Dynamical disentanglement in an analysis of oscillatory systems: an application to respiratory sinus arrhythmia

Abstract

We develop a technique for the multivariate data analysis of perturbed self-sustained oscillators. The approach is based on the reconstruction of the phase dynamics model from observations and on a subsequent exploration of this model. For the system, driven by several inputs, we suggest a dynamical disentanglement procedure, allowing us to reconstruct the variability of the system's output that is due to a particular observed input, or, alternatively, to reconstruct the variability which is caused by all the inputs except for the observed one. We focus on the application of the method to the vagal component of the heart rate variability caused by a respiratory influence. We develop an algorithm that extracts purely respiratory-related variability, using a respiratory trace and times of R-peaks in the electrocardiogram. The algorithm can be applied to other systems where the observed bivariate data can be represented as a point process and a slow continuous signal, e.g. for the analysis of neuronal spiking.

This article is part of the theme issue ‘Coupling functions: dynamical interaction mechanisms in the physical, biological and social sciences’.

1. Introduction

One of the basic problems in data analysis is to select or to eliminate a particular component of a given time series, e.g. to remove noise or a trend, or to single out an oscillation in a certain frequency band, etc. A whole variety of techniques has been designed to tackle this task by means of filtering in the frequency domain, smoothing in a running window, subtracting a fitted polynomial, and so on. Furthermore, a number of modern methods—principal component analysis, independent mode decomposition, empirical mode decomposition [1–6]—represent a signal of interest as a sum of modes such that (at least) dominating modes are assumed to represent certain relevant dynamical processes. Correspondingly, some of these modes can be analysed separately or, on the contrary, if they are considered as irrelevant, they can be subtracted from the original data, so that the cleansed signal can be further processed.

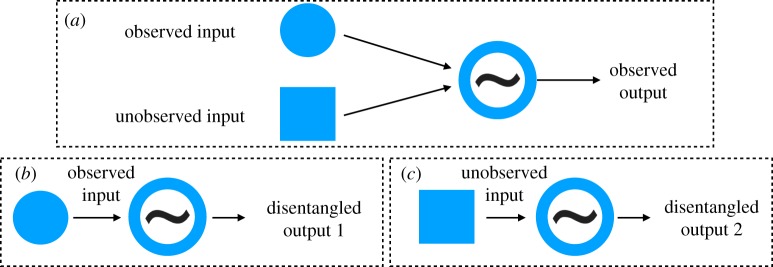
In this publication, we elaborate on a technique for a dynamical disentanglement of different components, designed for the analysis of signals, generated by coupled oscillatory systems. The disentanglement task is illustrated in figure 1. We assume that a signal from an oscillatory unit, which is driven by an observed nearly periodic signal and by other, non-observed inputs is known (figure 1a). (We treat the unobserved input as some noise, although generally, it may contain some regular components as well.) The technique is based on a reconstruction of the phase dynamics of the analysed unit. The obtained equation is then used for the generation of two new outputs. If only the observed input is used, i.e. the unobserved noise term is omitted, then the simulated equation yields a signal representing the dynamics of the noise-free system, i.e. the system driven by the observed input only (figure 1b). If, on the contrary, we eliminate from the equation the observed input, then the simulations yield the noise-induced output (figure 1c). This disentanglement procedure is neither the standard filtering (because the preserved and eliminated components can overlap in the frequency domain), nor the mode decomposition (because the sum of two disentangled outputs does not yield the original signal). Here, we consider the application of this approach to cardiac and respiratory data in humans. Our main oscillatory unit will be the cardiovascular system, and the observed input will be respiration. As the results of the analysis, we will obtain two heart rate variability (HRV) signals: one influenced purely by respiration, and one where the influence of respiration is excluded.

Figure 1.

Schematic of the disentanglement procedure. (a) Original set-up, where two inputs influence the oscillator, (b) reconstruction of the ‘noise-free’ dynamics and (c) reconstruction of the ‘signal-free’ dynamics. (Online version in colour.)

Understanding of the cardiac dynamics in terms of coupled oscillators goes back to the pioneering work by van der Pol & van der Mark [7]. Within the last two decades, this idea has been widely used to address the interaction between the cardiovascular and respiratory systems with the aim to reveal and quantify synchronization between them and to infer directionality and strength of their coupling under different conditions in adults and infants, with application to analysis of different sleep stages, apnoea, age-related changes, and effects of anaesthesia and hypertension [8–18]. In this paper, we discuss how the application of the coupled oscillators theory helps in the analysis of the main effect of the cardiorespiratory interaction, namely modulation of the heart rate by respiration, known for about a century as respiratory sinus arrhythmia (RSA) [19–23].

The separation and proper quantification of this respiratory component of HRV is of great importance for both fundamental physiological research and clinical medicine [24,25], due to the role vagal activity plays not only in cardiovascular but also in inflammatory control [26]. The isolated immune system is over-reactive and self-propagating by its nature. Germs or degraded cells in our body are detected by immune cells like macrophages floating in the interstitial space of the tissue. Macrophages detecting germ intruders produce inflammatory signals such as TNF-alpha and interleucine 1 [27], which attract other immune cells from nearby blood vessels. Without neuro-humoral control, the immune system would enter a dangerous state of generalized inflammation, well known as ‘sepsis’ in clinical medicine.

To prevent this generalized reaction, vagal afferents (transmitting from periphery to brain) also carry receptors for these signal substances and transmit the information on inflammation location and strength to brain stem areas [28]. After processing this information, vagal efferents (transmitting from brain to periphery) respond by release of acetylcholine at the location of the inflamed tissue [26]. Nicotinergic acetylcholine receptors have been identified on the surface of the macrophages, which downregulate the cytocine production as a response to the cholinergic stimulation [29], thereby reducing the attraction of additional inflammatory immune cells and downregulating immune response. This inflammatory feedback loop prevents over-activity of the immune system enabling the brain to locally control the immune activity. Therefore, a reduction of the vagal tone, e.g. by different forms of stress, is suspected to be related to several chronic diseases induced by inflammation, including type 2 diabetes, ulceral colitis, Hashimoto's thyreoiditis and even cancer [30]. Severe reductions of vagal tone have been observed in patients with these conditions [31–34]. The action of sympathetic activity in this system is not as well understood as vagal contribution at the moment. Therefore, it is important to measure the vagal component separated from the other components. Linear separation by filtering the signal can improve the estimation of pure vagal tone, but under certain conditions may fail to do so, when the respiratory frequency approaches other meta-cardiac cycles deriving from sympathetic origin, like the blood pressure rhythm of 0.1 Hz.

In our previous publications [15,35], we applied the dynamical disentanglement approach to the analysis of RSA in HRV records. In these publications, we used simultaneous measurements of electrocardiogram (ECG) and respiratory activity in order to reconstruct the equation of the phase dynamics of the cardiac oscillator. Next, we exploited this equation for a decomposition of the heartbeat intervals series into respiratory-related and non-respiratory-related components. This decomposition can be used as a general preprocessing tool for quantification of respiratory-related HRV and, in particular, opens a new way to address the clinically important problem of RSA quantification.

However, the results of refs. [15,35] can be considered only as a proof of principle, because they were obtained using a continuous phase of the cardiac oscillators. Determination of such a phase requires very clean high-quality measurements and a tedious preprocessing. Here, we suggest an easy-to-implement practical algorithm for achieving the same goal using the information about timing of the R-peaks only. The latter are well-defined events within each cycle of cardiac activity and they can be readily obtained with any standard equipment. From the viewpoint of data analysis, we deal with a relatively slow smooth signal (respiration), the phase of which can be easily estimated, e.g. by means of the Hilbert transform, and a point process (R-peaks) with a frequency about four times higher.

We emphasize that although we concentrate on cardiorespiratory interaction and explain the main idea in this context, our approach is of general use and can be applied to any weakly perturbed self-sustained oscillators, provided the observed signals allow for phase estimation. In particular, point processes frequently appear in neuroscience applications, and, thus, our algorithm can be helpful in the analysis of neural data, e.g. of spiking neurons affected by a slow observed continuous force. The restrictions here are that (i) neuronal spiking should be a dynamical, not a stochastic process; (ii) the forcing should be weak so that the first-order phase approximation is valid; and (iii) the variations of the instantaneous frequency of the forcing are slow.

2. Dynamical disentanglement based on the phase dynamics modelling

Our general goal is to identify dynamical properties of an oscillatory system, related to different influences, from the observations of its behaviour in a complex noisy environment. For example, one can be interested in the following questions: what would be the dynamics of the system if it were noise-free? Or how would the statistical properties of the oscillation change if one of the external forces were switched off? We address these and similar problems using the phase dynamics theory, see e.g. [36–38].

Consider a limit cycle oscillator, weakly perturbed by regular or stochastic known forces η_k(t), k = 1, 2, …. Then, according to the theory, in the first approximation in amplitude of these forces, the phase dynamics obeys

$$\dot{\phi }=\omega +\sum _k{Q}_k[\phi ,{\eta }_k(t)]+\zeta (t).$$ 2.1

Here, φ(t) and ω are the phase and the natural frequency of the system, and Q_k are the coupling functions; they quantify response of the oscillator to the corresponding perturbations. The random term ζ(t) accounts for intrinsic fluctuations of the system parameters. Note that the same equation describes dynamics of weakly chaotic systems; in this case, ζ(t) reflects effects of chaotic amplitude variations. In the second-order approximation in the force amplitudes, one expects the appearance of triple terms like Q₁₂[φ, η₁, η₂], etc [39,40], but these effects will be neglected below.

Let us suppose first that equation (2.1) is already known (practically, it is inferred from data, as discussed below). Then, if we are interested in properties of the purely deterministic phase dynamics, we can solve numerically equation (2.1) without the noise term ζ(t) (we speak of the deterministic dynamics here because the forces η_k(t) are known (recorded) functions of time, though they must not be completely regular). If the task is to analyse the response of the oscillator to a particular external force, e.g. η₁(t), then we omit in equation (2.1) the terms $\xi (t)=\sum _{k>1}{Q}_k[\phi ,{\eta }_k(t)]+\zeta (t)$, simulate the equation

$$\dot{\phi }=\omega +Q_1[\phi ,{\eta }_1(t)],$$ 2.2

and analyse the obtained result according to a particular problem in question. This approach was used in [41] for reconstructing the Arnold tongue of a noise-free oscillator (with strictly regular force η₁(t)) from a measurement of noisy system (where in addition to η₁(t) also pure noise ζ(t) is present). Alternatively, if we are interested in the effects of the random component ζ(t), e.g. in properties of phase diffusion, then we have to omit the deterministic perturbations and solve numerically

$$\dot{\phi }=\omega +\xi (t).$$ 2.3

In this way, we achieve the desired dynamical disentanglement. Below we apply this general idea to the analysis of cardiorespiratory interaction.

3. Disentanglement of the heart rate variability

In [15], we used the measurements of ECG and respiratory flow from healthy adults in order to reconstruct the model of cardiac phase dynamics in the form

$$\dot{\phi }=\omega +Q(\phi ,\psi )+\xi (t),$$ 3.1

where φ and ψ correspond to the instantaneous phases of the cardiac and the respiratory rhythms, respectively. This equation is a particular case of equation (2.1), with η₁(t) corresponding to the respiration dynamics. Since the latter is a rhythmical process with a well-defined phase ψ, we write the corresponding coupling function as a function of two phases, Q₁(φ, η₁(t)) = Q(φ, ψ), while the contribution of other, unobserved, perturbations and of intrinsic fluctuations is combined in the rest term $\xi =\sum _{k>1}{Q}_k(\phi ,{\eta }_k(t))+\zeta (t)$. Practically, Q(φ, ψ) as a function of two variables was constructed on a 64 × 64 equidistant grid in a domain (0, 2π) × (0, 2π).

Note that determination of the respiratory phase ψ is simple: since the respiratory signal looks like a modulated and slightly distorted sine-wave, its phase can be easily estimated, e.g. by means of the Hilbert transform. On the contrary, the ECG signal has a quite complicated form and computations of its phase represent a non-trivial stand-alone problem, see [15]: here one needs very high-quality data, and its processing is technically quite demanding. This fact motivates a development of techniques operating only with point processes, namely with instants of the R-peaks, corresponding to the peak of depolarization of the ventricles of the human heart. These events can be easily detected and therefore are commonly used in the analysis of HRV. Since these peaks appear once per heartbeat cycle, their continuous phase φ without loss of generality can be set to zero.

First, we discuss how the disentanglement of the HRV can be performed if both continuous phases φ(t) and ψ(t) are available [15]. For this goal, we note that, for a given time series φ(t) and ψ(t), the coupling function in equation (3.1) can be also interpreted as a time series Q[φ(t), ψ(t)] = Q(t). Correspondingly, knowledge of time series $\dot{\phi }(t)$ and Q(t) yields the rest term $\xi (t)=\dot{\phi }-Q$. Having all these time series, we easily construct the new disentangled ones. These are the respiratory-related (R) and the non-respiratory-related (NR) components of the instantaneous cardiac frequency, denoted as ${\dot{\phi }}^{(\mathrm{R})}$ and ${\dot{\phi }}^{(\mathrm{NR})}$, and obtained according to equations

$${\dot{\phi }}^{(\mathrm{R})}=\omega +Q({\phi }^{(\mathrm{R})},\psi )\text{and}{\dot{\phi }}^{(\mathrm{NR})}=\omega +\xi (t).$$ 3.2

Note that this is not a simple decomposition because $\dot{\phi }(t)\ne {\dot{\phi }}^{(\mathrm{R})}(t)+{\dot{\phi }}^{(\mathrm{NR})}(t)$. In [15], we have demonstrated that power spectrum of ${\dot{\phi }}^{(\mathrm{R})}$ nicely describes the spectral peaks corresponding to the frequency of respiration and to the side-bands of the heart rate.

In the subsequent study [35], we extended this idea and generated artificial sequences of heartbeat events (R-peaks) according to the conditions φ^(R)(t^(R)_k) = 2πk and φ^(NR)(t^(NR)_k) = 2πk, k = 1, 2, …, where the phases were obtained via numerical integration¹ of differential equation (3.2). The point process t^(R)_k represents instants of the heart beats as they would appear if there were no other perturbations to the cardiac oscillator, except for the respiration, while t^(NR)_k represents the HRV due to internal fluctuations and external non-respiratory rhythms, e.g. blood pressure and blood perfusion rhythms. It has been suggested that the described disentanglement into respiratory-related (R-HRV) and non-respiratory-related (NR-HRV) components should be used as a generic preprocessing technique prior to a quantification of the RSA in clinical practice. This suggestion has been supported by computation of different measures of RSA from the original series of inter-beat intervals as well as from respiratory-related intervals T^(R) = t^(R)_k+1 − t^(R)_k, see [35] for details. Note that our approach is intrinsically nonlinear, in contrast to ad hoc techniques used for the same purpose, like adaptive filtering and least-mean-square fitting of power spectra [42,43].

Summarizing, the disentanglement of the instantaneous cardiac frequency into R-HRV and NR-HRV components can be easily implemented, provided the continuous phases φ, ψ are known. However, as already mentioned, computation of the instantaneous cardiac phase φ requires high-quality measurements, visual inspection of the data, extensive preprocessing, and is currently solved by ad hoc, not automated, techniques only. On the other hand, determination of the R-peaks is a standard task and can be easily accomplished. Therefore, development of a disentanglement algorithm for the case when one observable, e.g. respiration, is continuous and appropriate for the phase estimation, and the other one, e.g. heartbeats, is a point process, represents an important unsolved problem. Below we present an approximate solution of this problem.

4. Dynamical disentanglement for the point process data

Our starting point is the description of the cardiorespiratory phase dynamics in the form of equation (3.1). We assume that the respiratory phase ψ is obtained from the respiratory time series and that the instants t_k, when the R-peaks appear in the ECG, are determined. The cardiac phase at these instants is φ(t_k) = 2πk. Let the inter-beat intervals be denoted as T_k = t_k+1 − t_k. Then, assuming weakness of the coupling, ∥Q∥≪ω, where ∥ · ∥ denotes the norm of the function, and keeping in equation (3.1) only the deterministic term, we write in the first approximation

$${\int }_{t_k}^{t_{k+1}}\mathrm{d}t=T_k={\int }_0^{2\pi }\frac{d\phi }{\omega +Q(\phi ,\psi )}\approx \frac{2\pi }{\omega }-\frac{1}{{\omega }^2}{\int }_0^{2\pi }Q(\phi ,\psi )\mathrm{d}\phi .$$ 4.1

Next, since the respiration is much slower than the heart rate, we assume that within the inter-beat interval T_k, the phase ψ grows linearly in time with the frequency ω^(r)_k, i.e. ψ(t) = ψ_k + ω^(r)_k(t − t_k), where ψ_k = ψ(t_k). Then the integral in equation (4.1) can be approximated as

$$-{\omega }^{-2}{\int }_0^{2\pi }Q(\phi ,\psi )\mathrm{d}\phi =-{\omega }^{-2}{\int }_0^{T_k}Q[\phi (t),\psi (t)]\mathrm{d}t\approx F({\psi }_k,{\omega }_k^{(r)}).$$

Taking for simplicity ${\omega }_k^{(r)}=\dot{\psi }(t_k)={\dot{\psi }}_k$ (corrections to this expression, due to slowness of the respiratory phase, appear in the higher orders) and denoting T = 2π/ω, we obtain

$$T_k=T+F({\psi }_k,{\dot{\psi }}_k)+{\chi }_k,$$ 4.2

where $F({\psi }_k,{\dot{\psi }}_k)$ can be understood as a discrete version of the coupling function (we denote it as the coupling map) and the rest term χ_k is the random component. Equation (4.2) can be considered as a direct discrete analogue of continuous equation (3.1).

Introducing the mean respiratory frequency $\overline{\omega }={⟨{\omega }_k^{(r)}⟩}_k={⟨{\dot{\psi }}_k⟩}_k$ and expressing F(ψ_k, ω_k) as a Taylor-Fourier series, we finally write

$$T_k\approx T+\sum _{n=1}^{N_F}\{\left[\sum _{m=0}^{N_T-1}{a}_{n,m}{({\dot{\psi }}_k-\overline{\omega })}^m\right]\cos (n{\psi }_k)+\left[\sum _{m=0}^{N_T-1}{b}_{n,m}{({\dot{\psi }}_k-\overline{\omega })}^m\right]\sin (n{\psi }_k)\}.$$ 4.3

Here, N_F and N_T are the orders of the Fourier and Taylor series, respectively. For a sufficiently long series of inter-beat intervals T_k, equation (4.3) can be considered as an overdetermined linear system for unknown parameters T, a_n,m, b_n,m. This system can be easily solved, e.g. by mean squares minimization.

Thus, the suggested algorithm yields a discrete dynamical model (4.2) for the inter-beat intervals. Now this model can be used for the dynamical disentanglement. In order to construct the respiratory-related component, we first take t^(R)₁ = t₁. Then, substituting ψ₁, ${\dot{\psi }}_1$ in (4.3) we obtain T^(R)₁ and t^(R)₂ = t^(R)₁ + T^(R)₁. Next, we compute ψ(t^(R)₂), $\dot{\psi }(t_2^{(\mathrm{R})})$ and use the model (4.3) to obtain T^(R)₂ and t^(R)₃, and so on² . For the construction of the non-respiratory-related component, we also start by assigning t^(NR)₁ = t₁ and then proceed as follows. Let the already determined t^(NR)_l fulfil t_k < t^(NR)_l < t_k+1. For t_k and t_k+1, we compute the rest term of the model (4.3) (effective noise), i.e. the difference between the true T_k, T_k+1 and their value predicted by equation (4.3); these terms are χ_k and χ_k+1. Then, using linear interpolation to find the effective noise at t^(NR)_l, we obtain

$$t_{l+1}^{(\mathrm{NR})}=t_l^{(\mathrm{NR})}+T+{\chi }_k+\frac{{\chi }_{k+1}-{\chi }_k}{t_{k+1}-t_k}(t_l^{(\mathrm{NR})}-t_k).$$ 4.4

The R-HRV component can be further used for an improved quantification of the RSA, while the NR-HRV time series can be exploited for the analysis of the other sources of the HRV.

5. Testing the approach on model data

First, we verify our approach using artificially generated data with known properties. For this goal, we use a simple phase model (3.1), where the coupling function Q(φ, ψ) is written in the Winfree form, i.e. as a product of the phase sensitivity function, or phase response curve (PRC), Z(φ), and forcing function I(ψ). Thus, introducing explicitly the coupling strength parameter ε, we write

$$\dot{\phi }=\omega +\epsilon Z(\phi )I(\psi )+\xi (t).$$ 5.1

Functions Z(φ), I(ψ) are modelled by Fourier series of order 15 and 4, respectively (figure 2), in such a way that they resemble experimentally obtained curves, cf. [15]. Instantaneous frequency of respiration was modelled as $\dot{\psi }={\omega }_r+\mu \nu$, where ν is an Ornstein–Uhlenbeck process, $\dot{\nu }=-{\gamma }_r\nu +{\eta }_1$. The random term ξ is given by the weighted sum of two components, i.e. of a low-pass and of a band-pass filtered noise: ξ = λ₁ζ₁ + λ₂ζ₂, where ${\dot{\zeta }}_1=-\gamma {\zeta }_1+{\eta }_2$ and ${\ddot{\zeta }}_2+\alpha {\dot{\zeta }}_2+{\omega }_{bp}^2{\zeta }_2={\eta }_3$. Here, η_k are independent Gaussian white noises with zero mean: 〈η_k(t)η_j(t′)〉 = δ_kjδ(t − t′).

Figure 2.

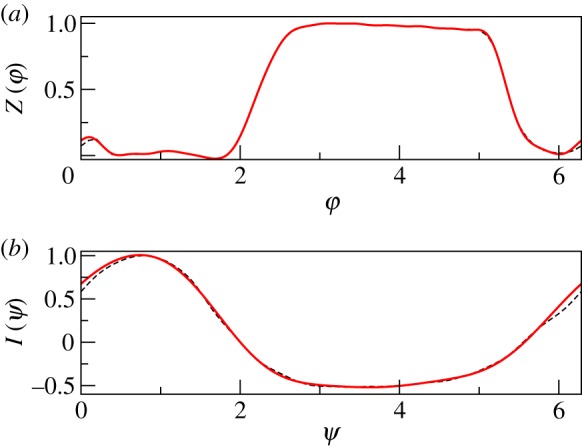
Model phase response curve of the cardiac oscillator (a) and model respiratory force (b) are shown by bold red lines. Dashed lines in both panels indicate the corresponding curves obtained in experiments, cf. [15]. (Online version in colour.)

Solving stochastic differential equation (5.1), we generate the artificial series of R-peaks. Without loss of generality, we say that these peaks occur when phase φ attains a multiple of 2π. Thus, we obtain a point process t_k such that φ(t_k) = 2πk. Correspondingly, we introduce series of RR-intervals T_k = t_k+1 − t_k. Similarly, solving the deterministic part of equation (5.1), i.e.

$${\dot{\phi }}^{(\mathrm{R})}=\omega +\epsilon Z(\phi )I(\psi ),$$ 5.2

we generate a series of respiratory-related R-peaks, t^(R)_k and corresponding intervals T^(R)_k³. Finally, the non-respiratory-related R-peaks, t^(NR)_k and the inter-beat intervals T^(NR)_k are obtained via solution of

$${\dot{\phi }}^{(\mathrm{NR})}=\omega +\xi (t).$$ 5.3

Thus, the data used for the disentanglement are: the times of R-peaks, t_k, and the respiratory phase and the frequency, ψ(t) and $\dot{\psi }(t)$, and in particular ψ(t_k) = ψ_k, and $\dot{\psi }(t_k)={\dot{\psi }}_k$. Note that in this test, two latter series are obtained from equations, while in fact respiratory phase and frequency should be estimated from data, which will certainly introduce an additional error. The respiratory-related and the non-respiratory-related components obtained via dynamic disentanglement shall be compared with t^(R)_k and t^(NR)_k, respectively.

Here, we illustrate the model data and the disentanglement results for the following values of the parameters: ω = 2π, ω_r = 2, ε = 0.1, ω_bp = 1.08π, α = 0.1, γ_r = 0.1, μ = 0.02, λ₁ = 0.03, λ₂ = 0.02. The records used for the subsequent analysis contained about 10⁴ inter-beat intervals, which correspond to about 2.5 h of natural heart beat. The model data are illustrated in figure 3. Here, we show a short epoch of the artificially generated sequences of RR-intervals. Figure 4 presents the respiratory-related component, extracted with the help of our algorithm with N_F = 8, N_T = 2, compared to the true one, i.e. generated by the model. Figure 5 illustrates the results of the disentanglement in the frequency domain. Namely, here we present spectra of point processes (Bartlett measure) [44]. As expected, spectral peaks induced by respiration are enhanced in the R-component and suppressed in the NR-component.

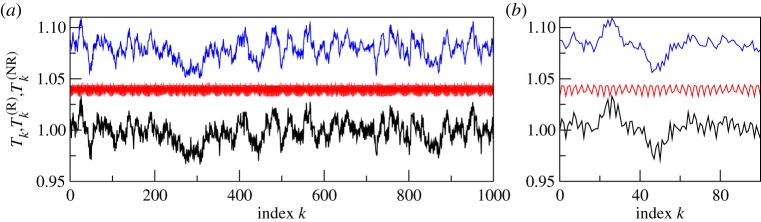
Figure 3.

An illustration of the model data. Panel (a) shows an epoch of 1000 inter-beat intervals and (b) is its zoomed version, with only 100 intervals shown. From bottom to top: artificial sequence of inter-beat intervals (black), its respiratory-related (red) and non-respiratory-related (blue) components. The latter two curves are shifted upwards for visibility. Panel (a) clearly shows that long-scale variability is preserved in the non-respiratory component, while in (b) one can see that variation with the respiration period is removed from this component. (Online version in colour.)

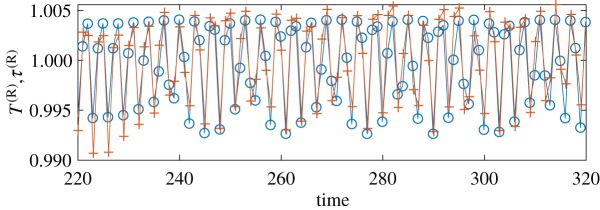
Figure 4.

True (blue circles) and recovered (red crosses) respiratory components of the HRV. The first one is generated by the model, while the second one is obtained from the point process by means of constructing the coupling map (4.3). (Online version in colour.)

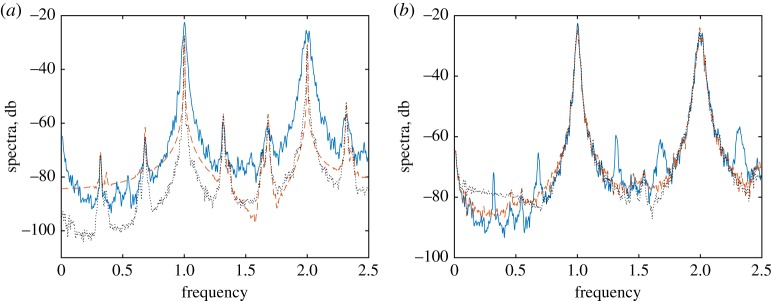
Figure 5.

Illustration of the disentanglement in the frequency domain. Here, we show the spectra of the point processes for the respiratory-related component (a) and for the NR component (b). Blue solid line shows the spectrum of model-generated series of instances of R-peaks t_k; red dashed curves show the spectrum of the model-generated series t^(R)_k, t^(NR)_k, while the black dotted curves present the spectra of the R- and NR-components obtained from t_k via disentanglement. (Online version in colour.)

We conclude the presentation of the technique by discussing a characterization of the quality of disentanglement. First, we note that, as it follows from equations (5.1), (5.2), (5.3) and as is expected for a disentanglement of independent components, $\mathrm{Var}(\dot{\phi })=\mathrm{Var}({\dot{\phi }}^{(\mathrm{R})})+\mathrm{Var}({\dot{\phi }}^{(\mathrm{NR})})$, where the variance is defined as Var(x(t)) = 〈(x − 〈x〉)²〉, $⟨(\cdot )⟩=T_{\mathrm{\Sigma }}^{-1}{\int }_0^{T_{\mathrm{\Sigma }}}(\cdot )\mathrm{d}t$, and T_Σ is the time interval over which the averaging is performed. We expect that a similar relation for variances obtained from the interval series T_k, T^(R)_k, T^(NR)_k shall also be valid, at least approximately. To compute the variance of the phase derivative for a point process, we consider the phase linearly growing between the events, so that $\dot{\phi }(t)=2\pi /T_k$ for t_k≤t≤t_k+1, k = 1, …, N. Then, for the variance we obtain

$${\sigma }^2=\frac{4{\pi }^2}{T_{\mathrm{\Sigma }}}\sum _{k=1}^N{(\frac{1}{T_k}-\frac{N}{T_{\mathrm{\Sigma }}})}^2{T}_k,$$ 5.4

where $T_{\mathrm{\Sigma }}=\sum _k{T}_k$, and similarly for the respiratory-related and non-respiratory-related components. We checked, for different N_F, N_T, that indeed (σ²_R + σ²_NR)/σ² ≈ 1 (for N_T ≤3 the worst case was 0.97).

6. An application to human cardiorespiratory data

Now we apply our algorithm to real data. For this goal, we analysed 26 multivariate records of ECG and respiration, registered in 17 healthy adults in supine position at rest, see [15,45,46] for a detailed description of the subjects, experimental protocol and measurement equipment⁴ . Since continuous phases φ(t), ψ(t) obtained in [15] are available, we compare the approximate disentanglement performed with the help of equations (4.2), (4.3) with the results obtained for continuous phases.

In order to quantify the quality of the disentanglement, we compute (σ²_R + σ²_NR)/σ² for all subjects with the help of equation (5.4). The results shown in figure 6 indicate that our algorithm works quite well. Here, we used N_F = 8, N_T = 1; for N_T > 1 the quality of the disentanglement was bad, probably because our point process series are quite short (about 400 heartbeats). Next, we compare the variance obtained from map-cleansed intervals with the variance for continuously cleansed data (figure 7). Both are in a good agreement.

Figure 6.

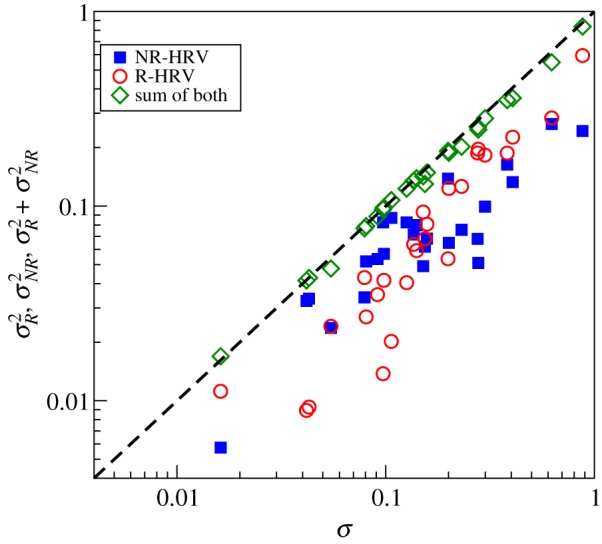
Quality of the point-process-based disentanglement for cardiorespiratory data from healthy subjects. Here, we plot, for each experimental record, variances of the respiratory and non-respiratory-related components and their sum versus variance of the original sequence of R-peaks. As expected for uncorrelated components, the sum of variances of disentangled processes is very close to the variance of original data. (Online version in colour.)

Figure 7.

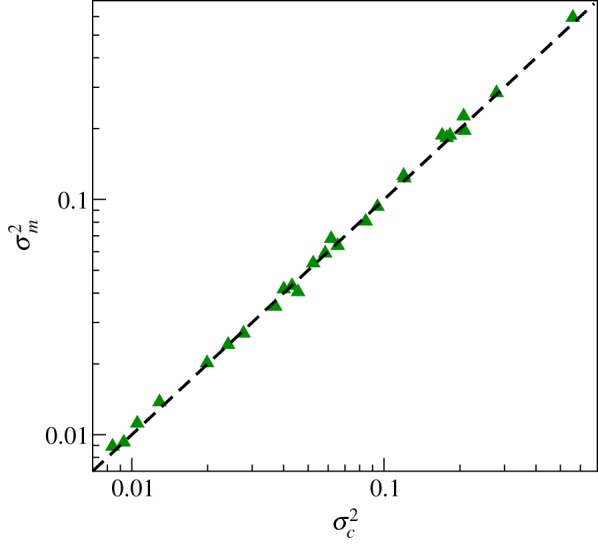
The efficiency of the map-based disentanglement is confirmed by plotting the variance σ²_m of the map-cleansed respiratory-related component versus the variance σ²_c of the continuously-cleansed respiratory-related component. (Online version in colour.)

An example of disentanglement (for a particular recording, dataset 3) is shown in figure 8. Here, we show the original series of RR-intervals and the two cleansed datasets, one obtained via the disentanglement with the continuous phase and one obtained using only the R-peaks. For better visibility, two cleansed datasets are shifted upwards by 0.2 s, their overlap indicates that the discrete dynamical disentanglement works well.

Figure 8.

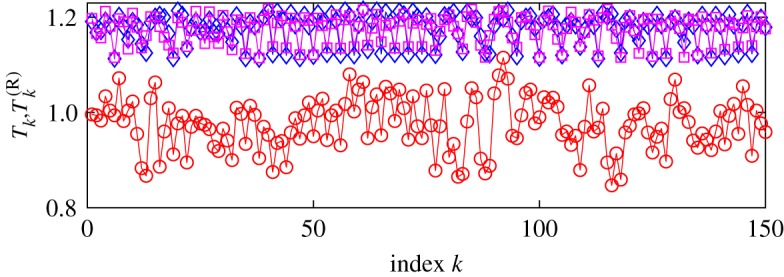
Original series of RR-intervals, T_k (in seconds), of a healthy subject (red circles) and its respiratory-related component, T^(R)_k, obtained either via continuous cleansing (blue diamonds) or by map cleansing (magenta squares). Both cleansed time series are shifted upwards for visibility. (Online version in colour.)

7. Conclusion

To summarize, we have presented a general approach that allows us, by means of the reconstruction of the dynamics of a driven oscillator, to predict its ‘virtual dynamics’ in which some of its inputs are cut off. The described disentanglement procedure differs from known mode decomposition algorithms, because it operates not with the given time series, but with a reconstructed phase dynamics equation. In this paper, we focused on the extension of the dynamical disentanglement to the case when the output of the investigated oscillator is a sequence of events (a point process), so that its instantaneous phase can hardly be estimated, while the observed input is a relatively slow and smooth process, suitable for the phase estimation. (Note that the slow process need not necessarily be close to a harmonic one, as the phase estimation works for rather complex waveforms as well). We applied this approach to analyse human HRV, where the available time series are a respiration signal and heart beat events. More precisely, we disentangled the respiratory-related variability, known to be mediated by the vagus nerve only, from that due to other sources. Using both model, data as well as instantaneous phases derived from an ECG, we have shown that our approximate procedure yields good results.

The developed technique can find applications in physiological as well as clinical studies. Indeed, quantification of different components of HRV is already an important diagnostic and prognostic tool in cardiology [47,48]. Several circulatory diseases show a strong difference in prognosis depending on vagal activity. As already mentioned, the simple spectral methods applied to RR interval analysis in many clinical studies are not performing well in separating vagal respiratory and other components of HRV. Since our technique provides respiratory-related variability cleansed from the effect of noise and other, unobserved rhythms, quantification of RSA and hence vagal tone from disentangled data is more precise. Note that the information theory-based approach has previously shown an improved capability to detect altered physiological conditions based on HRV analysed after discounting respiratory influences from HRV [49,50]. The separation of respiratory and non-respiratory components is physiologically and clinically especially important in the case of slow breathing (less than 0.12 Hz), where the vagal RSA intermixes with slower rhythms like the blood pressure rhythm, which derive from sympathetic and vagal components. Under such conditions, the two components of autonomic nervous system activity cannot be separated with linear models [51].

In [35], we compared the performance of different RSA measures applied to original and cleansed series. However, there the disentanglement was performed using instantaneous continuous phases. Now we show that the practical algorithm that operates not with a continuous ECG, but only with R-peaks, provides nearly the same results. This finding opens a further way to practical use. We anticipate that the developed technique can also be used in neuroscience, e.g. for analysis of spiking of sensory neurons in response to a slowly varying stimulus.

It is instructive to juxtapose the disentanglement approach described above with the methods of decomposition in bivariate systems, e.g. spectral- [52] and information-based ones [53]. In these decomposition methods one does not construct new time series, but rather determines which parts of statistical characteristics (e.g. spectral or information measures) are due to the coupling. Potentially, the disentanglement approach could be directly compared to decomposition methods, if one applies the spectral or information characterization to the original HRV signal and to the disentangled signals.

As a subject of future research, we mention a case of more than one observed input. Theoretically, it is not so difficult to perform the phase dynamics reconstruction for multivariate data; however, data requirements increase essentially so that reconstruction of a network of more than three oscillators becomes unfeasible, see [40]. Another interesting extension would be the case of non-oscillatory inputs, when parameterization of these inputs by a phase does not work. A possible solution for both problems might be reconstruction of the phase dynamics in the Winfree form, i.e. when the coupling function can be presented as a product of the phase response curve and of the driving signal, cf. equation (5.1). The Winfree representation can also be exploited to tackle the disentanglement problem in the case when the driven system is represented by a continuous signal while the observed input can be considered as a point process. The component related to this input can be constructed by taking into account phase resetting at the instants of spike appearance. The non-input-related, noisy, component can then be obtained in a way, similar to that presented in this paper, using the rest term of the reconstructed Winfree-type model.

Data accessibility

This article has no additional data.

Authors' contributions

M.R. and A.P. developed the algorithms for disentanglement. M.R. performed model study and data analysis. M.F. and M.M. provided the data and physiological interpretation of the results. M.R., M.M. and A.P. wrote the manuscript. All authors read and approved the manuscript.

Competing interests

We declare we have no competing interests.

Funding

M.R., M.M. and A.P. acknowledge financial support from the European Union's Horizon 2020 research and innovation programme under the Marie Sklodowska-Curie Grant Agreement No. 642563 (COSMOS). Development of methods presented in Section 4 was supported by the Russian Science Foundation under grant no. 17-12-01534.