On the concept of dynamical reduction: the case of coupled oscillators

Abstract

An overview is given on two representative methods of dynamical reduction known as centre-manifold reduction and phase reduction. These theories are presented in a somewhat more unified fashion than the theories in the past. The target systems of reduction are coupled limit-cycle oscillators. Particular emphasis is placed on the remarkable structural similarity existing between these theories. While the two basic principles, i.e. (i) reduction of dynamical degrees of freedom and (ii) transformation of reduced evolution equation to a canonical form, are shared commonly by reduction methods in general, it is shown how these principles are incorporated into the above two reduction theories in a coherent manner. Regarding the phase reduction, a new formulation of perturbative expansion is presented for discrete populations of oscillators. The style of description is intended to be so informal that one may digest, without being bothered with technicalities, what has been done after all under the word reduction.

This article is part of the theme issue ‘Coupling functions: dynamical interaction mechanisms in the physical, biological and social sciences’.

1. Introduction

The dynamics of nonlinear dissipative systems are most commonly modelled mathematically with coupled ordinary and partial differential equations [1]. The specific forms of evolution equations are often too complex to handle or may even be too poorly known. Thus, the effort of reducing them to a much simpler form by cutting off unessential parts would be extremely important to the understanding of nonlinear dynamical systems. We will call such work of purification dynamical reduction or simply reduction.

It seems widely accepted today that the concept of reduction has worked as a strong motivating force for the advancement of nonlinear science over the past half-century. As a remarkable fact, reduction provides, besides the explanation of how this or that dynamical behaviour observed occurs, a powerful tool for predicting utterly new types of behaviour whose existence in nature has never been imagined before. Since the result of reduction often takes a universal form, the predicted dynamics is also expected to appear universally. The universal form of the reduced evolution equation also implies that seemingly unrelated phenomena occurring in systems of completely different physical constitution may have something in common at a deeper mathematical level. Accumulation of such findings, each of which may be a small one, may ultimately lead to our refreshed view of nature.

Reduction is generally practicable when the dynamics of largely separated time scales coexist in the system of concern, that is, when dynamical variables of fast motion and those of much slower motion are coupled. Traditionally, two basic ideas have been known for the reduction of the dynamics of this type of system. One is the idea of the so-called adiabatic elimination and the other is that of averaging.

In adiabatic elimination, rapidly relaxing variables are eliminated by considering that they adiabatically follow the motion of slow variables. Consequently, the system's dynamics comes to be confined practically to a lower-dimensional subspace spanned only by a small number of slow variables. The broad applicability of this theoretical tool was emphasized by Hermann Haken under the term coined by him, slaving principle, i.e. the principle that slow modes slave fast modes [2,3].

In contrast to adiabatic elimination, the method of averaging is irrelevant to the reduction of dynamical degrees of freedom. This method can be applied typically when rapid oscillatory motion appears parametrically in the evolution equation governing the slow variables. Since such fast parametric modulation should have minor effects on the slow dynamics, it may safely be removed by time-averaging. Averaging represents a crucial tool in the asymptotic theory of weakly nonlinear oscillations developed extensively by Russian scientists such as Krylov, Bogoliubov and Mitropolsky [4]. We shall see in later sections that averaging is equivalent to slightly changing the definition of slow variables.

In this article, confining our concern to limit-cycle oscillator systems [5–10], we show how the above-described two traditional ideas of reduction can be incorporated more systematically into the form of a single asymptotic theory. Note that, in either adiabatic elimination or averaging, reduction is achieved most satisfactorily when the system involves special degrees of freedom whose time evolution is extremely slow or, to put it differently, their stability is nearly neutral. In the systematic reduction theory of our concern, which is a kind of a perturbation theory, the unperturbed part is chosen so as to include modes with perfect neutrality. The actual system is supposed to be a perturbed system in which the weak perturbation would cause a slow evolution of the otherwise neutral modes.

In order that such a reduction theory may enjoy a universal applicability, these neutral modes should also be of a universal nature. In our macroscopic and mesoscopic world, we know at least two universal situations where neutrally stable modes emerge. The first is met at the critical point of bifurcation where the critical eigenmodes are neutral in stability. The second is the situation where a certain continuous symmetry inherent in the system has been broken, producing a neutrally stable mode.¹ The second type of neutral mode may be called phase in a broad sense. The representative reduction theories making full use of these neutral modes are known, respectively, as centre-manifold reduction and phase reduction [5–9].

Fortunately, each of these theories is applicable to limit-cycle oscillator systems because in many cases the oscillation is a result of the Hopf bifurcation and the oscillation itself breaks the translational symmetry of time. The science of coupled oscillators is becoming a rapidly expanding field today. Since the reduction of coupled oscillator models provides a powerful tool for many practical purposes, reexamining its theoretical basis would be of considerable value.

Contrary to our intuition, the reduction theory for a single oscillator system and that for multi-oscillator systems can be formulated quite similarly [7]. In the centre-manifold reduction, the linearized system about the fixed point right at the Hopf bifurcation is chosen as the unperturbed system. The perturbation includes nonlinearity and the deviation from the bifurcation point, both of which are assumed to be sufficiently small. When we proceed to systems of weakly coupled oscillators, the coupling force from the other oscillators will simply be regarded as a sort of perturbation acting on the oscillator in question.

In the phase reduction, the unperturbed system is given by a single limit-cycle oscillator running along or near the closed orbit. There the phase of the oscillatory motion represents a neutrally stable degree of freedom. Similarly to the oscillator near the Hopf bifurcation, weak coupling force from the other oscillators and weak external drive, if necessary, are treated as perturbation.

The fact that the unperturbed system contains a neutral mode implies that its solution as $t\to \mathrm{\infty }$ includes at least one arbitrary parameter. For instance, the solution of the linearized system at the Hopf bifurcation as $t\to \mathrm{\infty }$ is given by a harmonic oscillation $\dot{z}=\mathrm{i}\omega z$, where the complex amplitude z may be multiplied by an arbitrary complex number. For a limit-cycle motion along the closed orbit, the phase ϕ changes as $\dot{\varphi }=\omega$ or ϕ = ωt + ψ, where the initial phase ψ is arbitrary.

The most basic idea of reduction is to reinterpret such an arbitrary constant as a dynamical variable, and absorb the effect of perturbation into this variable thereby causing its slow evolution. At the same time, the unperturbed form of the solution must inevitably be changed, but only a little. This small change modifies the dynamics of the slow variable, which in turn produces an even smaller correction of the solution form. Such processes of mutual correction between the solution form and the dynamics of the slow variables will repeat indefinitely. Still, this is not our goal of reduction.

In the evolution equation of the slow variable obtained at each stage of approximation, fast parametric oscillations will generally appear. Such a parametric modulation, which is much faster than the slow dynamics of our concern, could be removed by time-averaging. The same simplification of the evolution equation could be achieved more systematically through a variable transformation called near-identity transformation.

Our goal is to put the whole of the above-stated ideas into a mathematical form. We shall see how this can be achieved in each of the two representative theories of reduction.

Sections 2 and 3 will be devoted, respectively, to centre-manifold reduction and phase reduction. A few comments supplementary to these sections together with a general remark on the significance of reduction in nonlinear science will be given in the final section. In the appendix, some recent developments in the phase-reduction theory, such as the phase–amplitude reduction, Koopman-operator approach, and extension to non-conventional dynamical systems, are briefly described. Throughout the present paper, we only present the main line of the theory, ignoring all technical details.

2. Centre-manifold reduction

We begin with the centre-manifold reduction for a single oscillator, and then proceed to multi-oscillator systems. It will be seen how the two elements of reduction, namely, the reduction of dynamical degrees of freedom and transformation of the evolution equation to a canonical form, are incorporated into a systematic perturbation theory.

(a). Reduction of a single free oscillator

The situation of our concern is the neighbourhood of the Hopf bifurcation of an n-dimensional dynamical system $\dot{\mathbf{X}}=\mathbf{F}(\mathbf{X})$ with fixed point X = 0. We separate F into an unperturbed part and perturbation, where the former is chosen to be the linear part right at the bifurcation, and the latter includes the remainder, that is, the system's nonlinearity and the effect of small deviation from the bifurcation point. Thus, the system to be reduced is written as

$$\dot{\mathbf{X}}={\hat{L}}_0\mathbf{X}+ϵ{\hat{L}}_1\mathbf{X}+\mathbf{N}(\mathbf{X}).$$ 2.1

For simplicity, the small deviation from the bifurcation point, represented by the second term on the right-hand side, is given only by the linear term with small bifurcation parameter ϵ; the nonlinear part of F(X) is abbreviated as N(X). These two terms constitute the perturbation acting on the linear system at the criticality. The Jacobian ${\hat{L}}_0$ has a pair of pure imaginary eigenvalues ± iω, and the corresponding eigenvectors are denoted as u₀ and ${\overline{\mathbf{u}}}_0$, respectively, where the bar denotes complex conjugate; the real part of all the other eigenvalues are assumed negative. Thus, the unperturbed system $\dot{\mathbf{X}}={\hat{L}}_0\mathbf{X}$ is neutrally stable. Its solution as $t\to \mathrm{\infty }$, which is called the neutral solution, is given by

$${\mathbf{X}}_0=A\hspace{0.17em}{\mathrm{e}}^{\mathrm{i}\theta }{\mathbf{u}}_0+\overline{A}\hspace{0.17em}{\mathrm{e}}^{-\mathrm{i}\theta }{\overline{\mathbf{u}}}_0,$$ 2.2

where θ = ωt and A is an arbitrary complex amplitude. Note that e^iθu₀ and its complex conjugate are the eigenfunctions of the operator ${\hat{L}}_0-\omega (\mathrm{d}/\mathrm{d}\theta )$ with zero eigenvalue. This fact will be used later.

As was stated in the introductory section, the basic idea of reduction is to reinterpret the arbitrary parameter A appearing in the time-asymptotic solution as a dynamical variable and try to absorb the effect of perturbation into the slow evolution of A. At the same time, the change of the solution form from (2.2), however small it may be, is inevitable. Thus, a small correction term must be added to the right-hand side of (2.2) to express the true solution. The crucial assumption here is that this correction term is given by a functional of the neutral solution. As a result, the true solution takes the form

$$\mathbf{X}=A\hspace{0.17em}{\mathrm{e}}^{\mathrm{i}\theta }{\mathbf{u}}_0+\overline{A}\hspace{0.17em}{\mathrm{e}}^{-\mathrm{i}\theta }{\overline{\mathbf{u}}}_0+\sigma (A,\overline{A},\theta ).$$ 2.3

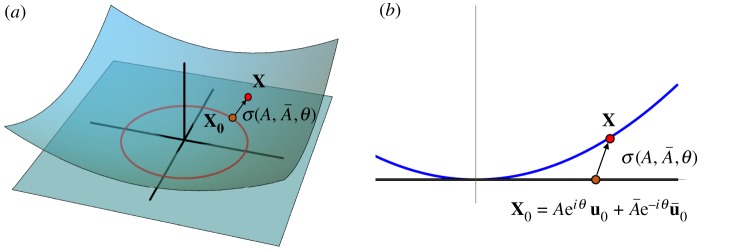
By assumption, the dependence of the small correction term σ on θ always appears as the combination A e^iθ or Ā e^−iθ. Since this time-asymptotic solution is parameterized with the two independent variables, i.e. the real and imaginary parts of A, the dynamics takes place on a 2D subspace. This subspace is the result of a slight deformation of the 2D critical eigenspace, and is called mathematically the centre manifold [5]. Figure 1 shows the neutral solution, centre manifold, and representation of the true solution schematically.

Figure 1.

Schematic figures of a neutral solution and a centre manifold. (a) The neutral solution X₀ in the two-dimensional plane spanned by u₀ and ${\overline{\mathbf{u}}}_0$, characterized by the complex amplitude A and phase θ = ωt. The centre manifold is tangent to this plane at X = 0. (b) Representation of the true solution X on the centre manifold by using the neutral solution X₀ and a small correction σ(A, Ā, θ). (Online version in colour.)

A few more remarks should be made on the above form of the true solution. Suppose first that the dynamical model to be reduced is already two-dimensional as exemplified by the FitzHugh–Nagumo oscillator and the Brusselator [6,7]. In such a case, the critical eigenspace itself spans the full phase space. It may then seem that the correction term σ is unnecessary, and that all the effects of perturbation can completely be absorbed into the slow evolution of A and Ā. This is true, but the existing theories of centre-manifold reduction still assume the solution form equivalent to (2.3) without inquiring into the dimension of the dynamical system model. There is actually no contradiction here, because the role played by the term σ is twofold. It certainly represents a slight deformation of the invariant space when the dimension of the dynamical system is higher than two. But what should never be overlooked is that σ also changes the definition of A slightly like $A\to A+s(A,\overline{A},\theta )$; when we have written down (2.3) with non-vanishing σ, the meaning of A has been changed a little. This transformation of A gives an example of the near-identity transformation. In short, for higher dimensional systems, σ plays double roles, while for two-dimensional systems it plays a single role.

While we say that variable transformation is necessary in order that the resulting evolution equation for A may take a canonical form, what is actually meant by canonical form? In the present reduction theory, it means that fast parametric oscillation does not appear in the evolution equation for A, that is, θ-dependence is excluded from that equation. Since θ always appears as the combination A e^iθ or its complex conjugate, $\dot{A}$ is required to assume the form

$$\dot{A}=G(A,\overline{A})=H(|A{|}^2)A$$ 2.4

as long as G can be expanded in powers of A and Ā. The unknown quantities G and σ are small because they are non-vanishing only because the perturbation is non-vanishing.

Another point to be noticed about the solution form (2.3) is that the separation between the neutral part and the correction term σ is not unique without imposing some additional condition. To make this separation unique, we should remember that e^iθu₀ and ${\mathrm{e}}^{-\mathrm{i}\theta }{\overline{\mathbf{u}}}_0$ are the zero eigenfunctions of ${\hat{L}}_0-\omega (\mathrm{d}/\mathrm{d}\theta )$. Thus, as the most natural choice, we exclude these components from σ; still σ may include the vector components u₀ and ${\overline{\mathbf{u}}}_0$, but only in combination with higher harmonics e^imθ(m≠ ± 1). This method of separation is crucial to the formulation of the present reduction theory, because, as we see below, it enables us to achieve the two tasks, i.e. reduction of the degrees of freedom and transformation of the reduced equation into a canonical form, at one stroke rather than stepwise.

We are now left with the two unknown quantities G and σ, and try to find them perturbatively by inserting (2.3) into (2.1) and using (2.4). Our direct concern is the functional form of G which determines the reduced evolution equation; σ is necessary only for finding small, but not always negligible, corrections to G beyond the lowest-order approximation.

When we refer to a perturbation theory, some small parameter usually appears explicitly in the theory. Although a small parameter ϵ appears in (2.1) measuring the small distance from the bifurcation point, this smallness causes small-amplitude oscillations, so that the amplitude X or A should also be treated as a small quantity. This is, so to speak, an implicit small parameter. How the smallness of A is related to ϵ is not known in advance. In some existing reduction theories, however, the smallness ϵ^1/2 is assigned to A a priori, but such an assignment should be justified only a posteriori. Therefore, we have to proceed for the moment only with the assumption that the smallness of ϵ and that of A are independent. Similarly, the smallness of G and σ should also be regarded as implicit small quantities whose smallness is independent of ϵ at this stage of the theory.

We now substitute (2.3) into (2.1). Since the time derivative is only through A, Ā and θ, d/dt is replaced with $\omega (\mathrm{d}/\mathrm{d}\theta )+G(\mathrm{d}/\mathrm{d}A)+\overline{G}(\mathrm{d}/\mathrm{d}\overline{A})$. The equation obtained in this way can be expressed in the concise form

$$G\hspace{0.17em}{\mathrm{e}}^{\mathrm{i}\theta }{\mathbf{u}}_0+\overline{G}\hspace{0.17em}{\mathrm{e}}^{-\mathrm{i}\theta }{\overline{\mathbf{u}}}_0-({\hat{L}}_0-\omega \frac{\mathrm{d}}{\mathrm{d}\theta })\sigma =\mathbf{B}(A,\overline{A},\theta ).$$ 2.5

In the above equation, B is dominantly composed of the perturbation terms $ϵ{\hat{L}}_1\mathbf{X}+\mathbf{N}(\mathbf{X})$ with X replaced with (2.3), plus, less importantly, the time-derivatives of σ through A and Ā, e.g. the term −G(∂σ/∂A) and its complex conjugate, are also included.

We now pretend that B is a known quantity. Then, (2.5) formally represents a linear equation for the unknowns $G,\overline{G}$ and σ with the inhomogeneous term B. Noting that e^iθu₀ and its complex conjugate appearing on the left-hand side are the zero eigenfunctions of ${\hat{L}}_0-\omega (\mathrm{d}/\mathrm{d}\theta )$, while by assumption σ is free from these components, we can find the unique solution to this linear equation. This is achieved by decomposing σ into various eigenfunctions ${\mathrm{e}}^{\mathrm{i}m\theta }({\mathbf{u}}_l,{\overline{\mathbf{u}}}_l)$ of ${\hat{L}}_0-\omega (\mathrm{d}/\mathrm{d}\theta )$ with non-zero eigenvalue, where m is an integer and u_l denotes the lth eigenvector of ${\hat{L}}_0$. The equation for the zero eigenfunction components determines G and $\overline{G}$. The result is given by

$$G=\frac{1}{2\pi }{\int }_0^{2\pi }{\mathrm{e}}^{-\mathrm{i}\theta }{\mathbf{u}}_0^{\ast }\mathbf{B}(A,\overline{A},\theta )\hspace{0.17em}\mathrm{d}\theta ,$$ 2.6

where u*₀ is the left eigenvector of ${\hat{L}}_0$ with eigenvalue iω, and hence, e^−iθu*₀ is the zero eigenfunction of the adjoint operator of ${\hat{L}}_0-\omega (\mathrm{d}/\mathrm{d}\theta )$. We have assumed that the left and right eigenvectors of ${\hat{L}}_0$ are biorthonormalized as u*_lu_m = δ_l,m.

Up to this point, we have pretended that B is a known quantity. Actually, however, B includes the unknowns G and σ. Still the problem can be solved iteratively. The starting point is to neglect G and σ appearing in B as relatively small. Then, (2.5) becomes a truly linear inhomogeneous equation from which G and σ are determined. These solutions are then inserted into B. By using this improved B, improved G and σ are obtained. Such processes can be repeated indefinitely, by which G and hence the reduced evolution equation is derived. It takes the form of a power series expansion in A like

$$\dot{A}={\alpha }_{0}A+{\alpha }_1|A{|}^{2}A+{\alpha }_2|A{|}^{4}A+\cdots ,$$ 2.7

where α₀ = O(ϵ) and α_l = O(1) (l = 1, 2, …) are complex coefficients.

Although all calculational details are omitted here, it should be pointed out that there is no precise correspondence between the iteration step and the resulting power of A. For instance, when N(X) includes quadratic and cubic nonlinearity, the contribution to the cubic term |A|²A in the $\dot{A}$ equation comes not only from the lowest-order B but also from the corrected B resulting from the first iteration. Thus, non-vanishing σ is responsible for the correct expression of the cubic nonlinearity in the $\dot{A}$ equation.

If we drop in (2.7) all the nonlinear terms higher than the cubic term, the so-called Stuart–Landau equation is obtained. We find that the solution of this equation takes the scaling form A(t) = ϵ^1/2Ã(ϵ²t), implying that the first three terms on the right-hand side of (2.7) have the same order of magnitude. Admittedly, the condition ℜα₁ < 0 must be satisfied so that |A| may not escape to infinity. Under this condition or, in other words, if the Hopf bifurcation is of a supercritical type, then the contribution from the terms higher than the cubic turns out negligibly small. Thus, unlike usual perturbation theories, the meaningful truncation of the perturbation expansion does not result automatically, but some arguments of physical flavour are required.

(b). Reduction of a perturbed oscillator and coupled oscillators

The above arguments leading to the well-known one-oscillator model would not be of much practical interest. Moreover, for such a one-oscillator reduction problem, far more precise mathematical arguments could be developed [5]. By contrast, for large systems of coupled oscillators, which are our main target of study, no mathematical theory equally rigorous to the one-oscillator theory seems to exist. Therefore, it seems difficult to proceed further without relying upon some unverifiable intuition.

We consider first diffusively coupled homogeneous fields of oscillators with sufficient spatial extension described typically with reaction–diffusion equation $\dot{\mathbf{X}}=\mathbf{F}(\mathbf{X})+\hat{D}{\mathrm{\nabla }}^2\mathbf{X}$, where X is now a function of spatial coordinate r and time t, and $\hat{D}$ is a matrix of diffusion coefficients. Mathematically, how to do reduction for such systems may seem desperately difficult as compared with the reduction of a single oscillator. This difficulty could be imagined, e.g. from the fact that we do not have a clear concept of infinite-dimensional centre manifold. Incidentally, the naming ‘centre-manifold reduction’ commonly used may therefore be inappropriate for many-oscillator problems. Instead, we sometimes used the term ‘reductive perturbation’ in the past, although this term will not be used in this article.

From a physicist's point of view, reduction of reaction–diffusion systems can be achieved only by slightly modifying the reduction of single oscillator dynamics. Let us confine our arguments to the reaction–diffusion equation. The key idea is that we still treat the problem as a one-oscillator problem by regarding the diffusion coupling $\hat{D}{\mathrm{\nabla }}^2\mathbf{X}$ as a weak perturbation acting on a local oscillator. Here again, the assumed weakness of the diffusion coupling could only be justified a posteriori by making use of what is expected physically, that the length scale of the spatial variation of X will become increasingly longer as the Hopf bifurcation is approached.

We try to find the solution to the problem by generalizing the form of (2.3) and (2.4). The only difference from those equations is that A and Ā are now functions of r and t and the unknown quantities G and σ are assumed to depend also on various spatial derivatives of A and Ā. These spatial derivatives may be looked upon as infinitely many parameters parameterizing the 2D centre manifold of a local oscillator. How to solve the problem is almost the same as the above. An equation similar to (2.5) is obtained, where the B term includes, most importantly, $\hat{D}{\mathrm{\nabla }}^2\mathbf{X}$, and less important terms arising from the time derivatives of σ through A, Ā and their various spatial derivatives. G and σ can be found iteratively again by starting with the B in the lowest-order approximation which is free from the unknowns G and σ.

In the resulting $\dot{A}$ equation, the new terms ∇²A and various spatial derivatives of A higher than the second order appear. To see how to find a meaningful truncation of this series expansion, we have to resort to a scaling argument again. The assumed scaling form of A includes spatial scaling as A(t, r) = ϵ^1/2Ã(ϵ²t, ϵ^1/2r). As a result, we find that the most dominant new term to be included in the $\dot{A}$ equation is the diffusion term β∇²A. The diffusion coefficient β is a complex number given by $\beta ={\mathbf{u}}_0^{\ast }\hat{D}{\mathbf{u}}_0$. In this way, the non-trivial lowest-order equation becomes the so-called complex Ginzburg–Landau equation [7]

$$\dot{A}={\alpha }_{0}A+{\alpha }_1|A{|}^{2}A+\beta {\mathrm{\nabla }}^{2}A,$$ 2.8

which in turn proves its consistency with the above-assumed scaling form.

Once the Stuart–Landau equation has been established as the non-trivial lowest-order evolution equation for A, the complex Ginzburg–Landau equation results from a much easier argument than the above: First, replace the diffusion coupling $\hat{D}{\mathrm{\nabla }}^2\mathbf{X}$ with its approximation $\hat{D}{\mathrm{\nabla }}^2{\mathbf{X}}_0$. Then, take its inner product with u*₀ e^−iθ, i.e. the zero eigenfunction of the adjoint of ${\hat{L}}_0-\omega (\mathrm{d}/\mathrm{d}\theta )$. Add the resulting term to the right-hand side of the Stuart–Landau equation, producing the complex Ginzburg–Landau equation. Any other types of perturbation than the diffusion coupling can be treated in a similar manner. As long as the lowest-order effect of the perturbation is concerned, each perturbation can be treated independently. In this way, many variants of the Stuart–Landau or complex Ginzburg–Landau equation could be obtained. The practical significance of such equations is great. For instance, besides the diffusion coupling, weak periodic forcing with nearly resonant frequency may be introduced; weak spatial heterogeneity may also be taken into account; diffusion coupling could be replaced with weak non-local coupling, etc [7,10,12–16].

3. Phase reduction

We now proceed to another representative theory of reduction called phase reduction, whose broad applicability to large populations and networks of coupled oscillators is well-recognized today [6–9].

In contrast to the centre-manifold reduction, phase reduction is applicable to general large-amplitude oscillations far from the bifurcation point. Consider a well-developed limit-cycle oscillator described by a general n-dimensional dynamical system $\dot{\mathbf{X}}=\mathbf{F}(\mathbf{X})$. Its periodic motion along the closed orbit itself is regarded as an unperturbed motion to start with. Admittedly, no analytical solution of such a general oscillation is available. Historically, this fact might have worked as an obstacle to hitting on the idea that this intractable mathematical object can still be chosen as the starting point of a perturbation theory of reduction. This may partly explain the reason why the appearance of the phase reduction theory is relatively new compared, e.g. with the asymptotic theory of weakly nonlinear oscillations.

(a). Definition of phase

Let the time-periodic solution of $\dot{\mathbf{X}}=\mathbf{F}(\mathbf{X})$ with frequency ω be given by a 2π-periodic function χ(ϕ), where the phase ϕ varies as ϕ = ωt + ψ. The initial phase ψ is an arbitrary constant. As noted in the introductory section, when the system's continuous symmetry has been broken, an arbitrary parameter must appear in the mathematical expression of the symmetry-broken state. This fact is true of the present case, because the limit-cycle oscillation breaks the translational symmetry in time, resulting in an arbitrary parameter ψ.

In conformity to the basic idea of phase reduction, we reinterpret the arbitrary constant ψ as a dynamical variable, and absorb the effect of perturbation into ψ(t) to cause its slow evolution.

Up to this point, the phase ϕ represents a one-dimensional coordinate defined along the closed orbit C in such a way that the free motion of the oscillator on C satisfies $\dot{\varphi }=\omega$. When the oscillator is perturbed, however weak the perturbation may be, it will generally be kicked off the closed orbit C. In order that the phase may still have a definite meaning, we have to extend its definition outside C. Although we only need to define it in the vicinity of C, let us begin with its global definition by defining a scalar field ϕ(X) for a general point X in the phase space [17].

The most natural and frequently used definition of ϕ(X) is such that the unperturbed motion of the oscillator identically satisfies $\dot{\varphi }=\omega$. The phase space will then be filled with an infinite family of the (n − 1)-dimensional hypersurface of equal phase. An isophase hypersurface thus defined is called the isochron [6,7,18,19]. The isochron of phase ϕ will be denoted by I_ϕ.

Since the time-evolution of the oscillator's phase ϕ(X) is only through the evolution of X, our unperturbed oscillator satisfies

$$\dot{\varphi }={\mathrm{grad}}_{\mathbf{X}}\varphi \cdot \mathbf{F}(\mathbf{X})=\omega .$$ 3.1

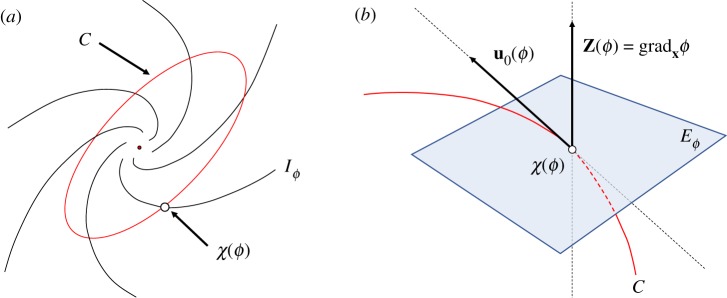
The second equality of the above equation gives the identity to be satisfied by the scalar field ϕ(X). Note that the vector grad_Xϕ is vertical to I_ϕ along which the slope of ϕ is the steepest. Equation (3.1) may, therefore, be understood as the natural requirement that the rate of change of ϕ must be given by how many isochrons are crossed by the oscillator per unit time. Figure 2a schematically shows a limit cycle and isochrons.

Figure 2.

Schematic figures of a limit cycle and isophase hypersurfaces. (a) An isochron I_ϕ is a n − 1-dimensional hypersurface, which intersects with the limit cycle C at the point χ(ϕ). (b) An isophase E_ϕ used in Method II is identified with the tangent space of I_ϕ at point χ(ϕ). (Online version in colour.)

(b). Method I

Our goal is to reduce the perturbed equation $\dot{\mathbf{X}}=\mathbf{F}(\mathbf{X})+\mathbf{P}(t)$ to an evolution equation of the phase alone. The perturbation P(t) is assumed to be sufficiently weak. For most practical purposes, the lowest-order perturbation theory would suffice. Then, a simple method of reduction, which we call Method I, is applicable. We begin with a brief presentation of Method I, and then proceed to a more systematic method including higher-order effects of perturbation, called Method II.

When the perturbation P is introduced, (3.1) is changed to

$$\dot{\varphi }={\mathrm{grad}}_{\mathbf{X}}\varphi \cdot (\mathbf{F}(\mathbf{X})+\mathbf{P}(t))=\omega +{\mathrm{grad}}_{\mathbf{X}}\varphi \cdot \mathbf{P}(t).$$ 3.2

Since our oscillator should still stay near the closed orbit C, the grad_Xϕ vector may approximately be evaluated at phase ϕ point on C or, equivalently, at the point of intersection between I_ϕ and C. This intersection point is also represented by χ(ϕ). Thus, in what follows, when we say ‘point χ(ϕ)’, it means the phase ϕ point on C.

Let us use the symbol Z(ϕ) for this gradient vector evaluated at χ(ϕ) on C, and rewrite (3.2) as

$$\dot{\varphi }=\omega +\mathbf{Z}(\varphi )\cdot \mathbf{P}(t).$$ 3.3

The quantity Z(ϕ) is crucial to the study of oscillator dynamics, because it measures the sensitivity of an oscillator to external stimuli, assumed not too strong, whatever the kind of the stimuli may be.

We have now to specify the kind of perturbation P(t). For simplicity, let us first consider a weakly coupled pair of identical oscillators labelled α and β. Then, P(t) represents the coupling force V(X_α, X_β) acting on oscillator α. The mutual coupling is assumed symmetric only for saving suffixes. The dynamical variables of each oscillator will be specified below by the suffixes α or β, such as X_α, X_β, ϕ_α and ϕ_β. In terms of the coupling V(X_α, X_β), we have for oscillator α

$${\dot{\varphi }}_{\alpha }=\omega +\mathbf{Z}({\varphi }_{\alpha })\cdot \mathbf{V}({\mathbf{X}}_{\alpha },{\mathbf{X}}_{\beta })$$ 3.4

and similarly for oscillator β. In what follows, we do not refer explicitly to oscillator β, because the same argument as for oscillator α holds simply by interchanging the suffixes α and β.

Since we are only concerned with the lowest-order approximation in this subsection, V(X_α, X_β) may be replaced with V(χ(ϕ_α), χ(ϕ_β)). This is a 2π-periodic function of either ϕ_α or ϕ_β, and below we abbreviate it as V(ϕ_α, ϕ_β). In this approximation, the phase equation becomes

$${\dot{\varphi }}_{\alpha }=\omega +\mathbf{Z}({\varphi }_{\alpha })\cdot \mathbf{V}({\varphi }_{\alpha },{\varphi }_{\beta }).$$ 3.5

The above equation combined with the similar equation for oscillator β completes the description of the dynamics only in terms of phases.

However, this is not the end of the story. To see why, we rewrite (3.5) in terms of the slow variables ψ_α,β = ϕ_α,β − ωt. We have

$${\dot{\psi }}_{\alpha }=\mathbf{Z}(\omega t+{\psi }_{\alpha })\cdot \mathbf{V}(\omega t+{\psi }_{\alpha },\omega t+{\psi }_{\beta }).$$ 3.6

The above equation is not of a canonical form in the sense that fast oscillation appears parametrically in the evolution equation describing slow dynamics. How to remove such fast modulation from the evolution equation constitutes the second step of reduction. This could be achieved by slightly changing the definition of ϕ_α,β. However, since we are only concerned with the lowest approximation, the same results can be obtained more directly by time-averaging [7–9,20]. Noting that, on the right-hand side of (3.6) the slow variables ψ_α,β approximately stay constant over one cycle of oscillation of frequency ω because V(X_α, X_β) is assumed weak, we time-average (3.6) over this period under fixed ψ_α,β. The resulting equation takes the simple form

$${\dot{\psi }}_{\alpha }=\mathit{\Gamma }({\psi }_{\alpha }-{\psi }_{\beta }).$$ 3.7

The effective phase coupling Γ, which is a 2π-periodic function of the phase difference, is given by

$$\mathit{\Gamma }({\psi }_{\alpha }-{\psi }_{\beta })=\frac{1}{2\pi }{\int }_0^{2\pi }\mathbf{Z}(y+{\psi }_{\alpha })\cdot \mathbf{V}(y+{\psi }_{\alpha },y+{\psi }_{\beta })\hspace{0.17em}\mathrm{d}y.$$ 3.8

In terms of the original phases ϕ_α,β, (3.7) becomes

$${\dot{\varphi }}_{\alpha }=\omega +\mathit{\Gamma }({\varphi }_{\alpha }-{\varphi }_{\beta }).$$ 3.9

Derivation of the corresponding phase equation for oscillator β is trivial. It is given by ${\dot{\varphi }}_{\beta }=\omega +\mathit{\Gamma }({\varphi }_{\beta }-{\varphi }_{\alpha })$.

In the above derivation, the two oscillators were assumed identical. However, this condition can be relaxed. Assuming that they are slightly different in nature, we put F_α,β(X_α,β) = F(X_α,β) + δF_α,β(X_α,β), where δF_α,β(X_α,β) represents a small difference of the dynamical system from a suitably defined ‘average’ system represented by F(X). How to choose this ‘average’ vector field F(X) does not affect the final phase equation as long as δF_α,β remain small. Let δF_α(X_α) be included in P(t) of oscillator α's equation as an additional perturbation. Then, the new term

$$\delta {\omega }_{\alpha }({\varphi }_{\alpha })\equiv \mathbf{Z}({\varphi }_{\alpha })\cdot \delta {\mathbf{F}}_{\alpha }(\chi ({\varphi }_{\alpha }))$$ 3.10

must be added to the right-hand side of (3.5). Similarly to what we did for the coupling function, δω_α(ϕ_α) is time-averaged, resulting in a frequency change by a small constant from ω.

The theory developed above can easily be extended so that it may become applicable to systems of large numbers of weakly coupled oscillators. The oscillators may be non-identical, but only slightly. Asymmetry of mutual coupling is also allowed. The result is a popular model of coupled phase oscillators given by [7]

$${\dot{\varphi }}_{\alpha }={\omega }_{\alpha }+\sum _{\beta }{\mathit{\Gamma }}_{\alpha \beta }({\varphi }_{\alpha }-{\varphi }_{\beta }).$$ 3.11

See, for example, refs. [6–10,21–24] for the analysis of synchronization in systems of limit-cycle oscillators using the phase model.

(c). Method II

In Method I, a number of approximations have been used in each step of reduction. These approximations are allowed as long as we are concerned with the lowest-order theory. However, by working with this sort of approach, we do not see how to generalize the theory to include systematically higher-order effects. Thus, we now come back to the starting point and move to a more systematic method which we call Method II. The theoretical framework of Method II is considerably different from Method I. Instead, it bears a strong resemblance to the centre-manifold reduction in §2.

The crucial difference from Method I is that we consider explicitly a small deviation ρ of the state vector X from the closed orbit due to the perturbation P. Similarly to (2.3), we thus put

$$\mathbf{X}(\varphi )=\chi (\varphi )+\rho (\varphi ),$$ 3.12

and let the above equation couple with the phase equation

$$\dot{\varphi }=\omega +G(\varphi ).$$ 3.13

The above reduction form is quite similar to (2.4). Our problem is how to determine the small unknown quantities ρ and G as functions of the phase alone. Note that the way of splitting the true state vector X(ϕ) into the reference state χ(ϕ) lying on the closed orbit and the deviation ρ(ϕ) from this orbit is generally not unique; we have to fix from what point on C the deviation ρ should be measured. However, implicit in (3.12), it has already been assumed that X and χ have the same phase. That is, the true state point and the reference state point lie on the same isochron I_ϕ. ρ may then be regarded as purely representing amplitude disturbance and is completely free from phase disturbance.

In order to formulate a systematic perturbation theory, however, curved hypersurfaces like isochrons will not be an easy object to handle. Therefore the definition of isophase manifold may desirably be changed slightly. In the new definition, the space of equal phase is identified with the tangent space of I_ϕ, tangent at point χ(ϕ). Let this tangent space be denoted by E_ϕ. In order that the disturbance vector ρ may completely be free from phase disturbance, ρ has to be so redefined as to lie on E_ϕ. Figure 2b shows the isophase surface E_ϕ schematically.

The advantage of working with E_ϕ is that it spans an eigenspace defined for the linearized system about C or, more precisely, E_ϕ is an (n − 1)-dimensional subspace of this eigenspace. Note that for any ϕ such an eigenspace can be defined. The small-amplitude disturbance ρ(ϕ) may then be decomposed into n − 1 eigenvector components.

In a similar way to (2.1), we expand F, now around χ(ϕ), as $\mathbf{F}(\mathbf{X})=\mathbf{F}(\chi (\varphi ))+ϵ\hat{L}(\varphi )\rho (\varphi )+\mathbf{N}(ϵ\rho (\varphi ))$, where $\hat{L}(\varphi )$ is the Jacobian of F evaluated at χ(ϕ) and N(ϵρ) represents higher-order terms of O(ϵ²). The eigenspace and eigenvectors are defined for the linearized equation

$$\dot{\rho }=\hat{L}(\omega t)\rho$$ 3.14

about the limit-cycle solution χ(ωt). Since the Jacobian $\hat{L}$ is time-periodic, using the Floquet theorem [5], the solution ρ can be written in the form $\rho (\varphi )=\hat{S}(\varphi )\hspace{0.17em}{\mathrm{e}}^{(\varphi /\omega )\hat{\mathit{\Lambda }}(0)}\rho (0)$ or, more generally, $\rho (\varphi +\psi )=\hat{S}(\varphi +\psi )\hspace{0.17em}{\mathrm{e}}^{(\psi /\omega )\hat{\mathit{\Lambda }}(0)}{\hat{S}}^{-1}(\varphi )\rho (\varphi )$, where $\hat{S}(\varphi )$ satisfies $\hat{S}(\varphi +2\pi )=\hat{S}(\varphi )$ and $\hat{S}(0)=I$. If we make a stroboscopic observation of ρ at time interval of the period T = 2π/ω, we obtain $\rho (\varphi +2\pi )=\hat{S}(\varphi )\hspace{0.17em}{\mathrm{e}}^{T\hat{\mathit{\Lambda }}(0)}{\hat{S}}^{-1}(\varphi )\rho (\varphi )={\mathrm{e}}^{T\hat{\mathit{\Lambda }}(\varphi )}\rho (\varphi )$, where $\hat{\mathit{\Lambda }}(\varphi )$ is a time-independent but ϕ-dependent n × n matrix given by $\hat{\mathit{\Lambda }}(\varphi )=\hat{S}(\varphi )\hat{\mathit{\Lambda }}(0){\hat{S}}^{-1}(\varphi )$. Thus, the above linear equation is transformed to an ordinary eigenvalue problem ${\mathrm{e}}^{T\hat{\mathit{\Lambda }}(\varphi )}\rho (\varphi )={\mathrm{e}}^{\mathrm{\lambda }T}\rho (\varphi )$, or $\hat{\mathit{\Lambda }}(\varphi )\rho (\varphi )=\mathrm{\lambda }\rho (\varphi )$, where λ is the eigenvalue called the Floquet exponent. There are n eigenvalues, λ_0,…,n−1. Among them, one eigenvalue is zero and denoted as λ₀ = 0. All other eigenvalues have negative real parts, Reλ_1,…,n−1 < 0, because the limit cycle is stable.

Let the eigenvectors of $\hat{\mathit{\Lambda }}(\varphi )$ be denoted by u_l(ϕ) (l = 1, 2, …, n). Out of these eigenvectors, n − 1 eigenvectors u₁(ϕ), u₂(ϕ), …, u_n−1(ϕ) with non-zero eigenvalues span E_ϕ. The remaining eigenvector u₀(ϕ) with zero eigenvalue corresponds to infinitesimal phase disturbance. The direction of u₀(ϕ) is tangential to the limit-cycle orbit C at χ(ϕ). Thus, this eigenvector is parallel with dχ(ϕ)/dϕ. In what follows, as a convenient choice, u₀(ϕ) will be identified with dχ(ϕ)/dϕ.

One may also define left-eigenvectors of $\hat{\mathit{\Lambda }}(\varphi )$, which we denote by u*₀(ϕ), u*₁(ϕ), u*₂(ϕ), …, u*_n−1(ϕ) satisfying biorthonormal relations with the right eigenvectors as u*_l(ϕ)u_m(ϕ) = δ_l,m. It should be noted that the sensitivity vector Z(ϕ) is identical with u*₀(ϕ)^†, where † denotes transpose. The reason is that the orthonormal condition required for u*₀(ϕ)^† is also satisfied by Z(ϕ). Regarding the orthogonality condition, remember that the phase gradient vector grad_Xϕ must be vertical to the isophase hypersurface. This means that Z(ϕ) is vertical to E_ϕ, or Z(ϕ) · u_l(ϕ) = 0 (l≠0). Normalization condition is clearly satisfied because Z(ϕ) · u₀(ϕ) = (grad_Xϕ)_X=χ(ϕ) · (dX/dϕ)_X=χ(ϕ) = 1.

Another technical remark should be made. As stated above, the eigenspace is defined at each phase on C. There is a relationship between the eigenvectors belonging to the same eigenvalue at different ϕ. By choosing the zero phase ϕ = 0 as the reference phase, u_l(ϕ) is given by a transformation of u_l(0) with the matrix $\hat{S}(\varphi )$ common to all l:

$${\mathbf{u}}_l(\varphi )=\hat{S}(\varphi ){\mathbf{u}}_l(0).$$ 3.15

Clearly, there is also a corresponding relation for the left-eigenvectors:

$${\mathbf{u}}_l^{\ast }(\varphi )={\mathbf{u}}_l^{\ast }(0){\hat{S}}^{-1}(\varphi ).$$ 3.16

It can also be shown by differentiating the solution ρ(ϕ) that the Jacobian $\hat{L}(\varphi )$ is related to $\hat{\mathit{\Lambda }}(0)$ through

$$\hat{\mathit{\Lambda }}(0)={\hat{S}}^{-1}(\varphi )(L(\varphi )-\omega \frac{\mathrm{d}}{\mathrm{d}\varphi })\hat{S}(\varphi ).$$ 3.17

In the past, Method II was not formulated for multi-oscillator systems except for oscillatory reaction–diffusion systems; space-discrete systems such as networks and populations of oscillators were carefully avoided [7]. In discrete systems, the pair coupling, which has to be treated as a perturbation, depends on the two-state vectors of the coupled pair like V(X, X′). This fact seemed to make it difficult to treat the problem formally as a one-oscillator problem. As we see later in this section, this seeming difficulty can be circumvented easily. However, before going into this problem, we begin with an easier case to treat, because the formulation is almost the same as for discrete systems except for one essential point.

The following example may be practically uninteresting but seems quite instructive for illustrating the general structure of the theory. Suppose that the perturbation P(t) is simply given by a function only of X of the oscillator of concern. This means that the nature of the oscillator has been slightly changed. By putting P(t) = ϵδF(X), where δF(X) represents the change in the oscillator dynamics, the equation to be reduced is given by

$$\dot{\mathbf{X}}=\mathbf{F}(\mathbf{X})+ϵ\delta \mathbf{F}(\mathbf{X}).$$ 3.18

We have introduced parameter ϵ as an indicator of the smallness of the perturbation, but we put ϵ = 1 at the end of the calculation. Our goal is to find the solution of the problem in an ϵ-expansion form.

As stated repeatedly, we try to solve the reduction problem in the following form:

$$\mathbf{X}(t)=\chi (\varphi )+ϵ\rho (\varphi ),$$ 3.19

and

$$\dot{\varphi }=\omega +ϵG(\varphi ).$$ 3.20

In the above equation, ρ(ϕ) and G(ϕ) generally include higher-order corrections and can still be expanded in powers of ϵ.

To determine the functional form of the unknowns ρ(ϕ) and G(ϕ), we insert (3.19) into (3.18), and use (3.20) to replace the time-derivative with ϕ-derivative. With the use of the identity (3.17), the result is concisely summarized in the form

$$G(\varphi ){\mathbf{u}}_0(0)-(\hat{\mathit{\Lambda }}(0)-\omega \frac{\mathrm{d}}{\mathrm{d}\varphi }){\hat{S}}^{-1}(\varphi )\rho (\varphi )={\hat{S}}^{-1}(\varphi )\mathbf{B}(\varphi ).$$ 3.21

The B term consists primarily of the lowest-order perturbation δF(χ(ϕ)) but also includes smaller quantities depending on ρ and G. That is,

$$\mathbf{B}(\varphi )=\delta \mathbf{F}(\chi (\varphi )+ϵ\rho (\varphi ))-ϵG(\varphi )\frac{\mathrm{d}\rho (\varphi )}{\mathrm{d}\varphi }+{ϵ}^{-1}\mathbf{N}(ϵ\rho (\varphi )).$$ 3.22

There is a strong similarity of (3.21) to the corresponding equation (2.5) in the centre-manifold reduction. The only important difference between these equations is that the reduced phase equation or G(ϕ) to be obtained from (3.21) does not have a canonical form yet, while in the centre-manifold reduction the canonical form was directly obtained by solving (2.5).

Note that G(ϕ) appears as the coefficient of the zero eigenvector u₀(0) of $\hat{\mathit{\Lambda }}(0)$. Note also that, by decomposing ρ(ϕ) as $\rho (\varphi )=\sum _{l\ne 0}{c}_l(\varphi ){\mathbf{u}}_l(\varphi )$, we have

$${\hat{S}}^{-1}(\varphi )\rho (\varphi )=\sum _{l\ne 0}{c}_l(\varphi ){\hat{S}}^{-1}(\varphi ){\mathbf{u}}_l(\varphi )=\sum _{l\ne 0}{c}_l(\varphi ){\mathbf{u}}_l(0).$$ 3.23

Thus, if we pretend that B is a known quantity, then (3.21) represents a set of linear uncoupled equations for the ϕ-dependent coefficients of the eigenvectors u_l(0). The coefficient of u₀(0) is given by G(ϕ) which is the only quantity of our ultimate concern. Each coefficient will be found by taking the scalar product of the left eigenvector u*_l(0) with each side of (3.21). In particular, by taking a scalar product with u*₀(0), G(ϕ) is given by

$$G(\varphi )={\mathbf{u}}_0^{\ast }(0){\hat{S}}^{-1}(\varphi )\mathbf{B}(\varphi )={\mathbf{u}}_0^{\ast }(\varphi )\mathbf{B}(\varphi ).$$ 3.24

Each of the other coefficients c_l(ϕ) is given by the solution of the first-order differential equation

$$({\mathrm{\lambda }}_l-\omega \frac{\mathrm{d}}{\mathrm{d}\varphi })c_l(\varphi )=-{\mathbf{u}}_l^{\ast }(\varphi )\mathbf{B}(\varphi ).$$ 3.25

The above equation is solved by integration, whose solution c_l(ϕ) must be a periodic function. Noting that the real part of the eigenvalue λ_l is negative, one may easily show that the periodicity condition can be satisfied by taking the lower limit of the integral to be −∞.

By starting with the B in the lowest approximation, which is given by B(ϕ) = δF(χ(ϕ)), the unknowns ρ(ϕ) and G(ϕ) will be found iteratively in the form of ϵ-expansion. In particular, the lowest-order G becomes G(ϕ) = u*₀(ϕ)δF(χ(ϕ)), and this coincides with the result from Method I given by (3.10). How to solve the problem to any desired order in ϵ by iteration will no longer need explanation.

We are now ready to deal with populations of weakly coupled oscillators. In order to see the source of the aforementioned difficulty about such systems and how this difficulty is circumvented, the study of the following simple system would be sufficient. This is a pair of identical oscillators with weak symmetric coupling, which was also studied in Method I. The governing equation for oscillator α is given by

$${\dot{\mathbf{X}}}_{\alpha }=\mathbf{F}({\mathbf{X}}_{\alpha })+ϵ\mathbf{V}({\mathbf{X}}_{\alpha },{\mathbf{X}}_{\beta })$$ 3.26

and similarly for oscillator β.

As a generalization of (3.19) and (3.20), it seems natural to assume the reduction form as

$${\mathbf{X}}_{\alpha }(t)=\chi ({\varphi }_{\alpha })+ϵ\rho ({\varphi }_{\alpha },{\varphi }_{\beta })$$ 3.27

and

$${\dot{\varphi }}_{\alpha }=\omega +ϵG({\varphi }_{\alpha },{\varphi }_{\beta }).$$ 3.28

A similar reduction form is also assumed for oscillator β. The above form must satisfy (3.26). This requirement leads to the following equation similar to (3.21):

$$G({\varphi }_{\alpha },{\varphi }_{\beta }){\mathbf{u}}_0(0)-(\hat{\mathit{\Lambda }}(0)-\omega \frac{\mathrm{d}}{\mathrm{d}{\varphi }_{\alpha }}){\hat{S}}^{-1}({\varphi }_{\alpha })\rho ({\varphi }_{\alpha },{\varphi }_{\beta })={\hat{S}}^{-1}({\varphi }_{\alpha })\mathbf{B}({\varphi }_{\alpha },{\varphi }_{\beta }).$$ 3.29

The problem arising here is that the lowest-order B contains an unknown quantity ρ. In fact, we have

$$\mathbf{B}({\varphi }_{\alpha },{\varphi }_{\beta })=\mathbf{V}(\chi ({\varphi }_{\alpha }),\chi ({\varphi }_{\beta }))-\omega \frac{\mathrm{\partial }\rho ({\varphi }_{\alpha },{\varphi }_{\beta })}{\mathrm{\partial }{\varphi }_{\beta }}+O(ϵ)\hspace{0.17em}\mathrm{terms},$$ 3.30

where the ∂ρ/∂ϕ_β term is comparable with the V term in magnitude. Thus, finding the solution by successive iterations seems impossible. Still, G in the lowest order can be determined, because the unwanted quantity ρ, and hence the ∂ρ/∂ϕ_β term, contained in B, is free from the u₀(0) component.

As stated before, in phase reduction and also in centre-manifold reduction, the problem should be treated formally as a one-oscillator problem even if we are dealing with many-oscillator systems. In the present case, this means that no quickly changing variable other than ϕ_α must appear in the formulation. If this is violated, then the time derivatives of ρ through such fast variables can not be small and contribute to the lowest-order terms in B, thus making iteratively solving the problem unfeasible from the outset.

Actually, how to circumvent this difficulty is simple. We only need to change the independent variables from ϕ_α and ϕ_β to ϕ_α and ψ≡ϕ_α − ϕ_β. With the use of simplified notations ρ(ϕ_α, ψ), G(ϕ_α, ψ), … in place of ρ(ϕ_α, ϕ_α − ψ), G(ϕ_α, ϕ_α − ψ), …, we have now to find the solution in the form

$${\mathbf{X}}_{\alpha }(t)=\chi ({\varphi }_{\alpha })+ϵ\rho ({\varphi }_{\alpha },\psi )$$ 3.31

and

$${\dot{\varphi }}_{\alpha }=\omega +ϵG({\varphi }_{\alpha },\psi ).$$ 3.32

By interchanging the suffixes α and β and replacing ψ with −ψ, we have the corresponding equations for oscillator β. As a result, in place of (3.29), we have

$$G({\varphi }_{\alpha },\psi ){\mathbf{u}}_0(0)-(\hat{\mathit{\Lambda }}(0)-\omega \frac{\mathrm{d}}{\mathrm{d}{\varphi }_{\alpha }}){\hat{S}}^{-1}({\varphi }_{\alpha })\rho ({\varphi }_{\alpha },\psi )={\hat{S}}^{-1}({\varphi }_{\alpha })\mathbf{B}({\varphi }_{\alpha },\psi ).$$ 3.33

No unpleasant term appears in B now, and the lowest-order B is simply given by B(ϕ_α, ψ) = V(χ(α), χ(ϕ_α − ψ)). Although B still includes the time derivative of ρ through the second variable ψ, this gives a small quantity because $\dot{\psi }=ϵ(G({\varphi }_{\alpha },\psi )-G({\varphi }_{\alpha }-\psi ,-\psi ))$.

In this way, G(ϕ_α, ψ) and ρ(ϕ_α, ψ) can be determined by successive iterations to any desired order in ϵ, although all calculational details are omitted here. Coming back to the representation in terms of the original phase variables ϕ_α and ϕ_β, we arrive at the ϵ-expansion form

$${\dot{\varphi }}_{\alpha }=\omega +ϵG_1({\varphi }_{\alpha },{\varphi }_{\beta })+{ϵ}^2{G}_2({\varphi }_{\alpha },{\varphi }_{\beta })+\cdots .$$ 3.34

Note that the above idea of treating the phase difference as a new independent variable is similar to the past study in which we applied Method II to diffusion-coupled systems where spatial derivatives of the phase were regarded as independent variables [7].

Although the calculation becomes even more involved, there is no essential difficulty in extending the above-developed method to a large assembly of weakly coupled oscillators. The only point to be noticed is that, since no fast variables other than ϕ_α must appear, we have to introduce many ψ-variables as ψ_β = ϕ_α − ϕ_β, ψ_γ = ϕ_α − ϕ_γ, …. The resulting phase equation in terms of the original phases takes the form

$${\dot{\varphi }}_{\alpha }=\omega +ϵ\sum _{\beta }{G}_1({\varphi }_{\alpha },{\varphi }_{\beta })+{ϵ}^2(\sum _{\beta }{G}_2^{(1)}({\varphi }_{\alpha },{\varphi }_{\beta })+\sum _{\beta ,\gamma }{G}_2^{(2)}({\varphi }_{\alpha },{\varphi }_{\beta },{\varphi }_{\gamma })+\cdots ).$$ 3.35

As a non-trivial feature of the above equation, many-body coupling appears in the second and higher-order terms. One of the ϵ²-order terms depends on 3 variables. Generally, the maximum number of phase variables appearing in the coupling terms increases one by one with the increasing power of ϵ.

We now move to the second step of reduction where we transform the phase equation to a canonical form. As noted in Method I, the canonical form means that the coupling function depends only on the phase difference. To illustrate how this is achieved, let us work with the lowest-order phase equation for a pair of symmetrically coupled oscillators. Thus, we consider the equation

$${\dot{\varphi }}_{\alpha }=\omega +ϵG({\varphi }_{\alpha },{\varphi }_{\beta })$$ 3.36

coupled with the equation for oscillator β, i.e. ${\dot{\varphi }}_{\beta }=\omega +ϵG({\varphi }_{\beta },{\varphi }_{\alpha })$. The essentials of the theory could fully be explained with this example.

To transform the above coupled phase equations to a desired form, we require a near-identity transformation from ϕ_α and ϕ_β to new variables ${\tilde{\varphi }}_{\alpha }$ and ${\tilde{\varphi }}_{\beta }$. The new variables will be so chosen that the coupling may become a function of the phase difference alone. Thus, in terms of the phase difference $\psi \equiv {\tilde{\varphi }}_{\alpha }-{\tilde{\varphi }}_{\beta }$, we require for oscillator α the following reduction form similar to (3.31) and (3.32):

$${\varphi }_{\alpha }={\tilde{\varphi }}_{\alpha }+ϵ\sigma ({\tilde{\varphi }}_{\alpha },\psi )$$ 3.37

and

$${\dot{\tilde{\varphi }}}_{\alpha }=\omega +\mathit{\Gamma }(\psi ).$$ 3.38

To make the above transformation unique, we impose the boundary condition σ(0, ψ) = 0 which means that ${\tilde{\varphi }}_{\alpha }=0$ implies ϕ_α = 0. As in the first step of reduction, working with ϕ_α and ψ and not with ${\tilde{\varphi }}_{\alpha }$ and ${\tilde{\varphi }}_{\beta }$ is crucial.

The reduction form (3.37) and (3.38) must satisfy (3.36). The result of substituting (3.37) and (3.38) into (3.36) may be summarized as

$$\frac{\mathrm{\partial }\sigma ({\tilde{\varphi }}_{\alpha })}{\mathrm{\partial }{\tilde{\varphi }}_{\alpha }}={\omega }^{-1}(-\mathit{\Gamma }(\psi )+B({\tilde{\varphi }}_{\alpha },\psi ))$$ 3.39

and

$$B({\tilde{\varphi }}_{\alpha },\psi )=G({\tilde{\varphi }}_{\alpha },{\tilde{\varphi }}_{\alpha }-\psi )+O(ϵ)\hspace{0.17em}\mathrm{terms}.$$ 3.40

The quantity B consists primarily of the coupling term in the lowest-order approximation but also contains some other terms depending on the unknown quantities. The situation is similar to the first step, that is, if σ and Γ(ψ) are determined simultaneously from (3.39) with B supposed known, then they must be found to any desired precision by iteration. This is in fact possible. Note that σ is a 2π-periodic function of ${\tilde{\varphi }}_{\alpha }$, which means that it vanishes by integration over one period. This condition determines Γ as

$$\mathit{\Gamma }(\psi )=\frac{1}{2\pi }{\int }_0^{2\pi }B(y,\psi )\hspace{0.17em}\mathrm{d}y\equiv B_{av}(\psi ).$$ 3.41

Then, $\sigma ({\tilde{\varphi }}_{\alpha },\psi )$ is obtained by integrating the right-hand side of (3.39):

$$\sigma ({\tilde{\varphi }}_{\alpha },\psi )={\omega }^{-1}{\int }_0^{{\tilde{\varphi }}_{\alpha }}(B(y,\psi )-B_{av}(\psi ))\hspace{0.17em}\mathrm{d}y.$$ 3.42

It is clear that, starting with the lowest-order B obtained by dropping the O(ϵ) terms in (3.40), we can achieve successive approximations for σ and Γ.

This completes the second step of reduction, but only for the simple phase equation (3.36). There are at least four conditions to be relaxed by which the formulation of the second step of reduction can be generalized. First, higher-order terms may be included in (3.36) with which we start. As a result, many-body coupling will necessarily be included. Second, larger assembly of oscillators than an oscillator pair can be treated. Third, the coupling may be asymmetric. Fourth, the oscillators may be slightly non-identical. The phase equation including all these facts will take the form

$${\dot{\varphi }}_{\alpha }={\omega }_{\alpha }({\varphi }_{\alpha })+ϵ\sum _{\beta }{G}_{\alpha ,\beta ,1}({\varphi }_{\alpha },{\varphi }_{\beta })+{ϵ}^2(\sum _{\beta }{G}_{\alpha ,\beta ,2}^{(1)}({\varphi }_{\alpha },{\varphi }_{\beta })+\sum _{\beta ,\gamma }{G}_{\alpha ,\beta ,\gamma ,2}^{(2)}({\varphi }_{\alpha },{\varphi }_{\beta },{\varphi }_{\gamma }))+\cdots$$ 3.43

To integrate all such complex situations into the theory would not be a difficult matter if we do not mind lengthy calculations. Omitting all calculational details, we arrive at the final form of phase reduction

$${\dot{\varphi }}_{\alpha }={\omega }_{\alpha }+ϵ\sum _{\beta }{\mathit{\Gamma }}_1({\varphi }_{\alpha }-{\varphi }_{\beta })+{ϵ}^2(\sum _{\beta }{\mathit{\Gamma }}_2^{(1)}({\varphi }_{\alpha }-{\varphi }_{\beta })+\sum _{\beta ,\gamma }{G}_2^{(2)}({\varphi }_{\alpha }-{\varphi }_{\beta },{\varphi }_{\alpha }-{\varphi }_{\gamma }))+\cdots .$$ 3.44

Finally, one may wonder if there is any practical use of the theory of higher-order phase reduction. It seems difficult to give a definite answer as yet, but it may at least be said that the higher-order corrections will become important when the lowest-order phase equation breaks down. For the phase reduction of reaction–diffusion system [7], this is actually the case because the lowest-order equation of the Burgers type breaks down when the phase diffusion constant ν becomes negative. As long as ν remains small negative, the next order theory which produces the fourth-order spatial derivative of phase becomes quite meaningful. Although not confirmed yet, a similar situation could be met in discrete assemblies of oscillators as well. Imagine either a short-range coupled oscillator lattice or all-to-all coupled population. It may happen that the lowest-order coupling function stays near the threshold between the in-phase and anti-phase types. The resulting dynamical state, whatever it may be, will have a weak stability, and some additional perturbation may easily cause a drastic change in the dynamics. It seems reasonable to expect that the higher-order terms in the phase equation will play the role of such an extra perturbation.

4. Concluding remarks

We have seen how the two representative theories of reduction are similar to each other in their basic way of thinking as well as their theoretical structure. Each theory must involve two essential steps, namely, reduction of dynamical degrees of freedom on one hand and transformation of the reduced equation to a canonical form on the other hand. In the centre-manifold reduction, however, these steps need not be taken one by one but could be achieved simultaneously. This was possible because the complete set of eigenfunctions of the operator ${\hat{L}}_0-\omega \mathrm{d}/\mathrm{d}\theta$ is simply given by the product of the eigenvectors of ${\hat{L}}_0$ and the various harmonics e^imθ, thus making the coefficients of these eigenfunctions become independent of θ. Such a nice property cannot be expected for the phase reduction, because this theory, unlike the centre-manifold reduction, deals with periodic orbits without high symmetry.

Another important feature common to the two reduction theories is that even when we deal with multi-oscillator systems the theory is formulated formally as a perturbed one-oscillator problem. Thus, when the centre-manifold reduction is applied to reaction–diffusion systems, for example, we still imagine a two-dimensional centre manifold depending on various spatial derivatives of the amplitude A as parameters.

Finally, a few remarks will be given on the significance of dynamical reduction from a broader perspective of science in general. There seem to be several roles to be played by the reduction theories for our understanding, controlling and designing systems around us. The most primitive motivation of the reduction theories was that, when we were given a complex dynamical system model, we expected that its analysis would become far easier by reduction. However, it is important to notice that reduced equations are derived without knowledge of the specific form of the original evolution equation. With the help of reduction theories, we often understand the reason for this or that observed behaviour of complex systems for which we are unable to construct a dynamical system model.

Predictive power of reduction is also great. Indeed, it sometimes happens that unexpectedly new types of dynamics are discovered through the analysis of reduced equations. Such dynamical behaviour is expected to exist universally because the reduced equations themselves are universal. For example, we owe much to the complex Ginzburg–Landau equation and its variants for our far deeper understanding of continuous fields of oscillators than before. Discovery of the concept of phase turbulence is also a fruit of dynamical reduction [7].

Implicit in the above arguments, we are thinking of qualitative understanding rather than quantitative understanding of the nature. Although quantitative validity of the reduced equations is limited to the vicinity of exceptional situations such as the near-critical situation of bifurcation and vanishingly small coupling strength, such restriction is not so severe for qualitative understanding. Whenever necessary, one may come back to more realistic mathematical models. Their analysis will become far easier with the help of the suggestions provided by the analysis of the reduced equations. Furthermore, regarding how to control coupled oscillator systems as desired, there may be a lot to learn from the analysis of reduced equations. This seems true whether the coupled oscillators concerned exist as a natural system or are designed as a man-made system.

Appendix A

In this appendix, we briefly describe some of the recent developments in the phase-reduction approach to limit-cycle oscillators, that is, the phase–amplitude reduction, Koopman-operator viewpoint, and some extensions of the phase reduction to non-conventional dynamical systems.

(a) Phase–amplitude reduction

In §3, we formulated the phase reduction for weakly perturbed limit-cycle oscillators. As we explained, the phase is the only slow variable describing the long-time asymptotic dynamics of the oscillator. The amplitude disturbance, representing deviation of the oscillator state from the limit cycle, was neglected in Method I or eliminated in Method II. However, when we are interested in the transient dynamics of the oscillator at shorter timescales, such as the relaxation dynamics to the limit cycle or small variation from the limit cycle caused by applied perturbations, the amplitude degrees of freedom may also be important.

Recently, phase–amplitude reduction of the oscillator dynamics, which explicitly takes the amplitude degrees of freedom into account, has been formulated [25–28]. These studies are partly inspired by the recent development of the Koopman-operator approach to nonlinear dynamical systems, which we briefly discuss in the next subsection, though the idea of the phase–amplitude description of the oscillator state around a limit cycle had already been discussed, for example, in the classical textbook of differential equations by Hale [29]. In this subsection, we briefly describe the extension of Method I of phase reduction to phase–amplitude reduction.

First, we need to introduce the amplitude variables that describe deviations of the oscillator state from the limit cycle C. In §3, the phase ϕ(X) of the oscillator state X was defined to satisfy equation (3.1), i.e. $\dot{\varphi }=\mathbf{F}(\mathbf{X})\cdot {\mathrm{grad}}_{\mathbf{X}}\varphi =\omega$, where ω is the frequency of the oscillator. Considering that small deviation of the unperturbed oscillator state from C decays exponentially on average, it seems natural and convenient to introduce an amplitude function r(X) which satisfies

$$\dot{r}=\mathbf{F}(\mathbf{X})\cdot {\mathrm{grad}}_{\mathbf{X}}r=\mathrm{\lambda }r$$ A 1

in the basin of C, where λ is the decay rate. The amplitude r vanishes on the limit cycle, i.e. r(χ(ϕ)) = 0 where χ(ϕ) is the point of phase ϕ on C. From the Floquet theory, it is expected that λ should be equal to one of the Floquet exponents λ_1,…,n−1 with negative real parts (sorted as λ₀ = 0 > Re λ₁≥Re λ₂ · s≥Re λ_n−1) and that n − 1 such amplitude variables can be introduced. This is actually the case as explained below. For simplicity, we assume that the Floquet exponents are simple and real; extension to the complex case is straightforward.

Suppose that such amplitude functions r_l(X) (l = 1, …, n − 1) exist. Then, as in §3, the amplitude r_l of a weakly perturbed oscillator $\dot{\mathbf{X}}=\mathbf{F}(\mathbf{X})+\mathbf{P}(t)$ obeys

$${\dot{r}}_l={\mathrm{grad}}_{\mathbf{X}}{r}_l\cdot (\mathbf{F}(\mathbf{X})+\mathbf{P}(t))={\mathrm{\lambda }}_l{r}_l+{\mathrm{grad}}_{\mathbf{X}}{r}_l\cdot \mathbf{P}(t)$$ A 2

for each amplitude variable. Moreover, if P(t) is sufficiently weak and X stays in the close vicinity of C, the gradient vector of r_l(X) may be approximately evaluated on C in the lowest-order approximation. We thus obtain an approximate amplitude equation

$${\dot{r}}_l={\mathrm{\lambda }}_l{r}_l+{\mathbf{I}}_l(\varphi )\cdot \mathbf{P}(t)$$ A 3

for l = 1, …, n − 1, where I_l(ϕ) = grad_Xr_l|_X=χ(ϕ) is the gradient vector of r_l evaluated at χ(ϕ) on C characterizing the sensitivity of r_l to external stimuli. It is important to note that I_l(ϕ) depends only on the phase and not on the amplitudes, because it is evaluated on the limit cycle C. Note the similarity of equation (A 3) and the function I_l(ϕ) for the amplitude to equation (3.3) and the sensitivity function Z(ϕ) for the phase. In §3, it was shown that the sensitivity function Z(ϕ) of the phase is equal to the transpose of the left eigenvector u*₀(ϕ) of $\hat{\mathit{\Lambda }}(\varphi )$ associated with the zero eigenvalue. Similarly, I_l(ϕ) can be chosen as the lth left eigenvector of $\hat{\mathit{\Lambda }}(\varphi )$ as I_l(ϕ) = u*_l(ϕ)^† as shown below.

Let us now derive the above facts, namely, the decay rate λ of r in equation (A 1) is equal to one of the Floquet exponents λ_1,…,n−1 and I_l(ϕ) = u*_l(ϕ)^† (l = 1, …, n − 1). Suppose that an initial oscillator state at t = 0 is chosen as X(0) = χ(0) + ϵρ(0) with ϕ = 0, where ρ(0) = u_j(0) (j = 0, …, n − 1) and ϵ is an arbitrary tiny parameter; namely, we add a tiny amplitude disturbance to the oscillator state in the direction of jth eigenvector of $\hat{\mathit{\Lambda }}(0)$ with eigenvalue λ_l. Evolving the oscillator without perturbation from this initial state under the linear approximation, the oscillator state at t = ϕ/ω can be expressed as $\mathbf{X}(t)=\chi (\varphi )+ϵ\rho (\varphi )=\chi (\varphi )+ϵ\hat{S}(\varphi )\hspace{0.17em}{\mathrm{e}}^{(\varphi /\omega )\hat{\mathit{\Lambda }}(0)}{\mathbf{u}}_j(0)=\chi (\varphi )+ϵ\hat{S}(\varphi )\hspace{0.17em}{\mathrm{e}}^{{\mathrm{\lambda }}_j(\varphi /\omega )}{\mathbf{u}}_j(0)$ as in §3. Expanding r(X) in Taylor series as r(χ(ϕ) + ϵρ(ϕ)) = r(χ(ϕ)) + grad_Xr|_X=χ(ϕ) · ϵρ(ϕ) + O(ϵ²) = ϵI(ϕ) · ρ(ϕ) + O(ϵ²), where I(ϕ) = grad_Xr|_X=χ(ϕ) is the gradient of r on C, the amplitude r of X(t) can be expressed as $r(\mathbf{X}(t))=ϵ\mathbf{I}(\varphi )\cdot \rho (\varphi )+O({ϵ}^2)=ϵ\mathbf{I}(\varphi )\cdot \hat{S}(\varphi )\hspace{0.17em}{\mathrm{e}}^{{\mathrm{\lambda }}_j(\varphi /\omega )}{\mathbf{u}}_j(0)+O({ϵ}^2)$. On the other hand, the amplitude r should obey equation (A 1) by assumption and thus r(X(t)) = e^λtr(X(0)) = ϵ e^λtI(0) · u_j(0). Therefore, $\mathbf{I}(\varphi )\cdot \hat{S}(\varphi )\hspace{0.17em}{\mathrm{e}}^{{\mathrm{\lambda }}_j(\varphi /\omega )}{\mathbf{u}}_j(0)={\mathrm{e}}^{\mathrm{\lambda }(\varphi /\omega )}\mathbf{I}(0)\cdot {\mathbf{u}}_j(0)$ should hold for any ϕ within the linear approximation. This requires the following two conditions to be satisfied: (i) I(0) · u_j(0) = 0 if λ≠λ_j, and (ii) $\mathbf{I}(\varphi )\cdot \hat{S}(\varphi )=\mathbf{I}(0)$ if λ = λ_j. From the condition (i), it turns out that a non-trivial amplitude r can only be defined when λ is equal to any of λ_1,…,n−1, otherwise r takes constantly 0 for any ρ(0) within the linear approximation. We thus assume λ = λ_l and denote the corresponding amplitude and gradient as r_l and I_l, respectively. Then, if l≠j, I_l(0) · u_j(0) should be 0, and if l = j, I_l(0) · u_l(0) should not be 0. These conditions can be satisfied only if we take I_l(0)∝u*_l(0)^† for l = 1, …, n − 1, and we simply adopt I_l(0) = u*_l(0)^†. We then obtain ${\mathbf{I}}_l{(\varphi )}^{†}={\mathbf{I}}_l{(0)}^{†}{\hat{S}}^{-1}(\varphi )$, i.e. I_l(ϕ) = u*_l(ϕ)^† from the condition (ii).

It is also important that these left eigenvectors, or sensitivity functions, can be numerically evaluated much more easily than the amplitude function itself. For the sensitivity function of the phase, it is well known that Z(ϕ) = u*₀(ϕ)^† is a 2π-periodic solution to an adjoint linear equation $\omega \hspace{0.17em}\mathrm{d}\mathbf{Z}(\varphi )/\mathrm{d}\varphi =-\hat{L}{(\varphi )}^{†}\mathbf{Z}(\varphi )$ with normalization condition Z(ϕ) · F(χ(ϕ)) = ω [21]. See also ref. [22] for a very concise derivation and the functional forms of Z(ϕ) for typical bifurcations of limit cycles. Using a similar argument, it can be shown that I_l(ϕ) = u*_l(ϕ)^† is a 2π-periodic solution to an adjoint linear equation, $\omega \hspace{0.17em}\mathrm{d}{\mathbf{I}}_l(\varphi )/\mathrm{d}\varphi =-[\hat{L}{(\varphi )}^{†}-{\mathrm{\lambda }}_l]{\mathbf{I}}_l(\varphi )$ [26–28].

In many cases, the slowest-decaying amplitude associated with λ₁, which dominates the relaxation dynamics toward the limit cycle, is of interest to us. Retaining only this amplitude, we obtain a pair of phase–amplitude equations in the lowest-order approximation as

$$\dot{\varphi }=\omega +\mathbf{Z}(\varphi )\cdot \mathbf{P}(t)\mathrm{and}\dot{r}=\mathrm{\lambda }r+\mathbf{I}(\varphi )\cdot \mathbf{P}(t),$$ A 4

where the subscript 1 is dropped from the amplitude equation. At the lowest order, the phase is not affected by the amplitude, while the amplitude is modulated by the phase.

By using the amplitude equation in addition to the phase equation, we can analyse the dynamics of the oscillator state around the limit cycle in more detail. For example, the first-order approximation to the oscillator state is given by X(t) = χ(ϕ(t)) + r(t)u₁(ϕ(t)), which would be useful if a more precise oscillator state than the lowest-order approximation χ(ϕ(t)) is required in the analysis. We may also use the amplitude equation for suppressing deviation of the oscillator state from the limit cycle by applying a feedback input to the oscillator in the control problem of synchronization [30,31]; for example, if we apply P(t) =  − cu₁(ϕ(t))r(t) with c > 0, the amplitude dynamics is given by $\dot{r}=(\mathrm{\lambda }-c)r$ and r decays more quickly than the case without the feedback. Keeping the oscillator state in the close vicinity of the limit cycle by such an additional feedback may allow us to apply stronger input for controlling the oscillator phase to realize desirable synchronized states.

The lowest-order formulation of the phase–amplitude reduction discussed in this subsection corresponds to Method I in §3. Although the phase is not affected by the amplitudes at this order, it is not the case at the second or higher orders; for stronger perturbations, more complex dynamics caused by the interaction between the phase and amplitude are expected. Higher-order generalization of the phase–amplitude reduction and its relation to Method II in §3 needs to be further investigated for a more detailed analysis of the phase–amplitude dynamics.

(b) Koopman-operator viewpoint

In the previous subsection, we mentioned that the recent formulations of the phase–amplitude reduction is closely related to the Koopman-operator approach to nonlinear dynamical systems, which has been intensively studied by Mezić and collaborators [32,33] and has attracted much attention. In this subsection, we discuss this relation very briefly.

Suppose a dynamical system $\dot{\mathbf{X}}=\mathbf{F}(\mathbf{X})$ with an exponentially stable limit-cycle solution. We are usually interested in the evolution of the system state X in the basin of the limit cycle. In the Koopman-operator approach, rather than the evolution of the system state X itself, we focus on the evolution of the observable g, which is a smooth function that maps the system state X to a complex value g(X). We denote by ${\hat{\mathit{\Psi }}}^{\tau }$ the flow of the system, which maps a system state at time t to a system state at time t + τ as $\mathbf{X}(t+\tau )={\hat{\mathit{\Psi }}}^{\tau }\mathbf{X}(t)$. The evolution of an observable g from time t to time t + τ is described as $g_{t+\tau }(\mathbf{X})=({\hat{U}}^{\tau }{g}_t)(\mathbf{X})$ by using the Koopman operator ${\hat{U}}^{\tau }$ define by

$$({\hat{U}}^{\tau }g)(\mathbf{X})=g({\hat{\mathit{\Psi }}}^{\tau }\mathbf{X}).$$ A 5

It can easily be shown that ${\hat{U}}^0=I$ (identity), ${\hat{U}}^{t+\tau }={\hat{U}}^t{\hat{U}}^{\tau }$, and ${\hat{U}}^t$ is a linear operator, i.e. ${\hat{U}}^{\tau }(c_a{g}^a(\mathbf{X})+c_b{g}^b(\mathbf{X}))=c_a{\hat{U}}^{\tau }{g}^a(\mathbf{X})+c_b{\hat{U}}^{\tau }{g}^b(\mathbf{X})$, where c_a,b are arbitrary constants and g^a,b are two observables. Thus, the observable obeys a linear equation even if the original dynamical system is nonlinear; the cost is that ${\hat{U}}^{\tau }$ is now acting on an infinite-dimensional function space of observables, in contrast to ${\hat{\mathit{\Psi }}}^{\tau }$ acting on the finite-dimensional phase space of the oscillator states.

Since U^τ is a linear operator, it is useful to consider its eigenvalues and eigenfunctions. To see the relation with the phase–amplitude reduction, it is convenient to introduce the infinitesimal generator of ${\hat{U}}^{\tau }$, given by $\hat{A}g=\underset{\tau \to +0}{lim}({\hat{U}}^{\tau }g-g)/\tau$. By expanding the flow as ${\hat{\mathit{\Psi }}}^{\tau }\mathbf{X}=\mathbf{X}+\tau \mathbf{F}(\mathbf{X})\tau +O({\tau }^2)$ for small τ, we can expand the action of the Koopman operator on g as $({\hat{U}}^{\tau }g)(\mathbf{X})=g({\hat{\mathit{\Psi }}}^{\tau }(\mathbf{X}))=g(\mathbf{X})+{\mathrm{grad}}_{\mathbf{X}}g(\mathbf{X})\cdot \tau \mathbf{F}(\mathbf{X})+O({\tau }^2)$. We thus obtain

$$\hat{A}=\mathbf{F}(\mathbf{X})\cdot {\mathrm{grad}}_{\mathbf{X}}$$ A 6

and the continuous evolution of the observable g is given by ${\dot{g}}_t=\hat{A}{g}_t$. Note that this generator $\hat{A}$ of the Koopman operator is exactly the operator that appeared in equations (3.1) and (A 1) defining the phase and amplitude functions ϕ(X) and r(X).

We denote the eigenvalue and the associated eigenfunction of $\hat{A}$ as μ and φ_μ(X), respectively, which satisfies $\hat{A}{\phi }_{\mu }(\mathbf{X})=\mu {\phi }_{\mu }(\mathbf{X})$. There can be infinitely many such eigenvalues and eigenfunctions. Most importantly, it can be shown that the eigenvalue iω and the Floquet exponents λ_1,…,n−1 of the limit cycle are included in these eigenvalues and they are called the principal eigenvalues [34,35]. We denote these eigenvalues as μ₀ = iω and μ_l = λ_l (l = 1, …, n − 1).

By using the eigenfunctions associated with the principal eigenvalues, we can introduce new coordinates y_μ(t) = φ_μ(X(t)). It then follows that

$${\dot{y}}_{\mu }=\dot{\mathbf{X}}\cdot {\mathrm{grad}}_{\mathbf{X}}{\phi }_{\mu }(\mathbf{X})=\mathbf{F}(\mathbf{X})\cdot {\mathrm{grad}}_{\mathbf{X}}{\phi }_{\mu }(\mathbf{X})=\hat{A}{\phi }_{\mu }(\mathbf{X})=\mu {\phi }_{\mu }(\mathbf{X})=\mu y_{\mu },$$ A 7

i.e. each y_μ obeys a simple linear equation ${\dot{y}}_{\mu }=\mu y_{\mu }$. Thus, the Koopman eigenfunctions give a global linearization transformation of the system dynamics in the basin of the limit cycle. It is also known that analytic observables can be expanded in series by using the principal eigenfunctions [33]. Therefore, we can reconstruct the observables, including the system state itself, from the new variables {y_μ(t)}.

The amplitude functions r_1,…,n−1(X) defined in the previous subsection are actually principal Koopman eigenfunctions associated with μ_1,…,n−1. Indeed, we have $\hat{A}{r}_l(\mathbf{X})=\mathbf{F}(\mathbf{X})\cdot {\mathrm{grad}}_{\mathbf{X}}{r}_l(\mathbf{X})={\mu }_l{r}_l(\mathbf{X})$, which is equivalent to the definition equation (A 1) of r_l. The phase function ϕ(X), which satisfies F(X) · grad_Xϕ(X) = ω as defined in equation (3.1), is also closely related to the principal Koopman eigenfunction. If we consider an observable e^iϕ(X), we have

$$\hat{A}\hspace{0.17em}{\mathrm{e}}^{\mathrm{i}\varphi (\mathbf{X})}=\mathbf{F}(\mathbf{X})\cdot {\mathrm{grad}}_{\mathbf{X}}\hspace{0.17em}{\mathrm{e}}^{\mathrm{i}\varphi (\mathbf{X})}=\mathrm{i}\mathbf{F}(\mathbf{X})\cdot [{\mathrm{grad}}_{\mathbf{X}}\varphi (\mathbf{X})]\hspace{0.17em}{\mathrm{e}}^{\mathrm{i}\varphi (\mathbf{X})}=\mathrm{i}\omega \hspace{0.17em}{\mathrm{e}}^{\mathrm{i}\varphi (\mathbf{X})}.$$ A 8

Therefore, e^iϕ(X) is also a principal Koopman eigenfunction associated with the eigenvalue iω.

Thus, we can see a clear correspondence between the Koopman-operator approach, in particular, the global linearization of the system dynamics using the principal Koopman eigenfunctions, and the phase or phase–amplitude reduction of limit-cycle oscillators using the phase and amplitude functions. Such a relation has recently been clarified by Mauroy et al. [35]. They proposed to call the level sets of the amplitude functions as isostables, which complement the notion of the classical isochrons, i.e. the level sets of the phase function. Using the idea from the Koopman-operator analysis, they have also proposed a convenient numerical method, called Fourier and Laplace averages, to calculate the phase function ϕ(X) and amplitude functions r_l(X) [34,35]. The recent developments in the Koopman-operator approach appear to shed new light on the conventional theories of dynamical reduction and further developments in various related fields are expected.

(c) Generalization of phase reduction to non-conventional systems

In §3, the phase reduction is developed for limit cycles described by ordinary differential equations. Recently, several extensions of the method to non-conventional dynamical systems have been made. We briefly mention some such attempts here.

(i) Collective oscillations in large populations of globally coupled dynamical elements. Large populations of coupled dynamical elements often undergo collective synchronization transition and exhibit stable collective oscillations [7,10,18]. A system of globally coupled noisy phase oscillators is a typical example that exhibits such a collective synchronization transition [7]. In the large-population limit, the system is represented by a probability density function P(ϕ, t) of the phase, which obeys a nonlinear Fokker–Planck equation. This equation has a stable periodic solution satisfying P(ϕ, t) = P(ϕ, t + T) with period T, which represents collective synchronized oscillations of the whole system. This solution can be considered a limit-cycle solution to the nonlinear Fokker–Planck equation, which should be considered an infinite-dimensional dynamical system. In ref. [36], an equation of the form (3.3) for the collective phase of the nonlinear Fokker–Planck equation is obtained and synchronization between a pair of such collectively oscillating systems is analysed. In [37], a similar phase equation is also derived for the collective phase of a system of globally coupled noiseless phase oscillators with sinusoidal coupling and Lorentzian frequency heterogeneity, which also exhibits collective synchronization transition, in the large-population limit by using the Ott-Antonsen ansatz [38]. Such dynamical reduction for collective oscillations, which we called collective phase reduction, would be useful in analysing collective oscillations in large populations of dynamical elements at the macroscopic level. For example, macroscopic rhythms arising in a mathematical model of neural populations have been analysed by using a similar approach [39].

(ii) Collective oscillations in networks of coupled dynamical systems. Stable collective oscillations in networks of coupled dynamical systems often play important functional roles in real-world systems such as neuronal networks and power grids. When the collective oscillations correspond to a limit-cycle orbit in the high-dimensional phase space of the network, we can develop a phase reduction theory, namely, we can define a phase of the collective oscillation of the network and represent the network dynamics by a single phase equation. In [40], such a phase reduction theory has been developed for collective oscillations in a network of coupled phase oscillators, where the network topology can be arbitrary. The sensitivity functions of the individual elements, characterizing how tiny perturbations applied to each element affect the collective phase of the network, have been derived. In [41], the theory has further been generalized to arbitrary networks of coupled heterogeneous dynamical elements, where the dynamics of individual elements can also be arbitrary. As long as the network exhibits stable collective limit-cycle oscillations as a whole, the network dynamics can be reduced to a single phase equation for the collective phase and, for example, synchronization between a pair of such networks can be analysed by using the same classical methods as those for ordinary low-dimensional oscillators. The interplay between the individual dynamics of the elements and network topology can lead to strongly heterogeneous sensitivities of the individual dynamical elements; for example, some special elements in the network can possess much stronger sensitivity than the other elements. Such information would be useful, for example, in developing a method to control the collective oscillations of the network by external input signals.

(iii) Delay-induced oscillations. Delay differential equations are used in various fields of science and engineering, e.g. in mathematical models of biological oscillations caused by delayed feedback. Since delay-differential equations are infinite-dimensional dynamical systems that depend on their past states, the conventional method of phase reduction for ordinary differential equations cannot be used for them. In [42,43], phase reduction methods for limit-cycle oscillations in delay-differential equations with a single delay time have been developed. The difficulty is that the oscillator state is given by a function representing its past history and not simply by an ordinary finite-dimensional vector. In [42] by Kotani et al., the adjoint equation for the sensitivity function is derived on the basis of the abstract mathematical theory of functional differential equations, while in [43] by Novičenko and Pyragas, a physically more intuitive approach has been taken to derive the phase equation. Both of these results are consistent with each other and enable us to reduce infinite-dimensional delay-differential equations to a one-dimensional phase equation, thereby providing a powerful method to analyse synchronization properties of delay-induced oscillations under weak perturbations. Though [42,43] treated oscillator models with a single delay time, one should be able to generalize the theory to allow multiple or distributed delay times.

(iv) Oscillations in spatially extended systems. Nonlinear oscillatory dynamics in real-world systems often arise in spatially extended systems. The target or spiral waves in chemical or biological systems described by reaction–diffusion equations [14] and oscillatory fluid flows described by Navier–Stokes equations [44] are typical examples. Similar to the delay-differential equations, these partial differential equations are also infinite-dimensional dynamical systems and the conventional method of phase reduction cannot be applied to them; even so, as long as the system exhibits stable limit-cycle oscillations, one should be able to assign a phase value to the system state described by a spatially extended field variable, and derive a phase equation describing the whole system. In [45], a phase reduction method for a fluid system has been developed, where a phase equation describing oscillatory convection in a Hele-Shaw cell is derived from the fluid equation, and synchronization between two coupled convection cells are analysed. The sensitivity function for the phase is represented by a two-dimensional field with characteristic localized structures, representing strong spatial heterogeneity of the response properties of the oscillatory convection to applied perturbations. In [46], a general phase reduction method for reaction–diffusion systems exhibiting rhythmic spatiotemporal dynamics has been developed and typical rhythmic patterns, such as oscillating spots, target waves, and spiral waves arising in the FitzHugh–Nagumo reaction–diffusion system, are analysed using the reduced phase equation. The notion of phase functional, which generalizes the phase function in §3, is introduced, and the sensitivity function of the phase is defined as a functional derivative of the phase functional. An adjoint partial differential equation describing the sensitivity function of the system is also derived. The sensitivity function exhibits strong spatial heterogeneity also in this case, reflecting spatiotemporal structures of the rhythmic patterns. It also seems possible to develop similar phase-reduction theories for other types of partial differential equations exhibiting spatiotemporally rhythmic patterns, and such theories would be useful in the analysis and control of rhythmic spatiotemporal patterns.

(v) Hybrid nonlinear oscillators. Hybrid, or piecewise-smooth dynamical systems, consisting of smooth dynamics described by ordinary differential equations and discontinuous jumps connecting them, are often used in mathematical models of real-world phenomena; the simplest example is the bouncing ball with discontinuity in the vertical velocity. Stable limit cycles can also arise in such systems, for example, in mathematical models of passively walking robots or electric oscillators with switching elements. The conventional phase reduction method cannot be applied to such hybrid systems because of the discontinuity. However, again, as long as the system exhibits stable limit-cycle oscillations, one should be able to define a phase and derive a phase equation. In [47,48], phase equations for hybrid limit-cycle oscillators have been derived. A generalized adjoint equation with discontinuous jumps is derived and the sensitivity function for the phase is obtained. Due to the jumps, the sensitivity function can possess non-smooth discontinuities, which can lead to non-trivial synchronization dynamics that cannot occur in smooth dynamical systems.

(vi) Strongly perturbed and non-autonomous oscillators. In this article and in all generalizations mentioned above, the property of the oscillatory system, whether it is low-dimensional or infinite-dimensional, is assumed to be constant, namely, the limit-cycle orbit, natural frequency, and phase sensitivity function do not vary with time. However, this may not be the case in some realistic problems, for example, when we consider biological oscillators that are subjected to slow but strong effect of parametric modulation due to circadian rhythms in addition to small perturbations coming from other oscillators. In such cases, it is convenient to regard the oscillator as a non-autonomous system whose parameter varies slowly with time while being subjected to fast small perturbations. In [49–51], the phase reduction method has been generalized to such non-autonomous oscillators. By considering a continuous family of limit cycles parameterized by the slowly varying input, a closed phase equation for the oscillator can be derived, which is characterized by the instantaneous frequency and two sensitivity functions. One of the sensitivity functions is the ordinary phase sensitivity function to small perturbations, and the other is a newly introduced sensitivity function to characterize the effect of deformation of the limit cycle due to slow parametric variation. Using the extended phase equation, non-trivial synchronization of a limit-cycle oscillator subjected to strong periodic forcing [49] and between a pair of coupled oscillators subjected to parametric variation [51] have been analysed. As emphasized in [52], non-autonomous systems can be crucially important in modelling real biological oscillations and further studies into this direction, e.g. collective phase synchronization of non-autonomous oscillators, would provide useful information for understanding real biological systems.

In this subsection, we have briefly described some of the recent extensions of the phase reduction to non-conventional rhythmic systems. The simplicity and flexibility of the phase reduction, whose key ideas have been discussed in the main text, allow us to extend the method to a wide class of nonlinear oscillatory dynamical systems. Moreover, once individual systems are reduced to phase equations, synchronization between coupled oscillatory systems of different types, e.g. networked systems and spatially extended systems, can readily be analysed within the framework of the phase reduction. Such an approach would be useful in analysing complex multiscale systems consisting of oscillatory subsystems of different types like neuronal systems. Further extensions of the phase-reduction approach would also be possible for other classes of nonlinear oscillatory systems, including stochastic, chaotic, and even quantum systems [53].

Finally, although not considered in the present paper, data-driven inverse-type approaches, which infer reduced dynamical equations from experimental data without knowing the precise mathematical models of the oscillatory phenomena, are becoming increasingly important recently. As discussed in §4, reduced equations can often be obtained without the detailed knowledge of individual systems in the dynamical reduction theory. This implies that one can infer appropriate reduced equations only from the experimental data of complex oscillatory phenomena and use them to predict their dynamics without knowing their precise physical, chemical, or biological origins. See, for example, refs. [54–57] for such inverse approaches to infer reduced phase equations from complex oscillatory phenomena.

Data accessibility

This article has no additional data.

Authors' contributions

Y.K. formulated the theories of centre-manifold and phase reduction for limit-cycle oscillators in the main text. H.N. discussed the phase-amplitude reduction and relation to the Koopman-operator approach in the appendix. Both authors read and approved the manuscript.

Competing interests

The authors declare that they have no competing interests.

Funding

H.N. is supported by the JSPS KAKENHI grant nos. JP16K13847, JP17H03279, 18K03471 and JP18H03287.