Shear-sensitive adhesion enables size-independent adhesive performance in stick insects

Abstract

The ability to climb with adhesive pads conveys significant advantages and is widespread in the animal kingdom. The physics of adhesion predict that attachment is more challenging for large animals, whereas detachment is harder for small animals, due to the difference in surface-to-volume ratios. Here, we use stick insects to show that this problem is solved at both ends of the scale by linking adhesion to the applied shear force. Adhesive forces of individual insect pads, measured with perpendicular pull-offs, increased approximately in proportion to a linear pad dimension across instars. In sharp contrast, whole-body force measurements suggested area scaling of adhesion. This discrepancy is explained by the presence of shear forces during whole-body measurements, as confirmed in experiments with pads sheared prior to detachment. When we applied shear forces proportional to either pad area or body weight, pad adhesion also scaled approximately with area or mass, respectively, providing a mechanism that can compensate for the size-related loss of adhesive performance predicted by isometry. We demonstrate that the adhesion-enhancing effect of shear forces is linked to pad sliding, which increased the maximum adhesive force per area sustainable by the pads. As shear forces in natural conditions are expected to scale with mass, sliding is more frequent and extensive in large animals, thus ensuring that large animals can attach safely, while small animals can still detach their pads effortlessly. Our results therefore help to explain how nature’s climbers maintain a dynamic attachment performance across seven orders of magnitude in body weight.

1. Introduction

Many arthropods and small vertebrates use adhesive pads for climbing. These animals cover approximately seven orders of magnitude in body weight. Safe and effective climbing despite such enormous size differences requires that the employed adhesive systems maintain performance even over large areas of contact, which is a fundamental challenge in adhesion science. In technical adhesives, this challenge typically arises from stress concentrations, which cause adhesive force per area (mean adhesive stress) to decrease as the contact area increases, σ ∝ A^≤0 [1,2]. As an illustrative example, the force required to peel a thin strip of adhesive tape does not change whether the tape has a length of 2 cm or 500 km; instead, the peel force is proportional to a characteristic length—in this case, the width of the tape—as normal stresses are concentrated at the peeling edge [3]. In biological adhesive systems, this problem is exacerbated further, because the mass which needs to be supported is proportional to a volume, and hence scales as the cube of a characteristic length, m ∝ V ∝ L³. Adhesive pad area, in turn, is expected to grow more slowly, A ∝ L² ∝ m^2/3, assuming geometric similarity (or ‘isometry’). Emerging from this simple geometrical argument is thus a non-trivial problem: size-independent adhesive performance requires that the ratio of the maximum adhesive force an animal can sustain to its body mass, m, is constant

$$S\propto \frac{A\sigma }{m}\propto \frac{m^a{m}^b}{m}\propto \frac{L^{3a}{L}^{3b}}{L^3}=\text{constant, }$$

Here, S is a ‘safety factor’, and a and b are the scaling coefficients describing the relationship between pad area, adhesive stress and body mass, respectively. Size-independent performance requires a + b = 1, so that larger animals need to either (i) systemically increase the adhesive stress their pads can sustain (b > 0; ‘efficiency’); (ii) break with the condition of geometric similarity, and systematically increase the fraction of body surface area used for adhesive pads (a > 2/3; ‘positive allometry’); or (iii) combine both strategies [2]. What do climbing animals do?

Perhaps surprisingly, it appears that climbing animals make use of both strategies, albeit at different phylogenetic levels: across distantly related animals, pad area grows in direct proportion to mass, A ∝ L³ ∝ m, whereas it is approximately isometric within more closely related groups, A ∝ l² ∝ m^2/3 [4]. This difference presumably reflects phylogenetic and developmental constraints: the fraction of available surface area used for adhesive pads differs by a factor of about 200 between large geckos and tiny mites, and such extreme differences require substantial anatomical changes, which in turn may only be achievable over long evolutionary timescales.

While strong positive allometry hence provides a partial answer to the puzzle of how larger climbing animals maintain adhesive performance, it leaves unresolved the question of whether animals within closely related groups compensate for the lower safety factor predicted from their isometric adhesive pads, and if so how. Strikingly, there is robust evidence that within closely related groups, pad efficiency increases with body size, and this increase can indeed be large enough to achieve constant safety factors despite an isometric growth of pad area, i.e. σ ∝ L ∝ m^1/3 [2,4,5]. However, the mechanisms underlying this biologically important increase in pad efficiency have remained unclear (though several authors have suggested corresponding hypotheses [2,4–7]).

In this article, we show that an increase of pad efficiency with body size can arise as a direct consequence of the coupling between adhesive and shear forces widespread in animal adhesive pads [2,8–11], thereby providing new insights into how both small and large animals can climb effectively with sticky feet.

2. Results and discussion

(a). Shear forces control scaling of adhesion

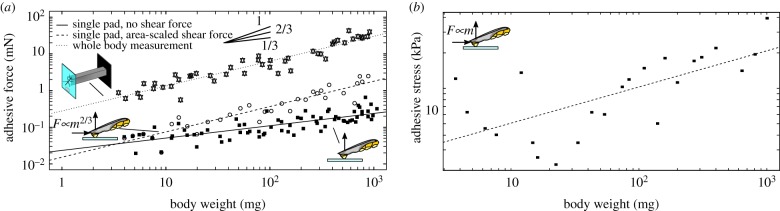
We used a centrifuge to measure whole-body adhesion performance on smooth glass across all instars of Indian stick insects (Carausius morosus, Sinety, 1901; figure 1a,b; for details on this method, see [12]). Across more than two orders of magnitude in body mass, m, adhesive force scaled as m^0.69 (95% CI: 0.59–0.79, n = 45), suggesting a direct proportionality to the area of the adhesive pads, which is approximately isometric (see figure 2a and electronic supplementary material, table S1 for statistics on pad allometry. All slopes cited in this study were obtained with ordinary least-squares (OLS) regression, but the main conclusions are unaffected by the regression technique used, see electronic supplementary material, table S1). However, the scaling coefficient of adhesion changed dramatically when forces of individual pads were measured by performing perpendicular pull-offs (figure 1c; [13]). In sharp contrast to whole-body measurements, single-pad adhesive force scaled with m^0.34 (95% CI: 0.27–0.40, n = 72), suggesting that it is proportional to a characteristic length of the isometric adhesive pads (figure 2a). What is the origin of this discrepancy between single-pad and whole-body measurements?

Figure 1.

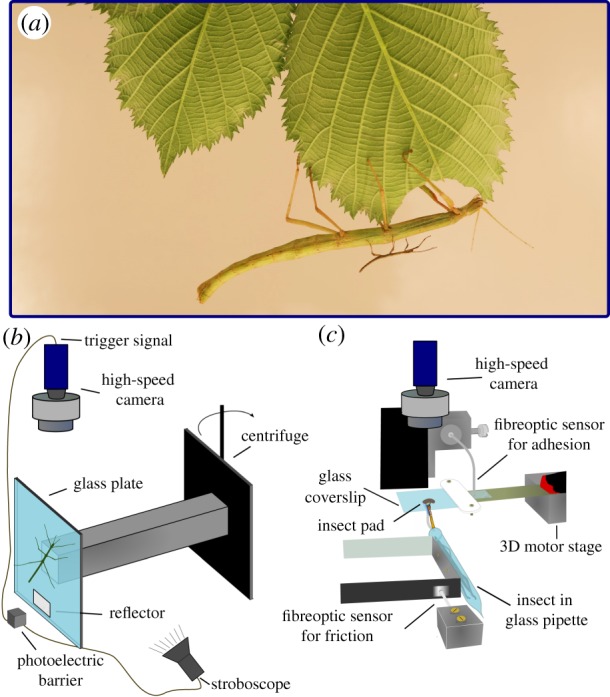
(a) Indian stick insects (Carausius morosus) vary by almost three orders of magnitude in body mass (image Simon Chen). We measured the attachment performance across all instars using (b) a centrifuge, and (c) a custom-built 2D fibre-optic set-up. (Online version in colour.)

Figure 2.

(a) Across all instars, whole-body adhesive performance scaled as m^0.69 (95% CI: 0.59–0.79, n = 45; dotted line), whereas adhesive forces measured with perpendicular pull-offs of individual pads scaled as m^0.34 (95% CI: 0.27–0.40, n = 72; solid line). The discrepancy arises from the absence of shear forces during perpendicular pull-offs. When shear forces scaled with pad area were applied prior to detachment, adhesive forces scaled as m^0.71 (95% CI: 0.61–0.82, n = 32; dashed line). More detailed statistics can be found in the main text. (b) Because of the linear relationship between applied shear force and measured adhesion, applying a shear force corresponding to the insect’s body weight increases the scaling coefficient of adhesion, leading to an apparent increase in pad efficiency. When shear forces equivalent to one body weight were applied prior to detachment, adhesive stress increased with m^0.31 (95% CI: 0.16–0.45, n = 23), sufficient to achieve size-independent safety factors. Note that both plots are double-logarithmic. (Online version in colour.)

A key difference between the two measurements arises from the sprawled leg posture of stick insects, which results in an inward shear component of the force vector detaching individual pads during whole-body measurements. As a consequence, centrifuge measurements simultaneously induce both normal and shear forces. Our single-pad measurements, in contrast, only induced normal forces. In order to investigate if the discrepancy between whole-animal and single-pad scaling arises from the presence or absence of shear forces, we repeated the single-pad measurements, but this time applied a feedback-controlled shear force to the pads prior to detachment (see [14] for details on this method). This shear force was scaled in proportion to m^0.67 to achieve an approximately constant shear stress of about 25 kPa, just above the static shear stress of the pads (approx. 20 kPa, corresponding to a shear force of 0.1 mN for a stick insect of 5 mg weight [10]). Single-pad adhesion forces measured in the presence of area-specific shear forces scaled as m^0.71 (95% CI: 0.61–0.82, n = 32), virtually identical to the result obtained with whole-animal centrifuge measurements (ANCOVA, F_1,73 = 0.36, p = 0.55, figure 2a), but significantly higher than for single-pad measurements in the absence of shear forces (ANCOVA, F_1,100 = 40.81, p < 0.001, figure 2a). Hence, shear forces alter the scaling of adhesive forces, confirming our previous hypothesis [2].

Strikingly, our results also shed light on the conflict between the vast majority of theoretical adhesion models—which predict adhesive forces to grow more slowly than adhesive contact area [1,2,15]—and the majority of experimental data on biological adhesives—which imply area—or even above area scaling [2]. This remarkable contradiction can be resolved by accounting for the size-related variation in shear forces acting during whole-body detachments, as we will show below. In the following, we will discuss why altering the magnitude and scaling of adhesion via shear forces is biologically important, and what mechanisms might explain the link between adhesion and shear force.

(b). Shear forces help to maintain size-independent safety factors across body sizes

Animals climbing with adhesive pads vary by almost seven orders of magnitude in mass, which poses a significant challenge: the weight that needs to be supported grows faster than the area available for adhesive structures (assuming isometry). Across the entire size range of animals climbing with adhesive pads, this change in surface-to-volume ratio is predicted to reduce safety factors (i.e. adhesion per body weight) more than 200-fold (10^7/3 ≈ 200; here, we also assumed area scaling of adhesion, and size-independent maximum adhesive stress [4]). Recently, we showed that heavier climbing animals partially solve this problem by allocating a larger fraction of the total available body surface area to adhesive structures [4]. However, this disproportionate increase in pad area was not observed within closely related taxa. Instead, the mass-specific pad area differed considerably between vertebrates and invertebrates, but was approximately consistent with isometry within clades, indicating that pad size is constrained by phylogeny [4]. Strikingly, some vertebrate and invertebrate taxa are nevertheless able to achieve size-independent adhesion: their pads appear to get more effective as they grow in size [2,4,5]. Larger climbing animals hence appear to maintain size-independent safety factors by employing two distinct strategies—disproportionately larger versus more effective pads—at different phylogenetic levels [2,4]. However, the underlying mechanism of the systematic increase in pad efficiency, observed within closely related groups [2,4,5], has remained unclear.

Based on the empirical observation that adhesive forces of invertebrate and vertebrate pads are an approximately linear function of the shear force acting during detachment [8,10], one may speculate that shear forces can in principle be used to achieve an arbitrary scaling of adhesive forces, if they are varied systematically with size (with an upper limit set by the maximum sliding shear stress sustainable by the adhesive pads). In order to test this hypothesis, we conducted another series of single-pad measurements, this time applying a shear force equal to the weight of the individuals. The resulting adhesive force scaled with m^0.87 (95% CI: 0.70–1.03, n = 23), an increase significantly exceeding that of adhesive pad area (t₅₄ = 2.5, p < 0.05). Force per pad area increased with m^0.31 (95% CI: 0.16–0.45, n = 23, figure 2b), consistent with previous reports on tree frogs and ants [2,4]. The relationship between shear force and adhesion may hence underlie the previously unexplained increases in pad efficiency with size [2,4], and may even suffice to achieve size-independent safety factors (i.e. σ A ∝ m or σ ∝ m^1/3 for isometric animals). We therefore propose that the link between shear force and adhesion plays a key role not only in controlling attachment during locomotion [10,16,17], but also avoids the predicted decrease of safety factors in larger animals [2].

(c). Biomechanics of shear-sensitive adhesion

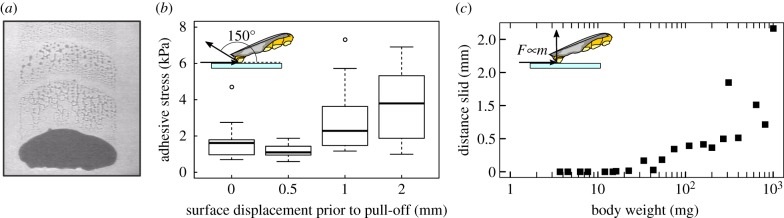
While our data provide strong evidence that shear forces influence both the scaling and magnitude of adhesive forces [2], the physical basis for this effect remains unclear. Shearing pads towards the body is known to increase the adhesive contact area of smooth and hairy pads [18–20], but this does not explain the shear-dependence of adhesive stress observed here and in previous studies [14]. Numerous theoretical models have been proposed for the performance of animal adhesive pads (for a review, see [15]), but to our knowledge no theory has been able to quantitatively predict the effect of shear forces on adhesion from first principles [10]. For example, the peeling theory for inextensible tape predicts that adhesion increases with applied shear force [2,10,15,16,21–23], and that it scales with length, seemingly consistent with our no-shear single-pad measurements (figure 2a). However, peeling theory fails to explain the well-established linear relationship between shear force and adhesion [10,16], and is also inconsistent with the area scaling of adhesive forces observed in pull-off measurements involving shear (figure 2a). This inconsistency may arise because shear forces increase the length of the peel zone, thereby leading to a more uniform stress distribution within the contact zone, and hence to area scaling [2,24,25]. Notably, single-pad adhesion forces of stick insects followed peeling theory for small shear forces (or large peel angles) and only departed from theoretical predictions for large shear forces (or small peel angles [10]). The departure from peeling theory coincided with the onset of whole-pad sliding during detachment [10], and two explanations for this observation have been proposed: first, pads that slide will be stretched, which increases their effective stiffness, thereby preventing the drop in adhesion predicted by the theory for extensible tape as peeling angles approach 0° (for a more detailed discussion, see [10,23,26]). While this effect is undoubtedly important, it cannot explain the departure from the theory for inextensible tape, which underestimates adhesion for small peel angles and still predicts adhesive forces to scale with a linear dimension of the contact [3,10,23]. Second, sliding results in the depletion of the contact-mediating liquid secreted by the adhesive pads (figure 3a, [10,27,28]; for more details on the function and chemical composition of the secretion, see [13,29]). Such a reduction in the amount of pad fluid has been hypothesized to increase pad adhesion, for example by increasing the contribution of ‘wet’ forces arising from the secretion’s surface tension and viscosity [19,30], or by reducing the ‘interfacial mobility’ [13]. However, direct experimental evidence for a link between sliding and changes in the force required to detach the pads is still missing.

Figure 3.

(a) Pads that slid left behind trails of contact-mediating fluid. (b) Adhesive force of pads that slid over different distances, prior to the detachment at 150°, significantly increased with sliding distance (repeated measures ANCOVA, F_1,37 = 20.1, p < 0.01, n = 10). (c) Sliding distance of stick insect pads prior to detachment in adhesion tests where shear forces equivalent to one body weight were applied. Because pad area grows more slowly than mass, larger insects are more likely to slide. Sliding occurred only for insects weighing more than approximately 20 mg, consistent with a simple estimate based on the pad allometry and the static shear stress (see the main text). Because sliding increases adhesive strength, the variable sliding distance of pads helps large animals to attach safely, while small animals can still detach their pads effortlessly. (Online version in colour.)

We experimentally tested the hypothesis that pad sliding increases the strength of the adhesive contact. In brief, we conducted single-pad adhesion measurements in which pads of adult stick insects were initially subjected to proximal shear displacements of 0, 0.5, 1 or 2 mm, in a direction corresponding to a pull of the pad towards the body. Subsequently, the pads were detached with an angle of 150° relative to the surface. This experimental design allowed us to separate the effect of pad sliding from a possible effect of the shear force itself. Although the shear force acting on the pads at peak adhesion did not differ between treatments (repeated measures ANCOVA, F_1,36 = 0.41, p = 0.53, n = 10), adhesion significantly increased with the applied shear displacement (repeated measures ANCOVA, F_1,37 = 20.1, p < 0.01, n = 10), providing direct evidence for a sliding-induced change in interface strength (figure 3b, [10,13]).

(d). The limits of shear-sensitive adhesion

We have demonstrated that shear forces control the magnitude of adhesive forces, and can therefore modify the scaling of adhesive forces. The adhesion-enhancing effect of shear force arises at least partly from pad sliding, which stretches the pad, and strengthens the contact. Does the amount of sliding differ between animals of different size, and if so, what are the consequences for the scaling of attachment performance?

Under natural conditions, pads will be sheared passively whenever adhesive forces are required, due to the insects’ sprawled leg posture. These passive shear forces likely scale with body mass, leading to higher shear stress acting on the adhesive pads of larger animals, which are therefore more likely to slide. As an illustrative example, the shear stress acting on the pads of a 1000 mg adult stick insect in our single-pad experiments with mass-scaled shear forces was approximately 70 kPa, or 3.5 times the static shear stress. For a first-instar insect weighing 5 mg, in turn, one body weight in shear force resulted in a stress of approximately 10 kPa, about half the static shear stress. As a consequence, the transition to sliding occurred at some intermediate body mass, m_c. We estimated m_c using the allometric relationship of the adhesive pad area, and the approximate static shear stress of 20 kPa, yielding m_c = 21.8 mg. This estimate is in excellent agreement with direct observations of pad sliding extracted from video recordings (figure 3c). It is remarkable that the static shear stress of the pads is of the same order of magnitude as the stresses expected from one body weight acting on a single foot, as sliding is considered detrimental for the function of conventional adhesives (although under natural conditions, the stresses might be smaller as the force is shared between multiple pads). We believe this is no coincidence: the problem of surface attachment at varying body sizes can be seen from two perspectives: it is hard to detach when small, but challenging to attach when large. The magnitude of the static shear stress of adhesive pads might hence be adaptive, as it can enable similar attachment performance for both small and large insects. Small animals are less likely to slide and hence can more easily detach their pads. Large animals, in turn, benefit from the weight-specific adhesion enhancement caused by larger amounts of pad sliding, and hence are able to maintain adhesive performance. For pads tested at shear stresses in excess of their static shear stress, the distance slid increased as m^1.1 (95% CI: 0.75–1.43, n = 15, figure 3c). At present, the quantitative relationship between the distance slid and the increase in adhesive strength is still unclear, and will be addressed in future work. It is plausible that adhesion enhancement depends on distance slid per unit pad length, adding further complexity to the scaling of shear-sensitive adhesion.

It appears relevant to distinguish between two types of sliding: (i) local sliding of parts of the pad’s contact zone near the peel front, which stretches the pad and thereby increases its stiffness, but does not lead to much fluid depletion; (ii) sliding of the entire pad, which will be most effective at depleting fluid by leaving it behind at the trailing edge [31]. This distinction can be used to illustrate a significant complication which we have thus far ignored for simplicity: during detachment, the contact area of the pads will decrease to zero, and the shear stress will therefore tend to notational infinity. Hence, even for size-invariant shear stress that was initially below the static shear stress, the pads of all instars must slide at some point during detachment. If the shear stress exceeds the static shear stress only after peak adhesion has been reached, sliding will have no effect on adhesive performance. If pads slide prior to reaching the adhesion peak, however, the critical parameter governing attachment performance is the distance slid before detachment (figure 3c). In insects, sliding speed increases in an approximately linear fashion with shear stress after the static shear stress is surpassed [32], but it is unclear if this relationship is affected by animal size. The time to detachment, in turn, depends on a number of factors, such as contact size and pad modulus, which ultimately together control the speed of crack propagation [13]. While a detailed investigation of the size-dependence of these factors will have to await future work, we point out that the need to generate some static shear stress provides a potential explanation for the increase in mass-specific pad area from invertebrate to vertebrate taxa [10]: from the previous discussion, it is unclear why vertebrates evolved pads much larger relative to their size, instead of just relying on the adhesion enhancement provided by pad sliding. However, the maximum static shear stress sustainable by the pads is finite, and hence there must be a critical size at which the pad area must increase disproportionally to prevent large animals from sliding excessively. Future research should clarify the factors that determine sliding distance before detachment, its role for adhesion enhancement, as well as detachment dynamics across body sizes. Such work will ultimately further our understanding of how nature’s best climbers maintain performance across considerable variations in body size, and potentially allow us to transfer their tricks to scalable bioinspired adhesives.

3. Material and methods

(a). Experimental model organism

We used Indian stick insects (Carausius morosus) as model species, because they vary by almost three orders of magnitude in body weight between first-instar nymphs and adults (figure 1a). Individuals from all instars were taken from a laboratory colony kept at ambient conditions, and fed with water, ivy and bramble leaves ad libitum. All individuals were weighed to the nearest 10 μg (MC 5, Sartorius AG, Göttingen, Germany). Prior to further preparation, all distal pads (arolia) were investigated using light microscopy, to exclude individuals with damaged pads.

All experiments were conducted in ambient laboratoryconditions (temperature: 19–23°C, relative humidity: 30–50%). In order to avoid pseudo-replication, all animals were kept in a different cage once tested.

Throughout this manuscript, we use ‘shear force’ to refer to forces applied parallel to the surface (they are counteracted by ‘friction forces’). ‘Adhesive force’, in turn, refers to the normal component of the force resisting detachment for whole animals or individual adhesive pads. ‘Shear stress’ and ‘adhesive stress’ refer to these forces when normalized by contact area. We use ‘pad efficiency’ for the maximum adhesive stress a pad can sustain. ‘Static shear stress’ is the maximum stress which can be applied parallel to the surface without causing the pads to slide, i.e. to move relative to the surface.

(b). Whole-body measurements

Whole-body adhesion measurements were conducted using a custom-built centrifuge (figure 1b) [12]. Animals were placed on vertical glass plates mounted on a custom-made holder attached to the centrifuge, which was gradually accelerated until the insects detached. A DMK 23UP1300 high-speed camera (Imaging Source Europe GmbH, Bremen, Germany) was mounted above the set-up, and triggered by a photoelectric barrier to synchronize with the rotational speed of the centrifuge. To achieve sharp images, the set-up was illuminated with a stroboscope, also triggered by the photoelectric barrier. We digitized the insect’s radial position on the centrifuge just before detachment, allowing us to calculate centrifugal acceleration; detachment force was then calculated as the product of body mass and centrifugal acceleration. Each insect was only measured once.

(c). Single-pad measurements

In order to isolate individual pads, stick insects were put into glass pipettes, and one of the two protruding front legs was attached onto a metal wire using dental wax (Elite HD, Zhermack, Badia Polesine, Italy), so that the ventral side of the arolium was facing up. To avoid interference with the measurements, the claw tips were cut-off under a stereo-microscope (MZ16 Leica Camera AG, Wetzlar, Germany) using sharp tweezers, and dust particles were removed from the pad using a piece of sticky tape (Tesa SE, Norderstedt, Germany).

Single-pad forces were measured with a custom-built 2D fibre-optic transducer set-up (figure 1c). In order to eliminate cross-talk between the shear force and adhesion channels, they were physically separated: adhesion was measured by the deflection of a cantilever beam to which a glass coverslip was attached, and friction was measured by the deflection of an independent double cantilever beam to which a plastic tube holding the stick insect was attached (figure 1c). This separation also allowed us to perform a straightforward independent manipulation of the beams’ spring constants. For both beams, the deflection was sensed with fibre-optic sensors (D12, Philtec, Inc., Annapolis, USA), via small pieces of reflective foil glued to the far end of the beams (figure 1c). More details regarding the set-up and the calibration procedure can be found in [13].

In order to perform controlled experiments, the adhesion beam was mounted on a 3D motor positioning stage (M-126PD, Physik Instrumente, Karlsruhe, Germany), which was controlled with a custom-made Labview script [30]. A high-speed camera (DMK 23UP1300, The Imaging Source Europe GmbH, Bremen, Germany), mounted on top of a stereo-microscope (Wild M8, Wild Heerbrugg AG, Gais, Switzerland), allowed us to record the contact area of the pads during the measurements using reflected light. The output from both fibre-optic sensors, and the camera trigger signal were recorded at 1 kHz with a data acquisition board (USB-6002, National Instruments, Austin, USA), allowing us to synchronize the contact area images with the measured forces.

For all single-pad measurements, pads were first brought in contact with clean glass coverslips for a period of 8 s, at a constant load of 0.5 mN unless otherwise specified (the normal load has no significant influence on adhesion measurements on smooth surfaces [14]). The normal load was kept constant using a force-feedback algorithm implemented in the LabView software [30], and the same algorithm was used to apply constant shear forces for a period of 10 s in all experiments involving controlled shear forces, detailed in the results section. All measurements ended with an upward movement of the motor stage holding the glass coverslip, at a speed of 0.5 mm s⁻¹, which led to complete detachment of the pads.

(d). Quantification and statistical analysis

All force data were filtered with a low-pass Butterworth filter in MatLabR2013a (Mathworks Inc., Natick, MA, USA), from which we extracted the peak adhesion force. The contact area and sliding distance of the pads were measured with ImageJv1.49 (National Institutes of Health, Bethesda, MD, USA). The video recordings were binarized by thresholding, and contact area was then extracted using native particle analysis routines. Scaling data were analysed using OLS regression, because the error in the determination of mass is likely much smaller than that in the measurement of adhesive forces. There is some controversy as to whether OLS or standardized major axis procedures are more appropriate for analysing scaling data [33–36], and we verified that all main conclusions of the paper hold independent of the regression technique, using the R-package smatr v3.4.4 [37]. The exact tests used, and sample size n, indicating the number of individuals, are specified both in the results text and in the relevant figure captions. Effects were considered significant if p < 0.05. Boxplots show the median and the 25%/75% quartiles; whiskers indicate 1.5—the interquartile range. All statistical analyses were performed in R v.3.4.4.

Data accessibility

All data used in this manuscript are available from the Dryad Digital Repository: https://doi.org/10.5061/dryad.gp44678 [38].

Authors' contributions

D.L. and W.F. conceived of the study, D.L., M.-Y.S. and A.V.B.-J. conducted the experiments, and performed data analysis. D.L. wrote drafts of the manuscript, which were edited further in collaborative work involving all authors.

Competing interests

We declare we have no competing interests.

Funding

This study was supported by research grants by the Human Frontier Science Programme Grant RGP0034/2012 (to W.F.), and the Biotechnology and Biological Sciences Research Council (grant nos. BB/I008667/1 and B/R017360/1) to W.F. and D.L., respectively.