Abstract
We use the PBE0/6-31G* density functional method to perform ab initio quantum mechanical/molecular mechanical (QM/MM) molecular dynamics (MD) simulations under periodic boundary conditions with rigorous electrostatics using the ambient potential composite Ewald method in order to test the convergence of MM→QM/MM free energy corrections for the prediction of 17 small-molecule solvation free energies and 8 ligand binding free energies to T4 lysozyme. The “indirect” thermodynamic cycle for calculating free energies is used to explore whether a series of reference potentials improve the statistical quality of the predictions. Specifically, we construct a series of reference potentials that optimizes a molecular mechanical (MM) force field’s parameters to reproduce the ab initio QM/MM forces from a QM/MM simulation. The optimizations form a systematic progression of successively expanded parameters that include bond, angle, dihedral and charge parameters. For each reference potential, we calculate benchmark quality reference values for the MM→QM/MM correction by performing the mixed MM and QM/MM Hamiltonians at 11 intermediate states, each for 200 ps. We then compare forward and reverse application of Zwanzig’s relation, thermodynamic integration, and Bennett’s acceptance ratio (BAR) methods as a function of reference potential, simulation time, and the number of simulated intermediate states. We find that Zwanzig’s equation is inadequate unless a large number of intermediate states are explicitly simulated. The TI and BAR mean signed errors are very small even when only the end-state simulations are considered, and the standard deviation of the TI and BAR errors are decreased by choosing a reference potential that optimizes the bond and angle parameters. We find a robust approach for the data sets of fairly rigid molecules considered here is to use bond+angle reference potential together with the end-state-only BAR analysis. This requires a QM/MM simulations to be performed in order to generate reference data to parameterize the bond+angle reference potential, and then this same simulation serves a dual purpose as the full QM/MM end-state. The convergence of the results with respect to time suggests that computational resources may be used more efficiently by running multiple simulations for no more than 50 ps, rather than running one long simulation.
Graphical Abstract
1. Introduction
Reliable simulations of complex biological processes whereby molecules undergo significant changes in their environment require robust force field models as well as efficient sampling methods to enable both the electronic and conformational degrees of freedom to accurately respond.1 These requirements present challenges for conventional molecular mechanical (MM) force fields,2 particularly with chemically diverse molecules for which tested parameters do not exist (and often selection of parameters is not clear).3 Further, modeling of more complex interactions such as formation/cleavage of ionic or covalent bonds may require more sophisticated quantum mechanical (QM) models.4 These challenges all culminate in free energy simulations applied to drug discovery applications, creating a critical barrier to progress for structure-based drug design.2-5
Free energy simulations with combined quantum mechanical/molecular mechanical (QM/MM) potentials or fully quantum mechanical force fields (QMFFs) garner increasing interest for improving the accuracy of prediction6-10 particularly for solvation and relative ligand binding free energies that are important for drug design applications.11 Quantum models, if made affordable, are attractive for these applications owing to their accuracy, robustness and lack of adjustable free parameters relative to MM force fields. Although dual-topology single-coordinate QM/MM free energy calculations can be performed for some specific applications,12,13 a more common strategy is to use a “reference potential approach” for calculating the free energy change via an indirect route. That is, one can perform the alchemical transformation with a MM method, and then apply MM→QM/MM free energy corrections to the end-states. The reference potential approach was pioneered by Gao14,15 and Warshel,16 and advanced recently by Woodcock, Boresch, König, Brooks and others.17-26
The high cost of quantum mechanical (QM) calculations has led to the exploration of various methods to reduce the number of energy (and force) evaluations necessary to converge the free energy estimate. These include the use of frozen density functional approximations,27,28 orthogonal space random walk strategies,29 integrated Hamiltonian sampling,30 paradynamics,31,32 and trajectory reweighting.25,33-36 Others have noted the importance of choosing the most compatible reference potential37-40 or have sought to improve the reference potential to increase the distribution overlap between reference and QM/MM potential energy surfaces.32,38,41,42 Of particular note are those methods that perform ad hoc parametrization of the MM reference potential via “force matching” to the QM/MM potential19,39,43-50 to enhance the conformational overlap between the levels of theory.18,19,47,50 In the present work, we use the phrase “reference potential” to refer to the low-level MM Hamiltonian used to connect the high-level QM/MM Hamiltonian to the free energy cycle. In other words, if an ad hoc MM force field model is parametrized to match the high-level QM/MM forces, then the reference potential is the force-matched MM model.
One can greatly reduce the number of QM/MM evaluations by re-analyzing a distribution generated from simulations using an MM reference potential, because only the statistically independent samples (typically 103 times less than that needed to produce the simulation distribution) need to be considered. The simplest form of re-analysis is the evaluation of Zwanzig’s relation,51 which is theoretically exact in the limit of infinite sampling;52 however, forward and reverse analysis (that is, evaluating Zwanzig’s relation from MM and QM/MM distributions, respectively) can be in serious error for finite sampling realized in practice,24,25,33,38,53-57 which has lead some to doubt the feasibility of converging the total energy calculations within a reasonable simulation time.55 Nevertheless, procedures have been sought to improve the convergence; for example, by fixing the internal-coordinates of the “QM region” during dynamics,58,59 representing the environment through a mean-field approximation,60 averaging many, short simulations,61,62 performing nonequilibrium work simulations,20,21,62-65 or by using interaction energies rather than total energies.66-68 It has been demonstrated, however, that the use of interaction energies can yield incorrect solvation free energies with respect to rigorously obtained values.68,69
In this work, we compare MM→QM/MM free energy corrections calculated from Zwanzig’s relation (forward and reverse), Bennett’s acceptance ratio70 (BAR), and thermodynamic integration71 (TI) for a series of solvation free energies and ligand binding free energies to the T4 lysozyme.72 We perform dynamics with the PBE0/6-31G* hybrid density functional method and obtain reference free energy correction values by performing simulations at 11-intermediate states connecting the MM and QM/MM Hamiltonians. Unlike previous works that performed ab initio QM/MM free energy simulations, we are able to perform condensed phase electrostatics using a robust ambient potential composite Ewald method to account for long-range interactions.73 We explore the benefits of using various reference potentials produced from force matching parametrization. Specifically, we use force matching parametrizations to construct a series of ad hoc MM′ reference potential models that are used as an intermediate stage within the thermodynamic cycle, so that the free energy correction becomes: MM→MM′→QM/MM. The MM′ reference potential models are parametrized to reproduce the target QM/MM forces by changing either: (1) the MM bond parameters, (2) the MM bond and angle parameters, (3) the MM bond and angle parameters and the dihedral force constants, or (4) the MM bonded parameters and (fixed) atomic charges. Convergence of the analysis methods is performed with respect to sampling time and the number of intermediate-Hamiltonian simulations.
The studies in the literature most closely related to the present work are those that directly assess the quality of the free energy corrections through extensive generation of QM/MM MD trajectories, including intermediate MM→QM/MM alchemical Hamlitonians as a reference for comparison.17,55,57 Of particular note is the work of Kearns et al.,17 which was published during the preparation of our manuscript. They developed a dataset for validating QM/MM free energy corrections consisting of 22 drug-like small molecules, and gas-phase QM corrections are obtained for a self-consistent charge density functional tight-binding (SCC-DFTB) semiempirical Hamiltonian.17 The authors obtain accurate free energy estimates and compare several analysis methods (Zwanzig’s relation, BAR, Jarzynski’s equation). Our present work differs in several ways: we use the PBE0/6-31G* ab initio Hamiltonian and obtain accurate estimates in both condensed- and gas-phases (for solvation free energies), and bound- and unbound-states (for ligand-binding free energies). Furthermore, our work is more heavily focused on the use of reference potentials obtained from force-matching parametrization.
2. Methods
2.1. Thermodynamic cycles and test sets
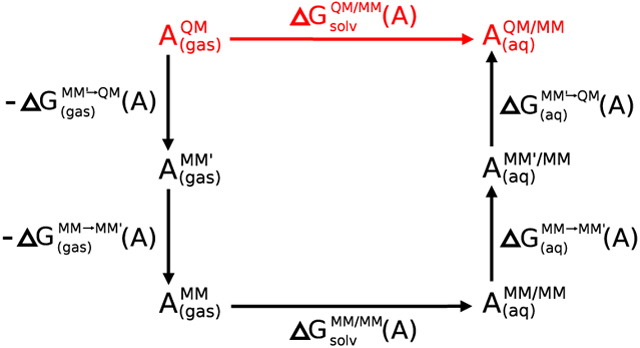
Figure 1 illustrates thermodynamic cycles for computing QM/MM solvation and ligand binding free energies by correcting the end-states of a MM-computed alchemical free energy calculation. The MM→QM end-state transformations avoid the need for performing direct alchemical transformations with a QM method. The thermodynamic cycle contains an intermediate step that transforms the MM Hamiltonian to a MM′ model, which differs only by the MM parameter values that are used. The purpose of including this additional step is to improve the overlap between the MM′ and QM distributions to enhance the converge of the thermodynamic estimate with respect to the number of QM energy evaluations (and in particular to minimize the amount of simulations that requires expensive QM/MM energy and force evaluation at every time step). In comparison, the MM→MM′ transformation requires a trivial amount of computational resources to obtain adequate sampling. Note: the schematic in Figure 1 illustrates the absolute ligand binding free energy, ΔAb(L ∙ P), whereas in practice, it is often the relative ligand binding free energy between two closely related ligands, ΔAb(L ∙ P) − ΔAb(L′ ∙ P), representing a much smaller perturbation, that is actually computed. This type of calculation involves an additional alchemical transformation between the ligands, in both an aqueous environment and bound to the protein. These transformations can be conducted completely within the MM framework, and the exact same QM/MM end-state free energy corrections as shown in the illustration can be used to make QM corrections to the relative ligand binding free energy calculations computed at the MM level.
Figure 1:
Thermodynamic cycles for correcting solvation free energies (left) and ligand binding free energies (right) with QM “book-ending” corrections. It is assumed that the molecule/ion being solvated or the ligand that is binding is to be treated as the QM region, and the surrounding region that makes up the aqueous solution or aqeuous protein environment is modeled using an MM framework to give rise to the final QM/MM potential. In the case that an MM′ reference potential is used for the QM atoms as an intermediate, we designate the combined potential as MM′/MM, and for consistency, when the unmodified MM potential is used for both we designate the potential as MM/MM.
One can write the QM-corrected solvation free energy of molecule A as
| (1) |
where is the net MM→QM correction
| (2) |
We calculate by transforming the solute, A, to a set of dummy particles that do not interact with the solvent, A*, in both aqueous and gas phases; that is
| (3) |
The simulations that were explicitly performed correspond to the terms: and in Eq. 3, and , , , in Eq. 2. We examine the accuracy and the convergence of , , and for the following set of 17 molecules/ions: , , , , H3O+, C6H5Cl, C6H14, CH3OH, C2H6, (CH2)4O, , C6H5NH2, CH3CONH2, H2O, C2H5OH, C6H6, and C6H5OH. These are designated the “Solvation test set” and are shown in Figure 2.
Figure 2:
List of 17 molecules/ions in the solvation test set, and 8 molecules in the T4 lysozyme ligand binding test set.
The QM-corrected ligand binding free energy of ligand L to protein P is
| (4) |
where is the free energy of transforming the ligand from MM→QM while the protein continues to be modeled with MM.
| (5) |
The notation L ∙ P and L + P indicates that the ligand is bound and unbound to the protein, respectively.
In practice, we compute the relative ligand binding free of ligand L (relative to ligand L′), which requires a much smaller perturbation to the system. The relative ligand binding free energy is:
| (6) |
where
| (7) |
The simulations that were explicitly performed correspond to the terms: and in Eq. 7, and , , , and in Eq. 5. We examine the accuracy of and the convergence of , , and for the following 8 ligands bound to T4 lysozyme:72 BNZ (benzene, PDBID: 181l), PXY (p-xylene, PDBID: 187l), I4B (isobutylbenzene, PDBID: 184l), BZF (benzofuran, PDBID: 182l), DEN (indene, PDBID: 183l), IND (indole, PDBID: 185l), OXE (o-xylene, PDBID: 188l), and N4B (n-butylbenzene, PDBID: 186l). These ligands are designated the “T4 lysozyme test set” and are illustrated in Figure 2. All ligands in the T4 lysozyme test set are electrically neutral, and the partial atomic charges were determined using the AM1-BCC procedure.74,75
2.2. Reference potentials
The free energy calculations begin by solvating the system and equilibrating the unit cell density using a MM Hamiltonian. A 200 ps QM/MM NVT simulation is then performed, and the trajectories of coordinates and atomic forces are saved every 0.5 ps. This simulation will later be reused to perform free energy analysis.
The MM′ reference potential models are created by adjusting the MM parameters to reproduce the saved QM/MM forces within a nonlinear optimization procedure. The merit function used in the optimization is:
| (8) |
where is the QM/MM atomic force vector of atom a in trajectory frame i and is the force vector produced by the MM Hamiltonian with the trial set of MM parameters p. All atoms, including MM solvent, contribute to the merit function. For the molecules in the solvation test set, the merit function uses the solvated simulation trajectories. For the T4 lysozyme ligand binding test set, the merit function uses the unbound/solvated simulation trajectories. One could perform the parameter optimization using the bound simulations; however, we chose to perform the optimizations using the unbound trajectories to make the procedure more consistent between the two test sets, and applicable to drug-like molecules for which binding to a specific target might not be known in advance.
The MM′ reference potentials considered in this work form a systematic progression in which MM bond, angle, dihedral and charge parameters form aggregate reference potential sets as follows:
The “b” model adjusts the solute/ligand bond force constants and equilibrium values, but leaves all other MM parameters unchanged.
The “ba” model adjusts the solute/ligand bond and angle force constants and equilibrium values, but leaves all other MM parameters unchanged.
The “bad” model adjusts the solute/ligand bond, angle, and dihedral force constants and the bond and angle equilibrium values, but leaves all other MM parameters unchanged.
The “badq” model adjusts the atomic charges, in addition to the parameters optimized within the “bad” model, under the constraint that the net-charge is preserved and equivalent-atom charges are maintained.
The GAFF force field chooses the MM parameters based upon atom-type assignment. That is, there are bond parameters of each pair of atom-types, angle parameters for each triplet of atom-types, and torsion parameters for each quadruplet of atom-types. For example, a 3-site water molecule consists of two atom types: “ow” for the oxygen and “hw” for each of the two hydrogens. There is only 1 set of bond parameters, corresponding to a ow-hw bond, and 1 set of angle parameters for the hw-ow-hw angle. The MM′ potential uses the same atom-type assignments as the GAFF force field – only the values of the parameters are allowed to change – therefore, the “b” MM′ model optimizes a total of 2 parameters for water: the force constant and equilibrium value of all ow-hw bonds.
The nonlinear optimization was performed using a custom python script that utilizes binding to the NLopt library.76 Trial parameters were successively chosen using the Constrained Optimization BY Linear Approximations (COBYLA) algorithm.77 The optimization script is provided the original MM (GAFF) parameter file, a list of parameters to optimize, a trajectory of atomic coordinates, and a corresponding trajectory of atomic forces evaluated with the QM/MM Hamiltonian (the in Eq. 8. At each step in the optimization procedure: 1. A new set of trial parameters are obtained from the COBYLA algorithm. 2. An Amber parameter file is written for the solvated system. 3. The SANDER program reads the parameter and coordinate trajectory files, re-evaluates the MM energy and forces for each trajectory frame (rather than performing dynamics) and writes the atomic forces to a file (the in Eq. 8). 4. The optimization script reads the new set of atomic forces from file and evaluates χ2 from Eq. 8. All parameters are allowed to change by 40% of their initial value. The “badq” model also changes the atomic charges within the nonlinear optimization procedure in a manner that is no different from any other optimization parameter with 2 exceptions: 1. Only the unique charges are optimized; that is, if two-or-more atoms share a common charge in the MM force field, then they will continue to share a common charge in the MM′ force field. 2. A constraint is placed on the optimization that maintains a fixed molecular charge. Finally, we emphasize that the optimization procedure evaluates the atomic forces of the entire system (including solvent) in the same manner as would be calculated during molecular dynamics. In contrast, the force-matching protocol used in some other works may only evaluate the forces of the solute in a vacuum environment, rather than the solvated system. In that case, one would not want to include the solute-solvent contributions within , as this would effectively doublecount the environment’s influence on the forces when it is applied to a condensed phase simulation. Technical advances in force matching procedures for force field development have been described in detail in several other seminal works.44-46,50,78-80
2.3. Simulation details
The solute and ligand molecule MM parameters were taken from the GAFF force field.81 The T4 lysozyme MM parameters are from the ff14SB protein force field.82 Water solvent molecules use the TIP4P-Ew model.83 The simulated T4 lysozyme structure has a net charge of 9+. This charge is counterbalanced by 16 Na+ and 25 Cl− ions chosen to achieve a 140 mM near-physiological salt concentration after neutralization. All QM calculations are performed with the PBE0/6-31G* hybrid density functional implemented within a development version of the SANDER molecular dynamics program.84 Condensed phase simulations are performed within a periodic truncated octahedron with at least 13 Å of solvent around all sides of the solute. Long-range electrostatics are evaluated with the Particle Mesh Ewald method with 10 Å real-space cutoffs and the reciprocal-space energy is evaluated with a 1 point/Å Fast Fourier Transform grid spacing, fourth order cubic B-spline interpolation, and tin-foil boundary conditions.85 A charge-canceling uniform background plasma correction was applied to those systems with a net charge.86,87 The condensed phase QM/MM simulations use the ambient potential composite Ewald method73 with the same cutoff and grid spacing. Nonbond interactions were explicitly computed within a 10 Å direct-space cutoff, and the LJ interactions beyond the cutoff were modeled with a long-range tail correction. All simulations are performed with a 1 fs timestep, and the SHAKE algorithm88 is used to remove hydrogen vibrations except the ligand or solute molecule that is (or will become) evaluated with the QM Hamiltonian. The condensed phase simulations were initially equilibrated with the MM Hamiltonian in the NPT ensemble (1 ATM pressure, 298K temperature) for 2 ns using the using the Berendsen barostat. After the initial equilibration of the density, all condensed phase simulations were performed in the NVT ensemble at 298 K using the Langevin thermostat (5 ps collision frequency).89 The gas-phase simulations are aperiodic, they use the weak-coupling algorithm90 to mantain a temperature of 298 K, and direct electrostatic evaluations are performed with a cutoff of 999 Å.
Free energy values are calculated from a series of simulations that propagate the dynamics using a λ-dependent potential energy:
| (9) |
where U(0) and U(1) are the potential energy functions of the initial and final states, respectively. The free energy simulations are performed using the single-coordinate dual-topology framework implemented with the Amber software; however, the MM→MM′ simulations could also be performed using the single-topology parameter interpolation approach.91 We use fixed values of λ that evenly divide the range [0,1]. The reference free energy values use a large number of λ simulations (the MM-calculated direct alchemical transformations use 12 λ values and the indirect stages of the MM→QM transformations each use 11 simulations). The latter was chosen such that we could examine subsets of 2, 3, and 6 evenly spaced λ windows with the same endpoints in order assess convergence with number of windows. The reference values are used to compare how the results differ when fewer λ values are considered. From these simulations, the free energy can be calculated from a variety of methods, discussed in the “Free energy analysis” section.
Additional simulation details are itemized below for specific energy terms. The listed simulation lengths are the total amount of sampling performed; the first half of each simulation is discarded as equilibration.
(in Eq. 3). This is performed in two stages. The first stage simulated 12 uniformly-spaced λ values in which the solute charges were set to zero. The second stage used a softcore Lennard-Jones potential in 12 uniformly-spaced λ values to transform the atoms into dummy particles consisting of only nonelectrostatic, nonbond energy terms. Each of these 24 simulations were run for 10 ns, and each 10 ns simulation was repeated 3 times, for an aggregate total of 720 ns of sampling. These simulations were run on a single GPU. The energies and dU/dλ were sampled every 1 ps, and the autocorrelation times of dU/dλ were found to typically range between 1 and 2 ps.
(in Eq. 3). This is performed in two stages, analogous to the description of , yielding 720 ns of aggregate sampling in the gas phase. These simulations were run on a single CPU core. The energies and dU/dλ were sampled every 1 ps, and the autocorrelation times of dU/dλ were found to typically range between 0 and 20 ps.
(in Eq. 2). This is performed in a single stage consisting of 11 uniformly-spaced windows, each run for 2 ns for an aggregate total of 22 ns of sampling. The simulations were performed on a single GPU. The energies and dU/dλ were sampled every 10 ps, and the autocorrelation times of dU/dλ were found to be less than 10 ps.
(in Eq. 2). This is performed in a single stage consisting of 11 uniformly-spaced windows, each run for 20 ns and repeated twice, for an aggregate total of 220 ns of gas phase sampling. These simulations were performed on a single CPU core. The energies and dU/dλ were sampled every 10 ps, and the autocorrelation times of dU/dλ were found to be less than 10 ps.
(in Eq. 2). This is performed in a single stage consisting of 11 uniformly-spaced windows, each run for 200 ps, for an aggregate total of 2.2 ns of sampling. Each simulation was performed on a 36-core node. A single core was reserved for evaluating the pure-MM energy and forces, and 35 of the cores were used to evaluate the ab initio QM/MM energy and forces. The energies and dU/dλ were sampled every 0.5 ps, and the autocorrelation times of dU/dλ were found to typically range between 0 and 1 ps.
(in Eq. 2). This is performed in a single stage consisting of 11 uniformly-spaced windows, each run for 200 ps, for an aggregate total of 2.2 ns of sampling. Each simulation was performed on a 36-core node. The energies and dU/dλ were sampled every 0.5 ps, and the autocorrelation times of dU/dλ were found to typically range between 0 and 2 ps.
(in Eq. 7) The relative ligand binding free energy simulations are performed in 3 stages which transform a benzene ligand to the target ligand. The first stage simulated 12 uniformly-spaced λ values to remove the atomic charges of those atoms present only in benzene, but not the target ligand. The second stage used a softcore Lennard-Jones potential to remove nonbonded, nonelectrostatic interactions of the “disappearing atoms” while simultaneously introducing the target ligand’s missing nonbonded, nonelectrostatic interactions. The atomic charges of those atoms common to the benzene and target ligand are also linearly-transformed in the second stage. The third stage reintroduces the atomic charges of the “appearing atoms”. Each of these 36 simulations was run for 2 ns, and each 2 ns simulation was repeated in 3 independent trials, yielding an aggregate total of 216 ns of sampling. The simulations were performed on a single GPU. The energies and dU/dλ were sampled every 20 ps, and the autocorrelation times of dU/dλ were found to typically range between 30 and 90 ps.
(in Eq. 7) The unbound ligand simulations were performed in the same manner as the bound-ligand simulations discussed above to produce 216 ns of aggregate sampling. The simulations were performed on a single GPU. The energies and dU/dλ were sampled every 20 ps, and the autocorrelation times of dU/dλ were found to be less than 20 ps.
and (in Eq. 5). These two terms are each performed using 11 uniformly-spaced windows simulated for 2 ns. Each term was sampled for an aggregate total of 22 ns, and each simulation was performed on a single GPU. The energies and dU/dλ were sampled every 10 ps, and the autocorrelation times of dU/dλ were found to be less than 10 ps.
and (in Eq. 5). These two terms are each performed using 11 uniformly-spaced windows simulated for 200 ps. Each term was sampled for an aggregate total of 2.2 ns, and each simulation was performed on a 36-core CPU node. The energies and dU/dλ were sampled every 0.5 ps, and the autocorrelation times of dU/dλ were found to be less than 0.5 ps.
2.4. Free energy analysis
The free energy analysis was performed using the alchemical-analysis program.92 The alchemical-analysis program makes use of the pymbar library, which implements time-series algorithms93 and various free energy analysis methods, including exponential averaging (the Zwanzig relationship51), Bennett acceptance ratio70,94 (BAR), multistate Bennett acceptance ratio95 (MBAR), and thermodynamic integration (TI) methods using either the trapezoidal rule or cubic spline integration.96 To perform the TI calculation, the mean value of ∂U(λ)/∂λ is calculated for each λ-state, and the autocorrelation time is used to prune the data into statistically independent samples for estimating the standard error. The energy of the λ = 0 and λ = 1 states are printed in the output files; therefore, the required derivative is easily calculated. The exponential averaging, BAR, and MBAR analysis require the energies of the λ-states, which are also readily available. The exponential averaging method can be performed in two directions, yielding two results that are referred to as DEXP and IEXP. The “D” and “I” are suggestive of processes that that delete or insert atoms in an alchemical transformation, respectively; however, in the present context, they merely assign a direction in which the data is analyzed. Specifically, the IEXP method uses the distribution sampled at λi and evaluates the energies at λi and λi−1, whereas the DEXP requires the energies at λi and λi+1. For the MM′→QM transformation, the λ=0 and 1 states correspond to the MM′/MM and QM/MM potentials, respectively. The BAR method requires energy evaluations from adjacent neighbors λi−1, λi, and λi+1. The MBAR method further uses the energies from all λ-states.
We calculated the MM′→QM transformations using 11 λ-states, each simulated for 200 ps. As will be shown below, this degree of λ and time sampling are very highly converged, and we have chosen it to enable clean comparisons and analysis. For example, 11 equally spaced λ windows as reference also allows comparison of 2, 3 and 6 intermediate λ windows by taking subsets of the reference data. From the 200 ps of total sampling, 100 ps is discarded as equilibration and the last 100 ps is analyzed. The large number of intermediate states used to calculate the reference free energy values resulted in nearly identical results between TI, BAR, and MBAR. We use the TI results as high-level reference values in the remainder of the paper.
3. Results and Discussion
Here we present benchmark reference results for a set of absolute solvation free energies and relative ligand binding free energies in order to investigate MM′→QM transformations using different reference potentials, methods and procedures. In particular, this study sets out to answer the following questions: 1. How linear are the MM′→QM transformations (in terms of dU/dλ profile) as a function reference potential? 2. How do the TI, BAR, DEXP, and IEXP methods perform when fewer λ-states are used? 3. How do the methods compare to the reference values when less sampling is used? 4. Does the use of reference potentials for MM′ intermediate states improve the accuracy of the MM→QM transformation, and which reference potential is best? 5. How does the accuracy of fast “1-state” and moderately fast “2-state” approaches compare? 6. How does the performance of fast “1-state” and moderately fast “2-state” approaches compare? We designate a “1-state” simulation approach to involve simulation at only one end-state (here, the λ=0 MM/MM or MM′/MM state), and free energy analysis using the Zwanzig equation that involves evaluation of ΔU = U1 − U0. A “2-state” simulation approach, on the other hand requires simulations at both end-states.
Toward this end, we have organized this section as follows. In the first subsection, we evaluate the linearity of the thermodynamic integration profiles for MM′→QM transformations using different reference potentials in order to gain insight that will be valuable in developing robust, efficient methods. In the second subsection, we examine the convergence of the MM′→QM transformation for solvation and relative ligand binding free energies with respect to number of λ windows and sampling. In the third subsection, we analyze phase space overlap of ΔU(λ) distributions from end-state simulations as a function of reference potential to better understand the origin of observed errors. In the fourth subsection, we examine the use of the indirect method with a force-matched reference potential analyzed with Bennett’s acceptance ratio for calculating free energies. For brevity, we refer to this as the BAR Book-ending to QM (BBQm) method, and we compare its accuracy to fast “1-state” approaches, designated “EA”, that use the Zwanzig equation to perform exponential averaging based only on MD trajectories using pure MM potentials. Finally, in the fifth subsection, we gauge the perforance of the BBQm and 1-state EA methods.
3.1. Linearity of the thermodynamic integration profiles for MM′→QM transformations
The goal of this paper is to examine the convergence properties of QM/MM alchemical free energy methods, and ultimately develop a procedure for robust and accurate MM′→QM transformations that requires minimal sampling involving evaluation of the expensive QM/MM potentials. To motivate design of such a method, it is important to understand the nature of the transformation itself, and in particular, the linearity of the ⟨∂U/∂λ⟩λ thermodynamic integration profiles for MM′→QM transformations using different MM′ reference potentials. The more linear the ⟨∂U/∂λ⟩λ profiles, the better justified thermodynamic integration becomes when only the end-point states, or simply “end-states” (λ=0 or 1), are sampled because the numerical integration of the profile (approximated as a line) is then accurate.
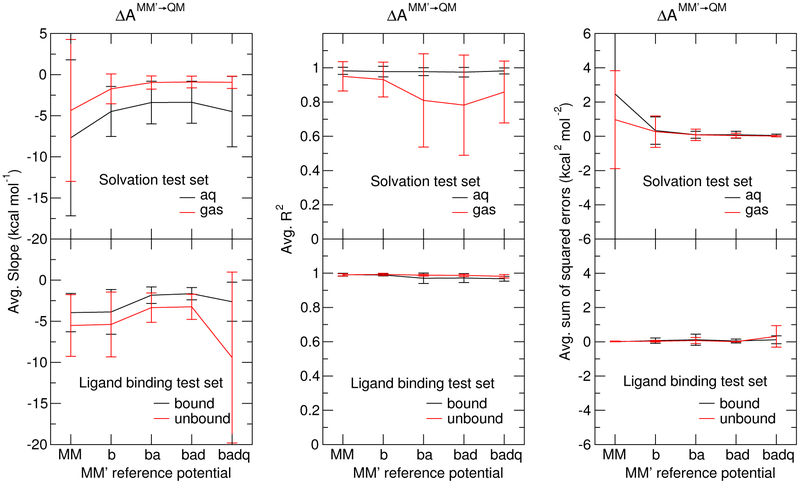
Figure 3 compares the average slopes, R2 coefficient of determination, and sum of squared errors produced from linear regressions of the ⟨∂U/∂λ⟩λ profile generated from 11 λ-state simulations for each MM′→QM transformation. The vertical bars are the standard deviations. For each MM′→QM transformation, we fit the 11 ⟨∂U/∂λ⟩λi values (corresponding to each λi window, i = 1, ⋯ 11) to a line, and the sum of squared errors (⟨err2⟩) is:
Figure 3:
Analysis of linearity of the ⟨∂U/∂λ⟩λi profiles for reference simulations using 11 λ windows (λi = 1, ⋯ 11). Average slopes, squared linear correlation coefficients, or coefficients of determination (R2), and sum of squares deviations from linear regression of the ⟨∂U/∂λ⟩λi profiles are shown for the unmodified MM potential, and intermediate MM′ reference potentials using both the solvation test set (top) and T4 lysozyme ligand binding test set (bottom).
| (10) |
where y(λi) is the value of the line at λi.
Figure 3 illustrates that the MM′→QM ∂U/∂λ profiles examined in this work are quite linear. The linearity of the profiles is best expressed by how close the R2 coefficients are to unity. The largest deviations of R2 from unity occur for the gas phase transformations performed in the solvation test set using the “ba”, “bad”, and “badq” MM′ parameters; however, linear fits of these profiles have a slope very close to zero, which artifically amplifies the apparent randomness of the data. In fact, it is precisely these transformations that have some of the smallest sum of squared errors. If the MM′ and QM models produced the same ensemble distributions, then the ∂U/∂λ profiles would be a line with zero slope. The slopes shown in Figure 3 become more linear from MM to “b” and “ba”; however, no improvement to the slope is made in going to “bad” nor “badq”.
These results suggest that the MM′→QM transformations are all highly linear and there is, at best, limited improvement in the linearity going beyond the “ba” reference potential. This observation is probably due to the small size of the molecules, which lack a high degree of torsional flexibility. This motivates us to explore the convergence of faster approaches that require less sampling with the expensive QM/MM potentials in order to inform the design of an optimal method.
3.2. Convergence of the MM′→QM transformation for solvation and relative ligand binding free energies with respect to number of λ windows and sampling
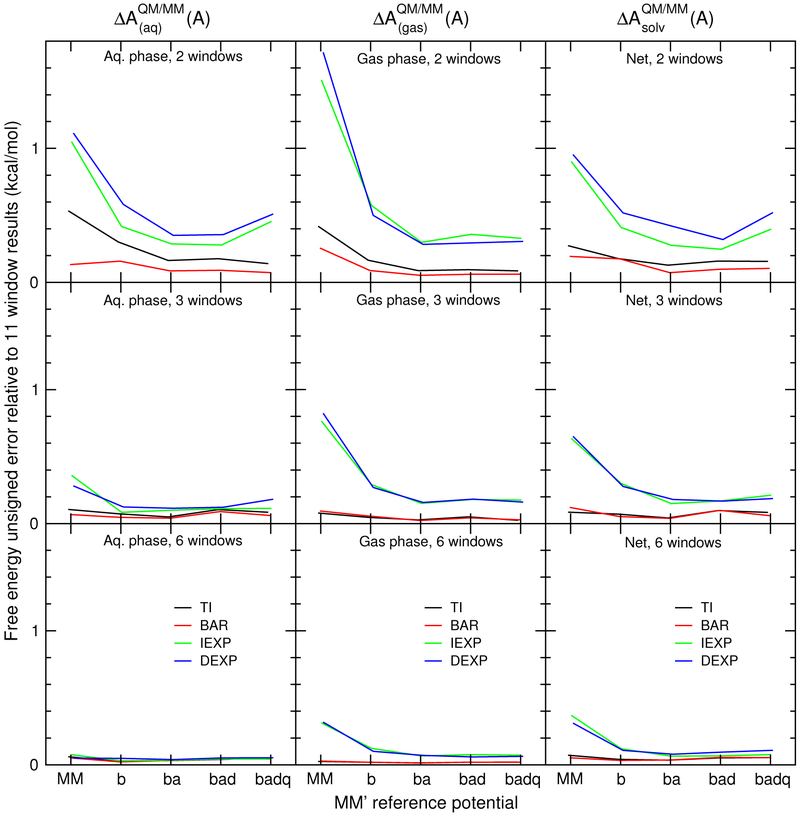
Figure 4 summarizes the MM′ →QM transformation errors of in the free energy estimates for the 17 molecules in the solvation test set as a function of the number of λ windows using 200 ps of sampling per window. The figure compares the solvation free energy mean signed errors between the TI, BAR, DEXP, and IEXP methods for each MM′ reference potential, relative to the reference TI results. The vertical bars are standard deviations. The left, center, and right columns are errors in , , and , respectively. The top row of plots evaluate the free energy using only the λ = 0 and λ = 1 states; that is, the BAR and TI methods use the two end-state simulations, the DEXP method evaluates Zwanzig’s equation using the λ = 1 simulation, and the IEXP method evaluated Zwanzig’s equation using the λ = 0 simulation. The middle row of plots perform the analysis with the λ = (0, 0.5, 1) states. The bottom row of plots compute the free energy using the λ = (0, 0.2, 0.4, 0.6, 0.8, 1) states.
Figure 4:
The solvation free energy mean unsigned errors of the MM→QM transformations using different analysis methods and MM′ intermediate Hamiltonian states. See Supporting Information for corresponding plot of mean signed errors.
On average, one observes improvement of aqueous and gas phase MM′→QM transformation free energies in going from MM to “ba”, but little to no improvement is made by further optimizing the dihedral force constants and atomic charges (i.e., to “bad” and “badq” reference potentials). We suspect that optimization of the dihedral force constants would make a larger impact if the solvation test contained molecules that exhibited larger conformational flexibility. The mean errors produced by Zwanzig’s equation (IEXP and DEXP) in solvent and gas phases are demonstrably worse than the BAR and TI errors; however, these errors cancel such that the net error is much closer to zero, on average. The standard deviation of the IEXP and DEXP net errors are approximately twice as large as TI or BAR. Because the IEXP and DEXP net errors rely on a precarious balance of the solvated and gas phase errors, one does not observe a systematic decrease in their mean errors within the series Nλ = 2, 3, and 6; however, increasing the number of intermediate simulations decreases the standard deviation of the errors.
The MM′→QM free energy values produced by the TI and BAR methods, on the other hand, are quite accurate for the solvation test set, even when only the end-state simulations are used for the analysis. Rather than significantly reducing the mean signed errors, which are already very small, the parametrized MM′ reference potentials act to reduce the standard deviation of errors. For example, the standard deviation of the net free energy corrections using the MM model and BAR analysis is 0.40 kcal/mol, whereas simulations using the “ba” model reduce the standard deviations to 0.11 kcal/mol. Increasing the number of windows further decreases the standard deviations; with 3 windows, the MM and “ba” net free energy correction standard deviations are 0.20 and 0.05 kcal/mol, respectively.
Overall, the use of the reference potentials improves the errors going from MM (no reference potential) to “b” and “ba”, but limited if any further improvement in going to “bad” and “badq” reference potentials. These results suggest that – for the molecules within the solvation test set – the “ba” reference potential, together with TI or BAR, are highly accurate using 200 ps of sampling per window, and motivates us to compare the convergence of the errors for the “ba” reference potential (relative to MM with no reference potential) as a function of simlation time.
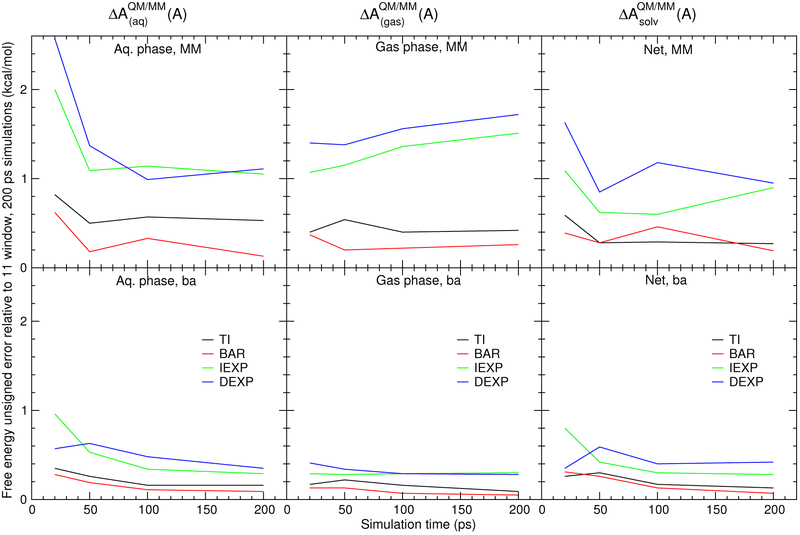
Figure 5 compares the solvation free energy mean signed errors of the MM′→QM transformations for the TI, BAR, DEXP, and IEXP methods as a function of simulation time for MM and the “ba” reference potential. These results were computed using the most computationally cost-effective “2-window” end-state simulations (λ=0 and/or 1). The vertical bars are standard deviations. The left, center, and right plots are errors in , , and , respectively. The top row is the direct MM→QM transformation, and the bottom row is the ba→QM transformation. For each analysis, we exclude the first half of the simulation as equilibration; for example, the 200 ps simulation results only analyze the last 100 ps of data.
Figure 5:
Convergence of the solvation free energy mean unsigned errors of the MM→QM transformations for 2 λ window (i.e., end-state only) simulations as a function of simulation time in ps. In each case, the first half of the simulations were considered as “equilibration” and the second half considered as “production” and used for statistical data collection. See Supporting Information for corresponding plot of mean signed errors.
The TI and BAR results are markedly more accurate than the IEXP and DEXP results, and are considerably improved with the use of the “ba” reference potential. The mean signed errors for all the reference potential and analysis methods do not significantly change after 50-100 ps of sampling. Furthermore, the standard deviations do not decrease when the simulations are extended to 200 ps. This is suggestive that computational resources could be better utilized by repeating many, short simulations from different starting positions rather than performing extended sampling of a single simulation, as is done here.61,62
Table 1 lists the mean signed and unsigned errors of BAR analysis for the ligand binding free energies. The errors are shown for the MM→QM and ba→QM transformations evaluated with 2, 3, or 6 evenly spaced λ-states and as a function of simulation time. The rows labeled L∙P, L+P, and net correspond to errors in , , and , respectively. For each analysis, we exclude the first half of the simulation as equilibration.
Table 1:
Mean signed and unsigned errors of the MM→QM and ba→QM ligand binding free energies computed from BAR, relative to the 11 λ-state reference TI calculations.
| MM |
ba |
||||||
|---|---|---|---|---|---|---|---|
| Env. | Time | Nλ =2 | Nλ =3 | Nλ =6 | Nλ =2 | Nλ =3 | Nλ =6 |
| Mean signed errors (kcal/mol) | |||||||
| L∙P | 200 ps | −0.03 ± 0.08 | −0.02 ± 0.08 | −0.04 ± 0.03 | 0.01 ± 0.08 | −0.00 ± 0.07 | −0.02 ± 0.03 |
| 100 ps | −0.05 ± 0.15 | −0.03 ± 0.12 | −0.03 ± 0.03 | −0.06 ± 0.09 | −0.02 ± 0.06 | −0.02 ± 0.06 | |
| 50 ps | −0.06 ± 0.17 | −0.11 ± 0.18 | −0.05 ± 0.11 | 0.02 ± 0.17 | −0.01 ± 0.10 | −0.00 ± 0.10 | |
| 20 ps | 0.04 ± 0.39 | 0.03 ± 0.32 | 0.08 ± 0.20 | −0.04 ± 0.23 | −0.03 ± 0.20 | −0.00 ± 0.18 | |
| L+P | 200 ps | 0.00 ± 0.25 | −0.10 ± 0.13 | −0.03 ± 0.11 | −0.00 ± 0.12 | 0.02 ± 0.09 | −0.02 ± 0.05 |
| 100 ps | −0.04 ± 0.16 | −0.02 ± 0.13 | 0.01 ± 0.08 | 0.06 ± 0.10 | 0.09 ± 0.16 | 0.05 ± 0.10 | |
| 50 ps | 0.13 ± 0.42 | 0.03 ± 0.25 | 0.05 ± 0.13 | 0.11 ± 0.36 | 0.10 ± 0.22 | 0.04 ± 0.15 | |
| 20 ps | −0.07 ± 0.67 | −0.11 ± 0.32 | −0.10 ± 0.14 | −0.02 ± 0.42 | 0.24 ± 0.43 | −0.08 ± 0.34 | |
| Net | 200 ps | −0.03 ± 0.25 | 0.08 ± 0.17 | −0.00 ± 0.10 | 0.02 ± 0.14 | −0.02 ± 0.11 | 0.01 ± 0.05 |
| 100 ps | −0.00 ± 0.14 | −0.01 ± 0.11 | −0.05 ± 0.06 | −0.11 ± 0.17 | −0.11 ± 0.19 | −0.07 ± 0.11 | |
| 50 ps | −0.19 ± 0.47 | −0.15 ± 0.37 | −0.10 ± 0.16 | −0.09 ± 0.47 | −0.11 ± 0.30 | −0.05 ± 0.23 | |
| 20 ps | 0.11 ± 0.75 | 0.14 ± 0.51 | 0.18 ± 0.23 | −0.01 ± 0.60 | −0.27 ± 0.54 | 0.08 ± 0.47 | |
| Mean unsigned errors (kcal/mol) | |||||||
| L∙P | 200 ps | 0.05 ± 0.08 | 0.06 ± 0.05 | 0.04 ± 0.03 | 0.06 ± 0.05 | 0.06 ± 0.03 | 0.03 ± 0.02 |
| 100 ps | 0.13 ± 0.09 | 0.09 ± 0.08 | 0.04 ± 0.03 | 0.09 ± 0.06 | 0.04 ± 0.04 | 0.05 ± 0.04 | |
| 50 ps | 0.12 ± 0.13 | 0.15 ± 0.15 | 0.09 ± 0.06 | 0.12 ± 0.10 | 0.06 ± 0.07 | 0.08 ± 0.06 | |
| 20 ps | 0.31 ± 0.21 | 0.26 ± 0.16 | 0.16 ± 0.13 | 0.17 ± 0.14 | 0.14 ± 0.14 | 0.13 ± 0.11 | |
| L+P | 200 ps | 0.15 ± 0.19 | 0.10 ± 0.13 | 0.08 ± 0.08 | 0.09 ± 0.08 | 0.07 ± 0.05 | 0.03 ± 0.04 |
| 100 ps | 0.13 ± 0.09 | 0.10 ± 0.09 | 0.06 ± 0.04 | 0.09 ± 0.07 | 0.14 ± 0.11 | 0.08 ± 0.07 | |
| 50 ps | 0.32 ± 0.29 | 0.22 ± 0.11 | 0.10 ± 0.09 | 0.28 ± 0.24 | 0.16 ± 0.18 | 0.12 ± 0.09 | |
| 20 ps | 0.53 ± 0.36 | 0.28 ± 0.16 | 0.14 ± 0.09 | 0.35 ± 0.19 | 0.39 ± 0.28 | 0.31 ± 0.13 | |
| Net | 200 ps | 0.15 ± 0.19 | 0.11 ± 0.15 | 0.08 ± 0.06 | 0.11 ± 0.08 | 0.10 ± 0.05 | 0.03 ± 0.05 |
| 100 ps | 0.10 ± 0.08 | 0.09 ± 0.06 | 0.06 ± 0.05 | 0.15 ± 0.12 | 0.17 ± 0.13 | 0.10 ± 0.08 | |
| 50 ps | 0.38 ± 0.31 | 0.25 ± 0.30 | 0.13 ± 0.13 | 0.29 ± 0.36 | 0.19 ± 0.25 | 0.14 ± 0.18 | |
| 20 ps | 0.63 ± 0.35 | 0.39 ± 0.33 | 0.23 ± 0.18 | 0.47 ± 0.33 | 0.49 ± 0.32 | 0.43 ± 0.14 | |
The mean signed errors produced by BAR are quite small for both reference potentials, irrespective of simulation time (20 ps versus 200 ps) or the number of simulated states (Nλ = 2 or Nλ = 6). Like the solvation free energy test set, the net free energy signed error standard deviations decrease when the number of simulated states increases from Nλ = 2 to Nλ = 3 and Nλ = 6. The net free energy mean unsigned errors generally decrease from 0.4 to 0.1 kcal/mol as the length of the simulation is increased from 20 ps to 200 ps; however, the benefit of using the “ba” reference potential is not as apparent for the T4 lysozyme ligand binding test set than it was for the set of solvation free energy calculations.
The aggregate results up to this point suggest that TI and BAR results are very accurate even using only end-state simulations, particularly with the use of reference potentials. On the other hand, the IEXP and DEXP methods, have large errors using only end-state simulations that can be only modestly improved by use of the reference potentials. This is an important negative result to report, as the IEXP and DEXP methods with 2 windows require an actual simulation at only one end-state state, and thus are designated as “1-state” approaches, which could be made highly efficient if simulation with the expensive QM/MM potentials could be avoided completely. Hence, before proceeding further, we strive to gain some insight as to the origin of the accuracy of the TI/BAR versus IEXP/DEXP methods and their dependence on reference potential in the context of phase space overlap.
3.3. Analysis of phase space overlap of ΔU(λ) distributions from end-state simulations as a function of reference potential
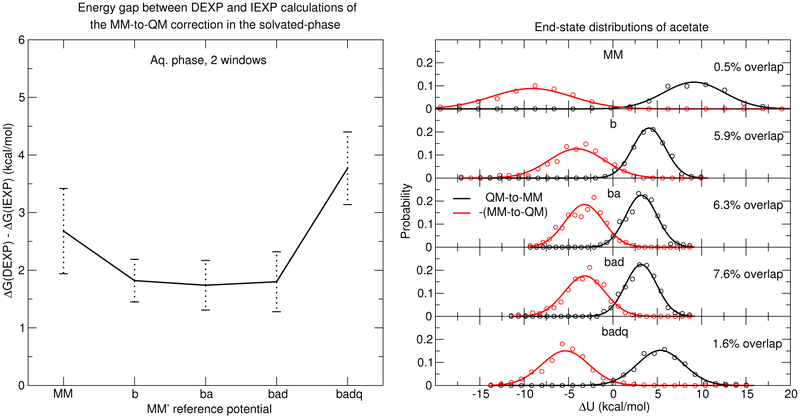
Here we examine the phase space overlap between end-states, as measured by the probability distribution of ΔU(λ) values.53 This overlap is a means of establishing similarity of the trajectories of the end-states. Figure 6 uses the acetate molecule as a representative example to compare the discrepancy between the DEXP and IEXP free energy calculations and end-state energy distribution overlap for the MM→QM transformation of acetate in solution.
Figure 6:
Left: Free energy gap between DEXP and IEXP. Right: Energy-difference histograms of the MM→QM transformations of acetate in aqueous environments.
The overlap of the end-state distributions are constructed by generating histograms of potential energy differences between the two states. Dynamics are performed with the QM/MM Hamiltonian, the MM and QM/MM energies are evaluated, and the difference ΔU = UMM − UQM/MM is histogrammed (the black circles in Figure 6). An analogous histogram of energy differences is made by analyzing the frames of the MM trajectory (the red circles in Figure 6). The distributions are well approximated by Gaussian functions, which are the solid lines in Figure 6. The Gaussian representation of the ΔU distribution generated by the QM/MM trajectory is
| (11) |
where μQM/MM is the mean ΔU value, the exponent is , and σQM/MM is the standard deviation of ΔU values. The Gaussian representation from the MM trajectory is written analogously. We measure the “percent overlap” between the two distributions according to Eq. 12
| (12) |
where ⟨u, ν⟩ = ʃ u(x)ν(x)dx is an inner-product. Equation 12 is maximum (with a value of 100) when the two distributions have the same mean and standard deviation. The distributions shown in Figure 6 have been translated along the ΔU axis such that ΔU = 0 is the midpoint between the two distribution means.
The percent overlap of the distributions in Figure 6 increase when the reference potential is changed from MM to “b”, “ba”, and “bad”; however, the “badq” model lowers the overlap relative to “bad”. The difference between the DEXP and IEXP estimates of the free energy similarly decrease by changing the reference potential from MM to “b”, “ba”, and “bad”, but the “badq” model increases the error relative to “bad”.
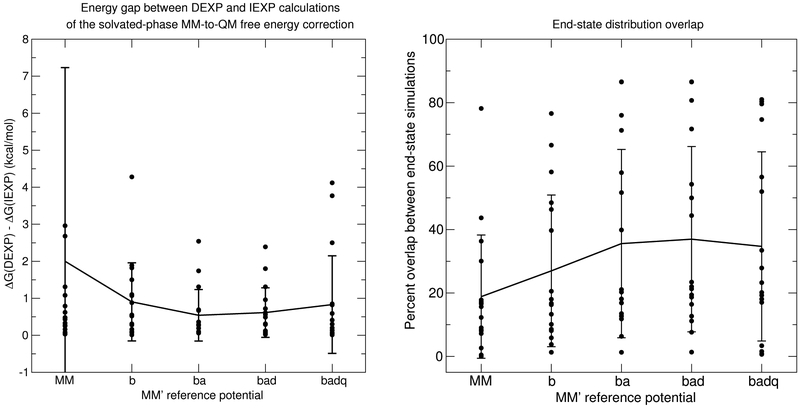
Figure 7 illustrates the behavior of the end-state overlaps (Eq. 12) for the entire solvation test set as a function of reference potential. Figure 7 similarly shows the average free energy gap between the DEXP and IEXP free energy calculations. There are 17 black circles for each reference potential, which correspond to the 17 small molecules in aqueous phase. The solid line and vertical bars are the mean and standard deviations. The trend of the overlaps with respect to reference potential are similar to that of the acetate molecule in that overlap is minimal for the MM model (no reference potential) and maximum for “ba” and “bad” reference potentials. The difference between the DEXP and IEXP calculations closely follow the inverse-correlation trend of mean percent overlap between the two end-states. Kofke and collaborators have developed other descriptors of phase space overlap between two states A and B.97-103 We shall focus on two metrics that Wu and Kofke have devised.101,102 The first is based on the overlap of total energy distributions:
Figure 7:
Left: Average gaps between DEXP and IEXP for the solvated-phase MM-to-QM free energy calculations. Right: End-state distribution overlaps in the aqueous phase. The circles are individual data points. The solid line traces the mean, and the vertical bar is the standard deviation.
| (13) |
where pAA(U) and pBA(U) are the probability distributions of state A energies observed within the simulations of state A and B, respectively. The expression for KAB is similarly written. The value of KBA varies from 0 to 2 and is an indicator of an offset of pBA(U) relative to pAA(U). That is, if pBA(U) is centered left (the negative U direction) of pAA(U), then 1 < KBA ≤ 2, and if pBA(U) is centered right of pAA(U), then 0 ≤ KBA < 1. In the present work, states A and B are the MM′ and QM/MM models, respectively, and we numerically evaluate KBA and KAB upon fitting the observed potential energies to Gaussian distributions. The integration was performed using SciPy’s “quad” function to numerically approximate the integral with a precision of 10−10.104 The second metric is based on the idea of relative entropy, which is related to the transformation’s dissipated work.101,102 The relative entropies can be used to define measures that indicate whether the sampling between the two states is adequate:
| (14) |
where N is the number of samples, WL(x) is the Lambert W function, and
| (15) |
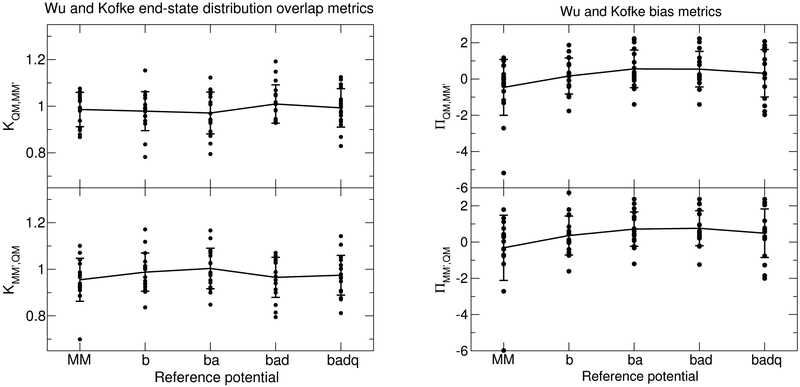
The expressions for ΠB,A and sB are written similarly. The energy difference UB − UA within Eq. 15 can be replaced by the work required to transform state A to B wA→B if Jarzynski’s equation is used in nonequilibrium work simulations. Wu and Kofke proposed the heuristic ΠA,B > 0 as indicating the presence of sufficient sampling for an accurate free energy evaluation. As pointed out by Boresch and Lee Woodcock,53 the rigorousness of the criteria can be questioned when it is applied to real world data, which often does not satisfy the implicit conditions assumed within the metric’s formulation. The Π metric assumes the observed phase spaces between the forward and reverse directions are subsets of one another but, in practice, only a partial overlap relation is often fulfilled. We evaluated the K and Π metrics for the end-states of and summarize the results in Figure 8.
Figure 8:
Left: Wu and Kofke overlap metrics between the end-states of . Right: Wu and Kofke Π metrics. Each dot corresponds to one of the molecules in the solvation test set. The line passes through the mean value. The vertical bars are the standard deviation.
The Wu and Kofke overlap metrics are very close to unity and exhibit anticorrelation between KMM′,QM and KQM,MM′. The overlap metric based on the energy difference ΔU (Eq. 12) appears to be a better qualitative indicator of the trend of energy gaps between the DEXP and IEXP estimates of the free energy correction. The ΠMM′,QM and ΠQM,MM′ bias metrics are very similar to each other and its mean value mimics the differences in the DEXP and IEXP energy gaps shown in Figure 7 That is, the Π values are largest for the “ba” and “bad” models and the energy gaps are smallest for those models as well.
At this stage it is clear that the IEXP and DEXP methods alone are not easily made accurate unless many λ windows are used. For end-state-only approaches, the IEXP and DEXP methods are not very accurate, and can be only modestly improved by use of reference potentials. The TI and BAR methods, on the other hand, are both accurate even in the absence of an ad hoc reference potential due mainly to the linearity of the thermodynamic integration profile, and can be made highly accurate with the use of reference potentials (particularly the “ba” reference potential) that increase the phase space overlap between end-state distributions. These results provide the foundation from which we propose a robust, accurate method for MM′→QM free energy transformations.
3.4. BAR Book-ending to QM (BBQm) method for robust, accurate MM′→QM free energy transformations
Here we consider two efficient end-state approaches for MM′→QM free energy transformations, and compare their accuracy for solvation free energies and relative ligand binding energies. As described previously, the λ=0 state will be the full MM/MM or MM′/MM state with energy U0, and the λ=1 state will be the full QM/MM state with energy U1.
Simulations for a λ state require energy and force evaluations at very short time step intervals (typically every 1 fs, as in the present work) in order to propagate the equations of motion. Once the simulation is performed, only the statistically independent samples from the trajectory need be revisited for calculating the relavant average, ⟨e−βΔU⟩, to obtain a free energy estimate. That is, a 1-state approach is most efficient, as it requires a molecular simulation only for the fast MM/MM or MM′/MM end-state models. On the other hand, a “2-state” approach requires molecular simulations at both the λ=0 (fast MM/MM or MM′/MM end-state models) and λ=1 (slow QM/MM end-state model). However, if a simulation at the λ=1 QM/MM end-state is performed, the trajectory data from the simulation can be used to develop an optimized “ba” reference potential using the force matching scheme described above to improve phase space overlap and accuracy in the MM′→QM free energy transformation. The additional MM→MM′ free energy component is trivial to conduct. In light of these consideation, we examine the accuracy of “1-state” and “2-state” approaches, both with and without the “ba” reference potential as follows:
EA - A “1-state” approach whereby simulations are performed at only the λ=0 (MM/MM) state, and the Zwanzig equation is used to determine the free energy. The unmodified MM potential (GAFF) is used as the reference potential.
EA* - Identical to EA, except the “ba” reference potential is used.
BBQm - A “2-state” approach whereby simulations are performed at both the λ=0 (MM/MM) and λ=1 (QM/MM) states, and the BAR method is used to determine the free energy. The unmodified MM potential (GAFF) is used as the reference potential.
BBQm* - Identical to BBQm, except the “ba” reference potential is used.
As will be demonstrated in the next section, the “1-state” approaches are more efficient than the “2-state” approaches, but as we show in this section, are not always accurate. Also note that we consider a “1-state” approach using the “ba” reference potential, which may seem paradoxical as this reference potential required optimization with respect to a QM/MM simulation at the λ=1 end-state. We did this in order to explore the degree to which such a reference potential might improve the accuracy of the “1-state” approach, and if this appeared promising, it might motivate the development of a transferable reference potential that did not require an explicit QM/MM simulation.
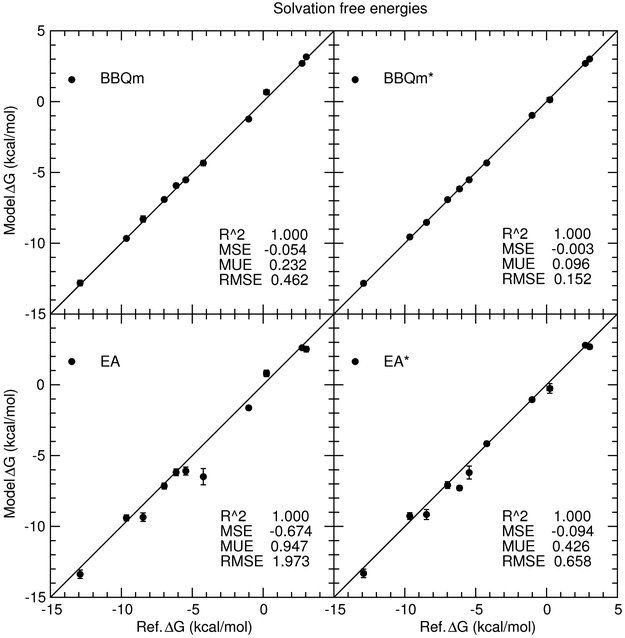
Figure 9 compares the accuracy of the absolute solvation free energies between the 1-state EA/EA* and 2-state BBQm/BBQm* approaches. The reference values are calculated from pure-MM simulations with our best estimates of the MM→QM corrections. Our best estimate of the MM→QM corrections are the average of the 5 values corresponding to the estimates made by the 5 reference potentials (MM, “b”, “ba”, “bad”, and “badq”), each simulated at 11 λ values for 200 ps and analyzed with TI. That is, we calculated (Eq. 2) and (Eq. 5) five times. The calculation of the 5 values differ only by the free energy pathway. The pathways differ by which MM′ is used as an intermediate state. The free energy value is pathway independent, however, so our best (most unbiased) estimate of the free energy correction is the average of our 5 calculated values. The predicted solvation free energies are based on the same pure-MM simulations as the reference values, but different procedures are used for calculating the MM′→QM correction as described above. Figure 10 differs from Figure 9 only by removing the pure-MM component of the calculations, such that the plot shows the predicted MM→QM corrections versus the reference MM→QM corrections. The vertical and horizontel bars in Figs. 9-10 are the standard errors of the model and reference free energy values, respectively.
Figure 9:
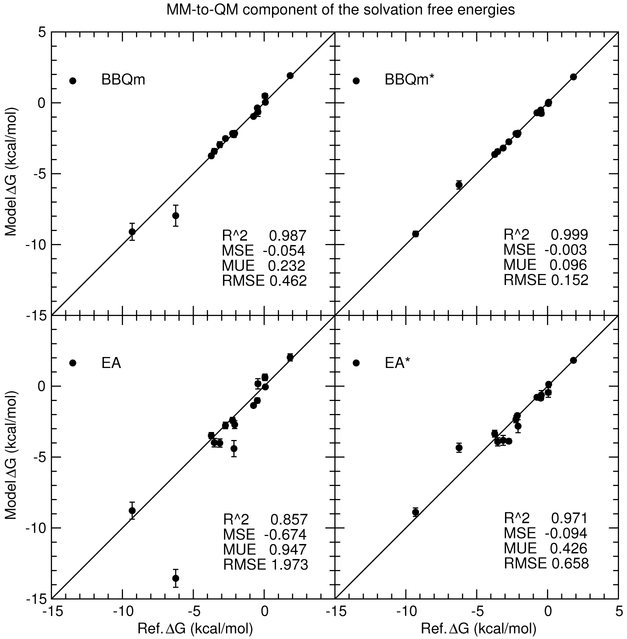
Predicted solvation energies versus reference values for 1-state EA/EA* and 2-state BBQm/BBQm* methods. These methods use either GAFF (EA/BBQm) or “ba” (EA*/BBQm*) as a reference potential. Only the neutral molecule solvation free energies can be viewed on the scale being shown, but the coefficient of determination (R2) and mean signed, unsigned and root-mean-square errors correspond to the entire solvation test set including the ions not shown in the figure.
Figure 10:
Predicted MM→QM corrections to the MM solvation energies versus reference values for 1-state EA/EA* and 2-state BBQm/BBQm* methods. These methods use either GAFF (EA/BBQm) or “ba” (EA*/BBQm*) as a reference potential. Data for the entire solvation test set (including ions) are shown.
Comparing the accuracy of the absolute solvation free energy values (Figure 9), the EA mean unsigned error is 0.95 kcal/mol improves to 0.43 kcal/mol when the ba reference potential is used. The BBQm mean unsigned error, on the other hand, is 0.23 kcal/mol and is reduced to 0.10 kcal/mol for BBQm*. In other words, the “ba” reference potential significantly improves the EA estimate, but the EA* errors continue to be far worse than the BBQm and BBQm* results. The coefficient of determination (R2 values are very close to unity in all cases because the absolute solvation free energy of the ions (not shown on the scale of the figure) are reasonably well accounted for by the underlying pure-MM contribution to the free energy. Figure 10 removes the pure-MM contribution to the reference and model free energies; it more clearly shows the correlation between the model and reference MM→QM corrections for all data in the solvation energy test set. The highest coefficient of determination occurs for BBQm* with the “ba” reference potential (R2 = 0.999). The EA and EA* coefficients of determination are considerably lower (0.857 and 0.971, respectively).
We now turn our attention to analysis of the accuracy of relative ligand binding free energy values for the T4 lysozyme ligand binding test set (Figure 2). These transformations require consideration of not only unbound ligands in a homogeneous aqueous environment, but also bound ligands in the heterogeneous environment of a solvated protein (T4 lysozyme).
Figure 11 compares predicted relative ligand binding free energies for the 1-state EA/EA* and 2-state BBQm/BBQm* approaches to reference values; that is, ΔΔA(lig) = ΔA(lig) − ΔA(BNZ). The reference values are calculated from pure-MM simulations with our best estimates of the MM→QM corrections. The predicted free energies are based on the same pure-MM simulations as the reference values, but different procedures for calculating the MM′→QM correction are used, as described above. Figure 12 differs from Figure 11 only by removing the pure-MM component of the calculations, such that the plot shows the predicted MM→QM corrections versus the reference MM→QM corrections. The vertical and horizontel bars in Figs. 11-12 are the standard errors of the model and reference free energy values, respectively.
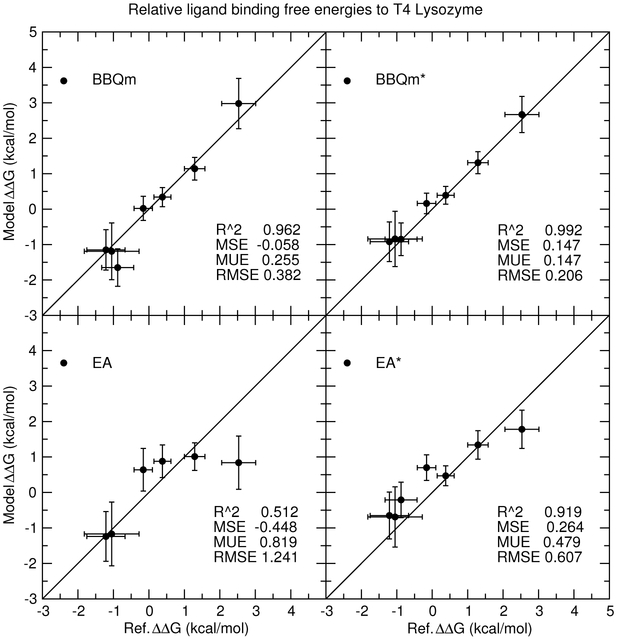
Figure 11:
Predicted relative ligand binding free energies versus reference values for 1-state EA/EA* and 2-state BBQm/BBQm* methods. These methods use either GAFF (EA/BBQm) or “ba” (EA*/BBQm*) as a reference potential. The free energy values are relative to benzene.
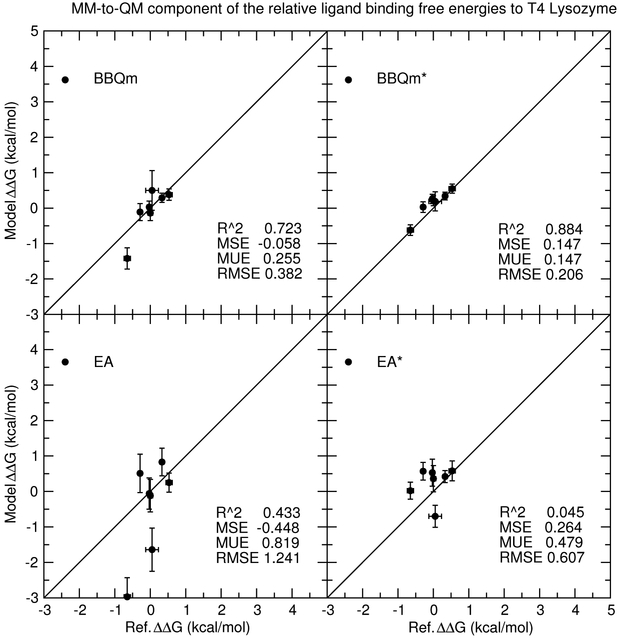
Figure 12:
Predicted MM→QM corrections to the ligand binding relative free energy differences versus reference values for 1-state EA/EA* and 2-state BBQm/BBQm* methods. These methods use either GAFF (EA/BBQm) or “ba” (EA*/BBQm*) as a reference potential. The free energy values are relative to benzene.
The comparison of the relative ligand binding free energy errors yield similar results to those made above for the solvation free energy test set. Specifically, the EA* errors are approximately half of the EA errors, the BBQm errors are nearly half the size as the EA* errors, and the BBQm* errors are nearly half those of BBQm. The use of a “ba” reference potential significantly improves both “1-state” and “2-state” methods. The ligands are structurally similar to one another; they are all beznene-like structures with little-to-no polarity, and most of them lack signficant conformational flexibility. It is not surprising that their ligand binding free energies are all within 4 kcal/mol of each other. This is in contrast to the range of solvation free energies, which considered polar and nonpolar molecules and even some charged ions. The challenge often encountered in ligand binding applications is not necessarily to estimate the binding free energies in lieu of experiment, but to simply rank the ligands from strongest to weakest binding. In this respect, we are particularly interested in whether the 1- and 2-state analysis methods are well-correlated with the reference calculations. The coefficient of determination (R2) values for EA/EA* methods are 0.512/0.919, whereas for BBQm/BBQm* they increase to 0.962/0.992. Figure 12 removes the pure-MM contribution to the reference and model free energies, and it more clearly shows the correlation between the model and reference MM→QM corrections for all data in the T4 lysozyme ligand binding test set. The highest coefficient of determination occurs for BBQm* with the “ba” reference potential (R2 = 0.884), whereas for all other methods the coefficients of determination are considerably lower (0.045-0.723).
3.5. Performance of the BBQm and EA methods
In this section we examine the performance of the MM′→ QM transformations for the BBQm and EA methods discussed in the previous section. Recall, the BBQm is a “2-state” approach that requires a QM/MM simulation to be performed at one of the end-states, and it was demonstrated to be accurate and robust. The EA method is a “1-state” approach requiring only reanalysis of an MM simulation trajectory at statistically independent points, and it was demonstrated to be much less accurate and robust. The timing results here are only for the MM′→ QM transformations, and does not depend on the particular MM reference potential.
The observed molecular dynamics sampling rates of the MM′→QM simulations, using a 1 fs timestep, are shown in tables 2 (absolute solvation test set) and 3 (T4 lysozyme ligand binding test set). These timings are of particular interest because the ab initio QM/MM energy and forces are evaluated at each step of dynamics. The “Reanalysis Rate” columns do not perform the dynamics using a QM/MM potential; instead, these calculations evaluate the QM/MM potential at each saved frame from a pure-MM trajectory. The trajectory frames are written once every 500 steps, so these rates are roughly 500 times larger than the simulation rates. The QM/MM simulations are performed on a single node equipped with two, 18-core Intel Xeon E5-2695 v4 processors running at 2.1 GHz. Of the 36 cores, 1 core is reserved for calculating the pure-MM energy and forces, and 35 cores are used to evaluate the QM/MM energy and forces. The columns labeled “CPU cost” are the total number of wallclock hours required to evaluate the absolute solvation energy (table 2) or relative ligand binding free energy (table 3) on 1 node. These costs do not include GPU usage, which is nearly the same for all molecules/ligands. The pure-MM simulations performed for the evaluation of , , , and approximately yield 62 ns/day on 1 GPU for all solutes/ligands. Similarly, the pure-MM simulations performed for the evaluation of and yield 28 ns/day on 1 GPU for all ligands. In table 3, the total CPU cost is completely determined by the evaluation of the MM′→QM simulations, whose sampling rates are provided. In table 2, the total CPU cost also includes a minor contribution from the gas-phase simulations used to calculate and , which approximately yield 4000 ns/day on 1 CPU core for all molecules.
Table 2:
Ab initio QM/MM simulation and reanalysis rates of the condensed and gas-phase simulations used to calculate solvation free energies. The columns of CPU cost are the number of wallclock hours required to calculate using 1 node to produce 200 ps of sampling for the MM′→ QM transformations. QM/MM simulations are performed on a single node equipped with two, 18-core Intel Xeon E5-2695 v4 processors running at 2.1 GHz.
| Solute | Simulation Rate ps day−1 |
Reanalysis Rate ns day−1 |
CPU cost wallclock hours |
|||
|---|---|---|---|---|---|---|
| aq | gas | aq | gas | BBQm* | EA* | |
| H2O | 640 | 6600 | 320 | 3300 | 8.4 | 0.2 |
| H3O+ | 640 | 4850 | 320 | 2425 | 8.7 | 0.2 |
| 640 | 3600 | 310 | 1800 | 9.0 | 0.2 | |
| 602 | 1080 | 301 | 540 | 12.6 | 0.2 | |
| CH3OH | 589 | 1700 | 294 | 850 | 11.2 | 0.2 |
| 580 | 980 | 290 | 490 | 13.4 | 0.2 | |
| C2H6 | 571 | 1180 | 285 | 590 | 12.7 | 0.2 |
| C2H5OH | 464 | 695 | 232 | 347 | 17.4 | 0.2 |
| 425 | 555 | 212 | 277 | 20.2 | 0.2 | |
| CH3CONH2 | 344 | 474 | 172 | 237 | 24.3 | 0.2 |
| 312 | 378 | 156 | 189 | 28.3 | 0.2 | |
| (CH2)4O | 183 | 219 | 91 | 109 | 48.4 | 0.3 |
| C6H6 | 147 | 169 | 73 | 84 | 61.3 | 0.3 |
| C6H5OH | 108 | 137 | 54 | 68 | 79.8 | 0.3 |
| C6H5Cl | 104 | 120 | 52 | 60 | 86.5 | 0.3 |
| C6H5NH2 | 98 | 118 | 49 | 59 | 90.0 | 0.3 |
| C6H14 | 94 | 109 | 47 | 54 | 95.4 | 0.4 |
Table 3:
Ab initio QM/MM simulation and reanalysis rates of the bound and unbound-state simulations used to calculate the ligiand binding free energies. The columns of CPU cost are the number of wallclock hours required to calculate using 1 node to produce 200 ps of sampling for the MM′→ QM transformations. QM/MM simulations are performed on a single node equipped with two, 18-core Intel Xeon E5-2695 v4 processors running at 2.1 GHz.
| Ligand | Simulation Rate ps day−1 |
Reanalysis Rate ns day−1 |
CPU cost wallclock hours |
|||
|---|---|---|---|---|---|---|
| L∙P | L+P | L∙P | L+P | BBQm* | EA* | |
| BNZ | 131 | 147 | 66 | 74 | 69.4 | 0.1 |
| PXY | 63 | 65 | 32 | 33 | 150.3 | 0.3 |
| OXE | 60 | 62 | 30 | 31 | 157.7 | 0.3 |
| BZF | 60 | 61 | 30 | 31 | 159.0 | 0.3 |
| DEN | 53 | 54 | 27 | 27 | 179.8 | 0.4 |
| IND | 56 | 57 | 28 | 29 | 170.3 | 0.3 |
| N4B | 36 | 36 | 18 | 18 | 267.2 | 0.5 |
| I4B | 34 | 34 | 17 | 17 | 282.9 | 0.6 |
Clearly there is tremendous computational cost advantage in using a “1-state” EA approach that does not require an explicit QM/MM simulation (requiring 1 fs time steps) at the final end-state. However, as discussed in the previous section, this computational advantage is counterbalanced by a significant loss of accuracy that can only partially be improved by inclusion of an optimized reference potential. In the present demonstration that reference potential was derived from a QM/MM simulation at the end-state, which of course would not be practical in the sense that if such a simulation were performed, it may as well be used for the more accurate BBQm approach. This nonetheless suggests that, should sufficiently enhanced reference potentials become available that do not require explicit QM/MM simulations at the final end-state, one might be able to considerably improve the accuracy of the fast “1-state” EA-type methods. A promising direction for exploration of such reference potentials may be possible through new machine learning approaches.105,106 In the future, it would be of interest to test whether ad hoc MM′ parametrizations could be avoided by using modified GAFF force field parameter files specifically designed to be consistent with the QM Hamiltonian of choice based on the existing infrastructure for atom-type assignment.
4. Conclusions
In this work we performed MM→QM/MM free energy corrections for solvation and T4 lysozyme ligand binding free energy test sets using a series of reference potentials that reparametrized the MM bond parameters; bond and angle parameters; bond, angle, and dihedral parameters; or the bonded parameters and atomic charges, using a force-matching nonlinear optimization procedure to reproduce ab initio QM/MM forces in aqueous solution. For each reference potential, a benchmark reference free energy correction was generated by performing 200 ps of sampling using periodic PBE0/6-31G* QM/MM simulations at 11 intermediate-states. Convergence of the free energy corrections was examined as a function of simulation time, analysis method (TI, BAR, and forward and reverse Zwanzig’s relation), the number of intermediate simulations used in the analysis, and the reference potential.
We found that optimizing the MM reference potential’s bond and angle parameters decreased the mean unsigned errors produced by either forward or reverse application of Zwanzig’s equation; however, no significant reductions were made by further parametrizing the dihedral force constants nor atomic charges. This observation is likely related to the chosen data sets, which contain a number of small molecules and relatively rigid fragments (e.g., benzene rings) that lack significant dihedral flexibility and whose torsions are already well-modeled by the MM force field. Previous work has also concluded that bond stretching and angle bending differences between the low- and high-level potentials are partially responsible for the poor convergence of Zwanzig’s equation24,25,33,36,38,54-56,107 and, for moderately large molecules, the torsion potentials may be responsible for observed differences in preferred conformations.107 As should be expected,38,68,108,109 free energy estimates based on Zwanzig’s equation did not converge to the reference free energy estimate without using a number simulated intermediate states, whereas TI and BAR analysis both yielded excellent mean unsigned errors, even when only the two end-state simulations were used. It is also not suprising that the use of force-matched referenced potentials reduced the mean unsigned errors. We did, however, assess the improvements made by a systematic series of force-matched potentials to ascertain the relative importance of the various force field terms in the fit. With respect to the solvation free energy test set, the standard deviation of the TI and BAR signed errors decreased when the MM reference potential’s bond parameters were optimized, and the further decreased when the bond and angle parameters were optimized; however, no significant benefit was found upon optimizing the dihedral force constants nor atomic charges. The MM and force-matched optimized reference potentials yielded very small errors when applied to the T4 lysozyme ligand binding free energy test set. The accuracy of all methods often did not significantly improve upon extending the simulation sampling from 50 ps to 200 ps, which suggests that computational resources could be better utilized by reperforming short simulations several times and averaging the results.61,62
Overall, we demonstrate the BAR book-ending to QM (BBQm) method, a 2-end-state approach that uses a QM/MM simulation for both reference potential generation and free energy sampling, is highly accurate and robust, and ready to take on broad applications. The “1-state” exponential averaging (EA) approach that requires only MM simulation is extremely fast, but does not achieve good accuracy. Use of a tailored reference potential improves the accuracy, but the resulting errors are still 2 to 4 times larger than BBQm. Nonetheless, the efficiency of the “1-state” EA approach motivates the idea of developing enhanced reference potentials, possibly through machine learning techniques, that improve accuracy while not sacrificing speed.
Supplementary Material
Acknowledgments
The authors are grateful for financial support provided by the National Institutes of Health (No. GM107485). Computational resources were provided by the Office of Advanced Research Computing (OARC) at Rutgers, The State University of New Jersey, the National Institutes of Health under Grant No. S10OD012346 and by the Extreme Science and Engineering Discovery Environment (XSEDE),110 which is supported by National Science Foundation (grant numbers ACI-1548562 and OCI-1053575).
References
- (1).Zhang C; Lu C; Jing Z; Wu C; Piquemal JP; Ponder JW; Ren P Amoeba Polarizable Atomic Multipole Force Field for Nucleic Acids. J. Chem. Theory Comput 2018, 14, 2084–2108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (2).Cavasotto CN; Adler NS; Aucar MG Quantum Chemical Approaches in Structure-Based Virtual Screening and Lead Optimization. Front. Chem 2018, 6, 188. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (3).Cournia Z; Allen B; Sherman W Relative Binding Free Energy Calculations in Drug Discovery: Recent Advances and Practical Considerations. J. Chem. Inf. Model 2017, 57, 2911–2937. [DOI] [PubMed] [Google Scholar]
- (4).Ehrlich S; Göller AH; Grimme S Towards full Quantum-Mechanics-based Protein-Ligand Binding Affinities. Chem. Phys. Chem 2017, 18, 898–905. [DOI] [PubMed] [Google Scholar]
- (5).Jorgensen WL Computer-aided discovery of anti-HIV agents. Bioorg. Med. Chem 2016, 24, 4768–4778. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (6).Giese TJ; Chen H; Huang M; York DM Parametrization of an orbital-based linear-scaling quantum force field for noncovalent interactions. J. Chem. Theory Comput 2014, 10, 1086–1098. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (7).Giese TJ; Huang M; Chen H; York DM Recent Advances toward a General Purpose Linear-Scaling Quantum Force Field. Acc. Chem. Res 2014, 47, 2812–20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (8).Lu X; Fang D; Ito S; Okamoto Y; Ovchinnikov V; Cui Q QM/MM free energy simulations: recent progress and challenges. Mol. Simul 2016, 42, 1056–1078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (9).Kamerlin SCL; Haranczyk M; Warshel A Progress in Ab Initio QM/MM Free-Energy Simulations of Electrostatic Energies in Proteins: Accelerated QM/MM Studies of pKa, Redox Reactions and Solvation Free Energies. J. Phys. Chem. B 2009, 113, 1253–1272. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (10).Duarte F; Amrein BA; Blaha-Nelson D; Kamerlin SC Recent advances in QM/MM free energy calculations using reference potentials. Biochim. Biophys. Acta 2015, 1850, 954–965, Recent developments of molecular dynamics. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (11).Rathore RS; Sumakanth M; Siva Reddy M; Reddanna P; Rao AA; Erion MD; Reddy MR Advances in Binding Free Energies Calculations: QM/MM-Based Free Energy Perturbation Method for Drug Design. Curr. Pharm. Des 2013, 19, 4674–4686. [DOI] [PubMed] [Google Scholar]
- (12).Li G; Cui Q pKa calculations with QM/MM free energy perturbations. J. Phys. Chem. B 2003, 107, 14521–14528. [Google Scholar]
- (13).Li G; Zhang X; Cui Q Free energy perturbation calculations with combined QM/MM potentials complications, simplifications, and applications to redox potential calculations. J. Phys. Chem. B 2003, 107, 8643–8653. [Google Scholar]
- (14).Gao J Absolute Free Energy of Solvation from Monte Carlo Simulations Using Combined Quantum and Molecular Mechanical Potentials. J. Phys. Chem 1992, 96, 537–540. [Google Scholar]
- (15).Gao J; Xia X A priori evaluation of aqueous polarization effects through Monte Carlo QM-MM simulations. Science 1992, 258, 631–635. [DOI] [PubMed] [Google Scholar]
- (16).Luzhkov V; Warshel A Microscopic models for quantum mechanical calculations of chemical processes in solutions: LD/AMPAC and SCAAS/AMPAC calculations of solvation energies. J. Comput. Chem 1992, 13, 199–213. [Google Scholar]
- (17).Kearns FL; Warrensford L; Boresch S; Woodcock HL The Good, the Bad, and the Ugly: "HiPen", a New Dataset for Validating (S)QM/MM Free Energy Simulations. Molecules 2019, 24, 681. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (18).Hudson PS; Han K; Woodcock HL; Brooks BR Force matching as a stepping stone to QM/MM CB[8] host/guest binding free energies: a SAMPL6 cautionary tale. J. Comput.-Aided Mol. Des 2018, 32, 983–999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (19).Hudson PS; Boresch S; Rogers DM; Woodcock HL Accelerating QM/MM Free Energy Computations via Intramolecular Force Matching. J. Chem. Theory Comput 2018, 14, 6327–6335. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (20).Kearns FL; Hudson PS; Woodcock HL; Boresch S Computing converged free energy differences between levels of theory via nonequilibrium work methods: Challenges and opportunities. J. Comput. Chem 2017, 38, 1376–1388. [DOI] [PubMed] [Google Scholar]
- (21).Hudson PS; Woodcock HL; Boresch S Use of Nonequilibrium Work Methods to Compute Free Energy Differences Between Molecular Mechanical and Quantum Mechanical Representations of Molecular Systems. J. Phys. Chem. Lett 2015, 6, 4850–4856. [DOI] [PubMed] [Google Scholar]
- (22).König G; Pickard FC; Huang J; Thiel W; MacKerell AD; Brooks BR; York DM A Comparison of QM/MM Simulations with and without the Drude Oscillator Model Based on Hydration Free Energies of Simple Solutes. Molecules 2018, 23, 2695–2720. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (23).König G; Brooks BR; Thiel W; York DM On the convergence of multi-scale free energy simulations. Mol. Simul 2018, 44, 1062–1081. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (24).König G; Brooks BR Correcting for the free energy costs of bond or angle constraints in molecular dynamics simulations. Biochim. Biophys. Acta 2015, 1850, 932–943. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (25).König G; Hudson PS; Boresch S; Woodcock HL Multiscale Free Energy Simulations: An Efficient Method for Connecting Classical MD Simulations to QM or QM/MM Free Energies Using Non-Boltzmann Bennett Reweighting Schemes. J. Chem. Theory Comput 2014, 10, 1406–1419. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (26).Olsson MA; Ryde U Comparison of QM/MM Methods To Obtain Ligand-Binding Free Energies. J. Chem. Theory Comput 2017, 13, 2245–2253. [DOI] [PubMed] [Google Scholar]
- (27).Wesolowski T; Warshel A Ab Initio Free Energy Perturbation Calculations of Solvation Free Energy Using the Frozen Density Functional Approach. J. Phys. Chem 1994, 98, 5183–5187. [Google Scholar]
- (28).Olsson MHM; Hong G; Warshel A Frozen Density Functional Free Energy Simulations of Redox Proteins: Computational Studies of the Reduction Potential of Plastocyanin and Rusticyanin. J. Am. Chem. Soc 2003, 125, 5025–5039. [DOI] [PubMed] [Google Scholar]
- (29).Min D; Zheng L; Harris W; Chen M; Lv C; Yang W Practically Efficient QM/MM Alchemical Free Energy Simulations: The Orthogonal Space Random Walk Strategy. J. Chem. Theory Comput 2010, 6, 2253–2266. [DOI] [PubMed] [Google Scholar]
- (30).Mori T; Hamers RJ; Pedersen JA; Cui Q Integrated Hamiltonian Sampling: A Simple and Versatile Method for Free Energy Simulations and Conformational Sampling. J. Phys. Chem. B 2014, 118, 8210–8220. [DOI] [PubMed] [Google Scholar]
- (31).Plotnikov NV; Kamerlin SCL; Warshel A Paradynamics: an effective and reliable model for ab initio QM/MM free-energy calculations and related tasks. J. Phys. Chem. B 2011, 115, 7950–7962. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (32).Plotnikov NV; Warshel A Exploring, refining, and validating the paradynamics QM/MM sampling. J. Phys. Chem. B 2012, 116, 10342–10356. [DOI] [PubMed] [Google Scholar]
- (33).Sampson C; Fox T; Tautermann CS; Woods C; Skylaris C-K A "Stepping Stone" Approach for Obtaining Quantum Free Energies of Hydration. J. Phys. Chem. B 2015, 119, 7030–7040. [DOI] [PubMed] [Google Scholar]
- (34).Olsson MA; Söderhjelm P; Ryde U Converging ligand-binding free energies obtained with free-energy perturbations at the quantum mechanical level. J. Comput. Chem 2016, 37, 1589–1600. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (35).Dybeck EC; König G; Brooks BR; Shirts MR Comparison of Methods To Reweight from Classical Molecular Simulations to QM/MM Potentials. J. Chem. Theory Comput 2016, 12, 1466–1480. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (36).Genheden S; Ryde U; Söderhjelm P Binding affinities by alchemical perturbation using QM/MM with a large QM system and polarizable MM model. J. Comput. Chem 2015, 36, 2114–2124. [DOI] [PubMed] [Google Scholar]
- (37).Shaw KE; Woods CJ; Mulholland AJ Compatibility of quantum chemical methods and empirical (MM) water models in quantum mechanics/molecular mechanics liquid water simulations. J. Phys. Chem. Lett 2010, 1, 219–223. [Google Scholar]
- (38).Heimdal J; Ryde U Convergence of QM/MM free-energy perturbations based on molecular-mechanics or semiempirical simulations. Phys. Chem. Chem. Phys 2012, 14, 12592–12604. [DOI] [PubMed] [Google Scholar]
- (39).Li P; Jia X; Pan X; Shao Y; Mei Y Accelerated Computation of Free Energy Profile at ab Initio Quantum Mechanical/Molecular Mechanics Accuracy via a Semi-Empirical Reference Potential. I. Weighted Thermodynamics Perturbation. J. Chem. Theory Comput 2018, 14, 5583–5596. [DOI] [PubMed] [Google Scholar]
- (40).Wang M; Mei Y; Ryde U Host-Guest Relative Binding Addinities at Density-Functional Theory Level from Semiempirical Molecular Dynamics Simulations. J. Chem. Theory Comput 2019, in press. [DOI] [PubMed] [Google Scholar]
- (41).Štrajbl M; Hong G; Warshel A Ab initio QM/MM simulation with proper sampling: “first principle” calculations of the free energy of the autodissociation of water in aqueous solution. J. Phys. Chem. B 2002, 106, 13333–13343. [Google Scholar]
- (42).Bentzien J; Muller RP; Florián J; Warshel A Hybrid ab Initio Quantum Mechanics/Molecular Mechanics Calculations of Free Energy Surfaces for Enzymatic Reactions: The Nucleophilic Attack in Subtilisin. J. Phys. Chem. B 1998, 102, 2293–2301. [Google Scholar]
- (43).Ercolessi F; Adams JB Interatomic Potentials from First-Principles Calculations: The Force-Matching Method. EPL 1994, 26, 583. [Google Scholar]
- (44).Maurer P; Laio A; Hugosson HW; Colombo MC; Rothlisberger U Automated Parametrization of Biomolecular Force Fields from Quantum Mechanics/Molecular Mechanics (QM/MM) Simulations through Force Matching. J. Chem. Theory Comput 2007, 3, 628–639. [DOI] [PubMed] [Google Scholar]
- (45).Izvekov S; Parrinello M; Burnham CJ; Voth GA Effective force fields for condensed phase systems from ab initio molecular dynamics simulation: A new method for force-matching. J. Chem. Phys 2004, 120, 10896. [DOI] [PubMed] [Google Scholar]
- (46).Zhou Y; Pu J Reaction Path Force Matching: A New Strategy of Fitting Specific Reaction Parameters for Semiempirical Methods in Combined QM/ MM Simulations. J. Chem. Theory Comput 2014, 10, 3038. [DOI] [PubMed] [Google Scholar]
- (47).Kroonblawd MP; Pietrucci F; Marco Saitta A; Goldman N Generating Converged Accurate Free Energy Surfaces for Chemical Reactions with a Force-Matched Semiempirical Model. J. Chem. Theory Comput 2018, 14, 2207–2218. [DOI] [PubMed] [Google Scholar]
- (48).Akin-Ojo O; Song Y; Wang F Developing ab initio quality force fields from condensed phase quantum-mechanics/molecular-mechanics calculations through the adaptive force matching method. J. Chem. Phys 2008, 129, 64108. [DOI] [PubMed] [Google Scholar]
- (49).Akin-Ojo O; Wang F The quest for the best nonpolarizable water model from the adaptive force matching method. J. Comput. Chem 2011, 32, 453–462. [DOI] [PubMed] [Google Scholar]
- (50).Pinnick ER; Calderon CE; Rusnak AJ; Wang F Achieving fast convergence of ab initio free energy perturbation calculations with the adaptive force-matching method. Theor. Chem. Acc 2012, 131, 1146. [Google Scholar]
- (51).Zwanzig RW High-temperature equation of state by a perturbation method. I. Nonpolar gases. J. Chem. Phys 1954, 22, 1420–1426. [Google Scholar]
- (52).Beierlein FR; Michel J; Essex JW A Simple QM/MM Approach for Capturing Polarization Effects in Protein-Ligand Binding Free Energy Calculations. J. Phys. Chem. B 2011, 115, 4911–4926. [DOI] [PubMed] [Google Scholar]
- (53).Boresch S; Woodcock HL Convergence of single-step free energy perturbation. Mol. Phys 2017, 115, 1200–1213. [Google Scholar]
- (54).Genheden S; Cabedo Martinez AI; Criddle MP; Essex JW Extensive all-atom Monte Carlo sampling and QM/MM corrections in the SAMPL4 hydration free energy challenge. J. Comput.-Aided Mol. Des 2014, 28, 187–200. [DOI] [PubMed] [Google Scholar]
- (55).Cave-Ayland C; Skylaris C-K; Essex JW Direct validation of the single step classical to quantum free energy perturbation. J. Phys. Chem. B 2015, 119, 1017–1025. [DOI] [PubMed] [Google Scholar]
- (56).Hudson PS; White JK; Kearns FL; Hodoscek M; Boresch S; Woodcock HL Efficiently computing pathway free energies: New approaches based on chain-of-replica and Non-Boltzmann Bennett reweighting schemes. Biochim. Biophys. Acta 2015, 1850, 944–953, Recent developments of molecular dynamics. [DOI] [PubMed] [Google Scholar]
- (57).Ryde U How Many Conformations Need To Be Sampled To Obtain Converged QM/MM Energies? The Curse of Exponential Averaging. J. Chem. Theory Comput 2017, 13, 5745–5752. [DOI] [PubMed] [Google Scholar]
- (58).Rod TH; Ryde U Accurate QM/MM Free Energy Calculations of Enzyme Reactions: Methylation by CatecholO-Methyltransferase. J. Chem. Theory Comput 2005, 1, 1240–1251. [DOI] [PubMed] [Google Scholar]
- (59).Rod TH; Ryde U Quantum Mechanical Free Energy Barrier for an Enzymatic Reaction. Phys. Rev. Lett 2005, 94, 138302. [DOI] [PubMed] [Google Scholar]
- (60).Rosta E; Haranczyk M; Chu ZT; Warshel A Accelerating QM/MM Free Energy Calculations: Representing the Surroundings by an Updated Mean Charge Distribution. J. Phys. Chem. B 2008, 112, 5680–5692. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (61).Steinmann C; Olsson MA; Ryde U Relative Ligand-Binding Free Energies Calculated from Multiple Short QM/MM MD Simulations. J. Chem. Theory Comput 2018, 14, 3228–3237. [DOI] [PubMed] [Google Scholar]
- (62).Wang M; Mei Y; Ryde U Predicting Relative Binding Affinity Using Nonequilibrium QM/MM Simulations. J. Chem. Theory Comput 2018, 14, 6613–6622. [DOI] [PubMed] [Google Scholar]
- (63).Jarzynski C Nonequilibrium equality for free energy differences. Phys. Rev. Lett 1997, 78, 2690–2693. [Google Scholar]
- (64).Jarzynski C Equilibrium free-energy differences from nonequilibrium measurements: a master-equation approach. Phys. Rev. E 1997, 56, 5018–5035. [Google Scholar]
- (65).Crooks GE Nonequilibrium measurements of free energy differences for microscopically reversible Markovian states. J. Stat. Phys 1998, 90, 1481–1487. [Google Scholar]
- (66).Fox SJ; Pittock C; Tautermann CS; Fox T; Christ C; Malcolm NOJ; Essex JW; Skylaris C-K Free Energies of Binding from Large-Scale First-Principles Quantum Mechanical Calculations: Application to Ligand Hydration Energies. J. Phys. Chem. B 2013, 117, 9478–9485. [DOI] [PubMed] [Google Scholar]
- (67).Wood RH; Yezdimer EM; Sakane S; Barriocanal JA; Doren DJ Free energies of solvation with quantum mechanical interaction energies from classical mechanical simulations. J. Chem. Phys 1999, 110, 1329–1337. [Google Scholar]
- (68).Jia X; Wang M; Shao Y; König G; Brooks BR; Zhang JZH; Mei Y Calculations of Solvation Free Energy through Energy Reweighting from Molecular Mechanics to Quantum Mechanics. J. Chem. Theory Comput 2016, 12, 499–511. [DOI] [PubMed] [Google Scholar]
- (69).Hudson PS; Lee Woodcock H; Boresch S Use of interaction energies in QM/MM free energy simulations. J. Chem. Theory Comput 2019, 10.1021/acs.jctc.9b00084. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (70).Bennett CH Efficient estimation of free energy differences from Monte Carlo data. J. Comput. Phys 1976, 22, 245–268. [Google Scholar]
- (71).Kirkwood JG Statistical mechanics of fluid mixtures. J. Chem. Phys 1935, 3, 300–313. [Google Scholar]
- (72).Morton A; Matthews BW Specificity of ligand binding in a buried nonpolar cavity of T4 Lysozyme: Linkage of dynamics and structural plasticity. Biochemistry 1995, 34, 8576–8588. [DOI] [PubMed] [Google Scholar]
- (73).Giese TJ; York DM Ambient-Potential Composite Ewald Method for ab Initio Quantum Mechanical/Molecular Mechanical Molecular Dynamics Simulation. J. Chem. Theory Comput 2016, 12, 2611–2632. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (74).Jakalian A; Bush BL; Jack DB; Bayly CI Fast, efficient generation of high-qualigy atomic charges. AM1-BCC model: I. method. J. Comput. Chem 2000, 21, 132–146. [DOI] [PubMed] [Google Scholar]
- (75).Jakalian A; Jack DB; Bayly CI Fast, efficient generation of high-quality atomic charges. AM1-BCC model: II. parameterization and validation. J. Comput. Chem 2002, 23, 1623–1641. [DOI] [PubMed] [Google Scholar]
- (76).Johnson SG The NLopt nonlinear-optimization package. 2007. –; http://http://github.com/stevengj/nlopt, [Online; accessed 2019-03-01]. [Google Scholar]
- (77).Powell MJD A direct search optimization method that models the objective and constraint functions by linear interpolation In Advances in Optimization and Numerical Analysis; Gomez S, Hennart JP, Eds.; Kluwer Academic: Dordrecht, 1994; pp 51–67. [Google Scholar]
- (78).Wang L-P; Van Voorhis T Communication: Hybrid ensembles for improved force matching. J. Chem. Phys 2010, 133, 231101. [DOI] [PubMed] [Google Scholar]
- (79).Wang L-P; Chen J; Van Voorhis T Systematic Parametrization of Polarizable Force Fields from Quantum Chemistry Data. J. Chem. Theory Comput 2013, 9, 452–460. [DOI] [PubMed] [Google Scholar]
- (80).Wang L-P; McKiernan KA; Gomes J; Beauchamp KA; Head-Gordon T; Rice JE; Swope WC; Martínez TJ; Pande VS Building a More Predictive Protein Force Field: A Systematic and Reproducible Route to AMBER-FB15. J. Phys. Chem. B 2017, 121, 4023–4039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (81).Wang J; Wolf RM; Caldwell JW; Kollman PA; Case DA Development and testing of a general amber force field. J. Comput. Chem 2004, 25, 1157–1174. [DOI] [PubMed] [Google Scholar]
- (82).Maier JA; Martinez C; Kasavajhala K; Wickstrom L; Hauser KE; Simmerling C ff14SB: Improving the Accuracy of Protein Side Chain and Backbone Parameters from ff99SB. J. Chem. Theory Comput 2015, 11, 3696–3713. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (83).Horn HW; Swope WC; Pitera JW; Madura JD; Dick TJ; Hura GL; Head-Gordon T Development of an improved four-site water model for biomolecular simulations: TIP4P-Ew. J. Chem. Phys 2004, 120, 9665–9678. [DOI] [PubMed] [Google Scholar]
- (84).Case DA; Ben-Shalom IY; Brozell SR; Cerutti DS; Cheatham III TE; Cruzeiro VWD; Darden TA; Duke RE; Ghoreishi D; Gilson MK; Gohlke H; Goetz AW; Greene D; Harris R; Homeyer N; Izadi S; Kovalenko A; Kurtzman T; Lee T; Le-Grand S; Li P; Lin C; Liu J; Luchko T; Luo R; Mermelstein DJ; Merz KM; Miao Y; Monard G; Nguyen C; Nguyen H; Omelyan I; Onufriev A; Pan F; Qi R; Roe DR; Roitberg A; Sagui C; Schott-Verdugo S; Shen J; Simmerling CL; Smith J; Salomon-Ferrer R; Swails J; Walker RC; Wang J; Wei H; Wolf RM; Wu X; Xiao L; York DM; Kollman PA AMBER 18. University of California, San Francisco: San Francisco, CA, 2018. [Google Scholar]
- (85).Essmann U; Perera L; Berkowitz ML; Darden T; Hsing L; Pedersen LG A smooth particle mesh Ewald method. J. Chem. Phys 1995, 103, 8577–8593. [Google Scholar]
- (86).Giese TJ; Panteva MT; Chen H; York DM Multipolar Ewald methods, 1: Theory, accuracy, and performance. J. Chem. Theory Comput 2015, 11, 436–450. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (87).Bogusz S; Cheatham III TE; Brooks BR Removal of pressure and free energy artifacts in charged periodic systems via net charge corrections to the Ewald potential. J. Chem. Phys 1998, 108, 7070–7084. [Google Scholar]
- (88).Ryckaert JP; Ciccotti G; Berendsen HJC Numerical Integration of the Cartesian Equations of Motion of a System with Constraints: Molecular Dynamics of n-Alkanes. J. Comput. Phys 1977, 23, 327–341. [Google Scholar]
- (89).Turq P; Lantelme F; Friedman HL Brownian dynamics: Its application to ionic solutions. J. Chem. Phys 1977, 66, 3039–3044. [Google Scholar]
- (90).Berendsen HJC; Postma JPM; van Gunsteren WF; Dinola A; Haak JR Molecular dynamics with coupling to an external bath. J. Chem. Phys 1984, 81, 3684–3690. [Google Scholar]
- (91).Giese TJ; York DM A GPU-Accelerated Parameter Interpolation Thermodynamic Integration Free Energy Method. J. Chem. Theory Comput 2018, 14, 1564–1582. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (92).Klimovich PV; Shirts MR; Mobley DL Guidelines for the analysis of free energy calculations. J. Comput.-Aided Mol. Des 2015, 29, 397–411. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (93).Chodera JD; Swope WC; Pitera JW; Seok C; Dill KA Use of the weighted histogram analysis method for the analysis of simulated and parallel tempering simulations. J. Chem. Theory Comput 2007, 3, 26–41. [DOI] [PubMed] [Google Scholar]
- (94).Shirts MR; Bair E; Hooker G; Pande VS Equilibrium free energies from nonequilibrium measurements using maximum-likelihood methods. Phys. Rev. Lett 2003, 91, 140601. [DOI] [PubMed] [Google Scholar]
- (95).Shirts MR; Chodera JD Statistically optimal analysis of samples from multiple equilibrium states. J. Chem. Phys 2008, 129, 124105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (96).Paliwal H; Shirts MR A benchmark test set for alchemical free energy transformations and its use to quantify error in common free energy methods. J. Chem. Theory Comput 2011, 7, 4115–4134. [DOI] [PubMed] [Google Scholar]
- (97).Kofke DA; Cummings PT Quantitaive comparison and optimization of methods for evaluating the chemical potential by molecular simulation. Mol. Phys 1997, 92, 973–996. [Google Scholar]
- (98).Lu N; Kofke DA Accuracy of free-energy perturbation calculations in molecular simulation. I. Modeling. J. Chem. Phys 2001, 114, 7303–7311. [Google Scholar]
- (99).Lu N; Kofke DA Accuracy of free-energy perturbation calculations in molecular simulation. II. Heuristics. J. Chem. Phys 2001, 115, 6866–6875. [Google Scholar]
- (100).Wu D; Kofke DA Model for small-sample bias of free-energy calculations applied to Gaussian-distributed nonequilibrium work measurements. J. Chem. Phys 2004, 121, 8742–8747. [DOI] [PubMed] [Google Scholar]
- (101).Wu D; Kofke DA Phase-space overlap measures. I. Fail-safe bias detection in free energies calculated by molecular simulation. J. Chem. Phys 2005, 123, 54103. [DOI] [PubMed] [Google Scholar]
- (102).Wu D; Kofke DA Phase-space overlap measures. II. Design and implementation of staging methods for free-energy calculations. J. Chem. Phys 2005, 123, 84109. [DOI] [PubMed] [Google Scholar]
- (103).Kofke DA On the sampling requirements for exponential-work free-energy calculations. Mol. Phys 2006, 104, 3701–3708. [Google Scholar]
- (104).Jones E; Oliphant T; Peterson P SciPy: Open source scientific tools for Python. 2001. –; http://www.scipy.org/, [Online; accessed 2019-03-01]. [Google Scholar]
- (105).Smith JS; Isayev O; Roitberg AE ANI-1, A data set of 20 million calculated off-equilibrium conformations for organic molecules. Sci. Data 2017, 4, 170193–170200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (106).Smith JS; Nebgen B; Lubbers N; Isayev O; Roitberg AE Less is more: Sampling chemical space with active learning. J. Chem. Phys 2018, 148, 241733–241743. [DOI] [PubMed] [Google Scholar]
- (107).Kerns SJ; Agafonov RV; Cho Y-J; Pontiggia F; Otten R; Pachov DV; Kutter S; Phung LA; Murphy PN; Thai V; Alber T; Hagan MF; Kern D The energy landscape of adenylate kinase during catalysis. Nature Structural and Molecular Biology 2015, 22, 124. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (108).Vaidehi N; Wesolowski TA; Warshel A Quantum-mechanical calculations of solvation free energies. A combined ab initio pseudopotential free-energy perturbation approach. J. Chem. Phys 1992, 97, 4264–4271. [Google Scholar]
- (109).Armacost KA; Goh GB; Brooks CL Biasing Potential Replica Exchange Multisite λ-Dynamics for Efficient Free Energy Calculations. J. Chem. Theory Comput 2015, 11, 1267–1277. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (110).Towns J; Cockerill T; Dahan M; Foster I; Gaither K; Grimshaw A; Hazlewood V; Lathrop S; Lifka D; Peterson GD; Roskies R; Scott JR; Wilkins-Diehr N XSEDE: Accelerating Scientific Discovery. Comput. Sci. Eng 2014, 16, 62–74. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.