Dramatic Improvement in Sensitivity with Pulsed Mode Charge Detection Mass Spectrometry

Abstract

Charge detection mass spectrometry (CDMS) is emerging as a valuable tool to determine mass distributions for heterogeneous and high-mass samples. It is a single-particle technique where masses are determined for individual ions from simultaneous measurements of their mass-to-charge ratio (m/z) and charge. Ions are trapped in an electrostatic linear ion trap (ELIT) and oscillate back and forth through a detection cylinder. The trap is open and able to trap ions for a small fraction of the total measurement time so most of the ions (>99.8%) in a continuous ion beam are lost. Here, we implement an ion storage scheme where ions are accumulated and stored in a hexapole and then injected into the ELIT at the right time for them to be trapped. This pulsed mode of operation increases the sensitivity of CDMS by more than 2 orders of magnitude, which allows much lower titer samples to be analyzed. A limit of detection of 3.3 × 10⁸ particles/mL was obtained for hepatitis B virus T = 4 capsids with a 1.3 μL sample. The hexapole where the ions are accumulated and stored is a significant distance from the ion trap so ions are dispersed in time by their m/z values as they travel between the hexapole and the ELIT. By varying the delay time between ion release and trapping, different windows of m/z values can be trapped.

Graphical Abstract

Interest in measuring accurate masses for species with molecular weights much greater than 1 MDa has led to the development of a number of specialized single-particle techniques where masses are directly measured for individual molecules.¹ These techniques include nanomechnical oscillators^2,3 and a variety of approaches based on more traditional mass spectrometry methods.^4–21 Charge detection mass spectrometry (CDMS), which offers a good compromise between resolution, accuracy, and measurement speed, is one of the more promising approaches.^20–31 In particular, CDMS has recently been used to measure the molecular weight distributions for a number of heterogeneous, high-mass samples including amyloid fibrils,³² synthetic polymers,³³ nanoparticles,³⁴ gene therapy products,³⁵ and viruses and virus assembly intermediates.^36–39

In CDMS, the ions pass through a metal cylinder and the charge induced by the ion is detected by a charge-sensitive amplifier. If the cylinder is long enough, the induced charge equals the charge on the ion.^40,41 The ion’s m/z can be determined at the same time from its flight time through the cylinder, assuming that the ion energy is known. The mass of the ion is then obtained from the product of the charge and the m/z ratio.

In some measurements, particularly early ones, the CDMS detector was operated in a single-pass mode where the ion passes through the detection tube once.²¹ This leads to relatively high uncertainties in the m/z and charge measurements and hence low (single digit) mass-resolving powers. To improve the mass resolution, Benner embedded the detection cylinder in an electrostatic linear ion trap (ELIT) so that the trapped ions oscillate back and forth through the detection cylinder.⁴² The resulting time domain signal is now usually analyzed by fast Fourier transforms (FFTs).^43–46 The uncertainty in the charge measurement is proportional to t_trap^−1/2, where t_trap is the trapping time. With trapping times in the 3 s range, the uncertainty is low enough that the charge state can be assigned with almost perfect accuracy.⁴⁷ With perfect charge accuracy the mass-resolving power is limited by the uncertainty in the m/z determination. With a trapping time of 3 s, it takes a long time to accumulate enough single-ion measurements to assemble a spectrum; in most cases, a compromise is made and a trapping time of around 100 ms is used. With this trapping time, the mass resolution is typically in the 10² range.

An ELIT consists of two endcaps that can be switched between transmission and reflection modes. A trapping event starts with both endcaps in transmission mode. The rear endcap is then switched to reflection mode. With this configuration, ions that enter the ELIT through the front endcap and pass through the detection cylinder are reflected back through the detection cylinder and leave the trap through the front endcap. Ions are trapped by switching the front endcap from transmission mode to reflection mode. When the front endcap is switched, ions in the detection cylinder and in the rear endcap are trapped. Ions in the front endcap are usually not trapped because their kinetic energies are changed by switching the endcap voltages. The fraction of ions that are randomly trapped with this arrangement is given approximately by

$$F=\frac{2t_{\text{dc}}+t_{\text{ec}}}{t_{\text{trap}}}$$ (1)

where t_dc is the time it takes for ions to travel through the detection cylinder and t_ec is the time it takes for ions to be reflected in the endcap. The trapping time, t_trap, is usually ≥100 ms. The flight times through the detection cylinder and in the endcap depend on the ion’s kinetic energy and m/z, but the numerator in eq 1 is usually much larger than the denominator, so the fraction of ions that is trapped is small. For example, for an ion with a kinetic energy of 130 eV/z and an m/z of 28 800 Da (the average m/z for the hepatitis B virusT = 4 capsids studied here), the fraction trapped is around 1 in 620 for the cylindrical ELIT used in this work.⁴⁸ Thus, most of the ions from the source are wasted because the trap is closed for most of the time. We show here that the sensitivity can be increased by more than 2 orders of magnitude by storing the ions and pulsing them into the ion trap so that a time-compressed packet of ions is present in the trap when it closes.

Before describing pulsed mode CDMS in detail, we should mention that there is another way of increasing sensitivity in CDMS measurements: triggered trapping where the induced-charge signal of an ion entering the detection cylinder is used to trigger the closure of the trap. However, in this case the signal that triggers trap closure must be detected from a single pass of the ion through the ELIT. This has restricted the application of triggered trapping to highly charged ions where the signal is well above the noise floor.⁴² For high count rates, single-pass mode CDMS can detect more ions than triggered trapping. However, single-pass mode CDMS suffers from the same high charge threshold as triggered trapping, and also has poor mass-resolving power.

EXPERIMENTAL METHODS

Instrumentation.

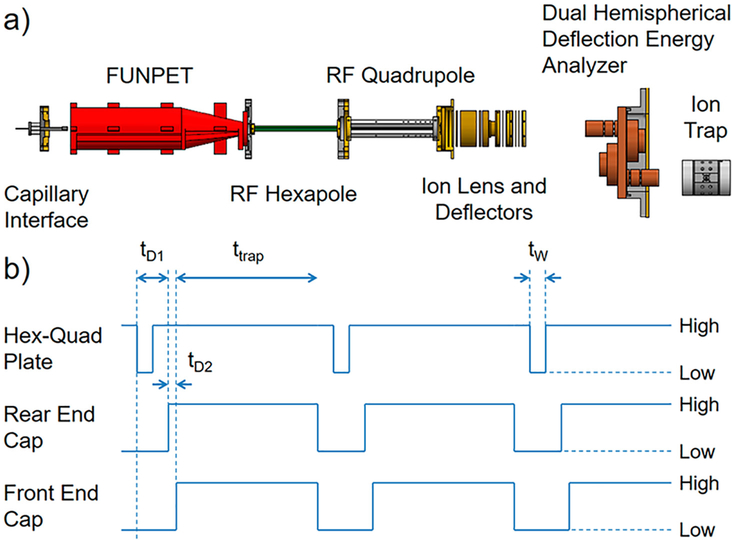
Figure 1a shows a schematic diagram of the home-built charge detection mass spectrometer used in the present study. Ions are generated by nanoelectrospray and enter the apparatus through a heated capillary. The first differentially pumped region contains a FUNPET,⁴⁹ a hybrid ion funnel/ion carpet interface designed to efficiently transmit ions with a broad mass distribution. The FUNPET incorporates a long drift region to break up the jet generated by gas flow through the capillary, followed by a funnel region⁵⁰ and ion carpet⁵¹ to focus the ions through a small aperture into the second differentially pumped region that houses a radio frequency (RF) hexapole. The third differentially pumped region houses a segmented RF quadrupole,⁵² and the fourth region contains an ion lens, deflectors, and a dual hemispherical deflection energy analyzer (HDA). The HDA transmits a narrow band of ion energies centered around the nominal ion energy of 130 eV/z. The final differentially pumped region houses the ELIT where the ions are trapped. The pressure in the ELIT chamber is around 10⁻⁹ mbar. This low pressure is necessary to minimize collisions with the background gas. Such collisions can reduce the ion energy which in turn causes the ion’s oscillation frequency to change.

Figure 1.

(a) Schematic diagram of the charge detection mass spectrometer used in this study. (b) Pulsing scheme used to accumulate and store ions in the hexapole and deliver them to the electrostatic linear ion trap just before the front endcap switches from transmission mode to reflection mode to trap the ions. High values for the hexapole-quadrupole (hex-quad) plate and front and rear endcaps indicate storage or trapping mode potentials. Low values indicate transmission mode potentials.

In this work, ions are accumulated and stored in the hexapole. The hexapole is operated at a pressure of 10−100 mbar, and collisions with the background gas thermalize any excess kinetic energy picked up by the ions from the gas flow through the FUNPET exit aperture. The direct current (dc) potential on the hexapole sets the ion energy, and the potential on the plate that separates the hexapole from the segmented quadrupole (the hex-quad plate) is usually set to a potential that is slightly less than the hexapole dc potential so that ions are efficiently transported from the hexapole to the segmented quadrupole. To accumulate and store ions, the potential on the hex-quad plate is raised to the point where ions were no longer transmitted. The pseudopotential from the RF on the hexapole rods confines the ions in the radial direction, and the gas flow through the FUNPET aperture forms a jet that prevents ions from diffusing backward. Thus, the ions are trapped.

Figure 1b shows a schematic of the pulse timing scheme used to accumulate and store the ions. A high value in Figure 1b for the hex-quad plate and the front and rear endcaps indicates potentials at the storage or trapping values and a low value indicates potentials at the transmission values. The sequence starts with the potential on the hex-quad plate switching to the transmission value. This pulse has a width t_W, which is adjustable. After a delay, t_D1, the potentials on the rear endcap are switched from transmission to reflection mode, and after an additional delay, t_D2, the potentials on the front endcap are switched from transmission to reflection mode. Any ions in the detection cylinder or the rear endcap are now trapped and remain trapped for the time t_trap in Figure 1b. At the end of the trapping period the potentials on the endcaps are returned to their transmission values to empty the trap and then the sequence starts again.

When an ion enters the detection cylinder, it induces a charge which dissipates when it leaves. The induced charge is detected by a charge-sensitive amplifier. The resulting signal is amplified, digitized, and then transferred to a computer for analysis in real time.⁵³ The time domain signals are analyzed by fast Fourier transforms (FFTs). The m/z is determined from the oscillation frequency and the charge is derived from the magnitudes. Trapping events where ions were not trapped for the full trapping period (t_trap) were discarded.

Sample Preparation.

Truncated hepatitis B virus (HBV) capsid protein (Cp149) (kindly provided by Prof. Adam Zlotnick of Indiana University) was assembled in 300 mM sodium chloride for 24 h, dialyzed into 100 mM ammonium acetate (Sigma-Aldrich, 99.999% trace metal basis), and stored for at least a week before use (to give assembly errors time to self-correct³⁹). The initial concentration of the capsid protein was 1 mg/mL. Assembly yields predominantly the icosahedral T = 4 capsid (around 32 nm in diameter) composed of 120 capsid protein dimers along with a smaller amount (around 5% in this case) of the icosahedral T = 3 capsid with 90 protein dimers. The pseudo critical concentration for HBV assembly in 300 mM NaCl is 3.7 μM and so the final capsid concentration is around 0.22 μM.⁵⁴ Samples of the stock solution were purified by size exclusion chromatography (SEC) with a 6 kDa cutoff (Bio Rad Micro Bio-Spin P-6 Column). Aliquots of the purified solution were then diluted with 100 mM ammonium acetate to the required concentration which ranged from 0.05 to 100 μg/mL.

Pyruvate kinase (PK), purchased from Sigma-Aldrich, was prepared at 10 mg/mL in ammonium acetate. Aliquots of the stock solution were purified by SEC with a 6 kDa cutoff (Bio Rad Micro Bio-Spin P-6 Column). The purified solution was then diluted to 2 mg/mL with 100 mM ammonium acetate.

RESULTS AND DISCUSSION

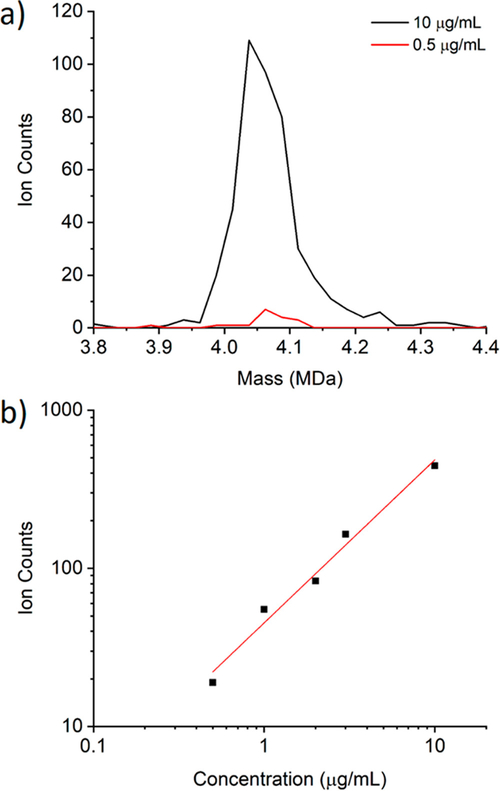
Figure 2a shows portions of two representative CDMS mass distributions measured for the HBV sample. Results are shown for two concentrations: 10 μg/mL (a 100-fold dilution of the HBV stock solution) and 0.5 μg/mL (a 2000-fold dilution). The CDMS distributions shown in Figure 2 were recorded for 16.6 min (10 000 trapping events) and are plotted with 25 kDa bins. With 10 μg/mL, there is a prominent peak at a mass of around 4.05 MDa, close to the expected mass for the T = 4 capsid of HBV Cp149.³⁹ With 0.5 μg/mL, the peak has almost disappeared. Note that the rate of spurious signals in CDMS is very small because the ions are measured for a relatively long time (100 ms). The HBV T = 4 capsid ions carry around 140 elementary charges and the probability that a random noise signal could masquerade as an ion signal of this magnitude over a time period of 100 ms is vanishingly small. Thus, the background noise in the region of interest is also vanishingly small.

Figure 2.

(a) CDMS mass distributions measured for HBV T = 4 capsids with sample concentrations of 10 and 0.5 μg/mL. Both distributions were recorded for 16.6 min (10 000 trapping events) and plotted using 25 kDa bins. The distribution measured with 0.5 μg/mL contains 19 ions. (b) shows a log−log plot of the number of ions detected in the 3.8−4.4 MDa mass window shown in (a) during 10 000 trapping events for a range of concentrations from 0.5 to 10 μg/mL. The points are the measured values and the line is a least-squares fit. The equation for the line is y = 1.66 + 1.031x. The slope (1.031) is close to the expected value of 1.0.

Analyte chargeability is a key factor determining detection efficiency in electrospray mass spectrometry of small molecules.⁵⁵ This is expected to be less important for the much larger species studied here because the ions are highly charged and there are many possible ionization sites. For large ions, the chargeability of a particular site may marginally affect the overall charge carried by the ion but not whether the ion is charged. Large ions are thought to be generated by the charge residue mechanism where the solvent evaporates from the electrospray droplet to leave behind a charged ion.⁵⁶ The number of analytes contained in an electrospray droplet could influence the detection efficiency. An estimate of the average number of capsids present in a droplet can be obtained from the concentration and droplet size. The average size of the primary electrospray droplets can, in turn, be estimated from the electrospray conditions.^57,58 For an estimated droplet size of 70 nm, the average number of capsids per droplet is around 0.025 (i.e., 1 in 40 droplets contain a capsid) at the concentration of the HBV stock solution (1 mg/mL).

Figure 2b shows a log−log plot of the integrated counts in the 3.8−4.4 MDa range against HBV concentrations from 0.5 to 10 μg/mL. The points are the measured values and the line is a least-squares fit. A slope of 1.0 is expected for a log−log plot of response versus concentration and slopes close to 1.0 were found. In this case the slope is 1.031. On the basis of these results, we take the limit of detection for HBV T = 4 capsids to be around 0.5 μg/mL. This corresponds to 1.1 × 10⁻¹⁰ mol/L or 6.6 × 10¹⁰ particles/mL. During the 16.6 min collection period, approximately 1.3 μL of solution was electrosprayed. Taking this into account, the limit of detection is around 0.14 fmol or 8.6 × 10⁷ particles. During the 16.6 min data acquisition time, 19 ions were detected. Thus, the detection efficiency for HBV T = 4 capsids is around 2.2 × 10⁻⁷.

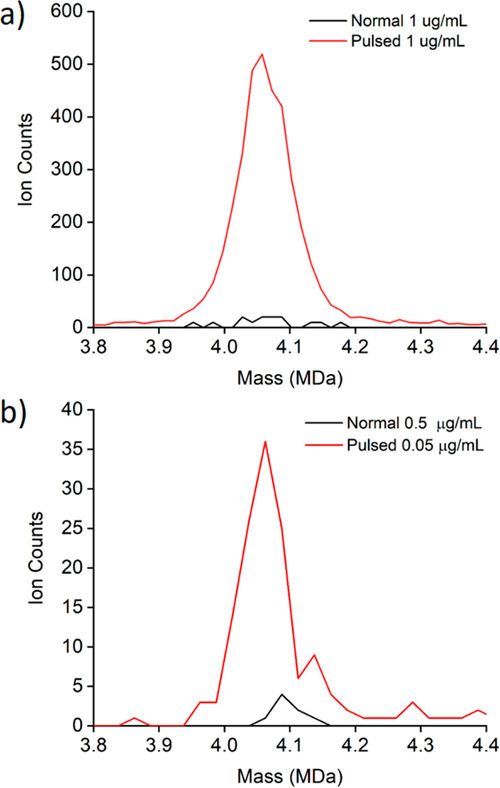
As noted above, the detection efficiency can be improved by accumulating and storing the ions in the hexapole and allowing them to exit so that their arrival at the ion trap is synchronized with the opening and closing of the trap. Figure 3a shows a comparison of CDMS mass distributions measured for the HBV capsids for a concentration of 1 μg/mL for both normal mode (i.e., nonpulsed) (black line) and pulsed mode (red line). Clearly, the intensity in the distribution measured with the pulsed mode is much larger than that with the normal mode; the normal mode distribution contains 15 ions and the pulsed contains 3695 so the intensity gain in this case is 246. Figure 3b shows another comparison between normal mode and pulsed mode. In this case the normal mode distribution was measured with a concentration of 0.5 μg/mL and the pulsed mode with a concentration of 0.05 μg/mL. The normal mode distribution contains 8 ions and the pulsed mode contains 145, so the intensity gain is 181 (taking into account the concentration difference).

Figure 3.

CDMS mass distributions measured for HBV T = 4 capsids. The black lines show distributions measured under normal (i.e., nonpulsed) conditions and the red lines show the distributions recorded with the hex-quad plate pulsed to store ions. In (a), both distributions were recorded with a protein concentration of 1 μg/mL. In (b), the concentrations were 0.5 μg/mL for the normal mode distribution and 0.05 μg/mL for pulsed mode. All distributions use 25 kDa bins.

The intensity gain depends on the trapping efficiency, the pulse width (t_W in Figure 1b), and delay times (t_D1 and t_D2). We found that the signal from ions trapped in the hexapole persists for more than 20 s after the electrospray source is turned off, indicating that ions are being efficiently trapped in the hexapole. On one hand, if the pulse width (t_W) is too short, there is not enough time for ions to leave the hexapole. On the other hand, if the pulse width is too long, the benefit of accumulating ions in the ion trap is lost and the signal approaches the value for nonpulsed mode. We found that the intensity gain from the pulsed mode of operation averaged around 200, with the pulse width and delay times optimized. As noted in the introduction, for an m/z of 28 800 Da, only around 1 ion in 620 can be trapped in the nonpulsed mode. By operating in pulsed mode, a large fraction of the lost signal is recovered. With the pulsed mode of operation, the limit of detection for HBV T = 4 capsids is around 200 times lower: 5.5 × 10⁻¹³ mol/L or 3.3 × 10⁸ particles/mL. This corresponds to around 0.7 amol or 4.3 × 10⁵ particles for a 1.3 μL sample. The detection efficiency for HBV T = 4 capsids with the pulsed mode of operation is around 4.4 × 10⁻⁵ (i.e., 200 times the detection efficiency with nonpulsed mode).

With the high sensitivity afforded by pulsed mode CDMS, it is relatively easy to simultaneously inject many ions into the ELIT. In our early work using CDMS, we restricted the measurements to single trapped ions and trapping events where more than one ion was trapped were discarded. It is feasible to analyze the multiple ion-trapping events and determine m/z values and charges for a few simultaneously trapped ions.^31,59 However, when two or more highly charged ions are simultaneously trapped in an ELIT, ion−ion interactions cause trajectory and energy fluctuations which degrade the m/z resolving power.⁵⁹ Because high m/z resolving power is not required for these studies, the multiple ion-trapping events were analyzed. However, the trapping of multiple ions with similar m/z values can lead to errors in the data analysis and so the measurements reported here were restricted to samples where on average one ion is trapped per trapping event. The distribution of trapped ions is a Poisson distribution, and when the average trapping efficiency is around 1.0, roughly one-third of the trapping events are empty, another one-third contain a single ion, and the remaining one-third contain two or more ions. For a sample concentration of 10 μg/mL, the number of trapped ions in pulsed mode is much larger than 1 per event on average and the sample must be diluted for measurements to be performed.

There is a substantial distance (0.86 m) between the hexapole, where the ions are stored, and the ELIT (see Figure 1a). The time it takes for an ion to travel this distance depends on its kinetic energy and m/z. The HDA transmits only ions within a narrow kinetic energy distribution, so the transit time depends mainly on the ion’s m/z. If the pulse width (t_W) is short, a range of m/z values will be trapped for a given delay time (t_D), where t_D is the time between the opening of the hex-quad plate and the closing of the front endcap of the ELIT (t_D = t_D1 + t_D2 in Figure 1b). The largest m/z (i.e., the slowest) ion that can be trapped, under these circumstances, is one that has just entered the detection cylinder when the front endcap switches to reflection mode:

$${\left\{\frac{m}{z}\right\}}_{\text{MAX}}=2eE\frac{t_D{}^2}{d_1{}^2}$$ (2)

In eq 2, e is the elementary charge, E is the ion energy, and d₁ is the distance from the hex-quad plate to the entrance of the detection cylinder. The smallest m/z (i.e., the fastest) ion that can be trapped is one that has traveled through the detection cylinder, been reflected by the back endcap, traveled back through the detection cylinder, and is just about to exit when the front endcap switches to reflection mode:

$${\left\{\frac{m}{z}\right\}}_{\text{MIN}}=2eE\frac{t_D{}^2}{{\left(d_1+3d_2\right)}^2}$$ (3)

In eq 3, d₂ is the length of the detection cylinder. 2d₂ of the 3d₂ in the equation results because the ion travels both back and forth through the detection cylinder and the other d₂ results from the time spent in the endcap (this time is equal to the time spent traveling through the detection cylinder for the cylindrical ELIT used here⁴⁸). The ratio of the maximum to minimum m/z that can be trapped is

$$\frac{{\left\{m/z\right\}}_{\text{MAX}}}{{\left\{m/z\right\}}_{\text{MIN}}}=\frac{{\left(d_1+3d_2\right)}^2}{d_1{}^2}$$ (4)

Thus, the range of m/z values that can be trapped is independent of the ion energy and the delay time. Longer delay times cause the m/z window to shift to larger m/z values but the relative width of the m/z window remains the same. The ratio of the maximum to minimum m/z values for the CDMS instrument employed here is 1.38, so the width of the m/z window that can be trapped with a single delay time is {m/z}_MIN to 1.38 × {m/z}_MIN. For example, if the delay time is set so that 25 kDa is the minimum m/z value that can be trapped, ions with m/z values up to 34.5 kDa can be trapped at the same time.

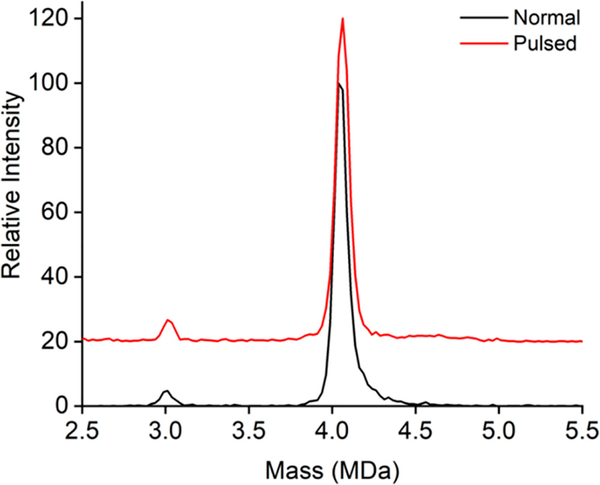
As noted above, assembly of the HBV capsid protein leads to a small amount of the smaller T = 3 capsid in addition to the T = 4. The average m/z for the T = 4 ions is 28 700 Da and the average m/z for the T = 3 ions is 25 500 Da. The ratio of these m/z values is 1.13, which falls within the range that can be trapped simultaneously. Figure 4 shows CDMS mass distribution measured for HBV showing the T = 3 peak at around 3.0 MDa and the T = 4 peak at 4.05 MDa. The black line in Figure 4 shows the distribution measured under normal operating conditions (i.e., nonpulsed) and the red line is the distribution measured with the hex-quad plate pulsed. The HBV protein concentration was 100 μg/mL for nonpulsed and 1 μg/mL for pulsed. The fraction of T = 3 capsids (from the integrated counts) is 0.0435 in the normal mode distribution and 0.0470 in the pulsed mode. However, the detection efficiency in the normal mode distribution is proportional to (m/z)^1/2 because larger m/z (i.e., slower) ions spend a longer time in the trappable region of the ELIT.⁶⁰ In the pulsed mode, all ions in the trappable region of the ELIT are trapped and the detection efficiency for those ions does not depend on the m/z ratio. After correction of the normal mode ratio for the detection efficiencies, the ratio increases to 0.0461 (compared to 0.0470 for pulsed mode). Thus, the intensity ratio is not significantly affected by the pulsed mode of operation.

Figure 4.

CDMS mass distributions measured for HBV capsids. There are peaks due to the T = 3 capsid at around 3.0 MDa and the T = 4 capsid at 4.05 MDa. The black line shows the distribution measured under normal (i.e., nonpulsed) conditions with an HBV protein concentration of 100 μg/mL. The red line shows the distribution recorded with the hex-quad plate pulsed to store ions with an HBV protein concentration of 1 μg/mL. The relative intensities of the T = 3 and T = 4 peaks are almost identical in the two distributions. The distributions were plotted with 25 kDa bins.

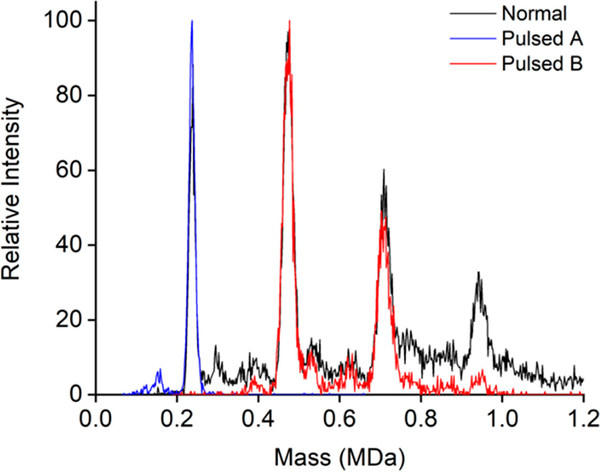
If the m/z distribution is broader that the {m/z}_MIN to 1.38 × {m/z}_MIN window, the delay time can be adjusted to trap different portions of the distribution. Figure 5a shows the CDMS mass distributions measured for a pyruvate kinase (PK) sample. The black line shows the distribution measured under normal (i.e., nonpulsed) conditions where peaks due to the PK tetramer (230 kDa), octamer (460 kDa), dodecamer (690 kDa), and hexadecamer (920 kDa) are evident. It is not possible to transmit all of the oligomers simultaneously in pulsed mode. However, by adjusting the delay time, it is possible to transmit different m/z bands. The blue CDMS mass distribution shown in Figure 5 was measured with the delay optimized to transmit m/z values that include the tetramer (m/z values ranging from around 6600 to 9150 Da were transmitted). The red distribution was measured with the delay optimized to transmit the octamer and dodecamer. In both cases, the ratios of the minimum and maximum m/z’s transmitted are close to the value predicted above (1.38). The ability to select portions of the m/z distribution is valuable in a number of applications. Because individual ions are processed in CDMS, it is beneficial to not spend time processing ions that do not contain useful information. Thus, a way to discriminate against portions of the m/z distribution that do not contain useful information is valuable. For example, many samples contain a substantial number of low mass ions that could be discriminated against using this approach.

Figure 5.

CDMS mass distributions measured for a pyruvate kinase (PK) solution. There are peaks due to the PK tetramer (230 kDa), octamer (460 kDa), dodecamer (690 kDa), and hexadecamer (920 kDa). The black line shows the mass distribution recorded under normal (i.e., nonpulsed) conditions. The red and blue lines show distributions recorded with the hex-quad plate pulsed to store ions. The delay time (t_D1 + t_D2) was adjusted to transmit ions with different m/z windows. For the blue line (pulsed A) the delay time was selected to transmit the tetramer, and for the red line (pulsed B) the delay time was selected to transmit the octamer and dodecamer.

CONCLUSIONS

Pulsed mode CDMS, where ions are accumulated and stored between trapping events, improves the sensitivity of CDMS by more than 2 orders of magnitude. In this work the ions were stored in a hexapole. When a pulse of ions exits the hexapole and travels to the ELIT, they disperse according to their m/z ratios. Because of this dispersion, a range of m/z values are trapped in the ELIT. With our current CDMS instrument, the range of m/z values has a relative width of 1.38. For a broad m/z distribution (i.e., relative width >1.38), the delay between when the ions exit the hexapole and ELIT closure can be adjusted so that different m/z windows are selected, making it possible to discard ions that do not contain useful information.

Titers are often low for high mass samples. Low solubility limits the maximum concentrations that can be obtained. However, more often than not the concentration is limited by the difficulty in generating the sample. The 2 orders of magnitude improvement in the sensitivity of pulsed mode CDMS will allow measurements to be performed for many samples where the signal was too low with normal mode CDMS. The improved sensitivity will also enable high-resolution measurements to be performed for more samples. High-resolution CDMS measurements require the ions entering the ELIT to have narrow energy, angular, and radial distributions. With the 2 orders of magnitude improvement in sensitivity, it is possible to trade signal for resolution and discard some ions to narrow the energy, angular, and radial distributions for ions entering the ELIT.