Abstract
We review the theory and algorithms of electrophysiological brain connectivity analysis. This tutorial is aimed at providing an introduction to brain functional connectivity from electrophysiological signals, including electroencephalography (EEG), magnetoencephalography (MEG), electrocorticography (ECoG), stereoelectroencephalography (SEEG). Various connectivity estimators are discussed, and algorithms introduced Important issues for estimating and mapping brain functional connectivity with electrophysiology are discussed.
Keywords: brain functional connectivity, electrophysiological connectivity, effective connectivity, EEG, MEG, intracranial EEG, electrophysiological Connectome
I. INTRODUCTION
Brain function and dysfunction are encoded in networks within the brain that are distributed over 3-dimensional space and evolves in time. It is of great importance to image brain activation and functional connectivity which are the building blocks of neural information processing. Such knowledge plays an important role for neuroscience research and clinical applications of managing various brain diseases. It is important to map the spatially distributed and temporally dynamic neural activity with high resolution in space and time domains. Noninvasive high-resolution imaging of spatio-temporal patterns of neural activation and connectivity would greatly improve our understanding of the mechanisms of perception, attention, learning, etc., and for managing neurological mental diseases such as epilepsy, stroke, neurodegeneration, depression, etc.
Various neuroimaging modalities have been pursued to achieve the afore-mentioned goal, including functional magnetic resonance imaging (fMRI), electrophysiological neuroimaging such as electroencephalography (EEG), magnetoencephalography (MEG), and electrocorticography (ECoG), as well as functional near-infrared spectroscopy (fNIRS) and positron emission tomography (PET). Of these imaging modalities, fMRI has relatively high spatial resolution but low temporal resolution, while electrophysiological methods have high temporal resolution but limited spatial resolution. fNIRS has the ability to measure both oxyhemoglobin and deoxyhemoglobin and can also be portable or wearable, allowing experiments in naturalistic environments for extended periods, yet it does not offer whole-brain coverage and has limited spatial and temporal resolution. fMRI is widely utilized for neuroscience research and plays a significant role in improving our multimodal imaging capability. However, due to its limited temporal resolution, fMRI currently cannot be used to image dynamic brain activity in the time frame in which these processes occur, i.e. in the sub-second range.
Innovations in source imaging have turned EEG and MEG from a 1-dimensional sensing or 2-dimensional mapping technique into a 3-dimensional source imaging modality for mapping dynamic distributed brain activity, arising primarily from the cortex, with high temporal (ms) and increasing spatial (5-10 mm) resolution. The availability of dense array EEG mapping systems has offered opportunities to sense the spatiotemporal distributions of brain electric activity over the scalp. Numerous investigations in cognitive neuroscience, clinical neurology, psychiatry, and neurosurgery have revealed the power of EEG source imaging in characterizing dynamic brain activity [111-112],[114],[116]. Recent advances in EEG source imaging have significantly improved performance in localizing brain activity from event-related potentials in healthy human subjects, and from interictal spikes in epilepsy patients. Advanced EEG source imaging techniques have also demonstrated the ability to image oscillatory brain activity at various frequencies, for example in human subjects performing motor imagery for brain computer interface applications and for directly imaging oscillatory seizure activity in patients suffering from epilepsy. Applications to psychiatric and neurological research and practice are also a clear opportunity.
As opposed to source imaging that aims for the identification of functional segregation, connectivity analysis provides an important tool for understanding brain networks through which our brain functions under a highly interconnected organization. Studies have suggested the definition of connectivity through anatomical connections that are based on brain structures, and functional and effective connectivity that is instead based upon the functional properties of the various cortical regions. Functional connectivity patterns have been estimated from fMRI using correlation mapping, revealing BOLD coherence and correlations among various brain regions. Intracranial EEG (iEEG), EEG/MEG, and the source signals reconstructed by EEG/MEG source imaging techniques have been proven efficient for measuring brain functional connectivity between various regions. Functional connectivity measures, such as coherence or causal directions, have been used to study brain networks associated with cognitive functions, spontaneous activities and neurological disorders. The goal of electrophysiological connectivity analysis is to infer neural connectivity: the causal influence that neural masses exert upon each other.
In this tutorial paper, we will describe the theoretical basis, computational algorithms, and applications of dynamic functional brain connectivity analysis from electromagnetic measurements. The merits, limitations, and needs for future development are also discussed.
II. Models and Methods for Connectivity Estimates
A. Conceptual framework for estimating neural connectivity
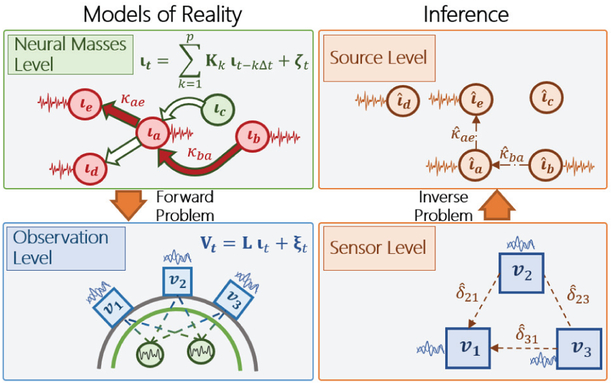
The ontology of the levels involved in neural connectivity are illustrated in Fig. 1. The relevant terms are defined as follows.
Fig. 1.
Levels involved in estimating neural connectivity from EEG and MEG. On the left models of brain reality. On the right, inferences made about this reality. Identifying neural connectivity is the ultimate objective. This is defined by the interactions (κ) between the activities of neural sources (ι). These in turn, determine the observed time series (ν) at the sensors. From these time series one can obtain measures of statistical dependence (δ). The attempt to use δ as a proxy for κ is known as “sensor level connectivity”. “Source level connectivity” solves the inverse problem to estimate κ. Estimated quantities at sensor and source levels are denoted as , , .
Neural entity: a set of neurons that are under consideration. The activity of a neural mass (measured as the amount of action potentials or ionic currents produced) will be denoted with the symbol ιn and that of N neural masses to be analyzed by the vector ιN×1.
Anatomical connectivity: the axonal, monosynaptic connection of one neural mass with another
Neural connectivity: the causal influence of one active neural mass upon another. The strength of the neural connectivity (causal effect) of the neural mass m upon the mass n shall be denote by K(m, n), with all connectivity strengths arranged into the matrix:
Sometimes, connectivity may also be referred as functional connectivity, which measures correlation between neural masses; or effective connectivity, which measures causal relationships among neural masses [97].
Neural connectivity is mediated by the transmission of action potentials over anatomical connections and therefore affect the target with a connectivity delay T(m, n) The set of all delays is denoted by the matrix:
The evolution of activity in a neural network is described by the state evolution equation formulated generally as a Nonlinear Autoregressive Moving Average Model with exogenous inputs ut (NARMAX):
where ιt is the state vector describing neural activity, f a nonlinear function that governs the dynamics of the neural network, ut an external input (e.g. a stimulus), ζt a noise input, Δt is the discretization period, and pι, pζ, pu, are, respectively, the time lags of the states, noise and input, required for the model to be Markovian. A very simple model (discussed below) assumes f to be linear, without external input and without dependence on past values of noise input (eliminating the MA component), This is the well-known linear p-order Multivariate Autoregressive Model:
| (1) |
The state evolution equation must be supplemented with the EEG/MEG observation equation:
| (2) |
Equations (1) and (2) define the EEG/MEG state space model and indicate that estimation of neural connectivity can fall within the framework of state-space estimation.
B. Cross-correlation and coherence
The simplest method to find statistical dependencies between signals is correlation (in the time domain) and coherence (in the frequency domain). Correlation between signals can arise when there is true connectivity between brain areas, but care must be taken for spurious sources of correlation such as common input. A simple model assuming linear relationship between signals is that one signal is a delayed and noisy version of the other:
| (3) |
where τ0 represents the time delay between signals x and y and e a noise term. The presence of a positive delay means that directionality goes from x to y.
Then the cross-correlation corr between x and y is expressed by the time domain expectation operation:
| (4) |
which is maximal for t = τ0. Normalizing the cross-correlation by the energy of each signal the correlation coefficient can be calculated.
In the frequency domain, the linear relationship between signals can be estimated based on the coherency – or ‘ complex coherence’ – measure [1], [2]:
| (5) |
where xv and yv are Fourier transforms of xt and yt, respectively. The squared module of C is the coherence, which ranks between 0 (no dependence and 1 (maximal dependency). The slope of the phase can be used to estimate the time delay between the signals. Indeed, if there is a delay τ0 between x and y, then
And,
| (6) |
Here (in a noise free situation), the coherence between the signals is 1, and the slope of the phase is proportional to the delay between signals [1] (this is called the ‘group delay’ in signal processing terms). It is important to note that in the presence of pure sine waves (i.e. Dirac in the frequency domain), then the delay measure at this single frequency is ambiguous (same dephasing would arise if a multiple of the period is added to the delay). It is only by having signals occupying a large frequency band than this can be disambiguated, using the group delay. Similar coherence measures can be performed in the wavelet domain [3]. Thus, Gotman measured connectivity on surface EEG in epilepsy patients with bilateral spike and wave [1]. Coherence was thus measured on symmetric channels in order to measure time differences. Channels were in order to reduce volume conduction effects, and delays between activities in the two hemispheres were measured based on the slope of the phase. More recently, Nolte et al. has proposed to use the imaginary part of the coherence in an attempt to remove the influence of zero-lag correlations arising from volume conduction [4].
C. Granger causality
Granger Causality (GC) was introduced in neuroscience to make inferences about directed brain functional connectivity. The method stems from the definition of causality in the statistical sense provided by Wiener in 1956 [5] according to which a time series has a causal (in the statistical sense) effect to another if the ability to predict the second time series worsens when information about the first one is removed from all the other available information. Granger [6] provided an implementation of Wiener’s definition using linear autoregressive models of stochastic processes. GC implies directionality, since a variable “causes” another variable if the former contains information that helps predict the future of the latter. This relationship is not symmetrical by construction, and can be bidirectional, thus enabling the detection of directed and reciprocal influences (which are common in brain coupling). The first - and most common - implementation of Granger Causality is based on linear Autoregressive (AR) modeling of time series, under the assumption that the two variables are stochastic and wide-sense stationary. Two time series x(1) and y(2) are modeled by a reduced AR (including just the past samples from the time series itself) and by a bivariate one BVAR (including also the past samples of the other time series), as follows:
AR
| (7) |
BVAR
| (8) |
where k is the time lag between samples and p is the model order, i.e. the maximum lag included in the model.
The improvement in the prediction of each time series due to the other one is assumed if the variability of the residual of the BVAR model (8) is significantly reduced with respect to the variability of the residual of the reduced AR model (7) , as expressed by the following indexes:
| (9) |
| (10) |
A reduction of the variance , of the residuals of the bivariate model (8) with respect to the variance , of the residuals of the univariate model (7) results in a GC index greater than zero, thus fulfilling the Wiener-Granger definition. Causality in the two directions is represented by different parameters of the model. This implies the directionality of the method: GCx→y ≠ GCy→x. It is important to stress that the reduced and the full model needs to be estimated at the same time in order to avoid high variance and bias [271]-[273].
The AR modeling allows an easy and straightforward implementation of Wiener-Granger causality under relatively wide assumptions, usually met by neuroimaging and neurophysiological data; it enables the estimation of the strength and the direction of the causal links as well as their statistical testing [6]. However, different implementations include nonlinear [274]-[276], non-parametric [7] and adaptive [277] modeling.
D. Multivariate time series
An important advancement in GC was provided by Geweke [8] with an extension of the basic Wiener-Granger concept to the frequency domain, through the spectral decomposition of the time domain statistics by Fourier transform of the VAR model. The spectral decomposition of GC is particularly important with neurophysiological data, which are based on oscillatory synchrony between neural populations. Importantly, Geweke also introduced an extension of GC to multivariate variables, by defining a conditional multivariate GC [9] and later an unconditional one [8].
The extension of (8) to the N time series xt = [xt(1), xt(2),…, xt(N)]T leads to the multivariate AR:
| (11) |
where A1, A2,…, Ap, are the N×N matrices of model coefficients Ak(m, n), A1 is equal to the identity matrix and et = [et(1), et(2),…, et(N)]T is the vector of the model residuals.
To analyze the spectral properties of the process, Eq. (11) is transformed to the frequency domain:
| (12) |
where
| (13) |
is the frequency transform of the model parameters A along the p lags considered, j is the imaginary unit and Δt is the temporal interval between two samples.
The model expressed by (12) can be also rewritten as:
| (14) |
where B(ν) is the transfer matrix of the system seen as an N-dimension generator filter.
From the transfer matrix, the power spectra S(ν) can be computed as follows:
| (15) |
where the superscript * denotes transposition and complex conjugate and Σee(ν) is the spectral matrix of the model residuals, including the variance of the m-th innovation process et(m) and the covariances Σee(ν; m, n) of all possible pairs of residuals et(m), et(n).
The use of a multivariate model is crucial when dealing with complex systems (like the brain) that are based on large networks. Moving from a pairwise to a multivariate approach can significantly increase the accuracy of the reconstructed connectivity pattern [10], even if at the expenses of an increased model complexity resulting in a more difficult model identification process.
D.1. Directed transfer function
A different approach to the spectral multivariate analysis proposed by Geweke was introduced (specifically for the brain functional connectivity) by Kaminski and Blinowska in 1991 [11]. Given the spectral representation of the MVAR model as in (14), the Directed Transfer Function (DTF) directed from m to n was defined as follows:
| (16) |
A normalization of DTF can be performed by dividing each value of the estimator by the squared sums of all elements of the relevant row [11]:
| (17) |
Normalized DTF values belong to the interval [0, 1], and satisfy the following condition:
| (18) |
D.2. Partial directed coherence
Partial Directed Coherence (PDC) was introduced in [12] as a factorization of Partial Coherence. Its basic structure, similarly to DTF, is based on a Multivariate Autoregressive modeling of the entire set of time series representing the brain activity at different sites. However, PDC is based on the transfer matrix A(ν) of the predictive MVAR filter (instead of its inverse B(ν), like DTF):
| (19) |
A comparison between the two approaches reveals more accuracy and a better interpretation of the quantitative values for DTF, but a more accurate reconstruction of the network structure by PDC [13].
D.3. Statistical assessment of DTF and PDC
The assessment of DTF and PDC against the null case can be achieved by the generation of empirical distributions of the null case [14] or by (less time consuming) asymptotic distributions [15], [16]. In fact, it was demonstrated [15] that the squared PDC estimator tends to a Gaussian distribution in the non-null case and to a χ2 distribution in the null case. Following this assumption, it is possible to derive the probability distribution of a function of the null-case squared PDC estimator (the χ2 distribution) by knowing its asymptotic variance.
The method consists of a generalization of the delta method consisting of an appropriate Taylor expansion of the estimator distribution. The null hypothesis is defined as follows:
| (20) |
In the case of null-hypotliesis rejection, is asymptotically normally distributed, and thus,
| (21) |
where Ns represents the number of data samples of the temporal time series, are the entries of the MVAR parameters matrix (explicit dependence from frequency is omitted for brevity), and γ is as follows:
| (22) |
where is the gradient of ∣Π(ν; m, n)∣2:
| (23) |
and Σ is the expected covariance matrix, contains on its main diagonal 2 N2xN2 matrices I{m,n} made by zeros except for the entry (k, l): ((n – 1)N + 1, (n – 1)N + m) which is equal to 1 and contains N2xN2 matrices I{n} made by zeros except for the entry (k, l): (n – 1)N + 1 ≤ k = l ≤ nN. If the null-hypothesis is verified, such gradient is zero; thus, it is necessary to use the Jacobian:
| (24) |
The statistical threshold of significance corresponds to the 95th percentile of this distribution. Details on the performance of such approach can be found in [16].
D.4. Different normalizations of DTF and PDC
Even if the basic meaning of DTF and PDC in terms of multivariate spectral distribution of GC is the same, and the fact that both approaches reveal similar network structures [13], the meaning of the estimators in terms of their value has been long discussed in the literature, and many different normalizations have been proposed. Squared versions of PDC in its different normalizations are usually adopted, due to higher stability and accuracy [17], [18]:
| (25) |
To improve the physiological interpretation of the estimated information flows, a row-wise normalization (rPDC) was proposed in [18], normalizing each contribution directed from m to n by dividing it by the sum of all links directed to the same target signal m and by squaring the index (similar to what was done for DTF):
| (26) |
A generalized version of PDC (gPDC) was introduced by [19] to improve the estimation of the causal coupling in the presence of scale differences between the multivariate signals used for the estimation:
| (27) |
Later, an extended version (ePDC) was introduced by [14] by computing (27) on an MVAR model including instantaneous interactions, i.e. by allowing the lag k to take the zero value as well, thus including instantaneous effects from xt(m) to xt(n) into the model, in the form of the coefficients A0(m,n) ≠ 0 even if m≠n.
Also, the information PDC (iPDC) has been introduced [20] to provide a precise interpretation of PDC in terms of the mutual information between partialized processes, establishing it as a measure of direct connectivity strength:
| (28) |
The same normalizations were provided for DTF [21].
Finally, in some normalizations the estimator is weighted by the power spectral density of the connectivity source, to improve the physiological interpretability of the results [18]:
| (29) |
where Sxx(ν; n, n) is the power spectral density of the source signal n, obtained by (15).
The equivalence of all these measures in terms of the connectivity pattern they provide was demonstrated in [21], [22]. However, the choice of the normalization is still crucial when dealing with the physiological interpretation of the estimator and its modifications between conditions or in time. This aspect will gain more and more importance with the use of these estimators to define quantitative indices of connectivity to be used for clinical applications.
E. Adaptive DTF and PDC
Traditional definitions of GC, DTF and PDC all rely on the hypothesis of wide-sense stationarity of the data, needed to build the MVAR model on which the estimators are computed. However, this can be an important limitation when the stationarity is not verified and when one is interested in the dynamic behavior of the brain in terms of connectivity (for a review, see [23]). To overcome this limitation, a number of approaches were developed to provide a time-varying extension of all MVAR- and GC-based connectivity estimators. All these approaches are based on adaptive MVARs with time-resolved parameters:
| (30) |
in which the AR parameters Ak,t are a function of time.
Among all time-varying MVAR estimation approaches, Kalman filter-bases MVAR modeling gained wider consent in high-dimensional EEG data due to their accurate estimation of non-stationary data [24], [25]. The application of the Kalman filtering algorithm to MVAR modeling is based on a linear state-space representation of the signal. The state equation relates the state of MVAR parameters A at time t + Δt to their state at time t plus the state white noise process gt:
| (31) |
The MVAR observation equation is provided by the AMVAR:
| (32) |
to obtain the adaptive MVAR parameters, these equations can be solved by classical Kalman filter through a Recursive Least Squares (RLS) approach with forgetting factor [13], [18], [24], [26] or by a general linear Kalman filter (GLKF) approach [25]. A comparison between different approaches in terms of performances in the accuracy and dynamics was provided in [13], [27].
The result of this procedure is an adaptive MVAR with time varying parameters. All the estimators previously described (in sections II.C and II.D) can be computed on the AMVAR, thus resulting in time-resolved GC, DTF and PDC that can return information about the dynamics of brain networks [18].
F. Phase-phase connectivity, amplitude-amplitude connectivity, cross-frequency interactions
A number of metrics have been used to estimate electrophysiological brain connectivity based on different aspects of neuronal activity [28]. While some of the earliest approaches focused on spectral coherence [4], [29] (see section IIB), most recent approaches examine either amplitude envelope correlations [30]–[34], or phase synchronization [35]–[38] between neuronal oscillations of the same frequency. Of these different metrics used to quantify connectivity, some are less prone than others to report spurious interactions due to volume conduction in M/EEG [39], [40], although none can alleviate the problem entirely [41] (also see sections IV.A and IV.B).
Analyses of electrophysiological data with phase- and amplitude-based metrics give partially overlapping, partially differing results; thus these metrics may reflect different processes. At the same time, it has been shown that in noisy signals, phase and amplitude dynamics influence each other [41]–[43] and the reliability of phase estimation inherently depends on signal-to-noise ratio (SNR) and may generally be more accurate in the presence of higher signal amplitudes [44].
Both instantaneous amplitude ρt and phase (φt are derived from the complex analytic signal zt. The analytic signal in a narrow frequency band can be constructed using the Hilbert transform H of a band-pass filtered signal xt in a simple manner: zt = xt + iH(xt) = ρtexp(iφt) [45] or convolving the broad-band signal with a Morlet wavelet centered around the frequency of interest [46].
Amplitude envelopes can capture slow fluctuations similar to those measured in fMRI [47]. The analysis of amplitude envelopes in MEG has revealed spatial patterns of activation that strongly resemble the topography of fMRI resting-state networks [32], [33], [48]. The amplitude correlation between two analytic signals can simply be estimated using the Pearson correlation coefficient:
| (33) |
where ρt(m) is the amplitude envelope, σρ(m) the variance of ρt(m) and cov(ρt(m), ρt(n)) the covariance of both signals. To exclude first-order spurious interactions arising from signal mixing, the signals can be orthogonalized prior to computation of r either in time [30] or frequency domain [33].
Phase synchronization is thought to facilitate improved communication and “binding” because it endows a neuronal assembly an advantage over competitors in engaging a postsynaptic target [49], [50]. During its high-excitability phases, an oscillating neuronal population can better process incoming signals than in its low-excitability phases. Populations whose signals arrive at this phase at an optimal phase may have an advantage over others. Thus, an optimal relationship between populations enhances communication while the opposite phase difference suppresses it [51]. The most standard metric of phase synchrony is the phase-locking value (PLV) [35] (φk corresponds to the k-th point in the time discretization Δt), but various other metrics have been introduced. Some metrics, like the [38] and the [41] only use the imaginary part of the signal, thus suppressing zero-lag interactions, which are partly due to instantaneous mixing.
| (34) |
where Im is the imaginary part, Szz(m, n) is the cross-spectrum of the complex signals zt(m) and zt(n) and E{ } is the expectancy value operator.
Phase synchronization has been reported at all frequency bands. A well-studied finding is gamma-band synchrony supporting processing of visual signals and visual attention [52]–[55]. In general, gamma activity and synchrony are supposed to underlie sensory-driven bottom-up feedforward processing, while synchronization in lower frequency bands may serve top-down feedback processing and regulation of activity [56], [57], with theta underlying attentional sampling, and alpha underlying inhibition and sustained attention [58], [59].
Several studies have also provided direct findings for the hypothesis that communication between regions depends on their phase relationships [60]. Selective synchronization enhances relevant input which can be modulated by sensory and motor events. Diversity of phase relationships among groups of neuronal oscillators supports rapid adaptability to novel signals and direction of attention [61]–[63].
Since relationships between same-frequency oscillations alone cannot explain cognition in its entirety, cross-frequency coupling (CFC) has also been studied. As the activity of a neuronal population can contain several frequency components, local CFC can occur, but inter-areal CFC has also been observed. The main two forms of CFC are phase-amplitude coupling (PAC), where the amplitude of the higher frequency oscillation is coupled to the phase of the lower frequency oscillation, and l0:l1 cross-frequency phase synchronization (CFS) [64], [65]. CFS can be seen as an extension of 1:1 phase synchrony, and computed as:
| (35) |
Where l0: l1 are points of the frequency domain discretization Δν that correspond to vlow : vhigh. PAC can be computed for example as the PLV of the slow-frequency phase and the phase of the amplitude envelope of the high-frequency signal filtered at νlow.
Local PAC between theta and gamma bands has been shown in many studies in the rat hippocampus, e.g. in [66], [67], but also in the human hippocampus [68] and cortex [69]. Several of these studies show that PAC supports task performance e.g. in working memory. Local CFS has also been observed in rat hippocampus [70], [71] and both local and inter-areal CFS have been observed in human cortex with MEG and EEG [36], [64], [65], [72] and in human hippocampus with intracranial EEG [73]. In contrast to PAC, CFS can operate at the faster timescale of the high-frequency oscillation [40] and occur even with weak coupling [74]. Similar to phase and amplitude metrics for within-frequency coupling, it is assumed that PAC and CFS, as well as cross-frequency amplitude correlations, capture different aspects of cross-frequency coupling [64], [65], [74], [75]. While most theoretical accounts of CFC so far have explicitly or implicitly assumed that the lower-frequency oscillation drives the higher-frequency in top-down manner, there is evidence that the reverse, ergo bottom-up-driven CFC, may also occur [76]. CFC might thus be involved in both feedforward and feedback processing.
Multiple studies have found evidence that working memory in humans is supported by PAC [68], [77] and CFS [64], [65], [73], [78]–[82] and theta-gamma CFC has been proposed to underlie representation of multiple items [83]. Also in resting state, there have been observations of PAC [76], [84], [85] and CFS [36], [86].
G. Dynamic causal modeling
Initially developed for the inference of effective connectivity in fMRI data, Dynamic Causal Models (DCMs) have been successfully extended to neuroelectromagnetic data (from local field potentials/intracranial recordings, to EEG and MEG).
The basic principle of DCM is the following: individual neural populations, and the connections between and within them, are described by biophysically plausible models. This simulated activity is then mapped to the measured data via a forward model appropriate for the recorded data (HRF, hemodynamic response function, convolution for BOLD, volume conduction for MEG/EEG, etc). Then the Likelihood (probability of the data given the model and its parameters), the Prior (probability of the parameters given a model), and the Model Evidence (probability of the data given a model) are combined through the Bayes’ theorem to estimate the Posterior (probability of the parameters given the data and the model). This Bayesian model inversion allows to answer the following questions: “which model architecture is most likely to generate the data?”, and “what parameter estimates have highest probability given the data and the model?” [87].
The models used to simulate neuroelectromagnetic data are neural mass models comprised of three subpopulations (Inhibitory Interneurons, Spiny Stellate Cells, and Pyramidal Cells), living on three connected cortical layers, as a simplified model of a macro-column. Directed connections between these layers are mapped according to the known cortical physiology. The set of first-order differential equations used for the simulation provide the input and output of these subpopulations. Ultimately, it is the potential generated by pyramidal cells which is projected to the sensors via a forward model [88]. Apart from the input coming from within the same population (intrinsic) and from other populations (extrinsic), each population can or cannot receive an external input (stimulus) or modulation (effect of attention, age, health status, time, etc…), according to the experimental design.
The model inversion needed to estimate the model parameters that best explain the observed data is a spatiotemporal one. The spatial part comes from the field distribution at all the sensors, that should be ascribed to a certain number of sources. It is important to note that when using neuroelectromagnetic data measured at the sensors, the source reconstruction is implicitly performed in the model inversion, and that DCM is itself a source reconstruction framework. Also, model comparison can be additionally used to determine the optimal number of nodes (regions among which the connectivity is evaluated), given that the data to which the model is fitted (field distribution at the sensors) is always the same [89]. Deep sources, whose activity could be difficult to reconstruct via an EEG/MEG inverse solution, can still be included in the model as hidden sources, although the fundamental challenge due to volume conduction effect remains [90], [91].
A list of general instructions in the form of a tutorial, including a flowchart depicting the inversion schemes appropriate for each case can be found in [92]; a MEG/EEG oriented primer, halfway between the software manual and a tutorial paper, is also available [93].
DCM has been applied to neuroelectromagnetic data across species and protocols. Some illustrative applications range from LFP rodent data under anesthesia [94], ERPs to probe consciousness [94], [95] or auditory processing [96], and recently fluctuations at rest.
The question might arise as whether is convenient to use DCM instead of data-driven methods such as Granger Causality and Transfer Entropy. This apparent dichotomy has been previously discussed, and boils down to asking what measure of causality we are after. The definition of causality can speak to temporal precedence, or (bio-)physical influence. Both these views can be encompassed by generative models and state-space models [97]. Whether these models should be biophysically plausible and based on differential equations (as in DCM), or aimed to estimate the state transition equation and the observation equation from the covariance of the data [98], the answer lies on our expectations from a causality measure in neuroscience. The directed influences between neural populations, inferred from Dynamic Causal Models, certainly imply a causal relation. On the other hand directed dynamical connectivity based on temporal precedence, without requiring an exact mapping onto the underlying physiology, can provide a convenient complementary view on the effect of the interaction between many variables, justified when we cannot be confident on the nature or the uniqueness of an underlying physical phenomenon [99].
H. Extension to information theory frameworks
The statistical dependencies among time series can be evaluated using information theory, using for example the concepts of joint entropy, conditional entropy, and mutual information [100]. In the presence of three or more (groups of) variables, the framework can be extended introducing the concept of interaction information, which can be used to decompose the joint informational contribution into redundant and synergetic [100]–[102].
The extension to directed dynamical influence is straightforward when the conditioning used above is applied to the past states of the system. In this formulation, Transfer Entropy [103] evaluates how much the driver time series influences the target by comparing the probability of finding the target in a present state given its past only, with the probability of the same state including the past of the candidate driver. This definition just expressed in terms of information (how is the probability of the current state of the target conditioned by the drivers?) can also be expressed in terms of predictability improvement (does the prediction of the current state of the target from its own past improve when the past of other variables is added to a model?). This distinction and the complementarity of these two frameworks have been clearly described in [104]. The two approaches are equivalent under the assumption of Gaussianity of the data, when a covariance-based estimator can be plugged in the probability-based framework, and Granger Causality is equal to twice the Transfer Entropy [105]. Similar to mutual information, also predictive information can be decomposed, defining synergy and redundancy in terms of directed influences [106], [107], as illustrated in Fig. 2. This representation can potentially solve algorithmic problems (conditioning to one variable per time in the presence of joint informational content would confound the retrieval of directed influences), and computational ones (reducing computational burden and curse of dimensionality by grouping variables). Furthermore, grouping variables in terms of their joint predictive information sheds further insight on the function of the system under study [107]–[110].
Fig. 2.
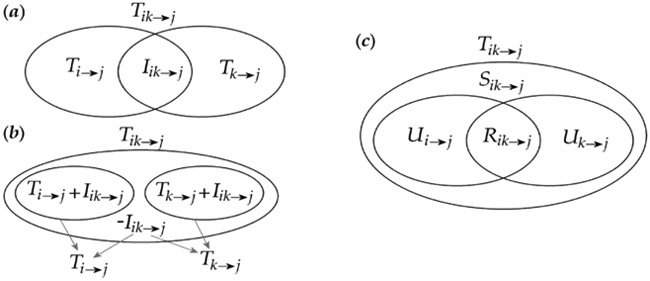
Venn diagrams depicting directed information decomposition. The terms Tx→y, denote Transfer Entropy, the terms Tik→j, denote Joint Transfer Entropy, Ixy→z the Interaction Information, Ux→y the Unique Information, Sxy→z and Rxy→z the Synergetic and Redundant joint information of variables x and y on variable z. Reproduced from [107].
III. METHODS
A. Source imaging and localization
The electrophysiological source imaging (ESI) is the process of estimating neural electrical activity underlying non-invasive electromagnetic measurements such as EEG and MEG [111]–[115] (see Fig. 3 for illustration). The principle of ESI is to reconstruct brain sources from EEG/MEG while accounting for the effect of volume conduction or field propagation. Solving this ill-posed problem encounters challenges if it is only treated mathematically. But significant progress has been made over the past 3 decades as anatomical and physiological a priori constraints can be utilized in source estimation.
Fig. 3.
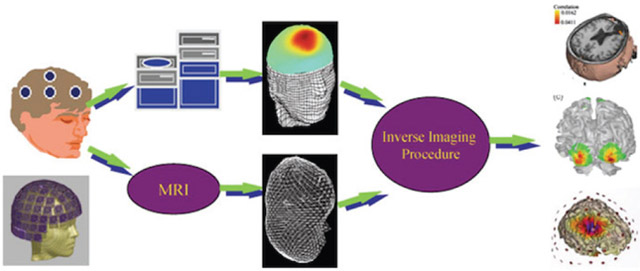
Schematic diagram of EEG/MEG source imaging (From [116]).
Given neuroelectric currents, finding the resulting electromagnetic signals on the scalp is called solving the forward problem of EEG/MEG. The electric/magnetic fields are generated by the currents that propagate through brain tissue and produce an effect at scalp sensors [113],[114]. When the average current density in each volumetric or areal element is modeled as a dipole, the forward problem can be solved with the superposition principle as the head is considered to be a linear system that generates additive effects of neuronal currents. Unlike the deterministic forward problem, the inverse problem (i.e. estimating source distribution given scalp measurements) is known to be under-determined. The number of current sources is significantly greater than the number of measurements, despite high-density EEG/MEG. Inferring source distribution from measurements is ill-posed without applying constraint or regularization based on a priori information about the desired source characteristics or physiological assumptions. Regularization also helps to stabilize the solution against noise.
Equivalent dipoles have been used to represent brain electrical activity. Such method – the so-called dipole source localization - produced estimates of the position and moment of one or several equivalent current dipoles localized within a brain model from the non-invasive EEG/MEG recordings [117], [118]. From the positions of the localized equivalent current dipoles, inferences about the neural sources in the real brain are obtained. The approximation is valid if the amount and the extension of the brain tissue excited is small with respect to the distance of the excited tissue from the recording sensors. If this is the case, then the region of active brain tissue can be approximated with an equivalent current dipole. Dipole source localization uses a non-linear minimization algorithm to estimate the dipole parameters since the relationship between the dipole locations and the EEG/MEG is nonlinear.
For spatially distributed sources, which are the general cases for EEG and MEG [111], source imaging techniques have been developed to estimate source distributions, usually a spatial distribution of equivalent current dipoles, from the scalp recorded EEG/MEG [119], [120]. In such cases, the observation system of brain electrical activity can be represented by equation (2). In such approaches, the source locations are fixed so the problem becomes linear. This is also often called linear inverse solution with various algorithms introduced and developed to minimize the error of model prediction in Eq. (2).
The minimum norm estimate (MNE) approach was the earliest solution to the EEG/MEG inverse problem with distributed source models [121]. Minimum norm (MN) solutions are biased for superficial sources, as superficial sources generate stronger fields with less energy due to their spatial vicinity to sensors. To mitigate this bias, one strategy is to weight current sources by the norm of the EEG/MEG signals that can be generated by each of them with a unitary magnitude. Introducing this weighting to MN regularization leads to the so-called weighted minimum norm (WMN) solution [120], [122]. A variation of WMN is the low-resolution electromagnetic tomography (LORETA) in which the norm of the second-order spatial derivative of the current source distribution is minimized to ensure spatial coherence and smoothness [120]. A variety of other source imaging algorithms based on WMN principle have also been reported. Alternatively, beamforming such as linearly constrained minimum variance or its variants [123], [124] or source scanning strategy such as MUSIC and its variants [125], [126], can be used to estimate source distributions. Recently, sparsity and other properties such as nonnegativity and orthogonality have been pursued to obtain enhanced source imaging and localization results [127]–[131]. See [111] for a recent review of EEG/MEG source imaging and localization methods.
An important issue in ESI is the adequate spatial sampling. While MEG uses ~150+ channels of recordings, clinical EEG often uses less channels (e.g. 19-32 electrodes). Studies indicate that higher spatial sampling helps improve substantially the precision of EEG based ESI [278],[279]. A recent guideline of the International Federation of Clinical Neurophysiology recommends that at least 64 channels of EEG should be used for ESI [132].
B. Connectivity inference in the sensor space
The work by Kaminski and Blinowska [11] have examined the connectivity inference or causal relationship over the scalp. Since EEG/MEG signals used for such connectivity inference are 2D surface manifestation of 3D brain electrical sources, the relationship derived between/among the recording sensors over the scalp provide a qualitative estimate of potential connectivity underlying the scalp recordings. This appreciation has been confirmed by several studies by means in which the use of simulations [41], [43], [133] show that sensor level connectivity can lead to erroneous conclusions with high probability. The reasons for this are easy to observe, illustrated here with the linear MVAR. Substituting (1) into the forward model (2) yields
| (36) |
If one estimates MVAR coefficients Ak for the Vt (as explained in II.D) there is no simple relation among those estimated (which show sensor connectivity) and the Kk of sources (underlying connectivity in source space).
Challenges with sensor connectivity are illustrated in Fig. 4, in an example in which sparse sources connected in a special manner are simulated and then applying different inverse solutions, the sources and the inter-nodal connectivity of the simulated network is estimated. Note that Fig. 4 shows a selected example of simulated source activity and connectivity, suggesting appropriate inverse algorithms are essential for estimating certain source distributions such as those with multiple focal sources. Further investigation, including extensive computer simulations and experimental studies, is needed to identify algorithms that would be less impacted by volume conduction effects for general brain activity and connectivity.
Figure 4.
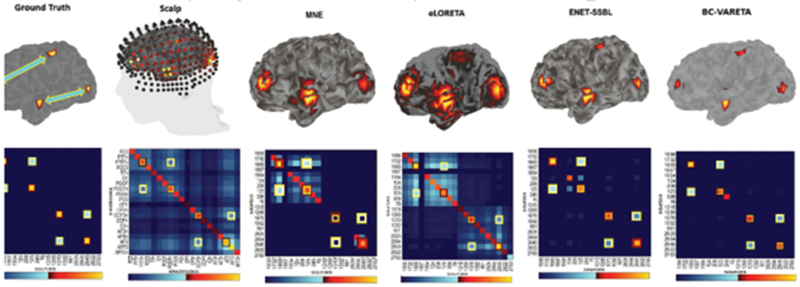
A computer simulation example to illustrate sensor and source connectivity issues. Four dipoles were placed upon the cortical surface. The forward field was generated by a BEM forward model. Activation is coded by a heat scale (red to yellow) and connectivity by a cool scale (blue to white). The projection to the scalp produces a very blurred activation and connectivity matrix due to volume conduction. On the right these same quantities are shown for four example inverse solutions - MNE, e-Loreta, ENET-SSBL, and BC-VARETA showing the appearance of “leakage” of both activation and connectivity estimates.
C. Connectivity inference in the source space
An important advancement in the field of EEG/MEG connectivity imaging is the introduction of functional and effective connectivity estimates at the source level, after solving the EEG/MEG inverse problem. Here two approaches are possible. One approach is to obtain estimates of the source time series and then to estimate association measures between the resulting time series. This approach has the merits of being intuitive and easy to interpret in the context of neuroscience research and clinical applications. The source imaging procedure reduces significantly the volume conductor effect of EEG/MEG, providing “equivalent” temporal profile of neural activity in source space. The general body of functional connectivity approaches can then be applied to such estimated “equivalent” source activity to estimate connectivity among brain regions. Such approach has been shown to provide meaningful results in a series of studies in both healthy human brains [13], [134] and epileptic brains [135]–[137], After solving the EEG source imaging and localization problem, functional connectivity among various cortical and brain regions can be quantitatively estimated and checked to assess if they are in agreement with the neuroscience knowledge about the brain functions and the known pathological information. This approach, namely estimating functional connectivity at the source space after solving the EEG/MEG inverse problem, has been referred as the “electrophysiological Connectome” (eConnectome) and open source codes are publicly available [138].
A second approach is to leverage the “state space” formulation of the EEG/MEG and to carry out source activity estimation and its connectivity simultaneously. Several attempts have been reported. In 2004, Galka et al. [139] reported parameter estimation based on the Kalman Filter. Due to the difficulty in scaling the Kalman filter the type of connectivity patterns studied were necessarily very simple. Scalability was dealt with by restricting the source model to a limited number of regions of interest and solve the linear or nonlinear state space model via the EM algorithm (in which the maximization step is the Kalman smoother) and to estimate the MVAR coefficients in the source space [140]. A sparsity assumption, paired to the joint estimation of demixing and source MVAR coefficients, has been reported [141]. This yields a type of “state space ICA” that carries out joint estimation of demixing and source MVAR coefficients, under the sparsity assumption. Current work continues in this direction by using hierarchical Bayesian modeling. Recently, the BC-VARETA approach was suggested [142] which carries out frequency domain source connectivity (partial correlation) estimation by formulating the problem as a Hierarchical Bayesian model and using the EM algorithm to iterate between estimation of sources and that of their precision matrix subject to a Graphical Lasso prior.
Experimental evaluations are much needed in order to fully assess the merits all source connectivity estimation methods. A rigorous comparison study, to assess the merits and limitations of the simultaneous estimation of source activity and connectivity vs. the sequential approach (first estimate sources and then functional connectivity), is warranted and remains to be seen in experimental evaluation.
D. Effects of volume conduction on functional connectivity
Similar to source imaging and localization from EEG/MEG, one needs to be cautious about the effect of volume conduction, since EEG/MEG is surface manifestation of mass responses from the underlying brain electrical activity. The volume conduction effect is unavoidable due to the transmission from neural excitation to the surface measurement.
At the sensor level, each (spatially limited) brain source is projected to several surface sensors as modelled by the gain matrix. This implies that connectivity measures can potentially detect spurious relations between pairs of sensors, trivially arising from the same brain source.
There are debates if the volume conduction effect can be avoided from scalp estimates of functional connectivity. These arguments include the considerations that volume conduction leads to instantaneous correlations on the scalp; and that measures robus t t to volume conduction are phase-lagged quantifiers of dependencies among pairs of channels, which may eliminate the instantaneous correlations and thus the effect of volume conduction.
To analyze this possibility, without loss of generality, we will analyze stationary sensor activity. According to Eq. (2) this activity is the instantaneous mixture (via the lead field) of simultaneous source activity. A consequence of this is that the cross-covariance matrix of the sensors at any time t with sensors at time t+τ is:
| (37) |
Where Σvv (τ), Σu(τ) are the covariances at lag τ of sensors and sources, respectively. Eq. (37) indicates that, the lead field will be affecting ALL lagged measurement and not only those derived from the instantaneous (zero lag) covariances Σvv (0). The effects of volume conduction are thus not eliminated by excluding the effects of zero lag interactions. This underscores that any measure attempting to counteract the effect of the lead field without taking it into account explicitly would fail.
As an application of this result consider the statement that “the imaginary coherence of sensor measurements can avoid the volume conduction effect”. As explained in [143], taking the Fourier transform of the lagged covariances in (37) leads to:
| (38) |
This simply states that the sensor cross-spectrum is the source cross-spectrum pre and post-multiplied by the lead field (volume conduction effect). This volume conduction effect extends to both the real and imaginary part of the source cross-spectrum as shown in the second line of (38). Since the sensor imaginary coherence is just a scaled version of the imaginary cross-spectrum it is also affected by the lead field, and its use in statistical estimation may facilitate inverse solutions but does not make them unnecessary.
A way to reduce these effects is to work at the source level, i.e. after applying source imaging and localization techniques that enable to reconstruct the source signal at each brain location. However, even in the source domain, the inverse operators produce ‘source leakage”: that a point-source will still be smeared across a region even after source localization and imaging.
Computer simulations allow to quantify and benchmark several connectivity estimates [13], [144], [145]. Real data arising from intracranial recordings are also useful for providing a “ground truth” (see IV.A.3)
E. Source leakage in connectivity estimates
Source leakage affects measures of connectivity by producing first-order and second-order false positive functional connections between brain regions [40]. First-order false positives or “artificial connections” occur between nearby regions as a direct consequence of source leakage between them. Since source leakage is instantaneous, all connectivity measures sensitive to zero-lag interactions are affected, e.g. Cross-correlation, Phase-Locking Value (PLV) [35]. Extensions have been proposed to reduce these false positives. For example, taking the imaginary part of the complex-valued PLV makes this measure less sensitive to zero-lag false positives. However, such a measure is confounded by the phase-angle at which the functional connection exists and is blind to interactions at angles of 0 or π [41]. Weighted Phase Lag Index (wPLI) [38] is another measure which is suggested to tackle the challenge of source leakage but is similarly confounded by phase-angle of the functional connection. The cross-correlation measure has also been extended, by mutual orthogonalization of pairs of signals before connectivity is estimated [33]. While it is a measure of connectivity between oscillatory amplitude envelopes, this orthogonalized Correlation Coefficient (oCC) measure is also confounded by the angle of concurrent phase-coupling when strong source leakage is present. It is less sensitive to source leakage in the absence of concurrent phase-coupling [41], [64], [65].
Second-order false positives or “spurious connections” occur in the vicinity of pairs of regions which have a true functional connection between them. Due to source leakage, the activities of regions near truly connected pairs also become correlated, resulting in second-order false positives [41]. Unlike first-order false positives, these spurious connections can be at non-zero lag and can be between distant regions. A method is recently reported by bundling sets of raw edges into “hyper-edges”, where edges within a hyper-edge are determined by clustering a matrix indicating source leakage between every pair of regions [146]. Each cluster represents a set of regions with strong source leakage between them, and each hyper-edge represents a true connection as well as likely spurious ones. The method has been demonstrated to appreciably reduce the ratio of false positives to true positives, and to yield a much-improved description of the underlying functional network. It can be used with any measure of interaction and with any source reconstruction method.
A complementary approach to the one just described is to address the cause of leakage by curtailing it at in the source reconstruction method itself. Substantially lower leakage may be obtained by appropriate priors. See for example [129] in which the use of non-negativity, orthogonality and sparseness reduce leakage. In a similar vein it has also been shown that Structured Sparse Bayesian Learning (SSBL) [127] may also achieve similar gains with respect to the usual linear minimum norm inverse methods.
F. Current limitations in functional connectivity in the source domain
Even though the estimation of functional connectivity in the source domain provides merits in terms of accuracy and interpretability of the obtained patterns, some aspects of the correct procedure to achieve this result are still unclear. Among these, the selection of the time series to represent the activity in each Region of Interest (ROI), see the discussion and comparative evaluation in [147]. Often, time series are averaged across the dipoles in a ROI, which leads to a signal smoothing. An alternative is to extract the time series from a single dipole [145], [148], [149]. The selection of such dipole can be based on the higher power density, the position within the ROI, the highest cross-talk function index in the region, or other data-driven approaches. A comparison of performances with different dipole selection approaches was provided in [27]. Recently, Rubega et al. [150] proposed to describe the activity of a ROI by the first singular vector computed from a singular-value decomposition of all dipoles belonging to the same ROI. A comparison with the above described methods showed improved connectivity results in simulations as well as evoked and epileptic data. Clearly, further investigation is needed to improve the performance of functional connectivity imaging in the source domain, including algorithm development and experimental validation.
IV. EEG/MEG Functional Connectivity
A. Event related activities
A classical method for measuring brain activity in response to external stimuli is event-related potentials in EEG or event related fields in MEG. This technique consists in presenting the subject with many repetitions of the same stimulation, and average the responses in order to improve signal to noise ratio. The underlying model is that the brain response is identical across stimuli, and corrupted by additive noise. In this ideal framework, the SNR improves as the square root of the number of trials. Similarly event-related potential/field can be obtained by averaging over multiple segments according to other events without external stimulation.
Functional connectivity among cortical regions have been estimated from scalp recorded EEGs during visually-triggered finger movements in human subjects, by means of directed transfer function technique on the estimated cortical current density waveforms in regions of interest on the modeled cortical mantle [134]. Connectivity patterns estimated for this task reveal an involvement of right parietal and bilateral premotor and prefrontal cortical areas. The reliability of these techniques was further demonstrated by the elaboration of high resolution EEG and fMRI signals collected. Determination of the priors in the resolution of the linear inverse problem was performed with the use of information from the hemodynamic responses of the cortical areas as revealed by block-designed (strength of activated voxels) fMRI. It is found that the approach allows to detect the changes in the time course of the information flow between cortical regions, in different frequency bands [134]. Fig. 5 shows an example of functional connectivity patterns associated with a motor paradigm using the EEG source imaging, constrained by fMRI, and Granger causality, in human subjects.
Fig. 5.
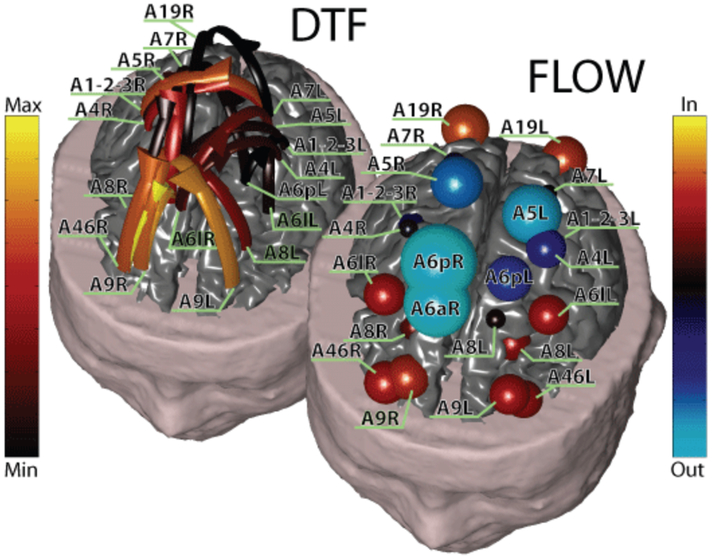
Top left: Functional connectivity patterns estimated in a subject during the performance of finger tapping movement, after the EMG onset. Each pattern is represented with arrows moving from one cortical area toward another. The color and size of the arrows code the level of strength of the functional connectivity observed between ROIs. The labels indicate the names of the ROIs employed. Bottom right: outflow patterns in all the ROIs obtained for the same connectivity pattern depicted in top left. The figure summarizes in red hues the behavior of a ROI in terms of reception of information flow from other ROIs, by adding all the value of the links arriving on the particular ROI from all the others. The information is represented with the size and the color of a sphere, centered on the particular ROI analyzed. The larger the sphere, the higher the value of inflow or outflow for any given ROI. The blue hues codes the outflow of information from a single ROI towards all the others. (From [134])
For cognitive activity, responses can vary in a trial to trial basis, in amplitude or delay. These fluctuations of activity can be used in order to infer connectivity between brain regions. For example, Wendling and colleagues have proposed in a language paradigm to measure instantaneous phase locking at each time point, with the measure being performed across trials [151]. Then, a clustering is performed in order to identify stable connectivity patterns. Going further in the single trial analysis, Brovelli has proposed to estimate Granger causality at the single trial level [152]. Using row-normalized, spectrally weighted partial directed coherence on single epochs transformed to source space, Plomp et al. [153] identified recurrent and top-down interactions between visual and attentional brain areas at short latencies after visual stimulation. Thereby, regions of interest were defined using fMRI localizer approaches and source localization was performed using the individual anatomical MRI of each participant.
Trial-to trial variation can be a source of information on the actual coupling between regions. It can also be a source of confound, in particular when subtracting the average signal from all trials. This subtraction can be performed in an attempt to remove the evoked part of the activity, keeping only the nonphase locked oscillatory part. Indeed, trial-to-trial variability can result in residual evoked activity in the signals, which can in turn lead to spurious interpretation of signal processing results. This was shown in connectivity [280] and phase resetting [281] analyses.
B. Oscillatory activities
Neuronal oscillations are rhythmic modulations in neuronal field and membrane potentials that reflect periodic modulations of neuronal excitability. Neuronal firing and associated neuronal processing is hence dependent on the position in an oscillatory cycle [51], [154]. Furthermore, oscillation phase intrinsically encompasses temporal information about the moments when neuronal processing is enhanced. Therefore, oscillations also imply a mechanism for representing temporal predictions. Experimental results show that the brain adaptively exploits oscillation phase to optimize processing of sensory stimuli [155]. Behavioral and electrophysiological evidence obtained with EEG and MEG indicate that visual perception is intrinsically sampled rhythmically, in at least the alpha frequency band, so that the pre-stimulus phase of alpha oscillations modulates the detection and discrimination of visual stimuli [156]–[160]. Also, attentional and other top-down temporal predictions guide the sampling of sensory information according to theta and alpha-band periodicity [157], [161]–[165].
Brain also adapts to the various temporal scales in the environmental context and rhythmic stimulus presentation entrains neuronal oscillations at the stimulus presentation frequency. Such alignment of neural oscillations with temporally systematic input has been observed in the auditory modality in the delta-frequency (1-4Hz) band [166]–[170]. Speech stimuli with rich temporal content [171]–[175] and natural-like visual stimuli [176], [177] entrain oscillations concurrently in multiple frequencies. Such alignment of neuronal oscillations to periodic stimulus streams has been suggested to facilitate sensory processing as well as to be crucial for segmentation of sensory input streams for further processing.
Neuronal phase-synchronization or phase-coupling between distinct oscillation assemblies has been suggested to be a mechanism for the coordination and regulation of neuronal processing in anatomically distributed neuronal circuits [50], [51]. This is because, synchronization is associated with millisecond-range spike-time correlations among anatomically distinct neuronal assemblies and temporally coincident spikes associated with synchronization are effective in evoking action potentials in downstream neurons [178], [179]. Furthermore, oscillations are thought to regulate neuronal communication by either facilitating it via aligned excitability windows or, conversely, inhibiting it by being out-of-phase [51]. Neuronal synchronization and consistent phase relationships of neuronal oscillations has hence been suggested to play an influential role in coordinating neuronal processing also in large-scale neuronal circuits in the whole brain level [40], [56], [180], [181]. Invasive local field potential (LFP) recordings from non-human primate [57], [182]–[185] and rodent [186] neuronal circuits have revealed inter-areal neuronal synchronization both among the neocortical and hippocampal sites, respectively. These data support the framework in where synchronization in gamma (40 – 120 Hz) frequencies underlie the bottom-up processing of visual information while concurrent theta (4–8 Hz), alpha (8 – 12 Hz) or beta (12 – 130 Hz) synchronization could be essential for top-down and feedback communication [57], [183], [184], [187].
In human non-invasive recordings with EEG and MEG, neuronal oscillations have been linked to variety of cognitive functions. Studies using source-reconstructed MEG data have shown that oscillations in alpha, beta, and gamma bands are modulated during perception [188]–[190], attention [58], [191], [192] and working memory [54], [192]–[195] tasks. The studies that have distilled the components underlying distinct cognitive functions support the hypothesis that local gamma oscillations are functionally significant in the neuronal representation of sensory information that is perceived [188], maintained in working memory [54], or attended [55], [196]. In line with these ideas, the load-dependent increase in the amplitude of gamma in oscillations in attention [55] and VW tasks [59] predicts cognitive capacity. Other lines of evidence implicate that alpha oscillations underlie attentional and executive top-down control of sensory processing [59], [197]–[199].
However, studies on large-scale inter-areal synchronization using source-reconstructed MEG have remained scarce and also more difficult to interpret [40]. These studies have revealed that endogenous attention is associated with inter-areal synchronization in the alpha [58], [200], [201] but also in the gamma [202] band frequencies. In contrast, working memory, enhances oscillations concurrently in multiple frequencies e.g. in alpha, beta, and gamma frequency bands in anatomically distributed networks [44]. Furthermore, in these data, the individual capacity limitations of VWM were predicted by concurrent large-scale high-alpha- (10-14 Hz,) and beta- (14-30 Hz) band phase synchronization. Similar observations of concurrent synchronization in many frequency bands, has been obtained in an attentional blink study [203] and during perception-action cycle in the somatosensory modality [204] suggesting that more complex tasks involve synchronization in multiple spectrally distributed networks.
Not only is large-scale synchronization important for healthy cognitive functions but its abnormalities have been proposed to be a systems-level mechanism of many neuropsychiatric diseases [205]–[207]. In line with this hypothesis, both local [208] and large-scale [209], [210] synchronization in the gamma frequency band are reduced in schizophrenia. Also attention deficits are associated with suppressed modulations in local alpha-band amplitudes [211] as well as in the functional coupling between brain regions [212]–[214]. Furthermore, also depression [215] and bipolar disorder [216] are associated with reduced synchronization.
In summary, healthy cognitive functions and behavioral performance are dependent on local neuronal oscillations that characterize activity in task-relevant cortical regions as well as on large-scale neuronal synchronization that connects the neuronal processing between the distributed brain areas. In contrast, neuropsychiatric diseases are associated with reduced task-dependent modulations in both local oscillations as well as large-scale network synchronization, which are thought to underlie the cognitive and behavioral deficits as well as other disease symptoms observed in the diseases.
C. EEG microstates as a measure of synchrony
Connectivity analysis of non-invasive electromagnetic data often ignores one particularly interesting phenomenon of brain network activity: Synchrony. Synchrony, generally speaking, refers to a state in which things happen, change, or exist at the same time.
Synchrony is particularly interesting in neuroscience, because from a theoretical point of view, the simultaneity of events excludes a causal relationship among the synchronized events, (this would require cause and effect to be temporally apart), but establishes a communality among events that gathers them into some functional unit. Synchrony has been regarded as a key mechanism of information integration in the brain [49], [217], [218] and dovetails with our subjective experience that we have a strong bias to consider simultaneous percepts as unitary objects or events.
However, from the mathematical point of view, in the analysis of scalp electromagnetic fields, synchrony is a very cumbersome term, because it is notoriously confounded with volume conduction. This is so because the lead-field operator of the EEG / MEG is a spatial low pass filter, such that already the activity of a single point source produces temporally synchronized dynamics in EEG and MEG measurements, both in the raw scalp recordings, and in estimates of inverse solutions (source leakage). In general, it seems however reasonable to explain observations of synchrony among scalp signals as a mixture of both source synchronization and volume conduction, because (a) we must reject the idea that it is source synchronization alone, as this would entirely disregard the effects of volume conduction, and (b) we have reasons to reject the idea that the observation is explained by volume conduction alone, as this constrain us to the typically unlikely scenario that the entire observed data is caused by a single point source in the brain.
From the empirical point of view, in EEG data, synchrony is a very typical and dominant phenomenon: This becomes evident through the observation that EEG data seem to consist of a sequence of transient, but non-overlapping states of nearly stable field configurations, so-called microstates. It is reasonable to assume that brain activity accounting for a particular microstate is not generated by one single source in the brain, but by a network of simultaneously active sources. The stability of the field configuration over the duration of a microstate (approx. 100 ms) then implies that these different sources must have exhibited highly synchronous dynamics, as differences in the time course of these sources would result in continuous changes of the generated scalp field. This global synchrony inherent to the microstate model corresponds very well with models of dynamic gating of brain functional connectivity through neuronal coherence [218]. Fig. 6 shows an example of microstates from scalp EEG.
Fig. 6.
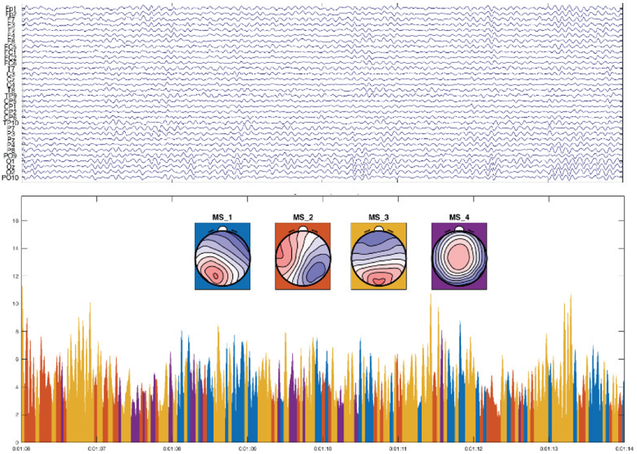
Example of a spontaneous 8 sec EEG epoch and the decomposition of the data into microstates. The Upper part shows the bandpass (2-20Hz) filtered EEG. In the lower part, we see the four microstate classes estimated in the individual subject and the GFP of the above EEG data, color labelled based on the assignment of the individual time points to the best-fitting microstate class.
Methodologically, the identification of microstates is a typical un-mixing problem of scalp field data, and aims to account for the observed scalp field differences by a weighted sum of potential vectors:
| (39) |
where vl is the vector of scalp measurements at the l-th point in the time discretization Δt, μk is the normalized measurement vector representing the spatial topography of the k-th microstate class, al(k) is the intensity of the k-th state at the time-point l and ξl is the residual variance. The microstate model assumes that there is no temporal overlap across different microstate classes in correspondence to functional theories that postulate that only one global functional state occurs at any given moment in time [219], [220]. Under this assumption, a unique solution to the above problem is obtained, given a series of measurement vectors ν1 … νNS, through minimizing the residual variance under the constraint that for each time-point l, all but one al(k) are zero. This type of problem is typically solved with clustering algorithms [221]. Microstates of class k are then defined as continuous time periods with al(k) ≠ 0. Microstate analysis is thus related to independent component analysis in the sense that it solves the same un-mixing problem, and because in the form of the prior of no temporal overlap, it imposes a particular form of independence among components.
The past 20 years of microstate research have shown that at least for awake, eyes closed resting state EEG data, empirically identified microstate classes generalize very well: Rather few (4+) classes of microstates usually explain an individual multichannel EEG to about 70 to 80%. Furthermore, the identified microstate topographies are similar across individuals and studies [222]. The generality of the phenomenon, together with the understanding of microstates as indices of large-scale synchronization, has invited researchers to speculate that microstates are electrophysiological counterparts of spontaneously, but lawfully forming patterns of resting state cortical networks that may have specific functional correlates. Indeed, a series of empirical findings found that specific microstates features, such as the relative presence and duration of certain microstate classes, were systematically related to task-demand, development, mental disorders and more (see [222] for a review). Resting state microstates may thus give us a unique possibility to observe global brain processes that actively and adaptively permit or suppress the communications among eventually remote cortical regions. This view has also some experimental support, as a recent multimodal imaging study showed that the presence of different classes of microstates correlated with BOLD changes in different sub-regions of the thalamus [285].
V. Evaluation of Brain Functional Connectivity
A. Patient studies using invasive EEG
A.1. Rationale and methods for invasive recordings
During presurgical evaluation of epilepsy, invasive recordings can be performed, which consist in placing electrodes at the brain surface (electrocorticography, ECoG [223]), or directly within the brain structures (stereotaxic EEG, SEEG [224]). Such recordings are often commonly referred to as “intracranial EEG” (iEEG). Thus, between 100 and 200 contacts can be recorded in a subdural or intracerebral manner. The implantation sites are planned on pure clinical grounds, but these invasive recordings give a unique opportunity for gathering data with unmatched spatial specificity and signal to noise ratio, without the limitations imposed by surface recordings (inverse problem, source leakage, artefacts…).
These invasive recordings can bring new insights both into pathological networks involved in epilepsy and in physiological networks in resting state or cognitive paradigms. They also permit direct probing of inter-regional connectivity through cortico-cortical evoked potentials (CCEPs, [225]). Moreover, and importantly, they offer opportunities to validate non-invasive imaging results by comparing with invasive recordings made directly within the brain.
A.2. Connectivity studies in iEEG
The goal of iEEG is to define the regions responsible for triggering epileptic seizures, which need to be removed by surgical intervention. It has thus been proposed to quantify the level of involvement of each brain region in the seizure start, based on the characterization of the fast (high frequency) discharge observed at seizure onset [226]. These measures are local, at the level of each contact; however, it is increasingly recognized that epilepsy is a disease of brain networks [224], [227]–[229]. As the actual seizure onset is generally a period of desynchronization [230] (even though this could vary with seizure patterns), the most useful periods are the interictal [231], [232], preictal [233] and post-fast discharge ictal periods [234]. Several connectivity measures have been used in epilepsy, including coherence [1], non-linear correlation [235], [236] and Granger causality [227], [228], [234], in time or time-frequency [237] domains. Graph-theory measures have been used in order to characterize the level of implication of each brain region (i.e., graph node) within the epileptic network [229]. Global metrics have been used in order to characterize global pathological brain states [238]. Clinically, local measures are useful in order to map the most important node networks, for example the OUT strength (sum of all outgoing links from a given brain region) which indicate the regions with higher outflow [137], [233], [234]. For this latter type of measure, inflow can also potentially interesting as it indicates the regions receiving abnormal number of inputs from other regions, which can in turn out to be hyperexcitable [233], [239].
A.3. Validation of non-invasive measures
The first aspect of validation consists in comparing the localization obtained by the inverse problem to the brain generators as seen in iEEG. The actual “field of view” of iEEG (i.e., the distance between a brain source and the activated contact in iEEG) is not completely clear, but it likely depends on the extent of cortex activated, the level of synchrony and the signal to noise ratio (which could be increased by averaging) [240]. Bipolar remontaging (i.e. difference between consecutive contacts) can help focusing iEEG towards nearby sources. Another important advantage of bipolar remontaging is that it enables to remove the influence of a common reference in two channels, which would lead to spurious high connectivity [282].
Electrical current dipoles have been tested in vivo by injecting currents on consecutive intracerebral contacts in cat [117], and human subjects [241]. Merlet and Gotman have shown for actual epileptic spikes a distance between active iEEG contacts and dipole localization of 11mm with 28 scalp electrodes [242]. Bai et al. [243] evaluated various source imaging algorithms from scalp EEG by comparing with ECoG the identified brain sources in patients undergoing presurgical planning, using a somatosensory evoked potential protocol. Lai et al. [244] validated their cortical potential imaging from scalp EEG during interictal spikes by comparing with ECoG recordings in the group of pediatric epilepsy patients. Yang et al. [245] further validated their EEG seizure source imaging from 76-ch EEG in a group of epilepsy patients comparing with iEEG findings. With a high density EEG (64 to 128 channels), Megevand et al. showed a median distance between EEG source and iEEG contact (ECoG grids) of 15 mm [246]. The estimation of the extent of activated cortex is a difficult issue, but has been shown on simulations to be potentially feasible [128], [247], [248].
The second aspect of validation is on the network dynamics, i.e. which region is leading in the network [249]. Baumgartner et al. have shown propagation of activity between mesiobasal and lateral temporal lobe, confirmed by sphenoidal electrodes [250]. Malinowska et al. have shown in MEG reconstruction of epileptic networks that, even though iEEG is more sensitive and captures more network nodes, the general pattern of propagation can usually be retrieved [251]. However, they also show that missing the leading region can lead to erroneous decision on the leading node in the network. This raises the important issue of sensitivity of the measures, as addressed below. Recently, Jmail et al. have compared the networks obtained in MEG for epileptic spikes and oscillations to their counterpart in iEEG, and found a better concordance for the spikes (possibly because of their SNR) [252].
A.4. Simultaneous depth/surface recordings
Many studies comparing iEEG and EEG/MEG have been performed on separate recordings. There is a current push towards simultaneous recordings, which guarantee that the exact same brain state is recorded at the two levels [253], [254], although the use of subdural electrode pad for ECoG recording may alter the current path so extra caution is needed for accurate modeling of head volume conductor, especially for EEG. Simultaneous acquisition of MEG /EEG and iEEG permit to capture the joint fluctuations of modalities at a single trial level. The measure of covariation constitutes a unique source of information on the coupling between depth and surface recordings [255].
A first question that simultaneous recordings can address is the sensitivity of the measures. Thanks to simultaneous EEG/SEEG recordings, Alarcon et al. have shown that activity from the surface can in fact be a propagation of discharges originating from deep sources (notably hippocampal sources) [256]. This poses the question of detectability of deep sources, which activity on the surface is likely to be very small. Yet, a few studies have suggested that it is possible to record on the surface a direct reflection of hippocampal and amygdala signals, based on simulations [257] or on simultaneous recordings [258], [259]. Recently, Pizzo et al. [286] have used independent component analysis to disentangle different networks including mesial structures, and found some components correlating with contacts in amygdala, hippocampus and even thalamic structures. Similarly, a recent study with simultaneous high-density EEG and intracranial recordings in thalamus or nucleus accumbens demonstrated correct localization of Alpha-activity generated in these deep structures [287].
The second question is the validation of signal processing measures, on signals corresponding to the exact same brain activity. Lantz et al. have shown by recording simultaneously EEG (22 sensors) and subdural electrodes that sources of epileptic activity can be reconstructed with sublobar accuracy [260]. Dubarry et al. have shown with simultaneous MEG/EEG that the local propagation of visual activity along the occipital lobe can be tracked with MEG [255]. Fig. 7 shows an example of networks derived i) from ICA applied on MEG [251] and ii) intracerebral EEG (stereotaxic EEG, SEEG) after registration of SEEG contacts on the brain [261], with data obtained during simultaneous MEG/SEEG recordings [255], [262].
Fig. 7.
Comparison of epileptic networks obtained on MEG-ICA and intracerebral EEG, with data recorded simultaneously (courtesy of S. Medina, methods in [251], [261], [262]).
Simultaneous recordings offer yet another opportunity, that of combining iEEG and MEG/EEG sensors into a common analysis, in order to benefit for the high spatial specificity of iEEG and the global view of MEG/EEG [263], [264], It has been shown that source localization can be performed in some cases on iEEG [265]–[269]. The next step is to combine all the data (EEG/MEG and iEEG) into a common inverse problem [263]. It is therefore expected that connectivity analysis will benefit from the multi-modal recording at several spatial scales.
B. Animal models
Various methods exist that can evaluate directed interactions between brain regions based on electrophysiological recordings, leading to sometimes dissimilar results. It is therefore unclear whether these connectivity results correctly reflect the underlying physiology. Real physiological benchmark data against which the different methods can be tested are therefore needed. Plomp et al. [18] used multichannel whisker stimulation-induced somatosensory evoked potentials recorded from epicranial electrodes distributed over the entire cortex in anesthetized rats to test different effective connectivity measures. Epicranial recordings in rats have been shown to be location-specific due to minimal effects of volume conduction in this lissencephalic brain with very thin bone. The spatiotemporal dynamics of evoked activity after unilateral whisker stimulation is well known from intracranial recordings and follows the underlying structural connectivity [270]. The stimulation first activates the contralateral barrel cortex at around 5 ms which ceases at around 25 ms. In line with structural connectivity, contralateral parietal and frontal sensory-motor regions become active immediately after the primary somatosensory cortex, followed by activity in the other hemisphere. Plomp et al. [18] compared the two time-varying multivariate Granger-causal models PDC and DTF in their capability to retrieve this spatio-temporal activation pattern. They also compared plain PDC and DTF with versions where the values were scaled by the power spectral density (PSD) and evaluated the difference between column-wise and row-wise normalization of the PDC. Column-wise normalization compromise the sensitivity to outflows, while row-wise normalization to inflows. Using three different performance criteria they showed that row-wise normalized and PSD-weighted PDC performed best in identifying the main drivers of the network at the correct latencies (see also discussion in [153]).
C. Patient studies using EEG/MEG
The functional connectivity estimates have been used to help delineate epileptic networks. At the same time, such studies also provided opportunities to evaluate the functional connectivity algorithms when brain pathology serves as reference. In 2007, Ding et al. [135] for the first time applied functional connectivity to EEG source imaging results to estimate primary seizure sources. They used source scanning approach to reconstruct brain sources from EEG, and then applied DTF to the waveforms of sources at ROIs to determine the information flow within the epilepsy network. Comparison to known epileptogenic zones revealed a high degree of concordance between the Granger causality estimates and the epileptogenic brain regions. In another study, Lu et al. [136] estimated brain sources from 76-ch EEG and applied Granger causality measure to the source waveforms in 10 partial epilepsy patients. Surgical resection outcome and the resected regions were used to serve as ground truth and high concordance was found between functional connectivity estimates and the seizure onset zones. Malinowska et al. computed the co-occurrence of epileptic events detected on the time courses of ICA components corresponding to interictal epileptic spikes in MEG [251]. Krishnan et al. [283] and Nissen et al. [284] have used resting state MEG connectivity in order to identify the pathological hubs in the brain networks, as a marker of the epileptogenic zone, even in the absence of visible interictal activity.
Sohrabpour et al. [145] compared the results from Granger causality estimates from EEG and MEG in the same patient, and concordance results were reported based on seizure onset zone confirmed by successful resection outcome. Fig. 8 illustrates an example of using EEG source imaging in combination of ICA and adaptive DTF was used to estimate the final result of seizure onset zone, which agrees well with the ECoG recordings in the patient.
Fig. 8.
Identifying epileptic networks from ictal signals in a patient. Dynamic seizure imaging is applied to the seizures recorded in the EEG of this patient prior to surgery to identify the nodes of the ictal network. ADTF analysis was then applied to combined source space signals to determine the driving IC (left). The identified IC is in good accord with clinical findings, i.e. SOZ electrodes and surgical resection (right). (From [145])
In another study, Granger causality (weighted PDC) in the frequency domain was computed at the source level in patients with left and right temporal lobe epilepsy, and the connectivity patterns within each region was evaluated with a graph measure of outflow [137]. They found that the strongest drivers of connectivity changes during interictal epileptic spikes (highest summed outflow) were concordant with the localization of temporal lobe epilepsy. Other important drivers were in the ipsilateral temporal and frontal regions but also in the contralateral hemisphere with a significant difference between right and left temporal epilepsy patients, paralleling the cognitive patterns at group level. Using the same analysis pipeline, Coito et al. [149] investigated connectivity alterations in temporal lobe epilepsy patients in the absence of visible epileptic activity. They showed evidence of EEG-based connectivity patterns concordant with the Default Mode Network, with reduced connectivity in patients vs controls. In addition, they identified the posterior cingulate cortex as the main driver in healthy subjects whereas the ipsilateral medial temporal lobe was the main driver in patients. Fig. 9 shows altered directed resting state connectivity in epilepsy patients.
Fig. 9.
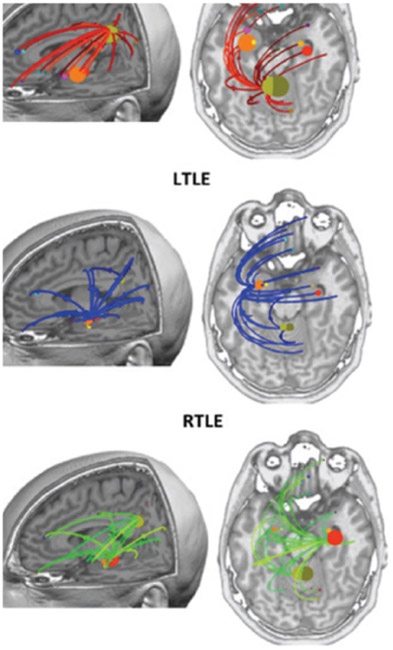
Altered directed resting-state connectivity in left and right temporal lobe epilepsy (TLE) measured by high density EEG in the absence of spikes. Main outflow in the posterior cingulate in controls (A) and ipsilateral medial temporal lobe in patients (B, C) (From [149]).
IV. Concluding Remarks
We have described various methods for estimating brain functional connectivity from electrophysiological signals and discussed relevant literature. It is generally accepted that functional connectivity analysis should be performed on the source space within the brain, instead of over the scalp, with a sufficient number of sensors. This can also be done sometimes from invasive recordings using intracranial EEG when it is available in special cases such as in patients undergoing presurgical planning. In most other cases, the general approach should be to perform functional connectivity analysis on source signals estimated from EEG or MEG. A number of studies have indicated the merits of such source space functional connectivity mapping of the brain for brain function studies or assisting clinical applications of managing brain disorders such as epilepsy. Efforts were also made to estimate sources and connectivity simultaneously from EEG/MEG. Studies using animal models or in patients where invasive data or pathological information are available, have also been reported to evaluate the functional connectivity algorithms. We hope this tutorial will serve readers who are interested in entering the field of electrophysiological connectivity analysis from EEG/MEG, and also for researchers who are working on a specific approach of functional connectivity analysis.
Acknowledgment
We thank Dr. Abbas Sohrabpour for useful comments on the manuscript, and Deirel Paz for unifying the format of equations throughout the paper.
This work was supported in part by NIH MH114223, EB021027, NS096761, AT009263.
Appendix
Notation
Matrix, vector and scalar quantities are differentiated by the typeface. Matrix: uppercase-roman-bold, e.g. X . Vectors: lowercase-italic-bold, e.g. x . Scalar: lowercase-roman-nonbold, e.g. x.
Observed quantities are represented with Latin letters, e.g. observed vector v. Unobserved quantities are represented with Greek letters, e.g. unobserved vector ι.
Association of quantities to different ontological levels (process type) is defined through right subscripts, e.g. Sxx represents a matrix quantity S associated to a vector process x.
Statistical versions of quantities are defined through left subscript, e.g. wS represents a statistical version indicated by w of a matrix quantity S.
Matrix, vector or scalar functions are defined through standard mathematical notation, e.g. X(ν) matrix quantity X defined as a function on the domain of the scalar magnitude ν.
Matrix elements/rows/columns and vector elements are indicated through MATLAB standard notation, the typeface differentiates weather the indicated quantity is an element or vector, e.g. x(l, m) element (scalar quantity) l, m-th or x(:, m) column (vector quantity) m-th of the matrix quantity X.
Elements/rows/columns of a matrix or vector function are indicated with indices after function argument and semicolon, e.g. x(v; l, m) element (scalar quantity) l, m-th or x(ν;:,m) column (vector quantity) m-th of the matrix function X(ν).
Integrals over the product of a pair of function arguments x and y on its entire domain of definition are represented by Dirac notation ⟨x∣y⟩, e.g. cross-correlation of x and y .
Nomenclature
| k,l,,m,n | Indices for vector/matrix elements, time points, frequency components. |
| t | Time. |
| ν | Frequency |
| ω | pulsation = 2 * π*ν |
| x,y | Generic vector processes. |
| e | Generic noise process. |
| ρ | Generic complex signal amplitude |
| φ | Generic complex signal phase |
| f | Generic scalar function. |
| V | Observations (M/EEG sensor signal) vector |
| ι | States (source activity) vector |
| ξ | Sensor signal noise vector |
| ζ | Biological noise vector |
| u | Exogenous inputs (stimulus) vector |
| L | Source to observations (M/EEG sensor signal) transfer function (Lead Field) matrix |
| s | Empirical covariance (cross-spectral) matrix. |
| Σ | Population covariance (cross-spectral) matrix. |
| K | Neural connectivity matrix or source connectivity. |
| T | Neural lag matrix |
| A | (uppercase alpha) Multivariate Autoregressive (MVAR) model coefficients matrix |
| B | (uppercase Beta) Multivariate Autoregressive (MVAR) model Transfer Function (TF). |
| GCx→y | Granger Causality from y to x |
| Multivariate Autoregressive (MVAR) model Directed Transfer Function (DTF) from m to n | |
| Normalized DTF | |
| Rm↔n | Pearson Correlation matrix coefficient of the m-th and n-th vector components |
| Γ | Normalized DTF |
| Π | Partial Directed Coherence (PDC) matrix |
| Squared amplitude of the PCD component m,n (magnitude of the influence from m to n) | |
| , , , , | PDC normalization versions: column-wise, row-wise, generalized, information, weighted |
| δ | Gradient of the PDC squared absolute values |
| γ2 | PCD’s normal tendency squared variance |
| H | Hilbert Transform |
| PLV | Phase locking value (PLV) |
|
, |
weighted PLV, information PLV |
Contributor Information
Bin He, Department of Biomedical Engineering, Carnegie Mellon University, Pittsburgh, USA..
Laura Astolfi, Department of Computer, Control and Management Engineering, University of Rome Sapienza, and with IRCCS Fondazione Santa Lucia, Rome, Italy..
Pedro Antonio Valdés-Sosa, University of Electronic Science and Technology of China, China and the Cuban Neuroscience Center..
Daniele Marinazzo, Ghent University, Ghent, Belgium..
Satu O. Palva, Helsinki Institute of Life Science, Finland.
Christian-George Bénar, Aix-Marseille Université/Inserm, Marseille, France..
Christoph M. Michel, University of Geneva, Switzerland.
Thomas Koenig, University of Bern, Switzerland..
References
- [1].Gotman J, “Measurement of small time differences between EEG channels: Method and application to epileptic seizure propagation,” Electroencephalogr. Clin. Neurophysiol, vol. 56, no. 5, pp. 501–514, 1983. [DOI] [PubMed] [Google Scholar]
- [2].Andrew C and Pfurtscheller G, “Event-related coherence as a tool for studying dynamic interaction of brain regions,” Electroencephalogr. Clin. Neurophysiol, vol. 98, no. 2, pp. 144–148, February 1996. [DOI] [PubMed] [Google Scholar]
- [3].Lachaux JP, Lutz A, Rudrauf D, Cosmelli D, Le Van Quyen M, Martinerie J, and Varela F, “Estimating the time-course of coherence between single-trial brain signals: An introduction to wavelet coherence,” Neurophysiol. Clin, vol. 32, no. 3, pp. 157–174, 2002. [DOI] [PubMed] [Google Scholar]
- [4].Nolte G, Bai O, Wheaton L, Mari Z, Vorbach S, and Hallett M, “Identifying true brain interaction from EEG data using the imaginary part of coherency,” Clin. Neurophysiol, vol. 115, no. 10, pp. 2292–2307, 2004. [DOI] [PubMed] [Google Scholar]
- [5].Wiener N, “The theory of prediction,” in Modern Mathematics for Engineers, Beckenbach E, Ed. McGraw-Hill, New York, 1956. [Google Scholar]
- [6].Granger CWJ, “Investigating Causal Relations by Econometric Models and Cross-spectral Methods,” Econometrica, vol. 37, no. 3, p. 424, 1969. [Google Scholar]
- [7].Dhamala M, Rangarajan G, and Ding M, “Analyzing information flow in brain networks with nonparametric Granger causality,” Neuroimage, vol. 41, no. 2, pp. 354–362, 2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Geweke JF, “Measures of conditional linear dependence and feedback between time series,” J. Am. Stat. Assoc, vol. 79, no. 388, pp. 907–915, 1984. [Google Scholar]
- [9].Geweke J, “Measurement of Linear Dependence and Feedback between Multiple Time Series,”J. Am. Stat. Assoc, vol. 77, pp. 304–313, 1982. [Google Scholar]
- [10].Kuś R, Kamiński M, and Blinowska KJ, “Determination of EEG activity propagation: Pair-wise versus multichannel estimate,” IEEE Trans. Biomed. Eng, vol. 51, no. 9, pp. 1501–1510, 2004. [DOI] [PubMed] [Google Scholar]
- [11].Kaminski MJ and Blinowska KJ, “A new method of the description of the information flow in the brain structures,” Biol. Cybern, vol. 65, no. 3, pp. 203–210, July 1991. [DOI] [PubMed] [Google Scholar]
- [12].Baccalä LA and Sameshima K, “Partial directed coherence: A new concept in neural structure determination,” Biol. Cybern, vol. 84, no. 6, pp. 463–474, 2001. [DOI] [PubMed] [Google Scholar]
- [13].Astolfi L, Cincotti F, Mattia D, Marciani MG, Baccala LA, Fallani FDV, Salinari S, Ursino M, Zavaglia M, Ding L, Edgar JC, Miller GA, He B, and Babiloni F, “Comparison of different cortical connectivity estimators for high-resolution EEG recordings,” Hum. Brain Mapp, vol. 28, no. 2, pp. 143–157, 2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].Faes L, Porta A, and Nollo G, “Testing frequency-domain causality in multivariate time series,” IEEE Trans. Biomed. Eng, vol. 57, no. 8, pp. 1897–1906, 2010. [DOI] [PubMed] [Google Scholar]
- [15].Takahashi DY, Baccal LA, and Sameshima K, “Connectivity inference between neural structures via partial directed coherence,”j. Appl. Stat, vol. 34, no. 10, pp. 1259–1273, 2007. [Google Scholar]
- [16].Toppi J, Mattia D, Risetti M, Formisano R, Babiloni F, and Astolfi L, “Testing the significance of connectivity networks: Comparison of different assessing procedures,” IEEE Trans. Biomed. Eng, vol. 63, no. 12, pp. 2461–2473, 2016. [DOI] [PubMed] [Google Scholar]
- [17].Astolfi L, Cincotti F, Mattia D, Marciani MG, Baccalà LA, De Vico Fallani F, Salinari S, Ursino M, Zavaglia M, and Babiloni F, “Assessing cortical functional connectivity by partial directed coherence: Simulations and application to real data,” IEEE Trans. Biomed. Eng, vol. 53, no. 9, pp. 1802–1812, 2006. [DOI] [PubMed] [Google Scholar]
- [18].Plomp G, Quairiaux C, Michel CM, and Astolfi L, “The physiological plausibility of time-varying Granger-causal modeling: Normalization and weighting by spectral power,” Neuroimage, vol. 97, pp. 206–216, 2014. [DOI] [PubMed] [Google Scholar]
- [19].Baccalá LA, Sameshima K, and Takahashi DY, “Generalized partial directed coherence, ” in 2007 15th International Conference on Digital Signal Processing, DSP 2007, 2007, pp. 163–166. [Google Scholar]
- [20].Takahashi DY, Baccalá6 LA, and Sameshima K, “Information theoretic interpretation of frequency domain connectivity measures,” Biol. Cybern, vol. 103, no. 6, pp. 463–469, 2010. [DOI] [PubMed] [Google Scholar]
- [21].Baccala LA, Takahashi DY, and Sameshima K, “Directed Transfer Function: Unified Asymptotic Theory and Some of Its Implications,” IEEE Trans. Biomed. Eng, vol. 63, no. 12, pp. 2450–2460, 2016. [DOI] [PubMed] [Google Scholar]
- [22].Baccala LA, de Brito CSN, Takahashi DY, and Sameshima K, “Unified asymptotic theory for all partial directed coherence forms.,” Philos. Trans. A. Math. Phys. Eng. Sci, vol. 371, no. 1997, p. 20120158, August 2013. [DOI] [PubMed] [Google Scholar]
- [23].Leistritz L, Schiecke K, Astolfi L, and Witte H, “Time-variant Modeling of Brain Processes,” Proc. IEEE, vol. 104, no. 2, pp. 262–281,2016. [Google Scholar]
- [24].Wilke C, Ding L, and He B, “Estimation of time-varying connectivity patterns through the use of an adaptive directed transfer function,” IEEE Trans. Biomed. Eng, vol. 55, no. 11, pp. 2557–2564, 2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [25].Milde T, Leistritz L, Astolfi L, Miltner WHR, Weiss T, Babiloni F, and Witte H, “A new Kalman filter approach for the estimation of high-dimensional time-variant multivariate AR models and its application in analysis of laser-evoked brain potentials,” Neuroimage, vol. 50, no. 3, pp. 960–969, 2010. [DOI] [PubMed] [Google Scholar]
- [26].Möller E, Schack B, Arnold M, and Witte H, “Instantaneous multivariate EEG coherence analysis by means of adaptive high-dimensional autoregressive models,” J. Neurosci. Methods, vol. 105, no. 2, pp. 143–158, 2001. [DOI] [PubMed] [Google Scholar]
- [27].Ghumare EG, Schrooten M, Vandenberghe R, and Dupont P, “A Time-Varying Connectivity Analysis from Distributed EEG Sources: A Simulation Study,” Brain Topogr, vol. 31, no. 5, pp. 721–737, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [28].O’Neill GC, Tewarie P, Vidaurre D, Liuzzi L, Woolrich MW, and Brookes MJ, “Dynamics of large-scale electrophysiological networks: A technical review,” Neuroimage, vol. 180, pp. 559–576, October 2018. [DOI] [PubMed] [Google Scholar]
- [29].Nunez PL, Srinivasan R, Westdorp AF, Wijesinghe RS, Tucker DM, Silberstein RB, and Cadusch PJ, “EEG coherency I: Statistics, reference electrode, volume conduction, Laplacians, cortical imaging, and interpretation at multiple scales,” Electroencephalogr. Clin. Neurophysiol, vol. 103, no. 5, pp. 499–515, 1997. [DOI] [PubMed] [Google Scholar]
- [30].Brookes MJ, Woolrich MW, and Barnes GR, “Measuring functional connectivity in MEG: A multivariate approach insensitive to linear source leakage,” Neuroimage, vol. 63, no. 2, pp. 910–920, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [31].Bruns A, Eckhorn R, and Jokeit H, “Amplitude envelope correlation detects coupling among incoherent brain signals,” Neuroreport, vol. 11, no. 7, pp. 1509–1514, 2000. [PubMed] [Google Scholar]
- [32].de Pasquale F, Della Penna S, Snyder AZ, Lewis C, Mantini D, Marzetti L, Belardinelli P, Ciancetta L, Pizzella V, Romani GL, and Corbetta M, “Temporal dynamics of spontaneous MEG activity in brain networks.,” Proc. Natl. Acad. Sci. U. S. A, vol. 107, no. 13, pp. 6040–5, March 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [33].Hipp JF, Hawellek DJ, Corbetta M, Siegel M, and Engel AK, “Large-scale cortical correlation structure of spontaneous oscillatory activity,” Nat. Neurosci, vol. 15, no. 6, pp. 884–890, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [34].O’Neill GC, Barratt EL, Hunt BAE, Tewarie PK, and Brookes MJ, “Measuring electrophysiological connectivity by power envelope correlation: A technical review on MEG methods,” Phys. Med. Biol, vol. 60, no. 21, pp. R271–R295, 2015. [DOI] [PubMed] [Google Scholar]
- [35].Lachaux JP, Rodriguez E, Martinerie J, and Varela FJ, “Measuring phase synchrony in brain signals,” Hum. Brain Mapp, vol. 8, no. 4, pp. 194–208, 1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [36].Palva JM, “Phase Synchrony among Neuronal Oscillations in the Human Cortex,” J. Neurosci, vol. 25, no. 15, pp. 3962–3972, 2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [37].Stam CJ, Nolte G, and Daffertshofer A, “Phase lag index: Assessment of functional connectivity from multi channel EEG and MEG with diminished bias from common sources,” Hum. Brain Mapp, vol. 28, no. 11, pp. 1178–1193, 2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [38].Vinck M, Oostenveld R, van Wingerden M, Battaglia F, and Pennartz CMA, “An improved index of phase-synchronization for electrophysiological data in the presence of volume-conduction, noise and sample-size bias,” Neuroimage, vol. 55, no. 4, pp. 1548–1565, April 2011. [DOI] [PubMed] [Google Scholar]
- [39].Colclough GL, Woolrich MW, Tewarie PK, Brookes MJ, Quinn AJ, and Smith SM, “How reliable are MEG resting-state connectivity metrics?,” Neuroimage, vol. 138, pp. 284–293, September 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [40].Palva S and Palva JM, “Discovering oscillatory interaction networks with M/EEG: Challenges and breakthroughs,” Trends Cogn. Sci, vol. 16, no. 4, pp. 219–229, 2012. [DOI] [PubMed] [Google Scholar]
- [41].Palva JM, Wang SH, Palva S, Zhigalov A, Monto S, Brookes MJ, Schoffelen JM, and Jerbi K, “Ghost interactions in MEG/EEG source space: A note of caution on inter-areal coupling measures,” Neuroimage, vol. 173, pp. 632–643, 2018. [DOI] [PubMed] [Google Scholar]
- [42].Daffertshofer A and van Wijk BCM, “On the Influence of Amplitude on the Connectivity between Phases,” Front. Neuroinform, vol. 5, p. 6, July 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [43].Schoffelen JM and Gross J, “Source connectivity analysis with MEG and EEG,” Hum. Brain Mapp, vol. 30, no. 6, pp. 1857–1865, 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [44].Palva JM, Monto S, Kulashekhar S, and Palva S, “Neuronal synchrony reveals working memory networks and predicts individual memory capacity,” Proc. Natl. Acad. Sci, vol. 107, no. 16, pp. 7580–7585, 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [45].Tass P, Rosenblum MG, Weule J, Kurths J, Pikovsky A, Volkmann J, Schnitzler A, and Freund HJ, “Detection of n:m phase locking from noisy data: Application to magnetoencephalography,” Phys. Rev. Lett, vol. 81, no. 15, pp. 3291–3294, 1998. [Google Scholar]
- [46].Le Van Quyen M, Foucher J, Lachaux JP, Rodriguez E, Lutz A, Martinerie J, and Varela FJ, “Comparison of Hilbert transform and wavelet methods for the analysis of neuronal synchrony,” J. Neurosci. Methods, vol. 111, no. 2, pp. 83–98, 2001. [DOI] [PubMed] [Google Scholar]
- [47].Laufs H, Kleinschmidt A, Beyerle A, Eger E, Salek-Haddadi A, Preibisch C, and Krakow K, “EEG-correlated fMRI of human alpha activity,” Neuroimage, 2003. [DOI] [PubMed] [Google Scholar]
- [48].Brookes MJ, Woolrich M, Luckhoo H, Price D, Hale JR, Stephenson MC, Barnes GR, Smith SM, and Morris PG, “Investigating the electrophysiological basis of resting state networks using magnetoencephalography,” Proc. Natl. Acad. Sci, vol. 108, no. 40, pp. 16783–16788, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [49].Singer W, “Temporal Coherence: A Versatile Code for the Definition of Relations,” Senses A Compr. Ref, vol. 2, no. 1, pp. 1–9, 2010. [Google Scholar]
- [50].Singer W, “Distributed processing and temporal codes in neuronal networks,” Cogn. Neurodyn, vol. 3, no. 3, pp. 189–196, 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [51].Fries P, “Rhythms for Cognition: Communication through Coherence,” Neuron, vol. 88, no. 1, pp. 220–235, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [52].Fries P, Reynolds JH, Rorie AE, and Desimone R, “Modulation of oscillatory neuronal synchronization by selective visual attention,” Science (80-. )., vol. 291, no. 5508, pp. 1560–1563, 2001. [DOI] [PubMed] [Google Scholar]
- [53].Gregoriou GG, Gotts SJ, Zhou H, and Desimone R, “High-Frequency, long-range coupling between prefrontal and visual cortex during attention,” Science (80-. )., 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [54].Honkanen R, Rouhinen S, Wang SH, Palva JM, and Palva S, “Gamma oscillations underlie the maintenance of feature-specific information and the contents of visual working memory,” Cereb. Cortex, vol. 25, no. 10, pp. 3788–3801, 2015. [DOI] [PubMed] [Google Scholar]
- [55].Rouhinen S, Panula J, Palva JM, and Palva S, “Load Dependence of and Oscillations Predicts Individual Capacity of Visual Attention,” J. Neurosci, vol. 33, no. 48, pp. 19023–19033, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [56].Bastos AM, Vezoli J, and Fries P, “Communication through coherence with inter-areal delays,” Curr. Opin. Neurobiol, vol. 31, pp. 173–180, 2015. [DOI] [PubMed] [Google Scholar]
- [57].Bastos AM, Vezoli J, Bosman CA, Schoffelen JM, Oostenveld R, Dowdall JR, DeWeerd P, Kennedy H, and Fries P, “Visual areas exert feedforward and feedback influences through distinct frequency channels,” Neuron, vol. 85, no. 2, pp. 390–401,2015. [DOI] [PubMed] [Google Scholar]
- [58].Lobier M, Palva JM, and Palva S, “High-alpha band synchronization across frontal, parietal and visual cortex mediates behavioral and neuronal effects of visuospatial attention,” Neuroimage, vol. 165, pp. 222–237, 2018. [DOI] [PubMed] [Google Scholar]
- [59].Palva S and Palva JM, “Functional roles of alpha-band phase synchronization in local and large-scale cortical networks,” Front. Psychol, vol. 2, no. September, p. 204, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [60].Womelsdorf T, Schoffelen JM, Oostenveld R, Singer W, Desimone R, Engel AK, and Fries P, “Modulation of neuronal interactions through neuronal synchronization,” Science (80-. )., vol. 316, no. 5831, pp. 1609–1612, 2007. [DOI] [PubMed] [Google Scholar]
- [61].Lakatos P, Musacchia G, O’Connel MN, Falchier AY, Javitt DC, and Schroeder CE, “The Spectrotemporal Filter Mechanism of Auditory Selective Attention,” Neuron, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [62].Maris E, Womelsdorf T, Desimone R, and Fries P, “Rhythmic neuronal synchronization in visual cortex entails spatial phase relation diversity that is modulated by stimulation and attention,” Neuroimage, vol. 74, pp. 99–116, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [63].Maris E, Fries P, and van Ede F, “Diverse Phase Relations among Neuronal Rhythms and Their Potential Function,” Trends Neurosci, vol. 39, no. 2, pp. 86–99, 2016. [DOI] [PubMed] [Google Scholar]
- [64].Siebenhühner F, Wang SH, Palva JM, and Palva S, “Cross-frequency synchronization connects networks of fast and slow oscillations during visual working memory maintenance,” Elife, vol. 5, no. September2016, p. e13451, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [65].Siebenhühner F, Lobier M, Wang SH, Palva S, and Palva JM, “Measuring Large-Scale Synchronization with Human MEG and EEG: Challenges and Solutions,” in Multimodal Oscillation-based Connectivity Theory, Springer, 2016, pp. 1–18. [Google Scholar]
- [66].Scheffer-Teixeira R, Belchior H, Caixeta FV, Souza BC, Ribeiro S, and Tort ABL, “Theta phase modulates multiple layer-specific oscillations in the CA1 region,” Cereb. Cortex, vol. 22, no. 10, pp. 2404–2414, 2012. [DOI] [PubMed] [Google Scholar]
- [67].Tort ABL, Kramer MA, Thorn C, Gibson DJ, Kubota Y, Graybiel AM, and Kopell NJ, “Dynamic cross-frequency couplings of local field potential oscillations in rat striatum and hippocampus during performance of a T-maze task,” Proc. Natl. Acad. Sci, vol. 105, no. 51, pp. 20517–20522, 2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [68].Axmacher N, Henseler MM, Jensen O, Weinreich I, Elger CE, and Fell J, “Cross-frequency coupling supports multi-item working memory in the human hippocampus,” Proc. Natl. Acad. Sci, vol. 107, no. 7, pp. 3228–3233, 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [69].Canolty RT, Edwards E, Dalal SS, Soltani M, Nagarajan SS, Kirsch HE, Berger MS, Barbare NM, and Knight RT, “High gamma power is phase-locked to theta oscillations in human neocortex,” Science (80-. )., 2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [70].Scheffer-Teixeira R and Tort ABL, “On cross-frequency phase-phase coupling between theta and gamma oscillations in the hippocampus,” Elife, vol. 5, no. December2016, pp. 423–435, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [71].Xu X, Zheng C, and Zhang T, “Reduction in LFP cross-frequency coupling between theta and gamma rhythms associated with impaired STP and LTP in a rat model of brain ischemia,” Front. Comput. Neurosci, vol. 7, p. 27, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [72].Sauseng P, Klimesch W, Gruber WR, and Birbaumer N, “Cross-frequency phase synchronization: A brain mechanism of memory matching and attention,” Neuroimage, vol. 40, no. 1, pp. 308–317, 2008. [DOI] [PubMed] [Google Scholar]
- [73].Chaieb L, Leszczynski M, Axmacher N, Höhne M, Elger CE, and Fell J, “Theta-gamma phase-phase coupling during working memory maintenance in the human hippocampus,” Cogn. Neurosci, vol. 6, no. 4, pp. 149–157, 2015. [DOI] [PubMed] [Google Scholar]
- [74].Hyafil A, Giraud AL, Fontolan L, and Gutkin B, “Neural Cross-Frequency Coupling: Connecting Architectures, Mechanisms, and Functions,” Trends in Neurosciences. 2015. [DOI] [PubMed] [Google Scholar]
- [75].Jensen O and Colgin LL, “Cross-frequency coupling between neuronal oscillations,” Trends Cogn. Sci, vol. 11, no. 7, pp. 267–269, 2007. [DOI] [PubMed] [Google Scholar]
- [76].Jiang H, Bahramisharif A, van Gerven MAJ, and Jensen O, “Measuring directionality between neuronal oscillations of different frequencies,” Neuroimage, vol. 118, pp. 359–367, 2015. [DOI] [PubMed] [Google Scholar]
- [77].Demiralp T, Bayraktaroglu Z, Lenz D, Junge S, Busch NA, Maess B, Ergen M, and Herrmann CS, “Gamma amplitudes are coupled to theta phase in human EEG during visual perception,” Int. J. Psychophysiol, vol. 64, no. 1, pp. 24–30, 2007. [DOI] [PubMed] [Google Scholar]
- [78].Hamidi M, “Repetitive transcranial magnetic stimulation affects behavior by biasing endogenous cortical oscillations,” Front. Integr. Neurosci, vol. 3, p. 14, 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [79].Holz EM, Glennon M, Prendergast K, and Sauseng P, “Theta-gamma phase synchronization during memory matching in visual working memory,” Neuroimage, vol. 52, no. 1, pp. 326–335, 2010. [DOI] [PubMed] [Google Scholar]
- [80].Sauseng P, Klimesch W, Heise KF, Gruber WR, Holz E, Karim AA, Glennon M, Gerloff C, Birbaumer N, and Hummel FC, “Brain Oscillatory Substrates of Visual Short-Term Memory Capacity,” Curr. Biol, vol. 19, no. 21, pp. 1846–1852, 2009. [DOI] [PubMed] [Google Scholar]
- [81].Schack B, Vath N, Petsche H, Geissler HG, and Möller E, “Phase-coupling of theta-gamma EEG rhythms during short-term memory processing,” Int. J. Psychophysiol, vol. 44, no. 2, pp. 143–163, 2002. [DOI] [PubMed] [Google Scholar]
- [82].Schack B, Klimesch W, and Sauseng P, “Phase synchronization between theta and upper alpha oscillations in a working memory task,” Int. J. Psychophysiol, vol. 57, no. 2, pp. 105–114, 2005. [DOI] [PubMed] [Google Scholar]
- [83].Lisman JE and Jensen O, “The Theta-Gamma Neural Code,” Neuron, vol. 77, no. 6, pp. 1002–1016, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [84].Roux F, Wibral M, Singer W, Aru J, and Uhlhaas PJ, “The Phase of Thalamic Alpha Activity Modulates Cortical Gamma-Band Activity: Evidence from Resting-State MEG Recordings,” J. Neurosci, vol. 33, no. 45, pp. 17827–17835, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [85].Florin E and Baillet S, “The brain’s resting-state activity is shaped by synchronized cross-frequency coupling of neural oscillations,” Neuroimage, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [86].Nikulin VV and Brismar T, “Phase synchronization between alpha and beta oscillations in the human electroencephalogram,” Neuroscience, vol. 137, no. 2, pp. 647–657, 2006. [DOI] [PubMed] [Google Scholar]
- [87].Friston KJ, Harrison L, and Penny W, “{D}ynamic causal modelling.,” Neuroimage, vol. 19, no. 4, pp. 1273–1302, 2003. [DOI] [PubMed] [Google Scholar]
- [88].Kiebel SJ, Garrido MI, Moran R, Chen CC, and Friston KJ, “Dynamic causal modeling for EEG and MEG,” Hum. Brain Mapp, vol. 30, no. 6, pp. 1866–1876, 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [89].Kiebel SJ, David O, and Friston KJ, “Dynamic causal modelling of evoked responses in EEG/MEG with lead field parameterization,” Neuroimage, vol. 30, no. 4, pp. 1273–1284, 2006. [DOI] [PubMed] [Google Scholar]
- [90].David O, Maess B, Eckstein K, and Friederici AD, “Dynamic Causal Modeling of Subcortical Connectivity of Language,” J. Neurosci, vol. 31, no. 7, pp. 2712–2717, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [91].Boly M, Moran R, Murphy M, Boveroux P, Bruno M-A, Noirhomme Q, Ledoux D, Bonhomme V, Brichant J-F, Tononi G, Laureys S, and Friston K, “Connectivity Changes Underlying Spectral EEG Changes during Propofol-Induced Loss of Consciousness,” J. Neurosci, vol. 32, no. 20, pp. 7082–7090, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [92].Stephan KE, Penny WD, Moran RJ, den Ouden HEM, Daunizeau J, and Friston KJ, “Ten simple rules for dynamic causal modeling,” Neuroimage, vol. 49, no. 4, pp. 3099–3109, 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [93].Litvak V, Mattout J, Kiebel S, Phillips C, Henson R, Kilner J, Barnes G, Oostenveld R, Daunizeau J, Flandin G, Penny W, and Friston K, “EEG and MEG data analysis in SPM8,” Comput. Intell. Neurosci, vol. 2011, no. March, p. 852961, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [94].Moran RJ, Jung F, Kumagai T, Endepols H, Graf R, Dolan RJ, Friston KJ, Stephan KE, and Tittgemeyer M, “Dynamic causal models and physiological inference: A validation study using isoflurane anaesthesia in rodents,” PLoS One, vol. 6, no. 8, p. e22790, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [95].Boly M, Garrido M, Gosseries O, Boveroux P, Schnakers C, Massimini M, Litvak V, Laureys S, and Friston K, “Preserved feedforward but impaired top-down processes in the vegetative state,” science.sciencemag.org, 2011. [DOI] [PubMed] [Google Scholar]
- [96].Garrido MI, Friston KJ, Kiebel SJ, Stephan KE, Baldeweg T, and Kilner JM, “The functional anatomy of the MMN: A DCM study of the roving paradigm,” Neuroimage, vol. 42, no. 2, pp. 936–944, 2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [97].Valdes-Sosa PA, Roebroeck A, Daunizeau J, and Friston K, “Effective connectivity: Influence, causality and biophysical modeling,” Neuroimage, vol. 58, no. 2, pp. 339–361, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [98].Barnett L and Seth AK, “Granger causality for state-space models,” Phys. Rev. E - Stat. Nonlinear, Soft Matter Phys., vol. 91, no. 4, p. 40101, 2015. [DOI] [PubMed] [Google Scholar]
- [99].Bressler SL and Seth AK, “Wiener-Granger Causality: A well established methodology,” Neuroimage, vol. 58, no. 2, pp. 323–329, 2011. [DOI] [PubMed] [Google Scholar]
- [100].Dimitrov AG, Lazar AA, and Victor JD, “Information theory in neuroscience,” J. Comput. Neurosci, vol. 30, no. 1, pp. 1–5, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [101].Bettencourt LMA, Gintautas V, and Ham MI, “Identification of Functional Information Subgraphs in Complex Networks,” Phys. Rev. Lett, vol. 100, no. 23, p. 238701, June 2008. [DOI] [PubMed] [Google Scholar]
- [102].Ince RAA, Giordano BL, Kayser C, Rousselet GA, Gross J, and Schyns PG, “A statistical framework for neuroimaging data analysis based on mutual information estimated via a gaussian copula,” Hum. Brain Mapp, vol. 38, no. 3, pp. 1541–1573, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [103].Schreiber T, “Measuring information transfer,” Phys. Rev. Lett, vol. 85, no. 2, pp. 461–464, 2000. [DOI] [PubMed] [Google Scholar]
- [104].Porta A and Faes L, “Wiener-Granger Causality in Network Physiology with Applications to Cardiovascular Control and Neuroscience,” Proc. IEEE, vol. 104, no. 2, pp. 282–309, 2016. [Google Scholar]
- [105].Barnett L, Barrett AB, and Seth AK, “Granger causality and transfer entropy Are equivalent for gaussian variables,” Phys. Rev. Lett, vol. 103, no. 23, p. 238701, 2009. [DOI] [PubMed] [Google Scholar]
- [106].Stramaglia S, Angelini L, Wu G, Cortes JM, Faes L, and Marinazzo D, “Synergetic and Redundant Information Flow Detected by Unnormalized Granger Causality: Application to Resting State fMRI,” IEEE Trans. Biomed. Eng, vol. 63, no. 12, pp. 2518–2524, 2016. [DOI] [PubMed] [Google Scholar]
- [107].Faes L, Marinazzo D, and Stramaglia S, “Multiscale information decomposition: Exact computation for multivariate Gaussian processes,” Entropy, vol. 19, no. 8, p. 408, 2017. [Google Scholar]
- [108].Stramaglia S, M Cortes J, and Marinazzo D, “Synergy and redundancy in the Granger causal analysis of dynamical networks,” New J. Phys, vol. 16, no. 10, p. 105003, 2014. [Google Scholar]
- [109].Wibral M, Priesemann V, Kay JW, Lizier JT, and Phillips WA, “Partial information decomposition as a unified approach to the specification of neural goal functions,” Brain Cogn, vol. 112, no. March, pp. 25–38, 2017. [DOI] [PubMed] [Google Scholar]
- [110].Wibral M, Finn C, Wollstadt P, Lizier J, and Priesemann V, “Quantifying Information Modification in Developing Neural Networks via Partial Information Decomposition,” Entropy, vol. 19, no. 9, p. 494, 2017. [Google Scholar]
- [111].He B, Sohrabpour A, Brown E, and Liu Z, “Electrophysiological Source Imaging: A Noninvasive Window to Brain Dynamics,” Annu. Rev. Biomed. Eng, vol. 20, no. 1, p. annurev-bioeng-062117– 120853, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [112].Michel CM, Murray MM, Lantz G, Gonzalez S, Spinelli L, and Grave De Peralta R, “EEG source imaging,” Clinical Neurophysiology. 2004. [DOI] [PubMed] [Google Scholar]
- [113].He B and Lian J, “Electrophysiological Neuroimaging,” in Neural Engineering, Boston, MA: Kluwer Academic/Plenum, 2005, pp. 221–261. [Google Scholar]
- [114].Michel C and He B, “EEG Mapping and Source Imaging,” in Niedermeyer’s Electroencephalography, , 6th edition, Schomer DL and Lopes da Silva F, Eds. Kluwer Wolters & Lippincott Williams & Wilkins, Philadelphia, 2011, pp. 1179–1202. [Google Scholar]
- [115].Ding M and He B, “Exploring Functional and Causal Connectivity in the Brain,” in Neural Engineering, He B, Ed. Springer, 2013, pp. 545–564. [Google Scholar]
- [116].He B and Ding L, “Electrophysiological Neuroimaging,” in Neural Engineering, He B, Ed. Springer, 2013, pp. 499–544. [Google Scholar]
- [117].He B, Musha T, Okamoto Y, Homma S, Nakajima Y, and Sato T, “Electric Dipole Tracing in the Brain by Means of the Boundary Element Method and Its Accuracy,” IEEE Trans. Biomed. Eng, vol. BME-34, no. 6, pp. 406–414, 1987. [DOI] [PubMed] [Google Scholar]
- [118].Scherg M, Cramon D, and Elton M, “Brain-stem auditory-evoked potentials in post-comatose patients after severe closed head trauma,” J. Neurol, vol. 231, no. 1, pp. 1–5, February 1984. [DOI] [PubMed] [Google Scholar]
- [119].Dale AM and Sereno MI, “Improved Localizadon of Cortical Activity by Combining EEG and MEG with MRI Cortical Surface Reconstruction: A Linear Approach,” J. Cogn. Neurosci, vol. 5, no. 2, pp. 162–176, April 1993. [DOI] [PubMed] [Google Scholar]
- [120].Pascual-Marqui RD, Michel CM, and Lehmann D, “Low resolution electromagnetic tomography: a new method for localizing electrical activity in the brain,” Int. J. Psychophysiol, vol. 18, pp. 49–65, 1994. [DOI] [PubMed] [Google Scholar]
- [121].Hämäläinen M, Hari R, Ilmoniemi RJ, Knuutila J, and Lounasmaa OV, “Magnetoencephalography—theory, instrumentation, and applications to noninvasive studies of the working human brain,” Rev. Mod. Phys, vol. 65, no. 2, pp. 413–497, April 1993. [Google Scholar]
- [122].Wang JZ, Williamson SJ, and Kaufman L, “Magnetic Source Images Determined by a Lead-Field Analysis: The Unique Minimum-Norm Least-Squares Estimation,” IEEE Trans. Biomed. Eng, vol. 39, no. 7, pp. 665–675, 1992. [DOI] [PubMed] [Google Scholar]
- [123].Van Veen BD, Van Drongelen W, Yuchtman M, and Suzuki A, “Localization of brain electrical activity via linearly constrained minimum variance spatial filtering,” IEEE Trans. Biomed. Eng, vol. 44, no. 9, pp. 867–880, 1997. [DOI] [PubMed] [Google Scholar]
- [124].Hossein Hosseini SA, Sohrabpour A, Akcakaya M, and He B, “Electromagnetic brain source imaging by means of a robust minimum variance beamformer,” IEEE Trans. Biomed. Eng, vol. 65, no. 10, pp. 2365–2374, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [125].Mosher JC, Lewis PS, and Leahy RM, “Multiple Dipole Modeling and Localization from Spatio-Temporal MEG Data,” IEEE Trans. Biomed. Eng, vol. 39, no. 6, pp. 541–557, 1992. [DOI] [PubMed] [Google Scholar]
- [126].Xu XL, Xu B, and He B, “An alternative substance approach to EEG dipole source localization,” Phys. Med. Biol, 2004. [DOI] [PubMed] [Google Scholar]
- [127].Paz-Linares D, Vega-Hernández M, Rojas-López PA, Valdés-Hernández PA, Martínez-Montes E, and Valdés-Sosa PA, “Spatio Temporal EEG Source Imaging with the Hierarchical Bayesian Elastic Net and Elitist Lasso Models,” Front. Neurosci, vol. 11, p. 635, November 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [128].Sohrabpour A, Lu Y, Worrell G, and He B, “Imaging brain source extent from EEG/MEG by means of an iteratively reweighted edge sparsity minimization (IRES) strategy,” Neuroimage, vol. 142, pp. 27–42, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [129].Valdés-Sosa PA, Vega-Hernández M, Sánchez-Bornot JM, Martínez-Montes E, and Bobes MA, “EEG source imaging with spatio-temporal tomographic nonnegative independent component analysis,” Hum. Brain Mapp, vol. 30, no. 6, pp. 1898–1910, June 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [130].Ding L and He B, “Sparse source imaging in electroencephalography with accurate field modeling,” Hum. Brain Mapp, vol. 29, no. 9, pp. 1053–1067, 2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [131].Vega-Hernández M, Martínez-Montes E, Sánchez-Bornot JM, Lage-Castellanos A, and Valdés-Sosa PA, “PENALIZED LEAST SQUARES METHODS FOR SOLVING THE EEG INVERSE PROBLEM,” Statistica Sinica, vol. 18 Institute of Statistical Science, Academia Sinica, pp. 1535–1551, 2008. [Google Scholar]
- [132].Seeck M, Koessler L, Bast T, Leijten F,Michel C, Baumgartner C, He B, and Beniczky S, “The standardized EEG electrode array of the IFCN,” Clin. Neurophysiol, vol. 128, no. 10, pp. 2070–2077, October 2017. [DOI] [PubMed] [Google Scholar]
- [133].van de Steen F, Faes L, Karahan E, Songsiri J, Valdes-Sosa PA, and Marinazzo D, “Critical Comments on EEG Sensor Space Dynamical Connectivity Analysis,” Brain Topogr, vol. {\textbull, pp. 1–12, 2016. [DOI] [PubMed] [Google Scholar]
- [134].Babiloni F, Cincotti F, Babiloni C, Carducci F, Mattia D, Astolfi L, Basilisco A, Rossini PM, Ding L, Ni Y, Cheng J, Christine K, Sweeney J, and He B, “Estimation of the cortical functional connectivity with the multimodal integration of high-resolution EEG and fMRI data by directed transfer function,” Neuroimage, vol. 24, no. 1, pp. 118–131, 2005. [DOI] [PubMed] [Google Scholar]
- [135].Ding L, Worrell GA, Lagerlund TD, and He B, “Ictal source analysis: Localization and imaging of causal interactions in humans,” Neuroimage, vol. 34, no. 2, pp. 575–586, 2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [136].Lu Y, Yang L, Worrell GA, and He B, “Seizure source imaging by means of FINE spatio-temporal dipole localization and directed transfer function in partial epilepsy patients,” Clin. Neurophysiol, vol. 123, no. 7, pp. 1275–1283, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [137].Coito A, Plomp G, Genetti M, Abela E, Wiest R, Seeck M, Michel CM, and Vulliemoz S, “Dynamic directed interictal connectivity in left and right temporal lobe epilepsy,” Epilepsia, vol. 56, no. 2, pp. 207–217, 2015. [DOI] [PubMed] [Google Scholar]
- [138].He B, Dai Y, Astolfi L, Babiloni F, Yuan H, and Yang L, “EConnectome: A MATLAB toolbox for mapping and imaging of brain functional connectivity,” J. Neurosci. Methods, vol. 195, no. 2, pp. 261–269, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [139].Galka A, Yamashita O, Ozaki T, Biscay R, and Valdés-Sosa P, “A solution to the dynamical inverse problem of EEG generation using spatiotemporal Kalman filtering,” Neuroimage, vol. 23, no. 2, pp. 435–453, October 2004. [DOI] [PubMed] [Google Scholar]
- [140].Cheung BLP and Van Veen BD, “Estimation of cortical connectivity from E/MEG using nonlinear state-space models,” in 2011 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), 2011, pp. 769–772. [Google Scholar]
- [141].Haufe S, Tomioka R, Nolte G, Müller KR, and Kawanabe M, “Modeling sparse connectivity between underlying brain sources for EEG/MEG,” IEEE Trans. Biomed. Eng, vol. 57, no. 8, pp. 1954–1963, 2010. [DOI] [PubMed] [Google Scholar]
- [142].Gonzalez-Moreira E, Paz-Linares D, Valdes-Sosa P, Abstract 2358 Organization for Human Brain Mapping, Singapore, 2018. [Google Scholar]
- [143].Nolte G, Marzetti L, and Valdes Sosa P, “Minimum Overlap Component Analysis (MOCA) of EEG/MEG data for more than two sources,” J. Neurosci. Methods, vol. 183, no. 1, pp. 72–76, September 2009. [DOI] [PubMed] [Google Scholar]
- [144].Haufe S and Ewald A, “A Simulation Framework for Benchmarking EEG-Based Brain Connectivity Estimation Methodologies,” Brain Topogr, pp. 1–18, 2016. [DOI] [PubMed] [Google Scholar]
- [145].Sohrabpour A, Ye S, Worrell GA, Zhang W, and He B, “Noninvasive Electromagnetic Source Imaging and Granger Causality Analysis: An Electrophysiological Connectome (eConnectome) Approach,” IEEE Trans. Biomed. Eng, vol. 63, no. 12, pp. 2474–2487, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [146].Wang SH, Lobier M, Siebenhühner F, Puoliväli T, Palva S, and Palva JM, “Hyperedge bundling: A practical solution to spurious interactions in MEG/EEG source connectivity analyses,” Neuroimage, vol. 173, pp. 610–622, 2018. [DOI] [PubMed] [Google Scholar]
- [147].Mahjoory K, Nikulin VV, Botrel L, Linkenkaer-Hansen K, Fato MM, and Haufe S, “Consistency of EEG source localization and connectivity estimates,” Neuroimage, vol. 152, pp. 590–601, 2017. [DOI] [PubMed] [Google Scholar]
- [148].Coito A, Michel CM, Van Mierlo P, Vulliemoz S, and Plomp G, “Directed Functional Brain Connectivity Based on EEG Source Imaging: Methodology and Application to Temporal Lobe Epilepsy,” IEEE Trans. Biomed. Eng, vol. 63, no. 12, pp. 2619–2628, 2016. [DOI] [PubMed] [Google Scholar]
- [149].Coito A, Genetti M, Pittau F, Iannotti GR, Thomschewski A, Höller Y, Trinka E, Wiest R, Seeck M, Michel CM, Plomp G, and Vulliemoz S, “Altered directed functional connectivity in temporal lobe epilepsy in the absence of interictal spikes: A high density EEG study,” Epilepsia, vol. 57, no. 3, pp. 402–411, 2016. [DOI] [PubMed] [Google Scholar]
- [150].Rubega M, Carboni M, Seeber M, Pascucci D, Tourbier S, Toscano G, Van Mierlo P, Hagmann P, Plomp G, Vulliemoz S, and Michel C, “Analysis, Estimating EEG source dipole orientation based on singular-value decomposition for connectivity,” Brain Topogr, vol. In press, 2018. [DOI] [PubMed] [Google Scholar]
- [151].Mheich A, Hassan M, Khalil M, Berrou C, and Wendling F, “A new algorithm for spatiotemporal analysis of brain functional connectivity,” J. Neurosci. Methods, vol. 242, pp. 77–81, March 2015. [DOI] [PubMed] [Google Scholar]
- [152].Brovelli A, “Statistical Analysis of Single-Trial Granger Causality Spectra,” Comput. Math. Methods Med, vol. 2012, pp. 1–10, May 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [153].Plomp G, Hervais-Adelman A, Astolfi L, and Michel CM, “Early recurrence and ongoing parietal driving during elementary visual processing,” Sci. Rep, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [154].Haegens S, Nacher V, Luna R, Romo R, and Jensen O, “ - Oscillations in the monkey sensorimotor network influence discrimination performance by rhythmical inhibition of neuronal spiking,” Proc. Natl. Acad. Sci, vol. 108, no. 48, pp. 19377–19382, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [155].VanRullen R, “Perceptual Cycles,” Trends Cogn. Sci, vol. 20, no. 10, pp. 723–735, 2016. [DOI] [PubMed] [Google Scholar]
- [156].Busch NA and VanRullen R, “Spontaneous EEG oscillations reveal periodic sampling of visual attention,” Proc. Natl. Acad. Sci, vol. 107, no. 37, pp. 16048–16053, 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [157].Dugué L, Marque P, and VanRullen R, “Theta oscillations modulate attentional search performance periodically,” J. Cogn. Neurosci, vol. 27, no. 5, pp. 945–958, 2015. [DOI] [PubMed] [Google Scholar]
- [158].Dugue L, Marque P, and VanRullen R, “The Phase of Ongoing Oscillations Mediates the Causal Relation between Brain Excitation and Visual Perception,”j. Neurosci., vol. 31, no. 33, pp. 11889–11893,2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [159].Hanslmayr S, Volberg G, Wimber M, Dalai SS, and Greenlee MW, “Prestimulus oscillatory phase at 7 Hz gates cortical information flow and visual perception,” Curr. Biol, vol. 23, no. 22, pp. 2273–2278, 2013. [DOI] [PubMed] [Google Scholar]
- [160].Mathewson KE, Gratton G, Fabiani M, Beck DM, and Ro T, “To See or Not to See: Prestimulus Phase Predicts Visual Awareness,” J. Neurosci, vol. 29, no. 9, pp. 2725–2732, 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [161].Chakravarthi R and VanRullen R, “Conscious updating is a rhythmic process,” Proc. Natl. Acad. Sci, vol. 109, no. 26, pp. 10599–10604, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [162].Landau AN and Fries P, “Attention samples stimuli rhythmically,” Curr. Biol, vol. 22, no. 11, pp. 1000–1004, 2012. [DOI] [PubMed] [Google Scholar]
- [163].Landau AN, Schreyer HM, Van Pelt S, and Fries P, “Distributed Attention Is Implemented through Theta-Rhythmic Gamma Modulation,” Curr. Biol, vol. 25, no. 17, pp. 2332–2337, 2015. [DOI] [PubMed] [Google Scholar]
- [164].Sherman MT, Kanai R, Seth AK, and Van Rullen R, “Rhythmic influence of top-down perceptual priors in the phase of prestimulus occipital alpha oscillations,” j. Cogn. Neurosci., vol. 28, no. 9, pp. 1318–1330, 2016. [DOI] [PubMed] [Google Scholar]
- [165].VanRullen R, Carlson T, and Cavanagh P, “The blinking spotlight of attention,” Proc. Natl. Acad. Sci, vol. 104, no. 49, pp. 19204–19209, 2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [166].Besle j., Schevon CA, Mehta AD, Lakatos P, Goodman RR, McKhann GM, Emerson RG, and Schroeder CE, “Tuning of the Human Neocortex to the Temporal Dynamics of Attended Events,” j. Neurosci., vol. 31, no. 9, pp. 3176–3185, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [167].Cramer j., “Styles, Stereotypes, and the South: Constructing Identities At the Linguistic Border,” Am. Speech, vol. 88, no. 2, pp. 144–167, 2013. [Google Scholar]
- [168].Lakatos P, Karmos G, Mehta AD, Ulbert I, and Schroeder CE, “Entrainment of neuronal oscillations as a mechanism of attentional selection,” Science (80-.)., vol. 320, no. 5872, pp. 110–113, 2008. [DOI] [PubMed] [Google Scholar]
- [169].Lakatos P, Barczak A, Neymotin SA, McGinnis T, Ross D, javitt DC, and O’Connell MN, “Global dynamics of selective attention and its lapses in primary auditory cortex,” Nat. Neurosci, vol. 19, no. 12, pp. 1707–1717, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [170].Stefanics G, Hangya B, Hernadi I, Winkler I, Lakatos P, and Ulbert I, “Phase Entrainment of Human Delta Oscillations Can Mediate the Effects of Expectation on Reaction Speed,” j. Neurosci, vol. 30, no. 41, pp. 13578–13585, 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [171].Arnal LH and Kleinschmidt AK, “Entrained delta oscillations reflect the subjective tracking of time,” Commun. Integr. Biol, vol. 10 no. 5–6, p. e1349583, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [172].Ding N, Melloni L, Yang A, Wang Y, Zhang W, and Poeppel D, “Characterizing Neural Entrainment to Hierarchical Linguistic Units using Electroencephalography (EEG),” Front. Hum. Neurosci, vol. 11, p.481,2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [173].Ding N, Patel AD, Chen L, Butler H, Luo C, and Poeppel D, “Temporal modulations in speech and music,” Neurosci. Biobehav. Rev, vol. 81, pp. 181–187, 2017. [DOI] [PubMed] [Google Scholar]
- [174].Keitel A, Gross j., and Kayser C, “Perceptually relevant speech tracking in auditory and motor cortex reflects distinct linguistic features,” PLoS Biol, vol. 16, no. 3, p. e2004473, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [175].Pefkou M, Arnal LH, Fontolan L, and Giraud A-L, “θ-Band and β-Band Neural Activity Reflects Independent Syllable Tracking and Comprehension of Time-Compressed Speech,” j. Neurosci, vol. 37, no. 33, pp. 7930–7938, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [176].Keitel C, Thut G, and Gross j., “Visual cortex responses reflect temporal structure of continuous quasi-rhythmic sensory stimulation,” Neuroimage, vol. 146, pp. 58–70, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [177].Montemurro MA, Rasch M. j., Murayama Y, Logothetis NK, and Panzeri S, “Phase-of-Firing Coding of Natural Visual Stimuli in Primary Visual Cortex,” Curr. Biol, vol. 18, no. 5, pp. 375–380, 2008. [DOI] [PubMed] [Google Scholar]
- [178].König P, Engel AK, and Singer W, “Integrator or coincidence detector? The role of the cortical neuron revisited,” Trends Neurosci., vol. 19, no. 4, pp. 130–137, 1996. [DOI] [PubMed] [Google Scholar]
- [179].Singer W, “Visual Feature Integration and the Temporal Correlation Hypothesis,” Annu. Rev. Neurosci, vol. 18, no. 1, pp. 555–586, 1995. [DOI] [PubMed] [Google Scholar]
- [180].Womelsdorf T, Valiante TA, Sahin NT, Miller K. j., and Tiesinga P, “Dynamic circuit motifs underlying rhythmic gain control, gating and integration,” Nat. Neurosci, vol. 17, no. 8, pp. 1031–1039, 2014. [DOI] [PubMed] [Google Scholar]
- [181].Siegel M, Donner TH, and Engel AK, “Spectral fingerprints of large-scale neuronal interactions,” Nat. Rev. Neurosci, vol. 13, no. 2, pp. 121–134, 2012. [DOI] [PubMed] [Google Scholar]
- [182].Womelsdorf T, Ardid S, Everling S, and Valiante TA, “Burst firing synchronizes prefrontal and anterior cingulate cortex during attentional control,” Curr. Biol., 2014. [DOI] [PubMed] [Google Scholar]
- [183].Buschman T. j. and Miller EK, “Top-down versus bottom-up control of attention in the prefrontal and posterior parietal cortices,” Science (80-.)., 2007. [DOI] [PubMed] [Google Scholar]
- [184].Michalareas G, Vezoli j., van Pelt S, Schoffelen j. M., Kennedy H, and Fries P, “Alpha-Beta and Gamma Rhythms Subserve Feedback and Feedforward Influences among Human Visual Cortical Areas,” Neuron, vol. 89, no. 2, pp. 384–397, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [185].Pipa G, “Performance- and stimulus-dependent oscillations in monkey prefrontal cortex during short-term memory,” Front. Integr. Neurosci, vol. 3, p. 25, 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [186].Colgin LL, Denninger T, Fyhn M, Hafting T, Bonnevie T, jensen O, Moser MB, and Moser EI, “Frequency of gamma oscillations routes flow of information in the hippocampus,” Nature, vol. 462, no. 7271, pp. 353–357, 2009. [DOI] [PubMed] [Google Scholar]
- [187].Voloh B, Valiante TA, Everling S, and Womelsdorf T, “Theta–gamma coordination between anterior cingulate and prefrontal cortex indexes correct attention shifts,” Proc. Natl. Acad. Sci, vol. 112, no. 27, pp. 8457–8462, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [188].Aru j., Axmacher N, Do Lam ATA, Fell j., Elger CE, Singer W, and Melloni L, “Local Category-Specific Gamma Band Responses in the Visual Cortex Do Not Reflect Conscious Perception,” j. Neurosci, vol. 32, no. 43, pp. 14909–14914, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [189].Hirvonen j. and Palva S, “Cortical localization of phase and amplitude dynamics predicting access to somatosensory awareness,” Hum. Brain Mapp, vol. 37, no. 1, pp. 311–326, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [190].Zumer j. M., Scheeringa R, Schoffelen j. M., Norris DG, and jensen O, “Occipital Alpha Activity during Stimulus Processing Gates the Information Flow to Object-Selective Cortex,” PLoS Biol, vol. 12, no. 10, p. e1001965, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [191].van Ede F, de Lange F, jensen O, and Maris E, “Orienting Attention to an Upcoming Tactile Event Involves a Spatially and Temporally Specific Modulation of Sensorimotor Alpha- and Beta-Band Oscillations,”j. Neurosci, vol. 31, no. 6, pp. 2016–2024, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [192].Park H, Lee DS, Kang E, Kang H, Hahm j., Kim j. S., Chung CK, and jensen O, “Blocking of irrelevant memories by posterior alpha activity boosts memory encoding,” Hum. Brain Mapp, vol. 35, no. 8, pp. 3972–3987, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [193].Palva S, Kulashekhar S, Hamalainen M, and Palva j. M., “Localization of Cortical Phase and Amplitude Dynamics during Visual Working Memory Encoding and Retention,” j. Neurosci, vol. 31, no. 13, pp. 5013–5025, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [194].johnson K, Keep j., and Philips j., “Sickness absence. Help staff with illness.,” Health Serv. j, vol. 115, no. 5946, p. 35, 2005. [PubMed] [Google Scholar]
- [195].Roux F, Wibral M, Mohr HM, Singer W, and Uhlhaas PJ, “Gamma-Band Activity in Human Prefrontal Cortex Codes for the Number of Relevant Items Maintained in Working Memory,” j. Neurosci., vol. 32, no. 36, pp. 12411–12420, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [196].Vidal j. R., Chaumon M, O’Regan j. K., and Tallon-Baudry C, “Visual grouping and the focusing of attention induce gamma-band oscillations at different frequencies in human magnetoencephalogram signals,” j. Cogn. Neurosci, vol. 18, no. 11, pp. 1850–1862, 2006. [DOI] [PubMed] [Google Scholar]
- [197].Palva and S Palva j. M., “New vistas for α-frequency band oscillations,” Trends Neurosci., 2007. [DOI] [PubMed] [Google Scholar]
- [198].Jensen O, Bonnefond M, Marshall TR, and Tiesinga P, “Oscillatory mechanisms of feedforward and feedback visual processing,” Trends Neurosci, vol. 38, no. 4, pp. 192–194, 2015. [DOI] [PubMed] [Google Scholar]
- [199].Klimesch W, Freunberger R, Sauseng P, and Gruber W, “A short review of slow phase synchronization and memory: Evidence for control processes in different memory systems?,” Brain Res, vol. 1235, pp. 31–44, 2008. [DOI] [PubMed] [Google Scholar]
- [200].Sacchet MD, LaPlante RA, Wan Q, Pritchett DL, Lee AKC, Hamalainen M, Moore CI, Kerr CE, and Jones SR, “Attention Drives Synchronization of Alpha and Beta Rhythms between Right Inferior Frontal and Primary Sensory Neocortex,” J. Neurosci, vol. 35, no. 5, pp. 2074–2082, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [201].Doesburg SM, Bedo N, and Ward LM, “Top-down alpha oscillatory network interactions during visuospatial attention orienting,” Neuroimage, 2016. [DOI] [PubMed] [Google Scholar]
- [202].Siegel M, Donner TH, Oostenveld R, Fries P, and Engel AK, “Neuronal Synchronization along the Dorsal Visual Pathway Reflects the Focus of Spatial Attention,” Neuron, vol. 60, no. 4, pp. 709–719, 2008. [DOI] [PubMed] [Google Scholar]
- [203].Glennon M, Keane MA, Elliott MA, and Sauseng P, “Distributed Cortical Phase Synchronization in the EEG Reveals Parallel Attention and Working Memory Processes Involved in the Attentional Blink,” Cereb. Cortex, vol. 26, no. 5, pp. 2035–2045, 2016. [DOI] [PubMed] [Google Scholar]
- [204].Hirvonen J, Monto S, Wang SH, Palva JM, and Palva S, Dynamic large-scale network synchronization from perception to action, vol. 2, no. 4 Network Neuroscience, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [205].Bassett DS and Bullmore ET, “Surface Basic Heat Transfer and Flow Friction Characteristics,” Fundam. Heat Exch. Des, vol. 22, no. 4, pp. 425–562, 2009. [Google Scholar]
- [206].Uhlhaas PJ and Singer W, “Oscillations and neuronal dynamics in schizophrenia: The search for basic symptoms and translational opportunities,” Biol. Psychiatry, vol. 77, no. 12, pp. 1001–1009, 2015. [DOI] [PubMed] [Google Scholar]
- [207].Voytek B and Knight RT, “Dynamic network communication as a unifying neural basis for cognition, development, aging, and disease,” Biol. Psychiatry, vol. 77, no. 12, pp. 1089–1097, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [208].Grent-‘t-Jong T, Rivolta D, Sauer A, Grube M, Singer W, Wibral M, and Uhlhaas PJ, “MEG-measured visually induced gamma-band oscillations in chronic schizophrenia: Evidence for impaired generation of rhythmic activity in ventral stream regions,” Schizophr. Res, vol. 176, no. 2–3, pp. 177–185, 2016. [DOI] [PubMed] [Google Scholar]
- [209].Bassett DS, Bullmore E, Verchinski BA, Mattay VS, Weinberger DR, and Meyer-Lindenberg A, “Hierarchical Organization of Human Cortical Networks in Health and Schizophrenia,” J. Neurosci, vol. 28, no. 37, pp. 9239–9248, 2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [210].Hirvonen J, Wibral M, Palva JM, Singer W, Uhlhaas P, and Palva S, “Whole-Brain Source-Reconstructed MEG-Data Reveal Reduced Long-Range Synchronization in Chronic Schizophrenia,” eneuro, vol. 4, no. 5, p. ENEURO.0338–17.2017, October 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [211].Vollebregt MA, Zumer JM, ter Huurne N, Buitelaar JK, and Jensen O, “Posterior alpha oscillations reflect attentional problems in boys with Attention Deficit Hyperactivity Disorder,” Clin. Neurophysiol, vol. 127, no. 5, pp. 2182–2191, 2016. [DOI] [PubMed] [Google Scholar]
- [212].Heinrichs-Graham E, Franzen JD, Knott NL, White ML, Wetzel MW, and Wilson TW, “Pharmaco-MEG evidence for attention related hyper-connectivity between auditory and prefrontal cortices in ADHD,” Psychiatry Res. - Neuroimaging, vol. 221, no. 3, pp. 240–245, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [213].Sudre G, Szekely E, Sharp W, Kasparek S, and Shaw P, “Multimodal mapping of the brain’s functional connectivity and the adult outcome of attention deficit hyperactivity disorder,” Proc. Natl. Acad. Sci, vol. 114, no. 44, p. 201705229, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [214].Wilson TW, Franzen JD, Heinrichs-Graham E, White ML, Knott NL, and Wetzel MW, “Broadband neurophysiological abnormalities in the medial prefrontal region of the default-mode network in adults with ADHD,” Hum. Brain Mapp, vol. 34, no. 3, pp. 566–574, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [215].Taybert J, Pronicki M, Bednarska-Makaruk M, and Sykut-Cegielska J, “Choroba spichrzania estrów cholesterolu- niedoceniana przyczyna hipercholesterolemii u dzieci,” Prz. Pediatryczny, vol. 41, no. 3, pp. 117–120, 2011. [Google Scholar]
- [216].Kim DJ, Bolbecker AR, Howell J, Rass O, Sporns O, Hetrick WP, Breier A, and O’ Donnell BF, “Disturbed resting state EEG synchronization in bipolar disorder: A graph-theoretic analysis,” Neuroimage Clin, vol. 2, no. 1, pp. 414–423, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [217].Varela F, Lachaux J-P, Rodriguez E, and Martinerie J, “The brainweb: Phase synchronization and large-scale integration,” Nat. Rev. Neurosci, vol. 2, no. 4, pp. 229–239, April 2001. [DOI] [PubMed] [Google Scholar]
- [218].Fries P, “A mechanism for cognitive dynamics: neuronal communication through neuronal coherence,” Trends Cogn. Sci, vol. 9, no. 10, pp. 474–480, October 2005. [DOI] [PubMed] [Google Scholar]
- [219].Baars BJ, “The conscious access hypothesis: origins and recent evidence,” Trends Cogn. Sci, vol. 6, no. 1, pp. 47–52, January 2002. [DOI] [PubMed] [Google Scholar]
- [220].Efron R, “The minimum duration of a perception,” Neuropsychologia, vol. 8, no. 1, pp. 57–63, January 1970. [DOI] [PubMed] [Google Scholar]
- [221].Pascual-Marqui RD, Michel CM, and Lehmann D, “Segmentation of brain electrical activity into microstates: model estimation and validation,” IEEE Trans. Biomed. Eng, vol. 42, no. 7, pp. 658–665, July 1995. [DOI] [PubMed] [Google Scholar]
- [222].Michel CM and Koenig T, “EEG microstates as a tool for studying the temporal dynamics of whole-brain neuronal networks: A review,” Neuroimage, vol. 180, pp. 577–593, October 2018. [DOI] [PubMed] [Google Scholar]
- [223].Wennberg R, Quesney F, Olivier A, and Rasmussen T, “Electrocorticography and outcome in frontal lobe epilepsy,” Electroencephalogr. Clin. Neurophysiol, vol. 106, no. 4, pp. 357–368, 1998. [DOI] [PubMed] [Google Scholar]
- [224].Bartolomei F, Lagarde S, Wendling F, McGonigal A, Jirsa V, Guye M, and Bénar C, “Defining epileptogenic networks: Contribution of SEEG and signal analysis,” Epilepsia, vol. 58, no. 7, pp. 1131–1147, 2017. [DOI] [PubMed] [Google Scholar]
- [225].Matsumoto R, Nair DR, Ikeda A, Fumuro T, Lapresto E, Mikuni N, Bingaman W, Miyamoto S, Fukuyama H, Takahashi R, Najm I, Shibasaki H, and Lüders HO, “Parieto-frontal network in humans studied by cortico-cortical evoked potential,” Hum. Brain Mapp, vol. 33, no. 12, pp. 2856–2872, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [226].Andrzejak RG, David O, Gnatkovsky V, Wendling F, Bartolomei F, Francione S, Kahane P, Schindler K, and de Curtis M, “Localization of Epileptogenic Zone on Pre-surgical Intracranial EEG Recordings: Toward a Validation of Quantitative Signal Analysis Approaches,” Brain Topogr, vol. 28, no. 6, pp. 832–837, November 2015. [DOI] [PubMed] [Google Scholar]
- [227].Wilke C, Van Drongelen W, Kohrman M, and He B, “Neocortical seizure foci localization by means of a directed transfer function method,” Epilepsia, vol. 51, no. 4, pp. 564–572, 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [228].Wilke C, Worrell G, and He B, “Graph analysis of epileptogenic networks in human partial epilepsy.” [DOI] [PMC free article] [PubMed] [Google Scholar]
- [229].Wilke C, Worrell G, and He B, “Graph analysis of epileptogenic networks in human partial epilepsy,” Epilepsia, vol. 52, no. 1, pp. 84–93, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [230].Wendling F, Bartolomei F, Bellanger JJ, Bourien J, and Chauvel P, “Epileptic fast intracerebral EEG activity: Evidence for spatial decorrelation at seizure onset,” Brain, vol. 126, no. 6, pp. 1449–1459, 2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [231].Badier JM and Chauvel P, “Spatio-temporal characteristics of paroxysmal interictal events in human temporal lobe epilepsy,” J. Physiol. - Paris, vol. 89, no. 4–6, pp. 255–264, 1995. [DOI] [PubMed] [Google Scholar]
- [232].Bourien J, Bartolomei F, Bellanger JJ, Gavaret M, Chauvel P, and Wendling F, “A method to identify reproducible subsets of co-activated structures during interictal spikes. Application to intracerebral EEG in temporal lobe epilepsy,” Clin. Neurophysiol, vol. 116, no. 2, pp. 443–455, 2005. [DOI] [PubMed] [Google Scholar]
- [233].Courtens S, Colombet B, Trébuchon A, Brovelli A, Bartolomei F, and Bénar CG, “Graph Measures of Node Strength for Characterizing Preictal Synchrony in Partial Epilepsy,” Brain Connect, vol. 6, no. 7, pp. 530–539, September 2016. [DOI] [PubMed] [Google Scholar]
- [234].Van Mierlo P, Carrette E, Hallez H, Raedt R, Meurs A, Vandenberghe S, Van Roost D, Boon P, Staelens S, and Vonck K, “Ictal-onset localization through connectivity analysis of intracranial EEG signals in patients with refractory epilepsy,” Epilepsia, vol. 54, no. 8, pp. 1409–1418, 2013. [DOI] [PubMed] [Google Scholar]
- [235].Lopes da Silva F, Pijn JP, and Boeijinga P, “Interdependence of EEG signals: Linear vs. nonlinear Associations and the significance of time delays and phase shifts,” Brain Topogr, vol. 2, no. 1–2, pp. 9–18, 1989. [DOI] [PubMed] [Google Scholar]
- [236].Wendling F, Bartolomei F, Bellanger JJ, and Chauvel P, “Interpretation of interdependencies in epileptic signals using a macroscopic physiological model of the EEG,” Clin. Neurophysiol, vol. 112, no. 7, pp. 1201–1218, 2001. [DOI] [PubMed] [Google Scholar]
- [237].Amini L, Jutten C, Achard S, David O, Soltanian-Zadeh H, Hossein-Zadeh GA, Kahane P, Minotti L, and Vercueil L, “Directed differential connectivity graph of interictal epileptiform discharges,” IEEE Trans. Biomed. Eng, vol. 58, no. 4, pp. 884–893, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [238].Ponten SC, Bartolomei F, and Stam CJ, “Small-world networks and epilepsy: Graph theoretical analysis of intracerebrally recorded mesial temporal lobe seizures,” Clin. Neurophysiol, vol. 118, no. 4, pp. 918–927, 2007. [DOI] [PubMed] [Google Scholar]
- [239].Vlachos I, Krishnan B, Treiman DM, Tsakalis K, Kugiumtzis D, and Iasemidis LD, “The Concept of Effective Inflow: Application to Interictal Localization of the Epileptogenic Focus from iEEG,” IEEE Trans. Biomed. Eng, vol. 64, no. 9, pp. 2241–2252, 2017. [DOI] [PubMed] [Google Scholar]
- [240].Cosandier-Rimele D, Badier J-M, Chauvel P, and Wendling F, “A Physiologically Plausible Spatio-Temporal Model for EEG Signals Recorded With Intracerebral Electrodes in Human Partial Epilepsy,” IEEE Trans. Biomed. Eng, vol. 54, no. 3, pp. 380–388, March 2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [241].Cohen D, Cuffin BN, Yunokuchi K, Maniewski R, Purcell C, Cosgrove GR, Ives J, Kennedy JG, and Schomer DL, “MEG versus EEG localization test using implanted sources in the human brain,” Ann. Neurol, 1990. [DOI] [PubMed] [Google Scholar]
- [242].Merlet I and Gotman J, “Reliability of dipole models of epileptic spikes,” Clin. Neurophysiol, vol. 110, no. 6, pp. 1013–1028, 1999. [DOI] [PubMed] [Google Scholar]
- [243].Bai X, Towle VL, He EJ, and He B, “Evaluation of cortical current density imaging methods using intracranial electrocorticograms and functional MRI,” Neuroimage, vol. 35, no. 2, pp. 598–608, 2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [244].Lai Y, Zhang X, van Drongelen W, Korhman M, Hecox K, Ni Y, and He B, “Noninvasive cortical imaging of epileptiform activities from interictal spikes in pediatric patients,” Neuroimage, vol. 54, no. 1, pp. 244–252, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [245].Yang L, Wilke C, Brinkmann B, Worrell GA, and He B, “Dynamic imaging of ictal oscillations using non-invasive high-resolution EEG,” Neuroimage, vol. 56, no. 4, pp. 1908–1917, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [246].Mégevand P, Spinelli L, Genetti M, Brodbeck V, Momjian S, Schaller K, M Michel C, Vulliemoz S, and Seeck M, “Electric source imaging of interictal activity accurately localises the seizure onset zone,” J. Neurol. Neurosurg. Psychiatry, vol. 85, no. 1, pp. 38–43, 2014. [DOI] [PubMed] [Google Scholar]
- [247].Grova C, Daunizeau J, Lina J-M, Bénar CG, Benali H, and Gotman J, “Evaluation of EEG localization methods using realistic simulations of interictal spikes,” Neuroimage, vol. 29, no. 3, pp. 734–753, February 2006. [DOI] [PubMed] [Google Scholar]
- [248].Maksymenko K, Giusiano B, Roehri N, Bénar CG, and Badier JM, “Strategies for statistical thresholding of source localization maps in magnetoencephalography and estimating source extent,” J. Neurosci. Methods, vol. 290, pp. 95–104, 2017. [DOI] [PubMed] [Google Scholar]
- [249].Lantz G, Spinelli L, Seeck M, De Peralta Menendez RG, Sottas CC, and Michel CM, “Propagation of Interictal Epileptiform Activity Can Lead to Erroneous Source Localizations: A 128-Channel EEG Mapping Study,” J. Clin. Neurophysiol, vol. 20, no. 5, pp. 311–319, 2003. [DOI] [PubMed] [Google Scholar]
- [250].Baumgartner C, Lindinger G, Ebner A, Aull S, Serles W, Olbrich A, Lurger S, Czech T, Burgess R, and Lüders H, “Propagation of interictal epileptic activity in temporal lobe epilepsy.,” Neurology, vol. 45, no. 1, pp. 118–22, January 1995. [DOI] [PubMed] [Google Scholar]
- [251].Malinowska U, Badier JM, Gavaret M, Bartolomei F, Chauvel P, and Bénar CG, “Interictal networks in Magnetoencephalography,” Hum. Brain Mapp, vol. 35, no. 6, pp. 2789–2805, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [252].Jmail N, Gavaret M, Bartolomei F, Chauvel P, Badier JM, and Bénar CG, “Comparison of Brain Networks During Interictal Oscillations and Spikes on Magnetoencephalography and Intracerebral EEG,” Brain Topogr, vol. 29, no. 5, pp. 752–765, 2016. [DOI] [PubMed] [Google Scholar]
- [253].Santiuste M, Nowak R, Russi A, Tarancon T, Oliver B, Ayats E, Scheler G, and Graetz G, “Simultaneous magnetoencephalography and intracranial EEG registration: Technical and clinical aspects,” J. Clin. Neurophysiol, vol. 25, no. 6, pp. 331–339, 2008. [DOI] [PubMed] [Google Scholar]
- [254].Kakisaka Y, Kubota Y, Wang ZI, Piao Z, Mosher JC, Gonzalez-Martinez J, Jin K, Alexopoulos AV, and Burgess RC, “Use of simultaneous depth and MEG recording may provide complementary information regarding the epileptogenic region,” Epileptic Disord, vol. 14, no. 3, pp. 298–303, 2012. [DOI] [PubMed] [Google Scholar]
- [255].Dubarry AS, Badier JM, Trébuchon-Da Fonseca A, Gavaret M, Carron R, Bartolomei F, Liégeois-Chauvel C, Régis J, Chauvel P, Alario FX, and Bénar CG, “Simultaneous recording of MEG, EEG and intracerebral EEG during visual stimulation: From feasibility to single-trial analysis,” Neuroimage, vol. 99, pp. 548–558, 2014. [DOI] [PubMed] [Google Scholar]
- [256].Alarcon G, Guy CN, Binnie CD, Walker SR, Elwes RDC, and Polkey CE, “Intracerebral propagation of interictal activity in partial epilepsy: Implications for source localisation,” J. Neurol. Neurosurg. Psychiatry, vol. 57, no. 4, pp. 435–449, 1994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [257].Attal Y and Schwartz D, “Assessment of Subcortical Source Localization Using Deep Brain Activity Imaging Model with Minimum Norm Operators: A MEG Study,” PLoS One, vol. 8, no. 3, p. e59856, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [258].Koessler L, Cecchin T, Colnat-Coulbois S, Vignal JP, Jonas J, Vespignani H, Ramantani G, and Maillard LG, “Catching the Invisible: Mesial Temporal Source Contribution to Simultaneous EEG and SEEG Recordings,” Brain Topogr, vol. 28, no. 1, pp. 5–20, 2014. [DOI] [PubMed] [Google Scholar]
- [259].Dalal S, Jerbi K, Bertrand O, Adam C, Ducorps A, Schwartz D, Martinerie J, and Lachaux J-P, “Simultaneous MEG-intracranial EEG: New insights into the ability of MEG to capture oscillatory modulations in the neocortex and the hippocampus,” Epilepsy Behav, vol. 28, pp. 283–302, 2013.23764496 [Google Scholar]
- [260].Lantz G, Menendez RGDP, Andino SG, and Michel CM, “Noninvasive localization of electromagnetic epileptic activity. II. Demonstration of sublobar accuracy in patients with simultaneous surface and depth recordings,” Brain Topogr, vol. 14, no. 2, pp. 139–147, 2001. [DOI] [PubMed] [Google Scholar]
- [261].Medina Villalon S, Paz R, Roehri N, Lagarde S, Pizzo F, Colombet B, Bartolomei F, Carron R, and Bénar CG, “EpiTools, A software suite for presurgical brain mapping in epilepsy: Intracerebral EEG,” J. Neurosci. Methods, vol. 303, pp. 7–15, 2018. [DOI] [PubMed] [Google Scholar]
- [262].Badier JM, Dubarry AS, Gavaret M, Chen S, Trébuchon AS, Marquis P, Régis J, Bartolomei F, Bénar CG, and Carron R, “Technical solutions for simultaneous MEG and SEEG recordings: Towards routine clinical use,” Physiol. Meas, vol. 38, no. 10, pp. N118–N127, 2017. [DOI] [PubMed] [Google Scholar]
- [263].Hosseini SAH, Sohrabpour A, and He B, “Electromagnetic source imaging using simultaneous scalp EEG and intracranial EEG: An emerging tool for interacting with pathological brain networks,” Clin. Neurophysiol, vol. 129, no. 1, pp. 168–187, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [264].Gavaret M, Dubarry A-S, Carron R, Bartolomei F, Trébuchon A, and Bénar C-G, “Simultaneous SEEG-MEG-EEG recordings Overcome the SEEG limited spatial sampling,” Epilepsy Res, vol. 128, pp. 68–72, December 2016. [DOI] [PubMed] [Google Scholar]
- [265].Le Cam S, Ranta R, Caune V, Korats G, Koessler L, Maillard L, and Louis-Dorr V, “SEEG dipole source localization based on an empirical Bayesian approach taking into account forward model uncertainties,” Neuroimage, vol. 153, pp. 1–15, 2017. [DOI] [PubMed] [Google Scholar]
- [266].Caune V, Ranta R, Le Cam S, Hofmanis J, Maillard L, Koessler L, and Louis-Dorr V, “Evaluating dipolar source localization feasibility from intracerebral SEEG recordings,” Neuroimage, vol. 98, pp. 118–133, 2014. [DOI] [PubMed] [Google Scholar]
- [267].Chang N, Gulrajani R, and Gotman J, “Dipole localization using simulated intracerebral EEG,” Clin. Neurophysiol, vol. 116, no. 11, pp. 2707–2716, 2005. [DOI] [PubMed] [Google Scholar]
- [268].Pascarella A, Todaro C, Clerc M, Serre T, and Piana M, “Source modeling of ElectroCorticoGraphy (ECoG) data: Stability analysis and spatial filtering,” J. Neurosci. Methods, vol. 263, pp. 134–144, 2016. [DOI] [PubMed] [Google Scholar]
- [269].Zhang Y, van Drongelen W, Kohrman M, and He B, “Three-dimensional brain current source reconstruction from intra-cranial ECoG recordings,” Neuroimage, vol. 42, no. 2, pp. 683–695, 2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [270].Quairiaux C, Megevand P, Kiss JZ, and Michel CM, “Functional Development of Large-Scale Sensorimotor Cortical Networks in the Brain,” J. Neurosci, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [271].Barnett L, Barrett AB, and Seth A,K, “Misunderstandings regarding the application of Granger causality in neuroscience,” Proceedings of the National Academy of Sciences, 115(29), E6676–E6677, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [272].Faes L, Stramaglia S, and Marinazzo D,”On the interpretability and computational reliability of frequency-domain Granger causality,” F1000Research, 6, 1710. doi: 10.12688/f1000research.12694.1, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [273].Dhamala M, Liang H, Bressler SL, Ding M, “Granger-Geweke causality: Estimation and interpretation,” NeuroImage, 175, 460–463, 2018. [DOI] [PubMed] [Google Scholar]
- [274].Freiwald WA, Valdes P, Bosch J, Biscay R, Jimenez JC, Rodriguez LM, Rodriguez V, Kreiter AK, Singer W, “Testing non-linearity and directedness of interactions between neural groups in the macaque inferotemporal cortex,” J. Neurosci. Methods, 94, 105–119, 1999. [DOI] [PubMed] [Google Scholar]
- [275].Marinazzo D, Pellicoro M, Stramaglia S, “Kernel Method for Nonlinear Granger Causality,” Physical Review Letters, 100, 144103, 2008. [DOI] [PubMed] [Google Scholar]
- [276].Li Y, Wei HL, Billings SA, and Liao XF, “Time-varying linear and nonlinear parametric model for Granger causality analysis,” Physical Review E, 85(4), p.041906, 2012. [DOI] [PubMed] [Google Scholar]
- [277].Sheikhattar A, Miran S, Liu J, Fritz JB, Shamma SA, Kanold PO, and Babadi B, “Extracting neuronal functional network dynamics via adaptive Granger causality analysis,” Proceedings of the National Academy of Sciences, 115(17), E3869–E3878, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [278].Lantz G, Grave de Peralta R, Spinelli L, Seeck M, Michel C, “Epileptic source localization with high density EEG: how many electrodes are needed,” Clin Neurophysiol, 114, 63–69, 2003. [DOI] [PubMed] [Google Scholar]
- [279].Sohrabpour A, Lu Y, Kankirawatana P, Blount J, Kim H, He B, “Effect of EEG Electrode Number on Epileptic Source Localization in Pediatric Patients,” Clinical Neurophysiology, 126(3), 472–480, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [280].Wang X, Chen Y, and Ding M, “Estimating Granger Causality after Stimulus Onset: A Cautionary Note,” NeuroImage, 41, 767–776, 2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [281].Krieg J, Trébuchon-Da Fonseca A, Martínez-Montes E, Marquis P, Liégeois-Chauvel C, Bénar CG, “A comparison of methods for assessing alpha phase resetting in electrophysiology, with application to intracerebral EEG in visual areas,” Neuroimage, 55(1), 67–86, 2011. [DOI] [PubMed] [Google Scholar]
- [282].Trongnetrpunya A, Nandi B, Kang D, Kocsis B, Schroeder CE, Ding M, “Assessing Granger causality in electrophysiological data: the importance of bipolar derivations,” Frontiers in Systems Neuroscience, 9, 18, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [283].Krishnan B, Vlachos I, Wang ZI, Mosher J, Najm I, Burgess R, Iasemidis L, Alexopoulos AV, “Epileptic focus localization based on resting state interictal MEG recordings is feasible irrespective of the presence or absence of spikes,” Clin Neurophysiol, 126(4), 667–674, 2015. [DOI] [PubMed] [Google Scholar]
- [284].Nissen IA, Stam CJ, Reijneveld JC, van Straaten IE, Hendriks EJ, Baayen JC, De Witt Hamer PC, Idema S, Hillebrand A, “Identifying the epileptogenic zone in interictal resting-state MEG source-space networks,” Epilepsia, 58(1), 137–148, 2017. [DOI] [PubMed] [Google Scholar]
- [285].Schwab S, Koenig T, Morishima Y, Dierks T, Federspiel A, and Jann K, “Discovering frequency sensitive thalamic nuclei from EEG microstate informed resting state fMRI” NeuroImage, vol. 118, pp. 368–375, 2015. [DOI] [PubMed] [Google Scholar]
- [286].Pizzo F, Roehri N, Medina Villalon S, Trébuchon A, Chen S, Lagarde S, Carron R, Gavaret M, Giusiano B, McGonigal A, Bartolomei F, Badier JM, and Bénar CG, “Deep brain activities can be detected with magnetoencephalography," Nat Commun,10(1): 971, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [287].Seeber M, Cantonas LM, Hoevels M, Sesia T, Visser-Vandewalle V, and Michel CM, “Subcortical electrophysiological activity is detectable with high-density EEG source imaging,” Nat Commun, 10(1):753, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]