Bivariate Logistic Bayesian LASSO for Detecting Rare Haplotype Association with Two Correlated Phenotypes

Abstract

In genetic association studies, joint modeling of related traits/phenotypes can utilize the correlation between them and thereby provide more power and uncover additional information about genetic etiology. Moreover, detecting rare genetic variants are of current scientific interest as a key to missing heritability. Logistic Bayesian LASSO (LBL) has been proposed recently to detect rare haplotype variants using case-control data, i.e., a single binary phenotype. As there is currently no haplotype association method that can handle multiple binary phenotypes, we extend LBL to fill this gap. We develop a bivariate model by using a latent variable to induce correlation between the two outcomes. We carry out extensive simulations to investigate the bivariate LBL and compare with the univariate LBL. The bivariate LBL performs better or similar to the univariate LBL in most settings. It has the highest gain in power when a haplotype is associated with both traits and it affects at least one trait in a direction opposite to the direction of the correlation between the traits. We analyze two datasets — Genetic Analysis Workshop 19 sequence data on systolic and diastolic blood pressures and a genome-wide association dataset on lung cancer and smoking, and detect several associated rare haplotypes.

1. Introduction

In health-related studies, multiple correlated traits and outcomes are often recorded (Teixeira-Pinto & Normand, 2009). These traits can have a shared genetic etiology, e.g, systolic and diastolic blood pressures (Schillert & Konigorski, 2016). In particular, one genetic variant may influence multiple phenotypes, a phenomenon referred to as cross-phenotype (CP) association or pleiotropy. The former typically refers to simply association without regard to the cause of association while pleiotropy refers to true effects of a genetic locus on multiple phenotypes (Solovieff, Cotsapas, Lee, Purcell, & Smoller, 2013).

There has been mounting scientific evidence that pleiotropy is widespread (Gratten & Visscher, 2016; Solovieff et al., 2013; C. Yang, Li, Wang, Chung, & Zhao, 2015). In fact, pleiotropy has been reported even between seemingly unrelated phenotypes, for example, between psychiatric disorders, autoimmune diseases, and metabolic disorders (Kember et al., 2018; Solovieff et al., 2013; Q. Wang, Yang, Gelernter, & Zhao, 2015), and between coronary artery disease and tonsillectomy (Gratten & Visscher, 2016). The shared variants can have concordant or discordant effects on the phenotypes. As Hackinger and Zeggini (2017) point out, understanding of pleiotropy is important not only from the point of view of association but it also holds potential for more accurate disease classification especially when aetiopathology of some disorders are ambiguous, e.g., in some psychiatric conditions. A deeper insight into the etiological overlap can have a wide-ranging implications for prevention and treatment strategies (Q. Wang et al., 2015; C. Yang et al., 2015). This is especially crucial as personalized and genomic medicines are gaining more traction. For example, if a specific variant is associated with multiple traits in opposite directions, the molecular targets for drug development and genome editing need to take it into account (Gratten & Visscher, 2016). Indeed, as the importance of uncovering pleiotropy is becoming clearer, it is motivating more large-scale PheWAS (phenome-wide association studies) wherein each genetic variant is tested for association with all available phenotypes (Hackinger & Zeggini, 2017).

The most common analytic approach to multiple outcomes is to consider each outcome separately in a univariate framework. However, such a strategy ignores the extra information contained in the correlation among the outcomes and amounts to a missed opportunity to gain insight into the underlying common genetic mechanism. Moreover, testing each outcome separately leads to loss of power especially after multiplicity adjustment. In fact, commonly used multiplicity adjustment approaches such as Bonferroni method assume that the tests are independent, which does not clearly hold as the outcomes are correlated. A better approach from both biological and statistical standpoint is to jointly model multiple correlated outcomes in a multivariate setting (Galesloot, van Steen, Kiemeney, & Janss, 2014; Mitteroecker, Cheverud, & Pavlicev, 2016; Teixeira-Pinto & Normand, 2009). It provides better control over type I error rates, increased power, and can answer intrinsically multivariate questions such as pleiotropy (Teixeira-Pinto & Normand, 2009).

In recent years, a number of methods have been proposed for testing genetic association with mutiple phenotypes jointly (Hackinger & Zeggini, 2017; Kaakinen et al., 2017; Klei, Luca, Devlin, & Roeder, 2008; Lee et al., 2017; O’Reilly et al., 2012; Pei, Zhang, Liu, & Deng, 2009; Ray & Basu, 2017; Ray, Pankow, & Basu, 2016). However, they almost exclusively use single-nucleotide polymorphisms (SNP) obtained from genome-wide association studies (GWAS) or next generation sequencing (NGS) as genetic variants. In particular, if the interest lies in testing rare SNPs, which are currently of great scientific interest as a key to missing heritability, then methods proposed for NGS data can be used. This is because rare SNPs are usually not genotyped in GWAS. Nevertheless, NGS data are typically of much smaller sample sizes than GWAS especially for the purpose of joint modeling of multiple phenotypes. Moreover, NGS data have several limitations such as genotype calling may not be accurate for extremely rare variants and how to distinguish and prioritize among different types of genetic variants may not be clear (Goldstein et al., 2013). Thus, for the purpose of testing common disease rare variant (CDRV) hypothesis, there is clearly a need for alternative approaches that do not necessarily rely on NGS data.

In this regard, haplotype-based tests are a powerful compliment to SNP-based tests. As common SNPs can combine to form rare haplotypes, tests using haplotypes as the basic genetic variant can not only be carried out using NGS data but also using GWAS data. This opens up enormous possibilities for investigating CDRV hypothesis especially because a vast array of GWAS data, still largely untapped, are already available and those datasets are typically of much larger sample sizes than NGS data. Thus, rare haplotype variants can be tested for association with one or multiple diseases using GWAS data without a need for collecting additional data. Apart from this specific rationale from the point of view of rare variants, a general motivation for studying haplotypes is that they have biological significance in terms of functionality of a genomic region as elucidated nicely in Chapter 13 of Ziegler and König (2010); also see Clark (2004); D. J. Schaid (2004). Indeed several haplotype-based association tests were proposed long before rare variants garnered attention of the scientific community (Burkett, Graham, & McNeney, 2006; Lake et al., 2003; D. Schaid, Rowland, Tines, Jacobson, & Poland, 2002). Conventionally, a haplotype analysis is conducted as a follow-up on regions deemed to be of interest using single-SNP genome-wide approaches. In fact, haplotype-based tests are powerful when there are multiple causal SNPs in a region acting in cis or if the causal variant is not genotyped (Morris & Kaplan, 2002; Ziegler & König, 2010). Moreover, following on the promise of the haplotype-based tests for investigating CDRV hypothesis, several tests have been proposed more recently and it has been also shown that rare haplotypes formed by common SNPs are likely to tag rare single nucleotide variants (Biswas & Lin, 2012; Guo & Lin, 2009; J. Li, Zhang, & Yi, 2011; Y. Li, Byrnes, & Li, 2010; Lin et al., 2013).

Specifically, logistic Bayesian LASSO (LBL) has been shown to be a powerful rare haplotype association method (Biswas & Lin, 2012; Biswas & Papachristou, 2014; Datta & Biswas, 2016; Datta, Zhang, Zhang, & Biswas, 2016; Papachristou & Biswas, 2019; M. Wang & Lin, 2015). The Bayesian framework of LBL is highly flexible and naturally allows for extensions in different directions. Indeed, LBL has been extended to incorporate gene-environment interactions (Biswas, Xia, & Lin, 2014; Zhang & Biswas, 2015; Zhang, Lin, & Biswas, 2017), data generated using complex sampling designs (Zhang, Hofmann, Purdue, Lin, & Biswas, 2017), and family data (Datta, Lin, & Biswas, 2018; M. Wang & Lin, 2014). These developments motivate us to consider extension of LBL for the purpose of modeling multiple phenotypes jointly. It is especially of practical interest because currently there is no method available for testing haplotype (rare or common) association with multiple binary traits, at least to the best of our knowledge. We could find only one haplotype-based test for two traits called Bivariate HTR (haplotype trend regression), however, it is applicable for quantitative traits only and is not targeted for detecting rare haplotype association (Pei et al., 2009). Thus, our goal is to fill this gap especially from the standpoint of detecting rare haplotype variants.

In this article, we propose bivariate LBL to jointly model two correlated binary (case/control) phenotypes. We adapt the general framework of LBL for each phenotype and model dependence between them by introducing latent variables in a way similar to how it is modeled in generalized linear mixed models through subject-specific random effect (Agresti, 2012). More specifically, in the framework of usual probit regression, Teixeira-Pinto and Normand (2009) use latent variables to induce correlation between a continuous and a binary outcomes. We adapt the idea in the context of LBL for two binary outcomes involving logistic regression under retrospective likelihood with regularization. We carry out extensive simulations under varying association scenarios to investigate the properties of bivariate LBL and compare with those of the original version of LBL (Biswas & Lin, 2012), which was proposed for analysis of a single phenotype (referred to as univariate LBL henceforth). We find that bivariate LBL has power higher or similar to that of univariate LBL in most scenarios. Finally we apply the methods to two datasets — exome sequence data from Genetic Analysis Workshop (GAW) 19 (Engelman et al., 2016) and GWAS data on lung cancer (database of Genotypes & Phenotypes, 2019). In the GAW data, we analyze haplotype blocks in several genes for testing association with systolic and diastolic blood pressures jointly. In the lung cancer data, we analyze haplotype blocks in chromosome 15q25.1 region for association with lung cancer and smoking jointly. In both analyses, we detect several haplotypes, including rare ones, to be associated with one or both phenotypes with same or opposite direction of effects. Some of these haplotypes are detected by bivariate LBL but not by univariate LBL.

2. Methods

2.1. Retrospective Likelihood for Bivariate LBL

Consider a sample consisting of two correlated disease statuses with each status being of binary type (case/control). Let Y_i1 = 0/1 and Y_i2 = 0/1 denote the ith individual’s affection statuses for diseases 1 and 2, respectively. Suppose n₀₀ subjects are free of both diseases, n₁₀ have disease 1 only, n₀₁ have disease 2 only, and n₁₁ have both diseases. Thus the two subscripts denote the two disease statuses. Let n = n₀₀+n₁₀+n₀₁+n₁₁ be the total sample size. Define Y₁ = (Y₁₁,…,Y_n1) and Y₂ = (Y₁₂,…,Y_n2). Let G_i denote the observed genotype of the ith individual and G = (G₁,…,G_n). As haplotype pair of a person may not be deduced unambiguously from the observed genotype data, we further let S(G_i) denote the set of haplotype pairs compatible with G_i, Z_ir denote the rth element of S(G_i), and Z denote a vector consisting of all elements of S(G_i) for all i (Zhang & Biswas, 2015). Further, we introduce a latent variable u_i for ith individual, which is shared between the disease models for Y_i1 and Y_i2 to model marginal dependence between them (Agresti, 2012; Teixeira-Pinto & Normand, 2009). Assume u_i follows $N\left(0,{\sigma }_u^2\right)$ distribution for all i. Let u = (u₁,u₂,…,u_n). Assume Y_i1 and Y_i2 are independent given u_i. That is, even though Y_i1 and Y_i2 are marginally dependent, they are conditionally independent given u_i. In other words, latent variables induce conditional independence between seemingly correlated outcomes. The retrospective likelihood can be written as:

$$\begin{gathered} L\left(\mathrm{\Psi }\right)=\prod _{i=1}^{n_{00}}\sum _{Z_{ir}\in S\left(G_i\right)}P\left(Z_{ir}|Y_{i1}=0,Y_{i2}=0,u_i\right)P\left(u_i|Y_{i1}=0,Y_{i2}=0\right) \\ ·\prod _{i=n_{00}+1}^{n_{00}+n_{10}}\sum _{Z_{ir}\in S\left(G_i\right)}P\left(Z_{ir}|Y_{i1}=1,Y_{i2}=0,u_i\right)P\left(u_i|Y_{i1}=1,Y_{i2}=0\right) \\ ·\prod _{i=n_{00}+n_{10}+1}^{n_{00}+n_{10}+n_{01}}\sum _{Z_{ir}\in S\left(G_i\right)}P\left(Z_{ir}|Y_{i1}=0,Y_{i2}=1,u_i\right)P\left(u_i|Y_{i1}=0,Y_{i2}=1\right) \\ ·\prod _{i=n_{00}+n_{10}+n_{01}+1}^n\sum _{Z_{ir}\in S\left(G_i\right)}P\left(Z_{ir}|Y_{i1}=1,Y_{i2}=1,u_i\right)P\left(u_i|Y_{i1}=1,Y_{i2}=1\right), \end{gathered}$$ (1)

where Ψ is the set of model parameters (${\sigma }_u^2$, regression coefficients, and parameters associated with haplotype frequencies). To completely write the likelihood in terms of the model parameters, we will go through the following steps. For ease of exposition, the subscripts i and r are suppressed and l = 1,2.

1. Write each probability term in the likelihood in terms of (i) ${\sigma }_u^2$, (ii) $a_Z^l=P\left(Z|Y_l=0\right)$, the frequency of haplotype pair Z in the control population for disease l, and (iii) ${\theta }_{Z,u}^l=P\left(Y_l=1|Z,u\right)/P\left(Y_l=0|Z,u\right)$, the odds of the disease l given Z and u. So we need to specify the models for $a_Z^l$ and ${\theta }_{Z,u}^l$ in terms of the model parameters, which we do in the next two steps.

2. Assume there are m possible haplotypes. Model $a_Z^l$ in terms of two sets of parameters: (1) ${\mathit{f}}^l=\left(f_1^l,\dots ,f_m^l\right)$, the frequencies of m haplotypes in the controls for disease l and (2) d, the within-population inbreeding coefficient, which can be used for modeling Hardy-Weinberg disequilibrium (Biswas & Lin, 2012; Weir, 1996). f¹ and f² are further expressed in terms of ${\mathit{f}}^{00}=\left(f_1^{00},\dots ,f_m^{00}\right)$, ${\mathit{f}}^{10}=\left(f_1^{10},\dots ,f_m^{10}\right)$, and ${\mathit{f}}^{01}=\left(f_1^{01},\dots ,f_m^{01}\right)$, the population frequencies of m haplotypes corresponding to the three sub-samples of sizes n₀₀, n₁₀, and n₀₁, respectively.

3. Model ${\theta }_{Z,u}^l$ in terms of regression coefficients β^l and u.

Thus, the set of model parameters in the likelihood is Ψ = (β¹,β²,f⁰⁰,f¹⁰,f⁰¹,d,${\sigma }_u^2$). The details of the steps 1 and 2 can be found in Appendix A1 while the step 3 is described in the following.

Modeling of ${\theta }_{Z,u}^1$ and ${\theta }_{Z,u}^2$. We model the two disease odds using the following logistic regression models:

$$\text{log}{\theta }_{Z,u}^l={\mathit{X}}_{\mathit{Z}}{\beta }^l+u,l=1,2.$$

Here X_Z = (1,x₁,x₂,…,x_m−1) is a (row) design vector, where x_k is the number of copies of haplotype z_k in a haplotype pair Z, k = 1,…,m − 1. The mth haplotype is assumed to be baseline without loss of generality. β¹ and β² are vectors of regression coefficients (including intercepts) representing the effects of haplotypes on the two diseases.

As the models for both disease odds share u (with same sign), the marginal correlation modeled between the two traits can only be non-negative (Agresti, 2012). If that is not the case in any particular application, one can flip the case/control status for one trait to make the correlation positive before applying bivariate LBL (Teixeira-Pinto & Normand, 2009). The marginal correlation between Y₁ and Y₂ can be found in Appendix A2; it is an increasing function of ${\sigma }_u^2$. This product moment correlation is referred to as ϕ coefficient from which odds ratio can be computed using the marginal probabilities of a 2 × 2 contingency table of Y₁ and Y₂ (Olivier & Bell, 2013). As $u_i~N\left(0,{\sigma }_u^2\right)$, when ${\sigma }_u^2=0$, all u_is are equal to 0, which corresponds to the two phenotypes being uncorrelated.

2.2. Priors

Following Biswas and Lin (2012), we use Bayesian LASSO to regularize the regression coefficients, which basically amounts to setting the prior for each element of β¹ and β² to be a double exponential distribution:

$$\pi \left({\beta }_j^l|\text{λ}\right)=\frac{\text{λ}}{2}\text{exp}\left(-\text{λ}\left|{\beta }_j^l\right|\right),-\infty <{\beta }_j<\infty ,l=1,2,j=0,1,\dots ,m-1.$$

The above distribution has mean 0 and variance 2/λ². We can use the hyper-parameter λ to control the degree of penalty in order to shrink the unassociated haplotype effects close to zero. This will allow the associated haplotypes, especially the rare ones, more likely to stand out with their coefficients estimated to be large (in absolute scale) and variance to be small. We let λ follow Gamma(a,b) distribution with a = b = 20 (Biswas & Lin, 2012; Zhang, Lin, & Biswas, 2017). As a = b, the prior variance of β is 2a²/((a − 1)(a − 2)), for a > 2. With a = b = 20, the standard deviation of β is 1.53.

Prior for each of f⁰⁰, f¹⁰, and f⁰¹ is set to be Dirichlet(1,…,1) consisting of m ones. For d, we use a uniform prior. However, d is not independent of f⁰⁰, f¹⁰, and f⁰¹ because $a_Z^1$ and $a_Z^2$ must be nonnegative. There is a constraint that $d>-\frac{f_k^l}{1-f_k^l},l=1,2$, and for all k (see Appendix A1 for more details). So the prior for d given f⁰⁰, f¹⁰, and f⁰¹ is set to be Uniform $\left(\underset{k}{\text{max}}\left\{\underset{l}{\text{max}}\left\{-\frac{f_k^l}{1-f_k^l}\right\}\right\},1\right)$. We use a non-informative uniform prior for σ_u, which is equivalent to $p\left({\sigma }_u^2\right)\propto {\sigma }_u^{-1},{\sigma }_u^2>0$ (Gelman, Carlin, Stern, & Rubin, 2003).

2.3. Posterior Distributions and MCMC Algorithm

Combining the likelihood and prior distributions, the joint posterior distribution of all parameters is:

$$\pi \left({\mathit{\beta }}^1,{\mathit{\beta }}^2,\text{λ},{\mathit{f}}^{00},{\mathit{f}}^{01},{\mathit{f}}^{10},d,{\sigma }_u^2,\mathit{Z}|{\mathit{Y}}_1,{\mathit{Y}}_2,\mathit{G},\mathit{u}\right)$$

$$\propto L\left(\mathrm{\Psi }\right)\pi \left({\mathit{\beta }}^1|\text{λ}\right)\pi \left({\mathit{\beta }}^2|\text{λ}\right)\pi (\text{λ})\pi \left({\mathit{f}}^{00}\right)\pi \left({\mathit{f}}^{01}\right)\pi \left({\mathit{f}}^{10}\right)\pi \left(d|{\mathit{f}}^{00},{\mathit{f}}^{01},{\mathit{f}}^{10}\right)\pi \left({\sigma }_u^2\right).$$

We use Markov chain Monte Carlo (MCMC) methods to estimate the posterior distributions of all parameters (Biswas & Lin, 2012) and these are described in Appendix A3.

2.4. Association Testing

After obtaining the posterior distribution of each β coefficient, we can use it to test for association. In order to compare the performance of our proposed bivariate LBL with univariate LBL and to take into account the fact that the phenotypes are correlated, we consider two sets of hypotheses: (1) Hypothesis 1 to test whether a specific haplotype is associated with any of the two phenotypes (2) Hypothesis 2 to test whether any haplotype (i.e., not a specific haplotype) in the block under study is associated with any of the two phenotypes. We will describe the testing procedure for the two sets of hypotheses in order in the following.

Hypothesis 1. For bivariate LBL, for testing association with jth haplotype, the null hypothesis of no association and the alternative hypothesis of association with at least one of the phenotypes are written as:

$H_0:\left|{\beta }_j^1\right|\le ϵ\text{\hspace{0.17em}and\hspace{0.17em}}\left|{\beta }_j^2\right|\le ϵ\text{\hspace{0.17em}versus\hspace{0.17em}}{H}_a:\left|{\beta }_j^1\right|>ϵ\text{\hspace{0.17em}or\hspace{0.17em}}\left|{\beta }_j^2\right|>ϵ\text{\hspace{0.17em}for\hspace{0.17em}a\hspace{0.17em}fixed\hspace{0.17em}}j$, where ϵ is a small number:

While for univariate LBL, we carry out two separate tests with the corresponding null and alternative hypotheses being:

$$H_{01}:\left|{\beta }_j^1\right|\le ϵ\text{ versus }{H}_{a1}:\left|{\beta }_j^1\right|>ϵ\text{ for a fixed }j,$$

$$H_{02}:\left|{\beta }_j^2\right|\le ϵ\text{ versus }{H}_{a2}:\left|{\beta }_j^2\right|>ϵ\text{ for a fixed }j.$$

These hypotheses are the same as what was proposed for the original LBL for one phenotype (Biswas & Lin, 2012).

We use ϵ = 0.1 following Biswas and Lin (2012) in our simulations and real data analyses. Bayes Factors (BF) are used to carry out the test of hypotheses, which is the ratio of the posterior odds to the prior odds of the alternative hypothesis. The unconditional joint prior distribution of β of dimension m is:

$$\pi (\mathit{\beta })=\frac{b^a\left(m+a-1\right)!}{2^m\left(a-1\right)!}\cdot \frac{1}{{\left({\sum }_{i=1}^m\left|{\beta }_i\right|+b\right)}^{m+a}},-\infty <{\beta }_i<\infty ,i=1,\dots ,m.$$

This is used to find the prior odds of a specific hypothesis. For the bivariate model, if a BF exceeds a certain threshold, we conclude association with at least one disease. While for a univariate model, if its BF exceeds a certain threshold, we conclude association with the corresponding disease. A threshold of 2 has been proposed earlier (Biswas & Lin, 2012), however, it may not be valid for testing with two or more phenotypes individually or jointly. We will discuss calculation of appropriate thresholds in the simulation study and real data application sections.

Hypothesis 2. For bivariate LBL, the null and the alternative hypotheses are:

$$H_0:\left|{\beta }_j^1\right|\le ϵ\text{\hspace{0.17em}and\hspace{0.17em}}\left|{\beta }_j^2\right|\le ϵ\text{\hspace{0.17em}for\hspace{0.17em}all\hspace{0.17em}}j\text{\hspace{0.17em}versus\hspace{0.17em}}{H}_a:\left|{\beta }_j^1\right|>ϵ\text{\hspace{0.17em}or\hspace{0.17em}}\left|{\beta }_j^2\right|>ϵ\text{\hspace{0.17em}for\hspace{0.17em}at\hspace{0.17em}least\hspace{0.17em}one\hspace{0.17em}}j.$$

While for the two univariate LBL models, we carry out two separate tests with the following two sets of null and alternative hypotheses:

$$H_{01}:\left|{\beta }_j^1\right|\le ϵ\text{ for all }j\text{ versus }{H}_{a1}:\left|{\beta }_j^1\right|>ϵ\text{ for at least one }j,$$

$$H_{02}:\left|{\beta }_j^2\right|\le ϵ\text{ for all }j\text{ versus }{H}_{a2}:\left|{\beta }_j^2\right|>ϵ\text{ for at least one }j.$$

The null hypothesis 2 for bivariate LBL is more difficult to hold than the corresponding null hypothesis 1 because the former requires all $\left|{\beta }_j^l\right|$ to be less than ϵ for l =1, 2 and j = 1,…,m−1, i.e., for a total of 2(m−1) β parameters. For large m, a small ϵ value can make the null hypothesis to be rejected easily, which will lead to high type I error rates. So we use a larger value of ϵ = 0.4 for testing hypothesis 2.

3. Simulation Study

3.1. Settings and Data Generation

In order to evaluate the performance of bivariate LBL and compare it with that of univariate LBL, we carry out a number of simulations under each combination of settings and association scenarios listed in Table 1. Specifically, we have three settings with 6, 9, and 12 haplotypes, respectively. Each haplotype is formed by 5 SNPs. Under each setting, we varied the type of association between haplotypes and traits to generate a scenario. In particular, a rare haplotype 11011 is associated with one or both diseases, i.e., its β coefficient(s) is/are set to be non-zero and the direction(s) of association(s) can be positive (risk) or negative (protective). Specifically, |β| = {2,2,1,1.5,1.5} in the five scenarios, respectively. Although these |β| values are relatively large, they were chosen to ensure that at least one of the two methods gives reasonable power at type I error rates of 1–10%. Moreover, |β| values around 1.5 do seem to occur in real data (e.g., in our GAW19 data analysis to follow). Rest of the haplotypes are null or non associated with their β coefficients set as 0. We choose to set only one haplotype to be associated so that we can easily examine how varying the directions of effects of the haplotype on one or both phenotypes influences the power. Also, in many real data applications (including ours), often only one haplotype is associated in a haplotype block.

Table 1:

Simulation settings and association scenarios.

			Scenario 1		Scenario 2		Scenario 3		Scenario 4		Scenario 5
Setting	Hap	Freq	β1	β2	β1	β2	β1	β2	β1	β2	β1	β2
1	01100	0.300	0	0	0	0	0	0	0	0	0	0
	10100	0.005	0	0	0	0	0	0	0	0	0	0
	11011	0.010	2	2	−2	−2	1	−1	1.5	0	−1.5	0
	11100	0.155	0	0	0	0	0	0	0	0	0	0
	11111	0.110	0	0	0	0	0	0	0	0	0	0
	10011	0.420	0	0	0	0	0	0	0	0	0	0
2	01010	0.060	0	0	0	0	0	0	0	0	0	0
	01100	0.250	0	0	0	0	0	0	0	0	0	0
	10000	0.080	0	0	0	0	0	0	0	0	0	0
	10100	0.005	0	0	0	0	0	0	0	0	0	0
	11011	0.010	2	2	−2	−2	1	−1	1.5	0	−1.5	0
	11100	0.090	0	0	0	0	0	0	0	0	0	0
	11101	0.085	0	0	0	0	0	0	0	0	0	0
	11111	0.100	0	0	0	0	0	0	0	0	0	0
	10011	0.320	0	0	0	0	0	0	0	0	0	0
3	00111	0.070	0	0	0	0	0	0	0	0	0	0
	01000	0.020	0	0	0	0	0	0	0	0	0	0
	01011	0.050	0	0	0	0	0	0	0	0	0	0
	01101	0.060	0	0	0	0	0	0	0	0	0	0
	01110	0.140	0	0	0	0	0	0	0	0	0	0
	10010	0.080	0	0	0	0	0	0	0	0	0	0
	10100	0.005	0	0	0	0	0	0	0	0	0	0
	11011	0.010	2	2	−2	−2	1	−1	1.5	0	−1.5	0
	11101	0.090	0	0	0	0	0	0	0	0	0	0
	11110	0.130	0	0	0	0	0	0	0	0	0	0
	11111	0.100	0	0	0	0	0	0	0	0	0	0
	10001	0.245	0	0	0	0	0	0	0	0	0	0

Hap: Haplotype, Freq: Haplotype frequency

To generate haplotype pairs for subjects, we first consider all possible haplotype pairs under each setting and use the frequencies listed in Table 1 to calculate their probabilities in the control population for both diseases by assuming Hardy-Weinberg equilibrium. Next, we use these haplotype pair probabilities to randomly choose one haplotype pair for each subject in a sample and form the design row vector X_Z. Once the haplotype pairs of all subjects are generated, we use a probit model to assign the subjects to be cases or controls for the two phenotypes (Teixeira-Pinto & Normand, 2009). Specifically, for each subject, we generate two continuous variables using the following bivariate normal (BVN) distribution:

$$\left(\begin{array}{l}{Y}_1^{*}\hfill \\ Y_2^{*}\hfill \end{array}\right)~BVN\left(\left(\begin{array}{c}{\mathit{X}}_Z{\mathit{\beta }}^1\\ {\mathit{X}}_Z{\mathit{\beta }}^2\end{array}\right),\left(\begin{array}{cc}{\sigma }_1^2& {\sigma }_1{\sigma }_2\rho \\ & {\sigma }_2^2\end{array}\right)\right),$$

where β¹ and β² (excluding intercepts ${\beta }_0^l,l=1,2$) are as shown in Table 1, ${\beta }_0^1={\beta }_0^2=\mathrm{-2.94}$, σ₁ = σ₂ = 3, and ρ = {0,0.3,0.7,0.99}. These ρ values correspond to empirically calculated approximate ϕ = {−0.15,0,0.3,0.83}, respectively. Next, the binary disease statuses (Y₁,Y₂) are generated in the following way (l = 1, 2):

$$Y_l=\{\begin{array}{ll}0,\hfill & \text{ if }{Y}_l^{*}\le 0,\hfill \\ 1,\hfill & \text{ if }{Y}_l^{*}>0.\hfill \end{array}$$

We generate a sample of size 2000 consisting of 1000 unaffected subjects and 1000 subjects affected with one or both diseases.

A total of 500 samples are generated for each simulation. We analyze each sample using bivariate LBL applied to the two phenotypes jointly. We run a total of 200,000 MCMC iterations with 50,000 burn-in to ensure satisfactory convergence. We also analyze each sample using univariate LBL (applied twice to the two phenotypes) for which the default total number of MCMC iterations is 50,000 with 20,000 burn-in. We apply appropriate cutoffs (to be described below) to the resulting BFs to declare significance. A significant result counts towards the calculation of power or type I error rate depending on whether the haplotype (for hypothesis 1) or haplotype block (for hypothesis 2) under study is truly associated or not. Then we compare powers of all methods using receiver operating characteristic (ROC) type curves wherein power is plotted against type I error rate.

3.2. Calculation of Cutoffs

We now describe how we calculate appropriate cutoffs for BF for both bivariate and univariate LBL (Galesloot et al., 2014). For each combination of simulation setting and a fixed value of ρ, we create a null sample of size 2000 (1000 controls and 1000 cases) in the same way as above but by setting all haplotype effects (βs) to be 0. We generate 1000 replicates for each null sample and use them to calculate cutoffs corresponding to varying type I error rates. These cutoffs are used in power calculations under the non-null settings listed in Table 1.

Cutoffs for hypothesis 1. For the bivariate model, we record BFs for hypothesis 1 for all haplotypes in a block and find their maximum. Then we sort the 1000 maximum BF values (one from each null sample) in descending order and use the value at a fixed top percent position as the cutoff. For example, we use the average of maximum BF values at the 50th and 51st positions as the cutoff for the type I error rate of 0.05. Note that the cutoffs calculated in this manner incorporate multiplicity adjustment for multiple testing within a haplotype block by taking maximum of BFs over all haplotypes in the block. For the univariate models, we first get the BFs for all haplotypes from the two univariate models and find the maximum of all those BFs. Note that as there are two univariate tests corresponding to each bivariate test, maximum is taken over twice as many BFs as in the bivariate model. For example, for the setting with 6 haplotypes, we get 5 × 2 = 10 univariate BFs (excluding the baseline) and find their maximum. Then we sort the 1000 maximum BF values in descending order and find the cutoffs in the same way as for the bivariate model.

Cutoffs for hypothesis 2. For the bivariate model, we sort all 1000 BFs for hypothesis 2 (there is only one BF per sample) in descending order and use the same way as mentioned above to find the cutoffs. For the univariate models, we get two BFs corresponding to hypothesis 2 from the two univariate tests and find their maximum. Then we sort the 1000 maximum BF values in descending order and find the cutoffs in the same way.

Note that an alternative way of calculating cutoffs for a given sample is to permute the case-control statuses of individuals to create a null sample and repeating the procedure a large number of times. However, it is more computationally intensive as this whole permutation procedure has to be carried out for every simulated sample to obtain a cutoff corresponding to that replicate. Moreover, the cutoffs will vary by sample.

3.3. Results

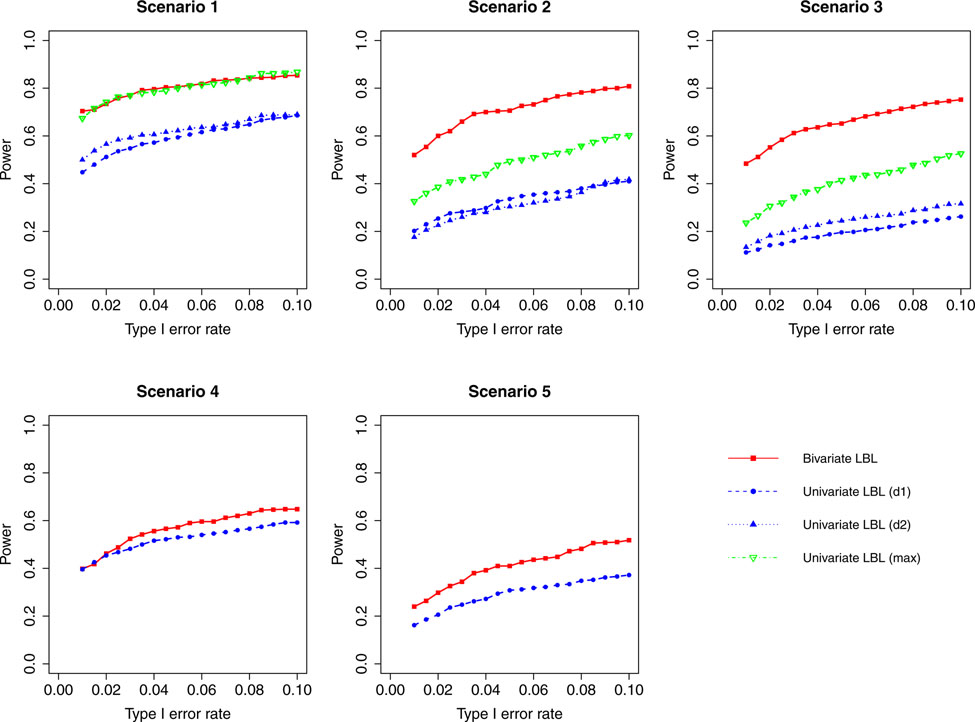
The results for hypothesis 1 for settings 1 and 3 are shown in Figures 1 to 8 and for setting 2 in Supplementary Figures S1 to S4. Depending on whether a haplotype is truly associated with one or both traits, we plot for univariate LBL, one or two curves for the power(s) to detect the haplotype by the respective model(s) individually. Also, in scenarios 1 – 3, where the haplotype is associated with both traits, we plot the results when maximum of BFs from the two univariate models is used for declaring significance. Here the maximum is calculated in the same manner as described in the sub-section “Calculation of Cutoffs”.

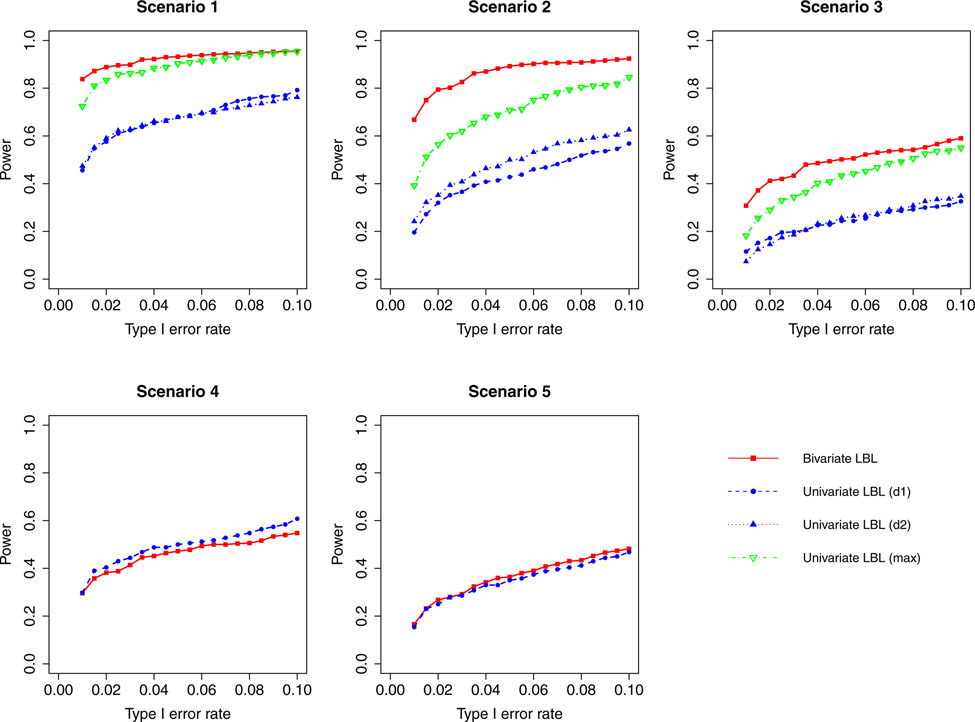
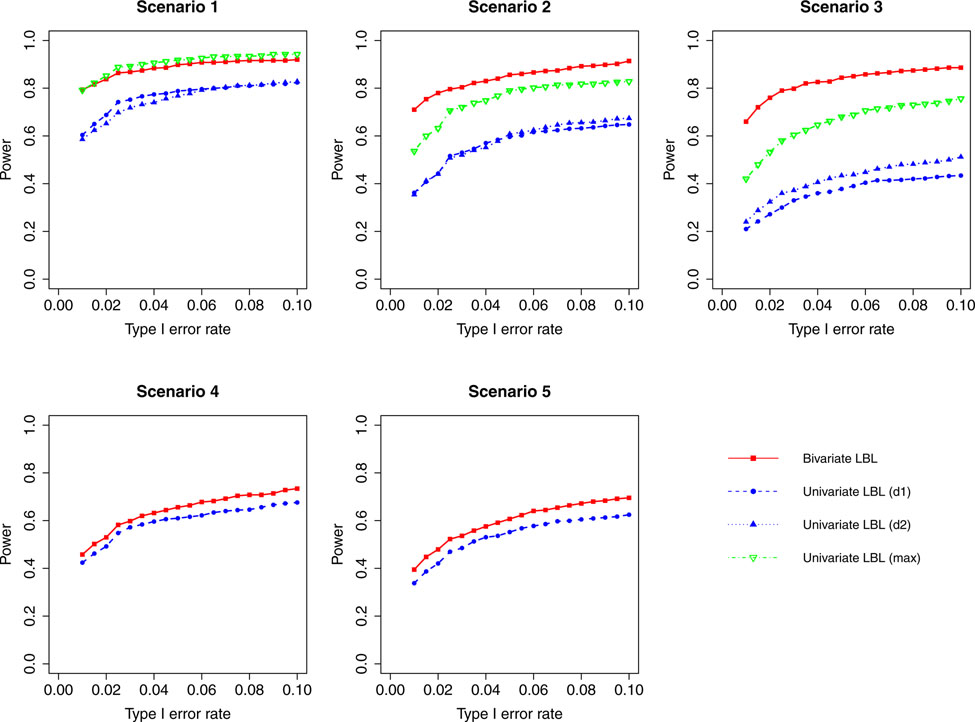
Figure 1:

Simulation results for hypothesis 1 under setting 1 (6 haplotypes) and ρ = 0. The scenarios are listed in Table 1. d1=disease 1, d2=disease 2.

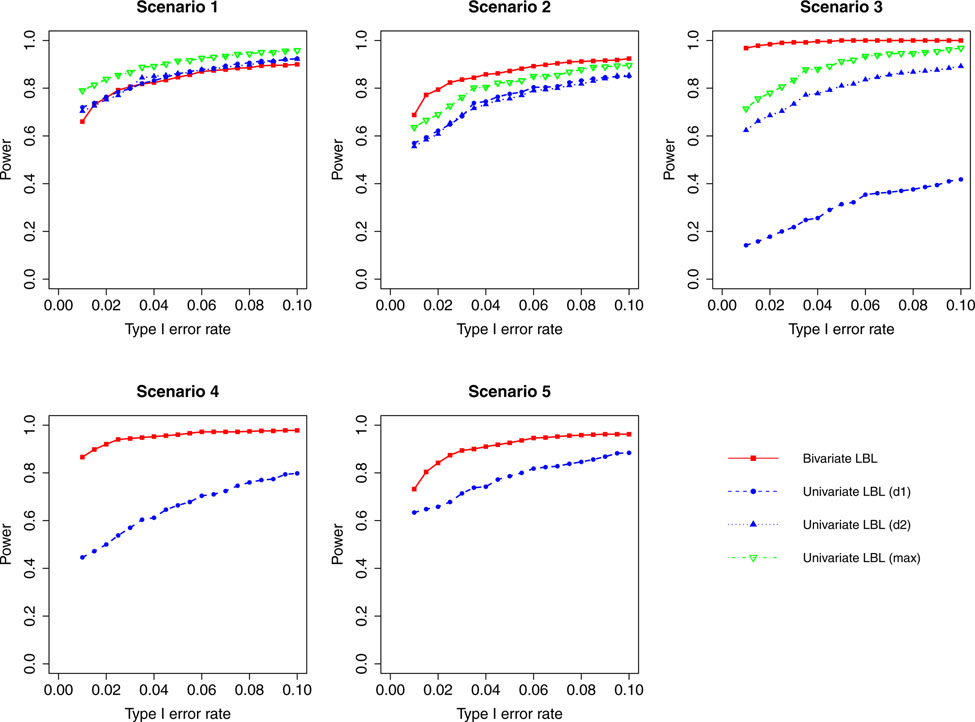
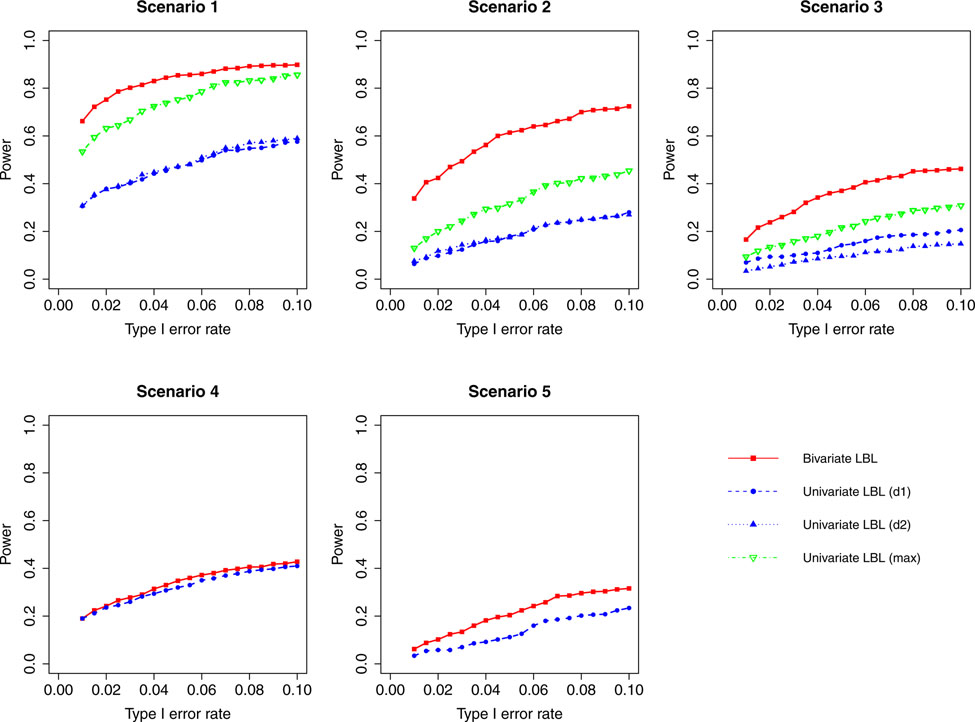
Figure 8:

Simulation results for hypothesis 1 under setting 3 (12 haplotypes) and ρ = 0.99. The scenarios are listed in Table 1. d1=disease 1, d2=disease 2.

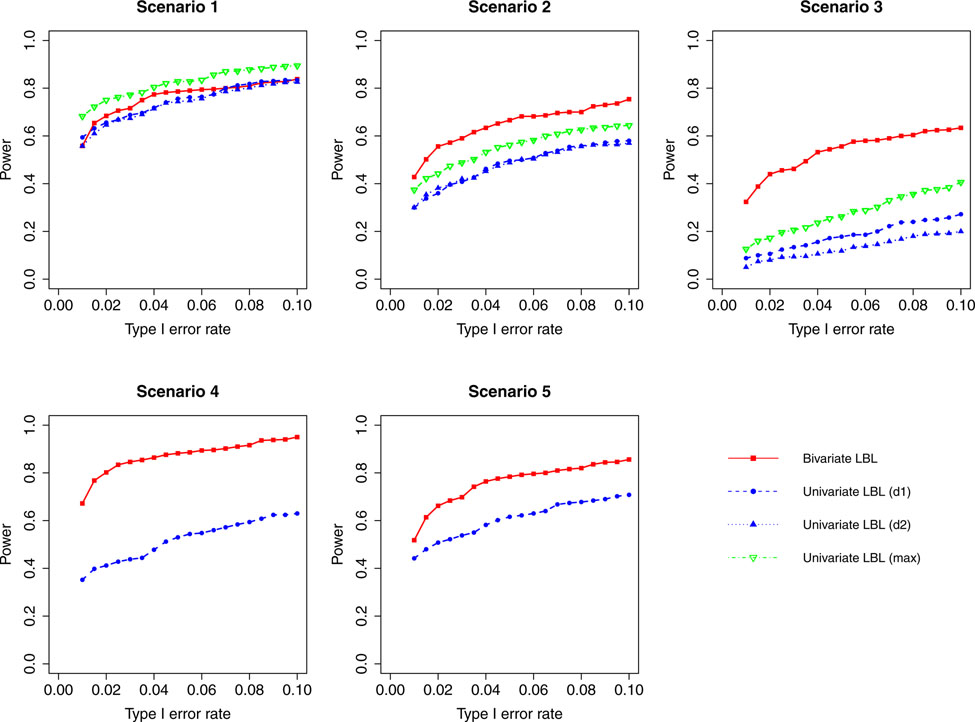
When the correlation between the two traits is zero or small (ρ = 0, 0.3), bivariate LBL has high power advantage over univariate LBL in scenarios 2 and 3 while in the other three scenarios the curves for bivariate LBL are close to those for univariate LBL using individual or maximum BF. When the two traits are moderately or highly correlated (ρ = 0.7,0.99), bivariate LBL has better performance in scenarios 2 – 5 especially when the target haplotype affects the two diseases in opposite directions (Scenario 3). However, for ρ = 0.99, it looses power slightly compared to univariate LBL using maximum BF in scenario 1 where the target haplotype is positively associated with both diseases as seen in Figures 4 and 8.

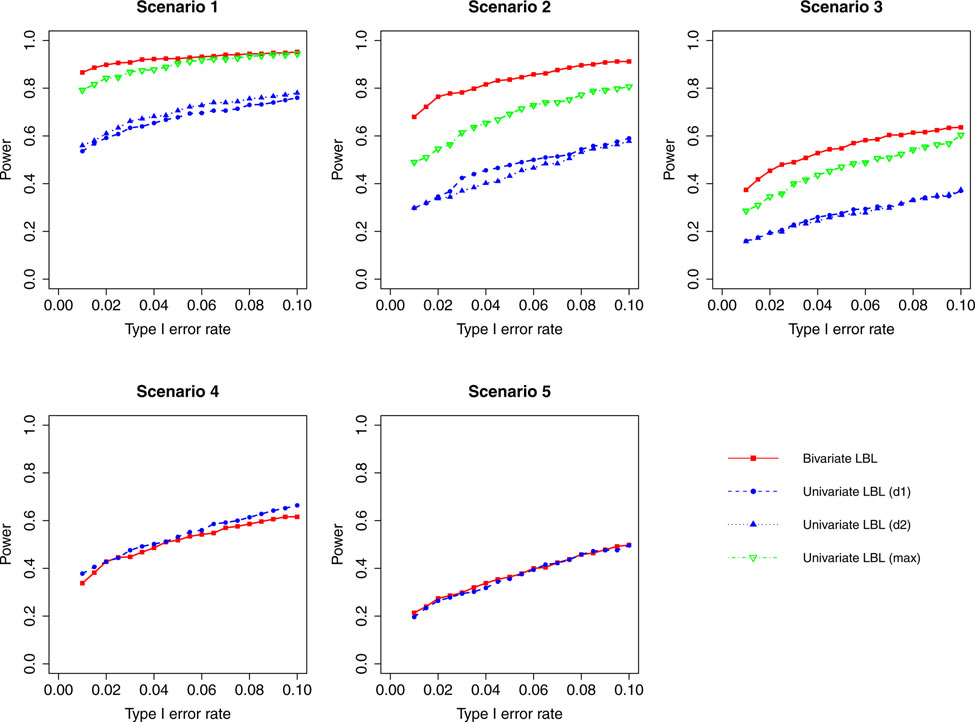
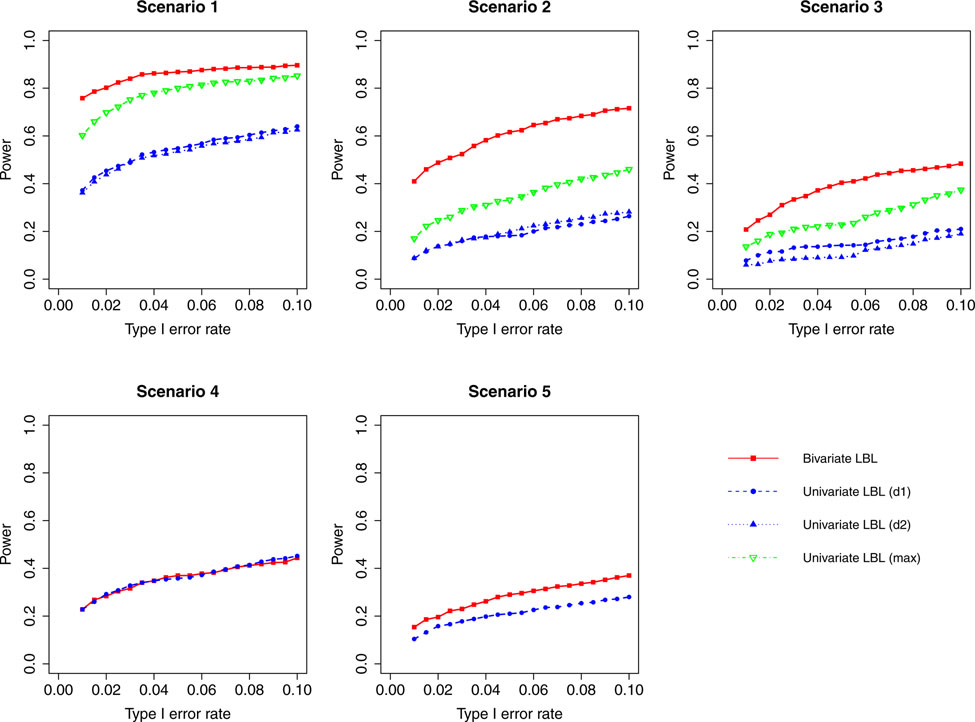
Figure 4:

Simulation results for hypothesis 1 under setting 1 (6 haplotypes) and ρ = 0.99. The scenarios are listed in Table 1. d1=disease 1, d2=disease 2.

For a different perspective into the results, we can compare the performances of the two models across different scenarios. For scenarios 2 and 3, in which the β coefficients of the target haplotype for the two traits are both negative or have different directions, the bivariate model clearly outperforms the univariate model for all ρ values. For scenarios 4 and 5, where only one of the two traits is associated, bivariate LBL has higher power when ρ = 0.7,0.99 especially for ρ = 0.99 while the methods exhibit similar powers when ρ is 0 or 0.3. For scenario 1, where both βs are positive, bivariate LBL has some advantage when ρ is 0 or 0.3 especially for settings with 9 and 12 haplotypes. However, when ρ = 0.99, bivariate LBL performs slightly worse compared to univariate LBL using maximum BF even though not using individual BFs as seen in Figures 4 and 8. Thus, overall we may conclude that bivariate LBL performs better or similar to univariate LBL in all situations except for scenario 1 under ρ = 0.99.

The results for testing hypothesis 2 for setting 2 (9 haplotypes) are shown in Figures S5 to S8. In general, the results that we reported above regarding comparison between bivariate and univariate LBL appear to hold for hypothesis 2 as well.

4. Application to GAW19 Blood Pressure Data

GAW19 data consist of multiple phenotypes including systolic and diastolic blood pressures (SBP and DBP) for each subject (Engelman et al., 2016). These two phenotypes are correlated (sample correlation coefficient = 0.549) and may have some common underlying genetic mechanism (Schillert & Konigorski, 2016). A common strategy to analyze data on the two blood pressure (BP) measurements is to combine them into a single binary hypertension phenotype by using a clinical threshold for each to declare if a BP is high and if any one of the two BPs are high for any subject, then labeling the subject as a case with hypertension (Datta et al., 2016). However, this leads to loss of information and does not allow investigation of potential pleiotropy. Being a sequence dataset, GAW19 data also contain a large number of rare SNPs, for example, more than 97% of variants on chromosome 3 have a minor allele frequency (MAF) less than 0.01 (Datta et al., 2016). We use bivariate LBL to study the association between the two related traits and haplotypes (specifically hypothesis 1) using data on unrelated individuals. After removing subjects with a missing value in either disease status, 1851 individuals remain in our study.

We analyze haplotype blocks in eight selected genes, namely, ULK4, MAP4, FBN3, HRH1, INMT, SAT2, SHBG, and ZNF280D. The first two were studied by Datta et al. (2016) while the rest were studied by Sun, Bhatnagar, Oualkacha, Ciampi, and Greenwood (2016). VCFtools is used to extract relevant genotype data from the provided data set. Following Datta et al. (2016), we use high quality genotypes listed under NALTT (the number of alternate alleles threshold) field. For each gene, we only include SNPs for which the proportion of subjects with missing genotypes is not more than 25% and whose MAF is at least 0.001. With these conditions, the total numbers of SNPs are 70 in ULK4, 18 in MAP4, 28 in FBN3, 10 in HRH1, 18 in INMT, 7 in SAT2, 15 in SHBG, and 30 in ZNF280D. We create sliding haplotype blocks by combining 5 successive SNPs starting from the first SNP and covering the whole gene. The haplotype blocks/windows are overlapping, i.e., windows are formed by SNPs 1–5, 2–6, and so on.

We convert the two continuous phenotypes SBP and DBP into two binary disease statuses in the following way. If a subject’s SBP value is greater than 140, we label him/her as a case (1) otherwise as a control (0). DBP is coded in the same way with a threshold of 90. Using the same notations as in the Methods section, we have n₀₀ = 1457, n₁₀ = 289, n₀₁ = 26 and n₁₁ = 79. After conversion of SBP and DBP values to binary variables, the ϕ coefficient between them is estimated to be 0.340.

We find appropriate cutoffs for BF for drawing inference at type I error rate of 1%. Recall that we had earlier calculated cutoffs for all simulation settings. Rather than using those directly, we supplement them with cutoffs calculated using real data with the goal of obtaining more robust cutoffs for real data application. To this end, we generate a large number of null samples using several windows in ULK4 and ZNF280D genes and setting βs for all haplotypes in a window to be 0. Then we use the same way as described in the simulation study to get the cutoffs for these windows. Finally, we put together the cutoffs from the simulation settings and the real data windows and plot them together.

The cutoffs for both models are plotted in Supplementary Figure S9. We see in the figure that the cutoffs for rare haplotypes are clearly higher than those for the common ones. So we dichotomize haplotype frequencies into rare or common with rare being of frequency less than or equal to 0.02. In the same figure, we also note that the cutoffs seem to be larger for smaller values of ρ especially for bivariate LBL (recall ρ = 0.55 for windows obtained from the GAW 19 data). We plot cutoffs versus ρ values in Figure S10 and cutoffs versus number of haplotypes in the corresponding window/block in Figure S11. We see that for bivariate LBL, the cutoff is higher when ρ value is smaller (Figure S10; left column plots) and the number of haplotypes in the block is smaller (for rare haplotypes; top left plot of Figure S11). Thus, we determine cutoffs separately for each combination of haplotype frequency (rare/common), ρ value (weak/moderate-strong), and # haplotypes (<= 8 or > 8; 8 is the median number of haplotypes across all windows). In particular, we use the mean of the cutoffs in each category for final inference and these are listed in Supplementary Table S1. We note that some cutoffs are less than 1. However, we confirm that the empirical type I error rates are indeed around 1% for bivariate LBL using the simulated data (shown in Table S2). For reference, if we average across all ρ values and number of haplotypes (rather than treating their categories separately), the cutoffs for rare haplotypes would be 2.16 and 5.26 for bivariate and univariate LBL, respectively, and for common haplotypes, these cutoffs would be 0.7 and 3.28.

We apply bivariate LBL to each haplotype block within each gene using both phenotypes jointly and apply univariate LBL to the same haplotype block twice using SBP and DBP separately. In each haplotype block, the haplotype with the highest frequency is used as the baseline. We run MCMC chain for each block for 300,000 iterations including 50,000 burn-in. The cutoffs we found above are applied to all the blocks in all genes. The haplotypes that show significance using at least one method are listed in Table 2. In this table, we see that the bivariate LBL produces more significant results. In some cases when the estimated β coefficients for SBP and DBP are both negative, the bivariate model detects the signals while univariate model does not, e.g., the haplotype in ZNF280D. When both βs are estimated to be positive, bivariate LBL also detects several haplotypes missed by univariate LBL such as the haplotype in window 7–11 in ULK4. We can see that the magnitudes of $\widehat{\beta }$ for those haplotypes are not too small as estimated by bivariate LBL. However, for haplotypes with small $\left|\widehat{\beta }\right|s$ (both less than 1), the univariate model may perform better as in the window 16–20 of FBN3. The results are consistent with the general pattern we found in the simulation study.

Table 2:

Results of GAW19 data analysis in the order of ULK4, FBN3, HRH1, and ZNF280D genes. Cutoffs are listed in Table S1. Significant results are shown in bold.

				$\widehat{\beta }(Bi)$		$\widehat{\beta }(Uni)$		BF (Bi)	BF (Uni)
Win	Hap	Freq	#Hap	SBP	DBP	SBP	DBP	Joint	SBP	DBP
3 – 7	h10101	0.0014	8	1.21	0.95	1.69	1.34	2.83	6.95	2.15
4 – 8	h01010	0.0012	9	1.45	1.06	2.04	1.54	3.54	11.01	2.54
5 – 9	h10101	0.0012	6	1.46	1.11	2.13	1.59	4.68	9.82	3.33
6 – 10	h01010	0.0014	4	1.05	0.95	1.46	1.24	2.42	5.20	1.91
7 – 11	h10100	0.0013	4	1.08	0.97	1.51	1.25	2.48	4.61	2.16
8 – 12	h01000	0.0014	6	1.06	0.94	1.53	1.28	2.36	4.57	2.29
9 – 13	h10000	0.0014	5	1.09	0.93	1.54	1.21	2.63	4.66	1.85
15 – 19	h00010	0.0125	8	−0.95	−1.60	−0.93	−1.59	3.78	3.25	2.44
16 – 20	h00101	0.0122	9	−0.92	−1.45	−0.93	−1.45	3.35	2.97	1.83
17 – 21	h01011	0.0121	9	−0.94	−1.51	−0.97	−1.48	3.29	3.3	1.84
18 – 22	h10111	0.0118	7	−0.75	−1.56	−0.75	−1.54	2.78	1.7	2.36
24 – 28	h10000	0.0275	8	−0.47	−0.52	−0.45	−0.53	0.75a	1.12	0.76
39 – 43	h11100	0.0055	11	1.15	−0.15	1.15	−0.01	3.60	10.75	0.58
40 – 44	h11000	0.0050	12	1.89	0.10	2.17	0.35	49.51	> 100	0.77
40 – 44	h11110	0.0466	12	0.79	0.22	1.28	0.58	3.99	> 100	1.22
41 – 45	h10001	0.0060	12	1.04	−0.17	1.03	−0.02	2.67	7.41	0.58
42 – 46	h00010	0.0062	9	0.88	−0.30	1.01	−0.15	1.70	5.25	0.53
42 – 46	h01100	0.0443	9	0.55	0.50	1.24	0.86	0.82a	> 100	2.69
43 – 47	h00100	0.0074	9	0.88	−0.28	0.93	−0.14	1.83	6.18	0.54
5 – 19	h00101	0.2501	6	0.35	0.23	0.35	0.30	0.98a	5.14	0.58
16 – 20	h01010	0.2400	7	0.33	0.12	0.33	0.19	0.59	4.40	0.28
17 – 21	h10100	0.2457	7	0.34	0.12	0.35	0.19	0.64	6.10	0.28
6 – 10	h00001	0.024	5	−0.8	0	−0.72	−0.04	1.83	3.96	0.38
24 – 28	h00001	0.0099	11	−0.94	−1.3	−1.01	−1.29	2.24	2.49	1.49

Hap: Haplotype, Freq: Haplotype frequency, # Hap: Number of haplotypes in the window, Bi: Bivariate, Uni: Univariate.

^aBF significant but less than 1

5. Application to Lung Cancer and Smoking Data

We consider the GWAS data collected in EAGLE (Environment And Genetics in Lung cancer Etiology) study and PLCO (Prostate, Lung, Colorectal, and Ovarian cancer) screening trial to illustrate the application of bivariate LBL on two related binary phenotypes of lung cancer and smoking status (database of Genotypes & Phenotypes, 2019). Several studies have shown that SNPs in the chromosomal region 15q25.1 are associated with lung cancer susceptibility as well as smoking behavior (Lassi et al., 2016; Liu et al., 2010; Spitz, Amos, Dong, Lin, & Wu, 2008; Thorgeirsson et al., 2008; VanderWeele et al., 2012; I. A. Yang, Holloway, & Fong, 2013; Yokota, Shiraishi, & Kohno, 2010; Yu et al., 2012). Indeed this was the motivation for the gene-environment interaction analysis of Zhang et al. (Zhang, Lin, & Biswas, 2017), where they specifically accounted for gene-environment dependence as smoking (the environmental covariate) is associated with (and hence is dependent on) the genetic region under study. Thus, following the findings from this body of literature, we analyze this region but from a different perspective wherein we investigate if it is jointly associated with lung cancer and smoking after taking into account the correlation between the two phenotypes.

We consider the same five haplotype blocks that Zhang et al. (Zhang, Lin, & Biswas, 2017) analyzed after locating them with Haploview (Barrett, Fry, Maller, & Daly, 2005). The blocks consist of the following SNPs: (i) Block 1 with 4 SNPs: rs1394371, rs12903150, rs12899131, and rs2656069 (ii) Block 2 with 2 SNPs: rs13180 and rs3743079 (iii) Block 3 with 4 SNPs: rs8034191, rs3885951, rs2036534, and rs2292117 (iv) Block 4 with 3 SNPs: rs12914385, rs1051730, and rs1948 and (v) Block 5 with 2 SNPs: rs11636753 and rs12441998. The total sample size is 5546 with the four sub-samples of sizes n₀₀ = 713, n₁₀ = 220, n₀₁ = 2108, n₁₁ = 2508, where the two subscripts denote the lung cancer and smoking statuses in order. Smoking status of 1 includes current and former smokers. The ϕ coefficient between the two phenotypes is estimated to be 0.23. Due to strong gene-environment dependence in this region, the haplotype frequencies differ substantially across the sub-groups (Zhang, Lin, & Biswas, 2017). Thus, we initially encountered an issue with the convergence of the frequency parameters (f⁰⁰,f¹⁰,f⁰¹) in the MCMC algorithm. However, with slight tuning of the C value used in updating these parameters (setting it to be 10000 for 00 and 01 sub-populations and 2000 for 10 sub-population; refer to the Appendix A3 for MCMC updates), we are able to achieve satisfactory convergence. Moreover, to ensure convergence, we ran the chain much longer for a total of 800,000 iterations with a burn-in of 200,000.

The haplotypes found to be significant by testing hypothesis 1 after applying the relevant cutoffs from Supplementary Table S1 are shown in Table 3. We see that at least one haplotype was found to be associated in all five blocks. Of these, the haplotype TTTG in the third block is a rare haplotype. Note that the effects of a haplotype on the two phenotypes can be concordant or discordant. For the sake of completeness, we also applied univariate LBL to each phenotype separately and found the same haplotypes to be significant as seen in the table. However, fitting a univariate model in this specific application is questionable as smoking is the most important and well-established risk factor for lung cancer. So testing for genetic association of lung cancer without accounting for smoking as a covariate is not sensible. On the other hand, bivariate LBL results are likely to be more credible as it accounts for the known correlation between lung cancer and smoking. Moreover, bivariate LBL results establish joint association of haplotypes with the two phenotypes unlike univariate LBL.

Table 3:

Results of lung cancer and smoking data analysis. Cutoffs are listed in Table S1. Significant results are shown in bold.

				$\widehat{\beta }(Bi)$		$\widehat{\beta }(Uni)$		BF (Bi)	BF (Uni)
Block	Hap	Freq	#Hap	Cancer	Smoke	Cancer	Smoke	Joint	Cancer	Smoke
1	hCAAG	0.2067	9	−0.25	−0.09	−0.24	−0.13	2.55	25.07	0.19
2	hCC	0.2109	2	−0.20	−0.11	−0.19	−0.12	0.72a	3.85	0.19
3	hCCTG	0.1250	9	0.28	−0.06	0.26	−0.04	2.59	19.81	0.04
3	hCTTG	0.2772	9	0.23	0.00	0.22	0.01	1.72	21.16	0.01
3	hTTTG	0.0149	9	0.62	0.08	0.58	0.13	11.15	44.22	0.21
4	hCCC	0.2594	6	−0.39	−0.05	−0.36	−0.10	> 100	> 100	0.1
4	hCCT	0.3019	6	−0.29	0.04	−0.27	0.00	57.04	524.37	0.02
5	hGG	0.2060	3	−0.33	−0.19	−0.31	−0.14	> 100	> 100	0.36
5	hTA	0.2396	3	0.03	0.89	0.17	2.53	> 100	0.94	> 100

Hap: Haplotype, Freq: Haplotype frequency, # Hap: Haplotype number, Bi: Bivariate, Uni: Univariate.

^aBF significant but less than 1

6. Discussion

Most health-related studies collect multiple outcomes and often several of them are correlated. Studying each trait separately can lead to loss of information contained in the correlation between the outcomes. Moreover, univariate analyses of correlated phenotypes misses an opportunity to investigate shared etiology such as pleiotropy, which is now widely believed to be pervasive. Many multivariate methods have been proposed to address this problem in the context of genetic association studies, however, none of them are haplotype-based applicable to case-control data. In order to fill up this gap, we proposed bivariate LBL, an extension of univariate LBL. It can detect association between a specific haplotype (or a haplotype block) and two binary phenotypes jointly.

Our simulation results show that bivariate LBL performs better or similar to univariate LBL in most of the scenarios when a rare haplotype is associated with one or both traits. The advantages of bivariate LBL become more pronounced when the two traits are highly correlated and the haplotype affects at least one of the two traits in direction opposite to the direction of correlation between the two traits. Recall that in our simulations, the correlation between the two traits was positive so direction opposite to the direction of correlation between the two traits amounts to the associated haplotype being negatively associated with a trait. However, when those effects are both positive and the two traits have high positive correlation, univariate LBL performs slightly better.

Although this result is counter-intuitive, it is consistent with the literature (Galesloot et al., 2014; Ray et al., 2016; Teixeira-Pinto & Normand, 2009). For example, Galesloot et al. (2014) found that a univariate approach outperforms multivariate approaches when traits were positively correlated and the genetic correlation (correlation between genetic effects) was positive. Essentially in this situation, the joint modeling does not add any independent piece of information beyond what a univariate model captures and as joint modeling is more complicated, slight power loss may ensue. On the other hand, when one or more genetic effects are of direction opposite to that of the correlation between traits (e.g., scenarios 2 and 3), then these different pieces of information cannot be captured adequately by a univariate model and it suffers power loss. Indeed, Teixeira-Pinto and Normand (2009) report that multivariate approach gives more efficient estimates when the outcomes depend on different set of covariates. This is also reflected in our results from scenarios 4 and 5 where a haplotype (covariate) affects only one disease.

We note that univariate LBL has been compared extensively with several existing haplotype association methods and LBL has been shown to be one of the most powerful methods (Biswas & Lin, 2012; Biswas & Papachristou, 2014; Datta & Biswas, 2016; Papachristou & Biswas, 2019; Zhang & Biswas, 2015; Zhang, Lin, & Biswas, 2017). Thus, we do not repeat the same exercise of comparison with other existing haplotype methods (all being univariate) in the current article.

In GAW19 data analysis, we detected a number of significant haplotypes in ULK4, FBN3, HRH1, and ZNF280D genes. These include both common and rare ones, and several of them could not be detected by univariate LBL. Thus, bivariate LBL can potentially help uncover cross-phenotype association, which could possibly be due to pleiotropic effects (establishing pleiotropy will require causal inference). Datta et al. (2016) reported haplotype association on ULK4 and MAP4 genes. Their phenotype was hypertension obtained by combining SBP and DBP. They reported several significant haplotypes using a BF threshold of 2, which may not be significant when a higher threshold is applied for multiplicity adjustment (as applied in our univariate LBL results). For example, they reported a rare haplotype on MAP4 gene with BF of 3.19, which is below the threshold used in our univariate LBL analysis (listed in Table S1). Sun et al. (2016) used the whole ZNF280D gene as a variable and found it to be significantly associated with DBP only. In our study, we find one haplotype significant in that gene using bivariate LBL only. They also detected significant associations between some SNPs in FBN3 and HRH1 genes and the two blood pressure traits jointly. We find some windows in those genes to be significant as well using bivariate LBL.

In our lung cancer data analysis, we found haplotypes in all five blocks that we analyzed to be associated with lung cancer and smoking jointly, consistent with the literature. In particular, two haplotypes in block 3, namely CTTG and TTTG were reported earlier to have significant interactions with smoking (Zhang, Lin, & Biswas, 2017). However, the results of that study and others on gene-environment interactions in this region are not directly comparable with our results as we investigated the region from a viewpoint different from gene-environment interaction. We did not treat smoking as a covariate rather as a phenotype correlated with lung cancer due to shared genetic mechanism. Thus our analysis does not investigate gene-environment interaction rather is intended to only answer whether carriers of certain haplotypes in this region have higher/lower susceptibility to lung cancer and/or smoking after accounting for the correlation between the two. A limitation of our application is that we had to treat smoking as a binary covariate whereas the literature suggests that a continuous measure such as smoking intensity is more strongly associated with this region (Lassi et al., 2016; I. A. Yang et al., 2013). Nonetheless, our analysis serves as an illustration of how the existing wealth of GWAS data can be mined for rare variant association with multiple phenotypes.

In addition to using BF for drawing inference, we also explored 95% simultaneous credible region (CR) for β parameters jointly (Besag, Green, Higdon, & Mengersen, 1995). However, we found that it is highly conservative in our setting. That is because the prior odds for the null hypothesis 1 is very large for bivariate LBL (105.17) making it highly likely for the simultaneous CR to cover the null vector of 0 for all β parameters involved in hypothesis 1. Thus, many haplotypes that were significant using BF were not significant using simultaneous CR method. We investigated few other variations of our model and MCMC updating steps but they produced similar or worse results compared to what we finally used. For example, we tried using two different λ parameters for the priors for β¹ and β² but that made little difference. For updating u jointly, we tried multivariate normal proposals and for ${\sigma }_u^2$ parameter, we explored a conjugate scaled inverse-χ² prior. However, those attempts gave slower convergence of the MCMC algorithm and so we did not pursue them further.

Bivariate LBL is much more computationally intensive compared to univariate LBL. That is because in bivariate LBL, the number of β parameters is doubled and there is additionally a parameter vector u of dimension equal to the total sample size. Furthermore, because of the more complicated model, it needs more iterations for convergence. However, we are able to control the computing costs to some extent by implementing some calculations using parallel computing (e.g., updating of u), which was not available in univariate LBL code. In our simulation study, using a sample of size 2000, the time costs of univariate LBL to finish two separate analyses (for two phenotypes) with 50,000 iterations for each analysis under Settings 1–3 are 60, 60, and 114, seconds, respectively. While the corresponding times for bivariate LBL to finish 200,000 iterations are 616, 1071, and 1770 seconds. These computing times are for a 3.40 GHz Xeon processor with 8 cores under Linux operating system and 32.89 GB RAM. Considering the computational burden, we recommend using bivariate LBL only when there is evidence of correlation between phenotypes or when the effect(s) of haplotype(s) on phenotypes are estimated to be negative because in these situations univariate LBL may miss association signals.

In spite of the computational limitation, bivariate LBL performs well for detecting associations between rare (and common) haplotypes and correlated phenotypes in most scenarios. The type I error rates are well-controlled and the powers are in a reasonable range. Thus, given that there is no haplotype association method available currently to jointly analyze two binary phenotypes, we believe that bivariate LBL is an important addition to the toolkit for genetic association studies especially for detecting rare variants. A relevant future work from practical standpoint will be to develop a more computationally efficient version of bivariate LBL. We also plan to extend bivariate LBL to jointly model correlated continuous phenotypes, a combination of binary and continuous phenotypes, and gene-environment interactions.

7. Software

An R package implementing the proposed bivariate LBL method is available at https://www.utdallas.edu/~swati.biswas/, CRAN (https://cran.r-project.org/web/packages/LBLGXE/index.html), and GitHub (https://github.com/MorningXY/LBLGXE_v1.4).

Figure 2:

Simulation results for hypothesis 1 under setting 1 (6 haplotypes) and ρ = 0.3. The scenarios are listed in Table 1. d1=disease 1, d2=disease 2.

Figure 3:

Simulation results for hypothesis 1 under setting 1 (6 haplotypes) and ρ = 0.7. The scenarios are listed in Table 1. d1=disease 1, d2=disease 2.

Figure 5:

Simulation results for hypothesis 1 under setting 3 (12 haplotypes) and ρ = 0. The scenarios are listed in Table 1. d1=disease 1, d2=disease 2.

Figure 6:

Simulation results for hypothesis 1 under setting 3 (12 haplotypes) and ρ = 0.3. The scenarios are listed in Table 1. d1=disease 1, d2=disease 2.

Figure 7:

Simulation results for hypothesis 1 under setting 3 (12 haplotypes) and ρ = 0.7. The scenarios are listed in Table 1. d1=disease 1, d2=disease 2.

Appendix

A1. Derivation of the Likelihood

Recall that $a_Z^1=P\left(Z|Y_1=0\right)$ and $a_Z^2=P\left(Z|Y_2=0\right)$ are the frequencies of haplotype pair Z in the control populations for diseases 1 and 2, respectively. We assume that $a_Z^1$ and $a_Z^2$ are independent of u. Next let $b_{Z,u}^1=P\left(Z|Y_1=1,u\right)$ and $b_{Z,u}^2=P\left(Z|Y_2=1,u\right)$ denote the frequencies of haplotype pair Z in the case populations of diseases 1 and 2. Recall that ${\theta }_{Z,u}^1=P\left(Y_1=1|Z,u\right)/P\left(Y_1=0|Z,u\right)$ and ${\theta }_{Z,u}^2=P\left(Y_2=1|Z,u\right)/P\left(Y_2=0|Z,u\right)$ are the odds of the two diseases given Z and u. We can express $b_{Z,u}^1$ in terms of $a_Z^1$ and ${\theta }_{Z,u}^1$ as follows:

$$b_{Z,u}^1=P\left(Z|Y_1=1,u\right)=\frac{{\theta }_{Z,u}^1{a}_Z^1}{{\sum }_H{\theta }_{H,u}^1{a}_H^1},$$

where H represents the set of all haplotype pairs (Biswas & Lin, 2012). Similarly, we can express $b_{Z,u}^2$ in terms of $a_Z^2$ and ${\theta }_{Z,u}^2$ as $b_{Z,u}^2={\theta }_{Z,u}^2{a}_Z^2/{\sum }_H{\theta }_{H,u}^2{a}_H^2$. The models for ${\theta }_{Z,u}^1$ and ${\theta }_{Z,u}^2$ were provided in the main text. In the following sub-sections, we will fully model $a_Z^1$ and $a_Z^2$ in terms of the model parameters, and then use $\left(a_Z^l,{\theta }_{Z,u}^l\right)$, l = 1,2 to represent the likelihood in (1).

Modeling of $a_Z^1$ and $a_Z^2$. Recall that $f^1=\left(f_1^1,\dots ,f_m^1\right)$ and $f^2=\left(f_1^2,\dots ,f_m^2\right)$ are the frequencies of the m haplotypes in the controls for diseases 1 and 2, and $f^{00}=\left(f_1^{00},\dots ,f_m^{00}\right)$, $f^{10}=\left(f_1^{10},\dots ,f_m^{10}\right)$, and $f^{01}=\left(f_1^{01},\dots ,f_m^{01}\right)$ are the frequency vectors of m haplotypes in the three corresponding disjoint sub-populations. There are constraints that $f_k^{00}>0$, $f_k^{10}>0$, and $f_k^{01}>0$ for all k, and ${\sum }_{k=1}^m{f}_k^{00}=1$, ${\sum }_{k=1}^m{f}_k^{10}=1$, and ${\sum }_{k=1}^m{f}_k^{01}=1$. Then we can represent the elements of f¹ and f² in terms of f⁰⁰, f¹⁰, and f⁰¹ in the following way:

$$f_k^1=\frac{f_k^{00}·n_{00}+f_k^{01}·n_{01}}{n_{00}+n_{01}},f_k^2=\frac{f_k^{00}·n_{00}+f_k^{10}·n_{10}}{n_{00}+n_{10}},k=1,\dots ,m.$$

For a haplotype pair Z = z_k/z_k′, we can model $a_Z^1$ and $a_Z^2$ as follows:

$$a_Z^l\left({\gamma }^l\right)=P\left(Z=z_k/z_{k^{\prime }}|Y_l=0,{\gamma }^l\right)={\delta }_{k{k}^{\prime }}d{f}_k^l+\left(2-{\delta }_{k{k}^{\prime }}\right)\left(1-d\right)f_k^l{f}_{k^{\prime }}^l,l=1,2,$$ (2)

where δ_kk′ = 1(0) if z_k = z_k′(z_k ≠ z_k′), γ^l = {f^l,d}, and d ∈ (−1,1) is the within-population inbreeding coefficient, which can be used to capture excess/reduction of homozygosity (Biswas & Lin, 2012; Weir, 1996). When d = 0, the expression in (2) reduces to the assumption of Hardy-Weinberg equilibrium (HWE) while other values of d allow for Hardy-Weinberg disequilibrium.

Modeling of P(u | Y₁,Y₂). Assuming the disease statuses (Y₁,Y₂) to be fixed, we can write

$$P\left(u|Y_1,Y_2\right)\propto P\left(Y_1,Y_2|u\right)P\left(u\right)=P\left(Y_1|u\right)P\left(Y_2|u\right)P\left(u\right),$$ (3)

where we used independence of Y₁ and Y₂ given u, as mentioned earlier. Consider

$$\begin{array}{l}P\left(Y_1=1|u\right)=\sum _{H}P\left(Y_1=1|H,u\right)P(H|u)=\sum _H{\theta }_{H,u}^{1}P\left(Y_1=0|H,u\right)P\left(H|u\right)\\ =\sum _H{\theta }_{H,u}^{1}P\left(H|Y_1=0,u\right)P\left(Y_1=0|u\right)=\sum _H{\theta }_{H,u}^1{a}_H^{1}P\left(Y_1=0|u\right)\\ =\sum _H{\theta }_{H,u}^1{a}_H^1\left(1-P\left(Y_1=1|u\right)\right).\end{array}$$

By combining the terms involving P(Y₁ = 1 | u) on both sides, we have

$$P\left(Y_1=1|u\right)=\frac{{\sum }_H{\theta }_{H,u}^1{a}_H^1}{1+{\sum }_H{\theta }_{H,u}^1{a}_H^1}\text{ and }P\left(Y_1=0|u\right)=\frac{1}{1+{\sum }_H{\theta }_{H,u}^1{a}_H^1}.$$ (4)

Similarly, we have

$$P\left(Y_2=1|u\right)=\frac{{\sum }_H{\theta }_{H,u}^2{a}_H^2}{1+{\sum }_H{\theta }_{H,u}^2{a}_H^2}\text{ and }P\left(Y_2=0|u\right)=\frac{1}{1+{\sum }_H{\theta }_{H,u}^2{a}_H^2}.$$ (5)

Substituting the expressions in (4) and (5) into (3), we have

$$P\left(u|Y_1,Y_2\right)\propto \frac{P\left(u\right){\left({\sum }_H{\theta }_{H,u}^1{a}_H^1\right)}^{Y_1}{\left({\sum }_H{\theta }_{H,u}^2{a}_H^2\right)}^{Y_2}}{\left(1+{\sum }_H{\theta }_{H,u}^1{a}_H^1\right)\left(1+{\sum }_H{\theta }_{H,u}^2{a}_H^2\right)}.$$ (6)

Modeling of P(Z | Y₁,Y₂,u). Consider

$$\begin{array}{l}P\left(Z|Y_1=0,Y_2=0,u\right)=\frac{P\left(Y_1=0|Z,Y_2=0,u\right)P\left(Z|Y_2=0,u\right)}{P\left(Y_1=0|u\right)}=\frac{P\left(Y_1=0|Z,u\right)a_Z^2}{P\left(Y_1=0|u\right)}\\ =\frac{P\left(Z,Y_1=0|u\right)}{P\left(Z|u\right)}\cdot \frac{a_Z^2}{P\left(Y_1=0|u\right)}=\frac{P\left(Z|Y_1=0\right)P\left(Y_1=0|u\right)}{P\left(Z|u\right)}\cdot \frac{a_Z^2}{P\left(Y_1=0|u\right)}\\ =\frac{a_Z^1{a}_Z^2}{P\left(Z|u\right)}.\end{array}$$ (7)

In this calculation, we use the facts that Y₁ and Y₂ are independent given u and that $a_Z^1=P\left(Z|Y_1=0\right)$ is independent of u. In the same way, we can get $P\left(Z|Y_1=1,Y_2=0,u\right)=b_{Z,u}^1{a}_Z^2/P\left(Z|u\right)$, $P\left(Z|Y_1=0,Y_2=1,u\right)=a_Z^1{b}_{Z,u}^2/P\left(Z|u\right)$, and $P\left(Z|Y_1=1,Y_2=1,u\right)=b_{Z,u}^1{b}_{Z,u}^2/P\left(Z|u\right)$. Now what remains to be modeled is P(Z | u). Using equations (4), (5), and (7), P(Z | u) can be written as:

$$\begin{array}{l}P\left(Z|u\right)=\sum _{Y_1=0}^1\sum _{Y_2=0}^{1}P\left(Y_1,Y_2,Z|u\right)=\sum _{Y_1=0}^1\sum _{Y_2=0}^{1}P\left(Z|Y_1,Y_2,u\right)P\left(Y_1|u\right)P\left(Y_2|u\right)\\ =\frac{a_Z^1{a}_Z^2}{P\left(Z|u\right)}·\frac{1}{1+{\sum }_H{\theta }_{H,u}^1{a}_H^1}·\frac{1}{1+{\sum }_H{\theta }_{H,u}^2{a}_H^2}+\frac{a_Z^1{b}_{Z,u}^2}{P\left(Z|u\right)}·\frac{1}{1+{\sum }_H{\theta }_{H,u}^1{a}_H^1}·\frac{{\sum }_H{\theta }_{H,u}^2{a}_H^2}{1+{\sum }_H{\theta }_{H,u}^2{a}_H^2}\\ +\frac{b_{Z,u}^1{a}_Z^2}{P\left(Z|u\right)}·\frac{{\sum }_H{\theta }_{H,u}^1{a}_H^1}{1+{\sum }_H{\theta }_{H,u}^1{a}_H^1}·\frac{1}{1+{\sum }_H{\theta }_{H,u}^2{a}_H^2}+\frac{b_{Z,u}^1{b}_{Z,u}^2}{P\left(Z|u\right)}·\frac{{\sum }_H{\theta }_{H,u}^1{a}_H^1}{1+{\sum }_H{\theta }_{H,u}^1{a}_H^1}·\frac{{\sum }_H{\theta }_{H,u}^2{a}_H^2}{1+{\sum }_H{\theta }_{H,u}^2{a}_H^2}.\end{array}$$

Multiplying both sides by P(Z | u) we get

$$P\left(Z|u\right)={\left\{\frac{a_Z^1{a}_Z^2\left(1+{\theta }_{Z,u}^2+{\theta }_{Z,u}^1+{\theta }_{Z,u}^1{\theta }_{Z,u}^2\right)}{\left(1+{\sum }_H{\theta }_{H,u}^1{a}_H^1\right)\left(1+{\sum }_H{\theta }_{H,u}^2{a}_H^2\right)}\right\}}^{\frac{1}{2}}.$$ (8)

By combining equations (6–8) and adding back the subscripts i and r, we can now write the likelihood in (1) completely in terms of the parameter vector Ψ = (β¹,β²,γ¹,γ²,${\sigma }_u^2$) in the following way:

$$L\left(\mathrm{\Psi }\right)\propto \prod _{i=1}^n\left\{\frac{P\left(u_i\right)}{{\left[\left(1+{\sum }_H{\theta }_{H,u_i}^1{a}_H^1\right)\left(1+{\sum }_H{\theta }_{H,u_i}^2{a}_H^2\right)\right]}^{\frac{1}{2}}}\sum _{Z_{ir}\in S\left(G_i\right)}{\left[\frac{{\left[{\left({\theta }_{Z_{ir},u_i}^1\right)}^2\right]}^{Y_{1i}}{\left[{\left({\theta }_{Z_{ir},u_i}^2\right)}^2\right]}^{Y_{2i}}{a}_{Z_{ir}}^1{a}_{Z_{ir}}^2}{1+{\theta }_{Z_{ir},u_i}^1+{\theta }_{Z_{ir},u_i}^2+{\theta }_{Z_{ir},u_i}^1{\theta }_{Z_{ir},u_i}^2}\right]}^{\frac{1}{2}}\right\}.$$

Recall that P(u_i) is $N\left(0,{\sigma }_u^2\right)$, i = 1,…,n.

A2. Correlation between Y₁ and Y₂

Consider the latent variable representation of Y_l (l = 1,2) as follows:

$$Y_l=\{\begin{array}{ll}1,\hfill & \text{ if }{Y}_l^{*}>0,\hfill \\ 0,\hfill & \text{ if }{Y}_l^{*}\le 0,\hfill \end{array}$$

where $Y_l^{*}=X_Z{\beta }^l+u+{ϵ}_l^{*},u~N\left(0,{\sigma }_u^2\right)$, and ${ϵ}_l^{*}~\text{logistic}\left(0,1\right)$. Here u, ${ϵ}_1^{*}$, and ${ϵ}_2^{*}$ are independent of each other. Then

$$\begin{array}{l}\text{Cov}\left(Y_1^{*},Y_2^{*}\right)=\text{Cov}\left(X_Z{\beta }^1+u+{ϵ}_1^{*},X_Z{\beta }^2+u+{ϵ}_2^{*}\right)=\text{Cov}(u,u)={\sigma }_u^2,\\ \text{Var}\left(Y_l^{*}\right)=\text{Var}(u)+\text{Var}\left({ϵ}_l^{*}\right)={\sigma }_u^2+\frac{{\pi }^2}{3},l=1,2,\text{ and Corr}\left(Y_1^{*},Y_2^{*}\right)=\frac{{\sigma }_u^2}{{\sigma }_u^2+{\pi }^2/3}.\end{array}$$

Thus, the correlation between $Y_1^{*}$ and $Y_2^{*}$ (and thus between Y₁ and Y₂) is an increasing function of ${\sigma }_u^2$. The exact correlation between Y₁ and Y₂ can be also derived by noting that

$$\text{Corr}\left(Y_1,Y_2\right)=\frac{E\left(Y_1{Y}_2\right)-E\left(Y_1\right)E\left(Y_2\right)}{\sqrt{E\left(Y_1\right)\left(1-E\left(Y_1\right)\right)E\left(Y_2\right)\left(1-E\left(Y_2\right)\right)}},$$

$E\left(Y_l\right)=E_u\left[P\left({ϵ}_l^{*}>-u-X_Z{\beta }^l|u\right)\right]=\frac{1}{\sqrt{2\pi }{\sigma }_u}{\int }_{-\infty }^{\infty }\frac{1}{1+\text{exp}\left(-u-X_Z{\beta }^l\right)}\text{\hspace{0.17em}exp}\left(\frac{-u^2}{2{\sigma }_u^2}\right)du$, l = 1,2, and similarly, $E\left(Y_1{Y}_2\right)=\frac{1}{\sqrt{2\pi }{\sigma }_u}{\int }_{-\infty }^{\infty }\frac{1}{\left(1+\text{exp}\left(-u-X_Z{\beta }^1\right)\right)\left(1+\text{exp}\left(-u-X_Z{\beta }^2\right)\right)}\text{\hspace{0.17em}exp}\left(\frac{-u^2}{2{\sigma }_u^2}\right)du$.

These expectations are functions of ${\sigma }_u^2$ and their values can computed using numerical integration. Moreover, approximate bounds can be obtained on Corr(Y₁,Y₂) by using normal approximation to the sum of independent and identically distributed standard logistic random variables (George & Mudholkar, 1983) and the distribution of sum of logistic and normal random variables (Nadarajah, 2005).

A3. MCMC Algorithm

Given the parameter estimates at the tth iteration (denoted by superscript t), we sample the new parameter values at the (t + 1)th iteration in the following way:

Updating of β¹ and β². These are the main parameters of interest. For each element ${\beta }_j^l\left(l=1,2,j=0,\dots ,m-1\right)$, we update it using Metropolis-Hastings algorithm. The proposal distribution is double exponential with mean ${\beta }_j^{l\left(t\right)}$ and SD $\sqrt{\left|{\beta }_j^{l\left(t\right)}\right|}$.

Updating of λ. We use a Gibbs sampler by directly sampling from the conditional distribution of λ, which is Gamma $\left(2m+a,{\sum }_{l=1}^2{\sum }_{j=0}^{m-1}\left|{\beta }_j^l\right|+b\right)$.

Updating of f⁰⁰, f¹⁰, and f⁰¹. We update f⁰⁰ using Metropolis-Hastings algorithm with proposal distribution Dir(a₁,a₂,…,a_m). The parameters satisfy $a_1/a_0=f_1^{00\left(t\right)},a_2/a_0=f_2^{00\left(t\right)},\dots ,a_m/a_0=f_m^{00(t)}$, with $a_0={\sum }_{i=1}^m{a}_i=C$ set equal to 1000, which gives reasonable acceptance rates and satisfactory convergence (Gelman et al., 2003). f⁰¹ and f¹⁰ are updated in the same way.

Updating of d. We update d using Metropolis-Hastings algorithm with proposal distribution Uniform(d^(t) − v, d^(t) + v) with v = 0.5. The updating is carried out subject to the constraint that $\text{max}\left\{-\frac{f_k^1}{1-f_k^1},-\frac{f_k^2}{1-f_k^2}\right\}<d^{\left(t+1\right)}<1,k=1,\dots ,m$.

Updating of u. We update u_i using Metropolis-Hastings algorithm with proposal distribution $N\left(u_i^{\left(t\right)},\left|u_i^{\left(t\right)}\right|\right)$, i = 1,…,n.

Updating of ${\sigma }_u^2$. We use a Gibbs sampler because the conditional distribution of ${\sigma }_u^2$ is Inverse $-{\chi }^2\left(n-1,{\sum }_{i=1}^n{u}_i^2/\left(n-1\right)\right)$, which is same as Inverse-gamma $\left(\left(n-1\right)/2,{\sum }_{i=1}^n{u}_i^2/2\right)$.