SiCloneFit: Bayesian inference of population structure, genotype, and phylogeny of tumor clones from single-cell genome sequencing data

Abstract

Accumulation and selection of somatic mutations in a Darwinian framework result in intra-tumor heterogeneity (ITH) that poses significant challenges to the diagnosis and clinical therapy of cancer. Identification of the tumor cell populations (clones) and reconstruction of their evolutionary relationship can elucidate this heterogeneity. Recently developed single-cell DNA sequencing (SCS) technologies promise to resolve ITH to a single-cell level. However, technical errors in SCS data sets, including false-positives (FP) and false-negatives (FN) due to allelic dropout, and cell doublets, significantly complicate these tasks. Here, we propose a nonparametric Bayesian method that reconstructs the clonal populations as clusters of single cells, genotypes of each clone, and the evolutionary relationship between the clones. It employs a tree-structured Chinese restaurant process as the prior on the number and composition of clonal populations. The evolution of the clonal populations is modeled by a clonal phylogeny and a finite-site model of evolution to account for potential mutation recurrence and losses. We probabilistically account for FP and FN errors, and cell doublets are modeled by employing a Beta-binomial distribution. We develop a Gibbs sampling algorithm comprising partial reversible-jump and partial Metropolis-Hastings updates to explore the joint posterior space of all parameters. The performance of our method on synthetic and experimental data sets suggests that joint reconstruction of tumor clones and clonal phylogeny under a finite-site model of evolution leads to more accurate inferences. Our method is the first to enable this joint reconstruction in a fully Bayesian framework, thus providing measures of support of the inferences it makes.

Acquisition of somatic mutations that confer selective growth advantage to the carrier cells drives initiation and progression of cancer (Vogelstein et al. 2013). From an evolutionary viewpoint, tumor progression is a somatic evolutionary process that gives rise to a composite mixture of genetically distinct subpopulations (clones) of cells through rounds of accumulation of somatic alterations, proliferation, and Darwinian selection in the tumor microenvironment (Nowell 1976; Merlo et al. 2006; Pepper et al. 2009; Yates and Campbell 2012). The genomic heterogeneity within a tumor, also known as intra-tumor heterogeneity (ITH) not only propels disease progression and metastasis (Turke et al. 2010; Wu et al. 2012) but can also lead to therapeutic relapse and drug resistance (Gillies et al. 2012; Burrell et al. 2013). High-throughput second-generation sequencing technologies have provided large-scale quantitative genomic data sets (Nik-Zainal et al. 2012; Kandoth et al. 2013) for investigating ITH. Most studies typically perform deep sequencing of bulk DNA retrieved from a single sample of the cancer tissue (Shah et al. 2012; Landau et al. 2015). Such data sets provide variant allele frequencies (VAFs) of somatic mutations, an aggregate signal averaged over the existing distinct tumor subclones as well as contaminating normal cells (Navin 2014), and VAFs are modeled as mixtures of subclones for their computational inference (Roth et al. 2014; Deshwar et al. 2015; El-Kebir et al. 2016; Jiang et al. 2016). However, the noisy aggregate signal of VAFs has limited resolution and thus restricts a comprehensive exploration of ITH (Navin 2014; Baslan and Hicks 2017). Sequencing multiple samples from different geographical regions of a tumor can improve upon single-sample bulk sequencing (Gerlinger et al. 2012, 2015; Yates et al. 2015) but cannot resolve spatially intermixed subpopulations (Navin 2015).

Ultimately, a single cell is the fundamental substrate of tumor evolution and single-cell DNA sequencing (SCS) has emerged as a powerful technique for resolving tumor evolution and ITH to a single-cell level (Hou et al. 2012; Gawad et al. 2014; Wang et al. 2014; Leung et al. 2017). Such technologies provide sequencing data pertaining to single cells, thus allowing for direct measurement of genotypes and prevalences of tumor subclones without requiring deconvolution of aggregate signals (Zafar et al. 2018). At the same time, they offer the possibility of reconstructing the clonal lineage tree. However, these tasks are challenged by a high level of experimental noise introduced in SCS data (Zafar et al. 2018) during the sample preparation and whole genome amplification (WGA) steps. WGA errors include false-positive (FP) and false-negative (FN) errors due to allelic dropout (ADO) (Navin 2014). FP errors are caused by deamination of cytosine bases and infidelity of polymerase enzymes. ADO affects the heterozygous loci as one of the alleles is preferentially amplified. Unintended isolation and processing of two cells together can result in cell doublets (characterized by merged genotype) (Zafar et al. 2018). Another problem with SCS data is missing entries due to coverage nonuniformity (Zafar et al. 2018).

Single-cell somatic point mutation profiles have been used to infer clonal subpopulations. Early studies (Li et al. 2012; Wang et al. 2014) used multidimensional scaling and hierarchical clustering for reconstructing the tumor subclones, but such approaches fail to account for errors. Gawad et al. (2014) used a Bernoulli mixture model (BMM) to infer clusters of cells and predict cluster genotypes and performed model selection via a Bayesian information criterion (BIC) score. This approach was extended in the SCG method (Roth et al. 2016) to accommodate errors due to ADO and doublets. However, such approaches neither utilize the evolutionary relationship between the clonal clusters nor infer any phylogeny that can convey the evolutionary history of the tumor cells. Another direction with SCS data has been the reconstruction of cell lineages to study tumor evolution. SCITE (Jahn et al. 2016) and OncoNEM (Ross and Markowetz 2016) probabilistically model WGA-specific errors for inferring tumor lineages from SCS data. However, both SCITE and OncoNEM operate under the infinite sites assumption (ISA), which posits that no genomic site mutates more than once and mutations are never lost. This assumption could get violated in tumor evolution due to events including convergent evolution, chromosomal deletions, and loss of heterozygosity (LOH) (Davis and Navin 2016; Kuipers et al. 2017). SiFit (Zafar et al. 2017) employs a finite-site model of evolution to allow for mutation recurrence and losses and employs a maximum-likelihood-based approach for reconstructing tumor phylogeny. Finally, PhISCS (Malikic et al. 2019) is a combinatorial approach that employs integer linear programming for inferring phylogenetic trees that deviate slightly from the ISA from single-cell and bulk-sequencing data. However, these phylogeny approaches (other than OncoNEM) do not provide straightforward reconstruction of the tumor subclones. At the same time, none of these phylogeny-based methods account for cell doublets as the merged genotypes cannot be represented by a cell lineage tree model.

Here, we propose SiCloneFit, a unified statistical framework and computational method that simultaneously addresses the problems of subclonal reconstruction and phylogeny inference from single-cell sequencing data. Our unified model simultaneously (1) estimates the number of tumor clones, (2) identifies the tumor clones as clusters of single cells, (3) predicts the mutations associated with each tumor clone (clonal genotype), and (4) under a finite-site model of evolution places the tumor clones at the leaves of a phylogenetic tree (clonal tree) that models their genealogical relationships.

Results

Overview of SiCloneFit

SiCloneFit integrates nonparametric Bayesian mixture modeling based on a Chinese restaurant process with the finite-sites-based phylogenetic approach introduced in SiFit (Zafar et al. 2017). Using single-cell somatic point mutation profiles as input, SiCloneFit introduces a nonparametric Bayesian mixture model based on a phylogeny-based Chinese restaurant process (clusters reside at the leaves of a phylogeny) to identify clusters (clones) of cells that share mutations and to resolve the clonal genotypes (mutations associated with a clonal cluster). The evolution of the clonal genotypes is modeled using a clonal phylogeny and a finite-site model of evolution that accounts for the effects of deletion, LOH, and point mutations at the genomic sites. SiCloneFit adopts the probabilistic error model of SiFit to account for FP and FN errors in SCS. The doublet-aware model of SiCloneFit employs a Beta-binomial distribution to accommodate for the presence of cell doublets and augments the nonparametric Bayesian mixture model with another finite mixture model to allow for the placement of a potential doublet in two clonal clusters. SiCloneFit employs a Gibbs sampling algorithm comprised of partial reversible-jump and partial Metropolis-Hastings updates to explore the joint posterior space of all parameters. To the best of our knowledge, SiCloneFit is the first Bayesian framework that jointly reconstructs clonal populations and their evolutionary history from SCS data sets under a finite-site model of evolution while accounting for cell doublets along with other WGA artifacts.

Description of SiCloneFit model

We start with a brief description of the formulation of the joint inference problem and the SiCloneFit model. Overview of the SiCloneFit model is given in Figure 1A.

Figure 1.

Overview of SiCloneFit Model. (A) From an observed noisy genotype matrix of single cells, SiCloneFit infers the clonal clusters, clonal phylogeny, and clonal genotypes of single cells. (B) A probabilistic graphical model representing the singlet model of SiCloneFit. Shaded nodes represent the observed values or fixed parameters; unshaded nodes are the latent variables that are of interest; a posterior distribution over the values of the unshaded nodes is approximated using samples from the proposed Gibbs sampler. The variables and indices are described in Supplemental Methods. (C) Distributional assumptions for the different variables in the SiCloneFit singlet model.

A tumor population (clone) refers to a set of cells that share a common genotype as they descend from a common ancestor (Merlo et al. 2006). In the context of single-cell sequencing, a clonal population refers to a maximal set of cells with identical genotype (with respect to the set of mutations under analysis) (Roth et al. 2016). We model the lineage of the clonal populations using a clonal phylogeny, a rooted directed binary tree, the root of which represents normal (unmutated) genotype, and somatic mutations are accumulated along the branches of the phylogeny. The sampling of single cells from the tumor at any point in time is analogous to horizontally slicing the clonal phylogeny to obtain samples from the leaves. The leaves of the clonal phylogeny represent the clonal populations, and the sampled cells are individuals sampled from each leaf. The DNA from each sampled cell goes through the process of single-cell DNA sequencing and mutation calling, which provides the observed genotype matrix D = D_n×m for m single cells and n somatic mutation sites.

In SiCloneFit, we model this generative process using the probabilistic graphical model shown in Figure 1B (also Supplemental Fig. S1). Here, we briefly describe the singlet model (all sampled cells are assumed to be singlets) of SiCloneFit. The probabilistic graphical model for the doublet-aware model is shown in Supplemental Figure S2. The model variables, hyperparameters, and associated indices are introduced in Supplemental Tables S1–S3. For a detailed description of the singlet and doublet-aware model of SiCloneFit, see Supplemental Methods.

We consider somatic single nucleotide variant (SNV) sites, where the input data is represented by a matrix that records the observed genotype for each cell for each mutation site. The input matrix can be binary, when the presence (denoted by 1) or absence (denoted by 0) of a mutation is noted. For a ternary matrix, the three possible genotype states, 0, 1, and 2 correspond to homozygous reference, and heterozygous and homozygous nonreference genotypes, respectively. We assume that there is a set of K clonal populations from which a total of m single cells are sampled and the clonal populations can be placed at the leaves of a clonal phylogeny, $\mathcal{T}$. Each clonal population contains a set of cells that have identical genotype and share a common ancestor. It is important to note that K is unknown. To infer the number of clones and assign the cells to clones, we introduce a tree-structured infinite mixture model. In our model, we extend the tree-structured Chinese restaurant process (CRP) prior from Meeds et al. (2008) to define a nonparametric Bayesian prior over binary trees, leaves of which represent the mixture components (clonal clusters). The clonal phylogeny represents the genealogical relationship between the clonal populations. A tree-structured infinite mixture model has been used for inferring tumor phylogeny from bulk-sequencing data (Deshwar et al. 2015). The genotype vector associated with a clone is called clonal genotype, and it records the genotype values for all mutation sites for the corresponding clone. To model the evolution of the clonal genotypes along the branches of $\mathcal{T}$, we employ a finite-site model of evolution, ${\mathcal{M}}_{\lambda }$, that accounts for the effects of point mutations, deletion, and LOH on the clonal genotypes. The model of evolution assigns transition probabilities to different genotype transitions along the branches of the clonal phylogeny. The true genotype of each cell is identical to the clonal genotype of the clonal cluster where it is assigned. However, observed genotypes of single cells can differ from their true genotype due to amplification errors introduced during the SCS work flow. The effect of amplification errors is modeled using an error model distribution parameterized by FP error rate α and FN error rate β. The generative process is described in detail in Methods and the distributional assumptions of the model are shown in Figure 1C.

SiCloneFit attempts to jointly reconstruct the tumor clones as clusters of single cells, clonal genotypes, and the clonal phylogeny. In doing so, it employs a likelihood function and a compound prior to define the posterior distribution over these latent variables. SiCloneFit employs a Markov chain Monte Carlo (MCMC) sampling procedure based on the Gibbs sampling algorithm comprised of partial reversible-jump and partial Metropolis-Hastings updates to estimate the latent variables. The posterior distribution and the inference algorithm are described in Methods and Supplemental Methods.

Benchmarking on simulated data sets

We performed comprehensive simulations to evaluate the performance of SiCloneFit in (1) clustering the cells into different clones, (2) inferring the genotypes of the cells via clonal genotyping, and (3) reconstructing the clonal lineage. To generate benchmarking data sets, we first sampled observed clonal prevalences for a fixed number of clones from a Dirichlet distribution, and the cells were assigned to different clones using a multinomial distribution. Then, we constructed linear and branching topologies for clonal phylogeny using the Beta-splitting model (Sainudiin and Véber 2016). The clonal genotypes at the leaves of the phylogeny were simulated in a similar fashion as described in Zafar et al. (2017). Different SCS artifacts were then introduced on the cellular genotypes to produce the noisy observed genotypes which were used as the input data for inference. The simulation process is described in detail in Supplemental Results.

To compare the results of SiCloneFit against the ground truth, we summarized the posterior samples from the Gibbs sampler of SiCloneFit. The clustering samples were summarized by the maximum posterior expected adjusted Rand (MPEAR) method (Fritsch and Ickstadt 2009). To summarize the clonal phylogeny samples, we constructed a maximum clade credibility topology (MCCT) from the posterior samples using DendroPy (Sukumaran and Holder 2010). From the posterior samples, we computed the posterior probability of the genotype of each cell at each mutation site, and the genotype with the highest posterior probability was assigned as the inferred genotype. When using the doublet-aware model of SiCloneFit, the doublets were inferred based on the posterior probability and were filtered out for subsequent analysis. The summarization methods are described in detail in Supplemental Results.

We compared SiCloneFit's performance against SCG (Roth et al. 2016), OncoNEM (Ross and Markowetz 2016), SiFit (Zafar et al. 2017), and SCITE (Jahn et al. 2016). SCG was used to infer clonal genotypes and clonal structures from the single cell somatic SNV profiles. The clonal phylogeny was obtained by running a maximum parsimony algorithm (Schliep 2011) on the clonal genotypes as suggested in the original study (Roth et al. 2016). OncoNEM was used to infer a clonal tree from the single cell somatic SNV profiles. Clonal genotypes were obtained by inferring the occurrence of the mutation on the branches of the clonal tree. SiFit inferred a cell lineage tree, the leaves of which represent the single cells. Mutations were inferred on the branches of this phylogeny using SiFit's mutation placement algorithm, which also resulted in inferring the genotype vector for each cell. The cells were clustered into a number of clones that resulted in the highest silhouette score for k-medoids clustering of the cells based on a distance matrix obtained from the inferred cell lineage tree. SCITE was used to infer a mutation tree from the noisy single-cell mutation profiles. The attachments of the cells on the nodes of the mutation tree also helped in inferring the genotype of each cell. We inferred the clonal populations by clustering the cells using a silhouette score-based k-medoids clustering based on a distance matrix obtained from the mutation tree. Details of how results were extracted for each method are described in Supplemental Results.

The clustering accuracy of each method was measured using the Adjusted Rand Index (ARI) and B-cubed F-score (Amigó et al. 2009) for data sets without and with doublets, respectively. For evaluating the genotyping performance of each method, we computed the genotyping error defined by the average Hamming distance (number of entries differing) per cell per site between the true and inferred genotypes of the cells. For an assessment of the phylogeny inference, we used the tree reconstruction error computed as the pairwise cell shortest-path distance (Ross and Markowetz 2016) between the true and inferred clonal phylogeny. The performance metrics are described in detail in Supplemental Results.

SiCloneFit employs a finite-site model of evolution along the branches of the clonal phylogeny to account for the effects of possible mutation losses and recurrence on the clonal genotypes. To analyze how well this finite-site model performs in conjunction with the tree-structured infinite mixture model in recovering the clonal genotypes of the single cells under varying rates of mutation recurrence and losses, we conducted three sets of experiments. For the three sets, varying probabilities for deletion (d), loss of heterozygosity (ω), and recurrent mutation (r) were used for simulation, respectively. An extreme setting (d = 0, ω = 0, r = 0) of these parameters also generated data sets under the infinite-sites model. The first two parameters resulted in loss of mutations; the third one introduced parallel recurrent mutations. For these experiments, we compared SiCloneFit's result against that of SiFit (the only other method employing a finite-site model) to test whether SiCloneFit's additional ability to cluster the cells results in improved performance. Details of these experiments have been described in Supplemental Results. For different values of deletion probability, SiCloneFit performed superiorly over SiFit based on all three metrics (Supplemental Fig. S3). Specifically, SiCloneFit achieved major improvement over SiFit in reducing the genotyping error and tree reconstruction error. Similarly, for different values of the probability of LOH, SiCloneFit achieved better or similar clustering accuracy (Supplemental Fig. S4A) and reasonably reduced tree reconstruction error (Supplemental Fig. S4B) and genotyping error (Supplemental Fig. S4C) compared to SiFit. For the data sets generated under the infinite-sites model (d = 0, ω = 0, r = 0), both SiCloneFit and SiFit achieved high clustering accuracy, but SiCloneFit outperformed SiFit in reconstructing the clonal genotypes and the phylogeny (Supplemental Fig. S5). For different values of recurrent mutation probability (r), SiCloneFit performed better than SiFit in inferring the clonal phylogeny and the genotypes (Supplemental Fig. S5).

To evaluate SiCloneFit's singlet model, we first conducted simulations excluding doublets. For a fixed number of clones, we simulated data sets with varying number of cells and varying number of sites. For these data sets, we compared against SCG, OncoNEM, SiFit, and SCITE. However, for larger sized data sets (m = 500), OncoNEM failed to run. Clustering accuracy (Fig. 2A; Supplemental Fig. S6) and phylogeny inference accuracy (Fig. 2C; Supplemental Fig. S8) of each method improved as the number of sites increased. Genotyping error (Fig. 2B; Supplemental Fig. S7) of each method reduced with an increase in the number of sites. For each experimental setting, SiCloneFit performed the best in terms of all performance metrics. For larger sized data sets, it achieved perfect clustering for almost all data sets. In the presence of a higher number of clonal populations, sampling the same number of cells leads to a more difficult inference problem. Even for such situations, SiCloneFit performed the best based on all three metrics (Supplemental Fig. S9), and it was robust against the increase in number of clones as evidenced by its low rate of reduction in clustering accuracy. SiCloneFit's performance was also robust against increasing error rate. With an increase in the FN rate, performance of each method degraded, but SiCloneFit had the lowest amount of reduction in performance, and it also outperformed all other methods for all values of FN rate (Supplemental Fig. S10). The same trend was observed when false positive rate was elevated (Supplemental Fig. S11). SiCloneFit's performance was robust to an increase in FP rate, and it performed superiorly over all other methods based on all three metrics. In this setting, for some data sets, SCG's genotyping failed to converge and resulted in a large number of false predictions. For larger data sets, we also tested the effect of missing data on inference accuracy. For these experiments, we compared SiCloneFit's results to that of only SCG as SCG was overall the second best performer (matched or outperformed by SiFit for some settings) in all our previous experiments. Even in the presence of a high amount of missing data, SiCloneFit performed well in clustering the cells into clones and inferring the clonal phylogeny. It consistently performed better than SCG (Supplemental Figs. S12–S14) in terms of all metrics. Only in one setting (n = 100, 30% missing data) did SCG achieve lower genotyping error than SiCloneFit.

Figure 2.

Performance comparison on simulated data sets containing 100 cells. SiCloneFit's performance is compared against that of SCG, OncoNEM, SiFit, and SCITE on simulated data sets containing 100 cells for varying numbers of sites. On the x-axis, we have results corresponding to n = 50 and n = 100. The cells were sampled from K = 10 clonal populations. Each box plot summarizes results for 10 simulated data sets with varying clonal phylogeny and varying size of clonal clusters. (A) Comparison of clustering accuracy measured in terms of Adjusted Rand Index that compares the inferred clustering against the ground truth. (B) Comparison based on the genotyping error measured in terms of Hamming distance per cell per site between the true genotype matrix and inferred genotype matrix. (C) Comparison based on the tree reconstruction error measured in terms of pairwise cell shortest-path distance between the true clonal phylogeny and inferred clonal phylogeny.

While most human tumors show evidence of at least weak selection leading to the prevalence of clonal subpopulations that harbor driver mutations (Greaves and Maley 2012), some tumors might undergo neutral evolution as shown in Ling et al. (2015) and Williams et al. (2016). To analyze SiCloneFit's performance under neutral evolution that can lead to an absence of clonal structure, we conducted simulation experiments under the neutral evolution model proposed in Williams et al. (2016). The neutral evolution model in Williams et al. (2016) posits that the number of subclonal mutations should follow the 1/f power law distribution (f being the allelic frequency of a mutation), and the cumulative distribution M(f) of subclonal mutations should have a linear relationship with 1/f. We simulated data sets satisfying these conditions (Supplemental Fig. S15) and compared SiCloneFit's results to that of SCG, SiFit, and SCITE (Supplemental Fig. S16). For these data sets, SiCloneFit performed either similarly or better than the other methods based on the different metrics (see Supplemental Results for details).

We further evaluated SiCloneFit's ability to estimate the error rates from the data sets. SiCloneFit performed very well for estimating both FP rate α and FN rate β (Supplemental Fig. S17). For data sets generated under a wide range of error rate values, SiCloneFit's estimated error rates were highly correlated (0.998 for α and 0.992 for β) to the original error rates used for generating the data sets. In order to evaluate SiCloneFit's ability to infer the correct number of clusters, we generated data sets under varying levels of sampling distortion. Higher sampling distortion leads to the sampled cells deviating from the true prevalences of the clonal clusters, making it more difficult to infer the actual number of clusters. SiCloneFit's performance in inferring the actual number of clusters improved as the amount of sampling distortion reduced from high to moderate to low (Supplemental Fig. S18). Even in the presence of high sampling distortion, it inferred the actual number of clusters for some data sets and only missed rare clusters (consisting of one cell). SiCloneFit also performed well for data sets containing a large number of cells (Supplemental Fig. S19) and large number of sites (Supplemental Fig. S20).

Next, we performed simulations including 10% doublets to evaluate SiCloneFit's doublet model. SCG is the only other method that accounts for the presence of doublets. As a consequence, for these data sets, we only compared SiCloneFit's results against that of SCG. For a fixed number of clones, we simulated data sets with varying number of cells and varying number of sites. SiCloneFit achieved higher clustering accuracy (Supplemental Fig. S21) and genotyping accuracy (Supplemental Fig. S22) compared to SCG. It also achieved lower tree reconstruction error (Supplemental Fig. S23) in all settings except for m = 500 and n = 100. For some data sets, SCG failed to converge and resulted in very low clustering accuracy and high genotyping error. In the presence of a higher number of clonal populations, SiCloneFit significantly outperformed SCG (Supplemental Fig. S24). Finally, we evaluated how inference is affected when missing data and doublets are simultaneously present. Even in the presence of a high amount of missing data (15%, 30%), both methods performed well in clustering (Supplemental Fig. S25) the cells to clones, with SiCloneFit performing better than SCG in all settings. For all settings, SiCloneFit's genotyping performance (Supplemental Fig. S26) was better than that of SCG's. For some data sets, SCG failed to converge and resulted in low clustering accuracy and high genotyping error. SiCloneFit's tree reconstruction error (Supplemental Fig. S27) was also smaller in all but one setting (n = 100 and 15% missing data).

Inference of clonal clusters, genotypes, and phylogeny from experimental SCS data

We applied SiCloneFit to two experimental single-cell DNA sequencing data sets from two metastatic colon cancer patients, obtained from the study of Leung et al. (2017). These data sets were generated using a highly multiplexed single-cell DNA sequencing method (Leung et al. 2016) and a 1000-cancer gene panel was used as the target region for sequencing. These are two of the most recent SCS data sets and contain a large number of cells and a small number of mutation sites, making the inference difficult.

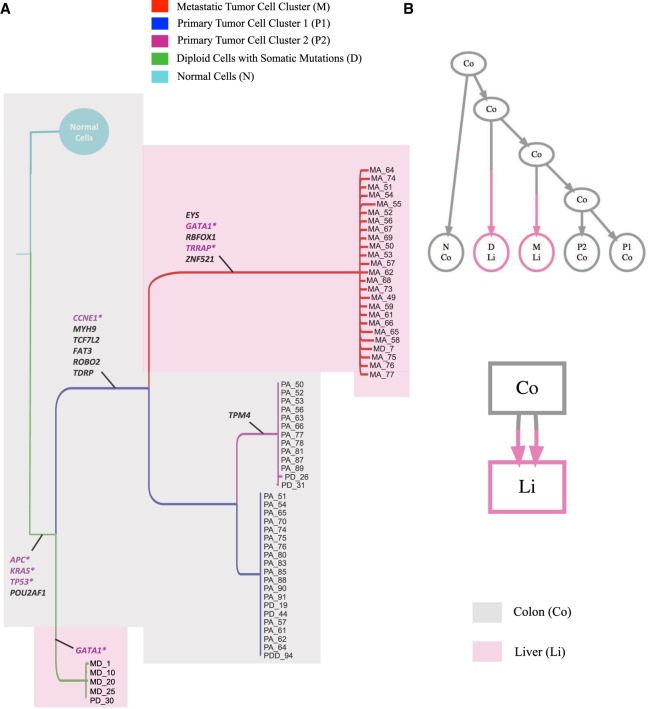
The first data set consisted of 178 cells (Leung et al. 2017) obtained from both primary colon tumor and liver metastasis. The original study reported 16 somatic SNVs after variant calling. The reported genotypes were binary values, representing the presence or absence of a mutation at the SNV sites. In the original study, SCITE (Jahn et al. 2016) was used for performing phylogenetic analysis of this tumor. However, SCITE operates under the infinite sites assumption and only infers the mutation tree. We ran the four-gamete test on this data set, which identified 104 (out of 120) pairs of SNV sites violating the four-gamete test, indicating potential violation of the infinite sites assumption. Multiple potential events including mutation recurrence and loss, FP and FN error could have caused such a high number of violations of the four-gamete test (Zafar et al. 2017). After running SiCloneFit on this data set, we collected the samples from the posterior and computed a maximum clade credibility tree based on the posterior samples, as shown in Figure 3A. Five different clusters were identified from the SiCloneFit posterior samples. The largest cluster (N) consisted of normal cells without any somatic mutation. The primary tumor cells were clustered into two subclones (P1 and P2). Metastatic aneuploid tumor cells were clustered into one subclone (M). There was another cluster (D) consisting of diploid cells (mostly metastatic). The clonal genotype of each cluster was inferred based on the posterior samples. The inferred genotypes are shown in Supplemental Figure S28. Based on the clonal genotypes, we inferred the ancestral sequences at the internal nodes, and this enabled us to find the maximum-likelihood solution for placing the mutations on the branches of the clonal phylogeny. First, a heterozygous nonsense mutation was acquired in APC along with mutations in the KRAS oncogene and TP53 tumor suppressor gene, and these initiated the tumor mass. The subclone (D) consisting of diploid cells acquired another mutation in GATA1 and branched out from the primary tumor mass. The primary tumor subclones developed by acquiring six more somatic mutations, including a mutation in the CCNE1 oncogene. These mutations were subsequently inherited in the metastatic tumor subclone (M). The accumulation of mutations in EYS, GATA1, RBFOX1, TRRAP, and ZNF521 marked the point of metastatic divergence. The two primary tumor subclones were distinguished by the presence/absence of TPM4 mutation. It was specific to the second primary subclone (P2) and was not identified in any of the metastatic tumor cells, suggesting that the first primary subclone (P1) disseminated and established the metastatic tumor mass. The clonal phylogeny displayed recurrence of the GATA1 mutation that was not identified in the original study. This finding was further supported by a mixture-model Bayesian binomial test (Leung et al. 2017) based on the read counts of the GATA1 mutation (see Supplemental Results for details). We ran MACHINA (El-Kebir et al. 2018) on the clonal phylogeny inferred by SiCloneFit for reconstructing the migration history of the tumor clones for this patient. The inferred migration graph (Fig. 3B) had two migrations with comigration number = 1. Since two anatomical sites were sequenced, the inference of a minimum possible comigration number indicates a single-source seeding pattern with colon being the source. The presence of a multiedge in the migration graph also indicates polyclonal seeding, where liver was seeded by two different clones that originated in colon. However, the first seeding did not result in the clonal expansion; metastatic tumor mass formed after the second seeding that was associated with the mutations in EYS, GATA1, RBFOX1, TRRAP, and ZNF521. None of the cells were inferred as doublets by the doublet-aware model of SiCloneFit. This finding was further supported by the doublet detection by SCG, which also did not find any doublet. This is expected, as the cells in this data set were isolated using FACS Aria II (Leung et al. 2017), which included a protocol for removing doublets.

Figure 3.

Inference of tumor clones and clonal phylogeny using SiCloneFit for metastatic colorectal cancer patient CRC1. (A) Maximum clade credibility tree reconstructed from the posterior samples obtained using SiCloneFit. Each tumor clone is a cluster of single cells, and their genotypes are also inferred. The temporal order of the mutations is reconstructed, and mutations are annotated on the branches of the clonal tree. The cancer genes and tumor-suppressor genes are marked in purple. The colors of the shades represent the organ/anatomical site of the origin of the cells. (B) Parsimonious migration history of the tumor clones inferred using MACHINA (El-Kebir et al. 2018) with the SiCloneFit inferred clonal tree as input. The top figure shows the clonal tree where the leaves are annotated by the anatomical sites and the anatomical sites annotation of the internal nodes and root are inferred by MACHINA. The bottom figure shows the migration graph of the cells with migration number 2 and comigration number 1. This indicates polyclonal single-source seeding from colon to liver.

For comparison, we ran SCG on this data set. SCG reported four clonal clusters, and the inferred clonal genotypes are shown in Supplemental Figure S29. SCG could not distinguish the primary tumor cells on the basis of the presence/absence of the TPM4 mutation and genotyped all of them to contain TPM4. Thus, it did not report two primary tumor subclones that were detected by SiCloneFit and instead only one primary tumor subclone (all primary tumor cells were assigned to this cluster) was inferred.

The second data set consisted of 182 cells (Leung et al. 2017) obtained from both primary colon tumor and liver metastasis. The original study reported 36 somatic SNVs after variant calling. The reported genotypes were binary values, representing the presence or absence of a mutation at the SNV sites. After running the four-gamete test on this data set, we identified 347 (out of 630) pairs of SNV sites violating the four-gamete test, indicating potential violation of the infinite sites assumption. After running SiCloneFit on this data set, we collected the samples from the posterior and computed a maximum clade credibility tree based on the posterior samples, as shown in Figure 4A. Six different clusters were identified in the MPEAR solution based on the posterior samples. The largest cluster (N) consisted of normal cells that did not harbor any somatic mutation. There were two clusters consisting of primary aneuploid tumor cells (P1 and P2) and two clusters consisting of metastatic aneuploid tumor cells (M1 and M2). There was one more cluster (I) comprised of diploid cells that harbored somatic mutations that were completely different from the primary or metastatic clusters, representing an independent clonal lineage consistent with the findings reported by Leung et al. (2017). The clonal genotype of each cluster was inferred based on the posterior samples. The inferred genotypes are shown in Supplemental Figure S30. Based on the clonal genotypes, we inferred the ancestral sequences at the internal nodes, and this enabled us to find the maximum-likelihood solution for placing the mutations on the branches of the clonal phylogeny. The first primary tumor clone (P1) evolved from the normal cells by acquiring eight mutations, including mutations in APC, NRAS, CDK4, and TP53. After that, four additional mutations (CHN1, APC, LINGO2, IL21R) were acquired before the first metastatic cluster (M1) diverged. After dissemination into liver, the first metatstatic subclone (M1) continued to evolve and acquired a number of metastasis-specific mutations (e.g., SPEN, IL7R, PIK3CG, F8, LINGO2). Before the divergence of the second metastatic subclone (M2), two more mutations (FHIT, ATP7B) were acquired that were also present in the second primary tumor subclone P2. The second primary tumor clone (P2) acquired two additional mutations in LRP1B and LINGO2 that were not present in either metastatic clone. The second metastatic clone disseminated after acquiring the ATP7B mutation and further expanded the liver tumor mass by acquiring seven additional mutations (e.g., PTPRD, NR4A3, HELZ, TSHZ3). In the original study, SCITE identified two different lineages for metastatic cells and inferred four mutations (FHIT, ATP7B, APC, and CHN1) between the two metastatic divergence events. These were called as “bridge mutations.” In contrast, SiCloneFit identified two mutations (FHIT and ATP7B) as “bridge mutations,” and the other two putative bridge mutations (APC, and CHN1) were identified as nonbridge and placed before the divergence of the first metastatic subclone. To evaluate these results, we performed the mixture-model Bayesian binomial test proposed in Leung et al. (2017) based on the read counts for these four mutations, which further indicated that SiCloneFit's placement of these mutations in the tumor phylogeny is more plausible than that of SCITE (see Supplemental Results; Supplemental Figs. S31, S32 for details). Other than the precursor mutations shared with the primary tumor clones, the metastatic tumor clones had three more mutations in common (PTPRD, FUS, and LINGO2). This is evidence for a potential convergent evolution. To evaluate the accuracy of this, we performed the mixture-model Bayesian binomial test (Leung et al. 2017), which provided strong evidence of recurrence for two of these mutations (FUS and LINGO2) (see Supplemental Fig. S33; Supplemental Results for details). Apart from the primary and metastatic tumor clones, there was another cluster (I) consisting of seven primary diploid cells that had completely independent somatic mutations. These cells acquired mutations in SPEN, ALK, ATR, NR3C2, and EPHB6 but did not share any other mutations with the primary or metastatic tumor cells, representing an entirely different tumor lineage that did not expand significantly. We reconstructed the migration history of the tumor clones by running MACHINA (El-Kebir et al. 2018) on the SiCloneFit inferred clonal phylogeny, whose leaves (clonal clusters) were annotated by the anatomical site of origin of the associated cells. The inferred migration graph (Fig. 4B) had two migrations with comigration number = 1 (also the minimum possible comigration number for two anatomical sites), indicating polyclonal single-source seeding from colon to liver. Here, both the seeding events led to expansion of tumor mass in liver and resulted in two different metastatic subclones. For this data set also, none of the cells were inferred as a doublet by SiCloneFit's doublet-aware model. Similarly, SCG did not detect any doublet in this data set.

Figure 4.

Inference of tumor clones and clonal phylogeny using SiCloneFit for metastatic colorectal cancer patient CRC2. (A) Maximum clade credibility tree reconstructed from the posterior samples obtained using SiCloneFit. Each tumor clone is a cluster of single cells, and their genotypes are also inferred. The temporal order of the mutations is reconstructed, and mutations are annotated on the branches of the clonal tree. The cancer genes and tumor-suppressor genes are marked in purple. The colors of the shades represent the organ/anatomical site of the origin of the cells. (B) Parsimonious migration history of the tumor clones inferred using MACHINA (El-Kebir et al. 2018) with the SiCloneFit inferred clonal tree as input. The top figure shows the clonal tree where the leaves are annotated by the anatomical sites and the anatomical sites annotation of the internal nodes and root are inferred by MACHINA. The bottom figure shows the migration graph of the cells with migration number 2 and comigration number 1. This indicates polyclonal single-source seeding from colon to liver.

SCG reported five clonal clusters from this data set (Supplemental Fig. S34). Clustering and genotyping results of SCG mostly agreed with that of SiCloneFit. However, SCG failed to detect two primary tumor subclones and instead clustered them together into one subclone, resulting in incorrect genotyping for those cells.

To validate SiCloneFit's doublet detection from experimental SCS data, we applied SiCloneFit on a high-grade serous ovarian cancer data set introduced in McPherson et al. (2016) consisting of 370 cells and 43 somatic mutations. Since, ground truth doublets were not known for this data set, we compared the results of the doublet-aware models of SiCloneFit and SCG on this data set. Seventeen cells were reported as doublets by both of these methods. SCG reported 11 additional doublets, 10 of which had similar posterior probabilities (computed by SCG) of being a doublet or a singlet (see Supplemental Fig. S35; Supplemental Results for details).

Discussion

Inference of tumor subclones and their evolutionary history is of paramount importance given their contribution to drug resistance and therapeutic relapse. While this problem has been investigated in depth in the context of bulk-sequencing data, methods are lacking for SCS data, the most promising and high-resolution data for studying tumor heterogeneity. Here, we reported on SiCloneFit, a novel probabilistic framework for inferring the number and structure of tumor clones, their genotypes, and evolutionary history from noisy somatic SNV profiles of single cells. Our unified framework jointly reconstructs the tumor clones as clusters of single cells as well as their genealogical relationship in the form of a clonal phylogeny. In this process, SiCloneFit accounts for the effects of mutational events (point mutations, LOH, deletion) in the evolutionary history of the tumor via a finite-site model of evolution and denoises the effects of technical artifacts such as allelic dropout, false-positive errors, missing entries, and cell-doublets to infer the clonal genotypes. SiCloneFit employs a Gibbs sampling algorithm consisting of partial reversible-jump MCMC and partial Gibbs updates for estimating the latent variables by sampling from the posterior distribution. A major distinguishing feature of SiCloneFit is that it jointly solves the subclonal reconstruction and tumor phylogeny inference problems from SCS data sets, whereas existing methods either cluster the cells into subclones or infer a tumor phylogeny. The phylogeny inference methods (except SiFit) also rely on infinite sites assumption to restrict the search space. On the contrary, SiCloneFit employs a finite-site model of evolution to account for mutation recurrence and losses. At the same time, SiCloneFit accounts for cell doublets, an important technical artifact that is not dealt with by existing single-cell phylogeny inference methods.

We assessed SiCloneFit's performance through a comprehensive set of simulation studies aimed at creating experimental settings corresponding to different aspects of modern SCS data sets. Data sets were generated with varying rates of mutation losses and recurrences, a varying number of cells, genomic sites, and tumor subclones, a wide range of error rates, and varying amounts of missing data and cell doublets. In simulated benchmarks, SiCloneFit outperformed the state-of-the-art methods based on different metrics for evaluating its performance in inferring the clonal clusters, clonal genotypes, and the clonal evolutionary history. SiCloneFit also performed well in estimating the error rates in SCS data. We also applied SiCloneFit on two targeted SCS data sets from two metastatic colon cancer patients for studying the intra-tumor heterogeneity. For these tumors, SiCloneFit inferred the primary and metastatic subclones as clusters of single cells, inferred their genotypes, reconstructed the genealogy of these subclones, and inferred the temporal order of the mutations in their evolutionary history, revealing mutations that potentially played an important role in metastatic divergence.

SiCloneFit's inference of clonal populations and clonal genotypes could potentially be improved by accounting for copy number alterations (CNAs) along with SNVs. The current model of SiCloneFit accounts for only LOH and deletion that can give rise to CNAs altering the genotype of a point mutation site. Similarly, copy number gain can also result in changing the genotype of a point mutation site. Copy number information for the mutation sites will be very helpful in a more accurate understanding of the genotype states of point mutations. While it is possible to approximate any copy number information via the ternary genotype states (e.g., for copy number 3, ternary genotype states will be 0 = {aaa}, 1 = {aaa, abb}, 2 = {bbb}; ‘a’: reference allele and ‘b’: variant allele) of our current model, the exact copy number information will help in more precise inference of the genotypes. Our finite-site model is flexible, and it can be easily extended by adding copy number gain and loss parameters to account for the possible genotype states emerged due to simultaneous occurrence of CNAs and SNVs. The inclusion of CNAs along with SNVs can also improve the inference of the mutational history of the tumor, as the placement of CNAs on the branches of the clonal phylogeny can help in understanding their role in subclonal expansion. However, owing to the difference of the whole genome amplification methods required for CNA and SNV detection, modern SCS data sets are generated with an aim to uncover either the CNAs or the SNVs. Most studies resort to targeted sequencing for SNV detection, and because of the uneven coverage of the targeted sequencing, inference of copy numbers from such data sets becomes extremely difficult. When technologies become available for producing SCS data sets enabling the measurement of both CNAs and SNVs from the same cell, SiCloneFit's finite-site model can be extended to account for more complex genotype states resulting from CNAs. If copy number information becomes available, SiCloneFit's error model can be further improved, as the mutated alleles present in multiple copies will be less prone to be affected by allelic dropout. SiCloneFit's error model can be further extended to utilize reference and variant read counts at each mutation site in each cell as the input data instead of presence/absence of mutation inferred by a variant caller.

In closing, SiCloneFit advances the understanding of intra-tumor heterogeneity and clonal evolution through improved computational analysis of SCS data. As SCS becomes more high-throughput, generating somatic SNV profiles for thousands of cells, SiCloneFit will be very helpful in reconstructing the tumor clones and clonal phylogeny from such large data sets. Being capable of handling doublets, SiCloneFit will find important applications in removing doublets, as their percentage can be high in more high-throughput data sets. Methods like SiCloneFit will have important translational applications for improving cancer diagnosis, treatment, and therapy in clinical applications.

Methods

Model description

We assume that we have measurements from m single cells. For each cell, n somatic single nucleotide variant sites have been measured. The data can be represented by a matrix D_n×m = (D_ij) of observed genotypes, where D_ij is the observed genotype at the i^th site of cell j. Let g_t be the set of possible true genotype values for the SNVs, and g_o be the set of observable values for the SNVs. For binary measurements for SNVs, g_t = {0, 1}, whereas g_o = {0, 1, X}, where 0, 1, and X denote the absence of mutation, presence of mutation, and missing value, respectively. If ternary measurements are available for SNVs, g_t = {0, 1, 2}and g_o = {0, 1, 2, X}, where 0 denotes homozygous reference genotype, and 1 and 2 denote heterozygous, and homozygous nonreference genotypes, respectively, and X denotes missing data.

We assume that there is a set of K clonal populations from which m single cells are sampled and the clonal populations can be placed at the leaves of a clonal phylogeny, $\mathcal{T}$. Each clonal population consists of a set of cells that have an identical genotype (with respect to the set of mutations in consideration) and a common ancestor. The genotype vector associated with a clone c is called clonal genotype (denoted by G_c, G_c ∈ {0, 1, 2}ⁿ), and it records the genotype values for all n sites for the corresponding clone. The true genotype vector of each cell is identical to the clonal genotype of the clonal population to which it belongs. The clonal genotype matrix, G_K×n, represents the clonal genotypes of K clones. It is important to note that, K, the number of clones is unknown. To automatically infer the number of clones and assign the cells to clones, we introduce a tree-structured infinite mixture model. Meeds et al. (2008) describes a nonparametric Bayesian prior over trees similar to mixture models using a Chinese restaurant process (Pitman 2006) prior. For this tree-structured CRP, each node of the tree represents a cluster. In our model, we extend this idea to define a nonparametric Bayesian prior over binary trees, leaves of which represent the mixture components (clonal clusters). A Chinese restaurant process defines a distribution for partitioning customers into different tables. In our problem, single cells are analogous to customers and clonal clusters are analogous to tables. Let c_j denote the cluster assignment for cell j and assume that cells 1:j − 1 have already been assigned to clonal clusters {1, …, |c_1:j−1|}, where |c_1:j−1| denotes the number of clusters induced by the cluster indicators of j − 1 cells. The cluster assignment of cell j, c_j is based on the distribution defined by a Chinese restaurant process and is given by

$$\begin{array}{r}p(c_j=c|c_{1:(j-1)},{\alpha }_0)=\frac{n_c}{j-1+{\alpha }_0}\\ p(c_j\ne c_k\mathrm{\forall }k<j|c_{1:(j-1)},{\alpha }_0)=\frac{{\alpha }_0}{j-1+{\alpha }_0}\end{array}$$ (1)

where n_c denotes the number of cells already assigned (excluding cell j) to cluster c. α₀ is the concentration parameter for the CRP model.

The clonal phylogeny, $\mathcal{T}$, is a rooted directed binary tree whose number of leaves is equal to the number of clonal clusters, K = |c| defined by the assignment of m cells to different clusters by the CRP. The root of $\mathcal{T}$ represents normal (unmutated) genotype, and somatic mutations are accumulated along the branches of the phylogeny. Each leaf in the clonal phylogeny corresponds to a clonal cluster, c ∈ {1, …, K}, and is associated with a clonal genotype G_c that records the set of mutations accumulated along the branches from the root. To model the evolution of the clonal genotypes, we employ a finite-site model of evolution, ${\mathcal{M}}_{\lambda }$, that accounts for the effects of point mutations, deletion, and loss of heterozygosity on the clonal genotypes. The model of evolution assigns transition probabilities to different genotype transitions along the branches of the clonal phylogeny. The true genotype of each cell is identical to the clonal genotype of the clonal cluster where it is assigned. However, observed genotypes of single cells differ from their true genotype due to amplification errors introduced during the single-cell sequencing work flow. The effect of amplification errors is modeled using an error model distribution parameterized by FP error rate, α and FN error rate, β. The generative process can be described as follows:

1. Draw ${\alpha }_0\sim \mathrm{Gamma}(a,b)$, $\alpha \sim \mathrm{Beta}(a_{\alpha },b_{\alpha })$, $\text{β}\sim \mathrm{Beta}(a_{\text{β}},b_{\text{β}})$.

2. For j ∈ {1, 2, …, m}, draw $c_j\sim CRP({\alpha }_0)$.

   From this, derive K = |c|, the total number of clusters (or clones) implicitly defined by c.

3. Draw $\mathcal{T}\sim T_{\mathrm{prior}}(K)$.

4. For $\lambda \in {\mathcal{M}}_{\lambda }$, draw $\lambda \sim \mathrm{Beta}(a_{M_{\lambda }},b_{M_{\lambda }})$.

5. For k ∈ {1, 2, …, K}, draw $G_k\sim F(G_k|\mathcal{T},{\mathcal{M}}_{\lambda })$.

6. For j ∈ {1, 2, …, m} and i ∈ {1, 2, …, n}, draw $D_{ij}\sim E(D_{ij}|G_{c_{j}i},\alpha ,\text{β})$.

c denotes the clonal assignments of all cells. T_prior is the prior distribution on phylogenetic trees for a fixed number of leaves. ${\mathcal{M}}_{\lambda }$ denotes the set of parameters in the finite-site model of evolution. F denotes a distribution on the genotypes at the leaves of a phylogenetic tree and can be computed using Felsenstein's pruning algorithm (Felsenstein 1981) given the phylogeny and a finite-site model of evolution. E is the error model distribution that relates the observed genotype at locus i for cell j, D_ij to clonal genotype $G_{c_{j}i}$. $a,b,a_{\alpha },b_{\alpha },a_{\text{β}},b_{\text{β}},a_M,b_M$ denote different hyperparameters used in this model.

Doublet-aware model description

The singlet model of SiCloneFit is extended to handle cases where some data points result from measuring two cells (doublets). The expected genotype for a doublet due to merging of two cells is defined by the $\oplus$ operator as shown in Supplemental Table S6 and the logical or operator for ternary and binary data type, respectively. The doublet-aware model of SiCloneFit incorporates all the variables in the singlet model. In addition, for each single cell j, it employs a Bernoulli variable Y_j for indicating whether the cell is a singlet or a doublet. A Beta distributed variable, δ, represents the probability of sampling a doublet. For each cell, two cluster indicators are used. $c_j^1$ is the primary cluster indicator for cell j with a Chinese restaurant process prior based on hyperparameter α₀, whereas $c_j^2$ is a secondary cluster indicator for cell j that can uniformly take values in the range {1, …, |c¹|}. If Y_j = 1, $c_j^2$ denotes the clone of origin of the cell that forms a doublet by merging with cell j from clone $c_j^1$. These additional variables are described in Supplemental Table S7. The generative process for the doublet-aware model is described in detail in Supplemental Methods.

Model of evolution and error model

To capture the effect of point mutations, LOH, and deletion on the clonal genotypes along the branches of clonal phylogeny, we employ a finite-site model of evolution similar to the one introduced in SiFit (Zafar et al. 2017). Point mutations can result in the genotype transition 0 → 1, whereas LOH and deletion can result in the genotype transitions 1 → 0 or 1 → 2. The finite-site model of evolution, ${\mathcal{M}}_{\lambda }$, is modeled using a continuous-time Markov chain that assigns a probability with each possible transition of genotypes. The transition rate matrix of the continuous-time Markov chain for binary and ternary genotypes can be defined based on branch length, t, and parameters λ_r and λ_l, accounting for the effects of recurrent mutation and mutation loss, respectively. These are described in detail in Supplemental Methods.

To account for FP and FN errors in SCS data, we introduce an error model distribution, $E(D_{ij}|G_{c_{j}i},\alpha ,\text{β})$, which gives the probability of observing genotype D_ij for locus i in cell j, given the true clonal genotype $G_{c_{j}i}$. The error model distributions for ternary and binary data are shown in Supplemental Tables S4 and S5, respectively.

Posterior distribution

The posterior distribution $\mathcal{P}$ over the latent variables of the SiCloneFit model is given by

$$\mathcal{P}(\mathcal{V}|\mathbf{D},\mathcal{H})\propto P(\mathbf{D}|\mathcal{V})\times P(\mathcal{V}|\mathcal{H}).$$ (2)

where $\mathcal{V}$ denotes the set of latent variables in the model, $\mathcal{V}=\left\{\mathbf{c},\mathbf{G},\mathcal{T},{\mathcal{M}}_{\lambda },\alpha ,\text{β},{\alpha }_0\right\}$. c is a vector containing cluster assignment for all cells, and it implicitly defines the number of clones K. $\mathcal{H}$ is the set of fixed hyperparameters of the model, $\mathcal{H}=\left\{a_{\alpha },b_{\alpha },a_{\text{β}},b_{\text{β}},a_M,b_M,a,b\right\}$. In Equation 2, the term $P(\mathbf{D}|\mathcal{V})$ denotes the likelihood of the model, and the term $P(\mathcal{V}|\mathcal{H})$ denotes the product of prior probabilities. The posterior distribution for the doublet-aware model is described in Supplemental Methods.

Likelihood function

The likelihood function employed by SiCloneFit is given by

$$P(\mathbf{D}|\mathcal{V},\mathcal{H})=E(\mathbf{D}|\mathbf{c},\mathbf{G},\alpha ,\text{β})=\prod _{i=1}^n\prod _{j=1}^{m}E(D_{ij}|G_{c_{j}i},\alpha ,\text{β}).$$ (3)

In Equation 3, $E(D_{ij}|G_{c_{j}i},\alpha ,\text{β})$ is given by the error model distribution of observing genotype D_ij for site i in cell j, given the true clonal genotype $G_{c_{j}i}$ and is parameterized by α and β. This error model is based on the error model of SiFit (Zafar et al. 2017). The likelihood of the doublet-aware model is described in Supplemental Methods.

Prior distributions

The SiCloneFit model incorporates a compound prior given by

$$\begin{array}{rl}P(\mathcal{V}|\mathcal{H})& =P(\mathbf{c},\mathbf{G},\mathcal{T},{\mathcal{M}}_{\lambda },\alpha ,\text{β},{\alpha }_0|\mathcal{H})\\ & =F(\mathbf{G}|\mathcal{T},{\mathcal{M}}_{\lambda })P(\mathbf{c}|{\alpha }_0)P(\mathcal{T})P(\alpha ,\text{β},\mathcal{M}\lambda ,{\alpha }_0|\mathcal{H})\end{array}$$ (4)

where

$$P(\alpha ,\text{β},{\mathcal{M}}_{\lambda },{\alpha }_0|\mathcal{H})=P(\alpha |a_{\alpha },b_{\alpha })P(\text{β}|a_{\text{β}},b_{\text{β}})P({\mathcal{M}}_{\lambda }|a_M,b_M)P({\alpha }_0|a,b).$$

$F(\mathbf{G}|\mathcal{T},{\mathcal{M}}_{\lambda })$ denotes the prior distribution on the clonal genotype matrix given a clonal phylogeny $\mathcal{T}$ and parameters of the model of evolution ${\mathcal{M}}_{\lambda }$, and it can be efficiently calculated using Felsenstein's pruning algorithm (Felsenstein 1981), assuming sites are independent and identically distributed. P(c|α₀) denotes the prior probability of partitioning m single cells into K (K is the number of clusters defined by c) clusters under a CRP with concentration parameter α₀. $P(\mathcal{T})$ denotes the prior probability on the clonal phylogeny. This is a product of the prior on topology and the prior on branch length. We consider uniform distribution for the prior on topology and exponential distribution for the prior on branch lengths. As the values of the error rate parameters α, β and the parameters of the model of evolution ${\mathcal{M}}_{\lambda }$ lie between 0 and 1, we use Beta distribution as their prior. For the concentration parameter α₀, we assume a Gamma prior as suggested in Escobar and West (1995). We set the value of hyperparameters for the Gamma distribution to a = 1 and b = 1 for all the analyses performed, but these are user-specified parameters in the software. All the prior distributions are described in detail in Supplemental Methods. The doublet-aware model of SiCloneFit contains additional parameters for indicating whether a cell is a singlet or a doublet; doublet rate and assigning a cell to two clonal clusters and the associated prior distributions are described in Supplemental Methods.

Inference

We designed a Markov chain Monte Carlo sampling procedure based on the Gibbs sampling algorithm to estimate the latent variables according to Equation 2. Our algorithm is inspired by a partial Metropolis-Hastings, partial Gibbs sampling algorithm described in Neal (2000). In each iteration, the sampler first samples new cluster indicators, c*, for all the cells using partial Metropolis-Hastings, partial Gibbs updates. During this, the dimensionality of the sample may change due to addition of a new cluster (resulting in addition of new edges in the clonal phylogeny) or removal of an existing singleton cluster (resulting in removal of existing edges from the clonal phylogeny). In case the dimensionality changes, the absolute value of the determinant of the Jacobian matrix is also taken into account, which results in partial reversible-jump MCMC (Green 1995) updates. When such dimension changing moves are accepted, the corresponding new clonal phylogeny ${\mathcal{T}}^{\ast }$ and new clonal genotype matrix G* are also accepted. The sampler next samples a new clonal phylogeny and new parameters of the model of evolution with the help of a Metropolis-Hastings MCMC sampler. After that, new clonal genotype for each clonal cluster is sampled from the conditional posterior distribution. To sample new values of the error rate parameters from their corresponding conditional posterior distributions, our sampler employs rejection sampling. Finally, the concentration parameter α₀ is sampled based on the method described in Escobar and West (1995). The sampling algorithms for both the singlet and doublet models of SiCloneFit are described in detail in Supplemental Methods.

Software availability

SiCloneFit has been implemented in Java and is freely available at https://bitbucket.org/hamimzafar/siclonefit, released under the MIT license. The binary file of SiCloneFit is also included in Supplemental Code.