Estimation of Plant and Canopy Architectural Traits Using the Digital Plant Phenotyping Platform^,

The Digital Plant Phenotyping Platform can be used to design and interpret phenotyping measurements for structural or functional trait extraction.

Abstract

The extraction of desirable heritable traits for crop improvement from high-throughput phenotyping (HTP) observations remains challenging. We developed a modeling workflow named “Digital Plant Phenotyping Platform” (D3P), to access crop architectural traits from HTP observations. D3P couples the Architectural model of DEvelopment based on L-systems (ADEL) wheat (Triticum aestivum) model (ADEL-Wheat), which describes the time course of the three-dimensional architecture of wheat crops, with simulators of images acquired with HTP sensors. We demonstrated that a sequential assimilation of the green fraction derived from Red–Green–Blue images of the crop into D3P provides accurate estimates of five key parameters (phyllochron, lamina length of the first leaf, rate of elongation of leaf lamina, number of green leaves at the start of leaf senescence, and minimum number of green leaves) of the ADEL-Wheat model that drive the time course of green area index and the number of axes with more than three leaves at the end of the tillering period. However, leaf and tiller orientation and inclination characteristics were poorly estimated. D3P was also used to optimize the observational configuration. The results, obtained from in silico experiments conducted on wheat crops at several vegetative stages, showed that the accessible traits could be estimated accurately with observations made at 0° and 60° zenith view inclination with a temporal frequency of 100 °Cd (degree day). This illustrates the potential of the proposed holistic approach that integrates all the available information into a consistent system for interpretation. The potential benefits and limitations of the approach are further discussed.

Crop genetic improvement consists in selecting or creating the best performing genotypes under a set of environmental and management conditions (Bustos-Korts, 2017). Performances are mainly based on the quantity and quality of the harvested organs. Yield results from complex interactions between the genotype and the environment that makes direct selection based on yield very inefficient. It is preferred to identify an ensemble of structural and functional traits that are less dependent on the environment, explain part of the yield, and are strongly related to the genome (Hammer et al., 2006; Tardieu and Tuberosa, 2010; Rutkoski et al., 2016; Bustos-Korts, 2017). High-throughput phenotyping (HTP) is expected to provide such structural traits over a large collection of genotypes under contrasting climate and management scenarios. Further, the noninvasive nature of HTP techniques allows repeat observations over time to possibly access functional traits.

HTP (Paproki et al., 2012) accesses structural traits including lamina shape in wheat (Triticum aestivum; Dornbusch and Andrieu, 2010), plant height (Hartmann et al., 2011; Madec et al., 2017), leaf angle (Cabrera-Bosquet et al., 2016), plant density (Liu et al., 2017c), ear density (Madec et al., 2019), or leaf area index (Liu et al., 2017a). Three-dimensional (3D) reconstruction of the canopy may provide more details to access canopy structural traits and the functioning of the canopy (Gibbs et al., 2017). This technique has been applied on individual plants under well-controlled illumination conditions by Duan et al. (2016), who used multiview images to reconstruct 3D wheat structure at early stages and extract morphological traits. Its transposition to field conditions, where observations are generally only possible from the top, is still challenging as they provide an incomplete description of the 3D plant structure because of the occlusions inherent to vision techniques (Gibbs et al., 2017). A detailed and explicit description of the characteristics of each organ to better understand the crop functioning is still a pending question. Nevertheless, monitoring the plants from the top would allow us to progressively build a description of the whole plant and infer the whole plant or stand characteristics. A dynamic plant architecture model will be very useful to keep a high degree of consistency between multidate observations, while providing sound assumptions on the fate of the organs at the bottom of the canopy that are partly occluded.

Functional structural plant models (FSPMs) describe the detailed evolution of plant architecture with relatively simple environmental inputs, mainly air temperature and sowing patterns and a set of parameters describing organ size, extension rate, and topology (Vos et al., 2010). They can be coupled to radiative transfer models (RTMs) such as Raytran (Govaerts and Verstraete, 1998) or LuxCoreRender (https://luxcorerender.org/) to simulate the corresponding 2D images acquired under a given observational geometry and waveband. The 3D nature of the FSPMs allows also simulating accurately the light detection and ranging (LiDAR) signal. The FSPMs are thus able to link 2D (camera) or 3D (LiDAR) measurements by HTP techniques with plant level architectural traits corresponding to FSPM parameters. These parameters are expected to be more strongly associated to genomic regions than direct HTP measurements. This approach applied to single date observations corresponds to an advanced RTM inversion (Baret and Buis, 2008). It has been applied by Liu et al. (2017a) to estimate the Green Area Index (GAI) over wheat crops from the combination of Red–Green–Blue (RGB) cameras and LiDAR observations. However, it did not exploit the temporal dimension that is described within FSPMs. Alternatively, comprehensive exploitation of multidate and/or multisensor observations to access FSPM parameters corresponds to a data assimilation approach that has been successfully applied to satellite observations (Moulin et al., 1998; Weiss et al., 2001; Bacour et al., 2015; Zhang et al., 2016). Data assimilation allows us to integrate consistently into a single modeling workflow all information available including the phenotyping observations, environmental variables, and the knowledge on the physical and biological processes integrated into FSPM and RTM. This approach benefits from the use of accumulated observations from several sensors and dates, which adds constraints in the parameter estimation process to get the set of optimal values (Combal et al., 2003; Baret and Buis, 2008). Consequently, more parameters of the FSPM can be estimated with increased accuracy. The resulting estimated parameters can then be used to derive emerging properties of the plant or the canopy such as the radiation interception efficiency.

The objective of this article is to describe the potentials of such an assimilation approach for retrieving detailed plant and canopy characteristics from multidate observations of the Green Fraction (GF) that can be measured from RGB or multispectral imageries. The study focuses on wheat crops monitored from emergence to the end of the tillering period and is based on in silico experiments to demonstrate the feasibility of the proposed approach, avoiding possible limitations due to the realism of the models used, particularly the FSPM. It is based on the digital plant phenotyping platform (D3P) that was specifically developed to simulate phenotyping measurements by coupling the Architectural model of DEvelopment based on L-systems (ADEL) wheat model (ADEL-Wheat; Fournier et al., 2003) to the RTM, Persistence of Vision Raytracer (POV-Ray 3.7; https://www.povray.org/download/). The D3P is first presented and then exploited to assimilate GF observations made at several dates and under several view directions to estimate 10 parameters of ADEL-Wheat. Finally, the approach is repeated for several temporal and directional samplings to select the optimal measurement configuration.

RESULTS

Assimilation of GF into the D3P

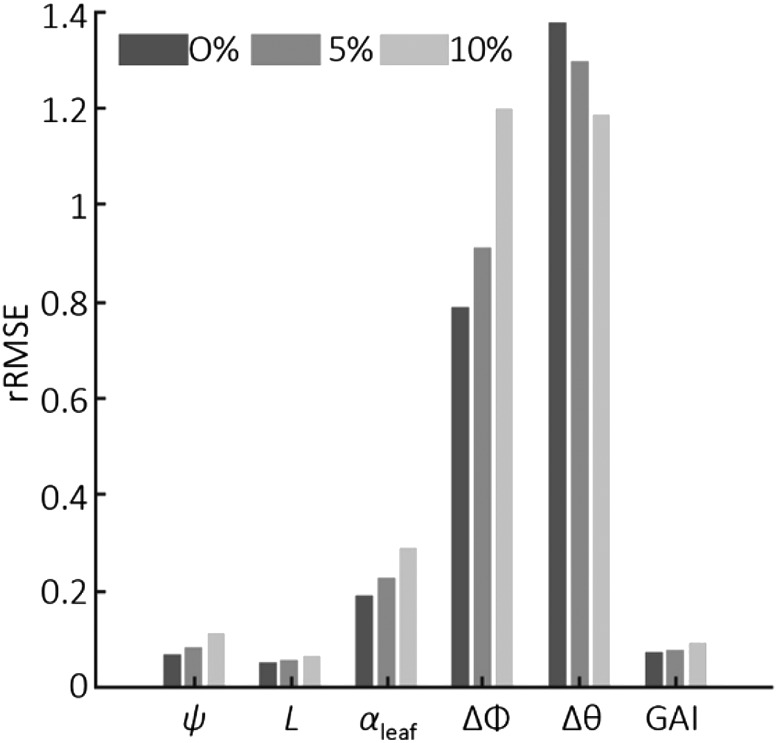
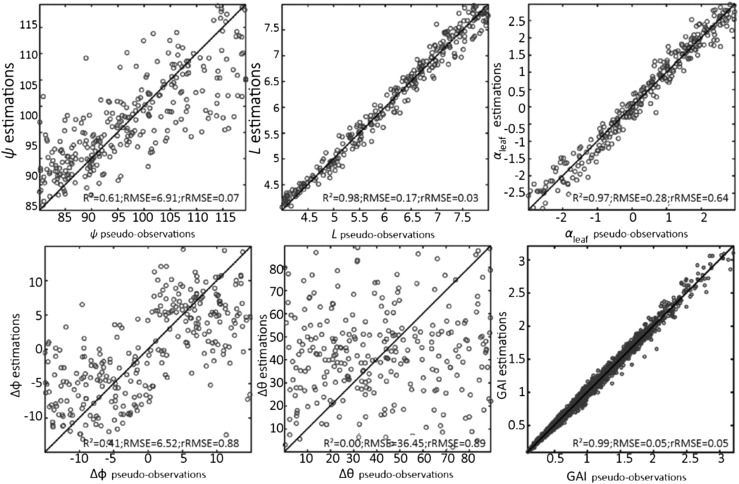
In silico experiments were conducted using five view directions and five dates before tillering to estimate the five parameters of ADEL-Wheat (ψ, L, α_leaf, Δφ, and Δθ; Table 1) and GAI. We obtained very good estimates of ψ and L, even considering a noise of 10% on GF (Figs. 1 and 2). The parameter α_leaf was retrieved with acceptable performances (Fig. 2). However, leaf orientation and inclination described by Δφ and Δθ appeared difficult to retrieve from the dynamics of the directional GF before tillering (Figs. 1 and 2). The parameter Δφ determines the clumping of neighboring leaves with potentially substantial impact on the canopy light interception (Maddonni et al., 2001). The first three leaves are very small with few interactions between leaves of the same plant and almost no interactions between neighboring plants. This may explain why the azimuthal orientation pattern of leaves is not accessible from observations at the canopy scale during this early development phase.

Table 1. Influential parameters of the simplified ADEL-Wheat model estimated in the D3P.

The range of variation as observed in field experiments is indicated from Abichou (2016).

Growth Period	Name	Descriptions	Value		Unit
			Minimum	Maximum
Before tillering	ψ	Phyllochron	80	120	°Cd
	L	Laminae length of leaf 1, rank from the bottom	4	8	Centimeters
	αleaf	Increase rate of lamina length	−3	3	Centimeters of phytomer−1
	Δφ	sd of the leaf azimuth compared to the previous one with mean 180°	0	90	Degree
	Δθ	Shift of leaf basal inclination	−15	15	Degree
During tillering	Nsen	Number of green leaves at the start of leaf senescence on the mainstem	3.5	6.5	Leaves
	Nmin	Minimum number of green leaves on the mainstem	1.5	3.5	Leaves
	Ntil	Final number of tillers per plant	0	5	Tillers
	θtil	Inclination of the base of tillers relative to mainstem inclination	10	85	Degree
	αtil	Change of tiller inclination angle with the number of emerged leaves	10	50	Degree of Haun stage−1

Figure 1.

rRMSE for five parameters of ADEL-Wheat and GAI estimated with the D3P using the GF observations under five view directions for five dates before tillering. Three levels of noise were considered (0%, 5%, and 10%) for the evaluation dataset. The five parameters are: ψ; L, rank from the bottom; α_leaf; Δφ; and Δθ.

Figure 2.

Comparison of the estimated and pseudo-observation values of the five parameters of ADEL-Wheat and the GAI computed for the five dates of GF measurements with the reference values for the first growth period (between crop emergence and ligulation of leaf 3). Synthetic GF data were obtained from five view directions with 5% noise. The five parameters are: ψ; L, rank from the bottom; α_leaf; Δφ; and Δθ.

The good retrieval performances of parameters driving the development of leaf area (ψ, L, and α_leaf) explains the good estimation of GAI (Fig. 1). The retrieval performance of GAI is little affected by the noise associated with GF observations.

The sequential assimilation scheme proposed exploits observations before and during the tillering period to estimate five new parameters (N_sen, N_min, N_til, θ_til, and α_til; Table 1) while refining the five parameters estimated before tillering (ψ, L, α_leaf, Δφ, and Δθ; Table 1). Results show that adding the five observation dates during the second subperiod improves substantially the estimation of the first set of parameters (Fig. 3). The improvement was very large for ψ and α_leaf. For the parameters describing canopy architecture (Δφ and Δθ), the relative root mean squared error (rRMSE) was also drastically improved, particularly for the larger noise levels, but it was still higher than 0.5. The improvement was marginal for L, which was already well estimated using the first five dates before tillering. The impact of noise affecting GF observations on rRMSE for the first set of parameters was much reduced (Fig. 3). This was probably due to the multiplicity of the observations (10 dates, five directions) that smoothed out the random noise associated with GF.

Figure 3.

rRMSE for 10 parameters of ADEL-Wheat, GAI, and the number of tillers with d_3l estimated with the D3P using the GF observations under five view directions for 10 dates between crop emergence and the beginning of stem elongation. Three levels of noise were considered (0%, 5%, and 10%) for the evaluation dataset. The 10 parameters include: ψ; L, rank from the bottom; α_leaf; Δφ; Δθ, shift of leaf basal inclination N_sen; N_min; N_til; θ_til; α_til.

Among the second set of parameters, N_sen that drives leaf senescence dynamics was relatively well estimated with rRMSE < 0.1 (Fig. 3). Conversely, N_min was more difficult to retrieve accurately with rRMSE ≈ 0.2 (Fig. 3). This can be explained by the fact that the influence of N_min on the dynamics of leaf senescence does not show up until the end of the tillering period, when the size of tillers is relatively small and partly hidden by the first leaves. The parameters driving the orientation of tillers (θ_tiller, α_tiller) were not retrieved accurately (Fig. 3). These parameters apply on tillers that are relatively small and partly hidden by the older leaves of the main stem. GAI was very well estimated, in agreement with the observations before tillering. In addition, d_3l (the number of axes with more than three leaves) was very well estimated.

Optimization of Measurement Configuration

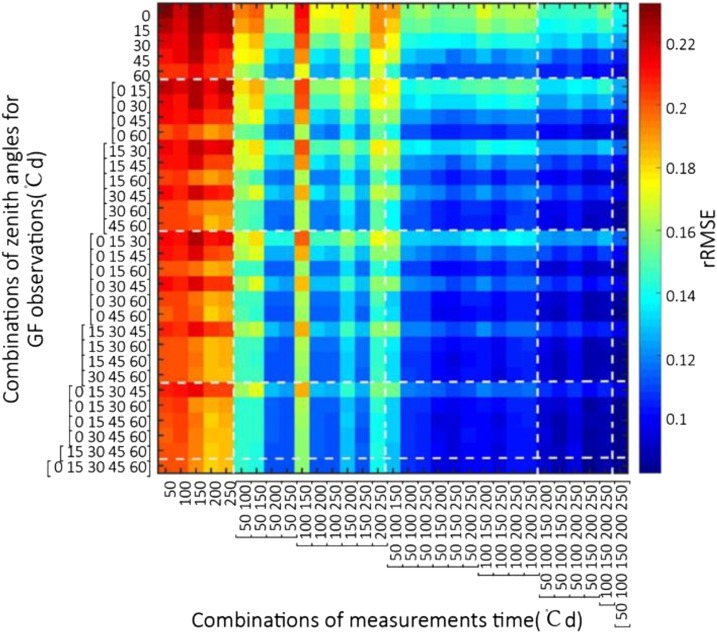
The optimal measurement configuration is defined by the combination of dates and directions that provides the best retrieval performances for the three parameters (ψ, L, and α_leaf) accessible before tillering in addition to GAI. Results showed that the average rRMSE on parameters (ψ, L, and α_leaf) varies between 0.23 for GF observations from a single direction on a single date, down to 0.09 for the most comprehensive set of observations including the five dates and the five directions (Fig. 4). Best performances were obtained when at least three observation dates were used and when they were sufficiently distinct in time with the optimal case being dates [50, 150, 250] °Cd (degree day) after crop emergence (Fig. 4). The multiplication of observation directions improved marginally the estimation of the parameters. For these early stages, Baret et al. (2010) already demonstrated that GF observed under 57° zenith angle provides an accurate estimate of GAI. Our results agree well with these findings, the best configurations always including a GF measurement at 60° zenith angle. The improvement when adding more directions might be mainly due to the reduction of the noise associated to the GF pseudo-measurements. Optimal performances were obtained when using two directions (0° and 60°) and three dates evenly distributed during the tillering period (Fig. 4). Adding more dates or directions improved only marginally the retrieval performances.

Figure 4.

Average rRMSE for the three estimated ADEL-Wheat parameters (ψ, L, and α_leaf) and GAI obtained from the 961 combinations of one to five directions and one to five dates before tillering.

DISCUSSION

Assimilation of GF Observations Provides Accurate Estimates of a Few Pertinent Wheat Architectural Traits

The GF is one of the most common canopy properties that can be derived from several HTP sensors including RGB high-resolution cameras (Guo et al., 2013), multispectral cameras based on vegetation indices (Comar et al., 2012), and RTM inversion (Li et al., 2015), as well as LiDAR systems (Liu et al., 2017a). These devices can be installed aboard a range of possible vectors including fixed sensors at the ground level (Guo et al., 2013), semiautomatic light carts (White and Conley, 2013) or tractor-based systems (Comar et al., 2012), fully automatic rover robots (Madec et al., 2017) running on the ground with active measurements, and unmanned aerial vehicles (Schirrmann et al., 2016). Our results clearly demonstrated that the assimilation of GF observations provide accurate estimates of the few ADEL-Wheat parameters that drive the dynamics of GAI: the phyllochron, ψ; the lamina length of the first leaf, L; the rate of elongation of leaf lamina, α_leaf; the number of green leaves at the start of leaf senescence, N_sen; and the minimum number of green leaves, N_min. The phyllochron that varies among cultivars (Hay and Kirby, 1991; He et al., 2012) is of high interest. The phyllochron describing leaf appearance rate responds nonlinearly to multienvironmental factors. When it is modeled using only temperature, residual environmental effects are often observed (Cao and Moss, 1989; Baumont et al., 2019). This can be partly removed using the photothermal time corresponding to temperatures accumulated during the light time period only (Masle et al., 1989). Environmental factors may have also substantial effects on the final length of leaves, L. Therefore, the influence of the environmental conditions on ψ and L should be explicitly modeled into ADEL-Wheat to characterize the early plant vigor that is a very pertinent trait to be selected (Blum, 1997; Monneveux et al., 2012). Parameter α_leaf that drives the lamina length of successive leaves may be also a good proxy of the early plant vigor. Parameters N_sen and N_min are traits of potential interest for drought tolerance (Araus et al., 1997; Hafsi et al., 2007). Conversely, parameters related to leaf or tiller orientation were poorly retrieved either because they vary within relatively narrow ranges or because they apply to organs with limited area or hidden by other organs. Nevertheless, the good estimates of ψ, L, α_leaf, N_sen, and N_min parameters that drive the dynamics of GAI allows simulating accurately GAI continuously with an rRMSE < 0.05. Baret et al. (2010) demonstrated that GAI could be estimated with an rRMSE = 0.12 using single GF measurements from 57.5° zenith angle when leaves are assumed randomly distributed in the canopy. The improved performances shown here comes from the additional information used in the assimilation scheme, with more directions and more dates of observations. Further, our assimilation method ensures us to get a consistent time course of GAI before tillering using the temporal constraints provided by the dynamic ADEL-Wheat model. In addition to GAI, d_3l was accurately computed from the estimated parameters (ψ, L, α_leaf, N_sen, and N_min). This trait is commonly used as a proxy of ear density and thereby of potential yield as tillers having three leaves at the start of stem elongation continue to grow and generally complete their development and produce an ear (Nerson, 1980; Whaley et al., 2000). Conversely, the other tillers generally regress due to the competition between neighboring tillers and plants (Masle, 1985).

Assimilation Exploits Consistently All the Available Information into a Single Workflow

The assimilation approach that integrates multidate remote sensing observations into process models was originally developed for satellite observations (Moulin et al., 1998; Weiss et al., 2001; Bacour et al., 2015; Zhang et al., 2016). It was applied here to HTP measurements. Data assimilation offers several advantages as compared to the more classical crop characteristics retrieval approaches. First, it integrates into a single and consistent workflow all the available information including phenotyping observations, environmental variables, and knowledge on the physical and biological processes embedded in the FSPM and RTM. Second, it capitalizes on the accumulation of observations from several sensors and dates and thereby facilitates the parameter estimation process (Combal et al., 2003; Baret and Buis, 2008). Third, data assimilation within such a modeling workflow permits us to access plant and canopy level architectural properties that cannot be directly measured in the field at high throughput. Finally, the combination of ADEL-Wheat with simulators of several phenotyping measurements allows assimilating concurrently observations coming from different sensors. This will allow adding more information in the interpretation system to provide more accurate parameter estimates or new traits.

Optimizing of the Measurement Configuration

The proposed approach allows defining the optimal measurement configuration that provides a trade-off between the accuracy of trait estimation and the cost/time associated to the multiplication of measurements and devices. This was demonstrated here by selecting the more parsimonious combination of dates and directions of observations. Results show that observations made at 0° and 60° and repeated every 100 °Cd provide the best estimates of the accessible traits. The optimization process allows playing on additional elements of the measurement configuration including the uncertainties associated to the measurements, the spatial resolution, or the interest of additional devices.

Potential Benefits and Limitations of the Assimilation Technique

The sequential assimilation scheme proposed here splits the retrieval problem into subproblems. It gradually adds parameters to be estimated as soon as they are required, limiting the complexity of the problem (Baret and Buis, 2008). Further, the values of the parameters needed for the first stages can be refined when exploiting later observations because they affect the fate of the canopy for the later growth stages. For the sake of simplicity, we focused on early growth stages that are recognized to be critical for the implantation of the crop and the competition with weeds. The traits estimated are therefore considered crucial to identify cultivars with higher early vigor and competitiveness with weeds or other crops/genotypes (Araus et al., 1997; Hafsi et al., 2007). However, the approach could be also applied to later stages to capture additional traits. This will be achieved at the expense of increased complexity because of the growing number of parameters to be considered. Additionally, our simulations are based on fixed thermal time and directions under which the GF are observed. However, the dynamics of GF is smooth because it results from incremental growth and senescence processes. Therefore, it would be possible to interpolate the GF values between the fixed dates simulated in this exercise to match the actual dates. Similar smooth variations of GF are expected as a function of the directions of GF observations. Therefore, it would also be possible to interpolate between the fixed directions to match the actual ones under which GF is observed.

The results presented here were based on in silico experiments where pseudo-observations were used instead of actual measurements. This probably boosts artificially the retrieval performances because the consistency of the ADEL-Wheat model with the actual canopy structure development was not challenged. The assimilation approach should therefore be further evaluated using actual observations to ensure that the possible systematic error on the description of the dynamics of canopy structure by the ADEL-Wheat model is limited. Nonetheless, the noise added on the GF observations demonstrates that the approach is relatively robust to random error thanks to the multiplicity of the observations.

The performances of the proposed approach when applied to actual observations rely on the realism of the FSPM, ADEL-Wheat in our case. In a previous work, we pointed out the limits of ADEL-Wheat to get realistic GF values acquired close to nadir directions because of the possible interactions between leaves at early growth stages that were not always accurately described (Liu et al., 2017b). However, it is possible to use only inclined observations for these early stages, which would limit the impact of model approximations on the estimation of the model parameters. Besides, ADEL-Wheat assumes that tillering ceases when the first internode starts to elongate (Kirby et al., 1985). However, the end of tillering can be strongly affected by external factors including light quality within the canopy (Evers et al., 2006) and photoperiod (Miralles and Richards, 2000). Although simplifications and assumptions on the description of some processes are always necessary, phenotyping observations will contribute to provide the required information for improving the realism of FSPMs.

As in many FSPMs, ADEL-Wheat incorporates very little functioning in terms of ecophysiological processes, which limits the type of traits that can be extracted by assimilating phenotyping observations into D3P. The next step should be to retrieve crop growth model parameters describing canopy response to environmental factors, i.e. truly functional traits, from the assimilation of the structural parameters retrieved from the proposed combination of HTP observations and D3P. Some wheat crop growth models such as “SiriusQuality” (Martre and Dambreville, 2018) describes the leaf area dynamics from the growth of individual leaves and tillers using an approach similar to that of ADEL-Wheat. To feed a crop model such as SiriusQuality with the FSPM parameters, they should be reparameterized so that the retrieved parameters have the same meaning in both models. Parameters determining the short-term responses of physiological processes to environmental factors are now also accessible in HTP platforms (Prado et al., 2018), which can limit the number of parameters that need to be retrieved by data assimilation.

MATERIALS AND METHODS

Description of the D3P

The D3P includes two components: a 3D canopy structure model and simulators of the phenotyping observations from LiDARs and multispectral or RGB cameras (Fig. 5). Three-dimensional canopy structures were simulated using the FSPM modeling platform “OpenAlea” (http://openalea.gforge.inria.fr/dokuwiki/doku.php; Pradal et al., 2008). OpenAlea is used in D3P to create 3D meshes of virtual canopies. LiDAR data are simulated using the 3D crop modeling library “Plantgl” (Pradal et al., 2009). Multispectral and RGB images are simulated with multispectral/RGB simulator using the software “POV-Ray 3.7” (https://www.povray.org/download/), which renders complex 3D scenes for a range of camera specifications. Optical properties of plant organs are simulated with the “PROSPECT” model (Jacquemoud and Baret, 1990) using the Python library “PyProSAIL” (https://pyprosail.readthedocs.io/en/latest/). By defining the sensor properties and the observational configuration (Supplemental Table S1), we can mimic with a very high realism any phenotyping measurement (Supplemental Video S1).

Figure 5.

Schema of the D3P that simulates phenotyping observations from environmental variables, crop management, and meteorological information.

The accuracy of the LiDAR simulator has been previously evaluated through comparison with LiDAR measurements (Liu et al., 2017a). The performance of POV-Ray–based radiative transfer simulation was evaluated through RTM intercomparison using an on-line model checker, ROMC (Widlowski et al., 2008). The evaluation of “POV-Ray” (Supplemental Fig. S1) shows satisfactory results.

D3P is programmed in the software Python (http://www.python.org). All D3P dependencies are open-source and their code is accessible from the code repositories and websites given in Supplemental Table S2. The code and user manual of D3P is freely available on GitHub (https://github.com/lsymuyu/Digital-Plant-Phenotyping-Platform). D3P is distributed under the free software open-source MIT license.

Simplification of ADEL-Wheat FSPM

Virtual wheat (Triticum aestivum) canopies were simulated with the wheat FSPM ADEL-Wheat implemented in the modeling platform “OpenAlea” (Fournier and Andrieu, 1999; Abichou et al., 2013; Liu et al., 2017b). Plant development is primarily driven by temperature and the thermal time between the appearance of two successive leaf tips, i.e. the phyllochron. The phyllochron is considered constant from seedling to flag leaf expansion (Hokmalipour, 2011). The current version of ADEL-Wheat needs more than 50 parameters to describe explicitly the dimension, orientation, and inclination of each organ (for a detailed presentation of ADEL-Wheat, see http://openalea.gforge.inria.fr/doc/alinea/adel/doc/_build/html/user/manual.html). Therefore, a reduced number of parameters was required to estimate them from HTP observations. We reparameterized the leaf dimension representation in ADEL-Wheat using a large dataset covering 28 winter wheat experiments conducted over several years in Grignon, France, with a range of sowing dates, cultivars, and nitrogen levels (Abichou, 2016). The modifications proposed are detailed in the Supplemental Methods and Supplemental Figure S3. A total of 10 influential parameters controlling the canopy development from emergence to the beginning of stem elongation was finally necessary to drive the simplified version of ADEL-Wheat model.

Before tillering starts, i.e. before ligulation of the third leaf on the main stem (Masle, 1985), five parameters drive the plant structure dynamics (Table 1). The phyllochron, ψ, controls the time of leaf appearance and the rate of leaf extension. The lamina length of the first three leaves is assumed to change linearly with leaf rank. It is parameterized by the lamina length of the first leaf L and the slope, α_leaf, of the relationship between lamina length and leaf rank. Leaf orientation is initialized from the seedling stage depending on seed orientation. Seeds are assumed to be sown with a random azimuth (Ledent and Moss, 1977). Evers et al. (2005) found that the azimuth of successive leaves is mainly opposite for the first three leaves. The azimuth angle of a leaf relative to the previous one was drawn from a Gaussian distribution with mean angle of 180° and sd Δφ accounting for the plasticity of the cultivar. The leaf inclination was described based on experimental observations (Abichou, 2016). Variations of leaf inclination is controlled by the basal inclination, Δθ.

During the tillering phase, i.e. between ligulation of the third leaf on the mainstem and the beginning of stem elongation (Abichou et al., 2018), five additional parameters drive tiller development and leaf senescence (Table 1). Leaf senescence is described by the number of green leaves on the mainstem when senescence starts, N_sen, and the minimum number of green leaves on the mainstem, N_min (Abichou et al., 2013); the final number of tillers is N_til, leaf inclination is θ_til, and change of tiller inclination angle with the number of visible leaves is α_til.

Simulation of Synthetic Datasets

We simulated RGB images of wheat canopies using D3P with our simplified version of ADEL-Wheat. We rendered 2 × 2 m scenes containing 11 rows with an inter-row spacing of 17.5 cm and a sowing density of 250 seeds∙m⁻². Note that plant density was not considered as an unknown parameter because high-resolution RGB imagery techniques have been developed to accurately measure it and document the associated sowing pattern (Jin et al., 2017; Liu et al., 2017b). A total of 2,500 combinations of the five influential parameters of ADEL-Wheat before tillering (Table 1) were randomly drawn using a “Latin Hypercube” sampling scheme. The parameters were assumed to follow a uniform distribution within their range of variation (Abichou, 2016; Table 1). During tillering, a similar sampling strategy was used for the five influential parameters during that period (Table 1). The canopies were simulated every 50 °Cd before tillering (between 50 and 250 °Cd after crop emergence) and every 100 °Cd during tillering (between 300 and 700 °Cd after crop emergence).

GF in a given direction is defined as the fraction of green elements viewed in this particular direction. It is computed from the classification of RGB images. The RGB camera with a ±10° field of view was placed at 1.5 m above the canopy, providing a footprint of 50 × 50 cm. The images had a resolution of 500 × 500 pixels with a 1-mm spatial resolution, which appears to be a good compromise between computation time and performances. Marginal classification errors were expected in the calculation of GF from our simulations. Noise was thus added to the simulated GF values to mimic the actual GF measurements where possible classification errors may be observed due to confusions between green vegetation and nongreen elements or the soil surface, depending on illumination conditions and camera spatial resolution. We assumed that the noise followed a Gaussian distribution with a mean of zero and sd of 0.05 and 0.10, which are typical values (Baret et al., 2010; Liu et al., 2017b). We then rendered the 3D scenes using the software “POV-Ray” every 15° between 0° and 60°. View azimuth was perpendicular to the row to maximize the sensitivity to canopy structure (López-Lozano et al., 2007, 2009).

GF was computed for the 10 dates and the five view directions for each of the 2,500 combinations of ADEL-Wheat parameters (Table 1). The 125,000 simulated RGB images and corresponding GF values will be called “pseudo-observations” in the following (illustrated in Supplemental Fig. S2). Each of the 2,500 input parameter combination were also associated to two additional traits: the GAI at each of the 10 dates and the number of axes with d_3l at the end of the tillering period. Training and validation processes were conducted with 85% and 15% of the synthetic dataset, respectively.

GF Assimilation

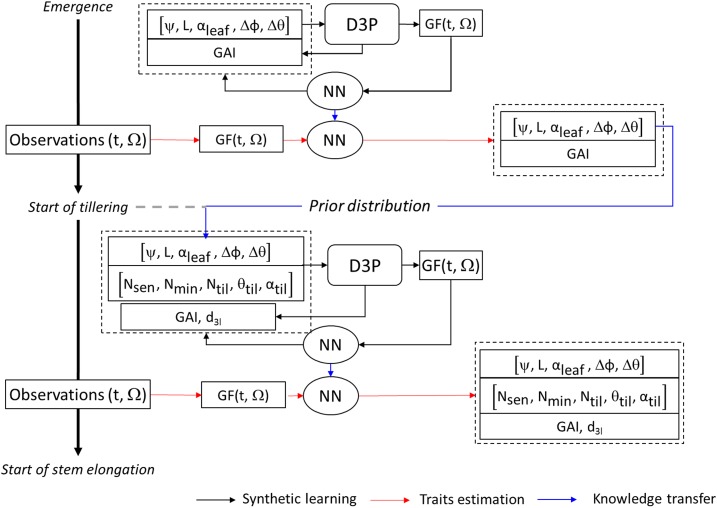
The assimilation process was conducted sequentially for the two growth periods as illustrated in Figure 6. The five parameters involved before tillering (ψ, L, α_leaf, Δφ, and Δθ) were first estimated. Then the five additional parameters required for the tillering period (N_sen, N_min, N_til, θ_til, and α_til) were estimated while the first five parameters were fine-tuned because they also influence the architecture of canopies during tillering. In the second assimilation step, GF data from crop emergence to beginning of stem elongation were also assimilated.

Figure 6.

Diagram showing the sequential scheme of GF assimilation. The assimilation was done in two consecutive steps: between crop emergence and the start of tillering (before tillering); and between crop emergence and the beginning of stem elongation (i.e. before stem elongation). In each step, an NN was first trained using the training GF dataset, GF(t,Ω). The trained NN was then used to estimate ADEL-Wheat parameters and GAI using the GF validation dataset, GF(t,Ω). The distribution of ADEL-Wheat parameters estimated in the first step (before tillering) were used as prior information when training the NN in the second step (before stem elongation). Finally, the tiller number with d_3l was computed from the estimated set of parameters.

For each of the two periods, the assimilation process consisted in adjusting the ADEL-Wheat parameters (Table 1) to get a good agreement between the simulated GF and the GF pseudo-observations for the 10 dates and five directions considered. Parameter adjustment was completed using a neural network (NN) machine learning approach, which is well adapted to our case where the simulations are time-consuming, preventing us from using iterative optimization approaches (Kimes et al., 2000; Baret and Buis, 2008). We used a one-layer feed-forward network with tangent sigmoid transfer functions in the first layer and a linear transfer function in the output layer. The number of neurons in the hidden layer is based on the geometric pyramid rule proposed by Masters (1993). The optimal number of neurons in the hidden layer should be close to , with n and m being the number of inputs and outputs, respectively. Then the synaptic weights and biases are tuned using the Levenberg–Marquardt optimization algorithm (Marquardt, 1963) to best match the output values over the training database. The accuracy of the estimated parameters was assessed with the rRMSE.

Defining the Optimal Observational Configuration

The optimal measurement configuration for the retrieval of plant and canopy architectural traits was investigated using D3P. We analyzed, among the 961 possible combinations of five dates and five directions, the ones providing the best retrieval performances for the ADEL-Wheat parameters and GAI. Pseudo measurements of GF were assimilated into D3P using the trained NN for each of the 961 configurations considered the same way as described above, the section “GF Assimilation,” for the five dates and five directions. A 5% Gaussian noise was applied on GF values simulated by D3P. Retrieval performances were quantified as the average rRMSE computed on the targeted traits and GAI for validation dataset (375 among the 2,500 combinations of the parameters presented in Table 1). For GAI, the rRMSE was computed for the five dates before tillering.

Supplemental Data

The following supplemental materials are available.

• Supplemental Methods. Description of the simplified ADEL-Wheat model.

• Supplemental Figure S1. Comparison between the reflectance simulations (named “Canray”) and the corresponding reference values.

• Supplemental Figure S2. RGB and the corresponding binary imagery of virtual wheat canopies simulated with the D3P.

• Supplemental Figure S3. Reparameterization of leaf dimension representation in ADEL-Wheat model.

• Supplemental Video S1. D3P mimicking unmanned aerial vehicle flight over wheat canopies.

• Supplemental Table S1. Input parameters of LiDAR and multispectral/RGB simulators for the D3P.

• Supplemental Table S2. Name and code repository of the D3P software and library dependencies.