Efficient multi-objective molecular optimization in a continuous latent space

We utilize Particle Swarm Optimization to optimize molecules in a machine-learned continuous chemical representation with respect to multiple objectives such as biological activity, structural constrains or ADMET properties.

Abstract

One of the main challenges in small molecule drug discovery is finding novel chemical compounds with desirable properties. In this work, we propose a novel method that combines in silico prediction of molecular properties such as biological activity or pharmacokinetics with an in silico optimization algorithm, namely Particle Swarm Optimization. Our method takes a starting compound as input and proposes new molecules with more desirable (predicted) properties. It navigates a machine-learned continuous representation of a drug-like chemical space guided by a defined objective function. The objective function combines multiple in silico prediction models, defined desirability ranges and substructure constraints. We demonstrate that our proposed method is able to consistently find more desirable molecules for the studied tasks in relatively short time. We hope that our method can support medicinal chemists in accelerating and improving the lead optimization process.

1. Introduction

A key challenge in small molecule drug discovery is to find novel chemical compounds with desirable properties. Computational methods have long been used to guide and accelerate the search through the huge chemical space of druglike molecules. In virtual screening, for instance, computational models can be utilized to rank virtual libraries of chemical structures regarding selected properties such as the predicted activity towards a target of interest.2,3 However, given the estimated vast amount of druglike molecules (10²³–10⁶⁰),4 a complete search through this space is computationally infeasible.

An alternative approach is to computationally generate new molecules (de novo design) with optimized properties without the need for enumerating large virtual libraries. Heuristic methods such as genetic algorithms were used to optimize selected properties on-the-fly.5–7 However, due to the discrete nature of the chemical space, defining rules to transform one molecule into another (e.g. mutation and crossover rules for the genetic algorithms) largely depends on human expert knowledge. Moreover, defining a finite set of possible transformation rules limits the optimization possibilities and thereby promising molecules might be missed.

With the recent rise of deep learning8,9 in the field of computational chemistry, new approaches for de novo drug design have emerged (for a comprehensive review of this field the interested reader is refered to ref. 10 and 11). Segler et al. trained a Recurrent Neural Network (RNN) to model a larger set of molecules represented by the Simplified Molecular Input Line Entry Specification (SMILES) notation.12 The resulting model was not only able to reproduce the molecules in the training set, but also to generate novel structures. By further training on a focused set of structures with a certain property distribution (e.g. the activity towards a biological target) the novel generated molecules could be enriched with structures following this desired property distribution. Another strategy for fine-tuning a generative model is Reinforcement Learning.13 Reinforcement Learning aims at learning the optimal set of actions to optimize a defined reward in a given environment. In the case of de novo design, the reward can e.g. be defined by the molecular properties to be optimized. Olivecrona et al. utilized this concept to alter the generative process of a pre-trained RNN, in order to generate more molecules with desirable properties.14

Besides RNNs trained on the SMILES representation, other groups also utilized Generative Adversarial Neural Networks15–17 or other molecular representations such as the molecular graph.18–20 While these method differ in how they generate molecules, they all apply Reinforcement Learning to enrich the generated molecules with structures that have desirable properties. The main drawback of such methods is the need to retrain the generative model every time the reward function changes. This becomes impractical in a typical drug discovery project as the optimization criteria usually change over time.

A method that decouples the generation of molecules from the optimization problem was originally proposed by Gómez-Bombarelli et al.21 In their work, a variational autoencoder was trained on the SMILES notation of a large set of molecules. As a result, a new continuous vector representation of chemical structures was obtained. Points in this continuous space correspond to molecules in the discrete chemical space (as represented by the SMILES notation) and vice versa. Novel structures can be generated by sampling arbitrary points in the continuous space and then transforming them back to the SMILES notation. A molecular transformation can be achieved by a simple shift in the vector representation. Thus, optimizing chemical structures with respect to selected properties can be directly performed by optimizing a reward function in the continuous space. In their work, Gómez-Bombarelli et al. utilized Bayesian Optimization to find points in the space that correspond to molecules with a high drug-likeness and synthetic accessibility. More recently, Jin et al. also used Bayesian Optimization to optimize molecules generated by a variational autoencoder based on molecular graphs.22 Bayesian Optimization is a powerful method that has proven useful in the optimization of functions that are computationally expensive to evaluate as it needs a comparably low amount of function evaluations.23 However, its computational complexity increases exponentially with the number of dimensions of the optimization space.24 In the case of molecular optimization, though, function evaluations are relatively cheap (prediction of molecular properties) and the dimensionality of the search space (continuous molecular representation) relatively high.

In this work, we propose the use of a more light weight heuristic optimization method termed Particle Swarm Optimization (PSO). Hartenfeller et al. already proposed in 2008 to apply PSO on a discrete chemical space represented by a large library of molecular building blocks and chemical reactions.25 Here, we apply PSO in our continuous chemical representation reported previously.26 As particles of the swarm navigating this representation correspond to actual molecules in the chemical space, we term our method Molecule Swarm Optimization (MSO). In three different experiments we show how our proposed method can be utilized to optimize molecules with respect to a single objective, under constraints with regard to chemical substructures and with respect to a multi-objective value function.

2. Methods

2.1. Continuous chemical representation

Our approach can be used with any continuous representation of the chemical space, such as those found in.21,22,27 In this study we build upon the continuous molecular representation framework reported earlier.26 This molecular representation was learned using a Deep Neural Network to translate from one molecular string representation (e.g. SMILES) to another. In this way, the model learns the common “essence” between both syntactically different string notations, i.e. the molecule which both notations are representing. By introducing a bottleneck in the architecture of the neural network, the molecule is encoded in a compressed embedding, that can be utilized as latent representation of the chemical space. As the model is trained on a huge dataset of approximately 75 million chemical structures stemming from various sources, the resulting latent space represents a wide range of the chemical space that can be explored.

In this earlier work, we also showed that the learned molecular representation can be utilized as powerful molecular descriptors for quantitative structure activity relationships (QSAR) models. Moreover, transformations in the latent space result, if decoded back, in smooth transformations in the discrete chemical space in regard of structural as well as molecular properties. The interested reader is directed to the original publication for technical details of our framework.26

2.2. Particle swarm optimization

Particle Swarm Optimization (PSO) is a stochastic optimization technique that mimics swarm intelligence to find an optimal point in a search space as defined by an objective function. The particle swarm consists of individual agents (particles) that explore the search space, utilizing information gained during their search and “communicating” with other particles in the swarm.28

This concept can be defined by a few simple equations. The N particles in the swarm are defined by their position x and velocity v. The potential surface of the search space can be evaluated by the objective function f. The movement of the i-th particle at iteration step k is influenced by the best point it has yet discovered

xbesti = argmaxf(x_i^k) 1

as well as the overall best point yet discovered

x^best = argmaxf(xbesti). 2

After each iteration, each particle updates its velocity v_i and position x_i in the following way:

v_i^k+1 = wv_i^k + c₁r₁(xbesti – x_i^k) + c₂r₂(x^best – x_i^k) 3

x_i^k+1 = x_i^k + v_i^k+1 4

where c₁ and c₂ are constants that weight the contribution of the particles individual experience versus the swarm experience. r₁ and r₂ are random numbers drawn from independent uniform distributions between 0 and 1. The so called inertia weight w is a constant that controls the momentum of the particle from the previous iteration.

2.3. Objective function

The search of the Particle Swarm is guided by the objective function that is defined to be maximized. In drug discovery, the optimized objective can be both complex, conflicting, ill-defined or evolving over time. For example, at the early stages of lead discovery, a higher emphasis is put on increasing biological activity and gaining structure-activity-relationship knowledge. A set of targets that should not be hit by the compounds can also be introduced at that stage. Later on, when the overall activity landscape is well understood by the team, the focus of the optimization evolves more towards pharmacokinetics-related properties (ADME) such as improving solubility, metabolic stability or cell permeability, etc. These different objectives can contradict themselves, for example increasing the solubility of a compound might lead to permeability problems. This makes a multi-parameter optimization notoriously challenging.

In order to keep the method flexible, we propose different individual objective functions that can be combined and weighted:

• Fixed ranges for molecular properties such as molecular weight, number of H-bond donors, octanol–water partition coefficient, stereocenters etc.

• Ad-hoc QSAR models to predict the biological activity of the molecules with respect to targets of interest.

• ADME models to predict solubility, metabolic stability, cell permeability and efflux rate.

• Scoring functions for chemical reasonableness like the synthetic accessibility (SA) score29 or drug-likeness (QED).30

• Penalties for unwanted (e.g. toxic) or uncommon substructures.

• Rewards for defined substructures (e.g. fixing a scaffold) or similarity to a certain compound.

These functions either work directly on the continuous representation (e.g. QSAR models, similarity) or on the decoded SMILES representation utilizing the chemoinformatics library RDKit.31 In this study, we build two biological activity models for prediction of Epidermal Growth Factor Receptor (EGFR) and asparyl protease b-site APP cleaving enzyme-1 (BACE1) activity. These targets were choosen as the QSAR models build for these targets showed reasonable predictive performance in our prior work.26 Compounds with reported IC₅₀ values were extracted from ChEMBL32 and preprocessed as described in this prior work. We encoded the molecules in the continuous representation and trained Support Vector Machine (SVM) regression models (as implemented in the Python library scikit-learn33) on predicting the IC₅₀ values of the compounds. Moreover, we trained SVMs on solubility, metabolic stability and membrane permeability endpoints utilizing in-house data. SVM hyperparameters were optimized in a 5-fold cross-validation.

In order to filter for unwanted substructures, we extracted known toxic substructures from a published collection by SureChEMBL.34,35 Moreover, to filter for possible unstable structures we created a list with extended-connectivity fingerprints (ECFP4) of substructures that occur in more than 5 individual compounds in ChEMBL. Roughly 1% of the compounds in ChEMBL have substructures that occur less often and are here considered as potentially unstable. During the optimization, generated structures are penalized if they contain such known toxic substructures or have uncommon ECFP4 bits.

In order to combine the scores of the different functions in a multi-objective setting, we follow the approach reported in36 and scale each function between 0 and 1 reflecting values of low to high desirability (see ESI† for more details). The scaled scores of each function are combined as the weighted average, where the weights correspond to priorities in different tasks. The resulting desirability score (dscore) is subsequently used as the objective function for the PSO algorithm.

2.4. Optimization model

The final optimization model combines the parts mentioned above, i.e. the continuous molecular representation, the optimization algorithm and the objective functions. Either a query molecule is encoded in the continuous space or a random point is sampled. The PSO algorithm is initialized by generating a fixed amount of particles (in the order of 100) at this position with randomly drawn initial velocities. After the first position update, the objective function is evaluated for each individual particle of the swarm. The search is continued until a certain number of iterations or a break condition (e.g. desired value) is met. Since the PSO algorithm is a stochastic optimization technique, multiple restarts are performed.

3. Results and discussion

By combining our encoder-decoder framework, computational models to predict properties and/or biological activities of compounds, and an optimization algorithm, we optimize a query molecule with respect to the objective function resulting in a set of compounds with more desirable (predicted) properties. In the first part we show the optimization of molecules with regard to a single objective. Next, we further restrict the optimization by adding substructure constraints and then demonstrate that our framework can be utilized to perform multi-objective optimization of compounds. In our final experiment we benchmark our proposed model with the GuacaMol1 package.

3.1. Single-objective optimization

As a first proof-of-principle, we run experiments on the optimization of molecules with respect to single molecular properties. Similar to related works,15,20,21,37 we perform individual optimizations on the drug-likeness, the octanol–water partition coefficient logP as well as the synthetic accessibility of a molecule. We utilize the RDKit implementation of the Quantitative Estimate of Druglikeness (QED) score to evaluate the drug-likeness and the penalized logP score37 that combines the partition coefficient and the synthetic accessibility (SA) score of a compound. Moreover, we optimize compounds with respect to their predicted biological activity on EGFR and BACE1.

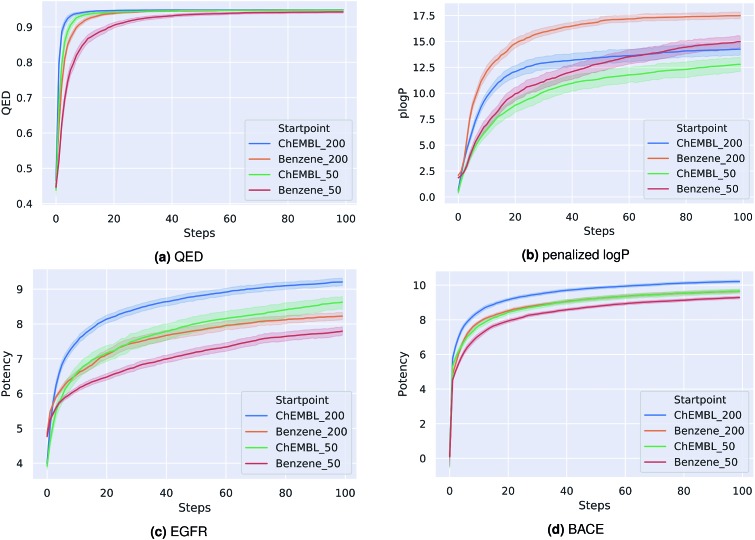
For each optimization task, we run the PSO algorithm 100 times for 100 steps each. Table 1 shows for each task the highest score achieved. For the drug-likeness and the penalized logP tasks, we compare our method to the best results of state-of-the-art optimization models as reported by You et al.20 Our proposed method achieves the same performance on the drug-likeness task as the best state-of-the-art approach and outperforms all other approaches on the penalized logP task. Moreover, our method consistently generated molecules with very high predicted binding-affinities (IC₅₀ < 1 nM) for both biological targets respectively. As the compounds used to train both QSAR models were not included in the pre-training dataset of the encoding-decoding framework, these high scores can not be attributed to an information leakage or bias in the generative model. In fact, we investigate if including these compounds in the pre-training influences the optimization results. We found that both models performed similarly with overlapping confidence intervals, suggesting that time-costly fine-tuning steps are not needed here. Fig. 1 depicts the average scores during the optimization process for the different tasks. To better understand the impact of the starting point for the optimization, we show results for a fixed starting point (benzene) and for variable starting points, randomly sampled from ChEMBL. In all tasks, the model consistently optimizes the respective property, reaching relatively high scores already after a few iterations. Although starting from different points, the variance between the scores at a given optimization step is similar to the variance obtained when repeatedly starting from benzene. As a matter of fact, the variance seems to be higher for the fixed starting point. Moreover, starting from a molecule picked from ChEMBL seems to result in faster and more successful optimizations, except for the optimization of the penalized logP score. This is probably due to the increased size and structural complexity of these molecules compared to a simple benzene ring. Moreover, initializing the particle swarm algorithm with more particles helps finding more optimal points in the search space in less iterations (at the expense of increased computational time).

Table 1. Best results for the different single-objective optimization tasks. Our Method is compared to the results of three recently published optimizations methods as reported by You et al.20.

	ORGAN	JT-VAE	GCPN	MSO
Reference	15	22	20	Ours
Penalized logP	3.63	5.30	7.98	26.1
QED	0.896	0.925	0.948	0.948
EGFR [pIC50]	—	—	—	10.3
BACE1 [pIC50]	—	—	—	11.5
Run time	∼1 d	∼1 d	∼8 h	∼10 m

Fig. 1. Best score of the particle swarm over the course of optimization averaged over 100 runs for four optimization tasks: (a) quantitative estimation of drug-likeness, (b) penalized octanol–water partition coefficient, (c) binding affinity (pIC₅₀) to Epidermal Growth Factor Receptor, (d) binding affinity (pIC₅₀) to asparyl protease b-site APP cleaving enzyme-1. Optimizations were either started from benzene or a random picked compound from ChEMBL with either 50 or 200 particles.

Similar to related work,21,22 we also tried to optimize the latent space of our autoencoder framework with Bayesian Optimization (BO). However, trying different BO frameworks, we were not able to find good solutions within reasonable computation time. This is probably due to the high dimensionality of our search space (512 dimensions), since BO's computational complexity grows exponentially with the number of dimensions.24

It has to be mentioned that the baseline methods in Table 1 were trained on significantly less data (≈250.000 compounds) which might lead to an unfair advantage for our proposed method. To investigate the impact of a smaller pre-training dataset on our optimization results, we retrained our encoder-decoder framework with the same dataset as used in ref. 20. We find that for this model different runs have a higher variance in performance, however, the best solutions still have a similar high score as the solutions reported in Table 1. Thus, the performance of our proposed model cannot only explained by the increased size of the pre-training dataset.

Using one GPU for passing the molecules in the swarm through the encoder-decoder model and one CPU core to perform the PSO algorithm and objective function evaluation, computational time is in the order of a few minutes for a 100-steps run. The run time on a 32-core CPU machine without GPU support is in the order of 10 minutes. This is in contrast to baseline methods in Table 1 which have a reported wall clock running time of multiple hours to one day on a 32-core CPU machine.20 This substantial speed-up is mainly due to the fact that our proposed method separates the training of the generative model (the decoder of the utilized encoder-decoder framework) and the optimization procedure. Since we use the same pre-trained generative model for each optimization task, we do not have to spend computational resources on training this model in every new run. This is in contrast to the methods used for comparison, as they approach the optimization task by re-training/fine-tuning the generative model for every new task.

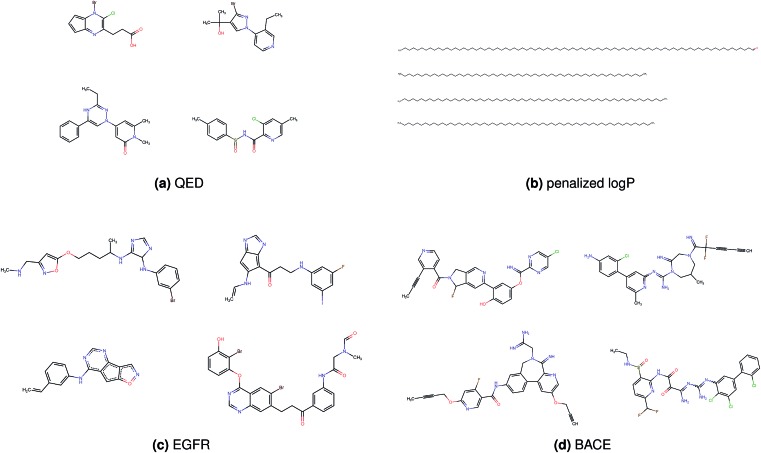
Fig. 2 shows a few example molecules randomly picked from the final iteration for each optimization task. It is evident that, by optimizing a single objective function, the model exploits its ability to freely navigate the chemical space and solely focuses on this very objective. While the optimization of drug-likeness obviously results in pleasant-looking molecules, the three other optimization tasks result into comparably “unusual” chemistry. Since long aliphatic chains are both maximizing the partition coefficient while being scored as easy to synthesize, they are the inevitable outcome when optimizing for penalized logP. Moreover, if the objective is solely maximizing the prediction of a QSAR model, the resulting molecules will aggregate the evidence the QSAR model found in the potent molecules of its training set. This, however, will most likely guide the optimizer into parts of the chemical space that are not well covered by training set molecules, leading to inaccurate and overoptimistic predictions. Thus, final molecules are likely to be artifacts of the underlying QSAR model.

Fig. 2. Compound examples resulting from optimizing (a) quantitative estimation of drug-likeness, (b) penalized octanol–water partition coefficient, (c) binding affinity to Epidermal Growth Factor Receptor, (d) binding affinity to asparyl protease b-site APP cleaving enzyme-1.

Summing up, we demonstrated that our method is able to very quickly improve upon a given starting molecule in terms of predicted drug-likeness or predicted biological activity. This confirms that our optimization method is able to navigate the chemical space defined by our pre-trained embedding and perform single-parameter optimization in a timely fashion. However, these examples are far from actual drug design cases. At this stage, we do not apply any structural constraints for guiding the structure generation. This means that the new, optimized compounds might be structurally remote from the defined starting points or contain toxic or unstable moieties (e.g. 1,3-pentadiyne substructure in Fig. 2d). Usually, drug discovery projects are confined within chemical series and closely related analogues. Hence, we propose to add constraints on the chemical structure during optimization in the following section.

3.2. Constrained single-objective optimization

In this experiment, we perform a single property optimization, while constraining the explorable chemical space using a defined molecular scaffold that needs to be present in the generated molecules. This task is more closely related to a real drug-development process, as it mimics a typical lead optimization task.

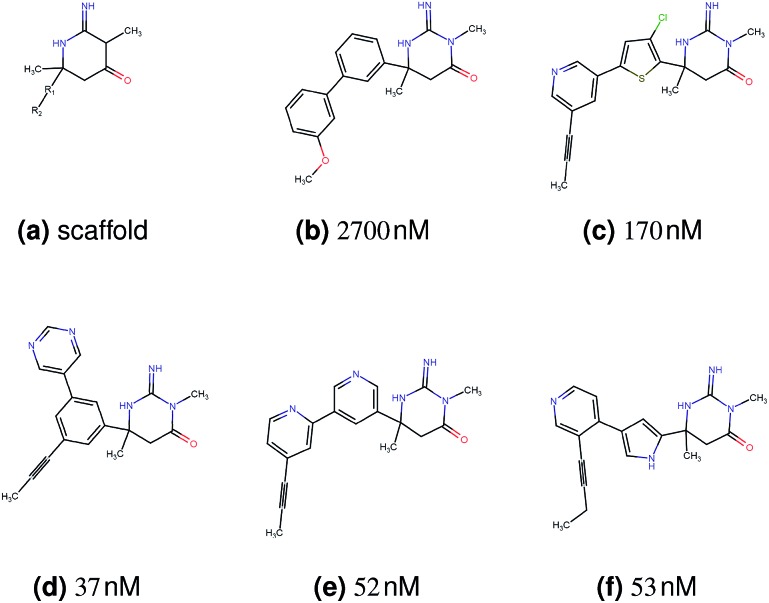
We base our experiment on a lead optimization paper by Stamford et al. in which an iminopyrimidine lead series was optimized for BACE1 inhibition.38 In order to evaluate whether our method can optimize for biological activity while constraining the explorable chemical space, we start the optimization from the same initial compound as in38 (Fig. 3b). We fix the iminopyrimidinone scaffold (Fig. 3a) by penalizing generated compounds that do not contain this substructure in the objective function. For the prediction of BACE1 activity we retrain the BACE1 model from the previous section, excluding all compounds with an iminopyrimidinone scaffold.

Fig. 3. (a) Iminopyrimidinone scaffold fixed in the optimization. R1 and R2 are aromatic rings. (b) Starting point of the optimization. (c) Best reported compound by Stamford et al. (d–f) Top 3 compounds found by our method. All compounds are depicted with their predicted binding affinity to asparyl protease b-site APP cleaving enzyme-1 (BACE1).

On the 17 iminopyrimidinone compounds reported by Stamford et al. the QSAR model achieves a Spearman correlation coefficient of ρ = 0.7 (p-value = 0.004) compared to the reported IC₅₀ values. This means that although we did not include compounds with an iminopyrimidinone scaffold in the training, the BACE1 activity prediction model shows a reasonable performance in the part of the chemical space we are interested in (i.e. compounds with iminopyrimidinone scaffold).

In addition to fixing the scaffold, we further restrict the chemical space by penalizing compounds with more than 26 heavy atoms (one more heavy atom than the best reported compound by Stamford et al. depicted in Fig. 3d). Moreover, we penalize for known toxic and uncommon substructures.

We run the optimization model for 100 steps and restart the optimization 200 times. Fig. 3d–f depicts the compounds with the best scores found in the in silico optimization. In the course of the optimization the most active BACE1 inhibitor (compound c) from Stamford et al. was passed by in 2 out of the 200 runs but was not part of the final set of proposed molecules. This can be explained as the members of the final set of molecules all have higher predicted activities than compound c. As a proof of principle, we also performed an experiment where the Euclidean distance of a particle to compound c's embedding was used as objective function. In this experiment, we could consistently (200 out of 200 times) recover compound c as the optimal solution. Hence, we suppose that our approach does not contain compound c within the final set of molecules because this region of chemical space is not the most attractive for the applied BACE1 model. Our reported in silico solutions do contain the required scaffold and are predicted to have a higher potency, so they might possibly give useful new ideas to medicinal chemists working on BACE1 inhibitors with an iminopyrimidone scaffold.

3.3. Multi-objective optimization

In this last section, we evaluate the ability of our proposed method to optimize a molecule with respect to a multi-objective value function. In accordance to a typical multi-objective lead optimization process, we define the value function as a combination of multiple molecular properties. We conduct three experiments:

1. Maximizing the predicted binding affinity to EGFR while minimizing the predicted binding affinity to BACE1.

2. Maximizing the predicted binding affinity to BACE1 while minimizing the predicted binding affinity to EGFR.

3. Maximizing the predicted binding affinity to both EGFR and BACE1.

Additionally for all experiments, we maximize the predicted solubility, metabolic stability, cell permeability, drug-likeness as well as the predicted synthetic accessibility (SA) of the molecule and penalize for known toxic or uncommon substructures and molecular weight below 200 or above 600 Dalton. Each of the ten different objectives was scaled by a desirability function between 0 and 1, where low values correspond to undesirable ranges and high values to acceptable or good ranges of a molecular property (see ESI† for details on the scaling functions). The final optimization objective is the weighted average of the different scaled objective functions. In all experiments, we weighted the maximization of binding affinities with a factor of 5, minimization of binding affinity with a factor of 3 and all other properties with 1.

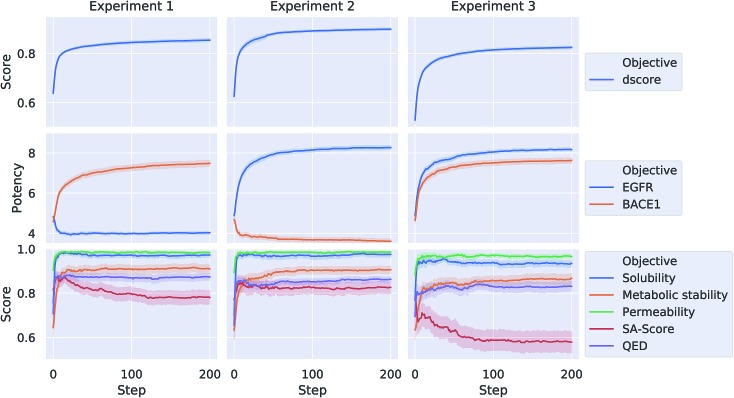
Each of the three optimization tasks was run 100 times for 200 steps, starting from a randomly picked molecule from ChEMBL. The aggregated results for the different properties over the course of the optimization are depicted in Fig. 4. Our proposed method is consistently able to optimize a query molecule with respect to the defined multi-objective value function. The weighted average of the different objective functions (dscore) increases on average from 0.64, 0.63 and 0.53 to 0.85, 0.9 and 0.82 for the three different experiments respectively. The method is able to find solutions that are predicted to meet the respective activity-profile while keeping desirable ADMET properties as well as QED and SA scores high. In experiment 3, however, the methods finds solutions that on average have a comparably lower SA score in order to meet the desired activity-profile.

Fig. 4. Results for the best scoring (dscore) particle in the swarm over the course of optimization for 200 steps averaged over 100 runs for the three different optimization tasks. In addition to the objective (dscore) that is optimized, the average predicted potency (pIC₅₀) on both BACE1 and EGFR as well as the average scaled predicted solubility, metabolic stability, permeability, SA score and QED of the best scoring (dscore) particle is shown.

Table 2 shows a few example molecules picked from the best final iteration for each of the three optimization tasks. Although the value function consists of many different and partially conflicting individual objectives our proposed method is consistently able to find molecules in the vast chemical space that meet the desirable ranges for all of the defined objectives.

Table 2. Four example compounds as result of the in silico optimization for experiment 1, 2 and 3 respectively, separated by blank rows. Each compound is shown with its calculated and predicted molecular properties: binding affinity (pIC₅₀) to target Epidermal Growth Factor Receptor (EGFR), binding affinity (pIC₅₀) to target asparyl protease b-site APP cleaving enzyme-1 (BACE), metabolic stability (Stab) in percent, solubility from powder (Sol) in mg L^–1, cell permeability (Perm) in nm s^–1, drug-likeness (QED) and synthetic accessibility (SA).

Compound	EGFR	BACE	Stab	Sol	Perm	QED	SA
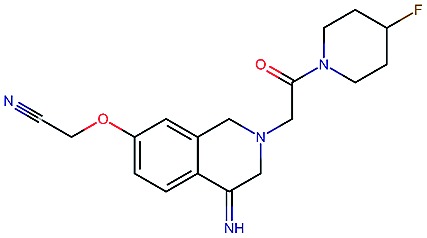
	3.7	8.0	86	390	72	0.90	3.0
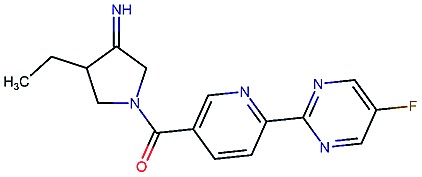
	4.4	8.5	86	500	130	0.94	3.4
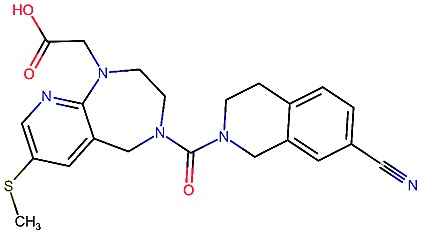
	4.1	8.3	78	570	90	0.73	3.0
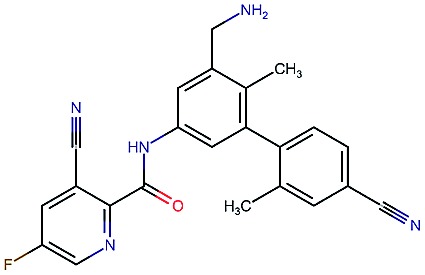
	4.3	8.3	86	25	69	0.69	2.8
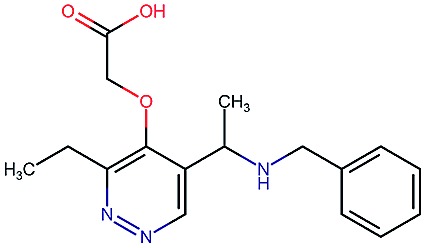
	8.6	2.4	82	1000	85	0.77	2.9
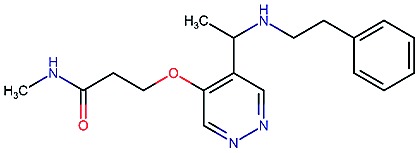
	9.1	3.1	68	610	100	0.73	2.9
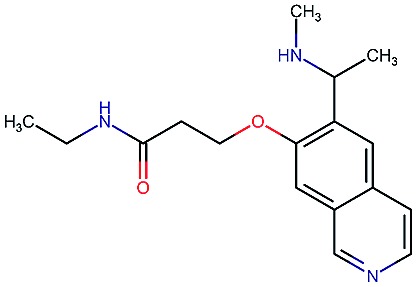
	8.4	3.5	86	280	67	0.82	2.8
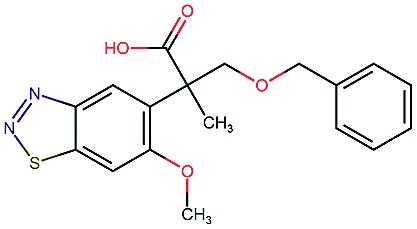
	9.0	3.6	80	230	74	0.70	3.2
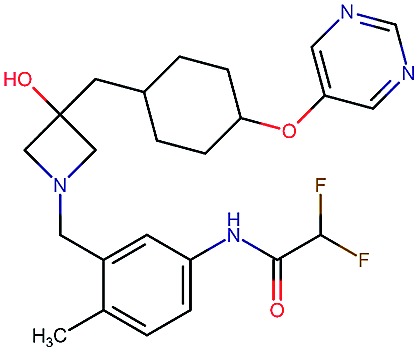
	8.7	8.2	59	838	80	0.63	3.0
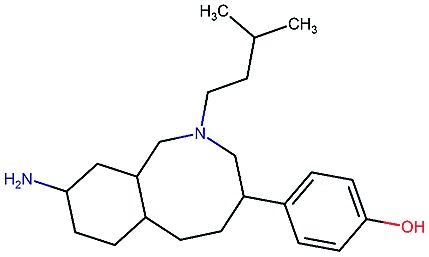
	8.1	8.0	53	531	120	0.85	3.4
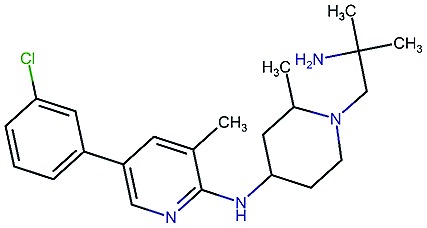
	8.1	7.7	85	390	84	0.78	3.3
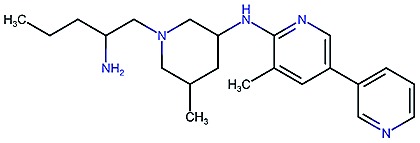
	7.9	7.9	68	1000	130	0.78	3.6

4. GuacaMol benchmark

In order to asses our proposed model's performance in a more standardized framework we utilized the recently published benchmark package GuacaMol proposed by Brown et al.1 The benchmark consists of 20 optimization tasks including a range of single-, constrained and multi-objective optimization tasks (goal-directed benchmarksuit v2). In contrast to the previous evaluations, this benchmark does not only consider the highest-scoring solution, but also takes up to top-250 solutions for scoring into account. For a fair comparison, we retrained our encoder-decoder framework with the same subset of ChEMBL that is defined in the benchmark. For each optimization task we used a particle swarm with 200 particles that was run for 250 iteration and 40 restarts.

We found that our proposed method achieves a higher average score when compared with the baselines methods included in the benchmark. We were able to outperform these methods in 9 out of the 12 tasks that were not already perfectly solved by the best baseline method (Graph-GA). For detailed (task-wise) solutions we refer the reader to Table 1 in the ESI.†

5. Conclusion

We propose the use of Particle Swarm Optimization (PSO) heuristic to optimize molecules in a continuous latent representation. We show that our model is able to consistently optimize molecules with respect to single objectives such as maximizing the predicted drug-likeliness, partition coefficient logP or target binding affinity as modeled by quantitative structure activity relationship (QSAR) model. Not only does our proposed method exhibit competitive or better performance in finding optimal solutions compared to baseline method, it also achieves significant reduction in computational time. In the more standardized benchmark package GuacaMol we outperform the baseline methods in 9 out of 12 tasks that were not already perfectly solved by the best baseline method. In further experiments we show how the proposed method can be utilized to support medicinal chemists in a lead optimization process by proposing in silico solutions for relevant tasks. Finally, we perform multi-objective optimizations of compounds with respect to relevant properties such as specific target activity profiles and pharmacokinetics-related properties. We demonstrate that our proposed method is consistently able to optimize the joined objective function and results in compounds that exhibit desirable ranges for all included computed properties. Although we show promising results for optimizing molecular properties in this work, it has to be noted that the optimization cycles are based on predicted values for the properties. This can be particularly problematic for QSAR models that are applied outside their domain of applicability. Hence, we advocate the use of our proposed method only in combination with reasonable constraints to parts of the chemical space that can be modeled by the applied functions with reasonable confidence. An even more suitable approach would be combining the in silico optimization with real world experiments in an active learning manner. By doing so, the QSAR model could be refitted while evolving into yet unexplored regions of the chemical space and hopefully remain reasonably accurate in its predictions.

Availability

Source code of the proposed model will be made openly available on GitHub (https://github.com/jrwnter/mso) upon publication.

Conflicts of interest

There are no conflicts to declare.