Computation of the bond dissociation enthalpies and free energies of hydroxylic antioxidants using the ab initio Hartree–Fock method

Abstract

Introduction

A new method for calculating theoretical bond dissociation enthalpy (BDE) and bond dissociation free energy (BDFE) of hydroxylic antioxidants is forwarded. BDE and BDFE may be understood as activation energies accompanying the formation of transition states, which may undergo downhill homolytic dissociation. The new method does not involve the complete fission of O–H bonds.

Method

Theoretical gas phase BDE values were calculated with the ab initio unrestricted Hartree–Fock (UHF) method, as changes in enthalpy between ground singlet states (GS) and triplet dissociative states (DS). Similarly, gas phase BDFEs were estimated from the corresponding changes in Gibbs free energy. The results were then compared with reliable experimental reports.

Results

The proposed theoretical approach of BDE and BDFE determination was tested using 10 simple phenols, 5 flavonoids, and l-ascorbic acid derivatives. The agreement between our calculated gas phase results and the adopted experimental values were generally within 0.5 kcal mol⁻¹, with a very few exceptions.

Discussion

Generally, steric interactions as well as intramolecular hydrogen bonding involving the dissociating OH group should be minimized in the GS. The DS are both electronically and vibrationally exited transition states. They have one unpaired electron on the carbon atom, which bears the homolytically dissociating OH group and are second order saddle points with a fixed <C–O–H bond angel of 180°.

Conclusion

It was concluded that ab initio UHF was well suited for the estimation of gas phase BDE and BDFE. The method presented has a good potential for application across a range of hydroxylic antioxidants. Currently, work is underway to extend its application in other class of antioxidants.

Introduction

It is generally believed that bond dissociation enthalpy (BDE)^1,2 strongly influences the rate of hydrogen atom abstraction from antioxidants.³ The existence of a reasonable correlation between radical scavenging activity and BDE has also been confirmed.⁴ Despite the widespread misconception that BDE may dictate the direction of hydrogen atom transfer reactions, in principle it cannot.⁵

A substantial effort has been dedicated to the determination of this basic physicochemical parameter affecting antioxidant activities with particular emphasis to BDE of O–H, S–H, N–H and C–H bonds.⁶ This introductory work solely focuses on the BDE of O–H bonds. For over half a century, the determination of the BDE of phenols and related hydroxylic antioxidants has been undertaken both experimentally^2,7–10 and using various computational tools.^11–17 All the same, the need for more reliable BDE values and accurate BDE determination techniques may not be quenched for some years to come.

In this report, a new, sound but yet simple computational approach for the approximation of the BDE of O–H bonds in phenolic and related antioxidants is presented. This work has appeared as an abstract recently.¹⁸ The newly proposed method stipulates a unimolecular dissociation mechanism involving a transition state.^18–20 It is based on the ab initio Hartree-Fock method and consistent with our reaction model for the radical scavenging activity of antioxidants.^5,21 Briefly, BDE is determined by approximating the enthalpy change required to obtain a relevant second order saddle point, which may undergo downhill homolytic dissociation. A similar approach is also used to estimate bond dissociation free energy (BDFE) from changes in Gibbs free energy. The proposed method would be demonstrated and tested using 10 simple phenols, 5 flavonoids, and ascorbic acid derivatives. Comparison of our calculated theoretical gas phase BDE and BDFE values against reported experimental values is discussed. Moreover, a preliminary assessment of the effect of basis set on calculated gas phase BDE and BDFE is presented.

Method

Computational details

The compounds studied were phenol, 2-methylphenol, 3-methylphenol, 4-methylphenol, 2-methoxyphenol, 2,6-dimethoxyphenol, BHT (2,6-di-tert-butyl-4-me thylphenol), 1-naphthol, 2-naphthol, 2-hydroxyphenol, l-ascorbic acid, l-ascorbate, 5,6-isopropylidene-l -ascorbic acid, 5,6-isopropylidene-l-ascorbate, 6,7-dihydroxyflavone, 7,8-dihydroxyflavone, chrysin (5,7-dihydroxyflavone), luteolin (5,7,3′,4′-tetrahydroxyflavone) and hesperetin ((S)-2,3-dihydro-5,7-dihydroxy-2-(3-hydroxy-4-methoxyphenyl)-4H-1-benzopyran-4-one). In addition to structural merits, the availability of reported experimental BDE (and BDFE) was the most important criterion in the selection of the above.

Our computational approach is essentially similar to the one elaborated by Woldu and Mai.⁵ All but a very few theoretical computations were carried out employing Gaussian 03^® E.01,²² on either the high-performance computation facilities of Intersect Australia Limited (mclaren.ac3.edu.au/shared memory SGI Altix 4700, 128 Dual-Core CPUs) or the National Computational Infrastructure (NCI) National Facility at the Australian National University (ANU) (vayu.nci.org.au/Sun Constellation Cluster, 1492 nodes, each containing 2 quad core Nehalem processors summing up to 11 936 cores). Visualization was carried out using the graphical interface Gabedit²³ and except in a couple of instances, all spin density distribution maps were generated from *.fchk files, at an isovalue of 0.005 au.

For convenience, we generated almost all of our input coordinates manually in Z-matrix. Routinely, the manually generated initial coordinates were directly optimized with the ab initio unrestricted Hartree–Fock (UHF) Hamiltonian, with very tight convergence criteria (Opt = VTight) (www.gaussian.com). Stability tests were regularly performed on the optimized wave functions before they were used for harmonic frequency analysis. For ground states (both singlet and triplet multiplicities) the minimum negative (imaginary) frequency tolerated was in most cases –1.5 cm⁻¹. In addition, the self-consistent field (SCF) spin-densities of the optimized structures were computed. Unless indicated differently, this introductory work was carried out with the basis set 6-31G(d,p) as it was found to be optimum. All thermochemical quantities are for 298.150 K and 1.00000 Atm.

Estimation of BDE and BDFE

Based on preliminary results, we focused on characterizing as many ground singlet states and a specific type of vibrationally excited triplet states. The later were non-planar, of lower energy and also had a fixed <C–O–H bond angel of 180°.²⁴ Characteristically, the vibrationally excited triplet states had an unpaired spin up electron on the carbon atom bearing the OH, which was designated to undergo homolytic dissociation. Moreover, we hypothesize that they may represent the dissociative states of hydroxylic antioxidants and be capable of undergoing downhill homolysis at the O–H bond.

Theoretical gas phase BDE was calculated as the enthalpy change (ΔH°(298 K)) accompanying the formation of a dissociative triplet state with respect to a suitable ground singlet state. Similarly, BDFE was calculated from the corresponding change in Gibbs free energy (ΔG°(298 K)). Enthalpy changes (Equation 1) were calculated by taking the appropriate sums and difference of the unscaled ‘Sum of electronic and thermal Enthalpies’ terms from the harmonic frequency job outputs (Equation 2).²⁵ The corresponding changes in Gibbs free energy were calculated using the ‘Sum of electronic and thermal Free Energies’ terms (Equation 3).²⁵ The conversion factor used was 627.50944796 kcal mol⁻¹ H⁻¹.

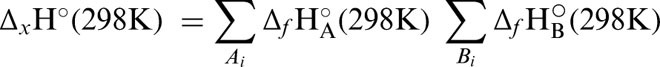1

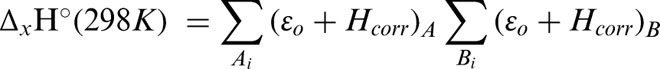2

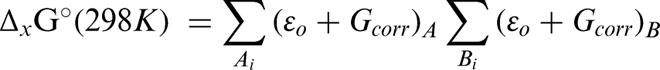3

where ΔH°(298 K) is change in enthalpy; ΔG°(298 K) is change in Gibbs free energy; Δ_f H°(298 K) is the enthalpy of formation; x: transformation, e.g. reaction (r), conformational change (c) etc; ɛ_o: total electronic energy (SCF); H_corr is the ‘Thermal correction to Enthalpy’ and G_corr, ‘Thermal correction to Gibbs Free Energy’ both from Gaussian frequency job output.

Results

Computational approach in focus

In order to test the methodological framework proposed, computational method to be used and selection of basis set, a proof of concept was first obtained using phenol as a model compound. To this effect an extensive investigation was carried out on the various singlet, doublet, triplet, quartet and quintet multiplicity states of phenol (Ph–O–H) and homolytically dissociated phenol (Ph-O^• + H^• or Ph-O^• alone), at UHF/6-31G(d,p) level. Part of the results obtained is depicted in Fig. 1. The enthalpy changes (ΔH°(298 K)) associated with the different transformations were carefully added and/or subtracted from each other, until they fell within the range 90 ± 3 kcal mol⁻¹.²⁶

Figure 1.

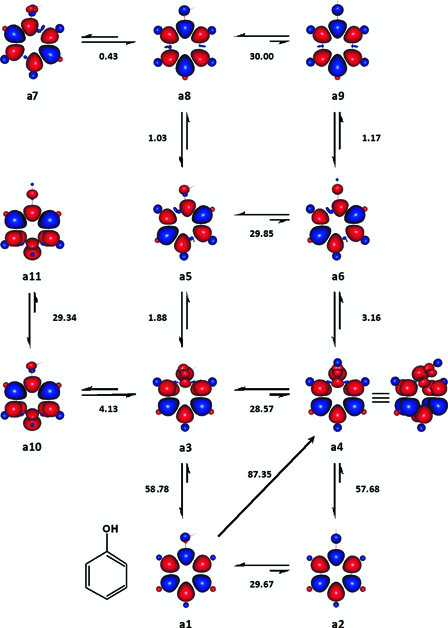
Enthalpy changes between selected states of phenol, which were considered for the estimation of its BDE (kcal mol⁻¹). Enthalpy changes (ΔH°(298 K)) are negative in the direction of the conformer the formation of which is favoured and conversely positive in the opposite direction. Red and blue are spin up and spin down regions, respectively.

In the case of phenol, a4 was chosen as the likely dissociative state among the potential candidates including a6, a9, and a11 (Fig. 1), since its relative enthalpy of formation, 87.3468 kcal mol⁻¹, was the lowest value that was closer to the recommended gas phase BDE of phenol. Once the structures and enthalpy changes of interest were identified, the dependence of enthalpy changes on the size of basis set was assessed (Fig. 2). All the basis sets tested (Fig. 2) except 6-31G + (d,p) and 6-31G + +(d,p), returned gas phase BDE, which fell between the two widely accepted BDE values of the compound.^27,28

Figure 2.

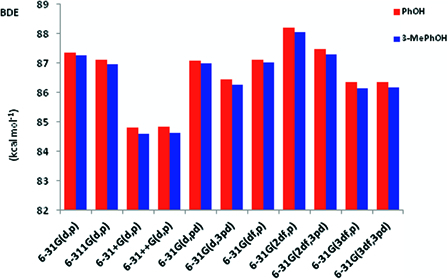
The relative performances of selected basis sets for the estimation of gas phase BDE.

According to Mulder et al.,²⁷ the recommended gas phase BDE of phenol is 86.7 ± 0.7 kcal mol⁻¹, while Borges dos Santos and Martinho Simões²⁸ have suggested the slightly higher value of 88.7 ± 0.5 kcal mol⁻¹. Using 6-31G(d,3pd), 6-31G(3df,p) and 6-31G(3df,3pd), theoretical BDE values ranging 86.35–86.44 kcal mol⁻¹ were obtained for phenol. 6-311(d,p), 6-31(d,pd), 6-31(df,p) and 6-31(2df,3pd) produced BDE values in the range 87.07–87.48 kcal mol⁻¹. Among the basis sets tested, only 6-31G(2df,p) returned an enthalpy change that was within the upper range BDE of phenol. Apparently, the new method of calculating gas phase BDE and BDFE may not benefit from the use of diffusion functions since both 6-31G + (d,p) and 6-31G + +(d,p) produced BDE values which were less than 85 kcal mol⁻¹. Ultimately, the use of 6-31G(d,p) was found to be adequate since increasing the ‘completeness’ of the basis set did not offer any apparent advantage as far as the purpose of this introductory study was concerned. Similar results for 3-methylphenol also lent support to the satisfactory performance of 6-31G(d,p) (Fig. 2 and Table 2).

Table 2.

Calculated gas phase bond dissociation enthalpies and bond dissociation free energies of the compounds studied together with literature values

Compound	Theoretical gas phase values (kcal mol−1)			Experimental literature values (kcal mol−1)
	BDE	ΔBDE∉	BDFE	BDE	ΔBDE	BDFE
Phenol	87.3	0.0	86.4	86.7 ± 0.727		79.8‡,48
				88.7 ± 0.528		84.9Æ,64
2-Methylphenol (o-cresol)	85.8	1.5	84.9	86.0 ± 0.433	2.233
				86.634	2.234
3-Methylphenol (m-cresol)	87.2 ± 0.0 (n = 2)	0.1	87.1 ± 0.0 (n = 2)	87.6 ± 0.133	0.533
4-Methylphenol (p-cresol)	86.9	0.4	86.5	86.6 ± 0.533	1.733	87.448
				86.834	1.934
2-Methoxyphenol (guaiacol)	83.7 ± 0.0 (n = 2)	3.6	82.9 ± 0.3 (n = 2)	84.2 ± 0.233	4.133
				84.734	4.134
2,6-Dimethoxyphenol	83.8 ± 0.2 (n = 3)	3.7	83.2 ± 0.4 (n = 3)	83.2 ± 0.241	5.141
				83.742	5.042
BHT	75.3	12.0	74.3	79.610	7.710	75.8Æ,64
1-Naphthol	80.5	6.8	79.7	82.133	6.133	75.4‡,64
				82.745	5.545	79.7§,64
2-Naphthol	85.0	2.3	84.1	84.633	2.433	78.7‡,64
				85.645	2.945	83.0§,64
2-hydroxyphenol	81.8	5.6	80.8	81.847	5.847
				81.634	7.234
l-Ascorbic acid	75.4 ± 0.7 (n = 6)	11.9	74.3 ± 0.6 (n = 6)	78.0,48	9.7,48	79.8,48
l-Ascorbate	66.2 ± 1.3 (n = 4)	21.1	65.2 ± 1.2 (n = 4)	71.8,48	15.9,48	73.6,48
				72.3Π,48		67.7Π,48
				72.2Θ,48	20.4Θ,48	67.6Θ,48
5,6-isopropylidene-l-ascorbic acid	76.0	11.3	74.8	75.1Π,48		70.5Π,48
5,6-Isopropylidene-l-ascorbate	67.3	20.0	66.0	70.0Π,48		65.4Π,48
				72.1Θ,48	20.6Θ,48	67.5Θ,48
6,7-Dihydroxyflavone	81.9 (6-OH)	5.4	80.2 (6-OH)	79.449	8.849
	79.7 (7-OH)	7.6	77.9 (7-OH)
7,8-Dihydroxyflavone	81.0 (7-OH)	6.3	79.9 (7-OH)	79.649	8.649
	79.6 (8-OH)	7.7	77.4 (8-OH)
5,7-Dihydroxyflavone	81.7 (5-OH)	5.6	80.3 (5-OH)	85.349	2.849
	88.9 (7-OH)	−1.6	87.2 (7-OH)
Luteolin	81.9 ± 0.1 (n = 8) (3′-OH)	5.4	81.1 ± 0.2 (n = 8) (3′-OH)	81.949	6.349
	78.0 ± 0.3 (n = 8) (4′-OH)	9.3	77.2 ± 0.2 (n = 8) (4′-OH)
Hesperetin	83.5 ± 0.4 (n = 8) (3′-OH)	3.8	82.6 ± 0.3 (n = 8) (3′-OH)	84.649	3.649

^∉ΔBDE = BDE_phenol – BDE_X

^‡Gas; ^ÆAlkane; Water; ^§Isopentane; ^ΠMeCN; ^ΘDMSO.

Similar types of extensive analyses were undertaken particularly for catechol and ascorbic acid only. It was eventually possible to narrow down the search parameters for dissociative triplet states and as a result, for the remaining compounds, mainly their ground singlet states and vibrationally excited triplet states, which were analogues to a4 were analysed. Where the conjugation between multiple ring systems could vary, it was carefully considered. The effects of possible intramolecular hydrogen bonding and steric interactions in a given compound were also analysed. Moreover, whenever possible, computed gaussian structures were verified using literature experimental and theoretical data.

In spite of its widely accepted shortcoming for the study of chemical bond breaking/ forming processes,²⁹ the ab initio Hartree–Fock method was used in this study for the determination of BDE and BDFE. This was owing to the fact that HF is one of the most suitable and economical methods for a rather accurate estimation of change in enthalpy of formation.^30,31 UHF in particular could even outperform some of the most widely employed correlated/perturbation corrected methods.⁵ To demonstrate this in relation to the present work, let us compare the relative performance of UHF with those of other computational methods.

Table 1 presents the enthalpy changes (and changes in Gibbs free energy) between the corresponding states of a1 and a4, as determined with some of the commonly used post-Hartree–Fock and advanced composite methods as well as two semi-empirical programs. Even though in this study it is strongly argued in its favour, admittedly, there is no concrete evidence at this stage, that the actual dissociative state of phenol closely resembles a4. If, however, the dissociative state of phenol does resemble a4, the results in Table 1 may indicate that UMP2, CBS, G3 and G4 and the semi-empirical program PM6 need to be revised. For the time being, at least, their usability for the intended study can be ruled out. AM1 on the other hand, produced an enthalpy change of 85.93 kcal mol⁻¹, which is relatively close to the lower range BDE of phenol.

Table 1.

Enthalpy changes (ΔH°(298 K)) and changes in Gibbs free energy (ΔG°(298 K)) between the ground singlet state and dissociative triplet state of phenol* determined with a few semi-empirical and post Hartree–Fock methods

	ΔH°(298 K) kcal mol−1	ΔG°(298 K) kcal mol−1
AM1**	85.93	84.96
PM6**	56.31	55.08
UMP2(Full)**	118.33	116.37
CBS-QB3	111.00	109.81
CBS-APNO	111.83	110.69
G3	111.14	109.95
G3B3	111.14	109.94
G3MP2	112.40	111.21
G4**	109.84	108.60

*Structures similar to a1 and a4 were fully optimized and thermochemical analyses carried out according to the respective methods.

**Gaussian 09^® B.01.³² on vayu.nci.org.au, was used for this work.

The results summarized below may illustrate the new method of calculating theoretical gas phase BDE and BDFE. Table 2 presents our calculated BDE and BDFE values together with the literature experimental values used for this study. The molecular orbitals of a4 and other details not included in the main paper are available as Supplementary Information and additional materials may also be obtained from the authors upon request.

Phenol

One of the two lowest energy isomers²⁴ of singlet state phenol is a1 (Fig. 1). a3, a5, a7, and a8 were four ground triplet states. a2 was a singlet state second-order saddle point, in which the <C–O–H bond angle is 180°. Similarly, a4, a6, a9 and a11 were a set of triplet state conformers, which were also second-order saddle points like a2. As far as the homolysis of the O–H bond was concerned, a10 and a11 were examples of less important triplet states in which the unpaired spin up electron is localized either ortho, meta or para to the carbon atom bearing the phenolic group. Unlike in the case of a6 and a9, the six-membered ring in a4 and a11 was non-planar

Relative to a1, the enthalpy changes associated with the formation of a4, a6, a9 and a11 were 87.35, 90.51, 91.68 and 92.25 kcal mol⁻¹, respectively. As mentioned earlier, we assume that the most stable of these four electronically and vibrationally exited states, a4, might represent the transition state of phenol that may undergo homolytic dissociation at its O–H bond. Therefore, based on our approach, the BDE of phenol was suggested to be 87.3 kcal mol⁻¹. From this point onwards, we would refer triplet states, which are analogous to a4 as dissociative states (DS), for the sake of convince.

The imaginary frequencies of a4 were −1318.8097 cm⁻¹ and −1256.7067 cm⁻¹ at 6-31G(d,p) level and −1307.1536 cm⁻¹ and −1241.7556 cm⁻¹ at 6-31G(3df,3pd). In a4, one of the two unpaired spin up electrons formed part of the residual aromatic π-electrons system while the other one mainly localized on the carbon atom bearing the phenolic group.

2-Methylphenol, 3-methylphenol and 4-methylphenol

Since the enthalpy change for b1 → b3, 85.80 kcal mol⁻¹, is much closer to the available experimental BDE values of 2-methylphenol (Table 2), we have considered b1 (Fig. 3A) to be the most appropriate reference ground state.^33,34 Apparently, b3 is the only DS of 2-methylphenol. Moreover, our estimation of the energy difference between b1 and b2, 0.77 kcal mol⁻¹, is roughly within ± 0.25 kcal mol⁻¹ of experimental and theoretical values.^35,36

Figure 3.

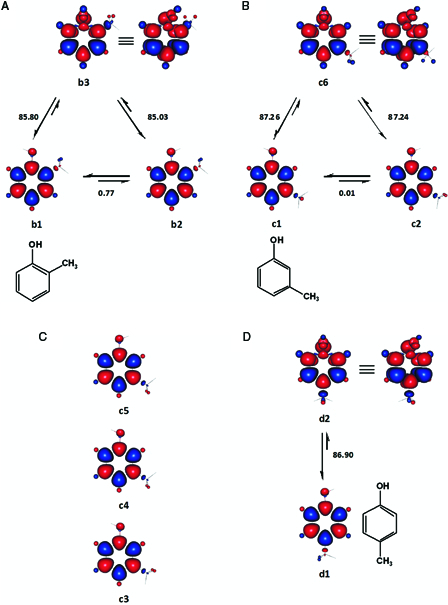
The relevant conformers and enthalpy changes (kcal mol⁻¹) considered for 2-methylphenol (A), 3-methylphenol (B) and 4-methylphenol (D). Singlet state transition conformers of 3-methylphenol (C) which were located at UHF/6–31G(d,p) are also shown for comparison. Red and blue are spin up and spin down regions, respectively.

c1 and c2 (Fig. 3B) were located as the two ground singlet states of 3-methylphenol at 6-31G(d,p) basis set. In c1, which is syn according to Hellweg et al.,³⁷ one of the methyl hydrogen atoms is almost perpendicular to the plane of the ring, while it is coplanar in the anti-conformer c2. All the other singlet state conformations tested, either failed to converge at all or converged to first-order saddle points (c3, c4, and c5) with respect to the torsional angle of the methyl group at 6-31G(d,p). Average BDE and BDFE were calculated using c1 and c2, which were energetically near degenerate.

The effects of the size of basis sets on the conformations and theoretical BDE (and BDFE) of 3-methylphenol were also assessed. Fig. 2 summarizes the BDE results together with those from phenol and additional conformational information may be found in the Appendix. As can be gathered from the figure, the relative performances of the basis sets on BDE were essentially similar to that outlined for phenol. Once again, the results from 3-methylphenol confirmed that our working basis set, 6-31G(d,p) was optimum for the purpose of this introductory work. However, the ground singlet state conformations changed at higher basis sets, mainly due to a shift in the preferred torsion angle of the methyl group³⁷ (see Appendix).

Fig. 3C shows that in the ground singlet state of 4-methylphenol (d1), the phenolic hydrogen atom, and one of the methyl hydrogen atoms face towards each other and are coplanar with the aromatic ring. These findings are in line with previous reports.^38,39 Similarly, the vibrationally activated OH group and one of the para methyl hydrogen atoms face towards each other in the DS of 4-methylphenol.

2-Methoxyphenol

e1-e4 (Fig. 4) are four ground singlet state conformations of 2-methoxyphenol, which differed in terms of hydrogen bonding and steric crowding. e1 and e2 exhibit intramolecular hydrogen bonding and in e2 and e4, the methoxyl groups are out-of-plan with torsion angels of ca. 74 and 105.4°, respectively. The methoxyl groups in the DS e5 and e6 have diametrically different torsion angles; ca. 0 and 149°, respectively. Owing to the near-degeneracy of e5 and e6, average BDE and BDFE were calculated for 2-methoxyphenol (Table 2) with respect to both DS conformers. Some of our singlet state structures are quite similar to the ones established by Agache and Popa using MP2/6-311G(d,p).⁴⁰

Figure 4.

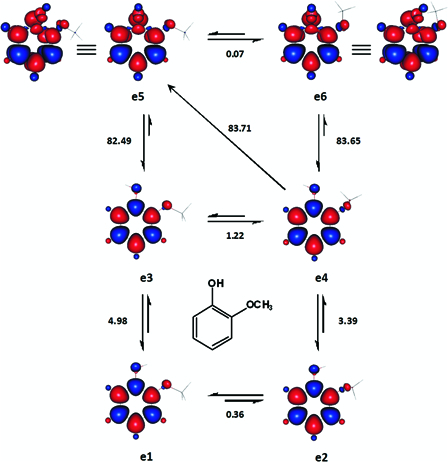
The important ground singlet and excited triplet states of 2-methoxyphenol analysed for the estimation of its BDE and BDFE. The enthalpy changes shown are in kcal mol⁻¹. Red and blue are spin up and spin down regions, respectively.

2,6-Dimethoxyphenol

Five energetically different ground singlet state conformations of 2,6-dimethoxyphenol were located. Four of these are shown in Fig. 5 (f1-f4). The singlet state, which is not shown (SCF ≈ −533.336564 and ɛ_o + H_corr = −533.144715 Hartree), was asymmetrical and had a methoxyl group facing each plane of the aromatic ring. In these conformers of 2,6-dimethoxyphenol (and to some extent 2-methoxyphenol), intramolecular hydrogen bonding and steric interactions may somehow counterbalance each other's effect on internal energy.

Figure 5.

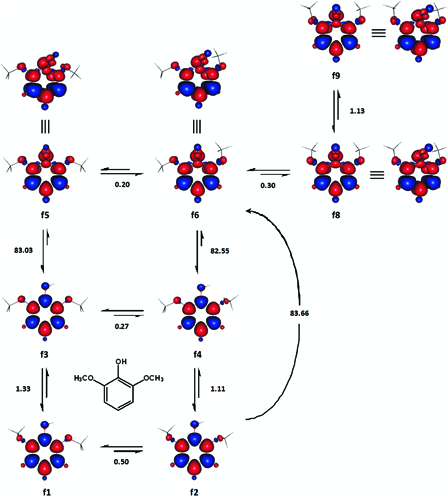
Selected transformations of 2,6-dimethoxyphenol together with the accompanying enthalpy changes (kcal mol⁻¹). Red and blue are spin up and spin down regions, respectively.

The DS of 2,6-dimethoxyphenol may also be found in at least five different conformations. The use of the relatively stable singlet state, f2, and one of the three dissociative states, f5, f6 and f8, resulted in BDE values, which were very close to the reported experimental BDE of the compound (Table 2).^41,42 Therefore, the BDE (and BDFE) of 2,6-dimethoxyphenol were estimated as the mean of the three enthalpy changes (and changes in Gibbs free energy) accompanying the formations of these dissociative states with respect to f2.

BHT

Two of the ground singlet states of BHT, g1 and g2, were essentially degenerate as the absolute enthalpy difference between them was only about 0.0006 kcal mol⁻¹ (Fig. 6A). In g1 and g2, the phenolic hydrogen atom is perpendicular to the average plane of the aromatic ring, with dihedral angles of 91.1 and 91.0°, respectively, for C6-C1-O39-H40. The structural results outlined above were in line with literature accounts.^3,43,44 When viewed along the side of the molecules, the two tert-butyl groups are precisely eclipsed in both g1 and g2. g4 was the only DS which could be located. In the DS, one of the methyl hydrogen atoms is preferentially coplanar and cis to the activated para phenolic group.

Figure 6.

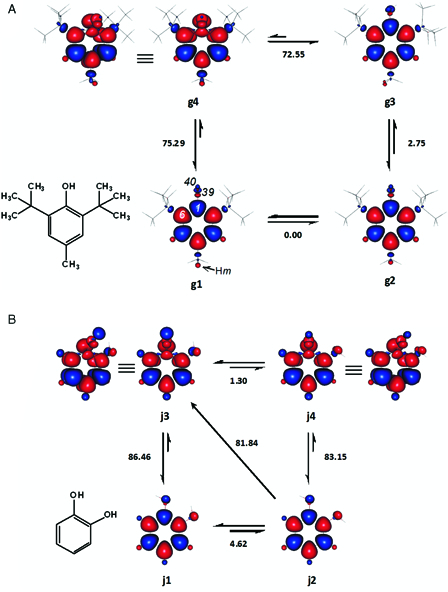
Enthalpy changes (kcal mol⁻¹) between the important conformers of BHT (2,6-di-tert-butyl-4-methylphenol) (A) and catechol (B). In BHT, one of the para methyl hydrogen atoms (Hm) is perpendicular to the average plane of the aromatic ring. Hm is above or below the ring in g1 and g2, respectively. Red and blue are spin up and spin down regions, respectively.

1-Naphtol and 2-naphtol

h1 (Fig. 7A) is apparently the global minimum of 1-naphtol. Rotating the hydroxyl group by about 136°, yielded the only local minimum we could locate (h2). Considering the relative agreement of the calculated BDE values of 1-naphtol, with a literature experimental BDE,³³ the singlet state with lower steric congestion, h1, may be suggested as a better reference state.

Figure 7.

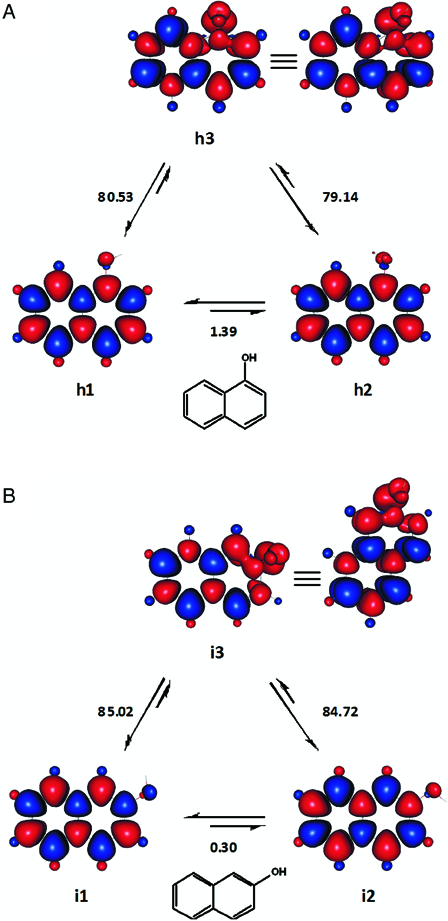
The ground singlet states and excited triplet states of 1-naphthol (A) and 2-naphthol (B) employed to study the homolytic dissociations of the compounds. Enthalpy changes shown are in kcal mol⁻¹. Red and blue are spin up and spin down regions, respectively.

Our results for 2-naphthol are shown in Fig. 7B. The enthalpy change for the transformation i2 → i3, 84.72 kcal mol⁻¹ agrees with the experimental BDE reported by Denisov and Denisova.³³ Similarly, the enthalpy change of 85.02 kcal mol⁻¹ for the alternative transformation could be considered to be quite closer to the experimental BDE forwarded by Das and Neta.⁴⁵ We have speculatively chosen the BDE and BDFE values calculated using i1 (Table 2). Optionally, average BDE and BDFE may be calculated for 2-naphthol with respect to both singlet states, i1 and i2. Nevertheless, a series of remotely substituted analogues (e.g. halogenated 2-naphthols) should be examined before labelling one of these two singlet states (cis and trans,⁴⁶ respectively), as a reasonable reference state.

Catechol

j2 and j3 in Fig. 6B were selected for the estimation of the BDE of catechol, owing to the facts that the former was devoid of any intramolecular hydrogen bond and the latter was the more stable DS. The associated enthalpy change of 81.84 kcal mol⁻¹, matched well with the gas phase BDE of the phenol recommended by Lucarini et al.⁴⁷ and Barzaghi and Herrmann.³⁴

5,6-Isopropylidene-l-ascorbic acid, l-ascorbic acid and α-hydroxytetronic acid

The side chain of 5,6-isopropylidene-l-ascorbic acid (IASA) can assume at least two non-equivalent local conformations. Yet, the conformers of IASA (Fig. 8) considered in this report were all based on the local conformation of the side chain, which by and large, imparted better stability. Depending on the combination of the ground singlet state and DS, four significantly different estimations for BDE were calculated. The transformation ka → kc might characterize the homolysis of IASA owing to the fact that its enthalpy change, 75.98 kcal mol⁻¹, was relatively closer to a solution experimental BDE of IASA (75.1 kcal mol⁻¹).⁴⁸ However, comparison between calculated gas phase BDE and experimental BDE in solutions should be carried out carefully and be regarded with caution.

Figure 8.

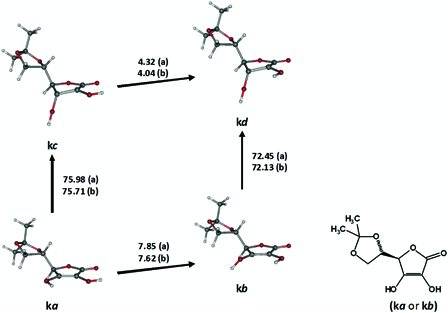
Transformations between selected ground singlet states and excited triplet states of 5,6-isopropylidene-l-ascorbic acid (IASA). ‘a’ designates the enthalpy changes (kcal mol⁻¹) for IASA and ‘b’ for α-hydroxytetronic acid, which is devoid of the side chain on C4.

Conformers analogous to ka-kd were consistently used in the case of α-hydroxytetronic acid (HTA) and l-ascorbic acid (AsH₂) as well. Since the dihydroxyethyl side chain of AsH₂ may assume several local conformations, six sets of conformations, SET m1-SET m6, were examined to get an average picture (Fig. 9A). Our best estimates for the gas phase BDE (75.4 ± 0.7 kcal mol⁻¹ (n = 6)) and BDFE (74.3 ± 0.6 kcal mol⁻¹ (n = 6)) were calculated using the transformations m1a → m1c, m2a → m2c, m3a → m3c, m4a → m4c, m5a → m5c, and m6a → m6c. Compared with the only available experimental BDE and BDFE values of AsH₂ in the aqueous phase,⁴⁸ the calculated values are lower by about 2.6 and 5.5 kcal mol⁻¹, respectively.

Figure 9.

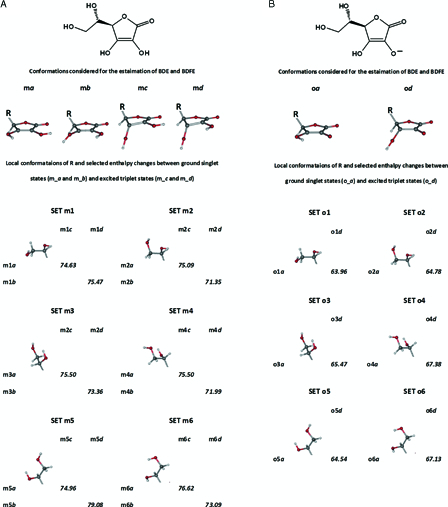
Six sets of conformers of l-ascorbic acid (A) and l-ascorbate (B) considered for the estimation of BDE and BDFE. Enthalpy changes shown are in kcal mol⁻¹.

5,6-Isopropylidene-l-ascorbate, l-Ascorbate and α-hydroxytetronate

Some of the important conformers of 5,6-isopropylidene-l-ascorbate (IASA⁻), which were considered for the calculation of gas phase BDE and BDFE are shown in Fig. 10. In light of the solution experimental BDE and BDFE values of IASA⁻ (Table 2), the key transformation for the homolytic dissociation of the anion may be na → nd. The calculated changes in enthalpy and Gibbs free energy for this transformation were 67.3 and 66.0 kcal mol⁻¹, respectively. Selected results for α-hydroxytetronate (HTA⁻) are also given in Fig. 10. Once again, average gas phase BDE and BDFE had to be calculated for l-ascorbate (AsH⁻) due to the variable local conformations of its dihydroxyethyl side chain. The four transformations in Fig. 9B, o2a → o2d, o3a → o3d, o4a → o4d and o6a → o6d were carefully selected to this end and considered with due regard to literature experimental BDE and BDFE values (Table 2).

Figure 10.

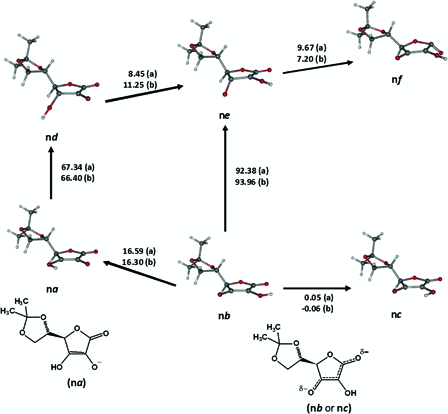
Transformations between selected ground singlet states and excited triplet states of 5,6-isopropylidene-l-ascorbate (IASA⁻). ‘a’ designates the enthalpy changes (kcal mol⁻¹) for IASA⁻ and ‘b’ for α-hydroxytetronate, which is devoid of the side chain on C4.

6,7-Dihydroxyflavone

Fig. 11 illustrates some conformers of 6,7-dihydroxyflavone. p1-p5 were different ground singlet states. p2 and p5, in particular had a discontinuity in their spin density distributions, which signified an incomplete conjugation between ring A and rings B and C. Similarly, several dissociative states were identified, which might lead to a homolytic dissociation from 6-OH (e.g. p6-p8) or 7-OH (e.g. p9 and p10). 7-OH may be the first hydroxyl group to undergo a homolytic dissociation as the transformation p5 → p9 was associated with an enthalpy change which was relatively close to the reported experimental BDE of the flavone, 79.4 kcal mol⁻¹ (Table 2). Additional results and some of the relevant considerations made in the analysis of our data can be found in the Appendix.

Figure 11.

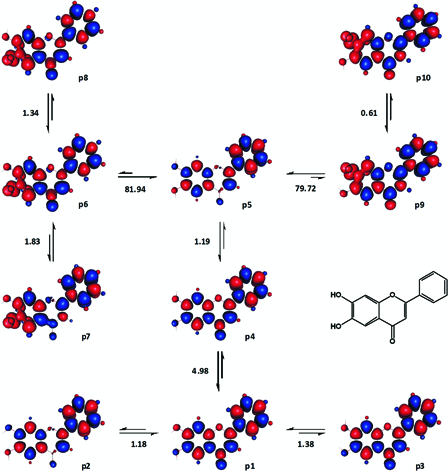
Various transformations of 6,7-dihydroxyflavone analysed for the estimation of its BDE and BDFE. Enthalpy changes shown are in kcal mol⁻¹. Red and blue are spin up and spin down regions, respectively.

7,8-Dihydroxyflavone

Six different ground singlet states and 14 DSs were characterized for 7,8-dihydroxyflavone and Fig. 12 depicts selected results. The patterns of spin density distribution in the conformers of 7,8-dihydroxyflavone were very much similar to those in 6,7-dihydroxyflavone (Fig. 11). In 7,8-dihydroxyflavone, the first hydrogen atom may be abstracted from 8-OH as the enthalpy change for q5 → q9 coincided with the reported experimental BDE of the compound (Table 2).

Figure 12.

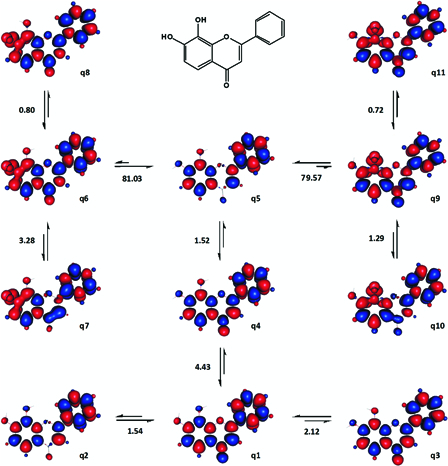
Various transformations of 7,8-dihydroxyflavone analysed for the estimation of its BDE and BDFE. Enthalpy changes shown are in kcal mol⁻¹. Red and blue are spin up and spin down regions, respectively.

5,7-Dihydroxyflavone

As can be seen from Fig. 13, the patterns of spin density distribution in the ground singlet state conformers of 5,7-dihydroxyflavone were quite different from those of the previous flavones'. Initially, both r1 and r4 were assessed as potential reference ground states for the computation of BDE and BDFE. However, based on this initial assessment, chemical intuition and experimental BDE⁴⁹ the former was found to be slightly more suitable. Accordingly, the gas phase BDE for 5-OH (81.7 kcal mol⁻¹) and 7-OH (88.9 kcal mol⁻¹) were calculated with respect to the transformations r1 → r5 and r1 → r7, respectively. Coincidentally, the only available experimental BDE⁴⁹ of the compound, 85.3 kcal mol⁻¹, was equal to the average value of the above two theoretical BDE values. We thus speculated that the actual experimental BDE of 5,7-dihydroxyflavone could be indeed the average of the individual BDE values of its two OH groups.

Figure 13.

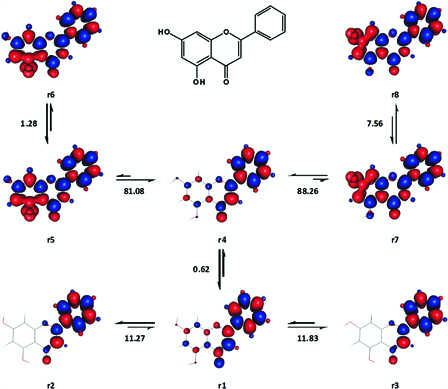
Various transformations involving the ground singlet states and excited triplet states of 5,7-dihydroxyflavone. Enthalpy changes shown are in kcal mol⁻¹. Red and blue are spin up and spin down regions, respectively.

Luteolin

The homolytic bond dissociation of luteolin was studied considering only 3′-OH and 4′-OH, assuming that the ring-A hydroxyl groups may not play an important role in the radical scavenging activity of the compound.²¹ This necessitated fixing the local conformation of ring A. As a result, four sets of luteolin conformers were generated, each consisting of 14 ground singlet states and dissociative states. The contributions of anti and syn conformers⁵⁰ were also examined.

The results from one of these four sets, where both 5-OH and 7-OH face towards the 4-oxo group, are shown in Fig. 14. Referring to Fig. 14 for illustration, the enthalpy changes accompanying the transformations s3 → s9 (syn conformers) and s6 → s13 (anti conformers) were relatively close to the reported experimental BDE⁴⁹ of luteolin, 81.9 kcal mol⁻¹. The enthalpy changes accompanying analogues transformations were generally comparable among anti and syn conformers and also across the four sets. Accordingly, the gas phase BDE of luteolin was calculated to be 81.9 ± 0.1 kcal mol⁻¹ (n = 8).

Figure 14.

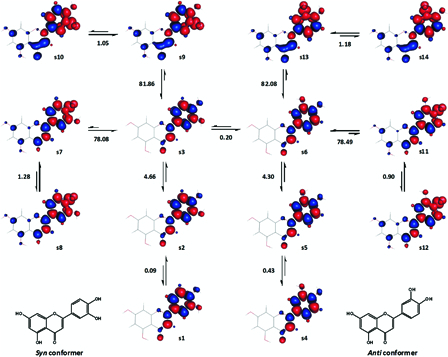
A set of related ground singlet state and excited triplet state conformers of luteolin. Half of the conformers (s1-s3 and s7-s10) have syn form and the remaining (s4-s6 and s11-s14), anti form. Enthalpy changes shown are in kcal mol⁻¹. Red and blue are spin up and spin down regions, respectively.

Hesperetin

Hesperetin has a 5,7-dihydroxy substituted ring A and a 3′-hydroxy-4′-methoxy substituted ring B. As in the case of luteolin, only ring B was analysed for hesperetin, with the assumption that the meta-substituted ring A was unimportant for the compound's radical scavenging activity. Nevertheless, in order to account for the structural variability of hesperetin arising from the relative orientations of ring A hydroxyl groups, two sets of conformers were considered. Each set of conformers consisted of 20 ground singlet states and dissociative states, which had the same form of ring A. Only two sets of conformers were considered, since the results for luteolin had indicated that remote substituents might not have a significant impact on calculated BDE and BDFE.

Fig. 15 shows part of the results from one of the two sets. The enthalpy changes of r5 → r7, r6 → r9 and six more analogous transformations were used for the estimation of the gas phase BDE of hesperetin as they were relatively close to its experimental BDE (Table 2). Similarly, the corresponding changes in Gibbs free energy of these transformations were used to estimate the gas phase BDFE of hesperetin. The ground singlet states in these eight transformations (e.g. r5 and r6) had an out-of-plane methoxyl group, which might minimize steric crowding. The relative position of the methoxyl group did not significantly alter the energy level of the dissociative states (for instance, compare r7-r10). However, only those dissociative states with an out-of-plane methoxyl group were considered for the estimation of BDE and BDFE.

Figure 15.

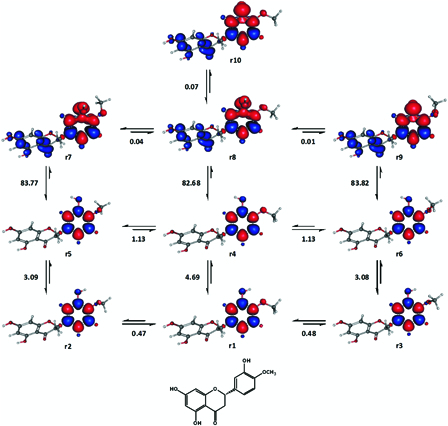
Some representative conformers of hesperetin analysed for the estimation of BDE and BDFE. Enthalpy changes shown are in kcal mol⁻¹. Red and blue are spin up and spin down regions, respectively.

Discussion

Mulder et al.²⁷ have stressed that the kinetics and thermodynamics of the radical scavenging reactions of phenols are intimately interrelated. However, the relative importance of these two aspects and how they interact with each other have largely remained unclear and misunderstood at best.⁵ Not surprisingly, the anchoring principles and unambiguous estimations of the energy changes which are characteristic of the kinetic and thermodynamic components of antioxidant reactions have been a source of an ongoing debate.^6,51 Nevertheless, if the thermodynamical aspect of radical scavenging activities is largely governed by the intrinsic properties of the radical scavenger, the same might be expected for the kinetic aspect.⁵

The new method of gas phase BDE and BDFE determination was formulated mainly based on an exploratory trial-and-error work. Understandably, the formalization is far from complete at this stage. However, certain fundamental assumptions, general considerations and consistent patterns can be highlighted. Since radical scavenging activity may be the property of compounds,⁵ it may be stipulated that the homolytic dissociations of radical scavengers might be a unimolecular process.⁵² The unpairing of bonding electrons during the homolysis of phenols may actually have its origin in an induced unpairing of their π-electrons.^52,53 Such a crossover to a triplet state prior to homolysis may be supported by accounts on photodissociation of aromatic compounds^54–56 and photochemical analyses of phenol.^57,58 Likewise, Nguyen et al.²⁴ have noted that vibrationally excited species of phenol may be implicated in its BDE.

General considerations

The homolytic dissociations of hydroxylic antioxidant molecules might invariably involve a combination of a one-step excitation of π-electrons (e.g. singlet → triplet or triplet → quintet) and vibrational excitations of OH groups. By and large, the ground states which would be suitable for the computation of BDE and BDFE with the proposed method would be singlet states, which are less stabilized by intramolecular hydrogen bonding and have minimum steric interactions. Since our results were mainly for compounds with isolated (non-fussed) aromatic rings, the significance and feasibility of using ground triplet states could not be ascertained.

Intramolecular hydrogen bonding and steric interactions play an important role in altering the internal energy of molecules. Unless they are systematically and consistently taken into account, they can be potential sources of error in the determination of theoretical BDE and BDFE. As already indicated, hydrogen bonding particularly involving the homolytically dissociating OH group, should be minimized in the ground state unless it is unavoidable (e.g. as in l-ascorbic acid). A transient stabilization afforded by intramolecular hydrogen bonding may result in the overestimation of enthalpy changes.⁵ On the other hand, steric interactions in the ground state should also be minimized as they may increase internal energy and result in the underestimation of calculated changes in enthalpy and Gibbs free energy.

In the DS, the formation of intramolecular hydrogen bonding involving the vibrationally activated OH group was stabilizing and apparently desirable in most cases. The important exceptions to this trend were the DSs of 5,6-isopropylidene-l-ascorbic acid (kc), l-ascorbic acid (m1c-m6c) and α-hydroxytetronic acid. The aforementioned dissociative states were stabilized by intramolecular hydrogen bonding which did not involve the dissociating OH group. This may indicate that while it affects internal energy, intramolecular hydrogen bonding in the DS may not have a mechanistic role.

As is evident from the results obtained, the new method holds promise for application across a range of hydroxylic antioxidants. The agreement between our calculated gas phase results and the adopted highly reliable experimental values were generally within 0.5 kcal mol⁻¹, with a relatively very few exceptions. Moreover, there is a good indication that, with proper modifications, the new method may be successfully applied for non-hydroxylic antioxidants as well (results not shown). In this regard, work currently is underway on thiol, alkyl and amine antioxidants.

2-Methoxyphenol, 2,6-dimethoxyphenol and hesperetin

Notwithstanding the fact that molecules possessing higher energy normally spearhead chemical transformations, they may acquire internal energies in ‘reaction coordinates’ that would not ultimately contribute to the reaction of interest. Steric interaction is a phenomenon that may create such a situation and this was well exemplified with the results for 2-methoxyphenol, 2,6-dimethoxyphenol and hesperetin. The experimental BDE of these compounds were best reproduced, only when both intramolecular hydrogen bonding and steric interactions in the ground singlet states were sufficiently reduced.

Despite the consistent and remarkable agreement between most of our theoretical BDE and BDFE and the adopted highly reliable experimental values (Table 2), there exist discrepancies of ca. 0.5–1.0 kcal mol⁻¹ and ca. 0.9 kcal mol⁻¹ in the cases of 2-methoxyphenol and hesperetin, respectively. Plausible explanations for this may include (a) failure to locate a better reference ground state (e.g. one that might lie between e2 and e4), (b) limitations of UHF and/ or the basis set 6-31G(d,p), and (c) inaccurate experimental values. There is also a good ground to speculate that the <C-O-H bond angle in the DSs of these two compounds should be slightly different from 180° owing to the presence of an ortho methoxyl group.

The reported experimental values for the intramolecular hydrogen bonding in 2-methoxyphenol include 3.3 kcal mol⁻¹ by Spencer et al.⁵⁹ and a recent gas phase value of 3.2 kcal mol⁻¹ by Varfolomeev et al.⁶⁰ The enthalpy difference between e2 and e4 (3.4 kcal mol⁻¹) is more consistent than the one between e1 and e3 (5.0 kcal mol⁻¹) with the aforementioned reported values. This might strongly indicate that ortho methoxyl groups would most likely be positioned in actual equilibrium structures as out-of-plane substituents, in order to minimize steric congestion. This may prevail for other bulky substituents as well.

BHT

Theoretical gas phase BDE values of BHT from this study (75.3 kcal mol⁻¹) and others^61,62 are about 4 kcal mol⁻¹ lower than a handful of very close experimental gas phase BDE^3,10,63 values of the compound. These discrepancies may possibly arise due to an increase in the BDE of BHT in solvents, as was pointed out by Singh et al.⁶¹ On the other hand, our calculated gas phase BDFE of BHT is appreciably close to the reported BDFE of the phenol in alkane solvents (Table 2).⁶⁴ Our calculated BDFE is also within an acceptable range of other BDFE values of the compound reported by Mayer group.^48,64 This is encouraging given the fact that BDFE values are more appropriate owing to enthalpy/entropy compensation.⁶⁵ Since calculated gas phase BDE and BDFE values only differ slightly (Table 2), we strongly believe that our BDE value for BHT may, at least, deserve the benefit of the doubt.

1-Naphtol and 2-naphtol

A rather comprehensive account on the different conformers of 1-naphthol and 2-naphthol can be obtained in reference 46 (and references therein) and some comparison of our results may be made with it. The monohydroxylated naphthols were among the few compounds tested which showed relatively considerable difference between our calculated BDE and BDFE values and experimental reports. Unfortunately, for these naphthols, the relative agreement among their respective experimental BDE values^{7,33,45,66,67} is not as such encouraging, even when the solvent variability was taken in to account.⁶⁴

Our BDE for 1-naphthol (Table 2) is about 1.6 and 2.2 kcal mol⁻¹ lower than the compound's experimental BDE according to Denisov and Denisova³³ and Das and Neta,⁴⁵ respectively. Our BDFE for this naphthol is also considerably higher than its reported experimental gas phase BDFE, while being identical with the corresponding value in isopentane.⁶⁴ Admittedly, we cannot provide satisfactory explanations for these discrepancies. For instance, there might exist a singlet state conformer which is more stable than h1. It can also be speculated that the experimentally determined BDE values of 1-naphtol (and potentially 2-naphtol) might contain some contributions from transformations involving higher spin states (e.g. triplet → quintet).

In order to assess the implication of higher spin state transformations in the BDE of 1-naphthol, the enthalpy changes between various ground triplet states and vibrationally excited quintet states have been examined (results not shown). Depending mainly on the ground triplet states, the results were usually either less than 72 kcal mol⁻¹ or greater than 87 kcal mol⁻¹. Nevertheless, an estimate for the relative prevalence of triplet ground states at a given temperature and pressure would be required to establish the relative significance of triplet → quintet transformations in the homolytic dissociation of 1-naphthol.

Catechol

Many authors consider that in the intramolecularly hydrogen bonded singlet state of catechol (j1, Fig. 6B), the strong hydrogen bonding weakens the free OH group. In addition, intramolecular hydrogen bonding is said to be behind the outstanding reactivity of catechol (and other compounds containing ortho phenolic group), since its strength is said to increase in the phenoxyl radical.^{47,49,68–71} Expectedly, however, intramolecularly hydrogen bonded ground conformations would result in higher BDE values, due to the need to overcome the extra stabilization rendered by the hydrogen bonding.^5,72

The BDE values calculated from j1 and j2 (Fig. 6B) may strongly corroborate the last statement. The BDE values calculated starting from j1 are significantly higher than the reported experimental BDE of catechol. On the other hand, an exceptionally good agreement with experimental values was achieved particularly with the enthalpy change for j2 → j3. This indicates that intramolecular hydrogen bonding in the ground state of catechol cannot be expected to facilitate the abstraction of the first (as well as the second) phenolic hydrogen atom.

At this juncture, we would also like to call attention to the alternative views on the nature of the intramolecular hydrogen bonding between the ortho hydroxyl groups of catechol in the gas phase, which stipulate either its total absence^73–75 or relatively weak strength.^76–78 The intramolecular hydrogen bonding in catechol may be overestimated by the cis-trans computational method since the O···O nonbonding interaction may be enhanced in the non-hydrogen bonded conformer.^78,79 Considering everything, it may safely be suggested that even at ambient reaction conditions, the relative proportion of the non-hydrogen bonded ground state (which may not necessarily resemble j2⁷³) may be significant enough in the Boltzmann population of catechol molecules, to result in a lower BDE.

A number of dissociative states and ground triplet states of catechol may also form intramolecular hydrogen bonding. For instance, a relatively weak (1.3 kcal mol⁻¹) intramolecular hydrogen bonding may be responsible for the slightly better stability of j3 over j4. The fact that j3 would be the preferred DS may not be surprising since activation often proceeds via the least energetic route. Therefore, as indicated earlier hydrogen bonding involving the dissociating hydroxyl group may be desirable in the dissociative states.⁸⁰

Flavonoids

The discussions for phenol and catechol also hold for the flavones studied. An additional element that should be considered for the theoretical determination of BDE and BDFE in flavones is the type of conjugations between ring-A and rings B and C. Complete conjugation of the ring systems generally lowered energy while decreased delocalization possibilities (incomplete conjugation) caused the opposite in both singlet and triplet states. Like in the case of intramolecular hydrogen bonding, the agreement with reported experimental BDE may be improved if the reference ground states have an incomplete conjugation (e.g. p5 and q5) and the DS, a complete conjugation (e.g. p9 and q9). Another consideration is that, ring-A of flavones may not be of consequence for the theoretical study of homolysis in ring-B.

7-OH in 6,7-dihydroxyflavone and 8-OH in 7,8-dihydroxyflavone, may be the hydroxyl groups which undergo the first homolytic dissociation and the BDE values associated with them were lower than the respective alternatives. The most stable semi-quinone phenoxyl radicals of these flavones are also derived from 7-OH and 8-OH, respectively.⁵ However, di- or polyhydroxyflavones and other compounds may alternatively form their less stable radical derivatives in the first instance of homolytic dissociation as was observed for luteolin.

The apparent discrepancy between the experimental BDE of 5,7-dihydroxyflavone⁴⁹ and the calculated BDE for its two OH groups may be a bit striking at the first glance. At the same time, our average gas phase BDE of 85.3 kcal mol⁻¹ was virtually identical with the experimental BDE of 5,7-dihydroxyflavone.⁴⁹ In order to rationalize the apparent discrepancy between the experimental and calculated BDE of the compound, we took into account the fact that 5,7-dihydroxyflavone was one of the least active hydrogen atom donors.⁵ Accordingly, we speculated that 5,7-dihydroxyflavone might be forced to undergo incomplete cycles of homolytic dissociations from either of its OH groups.⁵ Therefore, the experimental BDE of 5,7-dihydroxyflavone may actually be an average of the individual BDE values of 5-OH and 7-OH. Nevertheless, further experiential or theoretical lines of evidences may be in demand to definitively address this particular issue.

l-Ascorbic acid, l-ascorbate and their analogues

We have made the assumption that the hydrogen bond between 2-OH and 1C=O (Fig. 8 and 9A) may consistently be conserved during the transformation from the reference ground states (Ka and m1a-m6a) to the dissociative states (kc and m1c-m6c) of IASA and AsH₂. This assumption was made after critically scrutinizing a number of factors at hand. Nonetheless, its validation may require more reliable experimental gas phase BDE and BDFE values for IASA and AsH₂. The fact that the energy changes for corresponding transformations in IASA, HTA and AsH₂ were relatively similar may indicate that a side chain on 4C should not significantly affect calculated BDE and BDFE in these compounds. However, the BDE and BDFE of AsH⁻ were relatively sensitive to the local conformation of the dihydroxyethyl side chain.

The kinetically significant species of l-ascorbic acid depends on pH⁸¹ and while some may argue differently,⁸² generally the conjugate base is considered to be more active than the acid.⁸³ The superior radical scavenging activities of IASA⁻ and AsH⁻ may be rationalized in part by their appreciably lower BDFE values.⁸⁴ In relation to this, the deprotonation of 3-OH may be more favourable than that of 2-OH, since nb and nc in Fig. 10 are more stable than na by about 16 kcal mol⁻¹. This was also the case for AsH⁻ as well (data not shown). However, the deprotonation of 2-OH might be the one, which would be associated with the enhanced radical scavenging activities of AsH^- and IASA^-.

In the literature two opposing views are found regarding which one of the two enolic hydroxyl groups losses its proton first. In some of the earlier reports by Njus et al.,^85,86 2-OH has been deprotonated in the conjugate base. However, in a number of other reports the conjugate base forms of AsH₂ and its derivatives are depicted as to be deprotonated from 3-OH.^84,87,88 The later is consistent with the pK values of 2-O-methyl-l-ascorbic acid and 3-O-methyl-l-ascorbic acid, which are 3.2 and 7.8, respectively.⁸⁹ It may be noteworthy that the pK₁ of l-ascorbic acid, 4.04,⁸⁵ may not be entirely ascribed to only one of the enolic hydroxyl groups but rather be regarded as a weighed average of the individual pK values of both 2-OH and 3-OH.

Conclusion

A critical aspect of the present work is that it has clearly demonstrated that BDE and BDFE are not actually thermodynamical quantities⁵ but rather, activation barriers, which would be required to initiate equilibrium homolytic dissociation. This unequivocally challenges the traditional definitions of BDE and BDFE. Therefore, despite the wide spread misconception, BDE and BDFE cannot be expected to determine the direction of hydrogen atom transfer reactions.⁵ As would be expected, however, BDE and BDFE should be significant as kinetic parameters. With this in mind, it would be interesting to examine how the proposed method would perform in computational solvation models and simulated reaction conditions.

The method forwarded is reliable for application across a range of hydroxylic antioxidants. As was also noted previously,⁵ based on the results of this study we may conclude that ab initio Hartree–Fock method is adequate for the estimation of BDE and BDFE. At present the formalization of our method is far from complete. Work is underway on the postulate that the homolytic dissociation of O–H bonds from a4 and analogous species may involve the detachment of an excited electron from the highest occupied molecular orbital (HOMO). The detached electron would leave being accompanied with a proton. Short of further details, we would like to stress that the formalization of this new approach may hold the key to a better understanding of chemical bond formation and breakage.

Attribution

This work is attributed to - University of Western Sydney, Great Western Highway, Werrington 2747, Australia.

Appendix

3-Methyphenol

Up on optimization with 6-311G(d,p), 6-31 + G(d,p), 6-31 + +G(d,p), and increasing polarized basis sets at 6-31G level, the out of plane torsion angel of the methyl group was increasingly suppressed and finally disappeared completely at 6-31G(3df,3pd). Equilibrium conformations for c1 (Fig. 3B and 3C) could not be achieved at 6-31G(3df,p) and 6-31G(3df,3pd). At 6-31G(3df,p), c4 replaced c1 as one of the singlet minima. The three ground singlet states at 6-31G(3df,3pd) were c2, c3 and c4. The relative conformation of the DS, c6, remained unchanged across the basis sets tested.

Figure A1.

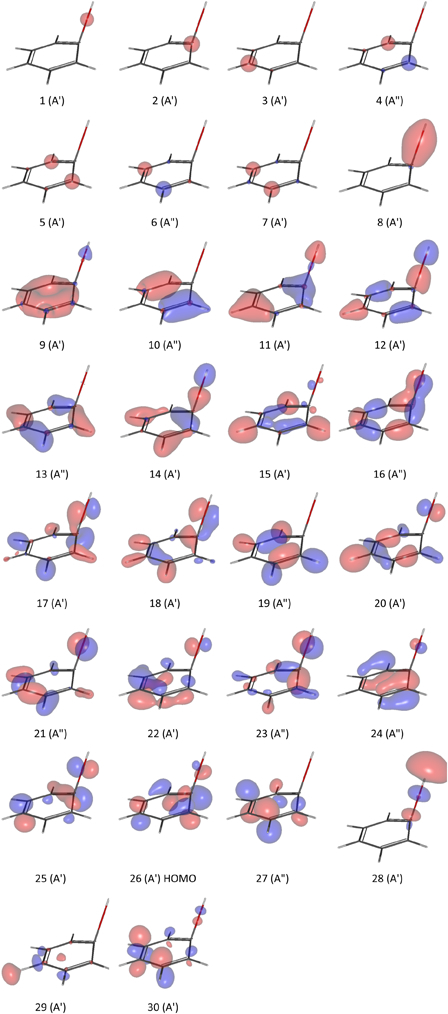
The first thirty alpha (α) molecular orbitals of a4 at UHF/6-31G(d,p). The Gabedit figures were generated at an isovalue of 0.085 au.

5,6-Isopropylidene-L-ascorbic acid, L-ascorbic acid and α-hydroxytetronic acid

We have mainly focused on the homolytic dissociation of 3-OH in 5,6-Isopropylidene-L-ascorbic acid (IASA), L-ascorbic acid (AsH₂) and α-hydroxytetronic acid (HTA), since it may donate the first hydrogen atom according to literature^1,2 and our preliminary results. Note that the DS for the homolysis of 3-OH, may exist in two diasteriomeric forms in IASA and AsH₂ depending on the position of the activated OH with respect to the side chian at 4C. Our reported results and discussions for IASA and AsH₂ in the main article were based on the dissociative state conformers, which had the activated OH on the opposite side of the isopropylidene substituent (Fig. 8 and Fig. 9A). Employing the ‘cis’ variations of kc or kd instead of kc or kd, would slightly decrease the associated BDE values by 0.13 and 0.24 kcal mol⁻¹, respectively. For AsH₂, the ‘cis’ forms of the dissociative states m1c-m6c (Fig. 9A) were on average less stable than m1c-m6c by ca. 0.9 ± 0.8 (n = 6) and similarly the ‘cis’ counterparts of m1d-m6d were less stable than m1d-m6d by ca. 0.8 ± 0.9 (n = 6).

5,6-Isopropylidene-L-ascorbate, L-ascorbate and α-hydroxytetronate

Considering the ‘cis’ conformer of nd (Fig. 10) would increase the apparent BDE and BDFE of 5,6-isopropylidene-L-ascorbate (IASA⁻) by about 1.0 and 1.7 kcal mol⁻¹, respectively. Considering all the six transformations in Fig. 9A (main article) for L-Ascorbate (AsH⁻) would give rise to BDE and BDFE values, which were slightly lower but slightly more variable than the corresponding values adopted for the anion (Table 2).

6,7-Dihydroxyflavone, 7,8-dihydroxyflavone, 5,7-dihydroxyflavone and luteolin

Initially, p4 (Fig. 11) was chosen for the calculation of BDE and BDFE owing to the absence of intramolecular hydrogen bonding in the structure. However, the BDE values calculated accordingly, 83.13 kcal mol⁻¹ (p4 → p6) and 80.91 kcal mol⁻¹ (p4 → p9), were both higher than the literature experimental value (Table 2). This prompted us to search for another singlet state, with a slightly higher energy than that of p4's, which might be able to close the gap between the theoretical and experimental values. This endeavour led to the identification of p5, which could reduce the aforementioned BDE values by about 1.19 kcal mol⁻¹.

The activated O-H in 6,7-dihydroxyflavone and the other flavones may flip upwards or downwards relative to the average plane of the aromatic ring. In order to avoid ambiguity, the common standard orientation of flavonoids has been consistently adopted in the study. Accordingly, p6-p10, q6-q11, r5-r8 and s7-s14 are all upward isomers. The upward and downward isomers of p6-p8 equilibrated to near degenerate diasteriomers. On the other hand, the upward and downward isomers of p9 and p10 were enantiomers. With respect to p6, p7 and p8, the relative enthalpies of formation of their downward counterparts were 0.000000, 0.001883 and −0.005020 kcal mol⁻¹, respectively. A more or less, comparable energy differences were also obtained for the upward and downward isomers of the dissociative states of 7,8-dihydroxyflavone, 5,7-dihydroxyflavone and luteolin. Since this type of conformational variation was relatively insignificant, it was not considered in the actual report.

Acknowledgement

This work was supported by UWSIPRS and the NCI National Facility at ANU (Australian National University, Canberra, Australia). Computational and storage resources used in this work were provided by Intersect Australia Limited.

Funding

This study was supported by UWSIPRS: University of Western Sydney International Postgraduate Research Scholarships and the NCI National Facility at the Australian National University (ANU), Canberra, Australia.