Tissue Fluidity Promotes Epithelial Wound Healing

Summary

The collective behaviour of cells in epithelial tissues is dependent on their mechanical properties. However, the contribution of tissue mechanics to wound healing in vivo remains poorly understood. Here we investigate the relationship between tissue mechanics and wound healing in live Drosophila wing imaginal discs and show that by tuning epithelial cell junctional tension, we can systematically alter the rate of wound healing. Coincident with the contraction of an actomyosin purse string, we observe cells flowing past each other at the wound edge by intercalating, reminiscent of molecules in a fluid, resulting in seamless wound closure. Using a cell-based physical model, we predict that a reduction in junctional tension fluidises the tissue through an increase in intercalation rate and corresponding reduction in bulk viscosity, in the manner of an unjamming transition. The resultant fluidisation of the tissue accelerates wound healing. Accordingly, when we experimentally reduce tissue tension in wing discs, intercalation rate increases and wounds repair in less time.

Epithelial tissues are inevitably damaged from time to time and must therefore have robust repair mechanisms. The behaviour of cells and tissues, for instance during wound healing and morphogenesis, depends on their mechanical properties and those of the surrounding environment¹. Previous studies have investigated the contribution of tissue mechanics to epithelial wound healing primarily using in vitro cell culture assays^2–7. However, whether these in vitro assays truly recapitulate the physiological response of in vivo tissues is unclear. Many in vivo models of epithelial wound healing have been developed⁷, although the mechanical basis of the wound healing process in such in vivo systems remains unclear. A number of in vivo epithelia have been shown experimentally to form contractile supracellular actomyosin cables^8–12 at the margin of epithelial wounds, which contract in a purse-string manner and bring the edges of the wound into apposition. While the mechanical role of the actomyosin purse string has begun to be investigated in vivo^13,14, the contribution of surrounding tissue mechanical properties to wound healing remains unclear.

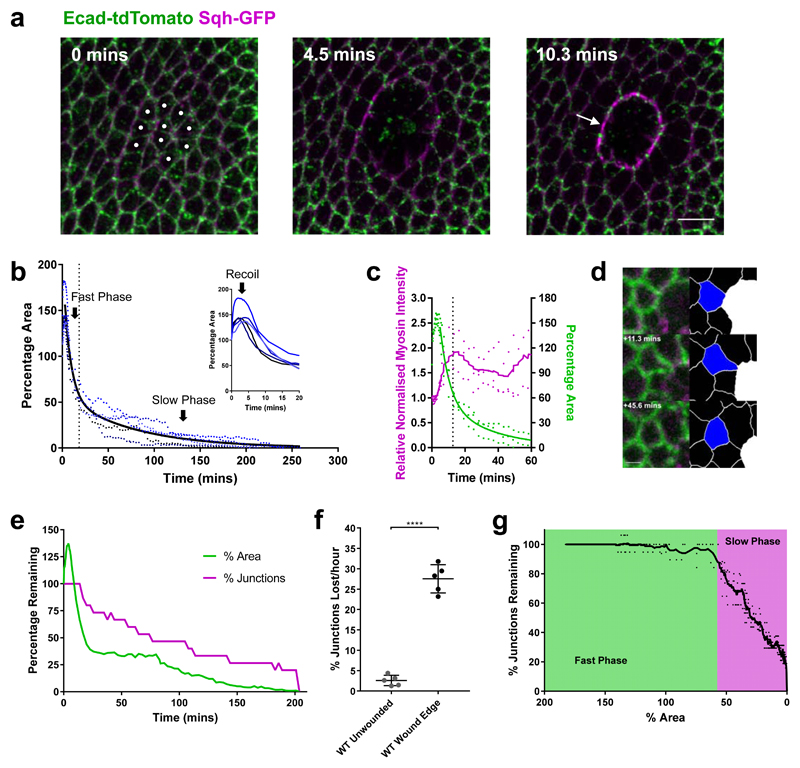
To investigate the role of tissue mechanics in wound healing in an in vivo system, we studied tissue repair in the epithelium of Drosophila wing imaginal discs by live time-lapse imaging. After wounding wing discs by laser ablation, an actomyosin purse string assembles at the wound’s leading edge (Fig. 1a, Supplementary Video 1), as in other systems^10,15–18. To understand the mechanisms controlling repair dynamics, we quantitatively analysed¹⁹ wound morphology over the time course of wound closure. We observe three distinct phases after wounding: recoil, fast closure and slow closure (Fig. 1b, Supplementary Video 2). Immediately after wounding, the wound area increases, due to a release of tissue tension by the ablation. The wound area then reduces in time, with an initial fast phase. However, after reaching approximately 50% of the original wound area, the rate of wound closure decreases dramatically, until closure. Myosin II (MyoII) intensity increases after wounding, before peaking at roughly twice the initial intensity (Fig. 1c). This peak coincides with the transition between fast and slow closure phases.

Figure 1. Wing disc wound closure is punctuated by wound edge intercalation, which can drive wound closure.

a, Early stages of wound closure in a sqh^AX3; sqh-GFP, Ecad-tdTomato wing imaginal disc. Cell outlines are marked by Ecad-tdTomato (green) and Myosin II by Sqh-GFP (magenta). Cells which will be ablated are marked by white circles at 0 mins. Within the first 10 minutes after wounding, a strong accumulation of Myosin II can be seen at the wound’s edge in the manner of a purse string (arrow). Images are maximum intensity projections of deconvolved image stacks. Scale bar = 5µm. b, Dynamics of wing disc wound closure. Percentage of original wound area is plotted over time for 5 WT wing discs expressing Ecad-GFP (blue dots, the same 5 wing discs are used for all subsequent WT analysis unless otherwise stated). Inset: first 20 mins, showing early expansion (recoil) of the wound. A two-phase exponential decay curve (black line) is fitted to the data after 3 minutes, when the wound begins to reduce in area until close. The transition between fast and slow closure phases of the two-phase exponential decay is marked by a dotted line (18.37 mins). c, Quantification of Myosin II purse string intensity (magenta, left y-axis) and wound percentage area (green, right y-axis) for 3 sqh^AX3; sqh-GFP, Ecad-tdTomato wing discs during the first hour of wound closure. A two-phase exponential decay curve has been fitted to the area data (green line) and a moving average (±4 time points) curve to the Myosin II intensity data (magenta line). The transition between fast and slow closure phases is shown with a dotted line (12.71 mins) d, Example of a single wound edge intercalation in an Ecad-GFP; sqh-mCherry, pnr-GAL4 wing disc. Raw maximum intensity projection (left) and skeletonised images (right, intercalating cell in blue, wound in white) are shown. The junction shared between the intercalating cell and the wound shrinks to a point and a new junction grows in the orthogonal direction. Scale bar = 3µm. e, Quantification of the percentage of starting wound edge junctions (magenta) and wound percentage area (green) for a single Ecad-GFP wing disc wound. The percentage of junctions remaining on the wound’s edge reduces as intercalations occur until the wound fully closes. f, Quantification of intercalation rate in unwounded WT tissues and at WT wound edges. The intercalation rate is significantly higher at the wound edge (unpaired t-test with Welch’s correction, n=5, t=15.15, df=5.089, p<0.0001). Error bars = SD. g, Relationship between percentage of wound start area and percentage of starting wound edge junctions remaining. The mean percentage area at which there is a transition between the fast (green) and slow (magenta) closure phases is highlighted (57.6%). A moving average curve (±4 time points) of the data is shown.

The dramatic reduction in wound closure rate at later stages suggested that different cell behaviours may be responsible for the fast and slow phases. By closely examining cell behaviours around the wound, we observe that cells at the wound edge readily undergo intercalation, particularly during the slow closure phase (Fig. 1d, e, g, Supplementary Video 2). This cell behaviour differs from those associated with wound healing in other Drosophila tissues, such as cell fusion^20,21, polyploidisation²¹ and cell intercalation further from the wound edge²². We also saw no evidence of protrusion-based active migration or cell extrusion. During wound edge intercalations, junctions in contact with the wound shrink to a single vertex and new junctions grow in the orthogonal direction (Fig. 1d). As a result, the number of cells in contact with the wound decreases over time (Fig. 1e, Supplementary Fig. 1a-d). These wound edge intercalations (involving three cells) are distinct from T1 transitions observed in many systems²³, as a T1 transition involves the rearrangements of four neighbouring cells (see methods). The rate at which wound edge cells intercalate is roughly eleven times that of an unwounded tissue (Fig. 1f) and there is a strong relationship between wound edge intercalation and the reduction in wound area during the slow phase of wound closure (Fig. 1g), indicating that wound edge cell intercalation might be required to promote the completion of wound closure.

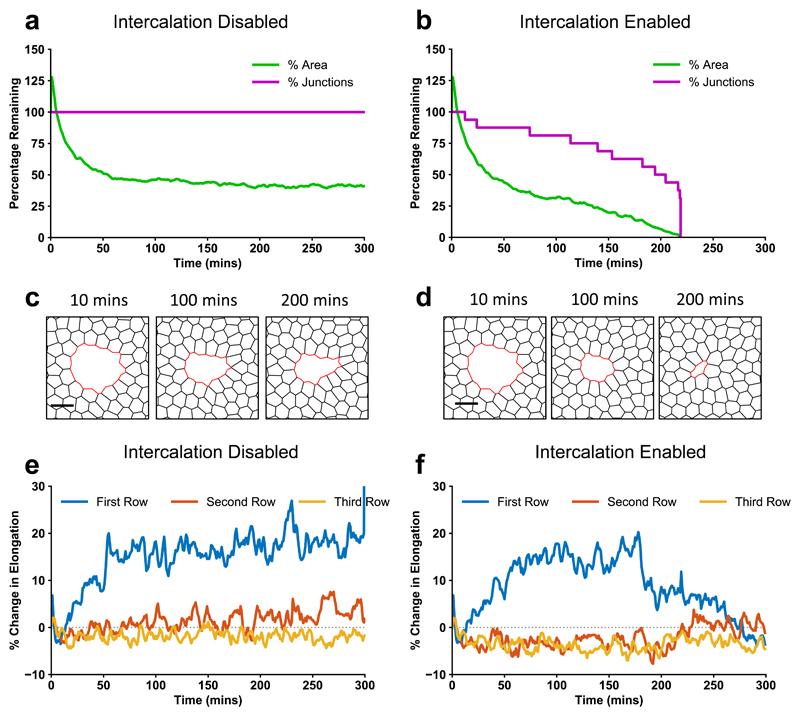
To quantitatively test the role of wound edge cell intercalation, we developed a computational vertex model²⁴ for wound closure in the wing disc (Supplementary Fig. 2, see methods). While the mechanics of wound healing has been previously modelled using continuum^2,4,6 or finite element approaches^5,25, more representative cell-based models, such as vertex models^26,27, have rarely been applied to replicate in vivo wound healing dynamics. We model each cell in the tissue as a two-dimensional polygon carrying variable tension on their edges, with bulk elasticity and peripheral contractility (Supplementary Fig. 2a-b, methods). We parameterised the model so that edges contacting the wound gradually increase in tension compared to the surrounding tissue, to mimic the assembly of the contractile actomyosin purse string, causing wound edge junctions to reduce in length. To capture experimentally observed fluctuations in junctional and purse-string MyoII²⁸, we introduced fluctuations in line tension at cell-cell interfaces and in the purse-string (Supplementary Fig. 2d). Without introducing intercalation events into the model, simulated wounds are unable to close (Figs. 2a, c, Supplementary Video 3). By contrast, when intercalations are enabled in the model (Supplementary Fig. 2c, see methods), wounds are able to close (Figs. 2b, d, Supplementary Video 4), supporting our hypothesis that intercalations at the wound edge are necessary to drive wound closure.

Figure 2. A vertex model of wound healing predicts that intercalation is necessary for wound closure and cell shape maintenance.

a-f, Vertex model simulations. a, b, Percentage of initial wound area and wound junctions after ablation with intercalations (a) disabled, and (b) enabled. c, d,Vertex model simulation images after ablation with intercalations (c) disabled, and (d) enabled. e, f, Percentage change in cell elongation over time during and after wound closure, calculated by dividing the major axis by the minor axis of an ellipse fit to each cell, for the first three rows of cells around the wound with intercalations (e) disabled, and (f) enabled.

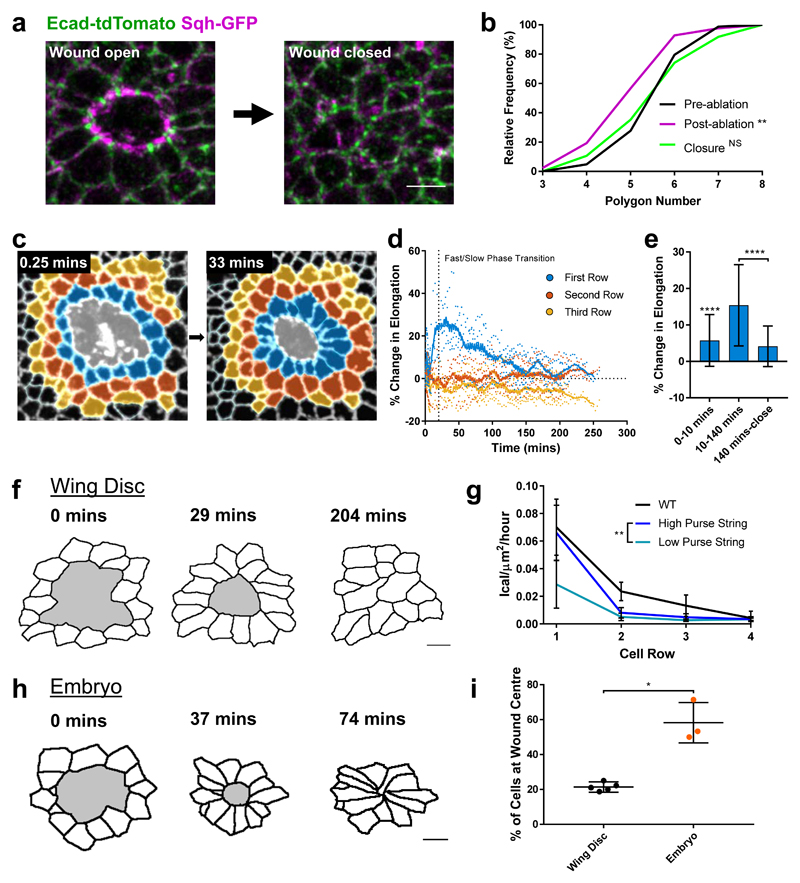
The vertex model predicts that in the absence of intercalation, cells around the wound become more elongated towards the centre of the wound (Fig. 2e) than in simulations with intercalations enabled (Fig. 2f). In both cases, the cells initially elongate as the purse-string contracts the wound. As cells begin to intercalate away from the wound edge their shapes relax, reducing the elongation over time. Towards the end of wound closure, many intercalations occur (Fig. 2b), at which point the elongation rapidly decreases, and the cells return to a fully relaxed state after healing (Fig. 2f). With intercalations disabled, the cells remain highly elongated (Fig. 2e). This led us to hypothesise that wound edge intercalations play a crucial role in maintaining cell shape and tissue patterning. Indeed, wing disc cells appear regularly packed immediately after wound closure (Fig. 3a) and the polygon distribution of wound edge cells is restored upon healing (Fig. 3b). The seamless closure we observe is distinct from a number of in vivo^22,29 and in vitro^5,30 systems that can form visible scar-like rosette structures upon closure. To test our vertex model’s prediction that intercalation preserves cell shape, we quantified cell elongation in the first three rows of cells away from the wound in wing discs (Fig. 3c, Supplementary Video 5). While cells in the second and third rows undergo little change in elongation during wound closure (Fig. 3d), cells in the first row undergo a transient increase in elongation towards the wound (Fig. 3c-f) before returning to their original shapes prior to wound closure (Figs. 3d-f). Cells return to their original shape during the slow phase of closure (Fig. 3d-e), when the majority of intercalations occur, supporting the role of intercalation in preserving cell shape.

Figure 3. Wound edge intercalation preserves cell shape.

a, Maximum intensity projection images of a wound in a sqh^AX3; sqh-GFP, Ecad-tdTomato wing disc before (left) and immediately after (right) wound closure (scale bar = 3µm). b, Quantification of wound edge cell polygon number before ablation, immediately after ablation and immediately after wound closure. The distribution of polygon number is significantly shifted left after ablation (Kolmogorov-Smirnov Test, D=0.2892, p=0.0019) but is restored upon closure (Kolmogorov-Smirnov Test, D=0.07583, p=0.9692). c, Colour coding of the first three rows away from the wound edge (first row blue, second row orange, third row yellow) for time points immediately after wounding (0.25 mins) and soon after the onset of wound edge intercalation (33 mins). Image is an adaptive projection of Ecad-GFP overlaid by skeletonised cell outlines. Scale bar = 5µm. d, Quantification of the percentage change in mean cell elongation for the first three rows of cells (colour coding as in c) over time for 5 WT wounds. Moving average curves (±4 time points) are shown. The transition between fast and slow closure phases is marked by a dotted line (18.37 mins). e, Percentage change in mean elongation of first row cells for three time windows; 0-10 mins (wound recoil), 10-140 mins (early wound closure), 140 mins – close (late wound closure). Data is pooled from the data set in d. Cells were significantly elongated during the recoil phase (Wilcoxon Signed Rank Test, p<0.0001). Cells were significantly more elongated during early wound closure than during late wound closure (Kolomogorov-Smirnov Test, D=0.5703, p<0.0001). Error bars = SD. f, h, Skeletonised cell outlines of cells starting at the wound edge (wound shaded in grey) at three time points in a (f) single WT wing disc (scale bar = 3µm) and a (h) single WT stage 13 embryo (scale bar = 5µm). g, Quantification of intercalation rates in rows of cells away from the wound for WT wing discs (black) and vertex model simulations with high (dark blue) and low (light blue) purse string strength. The intercalation rate in simulations is significantly higher in the first row of cells with a high purse string strength (Kolomogorov-Smirnov Test, D=0.6667, p=0.0097). i, Quantification of the percentage of cells remaining close to the wound’s centre after closure, as a measure of intercalation. A significantly higher percentage of cells remain close to the wound centre in embryos (n=3) compared to wing discs (n=5) (unpaired t-test with Welch’s correction, t=5.466, df=2.103, p=0.0285).

If intercalations are indeed required to maintain cell shape, we expect that the majority of cell intercalations should be localised to the first row of cells, as it is these cells that are being stretched (Fig. 3d). Indeed, when we quantify the intercalation rates in different rows of cells across the closure process, we find that the intercalation rate is significantly higher in the first row of cells and decays in increasing rows away from the wound edge (Fig. 3g, Supplementary Fig. 3 a-c). This prediction of a localised increase in intercalation rate also holds true for our vertex model (Fig. 3g, Supplementary Fig. 3b-c). However, when the strength of the purse string is reduced the intercalation rate in the first row of cells is significantly lower (Fig. 3g, Supplementary Fig. 3b-c). Therefore, the cell shape changes induced by the close proximity of a cell (or row of cells) to the purse string can explain the localised increase in intercalation rate that we observe. This mechanical function of the purse string contrasts previous work suggesting that the purse-string functions mainly in setting the direction of cell movement towards the wound during wound closure⁵.

Altogether, these findings suggested that intercalation events help maintain cell shape and that wound healing in an epithelium that does not intercalate will lead to cell deformation. To test this idea further, we compared wound edge intercalation in the wing disc to the Drosophila embryonic ectoderm, an epithelium in which cells do not return to their original shape (Fig. 3h). Following wound closure in the Drosophila embryonic ectoderm, cells can be up to twice as elongated as they were prior to wounding²². Supporting the model’s predictions, there are significantly fewer wound edge intercalations in embryos prior to wound closure (Fig. 3i).

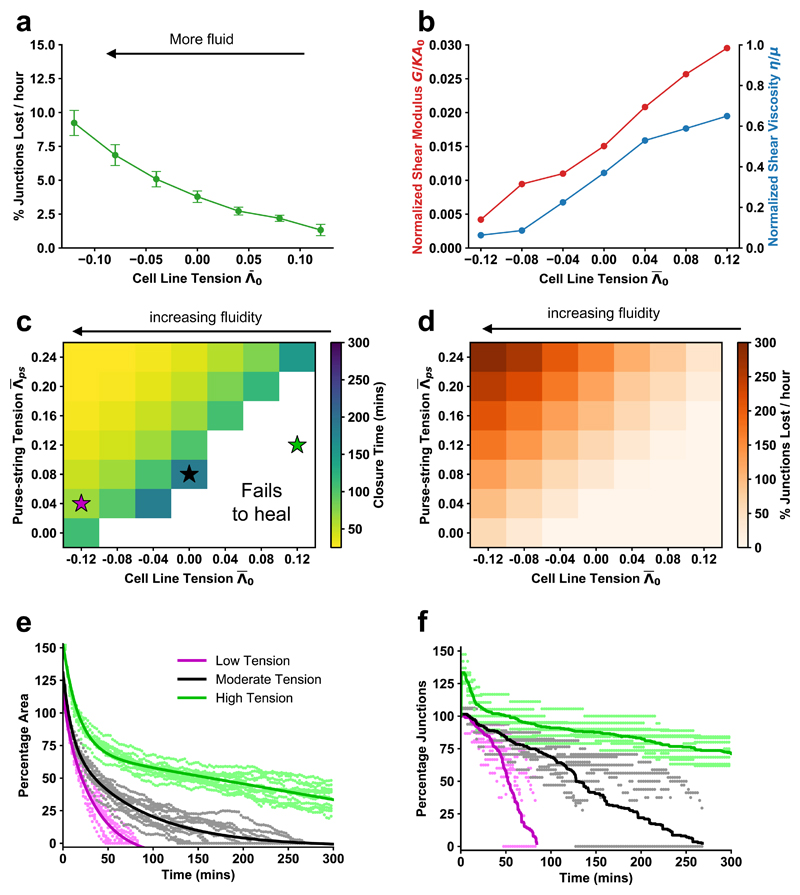
These results suggested that wound closure is controlled by two dynamic mechanical properties of the wounded tissue: the rate of wound edge intercalation and the tension in the purse string. We used the model to test the relative roles of intercalation rate and purse string tension in wounded tissues. We found that the rate of intercalation in the tissue can be tuned by modulating cell-cell interfacial tension (Fig. 4a). Likewise, intercalation rate can also be tuned by modulating the perimeter contractility of a cell (Supplementary Fig. 4a, b). As cell line tension decreases, the rate of intercalation in the tissue increases. This leads to an increase in “tissue fluidity” – the rearrangement of cells relative to each other, analogous to molecules in a liquid.

Figure 4. Reducing tissue contractility enhances fluidity and can speed wound closure.

All figures are vertex model simulations. a, Intercalation rate in an unwounded tissue against mean cell line tension. Error bars = SD. b, Normalized tissue shear modulus and viscosity against tension. c, Mean wound closure time against cell line tension and purse-string tension. The white region indicates parameter space where wounds fail to close within 300 minutes. The colored stars indicate the parameters used in (e) and (f). d, Mean wound edge intercalation rate against cell line tension and purse-string tension. e, Percentage of initial area over time for low, moderate, and high line tension cases. Points are from simulations, and lines are fit dual exponential curves. f, Percentage of initial wound junctions over time for low, moderate, and high tension cases. Points are from simulations; lines are the average over all simulations. For all combinations of tension, n = 12 simulations for each.

To demonstrate that a reduction in interfacial tension (increase in intercalations) indeed increases the fluidity of a tissue, we performed shear rheology simulations using our vertex model (Supplementary Fig. 5a), and computed the tissue shear modulus and viscosity with varying line tensions (Fig. 4b, Supplementary Fig. 5b-f). As line tension is gradually reduced in simulations, both the shear modulus and viscosity, the inverse of fluidity, approach zero³¹. Our findings stand in contrast to previous studies, which suggested that cell monolayers displaying viscous-like behaviours with many cell rearrangements³² fail to close wounds⁶. However, our results are consistent with the suggestion that increasing monolayer elasticity would prevent wound closure².

Simulations using our vertex model also demonstrate that the intercalation rate can increase rapidly when the magnitude of line tension fluctuations is increased (Supplementary Fig. 4d), leading to a smaller corresponding reduction in closure time (Supplementary Fig. 4c). However, when the tension fluctuations are large, the intercalation rate in unwounded simulations far exceeds what we observe in unwounded tissues (Fig. 1f) with many short timescale reversible intercalations. We do not observe large numbers of reversible intercalations in the wing disc, therefore it is unlikely that higher tension fluctuations are physiologically relevant. Simulations also demonstrate that cell division rates can affect closure time (Supplementary Fig. 4e). However, the range of cell division rates used in these simulations far exceeds the physiological range of cell division rates we have measured in a number of genetic conditions (Supplementary Fig. 4e). Therefore it is unlikely that cell division has a strong contribution to wing disc wound closure for wounds of this size, unlike for larger wounds³³. Although varying the magnitude of tension fluctuations and divisions rates is not physiologically relevant, the observation that both can be modulated to increase fluidity, and subsequently wound closure rate (Supplementary Fig. 4c-f), demonstrates that fluidity-driven wound closure is likely to be a general phenomenon.

Increasing either purse string tension or decreasing cell line tension reduces the time taken for wounds to close (Fig. 4c) and increases the rate of wound edge intercalations (Fig. 4d). Unexpectedly, we find a region of parameter space where a reduction in purse string tension is more than compensated for by an increase in tissue fluidity (decrease in tension), leading to accelerated wound closure (Figs. 4c, e-f, magenta compared to black). However, tissue fluidity can only rescue a reduced purse string up to a point, as the majority of simulations with the weakest purse string tension values fail to close, regardless of the level of tissue fluidity (Figs. 4c, e-f). This observation highlights the importance of the purse string for the increase in wound edge intercalation (Fig. 3g, Supplementary Fig. 3). Together, these results demonstrate that bulk tissue mechanical properties and the activity of the purse string cooperate to promote wound closure.

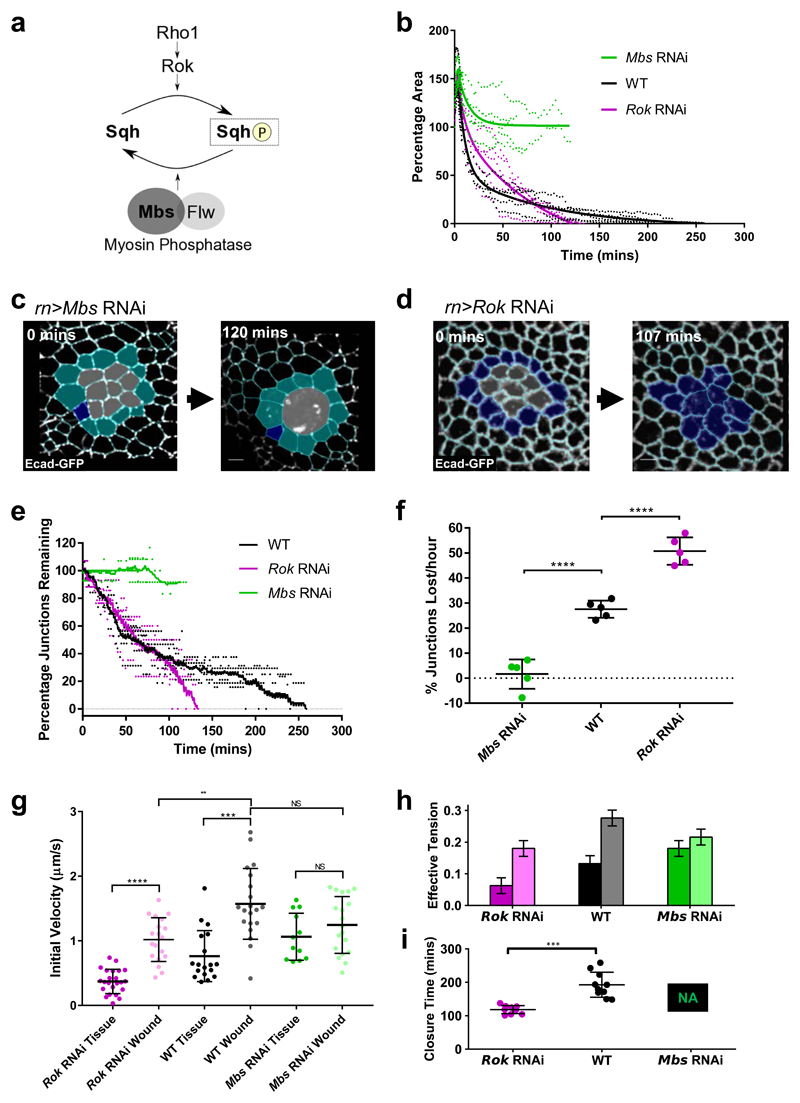
To test these predictions from our vertex model further, we sought to experimentally perturb cell edge tension. In epithelial tissues, cell edge tension is governed by the activity of non-muscle MyoII (Fig. 5a). To test the roles of purse string tension and tissue fluidity in the wing disc, we genetically modulated the activity of MyoII in the wing pouch epithelium. To increase tension, we performed RNAi against the Myosin binding subunit (Mbs) of the Myosin Phosphatase, a phosphatase that inactivates MyoII by dephosphorylating its regulatory light chain³⁴ (Spaghetti squash (Sqh) in Drosophila). To decrease tension, we performed RNAi against Rho-kinase (Rok), a kinase that activates MyoII by phosphorylating Sqh^35,36. We confirmed the effect of these genetic perturbations on tension by quantifying vertex recoil rates (a greater recoil rate implying higher tension) after single junction ablations in unwounded tissues (Fig. 5g). We then wounded these wing discs and compared the dynamics of wound closure to wildtype (WT) wing discs (Supplementary Fig. 6a-d). In Mbs RNAi wing discs, where tension is high, wounds fail to close within the imaging time window (Figs. 5b, c, Supplementary Fig. 6a, Supplementary Fig. 7, Supplementary Video 6). Furthermore, wound edge cell intercalation is almost entirely abolished (Figs. 5c, e-f, Supplementary Fig. 7, Supplementary Video 6), supporting the importance of intercalation in promoting wound closure.

Figure 5. Myosin activity controls tissue fluidity and wound closure rate.

a, Activation of Myosin II by phosphorylation of its regulatory light chain (Sqh) can be performed by Rho kinase (Rok) downstream of Rho1. Myosin II inactivation by Sqh dephosphorylation can be performed by the Myosin Phosphatase comprising the Myosin binding subunit (Mbs) and catalytic subunit (Flapwing, Flw). b, Quantification of wound closure (as percentage of start wound area) over time in Mbs RNAi (green, n=5) and Rok RNAi (magenta, n=5) wing discs, compared to WT wound closure (black, n=5). Two-phase exponential decays are fitted after 3 minutes. c, d, Examples of wound healing in (c) Mbs RNAi and (d) Rok RNAi before wounding (left) and after wound closure (right, Rok RNAi) or when further segmentation become impossible (right, Mbs RNAi). Cells are colour coded according to whether they undergo intercalation (dark blue) or not (cyan). Images are adaptive projections of Ecad-GFP overlaid by skeletonised cell outlines in cyan (scale bars = 3µm). e, Quantification of the percentage of initial wound edge junctions over time for Mbs RNAi and Rok RNAi wing discs (colours and n numbers as in b). Moving average curves (±4 time points) are shown. f, Quantification of mean intercalation rate for Mbs RNAi, WT and Rok RNAi wounds (colours and n numbers as in b). Intercalation rate is significantly higher in Rok RNAi wounds (unpaired t-test, n=5, t=8.026, df=8, p<0.0001) and significantly lower in Mbs RNAi wounds (unpaired t-test, n=5, t=8.503, df=8, p<0.0001) compared to WT. Error bars = SD. g, Quantification of initial vertex recoil rates after single junction ablations in WT (black), Mbs RNAi (green) and Rok RNAi (magenta) wing discs. Junction ablations were performed in unwounded tissues (“Tissue”) and at wound edges (“Wound”). Wound edge vertex recoil rates were significantly higher than in the surrounding tissue in WT and Rok RNAi discs, but not Mbs RNAi discs. Vertex recoil rates at the wound edge were significantly lower in Rok RNAi discs compared to WT discs, but were not significantly changed in Mbs RNAi discs. Full results of Kolmogorov Smirnov tests can be found in Supplementary Table 1. h, Input mean and standard deviation of effective tension, the total of line tension and contractility, for different simulated conditions. The left bars are for bulk edges, and right edges are for wound edges. i, Mean wound closure time for the simulated conditions. Mbs RNAi simulated wounds fail to heal. Error bars = SD. Wound closure time is significantly lower in Rok RNAi wounds than WT wounds (unpaired t-test, n=10, t=6.298, df=18, p<0.0001).

In Rok RNAi wing discs (Supplementary Fig. 8, Supplementary Video 7), in which tension is reduced, wounds close faster than in WT wing discs. While these wounds initially close more slowly than WT wounds, they eventually overtake them and unexpectedly close in roughly half the time of WT wounds (Figs. 5b, d, Supplementary Fig. 6a). This is accompanied by an increase in the rate of wound edge intercalation (Figs. 5d-f). A decrease in interfacial tension can also be achieved via an increase in cell-cell adhesion. An increase in cell-cell adhesion is thought to promote cell-cell contact formation, effectively counteracting junction contractility³⁷. In line with this prediction, we obtained intercalation and closure rates similar to Rok RNAi wing discs when we expressed double the number of copies of the adherens junction-associated cell-cell adhesion molecule E-cadherin (ubi-Ecad-GFP, Supplementary Fig. 6a-d, Supplementary Fig. 9a-h). Therefore, decreased interfacial tension appears to be a general route to increasing tissue fluidity and wound closure rate, regardless of the origin of the tension decrease.

One consequence of decreasing MyoII activity through Rok RNAi, is that it is likely to increase tissue fluidity, while simultaneously decreasing purse string tension^8,38. To quantify the effects of MyoII perturbations on tension in the surrounding tissue and in the purse string, we ablated single junctions at the wound edge and in the surrounding tissue in all three conditions and compared the initial vertex recoil velocities that serve as a measure of junctional tension³⁹ (Fig. 5g, Supplementary Table 1). In WT tissues, the junction recoil rate in the purse string is twice that of the surrounding tissue. This mimics the relative increase in MyoII intensity we observed in WT wing discs (Fig. 1c). In Rok RNAi wing discs, vertex recoil rates are reduced by 51% in the tissue and 35% in the purse string compared to WT. One would therefore predict that the increase in tissue fluidity in Rok RNAi discs, associated with a large decrease in tension in the surrounding tissue, may be able to more than compensate for the reduction in purse string strength, as predicted by our model (Fig. 4c). In Mbs RNAi wing discs, vertex recoil rates are increased by 40% in the tissue and decreased by 21% in the purse string compared to WT. The decrease in both tissue fluidity (due to increased tissue junctional tension) and purse string strength likely explains why wounds in Mbs RNAi discs fail to close. Interestingly, Mbs RNAi purse string vertex recoil rates are not significantly higher than vertex recoil rates in either the WT purse string or Mbs RNAi tissue (Fig. 5g, Supplementary Table 1). This suggests that we have elevated tension in the wing disc to its maximum possible level through Mbs RNAi, a level that is also achieved in the purse string of WT discs. To test whether measured vertex recoil rates in the three experimental conditions can predict wound closure rates, we used the measured vertex recoil rates as an input to our model by assuming that the total edge tension is proportional to the recoil rate (Fig. 5h, see methods). We also used experimentally measured division rates for WT, Rok RNAi, and Mbs RNAi (Supplementary Fig. 4e), although these rates show little variation and cannot explain changes in wound closure rate. We find that the differences in experimentally measured tensions are sufficient to explain the increased healing rate in Rok RNAi and failed healing in Mbs RNAi (Fig. 5i).

We have thus demonstrated that wing disc wound closure is dependent on cell-cell intercalation-driven tissue fluidity, downstream of interfacial junctional tension. The dynamics of wound closure in wing discs can be explained purely through junctional behaviours in our vertex model, rather than previously described cell-crawling based migration^30,40–42. In our system, fluidity may substitute for the propulsive action provided by cell crawling, as it provides a mechanism for energy dissipation, which leads to mechanical relaxation²⁷ (Supplementary Fig. 10a-c). The dispensability of crawling for our system is reminiscent of the closure of cell monolayer wounds over non-adherent environments^3,6, which entirely depends on purse string tensile activity. In these studies, wounds close much slower than in wing discs and a reinforcement of purse string strength is thought to be required for closure⁶. Both these differences may be explained by a failure of these monolayers to efficiently dissipate energy, unlike in wing discs (Supplementary Fig. 10a-c).

Changes in tension-based fluidity, such as those we have induced through MyoII perturbation, can be interpreted as an unjamming transition^43,44. Epithelial tissues can transition between a fluid-like state (unjammed) with many rearrangements and a solid-like jammed state, lacking the ability to rearrange^43–45. Theoretical models have described how jamming/unjamming transitions can be induced via changes in junctional tension and cell-cell adhesion⁴⁶. These two properties define a mechanical energy barrier, which must be overcome for cells to rearrange relative to each other^43,46, allowing an epithelium to behave as a fluid. By reducing tension in the wing disc, we are likely lowering this energy barrier, allowing cells to rearrange more. Simulations indeed demonstrate that, with increased intercalations, tissues can transit to a lower energy state during wound healing, which may allow further intercalations to occur (Supplementary Fig. 10a-c). The role we describe for tissue fluidity in wound healing, in addition to its known roles in developing^28,47–50 and mature tissues⁴⁶, reinforces the physiological importance of the fluid state of a tissue.