Abstract
Herein, we consider the process of force development along the adhesome within cell focal adhesions. Our model adhesome consists of the actin cytoskeleton-vinculin-talin-integrin-ligand-extracellular matrix-substrate force train. We specifically consider the effects of substrate stiffness on the force levels expected along the train and on the traction stresses they create at the substrate. We find that significant effects of substrate stiffness are manifest within each constitutive component of the force train and on the density and distribution of integrin/ligand anchorage points with the substrate. By following each component of the force train, we are able to delineate specific gaps in the quantitative descriptions of bond survival that must be addressed so that improved quantitative forecasts become possible. Our analysis provides, however, a rational description for the various levels of traction stresses that have been reported and of the effect of substrate stiffness. Our approach has the advantage of being quite clear as to how each constituent contributes to the net development of force and traction stress. We demonstrate that to provide truly quantitative forecasts for traction stress, a far more detailed description of integrin/ligand density and distribution is required. Although integrin density is already a well-recognized important feature of adhesion, our analysis places a finer point on it in the manner of how we evaluate the magnitude of traction stress. We provide mechanistic insight into how understanding of this vital element of the adhesion process may proceed by addressing mechanistic causes of integrin clustering that may lead to patterning.
Significance
Herein, we present a holistic analysis that explicitly includes the role of a major set of force-bearing proteins involved in force transmission along a “model adhesome” and that leads to the development of traction stress, rather than assuming adhesion is controlled by a single set of anonymous bonds attached to a rigid tether as has been typically done. In this, we demonstrate how the substrate’s physical characteristics such as stiffness and time-dependent force response are felt all along the adhesome, as opposed to being seen to be localized at a single anonymous site. The effects of the rate of retrograde flow of the actin cytoskeleton are also detailed in a, to our knowledge, novel manner and reveal effects not yet noted and reported. In addition, to our knowledge, new insights are introduced concerning the role of substrate stiffness and time-dependent response on the density of integrin clusters and thereby on traction force levels possible. Model parameters are discussed in terms of what is required for true predictive capability of traction stress.
Introduction
Mechanical forces, i.e., stimuli, transmitted between the intracellular matrix and its environment, e.g., the extracellular matrix (ECM), determine a wide range of cell functions such as motility (1), proliferation (2), and differentiation (3), as well as vital processes in cell development (4,5), tumorigenesis (6,7), cell growth (8, 9, 10), and wound healing (11,12), inter alia. Cells perform these functions and are so regulated via the formation of focal adhesions (FAs) (13, 14, 15, 16) that anchor the cell either transiently (i.e., dynamically) or permanently (17,18) to, e.g., the ECM (the substrate). The FA complex is formed via the assembly of a number of proteins and has the important ability to sense (via its mechanosensitivity) and react to (via mechanotransduction) the nature of the environment, in particular its mechanical stiffness (3,19, 20, 21, 22, 23, 24, 25, 26), as well as surface topography (27, 28, 29, 30, 31). The effect of substrate stiffness per se has been exemplified by observations of cell migration on substrates with stiffness gradients (23,24). Precisely how this happens, however, has yet to be clearly delineated because the interactive and coordinated roles of all the various proteins involved have yet to be described in a holistic manner. Hence, no predictive theory or models for traction force development exist as yet. Accordingly, our goal is to provide more insight into the roles played by the various molecular participants in this performance with the aim of providing more background for creating such predictive capability. Our hypothesis was that mechanosensitivity is manifested at each of the key elements that play vital roles in the generation of adhesion force; although this intuitively pleasing concept has not yet been demonstrated, it is what we find and report herein.
The cell’s adhesion complex and its protein components, the adhesome (32,33), transmits force generated by retrograde flow of its intracellular actin cytoskeleton (hereafter “actin”) via a series of proteins (33, 34, 35) that are bound to each other and ultimately to the cell’s extracellular matrix. In our case, we consider a model adhesome that includes the plaque proteins talin and vinculin; hence, our force train consists of actin(myosin)-vinculin-talin-integrin-ligand(ECM/substrate) (34, 35, 36) specifically suited for β1 integrins. Although this is a small subset of the full adhesome (33), it accounts for a vital set of force-bearing proteins, as required for our analysis of traction force and stress; many other adhesome members play important roles in their activation and recruitment. The substrate possesses a clearly defined elastic stiffness, and its cell interface has a certain density of receptors bound to ligands to which talin-integrin bonds. There has been considerable progress in delineating protein members of the adhesome and their individual properties and functionality—these are discussed below for our model adhesome as we present and incorporate them into a theoretical framework that follows the force pathway from actin to the ECM. Our goal leads us to several pointed observations of how the system functions or can function and to some insights into how certain key correlations come about, such as the observed effects of substrate rigidity, and points specifically to what quantitative knowledge is missing and requires resolution so that further understanding is possible. Our model system is minimal in that, although it includes major identified “players”—at least those known to date—it is yet deficient because the entire cast of characters has not been given sufficient quantitative definition; this theoretical recognition makes the specific contribution of crisply pointing to needed experimental inquiry. In summary, we find that mechanosensitivity and mechanotransduction rely on the full array of molecular constituents, at least for optimal performance, and cannot be attributed to any single set of model bonds, often anonymously referred to as “clutch bonds.”
As it happens, mechanosensing actually begins at the anchorage of the force train via integrin-ligand bonds whose density and survivability depend on ECM stiffness, viscoelastic response, and topology, as well as molecular constituency; how all these factors actually accomplish this is far from clear in a mechanistic sense, yet legions of empirical observations exist that may at least provide guidance for focused study. These are discussed herein. We begin, however, by providing a holistic, yet brief, conceptual overview of the adhesome considered here that provides a view of the various elements analyzed in our adhesome force train.
Plan of the presentation
After a brief overview of key force-train elements, we describe a mechanism in Integrin Clustering: Contributing Factors And Preforce that we believe contributes to and helps explain features of integrin clustering as described, for example, by Cluzel et al. (37) and Changede et al. (38,39). We then pass to a description of force development along talin rods in Force Response Of Talin And Its Connections To Actin; this analysis assumes talin is bound to integrins, analyzes the stochastic talin-actin bonding, and leads to a forecasted expected force versus time response along talin dubbed (t). In this, we demonstrate a mechanosensing effect not previously described. Individual talin rods are envisioned to be part of ensembles. It is then necessary to probe the stochastic bonding of talin rods to integrins under the (t) found in Force Response Of Talin And Its Connections To Actin to determine the population of talin rods actually engaged; this is done in Net Forces Generated On The Force Train. Without fidelity in the talin (t) response, the analysis of talin-integrin-ligand bonding would lack veracity. Net expectation forces and traction stresses are then estimated in Net Traction Stress And Assessments, and Discussion follows; the full dynamics of adhesion sites are not described herein because that is left for future study.
Materials and Methods
Overview of the force train’s key elements
Indeed, it is reported that nascent adhesions involve the clustering of integrins even before they are clearly visualized (37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47) and before traction forces are generated; hence, before mechanosensing occurs (38,39,45,46). The adhesome is then assembled at the nascent adhesion. Nascent adhesions may involve integrin densities of (500–1000/μm2); this may be a factor of at least 1.5 times the ambient integrin density (40), which indicates that clusters form. We realize that other reports cite different numbers, but this particular estimation appears appropriate for discussion’s sake. Integrins will be recruited into nascent adhesions as inactive integrins are converted to a talin-bound, relatively immobile specie. The resulting activity gradient of inactive integrins will lead to a diffusive influx. Once formed, diffusion within a mature clustered adhesion becomes occluded and slow (48) because integrins must diffuse through complex cytoskeleton corrals (39,49). Thus, integrins naturally cluster and are under bonding forces, the adhesome is mobilized, and integrins are corralled within the adhesion. Just below, we describe interactions among integrins that are (modestly) affected by substrate stiffness (and possible time-dependent response) that promote clustering.
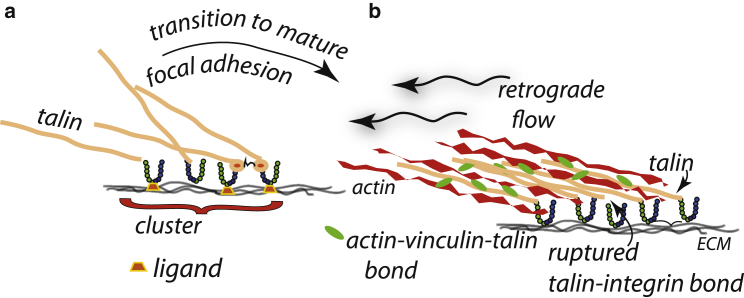
Nascent adhesion clustering is depicted in Fig. 1 a, which outlines mechanisms and steps described by Cluzel et al. (37) and also consistently with (39,50, 51, 52). Here, conformational changes in talin induced by PI(4,5)P2 activate integrins that bind to essentially immobile ligands. Talin heads, and hence integrins, can associate with other talin-integrin-ligand groups as illustrated. In this, Cluzel et al. (37) demonstrate a direct correlation between integrin activation and the formation of integrin clusters. They further discuss how “… actin fibers were dispensable for integrin clustering,” but that “talin is the cytoskeletal protein first recruited to high-affinity β3 and β1 integrins and may play a role in their clustering.” We have incorporated these observations into our Fig. 1 a. However, once FAs are established and linked to actin-myosin force generation, additional clustering occurs, as observed by Ballestram et al. (44). Moreover, an additional driving force for clustering would be the elastic interactions described below.
Figure 1.
(a) Integrin-talin cluster within a nascent adhesion; note the coclustering of unligated integrins. (b) A depiction of actin in retrograde flow, tugging on talin rods bound to integrins that are bound to the ECM (substrate), is given. Note the multiple connections between talin and actin filaments and the on-off bond rupture and reformation of integrins. Note also the depletion of inactive and unbound integrins that induces an influx of integrins into the adhesion. To see this figure in color, go online.
We now recall that talin binds actin—initially, we assume, at binding sites dubbed ABS3 and later at ABS2 and then with vinculin bonds on unfolded R3 domains; this is described below in Force Response Of Talin And Its Connections To Actin. Vinculin is activated, also via stimulation by PI(4,5)P2 (37), and binds actin as assessed above. This is depicted in Fig. 1 b. The net behavior of the adhesome’s force train now depends on integrin bond lifetimes and, of course, on bound integrin density. Hence, the extent of clustering and all the cumulative effects of substrate stiffness are important for the magnitude of force generated and its temporal behavior. The adhesion can then grow by continued integrin influx. As it happens, substrate stiffness promotes this process as discussed below. We now provide more detailed descriptions of the force-train elements; we begin, however, with additional comments on initial integrin clustering, i.e., nascent clusters.
Integrin clustering: Contributing factors and preforce
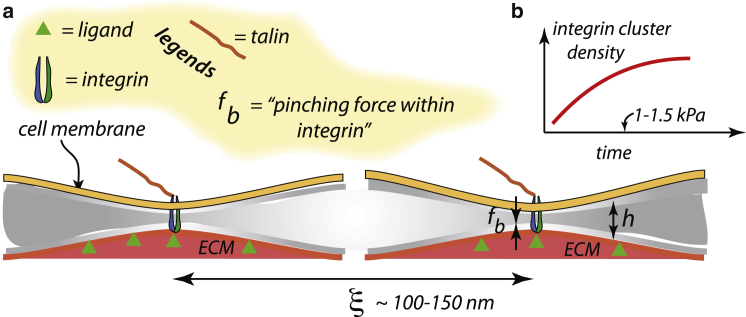
Here, we consider contributing factors to initial integrin clustering that are part of determining integrin density and distribution. We establish certain important realizations, including the fact that bound integrins are under “preforces” that are not dependent on the forces generated within the force train via actin retrograde flow; that is, preforces form in nascent adhesions. These preforces do, however, play a role in bond survival and hence in levels of force and thereby traction stresses that may develop. Indeed, preforces have been experimentally demonstrated to exist because of, for example, the need to compress the glycocalyx, as indicated in Fig. 2; in cases of cancer cells, this process may play a mediating role (43,53).
Figure 2.
(a) Integrins bound to ligands generate an internal force fb that induces local cell membrane and substrate bending. The interaction via the variation of free energy with translation of an integrin—e.g., an increase in ξ, the position integrin (1)—specifies a force, fint. (b) Expected integrin density versus time as nascent clusters form is shown. To see this figure in color, go online.
Mechanisms for integrin clustering have been discussed (38,39). However, clustering of integrins may be driven by, inter alia, the energetics of cell membrane deformation that is induced by the local bending deformations that are, in turn, caused by the force of the integrin bond (43). This force comes about because of the fact that integrins must “stretch” to “catch-bond” to ligands (54, 55, 56) and induces local membrane and substrate bending as depicted in Fig. 2, showing a pairwise integrin interaction. Here, we present a quite simple mechanistic analysis of the preforce that provides specific relations that allow for quantitative preforce estimates and naturally reveals the origin of the interaction forces that promote integrin clustering.
The dynamic picture we have presented, i.e., in Fig. 1 b, involves talin-integrin bonding and debonding from their integrin-ligand attachments within the ECM. We now recognize that these bonds are under a preforce and that they are catch bonds; hence, we use catch-bond theory (54) to describe their behavior, using the data of Kong et al. (55) for integrin-ligand (viz., α5β1 fibronectin) bonds as outlined in Appendix B. We compute the probability of bond survival under the actual expectation forces, , generated along talin, assuming they are bound to a ligated integrin. Our goal is to assess the ability of a typical talin rod to sustain such forces and remain bound.
For a linear elastic system, we may write for the free energy, (57),
| (1) |
because here, the symmetry of Fig. 2 suggests f(1) = f(2) = f.
In Eq. 1, W(e) = 1/2σijeij is the strain energy density, T the vertical component of surface traction, u(x) the net displacement field caused by f(1) and f(2), and δ(i) is the normal displacement caused solely by f(i) at the site of integrin i. The symbols u(1), u(2) are the components of displacement normal to the plane of the substrate evaluated at the points of force f(2) and f(1), respectively; negative u(1,2)-values point downward, as do f(1) and f(2).
The variation in ξ represents a translation in the displacement field of f(1) and yields, with η being the position of integrin 2 with respect to integrin 1,
| (2) |
Hence, the result we seek for the interaction force, fint, is simply
| (3) |
In the scenario of Fig. 2, because f(2) < 0 and (∂u(1)/∂x)η > 0, we indeed have fint > 0, which implies the point forces attract. The above analysis provides one mechanism for integrin clustering that we note is limited by several factors including, for example, steric interaction among integrins. What is needed now are specific model scenarios of Fig. 2 that allow calculation of the displacement fields and δ(i) vs. f(i) relations; we consider two cases.
Case #1
To estimate magnitudes for this interaction, we assume the integrins reside in a plate-like area of radius comparable to observed cluster sizes, say, 100 nm ≤ R ≤ 150 nm; there are two plates representing the cell and substrate with bending stiffness kc and ks, respectively. These dimensions reflect the reports of (38,39), who observe nascent adhesions with dimensions corresponding to R ≈ 50–75 nm. Again, assuming linearity, the relevant results are (58), with r being the radial distance from the point force,
| (4) |
Now, we require that a displacement δ★ = δc + δs be imposed for integrin bonding, and hence, we have
| (5) |
For the cell membrane stiffness, we take kc = 10−19 J. Hence, if R = 100 nm and δ★ = 10 nm (59, 60, 61), we find fb ≈ 3 pN if ks → ∞. If, on the other hand, the cell is bound to a supported lipid bilayer as used in (38,39), we would have something more like ks ∼ kc and fb ∼ 1.5 pN. Hence, there would appear to be slight mechanosensing to this interaction, yet we emphasize that the effect exists regardless of substrate rigidity. This interaction would clearly promote integrin clustering, but the effect would tend to dissipate once the reinforcing displacement fields of clustered integrins strongly overlap. Indeed, we would realize that the force fb within an isolated bound integrin would reduce when its required displacement, δ★, is partially provided by the displacement field of a nearby clustered integrin. This mechanism thereby supports a scenario of initial clustering of a number of integrins that saturates. The confinement of plaque protein corrals would also tend to stabilize the cluster size; this again would be modestly sensitive to substrate stiffness, as described in (37, 38, 39). We note, in addition, that as talin is recruited in the activation of integrins, talin would also associate with unligated integrins. Hence, nascent clusters would contain both ligated and unligated integrins, as noted earlier by (62, 63, 64) and more recently by (37, 38, 39).
The scenario of Fig. 2 is readily reinterpreted to suggest that integrin clustering will occur by the preferential activation and ligation of integrins to nearby ligated integrins. Clustering is then not only a natural result, but the effect would be self-limiting because once a number of integrins so cluster, with each contributing to the required displacement, the cluster would look like a single integrin to the far field of other integrins. Hence, these nascent clusters will form to limiting sizes.
Case #2
We also note that gray regions shown in Fig. 2 may indeed represent the cell’s glycocalyx. Analysis of this would not alter the essential points made here, but now the cell membrane and substrate would be modeled as plates deflecting on a deformable foundation. Glycocalyx properties in this context are, however, far from well-established, but we refer to O’Callaghan et al. (65) and our own theoretical model (66) that accounts for electrostatic repulsion. For standoff distances of, say, 10 nm ≤ h ≤ 15 nm, reasonable estimates of apparent stiffness would be 0.2 kPa ≤ Eg ≤ 1 kPa. Force versus deflection relations would now look like
| (6) |
with = 1/2Eg/(1 − ν2). Because values or even a precise definition of Poisson’s ratio ν is unavailable, we take ν = 1/4, and this leads to 1 pN ≤ fb ≤ 3 pN. The effect of variable properties such as ν is deemed to be quite small because for most biological materials of this type, Poisson’s ratio is typically taken in the range 0.3 ≤ ν ≤ 0.5 (67). We note that in this case, the effect of substrate stiffness is reduced somewhat, and a larger influence is made by the glycocalyx properties that are, unfortunately, not accurately known.
An effect that arises from integrin preforces, especially when the discussion surrounding Fig. 2, is recalled; this concerns the type of initial condition used to assess integrin catch-bond survivability as outlined in Appendix B. Given that talin-integrin complexes exist, perhaps under prestress such as with stiffer substrates that are then linked to actin-myosin contractility, we expect that the initial conditions are more appropriately of types II–II′ as in Appendix B; types II–II′ assume an equilibrium between states 1 and 2. In contrast, on compliant substrates, we expect that initial conditions are more like those described as types I–II. This apparently has not been previously considered.
We pass now to the description of talin’s force versus time response.
Force response of talin and its connections to actin
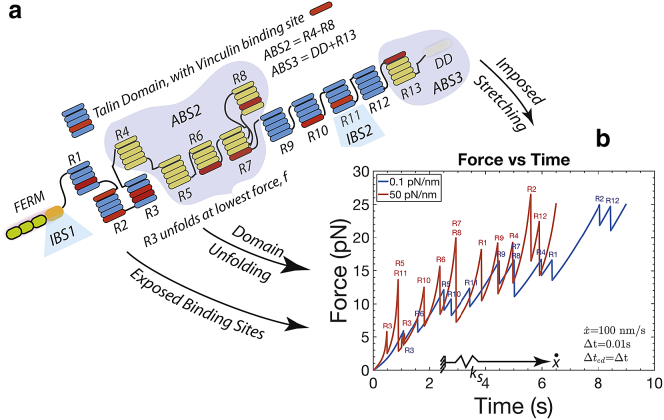
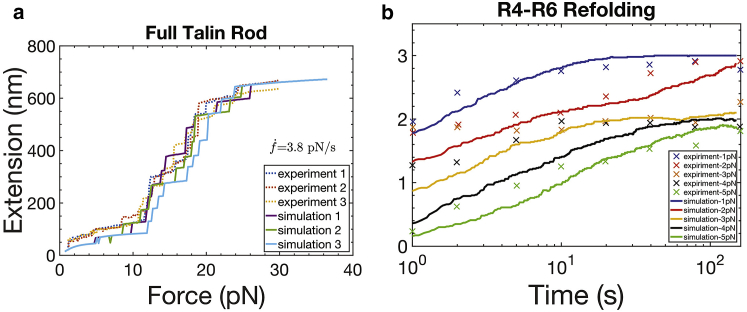
Fig. 3 a illustrates a schematic representation of talin (35) and its various binding sites (35,36). Integrin-binding sites are designated as “IBSi” and actin-binding sites by “ABSi” (35,36). Talin has two integrin-binding sites, IBS1 and IBS2, and can dimerize, as we shall consider below in Fig. 4. Actin-binding sites begin at ABS3 at the C-terminus (68); additional actin-binding sites are described as cryptic actin-vinculin-talin-binding sites (VBSs) and are buried within the folded domains R1–R3, R6–R8, and R10–R11. They are exposed upon the progressive force unfolding of ABS-containing domains (35,36,69, 70, 71, 72). We note that detailed and elegant experiments have been carried out that document the force-induced unfolding and refolding of talin; we have quantitatively described their data with our theoretical unfolding and refolding model (73), originally developed for spectrin. In Fig. 3 a, the cryptic vinculin-binding sites on the talin rod are specifically listed (35,36,69,70,72).
Figure 3.
(a) Model for a talin monomer. Note actin (ABSs), integrin (IBSs), and actin-vinculin-talin (VBSs) binding sites on talin. VBSs are shown in red in various domains. (b) Force along talin rod versus time at a stretching rate of = 100 nm s−1 is shown. Unfolding events of talin domains are indicated at the associated force peaks. To see this figure in color, go online.
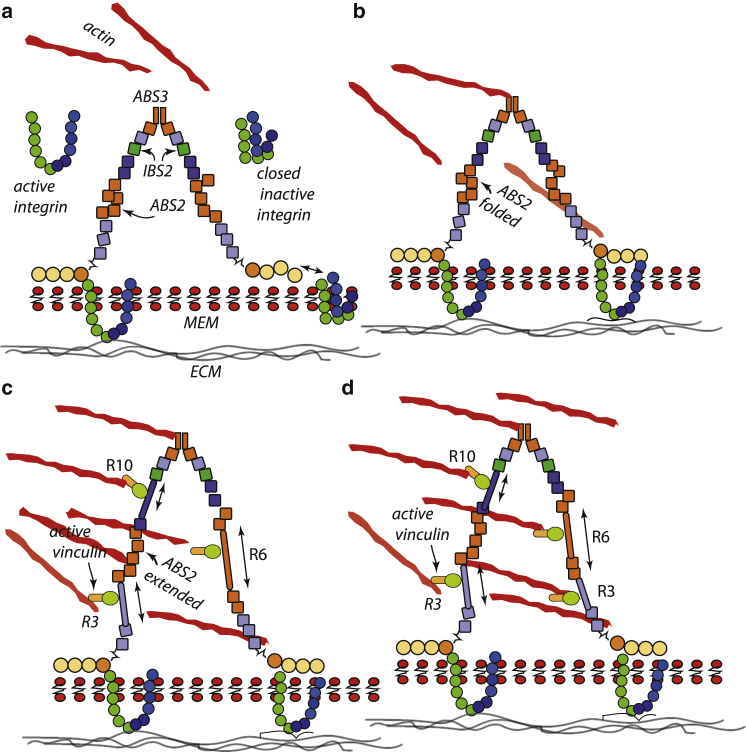
Figure 4.
(a–d) A talin dimer shown at various stages of unfolding and bonding via vinculin to actin. To see this figure in color, go online.
The calibration of the unfolding model is described in Appendix A, and in Fig. 3 b, we show a typical talin force versus time response to the stretching of a full talin rod at a constant rate of = 100 nm/s; the response at lower rates is considered later. Clearly, we assume here that talin is bound at both its ends, presumably to ABS3 (actin) and to integrin-substrate at IBS1; these prospects are analyzed later. Rearward actin speeds have been reported for various cell types and, depending on location within the cell, are in the range 1–600 nm/s (74, 75, 76, 77, 78); here, we use fixed rates of order 100 nm/s and later variable rates between 40 and 100 nm/s.
In Fig. 3 b, the substrate stiffness is taken as ks = 0.1 pN/nm or ks = 50 pN/nm; these roughly correspond to elastic moduli of E ∼ 0.4 kPa or ∼40 kPa, respectively, as discussed in Appendix A. As expected, and as already observed, it is common for R3 to unfold early, i.e., at the lowest force levels (36,69,70). The unfolding forces (i.e., the peak force at unfolding) are modestly dependent on loading rate because the activation lengths for unfolding are generally large (see Appendix A). Note, however, the example of unfolding of R4, shown in Fig. 3 b, which unfolds at a distinctly lower force when talin is stretched against a compliant substrate. Subsequently, we observe unfolding at domains within ABS2 (i.e., R4–R8) and R11 (which is also an integrin-binding domain). Other noteworthy features of the unfolding process include the fact that the load drops upon unfolding are larger with a stiffer substrate, and consequently, the unfolded forces (i.e., the forces after unfolding) can be larger on a compliant substrate. Also, it is noticed that refolding at low forces can and does occur (follow R3 at low forces) as long as an unfolded talin domain contains no vinculin bond, as discussed below.
At first glance, it may appear that the “general talin force versus time” is higher with a stiffer substrate, and yet the effect is seen to be modest because of the strong force-buffering effect of the unfolding of talin and would not seem to explain the generally larger traction forces generated on stiffer substrates. We note that although refolding is observed at low forces, viz., less than ∼3–5 pN, refolding is not expected at higher forces (see Appendix A; (69,70)).
Moreover, the responses shown in Fig. 3 b assume that the talin rod is indeed bound, say, to actin, as well as to integrin-ligand substrate. Hence, there is the question of whether these bonds can support the force versus time response of Fig. 3 b. Accordingly, we next explore this possibility but now assuming only a talin-integrin connection. We specifically explore the talin-actin and talin-vinculin-actin bonding dynamics.
We take the talin-actin bonds to involve at least three distinct contributions. Following Gingras et al. (68) and others (35,36,79), we assume an initial connection of talin to actin at ABS3; this initiates force on actin. However, we do not expect this bond to survive for forces greater than, say, 3–5 pN or for times greater than, say, 2–3 s. Hence, the activation (36; unpublished data) and then the unfolding of R3 is vital because it activates ABS2 (35,36,79) and then presents an erstwhile cryptic vinculin bond to talin and then to actin.
Vinculin-actin bonds have been quantified in the elegant experimental and analytical work of Huang et al. (80); in this, they document the behavior of vinculin-actin catch bonds and provide data that may be used to calibrate the catch-bond model as developed by Thomas et al. (54). We have thus calibrated the Thomas model (54) as described in Appendix B. By invoking such an actin-vinculin-talin catch bond, the talin rod is thereby reinforced against the prospect of a failing ABS3-actin initial bond. Moreover, the unfolding of R3 serves to activate ABS2 by allowing its conformational change (global domain, not helix, unfolding) to provide additional talin-actin reinforcement. Hence, we now present Fig. 4, which depicts a probable sequence of binding patterns.
Fig. 4 shows our talin dimer scheme, patterned after a scenario suggested by Klapholz and Brown (35). We begin with an integrin bond at the IBS1 of one monomer as in Fig. 4 a (left side), followed by an ABS3-actin bond as in Fig. 4 b. This engages and loads the talin rod (35,36). As force grows and R3 unfolds, we compute the probability of a vinculin bond from actin-R3-talin. We then continue stretching and compute the probability of bond rupture from catch-bond theory. The unfolding of R3 activates ABS2, as shown in Fig. 4 c; this engages another link to actin. We may assume that the dimer forms another talin-integrin-ligand bond and the process proceeds stochastically on the other monomer, as in Fig. 4 d.
Now, catch bonds are “two-state” bonds with state 1 stable at lower forces and state 2 at higher forces (54,81, 82, 83, 84, 85). We note that although unfolding forces tend to be higher on stiffer substrates, the unfolded forces are comparable on both compliant and stiffer substrates. This means that if we assume the bonds that form on a newly unfolded talin domain form in equilibrium with the prevailing force, they are likely to form in the same state on either stiff or compliant substrates—but what are their survival prospects, and how does substrate stiffness affect their survival?
We first describe the kinetics of actin-vinculin-talin bond formation. Following Huang et al. (80), we take the probability of vinculin bonding to actin to be of the form (86)
| (7) |
with ∼ 4–5 s−1 and where t is measured from the time of unfolding or the time that an erstwhile vinculin bond failed, the latter referring to rebinding. Although empirically calibrated by Huang et al. (80) for vinculin-actin bonding, the form of Eq. 7 follows from the more general analysis of Litvinov et al. (86).
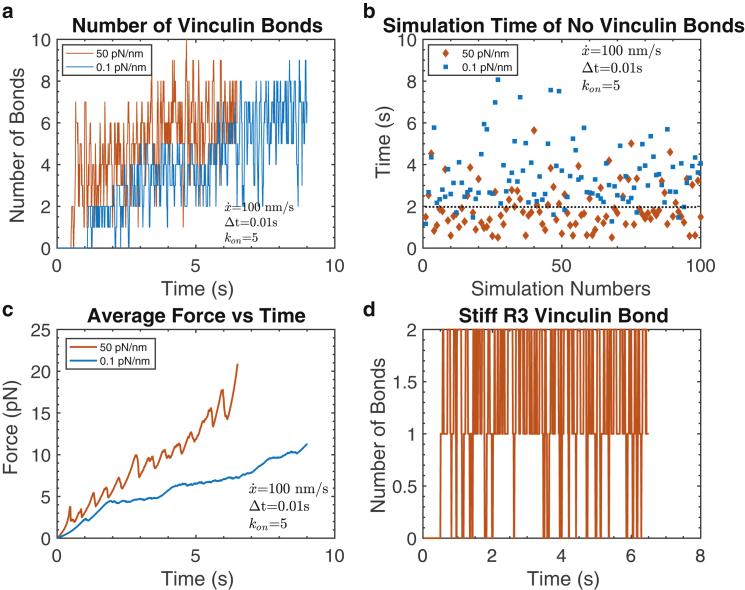
We note in passing that as long as a vinculin bond exists on an unfolded talin domain, no refolding is allowed (69,70). Once a bond is formed, the probabilities of transitions between states are computed as well as for the failures of either state; ultimately, the probability (t) of a bond of either state is computed (see Appendix B). In this, we assume that the full force is supported by all vinculin bonds equally, i.e., in parallel. In a simulation, we then poll each bond for failure. Some results are shown in Fig. 5 a, in which we show the vinculin bonds that come and go only at exposed VBSs on the unfolded talin rod; to be sure, the actin-talin bonds at ABS3 and ABS2 without unfolding are not included in the bond count of Fig. 5 a. We recall that this process is stochastic, and hence, the result of Fig. 5 a must be seen as one of many random processes. However, to gain some insight, we focus on the result with the stiffer substrate and note that we may suppose that the jump to two bonds just after t ≈ 0.5 s is the result of two bonds forming on the 2 VBSs on the unfolded R3 talin domain. Yet we then observe that these bonds fail thereafter at about t ≈ 1 s; in the interval 0.5 s ≤ t ≤ 1 s, we have bond failure and reforming events. At about t 1 s, we have three bonds because of the unfolding of R11 with one VBS (R5, which unfolds at this time, has no VBS); yet we observe that at a short time after, all three bonds have failed. Thereafter, we form more bonds that persist for the duration of the simulation. Similar observations can be made regarding the more compliant substrate but with rather significant differences. Firstly, the number of persistent bonds versus time and the time to establish persistent bonds, tp, are larger with a stiffer substrate. For this particular simulation, tp(stiff) ≈ 1 s and tp(compliant) ≈ 1.5 s. To explore this further, we performed large numbers of such simulations (100–2000); for clarity, we show the results for tp after 100 such simulations in Fig. 5 b. Such large numbers of simulations are required for obtaining expectation or average force versus time response, as shown next.
Figure 5.
(a) Evolution of the number of actin-vinculin-talin bonds after talin unfolding. (b) Results for the time beyond which persistent actin-vinculin-talin bonds exist, tp, after 100 simulations is shown. The dashed line drawn at 2 s is used for discussion purposes in the text. (c) The computed average forces versus time, , taken over a large number of simulations such as in Fig. 3b but assigning a null result for those that would be judged not to survive, is shown, where tp ≥ 2 s. Note that vs. time is seen to continuously rise here because of the fact that talin-vinculin-actin bonds survive for the limited time period shown; eventually, they will fail, but only after the time periods shown. (d) The number of bonds formed on R3 and that failed, Nf, in a particular simulation with a stiff substrate is shown. To see this figure in color, go online.
It is indeed noteworthy that we observe distinctly higher values for tp on more compliant substrates. The line drawn in Fig. 5 b at tp = 2 s suggests that because the initial bonds supporting talin are unlikely to survive for times t 2 s, a large fraction of talin rods would likely fail. To visualize this, we compute the force versus time responses shown in Fig. 5 c. In Fig. 5 c, we display the average force, , a large group (>100) of talin rods would support versus time, assuming that only those with tp ≥ 2 s survive. Hence, if the original number of talin rods was , then the total force they collectively exert would be . In this manner, we demonstrate that increased substrate stiffness causes an increased net force.
We note, in passing, that these results demonstrate that without talin unfolding, essentially no talin rods would survive longer than, say, 3 s, and hence, quite low or no sensible forces would be developed.
The rationale for making the above assumption is based on the dynamics of actin-talin or actin-vinculin-talin bonds as exemplified in Fig. 5 d; this shows the on-off dynamics of actin-vinculin-talin bonds on the unfolding R3 domain during the simulation of Fig. 3, calibrated as a catch bond using the data of Huang et al. (80). We cannot, at present, confirm the veracity of this correlation but we believe that it is representative enough to establish basic trends of the effect. Errors in time intervals on the order of, say, δt ∼ 0.1–0.2 s would be considered quite large and yet would not affect our argument in any measurable way.
Our simulations of the behavior of talin bound to actin and presumably bound to an anchoring integrin have shown a substantial effect of substrate stiffness in terms of talin’s ability to transmit force. In particular, the forces are observed to grow faster with stiffer substrates. We note that, because of the strong force-buffering effect of talin’s unfolding, this effect is not a trivial outcome of talin “pulling on a stiffer spring”; to appreciate this, simply observe the comparable force levels in Fig. 3 b for both stiff and compliant substrates.
We now must complete this force train by specifically considering the effects of the vital link to the integrin-substrate connection—that is, another catch bond.
Net forces generated on the force train
In analyzing the response of talin, we had assumed that talin was bound to an integrin-substrate complex. This assumption led to the expected force versus time of Fig. 5 c. Indeed, it is believed that nascent adhesions involve the clustering of integrins even before they are clearly visualized (37,40, 41, 42, 43, 44). The adhesome is then assembled at the nascent adhesion. We now must consider the expected survival of such catch bonds. These catch bonds are calibrated in Appendix B using data from Kong et al. (55).
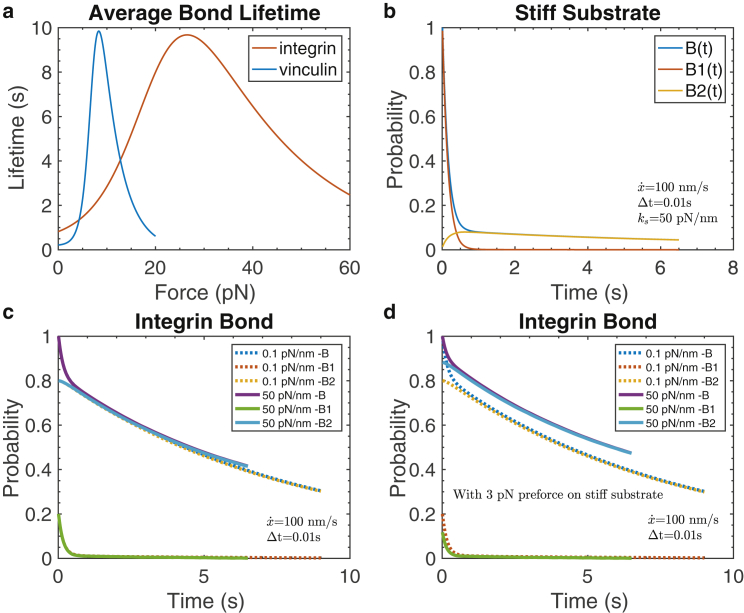
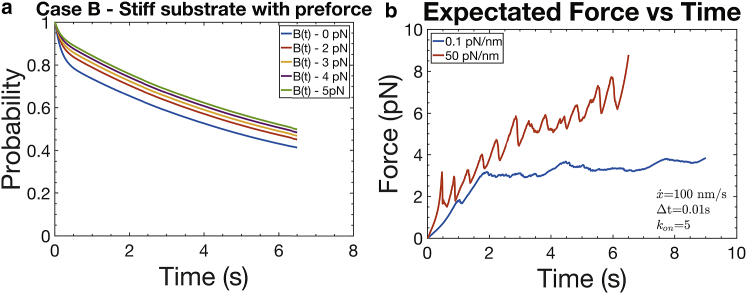
Fig. 10, a, c, and d show three scenarios for catch-bond behavior, each for a stiff and compliant substrate. The scenarios are characterized via the initial conditions taken for the initial bond types, i.e., bond states 1 or 2, which are called conditions I, II, or II′ in Appendix B. We note the above discussion regarding the time-dependent recruitment of integrins to the adhesion site and their association with talin, and the fact they are under a preforce suggests that initial conditions II or II′ are more appropriate; this condition was also used by Huang et al. (80). The significant differences between the cases using either initial conditions II or II′ and initial condition I are clear from the probability versus time plots. In Fig. 6 a, we explore this further and show the probability vs. time for a range of integrin preforce.
Figure 10.
(a) Average bond survival times versus an assumed constant force for both vinculin and integrin catch bonds. (b) shows the probability of integrin bond survival versus time using the force versus time responses shown in Fig. 5c using initial conditions based on the law of mass action, i.e., Eq. 25 (26). (c) Probability of integrin bond survival versus time using the force versus time responses shown in Fig. 5c is given but using for initial conditions of bonds in states 1 or 2 the criterion = k21/k12 and at zero initial force. (d) shows the same as (c), but here, it is assumed that a preforce of 3 pN exists when integrin bonds are formed. To see this figure in color, go online.
Figure 6.
(a) Probability vs. t using type II and II′ initial conditions; preforces are indicated. (b) Expectation force versus time with various integrin preforces is shown. Note that force vs. t for a compliant substrate is also indicated, with type II initial conditions. To see this figure in color, go online.
We recall that the average bond lifetime, , is computed from the integral in Eq. 24 of Appendix B. For that purpose, we use the bond rupture function, −d/dt, to describe the probability of a bond failing at time t. Note that from Eq. 23 we find, indeed, that
| (8) |
is the probable rate of bond rupture at time t. However, to compute the expected force surviving along a talin rod, we want the bond survival function, viz., (t). Hence, we arrive at
| (9) |
Clearly, (t) vanishes at t → ∞. This is shown, along with (t), in Fig. 6, a and b, respectively, for the case of a fixed = 110 nm/s.
Variable actin retrograde flow speed
To account for the effect of the “back force” the force train exerts on the actin-myosin motor system, we impose a force-dependent stretching speed as given by the phenomenological form used by Chan and Odde (87) and also by Elosegui-Artola et al. (88,89) and Huang et al. (80), viz., we set to the form
| (10) |
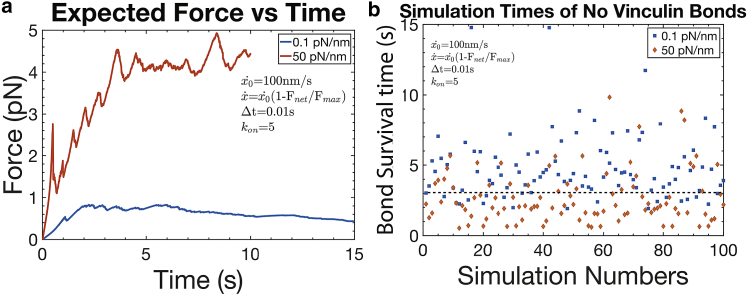
where fmax may lie in the range 8 pN ≤ fmax ≤ 30 pN. In what follows, we take = 100 nm/s and n = 1. We proceed to compute expectation forces as described above for constant . The two most useful results are shown in Fig. 7, a and b, for the case of a modest reduction in stretching speed obtained with fmax = 30 pN. In this case, we demonstrate that even a modest forecasted reduction in leads to a noticeably increased difference in expected force versus time between stiff and compliant substrates, as shown in Fig. 7 a.
Figure 7.
(a) Expectation force versus time with an integrin preforce of 3 pN. Note, as in Fig. 5c, that vs. time is seen to continuously rise here because of the fact that talin-vinculin-actin bonds survive for the limited time period shown; eventually, they will fail, but only after the time periods shown. (b) Results for the time beyond which persistent actin-vinculin-talin bonds exist, tp, after 100 simulations are shown. The dashed line drawn at 3 s is used for discussion purposes in the text. To see this figure in color, go online.
Fig. 7, a and b should be compared to Fig. 5 b for the times beyond which persistent actin-vinculin-talin bonds exist. As an example, the difference in the forecasted at t = 5 s between the stiff and compliant substrate is approximately a factor of 2 with a fixed speed but nearly a factor of 8 with the modestly variable speed we imposed. Part of the reason for this can be appreciated by examination and comparison to Fig. 5 b, which indicate a nearly 1 s increase in the time beyond which persistent actin-vinculin-talin bonds exist. This is actually a significant difference that accounts for the reduced number of active actin-vinculin-talin members in the net force train. This difference is also reflected in the “plateau-like” behavior of vs. time in Fig. 7 a. Simply put, as the force rises less rapidly with decreasing retrograde speed, there is more time for bond failure. We note in passing that, in principle, forces on talin would eventually fall to zero or saturate. Reasons for this include the understanding that conformational changes in talin under sufficiently large forces remove vinculin bonding sites (see, e.g., (69,70)). The relevant force ranges we consider do not reach such levels.
Net traction stress and assessments
As noted above, we expect the net traction stress, (t), to be determined by (t), the dynamic number of bound talin-integrins (per unit area), and the expectation force, (t), as, for example,
| (11) |
(t) may, indeed, be dynamic and display various forms of temporal and/or spatial patterns of turnover. We have discussed factors that clearly suggest that stiffer resistance to force, say, arising from stiffer substrates, tend to enhance (t) and, of course, (t). If, for instance, (400–600 μm−2), we would forecast (2–3 kPa), providing talin rods are expected to survive ∼10 s.
To compare the above forecasts with other modeling efforts, we observe the following. To essentially reproduce the results of Elosegui-Artola et al. (88,89) we would assign to a bonded integrin density, patterned after their reported measured densities, that displays a rather sharp rise at a critical substrate stiffness; this would suffice to explain the observed traction versus substrate stiffness. Elosegui-Artola et al. (88,89) used this empirically observed behavior to accurately “fit” their data.
The “clutch-bond” model of Chan and Odde (87) is more difficult to fit within this framework. The model does essentially provide a picture for increasing traction stresses with increasing “substrate stiffness”; this is due to the increasing forcing rate with actin retrograde flow. The force train is, however, not described except to connect it to a parallel array of “clutch bonds” of unspecified character.
Still other recent models are discussed in Conclusions in relation to the analysis presented herein.
Steady-state traction stresses
We conclude this section with estimating steady-state traction stress magnitudes in a stable FA complex. As noted above, integrins, once activated, bind talin and tend to cluster as depicted in Fig. 1. Clustering may depend on substrate stiffness as discussed by, e.g., (88,89), but to date, no explanation of this exists; we first estimate this via a particular integrin interaction mechanism. Next, we use this to estimate expected traction stresses.
Initial estimates of the mean expectation steady-state traction stresses
The expected force versus time curves along a given actin-vinculin-talin-integrin connection, shown in Figs. 6 b and 7 a, provide forecasted forces that would be expected along the force train as a function of the time that they may be active, i.e., actually connected all along the force train. However, these connections undergo continuous stochastic turnover—that is, they come and go. To assess this we assume that at steady state, their numbers remain stationary in that they last their average lifetimes, , as given by Eq. 24; these average lifetimes are listed for various cases in Table 1.
Table 1.
Integrin Bond Expected Lifetimes as Computed Using the Force versus Time Responses
| Substrate | Stretching Rate (nm/s) | (s) |
|---|---|---|
| compliant | fixed | 4.67 |
| stiff II | fixed | 3.84 |
| stiff II′ | fixed | 4.26 |
| compliant | variable | 5.85 |
| stiff II | variable | 5.01 |
| stiff II′ | variable | 5.60 |
Recall, for these cases, the fixed stretching rate was = 100 nm/s, and for the variable, force-dependent rate, = 100 nm/s, with (t) given by Eq. 10 and fmax = 30 pN.
Now, as these connections continuously turn over, and if we assume this occurs in a regular smooth pattern, the average force they contribute to an ensemble of such connections is . We use the case of variable stretching rate, and thus, we extract expected forces from Fig. 7 a. This leads to the following values, viz.,
| (12) |
We use the measured integrin densities reported by Elosegui-Artola et al. (88,89) of dint = 500 μm−2, as may exist on compliant substrates, and dint = 1000 μm−2, as may exist on stiffer substrates, because of the clustering tendencies we described above. This, however, does not yet fully specify of Eq. 11; for our steady-state scenario, we may call this .
To estimate , we require the probability, , of integrin binding to substrate ligands and, recalling they are catch bonds, in either states 1 or 2. We use the experimental results and accompanying kinetic analysis of Litvinov et al. (86) for αIIbβ3-fibrinogen bonds enhanced with Mn++. In this, they find, with timescales that exceed 0.5 s, → 0.175 approximately (86). As this is within our timescales of, say, , we use this as an appropriate estimate and thereby obtain
| (13) |
In this manner, we arrive at the following estimates for the expectation steady-state traction stresses, viz.,
| (14) |
The traction stresses obtained this way are certainly consistent with those measured by Elosegui-Artola et al. (88,89), who, incidentally, used the data and analysis of Litvinov et al. (86). These traction stress levels are also consistent with those reported by Gardel et al. (74) for PtK1 epithelial cells supported on acrylamide gel substrates with elastic moduli in the 3–5 kPa range. We note, however, that they (74) also report actin flow rates in the 10–30 nm/s range, i.e., considerably lower than used herein. Traction stresses in our above range <300 Pa are, however, much lower than reported by, e.g., (14,15,44,90), in which traction stresses are in the 1–10 kPa range. This is discussed below.
Specific estimates of the mean expectation steady-state traction stresses
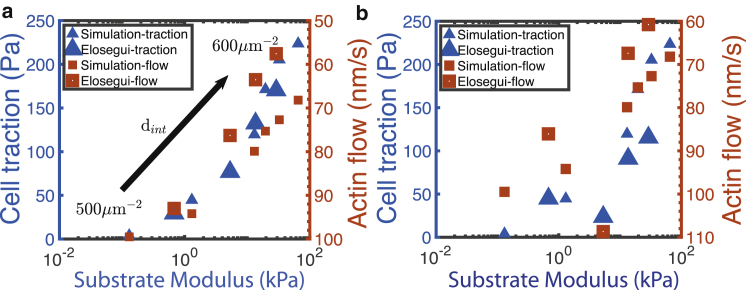
Elosegui-Artola et al. (88) provide a case study in which they measured traction stresses with variable substrate rigidity and in which they documented actin flow speed. The system they studied involved breast myoepithelial cells bound to fibronectin through either α5β1 (expressed constitutively) or αvβ6 integrins (selectively expressed in cancer development). Fig. 8, a and b show selected data for measurements performed on cells expressing one or both integrin types. Specifically, their data from their Fig. 4, j and k, along with our simulated results, are shown in Fig. 8 a for both types of integrins, whereas their data from their Fig. 4, d and e involving only α5β1 integrins, along with our forecasted results, are shown in Fig. 8 b.
Figure 8.
Traction stress versus substrate stiffness; comparison between experiments (88) and simulation. Note that the left-side expected-actin-flow-rate axis has been inverted to facilitate correlation with the traction-stress axis. To see this figure in color, go online.
We note that we were able to match their actin flow speeds reasonably well by simply using the variable speed relation given in Eq. 10 with = 100 nm s−1 and with an exponent of n = 0.8 and our forecasted (t). We also note that the expected actin flow rate is not (t), as computed from Eq. 10, because that rate depends on talin being actually engaged and under force; rather, the expected actin flow rate should be computed using the bonding survival function, −d/dt, as
| (15) |
where (t) is computed using the actual forecasted forces along talin (see Appendix B). The measured, i.e., observed, actin flow rate depends on an ensemble of talin rods bound to the actin skeleton and to integrins on the ECM. In the ensemble, individual talin rods that are engaged come and go, of course. We used initial integrin densities versus substrate stiffness in accord with those reported in (88) as listed in Fig. 8; in particular, we use integrin densities in the range 500 μm−2 ≤ dint ≤ 600 μm−2, as indicated in Fig. 8 a. To estimate , we again use the kinetic analysis of Litvinov et al. (86), whereby we estimate that for the two catch-bond states, i = 1, 2,
| (16) |
where . Because we lack sufficiently complete kinetic data for either α5β1 or αvβ6 integrins, we use data for αIIbβ3 integrins from (86), who report two-dimensional dissociation constants = 1.7 × 104, 2.6 × 103 μm−2. From these and Eq. 16, we estimate ∼ 0.175 as above. The expected steady-state traction stresses so determined are plotted versus those reported by Elosegui-Artola et al. (88).
Although the agreement shown in Fig. 8, a and b is encouraging, we note that whereas we use in Fig. 8 b the measured catch-bond parameters for α5β1 integrins (55) to estimate bond survival (see also Appendix B), we use the same parameters for the combination of α5β1 and αvβ6 integrins for the case of Fig. 8 a. This we have done because of a lack of independently measured catch-bond properties for αvβ6 integrin-fibronectin bonds. Moreover, although we have adequate catch-bond data for estimating α5β1 bond survival, we lack reliable kinetic data to estimate and hence used such data for αIIbβ3 from (86). We note, however, that Elosegui-Artola et al. (88) measured simple rate constants kon and koff and found ≈ 0.5 and ≈ 30. This they “compensated for” by also noting that, when observed on the substrate surface, ≈ 5. This ad hoc compensation is far from exact but may help explain the roughly similar behavior shown in Fig. 8, a and b. They reported ≈ 500 μm−2, as indicated in Fig. 8 a. Aside from that just mentioned, however, we make little other ad hoc “fitting.” Below, in the Discussion, we point out additional concerns and requirements for improved theoretical understanding and forecasting of cell adhesion and mechanotransduction.
Results and Discussion
General discussion and required parameters
The analysis presented above revealed a number of notable features of force transmission along the adhesome. Among these are that the effects of mechanosensitivity appear all along what we have dubbed the force train. Indeed, these effects are directly related to the time rate of force development, as seen in the behavior of both talin and integrin bonding. Hence, it would seem to be improper to simply relate force development to one particular set of “clutch bonds” that are envisioned to operate at one location or another along the actin-vinculin-talin-integrin-ligand-ECM train. We now discuss the various parameters and elements of our model that play important roles in the development of traction force and stress.
As an example, the response of talin vis-à-vis the actin-vinculin-talin reinforcement is intriguing, especially as it pertains to the early stage of talin force loading. The response of talin also illustrates the point made above that focusing attention on just a generic set of clutch bonds is misleading and renders the force-train system ill-described. Specifically, in Force Response Of Talin And Its Connections To Actin, we discussed the presumption that talin is initially “loaded” by actin bonding to ABS3 and then via the activation of ABS2 upon a conformational change of talin under modest forces (i.e., before talin domains unfold). The precise behavior of such bonding, however, is not yet quantitatively understood and hence is a topic of needed future study. Therefore, not being a simple parameter per se, the early engagement of talin to the actin skeleton requires more quantification in terms of bond strength, character, and survivability. We, in lieu of this quantitative information, made the assumption that actin-talin bonding had to survive for periods of time in the range of 2–3 s so that forces sufficient to induce talin unfolding (at, say, domain R3) and thereby vinculin reinforcement can be generated. Recently, however, Atherton et al. (unpublished data) have shed additional light on this phase of the loading process, as briefly discussed next.
Consistent with our view in Fig. 1, Atherton et al. (unpublished data) propose that talin is recruited to the RAP/RIAM complex (91) at nascent adhesions where it binds integrins. Interaction with integrin renders R3 accessible for vinculin activation and binding, and this leads to unmasking ABS2. At this point (before talin domain unfolding at, say, R3), the focal adhesion is ready to engage the actomyosin engine. We assume that this process “buys some time” for eventual talin unfolding that then allows for additional talin-vinculin bond reinforcement. We assume (see Figs. 5 b and 7 b) that this takes two to three critical seconds; this depends on loading rate and thereby on substrate stiffness. Those talin rods that do not survive such critical seconds are released from the ensemble of talin rods. Clearly, this phase of the force process requires additional quantitative study, as does the development of integrin density and distribution as discussed next. Indeed, Atherton et al. (36) have shown that fibroblast cells containing talin ABS2 mutants displayed traction stresses that were 45–50% less than TalFl. Hence, without a full account of the talin force versus time response, results from any assessments would be quite misleading.
Our model analysis makes use of the catch-bond theoretical framework of Thomas et al. (26) and the specific data of, inter alia, Huang et al. (80), Kong et al. (55), and Litvinov et al. (86). We note, however, that although adequate characterizations of catch-bond survivability are obtainable by the methods described in such work, kinetic parameters for bond formation are not always readily available, especially because bond formation and re-formation may occur under nonequilibrium conditions. The work of Litvinov et al. (86) is of specific interest here, and hence, we used their results as an example, as have others (e.g., (88,89)).
Integrin density and clustering
Estimations of traction stresses, as attempted in Initial Estimates Of The Mean Expectation Steady-State Traction Stresses and Specific Estimates Of The Mean Expectation Steady-State Traction Stresses, illustrate the vital need for quantitative perspective on integrin density, integrin-ligand bond survival, and, as we believe, integrin distribution. This will be vital to continue our analysis to describe the full time evolution of adhesion sites. We comment on several of these aspects below.
Elosegui-Artola et al. (88,89) have provided experimental data that showed a significant dependence of integrin density (dint) on substrate stiffness. By using this correlation as input to their simple “clutch-bond” model, they were able to rationalize their observations of increasing traction stress—which we call —with increasing substrate stiffness. Both the analysis of Initial Estimates Of The Mean Expectation Steady-State Traction Stresses and Specific Estimates Of The Mean Expectation Steady-State Traction Stresses and our mechanistic reasoning, however, clearly suggest that this aspect of the adhesion process requires a great deal more attention. This requires accounting for not only integrin type but also cell type, cell membrane and glycocalyx structure, and substrate morphology and topology. We note below that substrate viscoelasticity versus elasticity needs also to be considered.
ECMs—e.g., those composed of cross-linked polyacrylamide hydrogels, for one—display essentially elastic behavior characterized by time-independent linear force (stress) versus displacement (strain) response. Yet reconstructed cell matrices exhibit a time-dependent viscoelastic response, i.e., force (or stress) relaxation when held at a sustained displacement (or strain) or a relaxed rate of force (or stress) increase at a fixed rate of stretching (or straining). Indeed, effects of increased cell spreading, proliferation, and differentiation have been described for mesenchymal cells on substrates displaying increased viscoelastic stress-reduction behavior (47,92). The effects were attributed to increased integrin density and clustering, although no rationale was provided for why or how viscoelastic response contributes to integrin clustering (47,92). However, such an effect may be consistent with our model scenario for integrin clustering as shown in Fig. 2. The bonding of integrins to ECM ligands invokes an initially nearly elastic response of the cell’s membrane/substrate as we envisioned. This leads to enhanced clustering on stiffer substrates. Yet, once clustered and under force fb, the relaxation of the substrate will lead to a further reduction in energy and thereby stabilization of the clusters. We expect this process will reduce the internal force in the integrins but stabilize their positions.
On the latter point, we note that it now appears clear that ligand/integrin patterning, as well as substrate morphology and topology, must be explicitly accounted for. The effects of topology and patterning are distinct from density per se. The results of Maheshwari et al. (93) are most relevant here in that they demonstrated how fibroblast cell adhesion depended quite sensitively on ligand cluster patterns as well as on overall ligand density. But, to put an even finer point on this, we note the reported evidence of the effects of surface (nanoscale topology) on adhesion. Examples include, inter alia, the effect of patterns of nanoscale silica beads (27,30) and the nanoscale protrusions that exist on the surfaces of nanostructured metals and alloys (29,30).
Herein, we have not considered the full time evolution of integrin clustering and density per se but computed what we called steady-state expectation traction stresses; these were based on observed integrin densities as used to obtain, for example, the results of Fig. 8. Indeed, although much has been reported on the formation of nascent adhesion clusters (see, e.g., (38,39)), there does not exist as yet a fully predictive theoretical framework for such cluster development. A number of compelling ideas exist, however, that should eventually emerge into such a framework; examples include the role of membrane and glycocalyx distortions (see, e.g., (43,53,94) and the ideas presented herein). We present here a remarkably simple analysis that captures much of the effects and that leads to a simple pathway to computing integrin interaction forces that are readily incorporated into simulation models that would, in fact, reveal clustering. But that may not be nearly enough. Consider, for example, the reports of Cheresh and co-workers, e.g., (95, 96, 97), who uncover important effects on cancer cells of Galectin-3 and, indeed, the localization of gangliosides such as GD2 and GD3 on integrin aggregation and clustering. These observations—along with the reported diverse effects of substrate topography (30), cell glycocalyx (43,53), and membrane distortions (94), just to mention a few factors—suggest that far more study is required to even define a credible pathway for such predictive models. Such models may be quite system specific as general rules and principles have yet to emerge, even for say the effects of substrate topography (30).
Conclusions
This study has attempted to follow a minimal, yet detailed, account of the force train along a realistic model adhesome. In doing so, the analysis revealed that mechanosensitivity is manifest at each step and even substep along the force pathway. This, itself, makes the analysis unique and useful in that it illustrates where vital quantitative perspective is missing and how it would enable more definitive understanding of how a given system works.
A most vital issue would appear to be the question of integrin/ligand density and patterning on a given substrate and how these affect integrin-bond kinetics. Given the far-reaching implications of how cells sense, adapt, and develop based on their environments (26) this may well represent a prime focus for future study. We have modeled integrin bonding using available data, e.g., that of Kong et al. (55), and this would benefit from a more detailed assessment by looking individually at both the talin-integrin and integrin-ligand bonding as data become available. However, it is critical to understand that this will require a range of data and information typically unavailable in most published studies. Such detailed information will include, inter alia, substrate elasticity (3,28) (viscoelasticity) (92); substrate morphology, topography, and nanoscale roughness (in both detailed qualitative and quantitative character) (30); ligand type, density, and patterning (93); integrin type and (initial) density (88,89); cytoskeleton kinetics (80); and the presence of plaque proteins, as we have described (35,36; unpublished data). Indeed, as we have cited, there are many puzzle pieces of this grand puzzle to be found in the literature, but these pieces are incomplete and are often not necessarily from the same puzzle. Hence, we support the research suggestion of Lord et al. (30), viz., the “set up of very well-defined, much reduced model systems that can be thoroughly analyzed and large scale screening of cellular response to …” We add to this that a single such system will not suffice to navigate through the particularities of any given system, and hence, parallel systems are required. Therefore, a coordinated multigroup effort may be needed. The framework we have presented herein is indeed adaptable and readily expandable to provide quantitative verification of model concepts.
We conclude by noting that other models exist that consider a model adhesome such as ours and address questions such as adhesion growth and mechanosensitivity, but they analyze the adhesome’s elements in fundamentally different ways; an interesting case in point is the models of Cao et al. (98,99). For example, their model elements (98) are modeled as rate-independent, loading (or stretching) history-independent, linear elastic elements. In contrast, our model explicitly treats each element as a thoroughly nonlinear, stochastic, and hence rate- and history-dependent molecular-based element; moreover, we use a wide range of experimental biophysical data to calibrate each element, including the stochastic bonding of each element to each other. Hence, the two models have an entirely different composition. Moreover, our results demonstrate quite clearly that simply replacing linear elastic elements with an “effective nonlinear element” derived, for example, from our model may not produce similar outcomes; for example, and as just one example, the analysis of just the vs. time results obtained assuming a constant stretching versus a moderately variable rate of Figs. 5 a and 7 a illustrate that point clearly. Yet, what may be possible is to enhance our model adhesome by including a nucleus, as in the Cao et al. model (98), and pose questions as posed by them. Their framework would seem naturally suited to our molecular-based, stochastic approach. Likewise, models that describe either the growth or the survivability of FAs, e.g., (100,101), may be incorporated into a framework such as ours for a more complete description of the development of traction stress.
Author Contributions
R.J.A., K.L., and Q.Z. all contributed to and performed the research. The manuscript was written by R.J.A. and Q.Z.
Acknowledgments
The authors thank Drs. Christoph Ballestrem, University of Manchester; Wendy Thomas, University of Washington; and Michael Sheetz, Columbia University for valuable discussions related to this work.
Editor: Vivek Shenoy.
APPENDIX A: TALIN UNFOLDING
We use the framework of Zhu and Asaro (73) to describe the time-force evolution of folding and unfolding of talin; the parameters are listed in Table 2 and the resulting forecasts for unfolding refolding are shown in Fig. 9, a and b, respectively. We consider the transitions between two states , folded (f) and unfolded (u), separated by energy barriers ΔEf→u and ΔEu→f. The energy barriers are affected by force, and hence, e.g., for unfolding,
| (17) |
Table 2.
Parameters Used to Describe the Unfolding and Refolding of the Talin Rod Domains R1–R12
| Talin domain | 1 | 2 | 3 | 4 | 5 | 6 | 7–8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Folded size (nm) | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 |
| Unfolded size (nm) | 69.2 | 52.4 | 49.6 | 52.4 | 64 | 60.4 | 118.4 | 66.8 | 63.2 | 66.4 | 62.8 |
| kf→u(s−1) | 4.2 × 10−6 | 1.7 × 10−8 | 0.018 | 4.2 × 10−6 | 2.5 × 10−5 | 2.5 × 10−5 | 4.2 × 10−6 | 4.2 × 10−6 | 2.5 × 10−5 | 2.5 × 10−5 | 1.7 × 10−8 |
| Δxf→u (nm) | 3.1 | 3.4 | 5.7 | 3.1 | 4.1 | 4.1 | 3.1 | 3.1 | 4.1 | 4.1 | 3.4 |
| ku→f(s−1) | 1.606 | 0.1318 | 1 × 106 | 22.387 | 2.57 | 2.57 | 22.387 | 123 | 123 | 123 | 123 |
| −Δxu→f (nm) | 4.28 | 4.14 | 9.86 | 4.04 | 11.5 | 11.5 | 13.6 | 10.35 | 10.35 | 10.35 | 10.35 |
Figure 9.
(a) Unfolding of a full talin rod compared to the experimental measurements of Yao et al. (69,70); unfolding as observed under imposed force rate. (b) Talin domain refolding is shown. To see this figure in color, go online.
which formally and operationally define an unfolding activation distance as Δxf→u −∂ΔEf→u/∂f. For the unfolding rate, we thus have
| (18) |
A similar analysis leads to the refolding rate
| (19) |
where we note that the transition distance for refolding is such that Δxu→f < 0. The model continues by defining the end-to-end distance, x, as
| (20) |
with Lf and Lu being the contour lengths of the folded and unfolded domains, respectively, and xf and xu being the projection extensions in the direction of f of folded and unfolded domains, respectively; N is the total number of foldable plus unfoldable domains.
A freely jointed chain model (102) was then used, which led to the relation
| (21) |
where (ζ) = cothζ − 1/ζ and pi is the persistence length of a folded or unfolded domain, i.e., i = f, u.
The time step used was Δt = 0.01 ss.
APPENDIX B: CATCH BONDS
The model allosteric protein we envision has two minimal energy conformations separated by an energy barrier; the barrier height above state 1 is ΔE12 and above state 2 is ΔE21. The transition rates between these states in the absence of force are and , where these are in turn proportional to . Because the protein can bind the ligand from either state, we assume it can unbind from either state with unbinding energies ΔE10 and ΔE20; this leads to unbinding rates k10 and k20.
Upon the application of force, f, these energy barriers decrease by fΔxij so that the transition rates become
| (22) |
To compute bond lifetimes, we define (t) and (t) as the probability of occupancy of state 1 or state 2, respectively. Hence, these evolve from the coupled ODEs
| (23) |
The probability of a bond in either state be occupied is . Hence, Eq. 23 must be integrated through a given force versus time history, subject to initial conditions.
We note that the expectation lifetime of a bond may be computed from the negative derivative of the survival function, viz., − as
| (24) |
where the second equality follows via integration by parts provided . For actin-vinculin bonds, we have fitted the catch-bond model as described by Thomas et al. (54) to the data of Huang et al. (80). Results are listed in Table 3.
Table 3.
Kinetic Rate Constants for Vinculin-Actin Catch Bonds
| Transition | Rate Constant (1/s) | Transition Distance (Å) |
|---|---|---|
| 1 → 0 | = 5.3 | Δx10 = 0 |
| 2 → 0 | = 5.5 × 10−3 | Δx20 = 1.2 |
| 1 → 2 | = 6.1 | Δx12 = 0.4 |
| 2 → 1 | = 43 | Δx21 = −3.4 |
Integrin-fibronectin ligand bonds
For integrin catch bonds, we used the data of Kong et al. (55) for integrin-ligand bonds and determined, vis-à-vis the catch-bond model described by Thomas et al. (54), the parameters shown below in Table 4.
Table 4.
Kinetic Rate Constants for Integrin Catch Bonds
| Transition | Rate Constant (1/s) | Transition Distance (Å) |
|---|---|---|
| 1 → 0 | = 6.01 | Δx10 = 1.37 |
| 2 → 0 | = 0.021 | Δx20 = 2.112 |
| 1 → 2 | = 0.42 | Δx12 = 0.58 |
| 2 → 1 | = 0.105 | Δx21 = −0.42 |
With the calibrations given in Tables 3 and 4, we compute the average bond lifetimes at constant forces as shown in Fig. 6 b for both the actin-vinculin (80) and integrin-fibronectin bonds (55). In Fig. 10 b, we plot the probability versus time curves computed from the integration of Eq. 23 using the force versus time response of Fig. 5 c for an average talin rod of an integrin-ligand bond using the data of Table 4. In Fig. 10, we plot the probability versus time curves, again for an integrin-ligand bond, using initial conditions that differ from those used to compute Fig. 10 b.
The initial condition = k21/k12 assumes that bond states 1 and 2 equilibrate as we discuss in the text and has been assumed elsewhere (83). The survival versus time behavior, as we see, is quite sensitive to the initial conditions and for the initial probabilities of finding a bond in the low force state 1 and high force state 2. In Fig. 10, c and d, it is assumed that the bond state transitions equilibrate so that = k21/k12; we call these initial conditions II and II′, designating that the initial force on the bond is = 0 or > 0, respectively. For the case of Fig. 10 d, we used = 3 pN. However, Thomas et al. (26) point out that “the initial conditions depend on experimental conditions,” and for their conditions, they used a principle of “detailed balance” to estimate that, e.g.,
| (25) |
This initial condition, dubbed I, was used for Fig. 10 b.
Here again, the time step used was Δt = 0.01 s.
References
- 1.Janmey P.A., Winer J.P., Wen Q. The hard life of soft cells. Cell Motil. Cytoskeleton. 2009;66:597–605. doi: 10.1002/cm.20382. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Nelson C.M., Jean R.P., Chen C.S. Emergent patterns of growth controlled by multicellular form and mechanics. Proc. Natl. Acad. Sci. USA. 2005;102:11594–11599. doi: 10.1073/pnas.0502575102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Engler A.J., Sen S., Discher D.E. Matrix elasticity directs stem cell lineage specification. Cell. 2006;126:677–689. doi: 10.1016/j.cell.2006.06.044. [DOI] [PubMed] [Google Scholar]
- 4.Gorfinkiel N., Blanchard G.B., Martinez Arias A. Mechanical control of global cell behaviour during dorsal closure in Drosophila. Development. 2009;136:1889–1898. doi: 10.1242/dev.030866. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Mammoto T., Ingber D.E. Mechanical control of tissue and organ development. Development. 2010;137:1407–1420. doi: 10.1242/dev.024166. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Kumar S., Weaver V.M. Mechanics, malignancy, and metastasis: the force journey of a tumor cell. Cancer Metastasis Rev. 2009;28:113–127. doi: 10.1007/s10555-008-9173-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Paszek M.J., Zahir N., Weaver V.M. Tensional homeostasis and the malignant phenotype. Cancer Cell. 2005;8:241–254. doi: 10.1016/j.ccr.2005.08.010. [DOI] [PubMed] [Google Scholar]
- 8.Chen C.S., Mrksich M., Ingber D.E. Geometric control of cell life and death. Science. 1997;276:1425–1428. doi: 10.1126/science.276.5317.1425. [DOI] [PubMed] [Google Scholar]
- 9.Chrzanowska-Wodnicka M., Burridge K. Rho-stimulated contractility drives the formation of stress fibers and focal adhesions. J. Cell Biol. 1996;133:1403–1415. doi: 10.1083/jcb.133.6.1403. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Folkman J., Moscona A. Role of cell shape in growth control. Nature. 1978;273:345–349. doi: 10.1038/273345a0. [DOI] [PubMed] [Google Scholar]
- 11.Fenteany G., Janmey P.A., Stossel T.P. Signaling pathways and cell mechanics involved in wound closure by epithelial cell sheets. Curr. Biol. 2000;10:831–838. doi: 10.1016/s0960-9822(00)00579-0. [DOI] [PubMed] [Google Scholar]
- 12.Brugués A., Anon E., Trepat X. Forces driving epithelial wound healing. Nat. Phys. 2014;10:683–690. doi: 10.1038/nphys3040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Balaban N.Q., Schwarz U.S., Geiger B. Force and focal adhesion assembly: a close relationship studied using elastic micropatterned substrates. Nat. Cell Biol. 2001;3:466–472. doi: 10.1038/35074532. [DOI] [PubMed] [Google Scholar]
- 14.Beningo K.A., Dembo M., Wang Y.L. Nascent focal adhesions are responsible for the generation of strong propulsive forces in migrating fibroblasts. J. Cell Biol. 2001;153:881–888. doi: 10.1083/jcb.153.4.881. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Bershadsky A.D., Balaban N.Q., Geiger B. Adhesion-dependent cell mechanosensitivity. Annu. Rev. Cell Dev. Biol. 2003;19:677–695. doi: 10.1146/annurev.cellbio.19.111301.153011. [DOI] [PubMed] [Google Scholar]
- 16.Geiger B., Spatz J.P., Bershadsky A.D. Environmental sensing through focal adhesions. Nat. Rev. Mol. Cell Biol. 2009;10:21–33. doi: 10.1038/nrm2593. [DOI] [PubMed] [Google Scholar]
- 17.Winograd-Katz S.E., Fässler R., Legate K.R. The integrin adhesome: from genes and proteins to human disease. Nat. Rev. Mol. Cell Biol. 2014;15:273–288. doi: 10.1038/nrm3769. [DOI] [PubMed] [Google Scholar]
- 18.Maartens A.P., Brown N.H. Anchors and signals: the diverse roles of integrins in development. Curr. Top. Dev. Biol. 2015;112:233–272. doi: 10.1016/bs.ctdb.2014.11.020. [DOI] [PubMed] [Google Scholar]
- 19.Lo C.M., Wang H.B., Wang Y.L. Cell movement is guided by the rigidity of the substrate. Biophys. J. 2000;79:144–152. doi: 10.1016/S0006-3495(00)76279-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Saxena M., Liu S., Sheetz M.P. EGFR and HER2 activate rigidity sensing only on rigid matrices. Nat. Mater. 2017;16:775–781. doi: 10.1038/nmat4893. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Burridge K., Guilluy C. Focal adhesions, stress fibers and mechanical tension. Exp. Cell Res. 2016;343:14–20. doi: 10.1016/j.yexcr.2015.10.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Wang H.B., Dembo M., Wang Y.L. Substrate flexibility regulates growth and apoptosis of normal but not transformed cells. Am. J. Physiol. Cell Physiol. 2000;279:C1345–C1350. doi: 10.1152/ajpcell.2000.279.5.C1345. [DOI] [PubMed] [Google Scholar]
- 23.Hadden W.J., Young J.L., Choi Y.S. Stem cell migration and mechanotransduction on linear stiffness gradient hydrogels. Proc. Natl. Acad. Sci. USA. 2017;114:5647–5652. doi: 10.1073/pnas.1618239114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Plotnikov S.V., Pasapera A.M., Waterman C.M. Force fluctuations within focal adhesions mediate ECM-rigidity sensing to guide directed cell migration. Cell. 2012;151:1513–1527. doi: 10.1016/j.cell.2012.11.034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Yeung T., Georges P.C., Janmey P.A. Effects of substrate stiffness on cell morphology, cytoskeletal structure, and adhesion. Cell Motil. Cytoskeleton. 2005;60:24–34. doi: 10.1002/cm.20041. [DOI] [PubMed] [Google Scholar]
- 26.Thomas W.E., Discher D.E., Shastri V.P. Mechanical regulation of cells by materials and tissues. MRS Bull. 2010;35:578–583. [Google Scholar]
- 27.Lipski A.M., Pino C.J., Shastri V.P. The effect of silica nanoparticle-modified surfaces on cell morphology, cytoskeletal organization and function. Biomaterials. 2008;29:3836–3846. doi: 10.1016/j.biomaterials.2008.06.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Engler A.J., Carag-Krieger C., Discher D.E. Embryonic cardiomyocytes beat best on a matrix with heart-like elasticity: scar-like rigidity inhibits beating. J. Cell Sci. 2008;121:3794–3802. doi: 10.1242/jcs.029678. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Lowe T.C., Reiss R.A. Understanding the biological responses of nanostructured metals and surfaces. Mater. Sci. Eng. 2014;63:012172. [Google Scholar]
- 30.Lord M.S., Foss M., Besenbacher F. Influence of nanoscale surface topography on protein adsorption and cellular response. Nano Today. 2010;5:66–78. [Google Scholar]
- 31.Bagherifard S., Ghelichi R., Guagliano M. Cell response to nanocrystallized metallic substrates obtained through severe plastic deformation. ACS Appl. Mater. Interfaces. 2014;6:7963–7985. doi: 10.1021/am501119k. [DOI] [PubMed] [Google Scholar]
- 32.Horton E.R., Humphries J.D., Humphries M.J. The integrin adhesome network at a glance. J. Cell Sci. 2016;129:4159–4163. doi: 10.1242/jcs.192054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Zaidel-Bar R., Itzkovitz S., Geiger B. Functional atlas of the integrin adhesome. Nat. Cell Biol. 2007;9:858–867. doi: 10.1038/ncb0807-858. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Roca-Cusachs P., Iskratsch T., Sheetz M.P. Finding the weakest link: exploring integrin-mediated mechanical molecular pathways. J. Cell Sci. 2012;125:3025–3038. doi: 10.1242/jcs.095794. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Klapholz B., Brown N.H. Talin - the master of integrin adhesions. J. Cell Sci. 2017;130:2435–2446. doi: 10.1242/jcs.190991. [DOI] [PubMed] [Google Scholar]
- 36.Atherton P., Stutchbury B., Ballestrem C. Vinculin controls talin engagement with the actomyosin machinery. Nat. Commun. 2015;6:10038. doi: 10.1038/ncomms10038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Cluzel C., Saltel F., Wehrle-Haller B. The mechanisms and dynamics of (α)v(β)3 integrin clustering in living cells. J. Cell Biol. 2005;171:383–392. doi: 10.1083/jcb.200503017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Changede R., Xu X., Sheetz M.P. Nascent integrin adhesions form on all matrix rigidities after integrin activation. Dev. Cell. 2015;35:614–621. doi: 10.1016/j.devcel.2015.11.001. [DOI] [PubMed] [Google Scholar]
- 39.Changede R., Sheetz M. Integrin and cadherin clusters: a robust way to organize adhesions for cell mechanics. BioEssays. 2017;39:1–12. doi: 10.1002/bies.201600123. [DOI] [PubMed] [Google Scholar]
- 40.Wiseman P.W., Brown C.M., Horwitz A.F. Spatial mapping of integrin interactions and dynamics during cell migration by image correlation microscopy. J. Cell Sci. 2004;117:5521–5534. doi: 10.1242/jcs.01416. [DOI] [PubMed] [Google Scholar]
- 41.Roca-Cusachs P., Gauthier N.C., Sheetz M.P. Clustering of alpha(5)beta(1) integrins determines adhesion strength whereas alpha(v)beta(3) and talin enable mechanotransduction. Proc. Natl. Acad. Sci. USA. 2009;106:16245–16250. doi: 10.1073/pnas.0902818106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Cao L., Nicosia J., Barker T.H. Detection of an integrin-binding mechanoswitch within fibronectin during tissue formation and fibosis. ACS Nano. 2017;11:7110–7117. doi: 10.1021/acsnano.7b02755. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Paszek M.J., Boettiger D., Hammer D.A. Integrin clustering is driven by mechanical resistance from the glycocalyx and the substrate. PLoS Comput. Biol. 2009;5:e1000604. doi: 10.1371/journal.pcbi.1000604. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Ballestrem C., Hinz B., Wehrle-Haller B. Marching at the front and dragging behind: differential alphaVbeta3-integrin turnover regulates focal adhesion behavior. J. Cell Biol. 2001;155:1319–1332. doi: 10.1083/jcb.200107107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Bachir A.I., Zareno J., Horwitz A.R. Integrin-associated complexes form hierarchically with variable stoichiometry during nacent adhesion formation. Curr. Biol. 2014;24:1845–1853. doi: 10.1016/j.cub.2014.07.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Choi C.K., Vicente-Manzanares M., Horwitz A.R. Actin and α-actinin orchestrate the assembly and maturation of nascent adhesions in a myosin II motor-independent manner. Nat. Cell Biol. 2008;10:1039–1050. doi: 10.1038/ncb1763. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Chaudhuri O., Gu L., Mooney D.J. Substrate stress relaxation regulates cell spreading. Nat. Commun. 2015;6:6364–6378. doi: 10.1038/ncomms7365. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Lepzelter D., Zaman M.H. Clustered diffusion of integrins. Biophys. J. 2010;99:L106–L108. doi: 10.1016/j.bpj.2010.11.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Kusumi A., Nakada C., Fujiwara T. Paradigm shift of the plasma membrane concept from the two-dimensional continuum fluid to the partitioned fluid: high-speed single-molecule tracking of membrane molecules. Annu. Rev. Biophys. Biomol. Struct. 2005;34:351–378. doi: 10.1146/annurev.biophys.34.040204.144637. [DOI] [PubMed] [Google Scholar]
- 50.Welf E.S., Naik U.P., Ogunnaike B.A. A spatial model for integrin clustering as a result of feedback between integrin activation and integrin binding. Biophys. J. 2012;103:1379–1389. doi: 10.1016/j.bpj.2012.08.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Calderwood D.A. Talin controls integrin activation. Biochem. Soc. Trans. 2004;32:434–437. doi: 10.1042/BST0320434. [DOI] [PubMed] [Google Scholar]
- 52.Smith A., Carrasco Y.R., Hogg N. A talin-dependent LFA-1 focal zone is formed by rapidly migrating T lymphocytes. J. Cell Biol. 2005;170:141–151. doi: 10.1083/jcb.200412032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Paszek M.J., DuFort C.C., Weaver V.M. The cancer glycocalyx mechanically primes integrin-mediated growth and survival. Nature. 2014;511:319–325. doi: 10.1038/nature13535. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Thomas W., Forero M., Vogel V. Catch-bond model derived from allostery explains force-activated bacterial adhesion. Biophys. J. 2006;90:753–764. doi: 10.1529/biophysj.105.066548. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Kong F., García A.J., Zhu C. Demonstration of catch bonds between an integrin and its ligand. J. Cell Biol. 2009;185:1275–1284. doi: 10.1083/jcb.200810002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Bell G.I., Dembro M., Bongrand P. Cell adhesion. Competition between nonspecific repulsion and specific bonding. Biophys. J. 1984;45:1051–1064. doi: 10.1016/S0006-3495(84)84252-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Asaro R.J., Lubarda V.A. Cambridge University Press; New York: 2006. Mechanics of Solids and Materials. [Google Scholar]
- 58.Landau L.D., Lifshitz E.M. Addison-Wesley; New York: 1959. Theory of Elasticity. [Google Scholar]
- 59.Carman C.V., Springer T.A. Integrin avidity regulation: are changes in affinity and conformation underemphasized? Curr. Opin. Cell Biol. 2003;15:547–556. doi: 10.1016/j.ceb.2003.08.003. [DOI] [PubMed] [Google Scholar]
- 60.Li J., Su Y., Springer T.A. Conformational equilibria and intrinsic affinities define integrin activation. EMBO J. 2017;36:629–645. doi: 10.15252/embj.201695803. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Li J., Springer T.A. Integrin extension enables ultrasensitive regulation by cytoskeletal force. Proc. Natl. Acad. Sci. USA. 2017;114:4685–4690. doi: 10.1073/pnas.1704171114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Hughes P.E., Diaz-Gonzalez F., Ginsberg M.H. Breaking the integrin hinge. A defined structural constraint regulates integrin signaling. J. Biol. Chem. 1996;271:6571–6574. doi: 10.1074/jbc.271.12.6571. [DOI] [PubMed] [Google Scholar]
- 63.Lau T.L., Kim C., Ulmer T.S. The structure of the integrin alphaIIbbeta3 transmembrane complex explains integrin transmembrane signalling. EMBO J. 2009;28:1351–1361. doi: 10.1038/emboj.2009.63. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Ye F., Hu G., Ginsberg M.H. Recreation of the terminal events in physiological integrin activation. J. Cell Biol. 2010;188:157–173. doi: 10.1083/jcb.200908045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.O’Callaghan R., Job K.M., Hlady V. Stiffness and heterogeneity of the pulmonary endothelial glycocalyx measured by atomic force microscopy. Am. J. Physiol. Lung Cell. Mol. Physiol. 2011;301:L353–L360. doi: 10.1152/ajplung.00342.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Zhu Q., Salehyar S., Asaro R.J. Prospects for human erythrocyte skeleton-bilayer dissociation during splenic flow. Biophys. J. 2017;113:900–912. doi: 10.1016/j.bpj.2017.05.052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Guz N., Dokukin M., Sokolov I. If cell mechanics can be described by elastic modulus: study of different models and probes used in indentation experiments. Biophys. J. 2014;107:564–575. doi: 10.1016/j.bpj.2014.06.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Gingras A.R., Bate N., Critchley D.R. The structure of the C-terminal actin-binding domain of talin. EMBO J. 2008;27:458–469. doi: 10.1038/sj.emboj.7601965. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Yao M., Goult B.T., Yan J. Mechanical activation of vinculin binding to talin locks talin in an unfolded conformation. Sci. Rep. 2014;4:4610–4621. doi: 10.1038/srep04610. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Yao M., Goult B.T., Yan J. The mechanical response of talin. Nat. Commun. 2016;7:11966. doi: 10.1038/ncomms11966. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Humphries J.D., Wang P., Ballestrem C. Vinculin controls focal adhesion formation by direct interactions with talin and actin. J. Cell Biol. 2007;179:1043–1057. doi: 10.1083/jcb.200703036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.del Rio A., Perez-Jimenez R., Sheetz M.P. Stretching single talin rod molecules activates vinculin binding. Science. 2009;323:638–641. doi: 10.1126/science.1162912. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Zhu Q., Asaro R.J. Spectrin folding versus unfolding reactions and RBC membrane stiffness. Biophys. J. 2008;94:2529–2545. doi: 10.1529/biophysj.107.119438. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Gardel M.L., Sabass B., Waterman C.M. Traction stress in focal adhesions correlates biphasically with actin retrograde flow speed. J. Cell Biol. 2008;183:999–1005. doi: 10.1083/jcb.200810060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Fisher G.W., Conrad P.A., Taylor D.L. Centripetal transport of cytoplasm, actin, and the cell surface in lamellipodia of fibroblasts. Cell Motil. Cytoskeleton. 1988;11:235–247. doi: 10.1002/cm.970110403. [DOI] [PubMed] [Google Scholar]
- 76.Forscher P., Smith S.J. Actions of cytochalasins on the organization of actin filaments and microtubules in a neuronal growth cone. J. Cell Biol. 1988;107:1505–1516. doi: 10.1083/jcb.107.4.1505. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Theriot J.A., Mitchison T.J. Actin microfilament dynamics in locomoting cells. Nature. 1991;352:126–131. doi: 10.1038/352126a0. [DOI] [PubMed] [Google Scholar]
- 78.Cuda G., Pate E., Sellers J.R. In vitro actin filament sliding velocities produced by mixtures of different types of myosin. Biophys. J. 1997;72:1767–1779. doi: 10.1016/S0006-3495(97)78823-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Kumar A., Ouyang M., Schwartz M.A. Talin tension sensor reveals novel features of focal adhesion force transmission and mechanosensitivity. J. Cell Biol. 2016;213:371–383. doi: 10.1083/jcb.201510012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Huang D.L., Bax N.A., Dunn A.R. Vinculin forms a directionally asymmetric catch bond with F-actin. Science. 2017;357:703–706. doi: 10.1126/science.aan2556. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.Marshall B.T., Long M., Zhu C. Direct observation of catch bonds involving cell-adhesion molecules. Nature. 2003;423:190–193. doi: 10.1038/nature01605. [DOI] [PubMed] [Google Scholar]
- 82.Sarangapani K.K., Yago T., Zhu C. Low force decelerates L-selectin dissociation from P-selectin glycoprotein ligand-1 and endoglycan. J. Biol. Chem. 2004;279:2291–2298. doi: 10.1074/jbc.M310396200. [DOI] [PubMed] [Google Scholar]
- 83.Evans E., Leung A., Zhu C. Mechanical switching and coupling between two dissociation pathways in a P-selectin adhesion bond. Proc. Natl. Acad. Sci. USA. 2004;101:11281–11286. doi: 10.1073/pnas.0401870101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84.Bartolo D., Derényi I., Ajdari A. Dynamic response of adhesion complexes: beyond the single-path picture. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2002;65:051910. doi: 10.1103/PhysRevE.65.051910. [DOI] [PubMed] [Google Scholar]
- 85.Pereverzev Y.V., Prezhdo O.V., Thomas W.E. The two-pathway model for the catch-slip transition in biological adhesion. Biophys. J. 2005;89:1446–1454. doi: 10.1529/biophysj.105.062158. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 86.Litvinov R.I., Mekler A., Weisel J.W. Resolving two-dimensional kinetics of the integrin αIIbβ3-fibrinogen interactions using binding-unbinding correlation spectroscopy. J. Biol. Chem. 2012;287:35275–35285. doi: 10.1074/jbc.M112.404848. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87.Chan C.E., Odde D.J. Traction dynamics of filopodia on compliant substrates. Science. 2008;322:1687–1691. doi: 10.1126/science.1163595. [DOI] [PubMed] [Google Scholar]
- 88.Elosegui-Artola A., Bazellières E., Roca-Cusachs P. Rigidity sensing and adaptation through regulation of integrin types. Nat. Mater. 2014;13:631–637. doi: 10.1038/nmat3960. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 89.Elosegui-Artola A., Oria R., Roca-Cusachs P. Mechanical regulation of a molecular clutch defines force transmission and transduction in response to matrix rigidity. Nat. Cell Biol. 2016;18:540–548. doi: 10.1038/ncb3336. [DOI] [PubMed] [Google Scholar]
- 90.Munevar S., Wang Y., Dembo M. Traction force microscopy of migrating normal and H-ras transformed 3T3 fibroblasts. Biophys. J. 2001;80:1744–1757. doi: 10.1016/s0006-3495(01)76145-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 91.Lee H.S., Lim C.J., Ginsberg M.H. RIAM activates integrins by linking talin to ras GTPase membrane-targeting sequences. J. Biol. Chem. 2009;284:5119–5127. doi: 10.1074/jbc.M807117200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 92.Chaudhuri O., Gu L., Mooney D.J. Hydrogels with tunable stress relaxation regulate stem cell fate and activity. Nat. Mater. 2016;15:326–334. doi: 10.1038/nmat4489. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 93.Maheshwari G., Brown G., Griffith L.G. Cell adhesion and motility depend on nanoscale RGD clustering. J. Cell Sci. 2000;113:1677–1686. doi: 10.1242/jcs.113.10.1677. [DOI] [PubMed] [Google Scholar]
- 94.Sackman E., Subcana-Smith A. Physics of cell adhesion: some lessons from cell-mimetic systems. Soft Matter. 2014;10:1644–1659. doi: 10.1039/c3sm51910d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 95.Seguin L., Camargo M.F., Cheresh D.A. Galectin-3, a druggable vulnerability for KRAS-addicted cancers. Cancer Discov. 2017;7:1464–1479. doi: 10.1158/2159-8290.CD-17-0539. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 96.Desgrosellier J.S., Cheresh D.A. Integrins in cancer: biological implications and therapeutic opportunities. Nat. Rev. Cancer. 2010;10:9–22. doi: 10.1038/nrc2748. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 97.Cheresh D.A., Harper J.R., Reisfeld R.A. Localization of the gangliosides GD2 and GD3 in adhesion plaques and on the surface of human melanoma cells. Proc. Natl. Acad. Sci. USA. 1984;81:5767–5771. doi: 10.1073/pnas.81.18.5767. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 98.Cao X., Lin Y., Shenoy V.B. A Chemomechanical model of matrix and nuclear rigidity regulation of focal adhesion size. Biophys. J. 2015;109:1807–1817. doi: 10.1016/j.bpj.2015.08.048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 99.Cao X., Ban E., Shenoy V.B. Multiscale model predicts increasing focal adhesion size with decreasing stiffness in fibrous matrices. Proc. Natl. Acad. Sci. USA. 2017;114:E4549–E4555. doi: 10.1073/pnas.1620486114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 100.Walcott S., Kim D.H., Sun S.X. Nucleation and decay initiation are the stiffness-sensitive phases of focal adhesion maturation. Biophys. J. 2011;101:2919–2928. doi: 10.1016/j.bpj.2011.11.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 101.He S., Su Y., Gao H. Some basic questions on mechanosensing in cell-substrate interaction. J. Mech. Phys. Solids. 2014;70:116–135. [Google Scholar]
- 102.Weiner J.H. Dover; Mineola, NY: 1983. Statistical Mechanics of Elasticity. [Google Scholar]