Are the Effects of Independent Biophysical Factors Linearly Additive? A 3D Tumor Migration Model

Abstract

Interstitial fluid flow plays a critical role in tumor cell invasion, yet this role has not been explored extensively in combination with other microenvironmental factors. Here, we establish a novel computational model of three-dimensional breast cancer cell migration to unveil the effect of interstitial fluid flow in the dependence of various extracellular matrix (ECM) physical properties. Our model integrates several principal factors: fluid dynamics, autologous chemotaxis, collagen fiber network structure, ECM stiffness, and cell-fiber and cell-flow interaction. First, independently with an aligned collagen fiber network and interstitial fluid flow, this model is validated by successfully reproducing the cell migration patterns. In the model, the interstitial fluid flow leads to directional symmetry breaking of chemotactic migration and synergizes with the ECM orientation to regulate cell migration. This synergy is universal in both the mesenchymal and the amoeboid migration modes, despite the fact that the cell-ECM interaction are different. Consequently, we construct a cell displacement function depending on these factors. Our cell migration model enables three-dimensional cancer migration prediction, mechanism exploration, and inhibition treatment design in a complex tumor microenvironment.

Introduction

The primary cause of mortality in cancer is metastasis (1), in which tumor cells migrate from primary to secondary sites, such as surrounding tissues or distant organs. Single-cell migration is commonly divided into two modes: mesenchymal and amoeboid (2). The mesenchymal migration includes three steps: protrusion, adhesion to ECM, and contraction (3, 4). The protrusion step requires the actin filament polymerization and turnover. The adhesion step depends on the integrin amount and adhesion strength regulated by actomyosin. The contraction relies on myosin activity to detach cells from the old cell-ECM adhesion. On the other hand, the amoeboid migration lacks mature focal adhesion and stress fiber formation and largely depends on cell contractility (5).

The noncellular components surrounding cells are mainly the extracellular matrix (ECM) and the interstitial fluid. The major fraction of ECM is collagen and fibronectin (6). Collagen proteins self-assemble into load-bearing fibers, and they cross-link into network. In tumor, there is an increased collagen density, stiffness, or alignment. For example, collagen fibers become radially aligned around the tumor, which is a prognostic signature of human breast carcinoma (7) due to the correlation with metastasis (8). The increased collagen density can directly promote cell proliferation (9, 10, 11), and this hyperplasia reinforces the surrounding collagen density and alignment changes (12). Meanwhile, tumor expansion often leads to a higher interstitial fluid flow between tumor and stroma (13). The interstitial fluid transports ions, nutrients, and signaling chemicals around cells (14, 15, 16, 17) and therefore plays a crucial role in tumor progression and drug delivery (18). For example, high interstitial fluid flow can cause a notable gradient in some chemokine distributions (19). In this way, the interstitial fluid flow has been found to affect breast cancer migration through chemotactic membrane receptor CCR7 and self-secreted ligand CCL21 (20). Recent studies have revealed that cell-ECM interaction can be regulated by fluid shear stress (21). This shear stress increases the affinity and avidity of integrin and increases the activation of focal adhesion kinase (FAK) in various cell types (22, 23). As a result, it can promote cell motility (24).

A number of cell migration models have been developed to study single factor effect, including ECM stiffness (25, 26) and fluid flow field in depth. For example, Wu et al. has revealed the statistical distribution of cell motion in three-dimensional (3D) matrices (27). Kim et al. has studied thoroughly the local fiber stiffness deformation due to cell migration and filopodia dynamics (28). Fleury et al. has quantified the autologous morphogen gradients caused by subtle interstitial flow (19). Polacheck et al. has evaluated how interstitial flow affects the migration of tumor cell. The effects of chemotaxis and flow-activated FAK are competing factors that regulate cells to move either upstream or downstream (21).

However, few studies of cell migration have revealed the influence of interstitial fluid flow interacting with various ECM physical properties. The cell migration pattern varies with the change of microenvironment, so it is very hard to predict because of the complexity of the microenvironment. To address this gap, we developed a comprehensive model, including both mechanical and biochemical factors, to simulate the 3D cancer migration. These factors consist of fluid dynamics, collagen alignment, collagen stiffness, chemotaxis, durotaxis, and different cell migration modes. Our model combines the complexity of a 3D collagen fibrous network and hydrodynamic of interstitial flow at microscale. The parameters corresponding to these factors are varied in our model to study their individual and integrated effects. To characterize these effects on cancer migration, the model provides, as a quantitative output, important features of migration, such as displacement, speed, mean-square displacement (MSD), and directionality. In the model, the flow speed enhances the ECM alignment effect on promoting cancer migration regardless of the migration modes. That is, the interstitial fluid flow and ECM orientation synergistically affect cell migration displacement. Consequently, we abstract this displacement dependency on the microenvironmental factors with an allometric regression. This comprehensive model considering multiplexed factors will help to predict cancer migration in a complex microenvironment with different migration modes.

Model

Interstitial fluid flow dynamics

We solve the velocity v of the interstitial fluid flow through a porous ECM with the Brinkman equations (29), as follows:

$$\rho \frac{\partial \mathbf{v}}{\partial t}+\mathit{\nabla }p-\mu {\mathit{\nabla }}^2\mathbf{v}-\frac{\mu }{K}\mathbf{v}=0,$$ (1)

$$\mathit{\nabla }\cdot \mathbf{v}=0,$$ (2)

where ρ and μ are the density and viscosity of the fluid approximated by the values from water at 37°C. K is the permeability of the porous ECM, which is anisotropic when the ECM aligns directionally (30, 31, 32). The pressure p and the velocity v are calculated with the assigned initial and boundary conditions. At an upstream boundary, the velocity is designed to range from 0 to 3 μm/s in different conditions. There is a pressure outflow boundary at the downstream and no-slip boundaries at other sides. The standard atmospheric pressure is imposed on each boundary.

Autologous chemotaxis

There are more than 50 chemokines among different cell types to regulate cell migration (19, 20, 33). The breast cancer cell lines secrete chemokine CCL21, which binds to their autologous-specific membrane receptor CCR7 to regulate migration direction. The gradient of CCL21 is affected by interstitial fluid flow; thus, tumor cell migration aligns with the flow if without other influences (20). In our model, we use parameters that are breast cancer specific, yet they can be easily adapted to other cell lines. Because the speed of breast cancer cell migration is much smaller than the flow speed, the chemokine CCL21 concentration C is calculated at steady state of the diffusion-convection balance equation (19), as follows:

$$\mathbf{v}\cdot \mathit{\nabla }C-D{\mathit{\nabla }}^{2}C=0,$$ (3)

where v is the velocity of the interstitial fluid flow, and D is the diffusion coefficient of chemokine CCL21. Because of the autologous chemotaxis, we assume C = 1 at the surface of tumor cells and C = 0 at the computational domain boundaries. The chemokine CCL21 distribution and the interstitial fluid flow velocity in our computational domain are solved in the software ANSYS 14.0 (ANSYS, Pittsburgh, PA).

ECM network generation

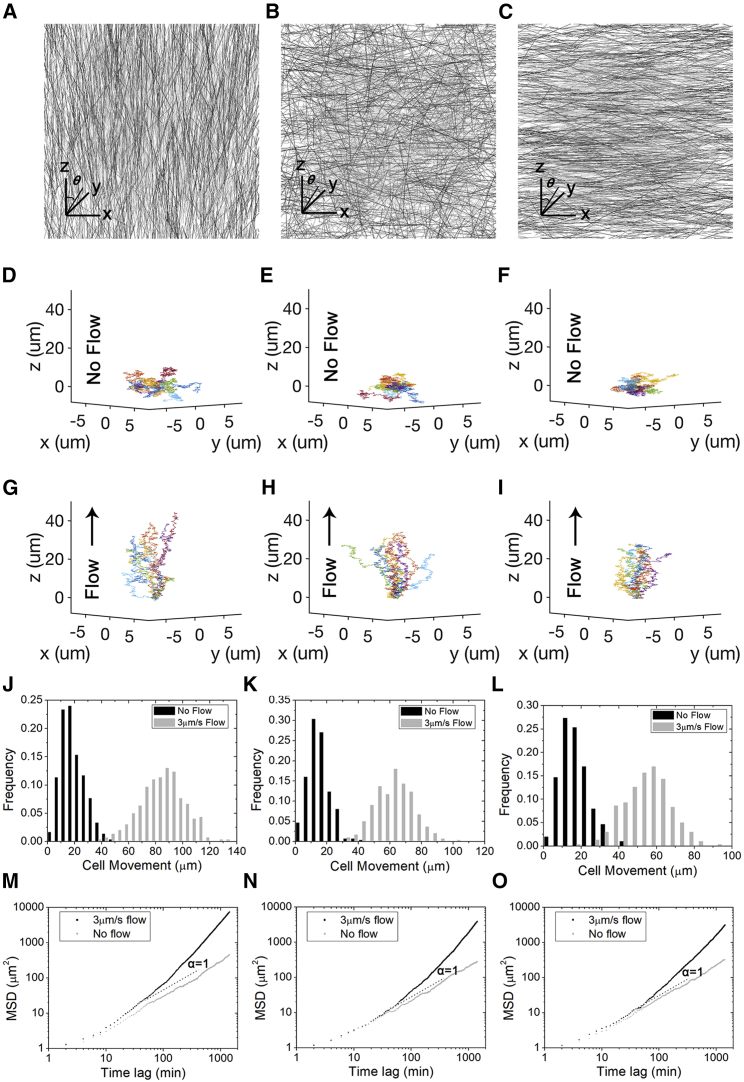
Because a major component of ECM in humans is collagen, in our model to study cell migration in the ECM, we develop a collagen network with an adjustable fiber density, positions, orientation, and stiffness (34). The parallel, random, and perpendicular alignments of collagen network are defined relative to the flow direction (z-positive direction) (Fig. 1, A–C). In the parallelly or the perpendicularly aligned collagen network, individual fiber orientation θ_i follows a normal distribution with predefined angular mean θ_average, and the is SD σ_θ. θ_average is either 0 or 90° to the flow direction, and σ_θ is estimated from the case of alignment index (AI) = 0.9 (35), where AI is defined as $AI=\left|\frac{1}{N}\sum _{i=1}^N\left(2{\text{cos}}^2\left({\theta }_i-{\theta }_{\text{average}}\right)-1\right)\right|$. On the other hand, the random aligned collagen network has fiber orientation θ_i following a uniform distribution between 0 and 180°. In our model, the collagen fibers are assumed to be fixed in their positions and orientations to minimize the influence of collagen remodeling during cancer migration.

Figure 1.

Distinct trajectories of tumor cell migration with various interstitial fluid flow speed and ECM alignments. (A)–(C) are the 3D ECM structures with different alignments generated with a previous method (33). The ECM alignments are parallel, random, or perpendicular to the flow direction, which is along the positive z axis. (D)–(F) are tumor cell migration trajectories in various aligned ECM without interstitial fluid flows. In contrast, (G)–(I) are migration trajectories in the same ECM with 3 μm/s interstitial fluid flow. (J)–(L) are the movement of cells in the corresponding ECM alignment. (M)–(O) are the MSDs of these cell migrations. The slope α = 1 in this log-log plot represents the diffusion like a random walk. The MSDs of cell migrations without interstitial fluid flow all have slopes larger than 1, whereas the ones with 3 μm/s interstitial fluid flow are significantly higher. (D), (G), (J), and (M) have ECM alignment in parallel to the flow direction. (E), (H), (K), and (N) have random ECM alignment. (F), (I), (L), and (O) have ECM alignment perpendicular to the flow direction. Each plot in (D)–(I) shows 20 tumor cell trajectories over 24 h, and the plots in (J)–(O) are based on 300 tumor cell trajectories over 24 h. To see this figure in color, go online.

Cell migration

Broadly speaking, there are three major steps in single-cell mesenchymal migration: protrusion, adhesion, and contraction. Accordingly, the forces regulating mesenchymal migration are protrusion force F_protrusion, traction force F_traction, and resistance force F_resistance (36, 37), which are adapted from Zaman et al. (25). In amoeboid migration, the adhesion step is not necessary (5); thus, the acting forces are reduced to protrusion force and resistance force. We choose this force model of cell migration developed from Zaman et al. because it partitions factors and represents each as a force, which may be phenological or simplified from real physical mechanism.

In details, the traction force F_traction is involved in the adhesion and contraction steps and is defined as a contractile force upon adhesion formed. It is transmitted through a cell-matrix bond, integrin. We assume that in 2 mg/mL collagen, the integrin concentration on cell surface is saturated and not rate limiting. Thus, once a fiber touches the cell surface, a cell-ECM bond is formed. It breaks immediately when this fiber detaches from the cell surface. A constant contractile force requiring adhesion is assumed to be at cell-fiber contact as a function of its Young’s modulus E because previous studies have shown that this force is proportional to ECM stiffness (38) The traction force is therefore modeled as follows:

$${\mathit{F}}_{\text{traction}}=\sum _i^{N_{\text{ECM}}}{c}_{\text{traction}}E{\mathit{l}}_f,$$ (4)

where N_ECM is the number of collagen fibers in touch with a cell instantaneously, and the coefficient c_traction measures phenomenologically the dependence of a contractile force at integrin on E. Thus, c_tractionE represents the force magnitude of a cell-fiber contractile bond, whose direction is along the fiber orientation pointing from cells (25) and is represented as l_f. Although more complex expressions of the traction force have been developed in other models, this simple form of F_traction in our model effectively reproduces durotaxis (see Results). On the other hand, in the amoeboid migration F_traction is assumed to be 0 because of a lack of cell-ECM adhesion.

To distinguish from the traction force in contact with ECM, the protrusion force F_protrusion is assumed to be regulated by chemotaxis and leads to a directional bias as follows:

$${\mathit{F}}_{\text{protrusion}}=c_{\text{propulsion}}{\mathit{l}}_{\text{protrusion}},$$ (5)

The magnitude of the protrusion force c_propulsion is estimated from previous experimental studies (39) and is assumed to be a constant here. In mesenchymal migration, F_protrusion arises from actin polymerization at sites of lamellipodia protrusion, whereas in amoeboid, cell migration is dominantly induced by cell contractility (39). Therefore, the force magnitudes are different in mesenchymal and amoeboid migration. At each migration time step, the direction of the cell protrusion force l_protrusion (a unit vector) is sampled from a probability function of CCL21 concentration in the surrounding regions. This probability $P_{\text{protrusion}}\left(\theta ,\phi \right)$ is calculated as follows:

$$P_{\text{protrusion}}\left(\theta ,\phi \right)=c_{\text{normalized}}\underset{r=0}{\overset{l}{\int }}C\left(r,\theta ,\phi \right)dr,$$ (6)

where the concentration of CCL21, $C\left(r,\theta ,\phi \right)$, is summed within 30 μm from the cell surface along the normal direction, and c_normalized is a coefficient for probability normalization.

The resistance occurs when cells move through ECM and viscous interstitial fluid flow. The viscosity of the interstitial fluid flow is significantly lower than the one of the ECM (25); thus, the fluidic drag of interstitial fluid flow is omitted. Consequently, the resistance has mainly two parts: isotropic viscous ECM resistance and ECM alignment resistance, as follows:

$${\mathit{F}}_{\text{resistance}}={\mathit{F}}_{\text{drag}}+{\mathit{F}}_{\text{ECM}\text{alignment}}.$$ (7)

On one hand, the ECM is approximated as a homogeneous viscous Newtonian medium with a low Reynolds number $\left(\mathrm{Re}\ll 1\right)$ (25). Thus, the resistance of this viscous ECM on a spherical cell is given by the classical Stokes solution, as follows:

$${\mathit{F}}_{\text{drag}}=-6\pi \eta R\mathit{U}\mathrm{,}$$ (8)

where η is the viscosity of the ECM, R is the cell radius, and U is the relative velocity between the cell and the ECM. Here, we assume a simplified geometry of ECM in this classical Stokes solution and do not incorporate dynamic, sub-microscale shape changes.

On the other hand, an object intuitively encounters a higher resistance across perpendicularly aligned fibers than the parallel ones because of fibrous bending stiffness (6). Thus, the resistance on cells due to ECM alignment is given by the following:

$${\mathbf{F}}_{\text{ECM}\text{alignment}}=c_{\text{resistance}}\sum _i^{N_{\text{ECM}}}{k}_b\mathit{\Delta }\theta {\mathit{l}}_{\perp f_i}/L_i,$$ (9)

where N_ECM is the number of collagen fibers instantaneously in touch with the cell. Fiber bending stiffness is calculated as k_b = EI/L_mean, where E is the Young’s modulus of a fiber, L_mean = 14 μm is the mean fiber length, I = πr⁴/4 is the second moment of inertia of a collagen fiber, and r is the fiber radius. Δθ_i is the angle between cell motion and fiber orientation. The resistance due to ECM bending stiffness is assumed to be linear with Δθ_i and cell speed independent. Namely, it is minimal when a cell moves along fiber orientations. The direction ${\mathbf{l}}_{\perp fi}$ of this resistance is perpendicular to the fiber orientation. L_i is the length of each fiber. c_resistance measures phenomenologically the dependence of the ECM alignment resistance on these variables.

As a result, the resultant force acting on a cell in mesenchymal migration mode is given by the following:

$${\mathit{F}}_{\text{total}}={\mathit{F}}_{\text{protrusion}}+{\mathit{F}}_{\text{traction}}+{\mathit{F}}_{\text{drag}}+{\mathit{F}}_{\text{ECM}\text{alignment}},$$ (10)

where F_traction and F_{ECM alignment} depend on ECM stochastic structures, F_protrusion represents the directional bias due to chemotaxis, and F_drag is used to determine the cell velocity. While in amoeboid mode, the term F_traction is absent. In each time step, a cell protrudes in a direction of chemotaxis calculated in F_protrusion, may form and lose ECM attachments in F_traction, and is resisted by ECM viscoelasticity in F_drag and F_{ECM alignment}. In this model, we only consider the translational movement of cells, the velocity of which is solved in Eq. 10 and is integrated with time to get the displacement. We simulate a large number of cells independently to generate cell migration statistics in MATLAB (The MathWorks, Natick, MA).

Parameter fitting

Aside from the parameters previously reported, we fit the parameters in our model from the previous experimental data in a heuristic manner (Table 1). Within the reported range of protrusion force, its force magnitude is first determined from the previous cell mesenchymal migration speed data in the randomly aligned ECM with no flow (39). In amoeboid migration, cells move faster; thus, there is a larger protrusion force (5). Next, the single-cell-ECM bond strength is used to calculate the traction strength coefficient (25). The resistance coefficient is obtained from the previous ECM alignment experiment without any flows (40). We also determine the asymmetric change of the cell-ECM traction force around a cell due to flow-induced FAK activation from the upstream directionality data (21). A sensitivity test of all parameters on the cell displacement in z direction is presented in the Results (Table 2). This sensitivity test is quantified in the percentage change calculated as follows:

$$\text{Percentage}\text{change}\text{on}\text{cell}\text{directional}\text{migration}=\frac{\text{cell}\text{z}\text{displacement}\left(105\%\text{parameters}\right)-\text{cell}\text{z}\text{displacement}\left(95\%\text{parameters}\right)}{\text{cell}\text{z}\text{displacement}\left(100\%\mathrm{parameters}\right)}\times 100\%.$$ (11)

Table 1.

The Parameters in the Tumor Cell Migration Model

Parameters	Values	References
Interstitial fluid density ρ	998.2 kg/m3	(19)
Interstitial fluid viscosity μ	7 × 10−3 poise	(19)
Permeability K through parallelly, randomly, and perpendicularly aligned ECM	2.856, 2.554, and 1.595 μm2	(42)
CCL21 diffusion coefficient D	140 μm2/s	(20)
Single fiber length	14 ± 7 μm	(43)
Single fiber diameter	100 nm	(43, 44)
Collagen concentration	2 mg/mL	(21)
Single fiber mass density	1.3 g/cm3	(45)
Traction strength coefficient ctraction	1 × 10−5μm2	Fitted from (25)
ECM resistance coefficient cresistance	500	Fitted from (40)
Collagen fiber Young’s modulus E	0.1 MPa	(25)
Protrusion force magnitude cpropulsion for mesenchymal migration	50 pN	Fitted from (25) and (39)
Protrusion force magnitude cpropulsion for amoeboid migration	100 pN	Fitted from (5) and (39)
ECM viscosity η	103 poise	(46, 47)
Tumor cell radius R	7.5 μm	(42)
Constant upstream interstitial fluid flow speed	0–3 μm/s	(21)

Table 2.

Sensitivity Analysis of the Parameters in the Model

Parameters	Percentage Change on Cell Directional Migration (%)	Ranking
Single fiber diameter	4.51	7
Collagen concentration	8.11	4
Traction strength coefficient	13.67	2
ECM resistance coefficient	6.67	5
Collagen fiber Young’s modulus	4.62	6
Protrusion force magnitude	10.92	3
ECM viscosity	17.80	1

Results

Our model presents multiple aspects of cell migration within various microenvironments. It initially places in silico tumor cells at coordinate origin and assumes a sparse cell density neglecting cell-cell interactions. Next, it generates the trajectories of tumor cells with mesenchymal migration mode (Fig. 1, D–I). In the condition with no interstitial fluid flow (Fig. 1, D–F), the cells exhibit random walks (41), and their migration is slightly affected by the ECM alignments. They tend to move along the prealigned ECM because of less resistance. In contrast, cells experience more resistance when moving perpendicularly to ECM alignment. In the condition with 3 μm/s flow speed (Fig. 1, G–I), cells are more likely to migrate along the flow direction, yet they are still partially influenced by the ECM alignment. Among their movements, the largest happens at nonzero interstitial fluid flow with the parallel ECM alignment (Fig. 1, J–L). All cell movements with interstitial fluid flow are significantly greater than the controls regardless of the ECM alignments (t-test, p < 0.0001). The MSDs of these cell migrations are presented in Fig. 1, M–O, with the slope at large time intervals corresponding to the diffusion coefficient in cell migration. The slopes with interstitial fluid flow are all significantly greater than 1, showing that cells do not follow random walks. Next, we closely study this directional migration with more aspects.

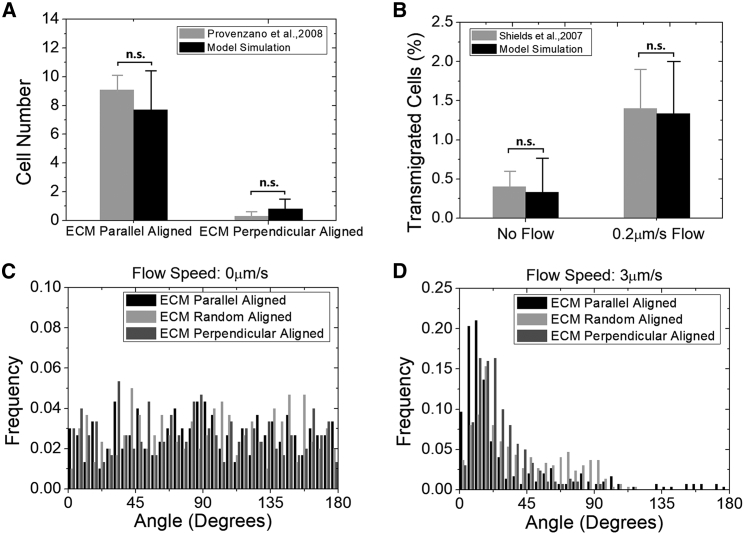
We first validate our model quantitatively by comparing to the previously published experimental data in breast cancer cell lines with different ECM alignments and no interstitial fluid flow (40). In silico tumor cells are initially placed in randomly aligned ECM flanked by parallelly and perpendicularly aligned ECM. A significantly larger number of cells migrate into the parallelly aligned ECM compared with the perpendicular one (Fig. 2 A). This quantitative accordance with the experiment well captures the effect of ECM alignment on cell migration. Our model is also validated by comparing the result to a previous experiment with a slow interstitial fluid flow in randomly aligned ECM (20). This quantitative coherence of flow-promoted migration (Fig. 2 B) testifies to the design of the autologous chemotaxis in our model. These together indicate that our model with a large population statistic reliably predicts the individual effect of the ECM and the interstitial fluid flow on tumor cell migration.

Figure 2.

Validations of our computational model by previous experimental data. (A) In our simulation, we reproduce the same experimental condition of collagen network and cell incubation time (40). More in silico tumor cells travel into the parallelly aligned collagen than into the perpendicular one, with a distance threshold defined at 30 μm. This result is in good agreement with the experimental data and does not depend significantly on the choice of the distance threshold (data not shown). Cell number is 300. Running time is 72 h. No significant difference is present between the groups (t-test, p > 0.05), indicating that the simulation agrees well with the experiment. Error bars show mean ± SD. (B) The simulation reproduces the experimental condition with the interstitial fluid flow (20). The flow significantly enhances tumor migration, which is in good agreement with the experimental data. Cell number is 300. ECM is randomly aligned. Running time is 15 h. No significant difference is present between the two groups, indicating that the simulation agrees well with the experiment. (C) It is a uniform distribution with no flow for the histogram of the polar angles between the cell’s last position to the origin and the z axis. Cells number is 300. ECM is randomly aligned. Running time is 24 h. (D) The histogram of the cell’s last position polar angle approaches zero at 3 μm/s flow. This corresponds to the cell migrating mostly around the flow direction. Cell number is 300. ECM is randomly aligned. Running time is 24 h.

After validation, the presence of flow is examined next to quantitatively study the cell movement pattern, particularly along the flow direction (z axis). 300 in silico cells are simulated in each condition with a different flow speed and ECM alignments for 24 h. Because the flow direction and the ECM alignment asymmetry in our study are both along the z axis to mimic the real tumor microenvironment, the cell movement in 3D is nearly symmetric along x and y axis. This migration directionality can be easily revealed by the histogram of the angle between the final position of the cell to the origin and the z axis. Without the flow, the angle histogram is random, indicating a random-walk pattern (Fig. 2 C). With the flow, it clearly changes from a random distribution to an asymmetric one, indicating that the flow changes the cell migration from random walk to a directional migration (Fig. 2 D). The angles are significantly different between no flow and 3 μm/s flow conditions with the same ECM alignment (Fig. 2, C and D, t-test, p < 0.001). Meanwhile, the angles with different ECM alignments are significantly different at 3 μm/s flow speed (Fig. 2 D, analysis of variance (ANOVA), p < 0.05).

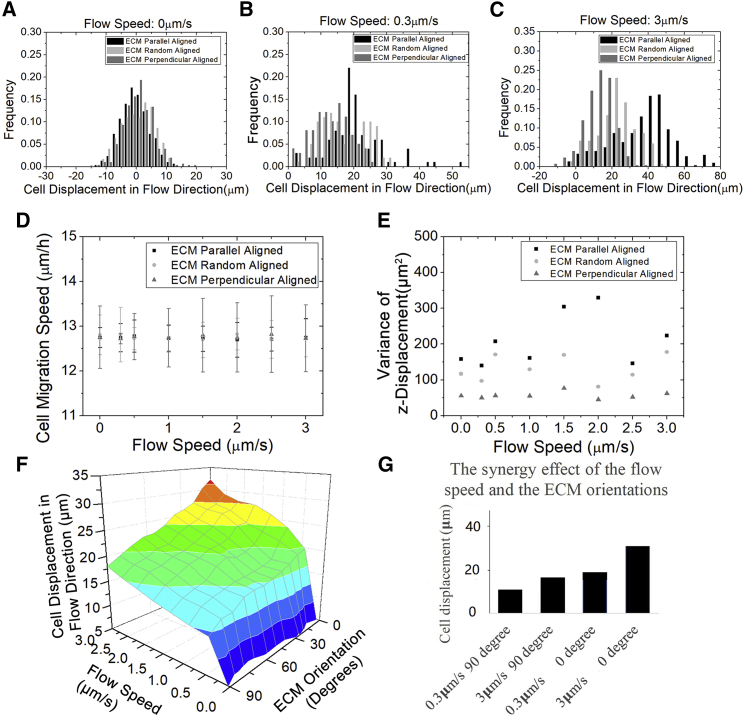
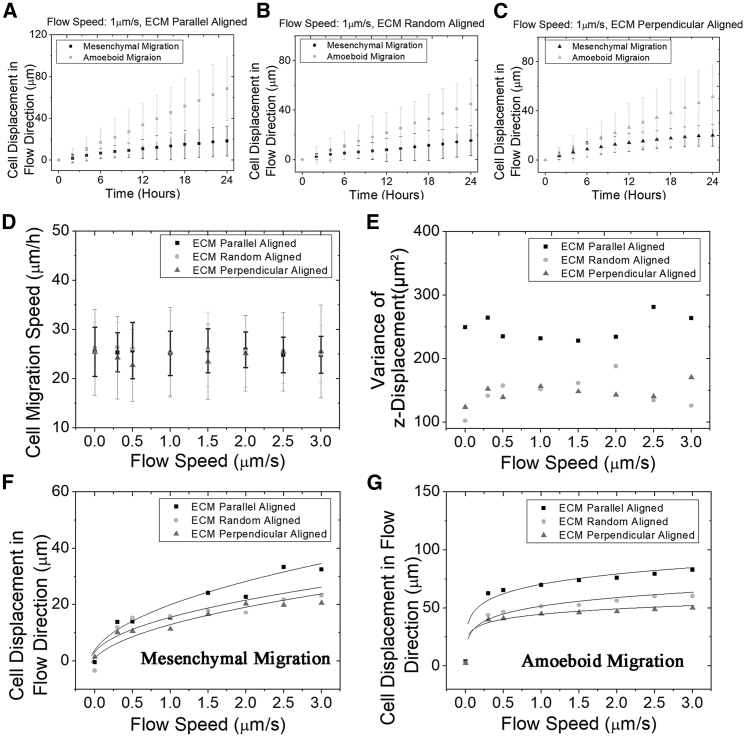
Varying flow speed is investigated further from more aspects to understand this directional tumor migration. Without the flow (Fig. 3 A), cell displacement along flow direction is limited in a small distance (less than 20 μm), with the mean value around zero. This is as expected because cells migrate like a random walk. At different flow speeds, the z displacements are all significantly larger than zero regardless of the ECM alignments (Fig. 3, B and C), which again quantitatively demonstrates a directional migration under the influence of the flow. A sensitivity test of the parameters (values ± 5%) regarding the z displacement at randomly aligned ECM and 3 μm/s flow speed is calculated to reveal their influence, and the top three ones are the ECM viscosity, the traction strength coefficient, and the protrusion force magnitude (Table 2). The effect of ECM alignment on the mean cell displacement varies among different flow speeds, which is demonstrated by the two-way ANOVA test (p < 0.05). This indicates an interaction between the ECM alignment and the flow speed on cell migration. Nevertheless, the cell speed does not change significantly with flow speed (Fig. 3 D, t-test, p > 0.05). That is, it is independent of interstitial flow, which concurs with the previous study (21). Therefore, the difference in z displacement due to the flow is only likely attributed to the migration directionality that is regulated by the chemotaxis. Though the mean of cell z displacement is largely regulated by the flow, its variance is only tightly regulated by the ECM alignment (Fig. 3 E). With the same flow speed, the variance in the parallel alignment is significantly larger than the perpendicular one (F-test, p < 0.01). Intuitively, in perpendicularly aligned ECM, cells are more limited to migrate along the z direction than in the parallel one. Thus, the variance of cell migration along the z direction is smaller in the perpendicularly aligned ECM. We also visualize the combinatory effect of varying interstitial fluid flow speed and ECM orientation on cell displacement along the flow direction in 3D (Fig. 3 F). When the flow speed is small, there is a small difference in the mean cell displacement among various ECM orientations. Although the flow speed is large, the difference becomes larger. Therefore, the cell migration is accelerated by the parallel ECM alignment and the flow in a synergistic manner (Fig. 3 G).

Figure 3.

The tumor cell migration along the flow direction is synergistically regulated by the flow speed and the ECM alignment. Cells number is 300. Running time is 24 h. (A) Without the flow, the mean values of cell displacement along the flow direction are close to zero and not significantly different apart in parallelly, randomly, and perpendicularly aligned collagen: −1.9, −1.1, and 1.7 μm (ANOVA, p > 0.05, mean values are not significantly different). (B) When the flow speed is 0.3 μm/s, the peak of the z displacement histogram shifts toward a larger displacement for various ECM alignments, whereas the width of each histogram does not change much, in comparison with the zero flow. At 0.3 μm/s flow speed, the mean values of z displacement for parallel, random, and perpendicular alignments are 20.9, 17.0, and 12.4 μm, respectively, which are significantly different (ANOVA, p < 0.001). (C) When the flow speed increases to 3 μm/s, the difference among the mean z displacement values for parallel, random, and perpendicular alignments is even larger: 33.4, 22.1, and17.4 μm, respectively (ANOVA, p < 0.001). (D) The cell migration speed does not change significantly with the interstitial fluid flow speed (t-test, p > 0.05) and the ECM alignments (ANOVA, p > 0.05). (E) The variance of the z displacement is plotted against various flow speed and ECM alignment. There is no clear monotonic relationship between the variance of the z displacement and the flow speed. However, the z displacement variance of the parallel alignment is always significantly larger than the perpendicular one at the same flow speed (F-test, p < 0.01). (F) The combinatorial effect of flow speed and ECM mean orientation relative to the flow direction on z displacement is visualized in this 3D plot. Along the ECM orientation axis, 0° represents the parallel ECM alignment, and 90° represents the perpendicular ECM alignment. (G) This bar plot demonstrates a synergistic effect on cell z displacement by aligning the ECM orientation around the flow direction and increasing the flow speed. That is, this combinatory effect is larger than the sum of the two individual effects. To see this figure in color, go online.

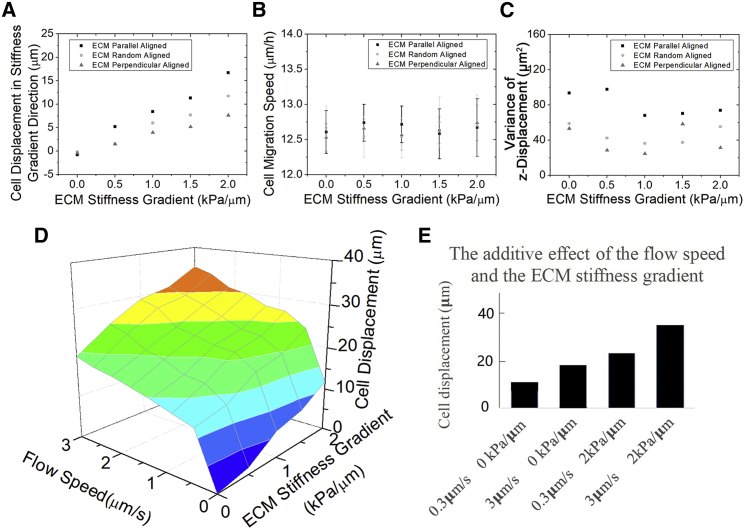
In addition to the ECM alignment, tumor cells sense the rigidity of surrounding ECM through integrin and migrate toward stiffer regions, termed as durotaxis (38). The stiffness gradient emerges with the ECM alignment change during tumor progression, but how it regulates cell migration with the interstitial fluid flow was unknown before our study. In our model, we first reproduce the durotaxis without the interstitial fluid flow (Fig. 4 A): the larger the stiffness gradient is, the further cells migrate into the stiffer regions. Interestingly, the speed magnitude of the moving cell is also not affected much by the ECM stiffness (t-test, p > 0.05, Fig. 4 B). Similarly, a possible explanation is that in durotaxis, the stiffness dominantly regulates the directionality of cell migration as regulated by the flow in chemotaxis. In addition, the ECM stiffness gradient also amplifies the ECM alignment effect on cell migration. These help to rule out that the synergy mechanisms are unique to our model design because the stiffness sensing and the chemotaxis have completely different force formula in our model. The variance of the cell z displacement (the gradient direction) is similar at different ECM stiffness gradient, but it still follows σ² _{Parallel aligned} > σ² _{Perpendicular aligned} (F-test, p < 0.01, Fig. 4 C). This shows that the parallel ECM alignment causes a large fluctuation in the cell displacement regardless of the stiffness gradient. Nevertheless, the ECM stiffness gradient does not synergize with the interstitial fluid flow on the cell directional displacement with random ECM alignment (Fig. 4 D). That is, the effects of ECM stiffness gradient and flow speed on cell migration are additive and thus independent (Fig. 4 E).

Figure 4.

The effects of the ECM stiffness gradient and the flow speed on tumor migration appear independent. Cell number is 300. Running time is 24 h. (A) The mean displacement along stiffness gradient direction increases with the ECM stiffness gradient magnitude visually. The displacement with ECM parallel alignment is always significantly higher than the perpendicular one at the same stiffness gradient (ANOVA, p < 0.001). (B) The speed of cell migration does not change much with the ECM stiffness gradient (t-test, p > 0.05) or alignment (ANOVA, p > 0.05). (C) The variance of the tumor z displacement is plotted against various ECM stiffness gradient and ECM alignments. There is no clear monotonic relationship between the z displacement variance and the ECM stiffness gradient. However, the z displacement variance with parallel alignment is always significantly larger than the perpendicular one with the same ECM stiffness gradient (F-test, p < 0.01). (D) The combinatory effect of flow speed and ECM stiffness gradient on cell displacement along the flow direction is visualized in a 3D plot. (E) The bar plot shows that the effects of increasing ECM stiffness gradient and the flow speed are independent. That is, this combinatory effect is similar to the sum of the individual effects. To see this figure in color, go online.

To understand whether the combinatorial effect of interstitial fluid flow and ECM orientation is universal, we further study the amoeboid migration mode of tumor cells in our model. Cells with amoeboid migration mode lack integrin-related cell-ECM adhesion, and thus, the cell-ECM traction force is zero. In our model, the amoeboid migration always represents a larger cell displacement along the flow direction regardless of the ECM alignments (Fig. 5, A–C). The displacement difference between the two migration modes is mostly the cell migration speed (Figs. 3 D and 5 D), which is attributed to the difference in cell protrusion force. The variances in amoeboid migration between the parallel and the perpendicular alignment are also significantly different (Fig. 5 E, F-test, p < 0.01), which is similar to the one in mesenchymal migration (Fig. 3 E). This common feature of variance between both migration modes is therefore likely to have resulted from the ECM resistance because of a lack of ECM traction force in amoeboid migration. The difference of cell displacement among various alignments amplifies with the flow speed in both mesenchymal and amoeboid migration (Fig. 5, F and G). This indicates that the flow promotes the effect of the ECM alignment on the cell migration, regardless of the migration modes, though this promotion effect is stronger in amoeboid at the same flow speed, potentially because of a higher cell speed.

Figure 5.

The cell displacement dependencies on the flow speed in mesenchymal and amoeboid migration have similar patterns. Cell number is 300. Running time is 24 h. (A)–(C) Directional displacement of tumor cell shows a linear correlation with the migration time in parallelly, randomly, and perpendicularly aligned ECM for both mesenchymal and amoeboid migration mode. Flow speed = 1 μm/s. (D) The speed of amoeboid migration is also independent of the flow speed (t-test, p > 0.05) and the ECM alignment (ANOVA, p > 0.05). (E) The variance of the z displacement of amoeboid migration is plotted against flow speed. There is no clear monotonic relationship between the variance of the z displacement and the flow. The cell displacement variance with parallel alignment is always larger than the perpendicular ECM alignment in the same flow speed (F-test, p < 0.01). (F) Displacement of tumor cells in the flow direction is plotted against the interstitial fluid flow speed with various ECM alignment for mesenchymal migration mode. (G) Displacement of tumor cells in the flow direction is plotted against the interstitial fluid flow speed with various ECM alignment for amoeboid migration mode.

Based on this finding, we use our model to predict the cell migration within multiplexed microenvironments. Surprisingly, the displacement as a function of interstitial fluidic flow speed follow a similar geometrical trend with various ECM alignments and migration modes (Fig. 5, F and G). We attribute this similar displacement dependency on the flow speed largely to the autologous chemotaxis. The flow delivers biochemical signals, which accumulate downstream of cells. As the flow speed increases, the increase of this accumulation effect saturates gradually. This is why the slopes of the displacement decrease to flat at large flow speed. The function describing the cell migration dependency on the interstitial fluid flow speed, ECM alignment, and migration mode is defined as follows:

$$S=c_{\mathrm{mod}\text{e}}{V}^{n}t,$$ (12)

where S is the displacement (the distance between the final z position and the origin) of tumor cells along the flow direction, V is the speed of the interstitial fluid flow, and t is the migration time interval. By fitting our simulation data (Table 3), n describes the shape of the cell displacement dependency on the flow speed. Their values for the mesenchymal and the amoeboid migration indicate a similar shape of cell displacement, depending on flow speed, which may result from the similar chemotactic regulation. c_mode is the parameter representing the ECM alignment regulation coupled with different migration modes. The adjusted R squares that measure the prediction strength imply that this allometric function of the migration displacement is convincing. Generally, the adjusted R squares of amoeboid migration are higher than mesenchymal ones. The rationale is that the amoeboid migration is dominated by the protrusion force, which is regulated by the chemotaxis and has lower fluctuations. In mesenchymal migration, the uncertainty occurs more because of the traction force and the ECM network generation. The nonlinear relation between S and V reflects the nature of solute spreading in fluid. When flow speed is small, this solute spreading is dominated by the isotropic diffusion. The fluid transportation grows stronger as the flow speed increases, leading to accumulations of biochemical signals downstream of cells until saturation. Notably, the effects of ECM alignment and the interstitial fluid flow regulations on cell migration are not linearly additive but entangled in such a nonlinear manner described by this allometric formula. The traction force among various ECM alignments is independent of the interstitial fluid flow speed. Therefore, this amplification of ECM alignment effect by the interstitial fluid flow is mostly likely due to the ECM resistance force.

Table 3.

Estimated Parameters in the Tumor Cell Migration Simulation Data Regression

	cmes	nmes	Adjust R-Square	camo	namo	Adjust R-Square
ECM parallel to flow	20.00	0.4	0.853	71.38	0.1	0.945
ECM random aligned	15.27		0.683	51.97		0.891
ECM perpendicular to flow	13.86		0.899	44.49		0.983

amo, amoeboid; mes, mesenchymal.

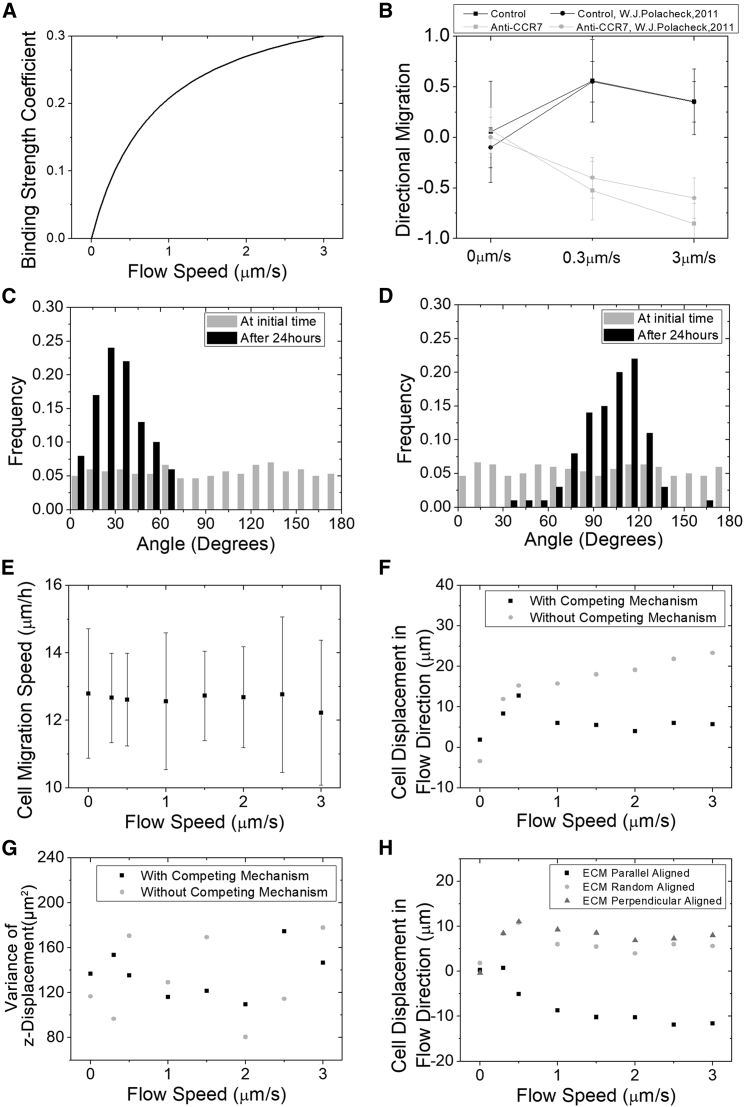
Some tumor cells tend to migrate upstream against interstitial fluid flow (21), which is of similar interest with the presence of other microenvironmental factors. The upstream migration is suggested because of asymmetry of fluid shear stress that promotes the FAK activation at the flow upstream side of cells (21). Accordingly, we first estimate this increase of cell-ECM traction strength within a cell at the flow upstream side from the experiment using a hill function (Fig. 6 A). With this effect of shear stress on cell-ECM traction strength, tumor cells experience a tendency to migrate against the flow, which is consistent with the experiment (Fig. 6 B). When flow speed is small (0.3 μm/s), the effect of migrating against the flow (the shear stress effect) is not big enough to overcome the one along it (the chemotaxis effect). As a result, most tumor cells migrate along the flow and are characterized by an angle less than 45° (Fig. 6 C). Here, the angle is defined the same as previously: the one between cell final position to the origin and the z axis. At 3 μm/s flow speed, the effect of shear stress is comparable to the effect of cytokine chemotaxis, leading some cells to migrate against flow (Fig. 6 D). The migration speed with this competing mechanism between the shear stress and the chemotaxis is also not affected by interstitial fluid flow (Fig. 6 E). However, the z displacements with and without shear stress effect are significantly distinguishable (Fig. 6 F, ANOVA, p < 0.01). With this competing mechanism, we observe a saddle point around 0.5 μm/s flow speed, after which the flow speed increase becomes notable to decrease the z displacement. The variance of the z displacement is not significantly affected by the competing mechanism or the speed flow (Fig. 6 G). We also present the cell displacement in flow direction with different ECM alignments (Fig. 6 H). Surprisingly, the parallel alignment promotes cells to migrate against the flow, whereas the perpendicular migrates along the flow. This may be because for the parallel aligned ECM, the cells have the most cell-ECM bonds at the upstream of the flow, whereas for the perpendicular one, they have the least. The amoeboid migration is not discussed here because the cell-ECM traction force is absent, and there is no competing mechanism.

Figure 6.

Tumor migration against flow direction is influenced by ECM alignment. (A) The increase of the traction force is estimated using a hill function from the directional migration data (B). With this setup, our simulation can reproduce the experimental data ((21), ANOVA, p > 0.05). (C) The population fraction of polar angles of cells in 0.3 μm/s flow case is shown. The polar angle is the angle between the cell’s location to the origin and the z axis. The polar angle less than 45° corresponds to cells migrating along the flow direction, or more than 135° corresponds to cells migrating against the flow direction. Cell number is 300. ECM is randomly aligned. Running time is 48 h. (D) The population fraction of polar angles of cells in 3 μm/s flow case is shown. Cell number is 300. ECM is randomly aligned. Running time is 48 h. (E) The speed of cell migration does not change much with the flow speeds (ANOVA, p > 0.05, mean values are not significantly different). Meanwhile, the cell speed does not significantly vary with that of the no competing mechanism case (not shown in the figure, ANOVA, p > 0.05). (F) Shown is the displacement of tumor cells in the flow direction versus flow speed for mesenchymal migration mode with the competing mechanism (21) (ANOVA, p < 0.01). Cell number is 300. ECM is randomly aligned. Running time is 24 h. (G) The variances of z displacement of the two cases are of no significant difference (F-test, p > 0.05, ANOVA, p > 0.05). (H) Directional displacement of cells in three ECM alignments with the competing mechanism is shown. The directional migration is defined as a population that has an average score that scored cells with a +1 if they migrated within 45° of the streamline in the downstream direction and a −1 if they migrated within 45° of the streamline in the upstream direction.

Discussion

In this article, we develop a computational model to investigate 3D tumor cell migration in various ECM network and interstitial fluid flow. We first validate that interstitial fluid flow facilitates tumor cell migration, and the parallel aligned ECM is optimal for cells to travel through. Though ECM and flow are independent inputs, their effects on cell migration are not independent. The resistance force that depends on cell migration speed and ECM serves as a nonlinear integrator. Meanwhile, the migration tendency toward stiffer ECM termed as “durotaxis” is influenced by the ECM alignment and the flow. The variance of cell displacement does not change with the flow speed nor the ECM stiffness gradient but is regulated by the ECM alignments. The comparison between the mesenchymal and amoeboid migration modes suggests that this is due to the presence of the cell-ECM traction force. Ultimately, we derive an analytical formula of this nonlinear cell directional displacement dependency on interstitial fluid flow speed and varied ECM alignments. Using this practical model, we can quantitatively predict the tumor cell invasion with multiplexed microenvironmental factors.

At the same time, this work can still be further refined. Our model is theoretical and is validated by some experiments on the effect of ECM alignment and fluid flow. Here, we assume the collagen fiber network as fixed during cell migration due to strong fiber cross-links. Though a dynamic collagen network can potentially provide more insights and practical application on cancer migration, it will be computationally expensive, and our current work manages to capture the effect of ECM on cell migration observed in the experiments. The deformability of tumor cell and the porosity of the ECM are also important factors during metastasis. In this article, we only focus on cell migration within sparse cell density. For higher cell density, the migration pattern is quite different, such as migration against flow direction at small flow speed (21). We hypothesize that with a very high cell density, the chemokine distribution field will be nearly homogeneous, and the receptor saturation will be more likely to happen, so that the migration pattern will be close to the result of zero flow speed. There are different modes of collective cell migration other than mesenchymal and amoeboid migrations, so in this work, we do not specifically study collective cancer migration with high cell density. With the help of our model, we will seek to design in vitro experiments to better understand the biomechanical mechanism of tumor metastasis and coordinate more data to improve this model.

The model adopts an innovative angle by considering the interaction between ECM and flow on cell migration. As a result, it connects the local nanoscale force integral, such as integrin-regulated traction forces, and the microscale cell migration regulation, such as the chemotactic protrusion and the ECM viscous resistance. Our cell migration model also embeds the stochastic effects arising from cell protrusion direction based on the chemokine concentration and the ECM network generation but leads to an analytical function to predict the average cell displacement within various microenvironments. Both single-cell migration modes and the migration against/along the flow are investigated, which is vital to consider for a tumor migration model due to tumor heterogeneity and migration transition in metastasis. Thus, our model provides a comprehensive picture of how the microenvironmental factors and the migration modes interact to optimize tumor migration.

Data and materials availability: All model parameters needed to evaluate the conclusions are present in the article. Simulation code is available in the GitHub (https://github.com/ttsunmeng/CollagenFiberModel_cfd).

Author Contributions

A.L., M.S., F.S., R.S., and M.H.Z. conceived and designed the study. A.L. and M.S. designed or implemented the mathematical model. A.L., M.S., F.S., R.S., and M.H.Z. have drafted the work or substantially revised it.

Editor: Kevin Janes.