Abstract
Assembly and deposition of insoluble amyloid fibrils with a distinctive cross-β sheet structure is the molecular hallmark of amyloidogenic diseases affecting the central nervous system as well as non-neuropathic amyloidosis. Amyloidogenic proteins form aggregates via kinetic pathways dictated by initial solution conditions. Often, early stage, cytotoxic, small globular amyloid oligomers (gOs) and curvilinear fibrils (CFs) precede the formation of late-stage rigid fibrils (RFs). Growing experimental evidence suggests that soluble gOs are off-pathway aggregates that do not directly convert into the final stage RFs. Yet, the kinetics of RFs aggregation under conditions that either promote or suppress the growth of gOs, remain incompletely understood. Here we present a self-assembly model for amyloid fibril formation in the presence and absence of early-stage off-pathway aggregates, driven by our experimental results on hen egg white lysozyme (HewL) and beta amyloid (Aβ) aggregation. The model reproduces a range of experimental observations including the sharp boundary in the protein concentration above which the self-assembly of gOs occurs. This is possible when both primary and secondary RFs nucleation rates are allowed to have a non-linear dependence on initial protein concentration, hinting towards more complex pre-nucleation and RFs assembly scenarios. Moreover, analysis of RFs lag period in the presence and absence of gOs indicates that these off-pathway aggregates have an inhibitory effect on RFs nucleation. Finally, we incorporate the effect of a Aβ binding protein on the aggregation process in the model that allows us to identify the most suitable solution conditions for suppressing gOs and RFs formation.
Graphical Abstract
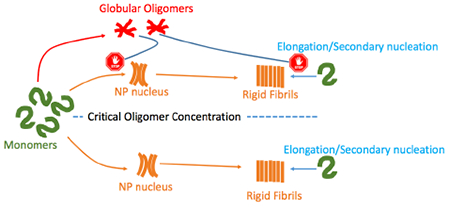
2. Introduction
Many neurodegenerative disorders, such as Alzheimer’s and Parkinson’s disease, are characterized by the formation and deposition of rigid fibrils (RFs)1–3. The kinetics of RFs formation can be monitored in vitro using Thioflavin T (ThT), a fluorescent dye that recognizes the amyloid cross-β sheet structural motif4;5. Under various growth conditions, ThT traces exhibit the classical nucleated polymerization kinetics with an initial lag period, during which a small amount of RF pre-nuclei form. Upon nucleation, an explosive upswing in the fluorescence signal ensues, which is associated with an accelerated fibril growth. The signal eventually plateaus, indicating the steady-state of the polymerization reactions.
Over the past several years, it has become evident that several additional molecular events can happen parallel to fibril elongation, namely fibril surface assisted or autocatalytic secondary nucleation, fragmentation of existing RFs (depending on the protein and growth conditions) leading to increase fibril number or fibril bundling leading to increased stability of existing fibrils6–12. The laboratories of Knowles, Radford, Linse and others have shown that half-time scaling (the time it takes for half of the protein to aggregate) behavior as a function of initial monomer concentration delineates the different nucleation mechanisms for RFs formation6;7;13;14. The two dominant RFs nucleation mechanisms identified by these studies are the primary (classical) and secondary nucleations15.
Under certain growth conditions, the formation of RFs is preceded by globular oligomers (gOs) and curvilinear fibrils (CFs)16–18. These early-stage species are believed to be the main source of cellular toxicity, with amyloidogenic diseases being strongly correlated with pathological levels of these aggregates19–21. Thus, it is important to understand the mechanism through which these oligomers form, and how their presence affects RFs nucleation and growth.
Though the particular mechanism by which early stage gOs/CFs emerge is unknown, there are three possible ways that have been proposed that could play into RF formation. (1) gOs/CFs are capable of internal restructuring into a RFs nuclei, acting as mandatory on-pathway intermediates (also known as nucleated conformational or structural conversion)22–24. (2) gOs/CFs are metastable aggregates that proceed along a separate pathway (off-pathway) and could serve as sites for RFs heterogeneous nucleation or assist in RFs pre-nuclei internal restructuring25;26 and subsequently dissolve, being replaced by the thermodynamically more stable RFs. In this scenario, both on- and off-pathways would proceed in parallel, with RFs being the end-products along both pathways. (3) gOs/CFs are kinetically favored metastable aggregates, incapable of facilitating RFs nucleation either by internal restructuring or surface assisted heterogeneous nucleation. Thus the nucleation and growth of RFs would proceed via a parallel mechanism, without any direct interaction with gOs/CFs growing along off-pathway27–31.
If the ThT signal was only representing the mass of protein that has converted to the aggregated state, distinguishing the above three scenarios from each other would not be possible. Even if one could differentiate the ThT signal originating from RFs from that due to gOs/CFs, the first and third scenarios would lead to identical ThT traces. In both cases, an initial rise in ThT signal would correspond to gOs/CFs formation, followed by another upswing that would indicate the formation and growth of RFs. In all three scenarios though, the lag period for RFs formation would continue to decrease as a function of initial monomer concentration (as opposed to the half-time that would continuously decrease in the first and second scenarios, but will first decrease and then increase in the third scenario as showed by Powers and Powers 32).
Recently, Miti et al.33 combined Static and Dynamic Light Scattering, Fourier-Transform Infrared Spectroscopy, and Atomic Force Microscopy with ThT spectroscopy to show that gOs/CFs form upon crossing a sharp boundary with respect to monomer concentration, known as the critical oligomer concentration (COC), for its similarities with the onset of micelle formation in charged surfactant system34. Monomer concentration below this threshold leads to RFs formation via classical nucleated polymerization where the lag period decreases with protein concentration according to a scaling law as described by Knowles’s group6;35. Above this threshold, the ThT signal exhibits biphasic behavior with an initial lag-free upswing, indicating gOs/CFs aggregation. Far above the COC, the first rise nearly plateaus before another upswing that represents the formation of RFs. Furthermore, this threshold depends on the salt concentration in the solution. Similar transitions were also observed in multiple beta amyloid (Aβ) variants36, IAPP37, and β2-microglobulin amyloid assembly upon changes in solution pH38;39. More recently, we reported the existence of such COC for Aβ dimer construct (dimAβ)40 (see also Figure 1). Interestingly, we found that below the COC, the lag period decreases as we increase the monomer concentration of both hen egg white lysozyme (HewL) and dimAβ. However, above the COC the lag period of RF formation increases as a function of monomer concentration. In other words, gOs/CFs seem to delay the formation of RFs. A similar self-inhibition was also reported for insulin amyloid-like aggregation 41, indicating that the observations we made could be common to several proteins.
Figure 1:
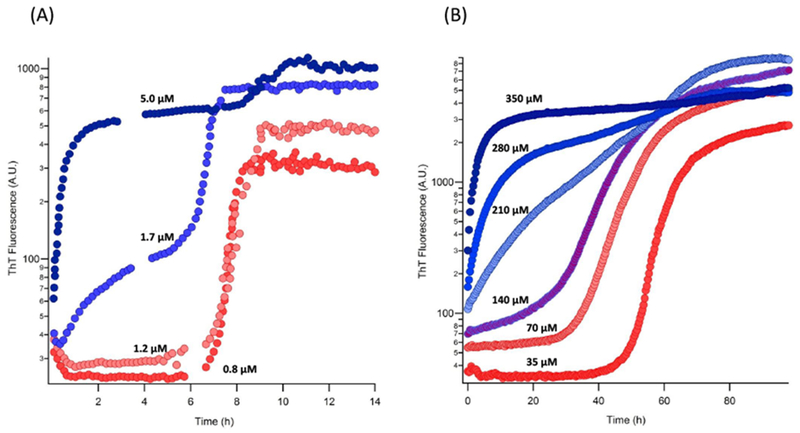
Oligomeric and fibril growth kinetics. Representative ThT traces showing the transition from sigmoidal growth representing the formation of only RFs below COC (red) to biphasic growth kinetics representing the fast formation of gOs followed by slower growth of RFs above COC (blue) for dimAβ (A) and HewL (B). For initial monomer concentration above COC in both cases, the first and second upswings represent the growth of gOs and RFs respectively. The number next to each curve represents the initial monomer concentration used.
Thus, our previous observations favor the third scenario for amyloid fibril self-assembly with two important modifications; (1) the off-pathway only exists when the monomer concentration is above COC and (2) gOs/CFs delay the formation of RFs33;40;42. Powers and Powers have previously formulated the third scenario32. In this work, we extend this formalism to include the two above mentioned adjustments. Unlike the Powers and Powers model, our model also incorporates the experimentally confirmed contribution of secondary nucleation to RFs formation. Furthermore, we replace the linear kinetics for nucleus formation along on-pathway and the gOs/CFs formation along the off-pathway by cooperative self-assembly formalism that is either warranted by the data or motivated by the desire to simplify the model without compromising the quality of the fits. Towards the end, we incorporate the effect of binding proteins on the amyloid fibril self-assembly.
3. Methods
Full details of experimental methods used in this study are reported previously40, and outlined below.
3.1. Protein and chemicals
Two times recrystallized, dialyzed, and lyophilized HewL was purchased from Worthington Biochemicals (Lakewood, NJ) and used for all experiments. Ultrapure grade ThT was obtained from Anaspec (Freemont, CA) and standard grade ThT from Sigma Aldrich. All other chemicals were from Fisher Scientific (Pittsburgh, PA) and were reagent grade or better.
3.2. Preparation of HewL solutions
HewL was dissolved at twice its final concentration in 25 mM KH2PO4 pH 2 buffer and was placed in a water bath for 3 minutes at 42° C to help dissolve preformed assemblies. Samples were successively filtered through 220 nm nitrile (Fisherbrand, Fisher Scientific, Pittsburgh, PA) and 50 nm polyethersulfone (Tisch Scientific, North Bend, OH) pore size syringe filters. The concentrated HewL stock was mixed 1:1 with a NaCl/25 mM KH2PO4 pH 2 stock solution at double the desired final salt concentrations. Final lysozyme concentrations were determined from UV absorption measurements at 280 nm (ϵ280 = 2.64mLmg−1cm−1).
3.3. Preparation of dimAβ
Following a strategy previously established for recombinant production of Aβ43, bacterial expression of dimAβ was achieved by co-expression of ZAβ3, a binding protein that shields aggregation-prone sequence segments of Aβ. The gene encoding dimAβ, including an N-terminal methionine, followed by a Aβ40 unit, a (G4S)4 linker, and a second Aβ40 unit, was obtained from Life Technologies, and was cloned into the pACYCDuet-1 vector for co-expression with the ZAβ3 gene using NcoI and HindIII restriction sites. The coexpression vector contains the genes for dimAβ and (His)6-tagged ZAβ3 in the following order: T7promoter-1 – dimAβ-T7promoter-2 – (His)6ZAβ3 – T7 terminator. The protein was expressed as described in Ref.43.
For purification, cell pellets were resuspended in 50 mM Na-phosphate, 0.3 M NaCl, 20 mM imidazole, pH 8, containing EDTA-free protease inhibitor (Roche Applied Sciences) and lysed by a cell disrupter (Constant Systems). The cell debris was removed by centrifugation in a Beckman J2-21 centrifuge mounting a JA20.1 rotor at 18,000 RPM, 4¼C for 40 minutes. For capture of the dimAβ:ZAβ3 complex by immobilized metal ion affinity chromatography (IMAC), the supernatant was loaded on a HisTrap FF column (GE Healthcare). DimAβ was separated from the resin-bound ZAβ3 and eluted with 8 M urea, 20 mM Na- phosphate, pH 7. For further purification, including removal of residual ZAβ3, reverse phase high-performance liquid chromatography (RP-HPLC) was performed. For this purpose the IMAC eluate was concentrated in a Vivaspin 20 centrifugal concentrator (Sartorius), followed by addition of 5 mM TCEP to reduce the disulfide bond of ZAβ3, and loading onto a semi-preparative Zorbax 300SB-C8 RP-HPLC column (9.4 mm × 250 mm, Agilent) connected to an Agilent 1260 Infinity system with UV detection at 214 nm. Monomeric dimAβ was eluted in a gradient from 30% (v/v) to 36% acetonitrile in water, 0.1% (v/v) trifluoroacetic acid at 80°C. DimAβ containing fractions were pooled, lyophilized, dissolved in HFIP, aliquoted in 1 mg portions, lyophilized again, and stored at −20°C. Immediately before use in experiments, lyophilized dimAβ was reconstituted in 6 M guanidinium-HCl, 50 mM Na-phosphate, 50 mM NaCl, pH 7.4, and sonicated for 30 minutes in a sonicator bath. Subsequently, the solution was loaded onto a Superdex 75 10/300 GL column (GE Healthcare) equilibrated with 35 mM Na2HPO4, 50 mM NaCl, 5 mM NaOH, pH 11. DimAβ was eluted at 13.5 ml. Protein concentration was determined by spectrophotometry. Immediately before the start of an experiment, 1.5% 1 M NaH2PO4 was added, yielding 50 mM Na-phosphate, 50 mM NaCl, pH 7.4, as final buffer.
3.4. ThT fluorescence-monitored amyloid formation
ThT stock solutions were prepared by dissolving 1 mM dye in DI (18 MΩ) water and then filtering through 220 nm syringe filters. Final ThT concentrations were obtained from absorption at λ = 412 nm (ϵ412 = 32000 M−1 cm−1)44. HewL amyloid growth kinetics was monitored with ThT using a Spectra-Max M5 fluorescence plate reader (Molecular Devices). ThT fluorescence was excited at 440 nm, and emission collected at 488 nm. Protein solutions at concentrations ranging from 0.1 mg/ml (7 μM, below the COC) to 5 mg/ml (350 μM, above the COC) and salt concentration of 450 mM were incubated in six 300 μL duplicates in a 96 well plate at 52°C. Protein concentrations were more closely spaced near the COC for a given salt concentration, and more widely spaced below and above the COC. ThT at final concentrations were 10 - 20 μM. Measurements were taken every 20 minutes and the plate was shaken for 3 seconds before each measurement.
DimAβ amyloid growth kinetics measurements were performed using an Infinite M200 Pro fluorescence plate reader (Tecan) with ThT excitation at 445 nm, and emission collected at 482 nm. Protein concentrations ranged from 0.6 μM (below the COC) to 5 μM (above the COC) in 50 mM Na-phosphate, 50 mM NaCl, pH 7.4. Typically, three identical 100 μL samples were incubated in a 96 well plate at 37°C. ThT at final concentrations of 100 μM was added to each well. Measurements were taken every 3 minutes and the plate was shaken for 2 seconds before each measurement. Typical aggregation kinetic curves for both HewL and dimAβ are shown in Figure 1.
3.5. Calibration of ThT signal
In most experiments on HewL, the ThT signal does not plateau even after 100 hours. Thus, normalizing the trace with respect to the peak intensity might lead to inaccurate conclusions as there are still leftover monomers that need to be converted to RFs at the end of the experiment. To overcome this issue, we grew gOs and CFs and separated them from monomers using 50 kDa cut-off filters and measured their concentration. This was followed by the addition of ThT, the purified gOs, and CFs. In Parallel, we grew RFs, separated them from monomers through 5 repeats of centrifugation (a protocol that we developed for a reliable separation of RFs from the remaining monomers in the solution), and measured their concentration. ThT at the same concentration as the gOs/CFs sample was added to the RFs. We first measured the ThT fluorescence from gOs/CFs sample by itself, then added known concentrations of RFs and measured the fluorescence again. We repeated this procedure for several RFs concentrations and found that 1 μM monomer concentration corresponds to 125 ThT intensity units in our experiments. This calibration is used below to compare the model to observations at different monomer concentrations.
In case of dimAβ experiments, the ThT traces always plateau before the end of the experiment. Therefore, we simply normalized the signal with respect to the peak intensity and use it for comparison with the model.
3.6. Numerical methods
The rate equations are solved in Fortran 90 using 4th order Runge-Kutta method, with a time step of 0.02 ms. Fitting to experimental data and statistical analysis was performed in Matlab R2014b. Codes reproducing key results are available upon request from authors.
4. Results and Discussion
4.1. Ad-hoc oligomer model
To replicate the kinetics of HewL aggregation, we previously adopted the formalism developed by Powers and Powers, modeling nucleated polymerization along with off-pathway aggregation32. To fit our data, we made three key changes to the model as was discussed in Ref.40. (1) In the original model, the pre-nucleus aggregation and fibril elongation rates were similar, while the dissociation rate for the pre-nucleus aggregates was larger than the dissociation rate for RFs. In our ad-hoc model, both the association and dissociation rates for the pre-nucleus were different from the association and dissociation rates for RFs (a1 vs. a and b1 vs. b in Figure S1). (2) To replicate the sharp autocatalytic rise upon RFs nucleation in the experimental traces, we included the secondary nucleation mechanism as proposed by Knowles et al.35 where already formed RFs facilitate the nucleation of new fibrils (blue arrow with binding constant k2 in Figure S1). (3) We described the third key change in the second last paragraph of this section.
The first two modifications resulted in a close fit of the model to the observed trajectories for HewL aggregation below the COC, including the long lag period and sharp rise in ThT signal during the RFs growth phase (Figure S2A). However, we observed that increasing the initial monomer concentration leads to a lag period for RFs growth that decreased disproportionately fast in comparison to the experimental observations (Figure S3). To overcome this discrepancy, we had to systematically change the primary and secondary nucleation rate constants. This led to a close fit to the RFs growth kinetics at different initial monomer concentrations below the COC (Figure S2A–C). As we will see later, the requirement to change the primary and secondary nucleation rate constants when fitting the growth kinetics of HewL RFs at varying initial monomer concentration is not limited to the Powers and Powers model. Fitting other leading models for protein aggregation to our data also demands similar changes in the two nucleation rate constants. In other words, the global fit with fixed primary and secondary nucleation rate constants as previously suggested6;7;15;35 is out of reach of our current model due to its inability to account for the disproportionately slow decrease in the lag period with respect to initial monomer concentration. This suggests a mechanism or reaction order that our model as well as many others do not account for. Our model includes most of the commonly identified mechanisms such as primary nucleation, elongation, dissociation, and secondary nucleation, suggesting an additional monomer dependent mechanism affecting RFs formation and the lag period that many models do not incorporate. It is worth noting that we have omitted the mechanism of fragmentation due to the fact that the samples are shaken for very short periods of time for the purpose of ensuring that our sample is well mixed. Furthermore, none of the current kinetic models incorporate the recently suggested roles of heterogeneous nucleation and surface effects in the deviations from the nucleation rates that these models would predict45;46.
As pointed out by Powers and Powers32, despite taking independent, parallel pathways, their original model could not reproduce the sharp transition from oligomer-free RFs growth to the biphasic oligomeric RFs aggregation observed in our experiments. To incorporate this feature into our ad-hoc model40, as the third key change we allowed the forward rate for the monomers assembly into dimers along the off-pathway to vary according to a sigmoid function that depends on monomer and salt concentrations, such that aggregation along off-pathway is only possible when the initial monomer concentration is above the COC. When the initial monomer concentration is lower than COC, the off-pathway is practically not available for aggregation and growth only occurs along on-pathway. In other words, to reproduce the observed transition from sigmoidal growth representing the formation of only RFs below COC to a biphasic growth representing the fast formation of gOs followed by slower growth of RFs above COC, we added an artificial switch that turns on and off as the monomer concentration crosses the COC. The full set of rate equations and the schematic of the model after making all these changes are given in section “Modified Powers and Powers Model” of Supplementary Information Text and Figure S1 respectively. This ad-hoc model closely fits the RFs and gOs growth kinetics at different initial monomer concentration both below and above COC (Figure S2).
One of the major limitations of the detailed ad-hoc model as described in Ref.40 is that the switch from sigmoidal to biphasic growth as the initial monomer concentration exceeds the COC is artificial. The model does not reflect the underlying physical mechanism of cooperative monomer assembly into gOs. In reality, such transition automatically arises from the amphiphilic nature of primary protein sequences. Consequently, the transition from sigmoidal to the biphasic growth is not limited to HewL. As pointed out above, there are several amyloid proteins which display COC-like transitions38;39;41. This indicates that the transition from sigmoid to biphasic growth and its downstream inhibitory effect on RFs formation could be a common phenomenon among several misfolded proteins. Since different proteins have different COC, the model parameters used in the subsequent simulations are specific to HewL growth under the above mentioned growth conditions. For example, we found that dimAβ and HewL have COC of 1.5 μM and 40 μM respectively. Similarly, the COC for HewL is strongly dependent on its solution environment33. Applying the model to another protein such as Aβ would require changing the sigmoid function and other rate constants accordingly. The value of the COC yields important information about gOs growth kinetics for a given protein that the simple formalism of a sigmoid function can not reveal. Moreover, as we shall see soon, our original model is unnecessarily complex for the growth kinetics of both Aβ and HewL.
4.2. Cooperative oligomer model
4.2.1. Cooperativity in aggregation leads to a simpler model
The Powers and Powers, as well as, our ad-hoc models use linear chains of reactions for pre-nucleus species along the on-pathway and entire off-pathway (Figure S1). However, a close inspection of the initial phase of the ThT signal representing the gOs growth indicates that the reactions along off-pathway are not linear. As we can see from Figure 2, the off-pathway aggregation exhibits a power law-like behavior with an exponent close to 4. Thus, the cooperative formation (non-linear dependence on the available monomer pool) of off-pathway gOs can be formulated as simultaneous aggregation of multiple monomers, or simply a nucleation step. Similarly, one can replace all the pre-nucleation reactions along the on-pathway by a single reaction step where N (where N is the nucleus size) monomers aggregate, similar to the models by Knowles et al15. This simplifies the model to the five rate equations given in the section “Reduced Model” of the Supplementary Information Text.
Figure 2:
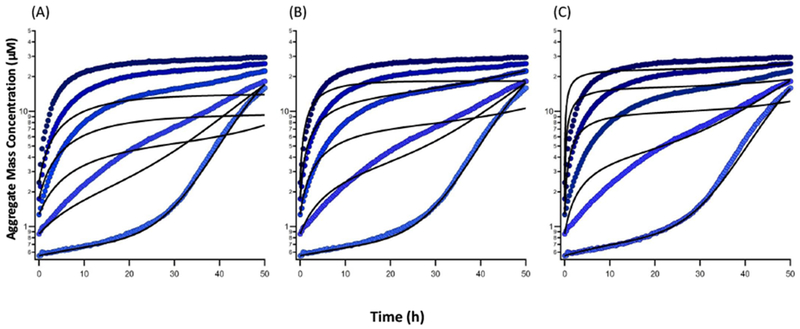
Non-linear behavior of the initial part of ThT signal representing the formation of gOs in HewL along off-pathway. Observed ThT traces (circles) for HewL concentrations of 70 μM, 140 μM, 210 μM, 280 μM and 350 μM (bottom to top) plotted alongside simulated results (solid lines) using a single step power law of degree 3 (A), 4 (B), and 5 (C).
This simpler model is capable of reproducing the observed transition from sigmoidal to biphasic growth as we increase initial monomer concentration from smaller to larger than the COC with reasonable oligomer sizes (3–8 monomers). It can also fit both sigmoidal and biphasic growths as we vary the initial monomer concentration within a narrow range around the COC. However, as we vary the monomer concentration over a wider range above the COC, the model results in either too rapid or too slow an increase in the initial gOs concentration compared to the observed time-traces (Figure S4). This made a global fit for the gOs segment of ThT signals at all initial monomer concentrations above the COC used in our experiments impossible.
To circumvent this shortcoming, we include an additional limiting intermediate step, in which the monomers first form an intermediate nucleus along the off-pathway before aggregating into a “full-size” gOs. To determine the sizes of intermediate (k) and final (m) aggregates, we simulated only the off-pathway (by setting the primary nucleation rate along the on-pathway equal to zero) with many combinations of m and k and fitting the model to the gOs segment of ThT traces recorded at a wide range of HewL concentrations above COC. Since the number of parameters remain the same, we used the Pearson’s chi-squared (χ2) test to determine the model with the best fit to the data, that is,
| (1) |
where xi and mi represent observation and model result at instant i respectively, and n is the total number of data points. As we point out in the next section, the model gives the best fit to the HewL data when k = 2 and m = 5 are used. We also note that the optimal values of k and m remain the same when both the on- and off-pathways are included in the model when fitting to the gOs segment of ThT traces (section “Fitting to off-pathway dynamics with varying aggregate sizes in the presence of on-pathway” of the Supplementary Information Text, compare Figures 4 and S5).
Figure 4:
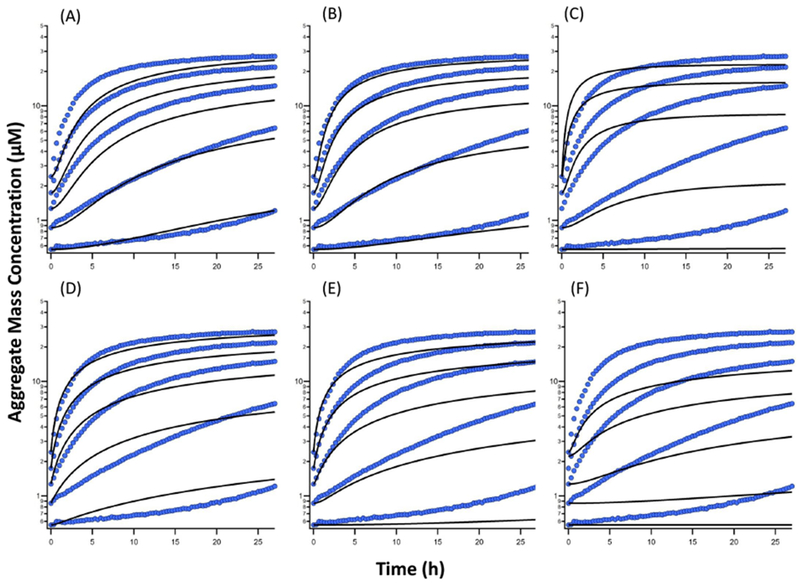
Fitting the model to the kinetics along off-pathway, representing the growth of gOs at HewL concentration of 70 μM, 140 μM, 210 μM, 280 μM, and 350 μM (bottom to top). Fits with different combinations of intermediate (Zk) and final (Zm) aggregates with different sizes (k and m respectively). Model fits with combination (A) Z2Z4, χ2=96.04, (B) Z2Z5, χ2=52.47, (C) Z2Z9, χ2=323.06, (D) Z3Z9, χ2=84.40, (E) Z4Z9, χ2=223.95, and (F) Z5Z9, χ2=214.87. Circles and lines represent experimental data and model fits respectively.
4.2.2. Final model for RFs growth in the presence and absence of off-pathway gOs
After the last modification, the final model has two assembly pathways: (1) on-pathway leading to RFs formation, and (2) off-pathway resulting in gOs assembly (Figure 3). Along the on-pathway, the fibril nucleation barrier is represented by the primary nucleation rate (a1 with nucleus size N = 5) and a dissociation rate constant b1. The reaction from nucleus to RFs is irreversible (note that c= 0). The RFs elongation proceeds via monomer addition beyond the nucleus with a rate constant a and dissociates with a rate constant b. In addition to primary nucleation, secondary nucleation proportional to the first moment of the RFs distribution occurs with a rate constant k2. gOs are treated as unstable aggregates that may grow to some specified maximum size, m, with an intermediate aggregate step of size k. In essence, the off-pathway buffers the monomers temporarily and releases them slowly. On the off-pathway, the transition from monomer to off-pathway intermediate is represented by a rate constant α1. These off-pathway intermediates then transition to larger aggregates with a rate constant α. Both intermediate and final aggregates dissociate with a rate β (see Table 1 for parameter values). The final model is represented by the following six rate equations.
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
where [X1], [Y5], [Zk], [Zm], [F(0)], and [F(1)] represent the concentration of free monomers, nuclei along the on-pathway, intermediate off-pathway species, final off-pathway species, the RFs number concentration, and the amount of monomers incorporated in RFs respectively in μM. We found the best fit to HewL data using k and m equal to 2 and 5 respectively. The last term in Eqs (2 and 3) corresponds to secondary nucleation for new RFs catalyzed by the already existing ones.
Figure 3:
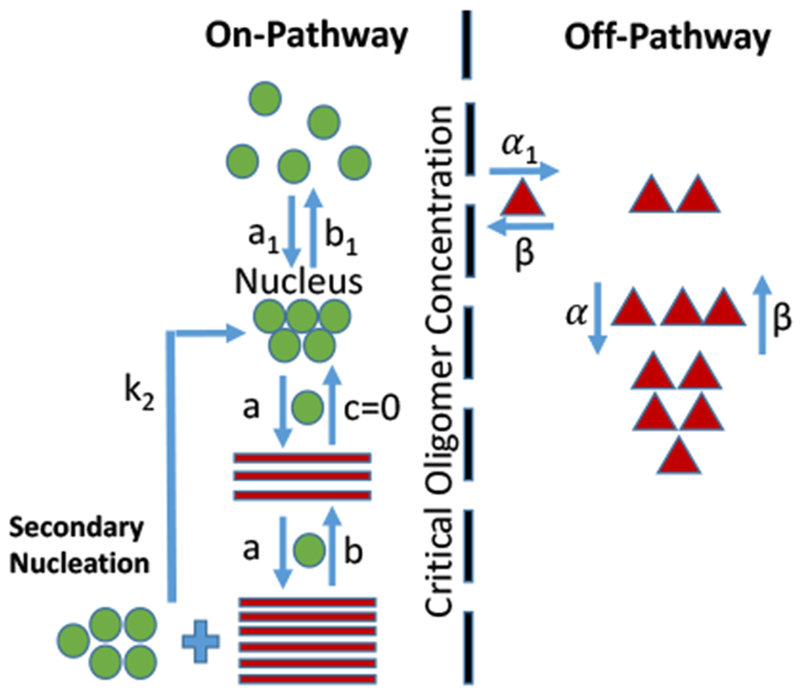
Schematic of the final coopertaive oligomer model. Monomers along the on-pathway are displayed with green spheres, where in addition to primary nucleation, secondary nucleation contributes to RFs seed formation. Within the on-pathway, N monomers associate cooperatively in one step to form a nucleus. Beyond the nucleus, fibril growth ensues (red bars), continuing till all monomers are consumed, progressively increasing the size of RFs. The irreversibility of RFs is indicated by the dissociation rate c = 0. The already existing RFs catalyze the formation of new ones through secondary nucleation with a rate constant k2. On the off-pathway, monomers first form the intermediate species, followed by final globular oligomeric species. gOs are metastable, dissolving into monomers that eventually end up in RFs along the on-pathway.
Table 1:
Rate constants used in the model for HewL and dimAβ
| Parameter | HewL | dimAβ |
|---|---|---|
| a1 (M−1hr−1) | 2.38×10−13 − 9.9×104 | 3.6× 10−22 − 5.76×1012 |
| b1 (hr−1) | 3.96×10−4 | 3.96×10−4 |
| a (M−1hr−1) | 1.98×1011 | 1.98×1011 |
| b (hr−1) | 1.98×107 | 1.98×107 |
| k2 (M−1hr−1) | 1.15×1011 − 9.0×1018 | 2.52×1023−1.8×1026 |
| α (M−1hr−1) | 1.8×104 | 3.6×1045 |
| β (hr−1) | 3.6×10−6 | 3.6×10−2 |
| α1 (M−1hr−1) | 1.8×104 | 2520 |
4.2.3. Dimers as the limiting step for the gOs assembly in HewL
The intermediate species along the off-pathway act as a buffer for impeding the extremely rapid gOs formation that results from the higher-order polynomial (as a function of available monomer pool) required to fit the initial phase of ThT traces representing the gOs. Extensive searches for the best combination of intermediate species and final aggregates suggests that Z2 and Z5 (i.e. k = 2, m = 5) yield the smallest χ2 score with respect to the data from HewL experiments (Figure 4, see also Figure S5). This combination of aggregate sizes also best reproduces the experimentally measured COC. Using larger final aggregate sizes requires the off-pathway forward rates to be much slower in order to fit the traces with larger initial monomer concentrations. However, this eliminates aggregate formation when the initial protein concentration is close to the COC. Also, larger final aggregate sizes cause the initial growth of these off-pathway species to be too rapid, resulting in premature oligomer plateauing. Smaller gOs sizes result in slower initial growth but due to the lower-order kinetics the gOs, growth lags behind the experimental observations at high initial protein concentrations. Thus, we believe that the model not only best represents the growth of gOs along off-pathway observed for HewL, but also best reproduces the observed COC using global fit for the kinetics along off-pathway.
4.3. Lack of global fit for RFs growth
Our final model closely fits the initial segment of the observed ThT traces representing off-pathway aggregation utilizing a global set of parameters along the off-pathway (α, α1, β). However, fitting the segment of ThT traces representing RFs growth at different initial monomer concentrations below and above the COC requires changing the primary and secondary nucleation rate constants (Figure 5). Interestingly, this apparent limitation is not restricted to our model. The model by Knowles and collaborators6;13;15 and Eden et al.47 also require similar changes in the primary and secondary nucleation rate constants. Although both these models do not incorporate the off-pathway aggregates, fitting the models globally to ThT traces representing the RFs growth only below the COC (where the contribution due to gOs is negligible) is not possible (see sections “Fits with the model by Knowles and collaborators” and “Fits with Eden et al. model” in Supplementary Information Text). Using a different version of the model by Knowles and collaborators 6 with primary nucleus size as a fitting parameter improves the global fit to the data (“Fits with the model by Knowles and collaborators” in Supplementary Information Text). However, there are still discrepancies between the model and the experimental results. Three different models behaving in the same manner most likely indicates more complex dynamics of fibril assembly rather than all models being fundamentally wrong. In the case of HewL, the rate of decrease in the primary and secondary nucleation rates appear to roughly compliment each other with the greatest drop in k2 occurring between 7 and 140uM when the change in a1 is smallest and vice versa above 140 μM (Figure 5H and I). As shown in the Supplementary Information Text, these large variations in the two nucleation rate constants make a global fit impossible, even if a few data sets are considered.
Figure 5:
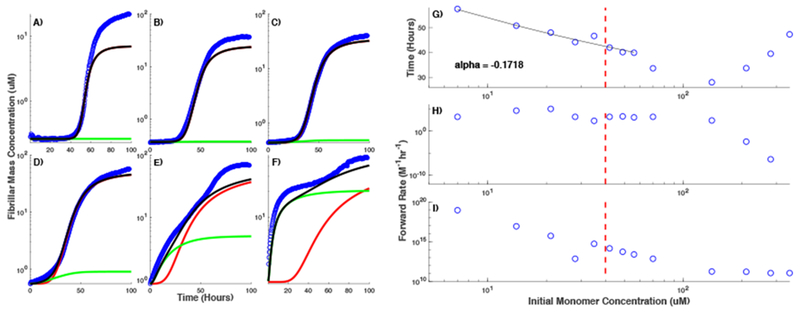
Model fit to ThT traces recorded at different HewL concentrations. Experimentally observed time traces (circles) are plotted alongside with the simulation results for RFs (red), gOs (green), and all on- and off-pathway species combined (model equivalent of ThT signal) (black) at HewL concentration of (A) 7 μM, (B) 28 μM, (C) 42 μM, (D) 70 μM, (E) 140 μM, and (F) 280 μM. (G) Lag period for RFs assembly given by the model as a function of HewL concentration, obtained after fitting the model to observed traces. Thin solid line represents exponential fit to the lag period for protein concentration below and around the COC with exponent −0.1718. Rate constants for the primary (H) and secondary (I) nucleation used to reproduce the experimental observations at different HewL concentrations. The dashed vertical line in panels (G-I) indicates the COC.
4.4. Inhibitory effect of gOs on RFs formation
To better understand the relationship between the changes in both nucleation rate constants and fibril assembly, we next analyze the lag period of RFs formation. We fit the model to ThT traces obtained at different initial monomer concentrations, and define the lag period as the time it takes for the mass concentration of RFs ([F(1)] in the model) to increase by more than 5% of its peak value at the end of simulations. To estimate the lag period of RFs in the experimental traces above the COC where gOs and RFs growth are indistinguishable, we first separated the portion of ThT traces representing RFs using a previously developed method40 and then use the same criterion as used for simulated RFs. The results are summarized in Figure 5G where the lag period of RFs is shown as a function of initial HewL concentration. Below the COC (vertical dotted line), the lag period exhibits an exponential behavior with exponent −0.1718. The lag period continues to decrease over a narrow range above the COC but as HewL concentration increases further, it begins to rise. Interestingly, the rise in the lag period occurs concurrently with a drop in the primary nucleation rate constant. This phenomenon indicates that the model predicts some sort of inhibition of RFs nucleation by gOs. We term it inhibition because if the role of the off-pathway was just to rapidly deplete the monomer concentration (for initial monomer concentration larger than the COC) down to their value at the COC, the lag period would have plateaued above COC at best, which is clearly not the case.
Our model is not equipped to provide a biophysical explanation for the inhibitory effect of gOs on fibril assembly. One can argue that gOs somehow change the free energy landscape33 through some sort of electrostatic shielding effect or changing the very nature of interaction through some unknown mechanism, but these would be mere speculations. Nevertheless, this very interesting interplay between RFs and gOs conceals key biological problems that warrants future experiments and modeling studies. Similarly, we can argue that the potential bundling of RFs provides a possible explanation for the decrease in the secondary nucleation rate constant. As the number of RFs progressively increases with increasing protein content, the probability of bundling would increase, decreasing the exposed area of RFs for secondary nucleation. Again, our current model in not equipped to test this hypothesis and would most likely require Monte Carlo simulations of this complex aggregation processes.
4.5. Modeling the fibril assembly of dimAβ
Recently, we showed that the transition from sigmoidal to biphasic behavior as the protein concentration exceeds the COC observed for HewL can also be seen in dimAβ fibril assembly40. To assess the similarities and differences between the aggregation of both proteins, we use the same procedure as described above to apply our model to dimAβ fibril assembly. Sample fits to the observed ThT traces for experiments on dimAβ are shown in Figure 6A–D. We found that as in HewL, the intermediate species along off-pathway have size 2 in case of dimAβ. However, the final oligomer size giving the best fit is 10. Much like our observations about HewL, the lag period for RFs assembly first decreases as a function of protein content and then begins to rise as we increase the initial monomer concentration above the COC (Figure 6E). The secondary nucleation rate constant initially decreases faster followed by a slower decrease as we increase initial monomer concentration beyond the COC (Figure 6G). Similarly, the primary nucleation rate remains almost fixed at first and then exhibits a rapid drop coincident with the increase in the lag period (Figure 6F).
Figure 6:
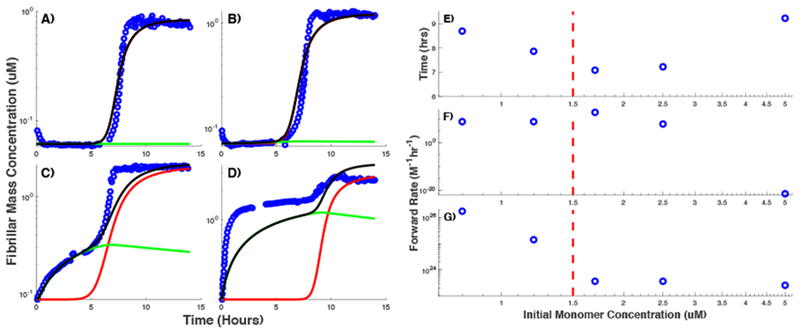
Model fits to ThT traces recorded at different initial dimAβ concentrations. Observed time traces (circles) are plotted alongside with the simulation results for RFs (red), gOs (green), and all on- and off-pathway species combined (model equivalent of ThT signal) (black) at dimAβ concentrations of (A) 0.8 μM, (B) 1.2 μM, (C) 2.5 μM, and (D) 5 μM. (E) Lag period for RFs assembly given by the model as a function of dimAβ concentration, obtained after fitting the model to observed traces. Rate constants for the primary (F) and secondary (G) nucleation used to reproduce the experimental observations at different dimAβ concentrations. The dashed vertical line in panels (E-G) indicates the COC.
4.6. Modeling the effect of binding protein ZAβ3 on fibril assembly of Aβ
Previously, Hoyer and collaborators showed that the binding protein ZAβ3, dissolves oligomeric forms of Aβ42 and Aβ40 by sequestering the monomeric species, but not RFs48–50. We incorporate the effect of ZAβ3 in the model using the following reaction equation
| (8) |
where [ZAβ3] and [ZAβ3·X1] represent the free and monomer-bound ZAβ3 concentrations. ζ and η are the binding and unbinding rates of Aβ monomers to ZAβ3. This leads to the modification of the rate equation for monomeric species and addition of one more rate equation. That is,
| (9) |
| (10) |
Where [ZAβ3]T is the total concentration of [ZAβ3] added to the solution. Luheshi et al. found an off-rate (η) of 1.1 × 10−4s−1 for Aβ42 dissociation from ZAβ350. The on-rate (ζ) is calculated from the dissociation constant, i.e. Kd = η/ζ, where Kd = 17nM for ZAβ348;51.
The numerical experiment shows that when ZAβ3 is added to the solution in the beginning of the experiment, it quickly buffers most of the available monomers and inhibits the formation of both gOs and RFs (compare Figure 7A & B). When the application of ZAβ3 is delayed long enough so that gOs have time to form, but RFs have not nucleated yet, it prevents the formation of RFs by immediately binding all free monomers and those that dissociate from gOs (Figure 7C). Finally, if ZAβ3 is added to the solution after both gOs and RFs are formed in sufficient numbers, RFs are clipped at fixed concentration (Figure 7D). Although, ZAβ3 continues to bind monomers that dissociate from gOs, resulting in a slow decay of overall ThT signal, RFs level off because in the model RFs are treated as irreversible. All these results are in line with our previous observations40, adding further validity to our model results.
Figure 7:
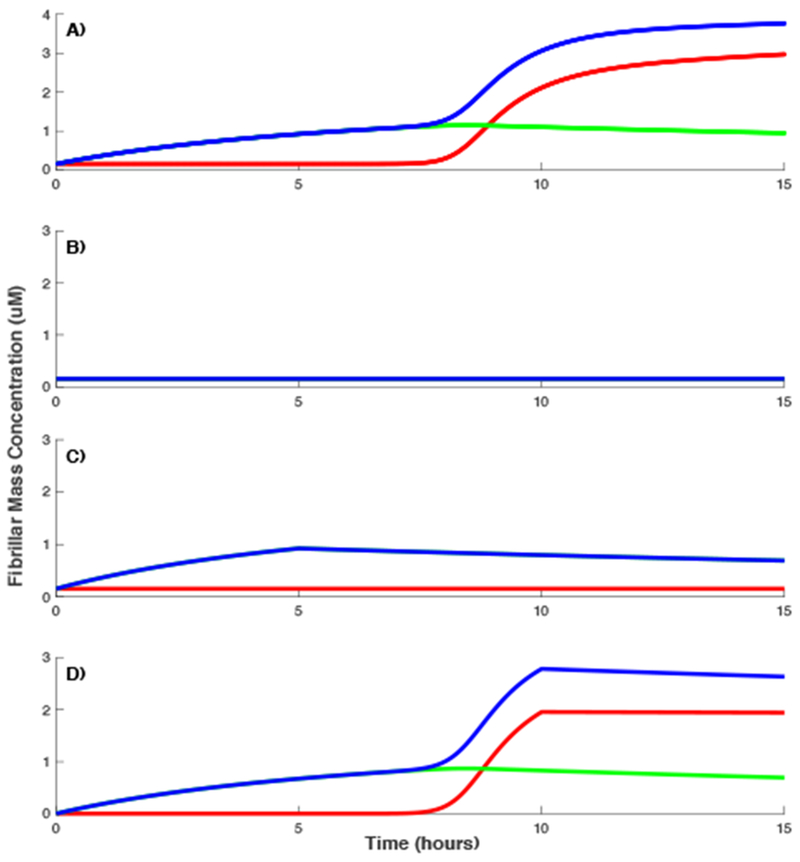
Fibril assembly of dimAβ in the presence of ZAβ3 added at different times. Oligomeric and fibril growth (A) without ZAβ3, (B) ZAβ3 added from the start of the experiment, (C) ZAβ3 added after 5 hours from the beginning of the experiment, and (D) ZAβ3 added after 10 hours from beginning of the experiments. In all panels, simulated contributions from both gOs, RFs, and all on- and off-pathway species combined (model equivalent of ThT signal) are represented with green, red, and blue lines respectively. dimAβ concentration used in the model is 5μM and the concentration of ZAβ3 added to the solution is 7μM.
5. Conclusions
Extensive evidence suggests that early-stage soluble gOs are the main cause of cytotoxicity in amyloid diseases19–21;52–57. However, the conditions that are suitable for the growth of these toxic species that are distinct from the inherently minor populations of small, on-pathway fibril nuclei and pre-nuclei, remain incompletely understood. Similarly, the mechanism of formation of gOs and the way they are replaced by the late-stage RFs continue to be elusive. The role played by metastable gOs in the nucleation and growth of RFs has important implications for our understanding of amyloid pathogenesis and informs efforts at intervening with their formation. Yet, it remains unresolved whether metastable gOs are obligatory or optional precursors of fibril growth, whether they serve as on-pathway precursors or represent off-pathway competitors of the RFs, and whether they affect the nucleation and growth of the RFs. The data-driven modeling study reported here sheds light on these key issues and leads to four main conclusions. (1) gOs are off-pathway aggregates that only form when the protein concentration crosses a well-defined threshold that we termed the “COC”. (2) The relationship between the lag period and protein content is non-linear and more complex than previously thought, even under the conditions where only RFs are formed. (3) Both primary and secondary nucleation are essential for the self-assembly of RFs in HewL and dimAβ. (4) gOs inhibit the nucleation and growth of RFs.
Our analysis of the lag period of fibril assembly reveals that gOs are kinetically favored, metastable aggregates that are incapable of facilitating RFs nucleation either by internal restructuring or surface assisted nucleation, and they form only above the COC. Thus, the growth of RFs and gOs proceed via two parallel mechanisms along on-pathway and off-pathway respectively. Our study also rules out the possibility of conversion of gOs into RFs along off-pathway in addition to RFs formation along on-pathway. In such a scenario, the lag period for RFs formation would progressively decrease as we increase initial monomer concentration, which is clearly not the case. The only way for gOs to convert to RFs is to dissociate into monomers that would then assemble into irreversible RFs.
Below the COC where the ThT signal exhibits sigmoidal behavior, representative of only RFs formation, the lag period shows a power-law behavior with exponent −0.17 and −0.32 for HewL and dimAβ respectively. This is significantly larger than the exponent ~ −0.5 estimated for β2-microglobulin, yeast prion Sup35, and insulin35, and requires a consistent decrease in one or both of the nucleation rate constants when fitting the model to experimental ThT traces at different monomer concentrations. This renders a global fit of the model to the data difficult even if first-order reactions are considered6. We show that this behavior is independent of the model as two other widely used models show a similar trend.
In line with the observations by Cohen and coworkers15;58;59, we found that both primary and secondary nucleations are necessary for reproducing the observations about the fibril self-assembly of HewL and dimAβ. Without the secondary nucleation, it is not possible to reproduce the rapid rise after RFs are nucleated, no matter how high primary nucleation is increased.
One of the key conclusions of this study is the inhibitory effect of gOs on RFs formation. If clipping the monomer content to the COC was the only way that gOs could delay RFs formation, the lag period would have at best leveled off as we increase monomer concentration above the COC. However, we noticed a significant elongation of the lag period as we increase initial monomer concentration beyond the COC. Reproducing the observed lag period requires decreasing the primary nucleation rate constant, indicating the inhibitory effect of gOs on the assembly of RFs. We remark that inhibition here does not necessarily mean the slowing down of primary nucleation only. We noticed that in case of dimAβ, it is possible to fit the lag period by keeping the primary nucleation rate constant nearly fixed but allowing the secondary nucleation rate constant to decrease at a faster rate as we increase the monomer concentration above the COC (results not shown). However, the quality of the fit was not as good as the case when the primary nucleation is allowed to decrease. If one disregards the slight differences in the quality of the fit to the experimental results, the inhibition of RFs’ assembly by gOs in the case of dimAβ can be modeled by decreasing both or either one of the nucleation rate constants. Nevertheless, the combined primary and secondary nucleation rates decrease at much faster rate once the initial monomer concentration increases beyond the COC.
In addition to understanding the mechanism of fibril self-assembly, significant time and expertise have gone into exploring different anti-amyloid therapies, specifically for the treatment of Alzheimer’s disease1;60;61, including anti-amyloid immunotherapy 61–65. One of the three suggested modes of action of anti-amyloid antibodies is to remove Aβ from the brain by binding to monomeric Aβ61;63 (dissolving gOs and RFs by directly binding to them, and phagocytosis by microglia are the other two modes). To mimic the effect of antibodies and provide the first step towards enabling the future fibril assembly models to search for the conditions (e.g. the amount and timing of the antibody application) that would lead to most favorable outcomes, we extended our model to include the effect of Aβ-binding affibody molecules ZAβ3. In line with our previous observations40, our model shows that ZAβ3 is most effective in buffering Aβ when applied before the onset of RFs. Once, a significant portion of monomers assemble into RFs, the effect of ZAβ3 significantly diminishes, allowing the RFs to survive for a very long time40.
To conclude, our model reproduces many observations about fibril formation in HewL and dimAβ in our experiments, both in the presence and absence of metastable gOs. Nevertheless, we do not consider our model to be the final mathematical framework for fibril self-assembly under different conditions. Instead, our model merely highlights the complexity of the amyloid fibril self-assembly, sheds light on some of the key questions that are embedded in this complexity, and provides a future direction for modeling the kinetics of oligomeric and fibril assembly.
Supplementary Material
Acknowledgements
This work was supported by NIH grant R01 AG053988 (GU), NIH grant R15GM097723 (MM), ERC Consolidator grant 726368 (WH), and Alzheimer Forschung Initiative (WH).
Footnotes
Supporting Information
(1) A detailed description of the augmented Powers and Powers model, along with fits produced by the model, as well as a model schematic.
(2) Examination of the results produced when the model is reduced and individual monomeric addition is treated as a single large step.
(3) Fits to the fibril growth kinetics using the models by Knowles et al6;15 and Eden et al47, and the examination of the change in association rates needed to accurately fit experimental data.
References
- [1].Hardy J; Selkoe DJ The Amyloid Hypothesis of Alzheimer’s Disease: Progress and Problems on the Road to Therapeutics. Science 2002, 297, 353–356. [DOI] [PubMed] [Google Scholar]
- [2].Fink AL The Aggregation and Fibrillation of α-synuclein. Accounts Chem. Res 2006, 39, 628–634. [DOI] [PubMed] [Google Scholar]
- [3].Koo EH; Lansbury PT; Kelly JW Amyloid Diseases: Abnormal Protein Aggregation in Neurodegeneration. Proc. Natl . Acad. Sci. U.S.A 1999, 96, 9989–9990. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Levine III H Thioflavine T Interaction with Synthetic Alzheimer’s Disease β-Amyloid Peptides: Detection of Amyloid Aggregation in Solution. Protein Sci. 1993, 2, 404–410. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].De Felice FG; Vieira MN; Meirelles MNL; Morozova-Roche LA; Dobson CM; Ferreira ST Formation of Amyloid Aggregates from Human Lysozyme and its Disease-Associated Variants Using Hydrostatic Pressure. FASEB J. 2004, 18, 1099–1101. [DOI] [PubMed] [Google Scholar]
- [6].Meisl G; Kirkegaard JB; Arosio P; Michaels TCT; Vendruscolo M; Dobson CM; Linse KTPJ, Sara. Molecular Mechanisms of Protein Aggre-gation from Global Fitting of Kinetic Models. Nat. Protoc 2016, 11, 252–272. [DOI] [PubMed] [Google Scholar]
- [7].Cohen SI; Vendruscolo M; Dobson CM; Knowles TP From Macroscopic Measurements to Microscopic Mechanisms of Protein Aggregation. J. Mol. Biol 2012, 421, 160–171. [DOI] [PubMed] [Google Scholar]
- [8].Psonka-Antonczyk K; Hammarstrom P; Johansson L. e. a. Nanoscale Structure and Spectroscopic Probing of A1-40 Fibril Bundle Formation. Front. Chem 2016, 4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Linse S Monomer-Dependent Secondary Nucleation in Amyloid Formation. Biophys. Rev 2017, 9, 329–338. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Fodera V; Librizzi F; Groenning M; van de Weert M; Leone M Secondary Nucleation and Accessible Surface in Insulin Amyloid Fibril Formation. J. Phys. Chem. B 2008, 112, 3853–3858. [DOI] [PubMed] [Google Scholar]
- [11].Nicoud L; Lazzari S; Balderas Barragn D; Morbidelli M Fragmentation of Amyloid Fibrils Occurs in Preferential Positions Depending on the Environmental Conditions. J. Phys. Chem. B 2015, 119, 4644–4652. [DOI] [PubMed] [Google Scholar]
- [12].Arimon M; Sanz F; Giralt E; Carulla N Template-assisted Lateral Growth of Amyloid-β42 Fibrils Studied by Differential Labeling with Gold Nanoparticles. Bioconjugate Chem. 2012, 23, 27–32. [DOI] [PubMed] [Google Scholar]
- [13].Arosio P; Knowles TPJ; Linse S On the Lag Phase in Amyloid Fibril Formation. Phys. Chem. Chem. Phys 2015, 17, 7606–7618. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].Xue W; Homans S; Radford S Systematic Analysis of Nucleation-dependent Polymerization Reveals New Insights into the Mechanism of Amyloid Self-assembly. Proc. Natl. Acad. Sci. U. S. A 2008, 105, 8926–8931. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15].Cohen SI; Linse S; Luheshi LM; Hellstrand E; White DA; Rajah L; Otzen DE; Vendruscolo M; Dobson CM; Knowles TP Proliferation of Amyloid-β42 Aggregates Occurs Through a Secondary Nucleation Mechanism. Proc. Natl. Acad. Sci. U. S. A 2013, 110, 9758–9763. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16].Pachahara SK NR, Adicherla H Self-assembly of Aβ40, Aβ42 and Aβ43 Peptides in Aqueous Mixtures of Fluorinated Alcohols. PLoS ONE 2015, 10, e0136567. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17].Modler A; Gast K; Lutsch G; Damaschun G Assembly of Amyloid Protofibrils via Critical Oligomers - A Novel Pathway of Amyloid Formation. J. Mol. Biol 2003, 325, 135–148. [DOI] [PubMed] [Google Scholar]
- [18].Breydo L; Uversky VN Structural, Morphological, and Functional Diversity of Amyloid Oligomers. FEBS Lett. 2015, 589, 2640–2648. [DOI] [PubMed] [Google Scholar]
- [19].Kayed R; Sokolov Y; Edmonds B; Mclntire TM; Milton SC; Hall JE; Glabe CG Permeabilization of Lipid Bilayers is a Common Conformation-dependent Activity of Soluble Amyloid Oligomers in Protein Misfolding Diseases. J. Biol. Chem 2004, 279, 46363–46366. [DOI] [PubMed] [Google Scholar]
- [20].Novitskaya V; Bocharova OV; Bronstein I; Baskakov IV Amyloid Fibrils of Mammalian Prion Protein are Highly Toxic to Cultured Cells and Primary Neurons. J. Biol. Chem 2006, 281, 13828–13836. [DOI] [PubMed] [Google Scholar]
- [21].Vieira MN; Forny-Germano L; Saraiva LM; Sebollela A; Martinez AMB; Houzel J-C; De Felice FG; Ferreira ST Soluble Oligomers From a Non-Disease Related Protein Mimic Ae-induced Tau Hyperphosphorylation and Neurodegeneration. J. Neurochem 2007, 103, 736–748. [DOI] [PubMed] [Google Scholar]
- [22].Lee J; Culyba EK; Powers ET; Kelly JW Amyloid-β Forms Fibrils by Nucleated Conformational Conversion of Oligomers. Nat. Chem. Biol 2011, 7, 602. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [23].Kelly J Mechanisms of Amyloidogenesis. Nat. Struct. Biol 2000, 7, 824. [DOI] [PubMed] [Google Scholar]
- [24].Serio T; Cashigar A; Kowal A; Sawicki G; Moslehi J e. a. Nucleated Conformational Conversion and the Replication of Conformational Information by a Prion Determinant. Science 2000, 289, 1317–1321. [DOI] [PubMed] [Google Scholar]
- [25].Hill SE; Robinson J; Matthews G; Muschol M Amyloid Protofibrils of Lysozyme Nucleate and Grow via Oligomer Fusion. Biophys. J 2009, 96, 3781–3790. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [26].Mulaj M; Foley J; Muschol M Amyloid Oligomers and Protofibrils, but not Filaments, Self-Replicate from Native Lysozyme. J. Am. Chem. Soc 2014, 136, 8947–8956. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [27].Ehrnhoefer DE; Bieschke J; Boeddrich A; Herbst M; Masino L; Lurz R; Engemann S; Pastore A; Wanker EE EGCG Redirects Amyloidogenic Polypeptides into Unstructured, Off-Pathway Oligomers. Nat. Struct. Mol. Biol 2008, 15, 558. [DOI] [PubMed] [Google Scholar]
- [28].Gosal WS; Morten IJ; Hewitt EW; Smith DA; Thomson NH; Radford SE Competing Pathways Determine Fibril Morphology in the Self-assembly of β2-microglobulin into Amyloid. J Mol Biol. 2005, 351, 850–864. [DOI] [PubMed] [Google Scholar]
- [29].Crespo R; Villar-Alvarez E; Taboada P; Rocha FA; Damas AM; Mar-tins PM What can the Kinetics of Amyloid Fibril Formation Tell about Off-pathway Aggregation? J. Biol. Chem 2015, 291. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [30].Necula M; Kayed R; Milton S; Glabe CG Small Molecule Inhibitors of Aggregation Indicate That Amyloid β Oligomerization and Fibrillization Pathways Are Independent and Distinct. J. Biol. Chem 2007, 282, 10311–10324. [DOI] [PubMed] [Google Scholar]
- [31].Souillac PO; Uversky VN; Millett IS; Khurana R; Doniach S; Fink AL Elucidation of the Molecular Mechanism During the Early Events in Immunoglobulin Light Chain Amyloid Fibrillation: Evidence for an Off-Pathway Oligomer at Acidic pH. J. Biol. Chem 2002, 277, 12666–12679. [DOI] [PubMed] [Google Scholar]
- [32].Powers ET; Powers DL Mechanisms of Protein Fibril Formation: Nucleated Polymerization with Competing Off-pathway Aggregation. Biophys. J 2008, 94, 379–391. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [33].Miti T; Mulaj M; Schmit JD; Muschol M Stable, Metastable, and Kinetically Trapped Amyloid Aggregate Phases. Biomacromolecules 2015, 16, 326–335. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [34].Israelachvili JN Intermolecular and surface forces; Academic Press, Burling-ton, MA, 3rd edn, 2011. [Google Scholar]
- [35].Knowles TP; Waudby CA; Devlin GL; Cohen SI; Aguzzi A; Vendruscolo M; Terentjev EM; Welland ME; Dobson CM An Analytical Solution to the Kinetics of Breakable Filament Assembly. Science 2009, 326, 1533–1537. [DOI] [PubMed] [Google Scholar]
- [36].Soreghan B; Kosmoski J; Glabe C Surfactant Properties of Alzheimer’s  Peptides and the Mechanism of Amyloid Aggregation. J. Biol. Chem 1994, 269, 28551–28554. [PubMed] [Google Scholar]
- [37].Brender JR; Krishnamoorthy J; Sciacca MF; Vivekanandan S; D?Urso L; Chen J; La Rosa C; Ramamoorthy A Probing the Sources of the Apparent Irreproducibility of Amyloid Formation: Drastic Changes in Kinetics and a Switch in Mechanism due to Micelle-Like Oligomer Formation at Critical Concentrations of IAPP. J. Phys. Chem. B 2015, 119, 2886–2896. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [38].Adachi M; So M; Sakurai K; Kardos J; Goto Y Supersaturation-Limited and Unlimited Phase Transitions Compete to Produce the Pathway Complexity in Amyloid Fibrillation. J. Biol. Chem 2015, jbc–M115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [39].Jahn TR; Radford SE Folding Versus Aggregation: Polypeptide Conformations on Competing Pathways. Arch. Biochem. Biophys 2008, 469, 100–117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [40].Hasecke F; Miti T; Perez C; Barton J; Scholzel D; Gremer L; Griming CS; Matthews G; Meisl G; Knowles T, et al. Origin of Metastable Oligomers and their Effects on Amyloid Fibril Self-assembly. Chem. Sci 2018, 9, 5937–5948. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [41].Ziaunys M; Sneideris T; Smirnovas V Self-Inhibition of Insulin Amyloid-Like Aggregation. Phys. Chem. Chem. Phys 2018, 20, 27638–27645. [DOI] [PubMed] [Google Scholar]
- [42].Hill SE; Miti T; Richmond T; Muschol M Spatial Extent of Charge Repulsion Regulates Assembly Pathways for Lysozyme Amyloid Fibrils. PLoS One 2011, 6, e18171. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [43].Macao B; Hoyer W; Sandberg A; Brorsson A-C; Dobson CM; Hard T Recombinant Amyloid Beta-Peptide Production by Coexpression with an Affibody Ligand. BMC biotechnol. 2008, 8, 82. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [44].Sulatskaya AI; Kuznetsova IM; Turoverov KK Interaction of Thioflavin T with Amyloid Fibrils: Stoichiometry and Affinity of Dye Binding, Absorption Spectra of Bound Dye. J. Phys. Chem. B 2011, 115, 11519–11524. [DOI] [PubMed] [Google Scholar]
- [45].Vacha R; Linse S; Lund M Surface Effects on Aggregation Kinetics of Amyloidogenic Peptides. J. Am. Chem. Soc 2014, 136, 11776–11782. [DOI] [PubMed] [Google Scholar]
- [46].Ris0r MW; Juhl DW; Bjerring M; Mathiesen J; Enghild JJ; Nielsen NC; Otzen DE Critical Influence of Cosolutes and Surfaces on the Assembly of Serpin-derived Amyloid Fibrils. Biophys. J 2017, 113, 580–596. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [47].Eden K; Morris R; Gillam J; MacPhee CE; Allen RJ Competition between Primary Nucleation and Autocatalysis in Amyloid Fibril Self-assembly. Biophys. J 2015, 108, 632–643. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [48].Hoyer W; Gronwall C; Jonsson A; Stahl S; Hard T Stabilization of a β-hairpin in Monomeric Alzheimer’s Amyloid-β Peptide Inhibits Amyloid Formation. Proc. Natl. Acad. Sci. U. S. A 2008, 105, 5099–5104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [49].Gruning CS; Klinker S; Wolff M; Schneider M; Toksoz K; Klein AN; Nagel-Steger L; Willbold D; Hoyer W The Off-Rate of Monomers Dissociating from Amyloid-β Protofibrils. J. Biol. Chem 2013, jbc-M113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [50].Luheshi LM; Hoyer W; de Barros TP; van Dijk Hard I; Brorsson AC; Macao B; Persson C; Crowther DC; Lomas DA; Stahl S, et al. Sequestration of the Ae Peptide Prevents Toxicity and Promotes Degradation in Vivo. PLoS biol. 2010, 8, e1000334. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [51].Grönwall C; Jonsson A; Lindström S; Gunneriusson E; Ståhl S; Herne N Selection and Characterization of Affibody Ligands Binding to Alzheimer Amyloid β Peptides. J. biotechnol 2007, 128, 162–183. [DOI] [PubMed] [Google Scholar]
- [52].Ono K; Condron MM; Teplow DB Structure-Neurotoxicity Relationships of Amyloid β-protein Oligomers. Proc. Natl. Acad. Sci. U. S. A 2009, 106, 14745–14750. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [53].Kalia LV; Kalia SK; McLean PJ; Lozano AM; Lang AE α-Synuclein Oligomers and Clinical Implications for Parkinson Disease. Ann. Neurol 2013, 73, 155–169. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [54].Dahlgren KN; Manelli AM; Stine WB; Baker LK; Krafft GA; LaDu MJ Oligomeric and Fibrillar Species of Amyloid-β Peptides Differentially Affect Neuronal Viability. J. Biol. Chem 2002, [DOI] [PubMed] [Google Scholar]
- [55].Lambert MP; Barlow A; Chromy BA; Edwards C; Freed R; Liosatos M; Morgan T; Rozovsky I; Trommer B; Viola KL, et al. Dif-fusible, Nonfibrillar Ligands Derived from Ae 1–42 are Potent Central Nervous System Neurotoxins. Proc. Natl. Acad. Sci. U. S. A 1998, 95, 6448–6453. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [56].Kayed R; Lasagna-Reeves CA Molecular Mechanisms of Amyloid Oligomers Toxicity. J. Alzheimers Dis 2013, 33, S67–S78. [DOI] [PubMed] [Google Scholar]
- [57].O’Nuallain B; Freir DB; Nicoll AJ; Risse E; Ferguson N; Herron CE; Collinge J; Walsh DM Amyloid β-Protein Dimers Rapidly Form Stable Synaptotoxic Protofibrils. J. Neurosci 2010, 30, 14411–14419. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [58].Cohen SI; Vendruscolo M; Welland ME; Dobson CM; Terentjev EM; Knowles TP Nucleated Polymerization with Secondary Pathways. I. Time Evolution of the Principal Moments. J. Chem. Phys 2011, 135, 08B615. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [59].Cohen SI; Vendruscolo M; Dobson CM; Knowles TP Nucleated Polymerization with Secondary Pathways. II. Determination of Self-Consistent Solutions to Growth Processes Described by Non-linear Master Equations. J. Chem. Phys 2011, 135, 08B611. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [60].Lansbury PT; Lashuel HA A Century-Old Debate on Protein Aggregation and Neurodegeneration Enters the Clinic. Nature 2006, 443, 774. [DOI] [PubMed] [Google Scholar]
- [61].Citron M Strategies for Disease Modification in Alzheimer’s Disease. Nat. Rev. Neurosci 2004, 5, 677. [DOI] [PubMed] [Google Scholar]
- [62].Masliah E; Hansen L; Adame A; Crews L; Bard F; Lee C; Seubert P; Games D; Kirby L; Schenk D Â Vaccination Effects on Plaque Pathology in the Absence of Encephalitis in Alzheimer Disease. Neurology 2005, 64, 129–131. [DOI] [PubMed] [Google Scholar]
- [63].Weiner HL; Frenkel D Immunology and Immunotherapy of Alzheimer’s Disease. Nat. Rev. Immunol 2006, 6, 404. [DOI] [PubMed] [Google Scholar]
- [64].Barrera-Ocampo A; Lopera F Amyloid-beta Immunotherapy: The Hope for Alzheimer Disease? Colomb. Med. (Cali) 2016, 47, 203–212. [PMC free article] [PubMed] [Google Scholar]
- [65].Schenk D; Barbour R; Dunn W; Gordon G; Grajeda H; Guido T; Hu K; Huang J; Johnson-Wood K; Khan K, et al. Immunization with Amyloid-β Attenuates Alzheimer-Disease-Like Pathology in the PDAPP Mouse. Nature 1999, 400, 173. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


