Abstract
The fluorescence lifetime of nicotinamide adenine dinucleotide (NADH) is commonly used in conjunction with the phasor approach as a molecular biomarker to provide information on cellular metabolism of autofluorescence imaging of cells and tissue. However in the phasor approach, the bound and free lifetime defining the phasor metabolic trajectory is a subject of debate. NADH increases the fluorescence lifetime when bound to an enzyme, in contrast to the short multiexponential lifetime displayed by NADH in solution. The extent of fluorescence lifetime increase depends on the enzyme to which NADH is bound. With proper preparation of lactate dehydrogenase (LDH) using oxalic acid as an allosteric factor, bound NADH to LDH has a lifetime of 3.4 ns and is positioned on the universal semi-circle of the phasor plot, inferring a mono-exponential lifetime for this species. Surprisingly, measurements in the cellular environments with different metabolic states show a linear trajectory between free NADH at about 0.37 ns and bound NADH at 3.4ns. These observations support that in a cellular environment a 3.4 ns value could be used for bound NADH lifetime. The phasor analysis of many cell types shows a linear combination of fractional contributions of free and bound species NADH.
Keywords: FLIM, NADH, Phasor, lifetime, Autofluorescence, TCSPC
INTRODUCTION
Endogenous fluorescence has long been used as a molecular marker of metabolic states in cells and tissues. Since the pioneer work of Briton Chance in the early ‘60 with fiber optics inside tissues, the fluorescence of NADH and FAD+ became very useful tools as metabolic fingerprints in physiology and pathology1–3. In particular, spectral measurements do not have enough sensitivity to separate and quantify bound from free NADH and this separation is needed because intensity per se cannot quantify how much of the NADH is bound and how much is free.. NAD+ and NADH are two important cofactors in various different cellular cycles including cell metabolism and salvage pathways4–6. Shifts in cellular metabolism have been shown to correlate with the NAD+/NADH ratio in the cell7,8. NAD+ is non-fluorescent and hence cannot be detected using fluorescence techniques. It has been shown that ratio of NAD+/NADH ratio, also known as metabolic index, is related to the free-to-protein-bound NADH ratio9. Changes in metabolism results in changes in NAD+/NADH ratios which can be related to the free to protein bound NADH ratio10,11. In reference 10 we reported the definition of metabolic index determined using only lifetime values at a single emission wavelength. In reference 11 we show that the concept of metabolic index can be applied to entire cells, although cells have different compartments. A shift towards the higher free NADH is indicative of a more glycolytic metabolism and a reverse shift is indicative of more oxidative phosphorylation12. These changes have been shown to be important for cancer cells, where normal metabolism can be replaced by the Warburg effect13–15. Free and protein bound NADH have been used often to non-invasively predict or determine the changes in cellular metabolism2. The metabolic index ratios have multiple definitions and often uses some variants of NADH and FAD autofluorescence resulting from two photon excitation fluorescence when the laser is tuned to around a 710–780 nm window16–18. NADH and FAD can be spectrally separated and are often used for this ratio17. Fluorescence intensity based measurements in a complex system are dependent on the quantum yields of the contributing species and are often dependent on the instrumentation. To alleviate these dependencies, fluorescence lifetimes are often employed as the method of choice19. The fluorescence lifetime is independent of the concentration and instrumental parameters including laser power and spectral window of observation. However the fractional contribution of species with different lifetime affects the measured fluorescence decay. Using the phasor approach, the phasor position of a pixel containing different amounts of free and bound NADH falls in the line joining the phasor of the free and bound NADH indicating that in those pixels there is a linear combination of two species with the lifetimes of the free and bound NADH (Figure 1). Hence, considering the ubiquitous presence of NADH and FAD autofluorescence, Fluorescence Lifetime Imaging Microscopy (FLIM) has become one of the most used non-invasive label-free techniques to study cellular metabolism9,19,20. The unique spatial and temporal resolution of the FLIM approach enables us to study cellular metabolism in great detail and to correlate metabolism changes with different parts of the cell with pixel resolution19.
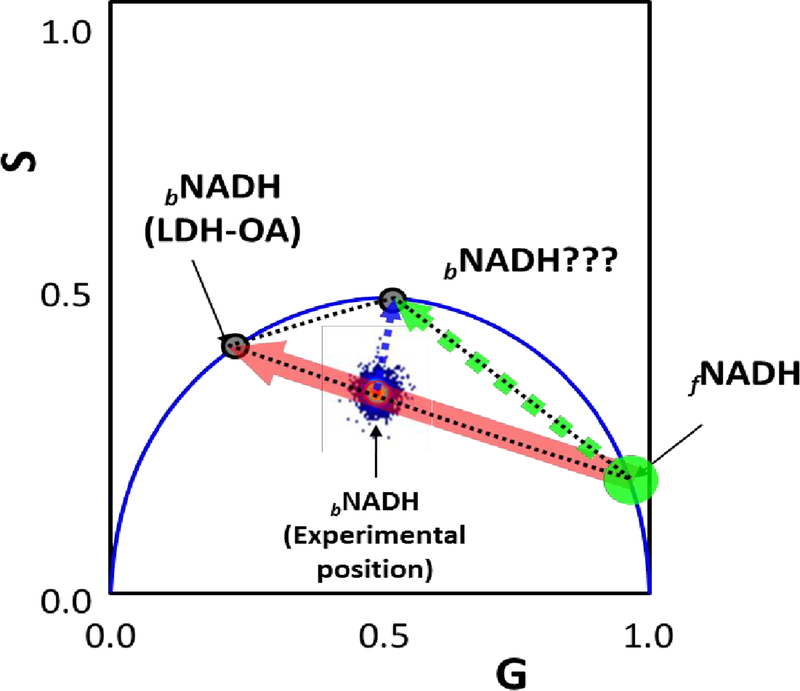
Figure 1: Phasor plot for the NADH lifetimes reported in the literature.
Free-NADH is positioned at the universal circle with a short lifetime around 0.4 ns, on the other hand, bound-NADH has reported different lifetimes. Two values are shown in the figure: 1.7 marked by question marks and 3.4. If the lifetime of 1.7ns should be be correct, then the position of the phasor for pixels in a cell should be inside the triangle represented by the black dashed lines. For the full bound-NADH (equilibrium displaced toward to the enzyme-ligand complex shown with the mark LDH-OA in the figure) the position for the phasor distribution should be at the universal circle, considering that should be single exponential. This fact is true for the bound-NADH when the enzyme is incubated with oxalic acid (black circle, bNADH/LDH-OA), but is not the case for all other lifetimes reported. The experimental position for the ‘others’ bNADH fall on the line that joins the free and bNADH (3.4 ns) marked as (experimental position in the figure); this is also true for the experimental data on cell (see Figure 4A). The metabolic trajectory obtained in the cell acquired by our lab is represented as a red arrow. On the other hand, the expected ‘metabolic trajectory’ by the linear combination between free-NADH and the short lifetime bound-NADH should be represented by the dashed green arrow in figure 1. It is interesting to point out that there is no literature (as far as we know) reporting cells with a linear combination between that region in the phasor plot. Instead, most of the values when resolved for 2 components are along the red arrow.
In this paragraph we report the large range of the values found in the literature for bound NADH and we discuss possible explanations for this very large range and the effect of using incorrect values for the determination of the metabolic index. The basis of these differences in cellular metabolism measurements assumes that the ratio of NAD+/NADH can be correlated to free and bound NADH and these two NADH species have very different lifetimes10,21. The similarity of the spectra of free and bound NADH makes it difficult to distinguish them22–24. Free NADH in solution has a lifetime which is the sum of several components with an average value of about 0.37 ns21,24. Although the free NADH shows a multiexponential decay, the line between bound and free moves very little when the value of 0.37ns or 0.40 ns is used in the phasor representation of the multiexponential decay of the free NADH decay. The lifetime of the bound NADH is dependent on the enzyme to which it is bound and on the presence of allosteric molecules. Reported values of the fluorescence lifetime of bound NADH are found in a very wide range, from 1 ns to 9 ns19,24–26. This change in lifetime is in part attributed to the interactions of NADH upon binding. In the free form the nicotinamide and adenine rings of NADH are adjacent and interacting and the π-π interaction self-quenches the fluorescence resulting in a short lifetime24,27. Binding to proteins causes the NADH structure to extend, disrupting the π-π interaction and increasing the fluorescence lifetime. These different structures27 have been shown by crystallographic structures of NADH bound to LDH28 and MDH29. Commonly for cellular imaging and for the purpose of illustration, lifetimes of NADH bound to lactate dehydrogenase (LDH) or malate dehydrogenases (MDH) have been used as the reference for the bound NADH lifetime19,26. However, discrepancies exist in between lifetime values measured for LDH and MDH. Often the way the lifetime of bound NADH is measured is not from separated solution systems, but from bi-exponential or multi-exponential fits of the fluorescence decays in the NADH channel and then assigning the long lifetime to bound NADH. Measurements of the lifetime of NADH bound to proteins are reported as follows: 2.0 ns (MDH)30, 9.0 ns (mMDH, mitochondrial MDH)26, 1.6 ns (LDH) and 2.5 ns (MDH)31, 4.0 ns (LDH)32, 1.5 ns with LDH and 6.53 ns (LDH and oxalic acid)24. One problem with using the values obtained by resolving multiexponential decays is the high signal-to-noise ratio needed for multiexponential analysis but also from the instrument used which need to have a relatively large time range. For example, the lifetimes of NADH in intact and pulverized mitochondria were measured and the long lifetime assigned to the bound NADH were 5.7 ± 0.5 ns (intact), and 4.1 ± 0.7 ns (pulverized)33. The rest of the bound NADH measurements involved measuring NADH lifetimes in cells, without accounting for specific binding to a protein and using the long lifetime of the multi-exponential fit as bound NADH lifetime. This approach includes: 2.03 ns13, 2.0 – 2.5 ns34, 1.5 ns (NADH) and 4.4 ns (bound NADPH)35, 3.65 ns (bound NADH from porcine eyes)36, 2.3 ± 0.5 ns37, 2.2 – 4.0 ns38, 3.4, 3.3 and 2.4 ns for bound NADH31, 2.0 – 5.0 ns associated with different parts of the cell39, and finally 1.99 – 1.57 ns13.
Using the fit-free phasor approach, a lifetime of 3.4 ns was determined for the NADH bound to LDH in the presence of 100 mM of oxalic acid. The phasor cloud was positioned in the universal semicircle revealing the single exponential character of this species19,40. However, previous phasor measurements have shown the position of bound NADH to be inside the universal semicircle with a phase lifetime (τP) of ~2.0 ns12. This apparent discrepancy can be attributed to a misnomer and in place of using ‘bound’, the term ‘higher fraction of bound’ should have been used since in these sample a mixture of free and bound NADH was present.
Recent work from Evans’ lab also shows the bound NADH lifetime to be ~ 3.3 to 4.3 ns using the phasor approach. Fitting of the original TCSPC decays used for this phasor analysis results in calculated NADH lifetimes of 2.64 ns and 3.85 ns, respectively41. Multi-exponential fits of NADH lifetime includes four exponentials42, where ~2 and ~ 6 ns were calculated as the long lifetime species. The difference in reported values of bound NADH can be observed from three separate values reported for NADH bound to mitochondrial MDH, 2.0 ns, 2.5 ns and 9.0 ns. One of the main differences between these measurements is the preparation and purification of the mMDH enzyme. Purification and differential activity of the enzyme affects the binding affinity as commonly observed in biochemistry19,26,43.
Explanation of the large differences between the NADH lifetimes and consequently its position on the phasor plot are the rationale behind this work since these differences have consequences in the evaluation of the metabolic index. Our approach was to measure the lifetime of NADH fully bound to LDH and to prove that the law of phasor addition holds for cellular imaging based on the positions of the free and LDH bound NADH phasors. Another aim of this work is to understand the effect of different data acquisitions setups and the consequences of proper and improper phasor transformations in determining the cellular metabolic index. To achieve these goals we paid special attention to the preparation of the LDH enzyme used for the calibration of the bound NADH phasor. It has been shown that KD of NADH binding to LDH decreases when oxalic acid is present as an allosteric molecule21. Oxalic acid results in a change in the NADH KD from 1.7 μM to 0.2 μM, shifting the equilibrium towards fully bound NADH. The presence of oxalic acid or oxamate does not change either the binding pocket of NADH or the structure of NADH when bound to LDH24,28. The sample with NADH+LDH and oxalic acid has 100% bound NADH and this sample is used to find the phasor position and lifetime of LDH bound NADH presented in this work. We hope that with the sample preparation and proper calibration protocols to determine the metabolic index, the results reported from different labs can be better understood and compared. We also note that what is measured with the protocols outlined in this works is the ratio of free and bound NADH in every pixel of an image. While this ratio is very useful, it could differ from other combination of parameters that have been previously described in the literature16.
MATERIALS AND METHODS
Preparation of Lactate Dehydrogenase enzyme:
To create the LDH bound NADH samples, an ammonium sulfate suspension of L-Lactic Dehydrogenase (LDH) from rabbit muscle (L2500, Millipore Sigma, St. Louis, MO, USA) was cleaned using a Vivaspin 20 Centrifugal Concentrator (Millipore Sigma, St. Louis, MO, USA). A 200 μM Tris-HCl buffer (pH 7.5), supplemented with 100 mM oxalic acid (75688, Millipore Sigma, St. Louis, MO, USA) was used for the cleaning the protein and as an exchange buffer. The Vivaspin 20 was used to change the buffer for 10 times. Following the concentration protocol, the supernatant from the Vivaspin 20 centrifugal tube was centrifuged at 9500 xg for 20 minutes to remove any precipitation. The concentration of the LDH was determined by the absorbance at 280 nm using a Perkin-Elmer Lambda 40 spectrophotometer and an extinction coefficient of 205000 M−1.cm−1 44. The final concentration of LDH was 220 μM, and the enzyme was always handled on ice or stored at 4°C for immediate use - no longer than 1 week. The β-Nicotinamide adenine dinucleotide (NADH, 10107735001 ROCHE, Millipore Sigma, St. Louis, MO, USA) was prepared fresh every day(~ 250 μM) using the same buffer as that used for LDH. The absolute concentration of the NADH was measured using an extinction coefficient 6200 M−1.cm−1 at 340 nm44. To calculate the amount of NADH and LDH needed to reach a percentage of enzyme/ligand complex (EL), we followed the thermodynamic reversible equilibrium rules45. We used a dissociation constant (KD) equal to 0.2 μM44 in 100 mM of the oxalic acid.
The calculation of the NADH fractions involved the following logic considering the equilibrium
| (1) |
Where, E, L and EL represent: the free LDH, free NADH and the LDH-NADH complex at the equilibrium, respectively.
The dissociation can be represented as:
| (2) |
Using the initial concentration of the E0 (E0 = E-EL) and L0 (L0 = L-EL), and reorganizing the terms in the KD expression, concentration of the complex EL can be calculated from the following equation:
| (3) |
The percentage of EL form is defined as:
| (4) |
Fluorescence lifetime imaging:
Samples were measured using a modified Zeiss Axiovert S100TV (Zeiss, Thornwood, NY) microscope equipped with a Spectra-Physics MaiTai HP laser (Spectra-Physics, Santa Clara, CA) for excitation and a photomultiplier tube (H7422P-40, Hamamatsu, Bridgewater, NJ) for detector. The samples were excited with the 740 nm laser line using a 40X water immersion objective (1.2 NA, Zeiss, Thornwood, NY) by two photon excitation. We note that the free form of NADH rotates fast so that the decay of the anisotropy could contribute to the lifetime of the free species. The calibration of the lifetime of the free species was done using the same setup used for the measurements in cells.
The fluorescence was passed through a filter (350 nm – 700 nm, BG39, Edmund Optics, Barrington, NJ) and collected using the photomultiplier tube (H7422P-40, Hamamatsu, Bridgewater, NJ), and recorded using two different time-resolved methods, FLIMbox (ISS , Champaign, IL) and SPC-830 (Becker & Hickl GmbH, Berlin, Germany) for the pure NADH sample. An additional bandpass filter 460/40 nm was used for the cell measurements.
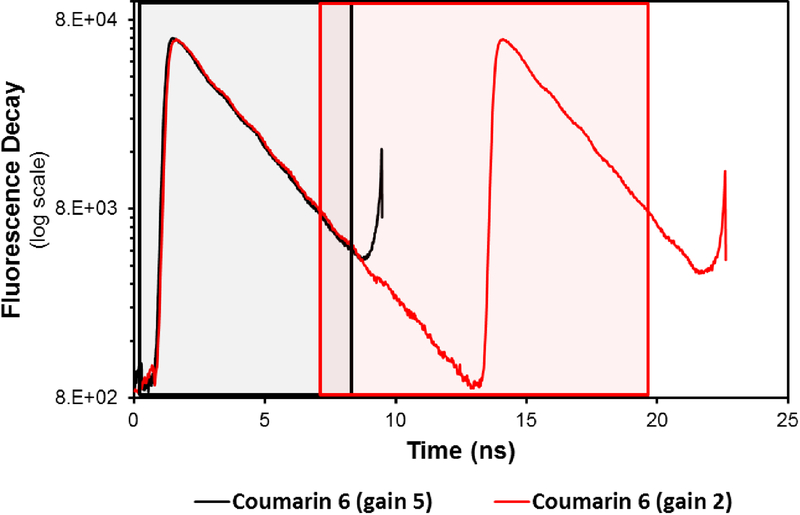
The pixel dwell time for the acquisitions was 32 μs and the images were taken with sizes of 256×256 pixels. To have a high signal to noise ratio, 30 – 50 frames were collected. To make a comparison between the FLIMbox and SPC-830 cards, the same numbers of maximum counts were recorded using each acquisition mode. The data collected using the FLIMbox is directly transformed to a phasor plot following the frequency domain approach. The data acquisition was controlled by SimFCS software (Globals Software·G-SOFT LLC., Irvine UCI-CA, USA). When using theSPC-830 B&H card the data acquisition was controlled by SPCM software (version 9.79, Becker & Hickl GmbH, Berlin, Germany). The intensity decays were analyzed using Globals for Spectroscopy software (https://www.lfd.uci.edu/globals/). The special feature of the Globals software is that the TCSPC analysis is carried over a periodic lamp, and the rise part of the fluorescence decay does not have to be at the start, and deconvolution can be applied if IRF is measured with the same procedure (or either calibration sample). Globals software can also employ global fitting procedures where the time decay parameter between multiple sets of data can be shared while calculating their relative amplitude. The decays were also analyzed with SPCM software. In this software, in absence of global fitting procedures, each individual decays were fitted with open sets of bi-exponential decays. Data acquisition using B&H SPC830 card provides the histogram of the TCSPC approach and here the data for TCSPC acquisition followed by phasor transformation was collected using two different set of parameters. The B&H card acquisitions use a company recommended gain of 5 when using high repetition lasers such as the Ti:Sa laser usually used for 2-photon excitation to increase the time resolution by increasing the time bins during the TAC time of 50 ns. This range equates to an acquisition window of 10 ns. A part of this time window was not used. The data acquisition was only recorded for an interval of this time range (black box, Figure 2). The recorded decay inside this window does not cover the period of the laser repetition and the recorded decay is incomplete, especially for long lifetimes, and thus transformation to the phasor plot should be done taking into account this effective reduced time window. The transformation of the signal acquired with gain 5 results in a repeating window of ~7 ns (black box, Figure 2) which is insufficient for the accurate determination of the lifetimes for the NADH experiments.
Figure 2. Collection of fluorescence lifetime decays by the SPC-830 B&H card.
Fluorescence lifetime decay of Coumarin 6 collected for different time windows using SPC-830 B&H card with the gains of 5 and 2 (Black and red lines). The boxes represent the range used for the phasor transformation for the corresponding B&H data collected in the time-domain.
However, our recommendation is to use a gain of 2 to recover the full decay46. A gain of 2 changes the total acquisition window to 25 ns and a 12.5 ns window (red box Figure 2)containing the full decay is in the middle of the 25 ns window can be selected for the phasor transformation. Figure 2 shows this acquisition scheme and one notes that the 12.5 ns window (red square) results in a periodic signal and thus adequate for the phasor transformation. The images in this scheme take longer to acquire as the total window of acquisition in this setting is 25 ns. But using this approach a complete period of the laser repetition frequency can be collected and a full decay can be acquired. In the vendor recommended gain of 5, the acquisition window is limited to 10 ns and the decay is often incomplete, especially for longer than 2 ns lifetimes, and the signal is non-periodic (Figure 2). This is a known problems with high repetition lasers like the TI:Sa laser used for autofluorescence of tissue. I pulse picker could be used to reduce the effective repletion rate of the laser, but at the expenses of extra cost. Instead using a different window or different acquisition and the phasor approach could avoid this effect,
Conversion to Phasors:
The X and Y phasor coordinates, gi,j(ω) and si,j(ω), are calculated from the intensity decays I(t) collected at each pixel of the image using the TCSPC approach and involve the following transformations:
| (5) |
| (6) |
where, n and ω represent the harmonic number and the angular light modulation frequency of excitation, respectively. Each point of an image gets transformed to a point in the phasor plot and the phasor plot contains lifetime decay information from every pixel of an image.
The transformation of the lifetime information following a frequency domain measurement to the phasor plot uses the relations,
| (7) |
| (8) |
where, mi,j and ϕi,j are the modulation and phase at the pixel i, j, respectively. The distribution of phasor points originating from FLIM measurements appear on (for the mono-exponential decays) or inside (for sum of exponential decays) the universal semicircle. Longer phase lifetimes are signified by increasing phase angles of the phasor plot.
One of the properties of phasor representation that the law of vector addition holds for phasor space and the law of linear addition dictates that if the fluorescence decay from a pixel has contributions from two different individual decays then the phasor position originating from this point lies on the line joining the phasor positions of the two independent decays. The distance from the original phasor position of the components to the new position from that pixel is inversely proportional to the fractional intensity contribution of that component. This fact can be shown from the following mathematical deduction:
A two-component system having contributions from two separate mono-exponential decays is represented by,
| (9) |
The calculated phasor positions by integrating this sum of exponentials from 0 to infinity are,
| (10) |
| (11) |
These equations can be simplified using the definition of the fractional intensity of each of the original components where fractional intensity is fi = Aiτi/ΣiAiτi
The expression for the coordinates transforms to,
| (12) |
Thus, for phasor coordinates, the exponential components are additive when combined with their relative fractional intensity contribution. This trait is known as the “law of addition of phasors” and is true for multiple decays as given by:
| (13) |
This results in ‘law of phasor addition’, in which the relative contribution of two or more phasor points towards another point in between them are inversely proportional to the distances between the point in the middle and their corresponding phasor points. A three component system results in the new phasor position being inside the triangle formed by the phasor positions of the corresponding individual decays. A detailed description related to phasor transformation and uses can be found in Ranjit et al.47.
RESULTS:
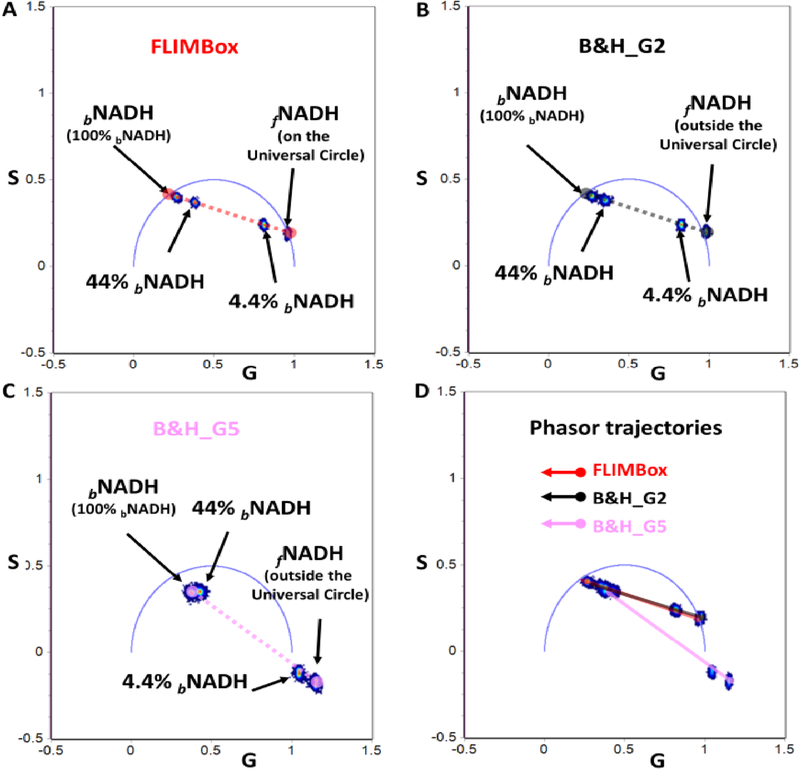
The results from the direct phasor transformations are shown in Figure 3. The transformation from the FLIMBox data, results in free and bound NADH phasor positions on top of the universal semicircle (blue semicircle, Figures 1 and 3) with average phase lifetimes of 0.4 ns and 3.4 ns. Phasor positions of the mixture of 4.4% bound NADH and 44% bound NADH lie on the line joining the phasor positions of free and bound NADH. This result follows the law of phasor addition. The distance from each individual component phasor position to that of the mixture is inversely proportional to the fractional intensity contribution of that component. A point of emphasis here is that this proportionality is dependent on fractional intensity contribution and not fractional species contribution. There is a quantum yield component to the law of phasor addition and brighter species contribute more to the final position of a mixture along the line of linear combination. Thus, the distance between the free and 4.4% LDH bound NADH is similar to that of 44% bound NADH and 100% bound NADH (Figure 3A).
Figure 3. Phasor trajectories for free and LDH bound NADH obtained using FLIMBox (A) or SPC-830 B&H card acquisition (B, C).
A) Phasor positions calculated using the FLIMBox for free and LDH bound NADH in increasing percentage (4.4%, 44% and 100% of bound NADH). The dashed red line illustrates the line joining the phasor positions of free to fully bound NADH, otherwise termed as the metabolic trajectory. The experimental points are along this line. B) Phasor positions for the same samples as that of (A) calculated from fluorescence lifetime decays obtained using B&H card and a gain of 2 (B&H_G2). Again, the experimental points are along the line combination line. C) Conversion of fluorescence intensity decays measured using B&H card with a gain of 5. The dotted black line (B) and dotted purple line (C) connect the phasor positions from free and fully bound NADH in each corresponding measurements. The experiment points are along a line, but the line shorter lifetime extreme is outside the universal circle and the fraction fo bound is also incorrect. D) The overlap of phasor trajectories obtained with the FLIMBox (red line) and B&H card (black line) with a gain of 5. The trajectories calculated for B&H card gain 2 (purple) is completely different and along the expected line of linear combination.
A similar result is observed in the phasor transformation of the data acquired with a gain of 2 using the SPC-830 B&H card. The phasor positions of free and LDH bound NADH are similar to that predicted for the mono-exponential 0.4 ns and 3.4 ns lifetimes on top of the universal semicircle (Figure 3A). The lower fractions of bound NADH have positions along the line joining these two points (gray line in Figure3B). The transformation of data acquired with a gain of 2 is proper as the data is periodic and the decay is complete. The data acquired with a gain of 5 using the SPC-830 B&H card is non-periodic and the decay is not complete. Thus, transformation of these data to a phasor plot is improper and results in calculation of incorrect phasor positions. As a consequence, free NADH and 4.4% LDH bound NADH are positioned outside the universal semicircle; 100% and 44% LDH bound NADH are also inside the universal semi-circle but not in the proper positions. Furthermore, 44% bound NADH does not appear in the same line joining the free and bound NADH (purple line Figure 3C). Instead the overlap of all trajectories in Figure 3D shows that the SPC-830 B&H card data with a gain of 2 and the FLIMBox are virtually identical and the two trajectories overlap with each other. The data for a gain of 5 is completely different and misleading. Since the position of the free and bound NADH phasor has consequences in the evaluation of the metabolic index based on the fraction of free and bound NADH we recommend using the specific protocol of data acquisition and calibration outlined in this section.
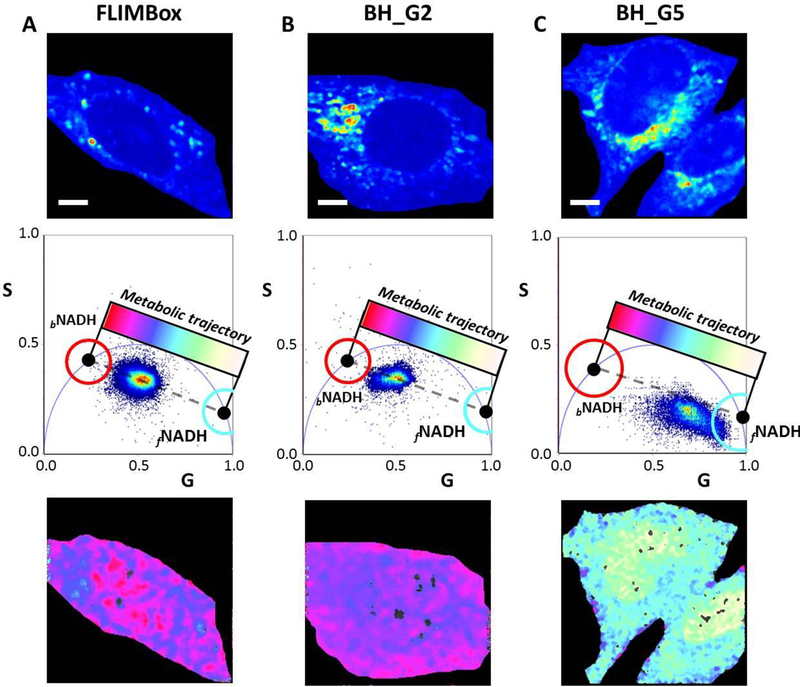
Phasor plots were obtained when the data were collected for autofluorescence in MEF cells. The cells were excited by 2-photon excitation with a 740 nm laser output and the fluorescence was collected using an observation window of 460/40 nm. FLIMBox acquisition and B&H acquisition with a gain of 2 have NADH autofluorescence where the phasor positions are along the metabolic trajectory, defined as the line connecting the phasor positions of free and fully bound NADH (to LDH for these calibration experiments). This trajectory is different for the B&H card with a gain of 5 as explained earlier and the cell phasor positions are also not on the correct line (Figure 4 column C). These plots show that a proper transformation is required for understanding cellular autofluorescence and to correlate the measurements with metabolism using the phasor plot. Another point of emphasis is the changing scale of the phasor plot. A small change in lifetime is reflected in a large change in phasor position around s=0, g=1. As the universal semi-circle comes closer to the origin (0, 0), a much larger change in the lifetime is reflected in a much smaller change in the phasor point position. This difference is due to the tangential nature of the phasor plot, where the position on the universal semicircle is proportional to tangent of the phase delay. This consideration results in the fact that a small lifetime change at one end of the metabolic trajectory results in a very large change in the phasor point position (close to s=0, g=1). The other end of phasor plot (s=0, g=0) is much less affected by a similar change in lifetime. Consequently, a change from 3.4 ns to 6.5 ns for bound NADH lifetime does not change the metabolic trajectory significantly. A small change in the lifetime of bound NADH is less significant for phasor analysis, which is advantageous in the absence of a proper lifetime calibration for bound NADH in cells.
Figure 4: Comparison between FLIMBox and SPC-830 B&H card acquisition of cellular autofluorescence in NADH channel.
A) FLIMBox, B) SPC-830 B&H card acquisition with gain of 2 and C) SPC-830 B&H card acquisition with a gain of 5 for cellular autofluorescence in the NADH channel for MEF cells. The top, middle and bottom row in each case show the intensity image, corresponding phasor plot and phasor mapped NADH cell autofluorescence, respectively. Red and cyan cursors are used to select the phasor positions of free and bound NADH (fNADH and bNADH), respectively. The dashed line indicates the linear trajectory between the free and bound NADH). The scale bars represent 5 μm. When the SPC-830 B&H is used with a gain of 5, the experimental phasors are not along the line of linear combination. If the metabolic index is calculated for this data set, it has an incorrect value as shown in column C. For this graph the values of bound (3.4ns) and free (0.4) ns for NADH are used, but the conversion to phasor is incorrect so that the phasors points are not in the line of linear combination. In this case, the cell shown in column C) will be misclassified.
In regard to the data on cellular systems (Figure 4), we don’t expect that at the pixel level each pixel will be exactly aligned along a straight line as shown for the solution values of figure 3. At the pixel level, the cloud of possible values of the s and g coordinates is distributed on a 2D Gaussian whose variance depends on the number of photons collected from a pixel, in addition of some biological variations from pixel to pixel that could modify the fluorescence lifetime. Finally, in a given pixel there should be enough free and bound NADH molecules to provide a representative average at that pixel. In our experience with this type of measurements, we always have distribution roughly along the average line between the free and bound ends on the universal semicircle.
As figure 4 (column C) shows, the representation in the phasor plot of data that were not acquired using the protocol indicated in this article will provide a wrong interpretation of the metabolism of cells. For example using a gain of 5 for the SPC-830 B&H card gives points outside the line of linear combination and using the color scale commonly used to color the metabolic state of cells gives a miss-classification of a specific cell (color white-green vs color pink-blue).
Results from fitting the experimental decay with bi-exponentials are shown in Table 1. The purpose of this table is that only with a gain of 2 we can obtain the correct values of the fractional intensities and the lifetimes. The data from a gain of 2 and a gain of 5 for the SPC-830 B&H card acquisitions were fitted with Globals Software for Spectroscopy (G-SOFT LLC) and SPCM 9.79 (Becker & Hickl GmbH) as mentioned earlier.
Table 1:
Global fitting of the SPC-830 B&H data (gain of 2 and 5) with deconvolution of the IRF using Globals for Spectroscopy (Globals Software G-SOFT Inc.) and SPCM 9.79 (Becker&Hickl GmbH).
| Software | Gain | PL% | τ1 ns | A1 | τ2 ns | A2 | χ2 |
|---|---|---|---|---|---|---|---|
| Globals | 2 | 0 | 3.58 | 0 | 0.35 | 9.60 | 2.96 |
| 4.4 | 3.58 | 0.20 | 0.35 | 8.49 | 4.75 | ||
| 44 | 3.58 | 1.64 | 0.35 | 3.00 | 14.35 | ||
| 100 | 3.58 | 2.20 | 0.35 | 1.64 | 13.29 | ||
| 5 | 0 | 3.11 | 0.01 | 0.35 | 16.94 | 2.47 | |
| 4.4 | 3.11 | 0.37 | 0.35 | 15.22 | 5.61 | ||
| 44 | 3.11 | 3.20 | 0.35 | 5.41 | 8.48 | ||
| 100 | 3.11 | 4.43 | 0.35 | 2.50 | 9.90 | ||
| SPCM | 2 | 0 | 0.79 | 13.1 | 0.46 | 86.9 | 3.21 |
| 4.4 | 2.42 | 6.1 | 0.50 | 93.9 | 1.39 | ||
| 44 | 3.97 | 59.1 | 1.87 | 40.9 | 1.23 | ||
| 100 | 3.51 | 67.6 | 2.17 | 32.4 | 1.07 | ||
| 5 | 0 | 0.82 | 13.5 | 0.42 | 86.6 | 2.97 | |
| 4.4 | 2.03 | 7.1 | 0.48 | 92.9 | 1.27 | ||
| 44 | 3.22 | 74.3 | 0.62 | 25.7 | 1.32 | ||
| 100 | 3.79 | 67.2 | 1.42 | 32.8 | 1.18 |
PL % = percentage of Protein-Ligand, τ1 and τ2 = Lifetime components in ns, A1 and A1 = Amplitude percentage, χ2 = Chi square (goodness of fit).
Globals fitting involves global analysis, where the lifetimes are open to change but are shared between the four sets of decays, only the amplitudes are free to vary and the decays are deconvoluted with a proper instrument response function (IRF) calculated as the difference between a calibration solution of coumarin 6 and a theoretical decay for the described lifetime (2.5 ns in ethanol). Global analysis requires best set of fits in between the samples and thus (χ2) values are generally higher, obtained by a global minimization. In comparison, SPCM uses individual fits and the IRF used for deconvolution is theoretical, obtained by fitting half of the peak with a combination of the IRF and lifetime decay, and the lifetimes cannot be shared in between. In this case, the calculated lifetime components are different for every intensity decay and the (χ2) values for individual fits are generally lower as there is no global minimization.
During the fitting procedure we applied two different methods: i) a global fit using all the NADH/LDH fractions and linking the lifetime across the four set of data; or ii) a single function fit using an IRF estimation as explained in Table 1. Global fitting determines the parameters that can represent the entire set of results and in this case free NADH and bound NADH lifetimes can be the shared parameters and from this type of fitting the pre-exponential factors that describes the molecular fractions of these two species can be determined. Another important point in the analysis of these decays is the fitting of the total time period of acquisitions, which has to be long enough for the intensity to decay to zero. This condition is possible when we use a gain of 2 as the decay time is longer than 20 ns. Using ‘Globals for Spectroscopy’ it is possible to setup a periodic lamp signal (IRF) that allows us to analyze the data as a recurrent pulse with a complete period. In comparison, SPCM software does not allow analysis of the data acquired after the second IRF and only a shortened window of ~8 ns after first IRF can be fitted, even though the total acquisition window is 25 ns long for a gain of 2. Table 2 shows the results of using the linear combination of components as obtained with the phasor approach. It is only when the phasor transformation is done properly that the results are in good agreement regardless of the technique used to measure the decay..
Table 2:
Fraction of free and bound NADH calculated by the phasor position in the phasor plot.
| Card | PL% | Free% | Amplitude% (Fitting) | Fraction phasor |
|---|---|---|---|---|
| B&H card G2 (Globals) | 4.4 | 95.6 | 8.49/(0.20+8.49)=0.98 | 0.80 |
| 44 | 56 | 1.64/(1.64+3.00)=0.67 | 0.18 | |
| 100 | 0 | 2.20/(2.20+1.64)= 0.43 | 0.05 | |
| B&H card G2 (SPCM) | 4.4 | 95.6 | 6.1/(6.1+93.9)= 0.94 | 0.80 |
| 44 | 56 | 59.1/(59.1+40.9)= 0.41 | 0.17 | |
| FLIMBox | 4.4 | 95.6 | 0.79 | |
| 44 | 56 | 0.21 | ||
| 100 | 0 | 0.05 |
For each fraction of the protein bound and free NADH reported in columns 2 and 3 we compare the amplitude of the 2 components as obtained by the fitting procedure using a gain of 2 for the SPCM and the values of fractional intensities as obtained with the FLIMbox method. Fliting using the Globals analysis method or the SPCM software give very similar result when compared with the FLIMbox data if the data are acquired with a gain of 2 in the setting of the B&H 830 card.
DISCUSSION
Our results indicate that there are two main problems in the literature associated with the calculation of metabolic trajectories using the NADH fluorescence lifetimes and the phasor approach. These problems are related to preparation of the bound NADH samples used for calibration and acquisition of the fluorescence decays and transformation to the phasor plot. These difficulties are explained below as well as the recommended protocol to be followed for the calculation of the metabolic index which will avoid both problems.
i). Difficulty associated with sample preparation and types of samples.
Sample preparation is one of the key aspects underlying the heterogeneity of the fluorescence lifetimes reported for bound NADH. In the past, enzymes were typically purified from tissue, but nowadays there are commercially available as lyophilized powders or in solutions containing anti-chaotropic salts like ammonium sulphate. Proper cleanup of the commercial enzyme preparation is an important consideration that needs to be addressed and done correctly to avoid miss folding of the enzyme. A second purification based on enzymatic activity (i.e., affinity chromatography) is recommended to obtain the most active version of the enzyme as regards NADH binding26. The addition of oxalic acid results in changes of KD by approximately an order of magnitude, giving a higher percentage of bound NADH fraction than that obtainable with pure LDH. These biochemistry related procedures are often not considered while preparing for enzymatic activity/ binding assays for NADH and can be responsible for the difficulty associated with preparation of completely bound NADH. Conversely, improper purification of the enzyme can produce non-specific binding of NADH in an environment where the NADH structure does not change and results in a change in fluorescent properties.
ii). Complications associated with improper instrument acquisition parameters.
The TCSPC card configuration and repeat frequency of the laser are relevant to the final decay that is recorded46. The commercial Ti-Sa laser is often used in biological measurements of NADH fluorescence and has a laser repetition frequency of 80 MHz and a corresponding period of 12.5 ns. Often the manufacturer recommended setting which results in a 10 ns window. The use of short windows in the TCSPC acquisition compromises the ability to measure long lifetime. In a mixture of short and long lifetimes, if the sum of exponentials does not decay to zero, then fitting that decay to a two component system will result in a smaller value of the long component. Thus the data often measured with a 10 ns repeat window and fitted to an even shorter range ends up severely underestimating the long lifetime component, e.g., the bound form of NADH in a mixture. During the phasor transformation associated with a short acquisition which is also non-periodic, the transformation is inaccurate and the positions of the converted phasor clouds are in the wrong positions. In comparison, a 25 ns TCSPC acquisition results in two partial intensity decays, where a repeating periodic pattern can be selected and properly transformed into phasor plot. This phasor clouds acquired from the proper transformation of a periodic function of the TCSPC acquisition of a gain of 2 are equivalent of that obtained from FLIMBox acquisition and proper analysis of TCSPCS/ phasor data results in a bound NADH (LDH) lifetime of ~3.4 ns. The results show that the global analysis using the ‘Globals software’ enables a proper deconvolution and the fitting results in shared lifetimes 0.35 ns for free and 3.5 ns for LDH bound NADH in presence of oxalic acid. These values are similar to the values mentioned in earlier manuscripts19 and are similar to the values measured in cellular systems9. On the contrary, the fitting by SPCM, which uses a Gaussian function for deconvolution, does not employ a global fitting algorithm and results in exponential components which are non-conforming, different for each data set, and do not match the lifetime of the individual components. Furthermore, the recommended gain of 5 with a TAC time of 50 ns results in an observation window of 10 ns and part of this time window contains the rise time and dead time. This situation results in the intensity decay not decaying completely and fitting a non-complete decay with sum of exponentials results in incorrect lifetime components. Proper conversion to phasor approach can only be achieved for a repeating signal and at a gain of 2. At gain 5 the decay is not complete and is non-periodic. This data cannot be properly converted to a phasor as shown in figure 3. In the absence of proper acquisition, phasor conversion becomes erroneous.
Values of the bound and free NADH lifetime in the phasor plot:
Finally, we want to discuss an important point related to the reported positions in the phasor plot for bound NADH lifetimes, often reported in the range between 1 to 2 ns. If these components were fully bound NADH, with a mono-exponential lifetime, the position of the cloud is expected to be at the universal semi-circle and not in a point inside, as positions inside are related to multi-exponentials and sum of exponentials (Figure 1). A phasor location between the positions of the free and bound NADH (3.4 ns) on the semicircle represents a mixture of the two components. The linear displacement along this line can only be obtained by changing the fraction of free and bound NADH (see Figure 4). In the case of three species, with mono-exponential decay times, the expected cloud should fall inside a triangle between the three components. This observation should be made if there were two different bound NADH lifetimes (1.7 and 3.4 ns) as some of the fitting procedures suggests19,25. However, this situation never takes place, neither in cells nor for in vitro experiments. The vector rule of phasor addition shows that the free and bound NADH species commonly observed can be explained by the linearity between the phasor positions of mono-exponential lifetime decays of 0.4 to 3.4 ns. In summary, we can conclude that to measure the metabolic index using FLIM data, proper sample preparation and instrument configuration is of outmost importance. Even when NADH lifetimes are used as simple fingerprints for tissues studies, the interpretation of the results can be erroneous if care is not taken.
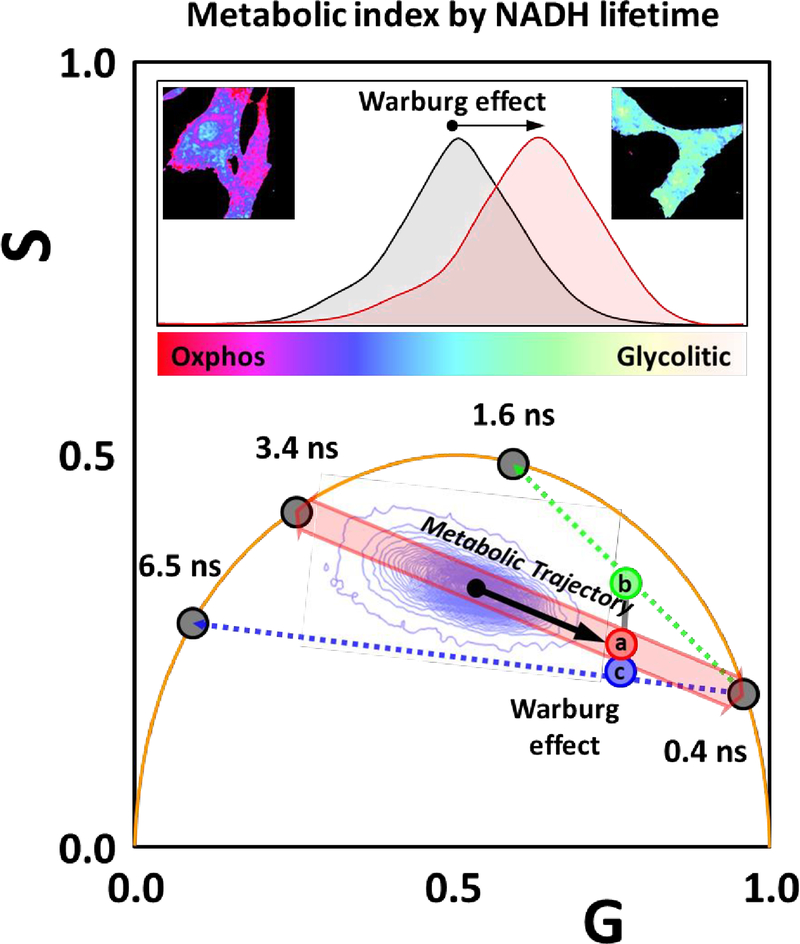
As an example, figure 5 illustrates the changes in the phasor position due to Warburg effect on metabolism depending on the lifetime that is assumed for the Bound NADH species. This effect shifts the metabolic index towards more free NADH when a longer (than 3.4 ns) lifetime is assumed and towards the more bound NADH if a shorter (than 3.4 ns) is assigned to the bound NADH species. As consequence of the wrong assignment of the lifetime of the bound spices, cells could be assigned to have undergone a change in metabolism toward more oxphos or more glycolytic. Determination of bound NADH lifetime is of a great interest as this gives the phasor position and the direction of the metabolic trajectory. In terms of fitting bi-exponentials, having a wrong lifetime assigned to the bound NADH species, will change the pre-exponential factors, giving wrong interpretation of the ratio of pre-exponential factors which is related to molar fractions. This is specifically true for global fitting algorithms, where the lifetimes are shared between decays. A second important point is that in our observations we have seen the metabolic trajectory along the axis (a) of Figure 5. Warburg effect changes the phasor coordinates along this trajectory. Assumption of other lifetimes for the bound NADH species modifies the trajectory to b or c in Figure 5. This indicates 3.4 ns as a good assumption for the bound NADH lifetime in cellular environment.
Figure 5.
Illustration of the error introduced in the calculation of the metabolic index by NADH FLIM if the lifetime of bound NADH is incorrectly assumed. In this example the metabolic index of cells in a cancer tissue changes toward the glycolytic direction due to the Warburg effect. Along the metabolic trajectory from 3.4ns to 0.4ns the cancer cells are colored and a fraction of free NADH of 0.8 is found. This fraction is intensity weighted. However if the same cells are analyzed using different values for the bound NADH species the position along the metabolic trajectory will move to a fraction of 0.6 for the case of 1.6ns and to 0.83 for the case of 6.5 ns. Cell displaying the Warburg effect will move from (b) to (c) given an erroneous value of the fraction of the bound NADH and the cancer cells could be improperly classified as “normal” for the case of 1.6ns. The point c shows how cancer cell affected by the Warburg effect will be at a different point in the phasor plot, in the case of using 6.5 ns for bound NADH.
In conclusion, the purpose of our paper is not to determine the value of the lifetime of NADH which was first measured more than 50 years ago in cuvettes, but to show that in FLIM analysis the current protocols used by the majority of researchers produce a wrong value of the metabolic index. This is not appreciated in the field and it originates from the assumed values of the lifetimes of free and bound NADH which are used for determining the metabolic index in cellular systems and tissues. The purpose of this work is to reveal the origin of the artifact in the FLIM measurements and to propose a simple protocol for fixing the problem. So even if the method is known and the lifetime of NADH is known, people publish papers which are based on wrong instrument setup and preparation artifacts. They find different values of the lifetime of NADH in biological systems and they attribute these differences to biological effects without realizing that what they report could be an artifact. This is a really difficult issue to reveal. Our purpose is clearly stated in the manuscript but its relevance in the field is missing. Although we show in a previous paper how to correct for the FLIM artifact in general46, it was not discussed in the field of tissue autofluorescence the consequence of this artifact for the correct determination of the metabolic index. We want to reiterate that there is nothing wrong with the FLIM approach or the instruments used, but each system must be properly setup and calibrated to obtain the correct value of the metabolic index.
ACKNOWLEDGMENTS
This work was supported in part by grants NIH P41-GM103540 and NIH P50-GM076516. LM is in part supported by the Universidad de la República-Uruguay as a full time professor. We are indebted to Prof. David Jameson for helping with the language and for valuable insights.
Footnotes
CONFLICT OF INTEREST
None to declare
Reference
- 1.Mayevsky A & Chance B Oxidation-reduction states of NADH in vivo: From animals to clinical use. Mitochondrion 7, 330–339 (2007). [DOI] [PubMed] [Google Scholar]
- 2.Chance B Mitochondrial NADH redox state, monitoring discovery and deployment in tissue. Methods Enzymol. 385, 361–370 (2004). [DOI] [PubMed] [Google Scholar]
- 3.Chance B, Nioka S, Warren W & Yurtsever G in Oxygen Transport to Tissue XXVI (eds. Okunieff P, Williams J & Chen Y) 231–242 (Springer; US, 2005). doi: 10.1007/0-387-26206-7_31 [DOI] [Google Scholar]
- 4.Kennedy BE et al. NAD+salvage pathway in cancer metabolism and therapy. Pharmacol. Res 114, 274–283 (2016). [DOI] [PubMed] [Google Scholar]
- 5.Yang Y & Sauve AA NAD+metabolism: Bioenergetics, signaling and manipulation for therapy. Biochim. Biophys. Acta - Proteins Proteomics 1864, 1787–1800 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Agerholm M et al. Perturbations of NAD + salvage systems impact mitochondrial function and energy homeostasis in mouse myoblasts and intact skeletal muscle. Am. J. Physiol. Metab 314, E377–E395 (2018). [DOI] [PubMed] [Google Scholar]
- 7.Winkler U & Hirrlinger J Crosstalk of Signaling and Metabolism Mediated by the NAD+/NADH Redox State in Brain Cells. Neurochem. Res 40, 2394–2401 (2015). [DOI] [PubMed] [Google Scholar]
- 8.Köhler S, Winkler U, Sicker M & Hirrlinger J NBCe1 mediates the regulation of the NADH/NAD + redox state in cortical astrocytes by neuronal signals. Glia 1–13 (2018). doi: 10.1002/glia.2350 [DOI] [PubMed] [Google Scholar]
- 9.Aguilar-Arnal L et al. Spatial dynamics of SIRT1 and the subnuclear distribution of NADH species. Proc. Natl. Acad. Sci. U. S. A 113, 12715–12720 (2016).10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Stringari C et al. Phasor approach to fluorescence lifetime microscopy distinguishes different metabolic states of germ cells in a live tissue. Nat Acad Sci Proc 108, 13582–13587 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Wright BK et al. NADH distribution in live progenitor stem cells by phasor-fluorescence lifetime image microscopy. Biophys. J 103, L7–9 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Stringari C, Nourse JL, Flanagan LA & Gratton E Phasor Fluorescence Lifetime Microscopy of Free and Protein-Bound NADH Reveals Neural Stem Cell Differentiation Potential. PLoS One 7, (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Skala MC et al. In vivo Multiphoton Fluorescence Lifetime Imaging of Protein-bound and Free NADH in Normal and Pre-cancerous Epithelia. J. Biomed. Opt 12, 024014 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Pate KT et al. Wnt signaling directs a metabolic program of glycolysis and angiogenesis in colon cancer. EMBO J. 33, 1454–1473 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Kim SM et al. PTEN deficiency and AMPK activation promote nutrient scavenging and anabolism in prostate cancer cells. Cancer Discov. 8, (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Skala MC et al. In vivo multiphoton microscopy of NADH and FAD redox states, fluorescence lifetimes, and cellular morphology in precancerous epithelia. Proc. Natl. Acad. Sci 104, 19494–19499 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Stringari C et al. Multicolor two-photon imaging of endogenous fluorophores in living tissues by wavelength mixing. Sci. Rep 7, 1–11 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Kolenc OI & Quinn KP Evaluating Cell Metabolism Through Autofluorescence Imaging of NAD(P)H and FAD. Antioxid. Redox Signal 00, ars.2017.7451 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Ma N, Digman MA, Malacrida L & Gratton E Measurements of absolute concentrations of NADH in cells using the phasor FLIM method. Biomed. Opt. Express 7, 2441 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Stringari C, Sierra R, Donovan PJ & Gratton E Label-free separation of human embryonic stem cells and their differentiating progenies by phasor fluorescence lifetime microscopy. J. Biomed. Opt 17, 046012 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Kolb DA & Weber G Quantitative demonstration of the reciprocity of ligand effects in the ternary complex of chicken heart lactate dehydrogenase with nicotinamide adenine dinucleotide oxalate. Biochemistry 10, 4471–6 (1975). [DOI] [PubMed] [Google Scholar]
- 22.Fereidouni F, Bader AN, Colonna A & Gerritsen HC Phasor analysis of multiphoton spectral images distinguishes autofluorescence components of in vivo human skin. J. Biophotonics 7, 589–596 (2014). [DOI] [PubMed] [Google Scholar]
- 23.Piersma SR, Visser AJWG, De Vries S & Duine JA Optical spectroscopy of nicotinoprotein alcohol dehydrogenase from Amycolatopsis methanolica: A comparison with horse liver alcohol dehydrogenase and UDP-galactose epimerase. Biochemistry 37, 3068–3077 (1998). [DOI] [PubMed] [Google Scholar]
- 24.Scott TG, Spencer RD, Leonard NJ & Weber G Emission Properties of NADH. Studies of Fluorescence Lifetimes and Quantum Efficiencies of NADH, AcPyADH, and Simplified Synthetic Models. J. Am. Chem. Soc 7302, 687–695 (1969). [Google Scholar]
- 25.Sharick JT et al. Protein-bound NAD(P)H Lifetime is Sensitive to Multiple Fates of Glucose Carbon. Sci. Rep 8, 1–13 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Jameson DM, Thomas V & Zhou D Time-resolved fluorescence studies on NADH bound to mitochondrial malate dehydrogenase. Biochim. Biophys. Acta 994, 187–190 (1989). [DOI] [PubMed] [Google Scholar]
- 27.Formoso E, Mujika JI, Grabowski SJ & Lopez X Aluminum and its effect in the equilibrium between folded/unfolded conformation of NADH. J. Inorg. Biochem 152, 139–146 (2015). [DOI] [PubMed] [Google Scholar]
- 28.Read JA, Winter VJ, Eszes CM, Sessions RB & Brady RL Structural basis for altered activity of M and H isozyme forms of human lactate dehydrogenase. Proteins Struct. Funct. Bioinforma 43, 175–185 (2001). [DOI] [PubMed] [Google Scholar]
- 29.Hung CH et al. Crystal structures and molecular dynamics simulations of thermophilic malate dehydrogenase reveal critical loop motion for co-substrate binding. PLoS One 8, (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Lakowicz JR, Szmacinski H, Nowaczyk K & Johnson ML Fluorescence lifetime imaging of free and protein-bound NADH. Proc. Natl. Acad. Sci 89, 1271–1275 (1992). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Yu Q & Heikal AA Two-photon autofluorescence dynamics imaging reveals sensitivity of intracellular NADH concentration and conformation to cell physiology at the single-cell level. J. Photochem. Photobiol. B Biol 95, 46–57 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Kierdaszuk B, Malak H, Gryczynski I, Callis P & Lakowicz JR Fluorescence of reduced nicotinamides using one- and two-photon excitation. Biophys. Chem 62, 1–13 (1996). [DOI] [PubMed] [Google Scholar]
- 33.Blinova K et al. Distribution of mitochondrial NADH fluorescence lifetimes: Steady-state kinetics of matrix NADH interactions. Biochemistry 44, 2585–2594 (2005). [DOI] [PubMed] [Google Scholar]
- 34.Schneckenburger H, Wagner M, Weber P, Strauss WSL & Sailer R Autofluorescence lifetime imaging of cultivated cells using a UV picosecond laser diode. J. Fluoresc 14, 649–654 (2004). [DOI] [PubMed] [Google Scholar]
- 35.Blacker TS et al. Separating NADH and NADPH fluorescence in live cells and tissues using FLIM. Nat. Commun 5, 1–9 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Schweitzer D et al. Towards Metabolic Mapping of the Human Retina. Microsc. Res. Tech 70, 410–419 (2007). [DOI] [PubMed] [Google Scholar]
- 37.Niesner R, Peker B, Schlüsche P & Gericke KH Noniterative biexponential fluorescence lifetime imaging in the investigation of cellular metabolism by means of NAD(P)H autofluorescence. ChemPhysChem 5, 1141–1149 (2004). [DOI] [PubMed] [Google Scholar]
- 38.Elson D et al. Time-domain fluorescence lifetime imaging applied to biological tissue. Photochem. Photobiol. Sci 3, 795–801 (2004). [DOI] [PubMed] [Google Scholar]
- 39.Vergen J et al. Metabolic imaging using two-photon excited NADH intensity and fluorescence lifetime imaging. Microsc. Microanal 18, 761–70 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Datta R, Alfonso-García A, Cinco R & Gratton E Fluorescence lifetime imaging of endogenous biomarker of oxidative stress. Sci. Rep 5, 9848 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Evers M et al. Enhanced quantification of metabolic activity for individual adipocytes by label-free FLIM. Sci. Rep 8, 1–14 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Vishwasrao HD, Heikal AA, Kasischke KA & Webb WW Conformational dependence of intracellular NADH on metabolic state revealed by associated fluorescence anisotropy. J. Biol. Chem 280, 25119–25126 (2005). [DOI] [PubMed] [Google Scholar]
- 43.Kiriyama S, Ichihara Y, Enishi A & Yoshida A Effect of purification and cellulose treatment on the hypocholesterolemic activity of crude konjac mannan. J. Nutr 102, 1689–1697 (1972). [DOI] [PubMed] [Google Scholar]
- 44.Scott TG, Spencer RD, Leonard NJ & Weber G Emmision properties of NADH. Studies of flourescence lifetimes and quantum properties of NADH, AcPyADH, and synthetic models. J. Am. Chem. Soc 92, 687–695 (1970). [Google Scholar]
- 45.Jameson DM . & Mocz G in Method in Molecular Biology 305 - Protein-Ligand Interactions (ed. Ulrich Nienhaus G) 301–322 (Humana Press, 2005). doi: 10.1385/1-59259-912-5:301 [DOI] [PubMed] [Google Scholar]
- 46.Ranjit S, Malacrida L & Gratton E Differences between FLIM phasor analyses for data collected with the Becker and Hickl SPC830 card and with the FLIMbox card. Microsc. Res. Tech 1–10 (2018). doi: 10.1002/jemt.23061 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Ranjit S, Malacrida L, Jameson DM & Gratton E Fit-free analysis of fluorescence lifetime imaging data using the phasor approach. Nat. Protoc 1 (2018). doi: 10.1038/s41596-018-0026-5 [DOI] [PubMed] [Google Scholar]