A modality-independent network underlies the retrieval of large-scale spatial environments in the human brain

Summary

As primarily visual creatures, the extent to which body-based cues, such as vestibular, somatosensory, and motoric cues, are necessary for the normal expression of spatial representations remains unclear. Recent breakthroughs in immersive virtual reality technology allowed us to test how body-based cues influence spatial representations of large-scale environments in humans. Specifically, we manipulated the availability of body-based cues during navigation using an omnidirectional treadmill and a head-mounted display, investigating brain differences in levels of activation (i.e., univariate analysis), patterns of activity (i.e., multivariate pattern analysis), and putative network interactions between spatial retrieval tasks using functional magnetic resonance imaging (fMRI). Our behavioral and neuroimaging results support the idea that there is a core, modality-independent network supporting spatial memory retrieval in the human brain. Thus, for well-learned spatial environments, at least in humans, primarily visual input may be sufficient for the expression of complex representations of spatial environments.

eTOC Blurb

Is movement of our body in space required for normal learning during navigation? By comparing navigation in virtual reality under different levels of immersion, Huffman & Ekstrom found that body movements are not necessary and that visual input is sufficient.

Introduction

When we navigate a new environment and remember it later, recalling the head, body turns, and steps we made previously can aid in our recall of where things are located. Such body-based cues, which include vestibular input about head turns and acceleration, as well as motoric and somatosensory cues related to moving our feet and bodies, provide ecologically relevant information regarding where we have been. In fact, several behavioral studies suggest that body-based cues enhance our spatial representations, aiding in the encoding and retrieval of spatial environments (Chance et al., 1998; Klatzky et al., 1998; Waller et al., 2003; Ruddle and Lessels, 2006; Ruddle et al., 2011a, b; Chrastil and Warren, 2013). Based on neural findings in the rodent, some have argued that body-based cues fundamentally influence spatial representations. For example, conditions of passive movement compared to active movement, as well as visual input lacking body-based cues, reduce place cell activity (Foster et al., 1989; Terrazas et al., 2005; Chen et al., 2013) and head direction cell activity (Stackman et al., 2003). Additionally, impaired vestibular input alters neural spatial codes related to place cells, head direction cells, and spatial memory more generally (Stackman and Taube, 1997; Russell et al., 2003a, b; Brandt et al., 2005). This, in turn, has led some to question the validity of conducting navigation studies using desktop virtual reality because participants do not have access to body-based cues other than those provided by vision (e.g., optic flow; Taube et al., 2013). We term the idea that the encoding modality fundamentally alters neural codes for spatial environments the modality-dependent spatial coding hypothesis.

Notably, many of the studies cited above investigated situations involving physically navigating, when vestibular, motoric, and somatosensory cues might be particularly critical, for example, for programming head turns, walking speed, or the direction and distance from a goal location. Some theoretical models and empirical work suggest that configural spatial representations, and their neural underpinnings, in contrast, should be largely modality-independent, particularly when representations are abstract, complex, or there is sufficient experience with and exposure to the different modality. In other words, regardless of how we learned a spatial layout and navigated it in the first place, all forms of input, including experiencing the environment somatosensorily or reading about it (rather than directly navigating it), should distill to the same fundamental spatial representations, although the rate of such learning may or may not differ between such conditions (Taylor and Tversky, 1992; Bryant, 1997; Loomis et al., 2002; Avraamides et al., 2004; Giudice et al., 2011). In support of this idea, some of the same brain regions are activated in blind and sighted individuals during imagined walking (Deutschländer et al., 2009) and touching and seeing complex scenes (vs. objects) elicited similar patterns of activation in retrosplenial cortex and parahippocampal place area (Wolbers et al., 2011). This hypothesis, often termed the modality-independent (Wolbers et al., 2011) or amodal (Bryant, 1997; Loomis et al., 2002; Avraamides et al., 2004) spatial coding hypothesis, argues that the representations involved in configural spatial knowledge, such as judging the relative distance or direction between objects, should not be significantly altered by how this information was encoded.

Due to technological limitations, little is known about the role that body based-cues play in the representation of spatial information in the human brain. Recent breakthroughs in virtual reality (VR) technology created the opportunity to study human spatial memory in an immersive, highly realistic environment, thus better approximating real-world navigation. Using this technology, participants can freely turn both their heads and bodies and walk on an omnidirectional treadmill while wearing a head-mounted display, experiencing a rich repertoire of visual, vestibular, motoric, and somatosensory cues related to free ambulation. Accordingly, we were able to directly pit the modality-dependent and modality-independent hypotheses against each other. Critically, by having participants learn the environments to comparable levels of performance but with different availability of body-based cues, we controlled for the possibility that task difficulty or retrieval performance, rather than the availability of body-based cues per se, could be driving differences in the brain. Participants subsequently retrieved this information by making judgments about the relative directions of objects in a virtual environment while undergoing whole-brain functional magnetic resonance imaging (fMRI). Specifically, we used the judgments of relative directions (JRD) task (see Figure S1B), in which participants answered questions of the following form: “Imagine you’re standing at A, facing B. Please point to C.” Previous research suggested that the JRD task would provide a reasonable measure of participants’ configural representation of the environment. For example, in a desktop-based navigation experiment of a large-scale environment, we found a strong correlation between the pattern of errors on the JRD task and a map-drawing task (Huffman and Ekstrom, 2019).

By comparing activation patterns and functional connectivity patterns during the JRD task, and additionally employing two positive controls involving an active and passive baseline task, we were able to directly compare whether individual brain regions and networks of brain regions differ as a function of encoding modality. Specifically, the modality-dependent spatial coding hypothesis predicts that there should be differences both in behavior and in the brain as a function of the availability of body-based cues. Alternatively, the modality-independent spatial coding hypothesis predicts that we should observe strong evidence in favor of the null hypothesis of no differences in behavior or in the brain networks or regions involved in spatial memory retrieval, which we assessed within a Bayesian framework. In addition, the modality-independent hypothesis predicts that neural codes from one modality (navigating with vision only) should be sufficient to decode behavior in a different modality (navigating with vision and body-based cues). We employed the method of converging operations to bolster our confidence in our results (McNamara, 1991). Our results support the notion that there is a core, modality-independent network underlying spatial memory retrieval in the human brain.

Results

The rate of spatial learning does not differ as a function of body-based cues

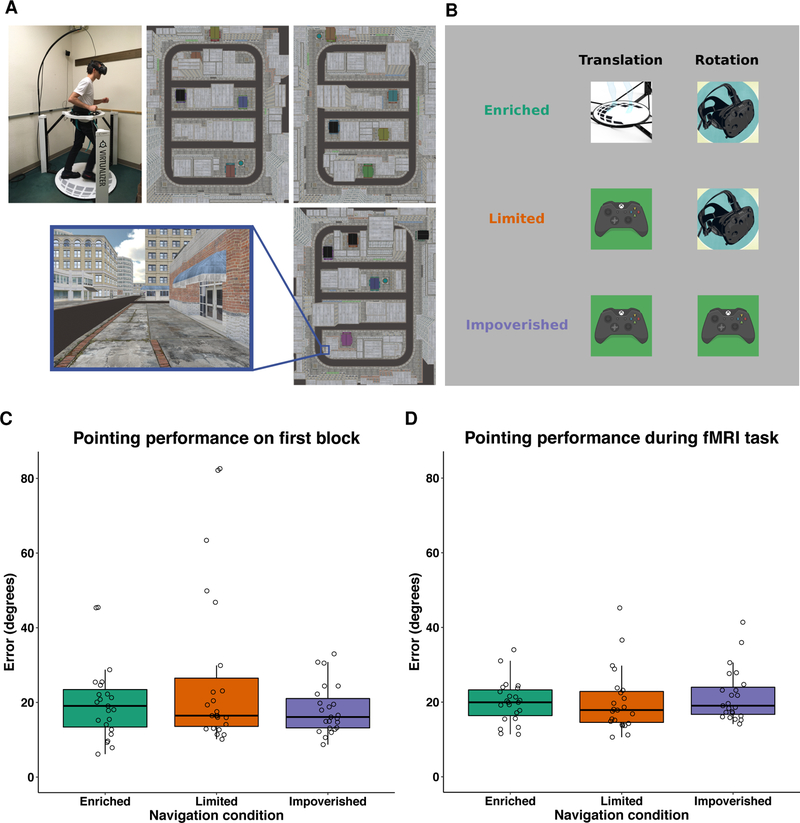
We first tested the hypothesis that differences in the availability of body-based cues would fundamentally influence spatial representations in the human brain by investigating whether there were differences in the rate of spatial learning. Participants learned three virtual environments under three body-based cues conditions: 1) enriched (translation by taking steps on the omnidirectional treadmill, rotations via physical head and body rotations), 2) limited (translation via joystick, rotations via physical head and body rotations), 3) impoverished (all movements controlled via joystick while standing on the treadmill wearing the head-mounted display; see Figure 1). Behaviorally, the modality-dependent hypothesis predicts that the rate of spatial learning of novel environments should differ as a function of body-based cues. To test this hypothesis, we employed a linear mixed model (see STAR Methods) to determine whether spatial memory performance—assessed by pointing error on the judgments of relative directions (JRD) pointing task (see Figure S1)—differed between body-based cues conditions after a single round of navigation.

Figure 1.

Images of the navigation task and of performance on our spatial memory task, the judgments of relative directions task. (A) Participants learned three virtual cities (which differed in store location and identity, see STAR Methods) by navigating to the task-relevant landmarks within the environment. (B) Each city was learned under one of three body-based cues conditions (enriched: all movements via body movements on the treadmill; limited: translation via joystick and rotations via body rotations on the treadmill; impoverished: all movements controlled via joystick while standing still on the treadmill with their head facing forward). (C) Pointing performance on the JRD task after one round of navigation was more consistent with the null hypothesis of no difference as a function of body-based cues (BF₀₁ = 3.7; bottom left panel). (D) Consistent with the goals of our training paradigm, pointing performance on the JRD task during fMRI scanning did not differ as a function of body-based cues (BF₀₁ = 5.1). Each dot represents the median absolute angular error for a single participant.

The results of this analysis revealed evidence in favor of the null hypothesis of no difference in pointing accuracy after a single round of navigation as a function of body-based cues (β = −0.90, Bayes factor in favor of the null [ BF₀₁ ] = 3.7, null model AIC = 571.6, full model AIC = 573.3, X² (1, N = 23) = 0.2, p = 0.65; see Figure 1). Nonetheless, participants performed better than chance on the first block of the JRD task for all conditions (all two-tailed group-level permutation p < 0.0001; group-level means of median absolute pointing error: enriched = 19.9 degrees, limited = 27.2 degrees, impoverished = 18.1 degrees). Given that the modality-dependent hypothesis would predict the largest difference between the enriched and impoverished conditions and because the errors were the most variable for the limited condition, we also compared the enriched and impoverished conditions and again observed evidence in favor of the null hypothesis of no difference in pointing error between these conditions (BF₀₁ = 3.4; t₂₂ = 0.80, p = 0.43). Similarly, we did not find differences in either the number of blocks required to reach criterion (Friedman X² (2, N = 23) = 0.14, p = 0.93) or path accuracy as a function of body-based cues during navigation (see Figure S2A), again suggesting that the presence body-based cues did not significantly enhance how participants learned the environments.

Additional analyses suggested that participants used similar strategies across conditions. Boundary-alignment effects, in which participants exhibit better pointing performance on the JRD task when the imagined heading is aligned with the salient axes of the environment, are well established and have been taken as evidence of configural spatial knowledge (Shelton and McNamara, 2001; Kelly et al., 2007; Mou et al., 2007; Manning et al., 2014). Our previous research suggested that alignment effects emerge over blocks of training for large-scale environments (Starrett et al., 2019); thus, we tested the hypothesis that participants would exhibit an effect of boundary alignment after they learned each city to criterion. Consistent with our hypothesis, we observed a significant main effect of boundary alignment (β = 0.32, null model AIC = 28, 300, full model AIC = 28, 283, X² (1, N = 23) =19.5, p < 0.0001). The interaction between alignment and body-based cues did not reach significance (alignment model AIC = 28, 283, alignment × cues interaction model AIC = 28, 286, X² (4, N = 23) = 5.1, p = 0.27), and the alignment effects were stable across body-based cues conditions (enriched: β = 0.33, null model AIC = 9, 526.1, full model AIC = 9, 518.8, X² (1, N = 23) = 9.4, p = 0.0022; limited: β = 0.32, null model AIC = 9, 311.8, full model AIC = 9, 305.9, X² (1, N = 23) = 7.9, p = 0.005; impoverished: β = 0.33, null model AIC = 9, 496.1, full model AIC = 9, 490.0, X² (1, N = 23) = 8.1, p = 0.0044; see Figure S2C). Moreover, in a post-session questionnaire, none of our participants reported using a different strategy across conditions. Altogether, these findings suggest that body-based cues neither enhanced the rate of spatial learning nor changed the strategies employed by our participants. These results are inconsistent with the modality-dependent hypothesis; however, we note that the modality-independent hypothesis does not necessarily make strong claims about the speed of learning, but rather suggests that the resultant spatial representations will be similar once the environments are well learned (Taylor and Tversky, 1992; Bryant, 1997; Loomis et al., 2002; Avraamides et al., 2004; Giudice et al., 2011), which we more directly tested in our fMRI analyses.

Our training paradigm resulted in similar spatial memory performance between body-based cues conditions during fMRI scanning

Our training paradigm had two main goals (see the Session 2 panel of Figure S1A). First, we aimed to ensure that performance during the fMRI retrieval phase was better than chance for all three cities. Our results revealed that this goal was realized—all 23 participants performed better than chance for each city during the fMRI retrieval phase, as determined by a permutation test (all p < 0.005). Second, by the end of training, we aimed to find no difference in pointing performance as a function of body-based cues. This was to ensure that our fMRI findings were in no way contaminated by differences in performance based on body-based encoding. Our results demonstrate that this condition was also met—a one-way repeated-measures ANOVA revealed that pointing performance during the fMRI retrieval task did not significantly differ as a function of based body-based cues (BF₀₁ = 5.1, F_2,44 = 0.63, p = 0.54; see Figure 1). These results are important because they suggest that the investigation of brain differences across these conditions is not confounded by differences in behavioral performance.

Neural interactions amongst brain regions differ between control and baseline tasks but do not differ as a function of body-based cues during encoding

Next, we combined resting state and task-based functional connectivity, which we refer to as functional correlativity, and a classification analysis based on these functional correlativity patterns to test whether interactions between brain regions could be dissociated as a function of the task that participants were performing. We hypothesized that if neural interactions are modulated specifically by condition, then we should observe significant classification accuracy specific to a task state as different from the others. Conversely, if tasks recruit similar cognitive and neural processes, then we should fail to observe significant classification accuracy between such tasks. Our first analysis focused on functional correlativity differences between different tasks—the JRD pointing task broadly (without consideration of body-based encoding), a visually matched active baseline task in which participants were asked to make math judgments (see Figure S1C), and the resting state condition (see Figure S1D). To ensure that differences in functional correlativity reflect putative differences in network interactions, as opposed to task-based co-activations, we performed this classification analysis using a “background” functional correlativity analysis (Norman-Haignere et al., 2012).

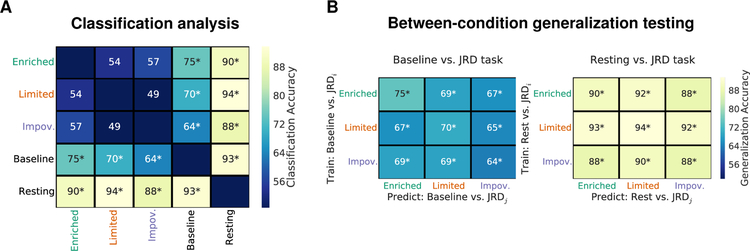
The classification analysis revealed that the resting state could be readily distinguished from all other task states (two-tailed permutation test; active baseline task: 93%, p < 0.0001; JRD-enriched: 90%, p < 0.0001; JRD-limited: 94%, p < 0.0001; JRD-impoverished: 88%, p = 0.0007). The classification analysis also readily distinguished the baseline task (i.e., the visually matched math judgments task; see STAR Methods and Figure S1C) relative to the JRD retrieval tasks (JRD-enriched: 75%, p < 0.0001; JRD-limited: 70%, p = 0.0006; JRD-impoverished: 64%, p = 0.019; Figure 2A). Conversely, however, when comparing classification between JRD task blocks involving different levels of body-based cues, classification accuracy was at chance (enriched vs. limited: 54%, p = 0.49; enriched vs. impoverished: 57%, p = 0.15; limited vs. impoverished: 49%, p = 0.80; Figure 2A). We also ran our classification analysis without regressing out task-based activation because such activations undoubtedly contain task-relevant information, thus this approach could potentially increase the sensitivity of discriminating between task conditions (e.g., between the different JRD task blocks). The pattern of classification results, however, was identical (see Figure S3B).

Figure 2.

Evidence that network interactions differ between tasks but the network underlying human spatial memory retrieval is stable across body-based cues conditions. (A) A classification analysis revealed that patterns of functional correlativity carried sufficient information for discriminating between task conditions (i.e., JRD task vs. active baseline task and all tasks vs. resting state), but there was no evidence of discriminability between the JRD tasks as a function of body-based cues (i.e., enriched vs. limited vs. impoverished). (B) Supporting the similarity of the networks across body-based cues conditions, a between-condition generalization test revealed significant classification accuracy between all three conditions for comparisons to both the active baseline task and the resting state. Classification accuracies indicate the average percent correctly classified across all participants for each binary classification. _* indicates two-tailed permutation p < 0.05 (note, these also survived FDR correction for multiple comparisons).

The results above suggest that there are not discriminable differences in the patterns of task-based functional correlativity as a function of body-based cues. An important additional test, which we performed as a positive control, is whether the classifier can generalize from one form of body-based cues condition to another. Specifically, if tasks recruit similar networks, then a classifier that has been trained to discriminate between two task conditions (e.g., JRD-enriched vs. resting state) should exhibit a high degree of classification accuracy when tested on a new task condition (i.e., good generalization performance; e.g., JRD-limited vs. resting state). Thus, we trained and tested a classifier using the same approach as our main analysis but instead of testing the same conditions on the held-out participant, we tested them on a complementary pair of conditions. This between-condition generalization test revealed significant classification accuracy between all three JRD task conditions for comparisons to both the active baseline task and the resting state (all p ≤ 0.017). Importantly, classification accuracy was similar to that of our main analysis (compare the main diagonal to the off diagonal classification accuracy in Figure 2B). These results provide an important positive control by suggesting that the patterns of functional correlativity for the JRD task are shared across body-based cues conditions.

The retrosplenial cortex, parahippocampal cortex, and hippocampus are activated by judgments of relative direction in a modality-independent manner

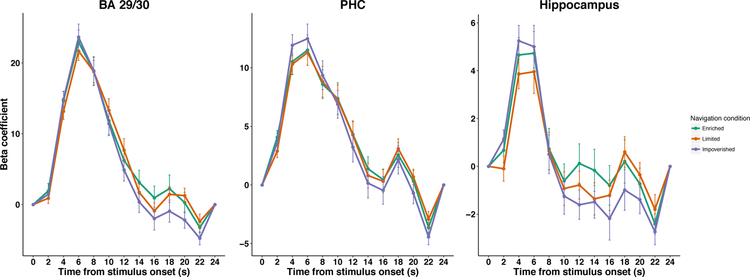
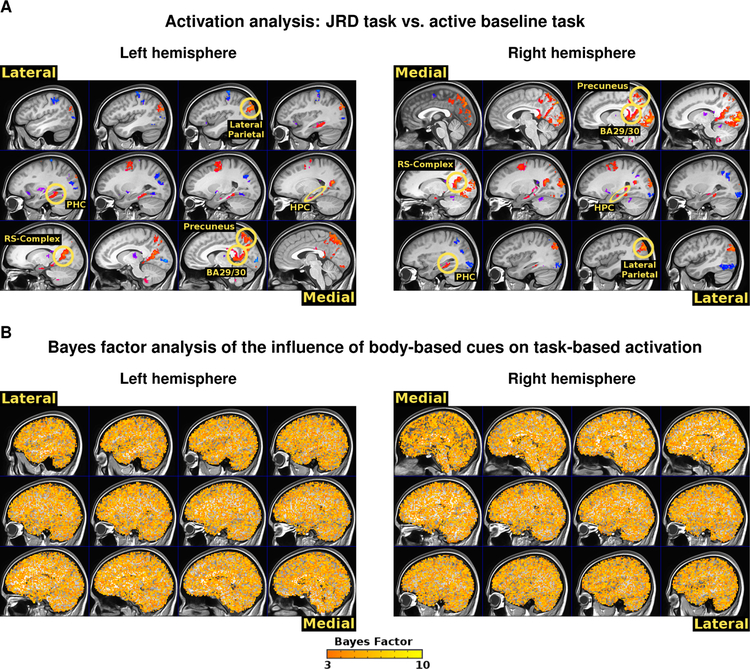
One possibility is that, instead of functional correlativity patterns, focal activation patterns would differentiate different levels of body-based encoding. For example, there is evidence that place cell (Foster et al., 1989; Terrazas et al., 2005; Chen et al., 2013) and head direction cell (Stackman et al., 2003) activity is diminished under conditions of passive movement relative to active movement, thus suggesting that activation levels would differ between body-based cues conditions. We therefore conducted a regions of interest (ROI) analysis to test the hypothesis that brain regions known to play a key role in human spatial cognition would be activated by spatial memory retrieval. We observed greater BOLD activation for the JRD task compared to the active baseline task in retrosplenial cortex (BA 29/30), parahippocampal cortex (PHC), and the hippocampus (see Figure 3). Specifically, the peak BOLD response, defined here as the sum of the beta weights from 4 to 8 seconds following stimulus onset, was significantly greater than zero in BA 29/30 (Enriched: BF₁₀ = 268, 293, 392, t₂₀ =13.00, p < 0.0001, Limited: BF₁₀ = 2,158, 262, 776, t₂₀ =14.69, p < 0.0001, Impoverished: BF₁₀ =118, 429, 200, t₂₀ =12.39, p < 0.0001), PHC (Enriched: BF₁₀ =1, 073, 034, t₂₀ = 9.23, p < 0.0001, Limited: BF₁₀ = 5, 238, 711, t₂₀ =10.22, p < 0.0001, Impoverished: BF₁₀ = 22, 217, 500, t₂₀ =11.19, p < 0.0001), and the hippocampus (Enriched: BF₁₀ = 219, t₂₀ = 4.72, p = 0.00013, Limited: BF₁₀ = 65, t₂₀ = 4.14, p = 0.00051, Impoverished: BF₁₀ = 847, t₂₀ = 5.4, p < 0.0001). A whole-brain contrast between the JRD task and the active baseline task demonstrated a similar pattern of activations, including retrosplenial cortex, retrosplenial complex (RS-Complex; note, this region is functionally defined and is typically anatomically distinct from retrosplenial complex, see Epstein, 2008), PHC, the hippocampus, lateral parietal cortex, and posterior parietal cortex (voxel-wise p < 0.001, cluster-corrected threshold p < 0.01; the voxel-wise threshold corresponds to an FDR q < 0.0196; see Figure 4A). These findings suggest that spatial retrieval activates a core set of brain regions that include the retrosplenial cortex, hippocampus, and parahippocampal cortex (Ekstrom et al., 2017; Epstein et al., 2017).

Figure 3.

Evidence that the retrosplenial cortex (BA 29/30), parahippocampal cortex (PHC), and hippocampus are activated by judgments of relative direction in a modality-independent manner. These figures depict the estimated impulse response functions for the JRD task versus the active baseline task in our regions of interest (data are represented at the mean ± the standard error of the mean). The peak responses (4–8 seconds following stimulus onset) were significantly greater than zero in all three regions for all three body-based cues conditions (all BF₁₀ ≥ 65). Additionally, the evidence was in favor of the null hypothesis of no difference in task-based activation as a function of body-based cues across all three regions (all BF₀₁ ≥ 3.4).

Figure 4.

Evidence that the core spatial navigation network is activated by judgments of relative direction in a modality-independent manner. (A) A task-based activation analysis across all body-based cues conditions revealed activations in the putative spatial cognition network. RS-Complex: retrosplenial complex; HPC: hippocampus. (B) A whole-brain ANOVA revealed no significant clusters for differences in task-based activation as a function of body-based cues and a Bayes factor analysis revealed widespread evidence in favor of the null hypothesis (thresholded at BF₀₁ > 3). Specifically, the majority of the brain showed a Bayes factor of at least 3 in favor of the null hypothesis.

We next tested whether task-based activations between the JRD task and the active baseline task differed in these regions as a result of the body-based cues available during encoding. Our results revealed no detectable evidence of a difference based on encoding condition. In fact, a Bayes factor ANOVA revealed evidence in favor of the null hypothesis of no difference between the peak responses based on encoding condition in BA 29/30 (BF₀₁ = 5.1, F_2,40 = 0.56, p = 0.58), PHC (BF₀₁ = 3.6, F_2,40 =1.04, p = 0.36), and the hippocampus (BF₀₁ = 3.4, F_2,40 =1.14, p = 0.33). These findings again suggest that differences in body-based input do not result in different levels of activation during spatial retrieval in these regions, thus supporting the modality-independent hypothesis.

Whole-brain analysis of different levels of body-based encoding: No brain areas showed differences based on the availability of body-based cues

It could be the case that brain regions outside of areas typically associated with navigation showed differences as a function of body-based immersion. To address this issue, we conducted a whole-brain ANOVA to determine whether there were brain regions that exhibited differences in task-based activation for the JRD task vs. the active baseline task as a function of body-based cues. The results revealed no significant clusters anywhere in the brain (voxel-wise p < 0.001, cluster-corrected threshold p < 0.01) and the minimum FDR q throughout the whole brain was q = 0.53. Indeed, the (unthresholded) activation maps were similar and the clusters observed across body-based cues conditions were overlapping (enriched vs. limited r = 0.90, dice overlap = 0.71; enriched vs. impoverished: r = 0.90, dice overlap = 0.71; limited vs. impoverished: r = 0.89, dice overlap = 0.69; see Figure S4). Importantly, a control analysis in which we compared activation between the JRD task versus blocks of the active baseline task (i.e., we ran the same analysis with “sham” regressors for the baseline task) revealed that the activation maps and the observed clusters were similar to the within-blocks analysis of the JRD task to the baseline task (enriched: r = 0.93, dice overlap = 0.73; limited: r = 0.93, dice overlap = 0.74; impoverished: r = 0.93, dice overlap = 0.72). In contrast, the activation maps and the observed clusters were not similar between the JRD task and the baseline task analysis (enriched: r = −0.16, dice overlap = 0.02; limited: r = −0.16, dice overlap = 0.02; impoverished: r = −0.17, dice overlap = 0.02).

To further interrogate whether the data were more consistent with the hypothesis of no difference in task-based activation as a function of body-based cues, we implemented a whole-brain Bayes factor ANOVA. We found that the vast majority of voxels throughout the brain were more consistent with the null hypothesis (thresholding at BF₀₁ >1 accounted for 92.5% of the voxels; thresholding at BF₀₁ > 3 accounted for 69.9% of the voxels; see Figure 4B). Together, our activation analysis suggests that judgments of relative direction activate a core set of brain regions involved in spatial cognition. Overall, we found strong evidence in favor of the modality-independent hypothesis that body-based cues exert little to no selective influence on the brain regions that are activated, as measured by fMRI, during the retrieval of configural spatial knowledge.

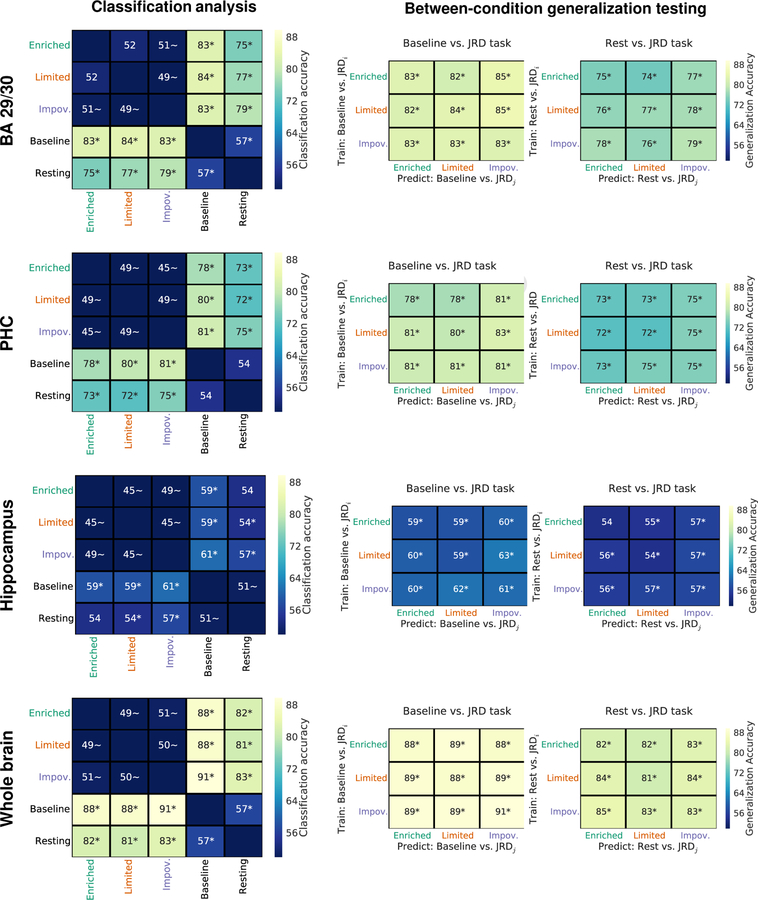
Single-trial patterns of activity differ between control and baseline tasks but do not differ as a function of body-based cues during encoding

It could be the case that differences between body-based cues manifest in a participant-specific manner; in other words, individual differences in retrieval of body-based cues could be masked by our group-based approach employed so far. Also, it could be that multivariate patterns of activation, rather than focal univariate activation, contained information about body-based cues during retrieval (Norman et al., 2006; Kriegeskorte and Bandettini, 2007). To address this possibility, we performed a within-subject single-trial classification analysis using patterns of activity within regions of interest (BA 29/30, PHC, hippocampus) and at the whole-brain level¹. The results of our analysis were consistent with our previous classification analysis of functional correlativity patterns—specifically, we observed significant classification accuracy between spatial memory retrieval and both the active baseline task and the resting state, but we observed chance-level classification accuracy between body-based cues conditions (see Figure 5). Moreover, we observed significant generalization accuracy when we trained and tested the classifier on different body-based cues conditions, and the generalization accuracy was similar to that of the main analysis (compare the main diagonal to the off diagonal classification accuracy for the between-condition generalization testing in Figure 5). Additionally, classification accuracy between body-based cues conditions was consistently in favor of the null hypothesis (i.e., BF₀₁ > 3) for the one-tailed comparison between 50% chance classification accuracy vs. classification accuracy greater than 50% (see STAR Methods). Altogether, these results accord with our between-subjects classification analysis and with our activation analyses, suggesting that patterns of activity differ between spatial memory retrieval and both the active baseline task and the resting state but that patterns of activity are similar between body-based cues conditions.

Figure 5.

Single trial classification analysis revealed evidence that patterns of activity differ between tasks but that patterns of activity during spatial memory retrieval are stable across body-based cues conditions. Across our ROIs, we observed significant classification accuracy between the JRD task and both the active baseline task and the resting state. In contrast, the evidence was in favor of the null hypothesis of chance-level classification accuracy between body-based cues conditions, and a between-condition generalization test revealed similar classification accuracy to the within-condition classifiers. * indicates two-tailed permutation p < 0.05. ~ indicates one-tailed BF₀₁ > 3.

Task-specific distance-related coding in retrosplenial cortex, parahippocampal cortex, and hippocampus which does not differ between body-based cues conditions

Previous research suggested that pattern similarity (i.e., correlations between patterns of activity across voxels in the brain) in the navigation network is related to the distance between positions within a virtual environment (Sulpizio et al., 2014) and the real world (Nielson et al., 2015). Therefore, as an exploratory analysis², we employed a linear mixed-model to investigate whether there was a relationship between pattern similarity and the distance between landmarks (see STAR Methods). If a region carries information regarding the locations and distances between landmarks, then we would expect to observe a negative relationship between pattern similarity and the distance between landmarks (i.e., lower pattern similarity for landmarks that are further apart). Further, if a region’s involvement in distance-related coding is dependent on body-based cues, then we would expect to observe a significant interaction between distance and body-based cues. We found a significant main effect of distance on pattern similarity in BA 29/30 (β = −0.000075, null model AIC = −9, 355.1, full model AIC = −9, 358.3, X² (1, N = 21) = 5.14, p = 0.023), PHC (β = −0.000042, null model AIC = −22, 338, full model AIC = −22, 341, X² (1, N = 21) = 4.57, p = 0.032), and a functionally defined hippocampal region of interest (β = −0.000040, null model AIC = −22, 576, full model AIC = −22, 578, X² (1, N = 21) = 4.35, p = 0.037; see Figure S5), consistent with Sulpizio et al. (2014). However, the interaction between distance and body-based cues was not significant (i.e., the distance × cues interaction model did not fit the data significantly better than the distance model) in BA 29/30 (distance model AIC = −9, 358.3, distance × cues interaction model AIC = −9, 356.4, X² (4, N = 21) = 6.14, p = 0.19), PHC (distance model AIC = −22, 341, distance × cues interaction model AIC = −22, 336, X² (4, N = 21) = 2.57, p = 0.63), and our functionally defined hippocampal region of interest (distance model AIC = −22, 578, distance × cues interaction model AIC = −22, 573, X² (4, N = 21) = 3.20, p = 0.52). While we approach these analyses with some caution (as they were exploratory), we note that they are consistent with the results of our other analyses, all of which provide evidence of differences as a function of spatial information but no significant effect of the body-based cues conditions.

Discussion

The influence of body-based cues on human spatial representations might depend on the nature of the task

Our behavioral results suggest that body-based cues did not significantly influence the rate of acquisition of configural spatial knowledge for large-scale environments in our task. Previous studies have revealed similar results for related tasks (e.g., map drawing; Waller et al., 2004; Waller and Greenauer, 2007; Ruddle et al., 2011b). Notably, there is also substantial evidence to support the idea that body-based cues facilitate performance on spatial tasks, although such experiments have used tasks which likely placed stronger demands on the navigator to actively maintain their orientation relative to landmarks in the environment (e.g., pointing to landmarks relative to their current position and heading; Chance et al., 1998; Klatzky et al., 1998; Waller et al., 2004; Ruddle and Lessels, 2006; Ruddle et al., 2011b; but see Waller et al., 2003). Thus, a potential explanation for the equivocal results from human behavioral studies that have manipulated body-based cues is that there might be different effects based on whether the task places stronger demands on configural spatial knowledge vs. actively maintaining orientation of oneself relative to landmarks in the environment. Waller et al. (2004) raise similar points, suggesting that “the effect of body-based information on developing complex configural knowledge of spatial layout (as opposed to knowledge of self-to-object relations) may be minimal.” Additionally, Waller and Greenauer (2007) suggested that “in contrast to the transient, egocentric nature of body-based information, the relative permanence of the external environment makes visual information about it more stable and thus likely more suitable for storing an enduring (and abstract) representation.” While configural and self-to-object representations likely exist along a continuum (Wolbers and Wiener, 2014; Ekstrom et al., 2014, 2017; Wang, 2017), our findings also involved spatial knowledge acquired from large-scale environments. This is precisely a situation in which path integration knowledge would likely be less reliable (Loomis et al., 1993; Foo et al., 2005; Chrastil and Warren, 2014; Warren et al., 2017), and together, our findings therefore provide important boundary conditions of when we might expect body-based cues to influence subsequent spatial retrieval.

A modality-independent network underlies human spatial retrieval

While our behavioral findings are not consistent with the modality-dependent hypothesis regarding the importance of body-based cues to navigation, we note that the modality-independent hypothesis does not necessarily make a strong prediction about the rate of spatial learning, but rather hypothesizes that the nature of spatial knowledge will be qualitatively similar once it is well learned (Taylor and Tversky, 1992; Bryant, 1997; Loomis et al., 2002; Avraamides et al., 2004; Giudice et al., 2011). Thus, our fMRI results provide a more direct test of the modality-dependent hypothesis vs. the modality-independent hypothesis. The results of our between-task (i.e., JRD task vs. active baseline task vs. resting state) functional correlativity analysis suggest that there are differences in network interactions between different tasks, supporting previous network results from decoding (Shirer et al., 2012) and graph theory analysis (Krienen et al., 2014; Braun et al., 2015; Spadone et al., 2015; Cohen and D’Esposito, 2016). Our results also revealed five pieces of neural evidence to suggest that the network underlying the retrieval of configural spatial knowledge for large-scale environments is modality independent. First, a classification analysis suggested that network interactions were similar across body-based cues conditions during performance of the JRD task. Specifically, we observed evidence of nearly equivalent generalization performance when the classifiers were trained and tested on functional correlativity patterns from the same body-based cues condition and when trained and tested on different conditions. Thus, in addition to the null classification between JRD tasks as a function of body-based cues, these results provide positive evidence to support the similarity of these conditions. Second, we observed a similar pattern of activations for the JRD task vs. active baseline in our ROI analysis (retrosplenial cortex, parahippocampal cortex, and the hippocampus) and in our whole-brain analysis. Third, a Bayes factor analysis revealed evidence in favor of the null hypothesis of no difference between task-based activations in both our ROI and whole-brain analyses. Fourth, single-trial classification analysis in regions of interest and at the whole-brain level revealed a similar pattern of results to the analysis of functional correlativity patterns. Fifth, an exploratory pattern similarity analysis revealed evidence of distance-related coding, but no significant effect of body-based cues conditions. Taken together, our results are consistent with the theory that aspects of human spatial cognition are supported by network interactions (Ekstrom et al., 2017), and further suggest that such interactions are stable across body-based cues conditions.

Our training paradigm sought to match performance across the body-based cues conditions during the final retrieval task, and we suggest that this type of training paradigm will be important for future studies regarding the nature of spatial representation in humans and in the rodent. We note that several studies that have shown effects of body-based cues have also observed differences in performance as a function of body-based encoding (Chance et al., 1998; Klatzky et al., 1998; Waller et al., 2003; Ruddle and Lessels, 2006; Ruddle et al., 2011a, b; Chrastil and Warren, 2013), but these same studies also involved situations in which matching the perceptual-vestibular details would generally be advantageous during retrieval (Tulving and Thomson, 1973). Our motivation here was to attempt to match task difficulty (i.e., during fMRI scanning) in addition to task engagement and other demands during the navigation task. For example, if a navigator does not have an understanding of where they are or how they are moving through an environment, then the spatial neural codes for that environment should be disrupted. While such a result is interesting in its own right, we argue that it is important to match behavioral performance across conditions to deconfound potential differences in task performance (e.g., the navigator’s knowledge of its location and heading) from the influence of body-based cues per se (i.e., the mode of transport). Previous research has also suggested that task demands can influence behavioral performance (and thus potentially the underlying neural processes) to be similar across visual and proprioceptive conditions (e.g., Experiment 3 of Avraamides et al., 2004), thus suggesting that task demands can shape cognitive representations to be more modality independent. Finally, it is worth noting that all three of our navigation conditions were active in the sense that participants were controlling their movements through the environment (cf. Chrastil and Warren, 2012).

Caveats and directions for future research

While our results are inconsistent with the modality-dependent hypothesis that body-based cues fundamentally influence the nature of spatial representations supporting spatial memory retrieval for large-scale environments, at least as assessed by the JRD task, there are several caveats to the interpretation of our results. First, as discussed above, different tasks or techniques might be required to elucidate differences as a function of body-based cues, for example, those placing more of an emphasis on active navigation and orientation during retrieval. Second, although each environment in our experiment involved different stores in different locations, and environment-type was counterbalanced across participants, it is possible that different environments could be learned in different ways dependent on body-based cues. For example, error accumulates in the (human) path integration system over longer distances (e.g., Loomis et al., 1993; Kim et al., 2013; cf. Eichenbaum, 2017) and because the environments we employed were large scale, on the order of a city neighborhood (i.e., “environmental space”; Montello, 1993), body-based cues (and body-rotation information in particular) might be of less importance for environments of this size compared to smaller-scale environments (e.g., room-sized environments; cf. Ruddle et al., 2011a). Consistent with this argument, past studies have suggested that participants may rely on visual input in such situations when path integration cues are unreliable (Foo et al., 2005; Chrastil and Warren, 2014; Warren et al., 2017). More generally, the cognitive and neural processes supporting spatial representations have been hypothesized to differ with the scale of space (e.g., Montello, 1993; Wolbers and Wiener, 2014), and it will be interesting for future studies to consider potential differences in the cues that are important at these different scales. Third, it is possible that different results would be obtained during real-world navigation, which involves aspects that are difficult to capture even during immersive virtual reality. We note, however, that the devices we employed (omnidirectional treadmill and head-mounted display), which have been used in other contexts to study human spatial navigation (Starrett et al., 2019; Liang et al., 2018), allowed us to carefully control body-based cues conditions and pre-exposure to the environments. Differences compared to real-world navigation could manifest for other reasons unrelated to body-based input, and thus using immersive VR was advantageous in this context for carefully controlling body-based cues. Moreover, if body-based cues exist along a spectrum, then our results suggest, at least for the spectrum considered here, that body-based cues do not fundamentally change the nature of spatial representations. Taken together, our results should be considered an important first step toward understanding the role of body-based cues on human neural representations of space, and future studies should address behavioral and neural differences between tasks that vary across these areas.

STAR Methods

LEAD CONTACT AND MATERIALS AVAILABILITY

Further information and requests for resources should be directed to and will be fulfilled by the Lead Contact, Arne Ekstrom (adekstrom@email.arizona.edu).

EXPERIMENTAL MODEL AND SUBJECT DETAILS

Participants

Participants were recruited from the local community and consented to participation according to the Institutional Review Board at the University of California, Davis. Participants were offered the option of receiving either course credit or monetary compensation ($10 per hour) for their participation. The experiment consisted of a total of approximately 7.5 hours of participation spread over two different days (note, there was variability in the length of time spent participating based on how quickly participants learned the cities in the treadmill portions of the experiment). Our analysis was conducted on the behavioral data from 23 healthy young adults (12 male, 11 female) between 18 and 27 years of age (mean = 20). Two participants (1 male, 1 female) were excluded from our fMRI analysis—the first was excluded due to scanner reconstruction errors that resulted in an incomplete fMRI dataset and the other was excluded due to excessive head motion, thus analysis was conducted on the fMRI data from 21 participants. Note, two additional participants (both female) participated in a portion of Session 2 but they were excluded because one failed to reach criterion after four rounds of navigation (see Pre-fMRI task) and one requested withdrawing because they were experiencing discomfort with the virtual environments (e.g., minor dizziness).

METHOD DETAILS

Pre-fMRI task

We designed our behavioral tasks using Unity 3D (https://unity3d.com). The experiment consisted of two sessions that took place on different days (Session 1: participants were trained to walk on the omnidirectional treadmill and we established a subject-specific criterion based on performance in this session; Session 2: participants performed behavioral tasks and underwent fMRI scanning [note, all of the data reported here are from this session]; see Figure S1A). In the first session, participants were trained to walk on an omnidirectional treadmill (Cyberith Virtualizer) while wearing an HTC Vive head-mounted display (see Figure 1). Previous VR research in the rodent found the full complement of spatial cells (e.g., place cells, grid cells, head direction cells, border cells) using a comparable omnidirectional treadmill (Aronov and Tank, 2014). Participants also performed a practice version of the main task, in which they navigated to five stores in a virtual city using the treadmill (note, all movements were controlled via movements on the treadmill). Participants performed four rounds of navigation and a judgments of relative directions (JRD) pointing task in which they were tested for their memory of the city. In the JRD task, participants were instructed to imagine that they are standing at one store, facing a second store, and to point in the direction of a third store (from the imagined location and orientation; see Figure S1B). Previous research suggested that the JRD task would provide a reasonable measure of participants’ configural representation of the environment. For example, in a desktop-based navigation experiment of a large-scale environment, we found a strong correlation between the pattern of errors on the JRD task and a map-drawing task, thus suggesting that the JRD task provides information about holistic, abstract, configural spatial representations of large-scale environments (Huffman and Ekstrom, 2019). At the end of the first session, we assessed whether the participant’s performance qualified for inclusion in the second session; inclusion criteria: 1) mean absolute angular error less than 30 degrees by the third block of the JRD task, 2) no sign of cybersickness (via questionnaire; Kennedy et al., 1993; March 2013 version).

During the second session, participants learned the layout of three virtual cities by performing the navigation task interspersed with the JRD task. Each city was large-scale (185 by 135 virtual meters) and contained five target stores, several non-target buildings, and other environmental stimuli that prevented participants from readily seeing stores from one another (see Figure 1). Thus, our environments were not “vista-spaces”, in which all landmarks can be viewed from one or a small number of locations, and instead required participants to actively navigate and integrate spatial knowledge to learn about the relative locations of the stores (Wolbers and Wiener, 2014). Accordingly, our cities can be considered “environmental scale” (Montello, 1993). We also note that the landmarks could occur at any position within a city block and were not arranged in a regular grid layout. In an attempt to match the difficulty of the cities, we matched the following between the three cities: 1) the distribution of imagined heading angles relative to the cardinal axes of the environment (e.g., to mitigate against potential differences in boundary-alignment effects across cities; McNamara et al., 2003), 2) the distribution of the distances between pairs of landmarks, and 3) the distribution of the angles of the answers. Note that we employed different store identities and locations, which past work suggests will result in independent spatial codes (Newman et al., 2007; Kyle et al., 2015), thereby significantly reducing the likelihood that participants simply used a copy of the same representation for each city (see Figure 1). All city types were counterbalanced across subjects and body-based encoding conditions to avoid any city-specific effects confounding our findings (note, there were 6 possible city-cues combinations and 36 city-cues-order combinations, thus we fully counterbalanced at the city-cues level and partially counterbalanced at the city-cues-order level; however, there were no significant differences in performance between the three cities, suggesting that they were comparably difficult).

There were two types of body-based cues in our experiment: 1) those related to translation (i.e., movement through the environment; e.g., leg movements), 2) those related to rotation (e.g., head and body rotations). Participants learned each of the three cities under one of the following body-based conditions: 1) enriched (translation by taking steps on the omnidirectional treadmill, rotations via physical head and body rotations), 2) limited (translation via joystick, rotations via physical head and body rotations), 3) impoverished (all movements controlled via joystick). Note, to experimentally manipulate body-based cues while matching visual information and immersion between conditions, participants stood on the treadmill and wore the head-mounted display for all three conditions (anecdotally, the impoverished condition in this format feels more immersive than a desktop-based virtual experiment; e.g., because you still appear to be standing in the environment). Additionally, the order in which participants received the different motion cues and the order in which participants learned the three cities was partially counterbalanced, thus mitigating the potentially confounding effect of order or city.

At the beginning of each round of navigation, participants were placed at the center of the city. Participants were asked to navigate to each of the five target stores (the order of which was random on each block), and then the JRD task began, with 20 questions per block. If a participant did not reach criterion (subject-specific mean error determined by performance in the first session; specifically, 10 degrees higher than their mean error after three rounds of navigation in the practice city), they then performed another round of navigation and the JRD task. This procedure continued until the participant reached criterion or for a maximum of four rounds (at which point they were excluded from further participation; note, as stated in Participants, one additional participant was run on a single city of Session 2 but they were excluded from further participation because they failed to meet this criterion).

After reaching criterion, participants learned about the next city. After participants learned all three cities, they were re-exposed to each city by performing an additional round of the navigation task. Then, we tested their memory for each of the three cities (20 questions on the JRD task). If a participant failed to perform better than chance for a city (we assessed significance via a permutation test because chance performance on the JRD task depends on how participants distribute their responses; for more details please see: Huffman and Ekstrom, 2019), then they were re-exposed to that city and then re-tested on their memory for all three cities. After we ensured that a participant was performing better than chance for all three cities, we went to the scanner for the MRI session.

fMRI task

The fMRI task consisted of ten blocks, which corresponded to the length of the functional scans (6 minutes and 16 seconds). Each block consisted of the JRD pointing task, a visually matched active baseline task, or a resting-state scan (see Figure S1). The JRD task was the same as described above with three differences. First, the blocks consisted of 15 questions. Second, there was a response limit of 16 seconds. Third, the JRD task blocks were randomly interspersed with the active baseline task (17 trials that were 8 seconds each). Note, in addition to these baseline trials, if participants submitted their response prior to the trial response timeout, then they performed the baseline task until that point. In the active baseline task, participants were instructed to make arrow movements based on math questions (the left/right and the correct/incorrect aspects were randomly assigned on each trial). The baseline task was self-paced and participants were instructed to respond as quickly and as accurately as possible (Stark and Squire, 2001), in this way, matching difficulty as closely as possible compared to the JRD task. Participants performed two blocks of the JRD task for each of the three body-based cues conditions, two blocks of the active baseline task, and two resting-state blocks, the order of which was pseudo-random such that each task was performed before any task repeated.

MRI acquisition

Participants were scanned on a 3-T Siemens Skyra scanner equipped with a 32-channel head coil at the Imaging Research Center in Davis. T1- (MP-RAGE, 1 mm³ isotropic) and T2-weighted (in-plane resolution = 0.4 × 0.4 mm, slice thickness = 1.8 mm, phase encoding direction = right to left) structural images were acquired (note, the T2 scan was not utilized for the present analyses). fMRI scans consisted of a 2 mm³ isotropic whole-brain T2*-weighted echo planar imaging sequence using blood-oxygenation-level-dependent contrast (BOLD; 66 slices, interleaved acquisition, in-plane resolution = 2 × 2 mm, slice thickness = 2 mm, TR = 2000 ms, TE = 25 ms, flip angle = 65 degrees, number of frames collected = 188, multi-band acceleration factor = 2, GRAPPA acceleration factor = 2, phase encoding direction = anterior to posterior).

QUANTIFICATION AND STATISTICAL ANALYSIS

Analysis of behavioral data

We conducted three sets of analyses of our behavioral data. First, if body-based cues fundamentally influence spatial representations in the human brain, then we should observe differences in the rate of learning as a function of body-based cues. We tested this hypothesis using linear mixed models within a Bayes factor framework using the BayesFactor package (version 0.9.12–2) in R (version 3.3.1; R Core Team, 2016) to fit a mixed linear regression model (using the lmBF function; the rscaleFixed parameter was set to the default: 1/ 2) to participants’ errors (here, median absolute angular error as in Huffman and Ekstrom, 2019) on the first block of the JRD task (our model included random intercepts across participants; the navigation conditions were coded as follows: enriched = −1, limited = 0, impoverished =1). For more details on the Bayes factor analysis we implemented, please see (Rouder and Morey, 2012). In other words, this model tested the hypothesis that performance would be best for the enriched condition, followed by the limited condition, followed by the impoverished condition. We also conducted a likelihood ratio test using the anova function within the R stats package and the lmer function within the lme4 package (1.1–14; Bates et al., 2015) to assess whether or not this full model fit the data better than a model that only included the random intercepts across subjects (i.e., our null model). We assessed whether performance was better than chance on the first round of the JRD task using a group-level permutation approach that we developed in our previous work (Huffman and Ekstrom, 2019). Briefly, we used a two step procedure. First, we randomly shuffled a participant’s responses and calculated the median angular error with these arbitrarily associated angles. We performed this procedure 10,000 times, separately for each participant. Second, we created group-level distributions by averaging these random distributions across participants (i.e., to obtain 10,000 shuffled group-level means). We then assessed whether the empirical value was significantly better than this resultant group-level null distribution using a two-tailed test (see Equation 1 below and Huffman and Ekstrom, 2019). As an additional test of significant spatial learning after a single round of navigation, we tested whether participants exhibited an improvement in navigation performance between blocks of navigation. Specifically, we calculated excess path (defined here as the length of a participant’s actual path between two landmarks minus the Euclidean distance between their start and finish locations for that trial) and assessed whether it decreased from the first to second block of navigation using a generalized linear mixed-effects model framework (using the glmer function within lme4 with a gamma function for our dependent variable—i.e., excess path—and a log link function; our models included random intercepts across subjects). We also assessed whether a model that included an interaction between body-based cues and block fit the data better than the block model. If body-based cues influence the rate of spatial learning, then we would expect to observe a significantly better fit of the interaction model than the block model. We also assessed whether there were differences in the number of rounds of navigation required to reach performance criterion between body-based cues conditions using a Friedman rank sum test using the friedman.test function within the stats package (3.3.1) in R.

Second, we used a Bayes factor ANOVA (using the anovaBF function; the rscaleFixed parameter was set to the default: 1/ 2) to assess whether performance differed on the JRD task as a function of body-based cues during fMRI scanning. One of the major goals of our training paradigm was to ensure that performance did not differ across body-based cues conditions. Thus, we tested the hypothesis that pointing performance would be in favor of the null hypothesis of no difference as a function of body-based cues. Note that in this case we conducted our analysis within an ANOVA framework (i.e., we treated the navigation conditions as categorical variables) because we did not have a specific prediction about the nature of the underlying relationship between performance after cities were learned to criterion. In contrast, we used a linear mixed model to test differences in the rate of learning based on the number of body-based cues available to participants because we were testing an a priori hypothesis about the nature of the relationship between these variables.

Third, we assessed whether there were boundary-alignment effects on pointing performance after participants had been trained to criterion (Shelton and McNamara, 2001; Kelly et al., 2007; Mou et al., 2007). Specifically, we included the data from the final pre-fMRI retrieval task (20 trials per city) and the fMRI retrieval task (30 trials per city), excluding “no response” trials. We restricted our analysis to blocks in which participants were trained to criterion because our previous research suggested that alignment effects are not present initially but rather emerge over blocks of training for large-scale environments (Starrett et al., 2019). We generated our alignment regressors using a sawtooth function, which alternated between −0.5 and +0.5 every 45 degrees (i.e., 0: −0.5, 45: +0.5, 90: −0.5, …, 360: −0.5), with intermediate values lying on the “line” between the two values (e.g., 11.25: −0.25, 22.5: 0; see Figure S2A; Meilinger et al., 2016). We accounted for the fact that the distribution of absolute angular errors is non-normal and positively skewed by using a generalized linear mixed-effects model framework using the glmer function within lme4 with a gamma function for our dependent variable (i.e., absolute angular error) and a log link function (Lo and Andrews, 2015). Our models included random slope and intercept terms for alignment across subjects. We compared models using likelihood ratio tests.

Regions of interest

Based on prior spatial cognition experiments, we defined three regions of interest (ROIs) in our analysis: retrosplenial cortex, parahippocampal cortex, and the hippocampus. As in Vass and Epstein (2017), we defined retrosplenial cortex as Brodmann Areas 29/30 from the MRIcron template and we also removed voxels that were ventral to Z = 2. We warped this mask from the MRIcron template to our model template and from our model template we warped this mask into each of our subjects’ native space using Advanced Normalization Tools (ANTs; Avants et al., 2011). We also used ANTs to warp hand-drawn labels for parahippocampal cortex and hippocampus from our model template into each of our subjects’ native space using templates from our previous research (for more details see: Huffman and Stark, 2014, 2017). For our functional correlativity analysis, we used an atlas of 264 functional nodes (from Power et al., 2011; Cole et al., 2014; see Figure S3A), which we warped from MNI space into our model template space and then into each participant’s native space. For all masks, we then resampled these to the fMRI resolution and masked to only include completely sampled voxels.

Standard fMRI preprocessing

Each participant’s functional runs were aligned to their MP-RAGE scan by a 12 parameter affine transformation, which also included motion correction and slice-time correction, using align_epi_anat.py (Saad et al., 2009) in AFNI (Cox, 1996). Additional preprocessing was conducted for our functional correlativity analysis (see Functional correlativity preprocessing).

Univariate analysis

We used the 3dDeconvolve function in AFNI to conduct a finite-impulse-response-based (FIR) regression analysis (using the TENTzero option; we modeled each TR from the stimulus onset to 24 seconds following stimulus onset; note, this model sets the initial and final values to zero; we set the polort option to 3, thus allowing up to 3rd order drifts to be removed from the data). Similar to our functional correlativity analysis, we censored frames using a framewise displacement threshold of 0.5 mm (see Functional correlativity preprocessing). We used an area-under-the-curve-type approach by summing the resultant betas from 4 to 8 seconds following stimulus onset. We first assessed the hypothesis that the retrosplenial cortex, parahippocampal cortex, and the hippocampus would exhibit task-based activations for the JRD task relative to our active baseline task by testing whether the resultant “peak” responses were greater than zero. Specifically, within each subject, we averaged all of the peak responses within each ROI and then we used a t-test (using the t.test function in R) and a Bayes factor t-test (using the ttestBF function within BayesFactor in R; note, the rscale factor was set to the default: $\sqrt{2}/2$) to assess whether these responses differed from zero at the group level. We also conducted a Bayes factor ANOVA to assess whether there was a difference in task-based activation within these regions as a function of body-based cues (see fMRI Bayes factor analysis).

We conducted a similar analysis at the whole-brain level. Here, we warped the resultant whole-brain peak response maps to our model template using ANTs. We then used 3dttest++ (compile date August 28, 2016) to determine brain regions that had peak responses that were significantly different than zero (note, we used the -clustsim option to calculate a cluster-corrected threshold for significance). For our main analysis of task-based activation (i.e., JRD task vs. active baseline task), we set a voxelwise threshold of p < 0.001 (this corresponded to a FDR q < 0.0196) and a corrected cluster threshold of p < 0.01 (here, 18 voxels). We implemented a whole-brain ANOVA (using the 3dANOVA2 function) to test the hypothesis that task-based activation would differ as a function of body-based cues. Because this analysis revealed no significant clusters throughout the entire brain, we implemented a whole-brain Bayes factor analysis to assess whether evidence throughout the brain was in fact more consistent with the null hypothesis (see fMRI Bayes factor analysis).

fMRI Bayes factor analysis

Similar to our analysis of the JRD task data during fMRI scanning (see Analysis of behavioral data), we implemented a Bayes factor ANOVA (Rouder et al., 2012) to assess whether the evidence was in favor of the null hypothesis or the alternative hypothesis of a difference in task-based activation (i.e., JRD task vs. the active baseline task) as a function of body-based cues conditions. First, we conducted an ROI analysis in which we used the anovaBF function (the rscaleFixed parameter was set to the default: 1/ 2) from BayesFactor to test whether task-based activation differed within our ROIs (see Regions of interest). Second, we conducted a whole-brain analysis in which we used oro.nifti (version 0.9.1; Whitcher et al., 2011) to load our fMRI data into R and we wrote code to implement anovaBF at every voxel of the brain. We then saved the results of our Bayes factor analysis as AFNI files for visualization.

Functional correlativity preprocessing

After the steps described in Standard fMRI preprocessing, the time-series were quadratically detrended using 3dDetrend and then normalized to zero mean and unit variance (i.e., within each voxel) using 3dTstat and 3dcalc. We then regressed out the six motion parameters generated from motion correction as well as their first derivatives (using 3dDeconvolve and 1d_tool.py). We then used the CompCorrAuto function within ANTs (i.e., within the ImageMath function) to calculate the first six principal components of the time-series across all voxels in the brain, including gray matter, white matter, and cerebrospinal fluid. We then regressed out these 6 components, and we bandpass filtered these time-series between 0.009 and 0.08 Hz.

We then regressed out the effect of task using a FIR deconvolution (using the TENT option within 3dDeconvolve; we modeled each TR from the stimulus onset to 24 seconds following stimulus onset). Importantly, this method makes no assumptions about the underlying shape of the hemodynamic response (cf. Norman-Haignere et al., 2012). We then extracted the first eigentimeseries from each of our ROIs (i.e., the 264 node atlas from Power et al., 2011) using 3dmaskSVD. Note, this process is akin to extracting the average time-series but has been shown to provide a more representative time-series of voxels throughout an ROI (e.g., O’Reilly et al., 2010). We followed the approach of Power et al. (2012) and censored frames with a framewise displacement greater than 0.5 mm as well as one frame before any such motion events and two frames following any such motion events. We then calculated Pearson’s correlation coefficient between each of our ROIs, separately for each run, and entered these values into a correlation matrix. We converted these matrices using Fisher’s r-to-z transformation (z[r])—i.e., the inverse hyperbolic tangent function. The lower triangle of these z[r] correlation matrices—i.e., the unique entries—were used in our classification analysis. Note, we only included ROIs that had coverage across all 21 participants.

Functional correlativity analysis

We performed a leave-one-subject-out cross-validation classification analysis using a linear support vector machine (SVM) in Python using the LinearCSVMC function in PyMVPA (0.2.6; Hanke et al., 2009) and custom-written code on a NeuroDebian platform (Halchenko and Hanke, 2012). For each iteration of the analysis, each feature (i.e., between-region correlation) was normalized to zero mean and unit variance using the StandardScalar function in scikit-learn (0.18.1; Pedregosa et al., 2011). We then performed principal components analysis (PCA) and extracted the minimum number of features required to explain 97.5% of the variance using the PCA function in scikit-learn. Importantly, both the normalization and PCA steps were fit using the training data and these models were then applied to the left-out test data (i.e., the test data were not used in the normalization or in the PCA steps). These features were then used to train a linear SVM, and the left-out participant was used to assess classifier accuracy (i.e., the percentage of correctly predicted task labels). This procedure was iterated until all participants served as the left-out test dataset, and we averaged the classification accuracy over all participants.

We assessed whether classification accuracy was better than chance using a randomization test in which the task condition labels in the training set were randomly shuffled and we tested performance using unshuffled labels in the test set. On each iteration, we randomized the training labels and then ran all iterations of testing. Note that our shuffling procedure matched the pseudo-randomization of our actual data collection. Specifically, the run labels were not shuffled between the first and second half of the runs because in our experimental design we ensured that every task type occurred prior to any repetitions; thus, fully randomizing the labels in our randomization test could have led to increased variability that was not present in our actual data. For each of the 10,000 iterations, we calculated the average classification accuracy. We then calculated two-tailed p-values by comparing the empirical classification accuracy to that across the 10,000 permutations (see Ernst, 2004; Huffman and Stark, 2017; Huffman and Ekstrom, 2019):

$$p=\frac{1+{\sum }_{i=1}^{10,000}I\left(\left|t_i-\overline{t}\left|\ge \right|t^{\ast }-\overline{t}\right|\right)}{1+10,000}$$ (1)

where $I\left(\cdot \right)$ is an indicator function that is set to 1 if the statement is true and to 0 otherwise, t_i represents the classification accuracy on the ith randomization, $\overline{t}$ represents the mean across all such randomizations, and t* represents the observed classification accuracy (i.e., the empirical classification accuracy). We set a significance threshold of a two-tailed p < 0.05. Note, any statistics that we report at p < 0.05 for our permutation test on classification accuracy also survived false discovery rate (FDR) correction for multiple comparisons using the Benjamini-Hochberg method (Benjamini and Hochberg, 1995) using p.adjust in R.

Single-trial classification analysis

We generated single-trial patterns of activity using an iterative approach across all trials within a run. Specifically, for each iteration we fit a FIR regression model (using the TENTzero function within 3dDeconvolve) which contained one regressor for the trial of interest and one regressor for all other trials (note, this is an FIR version of the Least Squares – Separate [LS-S] approach described in Mumford et al., 2012; Turner et al., 2012). Here, we ran this iterative approach within each run separately, thus each run solely contained trials of one type. Similar to our activation analysis, we summed the resultant betas from 4 to 8 seconds following stimulus onset and we censored frames using a framewise displacement threshold of 0.5 mm (see Univariate analysis and Functional correlativity preprocessing). Additionally, we excluded any trials with any censored frames during the duration of the modeled FIR response because 1) models with censored frames at the single-trial level resulted in matrix inversion errors due to insufficient data and 2) motion during a single trial would make its estimation inherently noisy in any case. Note, for cases in which trials were excluded, we balanced the number of trials in each condition of our classification analysis by randomly selecting the same number of trials for each condition (this procedure was performed separately within each split-halves of the data and for each binary classification).

We performed a within-subject split-halves classification analysis using a similar approach to our analysis of functional correlativity patterns. Specifically, for each pair of conditions, we normalized the patterns of activity within each split halves of the data to zero mean and unit variance. We used a linear SVM to classify individual trial patterns of activity, separately within each participant. We averaged the classification accuracy for each participant for each comparison and assessed whether these accuracies were significantly better than chance using a randomization test. We randomized the labels using the same pseudo-randomization as our empirical data. Specifically, for each participant there were 4 possible permutations (i.e., 2 ×2) of the labels. We generated a group-level null distribution by randomly selecting one value from each participant’s permutation vector 10,000 times (note, there were a total of 4^N = 4²¹ possible permutations). We assessed whether the classification accuracy was better than chance using a two-tailed test (see Equation 1).

Because classification accuracy was calculated within each participant individually, we were also able to compare whether classification accuracy was significantly better than chance using t-tests in which we compared the group of classification accuracies to an assumed chance accuracy of 50% (note, the means of the null distributions from our randomization tests were all around 50%). This procedure revealed nearly identical results to our randomization test. We extended this approach to a Bayes factor framework to assess whether the chance-level classification accuracy between body-based cues conditions was more consistent with the null hypothesis. Specifically, we used one-tailed Bayes factor t-tests to assess whether classification accuracy was more consistent with the hypothesis of the null hypothesis of 50% accuracy relative to the alternative hypothesis of greater than 50% accuracy (using the ttestBF function within BayesFactor in R; note, the rscale factor was set to the default: $\sqrt{2}/2$. We ran a one-tailed test was because classification accuracy between body-based cues conditions was occasionally less than 50%, thus we felt it was more intuitive to calculate one-tailed Bayes factors (i.e., because sometimes the Bayes factors were in favor of the alternative hypothesis of classification accuracy less than 50%). Additionally, we performed a between-condition generalization test, similar to our approach for functional correlativity patterns. Specifically, within each participant, we trained the classifier on a pair of conditions, and then tested the classifier on a complementary set of conditions. Importantly, we used the same split-halves approach as our main analysis, and we again assessed significance via a randomization test.

Single-trial pattern similarity analysis

We performed a split-halves pattern similarity analysis in which we calculated the correlation between all possible pairs of trials between different runs, separately within each body-based cues condition (for details on estimation of single-trial patterns of activity see Single-trial classification analysis). We also calculated the Euclidean distance between the imagined standing locations between trials. We used linear mixed models to assess whether the Euclidean distance model provided a better fit to the pattern similarity data than a null model. Additionally, we compared whether a model that included an interaction between body-based cues and Euclidean distance fit the pattern similarity values better than the Euclidean distance model. The random effects structure for the null model, the Euclidean distance model, and the interaction model included random intercepts and slopes for body-based cues conditions (note, this random effects model fit the data significantly better than a random effects model that only included random intercepts for participants; Matuschek et al., 2017). We performed likelihoood ratio tests to assess significance of the models (also see Analysis of behavioral data). Identical results for the effect of Euclidean distance were obtained when we used a permutation approach (using the function permlmer from the package predictmeans in R), which is subject to different assumptions than the likelihood ratio test. Note, an initial analysis using the anatomical hippocampus did not reach significance, so for the pattern similarity analysis we report the results from a functional region of interest for the hippocampus, in which we selected the 100 most active voxels (the voxels with the largest t-statistic for the JRD task vs. active baseline task) in each hemisphere and combined these to generate bilateral masks, similar to previous studies (Marchette et al., 2015; Vass and Epstein, 2017).

DATA AND CODE AVAILABILITY

The datasets and code from this study are available from the corresponding author on request.

Supplementary Material

2. Data File 1.

Related to Figure 4 and Figure S4. This file contains the “underlay” file for the activation and Bayes factor analysis. Specifically, this file contains our model template brain, which can be used for viewing the neuroimages in Data Files 2-6.

3. Data File 2.

Related to Figure 4A. This file contains a figure of the beta maps (sum of the beta coefficients from 4–8 seconds following stimulus onset) from the activation analysis for the judgments of relative directions task and it has been thresholded at a voxelwise p < 0.001 and cluster-corrected threshold of p < 0.01.

4. Data File 3.

Related to Figure 4B. This file contains a figure of the Bayes factor maps from the ANOVA investigating whether there were differences as a function of body-based cues. The values in this map represent the Bayes factors in favor of the null hypotheses (i.e., BF₀₁) and have been thresholded at BF₀₁ > 3.

5. Data File 4.

Related to Figure S4A. This file contains a figure of the beta maps (sum of the beta coefficients from 4–8 seconds following stimulus onset) from the activation analysis for the judgments of relative directions task for the “enriched” condition. This map has been thresholded at a voxelwise p < 0.001 and cluster-corrected threshold of p < 0.01.

6. Data File 5.

Related to Figure S4B. This file contains a figure of the beta maps (sum of the beta coefficients from 4–8 seconds following stimulus onset) from the activation analysis for the judgments of relative directions task for the “limited” condition. This map has been thresholded at a voxelwise p < 0.001 and cluster-corrected threshold of p < 0.01.

7. Data File 6.

Related to Figure S4C. This file contains a figure of the beta maps (sum of the beta coefficients from 4–8 seconds following stimulus onset) from the activation analysis for the judgments of relative directions task for the “impoverished” condition. This map has been thresholded at a voxelwise p < 0.001 and cluster-corrected threshold of p < 0.01.

KEY RESOURCES TABLE

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Software and Algorithms
AFNI (Debian precompiled binary; Debian-16.2.07~dfsg.1–2ñd80+1; August 28, 2016)	Cox (1996)	http://neuro.debian.net/pkgs/afni.html
ANTs (2.0.1)	Avants et al. (2011)	http://neuro.debian.net/pkgs/ants.html
BayesFactor (0.9.12) package for R	Rouder and Morey (2012)	https://cran.r-project.org/web/packages/BayesFactor
lme4 (1.1–14) package for R	Bates et al. (2015)	https://cran.r-project.org/web/packages/lme4
NeuroDebian	Halchenko and Hanke (2012)	http://neuro.debian.net/index.html
oro.nifti (0.9.1)	Witcher et al. (2011)	https://cran.r-project.org/web/packages/oro.nifti
PyMVPA (0.2.6)	Hanke et al. (2009)	http://neuro.debian.net/pkgs/python-mvpa2.html
Python (2.7.9)	Python Software Foundation	https://www.python.org
R (3.3.1)	R Core Team (2016)	https://www.r-project.org
scikit-learn (0.18.1) package for Python	Pedregosa et al. (2011)	http://neuro.debian.net/pkgs/python-sklearn.html
Unity 3D	Unity Technologies	https://unity3d.com

Highlights.

• What is the role of body-based cues, such as head turns, in human navigation?

• We tested this question using immersive virtual reality and neuroimaging

• Behavioral and brain data suggest that human spatial memory is modality independent

• Vision might play a dominant role in human memory for large-scale spaces