Development of a spatial model of age-related change in the macular ganglion cell layer to predict function from structural changes

Abstract

Purpose:

To develop location specific models of normal, age-related changes in the macular ganglion cell layer (GCL) from optical coherence tomography (OCT). Using these OCT-derived models, we predicted visual field (VF) sensitivity and compared these results to actual VF sensitivities.

Design:

Retrospective cohort study

Methods:

Single eyes of 254 normal participants were retrospectively enrolled from the Centre for Eye Health (Sydney, Australia). Macular GCL measurements were obtained using Spectralis OCT. Cluster algorithms were performed to identify spatial patterns demonstrating similar age-related change. Quadratic and linear regression models were subsequently utilized to characterize age-related GCL decline. 40 participants underwent additional testing with Humphrey VFs, and 95% prediction intervals were calculated to measure the predictive ability of structure-function models incorporating cluster-based pooling, age-correction and consideration of spatial summation.

Results:

Quadratic GCL regression models provided a superior fit (p = <0.0001-0.0066), establishing that GCL decline commences in the late 30’s across the macula. The equivalent linear rates of GCL decline showed eccentricity-dependent variation (0.13μm/year centrally versus 0.06μm/year peripherally), however average, normalized GCL loss per year was consistent across the 64 macular measurement locations at 0.26%. The 95% prediction intervals describing predicted VF sensitivities were significantly narrower across all cluster-based structure-function models (3.79-4.99dB) compared with models without clustering applied (5.66-6.73dB, p <0.0001).

Conclusions:

Combining spatial clustering with age-dependent regression allowed the development of robust models describing GCL changes with age. The resultant superior predictive ability of VF sensitivity from ganglion cell measurements may be applied to future models of disease development to improve detection of early macular GCL pathology.

Introduction

With the ongoing advances in optical coherence tomography (OCT) technology, high-resolution in vivo visualization of the retinal nerve fiber layer (RNFL) and ganglion cell layer (GCL) have become possible, providing invaluable information supplementing the clinical examination of glaucoma.^{1, 2} Although natural changes to the GCL should not be difficult to capture in theory, various biological factors including concurrent changes due to normal aging and inherent, normal inter-individual variation confound our ability to differentiate variations of normal from early disease states.^3-5 In conjunction with functional considerations such as variable spatial summation characteristics across different macular regions,^6-8 these factors have contributed to so-called discordance in the relationship between macular ganglion cell (GC) measurements and visual field (VF) sensitivity.^9-12 Theoretically, if approaches aimed towards characterizing these structural and functional factors in greater detail and limiting their complexity are successfully integrated, there is potential to develop relatively simple yet robust models describing both aging changes in the macular GCL and the structure-function relationship at the macula.

The rate of age-related decline in the macular GCL is a subject of controversy, and successful identification of age-related changes requires minimization of variability within individual groups, which may be attained by clustering data with similar properties. Hierarchical clustering, k-means clustering and pattern recognition analyses using Iterative Self-Organizing Data Analysis Technique Algorithm (ISODATA) clustering have been successfully applied in various contexts of vision science, including the identification of VF isocontours, pathological changes in retinal OCTs, and glaucomatous progression.^13-17 More recently, pattern recognition was applied to OCT structural measurements at the macula, demonstrating that the decline of GCs with age is neither random nor uniform, but organized in statistically separable clusters.¹⁸ However, partial dependency of this statistical method on initial input assumptions resulted in reasonable variation in the possible number of clusters and resultant cluster patterns. More importantly, the proposed segmented linear regression model applied in this study suggests that GCL loss occurs abruptly at a relatively late age,¹⁸ which is not consistent with aging in other visual processes that has been reported to deteriorate more gradually.^19-21 Models describing a gradual decline in the GCL may be more appropriate to describe normal aging in concordance with functional data.

In the current study, cluster based-regression models were employed to describe normal, age-related decline in the macular GCL using OCT measurements, which were consequently used to optimize the structure-function relationship between macula GC counts and co-localized VF sensitivities. We hypothesize that optimized application of such approaches will aid generation of robust spatial-temporal models describing age-related decline in the macular GCL, and that the combination of these models with functional data under consideration of spatial summation properties can improve structure-function correlations. As a consequence, we will demonstrate that the derived structure-function correlations allow for accurate prediction of VF sensitivity from structural measurements, which has important implications for detection of early disease states.

Method

Participant Recruitment

Data were retrospectively collected from patients attending the Centre for Eye Health (CFEH, Sydney, Australia) for glaucoma assessment, who did not display retinal or optic disc abnormalities on clinical examination using standard clinical protocols.^{18, 22} A total of 254 participants met inclusion criteria defined as: visual acuity better than 20/25 (logMAR > 0.1) or 20/32 (logMAR > 0.2) for individuals under and over 60 years respectively, intraocular pressure <22mmHg in both eyes, spherical equivalent refractive error between +3.00 and −6.00 diopters and astigmatism <3.00 diopters, no media opacity resulting in inadequate scan quality and the absence of any optic nerve or retinal pathologies that may affect GCL thickness or segmentation (Table 1). Ethics approval was provided by the University of New South Wales Australia Human Research Ethics Advisory panel, and the tenets of the Declaration of Helsinki were observed throughout the duration of this study.

Table 1.

Demographic characteristics of the study population. Decade brackets were derived by grouping together participants from the 5 year brackets within that decade; as an example, the 20-29 decade bracket consisted of participants in the 20-24 and 25-29 brackets.

Cohort	n	Age, y ± SD (range)	Gender, male:female	Ethnicity, European:Asian:Other	Eye tested, OD:OS	SE ± SD, Dioptres
All subjects	254	50.3 ± 14.4 (20.2-84.9)	109:145	156:91:7	132:122	−0.47 ± 1.74
Cohort characteristics per 5 years
20-24	13	22.6 ± 1.3	7:6	4:9:0	4:9	−1.33 ± 1.55
25-29	16	27.9 ±1.4	4:12	9:7:0	8:8	−1.55 ± 1.87
30-34	15	32.0 ±1.6	6:9	6:9:0	7:8	−1.30 ± 1.22
35-39	11	37.1 ±1.5	3:8	5:6:0	8:3	−1.58 ± 2.30
40-44	23	42.5 ±1.6	7:16	12:9:2	16:7	−0.68 ± 1.61
45-49	46	47.5 ±1.5	18:28	27:19:0	25:21	−0.75 ± 1.52
50-54	34	52.4 ± 1.4	14:20	20:12:2	19:15	−0.38 ± 1.49
55-59	32	57.3 ± 1.4	16:16	22:8:2	18:14	+0.07 ± 1.35
60-64	26	62.2 ± 1.6	13:13	20:6:0	11:15	−0.22 ± 2.29
65-69	14	67.4 ± 1.2	6:8	12:2:0	8:6	+0.31 ± 1.58
70-74	12	72.0 ± 1.8	8:4	8:3:1	4:8	+ 1.04 ± 1.30
75-84	12	79.4 ± 3.0	7:5	11:1:0	4:8	+0.72 ± 1.74
Cohort included in structure-function analyses
	40	46.1 ± 15.0 (20.8-71.6)	19:21	24:12:4	26:14	−1.12±2.47

y, years; SD, standard deviation; OD, right eye; OS, left eye; SE, spherical equivalent

Macular OCT

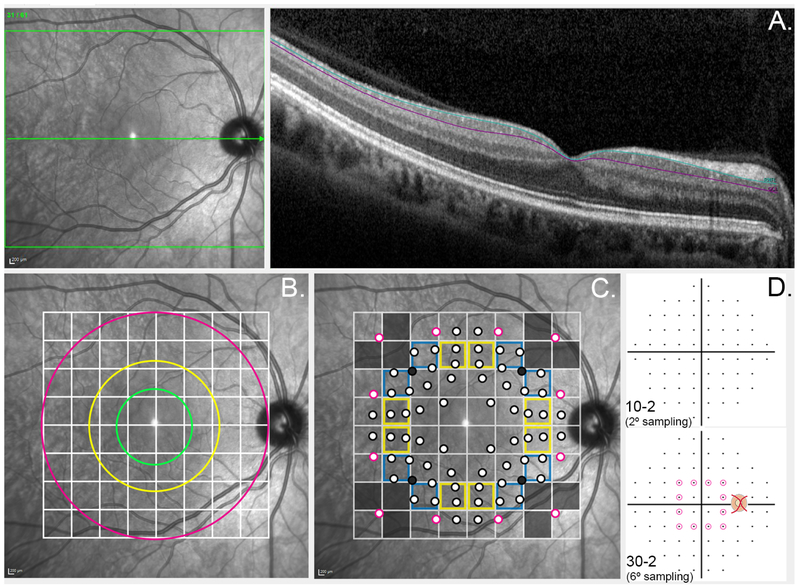
GCL thickness measurements were obtained at the posterior pole from Spectralis OCT (Heidelberg Engineering, Heidelberg, Germany), following manual correction of automated segmentation (Figure 1A). Posterior pole scans consisted of an 8 × 8 grid covering a total macula area of 6880μm × 6880μm centred on the foveal pit, and each posterior pole scan included a total of 61 OCT B-scans spaced 120μm apart. One eye per participant was randomly included, and all left eye scans were converted to right eye format to facilitate direct comparison between scans. Measurements with poor quality, poor segmentation that could not be corrected, or missing data were excluded as reported previously.^{18, 22} Average GCL thicknesses for each grid square were extracted directly from the instrument review software (Heidelberg Engineering, Heidelberg, Germany), with the exception of the 4 central grid squares including the foveal pit, as average GCL measurements in these locations systematically underestimate the true foveal GCL thickness. As per Yoshioka et al.,²² the projected location of the 4 innermost 10-2 HVF stimuli onto the macula was isolated to identify the primary location responding to each stimulus, with corrections applied to account for the relative displacement of the corresponding GC locations secondary to Henle’s fibers (Figure 1C).²³ The GCL thickness measurements from this point and 4 points in the 1-degree surrounding area were averaged to calculate the average GCL thickness at each foveal location. The remaining VF points were also corrected for displacement, as per Drasdo et al.,²³ so that each retinal test point location correlated with the corresponding GCL location.

Figure 1. Schematic illustrating methodology to obtain structural measurements.

(A) Ganglion cell layer thickness (GCL) measurements (depicted between aquamarine and purple lines) were extracted from Spectralis OCT B-scans oriented to the horizontal raphé (green arrow). (B) The default Spectralis OCT posterior pole grid centered on the horizontal raphé indicates 64 areas over which measurements were averaged. The green, yellow and fuchsia rings coincide with the outermost boundary of the fovea, parafovea and perifovea respectively. (C) Projected visual field test locations are indicated in relation to the Spectralis OCT posterior pole grid. Corrections were applied to account for the relative displacement of the corresponding GC locations secondary to relative elongation of Henle’s fibers at the central fovea.²³ Points outlined in black indicate points from the 10-2 testing paradigm, and points outlined in fuchsia indicate the 12 paracentral points from the 30-2 testing paradigm. For grids outlined in yellow or blue, 2 or 3 visual field measurements respectively were averaged to obtain an average visual field sensitivity corresponding to the GCL measurement for the particular grid square. Grey points and grid squares indicate visual field points and ganglion cell layer measurements were excluded from structure-function analyses. (D) The 10-2 (2° separation between test points) and 30-2 Humphrey visual field test paradigms (6° separation between test points). The visual field points on the 30-2 grid circled in fuchsia indicate the paracentral points utilized in the structure-function correlations in this study.

Cluster Analysis

Average GCL thickness measurements per grid square were grouped by patient age in decade intervals for consistency with previous studies^{4, 18} as well as in 5-year intervals (Table 1). As different clustering methods applied to VF data has previously yielded virtually identical cluster patterns,²⁴ we compared several clustering approaches to the obtained GCL thickness measurements to determine whether similar robustness could be observed in structural data. Hierarchical clustering was performed applying within-groups linkage based on squared Euclidean distance using SPSS Statistics Version 25.0 (IBM Corporation, New York, NY, USA). The maximum number of clusters identified with hierarchical clustering was subsequently used as the initial number of clusters in k-means cluster analysis, allowing for direct comparison of resultant cluster patterns from hierarchical and k-means methods. Statistically significant separability of clusters was verified by the d’ distance:²⁴

$$d^{\prime }=\frac{\mid x_1-x_2\mid }{\sqrt{0.5\times ({{\sigma }_1}^2+{{\sigma }_2}^2)}}$$

whereby clusters resulting in d’ < 1 were merged until all final cluster pairs were separated by d’ ≥ 1, indicating that the distributions were separated by at least 1 standard deviation (SD). Additionally, cluster distributions were compared using two-way ANOVA with correction for multiple comparisons using Tukey’s test (GraphPad Prism Version 7.04, La Jolla, CA, USA).

Pattern recognition analysis was employed to compare current outcomes to previously published data.^{13, 18} This method requires conversion of average GCL thicknesses per grid square and age bracket into pixel values between 0 (smaller measurement) to 255 (larger measurement), which are subsequently clustered using an unsupervised ISODATA approach (PCI Geomatica version 10; PCI Geomatics, Richmond Hill, Ontario, Canada). The separability of classes was determined through transformed divergence (D_T) statistic with a cut-off value of > 1.90 corresponding to >98% probability of correct classification.^{13, 18, 25}

Regression Analysis

Quadratic and linear regression models were calculated from average regression rates of GCL measurements per cluster and age bracket using GraphPad Prism Version 7.04. Vertex points were for quadratic regression curves were determined from axis of symmetry formula:

$$x(y^{\prime }=0)=-\frac{b}{2a}$$

Equivalent linear regression analyses were performed from the vertex point onwards, as an indication of mean annual reduction in GCL thickness.

Structure-Function Correlations

Forty participants experienced at undertaking VFs also underwent Humphrey VF testing (Carl Zeiss Meditec) using full threshold 10-2 and 30-2 testing strategies with the commonly used Goldman III (GIII) stimulus size as well as Goldman II (GII), which satisfies complete spatial summation criteria in the macula.^{6-8, 26-28} Each combination of stimulus size and testing grid was repeated, totaling 8 VFs for the eye that had undergone structural analyses, and the order in which VFs using different stimulus sizes and testing paradigms were performed was randomized to minimize the influence of potential systematic order effects. Rest breaks were offered to all participants between each VF to limit potential effects of fatigue on VF results. VF exceeding manufacturer-specified criteria of ≤20% fixation losses and ≤15% false positives, in conjunction with gaze tracker information, were considered unreliable and excluded from analysis. Results of all 10-2 test points and an additional paracentral 12 test points from the 30-2 grid were extracted and recorded in right eye format (Fig 1D).

All data were age-corrected to a 50-year-old equivalent to maintain consistency with previous work and SITA strategies that automatically modulate VF sensitivity based on patient age.^{7, 22, 29-32} GCL thickness data was accordingly age-corrected to a 50-year-old equivalent based on the outcome of regression analyses described above, and was used to calculate the estimated number of GCs stimulated by the projected VF stimuli (ganglion cells per stimulus area, GCpSA).^{22, 33} For linear correlation with VF sensitivity data,^{22, 34} average GCpSAs across all participants for each gridwise location were converted to a decibel (dB) scale:

$${\mathit{GCpSA}}_{dB}=10\times {\log }_{10}(\mathit{GCpSA})$$

Linear structure-function correlations were subsequently established from mean GCpSA and VF sensitivity values based on spatially co-localized areas under consideration of lateral displacement of GCs (Figs 1C, D).²³ Where more than one VF measurements corresponded to a structural measurement grid, arithmetic mean sensitivity for that location was calculated. VF test points that did not clearly correspond to one grid square and GC measurements at locations that did not correlate with a VF location were excluded from analyses.

Statistical Analysis

Statistical analyses were performed using GraphPad Prism Version 7.04. Normality of GCL thickness data was determined using D’Agostino and Pearson normality tests. To account for occasional variation in cluster assignment between different methods, Kruskal-Wallis tests with Dunn’s correction for multiple comparisons were applied. Final cluster assignments were decided using highest p-value ranking, indicative of poorer separability between grid square and overall cluster means. For each cluster and cluster pattern, sum-of-squares F tests were used to compare and determine whether quadratic and linear regressions better fit the data. F tests were used to compare regression models derived from different cluster patterns and age-intervals (e.g. 5-year vs decade grouping). Bonferroni correction at an α of 0.05 was applied to account for multiple comparisons.

F-test statistics was further applied to determine significant differences between structure-function correlations. The 95% prediction intervals for different models were compared to the expected variability of VF sensitivities for each stimulus size and location, defined as 2 SDs of expected VF sensitivity for each stimulus size,¹³ using Kruskal-Wallis tests with Dunn’s correction for multiple comparisons. Individual participants’ grouped GCpSA and VF sensitivity measurements were used to calculate the proportions captured by corresponding 95% prediction intervals. Differences between actual and predicted VF sensitivities were visualized with Bland-Altman methods. Outliers, defined as VF sensitivity corresponding to a GCpSA outside of the expected normal variability, were excluded and the described analysis process was repeated to determine potential improvement in accuracy of the 95% prediction intervals. Mann-Whitney test was performed to compare 95% prediction interval size between different stimulus sizes, cluster patterns and after exclusion of outliers. The threshold of statistical significance was set at p <0.05 for all analyses.

Results

Study Cohorts

Of the total study cohort 57% was female, with the majority (61.4%) of European descent (Table 1). As expected with a higher prevalence of ocular pathologies with increasing age, the participants aged over 75 years of age were comparatively sparse; to maintain comparable sample sizes between groups, participants aged 70 to 84 were not divided into 5-year brackets but analyzed as a single group. Characteristics of the subset of participants for structure-function comparisons (n = 40) were similar to those of the overall study population (Table 1).

Cluster Patterns

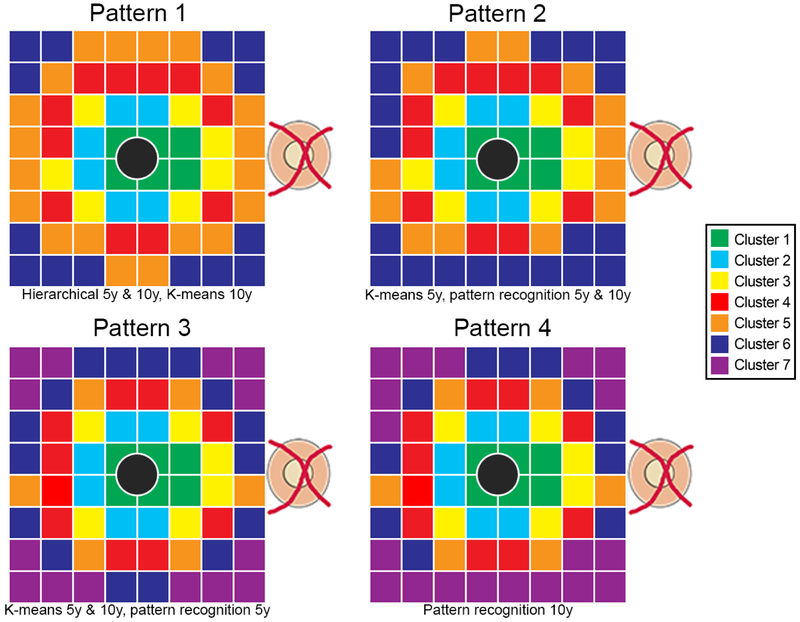
Hierarchical cluster analysis identifying patterns of age-related change in GCL thickness resulted in a maximum of 6 clusters (Figure 2, Pattern 1), regardless of whether decade or 5-year intervals were used. The corresponding k-means cluster algorithm with initial number of clusters set at 6 confirmed this pattern when based on decade intervals. K-means clustering based on 5-year interval data and pattern recognition based on decade and 5-year intervals resulted in some reassignments of the outermost perifoveal points to different clusters (Figure 2, Pattern 2). For comparison with previously published data,¹⁸ both pattern recognition and k-means cluster algorithms were applied with the initial number of clusters set at 7. K-means clustering irrespective of the underlying age brackets and pattern recognition based on 5-year intervals arrived at the same results (Figure 2, Pattern 3), with distinct differences in the two most peripheral clusters from the pattern obtained with pattern recognition based on decade data (Figure 2, Pattern 4). Of note, each of the identified patterns demonstrated an overall concentric cluster configuration, whereby all clusters were statistically separable using d’ calculations and displayed significantly different GCL thickness distributions using two-way ANOVA with Tukey’s test for multiple comparisons. The different cluster algorithms identified highly reproducible patterns, indicating that the observed classifications were highly robust and not dependent on the underlying approach, and further details on the minor variations between cluster algorithms are available in Supplementary Table 1.

Figure 2. Concentric pattern of GCL thickness indicative of locations demonstrating similar change with age.

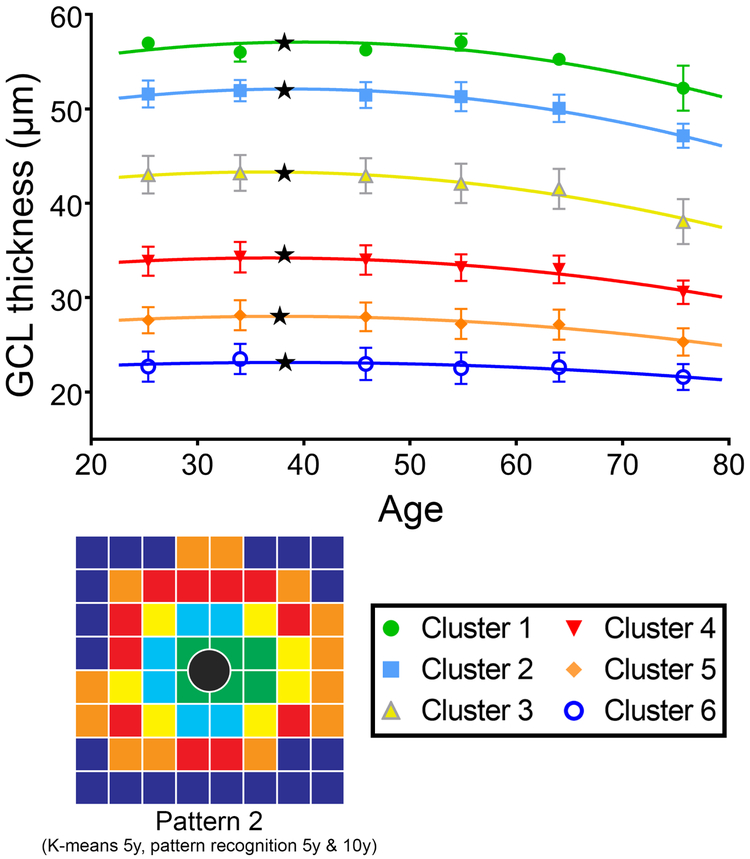
GCL thickness grid squares denoted by the same color depict clusters with similar age-related changes derived from hierarchical, k-means and pattern recognition analyses with data grouped into 5 year and decade brackets. The most robust outcomes resulted in a maximum of 6 statistically separable clusters (Patterns 1 and 2), and to maintain consistency with previous work k-means and pattern recognition clustering with 7 statistically separable clusters were generated (Patterns 3 and 4). The cluster algorithms utilized to generate individual cluster patterns are listed beneath each pattern, with 5y and 10y representing data grouped in 5-year and decade brackets respectively. Grey central circles correspond to the foveal pit, which was excluded from analysis due to the lack of ganglion cells within this region.

Regression Analyses

Regression analysis was performed on each of the identified clusters within each cluster pattern to quantify GCL change as a function of age. Models based on either 5-year or decade intervals were not significantly different for any of the cluster algorithms (p = 0.96-0.99). As a result, reported regression curves are displayed for decade data, but apply equally to data based on 5-year intervals. Most notably, quadratic regression models provided a superior fit for each of the examined clusters across all patterns in comparison to linear regression models (F-test, p = <0.0001-0.0066). Comparison of the fitted regression curves between clusters within each pattern revealed no significant difference between the regression coefficients excluding constants (p = 0.06-0.11) within foveal and parafoveal clusters (Figure 1B, corresponding to clusters 1-4 in Figure 2), indicative of similar rates of GCL change in the central retina. Similarly, patterns 3 and 4 exhibited consistent regression coefficients excluding constants (p = 0.22-0.78) between perifoveal clusters (Supplementary Table 2, corresponding to clusters 5-7 in Figure 2), but significant differences were observed between all other clusters (p = <0.0001-0.012), indicating different rates of GCL thickness change between the central and perifoveal regions.

Quadratic regression models indicate GCL thickness initially increases followed by a decrease past the vertex point, which was located at the late 30’s across all clusters (mean 38.0 years, range 36.2-38.7 years, Table 2). The mean absolute increase in GCL thickness between 20 years of age to the vertex points across all clusters was small (mean 0.86μm, range 0.36-1.52μm), equivalent to an annual increase of 0.048μm/year (range 0.020-0.084μm/year). Linear regression slopes were calculated past the vertex point to obtain estimates of annual rates of GCL decline, which were higher in the foveal and parafoveal (mean 0.13μm/year) than the perifoveal (mean 0.06μm/year) regions (Table 2). As the GCL of the central retina is invariably thicker than in more peripheral locations, average annual loss may be proportional to peak GCL thickness at each location. When expressed as percentage loss of peak GCL thickness, an equivalent mean rate of loss in GCL beyond 38 years of 0.260%/year was calculated across all clusters and cluster patterns (range 0.256-0.263%), without significant differences between clusters (p = 0.06-0.12).

Table 2.

Quadratic regression characteristics for the four cluster patterns described in Figure 2.

	R2	Vertex point	Slope of linear regression after vertex point (μm/year)
Pattern 1 (6 Clusters)
Cluster 1	0.81	38.19	0.13
Cluster 2	0.94	38.19	0.13
Cluster 3	0.94	38.19	0.13
Cluster 4	0.86	38.19	0.13
Cluster 5	0.92	38.66	0.07
Cluster 6	0.74	36.22	0.04
Mean	0.87	37.94	0.10
Pattern 2 (6 Clusters)
Cluster 1	0.81	38.19	0.13
Cluster 2	0.94	38.19	0.13
Cluster 3	0.94	38.19	0.13
Cluster 4	0.86	38.19	0.13
Cluster 5	0.92	37.75	0.07
Cluster 6	0.80	38.27	0.04
Mean	0.88	38.13	0.11
Pattern 3 (7 Clusters)
Cluster 1	0.81	38.23	0.13
Cluster 2	0.94	38.23	0.13
Cluster 3	0.92	38.23	0.13
Cluster 4	0.88	38.23	0.13
Cluster 5	0.93	38.30	0.07
Cluster 6	0.91	38.30	0.07
Cluster 7	0.74	36.22	0.04
Mean	0.87	37.96	0.10
Pattern 4 (7 Clusters)
Cluster 1	0.81	38.23	0.13
Cluster 2	0.94	38.23	0.13
Cluster 3	0.92	38.23	0.13
Cluster 4	0.88	38.23	0.13
Cluster 5	0.93	38.19	0.08
Cluster 6	0.93	38.19	0.08
Cluster 7	0.79	36.93	0.04
Mean	0.88	38.03	0.10

R², coefficient of determination, μm, microns

Structure-Function Correlations and 95% Prediction Intervals

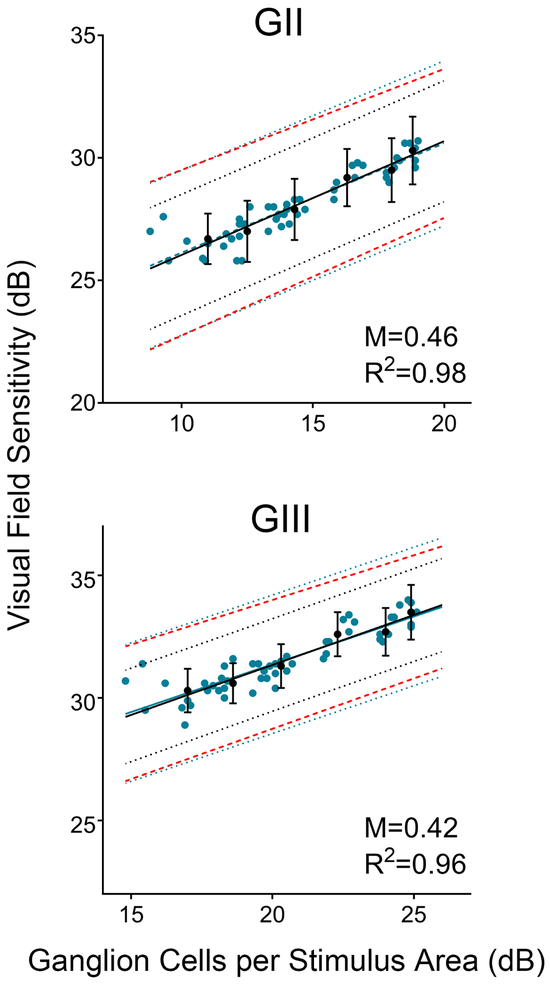
Regardless of the underlying cluster pattern and VF stimulus size, linear structure-function relationships for the developed pattern models showed a superior fit to those generated from gridwise comparisons, as indicated by higher coefficients of correlation (Figure 4, R² = 0.94-0.98 vs. R² = 0.79-0.84). Although overall high, R² values were slightly higher and resulted in a steeper slope (that is, closer to a 1:1 relationship) with correlations derived from GII compared to GIII. Slopes corresponding to each individual cluster pattern, however, were not statistically differentiated from those generated from gridwise slope values across both stimulus sizes (p = 0.90-0.99).

Figure 4. Structure function correlations result in narrow 95% prediction intervals.

Linear structure-function correlations for ganglion cell per stimulus area measurements derived from OCT and visual field locations grouped according to Pattern 2 (6 clusters), for GII and GIII visual field stimuli. Mean and standard deviation of clustered ganglion cells per stimulus area are plotted against the mean visual field sensitivity (●, black points) providing the basis for the corresponding indicated 95% prediction intervals (•••••, black dotted lines). The equivalent outcomes are illustrated for non-clustered, gridwise data (● blue points), resulting in much wider 95% prediction intervals (•••••, blue dotted lines). Intervals corresponding to 2× the standard deviation, commonly equated to the normal variability of visual field sensitivity data, is provided as reference from the current data set (- - - -, red dashed lines). Error bars indicate standard deviations per cluster. M and R² indicate the slope and coefficient of determination respectively of the structure-function relationships depicted.

The 95% prediction intervals established from structure-function correlation models utilizing clustered GCpSA and VF measurements that encumbered all GCpSA values fell within the range of normal VF variability, which was defined as 2 SDs around mean VF sensitivity. Additionally, 95% prediction intervals based on these models were significantly narrower than those corresponding to gridwise comparisons (Figure 5, Table 3, p <0.0001 for all comparisons). Prediction intervals were significantly wider for GII than GIII stimuli across all cluster patterns (interval size 4.92-5.06dB vs. 3.79-3.93dB, p <0.0001), reflecting the generally larger SD intervals for this stimulus size. Accordingly, 95% limits of agreement between actual and predicted VF sensitivities were larger for GII than GIII (Table 4, Bland-Altman comparisons interval sizes 4.84-4.97dB vs. 3.75-3.87dB).

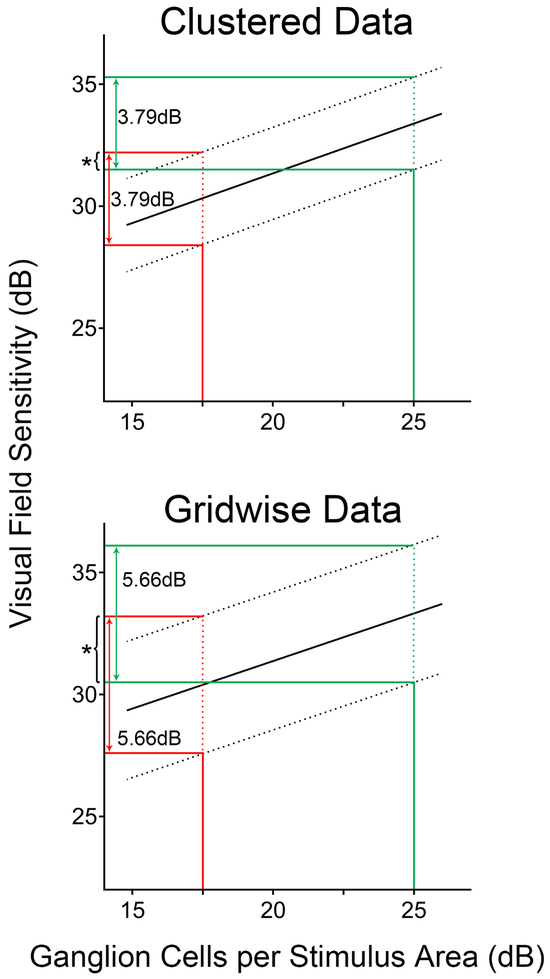
Figure 5. Comparison of 95% prediction interval widths between clustered and gridwise (i.e. not clustered) data.

Linear structure-function correlations of ganglion cells per stimulus area (GCpSA) versus visual field sensitivity a GIII size stimulus compared between data clustered according to Pattern 2 (6 clusters, top panel) and for gridwise data without clustering (bottom panel). Solid lines depict the linear structure-function relationship while dashed lines indicate the limits of the 95% prediction intervals. The red and green lines indicate the 95% prediction interval at GCpSA measurements of 17.5dB and 25dB respectively. While the 95% prediction intervals do not differ markedly at different GCpSA measurements within individual structure-function correlations, it is evident that clustered data resulted in significantly narrower 95% prediction intervals (p<0.0001) and reduced overlap in the range of predicted visual field sensitivities at different GCpSA measurements (*, asterisks), indicating superior predictive ability of these models.

Table 3.

Mean 95% prediction interval size for gridwise analyses and analyses clustered based on Patterns 1-4. Where no outliers were present, N/A indicates no adjustments to prediction interval were required.

	Mean 95% prediction interval size (dB, SD)	Mean 95% prediction interval size, adjusted for outlier exclusion (dB, SD)
Gridwise
GII	6.73 (0.002)	6.64 (0.002)
GIII	5.66 (0.001)	N/A
Pattern 1 (6 Clusters)
GII	4.92 (0.013)	4.69 (0.010)
GIII	3.93 (0.008)	3.87 (0.008)
Pattern 2 (6 Clusters)
GII	4.93 (0.010)	4.69 (0.013)
GIII	3.79 (0.007)	N/A
Pattern 3 (7 Clusters)
GII	4.99 (0.009)	4.72 (0.009)
GIII	3.90 (0.007)	3.84 (0.007)
Pattern 4 (7 Clusters)
GII	4.98 (0.009)	4.63 (0.010)
GIII	3.79 (0.008)	3.75 (0.008)

GII, Goldmann stimulus size II, GIII, Goldmann stimulus size III, SD, standard deviation

Table 4.

Width of the 95% limits of agreement as calculated using Bland-Altman comparisons between actual VF sensitivity and VF sensitivity predicted from the linear structure-function correlations. Where no outliers were present, N/A indicates no adjustments to the limits of agreement were required.

	Interval size of the 95% limits of agreement (dB)	Interval size of the 95% limits of agreement, adjusted for outliner exclusion (dB)
Pattern 1 (6 Clusters)
GII	4.84	4.65
GIII	3.85	3.80
Pattern 2 (6 Clusters)
GII	4.86	4.59
GIII	3.75	N/A
Pattern 3 (7 Clusters)
GII	4.89	4.59
GIII	3.86	3.81
Pattern 4 (7 Clusters)
GII	4.90	4.53
GIII	3.76	3.72

dB, decibels, GII, Goldmann stimulus size II, GIII, Goldmann stimulus size III

Increased variability within samples would invariably increase the size of the 95% prediction interval. To adjust for this potential inflation, linear structure-function correlations were repeated after the exclusion of outliers, and ≥95% of all individual points grouped in each individual cluster patterns fell within the 95% prediction interval regardless of whether outliers were excluded (Supplementary Table 5). Linear correlations calculated after the exclusion of outliers were not significantly different from initial results across all patterns and stimulus sizes (F-test, p = 0.76-0.95), but led to a significant reduction in 95% prediction interval size with all pattern and stimulus size combinations (Table 3, p <0.0001 for all comparisons).

Discussion

Concentric Organization of GCL Thickness

Cluster analyses are capable of describing GCL thickness as a function of age, by identifying patterns depicting discrete locations that change in a similar manner over time.¹⁸ Although gridwise regression analyses may be more sensitive to location-specific data, the vast amount of normal inter-individual variation in GCL thickness poses difficulties in discriminating true rates of normal regression.^{4, 5, 18} The cluster patterns identified in this study confirmed an overall concentric configuration, albeit slightly nasally skewed, which is consistent with histological studies showing highest GC density in the nasal parafovea and closely matches patterns of visual function.^{13, 35}

Hierarchical clustering consistently resulted in a maximum of 6 statistically separable clusters, with minimal variation in cluster assignment within individual patterns, while k-means and pattern recognition analyses with 7 clusters appeared to be less robust. The increased variability in cluster assignments in the perifoveal regions reflect higher variability in GCL thickness in these areas, which is not adequately described by averaged measurements across entire grid squares (Supplementary Figure 2). Consequently, the current review software’s automated method of extracting averaged GCL measurements may not be optimal to describe spatial GCL changes within the central retina.

Age-Related GCL Thickness Changes

We have established that normal, age-related changes in spatially clustered GCL thickness measurements at the macula can be accurately described with quadratic regression models identifying GCL thickness decline beginning at the late 30’s and indicating accelerated reduction with increasing age. Conversion of quadratic rates of decline to a linear equivalent per year indicated a mean rate of change of 0.10μm/year, which is reasonably consistent with previous studies based on similar methodology.^{5, 36-38} F test comparisons of regression rates between clusters in the current study implied that age-related changes in the macular GCL thickness are location-specific and occur in a non-linear fashion, with accelerated decline with increasing age and in the central macula when expressed in absolute thickness. Notably, once location-specific GCL thickness was taken into consideration, a mean rate of 0.26% loss in GCL thickness per year was calculated across the central 20 degrees of the retina. This strongly indicates that absolute location-specific rates of decline in GCL thickness were proportional to peak GCL thickness.

While existing models describing GCL change over time typically operate under the assumption of a linear change function either throughout the investigated age range or after an initial period without change,^{5, 18, 36, 39} quadratic regression models best described aging changes in the macular GCL in the present study, and such models are physiologically plausible on consideration of characteristics of aging in other ocular processes. Segmented linear regression models described by Yoshioka et al.¹⁸ predict an abrupt decline in GCL thickness only after the regression breakpoint placed at 50 to 70 years of age, which is inconsistent with the reported gradual aging changes in rod outer segment morphology, spatial contrast sensitivity and scotopic vision beginning in the early to mid-40’s.^{19, 40-42} These aging properties of anatomical and visual perceptual changes are more consistent with the calculated vertex points of the proposed quadratic models (mean 38.0 years, range 36.2-38.7 years). Furthermore, existing data describing aging changes in human macular GC density is best described with a quadratic model, as suggested by reanalysis of Harman et al.’s⁴³ data (Supplementary Figure 3). While quadratic models indicate an increase in GCL thickness prior to the vertex points (i.e. between 20 years of age and the late 30’s), it is important to note that the best fit quadratic functions are broad and exhibit a small change over this age range in the order of 0.048μm/year across all clusters (Figure 3). Investigations into the mechanisms behind this small increase is beyond the scope of the present study, however we postulate that this may be due to variations in inner retinal cell morphology over this age range. Variations in GC soma diameter with aging of up to 1.66μm have been reported in rat and human histological studies,^43-45 while hypertrophy of Müller cell bodies and processes has been described previously.^{46, 47} Nevertheless, we maintain that quadratic regression models are good descriptors of change in the macular GCL with age, and are physiologically valid given their compliance with established psychophysical and anatomical models of aging. However, further investigations into the mechanisms behind such patterns of change are warranted.

Figure 3. Quadratic regression models describing age-related change in ganglion cell thickness.

Regression analysis was performed for each pattern and cluster identified in Figure 2, however for clarity only regression analyses from Pattern 2 (6 clusters) are displayed. Since analysis was statistically not significantly different when data were grouped by age in either decade or 5-year intervals, only decade data are shown for clarity. Vertex points located in the mid to late 30’s age range are indicative of onset of ganglion cell loss (black stars), and regression analyses reflected an equivalent linear rate of GCL thickness decline of 0.26%/year across the macula. Error bars indicate standard deviations per age group and cluster.

Prediction of Functional Changes from Structural Measurements

The identified cluster analyses of structural data and age-correction of GCL thickness using the identified regression analyses were utilized to aid characterization of the structure-function relationship at the macula. Additionally, we demonstrate that these relationships can be applied to predict VF sensitivity with reasonable accuracy from GCpSA calculations derived from OCT measurements, as shown by 95% prediction intervals well within the range of normal VF variability.

While other models describing the structure-function relationship at the central retina have been previously reported,^{9, 10, 34, 48, 49} not only were these models based on assumptions of standard anatomical RNFL projections which may vary between individuals,^50-52 the VF paradigms utilized in these studies sample the macula sparsely and they typically utilized GIII stimuli that do not account for variable spatial summation characteristics within the macula.⁷ Additionally, models investigating the structure-function relationship of the macular GCL were based on global measurement indices and spatially oriented based on a semi-arbitrary distribution of OCT-derived macular GCL measurements, rather than incorporating structural or functional considerations.^53-56 By considering the above factors in conjunction with cluster and regression analyses, we have generated a comparatively simple model that robustly and accurately describes the structure-function relationship at the macula.

VFs can be notoriously variable both between individuals and between different visits for the same individual, and yet are the mainstay method of determining functional impairment in many ocular pathologies including glaucoma.²⁸ While structure-function correlations improved when the stimulus size remained within complete spatial summation (GII), the 95% prediction intervals were consistently wider than those derived from GIII stimuli (Table 3). Consequently, differences between actual and predicted VF sensitivities were on average 1dB larger for GII than GIII (Table 4). These outcomes clearly demonstrate the trade-off between increased measurement sensitivity, which may potentiate earlier detection of pathological changes,^{6, 7, 12, 22, 26, 27, 57} and increased variability when using smaller VF stimulus sizes.^{7, 13, 22} From a clinical perspective, the narrower prediction intervals found using GIII compared to GII may facilitate more accurate prediction of functional deficits from structural measurements. Given that GII has been shown to identify greater number and magnitude of functional deficits compared to GIII within the central VF even in the presence of greater measurement variability,⁵⁷ this framework can be used to guide additional confirmatory testing using GII.

Most importantly, accurate structure-function models allow for the prediction of changes in VF sensitivity from more objective and arguably easier to obtain structural GCL measurements. The 95% prediction intervals calculated from cluster pattern-derived structure-function correlations in this study were significantly narrower than those from gridwise correlations, and consistently fell well within 2 SDs of normal VF sensitivity (Figure 4). Additionally, for different GCpSA measurements, there was less overlap in the ranges of predicted VF sensitivities for cluster pattern derived correlations (Figure 5), indicating superior predictive ability upon utilization of cluster-based grouping strategies. Similarly, Leite et al.⁹ grouped RNFL thickness and VF sensitivity measurements according to the structure-function map proposed by Garway-Heath et al.⁵⁸ and demonstrated that 87-88% of their data points fell within the 95% prediction interval of the resulting model. On the other hand, models proposed by Guo et al.⁴⁹ to predict VF sensitivity from RNFL and GC-IPL measurements performed relatively poorly, with 95% prediction intervals exceeding 20dB for VF sensitivities of up to 26dB. The strategies developed in the present study may form the basis of future technologies to facilitate earlier detection of glaucoma.

Limitations

Cluster analyses based on individual GCL measurements might be advantageous over mean measurements for age-defined brackets, to improve precision within each age bracket. However, unavoidable OCT artefacts due to anatomical features, such as intraretinal vasculature, needed to be excluded from analysis to preserve accuracy of GCL thickness measurements. Consequently, averaged thickness data were the only reasonable alternative to maintain complete data sets across all investigated retinal regions.

The default posterior pole OCT measurement grid on the instrument review software posed multiple limitations in our study. Firstly, the GCL thickness varied more widely over some grid squares than others (Supplementary Figure 2), which is not captured through mean thickness data and likely contributed to the variations in cluster assignments. Secondly, several VF points and GCL measurement areas were excluded from structure-function analyses due to missing co-localization of data; a measurement grid that averages GCL measurements over regions directly corresponding to each VF test location may provide greater insight into the macular structure-function relationship.

Conclusions

The present study investigated the utility of cluster analysis and detailed characterization of aging in the macular GCL to predict VF sensitivity from structural data. We have established robust quadratic regression models indicating that normal aging of the macular GCL begins at the late 30’s with accelerated change with increasing age, with an equivalent mean rate of loss in GCL of 0.26%/year across the entire macula. The resultant cluster-based macular structure-function relationships allowed for accurate prediction of functional measurements in the form of VF sensitivity from structural GCL measurements. The findings of this study may be applied in future to further advance models of disease development and progression, and therefore may improve our ability to detect early pathological changes in the macular GCL due to their ability to minimize noise and produce more meaningful predictions.