Tunable corrugated patterns in an active nematic sheet

Significance

To what extent can we engineer matter that shapes itself? To investigate this question we study an aqueous solution containing molecular motors that walk on protein filaments. When the filaments are long and attract each other, bundles of filaments are parallelly oriented. We show that such a nematic solution in the presence of multimers of motors has an unexpected behavior: It forms a fluid film that autonomously wrinkles. The observed wrinkles have a well-defined wavelength that decreases with increasing motor concentration. The wrinkles either are stable or break into a chaotic flowing state at high motor concentration, providing insights into how to engineer static or dynamic materials with this class of active matter.

Abstract

Active matter locally converts chemical energy into mechanical work and, for this reason, it provides new mechanisms of pattern formation. In particular, active nematic fluids made of protein motors and filaments are far-from-equilibrium systems that may exhibit spontaneous motion, leading to actively driven spatiotemporally chaotic states in 2 and 3 dimensions and coherent flows in 3 dimensions (3D). Although these dynamic flows reveal a characteristic length scale resulting from the interplay between active forcing and passive restoring forces, the observation of static and large-scale spatial patterns in active nematic fluids has remained elusive. In this work, we demonstrate that a 3D solution of kinesin motors and microtubule filaments spontaneously forms a 2D free-standing nematic active sheet that actively buckles out of plane into a centimeter-sized periodic corrugated sheet that is stable for several days at low activity. Importantly, the nematic orientational field does not display topological defects in the corrugated state and the wavelength and stability of the corrugations are controlled by the motor concentration, in agreement with a hydrodynamic theory. At higher activities these patterns are transient and chaotic flows are observed at longer times. Our results underline the importance of both passive and active forces in shaping active matter and demonstrate that a spontaneously flowing active fluid can be sculpted into a static material through an active mechanism.

Active matter is composed of subunits that convert free energy into mechanical work. It comprises systems composed of objects with very different sizes, from flocks of animals (1) and bacterial colonies (2) to gels of cytoskeletal proteins (3, 4). Active matter has attracted much attention, both theoretically and experimentally, because it displays phase transitions and states that greatly differ from those observed at equilibrium, such as motile ordered states and spontaneous coherent or incoherent flow (5–9). Among the active systems that can be studied in the laboratory, those composed of the protein filaments and motors that constitute the cytoskeleton of the eukaryotic cell are of special interest for 3 reasons: 1) their biological importance (10, 11), 2) the possibility to make purified systems that can be easily controlled and studied (3, 4, 12), and 3) their potential to make self-organizing materials (13).

Depending on the conditions, cytoskeletal active systems display a wide array of dynamic behaviors. Isotropic systems contract (12, 14–16) and buckle (17) in 3 dimensions (3D). Polar ones generate density waves (18) and large-scale vortices (19) in 2D and asters and vortices (3) in 3D. Nematic systems display spatiotemporally chaotic flows both in 2D (4, 20, 21) and in 3D (4, 22) and also coherent flow (22) in 3D. This diversity of behaviors is qualitatively understood by a hydrodynamic theory (5–9). However, we currently do not fully understand why one behavior is observed in a given experimental system and not in another and which experimental parameter has to be modified to switch from one state to another. This is due, on the one hand, to the difficulty of measuring the phenomenological parameters of the hydrodynamic theory and, on the other hand, to the use of 2 experimental systems, actin/myosin and microtubule/kinesin, with very different microscopic properties. In this regard, the recent demonstration that global contractions (12, 15) and chaotic flows in 2D (4, 21) were present in both systems and the understanding of the nematic to polar transition in microtubule/kinesin systems (23) have clarified the design of these dynamic behaviors. Yet, the 2 aforementioned difficulties remain, hindering the development of controllable active materials.

In this work, we report the observation of a static patterned state in an active nematic fluid, we provide a semiquantitative interpretation to why this state is observed, and we show which experimental parameters need to be tuned to reach either this static state or a previously reported flow state. More precisely, we demonstrate that a microtubule/kinesin nematic fluid that is known to flow in 3D (4, 22) can be rationally engineered to form a thin static corrugated sheet in 3 dimensions, a behavior that has only recently been observed in isotropic and cross-linked actin/myosin gels (17) that cannot flow. Essentially, the fluid contracts anisotropically along its 2 shortest dimensions to form a thin sheet of gel that freely floats in the aqueous solution, mainly due to passive depletion forces. Simultaneously, the extensile active stress generated by the motors buckles the sheet along the direction perpendicular to its plane, forming a corrugated sheet of filaments with a well-controlled wavelength of the order of 100 $\mathrm{\mu }$m over an area of 10 ${\mathrm{m}\mathrm{m}}^2$. We demonstrate that this out-of-plane buckling differs both from classical Euler buckling in passive gels (24, 25) and from the flow-generating in-plane buckling that is common in 2D active nematic gels (4, 22, 26, 27). Importantly, nematic topological defects are not observed and we provide a theoretical prediction of the dependence of the wavelength with the motor concentration and with the thickness of the fluid that is in agreement with the experiments. Finally, we show that the transition between static corrugations and chaotic flow can be experimentally controlled by 2 parameters, the motor concentration and the attractive interactions between microtubule filaments.

Results and Discussion

A 3D Active Nematic Fluid Forms a Static Corrugated Sheet.

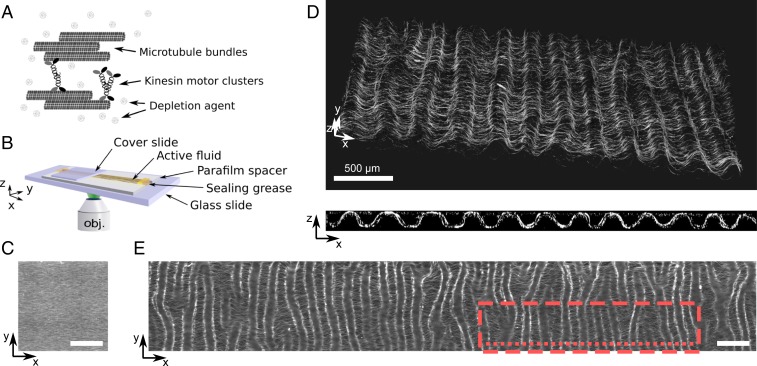
The active fluid is constituted of a dense suspension of nongrowing microtubules bundled together by a depletion agent and by clusters of kinesin-1 motors (Fig. 1A). We use the word fluid, instead of gel, to underline the fact that the system does not present irreversible cross-links, as actin gels do (17). It is supplemented with ATP and an ATP-regeneration system that drives the system out of equilibrium by keeping the motor active for at least 4 h. Additionally, the microtubule bundles are fluorescent because they bear a small fraction of fluorescent tubulin, allowing their observation by fluorescence microscopy. This system is similar to previously published active nematic fluids (4) but it differs in several important ways: The microtubules are longer ($8\pm 6\hspace{0.17em}\mathrm{\mu }$m instead of 1 $\mathrm{\mu }$m; SI Appendix, Fig. S1); and the kinesin used here (28), K430, is different from the standard K401 (it comes from a different organism and forms nonspecific clusters), and its typical concentration is 2 orders of magnitude lower (SI Appendix, section 1). The active fluid is prepared inside a long and shallow channel of rectangular cross-section, with length $L=22$ mm, width $W=1.5$ mm, and height $H=0.13$ mm. Initially, the density of microtubule bundles is homogeneous in 3D but they are aligned along the long axis of the channel, parallel to $x$ (Fig. 1 B and C). This nematic order arises spontaneously during the filling process of the channel by capillarity, the angle of the director of the nematic with the $x$ axis being $2^{○}\pm 16^{○}$ (SI Appendix, Fig. S2).

Fig. 1.

At low motor concentration a 3D active nematic fluid creates a thin corrugated sheet of well-defined wavelength. (A) Scheme of the components of the active fluid formed by nongrowing microtubules bundled together by a depletion agent and clusters of kinesin motors. (B) Scheme of the channel where the fluid (in yellow) is observed. (C) Epifluorescence image of the fluid at initial time. (D) Confocal images in 3D (Top) and cross-section in the $xz$ plane (Bottom) of the fluid after 300 min. (E) Epifluorescence image of the same sample after 24 h and over a $9.5\times 1.4$-${\text{mm}}^2$ area. The red dashed rectangle and the red dotted line respectively indicate the region where Top and Bottom images in D were recorded. (Scale bars, 500 $\mathrm{\mu }$m; motor concentration, 0.5 nM.)

In the presence of 0.5 nM of motors, confocal images recorded after 300 min show that the active fluid has contracted along $z$ and buckled in the $xz$ plane to form a corrugated sheet whose hills and valleys reach the top and bottom walls of the channel and whose grooves are strikingly parallel to the $y$ axis (Fig. 1D). The thickness of the sheet is ${\ell }_z=35\pm 5$ $\mathrm{\mu }$m and the wavelength of the corrugations is $\lambda =285\pm 15\hspace{0.17em}\mathrm{\mu }$m. This periodic pattern extends along an area of at least $9.5\times 1.4$ ${\mathrm{m}\mathrm{m}}^2$, with dislocations corresponding to the junction of 2 valleys or hills. Notably, these dislocations in the periodic undulatory pattern do not correspond to defects in the nematic field. The pattern can also be visualized in epifluorescence, where it appears in the form of focused and defocused bands (Fig. 1E).

During the Formation of the Corrugations the Fluid Buckles along $z$ and Contracts along $z$ and $y$.

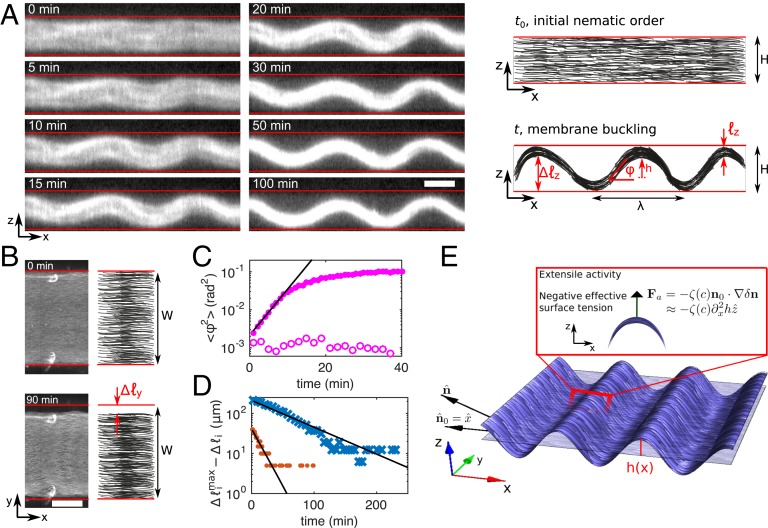
To elucidate the mechanism of pattern formation we recorded confocal (Movie S1) and epifluorescence time-lapse images of a buckling fluid at 0.5 nM motors (Fig. 2). Two processes are observed: buckling along the $z$ direction and contraction along $z$ and $y$. These processes are quantified by the angle $\varphi$ between the microtubule bundles and the $x$ axis in the $xz$ plane and by $\mathrm{\Delta }{\ell }_z$ and $\mathrm{\Delta }{\ell }_y$, the contracted lengths of the fluid along the $z$ and $y$ axes, respectively. Buckling initially proceeds at a rate ${\omega }_{\varphi }=0.3$ ${\mathrm{m}\mathrm{i}\mathrm{n}}^{-1}$ but later slows down until reaching a maximal buckling angle ${\varphi }^{max}=32.2^{○}\pm 0.5^{○}$ (Fig. 2C) and an amplitude $h^{max}=22\pm 3$ $\mathrm{\mu }$m after 100 min. Contraction along $z$ and $y$ is significantly slower with onset rates ${\omega }_z=6.4\times 10^{-2}$ ${\mathrm{m}\mathrm{i}\mathrm{n}}^{-1}$ and ${\omega }_y=1.5\times 10^{-2}$ ${\mathrm{m}\mathrm{i}\mathrm{n}}^{-1}$, respectively, to reach maximum amplitudes $\mathrm{\Delta }{\ell }_z^{max}=40$ $\mathrm{\mu }$m and $\mathrm{\Delta }{\ell }_y^{max}=210$ $\mathrm{\mu }$m (Fig. 2D). Note that the relative contraction amplitudes $\mathrm{\Delta }{\ell }_z^{max}/H=0.40$ and $\mathrm{\Delta }{\ell }_y^{max}/W=0.14$ are significantly different, indicating that the final contracted state does not correspond to a nematic liquid droplet at equilibrium (29).

Fig. 2.

Dynamics and mechanism of the formation of a thin corrugated sheet at low motor concentration. (A) Time-lapse confocal fluorescence images of the active fluid in the $xz$ plane (Left) and sketch of the observations indicating the measured quantities $\mathrm{\Delta }{\ell }_z$, $\varphi$, $h$, and ${\ell }_z$ (Right). (Scale bar, 100 $\mathrm{\mu }$m.) (B) Epifluorescence images of the fluid at $t=0$ and 90 min (Left) and sketch indicating the measured quantity $\mathrm{\Delta }{\ell }_y$ (Right). (Scale bar, $500\hspace{0.17em}\mathrm{\mu }$m.) Red lines in A and B indicate channel walls. (C) Average of ${\varphi }^2$ along the $x$ direction vs. time in the presence (solid circles) and in the absence (open circles) of motors. (D) Offset to the maximum contracted length along the $z$ (red circles) and $y$ (blue crosses) directions. Black lines in C and D are exponential fits. (E) Sketch of the mechanism for the active buckling of a thin membrane through the negative tension $F_a$ proportional to the active stress $\zeta \left(c\right)$ and the Laplacian of the height $h\left(x\right)$ of the sheet above its fiducial plane. All data correspond to 0.5-nM motors except open circles in C.

Buckling Is Active and Contraction Is Passive.

Passive gels of various compositions have been reported to form corrugations through Euler buckling when they are submitted either to an external contractile stress or to an extensile stress at constant length (24, 25). To assess whether this could explain our observations, we performed experiments that demonstrated, first, that buckling is principally an active process and, second, that a Euler mechanism is not compatible with the data.

In the absence of motors buckling is undetectable in confocal images with the same field of view in $x$ as above (660 $\mathrm{\mu }$m) (Fig. 2C and SI Appendix, Table S1), although it is weak but detectable in images acquired over a wider field of view (SI Appendix, Fig. S3). In contrast, contraction is similar in both passive and active fluids (SI Appendix, Fig. S3). The passive origin of contraction is further supported by the fact that its amplitude is strongly dependent on the concentration of depletion agent (SI Appendix, Fig. S4).

In passive fluids, depletion forces induce the condensation of microtubules into a dense nematic fluid phase, which, in the absence of confinement, would relax to a highly anisotropic tactoid droplet (30). In the geometry of our experiments, this results in the formation of a quasi-2D sheet that elongates along the nematic axis $x$, thereby leading to Euler buckling in the presence of boundaries. Indeed, a membrane with an excess area, which in this case arises from the excess length $\mathrm{\Delta }{\ell }_x={\ell }_x-L$, where ${\ell }_x$ is the length of the membrane along $x$, will have a buckled state beyond a critical $\mathrm{\Delta }{\ell }_x^c$ that depends on $H$. Note that this mechanism could in principle also explain active buckling if $\mathrm{\Delta }{\ell }_x$ depends on the activity. However, this sort of passive mechanism, reminiscent of the classic Euler buckling, is possible only if the membrane had a fixed projected area, i.e., if it were confined in the $x$ direction. On the contrary, if active buckling were generated by local extensile forces exerted by the motors, it would be independent of whether the fluid is constrained in length or not.

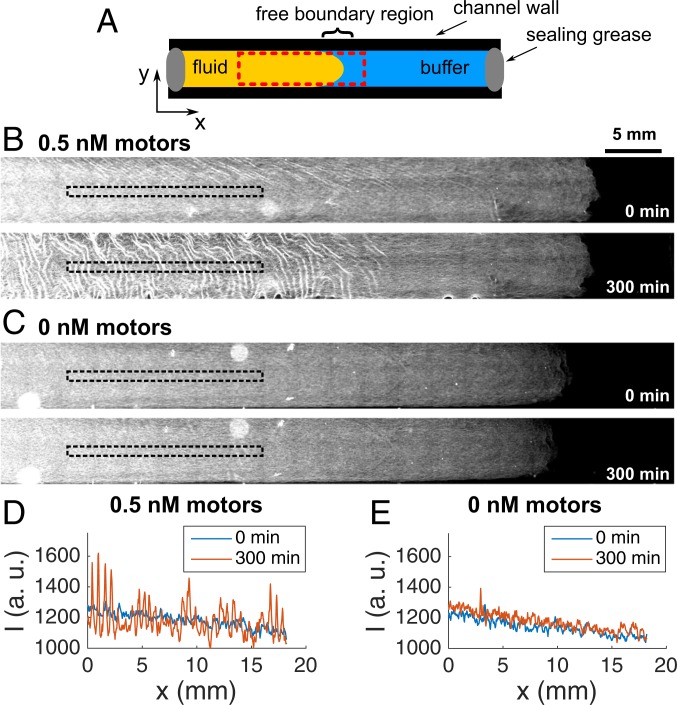
To test these 2 hypotheses, we performed experiments where one end of the fluid was in contact with an aqueous solution and thus free to change length. In this configuration (Fig. 3) the active fluid buckled everywhere except on the tip close to the free boundary, while the passive one did not buckle at all. We attribute the lack of buckling on the tip of the active fluid to a gradient of microtubule concentration across the free boundary arising during the preparation of the fluid (SI Appendix, section 1). These results suggest that, while the excess area mechanism explains passive buckling, it cannot fully account for the buckling of active films. We thus conclude, first, that passive buckling and active buckling happen through different mechanisms and, second, that in active fluids buckling is principally an active mechanism while contractions in $y$ and $z$ are mainly passive.

Fig. 3.

An active fluid buckles, in contrast with a passive one, in fluids with 1 free boundary. (A) Scheme of the experiment. The red dashed rectangle indicates the area where the images were recorded. (B and C) Epifluorescence images of an active (B) and a passive (C) fluid at the initial and the final time. The black, dashed rectangles show the zones where the intensity profiles in D and E were extracted.

A Hydrodynamic Theory That Predicts the Wavenumber of the Corrugations.

The behavior of active fluids, including those composed of microtubules and kinesins (4, 22, 31, 32), has been successfully described with the hydrodynamic theory of liquid crystals supplemented with a stress term resulting from activity. We now demonstrate that this framework applied to a thin film that can buckle in the third dimension can provide an explanation and theoretical estimates of the wavenumber $q^{*}=2\pi /\lambda$ and of the formation rate ${\omega }^{*}$ of the corrugated pattern (Fig. 2E and SI Appendix, section 2).

To do so, we consider the periodic undulation of the thin sheet made of microtubules and motors in the $xz$ plane, supposing that passive forces have already collapsed the 3D fluid into a thin 2D sheet. The nematic active fluid sheet has bending modulus $K$ and its director $\widehat{\mathbf{n}}$ is on average parallel to the $x$ axis: ${\widehat{\mathbf{n}}}_0=\widehat{x}$. The fluctuation of the membrane about a fiducial plane parallel to the $xy$ plane (here, taken to be the midplane of the channel) is denoted by $h\left(x,y\right)$. The deflection of the director in the $xz$ plane, $\delta {\mathbf{n}}_z$, leads to a buckling of the membrane in the $z$ direction: $\delta {\mathbf{n}}_z\approx {\partial }_{x}h\widehat{z}$. The passive elasticity of the nematic fluid $\propto {\left(\nabla \mathbf{n}\right)}^2$ then yields a bending energy $\propto \left(K/2\right){\left({\partial }_x^{2}h\right)}^2$ for the buckling of the thin sheet in the $z$ direction. The standard active force (5–9) is $-\zeta \left(c\right)\nabla \cdot \left(\mathbf{n}\mathbf{n}\right)$, where $\zeta \left(c\right)>0$ is the strength of the extensile activity that is a function of motor concentration $c$. This leads to a force $\propto -\zeta \left(c\right){\partial }_x^{2}h\widehat{z}$ that tends to destabilize the flat membrane and that is similar to an effective negative surface tension (33). The interplay between the negative surface tension, arising from activity, and the stabilizing bending modulus, due to nematic elasticity, leads to the selection of a pattern with wavenumber

$$q^{*}\sim \sqrt{\zeta \left(c\right)/K}.$$ [1]

The pattern arises with a rate $\omega$ whose exact expression is provided in SI Appendix, section 2. Note that in the absence of confinement, we expect the pattern to be unstable.

The theory thus shows that an out-of-plane buckling instability compatible with our observations results from the interplay of active forcing $\zeta \left(c\right)$ and passive elastic restoring forces, $K$, the same ingredients that in previous microtubule/kinesin active fluid provided dramatically different patterns (4, 31, 32, 34, 35). Here, the out-of-plane buckling of the active sheet precedes any planar pattern formation, in contrast to those experiments. In addition, the instability described here does not result in coherent or incoherent flow, of either the active or the embedding fluid, in contrast with theories describing 2D or 3D active fluids that do not form sheets (26, 27, 36).

This qualitative interpretation has 2 advantages. First, it is parsimonious because a single feature, activity, explains the 3D out-of-plane buckling observed here and the 2D in-plane buckling (4, 32) and 3D chaotic flows (22) observed previously in a similar system. Second, it predicts that decreasing depletion forces precludes the formation of the thin sheet and thus the emergence of out-of-plane buckling in favor of 3D chaotic flows. In the rest of this paper we analyze these 2 questions in more detail. However, although hydrodynamic theories, such as the one just described, provide an informative qualitative description of the physics of active fluids, they feature phenomenological parameters, such as $\zeta \left(c\right)$ and $K$, that are difficult to measure experimentally. To our knowledge, the only quantitative test of such theories in the kinesin-microtubule system was recently performed by Martínez-Prat et al. (32), where they obtained $\zeta \left(c\right)\sim c^2$. Using their scaling, our semiempirical prediction reads

$$q^{*}\sim c/\sqrt{K}.$$ [2]

Increasing the Motor Concentration Linearly Increases the Wavenumber of the Corrugations and Destabilizes the Patterns.

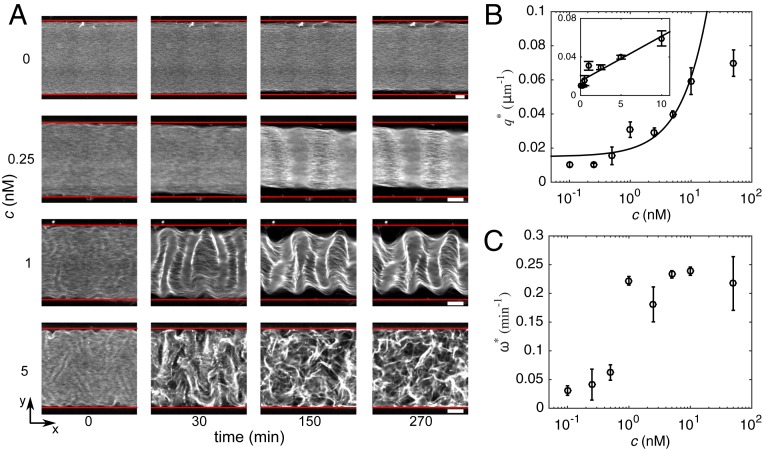
To test the prediction $q^{*}\sim c$ we investigated the behavior of the fluid over a range of motor concentrations $c$ spanning more than 2 orders of magnitude (Fig. 4 and Movie S2). Below 0.5 nM motors, the fluid behaves as described in Fig. 2: buckling in the $xz$ plane and contractions in the $z$ and $y$ directions. As $c$ increases, between 1 and 2.5 nM motors, buckling in the $xz$ plane is initially observed and followed by buckling in the $xy$ plane that distorts the corrugated pattern without breaking it. Finally, between 5 and 50 nM motors, buckling in the $xz$ plane is still observed at early times but the pattern breaks into a 3D active chaotic state similar to the one already reported in this active fluid (4, 22) (Movies S3 and S4). However, the velocity of this flow state is significantly lower in our case, possibly because the solution is more viscous.

Fig. 4.

Dynamics, shape, and stability of the patterns strongly depend on motor concentration. (A) Time-lapse epifluorescence images of fluids with different motor concentrations $c$. Red lines indicate channel walls. (Scale bars, 200 $\mathrm{\mu }$m.) (B) Wavenumber $q*$ of the corrugations vs. motor concentration. Inset is the lin-lin representation of the main plot and the line corresponds to a linear fit to the data in the range $c=0.1$ to 10 nM with regression coefficient $r^2=0.9$. (C) Growth rate vs. motor concentration. Error bars indicate the SD of a triplicate experiment where a single motor/filament mix was distributed into 3 different channels.

The transition to the chaotic state happens qualitatively through 2 processes: The accumulated tension on the hills and valleys of the corrugations breaks the microtubule bundles and the frozen fluid locally flows (Movie S2, 5-nM channel) or the dislocations in the corrugations become motile, leading to a shearing of the pattern and its consequent destruction (Movie S2, 10-nM channel). Note that, in our experiments, the chaotic state was never observed before the buckled state. However, if the characteristic time of active transport is much shorter than the time of passive contraction, one would observe only the spontaneous flow instability and would not observe the buckling instability (which happens in ref. 4). Nevertheless, first observing spontaneous flow instability and then the buckling instability is unlikely because the first one would destroy the nematic order that allows passive buckling.

Importantly, the measured wavenumber of the corrugations is in agreement with the predicted linear scaling (Fig. 4b), in particular in the range 0.5 to 10 nM. A linear fit $q^{*}=a_1+a_{2}c$ of the data yields $a_1=5\times 10^{-3}$ $\mathrm{\mu }{\mathrm{m}}^{-1}$ and $a_2=1.4\times 10^{-3}\mathrm{\mu }{\mathrm{m}}^{-1}{\mathrm{n}\mathrm{M}}^{-1}$, where the constant term $a_1$ results from the weak contribution of Euler buckling in the absence of motors. Indeed, activity controls the wavenumber only if the active wavenumber is larger than the one selected by passive Euler buckling, a crossover that in our experiments happens at $c=0.5$ nM.

The growth rate of the patterns, ${\omega }^{*}$, increases slightly with $c$ in the range 0.1 to 0.5 nM, then increases drastically between 0.5 and 1 nM, and saturates at higher $c$ (Fig. 4C and SI Appendix, Fig. S5), resulting in ${\omega }^{*}$ also increasing and then saturating with $q^{*}$. For the hydrodynamics-dominated approximation, the theory predicts ${\omega }^{*}\sim q^3$ for $q^{*}H\gg 1$ and ${\omega }^{*}\sim q^6$ for $q^{*}H\ll 1$, while our experiments correspond to $q^{*}H=1.3$ to $4$. In the range $c=0.1$ to 0.5 nM, the data are compatible with the scaling ${\omega }^{*}\sim q^3$, although their precision does not allow us to rule out other scaling laws (SI Appendix, Fig. S6).

Comparing the results of our out-of-plane instability with recent measurements of the in-plane buckling instability of a related system (32), we find similar wavenumbers ($1\text{to}7\times 10^{-2}$ $\mathrm{\mu }$m in our case vs. $0.5\text{to}3\times 10^{-2}$ $\mathrm{\mu }$m) but significantly slower dynamics ($1\hspace{0.17em}\text{to}\hspace{0.17em}4\times 10^{-2}$ ${\mathrm{m}\mathrm{i}\mathrm{n}}^{-1}$ vs. $6\hspace{0.17em}\text{to}\hspace{0.17em}240$ ${\mathrm{m}\mathrm{i}\mathrm{n}}^{-1}$, respectively). In addition, topological defects seem to play no role in the emergence of our patterns, in contrast with what happens in 2D active nematic systems (21, 34). We do observe dislocations in the corrugations that rarely move along the $y$ axis, although they do so too slowly to play a significant role. In contrast, defects in the nematic field would create nonperiodic buckled shapes in the $z$ direction (37, 38) and we never observe this in our conditions.

The Thickness of the Nematic Fluid Influences the Corrugations.

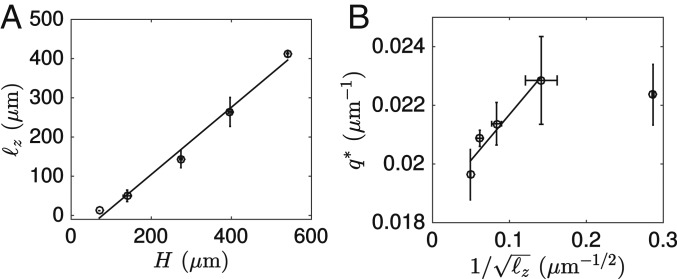
To test the prediction $q^{*}\sim 1/\sqrt{K}$ we varied the thickness and the aspect ratio of the confinement of the active fluid at low motor concentration, with the hypotheses $K\sim {\ell }_z$ and ${\ell }_z\sim H$. First, we measured ${\ell }_z$ and $q^{*}$ for $H$ in the range 70 to 540 $\mathrm{\mu }$m and confirmed that the data are in agreement with ${\ell }_z\sim H$ and with $q^{*}\sim 1/\sqrt{{\ell }_z}$, with the exception of this last scaling for the thinnest fluid (Fig. 5 and SI Appendix, Fig. S7 and Table S2). Second, reducing the aspect ratio of the channel section resulted in some portions of the fluid buckling in $xz$ and others in the $xy$ plane at $W/H=4.6$ (SI Appendix, Fig. S8) and no preferential direction of buckling at $W/H=1$ (SI Appendix, Fig. S9). In addition, in all of the cases where both $xy$ and $xz$ buckling was observed, the wavenumbers in the 2 planes were in qualitative agreement with the aforementioned argument that essentially yields $q^{*}\sim 1/\sqrt{H}>q_{xy}^{*}\sim 1/\sqrt{W}$ when $H<W$ and $q^{*}=q_{xy}^{*}$ when $H=W$.

Fig. 5.

Increasing the thickness of the fluid reduces the wavenumber. (A) Final thickness ${\ell }_z$ vs. channel height $H$. (B) Wavenumber vs. $1/{\ell }_z^{1/2}$. Error bars indicate the SD of a triplicate experiment where a single motor/filament mix was distributed into 3 different channels. Solid lines correspond to linear fits. Shown are 1-nM motors.

Another way to influence $K$ is to change the microtubule concentration $\mu$. Increasing $\mu$ in the range 0.5 to 2 mg/mL decreased $q^{*}$ in agreement with the expectation that $K$ should increase with $\mu$. In contrast, at $\mu =0.25$ mg/mL, global contraction, instead of corrugations, was observed, possibly because the initial nematic order was reduced (SI Appendix, Fig. S10).

Strong Attractive Interactions between the Microtubules Are Crucial to Form a Corrugated Sheet.

To the best of our knowledge, neither stable nor unstable out-of-plane buckling has been reported in nematic active fluids. We performed control experiments to determine which of the factors that differentiate our experiments from previously published 3D microtubule/kinesin nematics (4, 22, 39) was responsible for the observed phenomenology: the type of motor or the length of the microtubules. We obtained both stable and unstable $xz$ buckling with the kinesin K401 used in previous reports (4) (SI Appendix, Fig. S11). This means that, although the motor K430 is not designed to form specific multimers, in contrast with K401, it forms nonspecific ones. Our efforts to eliminate these nonspecific multimers by size exclusion chromatography did not change the observed patterns (SI Appendix, Fig. S12), suggesting that these clusters either form rapidly or do so in the working buffer.

In contrast with the nature of the motor, the length of the microtubules had a strong impact on the observed structures. When, instead of 8-$\mathrm{\mu }$m-long taxol-stabilized microtubules, 1.5-$\mathrm{\mu }$m-long GMPCPP-stabilized ones were used, no contraction of the fluid was observed along $z$ or $y$, with or without motors, precluding the formation of a thin sheet that could buckle out of plane (SI Appendix, Fig. S13). In this case, chaotic flow was observed at high activity, in agreement with previous reports (4). These observations are consistent with the expected linear dependence of the depletion free energy on filament length (40) which, in our geometry, makes long microtubules condense into a thin sheet. To further test this hypothesis we reduced the attractive force between negatively charged 8-$\mathrm{\mu }$m-long microtubules by lowering either the concentration of the depletion agent or the ionic strength of the buffer. In agreement with this interpretation, neither fluid contraction nor buckling in the $xz$ plane was apparent in these conditions, although the fluid remained active (SI Appendix, Figs. S14 and S15).

Comparison with Other Out-of-Equilibrium Membrane Buckling.

The active buckling instability described here needs 3 ingredients: a thin film, nematic order, and extensile activity. We thus expect any system displaying these properties, such as thin films that may be composed of living liquid crystals (41)—which are suspensions of living bacteria in an inert nematic solution—to buckle in a similar manner. Monolayers of polarized living cells could potentially buckle in the same way, although so far only buckling due to growth has been reported (42). Interestingly, a different type of active buckling has recently been observed in a contractile isotropic film made of a cross-linked actin gel and myosin (17). Despite their differences, for this contractile film to buckle, filaments also need to form bundles, motors have to make aggregates, and the observed thickness and wavelength were of the same order of magnitude as those reported here.

Finally, we have described our system as an active fluid and not a gel to stress that there are no permanent cross-links between the microtubule filaments. This is supported by the low concentration of motors relative to tubulin (1:1,000 wt/wt at 1 nM motors) and by the flows observed by us and others (4, 20–22, 32) at high motor concentration. We believe that the apparent contradiction of our observations with rheological measurements that reported the presence of an effective cross-linking in pure microtubule solutions (43) could be explained, either by the presence of microtubule bundles or by the longer timescale probed here ($10^3$ s compared with $10^2$ s in ref. 43). Ultimately, precise rheological measurements of this type of active fluids will provide a definite answer.

Conclusion

In summary, we demonstrate that in vitro active fluids can be designed to form static or transient suspended sheets with periodic corrugated patterns of tunable wavelength. The mechanism of pattern formation that we propose combines passive and active processes that can be controlled physicochemically. Passive depletion forces, which depend on depletion agent concentration, filament length, and ionic strength, induce the spontaneous condensation of a 3D nematic fluid into a thin 2D nematic sheet, and active stresses buckle the fluid sheet out of plane to form corrugations with well-defined wavelength that can be controlled by activity.

In addition, we use an active gel theory to demonstrate that the observed patterns result from an out-of-plane buckling instability induced by active extensile stresses along the nematic axis of the fluid sheet, in contrast with in-plane buckling patterns that have been observed in prestressed nematic fluids of either nongrowing F-actin (44) or growing microtubules (45) in the absence of motors. Our theory is appealing since it relies on the same essential physics that lead to 2D patterning and 2D and 3D spatiotemporal chaos. However, the buckling instability that we report does not involve filament flows and therefore fundamentally differs from both contractile instabilities in anisotropic active fluids and spontaneous flow transitions in nematic active fluids that have been described theoretically (6, 8, 26, 27, 36, 46) and shown to be characterized by hydrodynamic flows and in-plane buckling of the director field in the case of 2D systems. Such spontaneous flows have been observed in various active matter systems (4, 31, 32, 34, 35, 41, 47–50), which in practice yield either chaotic or large-scale coherent flows, but so far no static spatial patterns. In contrast, our results show that active matter can be shaped into long-lived static 3D patterns that can be tuned by activity, which may open the way to the design of 3D biomimetic materials capable of morphogenesis (51, 52).

Materials and Methods

Kinesin and Microtubule Preparation.

The K430 truncated kinesin-1 from Rattus norvegicus, containing a C-terminal SNAP tag, was the homodimer version of the kinesin-1 described in ref. 28. K430 was expressed in Escherichia coli, purified using a Nickel affinity column due to a His-tag, dialyzed, and flash frozen. K401 was purified as described in ref. 53. Tubulin and TRITC-labeled tubulin (Cytoskeleton) were dissolved at 10 mg/mL in 1$\times$ PEM buffer (80 mM Pipes, pH 6.8, 1 mM EGTA, 1 mM ${\text{MgSO}}_4$) supplemented with 1 mM GTP, flash frozen, and stored at $-80{}^{○}$C. They were polymerized in 1$\times$ PEM, 1 mM GTP, 10% (wt/vol) glycerol, and 5 mg/mL tubulin (including 2.5% fluorescent tubulin). Taxol-stabilized microtubules were incubated at 37 °C for 15 min followed by the addition of 20 $\mathrm{\mu }$M paclitaxel and stored at room temperature for few days. GMPCPP-stabilized microtubules were polymerized in the presence of 0.5 mg/mL GMPCPP (Jena Bioscience) from tubulin at 37 °C for 30 min and left at room temperature for 5 h. They were used within the same day. These procedures are described in more detail in SI Appendix, section 1.

Active Mix.

The active mix consisted of 1$\times$ PEM buffer, 10 mM K-acetate, 10 mM KCl, 5 mM ${\text{MgCl}}_2$, 2% (wt/vol) Pluronic F-127, 5 $\mathrm{\mu }$g/mL creatine kinase, 20 mM creatine phosphate, 20 $\mathrm{\mu }$M taxol, 2 mM ATP, 1 mg/mL BSA, 1 mM trolox, 20 mM d-glucose, 3 mM DTT, 150 $\mathrm{\mu }$g/mL glucose oxidase, 25 $\mathrm{\mu }$g/mL catalase, and 0.5 mg/mL taxol-stabilized microtubules.

Channel Assembly.

Channels were assembled using a microscope glass slide (26 × 75 × 1 mm) and a coverslip (22 × 50 × 0.17 mm) separated by strips of Parafilm cut with a Graphtec Cutting Plotter CE6000-40. Both microscope glass slides and coverslips were passivated using an acrylamide brush (54). The active mix was filled in the flow cell (22 × 1.5 × 0.130 mm) by capillarity and sealed with vacuum grease.

Imaging.

Epifluorescence images were obtained with a Zeiss Observer 7 automated microscope equipped with a Hamamatsu C9100-02 camera, a 10$\times$ objective, and a motorized stage and controlled with MicroManager 1.4. Images were recorded automatically every 3 min using an excitation at 550 nm with a CoolLED pE2. Confocal images were obtained with a Leica TCS SP5 II confocal microscope with a 25$\times$ water-immersion objective or an X-Light V2 Spinning Disk confocal system mounted on an upright Nikon Eclipse 80i microscope with a 10$\times$ objective. Images were recorded automatically every 1 to 10 min.

Image Analysis.

Fluorescent images were binarized to obtain $\mathrm{\Delta }{\ell }_z$ and $\mathrm{\Delta }{\ell }_y$. To measure $\varphi$ the binarized $xz$ confocal cross-sections were averaged over $x$ and smoothed along $x$ by applying a moving average filter with a 30-pixel window that was then differentiated. $\varphi$ was the arctangent of this derivative.

Note Added in Proof.

During the revision process a similar observation was reported in the arXiv (55).