Significance
Recent advances in artificial intelligence and deep learning have significantly improved the capability of recurrently connected artificial neural networks. Although these networks can achieve high performance on various tasks, they often lack basic biological constraints, such as communication via spikes. However, recurrent microcircuitry in the brain can attain similar or better performance with discrete spikes in a much more efficient manner. Here, we introduce an extremely simple platform to construct spiking recurrent neural networks capable of performing numerous cognitive tasks commonly studied in neuroscience. Our method utilizes a close relationship between rate-based and spike-based networks that emerges under certain conditions. By characterizing these conditions, we provide another avenue that can be probed for constructing power-efficient spiking recurrent neural networks.
Keywords: spiking neural networks, recurrent neural networks, rate neural networks
Abstract
Cortical microcircuits exhibit complex recurrent architectures that possess dynamically rich properties. The neurons that make up these microcircuits communicate mainly via discrete spikes, and it is not clear how spikes give rise to dynamics that can be used to perform computationally challenging tasks. In contrast, continuous models of rate-coding neurons can be trained to perform complex tasks. Here, we present a simple framework to construct biologically realistic spiking recurrent neural networks (RNNs) capable of learning a wide range of tasks. Our framework involves training a continuous-variable rate RNN with important biophysical constraints and transferring the learned dynamics and constraints to a spiking RNN in a one-to-one manner. The proposed framework introduces only 1 additional parameter to establish the equivalence between rate and spiking RNN models. We also study other model parameters related to the rate and spiking networks to optimize the one-to-one mapping. By establishing a close relationship between rate and spiking models, we demonstrate that spiking RNNs could be constructed to achieve similar performance as their counterpart continuous rate networks.
Dense recurrent connections common in cortical circuits suggest their important role in computational processes (1–3). Network models based on recurrent neural networks (RNNs) of continuous-variable rate units have been extensively studied to characterize network dynamics underlying neural computations (4–9). Methods commonly used to train rate networks to perform cognitive tasks can be largely classified into 3 categories: recursive least squares (RLS)-based, gradient-based, and reward-based algorithms. The first-order reduced and controlled error (FORCE) algorithm, which utilizes RLS, has been widely used to train RNNs to produce complex output signals (5) and to reproduce experimental results (6, 10, 11). Gradient descent-based methods, including Hessian-free methods, have also been successfully applied to train rate networks in a supervised manner and to replicate the computational dynamics observed in networks from behaving animals (7, 12, 13). Unlike the previous 2 categories (i.e., RLS-based and gradient-based algorithms), reward-based learning methods are more biologically plausible and have been shown to be as effective in training rate RNNs as the supervised learning methods (14–17). Even though these models have been vital in uncovering previously unknown computational mechanisms, continuous rate networks do not incorporate basic biophysical constraints, such as the spiking nature of biological neurons.
Training spiking network models where units communicate with one another via discrete spikes is more difficult than training continuous rate networks. The nondifferentiable nature of spike signals prevents the use of gradient descent-based methods to train spiking networks directly, although several differentiable models have been proposed (18, 19). Due to this challenge, FORCE-based learning algorithms have been most commonly used to train spiking recurrent networks. While recent advances have successfully modified and applied FORCE training to construct functional spike RNNs (8, 20–23), FORCE training is computationally inefficient and unstable when connectivity constraints, including separate populations for excitatory and inhibitory populations (Dale’s principle) and sparse connectivity patterns, are imposed (21).
Due to these limitations, computational capabilities of spiking networks that abide by biological constraints have been challenging to explore. For instance, it is not clear if spiking RNNs operating in a purely rate-coding regime can perform tasks as complex as the ones rate RNN models are trained to perform. If such spiking networks can be constructed, then it would be important to characterize how much spiking-related noise not present in rate networks affects the performance of the networks. Establishing the relationship between these 2 types of RNN models could also serve as a good starting point for designing power-efficient spiking networks that can incorporate both rate and temporal coding.
To address the above questions, we present a computational framework for directly mapping rate RNNs with basic biophysical constraints to leaky integrate-and-fire (LIF) spiking RNNs without significantly compromising task performance. Our method introduces only 1 additional parameter to place the spiking RNNs in the same dynamic regime as their counterpart rate RNNs and takes advantage of the previously established methods to efficiently optimize network parameters while adhering to biophysical restrictions. These previously established methods include training a continuous-variable rate RNN using a gradient descent-based method (24–27) and connectivity weight matrix parametrization method to impose Dale’s principle (13). The gradient descent learning algorithm allowed us to easily optimize many parameters, including the connectivity weights of the network and the synaptic decay time constant for each unit. The weight parametrization method proposed by Song et al. (13) was utilized to enforce Dale’s principles and additional connectivity patterns without significantly affecting computational efficiency and network stability.
Combining these 2 existing methods with correct parameter values enabled us to directly map rate RNNs trained with backpropagation to LIF RNNs in a one-to-one manner. The parameters critical for mapping to succeed included the network size, the nonlinear activation function used for training rate RNNs, and a constant factor for scaling down the connectivity weights of the trained rate RNNs. Here, we investigated these parameters along with other LIF parameters and identified the range of values required for the mapping to be effective. We demonstrate that, when these parameters are set to their optimal values, the LIF models constructed from our framework can perform the same tasks that the rate models are trained to perform equally well.
Results
Here, we provide a brief overview of the 2 types of RNNs that we used throughout this study (more details are in Materials and Methods): continuous-variable firing rate RNNs and spiking RNNs. The continuous-variable rate network model consisted of rate units with firing rates that were estimated via a nonlinear input–output transfer function (4, 5). The model was governed by the following set of equations:
| [1] |
| [2] |
where is the synaptic decay time constant for unit , is the synaptic current variable for unit , is the synaptic strength from unit to unit , and is the external current input to unit . The firing rate of unit () is given by applying a nonlinear transfer function [] to the synaptic current variable. Since the firing rates in spiking networks cannot be negative, we chose the activation function for our rate networks to be a nonnegative saturating function (standard sigmoid function) and parametrized the connectivity matrix () to enforce Dale’s principle and additional connectivity constraints (Materials and Methods).
The second RNN model that we considered was a network composed of spiking units. Throughout this study, we focused on networks of LIF units with membrane voltage dynamics that were given by
| [3] |
where is the membrane time constant (set to 10 ms throughout this study), is the membrane voltage of unit , is the synaptic strength from unit to unit , represents the synaptic filtering of the spike train of unit , and is the external current source. The discrete nature of (Materials and Methods) has posed a major challenge for directly training spiking networks using gradient-based supervised learning. Even though the main results presented here are based on LIF networks, our method can be generalized to quadratic integrate-and-fire (QIF) networks with only a few minor changes to the model parameters (SI Appendix, Table S1).
Continuous rate network training was implemented using the open source software library TensorFlow in Python, while LIF/QIF network simulations along with the rest of the analyses were performed in MATLAB.
Training Continuous Rate Networks.
Throughout this study, we used a gradient-descent supervised method, known as backpropagation through time (BPTT), to train rate RNNs to produce target signals associated with a specific task (13, 24). The method that we used is similar to the one used by previous studies (13, 25, 27) (more details are in Materials and Methods) with 1 major difference in synaptic decay time constants. Instead of assigning a single time constant to be shared by all of the units in a network, our method tunes a synaptic constant for each unit using BPTT (Materials and Methods). Although tuning of synaptic time constants may not be biologically plausible, this feature was included to model diverse intrinsic synaptic timescales observed in single cortical neurons (28–30).
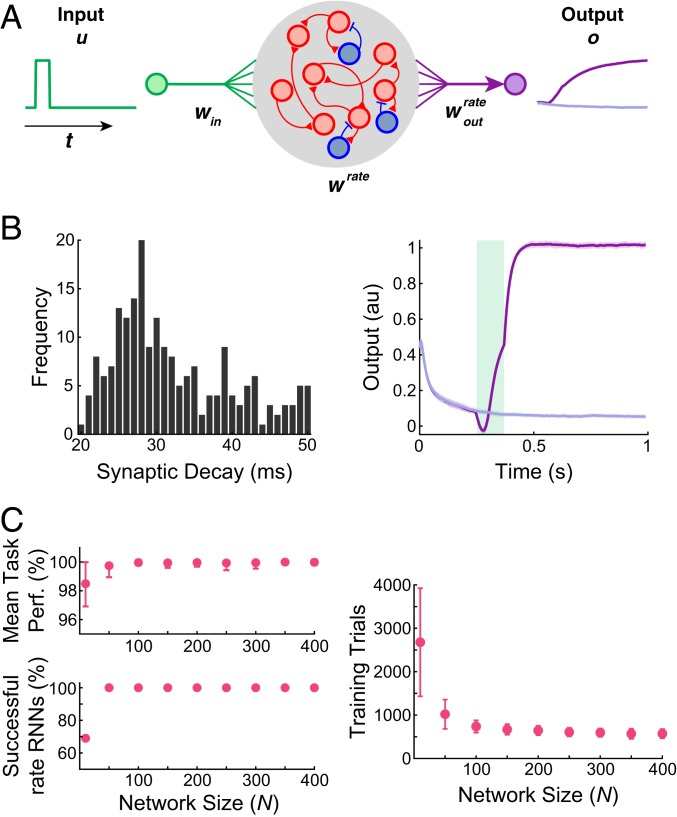
We trained rate RNNs of various sizes on a simple task modeled after a Go-NoGo task to demonstrate our training method (Fig. 1). Each network was trained to produce a positive mean population activity approaching +1 after a brief input pulse (Fig. 1A). For a trial without an input pulse (i.e., NoGo trial), the networks were trained to maintain the output signal close to 0. The units in a rate RNN were sparsely connected via and received a task-specific input signal through weights () drawn from a normal distribution with 0 mean and unit variance. The network output () was then computed using a set of linear readout weights:
| [4] |
where is the readout weights and is the firing rate estimates from all of the units in the network at time . The recurrent weight matrix (), the readout weights (), and the synaptic decay time constants () were optimized during training, while the input weight matrix () stayed fixed (Materials and Methods).
Fig. 1.
Rate RNNs trained to perform the Go-NoGo task. (A) Schematic diagram illustrating a continuous rate RNN model trained to perform the Go-NoGo task. The rate RNN model contained excitatory (red circles) and inhibitory (blue circles) units. (B) Distribution of the tuned synaptic decay time constants (mean SD, 28.2 9.4 ms; Left) and the average trained rate RNN task performance (Right) from an example rate RNN model. The mean SD output signals from 50 Go trials (dark purple) and from 50 NoGo trials (light purple) are shown. The green box represents the input stimulus given for the Go trials. The rate RNN contained 200 units (169 excitatory and 31 inhibitory units). (C) Rate RNNs with different network sizes trained to perform the Go-NoGo task. For each network size, 100 RNNs with random initial conditions were trained. All of the networks successfully trained performed the task almost perfectly (range from 96 to 100%; Left). As the network size increased, the number of training trials decreased (mean SD is shown; Right).
The network size () was varied from 10 to 400 (9 different sizes), and 100 networks with random initializations were trained for each size. For all of the networks, the minimum and maximum synaptic decay time constants were fixed to 20 and 50 ms, respectively. As expected, the smallest rate RNNs () took the longest to train, and only 69% of the rate networks with were successfully trained (Fig. 1C; SI Appendix has training termination criteria).
One-to-One Mapping from Continuous Rate Networks to Spiking Networks.
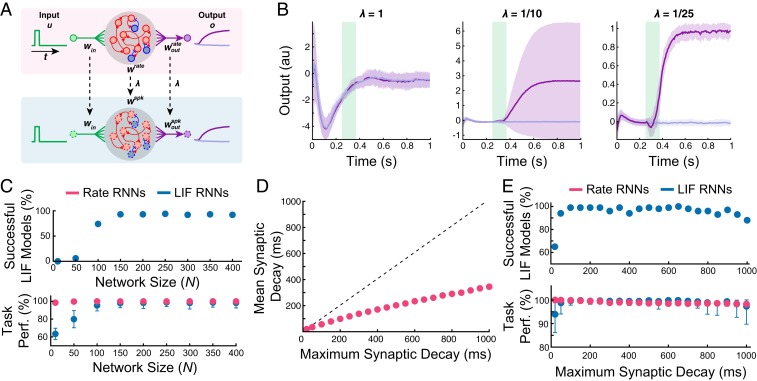
We developed a simple procedure that directly maps dynamics of a trained continuous rate RNN to a spiking RNN in a one-to-one manner.
In our framework, the 3 sets of the weight matrices (, , and ) along with the tuned synaptic time constants () from a trained rate RNN are transferred to a network of LIF spiking units. The spiking RNN is initialized to have the same topology as the rate RNN. The input weight matrix and the synaptic time constants are simply transferred without any modification, but the recurrent connectivity and the readout weights need to be scaled by a constant factor () in order to account for the difference in the firing rate scales between the rate model and the spiking model (Materials and Methods and Fig. 2A). The effects of the scaling factor are clear in an example LIF RNN model constructed from a rate model trained to perform the Go-NoGo task (Fig. 2B). With an appropriate value for , the LIF network performed the task with the same accuracy as the rate network, and the LIF units fired at rates similar to the “rates” of the continuous network units (SI Appendix, Fig. S1). In addition, the LIF network reproduced the population dynamics of the rate RNN model as shown by the time evolution of the top 3 principal components extracted by the principal component analysis (SI Appendix, Fig. S2).
Fig. 2.
Mapping trained rate RNNs to LIF RNNs for the Go-NoGo task. (A) Schematic diagram illustrating direct mapping from a continuous rate RNN model (Upper) to a spiking RNN model (Lower). The optimized synaptic decay time constants () along with the weight parameters (, , and ) were transferred to a spiking network with LIF units (red and blue circles with dashed outlines). The connectivity and the readout weights were scaled by a constant factor, . (B) LIF RNN performance on the Go-NoGo task without scaling (; Left), with insufficient scaling (Center), and with appropriate scaling (Right). The network contained 200 units (169 excitatory and 31 inhibitory units). Mean SD over 50 Go and 50 NoGo trials. (C) Successfully converted LIF networks and their average task performance on the Go-NoGo task with different network sizes. All of the rate RNNs trained in Fig. 1 were converted to LIF RNNs. The network size was varied from to 400. (D) Average synaptic decay values for across different maximum synaptic decay constants. (E) Successfully converted LIF networks and their average task performance on the Go-NoGo task with fixed network size () and different maximum synaptic decay constants. The maximum synaptic decay constants were varied from 20 to 1,000 ms.
Using the procedure outlined above, we converted all of the rate RNNs trained in the previous section to spiking RNNs. Only the rate RNNs that successfully performed the task (i.e., training termination criteria met within the first 6,000 trials) were converted. Fig. 2C characterizes the proportion of the LIF networks that successfully performed the Go-NoGo task ( accuracy; same threshold used to train the rate models) (SI Appendix) and the average task performance of the LIF models for each network size group. For each conversion, the scaling factor () was determined via a grid search method (Materials and Methods). The LIF RNNs constructed from the small rate networks ( and ) did not perform the task reliably, but the LIF model became more robust as the network size increased, and the performance gap between the rate RNNs and the LIF RNNs was the smallest for (Fig. 2C).
In order to investigate the effects of the synaptic decay time constants on the mapping robustness, we trained rate RNNs composed of 250 units () with different maximum time constants (). The minimum time constant () was fixed to 20 ms, while the maximum constant was varied from 20 to 1,000 ms. For the first case (i.e., ms), the synaptic decay time constants were not trained and fixed to 20 ms for all of the units in a rate RNN. For each maximum constant value, 100 rate RNNs with different initial conditions were trained, and only successfully trained rate networks were converted to spiking RNNs. For each maximum synaptic decay condition, all 100 rate RNNs were successfully trained. As the maximum decay constant increased, the average tuned synaptic decay constants increased sublinearly (Fig. 2D). For the shortest synaptic decay time constant considered (20 ms), the average task performance was the lowest at , and 65% of the converted LIF RNNs achieved at least 95% accuracy (Fig. 2E). The LIF models for the rest of the maximum synaptic decay conditions were robust. Although this might indicate that tuning of is important for the conversion of rate RNNs to LIF RNNs, we further investigated the effects of the optimization of in Analysis of the Conversion Method.
Our framework also allows seamless integration of additional functional connectivity constraints. For example, a common cortical microcircuitry motif where somatostatin-expressing interneurons inhibit both pyramidal and parvalbumin-positive neurons can be easily implemented in our framework (Materials and Methods and SI Appendix, Fig. S3). In addition, Dale’s principle is not required for our framework (SI Appendix, Fig. S4).
LIF Networks for Context-Dependent Input Integration.
The Go-NoGo task considered in the previous section did not require complex cognitive computations. In this section, we consider a more complex task and probe whether spiking RNNs can be constructed from trained rate networks in a similar fashion. The task considered here is modeled after the context-dependent sensory integration task used by Mante et al. (7). Briefly, Mante et al. (7) trained rhesus monkeys to integrate inputs from one sensory modality (dominant color or dominant motion of randomly moving dots) while ignoring inputs from the other modality (7). A contextual cue was also given to instruct the monkeys which sensory modality they should attend to. The task required the monkeys to utilize flexible computations, as the same modality can be either relevant or irrelevant depending on the contextual cue. Previous works have successfully trained continuous rate RNNs to perform a simplified version of the task and replicated the neural dynamics present in the experimental data (7, 13, 15). Using our framework, we constructed a spiking RNN model that can perform the task and capture the dynamics observed in the experimental data.
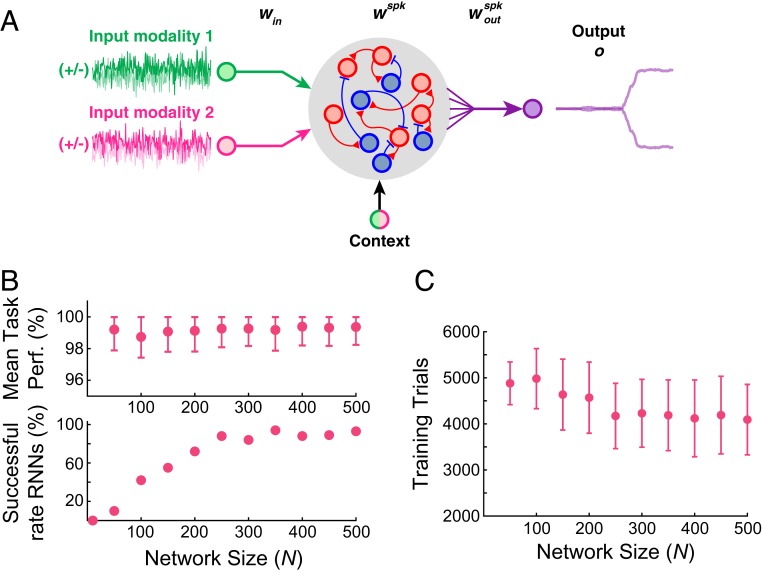
For the task paradigm, we adopted a similar design as the one used by the previous modeling studies (7, 13, 15). A network of recurrently connected units received 2 streams of noisy input signals along with a constant-valued signal that encoded the contextual cue (Materials and Methods and Fig. 3A). To simulate a noisy sensory input signal, a random Gaussian time series signal with 0 mean and unit variance was first generated. Each input signal was then shifted by a positive or negative constant (“offset”) to encode evidence toward the (+) or (−) choice, respectively. Therefore, the offset value determined how much evidence for the specific choice was represented in the noisy input signal. The network was trained to produce an output signal approaching +1 (or −1) if the cued input signal had a positive (or negative) mean. For example, if the cued input signal was generated using a positive offset value, then the network should produce an output that approaches +1 regardless of the mean of the irrelevant input signal.
Fig. 3.
Rate RNNs trained to perform the contextual integration task. (A) Diagram illustrating the task paradigm modeled after the context-dependent task used by Mante et al. (7). Two streams of noisy input signals (green and magenta lines) along with a context signal were delivered to the LIF network. The network was trained to integrate and determine if the mean of the cued input signal (i.e., cued offset value) was positive (+ choice) or negative (− choice). (B) Rate RNNs with different network sizes trained to perform the contextual integration task. The network size was varied from to 500. For each network size, 100 RNNs with random initial conditions were trained. The average task performance (Upper) and the proportion of the successful rate models (Lower) are shown. A model was successful if its mean task performance was 95%. (C) Average number of training trials required for each network size. As the network size increased, the number of training trials decreased (mean SD is shown).
Rate networks with different sizes () were trained to perform the task. As this is a more complex task compared with the Go-NoGo task considered in the previous section, the numbers of units and trials required to train rate RNNs were larger than those in the models trained on the Go-NoGo task (Fig. 3 B and C). The synaptic decay time constants were again limited to a range of 20 and 50 ms, and 100 rate RNNs with random initial conditions were trained for each network size. For the smallest network size (), the rate networks could not be trained to perform the task within the first 6,000 trials (Fig. 3B).
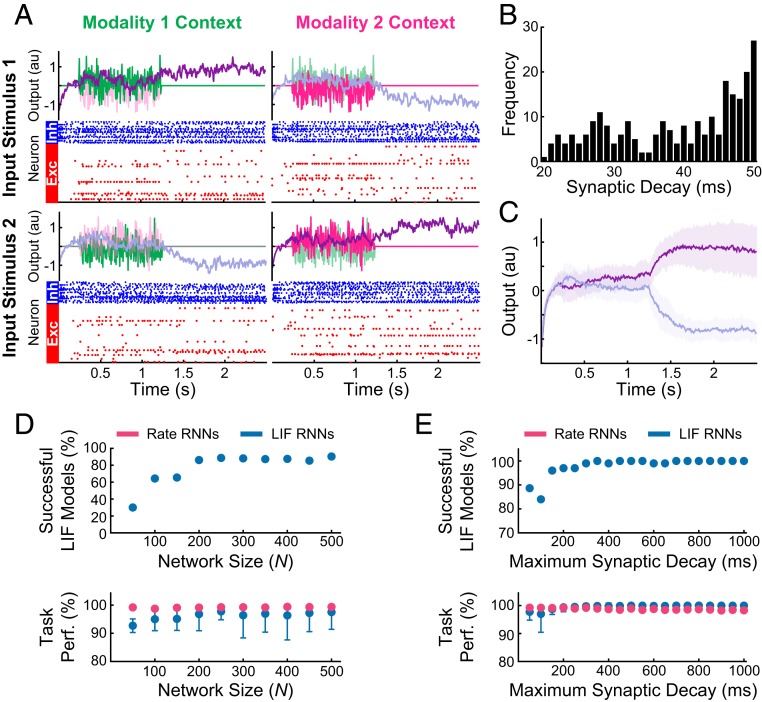
Next, all of the rate networks successfully trained for the task were transformed into LIF models. Example output responses along with the distribution of the tuned synaptic decay constants from a converted LIF model (, ms, ms) are shown in Fig. 4 A and B. The task performance of the LIF model was 98% and comparable with the rate RNN used to construct the spiking model (Fig. 4C). In addition, the LIF network manifested population dynamics similar to the dynamics observed in the group of neurons recorded by Mante et al. (7) and rate RNN models investigated in previous studies (7, 13, 15): individual LIF units displayed mixed representation of the 4 task variables (modality 1, modality 2, network choice, and context) (SI Appendix, Fig. S5A), and the network revealed the characteristic line attractor dynamics (SI Appendix, Fig. S5B).
Fig. 4.
LIF network models constructed to perform the contextual integration task. (A) Example output responses and spike raster plots from an LIF network model for 2 different input stimuli (rows) and 2 contexts (columns). The network contained 250 units (188 excitatory and 62 inhibitory units), and the noisy input signals were scaled by 0.5 vertically for better visualization of the network responses (purple lines). (B) Distribution of the optimized synaptic decay time constants () for the example LIF network (mean SD, 38.9 9.3 ms). The time constants were limited to range between 20 and 50 ms. (C) Average output responses of the example LIF network. Mean SD network responses across 100 randomly generated trials are shown. (D) Successfully converted LIF networks and their average task performance across different network sizes. The network size was varied from to 500. The rate RNNs trained in Fig. 3 were used. (E) Successfully converted LIF networks with and their average task performance across different maximum synaptic decay constants (varied from 20 to 1,000 ms).
Similar to the spiking networks constructed for the Go-NoGo task, the LIF RNNs performed the input integration task more accurately as the network size increased (Fig. 4D). Next, the network size was fixed to , and was gradually increased from 20 to 1,000 ms. For ms, all 100 rate networks failed to learn the task within the first 6,000 trials. The conversion from the rate models to the LIF models did not lead to significant loss in task performance for all of the other maximum decay constant values considered (Fig. 4E).
Analysis of the Conversion Method.
Previous sections illustrated that our framework for converting rate RNNs to LIF RNNs is robust as long as the network size is not too small (), and the optimal size was for both tasks. When the network size is too small, it is harder to train rate RNNs, and the rate models successfully trained do not reliably translate to spiking networks (Figs. 2D and 4D). In this section, we further investigate the relationship between rate and LIF RNN models and characterize other parameters crucial for the conversion to be effective.
Training synaptic decay time constants.
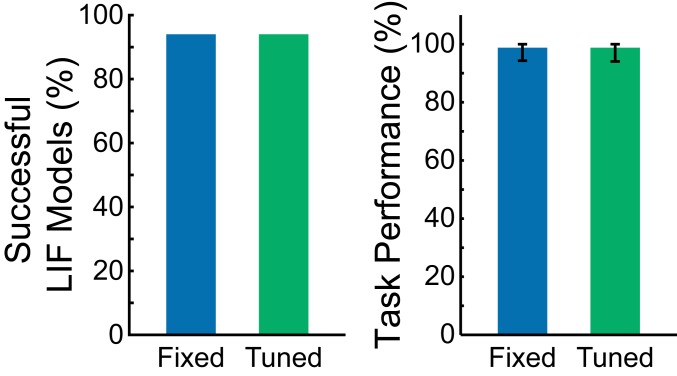
As shown in Fig. 5, training the synaptic decay constants for all of the rate units is not required for the conversion to work. Rate RNNs (100 models with different initial conditions) with the synaptic decay time constant fixed to 35 ms (average value for the networks trained with ms and ms) were trained on the Go-NoGo task and converted to LIF RNNs (Fig. 5). The task performance of these LIF networks was not significantly different from the performance of the spiking models with optimized synaptic decay constants bounded between 20 and 50 ms. The number of the successful LIF models with the fixed synaptic decay constant was also comparable with the number of the successful LIF models with the tuned decay constants (Fig. 5).
Fig. 5.
Optimizing synaptic decay constants is not required for conversion of rate RNNs. The Go-NoGo task performance of the LIF RNNs constructed from the rate networks with a fixed synaptic constant ( ms; blue) was not significantly different from the performance of the LIF RNNs with tuned synaptic decay time constants ( ms, ms; green).
Other LIF parameters.
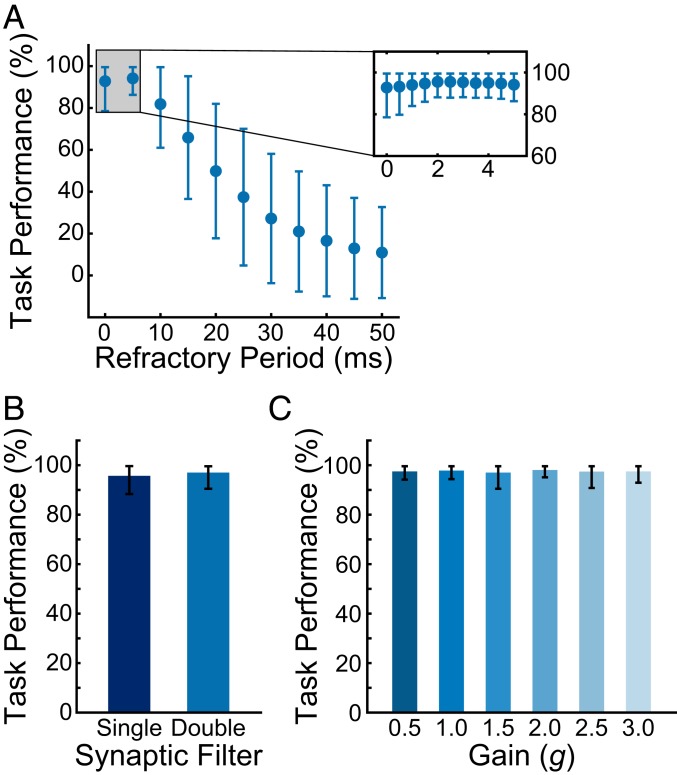
We also probed how LIF model parameters affected our framework. More specifically, we focused on the refractory period and synaptic filtering. The LIF models constructed in the previous sections used an absolute refractory period of 2 ms and a double-exponential synaptic filter (Materials and Methods). Rate models ( and ms) trained on the sensory integration task were converted to LIF networks with different values of the refractory period. As the refractory period became longer, the task performance of the spiking RNNs decreased rapidly (Fig. 6A). When the refractory period was set to 0 ms, the LIF RNNs still performed the integration task with a moderately high average accuracy (92.8 14.3%), but the best task performance was achieved when the refractory period was set to 2 ms (average performance, 97.0 6.6%) (Fig. 6A, Inset).
Fig. 6.
Effects of the refractory period, synaptic filter, and rate RNN connectivity weight initialization. (A) Average contextual integration task performance of the LIF network models () with different refractory period values. The refractory period was varied from 0 ms (i.e., no refractory period) to 50 ms. Inset shows the average task performance across finer changes in the refractory period. Mean SD is shown. (B) Average contextual integration task performance of the LIF network models ( and refractory period of 2 ms) with the single-exponential synaptic filter (dark blue) and the double-exponential synaptic filter (light blue). Mean SD is shown. (C) Average contextual integration task performance of the LIF network models (, refractory period of 2 ms, and double-exponential synaptic filter) with different connectivity gain initializations. Mean SD is shown.
We also investigated how different synaptic filters influenced the mapping process. We first fixed the refractory period to its optimal value (2 ms) and constructed 100 LIF networks () for the integration task using a double synaptic filter (Materials and Methods and Fig. 6B, light blue). Next, the synaptic filter was changed to the following single-exponential filter:
where represents the filtered spike train of unit and refers to the th spike emitted by unit . The task performance of the LIF networks with the above single-exponential synaptic filter was 95.7 7.3%, and it was not significantly different from the performance of the double-exponential synaptic LIF models (97.0 6.6%) (Fig. 6B).
Initial connectivity weight scaling.
We considered the role of the connectivity weight initialization in our framework. In the previous sections, the connectivity weights () of the rate networks were initialized as random, sparse matrices with 0 mean and an SD of , where is the gain term that controls the dynamic regime of the networks and is the initial connectivity probability (Materials and Methods). Previous studies have shown that rate networks operating in a high gain regime () produce chaotic spontaneous trajectories, and this rich dynamics can be harnessed to perform complex computations (6, 11). By varying the gain term, we determined if highly chaotic initial dynamics were required for successful conversion. We considered 6 different gain terms ranging from 0.5 to 3.5, and for each gain term, we constructed 100 LIF RNNs (from 100 rate RNNs with random initial conditions) (Fig. 6C) to perform the contextual integration task. The LIF models performed the task equally well across all of the gain terms considered (no statistical significance detected).
Transfer function.
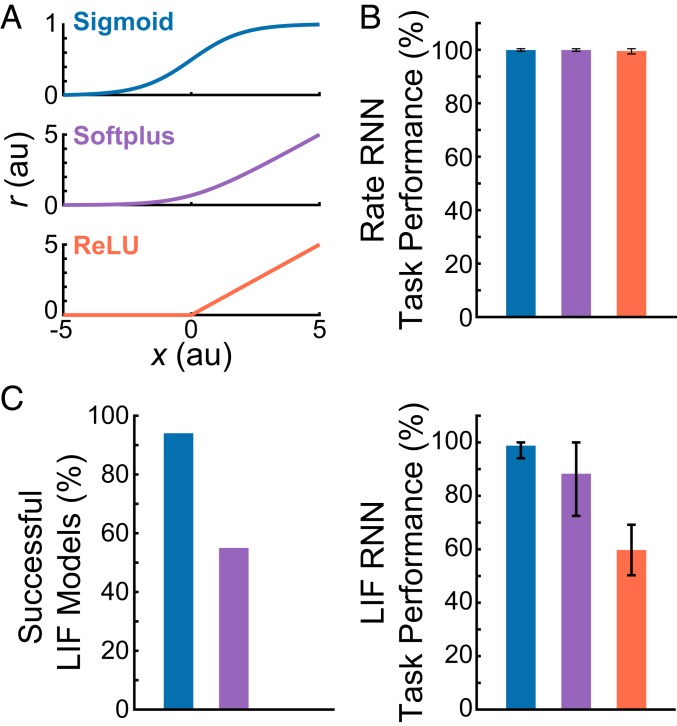
One of the most important factors that determines whether rate RNNs can be mapped to LIF RNNs in a one-to-one manner is the nonlinear transfer function used in the rate models. We considered 3 nonnegative transfer functions commonly used in the machine learning field to train rate RNNs on the Go-NoGo task: sigmoid, rectified linear, and softplus functions (Fig. 7A and SI Appendix). For each transfer function, 100 rate models ( and ms) were trained. Although all 300 rate models were trained to perform the task almost perfectly (Fig. 7B), the average task performance and the number of successful LIF RNNs were highest for the rate models trained with the sigmoid transfer function (Fig. 7C). None of the rate models trained with the rectified linear transfer function could be successfully mapped to LIF models, while the spiking networks constructed from the rate models trained with the softplus function were not robust and produced incorrect responses (SI Appendix, Fig. S6).
Fig. 7.
Comparison of the LIF RNNs derived from the rate RNNs trained with 3 nonnegative activation functions. (A) Three nonnegative transfer functions were considered: sigmoid, softplus, and rectified linear (ReLU) functions. (B) All 300 rate RNNs (100 networks per activation function) were successfully trained to perform the Go-NoGo task. (C) Of the 100 sigmoid LIF networks constructed, 94 networks successfully performed the task. The conversion rates for the softplus and ReLU LIF models were 55 and 0%, respectively. Mean SD task performance: 98.8 4.7% (sigmoid), 88.3 15.8% (softplus), and 59.7 9.5% (ReLU).
Discussion
In this study, we presented a simple framework that harnesses the dynamics of trained continuous rate network models to produce functional spiking RNN models. We identified a set of parameters required to directly transform trained rate RNNs to LIF models, thus establishing a one-to-one correspondence between these 2 model types. Despite of additional spiking-related parameters, surprisingly only a single parameter (i.e., scaling factor) was required for LIF RNN models to closely mimic their counterpart rate models. Furthermore, this framework can flexibly impose functional connectivity constraints and heterogeneous synaptic time constants.
We investigated and characterized the effects of several model parameters on the stability of the transfer learning from rate models to spiking models. The parameters critical for the mapping to be robust included the network size, choice of activation function for training rate RNNs, and a constant factor to scale down the connectivity weights of the trained rate networks. Although the softplus and rectified linear activation functions are popular for training deep neural networks, we demonstrated that the rate networks trained with these functions do not translate robustly to LIF RNNs (Fig. 7). However, the rate models trained with the sigmoid function were transformed to LIF models with high fidelity.
Another important parameter was the constant scaling factor used to scale and before transferring them to LIF networks. When the scaling factor was set to its optimal value (found via grid search), the LIF units behaved like their counterpart rate units, and the spiking networks performed the tasks that the rate RNNs were trained to perform (Fig. 2). Another parameter that affected the reliability of the conversion was the refractory period parameter of the LIF network models. The LIF performance was optimal when the refractory was set to 2 ms (Fig. 6A). Training the synaptic decay time constants, choice of synaptic filter (between single- and double-exponential filter), and connectivity weight initialization did not affect the mapping procedure (Figs. 5 and 6 B and C).
The type of approach used in this study (i.e., conversion of a rate network to a spiking network) has been previously used in neuromorphic engineering to construct power-efficient deep spiking networks (31–36). These studies mainly used feedforward multilayer networks or convolutional neural networks aimed to accurately classify input signals or images without placing too much emphasis on biophysical limitations. The overarching goal in these studies was to maximize task performance while minimizing power consumption and computational cost. However, the main aim of this study was to construct spiking recurrent network models that abide by important biological constraints in order to relate emerging mechanisms and dynamics to experimentally observed findings. To this end, we have carefully designed our continuous rate RNNs to include several biological features. These include 1) recurrent architectures, 2) sparse connectivity that respects Dale’s principle, and 3) heterogeneous synaptic decay time constants.
For constructing spiking RNNs, recent studies have proposed methods that built on the FORCE method to train spiking RNNs (8, 20–22). Conceptually, our work is most similar to the work by DePasquale et al. (21). The method developed by DePasquale et al. (21) also relies on mapping a trained continuous-variable rate RNN to a spiking RNN model. However, the rate RNN model used in their study was designed to provide dynamically rich auxiliary basis functions meant to be distributed to overlapping populations of spiking units. Due to this reason, the relationship between their rate and spiking models is rather complex, and it is not straightforward to impose functional connectivity constraints on their spiking RNN model. An additional procedure was introduced to implement Dale’s principle, but this led to more fragile spiking networks with considerably increased training time (21). The one-to-one mapping between rate and spiking networks used in our method solved these problems without sacrificing network stability and computational cost: biophysical constraints that we wanted to incorporate into our spiking model were implemented in our rate network model first and then, transferred to the spiking model.
While our framework incorporated the basic yet important biological constraints, there are several features that are also not biologically realistic in our models. The gradient-descent method used to tune the rate model parameters, including the connectivity weights and the synaptic decay time constants, in a supervised manner is not biologically plausible. Although tuning of the synaptic time constants is not realistic and has not been observed experimentally, previous studies have underscored the importance of the diversity of synaptic timescales both in silico and in vivo (8, 29, 30). In addition, other works have validated and uncovered neural mechanisms observed in experimental settings using RNN models trained with backpropagation (7, 13, 37), thus highlighting that a network model can be biologically plausible even if it was constructed using nonbiological means. Another limitation of our method is the lack of temporal coding in our LIF models. Since our framework involves rate RNNs that operate in a rate-coding scheme, the spiking RNNs that our framework produces also use rate coding by nature. Previous studies have shown that spike coding can improve spiking efficiency and enhance network stability (20, 38, 39), and recent studies emphasized the importance of precise spike coordination without modulations in firing rates (40, 41). Lastly, our framework does not model nonlinear dendritic processes, which have been shown to play a significant role in efficient input integration and flexible information processing (22, 42, 43). Incorporating nonlinear dendritic processes into our platform using the method proposed by Thalmeier et al. (22) will be an interesting next step to further investigate the role of dendritic computation in information processing.
In summary, we provide an easy-to-use platform that converts a continuous recurrent network model with basic biological constraints to a spiking model. The tight relationship between rate and LIF RNN models under certain parameter values suggests that spiking networks could be put together to perform complex tasks traditionally used to train and study continuous rate networks. Future work needs to focus on why and how such a tight relationship emerges. The framework along with the findings presented in this study lay the groundwork for discovering principles on how neural circuits solve computational problems with discrete spikes and for constructing more power-efficient spiking networks. Extending our platform to incorporate other commonly used neural network architectures could help design biologically plausible deep learning networks that operate at a fraction of the power consumption required for current deep neural networks.
Materials and Methods
The implementation of our framework and the codes to generate all of the figures in this work are available at https://github.com/rkim35/spikeRNN. The repository also contains implementation of other tasks, including autonomous oscillation and delayed match-to-sample tasks.
All of the trained models used in this study have been deposited into Open Science Framework (44).
Continuous Rate Network Structure.
The continuous rate RNN model contains units recurrently connected to one another. The dynamics of the model is governed by
| [5] |
where corresponds to the synaptic decay time constants for the units in the network (Training Details discusses how these are initialized and optimized), is the synaptic current variable, is the synaptic connectivity matrix, and is the output of the units. The output of each unit, which can be interpreted as the firing rate estimate, is obtained by applying a nonlinear transfer function to the synaptic current variable () elementwise:
We use a standard logistic sigmoid function for the transfer function to constrain the firing rates to be nonnegative:
| [6] |
The connectivity weight matrix () is initialized as a random, sparse matrix drawn from a normal distribution with 0 mean and an SD of 1.5/, where is the initial connectivity probability.
The external currents () include task-specific input stimulus signals (SI Appendix) along with a Gaussian white noise variable:
where the time-varying stimulus signals () are fed to the network via , a Gaussian random matrix with 0 mean and unit variance. corresponds to the number of input signals associated with a specific task, and represents a Gaussian random noise with 0 mean and variance of 0.01.
The output of the rate RNN at time is computed as a linear readout of the population activity:
where refers to the readout weights.
Eq. 5 is discretized using the first-order Euler approximation method:
where ms is the discretization time step size used throughout this study.
Spiking Network Structure.
For our spiking RNN model, we considered a network of LIF units governed by
| [7] |
In the above equation, ms is the membrane time constant shared by all of the LIF units, is the membrane voltage variable, is the recurrent connectivity matrix, and represents the spike trains filtered by a synaptic filter. Throughout the study, the double-exponential synaptic filter was used to filter the presynaptic spike trains:
where ms and refer to the synaptic rise time and the synaptic decay time for unit , respectively. The synaptic decay time constant values () are trained and transferred to our LIF RNN model (Training Details). The spike train produced by unit is represented as a sum of Dirac functions, and refers to the th spike emitted by unit .
The external current input () is similar to the one used in our continuous model (Continuous Rate Network Structure). The only difference is the addition of a constant background current set near the action potential threshold (see below).
The output of our spiking model at time is given by
Other LIF model parameters were set to the values used by Nicola and Clopath (23). These include the action potential threshold (−40 mV), the reset potential (−65 mV), the absolute refractory period (2 ms), and the constant bias current (−40 pA). The parameter values for the LIF and the QIF models are listed in SI Appendix, Table S1.
Training Details.
In this study, we only considered supervised learning tasks. A task-specific target signal () is used along with the rate RNN output () to define the loss function (), which our rate RNN model is trained to minimize. Throughout the study, we used the root mean squared error defined as
| [8] |
where is the total number of time points in a single trial.
In order to train the rate model to minimize the above loss function (Eq. 8), we used the adaptive moment estimation stochastic gradient descent algorithm. The learning rate was set to 0.01, and the TensorFlow default values were used for the first and second moment decay rates. The gradient descent method was used to optimize the following parameters in the rate model: synaptic decay time constants (), recurrent connectivity matrix (), and readout weights ().
Here, we describe the method to train synaptic decay time constants () using backpropagation. The time constants are initialized with random values within the specified range:
where is the sigmoid function (identical to Eq. 6) used to constrain the time constants to be nonnegative. The time constant values are also bounded by the minimum () and the maximum () values. The error computed from the loss function (Eq. 8) is then backpropagated to update the time constants at each iteration:
The method proposed by Song et al. (13) was used to impose Dale’s principle and create separate excitatory and inhibitory populations. Briefly, the recurrent connectivity matrix () in the rate model is parametrized by
| [9] |
where the rectified linear operation () is applied to the connectivity matrix at each update step. The diagonal matrix () contains +1 for excitatory units and −1 for inhibitory units in the network. Each unit in the network is randomly assigned to 1 group (excitatory or inhibitory) before training, and the assignment does not change during training (i.e., stays fixed).
To impose specific connectivity patterns, we apply a binary mask () to Eq. 9:
where refers to the Hadamard operation (elementwise multiplication). Similar to the diagonal matrix (), the mask matrix stays fixed throughout training. For example, the following mask matrix can be used to create a subgroup of inhibitory units (Group A) that do not receive synaptic inputs from the rest of the inhibitory units (Group B) in the network (SI Appendix, Fig. S3):
where establishes (if ) or removes (if ) the connection from unit to unit .
Transfer Learning from a Rate Model to a Spiking Model.
In this section, we describe the method that we developed to perform transfer learning from a trained rate model to an LIF model. After the rate RNN model is trained using the gradient descent method, the rate model parameters are transferred to an LIF network in a one-to-one manner. First, the LIF network is initialized to have the same topology as the trained rate RNN. Second, the input weight matrix () and the synaptic decay time constants () are transferred to the spiking RNN without any modification. Third, the recurrent connectivity matrix () and the readout weights () are scaled by a constant number, , and transferred to the spiking network.
If the recurrent connectivity weights from the trained rate model are transferred to a spiking network without any changes, the spiking model produces largely fluctuating signals (as illustrated in Fig. 2B), because the LIF firing rates are significantly larger than 1 (whereas the firing rates of the rate model are constrained to range between 0 and 1 by the sigmoid transfer function).
To place the spiking RNN in the similar dynamic regime as the rate network, we first assume a linear relationship between the rate model connectivity weights and the spike model weights:
Using the above assumption, the synaptic drive () that unit in the LIF RNN receives can be expressed as
| [10] |
where is the synaptic weight from unit to unit .
Similarly, unit in the rate RNN model receives the following synaptic drive at time :
| [11] |
If we set the above 2 synaptic drives (Eqs. 10 and 11) equal to each other, we have
| [12] |
Generalizing Eq. 12 to all of the units in the network, we have
Therefore, if there exists a constant factor () that can account for the firing rate scale difference between the rate and the spiking models, the connectivity weights from the rate model () can be scaled by the factor and transferred to the spiking model.
The readout weights from the rate model () are also scaled by the same constant factor () to have the spiking network produce output signals similar to the ones from the trained rate model:
In order to find the optimal scaling factor, we developed a simple grid search algorithm. For a given range of values for (ranged from 20 to 75 with a step size of 5), the algorithm finds the optimal value that maximizes the task performance.
Supplementary Material
Acknowledgments
We thank Ben Huh, Gerald Pao, Jason Fleischer, Debha Amatya, Yusi Chen, and Ben Tsuda for helpful discussions and feedback on the manuscript. We also thank Jorge Aldana for assistance with computing resources. This work was funded by National Institute of Mental Health Grant F30MH115605-01A1 (to R.K.), the Harold R. Schwalenberg Medical Scholarship (R.K.), and the Burnand–Partridge Foundation Scholarship (R.K.). We acknowledge the support of the NVIDIA Corporation with the donation of the Quadro P6000 graphics processing unit used for this research. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
Footnotes
The authors declare no competing interest.
Data deposition: The data reported in this paper have been deposited in Open Science Framework, https://osf.io/jd4b6/.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1905926116/-/DCSupplemental.
References
- 1.Goldman-Rakic P., Cellular basis of working memory. Neuron 14, 477–485 (1995). [DOI] [PubMed] [Google Scholar]
- 2.Felsen G., et al. , Dynamic modification of cortical orientation tuning mediated by recurrent connections. Neuron 36, 945–954 (2002). [DOI] [PubMed] [Google Scholar]
- 3.Wang X. J., Decision making in recurrent neuronal circuits. Neuron 60, 215–234 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Sompolinsky H., Crisanti A., Sommers H. J., Chaos in random neural networks. Phys. Rev. Lett. 61, 259–262 (1988). [DOI] [PubMed] [Google Scholar]
- 5.Sussillo D., Abbott L., Generating coherent patterns of activity from chaotic neural networks. Neuron 63, 544–557 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Laje R., Buonomano D. V., Robust timing and motor patterns by taming chaos in recurrent neural networks. Nat. Neurosci. 16, 925–933 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Mante V., Sussillo D., Shenoy K. V., Newsome W. T., Context-dependent computation by recurrent dynamics in prefrontal cortex. Nature 503, 78–84 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Kim C. M., Chow C. C., Learning recurrent dynamics in spiking networks. eLife 7, e37124 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Mastrogiuseppe F., Ostojic S., Linking connectivity, dynamics, and computations in low-rank recurrent neural networks. Neuron 99, 609–623.e29 (2018). [DOI] [PubMed] [Google Scholar]
- 10.Enel P., Procyk E., Quilodran R., Dominey P. F., Reservoir computing properties of neural dynamics in prefrontal cortex. PLoS Comput. Biol. 12, e1004967 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Rajan K., Harvey C. D., Tank D. W., Recurrent network models of sequence generation and memory. Neuron 90, 128–142 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Barak O., Sussillo D., Romo R., Tsodyks M., Abbott L. F., From fixed points to chaos: Three models of delayed discrimination. Prog. Neurobiol. 103, 214–222 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Song H. F., Yang G. R., Wang X. J., Training excitatory-inhibitory recurrent neural networks for cognitive tasks: A simple and flexible framework. PLoS Comput. Biol. 12, e1004792 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Song H. F., Yang G. R., Wang X. J., Reward-based training of recurrent neural networks for cognitive and value-based tasks. eLife 6, e21492 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Miconi T., Biologically plausible learning in recurrent neural networks reproduces neural dynamics observed during cognitive tasks. eLife 6, e20899 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Wang J. X., et al. , Prefrontal cortex as a meta-reinforcement learning system. Nat. Neurosci. 21, 860–868 (2018). [DOI] [PubMed] [Google Scholar]
- 17.Zhang Z., Cheng Z., Lin Z., Nie C., Yang T., A neural network model for the orbitofrontal cortex and task space acquisition during reinforcement learning. PLoS Comput. Biol. 14, e1005925 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Huh D., Sejnowski T. J., “Gradient descent for spiking neural networks” in Advances in Neural Information Processing Systems 31, Bengio S, et al., Eds. (Curran Associates, Inc., 2018), pp. 1433–1443. [Google Scholar]
- 19.Lee J. H., Delbruck T., Pfeiffer M., Training deep spiking neural networks using backpropagation. Front. Neurosci. 10, 508 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Abbott L. F., DePasquale B., Memmesheimer R. M., Building functional networks of spiking model neurons. Nat. Neurosci. 19, 350–355 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.DePasquale B., Churchland M. M., Abbott L. F., Using firing-rate dynamics to train recurrent networks of spiking model neurons. arXiv:1601.07620 (26 January 2016).
- 22.Thalmeier D., Uhlmann M., Kappen H. J., Memmesheimer R. M., Learning universal computations with spikes. PLoS Comput. Biol. 12, e1004895 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Nicola W., Clopath C., Supervised learning in spiking neural networks with force training. Nat. Commun. 8, 2208 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Werbos P. J., Backpropagation through time: What it does and how to do it. Proc. IEEE 78, 1550–1560 (1990). [Google Scholar]
- 25.Martens J., Sutskever I., “Learning recurrent neural networks with hessian-free optimization” in Proceedings of the 28th International Conference on International Conference on Machine Learning, ICML’11, Getoor L., Scheffer T., Eds. (Omnipress, 2018), pp. 1033–1040. [Google Scholar]
- 26.Pascanu R., Mikolov T., Bengio Y., “On the difficulty of training recurrent neural networks” Proceedings of the 30th International Conference on International Conference on Machine Learning - Volume 28, ICML’13, Dasgupta S., McAllester D., Eds. (JMLR, Atlanta, GA, 2013), pp. III–1310–III–1318. [Google Scholar]
- 27.Bengio Y., Boulanger-Lewandowski N., Pascanu R., “Advances in optimizing recurrent networks” in Proceedings of the 2013 IEEE International Conference on Acoustics, Speech and Signal Processing, Ward R., Deng L., Eds. (IEEE, Piscataway, NJ, 2013), pp. 8624–8628. [Google Scholar]
- 28.Stokes M. G., et al. , Dynamic coding for cognitive control in prefrontal cortex. Neuron 78, 364–375 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Wasmuht D. F., Spaak E., Buschman T. J., Miller E. K., Stokes M. G., Intrinsic neuronal dynamics predict distinct functional roles during working memory. Nat. Commun. 9, 3499 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Cavanagh S. E., Towers J. P., Wallis J. D., Hunt L. T., Kennerley S. W., Reconciling persistent and dynamic hypotheses of working memory coding in prefrontal cortex. Nat. Commun. 9, 3498 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Cao Y., Chen Y., Khosla D., Spiking deep convolutional neural networks for energy-efficient object recognition. Int. J. Comput. Vis. 113, 54–66 (2015). [Google Scholar]
- 32.Diehl P. U., et al. , “Fast-classifying, high-accuracy spiking deep networks through weight and threshold balancing” in Proceedings of the 2015 International Joint Conference on Neural Networks (IJCNN), Huang D.-S., Ed. (IEEE, Piscataway, NJ, 2015), pp. 1–8. [Google Scholar]
- 33.Diehl P. U., Zarrella G., Cassidy A., Pedroni B. U., Neftci E., “Conversion of artificial recurrent neural networks to spiking neural networks for low-power neuromorphic hardware” in Proceedings of the 2016 IEEE International Conference on Rebooting Computing (ICRC), Williams S., Ed. (IEEE, Piscataway, NJ, 2016), pp. 1–8. [Google Scholar]
- 34.Hunsberger E., Eliasmith C., Training spiking deep networks for neuromorphic hardware. CoRR abs/1611.05141 (16 November 2016).
- 35.Rueckauer B., Lungu I. A., Hu Y., Pfeiffer M., Theory and tools for the conversion of analog to spiking convolutional neural networks. arXiv:1612.04052 (13 December 2016).
- 36.Sengupta A., Ye Y., Wang R., Liu C., Roy K., Going deeper in spiking neural networks: Vgg and residual architectures. Front. Neurosci. 13, 95 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Chaisangmongkon W., Swaminathan S. K., Freedman D. J., Wang X. J., Computing by robust transience: How the fronto-parietal network performs sequential, category-based decisions. Neuron 93, 1504–1517.e4 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Denéve S., Machens C. K., Efficient codes and balanced networks. Nat. Neurosci. 19, 375–382 (2016). [DOI] [PubMed] [Google Scholar]
- 39.Alemi A., Machens C. K., Denéve S., Slotine J. J. E., “Learning nonlinear dynamics in efficient, balanced spiking networks using local plasticity rules” in Proceedings of the AAAI Conference, McIlraith S., Weinberger K., Eds. (AAAI Press, Palo Alto, CA, 2018), pp. 588–595. [Google Scholar]
- 40.Zick J. L., et al. , Blocking NMDAR disrupts spike timing and decouples monkey prefrontal circuits: Implications for activity-dependent disconnection in schizophrenia. Neuron 98, 1243–1255 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Shahidi N., Andrei A. R., Hu M., Dragoi V., High-order coordination of cortical spiking activity modulates perceptual accuracy. Nat. Neurosci. 22, 1148–1158 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Ujfalussy B. B., Makara J. K., Branco T., Lengyel M., Dendritic nonlinearities are tuned for efficient spike-based computations in cortical circuits. eLife 4, e10056 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Yang G. R., Murray J. D., Wang X. J., A dendritic disinhibitory circuit mechanism for pathway-specific gating. Nat. Commun. 7, 12815 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Kim R., Li Y., Sejnowski T. J., Simple framework for constructing functional spiking recurrent neural networks. Open Science Framework. https://osf.io/jd4b6/. Deposited 10 October 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.