Origin of horsetails and the role of whole-genome duplication in plant macroevolution

Abstract

Whole-genome duplication (WGD) has occurred commonly in land plant evolution and it is often invoked as a causal agent in diversification, phenotypic and developmental innovation, as well as conferring extinction resistance. The ancient and iconic lineage of Equisetum is no exception, where WGD has been inferred to have occurred prior to the Cretaceous–Palaeogene (K–Pg) boundary, coincident with WGD events in angiosperms. In the absence of high species diversity, WGD in Equisetum is interpreted to have facilitated the long-term survival of the lineage. However, this characterization remains uncertain as these analyses of the Equisetum WGD event have not accounted for fossil diversity. Here, we analyse additional available transcriptomes and summarize the fossil record. Our results confirm support for at least one WGD event shared among the majority of extant Equisetum species. Furthermore, we use improved dating methods to constrain the age of gene duplication in geological time and identify two successive Equisetum WGD events. The two WGD events occurred during the Carboniferous and Triassic, respectively, rather than in association with the K–Pg boundary. WGD events are believed to drive high rates of trait evolution and innovations, but analysed trends of morphological evolution across the historical diversity of Equisetum provide little evidence for further macroevolutionary consequences following WGD. WGD events cannot have conferred extinction resistance to the Equisetum lineage through the K–Pg boundary since the ploidy events occurred hundreds of millions of years before this mass extinction and we find evidence of extinction among fossil polyploid Equisetum lineages. Our findings precipitate the need for a review of the proposed roles of WGDs in biological innovation and extinction survival in angiosperm and non-angiosperm lineages alike.

1. Introduction

The prevalence of whole-genome duplication (WGD) in land plants has contributed to the widely held view that WGD is an agent of macroevolutionary change [1]. The most striking pattern to have emerged is the apparent temporal clustering of WGD events about the Cretaceous–Palaeogene (K–Pg) boundary interval [2,3]. Perhaps inevitably, this has led to suggestions that WGD facilitated the survival and success of plant lineages in the wake of the attendant ecological disturbance and mass extinction [4,5]. However, the WGD-K–Pg hypothesis is dependent on the accuracy and precision of estimates for the timing of WGD events.

Transcriptomics of Equisetum giganteum has revealed that, like many other land plant lineages, Equisetum underwent at least one round of WGD [6]. The phylogenetic position of Equisetum on a long depauperate branch makes direct molecular dating challenging and hence previous studies have broad confidence intervals around estimated ages. Nevertheless, age estimates from synonymous substitutions (K_s) between duplicate gene pairs have been interpreted cautiously to reflect a duplication age overlapping the K–Pg boundary [6].

WGD is often proposed as a driver of species diversification [7]. Equisetum seems to be an exception, as with only 15 extant species the genus hardly evidences a link between WGD and diversification. In lieu of high species diversity, Vanneste et al. [6] have suggested that the WGD event may have contributed to the longevity of the lineage, despite estimating a relatively recent Equisetum WGD. WGD is also generally proposed as a driver of phenotypic innovation [8], however, few studies consider the diversity of extinct forms in the context of WGD [9]. This is pertinent to Equisetum which exhibits a rich evolutionary history that has been revealed by several recent palaeontological discoveries [10–12].

To test the association of Equisetum WGD and the K–Pg extinction event, we present a thorough analysis of the timing of WGD within Equisetales and its putative macroevolutionary consequences. We refine the phylogenetic position of putative WGD events and use molecular clock methods to show that WGD occurred well before the K–Pg, closer in age to the more ancient and profound Permian–Triassic extinction event. Further, we show that the WGD is not responsible for the phenotypic distinctiveness of Equisetum. There is no evidence that WGD conferred extinction resistance to Equisetales with many Mesozoic lineages not making it through the K–Pg mass extinction.

2. Material and methods

(a). Transcriptome assembly

Assembled transcriptomes were collected from the 1KP dataset for Equisetum diffusum, Equisetum hyemale, Culcita macrocarpa, Ophioglossum petiolatum, Tmesipteris parva, Selaginella kraussiana, Danaea nodosa and Botrypus virginianus, and an additional transcriptome for Equisetum giganteum was obtained from Vanneste et al. [6].

Paired-end short reads were downloaded from the SRA archive for Equisetum arvsense (SRR4061754), Equisetum telmateia (SRR4061752) and Equisetum ramossisimum (SRR5499399), and assembled following [13]. Reads were trimmed of adapter sequences using Trimmomatic v. 0.35 [14] using default settings. Assembly was performed using Trinity [15] using default settings. Redundant transcripts were removed using CD-HIT with a cluster value of 0.9 [16]. The assembly of the E. arvense, E. ramosissimum and E. telmateia transcriptomes after clustering resulted in 24 187, 58 549 and 61 969 transcripts.

(b). K_s analysis

We compared rates of synonymous substitution between paralogous genes in E. hyemale and E. diffusum which represent the subgenera Hippochaete and Equisetum, respectively. Analyses were performed using default parameters and the ‘phyml’ node-weighting method in the wgd package [17–20]. K_s distributions were plotted based on node-averaged values as calculated in the wgd package. Gaussian mixture models (GMMs) were fitted to the K_s distribution following the wgd pipeline, with the optimal number of components assessed using the Bayesian information criterion.

(c). Gene family assignment

Orthogroups from the transcriptomes were inferred using Orthofinder v. 2.2.6 [21] under a Diamond sequence search. The Orthofinder analysis initially produced 27 038 orthogroups. An initial filtering step was performed to remove orthogroups that did not contain at least one representative from 75% of species. Remaining orthogroups were aligned using MUSCLE and trimmed using trimal [22]. A second filtering step removed all alignments shorter than 200 amino acids, resulting in 5009 orthogroups. Phylogenetic inference was performed on each remaining orthogroup under the best-fitting model and maximum-likelihood criterion in IQ-TREE [23], with 1000 ultra-fast bootstrap replicates [24].

(d). Species divergence time estimation

Single copy orthogroups from the Orthofinder output formed the basis of a dating analysis. An alignment of 45 977 amino acids was partitioned by the gene for a topology search using the edge-linked option (-spp) in IQ-TREE [23].

The topology formed the basis of a fixed-topology node-calibrated molecular clock analysis in MCMCtree [18]. Node calibrations were specified with a uniform distribution spanning the hard minimum and soft maximum constraints (with a 2.5% tail distribution) established using MCMCtreeR in R (electronic supplementary material, table S2) [25]. Previous studies have placed the fossil taxon Equisetum fluviatoides as sister to E. diffusum [12]. However, our analyses supported an E. fluviatoides as sister to both E. diffusum and E. arvense, and so we established a calibration for the divergence of the two subgenera (electronic supplementary material, Methods). The mean rate was assigned a gamma prior, based on the mean number of substitutions along the tree scaled by the approximate geological age, with a total of 0.12 substitutions per site per million years. To ensure the model sampled from this distribution, we fixed the shape parameter to 2 and adjusted the scale parameter to 16 [26,27]. The analysis was run without sequence data to ensure that the effective time priors were compatible with the palaeontological and phylogenetic constraints informing the specified node calibrations [28]. Using the approximate likelihood method [29], we ran two independent analyses, each for 5 000 000 generations, discarding the first 1 000 000 generations as burn-in. The convergence of each run was assessed using Tracer [30].

(e). Gene tree and species tree reconciliation

Gene trees inferred from Orthofinder were reconciled with the dated species tree. Gene trees were inferred under a duplication-transfer-loss model using a maximum-likelihood criterion in ALE (amalgamated likelihood estimation) [31]. The reconciliations were performed using 1000 ultra-fast bootstrap replicates as tree samples. As there is no prior hypothesis regarding an ancient hybridization (allopolyploidy) event in Equisetum, we set a low prior rate of gene transfer (0.1). The total number of duplications was summed for each branch in the phylogeny based on the number of inferred duplications across each of the 1000 sampled trees for each gene family.

(f). Dating whole-genome duplication

Gene families inferred to have duplicated along the branch leading to Equisetum were sampled from the ALE output (electronic supplementary material, figure S1). To evaluate the hypothesis of a single WGD event in Equisetum, we selected gene families that contained a single duplication along this branch for a molecular clock analysis. Following [32], gene families were used if they: (i) had a clear topological signal of the WGD event, were represented by two paralogous copies present in all Equisetum species forming two monophyletic groupings; (ii) had a topology congruent with current understanding of tracheophyte phylogeny; and (iii) did not have a signal of additional duplication events within Equisetum. We conducted a molecular clock analysis for each gene family with the same settings as used for the species divergence estimation. The 95% highest posterior densities (HPDs) were combined between all gene families. Peaks in this combined posterior distribution may represent duplication events common to multiple gene families. To determine which gene families coincide with each peak, the peaks in the combined posterior distribution were described using GMMs and the overlap between these peaks and the individual gene posterior distributions were estimated using an overlapping coefficient [33]. Gene families with an overlap greater than 0.8 for each respective peak were selected and concatenated. Molecular clock analyses were performed for families corresponding to each peak, with the same set of fossil calibrations employed as in the species divergence time estimation, with the exception that the calibration within Equisetum was cross-calibrated on both sides of the duplication. Analyses were performed as for the species divergence estimation.

To consider the possibility of multiple WGD events, we repeated the analysis with gene families containing at least two duplications (four copies of each gene) in all extant Equisetum species, allowing for simultaneous age estimation of two duplication nodes.

(g). Dating of fossils and extant taxa

We used previously assembled phenotypic and molecular matrices of 77 binary and multistate phenotypic characters and the rbcL, atpA, atpB and matK chloroplast genes [12]. The matrix contained 49 taxa, including 17 extant and 32 fossil taxa spanning the Sphenophyllales + Equisetales as well as outgroup taxa Hamatophyton verticillatum, Rotafolia songziensis, Ophioglossum reticulatum and Psilotum nudum.

We estimated divergence times using the estimates from the molecular species divergence analysis as priors on nodes present in this dataset. Fossil tip ages were based on a uniform distribution across their occurrence ranges (electronic supplementary material, table S1) and a uniform distribution was placed on the root between 451 and 384 Myr [27]. A stepping stone analysis was used to test for the best-fitting clock model in MrBayes v. 3.2.6 [34,35]; this showed significant support for the correlated model [36] over the independent gamma rates [37] and strict clock models. A correlated rates clock model [36] was implemented with the clock rate prior set as a lognormal distribution; the mean of the lognormal distribution was estimated from a topological analysis to estimate the tree height scaled by the approximate geological age of the root (0.02 substitutions/site/Myr) [38]. Finally, we set a uniform birth–death prior across the tree [35]. The phenotypic data and each gene were partitioned separately, with molecular data analysed under the GTR+Γ model and the phenotypic data under the MKv+Γ model [39]. Four independent chains were run for 20 000 000 generations. Convergence between the chains was assessed based on the average standard deviation of split frequencies (less than 0.01), effective sample size (target greater than 200) and by examining the parameters of the chain in Tracer [30].

(h). Rates of phenotypic evolution

To examine the rates of phenotypic evolution across the tree, we performed a morphological clock analysis using only the phenotypic dataset with the tree constrained to the topology resolved by the combined analysis. A relaxed clock model was used, allowing rates to vary between branches.

The rate of phenotypic evolution was estimated by sampling the effective branch lengths from 1000 points of the posterior distribution; the mean rates were estimated from these samples. Only branches from the majority-rule consensus topology were considered for further analyses; from the 1000 posterior samples, rates were summarized for branches on the posterior tree that matched branches on the majority-rule consensus tree.

(i). Phenotypic disparity

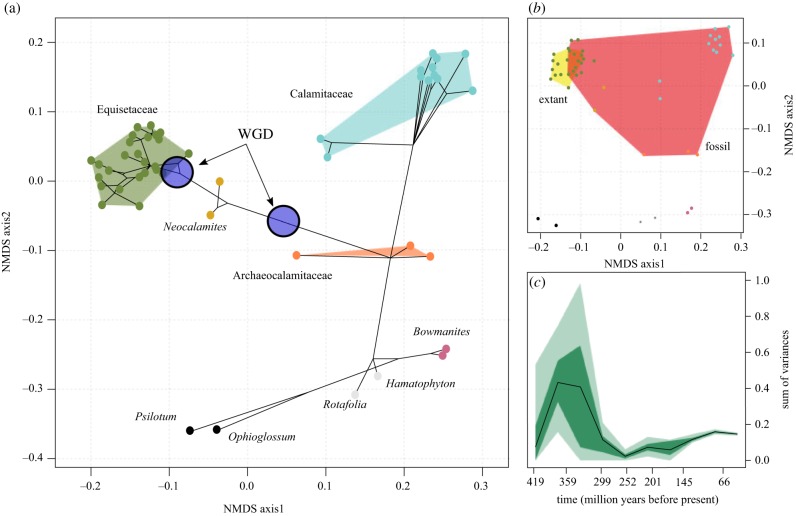
The phenotype matrix was recoded following [40], such that non-applicable states were coded as ‘0’ and missing data as ‘?’, to distinguish the two types of ‘missing data’ [41]. The distance between taxa was calculated using Gower's dissimilarity metric [42]. The distances were projected into two-dimensional space using non-metric multi-dimensional scaling (NMDS). We plotted a phylomorphospace using the majority-rule (50%) consensus tree from the total evidence analysis [43]. The most likely ancestral state was reconstructed along the tree by summarizing states across 1000 stochastic character maps [44]; the estimated states were used to position the nodes within the morphospace.

We calculated disparity as the sum of variances from the distance matrix [45] using dispRity in R [46]. Disparity through time was estimated using a time-slicing approach using 10 bins and the ‘gradual split’ model as implemented in dispRity, with an equal probability of a character state being that of either the descendant or the ancestor dependent on the length of the branch [46].

(j). Genome size analysis

Genome size estimates (1C-values) were downloaded from the C-value database [47]. The 1C-values were estimated for fossil taxa by Franks et al. [48] who derived a linear regression model for the relationship between 1C-value and stomata guard cell length. They estimated 1C-value for members of Sphenophyllales (Sphenophyllum) and Calamitaceae (Calamocladus) as well as Equisetum haukeanum. For this analysis, we took the values for Sphenophyllales and Calamitaceae to be representative of each lineage. We used the linear model (y = 1.83x + −5.46) to convert the logged guard cell widths of other fossil Equisetum and to a logged 1C-value [10,11,48–50]. In total, 21 1C-values were obtained (electronic supplementary material, table S1) and were analysed as continuous characters in BayesTraits v. 3 [51] using a homogeneous continuous random walk model to estimate the ancestral 1C-values at internal nodes. The MCMC was run for 15 000 000 generations, with the first 10 000 000 generations discarded as burn-in.

3. Results

(a). Transcriptomic analyses reveal Triassic and carboniferous whole-genome duplication events

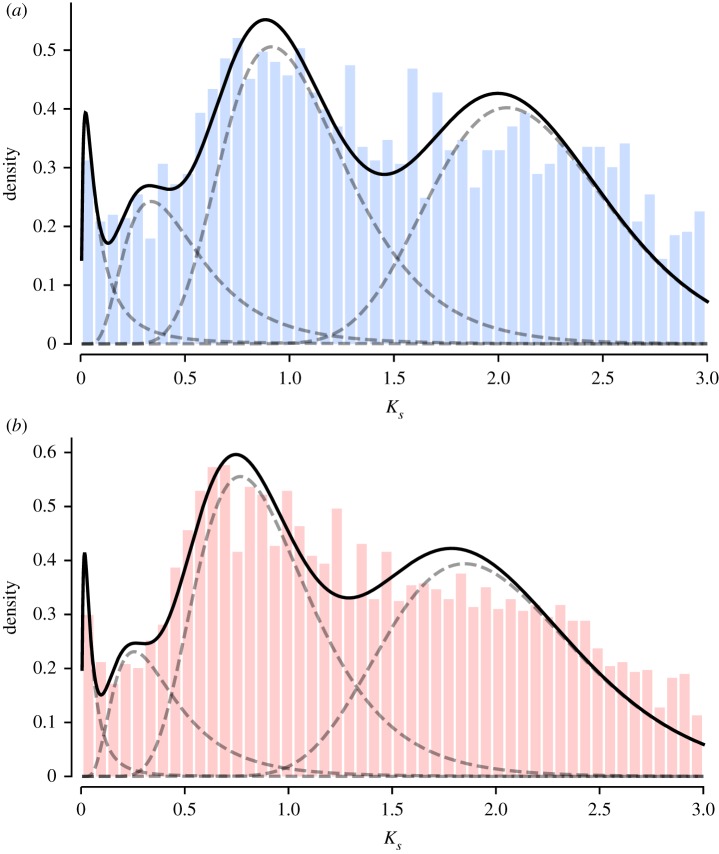
The distribution of K_s values in E. hyemale and E. diffusum exhibit at least three conspicuous peaks: one close to 0.1 representing recent duplicates, another with a mean close to 1 and third more ancient peak close to 2 (figure 1). Mixture modelling supported four components, but the fourth component had a low mean weight (figure 1; electronic supplementary material, figure S1). The coincidence of these peaks suggests that the WGD event initially identified in E. giganteum is shared between both subgenera, though K_s values > 2 are increasingly unreliable predictors of WGD [52].

Figure 1.

Node-averaged rates of synonymous substitution (K_s) between paralogous pairs for (a) E. diffusum and (b) E. hyemale. Components among the distributions were fitted using the function gmm() in the wgd pipeline. (Online version in colour.)

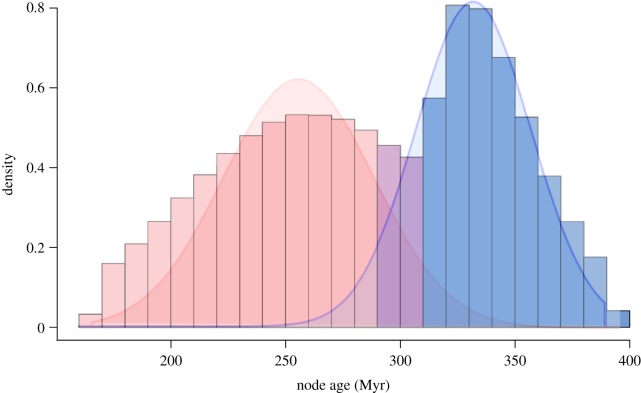
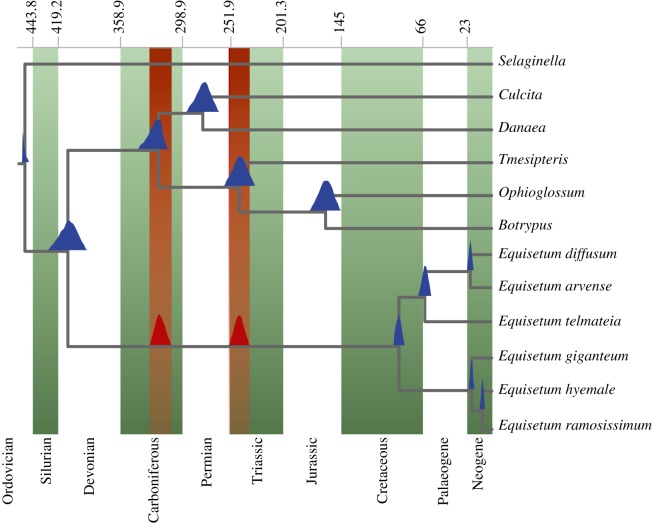
ALE analysis revealed rates of duplication that were generally higher on terminal branches (likely due to recent local duplication events) and some of the long branches included in the study. Among all branches, however, ALE provided strong support for a duplication event on the branch leading to total group Equisetum (electronic supplementary material, figure S2). Two hundred and forty gene families were selected from the ALE output that showed a clear signal of the duplication event. Molecular clock analyses of these gene families supported two clear clusters of ages (figure 2). For each cluster, we found 52 and 51 corresponding gene families that were concatenated to form alignments of 21 894 and 19 360 amino acids. These analyses suggested a first duplication within the interval 329–307 Ma (Serpukhovian–Moscovian: mid–late Carboniferous) and a second within 253–233 Ma (Changhsingian–Carnian: latest Permian to Late Triassic) (figure 3).

Figure 2.

A histogram showing the combined posterior distribution of ages for the duplication node among 240 gene families containing the signal of a gene duplication event in Equisetum. Two clusters are defined using mixture models. (Online version in colour.)

Figure 3.

Inferred age of the WGD event in Equisetum. Multi-copy gene families were concatenated to inform a molecular clock analysis for each putative WGD event. The 95% HPD is shown for each speciation node in blue, with the duplication events in red. (Online version in colour.)

We identified a further 14 gene families with a clear signal of two successive duplications with all four paralogues retained. The two successive duplications were estimated to 360–322 Ma (Fammenian–Bashkirian: latest Devonian to mid-Carboniferous) and 261–211 Ma (Capitanian–Norian: late Permian to Late Triassic; electronic supplementary material, figure S3).

(b). An evolutionary framework: Triassic–Jurassic origin of total group Equisetum

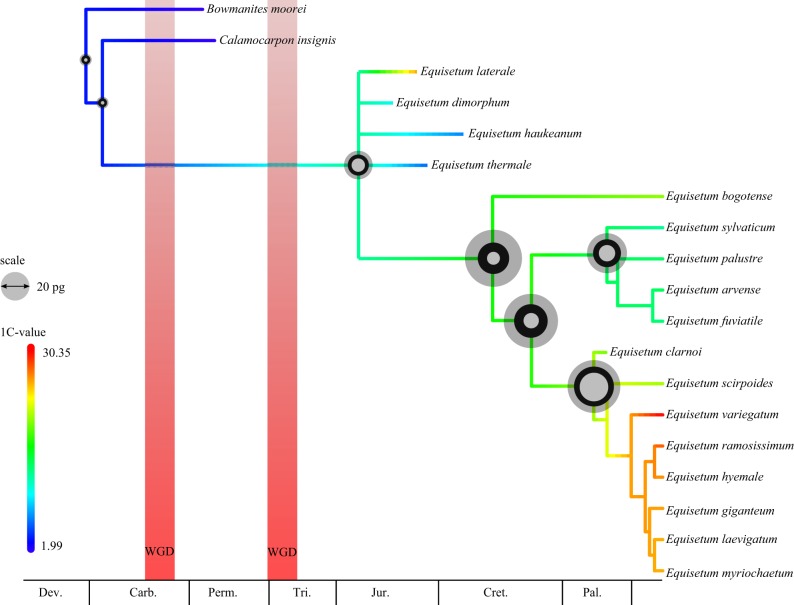
Analysis of the combined molecular and morphological dataset partially resolved the backbone phylogeny of Equisetales (figure 4). Monophyly of Equisetales is strongly supported, with Neocalamitaceae as sister to all remaining Equisetaceae, but there is only weak support for Neocalamitaceae. As with Elgorriaga et al. [12], we resolve Equisetites arenaceus and Spaciinodum collinsonii as sister to the total group Equisetum.

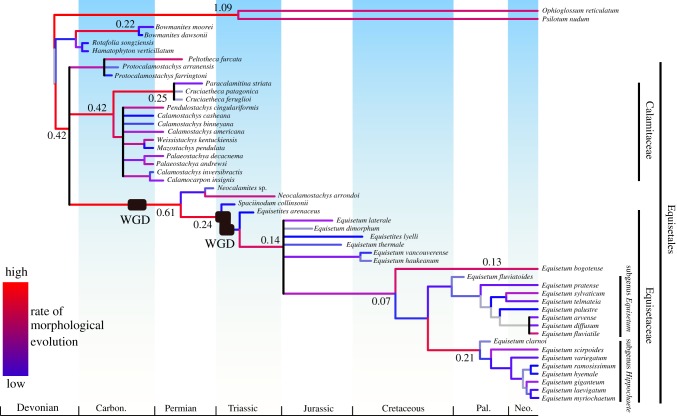
Figure 4.

Total evidence phylogeny of extinct and extant Equisetales. The tree was constructed using Bayesian analysis of phenotypic and molecular data with the ages of the fossils as tip calibrations and nodes calibrated using estimates from the molecular analysis. Rates of phenotypic evolution (low rates in blue, high rates in red) are from the mean effective branch rates from a posterior sample of 1000 trees estimated morphological data alone. High rates are shown in text next to branches. The position of each putative WGD is shown on the tree. (Online version in colour.)

Relationships within Equisetum are poorly resolved; the two subgenera (Equisetum and Hippochaete) are well supported, as are the positions of E. clarnoi and E. fluviatoides within each, respectively. The relationships of the outgroups are also poorly resolved, including the order of divergence of Archaeocalamitaceae and Calamitaceae, although as we confirm that Equisetaceae did not originate from within Calamitaceae.

We estimate a Devonian origin of both sphenopsids and ferns. Sphenophyllales and Equisetales diverged during the Carboniferous along with most of the extinct lineages of Equisetales, including the Archaeocalamitaceae and Calamitaceae. Equisetaceae and Neocalamitaceae diverged during the Permian. We report a Triassic–Jurassic origin of total group Equisetum, but a Cretaceous origin of the crown group, with both extant subgenera originating during the Palaeogene (electronic supplementary material, figure S4).

(c). High rates of phenotypic evolution at the origin of major clades

Rates of phenotypic evolution are heterogeneous across the tree (figure 4). The origin of major lineages is marked by the fastest rates of phenotypic evolution, including Equisetales, Equisetaceae and Hippochaete (figure 4). Generally, phenotypic evolution is much greater between higher-order lineages than within them, with slow rates observed within Equiseteceae and most lineages within Calamitaceae, except the branch leading to Cruciaetheca.

High rates of phenotypic evolution correspond to large distances in morphospace (figure 5a). Major lineages cluster tightly within morphospace across both axes, though on the individual axes, there is considerable overlap. The proportion of total disparity represented by extant taxa is low (figure 5b) and disparity through time analyses show that modern levels of disparity are a small fraction of a Carboniferous acme (figure 5c). The mean disparity, measured as the average Euclidean pairwise distance between taxa, is lower in Equisetaceae (0.195) than Calamitaceae (0.381), but they do occupy a novel region of morphospace.

Figure 5.

Phenotypic evolution within the Equisetales. (a) An empirical phylomorphospace showing the distribution of disparity within the order. The distances between taxa were calculated using Gower's index and ordinated using NMDS. Character states for all ancestral nodes were reconstructed and were projected into the morphospace with the tree. Convex hulls were fitted around each lineage. Colours correspond to different lineages. (b) The comparative morphospace occupation of extant and fossil Equisetales. (c) The evolution of disparity (sum of variances) through time estimated from the distance matrix. (Online version in colour.)

(d). Genome duplication and genome size

Reconstruction of ancestral genome size within Sphenopsida reveals that the largest genome sizes are found within extant Equisetum (mean ancestral 1C-value = 17.09 pg), in particular, the subgenus Hippochaete (ancestral 1C-value = 20.9 pg) (figure 6). Across nodes, we observed three large increases in genome size: from the base of Equisetum to Hippochaete (17.6–20.9 pg), from the base of Equisetales to total group Equisetum (3.9–11.01 pg) and from total group to crown group Equisetum (11.01–17.6 pg) (figure 6).

Figure 6.

The reconstruction of ancestral genome size across the Equisetales. The genome size was reconstructed based on both extant and fossil 1C-value estimates. The reconstructed size is shown at each node, with the width of the circle proportional to the 1C-value. The middle circle represents the mean estimate, while the small and large circles represent the lower and upper 95% HPD values, respectively. Branches are coloured to show the evolution of large (red) and small (blue) genome sizes. (Online version in colour.)

4. Discussion

(a). Duplication and evolution in Equisetum

The WGD shared by extant Equisetum was previously proposed as one of several WGD events that coincide with the K–Pg boundary [2,6]. The significance of this clustering of events has been explored from various angles: that WGD confers an ‘extinction resistance’, that WGD may have provided a means of rapid adaptation amidst ecological disturbance, that WGD may be a response to environmental stresses and that WGD itself might just be a non-selective consequence [53] of a switch to vegetative reproduction often associated with polyploidy [2,54,55]. The new age estimates presented here render these hypotheses unlikely given that the WGDs predate the K–Pg mass extinction by hundreds of millions of years. Indeed, we find no evidence of beneficial evolutionary consequences of WGD in Equisetum, suggesting that these events do not universally precipitate changes on the macroevolutionary scale across the tree of life.

Our analyses supported multiple bursts of gene duplication throughout the evolution of the Equisetum lineage. Their interpretation as WGD events can be difficult [56], yet their clustering within time and the repeated history of WGD across land plants suggests that there is a high probability that they represent WGD events. Though congruent with the findings of Vanneste et al. [6], we have better resolved the phylogenetic position of these putative WGD events and find that they are likely shared by both subgenera of Equisetum (figure 1). However, the WGD event proposed by Vanneste et al. [6] to have occurred in E. giganteum was known only from a single transcriptome and the geological age was difficult to constrain using both phylogenomic and K_s methods. Indeed, ages inferred directly from K_s distributions can be inaccurate due to sequence saturation and the assumption of a strict clock [52,57].

Using phylogenomic and molecular clock methods, we estimated both events to have occurred long before the K–Pg boundary. Rather, these WGD events are among the most ancient detected in land plants, occurring within the latest Devonian–mid-Carboniferous and late Permian–Late Triassic, respectively (figure 3). This estimate is comparable in precision to recent estimates for other WGD events associated with the K–Pg boundary [58] and serves to highlight the power of these methods to constrain the timing of the event to within 20 Myr, along one of the most isolated branches within living land plants. The discrepancy in age for the Equisetum WGD events reported here and by Vanneste et al. [6] may be due to the initial paucity of transcriptomic data representative of the lineage and highlights the benefits of increased taxonomic sampling and the value of concatenation in estimating the timing of WGD events [1].

We reconstructed the evolutionary history of Equisetales using a combination of molecular and phenotype data in a Bayesian framework (figure 4). Broadly, the relationships resolved are congruent with previous parsimony-based results [12], though the relationships of species are less well resolved. The lack of resolution in the phylogeny here may be the consequence of the previously used parsimony methods producing more highly resolved, but less accurate trees compared to Bayesian analyses of morphological data [59,60]. Nevertheless, our results corroborate the distinction between the Calamitaceae and Equisetaceae and the hypothesis that both lineages have evolved independently since the Carboniferous (figure 4).

Crucially, these analyses provide a framework in which WGD can be considered in the light of both extant and extinct diversity. We have shown that the more ancient WGD event took place prior to the divergence of Equisetaceae and Neocalamitaceae, and the more recent WGD event appears to coincide with the origin of Equisetaceae, either prior to or after the divergence of Spaciinodum. As well as establishing a more precise estimate for the timing of WGD, our analyses place WGD within the context of the gross historical diversity of the lineage, rather than merely the net diversity that has survived to the present. This represents a novel approach to understanding the role of WGD in land plant evolution that is likely to be key to more thoroughly testing existing hypotheses, such as the proposed link between WGD events and the K–Pg mass extinction event in angiosperm evolution.

(b). Evolutionary consequences of whole-genome duplication in a non-angiosperm lineage

The ancient timing of the Equisetum WGD events could be interpreted to strengthen the hypothesis that WGD has facilitated the longevity of the lineage [6]. The tentative hypothesis that the Equisetum WGD event conferred extinction resistance across the K–Pg seems unlikely given our estimates for the timing of the WGD events, and current hypotheses linking WGD to success emphasize only short-term advantages. Furthermore, our analyses have shown that many polyploid taxa descended from the WGD events are now extinct.

WGD events have also been implicated as drivers of phenotypic variance within the plant kingdom. Multiple models and a few examples demonstrate how novel traits have arisen in the wake of WGD that have been maintained and diversified on a macroevolutionary scale [8,61]. The precise estimates that we have obtained for the timing of the WGD events allow us to constrain them within tight bounds on the species phylogeny and to consider their impact within the context of subsequent phenotypic evolution. The evolution of Equisetales is generally associated with relative stability and few character state changes, yet the first WGD event coincides with higher rates of phenotypic evolution (figure 4) and each WGD event also coincides topologically with a movement into a novel area of morphospace (figure 5a).

However, extant Equisetum and the fossil taxa that descended from the WGD event represent only a fraction of the phenotypic diversity of Equisetales (figure 5b). In addition, both Equisetales and Calamitaceae exhibit fast early rates of phenotypic evolution (figure 4), yet Calamitaceae also achieved greater disparity (figure 3a). Indeed, while WGD may have played a role in promoting phenotypic novelty, it has not been sufficient to sustain disparity over time (figure 3c). Based on previously identified synapomorphies [12], the first WGD event coincides with the evolution of lacunae (vallecular canals), the loss of internode differentiation, alternating sporangiophore shields, an increase in sporangium numbers and, possibly, the expression of all three reproductive regulatory modules [12]. The second WGD also coincides with a number of synapomorphies, including alternating ribs, leaf tips and a reduction in the length of reproductive structures [12]. Throughout the evolutionary history of Equisetales, the accumulation and transformation of characters associated with the extant taxa is gradual and many of the distinguishing features, including a compacted strobilus and small size, have evolved slowly and in a mosaic pattern over several nodes [12,62,63]. This suggests that while WGD may have had a role in promoting the diversity of the Equisetaceae, it was not a prerequisite to the evolution of disparity within Equisetales.

(c). Genome size correlates with whole-genome duplication in Equisetum

Genome size evolution within Equisetales shows that the inferred WGD events may also correlate with an increase in ancestral genome size (figure 6). This is in some ways surprising since the signal of genome duplication in genome size estimates rapidly erodes across most plant genomes [64,65]. However, there is also a more recent shift towards much larger genomes that does not appear to be associated with a WGD event (figure 6). As there are no extant members of Calamitaceae, it is not possible to rule out the possibility that they may have undergone their own independent WGD event. However, the small genome size inferred for Calamitaceae [48] and relative stasis of fern genome evolution means that we may speculate that there may have been no further WGD events in this lineage [66]. Multiple WGD events may in part explain the fixed high chromosome numbers shared among extant species of Equisetum [66], yet does not appear to explain the distribution of genome sizes between the two extant subgenera.

Clearly, to elucidate a macroevolutionary role for WGD in land plant evolution, it is insufficient to consider only extant taxa. Equisetum is a good example, since its extant diversity is a poor representation of the taxonomic and phenotypic diversity that existed historically within Sphenopsida. Here, we suggest that a combination of palaeontological and genomic approaches provides additional power and greater insight when considering the impact of ancient or ‘palaeo’-polyploidy.

5. Conclusion

It is generally accepted that WGD events are agents of macroevolutionary change. Here, we have shown that a combination of macroevolutionary and comparative genomic approaches can be used to improve estimates of the timing and characterize outcomes of WGD. In Equisetum, WGD did not coincide with the K–Pg boundary, nor does it appear to have facilitated greater resistance to extinction. Rather, while WGD in Equisetum appears to correlate with the occupation of novel regions of morphospace, it has not led to significant morphological diversification. The formative role of WGD in the evolutionary history of many angiosperm lineages is generally accepted, yet its role remains to be explored in many other plant lineages where rates of WGD are expected to be high. It is possible that differing genome dynamics may determine equally different roles for WGD in macroevolution.

Data accessibility

This article has no additional data.

Authors' contributions

All authors contributed to the design of the analyses. J.W.C. performed the data analyses. All authors contributed to the drafting of the manuscript.

Competing interests

We declare we have no competing interests.

Funding

The authors thank members of the Bristol Palaeobiology Group, Jill Harrison and Andrew Leitch for helpful discussion. J.W.C was funded by a BBSRC SWBIO DTP studentship, M.N.P. by an 1851 Research Fellowship from the Royal Commission for the Exhibition of 1851 and P.C.J.D. by NERC (grant no. NE/N002067/1) and BBSRC (grant no. BB/N000919/1).