Kinematic patterns while walking on a slope at different speeds

Abstract

During walking, the elevation angles of the thigh, shank, and foot (i.e., the angle between the segment and the vertical) covary along a characteristic loop constrained on a plane. Here, we investigate how the shape of the loop and the orientation of the plane, which reflect the intersegmental coordination, change with the slope of the terrain and the speed of progression. Ten subjects walked on an inclined treadmill at different slopes (between −9° and +9°) and speeds (from 0.56 to 2.22 m/s). A principal component analysis was performed on the covariance matrix of the thigh, shank, and foot elevation angles. At each slope and speed, the variance accounted for by the two principal components was >99%, indicating that the planar covariation is maintained. The two principal components can be associated to the limb orientation (PC1*) and the limb length (PC2*). At low walking speeds, changes in the intersegmental coordination across slopes are characterized mainly by a change in the orientation of the covariation plane and in PC2* and to a lesser extent, by a change in PC1*. As speed increases, changes in the intersegmental coordination across slopes are more related to a change in PC1*, with limited changes in the orientation of the plane and in PC2*. Our results show that the kinematic patterns highly depend on both slope and speed.

NEW & NOTEWORTHY In this paper, changes in the lower-limb intersegmental coordination during walking with slope and speed are linked to changes in the trajectory of the body center of mass. Modifications in the kinematic pattern with slope depend on speed: at slow speeds, the net vertical displacement of the body during each step is related to changes in limb length and orientation. When speed increases, the vertical displacement is mostly related to a change in limb orientation.

INTRODUCTION

Walking is a rather complex task that involves the motion of all body segments at several degrees of freedom (45, 69). However, with an examination of the whole body dynamics, the description of walking appears remarkably simple and consistent: the out-of-phase fluctuations of the potential and kinetic energies of the center of mass (COM) of the body can be likened to an inverted pendulum (15). It has been suggested that these pendulum-like dynamics may serve as a target for motor control of walking (2, 26, 37, 48, 65). The displacement of the COM highly depends on the combined movements of the lower-limb segments (44, 45, 63). These segmental motions result from the interplay between passive dynamics and active neural control (37, 43), which in turn, contribute to whole body stability and economy.

In the mid-1990s, it was shown that the changes of the orientation of the lower-limb segments in the sagittal plane do not evolve independently during the stride (9, 12): when the orientation angles of the thigh, shank, and foot are plotted against each other in a three-dimensional (3D) space, they covary along a loop constrained close to a 2D plane. The orientation of this plane and the shape of the loop depend on the phase and amplitude relationships among the segmental angles. Changes in the planar covariation are related to how subjects perform in different walking conditions, e.g., with erect vs. bent posture (29), with different levels of body-weight unloading (38), along curved paths (19), or with slip-like perturbations (6). Furthermore, pathologies of the brain structures, such as the basal ganglia (28) or the cerebellum (51, 54), also affect the shape of the elevation angle loop and the orientation of the covariance plane.

With the analysis of the planar covariation of the lower-limb segments, Ivanenko et al. (35) has shown that the main axis of the covariance plane primarily represents the limb orientation, and the second axis primarily represents the limb length. In this way, the planar covariation of lower-limb segments describes the behavior of a “telescopic limb” (41) that shapes the COM trajectory as a function of body posture and gait (29, 35). However, open questions remain as to how the COM trajectories are achieved by the combined rotation and translation of the lower-limb segments when walking on various slopes and at different speeds.

The task of walking up or down slopes involves a modification of COM height with each step. At first approximation, the trajectory of the COM during level walking is often illustrated by a “compass gait” model (3, 56, 63, 66). In this model, the lower limbs are assimilated to rigid sticks, their mass is negligible, and the COM is located at the hip. In this way, the hip joint and the COM move along a series of arcs that are symmetric relative to the point of contact. In a previous study (21), we suggested that the changes in the transduction between kinetic and potential energies of the COM during walking on a slope can be illustrated by the tilting of the compass gait model backward in uphill walking and forward in downhill walking. However, these changes at the COM level could be accomplished in the following various ways: by changing 1) the limb length, 2) the limb orientation, or 3) both limb length and limb orientation in a coordinated fashion. Limb length and limb orientation are then a function of intersegmental coordination, particularly of the thigh, shank, and foot. The aim of the present study is to characterize how limb orientation and limb length, as well as intersegmental coordination patterns, change with walking slope and speed.

METHODS

Subjects and Experimental Procedure

Data were collected at the same time and on the same subjects as in the study of Dewolf et al. (21). Six men and four women (age: 22.2 ± 2.4 yr, mass: 69.2 ± 14.4 kg, height: 1.75 ± 0.10 m, means ± SD) participated in the study. All participants gave their written, informed consent. Experimental procedures were performed according the Declaration of Helsinki and were approved by the Ethics Committee of the Université Catholique de Louvain.

Subjects walked on an instrumented treadmill mounted on wedges. The instrumented treadmill consisted of a modified commercial treadmill (h/p/comos-Stellar, Nussdorf-Traunstein, Germany; belt surface: 1.6 × 0.65 m, mass: ~240 kg) combined with four force transducers (Arsalis, Louvain-la-Neuve, Belgium), measuring the components of the ground reaction forces (GRFs), parallel, normal, and lateral to the tread belt. Wedges of different size were attached under the four strain gages to incline the treadmill at different slopes.

The whole structure of the treadmill (i.e., the body, tread surface, belt, and motor) is mounted on force transducers. Since the fixed parts of the treadmill are rigid and firmly attached to each other and since the mobile parts are moving symmetrically, the acceleration and the velocity of the COM of the treadmill, relative to the reference frame of the laboratory, are nil. In this way, the forces exerted by the subject moving on the upper part of the treadmill are accurately transmitted to the transducers placed under it, and all internal forces, including friction, between the parts of the treadmill, are cancelling each other (68).

The trajectory of the COM was determined from the GRF using the procedure described in detail in Dewolf et al. (21, 22). The lateral (d_y) and fore-aft (d_x) position of the center of pressure was computed by the following

$$d_{\text{x}}=\frac{-M_{\text{y}}-h{F}_{\text{x}}}{F_{\text{z}}}$$ (1)

$$d_{\text{y}}=\frac{-M_{\text{x}}-h{F}_{\text{y}}}{F_{\text{z}}}$$ (2)

where F_x, F_y, and F_z are the lateral, fore-aft, and vertical GRFs; M_x and M_y are the moment components in the force transducer coordinate system; and h is the vertical distance between the force transducers and the tread surface (71). Note that the center of pressure is under one foot during the single-support phase and moves from one foot to the other during the double-support phase (59).

Reflective markers were glued on the skin of the subject at the following positions: chin-neck intersect, greater trochanter (GT), lateral femoral condyle, lateral malleolus, heel (HE), and fifth metatarsophalangeal joint (VM). An additional marker was also placed at a point midway between the GT and the lateral femoral condyle on the lateral side of the thigh in case the marker of the hip was hidden by the hand. The position of the markers in the sagittal plane was measured by means of a high-speed video camera (A501k; Basler, Ahrensburg, Germany; resolution 1,280 × 1,024 pixels, aperture time 3 ms), fixed on the ground, 3 m to the side of the treadmill, perpendicular to the plane of progression. Images were sampled at a rate of 100 frames/s. The horizontal and vertical coordinates of the reflectors in the sagittal plane were measured in each frame using Lynxzone software (Arsalis).

Seven different inclinations (0°, ±3°, ±6°, and ±9°) were explored: six subjects walked on all slopes. Due to the duration of the experiments, two subjects walked only at 0° and ±6° and two at 0° and ±9°. One-half of the subjects started with the belt turning forward to simulate uphill walking and the other half with the belt turning backward to simulate downhill walking. At each slope, subjects walked at seven different speeds, ranging between 0.56 m/s (slow walking speed) and 2.22 m/s (close to the walk-run transition), with at least a 3-min resting period between each speed. At 2.22 m/s, four subjects were spontaneously running, especially on steep slopes, and were thus not recorded. Each trial started with the belt still, and speed was ramped up until the desired speed. An average of 13.6 ± 5.6 strides (means ± SD) was recorded in each trial. The number of subjects recorded in each speed-slope class is presented in Table 1.

Table 1.

Number of subjects in each slope/speed class

Speed, m/s	−9°	−6°	−3°	0°	3°	6°	9°
0.56	8	8	6	10	6	8	8
0.83	8	8	6	10	6	8	8
1.11	8	8	6	10	6	8	8
1.39	8	8	6	10	6	8	8
1.67	8	8	6	10	6	8	8
1.94	8	8	6	10	6	8	8
2.22	5	6	5	8	5	6	5

Data Analysis

Stride period and stride length.

The stride was defined as the period between a right-foot contact (FC; 0%) and the next one (100%). FC and toe off (TO) were estimated from the displacement of the center of pressure on the belt (59). The stride duration T was calculated as the time between two successive right FCs.

Orientation of the body segments during the stride.

From the marker locations, the orientation of the thigh (GT–lateral femoral condyle), shank (lateral femoral condyle–lateral malleolus), foot (lateral malleolus–VM), and trunk (chin-neck intersect–GT), relative to the vertical axis (elevation angle), was computed, as described in Borghese et al. (12). The joint angles (hip, knee, and ankle) were computed from the elevation angle of adjacent segments. For each subject, the different strides of each trial were time interpolated to fit a normalized, 400-point time base and then averaged every 0.25% of the stride period.

To analyze the time course of the elevation angle during the stride, a Fourier series component was performed (9, 29). Amplitude (A), phase shift (P), and percentage of variance, accounted for by the first harmonic, were computed. The amplitude ratio and phase shift between two adjacent limb segments p and d (G_pd and ϕ_pd, respectively) were computed as G_pd = A(d)/A(p) and as ϕ_pd = P(d) − P(p).

Lower-limb length and orientation during the stride.

The length of the limb (L) was measured as the distance between the markers located on the GT and on the HE during standing. At each instant of stance, the actual limb axis should be defined as the connection of the proximal joint with the point of contact with the ground, i.e., with the instantaneous center-of-pressure position (35). However, during walking, the contact moves from the HE to the ball of the foot, as stance progresses from FC to TO. During double support, our system allows the measurement of only the global center of pressure under the two feet. Therefore, the angle, relative to vertical (θ_fc, θ_to), and the limb length (L_fc, L_to) were measured only at FC and TO. The angle θ_fc and the length L_fc were measured from the markers of the GT and the HE at FC, and θ_to and L_to were measured from the markers of the GT and the VM at TO.

Intersegmental coordination.

A principal component analysis was applied to the 3D covariance matrix of the segment elevation angles (thigh, shank, foot). Eigenvalues and eigenvectors u_i were computed by the factoring of the covariance matrix from the set of original signals by using a singular value decomposition algorithm. The first two eigenvectors (u₁ and u₂) lay on the best-fitting plane of angular covariation, and the data projected onto these axes corresponded to the first (PC1) and second (PC2) principal components. The planarity was evaluated for each condition by finding the percentage of variance that was explained by u₁ (PV₁) and u₂ (PV₂). If the data were lying perfectly on a plane, then 100% of the variance would be explained by u₁ and u₂. The eigenvectors u₁ and u₂ defined the shape of the loop, whereas the third eigenvector u₃, normal to the plane, provided a measure of its orientation. The parameters u_3t, u_3s, and u_3f corresponded to the direction cosines with the positive semiaxis of the thigh, shank, and foot angular coordinates, respectively.

In a next step, the principal components PC1 and PC2 were reoriented to be associated to the limb orientation (PC1*) and the limb length (PC2*), as proposed by Ivanenko et al. (35). The reference axis PC1* corresponded to the projection of the vector t = s = f on the covariance plane, where t, s, and f referred to the thigh, shank, and foot elevation angles. The orientation of the second axis PC2* was determined from a previous study (35), in which subjects were walking in place; in this case, there was no change in the limb orientation, and the covariance loop was a line that could be associated to the limb length L. In the present study, the orientation of the in-place covariance line, computed by Ivanenko et al. (35), was used to determine the orientation of PC2*.

Since the trunk orientation can be regulated independently of the covariation of the lower-limb angles, we have also included the trunk into the coplanar analysis and redid the principal component analysis performed on the 4D covariance matrix [as in Borghese et al. (12)]. Due to the limited range of motion (ROM) of the trunk during walking, whatever the slope, the projection of the 4D space on the principal plane is very similar to the projection of the 3D space (see Table 2). Therefore, to obtain a better visualization of the angular covariations, the analysis was limited to the 3D space.

Table 2.

Percent of variance accounted for by PV1 and PV2 when the principal component analysis is performed on the 3D covariance matrix (first line) and on the 4D covariance matrix (second line)

	0.56 m/s		1.39 m/s		2.22 m/s
Slope, °	PV1	PV1 + PV2	PV1	PV1 + PV2	PV1	PV1 + PV2
−9	89.4 ± 3.6	99.3 ± 3.4	90.7 ± 2.1	99.4 ± 2.1	90.9 ± 1.9	98.9 ± 2.2
	89.2 ± 3.4	99.2 ± 0.3	90.6 ± 2.1	99.3 ± 0.2	90.7 ± 1.8	98.8 ± 0.7
−6	87.0 ± 2.9	99.3 ± 2.6	89.5 ± 1.6	99.5 ± 1.6	90.8 ± 1.0	99.1 ± 1.4
	87.1 ± 2.9	99.1 ± 0.3	89.4 ± 1.6	99.4 ± 0.1	90.6 ± 0.9	99.0 ± 0.4
−3	85.1 ± 1.7	99.3 ± 1.6	88.5 ± 1.0	99.6 ± 1.1	89.4 ± 1.0	99.5 ± 1.1
	84.9 ± 1.6	99.0 ± 0.3	88.3 ± 1.0	99.4 ± 0.1	89.2 ± 1.0	99.3 ± 0.1
0	83.4 ± 3.0	99.4 ± 3.0	87.8 ± 1.4	99.5 ± 1.4	88.8 ± 1.0	99.4 ± 1.0
	83.1 ± 2.9	99.2 ± 0.4	87.6 ± 1.4	99.4 ± 0.1	88.6 ± 1.1	99.3 ± 0.3
3	80.6 ± 3.2	99.5 ± 3.3	86.0 ± 1.3	99.5 ± 1.3	86.9 ± 1.0	99.5 ± 1.1
	80.4 ± 3.2	99.4 ± 0.2	85.8 ± 1.3	99.4 ± 0.1	86.7 ± 1.0	99.4 ± 0.1
6	76.7 ± 3.6	99.5 ± 3.6	82.8 ± 2.6	99.5 ± 2.7	85.1 ± 1.9	99.5 ± 2.0
	76.4 ± 3.5	99.4 ± 0.1	82.6 ± 2.5	99.4 ± 0.1	84.9 ± 1.9	99.3 ± 0.1
9	70.6 ± 2.1	99.4 ± 2.1	79.2 ± 1.8	99.3 ± 2.0	83.1 ± 2.3	99.3 ± 2.4
	70.4 ± 2.1	99.2 ± 0.2	79.0 ± 1.8	99.2 ± 0.4	82.8 ± 2.2	99.2 ± 0.2

3D, 3-dimensional; 4D, 4-dimensional; PV1, variance explained by eigenvector 1; PV2, variance explained by eigenvector 2.

Estimation of the motion of the COM from the kinematic data.

One of the subgoals of our study was to investigate changes in kinematics of the lower-limb segments relative to changes in COM trajectory. Therefore, the trajectory of the COM, as estimated from the GRF, was compared with the trajectory of a point located at mid-distance between the two hips (on the assumption that the distance between this point and the COM remains constant during the stride). Due to the rotation of the pelvis in the frontal plane and in the transverse plane, the movements of one hip do not reflect the movements of the midpoint of the pelvis. To estimate the x–y position of this midpoint in the sagittal plane, we make the assumption that the x–y position of the hip on the nonrecorded side of the body during one-half of a stride is equal to the one on the side facing the cameras during the other one-half of the stride (9). From the coordinates of both hips, we estimate the projection on the sagittal plane of the point located at mid-distance between the two hips to assess if this point can be used as a surrogate for the COM.

Statistics

Data were grouped into speed-slope classes. To obtain one value per subject in each class, all strides of a subject in a given class were averaged. The mean and SD of the population were then computed in each class (grand mean). The variables (mean value per subject) were analyzed across all conditions using a repeated-measure ANOVA with post hoc Bonferroni correction (PASW Statistics 19; SPSS, IBM, Armonk, NY) to assess the individual and interaction effects of speed and slope on the calculated variables. Linear regression analysis, using Pearson’s correlation coefficient (r), was used to indicate the relationship between variables. An α threshold of 0.05 was used throughout to assess statistical significance.

RESULTS

General Gait Parameters and Limb Kinematics

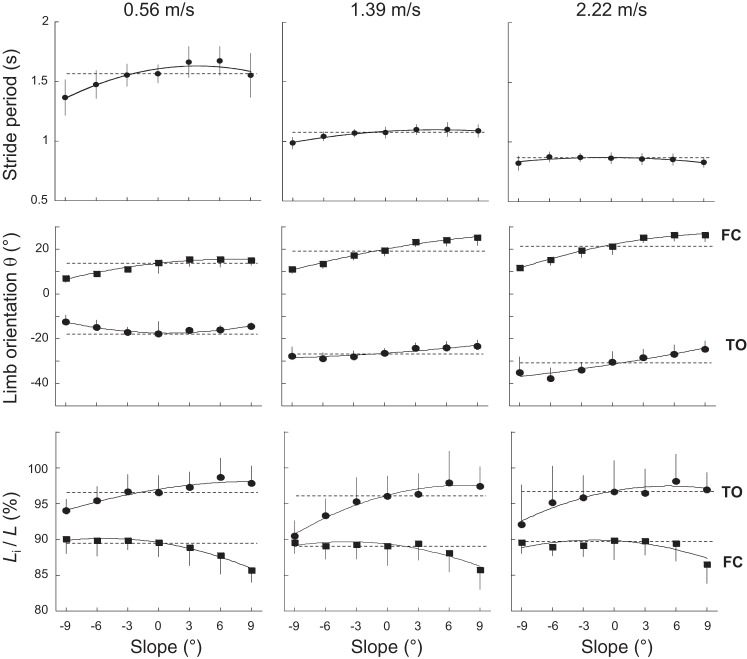
Stride period (T)—the angle between the limb axis and the vertical and the limb length at FC (θ_fc, L_fc) and at TO (θ_to, L_to)—is presented as a function of slope at three different speeds in Fig. 1. In accordance with Kawamura et al. (40) and Sun et al. (64), T decreases with speed (F_6,363 = 580.8, P < 0.001). Bonferroni post hoc shows that T is not significantly affected by the slope of the terrain compared with the level (P > 0.063), except at −9° at 0.56 m/s (P < 0.001), where T is shorter.

Fig. 1.

Stride period, limb orientation, and limb length as a function of slope at slow, intermediate, and fast walking speed. Top: stride period; middle: orientation of the limb relative to vertical at foot contact [FC; θ_fc (■)] and toe off [TO; θ_to (●)]; bottom: length of the limb (L_i), expressed as a percent of the length (L), measured during standing at FC [L_fc (■)] and at TO [L_to (●)]. Horizontal dotted lines correspond to the data obtained on the level. Symbols and bars represent the grand means of the subjects and the SDs (when the length of the bar exceeds the size of the symbol). The continuous lines were drawn through experimental data (using a weighted mean function, KaleidaGraph 4.5; Synergy Software, Reading, PA).

Compared with walking on the level at a given speed, θ_fc increases when walking uphill, whereas it decreases when walking downhill (F_6,363 = 100.1, P < 0.001). The angle θ_to is also affected by slope (F_6,363 = 24.6, P < 0.001): θ_to decreases from 0° to +9°. From 0° to −9°, θ_to decreases at low speeds, whereas θ_to increases at high speeds. At all slopes, both θ_fc (F_6,363 = 46.3, P < 0.001) and θ_to (F_6,363 = 163.2, P < 0.001) increase when speed becomes faster, because the stride length increases. Note that at 2.22 m/s, the change in orientation of the limb corresponds approximately to the change in inclination of the terrain.

The limb lengths at FC and at TO (respectively, L_fc and L_to; Fig. 1) are also affected by slope (F_6,363 = 20.5, P < 0.001 and F_6,363 = 25.9, P < 0.001, respectively) but not by speed (F_6,363 = 0.27, P = 0.948 and F_6,363 = 1.6, P = 0.150, respectively). When walking uphill, L_fc is shorter, and L_to is longer compared with the level. When walking downhill, L_to is longer, but L_fc remains unchanged compared with the level.

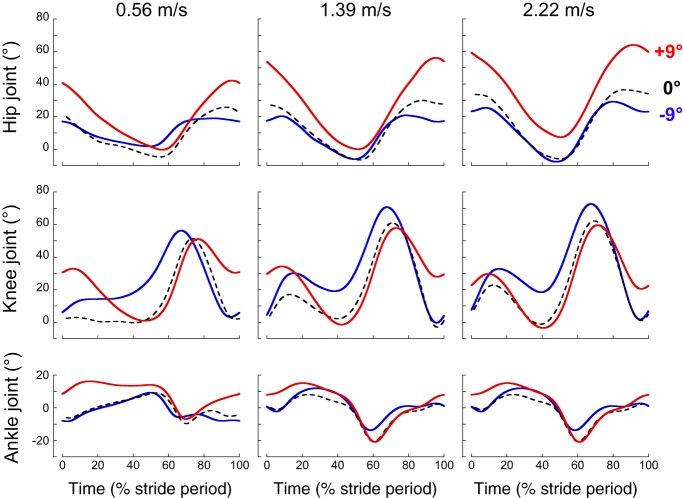
Figure 2 shows the average waveforms of lower-limb joint angles at low, intermediate, and high walking speeds on the level and on the steepest positive and negative slopes. The joint motion pattern observed on slope walking in this study shows good agreement with results obtained in other studies (24, 30, 49, 57). Compared with level walking, the major kinematic changes in uphill walking occur at FC, where the hip, knee, and ankle joints are more flexed. In downhill walking, the major kinematic modification is an increase of knee flexion during stance.

Fig. 2.

Lower-limb joint angles at 3 different slopes at slow-, intermediate-, and fast-walking speeds. Ensemble average of the hip (top), knee (middle), and ankle (bottom) joint angles over a stride during walking at +9° (red curves), −9° (blue curves), and 0° (black interrupted lines). All of the curves of each subject walking at a given speed and on a given slope were first averaged (mean curve). The curves presented here are the average of the mean curves of the 10 subjects (ensemble average). Zero percent and 100% correspond to the right-foot contact.

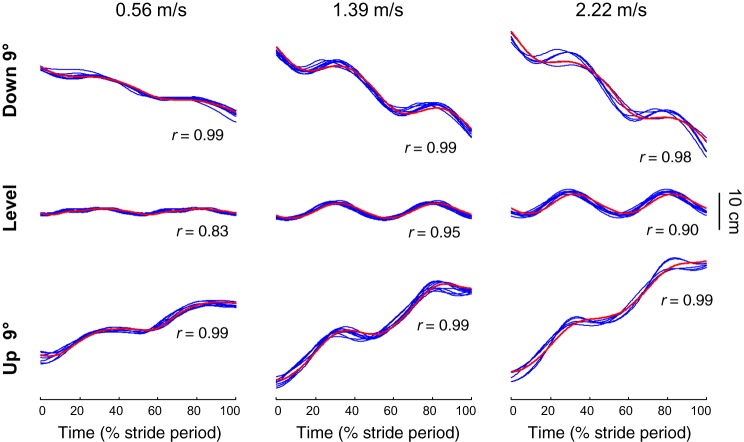
The vertical displacement of the midpoint between the two hips is presented in Fig. 3 at different slopes and speeds. The trajectory of this point is similar to the trajectory of the COM, measured from the GRF, both in uphill and downhill walking.

Fig. 3.

Center of mass (COM) and hips vertical displacement at slow-, intermediate-, and fast-walking speed. Ensemble-average vertical displacement of the COM of the 10 subjects (red curve) over a stride during walking at −9° (top), +9° (bottom), and on the level (middle). Each blue line represents the mean curve of the vertical displacement of the hips (see methods) of a subject. In each condition, r corresponds to the average Pearson’s correlation coefficient between the COM and the hips vertical displacement.

Lower-Limb Segment Angular Motion

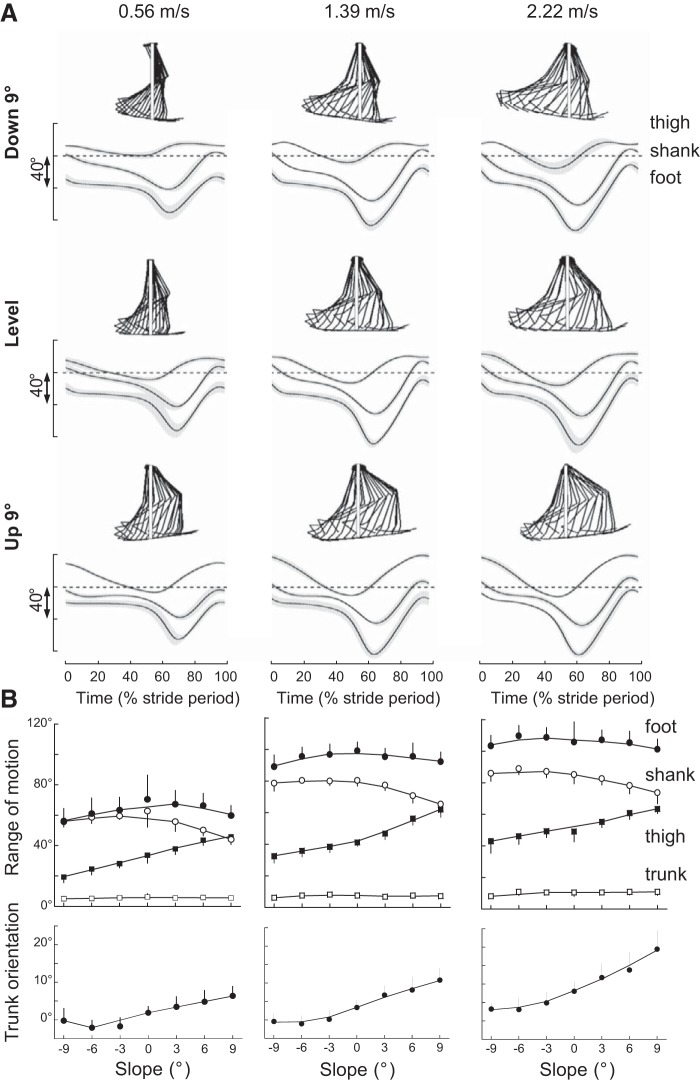
Figure 4A shows the time curve of the average elevation angles of lower-limb segments at low, intermediate, and high walking speeds on the level and on the steepest positive and negative slopes. All elevation angles display a typical biphasic shape (9, 12), and their ROM increases with increasing speed (Fig. 4B; F_6,363> 89.1, P < 0.001). Compared with level walking, when walking uphill, the shank ROM decreases (Bonferroni post hoc, P < 0.001), whereas the thigh ROM increases (Bonferroni post hoc, P < 0.001). When walking downhill, the foot and the shank ROM remain fairly similar, whereas the thigh ROM decreases (Bonferroni post hoc, P < 0.003).

Fig. 4.

Elevation angles of lower-limb segments during walking at slow-, intermediate-, and fast-walking speeds. A: ensemble-average elevation angles of the thigh, shank, and foot over a stride at −9° (top), +9° (bottom), and on the level (middle) at 0.56 (left), 1.39 (middle), and 2.22 (right) m/s. The gray zone represents ±1 SD. The interrupted lines correspond to 0° for the thigh and shank segments and to 90° for the foot segment. In each condition, the stickman illustrates the position of the segments, every 5% of a typical stride of 1 subject. The white continuous lines correspond to vertical. B: range of motion of all body segments over 1 stride (top) and average orientation of the trunk (bottom) as a function of slope at 0.56 (left), 1.39 (middle), and 2.22 (right) m/s. Other indications are as in Fig. 1.

Even if the orientation of the trunk changes little during the gait cycle (Fig. 4B), its average orientation is affected by both slope (F_6,363 = 134.8, P < 0.001) and speed (F_6,363 = 43.5, P < 0.001). Compared with level walking, the trunk shows a forward tilt during uphill walking and a backward tilt during downhill walking. At each slope, the body bends more forward with increasing speed.

Planar Covariation of the Limb-Segment Elevation Angles

In each speed-slope class, the variance accounted for by the two first eigenvectors of the data covariance matrix (PV₁ + PV₂; Table 2) was, on average, 99.45 ± 0.24%. The variance accounted for by each principal axis changes with speed (F_6,363 = 59.9, P < 0.001) and slope (F_6,363 = 253.8, P < 0.001): PV₁ decreases on positive slopes and increases on negative slopes and with increasing speed (Table 2).

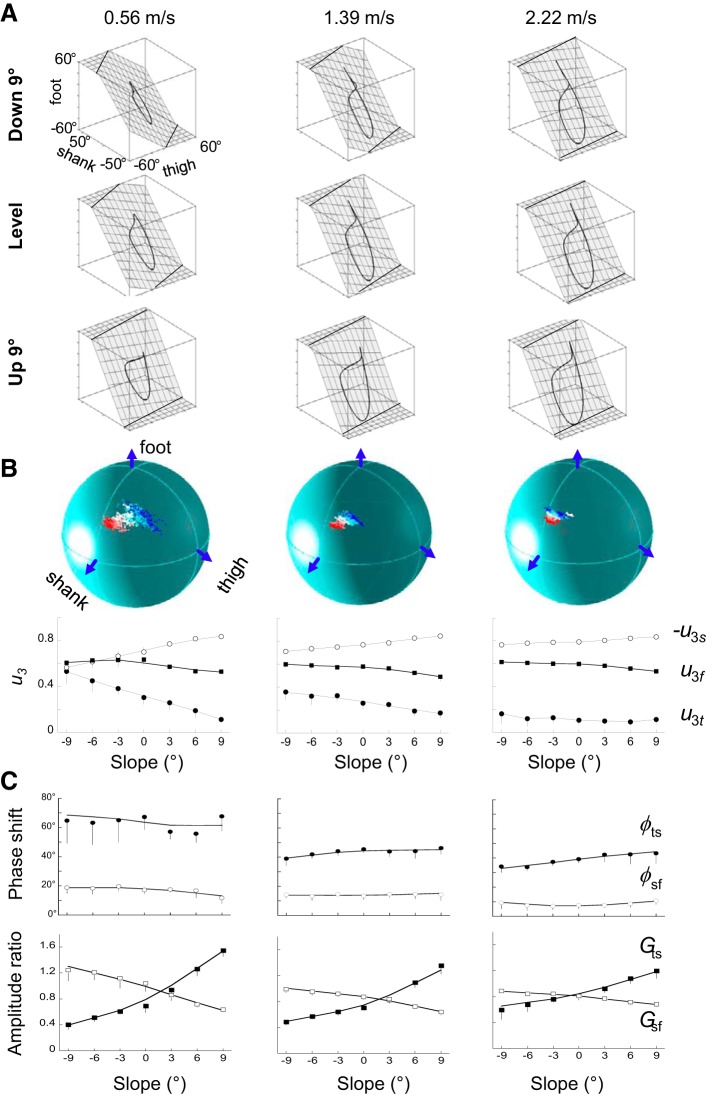
The principal planes are illustrated in Fig. 5A. In agreement with previous studies (8, 9, 18, 23, 36, 38, 60), both slope and speed involve a rotation, mainly along the long axis of the gait loop (Fig. 5B): the covariation plane rotates counterclockwise when viewed from above. At low walking speed, with increasing slope from −9° to +9°, u_3t and u_3s decrease, whereas u_3f remains fairly similar. As speed increases, both u_3t and u_3s are reduced. Note that the effect of speed is scaled with slope (F_36,363 = 4.6, P < 0.001): the change due to speed is greater in downhill walking and almost nil in uphill walking. As a result, at high walking speed, the effect of slope on u₃ tends to disappear. Because the effect of slope and speed is similar but greater on u_3t than on u_3s, we will only discuss the results for u_3t.

Fig. 5.

Planar covariation of elevation angles. A: covariation of the limb-segment elevation angles during walking at −9° (top), +9° (bottom), and on the level (middle) at 0.56 (left), 1.39 (middle), and 2.22 (right) m/s. Each trace represents the ensemble average (see definition in Fig. 2). Grids show the best-fitting plane. B, bottom: third eigenvector direction cosines for thigh, shank, and foot (u_3t, −u_3s, u_3f) of the normal to the covariation plane (u₃ vector) as a function of slope at 0.56 (left), 1.39 (middle), and 2.22 (right) m/s. Other indications are as in Fig. 1. Top: spatial distribution of the normal to the principal plane (u₃) in the 3-dimensional space, defined by the elevation angles in each slope at 0.56 (left), 1.39 (middle), and 2.22 (right) m/s. White symbols correspond to level walking. The red color gradients are for the positive slopes (the darker the color, the steeper the slope), whereas the blue color gradients are for the negative slopes. C: phase shift (ϕ; top) and amplitude ratio (G; bottom) between the first harmonics of adjacent lower-limb segments (ts, thigh/shank; sf, shank/foot). Other indications are as in Fig. 1.

The first harmonic of the elevation angles accounts for the major part of the variance for all segments in each speed-slope class (86.1 ± 4.8%, means ± SD). Thus the amplitude ratio (G) and the phase shift (ϕ) between pairs of adjacent lower-limb segments (thigh-shank and shank-foot) capture the amplitude and time relationship characteristics of the elevation angles (Fig. 5C). As slope changes from −9° to +9°, G_ts increases (F_6,363 = 281.7, P < 0.001), meaning that the amplitude of the thigh movements, relative to that of the shank movements tends to increase (Fig. 5B). To a lesser extent, G_sf shows the opposite tendency (F_6,363 = 313.2, P < 0.001), i.e., the amplitude of the shank movements, relative to that of the foot, tends to decrease from −9 to +9°. However, the effect of slope on G_ts and G_sf is lessened when walking speed increases. At each walking speed, the time changes of thigh-elevation-angle lead those of shank-elevation-angle, and the time changes of shank-elevation-angle lead those of foot-elevation-angle. However, both ϕ_ts and ϕ_sf are reduced when speed increases (F_6,363> 61.2, P < 0.001) but do not change with slope compared with the level (Bonferroni post hoc, P > 0.271), except at −9°, where ϕ_ts is slightly reduced (Bonferroni post hoc, P = 0.003).

The rotation of the plane described above is related to the changes in amplitude ratio and phase shift between adjacent segments (9, 35). A multiple linear regression is calculated to predict u_3t, based on G_ts and ϕ_sf. A significant regression equation is found (P < 0.001), with an r² = 0.92. Both G_ts and ϕ_sf are significant predictors of u_3t.

PC1* and PC2*: Length and Orientation of Limb Axis

Overall, PC1* and PC2* are in agreement with our lower-limb kinematics measurement. The time changes of PC1* are correlated with the time changes in lower-limb orientation. The lower-limb axis definition used here (i.e., GT-HE or GT-VM) did not affect appreciably the correlation between PC1* and limb orientation, likely because of a similar back-and-forth horizontal motion of any fixed point on the foot (35). The correlation is higher for the GT-VM (r² = 0.99 ± 0.01) than the GT-HE limb axis (r² = 0.96 ± 0.02). The behavior of PC2* is similar to that of knee-joint angle observed in Fig. 2. Indeed, PC2* is essentially correlated with knee angle (r² = 0.91 ± 0.07). As a result, the differences (Δ), observed in ΔPC2*, are essentially dependent on the change in knee angle during stance, which affects limb length.

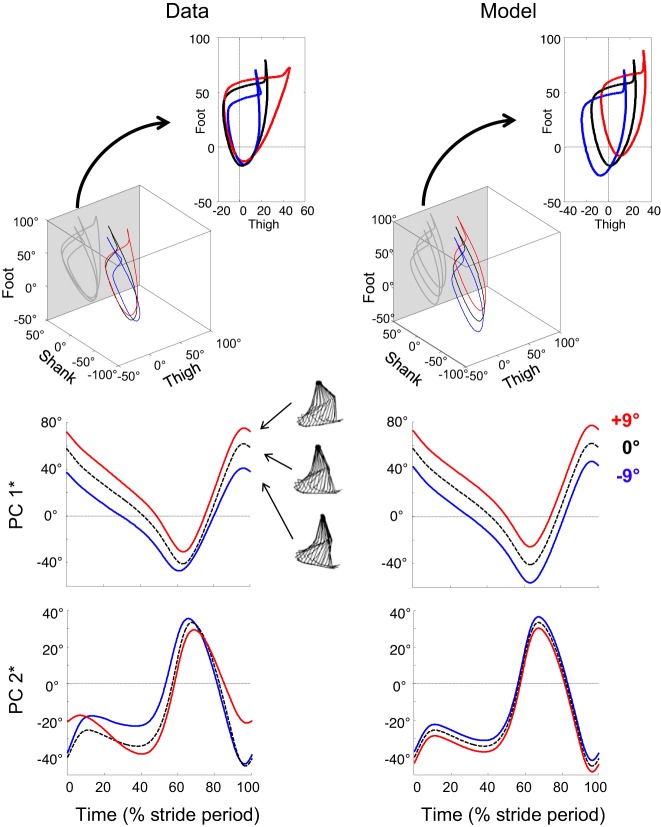
In a previous study (21), we suggested that the changes in the COM trajectory during walking on a slope can be illustrated by the tilting of the compass gait model backward in uphill walking and forward in downhill walking. In Fig. 6, the actual data of the covariation of limb-segment elevation angles are compared with data obtained by simulating a passive tilt of the compass-gait model relative to the slope: these last data are obtained by adding +9° (uphill) or −9° (downhill) to the elevation angles of the thigh, shank, and foot measured on the level. Changes in kinematic pattern across slope cannot be explained by a simple tilt of the compass gait model proportional to the inclination of the ground. The actual PC1* curves hardly differ from PC1* of the model, suggesting that there is a tilt of the limb-axis orientation. However, major differences in PC2* are observed with slope.

Fig. 6.

Decomposition of planar covariation in the reoriented principal component associated to limb orientation (PC1*) and to limb length (PC2*). Top: covariation of limb-segment elevation angles during walking at 1.39 m/s on a −9° (blue) and a +9° (red) slope and on the level (black interrupted line). Insets: projection of the gait loops on the thigh-foot plane (gray planes of the cubes). The loops were decomposed in PC1* and PC2* (see methods), corresponding to limb orientation and limb length, respectively. Middle and bottom: variation of PC1* and PC2* over a stride. All curves are ensemble average. Left: actual data of the covariation of limb-segment elevation angles. Right: data obtained by simulation of a passive tilt of the compass-gait model relative to the slope. Data on the level (black curve) are the same as the left. The red and blue loops and decomposition in PC1* and PC2* are obtained by addition of +9° (uphill) or −9° (downhill) to the elevation angles of the thigh, shank, and foot, measured on the level.

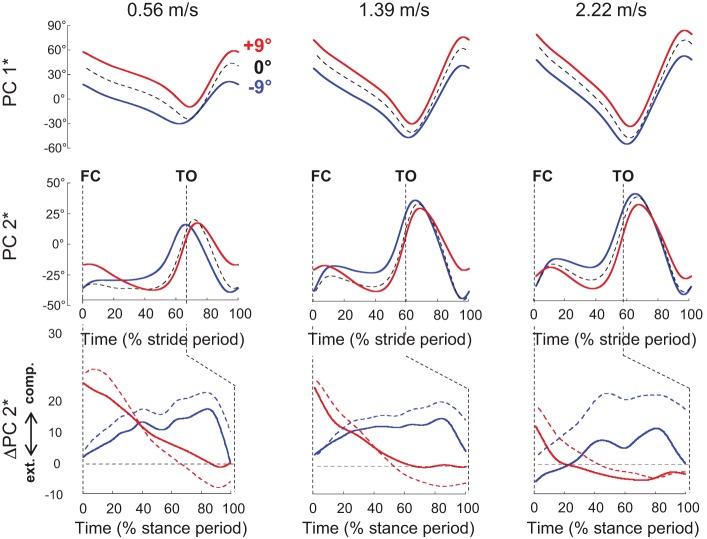
In uphill walking, the main change occurs at FC, where a higher PC2* is indicative of a more flexed limb (Fig. 7). In downhill walking, the major PC2* modification reflects an increase in limb flexion during stance. Compared with the level, ΔPC2* reflects that in uphill walking, the limb is extended throughout the stance, whereas in downhill walking, the limb is compressed during early stance and is extended before TO. However, both in uphill and downhill walking, the changes in limb length are reduced with increasing speed.

Fig. 7.

Limb length- and limb orientation-related angular covariance at slow-, intermediate-, and fast-walking speed. Top and middle: ensemble-average reoriented principal component associated to limb orientation (PC1*) and to limb length (PC2*) over a complete stride during walking at +9° (red), −9° (blue), and on the level (black interrupted line). Bottom: ΔPC2* is computed by subtracting PC2* on the level from PC2* at +9° (continuous red lines) and from PC2* at −9° (continuous blue lines) during the stance period. Likewise, the knee-angle time curves (presented in Fig. 2) on the level were subtracted from those at +9° (interrupted red lines) and at −9° (interrupted blue lines). comp., compressed; ext., extended; FC, foot contact; TO, toe off.

DISCUSSION

In this study, we investigated the combined effect of slope and speed on the lower-limb intersegmental coordination, limb orientation, and limb length. Whereas other studies have also reported the impact of speed and slope on joint kinematics and kinetics during walking (1, 4, 30–33, 39, 42, 46, 47, 49, 57, 61, 67, 74), here, we built on this work by the characterization of changes in intersegmental coordination to slopes.

Our findings extend previous observations that the limb-segment elevation angles covary along a plane, not only during level (9) or uphill walking (60) but also during downhill walking (Fig. 5), despite considerable differences in the joint kinetics and in the relative amplitude of proximal vs. distal segment motion across slopes (Fig. 4). It is worth stressing that the changes in the kinematic pattern across slopes cannot be accounted for by a simple tilt of the compass gait model proportional to the inclination of the ground, i.e., a simple tilt of the “dynamic template” of limb-segment motion (Fig. 6). Furthermore, we observe a cross-effect of speed and slope on the characteristics of the limb-segment covariation (orientation of the covariance plane and the width of the gait loop): at slow speeds, more changes were observed across slope, whereas at high walking speed, the effect of slope tends to disappear (Fig. 5). Below, we discuss the results in the context of the telescopic limb behavior (35, 41) and phase relationships among limb-segment motions during walking on a slope.

Effect of Speed and Slope on Limb-Segment Planar Covariation

At slow speeds, the effect of slope on covariance plane orientation, the shape of PC2*, and the shape of the gait loop is considerable (Fig. 5), whereas at higher speeds, this effect fades away. The fact that at fast walking speeds, the intersegmental coordination hardly changes with slope is not a simple result of high inertia, making it difficult for the planar covariation characteristics to adapt quickly to slope. Indeed, when running at ~3 m/s, for example, the characteristics of planar covariation change significantly: the compression of the limb at midstance corresponds to adjustments of the planar covariation (35).

At slow speed, when walking uphill or downhill, the difference in limb length between FC and TO is modified compared with the level and affects the net vertical displacement of the COM (Fig. 1). The change in covariation plane orientation across slopes is related to a change in the amplitude ratio between thigh- and shank-elevation angles (G_ts). In turn, the modification of G_ts affects the shape of the loop. In uphill walking, the greater G_ts is associated with a larger PV₂ (Table 2), indicating a wider loop most likely to facilitate the increase in toe clearance (51). On the contrary, in downhill walking, the smaller G_ts is associated with a lower PV₂ and thus a narrower loop.

The changes in limb orientation (and thus in PC1*) and in limb length (and thus in PC2*) confirm that there is a tilt in the orientation of the limbs but also an adjustment of limb length (Fig. 7). Because of the high correlation between PC2* (Fig. 7) and the knee joint angle (Fig. 2), the adjustment of limb length is thought to depend mainly on knee motion. ΔPC2* indicates that in uphill walking, the limb is compressed at FC and extends during stance, whereas in downhill walking, the limb is extended at FC and compressed during stance.

When walking downhill, the COM moves forward and downward, aided by gravity. Body balance must be ensured to avoid either foot slipping or a headlong rush, due to a greater forward “toppling moment.” Greater knee flexion throughout the stance (Fig. 2) has been related to shorter strides (Fig. 1) (31, 49), which may reduce the likelihood of slipping (31, 57). Greater knee flexion also tends to decrease the COM height, which may help reduce instability issues (10, 16, 34, 49, 55, 62). In addition, compared with the level, the trunk is tilted backward (Fig. 4) (49). When walking uphill, the COM moves forward and upward, against gravity. At the same time, body balance must be ensured to avoid a backward toppling moment. At low speeds, the increase in knee but also in hip and to a lesser extent, in ankle flexion at FC (Fig. 2) results in a shorter L_fc (49, 51, 57). Furthermore, the greater difference between L_fc and L_to (Fig. 1) leads to a higher range of limb-length change compared with the level. Compared with the level, the trunk is tilted forward in uphill walking (Fig. 4) (49). The more crouched posture brings the COM closer to the ground, which helps to counteract the issue of the toppling moment (10, 14).

When speed increases, the net vertical displacement of the COM during each stride increases (Fig. 3) in uphill and downhill walking. However, we did not observe any effect of speed on L_fc and L_to. With increasing speed, the orientation of the covariation plane tends to be independent of slope. Indeed, the gait loop is progressively stretched lengthwise with increasing speed (11, 38), as indicated by the increase in PV₁ (Table 2). As a result, the changes in G_ts and in PV₂ with slope progressively fade away. Likewise, the time changes in ΔPC2* throughout the stance are reduced (Fig. 7). Thus at fast speeds, the change in COM height is more related to a tilt of the compass gait than at slow speeds (Figs. 6 and 7): the portion of the stance in which the foot is posterior to the hip joint decreases in uphill walking (backward tilt of the compass gait) and increases in downhill walking (forward tilt of the compass gait). Likewise, the fraction of stance dedicated to increase/decrease the gravitational potential energy of the COM also increases in uphill/downhill walking (21).

Changes in planar covariation are thought to be related to an ability to adapt to different walking conditions (9, 54). For instance, when toddlers walk on terrains with different inclinations, their ability to adapt is very limited, and they maintain a roughly constant planar orientation, suggesting a reduced flexibility of the kinematic pattern (23). The selection of the appropriate motor strategy from a large number of possibilities could indicate optimization of some physiological goals and properties (e.g., stability, energy expenditure, mechanical stress, etc.). The present results suggest that modifications of the kinematic coordination pattern highly depend on walking speed. At slow speeds, these changes might be necessary to maintain stability (17). Indeed, the COM remains within (or close to) the polygon of support formed by the foot/feet in contact with the ground. At fast speeds, the lack of modification observed may highlight a more active selection pressure on the walking gait. Indeed, it has been shown that the progressive reduction of u_3t with increasing speed contains the increase in the mechanical energy expenditure (8). Furthermore, the trunk tilts forward with speed both in uphill and downhill walking (Fig. 4B). This forward leaning may be pursued to assist lower limbs in generating greater forward propulsion (49, 50).

Neural Underpinnings for the Differential Effect of Speed on Intersegmental Coordination

It has been hypothesized that the intersegmental coordination results from interplay between the activity of central pattern generators (CPGs; neural circuits that can generate rhythmic motor activity) and sensory signals originating in the limbs (13). The effect of speed on coordination patterns during walking has also been found in insects (20, 27, 70). It has been suggested that this change in coordination may be due to the contribution of central CPG coupling mechanisms for coordination and its dependence of walking speed (7). Indeed, the coordination in slow-walking insects is thought to be largely based on sensory input contributions, whereas in fast-walking insects, the central CPG coupling is thought to play a more important role (25, 53). In humans, Yokoyama et al. (73) showed that the neural control strategies for activating muscles depend on locomotor speed, which suggests that human locomotor networks may have speed dependency as in insects.

In sum, our results show that the kinematic patterns highly depend on the walking speed. The effect of speed on motor control of locomotion has been observed in animal studies (5, 58, 75), which have demonstrated distinct recruitment of spinal neuronal groups, depending on the speed of progression. In humans, different networks are recruited at various speeds as well (72, 73). Here, we report a speed-dependent modification in the intersegmental coordination to walking on slopes (Figs. 5 and 7). This observation might reflect the fact that the CPG neural networks are not overlapping for high and slow speeds (i.e., there is no simple scaling of motoneuron and interneuron activity with speed but the involvement of somewhat different neural circuits), since slow and fast speeds of progression exhibited different telescopic limb behavior on slopes.

Limitations of the Study

In this study, the movements were only analyzed in the sagittal plane, because those represent the major and most systematic component of walking gait (12, 52). Given the small ROM and low signal-to-noise ratio in the frontal plane, a larger sample size should be necessary to achieve reliable results. Indeed, at the highest speed and on the steepest slopes, due to their physical ability, only five of the 10 subjects were able to perform the walking task.

Conclusion

In conclusion, this study provides new quantitative details, consistent with prior literature (26, 72, 73), on how intersegmental coordination changes during uphill, downhill, and level walking. The results demonstrate that the kinematic patterns highly depend on both ground slope and walking speed.

GRANTS

Funding for this study was provided by the Université Catholique de Louvain (Belgium), Fonds de la Recherche Scientifique (Belgium), Italian Ministry of Health (IRCCS Ricerca Corrente), Italian Space Agency (Contract No. I/006/06/0), Italian Ministry of University and Research (PRIN Grant 2015HFWRYY_002), Horizon 2020 Robotics Program (ICT-23-2014 under Grant Agreement 644727-CogIMon), Lazio Region (INNOVA.1 FILAS-RU 2014_1033), Whitaker International Program, and in part by NIH Grant K12HD073945 (to K. E. Zelik).

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

K.E.Z. and P.A.W. conceived and designed research; K.E.Z. and P.A.W. performed experiments; A.H.D., Y.I., F.L., and P.A.W. analyzed data; A.H.D., Y.I., K.E.Z., F.L., and P.A.W. interpreted results of experiments; A.H.D., Y.I., and P.A.W. prepared figures; A.H.D. and P.A.W. drafted manuscript; A.H.D., Y.I., K.E.Z., F.L., and P.A.W. edited and revised manuscript; A.H.D., Y.I., K.E.Z., F.L., and P.A.W. approved final version of manuscript.