Neural coding and perception of auditory motion direction based on interaural time differences

Abstract

While motion is important for parsing a complex auditory scene into perceptual objects, how it is encoded in the auditory system is unclear. Perceptual studies suggest that the ability to identify the direction of motion is limited by the duration of the moving sound, yet we can detect changes in interaural differences at even shorter durations. To understand the source of these distinct temporal limits, we recorded from single units in the inferior colliculus (IC) of unanesthetized rabbits in response to noise stimuli containing a brief segment with linearly time-varying interaural time difference (“ITD sweep”) temporally embedded in interaurally uncorrelated noise. We also tested the ability of human listeners to either detect the ITD sweeps or identify the motion direction. Using a point-process model to separate the contributions of stimulus dependence and spiking history to single-neuron responses, we found that the neurons respond primarily by following the instantaneous ITD rather than exhibiting true direction selectivity. Furthermore, using an optimal classifier to decode the single-neuron responses, we found that neural threshold durations of ITD sweeps for both direction identification and detection overlapped with human threshold durations even though the average response of the neurons could track the instantaneous ITD beyond psychophysical limits. Our results suggest that the IC does not explicitly encode motion direction, but internal neural noise may limit the speed at which we can identify the direction of motion.

NEW & NOTEWORTHY Recognizing motion and identifying an object’s trajectory are important for parsing a complex auditory scene, but how we do so is unclear. We show that neurons in the auditory midbrain do not exhibit direction selectivity as found in the visual system but instead follow the trajectory of the motion in their temporal firing patterns. Our results suggest that the inherent variability in neural firings may limit our ability to identify motion direction at short durations.

INTRODUCTION

The ability to perceive moving sounds is important for parsing an auditory scene into separate auditory objects. Humans can perceptually track moving sounds in the environment (Leung et al. 2016) and segregate moving sound sources from static ones (Davis et al. 2016), but how the auditory system processes moving sounds is still poorly understood.

Motion perception produced by time-varying interaural time differences (ITD), an important binaural cue for sound localization and for parsing an auditory scene (van der Heijden and Joris 2010), has been studied for pure tones (Perrott and Musicant 1977), broadband noise (Grantham and Wightman 1978; Siveke et al. 2008), and clicks (Blauert 1972) (for review see Carlile and Leung 2016; Shackleton and Palmer 2010). These studies showed that a sound is no longer perceived as moving when the rate of periodic ITD motion exceeds ~8 Hz. Similarly, the smallest angle at which a sound is recognized as moving rapidly deteriorates once the stimulus duration falls below 100–200 ms (see Fig. 2 in Carlile and Leung 2016). If there are direction-selective neurons or circuits in the auditory system, they should exhibit a similar temporal limitation.

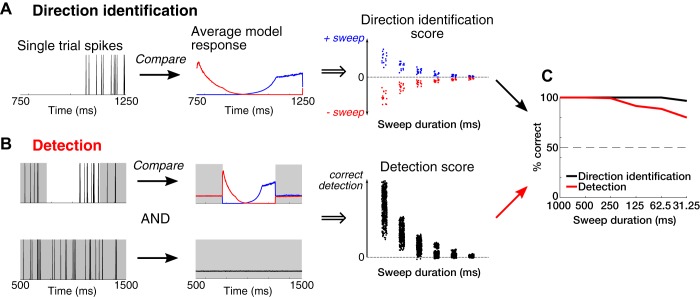
Fig. 2.

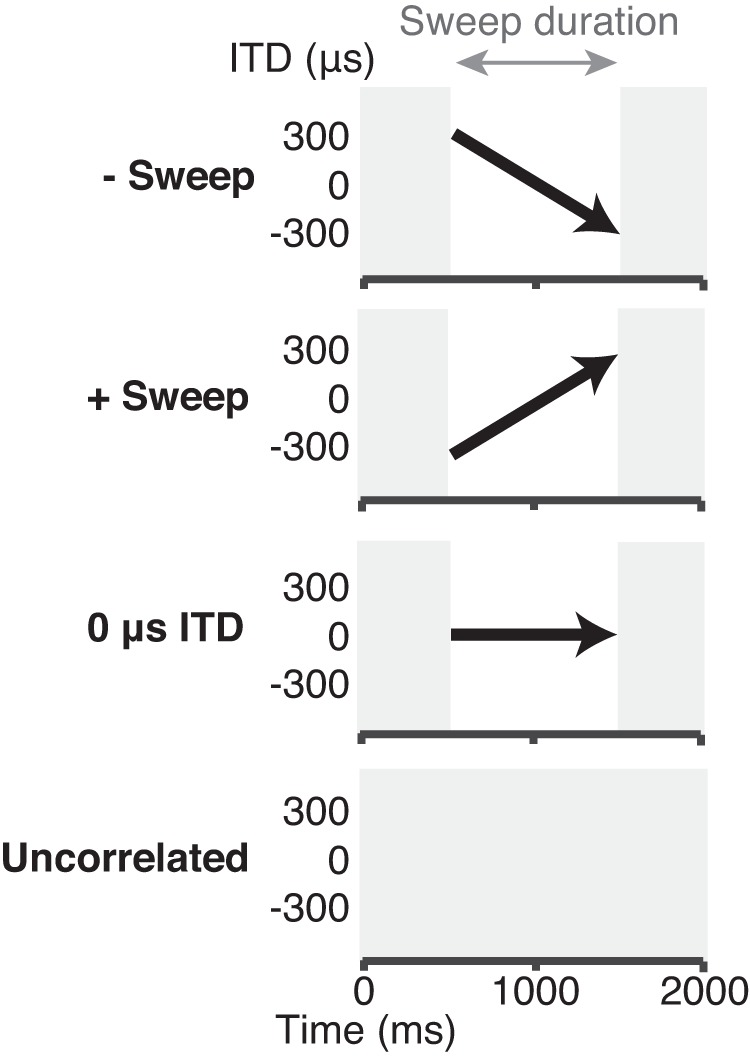
Stimuli for the neurophysiological experiments: negative-going sweep (−sweep), positive-going sweep (+sweep), 0-μs interaural time difference (ITD) stimulus, and interaurally uncorrelated noise, all 2 s in duration. Each of these stimuli were presented 15 times for 6 different sweep durations: 1,000, 500, 250, 125, 62.5, and 31.25 ms. All the sweeps had an ITD range of 600 μs and were centered on 0-μs ITD. Positive ITDs are leading in the ear contralateral to the inferior colliculus recording site.

The inferior colliculus (IC) is the earliest stage of the auditory system for which motion direction selectivity has been reported (Altman 1968; Fitzpatrick et al. 2009; Ingham et al. 2001; McAlpine et al. 2000; Spitzer and Semple 1991, 1993, 1998; Wagner and Takahashi 1992; Wang and Peña 2013; Yin and Kuwada 1983). These studies observed differences in firing rates depending on the motion direction of an acoustic source. However, modeling studies suggest that this apparent direction selectivity can largely be explained by firing rate adaptation (Borisyuk et al. 2002; Cai et al. 1998; Wang and Peña 2013), because high firing rates are followed by firing rate suppression irrespective of the starting position of the sound source and the direction of motion (McAlpine et al. 2000). In addition, Joris (2019) found no evidence for direction selectivity in IC neurons using linear variations in ITD imposed on broadband noise. Thus “direction selectivity” in the IC appears to differ from the visual system, where selectivity to a particular motion direction is invariant to the spatial extent of the motion (Albright 1984; Barlow and Levick 1965). To properly identify direction selectivity, the directionally dependent component of a neuron’s response needs to be dissociated from the effects of firing rate adaptation.

Even when we are unable to perceive motion in short duration sounds emanating from a single source, we may still be able to “glimpse” the ITD of a source and use this information to perceptually separate it from other sources (Bernstein et al. 2001; Faller and Merimaa 2004). The ability to detect a short probe noise temporally embedded in a noise background differing in interaural correlation is known as “binaural gap detection” (Akeroyd and Summerfield 1999) or “interaural correlation-change interval detection” (Boehnke et al. 2002). When the embedding noise is interaurally uncorrelated, and the probe is diotic, threshold durations for detection are 20–40 ms (Boehnke et al. 2002; Lüddemann et al. 2016). This threshold duration is longer than the timescale over which auditory midbrain neurons can encode time-varying interaural correlations (Joris et al. 2006; Shackleton and Palmer 2010; but see Siveke et al. 2008), suggesting that the perceptual limit is either created more centrally or caused by internal neural noise.

To determine whether the temporal limits on the perception of acoustic motion are also observed in neural responses, we recorded from neurons in the IC of unanesthetized rabbits in response to noise with linearly time-varying ITDs (“ITD sweep”) temporally embedded in interaurally uncorrelated noise. To distinguish true direction selectivity from the effects of firing rate adaptation, we modeled each neuron’s response by using a point-process model in which spiking probability was dependent on three components: 1) ITD following, 2) direction selectivity, and 3) spiking history. We used a generalized linear model (GLM) to describe the joint dependence of instantaneous firing rate on stimulus variables and spiking history. This mathematical framework (Paninski 2004; Truccolo et al. 2005) is increasingly used in studies of sensory systems because it can describe quantitatively both how stimuli are encoded in the activity of single neurons and neural populations and how stimulus information can be decoded from the patterns of neural activity. We find that the responses of IC neurons are largely dominated by the ITD-following component in that the time-varying firing rate depends primarily on the instantaneous ITD of the stimulus and the neuron’s static ITD tuning. We also tested the ability of human listeners to both detect the presence of the ITD sweep and identify its direction. An optimal classifier operating on single-neuron responses produced thresholds that were closer to human perceptual thresholds for both tasks than would be expected given the neurons’ ability to track fast-moving ITDs. This study is the first to apply the point process-GLM framework to studies of spatial hearing.

METHODS

ITD sweep stimuli.

All ITD sweep stimuli were derived from broadband noise (50 Hz to 15 kHz), and noise tokens were freshly generated on each stimulus presentation (each trial). In the neural experiments, the “sweeps” had a linearly time-varying ITD that ranged from either −300 to +300 μs (“positive-going” sweep, or “+sweep”) or +300 to −300 μs (“negative-going” sweep, or “−sweep”; see Fig. 1A and Fig. 2). For these stimuli, a positive ITD refers to a stimulus leading in the ear contralateral to the recording site. For the psychophysical experiments, the sweeps always had a range of 600 μs, as in the neural experiments, but the stimuli could be centered at an ITD of −300, 0, or +300 μs. In this case, a positive ITD refers to an ITD that is leading in the right ear. Sweep durations were varied from 1,000 ms down to 31.25 ms in halving steps. Because the range of the ITD sweep was always the same 600 μs, shorter sweep durations resulted in faster rates of change of ITD. Specifically, rates of ITD motion ranged from 600 μs/s for the 1-s sweep to 19,200 μs/s for the 31.25-ms sweep. Each sweep was preceded and followed by interaurally uncorrelated broadband noise such that the total duration of each stimulus was always 2 s (1 s in the psychophysical detection task, see Psychophysics). The flanking uncorrelated noise was included to separate the sweep from the stimulus onset and offset, which could interfere with both the neural coding and perception of the sweeps. Because there is no change in stimulus amplitude in each ear at the transition between the uncorrelated noise and the ITD sweep, the flanking noise also eliminates adaptation that would otherwise occur during the sweep in monaural neurons of the auditory nerve and cochlear nucleus. Subjectively, the interaurally uncorrelated noise was perceived as spatially diffuse or split into two different noises, one at each ear. For sufficiently long sweep durations, the noise during the ITD sweep produced a moving, spatially focused perceptual image.

Fig. 1.

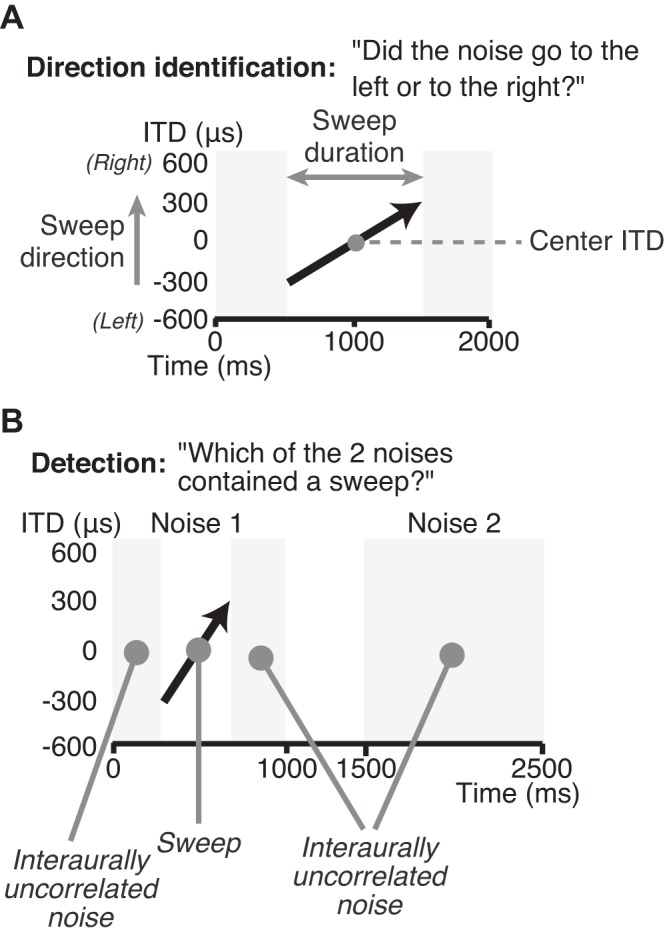
A: interaural time difference (ITD) sweep stimulus for the direction identification task. Participants were presented with a 2-s-long noise that contained a sweep (black arrow) flanked by interaurally uncorrelated noise (light gray region). Participants were asked to identify the direction of motion of the sweep, either to the left or to the right; a sweep moving to the right is shown, with the corresponding ITD trajectories. Center ITDs were either −300, 0, or +300 μs and randomly varied between trials in a block; a center ITD of 0 μs is shown. B: stimuli for the sweep detection task. Participants were presented with two 1-s-long noises separated by 500 ms of silence. One of the two intervals (noise 1) contained a sweep with a center ITD of 0 μs, and the sweep direction could be to the left or to the right. The second interval (noise 2) contained interaurally uncorrelated noise. Participants were asked to identify which of the two intervals contained a sweep.

The method to generate time-varying ITDs was identical to previous work (Zuk and Delgutte 2017). Broadband noise was synthesized using a 100-kHz sampling rate (40 kHz for psychophysics). In one ear (the left ear for psychophysics, the ipsilateral ear for neurophysiology), the noise was upsampled by 10 times to a sampling rate of 1 MHz (400 kHz for psychophysics). The upsampled noise was then downsampled to the original sampling rate after the application of delays based on the desired linear ITD trajectory of the sweep with a resolution of 1 μs (2.5 μs for psychophysics). The noise with time-varying delay was then preceded and followed by an independent noise, resulting in an interaurally uncorrelated noise flanking the sweep with a total stimulus duration of 2 s (1 s in the psychophysical detection task). The overall stimulus was then filtered between 50 Hz and 15 kHz in each ear. Qualitatively, we were unable to perceive any spectral distortions in the ear containing the time-varying delay, and the ITD sweep could not be detected monaurally for any duration.

Psychophysics.

Thirty-three self-described normal hearing listeners (21 men, 12 women), age 21–64 yr (median = 31 yr) participated in the psychophysical experiments. The experiments were done in a sound-treated booth in the McDermott laboratory at the Massachusetts Institute of Technology (MIT). All stimuli were presented at 65 dB SPL. The procedures were approved by the MIT Internal Review Board for human subjects, and all participants provided written, informed consent.

Participants first performed a motion direction identification task and then a detection task using similar stimuli. For the direction identification task, they were presented with ITD sweep stimuli flanked by interaurally uncorrelated noise such that the overall duration of each stimulus was always 2 s. Different center ITDs (−300, 0, and +300 μs) were used to prevent participants from identifying the motion direction based on the lateral position of the sweep at a particular moment in time (e.g., at the beginning or the end of the trajectory).

Before performing the direction identification task, participants were trained to identify the motion direction of 2-s-long ITD sweeps that started and ended with 0.5 s of interaurally uncorrelated noise (total stimulus duration of 3 s). On each trial, participants were presented with either a +sweep or a −sweep stimulus. After the stimulus presentation, they were prompted to press “1” or “2” on the keyboard if they heard the sweep go to the left (−sweep) or to the right (+sweep), respectively. They were provided with feedback after each response. Stimuli were presented in blocks of 12 trials, 6 of which were centered on 0 μs, 3 centered on −300 μs, and 3 centered on +300 μs. Center ITDs were randomly varied within a block. Participants completed two to six blocks of training. In early experiments, 6/33 participants were trained instead on 1-s-long sweeps that started and ended with 0.5 s of uncorrelated noise (2-s total duration), which are identical to the longest sweep durations tested in the main experiment. We switched to the training regimen with 3-s stimuli after the first six participants because results might have been biased by the fact that the training stimuli were a subset of the stimuli used in the main experiment. These six subjects performed similarly to the other subjects for the 1,000-ms-long sweep, so the results from the two training regimens were combined (see results).

After training, participants performed the ITD sweep direction identification task using 2-s-long ITD sweep stimuli (Fig. 1A). Within a block, all ITD sweeps had the same duration. Each block consisted of 20 trials: 10 trials with sweeps centered on 0 μs, 5 with sweeps centered on −300 μs, and 5 with sweeps centered on +300 μs. Initially, listeners were given six blocks where ITD sweep durations successively decreased from 1,000 to 31.25 ms in halving steps. After these first six blocks, the sweep durations were randomized. Participants completed 24 blocks, 4 for each of the 6 sweep durations, giving a total of 80 trials for each sweep duration. Five subjects performed below 75% correct for the training block as well as for all sweep durations. To reduce exhaustion due to their difficulty with the task, these subjects only completed 12–18 of the 24 blocks. As per our criterion for removing subjects on the direction identification task (see results), these subjects were excluded from the psychometric threshold analysis.

The shortest sweep durations were close to binaural gap detection thresholds for diotic noise embedded in interaurally uncorrelated noise (20–40 ms; see Boehnke et al. 2002; Lüddemann et al. 2016). For this reason, direction identification performance at short sweep durations could be limited by the participant’s ability to detect the sweep rather than an inability to identify motion direction per se. Alternatively, the thresholds for sweep detection and direction identification could be distinct. To distinguish between these two possibilities, all 33 participants performed a sweep detection task after completing the direction identification task. A two-interval, two-alternative forced choice procedure was used. Participants were presented with two 1-s-long stimuli on each trial separated by 0.5 s of silence. (We used a shorter stimulus duration for the detection task to reduce testing time. This was possible because, based on previous work, we only tested shorter sweep durations for this task.) One of the two intervals contained a sweep, and the other interval contained interaurally uncorrelated noise (Fig. 1B). The sweep was 125, 62.5, or 31.25 ms in duration and was flanked by interaurally uncorrelated noise on both sides to maintain an overall stimulus duration of 1 s. The sweeps were centered on 0 μs, and the motion direction was randomized across trials. Participants were asked to identify which of the two intervals contained a “sweep,” a term that they were familiar with from the previous direction identification task. Participants reported that they performed this task by identifying a “gap” in the interaurally uncorrelated noise. Sweep durations were constant within each block of 20 trials and randomized across blocks. Participants completed 12 blocks of this task, 4 for each sweep duration, giving a total of 80 trials for each sweep duration. Because the participants were familiar with the stimuli from the direction identification task, no additional training was provided in this task. Only one participant performed below 75% correct for the longest sweep duration (125 ms) and was excluded from psychometric threshold analysis.

Psychophysics analysis.

We computed the percentage of correct responses for direction identification separately for each sweep duration and for each center ITD. Nearly all participants showed a sigmoidal trend in performance going from around 100% correct at the longest sweep durations to around 50% correct (chance performance) at the shortest durations. However, there was a wide variability in the slopes and midpoints of these curves. We used nonlinear least squares in MATLAB to fit a sigmoid model to the percentage of correct responses for sweeps centered on 0 μs. The model took the form

$$PC\left(d\right)=\frac{50}{1+\text{exp}\left[\frac{-({\log }_{2}d-{\log }_2{d}_{75})}{\tau }\right]}+50,$$

where d is the sweep duration, d₇₅ is the “threshold duration” at 75% correct, and τ determines the slope through d₇₅ [units of %/log₂(duration)], which is equal to 50/4τ.

Similarly, the percentage of correct responses for the sweep detection task tended to be near 100% for the longest sweep durations tested and dropped below 75% at 31.25 ms. We fit the same sigmoid model to the sweep detection percentage of correct responses to identify the threshold duration d₇₅ and the slope through d₇₅.

Neurophysiology.

We recorded from single units in the IC of two unanesthetized female Dutch-belted rabbits. We used unanesthetized rabbits to avoid the known effects of anesthesia on ITD tuning (Kuwada et al. 1989; Song et al. 2011) and temporal coding (Chung et al. 2014), both of which may also play a role in encoding ITD motion and adaptation (Cai et al. 1998; Ingham and McAlpine 2004; McAlpine et al. 2000). The procedures for attaching a head post, craniotomy, and neural recording have been described previously (Day et al. 2012; Devore and Delgutte 2010; Zuk and Delgutte 2017) and were approved by the Animal Care Committee of Massachusetts Eye and Ear. Briefly, a small craniotomy (~2 mm in diameter) was performed to access the IC dorsally. Neural recordings were performed while the rabbit’s head was fixed using a head bar previously attached to the skull. All sound stimuli were presented using a pair of speakers (Beyer-Dynamic DT-48) attached to sound tubes running through custom-fitted ear inserts. A probe tube placed at the end of the ear insert was used to measure the sound pressure within 2 cm of the eardrum. The impulse response measured at the probe tube was used to create an inverse filter to generate a flat spectral response at the tip of the ear inserts. The inverse filter was applied to all signals used in this experiment.

Single-unit recordings were made using flexible polyimide four-channel linear multielectrode arrays (Microprobe). IC neurons were identified based on their response to a search stimulus consisting of two 200-ms bursts of broadband noise, with ITDs of 0 and +300 μs, respectively, separated by 200 ms and repeating every 1,000 ms. Spike times from well-isolated single units were measured by threshold crossing.

Stimulation protocols.

Once a neuron was isolated, we measured its frequency-response map to 100-ms pure tone bursts separated by 100-ms silent intervals. The tones were randomly varied between frequencies of 20 Hz and 18 kHz in quarter-octave steps and sound levels of 5 to 70 dB SPL in 5-dB steps. Each frequency-level pairing was repeated one to three times. The characteristic frequency (CF) of the neuron was identified from frequency-response maps using the method of Palmer et al. (2013) by using quadratic interpolation to compute the frequency at the lowest sound level that evoked a number of spikes greater than (or less than for an inhibitory neuron) the average spike count at the lowest sound level (5 dB) across all frequencies by at least four standard deviations. We think most of our recordings were from the central nucleus of the IC because CF increased systematically with increasing electrode depth and there was no strong habituation to successive repetitions of the tonal stimuli. Both of these properties are characteristics of the central nucleus (Aitkin et al. 1972, 1975).

Static ITD tuning was characterized using 300-ms bursts of broadband noise separated by 300 ms of silence. The ITD of the noise was varied between −1,500 and +1,500 μs in 150-μs steps, and each ITD was presented 10 times in random order. The firing rate was averaged over the stimulus duration and plotted as a function of ITD to characterize “static” ITD tuning. The statistical significance of the dependence of firing rate on ITD was assessed by a one-way ANOVA (Chung et al. 2016; Day et al. 2012; Hancock et al. 2010; Zuk and Delgutte 2017). A total of 101/157 neurons showed significant ITD sensitivity (P < 0.001) and were then tested with ITD sweep stimuli.

Once static ITD tuning was characterized, neural responses to ITD sweep stimuli were measured, randomly interleaving the presentations of each sweep duration and direction. All stimuli were presented at 65 dB SPL. In addition to the positive-going and negative-going sweeps, 2-s-long “0-ITD stimuli” were also presented, randomly interleaved with the ITD sweeps (see Fig. 2). The 0-ITD stimuli started and ended with interaurally uncorrelated noise as for the ITD sweep stimuli, but the sweep segment was replaced by a same-duration noise segment with a constant 0-μs ITD. In later experiments, we also presented a 2-s-long interaurally uncorrelated noise stimulus (Fig. 2). Each of the ITD sweeps, 0-ITD stimuli, and the uncorrelated noise was presented 10–15 times with an interstimulus interval of 1 s.

Single-unit spike isolation and stability.

A neural recording was identified as a single unit based on visual inspection of the spike shape variability, spike sorting following principal component analysis of the spike waveforms, and the percentage of interspike intervals (ISIs) <1 ms, which was typically <1% (Day and Delgutte 2016). The latter criterion was met for all recordings with 0-ITD and ITD sweep stimuli.

Presenting our complete stimulus set required at least 25 min of recording time during which the spike height and shape of single units could vary. The isolation of the neuron and the stability of the recording were tested post hoc based on two criteria. First, a signal-to-noise ratio (SNR) was calculated in each 10-s period of the recording. The SNR is defined as the ratio of the mean peak-to-peak spike amplitude to the mean peak-to-peak amplitude of the background noise. A neuron was excluded if its SNR dropped below 2.5 during any 10-s period over the course of recording. Second, in each trial, the “d-prime distance” between the spike shapes in consecutive recordings as well as the d-prime distance between the spikes and a “noise” distribution was computed. The d-prime distance is the difference in means between the two samples being compared divided by the geometric mean of their standard deviations. The noise distribution was created by randomly sampling the same number of nonoverlapping 1-ms intervals (same interval size as the spike waveform) that did not contain spikes. A recording was rejected if either the d-prime distance between the spikes and the noise was <4 or if the d-prime between successive recordings of the same neuron was >2.5. Typically, the d-prime distance between different neurons had values of 5 and above.

Modeling the response to ITD sweeps.

We used a point-process GLM (Paninski 2004; Truccolo et al. 2005) to quantitatively characterize the temporal dependence of firing rate in response to ITD sweeps. Point processes are the appropriate mathematical framework for modeling discrete, stochastic events such as neural spike trains (Johnson 1978; Johnson et al. 2001). A point process in which the instantaneous firing rate (or spiking probability) depends on both stimulus variables and spiking history via a GLM can be used both to accurately predict neural responses to new stimuli (Calabrese et al. 2011; Fontaine et al. 2014; Goldwyn et al. 2012; Plourde et al. 2011a; Steinberg et al. 2013; Trevino et al. 2010) and to implement optimal decoders that identify stimulus properties from the neural spike trains (Goldwyn et al. 2010; Pillow et al. 2005; Siahpoush et al. 2015).

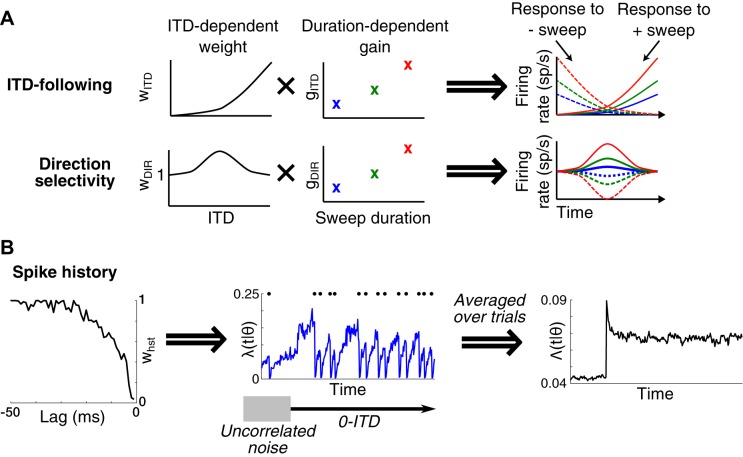
In our model, the instantaneous spiking probability of each neuron is the product of three distinct components (see appendix a for details): 1) an ITD-following component representing tuning to the instantaneous ITD of the sweep; 2) a direction selectivity component that captures dependence on the direction of motion of the ITD sweep, and 3) a spiking history component to incorporate the effects of adaptation and refractoriness. Because the sweep rate can affect the strength of a neuron’s ITD tuning or direction selectivity (Spitzer and Semple 1991, 1993), the ITD-following and direction selectivity components are dependent on ITD (sampled at −300, −150, 0, 150, and 300 μs) and also include a duration-dependent gain, resulting in 11 ITD-following terms and 11 direction selectivity terms. The ITD-following component is proportional to the neuron’s firing rate at the instantaneous ITD of the sweep and can be directly compared with the static ITD tuning curve. The duration-dependent gain, the direction selectivity component, and the spiking history component modify the dependence of spiking probability on instantaneous ITD based on the sweep duration, direction, and previous spiking history. The spike history component incorporated spiking activity over the past 300 ms with 1-ms resolution, resulting in 300 additional free parameters that were the same for all sweep durations and directions.

We used a GLM to estimate the time-varying firing rate of this point process and used the time-rescaling test to assess the goodness of fit of the model (Brown et al. 2002; Haslinger et al. 2010). The best-fitting model was used to implement a maximum-likelihood decoder for the sweep direction based on the neural response (spike train) to individual stimulus trials. The mathematical specification of the model and methods for evaluating goodness of fit can be found in appendix a and appendix b, respectively.

Quantifying the relative contributions of each of the three model components.

The complete model used to describe responses to ITD sweep stimuli had three components. We also fit three reduced models, called “no-ITD-following,” “no-direction-selectivity,” and “no-spiking-history” models, respectively, to test the degree to which each of the full model components contributes to the model’s ability to predict the observed responses (spike trains). To create the no-ITD-following model, the ITD-following component was replaced by a single term representing the average firing rate across all ITDs. For the no-direction-selectivity model, the direction selectivity component in the full model was set to unity. For the no-spiking-history model, the history component was set to unity so that the model had the form of a nonhomogeneous Poisson process.

We used a likelihood ratio test (appendix c) to compare the full model with each of the three reduced models and thereby assess the contribution of each model component to the ability of the full model to fit the observed spike trains. Specifically, if the likelihood ratio statistic for the no-direction-selectivity model is significantly greater than 0 (note that the ratio is log-transformed to get the statistic; see appendix c, Eq. A6), then the direction selectivity component contributes significantly to the overall fit of the model. Likewise, if the likelihood ratio statistic for the no-ITD-following model is significant, then the ITD-following component significantly contributes to the model fit.

We also used a separate likelihood ratio test (appendix c) to compare the ability of the no-direction-selectivity and no-ITD-following models to fit the spike trains for each stimulus trial. This test directly evaluates which of the direction selectivity and ITD-following components is most important to predict the data. A likelihood ratio >1 implies that the model with no direction selectivity captures the timing of spikes better than the model with no ITD following. This was done for each sweep duration. The details of the likelihood computations are given in appendix c.

Direction identification of ITD sweeps from neural responses.

Neurons in the IC respond to ITD sweeps with spikes whose timing provides information about the direction of motion of the sweep. Although the spiking of these neurons is generally highly variable, on average, there is a trend in the time-varying firing rate that should be distinct for different sweep directions if the neuron is properly capturing the variation in ITD. Theoretically, an optimal processor or ideal observer that judges the direction of the sweep would have implicit knowledge about the average response of the neuron to each sweep direction and would use this information to determine the likelihood that the observed spike train was produced by a positive-going sweep or a negative-going sweep. Thus, to assess how well the ITD sweep direction could be decoded from a neuron’s response on each trial, we compared the spike train to an average response template generated by the full model (including ITD-following, direction selectivity, and spike history components) and quantified performance of an optimal classifier of the single-neuron responses to do the task. For each stimulus trial, the model was fit to all the data excluding that trial to avoid overfitting, and then the trial was classified as a +sweep or –sweep depending on which model was most likely to have generated the observed spike train. Details of the implementation of this maximum-likelihood decoder are given in appendix d.

The percentage of correct classifications was then computed by dividing the number of correctly classified trials by the total number of trials (2 times the number of trials for each sweep direction; 30 trials for most neurons). This percentage was computed independently for each stimulus duration.

After the percentage of correct responses at each sweep duration was computed, the same sigmoid model used to analyze the psychophysical data was fit to the percent correct curve (a.k.a. “neurometric function”) for each neuron. During the fitting procedure, the thresholds were limited to values between 10 and 2,000 ms to ensure that the fitted curve would be well behaved. The fitted curves were used to determine the threshold duration and slope of the neurometric function.

ITD sweep detection from neural responses.

We implemented a similar neural decoder to assess each neuron’s ability to detect the sweep against interaurally uncorrelated noise. This classifier compared the response during each trial to the expected response (the model’s average time-varying firing rate) for either sweep direction against the expected response to interaurally uncorrelated noise. Specifically, we selected a pair of trials, one containing a sweep in either direction and one containing uncorrelated noise. Using the model fit to all the data excluding this pair of trials, we simulated a two-interval, two-alternative forced choice task similar to the psychophysical detection task and determined whether the decoder correctly identified the pair of trials. This test was repeated for each possible pairing of one trial with interaurally uncorrelated noise and one trial for either sweep direction (2 times the number of trials squared, including both +sweeps and -sweeps; 450 pairings for most neurons). The percentage of correct responses, neurometric function, and threshold duration for detection were computed as for the direction identification task. Details of the implementation of this maximum likelihood decoder are given in appendix d.

RESULTS

Psychophysics.

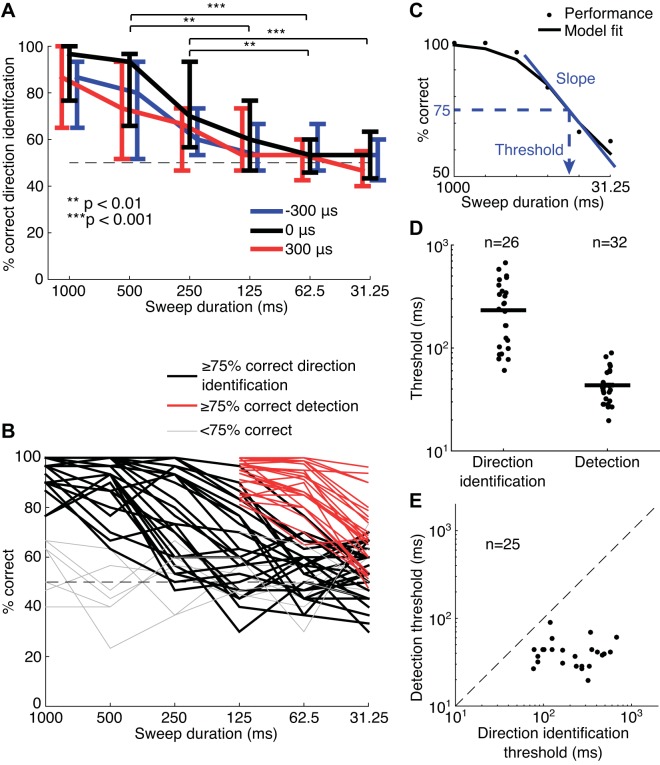
Thirty-three normal-hearing subjects performed first a direction identification task and then a sweep detection task with ITD sweep stimuli of different durations. Both tasks were performed in blocks of 20 trials, where each block contained stimuli with the same sweep duration to reduce the difficulty of the task and optimize subject performance. Listeners performed four blocks of trials for each sweep duration. Across all participants, there was a weak but significant difference in direction identification performance across blocks for the 1,000-ms sweep duration (Kruskal–Wallis test with Bonferroni correction for 6 sweep durations: χ² = 14.0, P = 0.026), but not for any of the other sweep durations (P > 0.05). For the 1,000-ms sweeps, a significant increase in performance was only found between the first block and the last two blocks (Mann–Whitney U test with Bonferroni correction for 6 comparisons: block 1 versus block 3, P = 0.011; block 1 versus block 4, P = 0.026). For this reason, we only analyzed the percent correct scores for direction identification averaged over the last three blocks (last 2 blocks for the 5 poorly performing subjects who completed only 3 blocks) for each sweep duration, after the participant’s performance seemed to have reached an asymptote. This left a total of 30 trials per sweep duration at a center ITD of 0 μs, 15 trials at −300 μs, and 15 trials at +300 μs. There was no effect of block number on performance for the detection task (Kruskal–Wallis test, P > 0.05), so all four blocks (80 trials) were included in the analysis for each sweep duration.

On average, there was a clear decrease in direction identification performance with decreasing sweep durations for all three center ITDs (Kruskal–Wallis test, −300 μs: χ² = 43.5, P < 0.001; 0 μs: χ² = 65.7, P < 0.001; +300 μs: χ² = 52.6, P < 0.001; Fig. 3A). The largest drop in performance occurred between 250 and 125 ms. We also observed a significant difference in performance between center ITDs (Friedman test: χ² = 7.32, P = 0.026). Performance was significantly better for sweeps centered on ITDs of 0 μs than for sweeps centered on −300 and +300 μs (Wilcoxon signed-rank test with Bonferroni corrections, −300 versus 0 μs: W = 3273, P < 0.001; 0 versus +300 μs: W = 8710, P < 0.001; −300 versus +300 μs: W = 5366, P = 0.26). Even though we used two different training protocols (27 participants were trained with 2,000-ms sweeps and 6 with 1,000-ms sweeps), there was no significant difference in performance between the two groups for the 1,000-ms sweeps during testing (Mann–Whitney U test: U = 107.5, P = 0.63), so data from the two groups were combined for subsequent analyses.

Fig. 3.

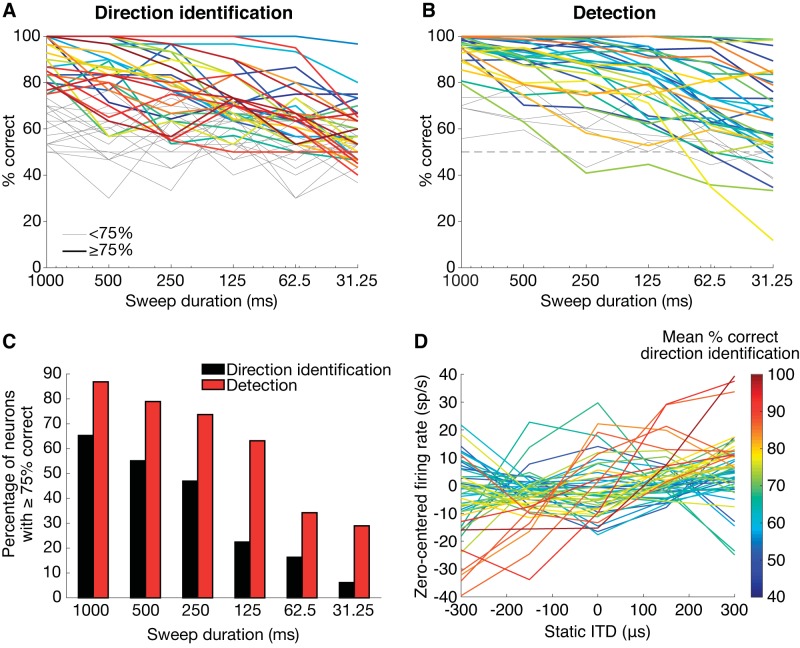
A: average performance across the participants in direction identification against sweep duration for center interaural time differences of −300 (blue), 0 (black), and +300 μs (red). Red and blue curves have been shifted slightly along the horizontal axis for clarity. Error bars designate the interquartile range. Significance values were calculated by Tukey’s honestly significant difference test. B: overall average performance of each participant against sweep duration for direction identification (black) and sweep detection (red). Thick lines show data from participants who performed at or above 75% correct for at least one sweep duration, and thin gray lines show participants with %correct below this criterion. Data from participants that performed at or above 75% correct are in D and E. C: a sigmoid model was fit to the %correct scores against duration to compute the threshold duration yielding 75% correct (black) and the slope through the threshold duration (blue). D: distribution of threshold durations for direction identification and detection for the participants that passed the 75% correct criterion. E: comparison of individual direction identification and detection thresholds in participants that passed the 75% correct criterion for both tasks. n, Number of participants.

In each block, we presented sweeps with center ITDs of either −300 or +300 μs in addition to 0 μs to prevent listeners from identifying the direction of motion based on the lateralization of the sounds at the beginning or end of the trajectory. However, this approach does not completely rule out the possibility of judging the direction based on static lateralization. For instance, for a sweep moving from an ITD of −600 to 0 μs, the listener could theoretically identify the motion as rightward (a positive-going ITD) by recognizing that −600 μs was the leftmost (most negative) possible starting ITD within the set of ITDs tested in the experiment. The same logic can be applied if the sweep ended at −600 μs, which would necessarily be a negative-going sweep. To test whether participants used such a strategy, the percentages of correct responses for direction identification were recalculated based on the lateral position at the start of the sweep. If listeners identified the direction based on the lateral position at the start of the sweep, they should do better for sweeps starting from a position on the left or a position on the right than for sweeps with a starting position in the center, because, in the latter case, this strategy would result in chance performance. Alternatively, if listeners identified the direction based on the end of the sweep, they should do better for sweeps starting at the center than for sweeps starting on either side. We found no effect of starting position on performance (Friedman test: χ² = 4.08, P = 0.13). Thus we conclude that participants were indeed identifying the direction of the ITD sweeps based on the change in ITD rather than identification of specific static ITDs at either end of the trajectory.

Whereas all participants showed a decrease in performance with decreasing sweep duration for both direction identification and sweep detection, the durations at which this decrease was steepest varied across individuals and between the two tasks. As shown in Fig. 3B, the performance of most participants (26/33, which also excludes the subjects who performed only 3 blocks) for direction identification exceeded 75% correct for at least one sweep duration and showed a sigmoid trend. However, there was a large variability in performance around 250-and 125-ms sweep durations corresponding to differences in threshold durations. Importantly, the median performance was significantly better for detection (excluding 1 subject who performed <75% correct) than for direction identification at 125 ms and below (Mann–Whitney U test with Bonferroni correction: 125 ms, U = 642.5; 62.5 ms, U = 581; 31.25 ms, U = 785; P < 0.001 for all sweep durations; Fig. 3B). Thus the limitation on performance for direction identification at short sweep durations cannot be explained by an inability to hear the sweep amidst the flanking interaurally uncorrelated noise.

We quantified the dependence of performance on sweep duration for direction identification and detection by fitting a sigmoid function to the percentages of correct responses (“psychometric function”) for each individual (Fig. 3C). The sigmoid model assumed that all participants exhibited a maximum performance of 100% correct for long sweep durations and a minimum performance of 50% correct (chance) for short durations. Model fitting yielded two parameters for each task and individual: the threshold sweep duration yielding a performance of 75% correct and the slope through that midpoint [in %correct/log₂(duration)]. We only fit this model for individuals that performed at 75% correct or above for at least one sweep duration (n = 26/33 for direction identification, n = 32/33 for detection). On average, threshold durations were 5.4 times larger for direction identification than for detection (median direction identification threshold = 232.3 ms, median detection threshold = 43.4 ms; Fig. 3D), and the difference between the two was highly significant (Mann–Whitney U test: U = 1172, P < 0.001). However, the slopes of the psychometric functions were similar for both tasks [median direction identification slope = 24.9%/log₂(duration), median detection slope = 20.0%/log₂(duration); U = 809, P = 0.52]. Further insights into the differences between the two tasks can be obtained by plotting the threshold for detection against the threshold for direction identification for the 25 participants who passed the 75% criterion for both tasks (Fig. 3E). With no exception, the data lie below the line of equality, further reinforcing the finding that the detection thresholds were smaller. For these participants, there was no correlation between the threshold durations for the two tasks (Kendall’s tau: τ = 0.14, P = 0.33), suggesting that the factors limiting performance are distinct for the two tasks.

The present threshold durations are in broad agreement with previous studies of direction identification and motion detection thresholds (see Carlile and Leung 2016 for review). The threshold durations for detection are consistent with previous studies of interaural correlation-change interval detection when noise with constant ITD is temporally embedded in uncorrelated noise (Boehnke et al. 2002) (see discussion).

Neural responses to ITD sweeps.

We recorded from 101 ITD-sensitive neurons in the IC of unanesthetized female rabbits. ITD sensitivity was determined based on an ANOVA test (P < 0.001) of the effect of ITD on firing rate for 300-ms stimuli with static ITD (Chung et al. 2016; Day et al. 2012; Hancock et al. 2010; Zuk and Delgutte 2017). For 62 of these neurons, responses to a complete set of ITD sweep stimuli were measured for 10–15 trials, and the recordings were deemed sufficiently stable and well isolated to be included in later analyses. CF values ranged from 293 Hz to 18.1 kHz (median 3.81 kHz, 19 neurons with CF < 2 kHz, 43 with CF > 2 kHz). For rabbit IC neurons stimulated by broadband noise, 2 kHz is approximately the CF boundary between ITD sensitivity based on the temporal fine structure and ITD sensitivity based on the cochlear-induced envelope (Day et al. 2012; Devore and Delgutte 2010).

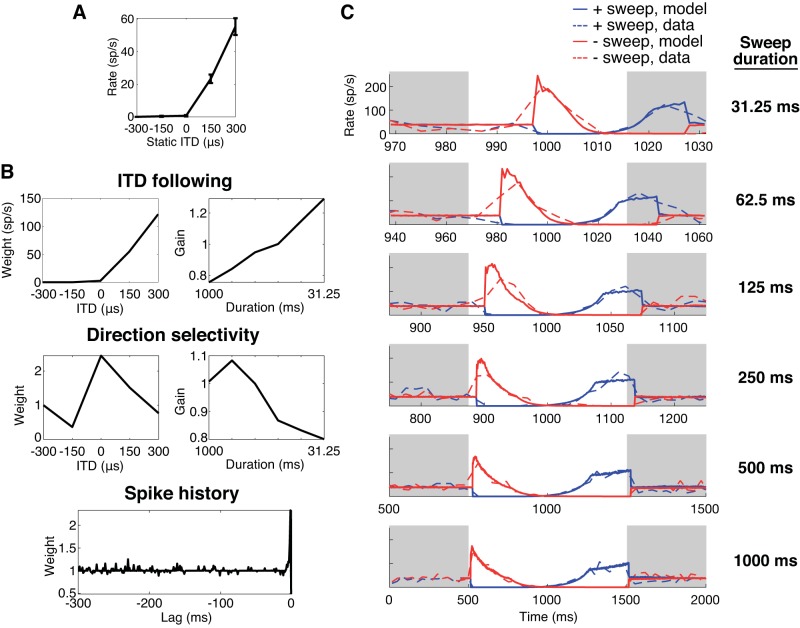
Figure 4A shows the static ITD tuning curve for an example neuron (CF = 475 Hz) with a best ITD near +300 μs. Figure 4B shows the temporal response patterns [peristimulus time (PST) histograms] to negative-going sweeps, positive-going sweeps, and 0-ITD stimuli of different durations, as well as the response to interaurally uncorrelated noise (bottom). The average firing rate across 15 trials is shown using a bin width equal to the square root of the sweep duration (in ms) and using a normalized timescale so that all sweep durations are displayed over the same width. Consistent with the neuron’s static ITD tuning, the firing rates during negative-going sweeps start high and decrease over time as the ITD decreases from +300 to −300 μs. (Because of the normalized timescale, the peak response occurs increasingly to the right in Fig. 4B with decreasing duration, reflecting a nearly constant response latency.) Conversely, the firing rates for positive-going sweeps tend to increase over time as expected based on static ITD tuning.

Fig. 4.

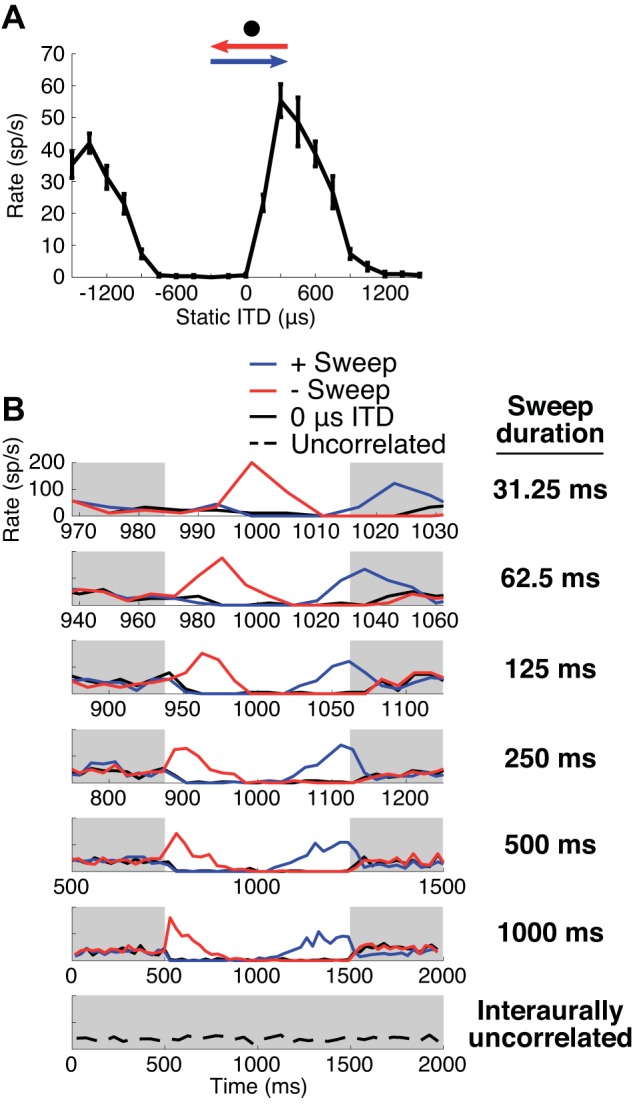
A: static interaural time difference (ITD) tuning curve of an inferior colliculus neuron. Characteristic frequency (CF) = 475 Hz. Trajectories of the ITD sweep stimuli are indicated by arrows (blue, positive-going sweep; red, negative-going sweep; black circle, 0-ITD stimulus). Error bars are SE of mean firing rate in spikes/s (sp/s). B: peristimulus time histograms of the neuron in A in response to the positive-going (+sweep; blue) and negative-going (−sweep; red) ITD sweeps and the 0-μs ITD stimulus (black). Each row shows the response for 1 sweep duration; bottom row shows a response to interaurally uncorrelated noise. Bin widths for the histograms for the sweeps are equal to the square root of the sweep duration, and bin width for the histogram for uncorrelated noise is 50 ms. In each plot the light gray shading marks intervals when the noise is interaurally uncorrelated, and the white regions represent the intervals of ITD sweeps.

The neuron appears to produce a distinguishable response to the positive-going and negative-going sweep for every sweep duration (Fig. 4B), but this could only be observed by using a variable bin width depending on sweep duration. If a constant bin width is used across sweep durations, the bin width must be substantially smaller than the duration of the shortest sweep (31.25 ms) to distinguish the responses to opposite sweep directions. At these short bin widths, neural noise makes the overall trends in firing at the longest sweep durations hard to see. Our goals in this study were to quantify the sweep direction information available in the neural responses to ITD sweep stimuli and to compare the performance of a neural decoder that identifies the sweep direction with human psychophysical performance. Clearly, analyzing responses using PST histograms as in Fig. 4B yields results that heavily depend on the choice of bin width. To overcome this difficulty, we modeled the variations in firing rates as a point process with a dependence on stimulus parameters in the form of a GLM (Paninski 2004; Truccolo et al. 2005). The model reduced the temporal response patterns to a smaller number of parameters to avoid overfitting while also capturing the fast dynamics in the response that are present at short sweep durations. The model could also represent effects of adaptation by including a term dependent on recent spiking history. Importantly, the same model led to the straightforward implementation of a neural decoder that optimally identified the sweep direction based on the response of a neuron to individual stimulus trials.

Modeling responses to ITD sweeps.

In our point-process GLM, the instantaneous firing rate is the product of three components (see methods and appendix a): 1) an ITD-following component, 2) a direction selectivity component, and 3) a spiking history component dependent on the timing of spikes over the preceding 300 ms. The ITD-following and direction selectivity components each had separate ITD-dependent weights and duration-dependent gain terms. For a neuron in which the ITD-following component dominates, the responses to opposite sweep directions are identical but flipped in time and should resemble the static ITD tuning curve (Fig. 5A). In contrast, the direction selectivity component flips in sign depending on the sweep direction. If a neuron consistently “preferred” one of the two motion directions, its direction selectivity component would always be either >1 or <1, regardless of the instantaneous ITD and duration of the sweep (Fig. 5A). In the rabbit retina, for example, direction-selective ganglion cells have a preferred direction irrespective of the initial position of the stimulus (Barlow and Levick 1965) and over a wide range of motion speeds and displacements (Grzywacz and Amthor 2007). Whether or not neurons in the IC have a preferred direction in this strong sense is unclear. There is some evidence for preferred motion directions for stimuli with time-varying ITDs (Dietz et al. 2014; Fitzpatrick et al. 2009; Spitzer and Semple 1993, 1998; Yin and Kuwada 1983), but at least some of this apparent selectivity is likely due to firing rate adaptation (Cai et al. 1998; McAlpine et al. 2000; Wang and Peña 2013). By allowing the time-varying firing rate in our model to depend on both instantaneous ITD and sweep direction, and by also including a spiking history component, we intended to test empirically whether direction selectivity in a strong sense exists in the IC.

Fig. 5.

Point-process generalized linear model (GLM) of neural responses to interaural time difference (ITD) sweep stimuli. The model has 3 components: ITD-following, direction selectivity, and spiking history. A: if a neuron shows a variation in ITD-following weights (w_ITD), then the neuron’s response to the negative-going sweep (−sweep) would be a time-reversed version of the response to the positive-going sweep (+sweep). If a neuron’s direction selectivity weights (w_DIR) are >1 (assuming the ITD-following weights are constant for all ITD), then the neuron’s firing rate would be enhanced for the +sweep and suppressed for the −sweep. For both ITD-following and direction selectivity, the duration-dependent gain term (g_ITD and g_DIR, respectively) amplifies or suppresses the neuron’s firing rate (spikes/s, sp/s). B: spike history quantifies the amount of suppression in the probability of firing following a spike. Example shown at left suggests a decaying amount of suppression as the time relative to the spike increases; this was a common trend across the neurons we recorded. Example in middle shows time-varying firing rate [λ(t|θ)] of the model for a neuron with the spike history component shown at left in response to a 0-μs ITD stimulus. Spike times are indicated by black dots at top. The effect of the spike history component is to reduce the probability of firing immediately after each spike. When averaged across trials [Λ(t|θ)], this results in a gradual decay in firing rate after the transition from interaurally uncorrelated noise to the 0-μs ITD noise (shown at right). Conversely, if the 0-μs ITD noise evoked lower average firing rates than uncorrelated noise, there would be a gradual increase in firing rate following the transition.

In general, the model’s ITD-following components for our IC neurons resembled the static ITD tuning curve. For example, the ITD-following component in the neuron of Fig. 6B (CF = 475 Hz; same neuron as in Fig. 4) has a peak at 300 μs, and its shape is similar to that of the static ITD tuning curve in Fig. 6A. The duration-dependent gain for ITD-following (Fig. 6B, top right) increased monotonically with decreasing sweep duration, meaning the range of instantaneous firing rates produced by the sweep was larger for short durations. The direction selectivity component for this neuron (Fig. 6B) showed both amplification (values >1) and suppression (values <1). However, the largest amplification occurred at an ITD where the neuron’s firing rate is near zero, making the direction selectivity components for this neuron difficult to interpret.

Fig. 6.

Components of the point-process generalized linear model (GLM) and analysis for the same neuron as in Fig. 4. A: for comparison, the static interaural time difference (ITD) tuning between −300 and +300 μs is shown, with error bars showing SE of the firing rate (spikes/s, sp/s) over 10 trials. B: ITD-following, direction selectivity, and spike history components. For the ITD-following and direction selectivity components, the ITD-dependent weights are shown at left, and the duration-dependent gains at right. This neuron was 1 of 8 that had spike history weights >1.4. Half width (the lag at which the history weight is 0.5) of the spike history component was 1 ms. C: peristimulus time (PST) histograms (dashed lines) and average model responses (solid lines) for the positive-going sweep (+sweep; blue) and negative-going sweep (−sweep; red) at the different sweep durations. Gray regions designate the times when interaurally uncorrelated noise was presented, as in Fig. 4. PST histograms shown are identical to those in Fig. 4. These plots show a reasonably good fit of the model to the neuron’s recorded average firing rates.

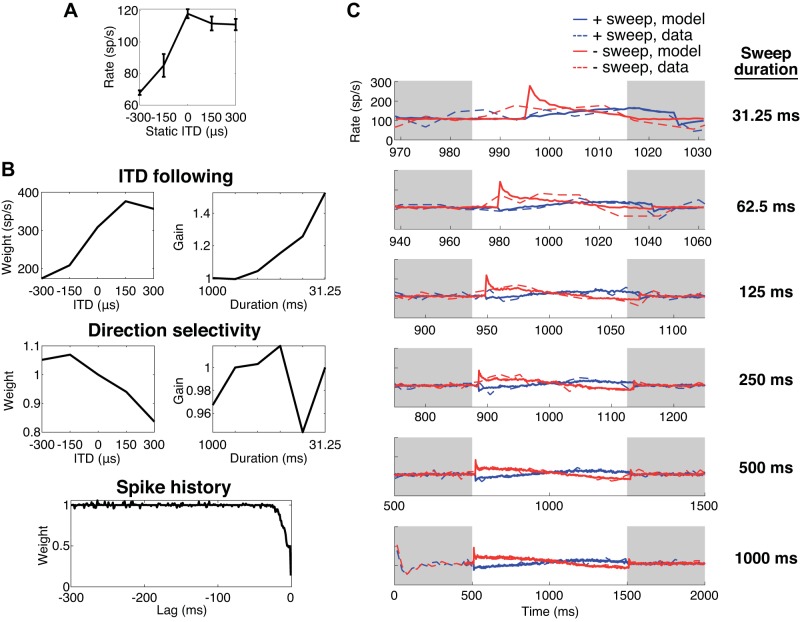
Data from another neuron with a high CF (5,380 Hz) are shown in Fig. 7. Again, the neuron’s ITD-following component (Fig. 7B) resembles the static ITD tuning curve (Fig. 7A): the firing rate increased with ITD and then plateaued for positive ITDs. Again, the duration-dependent gain for ITD following increased monotonically with decreasing duration. For this neuron, the direction selectivity component decreased with increasing ITD and was mostly suppressive. We observed such a sloping trend in the direction selectivity components of several other neurons. If we consider a neuron in which the ITD-following component is constant, such a sloping trend would result in a steady decrease in firing rate over time for both positive-going and negative-going sweeps. Specifically, for positive-going sweeps, the direction selectivity weights enhance firing at the beginning of the sweep and suppress firing at the end, and for negative-going sweeps, the reciprocal of the direction selectivity weights is applied, resulting in the same pattern of enhancement and suppression (see appendix a). Such a pattern may represent a form of adaptation not fully captured by the spike history component rather than direction selectivity per se.

Fig. 7.

Generalized linear model (GLM) analysis for a neuron with a high characteristic frequency (CF = 5,380 Hz). A: static interaural time difference (ITD) tuning between −300 and +300 μs. Error bars are SE of firing rate (spikes/s, sp/s) over 10 trials. B: ITD-following, direction selectivity, and spike history components. For the ITD-following and direction selectivity components, the ITD-dependent weights are shown at left and the duration-dependent gains at right. This neuron’s spike history only showed a decaying suppression at short time lags. For this neuron, the half width was 7 ms. C: peristimulus time (PST) histograms (dashed lines) and average model responses (solid lines) for the positive-going sweep (+sweep; blue) and negative-going sweep (−sweep; red) at the different sweep durations. Gray regions designate the times when interaurally uncorrelated noise was presented, as in Fig. 6. PST histograms shown are identical to those in Fig. 6.

The third component in the model is the spiking history component, which is intended to capture effects of adaptation and refractoriness (Fig. 5B). Often, the spike history component was only prominent at short time lags and then rapidly moved toward 1, meaning remote spiking history did not influence responses (Figs. 6B and 7B). In the neuron of Fig. 6B, the spike history component showed an enhancement in spiking probability (values >1) at time lags from −2 to −3 ms rather than the expected suppression. This enhancement may be related to the frequent occurrence of spike doublets or triplets (“bursting”) in the spike train of this neuron. Such apparent enhancement at short time lags was rarely observed: Only 8/62 neurons had spike history components that exceeded a magnitude of 1.4 for any lag. The neuron in Fig. 7B had spike history components smaller than 1 (indicating suppression of firing) for short lags, which is consistent with the expected effect of short-term adaptation and refractoriness. The vast majority of neurons (50/62) had spike history components <0.5 for short delays, indicating suppression. For each of these neurons, we computed the “half width,” the time lag for which the spike history component crossed 0.5. The median half width among the 50 neurons with suppressive history was 7 ms (interquartile range of 3 to 9 ms). This is short compared to the 20- to 120-ms time constants of binaural adaptation reported for IC neurons in anesthetized guinea pigs by Ingham and McAlpine (2004).

Taken together with the trends in the direction selectivity components, the spike history components seem to capture only very short-term adaptation, perhaps associated with refractoriness, whereas the direction selectivity components may have indirectly captured longer term forms of adaptation. Specifically, the sloping trend in the direction selectivity component observed in some of our neurons (e.g., Fig. 7B), which results in falling firing rates for both sweep directions, is consistent with an adaptive component, perhaps dependent on subthreshold events that would not be captured by the spike history component.

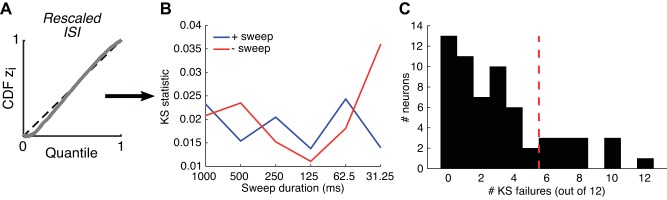
By combining the three components of the model (using ITD-following, direction selectivity, and spike history), we can generate an average model response that can be compared with measured PST histograms for both sweep directions (Figs. 6C and 7C). In these two examples, the average model firing rate appeared to capture the PST histogram adequately for both long and short sweep durations. However, comparing the model’s average firing rate to the PST histogram neglects the effects of spike history on short-term spiking probabilities and is therefore a poor measure of goodness of fit for a point-process model. Instead, we used a more rigorous test based on the time rescaling theorem for ISIs, which is specifically designed for point-process models (Brown et al. 2002; Haslinger et al. 2010). Details of the analysis of the model goodness of fit are given in appendix b. Only a modest fraction of our neurons (13/62) passed the goodness-of-fit test for all 12 stimuli. However, most of the neurons only exhibited a few failures, and there was no general tendency for the model to fit better for specific sweep durations or directions (the neurons in Figs. 6 and 7 failed the goodness-of-fit test 2/12 and 1/12 times, respectively). The failures may be due to the high sensitivity of our goodness-of-fit measure as well as the inability of the model’s spike history component to capture forms of adaptation occurring over long timescales. The following analyses were restricted to the 49/62 neurons for which the time-rescaling test failed for ≤5 of the 12 sweep stimuli.

Relative importance of the three model components.

Next, we examined the relative fits of three reduced models: 1) a no-direction-selectivity model in which the direction selectivity components were removed, 2) a no-ITD-following model in which the ITD-following components were removed, and 3) a no-spiking-history model where the spiking history components were removed (Fig. 8A). By removing components, we tested the degree to which each of these components contributes to the overall model fit. This was quantified by the likelihood of the data given the reduced models. Figure 8A shows the likelihood of the full model relative to the likelihoods of each reduced model, where higher values indicate a worse fit for the reduced model. On average, the no-direction-selectivity model fit better than the no-history and no-ITD-following models.

Fig. 8.

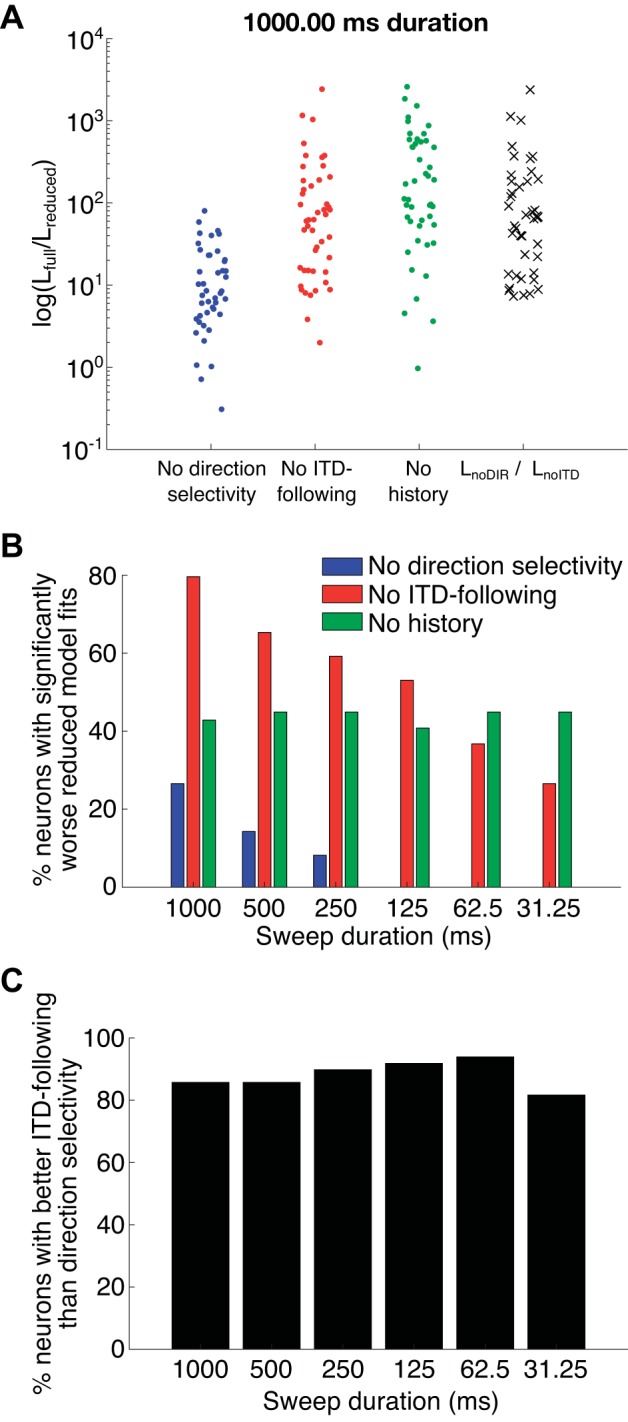
A: data points show the log of the likelihood ratio of the full model (L_full) relative to each reduced model (L_reduced) [no direction selectivity, no interaural time difference (ITD)-following, and no history] for the longest sweep duration (1,000 ms), summed across sweep directions for all units included in the population analysis (n = 49). Larger values mean a worse model fit relative to the full model. Black crosses at right show the log of the likelihood ratio comparing the model without direction selectivity components (L_noDIR) to the reduced model without ITD-following components (L_noITD), which is the measure used in C. Seven neurons had log L_noDIR/L_noITD ratios <0 and are not shown. B: percentage of neurons for which including the ITD-following component (blue), the direction selectivity component (red), or the spike history component (green) significantly improved the goodness of fit of the model to the data. Significance of the improvement in goodness of fit was assessed by a statistical test (χ²) on the likelihood ratio comparing each reduced model with the full model including all components. C: percentage of neurons in which the neural response was better fit by the no-direction-selectivity model than by the no-ITD-following model as a function of sweep duration. Relative goodness of fit of the two models to the data was evaluated by a likelihood ratio.

We used a likelihood ratio statistic to test whether including each model component improved the model’s ability to fit the data by comparing the goodness of fit of the full model to that of each reduced model (Fig. 8B). For all but the shortest durations, the no-ITD-following model produced a significantly worse fit to the data than the full model in over 50% of the neurons, indicating that the ITD-following component made a major contribution to the full model. In contrast, the direction selectivity component contributed to the full model fit in only 27% of the neurons at the longest duration. Thus the ITD-following component dominates in most IC neurons, but the contribution of direction selectivity cannot be completely ignored, especially at long durations where the tests are more powerful due to the larger number of spikes. Importantly, for each sweep duration, 42–44% of the neurons had significantly worse model fits when the history component was removed. Although this proportion is smaller than reported in a previous study of auditory neurons (Plourde et al. 2011b), the history component does contribute to the model fit for a large number of neurons. Including an adaptation term dependent on subthreshold events in the model might further improve the goodness-of-fit of the model.

We further assessed the relative contributions of the ITD-following and direction selectivity components to each neuron’s temporal firing patterns by comparing the likelihoods of the data given the models with no ITD-following and no direction selectivity (Fig. 8C; also see Fig. 8A for the exact values for the 1,000-ms sweep duration). If a neuron’s response is dominated by ITD following, then the model with no direction selectivity will better capture the temporal pattern of the response than the model with no ITD following, and the likelihood ratio will be >1. On the other hand, if the neuron’s response is dominated by direction selectivity, then the likelihood ratio will be <1. Over 80% of the neurons (n = 49) had likelihood ratios >1 for all sweep durations. Thus most of the neurons in our sample were dominated by ITD following.

Comparison of ITD following to static ITD tuning.

Because the ITD-following component captured a large portion of the temporal firing patterns in most neurons, we analyzed how this component compares with the static ITD tuning curve and how it is modulated by the duration-dependent gain. If the decrease in direction identification performance at short sweep durations was due to an inability of auditory neurons to follow the ITD at high rates, then we would expect the gain of the ITD-following component to decrease with decreasing sweep duration. Instead, we found that the gain tended to increase with decreasing sweep duration, as shown in Figs. 6B and 7B. This trend was also apparent across the sample of neurons (Fig. 9A): there was a significant increase in gain with decreasing sweep duration (Kendall: τ = −0.133, P = 0.002).

Fig. 9.

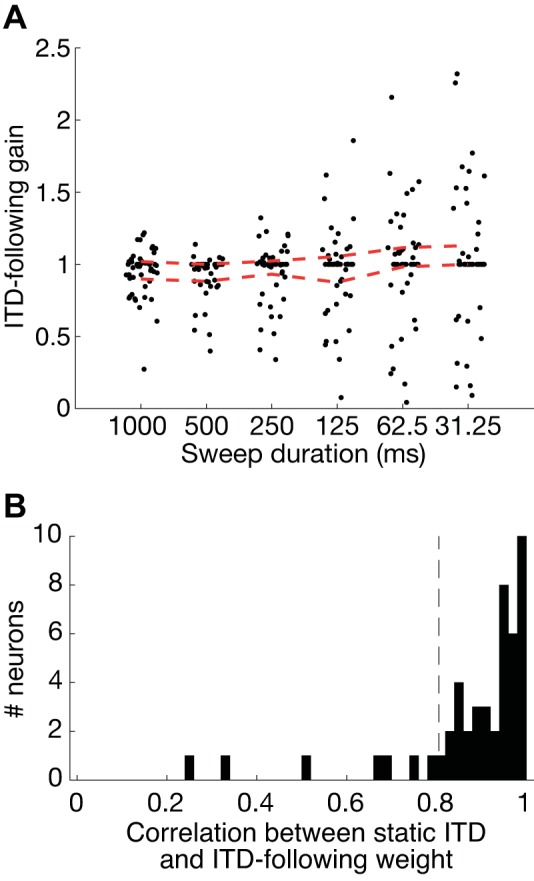
A: interaural time difference (ITD)-following gain against sweep duration for 49 neurons. Dashed red lines indicate the interquartile range of the gains. B: distribution of Pearson’s correlation between each neuron’s ITD-dependent ITD-following weight and their static ITD tuning as a function of sweep duration. Dashed horizontal black line shows the threshold for significant correlation with P < 0.05 based on a one-tailed Student’s t test. Forty-one of 49 neurons had correlations above this threshold.

To analyze the similarity in shape between the ITD-following component and the static ITD tuning curve, we computed the Pearson’s correlation between the two. A vast majority of the neurons (41/49) had ITD-following components that were significantly correlated with their static ITD tuning curve (threshold correlation = 0.805, one-tailed Student’s t test, P < 0.05; Fig. 9B). Furthermore, the median correlation across the population (0.937) was significantly larger than this threshold (Wilcoxon signed-rank test: W = 979, P < 0.001).

Taken together, these results show that the ITD-following component resembles the static ITD tuning curve and spans a wider range of firing rates across ITD for shorter sweeps. These findings are contrary to the hypothesis that direction identification performance is limited by the ability of IC neurons to follow the ITD at high rates.

Direction identification and detection performance based on single-trial neural response.

In general, our IC neurons appeared to follow the ITD and maintained their static ITD tuning for all sweep durations. These attributes suggest that a classifier based on single-trial neural responses may be able to both detect the presence of a sweep and identify the sweep direction. We used the average firing probability (intensity function) of the point-process model fit to a particular neuron’s response to quantify the likelihood that the observed spike train on a particular trial occurred in response to a positive-going sweep, a negative-going sweep, or (in the detection task) interaurally uncorrelated noise. Likelihood ratio tests (Green and Swets 1988) were used to determine the performance of optimal classifiers (or “ideal observers”) that use responses of a single neuron to a single stimulus trial to perform the direction identification and detection tasks.

To model the direction identification task, we calculated the average time-varying firing rate of the point-process model to each sweep direction and each sweep duration by iteratively generating a model response to each sweep stimulus and averaging the responses over 500 iterations (Fig. 10A; see also Figs. 6C and 7C). The model used in these calculations was fit to all trials except one left-out trial to ensure cross-validation. We then scored the spike train in the left out trial by computing the log of the ratio of the likelihood for the spike train given the average model response to the positive-going sweep relative to the likelihood for the spike train given the average model response to the negative-going sweep (Fig. 10A, middle). A positive score means that the spike train on a given trial is more likely to match the average model response to the positive-going sweep, whereas a negative score means that the spike train better matches the negative-going sweep. We then classified the trial as correct or not based on whether the sign of its score matched the stimulus that was actually presented on this trial. We calculated the percentage of correct responses over all 20–30 trials for each sweep duration (Fig. 10C).

Fig. 10.

Steps for computing direction identification and detection neurometric functions. Examples shown are based on data from the neuron represented in Figs. 4 and 6. A: direction identification. The neuron’s response on each trial (left) is compared with the model’s probability of firing averaged over 500 simulated responses during the duration of the sweep (middle). The model is refit to all of the data, excluding the trial being compared. The log of the likelihood ratio comparing the trial to a +sweep response and a −sweep response is then used to compute the direction identification score (right), where positive values mean that the trial is a +sweep (blue dots) and negative values mean a −sweep (red dots) (see appendix d). The neurometric function is then computed by adding up the correct identifications (>0 for +sweep, <0 for −sweep) and dividing by the total number of trials (30 trials; black line in C). B: detection. One trial containing either a +sweep or −sweep and one trial containing continuous interaurally uncorrelated noise were chosen (left) and compared with the average model responses for either sweep direction and interaurally uncorrelated noise (middle). Comparisons were done for the 1,000-ms interval surrounding the sweep to match the interval of time used for psychophysics. Sweep detection was then scored using the log of the ratio of these likelihoods, as in a 2-interval, 2-alternative forced choice task (black dots; right) (see appendix d). The number of correct detections (scores >0) divided by the total number of trial pairings (200–450 trials) was equal to the %correct (red line in C).

Similarly, for modeling the detection task, we calculated the average model firing rate to interaurally uncorrelated noise and then scored the neural responses in a pair of left-out trials corresponding to the two intervals in each trial of the psychophysical detection task. The first interval contained the response to a sweep in either direction, and the second interval contained the response to interaurally uncorrelated noise (Fig. 10B). The detection score was computed based on the likelihood ratio for a two-interval two-alternative forced choice task (Green and Swets 1988) similar to the task performed by the human participants in our study (Fig. 10B, right). A positive score means that the sweep was detected in the first interval (the correct classification), whereas a negative score means a sweep was detected in the second interval (the incorrect classification). The percent correct is defined as the number of positive scores out of the total number of possible pairings (200–450 total pairings; Fig. 10C).

The direction identification task was modeled in 49 neurons and the detection task in the 38 neurons for which we measured responses to interaurally uncorrelated noise. These neurons passed the goodness-of-fit test for the GLM for at least 7/12 stimuli. Figure 11, A and B, shows the neurometric functions (percentage of correct responses against sweep duration) of all of these neurons for the direction identification and detection, respectively. Performance varied widely across neurons. Some neurons performed direction identification very accurately; for example, the neuron in Fig. 10 (same neuron as in Figs. 4 and 6) produced one of the highest average performances for direction identification. Likewise, the performance of many neurons for sweep detection was very high. Figure 11C shows the percentage of neurons for which the percentage of correct responses was above 75% as a function of sweep duration. Overall, a higher percentage of neurons reached this criterion level of performance in the detection task compared with the direction identification task.

Fig. 11.

A: %correct of the optimal classifier for direction identification as a function of sweep duration for 49 neurons. B: %correct detection for 38 neurons. Thick lines in A and B mark neurons in which the performance was at or above 75% correct for the 1,000-ms sweeps. Thick lines are colored to separate individual neurometric curves. All neurometric curves that did not pass this criterion are shown in gray. C: for all sweep durations, there are more neurons for which the classifier performed above 75% for detection (red) than for direction identification (black). Both numbers decrease with decreasing sweep duration. D: static interaural time difference (ITD) tuning curves color coded by performance (spikes/s, sp/s) averaged across all sweep durations for the direction identification task. The best-performing neurons for direction identification tended to have monotonic ITD tuning curves between −300 and 300 μs.

We next examined the relationship between a neuron’s static ITD tuning and the performance of the optimal classifier for direction identification. The neurons providing the best direction identification performance tended to have monotonic ITD tuning spanning a wide range of firing rates within the range of the ITD sweep (Fig. 11D). In contrast, neurons with nonmonotonic ITD tuning curves typically did not provide good classification for direction identification. If a neuron’s firing rate followed the instantaneous ITD of the sweep, then a monotonic ITD tuning curve would yield distinct responses for positive-going sweeps relative to negative-going sweeps (see Fig. 4 for example). If instead the neuron’s ITD tuning curve was symmetrical around the sweep’s center ITD, then the response should be identical for both sweep directions. Thus the observed relationship between direction identification performance and the shapes of static ITD tuning curves is consistent with our finding that ITD following is more important than direction selectivity in accounting for temporal response patterns to ITD sweeps.

There was no significant correlation between a neuron’s CF and the average percent correct for direction identification (Kendall’s tau: τ = 0.04, P = 0.67) or detection (τ = −0.08, P = 0.46). Additionally, there was no significant difference between low-CF (<2 kHz) and high-CF (>2 kHz) neurons in their average percent correct for direction identification (Mann–Whitney U test: U = 416, P = 0.74) or for detection (U = 265, P = 0.33). A 2-kHz cutoff approximately separates IC neurons sensitive to ITD in the temporal fine structure of noise from neurons sensitive to ITDs in the cochlear-induced envelope (Day et al. 2012; Devore and Delgutte 2010; Joris 2003). This observation is consistent with a previous finding (Devore and Delgutte 2010) that the strength of ITD coding (as measured by mutual information between firing rate and ITD) for broadband noise is nearly constant across the tonotopic axis of the IC.

Comparison of neural and psychophysical thresholds.

Similar to our analysis of psychometric functions, we determined threshold durations for detection and direction identification by fitting a sigmoid curve to the neurometric function. We did this only for neurons that performed at or above 75% correct for the longest sweep duration (direction identification: n = 32 neurons; detection: n = 33 neurons). Despite the large spread in threshold durations for both tasks, the median neural thresholds for detection were significantly lower than thresholds for direction identification (median direction identification threshold = 191 ms, median detection threshold = 73 ms; Mann–Whitney U test: U = 1208, P = 0.0032; Fig. 12A). There were 21 neurons that reached performances at or above 75% correct for both direction identification and detection (Fig. 12B). The difference in threshold durations for detection and direction identification for this subset of neurons did not quite reach statistical significance (Wilcoxon signed-rank test: W = 167, P = 0.073), and there was no correlation between thresholds for the two tasks (Kendall’s tau: τ = −0.12, P = 0.46), suggesting that different factors limit performance.

Fig. 12.

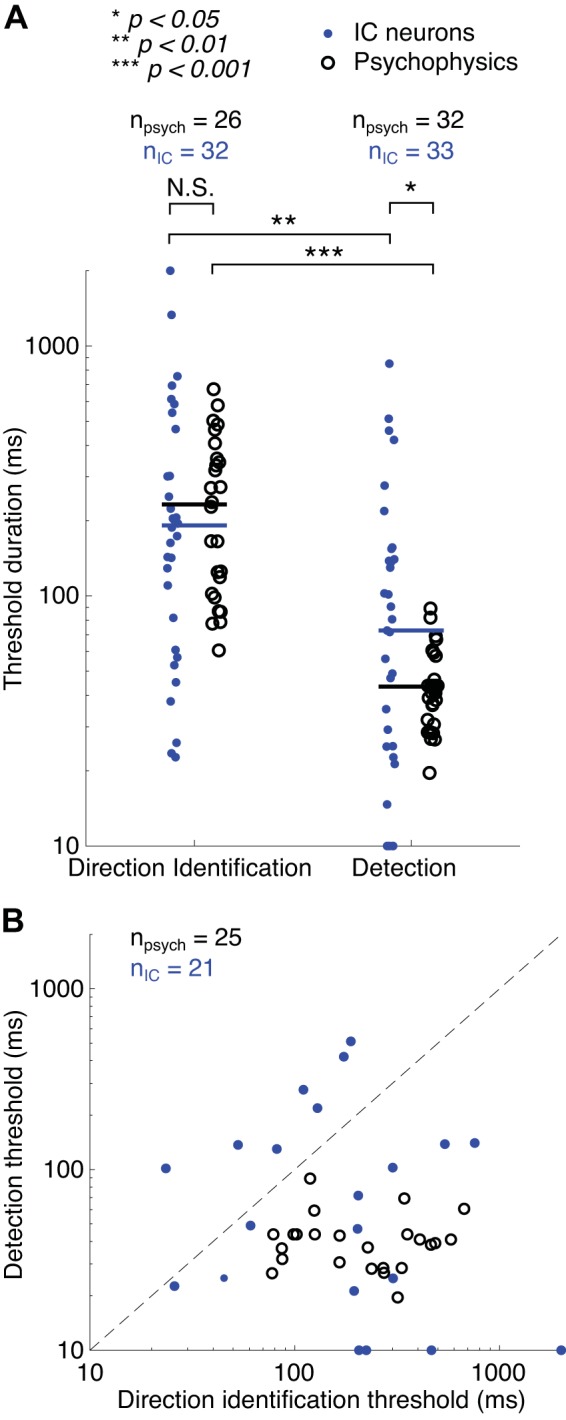
A: distribution of psychophysical (black circles) and single-neuron (blue dots) threshold duration for direction identification and detection. Psychophysical thresholds shown are identical to those in Fig. 3D. Neural and psychophysical thresholds were only determined if the %correct was at or above 75% for the longest sweep duration. Significance values are based on a Mann–Whitney U test. B: thresholds for direction identification plotted against detection thresholds for individual neurons (blue dots) and individual participants (black circles). Psychophysical data are identical to those in Fig. 3E. n_IC, number of inferior colliculus (IC) neurons; n_psych, number of participants; N.S., not significant.

We then compared the neural threshold durations and slopes with those calculated from the psychometric functions in the human perceptual experiments. There was no significant difference between the neural and psychophysical thresholds for direction identification (U = 909, P = 0.59), but median neural thresholds were significantly higher than median psychophysical thresholds for detection (U = 1202, P = 0.03; Fig. 12A). Neurometric slopes were significantly shallower than psychometric slopes for both tasks (direction identification: U = 651, P < 0.001; and detection: U = 884, P = 0.007), as found in other studies (Tolhurst et al. 1983; von Trapp et al. 2016).

The overlap between neural and psychophysical thresholds suggests that temporal coding in IC neurons may limit motion direction identification in humans. Although the average response of IC neurons could follow the instantaneous ITD quite well even at the shortest sweep durations, performance in direction identification did degrade at short sweep durations. This degradation in performance is due to neural noise limiting the classifier’s ability to identify the motion direction from single-trial neural responses. For short sweep durations, neurons fire fewer spikes during the sweep, and the inherent variability in firing makes the responses less reliable for both tasks.

DISCUSSION

We recorded from single units in the IC of unanesthetized rabbits in response to broadband noises containing a segment with linearly time-varying ITD (ITD sweep). We also asked human participants in two separate tasks to identify the motion direction of the ITD sweeps and detect the sweeps. We found that IC neurons responded dynamically to the ITD sweeps and that their responses were dominated by their ability to follow the instantaneous ITD rather than by true direction selectivity. Optimal classifiers that used the single-trial responses of individual neurons to identify the direction of the ITD sweeps exhibited similar threshold durations to the human participants, even though the neurons could still track the instantaneous ITD for sweep durations shorter than psychophysical thresholds when the responses were averaged across stimulus trials.

We used a point-process GLM to quantitatively characterize how the time-varying firing rate of IC neurons depends on the ITD sweep stimuli and previous spiking history. GLMs are increasingly used in studies of auditory neurons with the goal of improving estimates of spectrotemporal receptive fields by incorporating the effects of spiking history (Calabrese et al. 2011; Carruthers et al. 2013; Jenison et al. 2015; Siahpoush et al. 2015; Steinberg et al. 2013). We also included a spiking history component in our GLM with the goal of separating genuine direction selectivity from the effects of firing rate adaptation. This goal was only partly met because the spiking history component only captured adaptation occurring on a short timescale, perhaps related to neural refractoriness. In general, a model dependent on spiking history cannot capture forms of adaptation related to the dynamics of subthreshold events.

A major advantage of point-process GLMs is that the same mathematical framework can be used to describe both how sensory stimuli are encoded in neural response and how stimulus information can be decoded from neural activity (Paninski 2004; Paninski et al. 2007; Truccolo et al. 2005). We used the best-fitting GLM to implement an optimal neural classifier that predicted performance in sweep detection and direction identification based on single-trial responses. To our knowledge, this is the first application of point-process GLMs to a dynamic spatial hearing task. Our approach is similar to that of Goldwyn et al. (2010), who used a point-process GLM to predict the detection thresholds for amplitude modulation based on spike trains generated by a model of auditory nerve activity.

We found that a point-process model incorporating an ITD-following component but no direction selectivity matched the response for nearly all neurons better than a model with direction selectivity and no ITD following, suggesting that neurons primarily responded by following the ITD. Furthermore, the neurons that produced the best performance for direction identification were usually neurons with monotonic static ITD tuning curves within the range of the ITD sweeps, again suggesting that ITD following is dominating performance for direction identification. The direction selectivity components in our model appeared to capture slower forms of adaptation in several neurons rather than true direction selectivity. Still, it is unlikely that direction-selective responses in the IC play a major role in inferring the trajectory of the ITD sweeps.

The average time-varying firing rate of many IC neurons could follow the ITD of the sweeps at the shortest sweep durations tested but could not be used reliably for direction identification when the classification was based on single-trial responses. Joris (2019) similarly found that IC neurons in anesthetized cat could, on average, maintain their ITD tuning even at very fast ITD motion speeds. Additionally, the firing rates of his neurons increased with the speed of the ITD, which agrees with our finding that the gain of the ITD-following component increases with increasing sweep rate. Joris argued that neurons could follow the ITD up to the highest speeds measured in their study, 128,000 μs/s, which is well above the maximum speed used in this study (19,200 μs/s). However, in an earlier study (Zuk and Delgutte 2017), we found that most IC neurons were unable to track triangular modulations in ITD for modulation frequencies of 128 and 256 Hz, which, for an ITD span of 600 μs, correspond to ITD motion speeds of 153,600 and 307,200 μs/s, respectively, showing that there is indeed a limit to the rates of change in ITD that IC neurons can track. Because the stimuli in Joris (2019) were isolated ITD sweeps, the apparent modulation of responses by ITD at high rates could have been exaggerated by the presence of a prominent onset response (see Fig. 2, D and E, in Joris 2019, for example). Onset responses are not an issue in the present study, because our ITD sweeps were flanked by uncorrelated noise, and it not an issue in the Zuk and Delgutte (2017) study, which used 5 s of continuous noise with modulated ITD. Importantly, we also found in the present study that although IC neurons were able to track our fastest ITD sweeps, neural noise appeared to limit the ability to extract directional information about the ITD sweeps, resulting in neurometric thresholds that did not significantly differ from psychometric thresholds for direction identification.

We used responses of individual neurons to compute neurometric thresholds for the direction identification and detection tasks. However, it is unlikely that the participants in our study were using just one IC neuron to perform the task, but instead they probably “pooled” together information from multiple neurons. This may be especially true for the sweep detection task, where the median neurometric threshold was significantly higher than the median psychometric threshold. When information from multiple neurons is pooled, performance of optimal classifiers generally improves (Delgutte 1996; Green 1958; Parker and Newsome 1998). Performance gains from pooling can be limited by correlations in neural noise between pairs of neurons, also called noise correlations (Averbeck et al. 2006). Based on a few studies in anesthetized animals (Belliveau et al. 2014; Garcia-Lazaro et al. 2013), noise correlations in the IC appear to be small and thus would only limit the information gained by pooling over large numbers of neurons. Also, information may be pooled across IC neurons but may be further degraded in the thalamus or cortex. Understanding how single-neuron information can be used to perform a task is essential for understanding how information is encoded in the brain (Parker and Newsome 1998), but how this information may be pooled across neurons is still an active area of research (Averbeck et al. 2006; Kohn et al. 2016; Nienborg et al. 2012).

The range of neural and psychometric threshold durations for direction identification has important implications for the coding of time-varying ITD. Natural head rotations can reach angular velocities of up to 400 deg/s (Carriot et al. 2014), which, assuming 10-μs ITD per degree at the front of the head (Kuhn 1977), correspond to ITD speeds of 4,000 μs/s. This is well within the range of ITD speeds used in our study, and it is also within the range of neurometric and psychometric thresholds for direction identification that we observed on average (a threshold sweep duration of 125–250 ms corresponds to ITD motion speeds of 2,400–4,800 μs/s). Several studies have suggested that the temporal precision of firing in the IC allows neurons to respond to time-varying binaural cues, such as changes in interaural correlation, faster than humans can detect them psychophysically (Joris 2019; Joris et al. 2006; Shackleton and Palmer 2010; but see Siveke et al. 2008; Zuk and Delgutte 2017). Some of our neurons had threshold durations for direction identification and detection that were shorter than the human thresholds, suggesting that direction identification and detection may be suboptimally coded. However, the optimal classifier we used to derive neural thresholds requires implicit knowledge of the time-dependent probability of firing for every sweep duration and direction, and thus may be too complex (or too specialized) to be implemented neurally. Alternatively, our human participants received very little training, and training has been shown to greatly improve direction identification of moving sounds (Perrott and Marlborough 1989; Strybel et al. 1992). With additional training, it is possible that participant performance would improve to levels close to the best-performing neurons.

The average psychophysical thresholds we observed were 232 ms for direction identification and 43 ms for detection. Neural thresholds were similar (191 ms for direction identification and 73 ms for detection), and although we did find a significant difference between psychometric and neurometric detection thresholds, there was considerable overlap between the distributions of neurometric and psychometric thresholds for both tasks. The median neurometric thresholds are within the range of thresholds observed in other studies. Lüddemann et al. (2016) cited “binaural integration times” (the perceptual temporal integration window used to identify changes in interaural correlation), between 50 and 210 ms across various studies. They argued that the variation across studies may be largely explained by task differences. In tasks involving direction identification or motion detection relative to a stationary sound, threshold durations were 100–200 ms (Grantham 1986; for review see Carlile and Leung 2016). In contrast, when subjects had to detect changes in interaural correlation, binaural integration times were shorter: 20–40 ms for an interaurally coherent target flanked by uncorrelated noise, and 2–8 ms for an uncorrelated target flanked by correlated noise (Akeroyd and Summerfield 1999; Boehnke et al. 2002; Lüddemann et al. 2016). The difference in threshold durations that we observed between the two tasks supports the view that the variability in binaural integration times is due in part to task differences.

Our present focus was on manipulating ITD to examine motion direction identification without monaural changes in loudness, but motion direction can be identified monaurally in free field, when other localization cues involving time-varying sound level (such as interaural level differences, ILD) are present (Harris and Sergeant 1971). Auditory motion aftereffects are stronger when the adapting stimulus is a time-varying ILD instead of an ITD sweep (Carlile and Leung 2016), which suggests that neural direction selectivity may be stronger when both ITD and ILD are present.

Grantham (1986) suggested that the auditory system detects motion by taking “snapshots” of the moving sound at two different times and identifying the difference between the two locations in each snapshot (see also Middlebrooks and Green 1991). Our results are consistent with this hypothesis. Neural responses in the IC are dominated by ITD following rather than direction selectivity, so it is possible that a higher area of the brain is determining the direction of motion by comparing the firing rates of the neurons at two different points in time. There is some evidence that higher order cortical areas in humans, such as the medial temporal area, are direction selective, because auditory motion direction can be decoded from functional MRI activity in these areas (Jiang et al. 2014, 2016; for review see Chaplin et al. 2018). It is possible that this comparison occurs somewhere between the IC and the cortex, but even in the primary auditory cortex of macaques, direction selectivity in single neurons appears to be fairly weak (Ahissar et al. 1992; Scott et al. 2009). Thus exactly where the decoding of motion direction occurs is still unclear.

Our results demonstrate that the differences in threshold durations between ITD sweep direction identification and detection are consistent with differences in optimum classifier performance with the use of single-neuron responses in the IC. The coding schemes described in this report may be relevant not only to the perception of moving sounds but also for detecting glimpses of objects of interest in complex auditory scenes.

GRANTS

This work was supported by NIH Grant R01 DC002258, and by an Amelia-Peabody Scholarship from Massachusetts Eye and Ear.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

N.J.Z. and B.D. conceived and designed research; N.J.Z. performed experiments; N.J.Z. analyzed data; N.J.Z. and B.D. interpreted results of experiments; N.J.Z. prepared figures; N.J.Z. drafted manuscript; N.J.Z. and B.D. edited and revised manuscript; N.J.Z. and B.D. approved final version of manuscript.

APPENDIX A: IMPLEMENTATION OF THE GENERALIZED LINEAR MODEL

The time-varying firing rate λ (a.k.a. conditional intensity function) of the GLM for ITD sweep and 0-ITD stimuli has the form

$$\begin{array}{c}\lambda \left(t,d\text{|}\theta \right)=\exp \left(w_{ITD}\left[ITD\left(t\right)\right]+g_{ITD}\left(d\right)+DIR\times \left\{w_{DIR}\left[ITD\left(t\right)\right]+g_{DIR}\left(d\right)\right\}+{\displaystyle \sum }_{u=1}^U{h}_u{n}_{t-u}\right)\end{array}$$ (A1)

The rightmost term is the spike history component, which weights each of the spike counts n_t−u in 1-ms bins at time lags up to U = 300 ms preceding the current time t, by the terms h_u. The terms w_ITD and g_ITD specify the ITD-following component. Due to the fundamental property of exponentials, this component is the product of an ITD-dependent term defined by w_ITD and a duration-dependent gain defined by g_ITD. Similarly, w_DIR and g_DIR define the direction selectivity component. The ITD-dependent weights are only defined for a discrete set of ITDs, specifically −300, −150, 0, +150, and +300 μs. At times when the instantaneous ITD falls in between these discrete ITDs, w_ITD and w_DIR are determined using linear interpolation. The direction selectivity component is multiplied by the sign of the motion direction (DIR), which is +1 for a positive-going sweep, −1 for a negative-going sweep, and 0 for the 0-ITD stimulus. The exponential in Eq. A1 ensures that the model’s instantaneous firing rate is always nonnegative and also that the GLM has a unique minimum for the parameter vector (Hastie et al. 2009; McCullagh and Nelder 1989).

The logarithm of the time-varying firing rate in response to the interaurally uncorrelated noise segments preceding and following each sweep (or 0-ITD stimulus) was fit by the sum of a constant term for the interaurally uncorrelated noise (w_Uncor) and the same spike history weights as in Eq. A1: λ_uncor = exp(w_Uncor + Σh_un_t−u).

Overall, the set of parameters θ includes the 5 ITD-dependent weights each for ITD following (w_ITD) and direction selectivity (w_DIR), the 6 duration-dependent components each for ITD following (g_ITD) and direction selectivity (g_DIR), the weight for the uncorrelated noise (w_Uncor), and the 300 spike history weights (h). Thus the total number of free parameters (323) is very small compared with the dimensionality of the raw spike data.

Equation A1 uniquely specifies the variations in firing rate for both positive-going and negative-going sweeps. This can be observed by recognizing that the logarithm of the variation in firing rate as a function of ITD for the positive sweep (λ₊) is proportional to the sum of the ITD-following and direction selectivity weights, whereas the logarithm of the firing rate for the negative sweep (λ₋) is proportional to their difference:

$${\lambda }_{+}\left(t,d\text{|}\theta \right)\propto \text{exp}\left[(w_{ITD}+g_{ITD}\right)+\left(w_{DIR}+g_{DIR}\right)]$$

$${\lambda }_{-}\left(t,d\text{|}\theta \right)\propto \text{exp}\left[(w_{ITD}+g_{ITD}\right)-\left(w_{DIR}+g_{DIR}\right)]$$

By the fundamental property of exponentials, Eq. A1 can be rewritten as the product

$$\begin{array}{c}\lambda \left(t,d\text{|}\theta \right)=\exp \left(w_{ITD}\right)\times \exp \left(g_{ITD}\right)\times {\left[\exp \left(w_{DIR}\right)\times \exp \left(g_{DIR}\right)\right]}^{DIR}\times \prod \text{exp}(h_u{n}_{t-u})\end{array}$$ (A2)

In this form, it is clearer that the ITD-dependent weights for ITD following (w_ITD) capture the one-to-one mapping between the instantaneous ITD and the neuron’s probability of firing, and for clarity we express these weights in spikes per second (Figs. 6B and 7B). This firing rate is modulated by a duration-dependent gain, g_ITD. The direction selectivity components multiplicatively enhance or suppress the instantaneous firing rate of the neuron, depending on the direction of the sweep.

Model fitting.

The model parameters were fit in three steps. First, the response latency was estimated by first computing a temporal filter that modeled the firing rate following a step change from uncorrelated noise to 0-μs ITD and then finding the filter delay with the maximum weight (or minimum weight for a decrease in firing rate). In subsequent modeling steps, the stimulus vector ITD(t) was shifted by this measured response latency. Next, the model was fit to the responses to all 0-ITD stimuli simultaneously (6 durations, 10–15 trials), which determined w_Uncor and h. Importantly, the transitions from uncorrelated noise to 0-ITD segments and back produced substantial firing rate adaptation that was important in estimating the history term h. Finally, the remaining components, w_ITD, g_ITD, w_DIR, and g_DIR were estimated by fitting the model simultaneously to the responses to ITD sweeps for all sweep directions and durations while holding w_Uncor and h at their previously fitted values. In doing so, we assume that the intensity function for the uncorrelated noise and the history component are invariant to the sweep duration and ITD motion direction. All model fitting was done on the spike times binned at 1 ms to ensure that there would be at most one spike in each bin, which is a fundamental assumption of the point-process GLM. To prevent overfitting, we used elastic-net regularization, which enforces sparsity of the parameters in the model, setting unused parameters to zero, while still limiting magnitudes of the used parameters as in ridge regression (lassoglm function in MATLAB, see Friedman et al. 2010; Zou and Hastie 2005). Across neurons, the optimal regularization constant ranged from 10⁻⁶ to 10⁻⁴ for both the 0-ITD stimulus fitting and the ITD sweep fitting.

APPENDIX B: EVALUATION OF GOODNESS-OF-FIT

We assessed the goodness of fit of the model using the time-rescaling test (Brown et al. 2002; Truccolo et al. 2005) as modified by Haslinger et al. (2010). This is a direct test of goodness-of-fit for point-process models that, unlike methods based on the PST histogram, accounts for the effects of spike history. Specifically, the ISIs were rescaled by the monotonic transform

$$z_i=1-\exp \left[-{\displaystyle \underset{t=s_{i-1}}{\overset{s_i}{\int }}\lambda (t,d|\theta )dt}\right]$$ (A3)

In Eq. A3, the model’s time-varying firing rate is integrated from the previous spike time s_i−1 to the current spike time s_i. We then simulated a set of time-rescaled ISIs by generating spikes for 750 stimulus trials using the model. If the model’s time-varying firing rate properly captures the variation in firing rate in the data, the measured distribution of z_i should be no different than the simulated distribution (Haslinger et al. 2010). We thus assessed the goodness of fit using a Kolmogorov–Smirnov test comparing the cumulative distribution function of z with the simulated distribution (Fig. A1A). The goodness of fit was evaluated for each ITD sweep stimulus independently (Fig. A1B).

Using a significance criterion of P < 0.01 for the time-rescaling test, most of the neurons failed for at least one of the sweep conditions (49/62 of the neurons), but many of them did not have very many failures (Fig. A1C). All population analyses reported in this article used a subset of 49/62 neurons that had 5/12 or fewer failures. Including a stimulus-dependent time lag component (e.g., Weber and Pillow 2016; Williamson et al. 2016) may further improve the model fit for the high-firing neurons and better separate true direction selectivity from adaptation.

APPENDIX C: LIKELIHOOD RATIO TESTS FOR COMPARING THE REDUCED MODELS WITH EACH OTHER AND WITH THE FULL MODEL

In addition to the full GLM comprising three components (ITD following, direction selectivity, and spiking history), we implemented three reduced models in which one of the components was set to a constant. In the no-direction-selectivity model, the direction selectivity component weights and gains were removed. In the no-ITD-following model, the ITD-following component was replaced by a single constant representing the average firing rate. In the no-spiking-history model, the history terms h were removed.

To quantitatively assess which of the no-ITD-following and no-direction-selectivity models best accounts for the neural responses, we computed the likelihood of the observed spike trains, defined by a Poisson distribution, given each reduced model for each stimulus trial and each ITD sweep stimulus:

$$\begin{array}{c}l\left(n\text{|}\lambda \right)={\displaystyle \prod }_t\frac{{\lambda }_t^{n_t}{e}^{-{\lambda }_t}}{n_t!}\end{array}$$ (A4)

where λ_t is the time-varying firing rate of the model at time t, and n_t is the observed spike count at time t. The likelihoods for the different stimulus trials and for the positive- and negative-going sweeps were all multiplied together to get the overall likelihood for each sweep duration. We then calculated the likelihood ratio (LR) between the no direction selectivity model and the no ITD-following model:

$$\begin{array}{c}LR=\frac{l\left(n\text{|}{\lambda }_{no\_DIR}\right)}{l\left(n\text{|}{\lambda }_{no\_ITD}\right)}\end{array}.$$ (A5)

A likelihood ratio >1 implies that the no direction selectivity model captures the timing of spikes better than the no ITD-following model.

We also implemented likelihood ratio tests to determine whether the full model with three components produced a significant improvement in goodness of fit over each of the three reduced models. For each reduced model, we calculated the likelihood ratio statistic, which has a chi-squared distribution (Wilks 1938):

$$\begin{array}{c}{\chi }^2=-2\log \left[\frac{l\left(n\text{|}{\lambda }_{reduced}\right)}{l\left(n\text{|}{\lambda }_{full}\right)}\right]\end{array},$$ (A6)

where λ_reduced is the time-varying firing rate of the reduced model (either the no-ITD-following model, no-direction-selectivity model, or no-spiking-history model), and λ_full is the time-varying firing rate for the full model. If the likelihood ratio statistic for the no-direction-selectivity model is significantly greater than 0, then the direction selectivity component contributes significantly to the overall fit of the model. Likewise, if the likelihood ratio statistic for the no-ITD-following model is significant, then the ITD-following component significantly contributes to the model fit. Finally, if the likelihood ratio statistic for the no-spiking-history model is significant, then the spiking history component significantly contributes to the model fit. For population analysis, we looked at the number of neurons with likelihood ratio statistics that were significant relative to a chi-squared distribution with P < 0.001.

APPENDIX D: MAXIMUM-LIKELIHOOD NEURAL DECODERS FOR DIRECTION IDENTIFICATION AND SWEEP DETECTION

We implemented a maximum-likelihood neural decoder that classified the sweep direction based on the response of one neuron to one stimulus trial. The procedure was iteratively repeated for all trials to obtain a percent correct score for each neuron and each sweep duration.

For each sweep duration, the GLM was fit to the responses to positive-going sweeps, negative-going sweeps, and 0-μs ITD stimuli with one trial of each stimulus left out. With the fitted model, a new spike train was synthesized by stepping through each time bin, from 450 to 2000 ms following stimulus onset, and computing spike times from the intensity function, λ(t), taking prior spiking history into account. The average time-varying firing rate of the model, Λ(t), was computed by iteratively regenerating the time-varying firing rate and spike trains 500 times and averaging the rates:

$$\begin{array}{c}\Lambda \left(t\right)=\frac{1}{M}{\displaystyle \sum }_{m=1}^M\lambda \left(t\text{|}{\tilde{\theta }}^m\right)\end{array},$$ (A7)

where ${\tilde{\theta }}^m$ includes the history of simulated spikes generated on iteration m in addition to ITD-following and direction selectivity, and M = 500. We computed the average time-varying firing rate for each sweep direction [Λ₊(t) for positive-going sweeps and Λ₋(t) for negative-going sweeps].

We then scored the response in the left-out trial based on its similarity to the model’s average response to each sweep direction by computing the log of the likelihood ratio of the spike train for the left-out trial given the average model responses for each of the sweep directions. This procedure implements the optimal classifier for a one-interval, two-alternative forced choice task (Green and Swets 1988). The log of the likelihood ratio was computed by

$$\begin{array}{c}Scor{e}_{DIR}=\log \left[p\left(n{\text{|Λ}}_{+}\right)\right]-\log \left[p\left(n\text{|}{\Lambda }_{-}\right)\right]\end{array}$$ (A8)

where n is the array of spike counts in 1-ms bins for the left-out trial, and the likelihood of n given the average time-varying firing rate is

$$\begin{array}{c}p\left[n\text{|Λ}\left(t\right)\right]={\displaystyle \prod }_t\frac{\text{Λ}{\left(t\right)}^{n_t}\hspace{0.17em}\exp \left[-\text{Λ}\left(t\right)\right]}{n_t!}\end{array}$$ (A9)

where n_t is the spike count at time t. Each trial was then classified as a positive-going sweep if the score was ≥0 and a negative-going sweep otherwise. This score was determined as correct or not depending on whether it matched the stimulus actually presented on the left-out trial, and percent correct performance was computed by repeating this procedure for all trials (typically 20–30 trials).

The implementation of the neural classifier for sweep detection was similar to that for direction identification, with modifications to account for the fact that the psychophysical detection task used a two-interval paradigm, whereas the direction identification task used a single interval. First, we picked one trial containing a sweep in either direction (n₁) and one trial containing interaurally uncorrelated noise (n₂). Next, we computed the average response of the model for both sweep directions [Λ₊(t) and Λ₋(t)] as well as the average response to interaurally uncorrelated noise [Λ_uncor(t)]. The average time-varying firing rates were generated based on model fits to all stimulus trials except the selected pair of trials. For each interval, we then computed the likelihoods of the observed spike counts n₁ and n₂ given each average time-varying firing rate as described above. The score for sweep detection was given by

$$\begin{array}{c}Scor{e}_{DET}=\log \left(\frac{\left\{p\left[n_1\text{|}{\Lambda }_{+}\left(t\right)\right]+p\left[n_1\text{|}{\Lambda }_{-}\left(t\right)\right]\right\}\times p\left[n_2\text{|}{\Lambda }_{unc}\left(t\right)\right]}{\left\{p\left[n_2\text{|}{\Lambda }_{+}\left(t\right)\right]+p\left[n_2\text{|}{\Lambda }_{-}\left(t\right)\right]\right\}\times p\left[n_1\text{|}{\Lambda }_{unc}\left(t\right)\right]}\right)\end{array},$$ (A10)

The detection score is equivalent to the likelihood ratio test for a two-interval, two-alternative forced choice task (Green and Swets 1988), where each interval is twice as likely to contain interaurally uncorrelated noise than either sweep direction and detection can be based on either a positive-going sweep or a negative-going sweep. This procedure was repeated for all possible pairs of trials (200–450 pairs) to obtain percent correct performance for each neuron and sweep duration.

Fig. A1.

A: the Kolmogorov–Smirnov (KS) statistic is equal to the maximum distance between the cumulative distribution function (CDF z_i) for the time-rescaled interstimulus intervals (ISIs) and the unity line. B: KS statistics from the time-rescaling test against sweep duration for positive-going sweeps (blue) and negative-going sweeps (red) for the neuron in Fig. 7. For this neuron, all of the KS statistics pass the test except for the statistic for the negative-going sweep at 31.25 ms. C: histogram of the number of neurons with 0–12 failures of the KS test for the positive-going sweeps (+sweep) and negative-going sweeps (−sweep) where 12 is the total number of stimulus conditions. All population analyses were based on neurons that failed the KS test 5 or fewer times, as designated by the dashed red line in the plot.