Electronic Medical Record Context Signatures Improve Diagnostic Classification using Medical Image Computing

Abstract

Composite models that combine medical imaging with electronic medical records (EMR) improve predictive power when compared to traditional models that use imaging alone. The digitization of EMR provides potential access to a wealth of medical information, but presents new challenges in algorithm design and inference. Previous studies, such as PheWAS (Phenome Wide Association Study), have shown that EMR data can be used to investigate the relationship between genotypes and clinical conditions. Here, we introduce PheDAS (Phenome-Disease Association Study) to extend the statistical capabilities of the PheWAS software through a custom Python package which creates diagnostic EMR signatures to capture system-wide comorbidities for a disease population within a given time interval. We investigate the effect of integrating these EMR signatures with radiological data to improve diagnostic classification in disease domains known to have confounding factors because of variable and complex clinical presentation. Specifically, we focus on two studies: (1) a study of four major optic nerve related conditions and (2) a study of diabetes. Addition of EMR signature vectors to radiologically-derived structural metrics improves the area under the curve (AUC) for diagnostic classification using elastic net regression, for diseases of the optic nerve. For glaucoma, the AUC improves from 0.71 to 0.83, for intrinsic optic nerve disease it increases from 0.72 to 0.91, for optic nerve edema it increases from 0.95 to 0.96, and for thyroid eye disease from 0.79 to 0.89. The EMR signatures recapitulate known comorbidities with diabetes, such as abnormal glucose but do not significantly modulate image-derived features. In summary, EMR signatures present a scalable and readily applicable.

I. Introduction

With the advent of digitization of medical records, extensive medical data are available to perform large-scale studies that were previously difficult to implement[1]. However, so-called “big data” analyses also present new challenges for consolidation of information and integration of newer methods with established practices in the medical image processing community.

For example, automatic detection and diagnosis systems have been developed for medical image processing [2], [3], brain tumor classification[4], detection of prostate lesions[5], risk assessment in traumatic brain injury[6], and detection of breast cancer[7], demonstrating that medical images contain quantitative diagnostic information. However, when physicians make diagnoses in practice, they integrate multi-modal patient information, including medical history, laboratory tests, medication exposures, etc. Because much of this information can be extracted computationally from the electronic medical record (EMR)[8]-[10], we propose using EMR-derived patient signatures alongside imaging data to improve the accuracy of image analysis.

Specifically, we build on the Phenome Wide Association Study (PheWAS) [11], [12] paradigm that identifies relationships between targeted genotypes and clinical phenotypes. The phenotypes are clinical diseases represented by codes derived from EMR billing codes such as the International Classification of Diseases, Ninth Revision (ICD-9) codes. ICD9 codes are hierarchical, with the three digits codes representing a major disease category, followed by a decimal or two to describe subtypes and specific symptoms. For example, Code 377 represents “Disorders of the optic nerve and visual pathway”; 377.0 represents “Papilledema”, a specific disorder of the optic nerve pathway; and 377.01 represents “Papilledema with decreased ocular pressure”. However, there are a few issues with the use of ICD9 codes directly for scientific research [13]. 1. The number of digits or the type of code used to describe a sign or symptom is inconsistent among doctors. 2. The hierarchical system here is designed such that there are multiple categories for common diseases and sometimes, just a single code for a complex disease—since they’re primarily designed for the purposes for measuring hospital utilization and billing[12]. To overcome these problems, Denny et al designed a conversion system from ICD9 codes to PheWAS codes such that the conceptual granularity of the codes is consistent across diseases with the help of medical experts[11]. PheWAS codes are widely used in genomic research and are generally considered an acceptable standard in medical conceptual categorization. In this work, we convert the ICD9 codes to PheWAS codes for EMR feature extraction. We developed a Python package that uses the same PheWAS-ICD-9 mappings to study the associations of these clinical phenotypes with a particular disease of interest [14]. We refer to this approach as a phenome-disease association study (PheDAS). With PheDAS, we isolate the phenotypes most associated with a disease group prior to the diagnosis of the disease. In other words, we develop an “EMR context signature” that consolidates a patient’s history of diagnoses and symptoms into a binary vector. We add this signature to radiological image features and evaluate the improvement it provides in disease classification.

We illustrate the PheDAS approach using two studies. In the first study, we evaluate the role of EMR context signatures in improving classification accuracy of four disease groups affecting the optic nerve: glaucoma, intrinsic optic nerve disease (optic neuritis and other optic nerve disorders), thyroid eye disease (TED), and optic nerve edema (papilledema and idiopathic intracranial hypertension). These groups were chosen because the conditions can present with similar initial symptoms and co-morbidities, making detection challenging. However, early classification and intervention are often needed to preserve visual function. Xiuya et al and Chaganti et al have also shown that visual function for these subjects is correlated with radiological features derived from computed tomography (CT) and magnetic resonance (MR) imaging [15], [16]. Herein, we evaluate the role of EMR context signatures in improving classification accuracy for each of the four disease groups. In the second study, we use EMR to extract the context signature of a well-defined disease, and assess the classification accuracy gained by integrating this with neuroimaging information. For this study, we examine diabetes in an aging population [17]. Symptomatic risk factors for diabetes are well understood, for example impaired glucose levels are highly predictive of future diabetes [18]. Recent studies have also shown that diabetes is mildly correlated with cortical and white matter signal changes and white matter hyper intensities in the brain[17], [19]. However, classification of diabetes based on imaging remains a harder problem, as it depends on various other issues such as variance in disease population, disease stage etc. We use EMR signatures and brain MRI data acquired in the aging study to investigate the classification accuracy for Diabetes.

II. METHODS

A. Glossary of terms

We use the following terms to disambiguate between the multiple levels of our study design:

• Study: An observational study of a group of individuals sharing similar type of data collected at the same center. Each study has one or more case-control experiments designed to compare subjects who have a disease and those who do not.

• Disease group: A clinical classification of individuals having a health condition.

• Control group: Individuals in a study that are not classified as belonging to a disease group are considered as the control group.

• Case-control experiment: An experiment within a study to compare a disease group with a control group.

• Dataset: A type of data collected within a study. Dataset E has a set of individuals with only EMR data, while dataset RE has a different set of individuals with both EMR and radiological imaging data.

• Class: An engineering term for group (disease or control). An individual’s class label is a categorical indicator of which class the patient belongs to. The algorithms presented fall under classification approaches in which a procedure is created to infer a class label for each subject.

• ICD-9 code: A code used to describe a diagnosis or a health problem as defined by the International Classification of Diseases version 9 (ICD-9). There are roughly ~15,000 ICD-9 codes defined.

• PheWAS code: A code based on hierarchical categorization of ICD-9 codes that describes a diagnostic “phenotype” by grouping a set of related ICD-9 codes. The ~15,000 ICD-9 codes are mapped to 1865 PheWAS codes [20].

• PheDAS: A phenome-disease association study, which is used to identify all the diagnostic phenotypes associated with a disease group.

• EMR context signature: A binary vector describing an individual’s history that is calculated using PheDAS.

B. Overview

We use data from two studies to evaluate the PheDAS framework (Table I). The first study, collected at Vanderbilt University Medical Center (VUMC), characterizes diseases of the optic nerve within four major disease groups: glaucoma, intrinsic optic nerve disease, thyroid eye disease and optic nerve edema. These diseases have a complex presentation, similar symptoms, and frequently co-occur. The control group for this study is a group of individuals with hearing loss who were chosen for having similar imaging data available. In the first study, we build classifiers to classify disease groups from control group. Additionally, we build a one v. all to classify each optic nerve disease group from the other optic nerve diseases.

TABLE I.

Overview of the data used and analyses performed from the two studies.

Center	Study 1: VUMC	Study 2: BLSA
Data
Study population	Individuals with disease codes for glaucoma, intrinsic optic nerve disease, thyroid eye disease, optic nerve edema. Individuals with hearing loss for controls.	Individuals from the Baltimore Longitudinal Study of Aging (BLSA).
Dataset E	ICD-9 codes and demographic data for 29,214 individuals from the study population collected over all visits.	ICD-9 codes and demographic data for 1,715 individuals from the study population collected over all visits.
Dataset RE	Computed tomography (CT) imaging of the eye orbit for 1,451 subjects along with ICD-9 codes for all visits, and demographic data.	Magnetic resonance imaging (MRI) of the brain of 124 subjects along with ICD-9 codes for all visits, and demographic data.
Analyses
Case-control experiments	Glaucoma vs. healthy control Intrinsic optic nerve disease vs. healthy control Thyroid eye disease vs. healthy control Optic nerve edema vs. healthy control Glaucoma vs. other Intrinsic optic nerve disease vs. other Thyroid eye disease vs. other	Diabetes vs. control

The second study uses data from the Baltimore Longitudinal Study of Aging (BLSA)[21], a study that collects longitudinal data of an aging population in order to examine changes in the brain as a person ages. In this study, our “treatment” group are individuals who were diagnosed with diabetes. The control group for this study is individuals in BLSA who had no diagnosis of diabetes. Since risk factors for diabetes are well understood, it is used as a validation for our method for deriving EMR phenotypes.

For each study, we examine two separate datasets: dataset E, which is a large EMR-only dataset and dataset RE, which is a smaller EMR and radiological dataset. Dataset E is used to identify EMR phenotypes that are most associated with a given disease group using PheDAS. These phenotypes are used to construct EMR context signatures in the dataset RE to evaluate additional predictive value that EMR data provides to imaging studies. X_E, an N₁ × P₁ matrix, is constructed using dataset E with demographic data and ICD-9 data, where N₁, is the number of subjects and P₁ is the number of significant EMR phenotypes identified. X_RE, an N₂ × P₂ matrix, is constructed using dataset RE which comprises of radiological imaging data and EMR data for both control and treatment groups, where N₂ is the number of subjects and P₂ is the number of parameters. X_RE can be written as,

$$X_{RE}=[X_{\mathit{Rad}}{X}_{\mathit{EMR}}]$$ (1)

where, X_Rad contains the radiological imaging features for all the subjects and X_EMR contains binary vectors describing the EMR context signature for all the subjects. N₁ equals 29,214 in study 1 and 1,715 in study 2. N₂ equals 1,451 in study 1, and 124 in study 2.

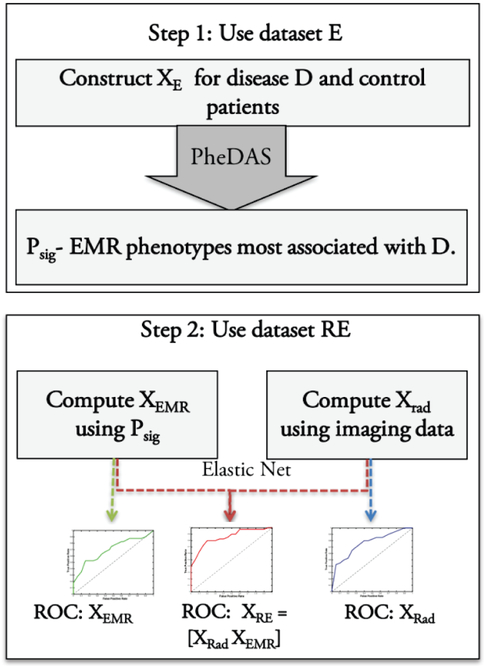
We conduct seven case-control experiments in study 1. The first four experiments, where each of the four disease groups is compared with controls. And an additional three experiments, where each disease group is compared with other disease groups in a one v. all fashion. We conduct one case-control experiment in study 2, comparing individuals with diabetes to those without the disease. The data for each case-control experiment is described in section 2C. The procedure for a case-control experiment is shown in Fig. 1. In the first step, we construct X_E from dataset E and use PheDAS to find the EMR phenotypes associated with the disease in the experiment as described in section 2D. In step two, we use dataset RE to construct radiological imaging features X_Rad, as described in section 2E and EMR context signature vectors X_EMR, as described in the end of section 2D. Finally, we evaluate the EMR context signatures X_EMR, the imaging features X_Rad, and the combination of the two, using an elastic net paradigm [22] as described in section 2F and constuct their Receiver Operating Characteristic (ROC) curves [23] for comparison.

Fig. 1.

Overview for each case control experiment. In step 1, the EMR phenotypes associated with disease D, P_sig are learnt from dataset E. In Step 2, EMR context signature vectors, X_EMR are calculated from P_sig and X_Rad is calculated from imaging. X_RE, X_Rad, and X_EMR are used to train an elastic net classifier and ROC curves are computed.

C. Data

1). Study 1: Diseases of the Optic Nerve

We collect ICD-9 codes, and demographic data for datasets E for each of the four disease groups and controls. For datasets RE, we collect computed tomography (CT) imaging of the eye orbit for each of the four disease groups and controls. The anonymized CT images were acquired clinically at Vanderbilt University Medical Center (VUMC) under varied settings and a wide range of scanners such as Phillips, Marconi, and GE (detailed acquisition parameters were not available). The CT imaging for disease population was acquired for subjects who have had an ICD-9 code belonging to one of the four main disease groups: glaucoma, intrinsic optic nerve disease, thyroid eye disease, and optic nerve edema. The detailed description of ICD-9 codes to identify a disease group is shown in Table II. The CT imaging for control subjects was acquired from subjects with hearing loss who had no other known vision problems as the clinical imaging protocols for these subjects was similar to the imaging acquired for those with optic nerve disorders in terms of acquisition parameters and field of view.

TABLE II.

Disease groups in Study 1 and the ICD-9 codes used to identify them

Disease group	ICD-9 codes
Glaucoma	365.0* (Borderline glaucoma), 365.1* (Open-angle glaucoma), 365.2* (Primary angle-closure glaucoma), 365.3* (Corticosteroid-induced glaucoma), 365.4* (Glaucoma associated with congenital anomalies, dystrophies, and systemic syndromes), 365.5* (Glaucoma associated with disorders of the lens), 365.6* (Glaucoma associated with other ocular disorders), 365.7* (Glaucoma stage, unspecified), 365.8* (Other specified forms of glaucoma), and 365.9*(Unspecified glaucoma)
Intrinsic Optic Nerve Disease	377.3* (Optic Neuritis), and 377.4* (Other disorders of optic nerve)
Optic Nerve Edema	348.2 (Idiopathic intracranial hypertension), 377.0 and 377.00 (Papilledema), 377.01 (Papilledema, increased intracranial pressure), and 377.02 (Papilledema, decreased ocular pressure)
Thyroid Disease	242.00 (Toxic diffuse goiter without thyrotoxic crisis or storm), 376.2 (Endocrine exophthalmos), 376.21 (Thyrotoxic exophthalmos), and 376.22 (Exophthalmic ophthalmoplegia)

For each disease group d, the counts and ages for datasets $X_E^{\{d\}}$, and $X_{RE}^{\{d\}}$, are shown in Table III, along with age-matched controls. The controls for $X_E^{\{d\}}$, are all individuals in study 1 who do not belong to disease group d, i.e. individuals belonging to other disease groups and hearing loss patients not included in $X_{RE}^{\{d\}}$. $X_E^{\{d\}}$ is used to learn EMR context signatures for each d.

TABLE III.

Average ages (in years) for control and disease population for Study 1 and Study 2.

Disease Group	Dataset E		Dataset RE (Disease vs. Healthy)		Dataset RE (Disease vs. Other)
	Control	Disease	Control	Disease	Control	Disease
Glaucoma	55.31±18.59 (n=11,474)	55.31±18.76 (n=11, 499)	56.12±17.6 (n=75)	56.2±17.67 (n=75)	58.10±9.40 (n=25)	58.12±9.76 (n=25)
Intrinsic Optic Nerve Disease	43.6±23.2 (n=2198)	43.55±23.24 (n=1, 099)	43.29±21.02 (n=135)	43.3±21.0 (n=135)	47.41±16.97 (n=27)	47.51±16.91 (n=27)
Optic Nerve Edema	28.32±19.09 (n=1604)	28.25±19.06 (n=802)	28.25±19.06 (n=115)	30.47±16.58 (n=115)	-	-
Thyroid Eye Disease	43.1±19.06 (n=3114)	43.32±18 (n=1557)	50.73±15.20 (n=40)	50.65±15.27 (n=40)	49.98±17.86 (n=15)	50.26±17.30 (n=15)

$X_{RE}^{\{d\}}$ is used to conduct two experiments to evaluate the predictive value of EMR and imaging data for each d:

1. Disease vs. healthy control subjects: The predictive value of EMR and imaging data is evaluated when compared to healthy control subjects. The controls for in this case are age-matched hearing loss patients. There are four case-control studies, one for each disease.

2. Disease vs. other disease groups: The predictive value of EMR and imaging data is evaluated when compared to subjects with other optic nerve diseases. The controls for this case are subjects who have never had disease d, but had one of the other three eye diseases. For example, subjects with glaucoma are compared with subjects who have never had glaucoma but had one of the following: intrinsic optic nerve disease, optic nerve edema or thyroid eye disease. In this category, subjects with optic nerve edema did not have enough age-matched controls, resulting in only three case-control studies.

Only ICD-9 codes recorded one year prior to of the diagnosis are included for both $X_E^{\{d\}}$, and $X_{RE}^{\{d\}}$.

2). Study 2: Diabetes

We collect ICD-9 codes, and demographic data for dataset E. For dataset RE, we collect magnetic resonance (MR) imaging of the brain for the disease group and controls along with ICD-9 codes.

The EMR dataset $X_E^{\{diab\}}$, has 245 patients with diabetes and 1470 age-matched controls, comprised of other subjects in the study without diabetes. The dataset with radiology data and EMR $X_{RE}^{\{diab\}}$, has 62 participants with diabetes and 62 age-matched controls. Their average ages are shown in Table III. Only ICD-9 codes recorded one year prior to of diagnosis are included for both $X_E^{\{diab\}}$ and $X_{RE}^{\{diab\}}$.

D. Phenome-Disease Association Study (PheDAS)

We use our custom package pyPheWAS to extract EMR context signatures as described in this section[14]. First, phenome-disease associations are identified from EMR dataset E as shown in Fig. 2, for each case-control experiment. Two tables are extracted from dataset E for each disease group and their respective controls. The first table contains the subject identifier and each ICD-9 recorded for that subject along with the date. The second table consists of demographic information for each subject including current age, diagnosis class (1=disease group, 0=controls), age of the subject at the diagnosis, and sex. Next, the data are right censored such that all the time points that occur up to t_c years before the diagnosis are eliminated, so that conditions that are temporally predictive of, or precursors to the diagnosis can be identified. In this paper. t_c = 1. The first table now contains only ICD-9 codes for visits before the diagnosis. The ages of the subjects are recalculated to reflect the censoring. Next, the ICD-9 codes are mapped to 1865 diagnostic phenotype codes or PheWAS codes as defined in Denny et al[11]. These codes are denoted by C, where C = {c_k∣k = 1 … 1865}. Next, the diseases and controls are age-matched in a 1:2 ratio, when available, i.e., for each subject in the disease group, two subjects in the control group are selected whose ages are within 2 years. For each subject, an aggregate measure, M_ck, of the PheWAS code c_k, is calculated. The PheDAS software supports computing M_ck by one of the following:

Fig. 2.

Process flow of PheDAS. ICD-9 data for each visit and class information is extracted from EMR in step 1. Next, the data is censored by eliminating visits up to t_c years before the time of diagnosis, t_dx. In step 3, ICD-9 codes are mapped to the PheWAS codes. In step 4, the data is age matched in 1:2 ratio with controls. In step 5, a logistic regression model is trained for each PheWAS code to determine if it is associated with the disease. In step 6, the EMR signature vector is constructed with conditions that are positively associated with the disease.

1. A binary variable, indicating presence or absence of the code in the subject’s history.

2. A count, indicating the number of times the code was recorded in the subject’s history.

3. Duration, indicating the time between the first time the code was recorded and the last time it was recorded.

In this paper, the binary measure is computed. Finally, the last recorded age of the subject for the given code, A_ck, is calculated. Sex is the only other covariate that is considered. From this data, X_E is given by,

$$X_E=[{\mathit{sex}}^{N_1\times 1}{M}_{c_1}^{N_1\times 1}{A}_{c_1}^{N_1\times 1}\dots M_{c_{1865}}^{N_1\times 1}{A}_{c_{1865}}^{N_1\times 1}{]}^{N_1\times P_1}$$

Each subject belongs to class 1 (disease) or 0 (control). Each diagnostic phenotype c_k is associated either with 1 or with 0 or is not associated with either. Logistic regression is used to determine the association between each c_k and the disease of interest:

$$\begin{gathered} p(\mathit{class}=\mathit{disease}\mid c_k)~\text{logit}({\beta }_{0_k}+{\beta }_{1_k}{M}_{c_k}+{\beta }_{2_k}{A}_{c_k}+ \\ {\beta }_{3_k}\mathit{sex}) \end{gathered}$$

The p-value of β_1k, the coefficient of the binary aggregate measure, is used to determine the significance of the association between the PheWAS code c_k and the diagnosis of the disease. The sign of the co-efficient determines the direction of the association. The threshold for significance, p_bh, is given by the false discovery rate[24]. The set of significant PheWAS codes that are positively correlated with the disease is given by C_sig = {c_k* ∣ p – value of β_1k* < p_bh and β_1k* > 0}. To illustrate this process, Fig. 3 presents C_sig for Glaucoma dataset, $X_E^{\{glauc\}}$.

Fig. 3.

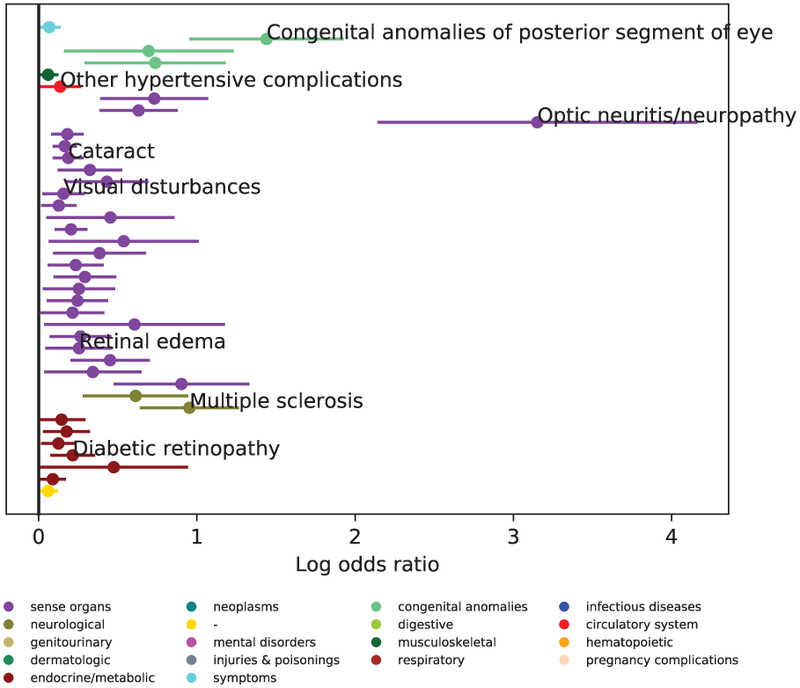
Example result of phenotype extraction. Shown here are all the positively correlated phenotypes with Glaucoma. A few key associations are labelled. The complete list of associated conditions is shown in Table B1 of the supplementary material.

Next, the ICD-9 codes are mapped to PheWAS codes in dataset RE of the as described above, for each disease group. The set of phenotypes positively associated with the disease D, C_sig, that was identified using dataset E is used to construct EMR context signature vectors X_EMR, from dataset RE (refer to equation (1)),

$$X_{\mathit{EMR}}={\left[\mathrm{sex}\mathrm{age}{M}_{c_{1^{\ast }}}^{N_2\times 1}{M}_{c_{2^{\ast }}}^{N_2\times 1}\dots \right]}^{N_2\times P_2}$$ (2)

where c_k* ∈ C_sig and $M_{c_{k^{\ast }}}^{N_2\times 1}$ is the binary vector of aggregate measures for c_k* for each of the N₂ subjects.

E. Image processing

1). Study 1: Diseases of the Optic Nerve

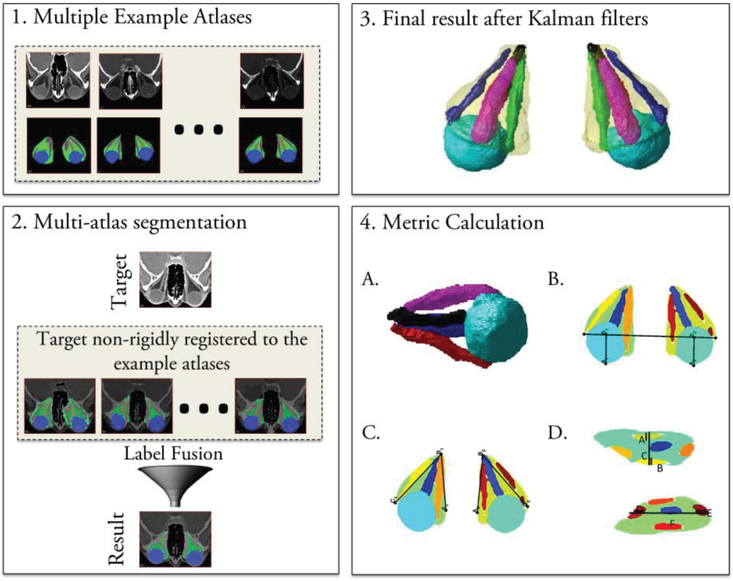
CT imaging from dataset RE is used in study 1 to extract radiological imaging features, X_Rad. Multi-atlas segmentation [25] is used to segment the optic nerve, globes, extraocular rectus muscles, and orbital fat from CT imaging, as illustrated in Fig. 4. A set of 25 example atlases with expertly marked labels for the orbital structures are used to segment the structures in a new target scan. First, the target image is registered to the example atlases to localize the eye orbit and crop it using a bounding box[26]. This is done since target atlases can have varying fields of view from a whole head scan to a scan limited to the eye orbit. A down-sampled version of the target image is used for this step since it is faster, and a rough registration is sufficient to identify a bounding box. Once the eye orbit is localized, the full-resolution images of the cropped target space are used. Next, the example scans are non-rigidly registered [27] to the cropped target space and the expertly labeled structures are propagated to the target space. The registered labels in the target space are combined using non-local statistical label fusion [28] to identify the globe, optic nerve, muscles, and fat. However, challenges arise in the identification of the individual extraocular rectus muscles that control eye movement. This is increasingly problematic in diseased eyes, where these muscles often appear to fuse at the back of the orbit (at the resolution of clinical computed tomography imaging) due to inflammation or crowding. Kalman filters are used to isolate the individual extraocular muscles from the muscle labels obtained from the multi-atlas segmentation pipeline as described by Chaganti et al[15]. We start at a coronal slice at the center of the globe, where the muscles are well-separated, and use Kalman filters to track each muscle in z-direction. After the segmentation, thirty-six volume, size and intensity metrics are calculated as described in Chaganti et al[15]. These orbital structural metrics included the (#1-#20) volume, maximum diameter, average diameter, median intensity, and interquartile range of the intensities for the superior, inferior, medial, and lateral rectus muscles and total rectus muscle volume; (#21) Barrett muscle index; (#22-#25) volume, diameter, median intensity and the interquartile range of the intensities of the globe; (#26) orbital volume; (#27) volume crowding index; (#28) orbital angle; (#29) degree of proptosis; (#30) length along the optic nerve, and (#31-#36) traditional length, volume, average area, maximum diameter, median intensity, and the interquartile range of intensities of the optic nerve. All structural metrics are computed bilaterally, and their mean is used for analysis. The radiological imaging data vector X_Rad, in equation (1) is formed from these metrics,

$$X_{\mathit{Rad}}=\left[{\mathit{sm}}_1^{N_2\times 1}{\mathit{sm}}_2^{N_2\times 1}\dots {\mathit{sm}}_{36}^{N_2\times 1}\right]$$ (3)

where, sm_k is the average of the k^th structural metric of the left and right eye.

Fig. 4.

Process flow of image segmentation for study 1. In the first block, a set of atlases along with expertly marked labels for multi atlas segmentation protocol are shown. In the second block, the multi-atlas segmentation process where each of the example atlases is non-rigidly registered to the target atlas, and the labels are propagated using this deformation are shown. Statistical label fusion is used to achieve the final labels. In the third block, the muscle label obtained from multi-atlas segmentation is further split into four extraocular rectus muscles using Kalman filters are shown. In the fourth block, the structural metrics calculated from the segmentation are shown.

2). Study 2: Diabetes

In study 2, X_Rad is calculated from segmented MR images of the brain as described in [29]. A multi-atlas segmentation paradigm is used for the segmentation. Briefly, scans are first affinely registered [30] to the MNI305 atlas[31]. Then, multi-atlas segmentation is performed on each subject. 45 MPRAGE images from OASIS dataset are used as original atlases which are manually labeled with 133 labels (132 brain regions and 1 background) by the BrainCOLOR protocol[32]. Multi-atlas segmentation produces regional masks for each of the 133 labels. The volume of each label, except the background, is computed by integrating the individual masks, and a radiological imaging data vector X_Rad, is formed,

$$X_{\mathrm{Rad}}=[{\mathrm{sm}}_1^{{\mathrm{N}}_2\times 1}{\mathrm{sm}}_2^{{\mathrm{N}}_2\times 1}\dots {\mathrm{sm}}_{132}^{{\mathrm{N}}_2\times 1}]$$

where, sm_k is the volume of the k^th brain region.

F. Classification

A binary classifier is trained on dataset RE for each case-control experiment to distinguish subjects belonging to the disease group from the control group. The data vector X_RE, is calculated from equations 2, 3, and 4 as follows,

$$X_{\mathit{RE}}=[X_{\mathit{Rad}}{X}_{\mathit{EMR}}{]}^{N_2\times P_2}$$

The relative performance of each of X_RE, X_Rad, and X_EMR is evaluated. For each X, we model

$$P(y_i=\mathit{disease}\mid X=x_i)=\frac{e^{{\beta }_0+{\beta }^T{x}_i}}{1+e^{{\beta }_0+{\beta }^T{x}_i}}$$

We use logistic regression with elastic net regularization[22]. The following penalized log likelihood function is minimized to derive the β for the logistic regression model,

$$\begin{gathered} \min -\left[{\sum }_{i=1}^N{y}_i({\beta }_0+{\beta }^T{x}_i)-\log (1+e^{{\beta }_0+{\beta }^T{x}_i})\right]+\lambda [(1 \\ -\alpha )\Vert \beta {\Vert }_2^2∕2+\alpha \Vert \beta {\Vert }_1] \end{gathered}$$

Here, α is fixed at 0.5, and λ that provides the optimal test error is selected. $\Vert \beta {\Vert }_2^2$ is the ridge penalty and ∥β∥₁ is the lasso penalty[33].

We use ROC curves to evaluate the performance of the model. We build the final model using all of the data, and the extra-sample ROC estimate is computed using bootstrapping for optimism correction[34]–[36]. The extra sample error is the generalization error of the model, which is estimated as described in this section.

From the original X^N₂×P₂, a sample, $X_s^{N_2\times P_2}$, of size N₂ is selected with replacement and the model is fitted to it. Let $X_s^{+}$ denote the positive class samples, and $X_s^{-}$ denote negative class samples of X_s. Let $X_{orig}^{+}$ denote the positive class samples, and $X_{orig}^{-}$ denote negative class samples of X. Let ${\widehat{f}}_s$ be the classification rule for the model fitted over the dataset X_s. The true and false positive rates, tpr_s,s(t) and fpr_s,s(t), of applying ${\widehat{f}}_s$ to X_s are calculated over thresholds t,

$$tp{r}_{s,s}(t)=\frac{1}{\mathit{size}(X_s^{+})}\sum _{x_i,y_i\in X_s^{+}}I({\widehat{f}}_s(x_i)\ge t),t\in [0,1]$$

$$fp{r}_{s,s}(t)=\frac{1}{\mathit{size}(X_s^{-})}\sum _{x_i,y_i\in X_s^{-}}I({\widehat{f}}_s(x_i)\ge t),t\in [0,1]$$

Similarly, the true and false positive rates, tpr_s,orig(t) and fpr_s,orig(t), of applying ${\widehat{f}}_s$ to X are calculated over thresholds t,

$$tp{r}_{s,orig}(t)=\frac{1}{\mathit{size}(X_{orig}^{+})}\sum _{x_i,y_i\in X_{orig}^{+}}I({\widehat{f}}_s(x_i)\ge t),t\in [0,1]$$

$$fp{r}_{s,orig}(t)=\frac{1}{\mathit{size}(X_{orig}^{-})}\sum _{x_i,y_i\in X_{orig}^{-}}I({\widehat{f}}_s(x_i)\ge t),t\in [0,1]$$

Now, we model all of the points in the original dataset X using elastic net regression to obtain a new classification rule, ${\widehat{f}}_{orig}$. Next, we calculate the apparent true and false positive rates, tpr_app(t) and fpr_app(t), of applying ${\widehat{f}}_{orig}$ to X. This would give an optimistic estimate, but we correct for that using the optimism correction approach[34]:

$$\begin{gathered} tp{r}_{\mathit{corrected}}(t)=tp{r}_{\mathit{app}}(t) \\ -\left(\frac{1}{{\text{num}}_{\text{bootstrap}}}\right)\sum _s\left(tp{r}_{s,s}(t) \\ -tp{r}_{orig,s}(t)\right),t\in [0,1] \end{gathered}$$

$$\begin{gathered} fp{r}_{\mathit{corrected}}(t)=fp{r}_{\mathit{app}}(t) \\ -(\frac{1}{{\text{num}}_{\text{bootstrap}}})\sum _s\left(fp{r}_{s,s}(t) \\ -fp{r}_{orig,s}(t)\right),t\in [0,1] \end{gathered}$$

The optimism corrected receiver operating characteristic curve is given by,

$$\mathit{ROC}(.)=\{(tp{r}_{\mathit{corrected}}(t),fp{r}_{\mathit{corrected}}(t))\mid t\in 0:0.01:1\}$$

The corrected area under the curve is calculated for the ROC using the trapezoidal rule[23].

III. RESULTS

A. Study 1: Diseases of the Optic Nerve

1). Case-control experiment: Glaucoma vs. healthy controls

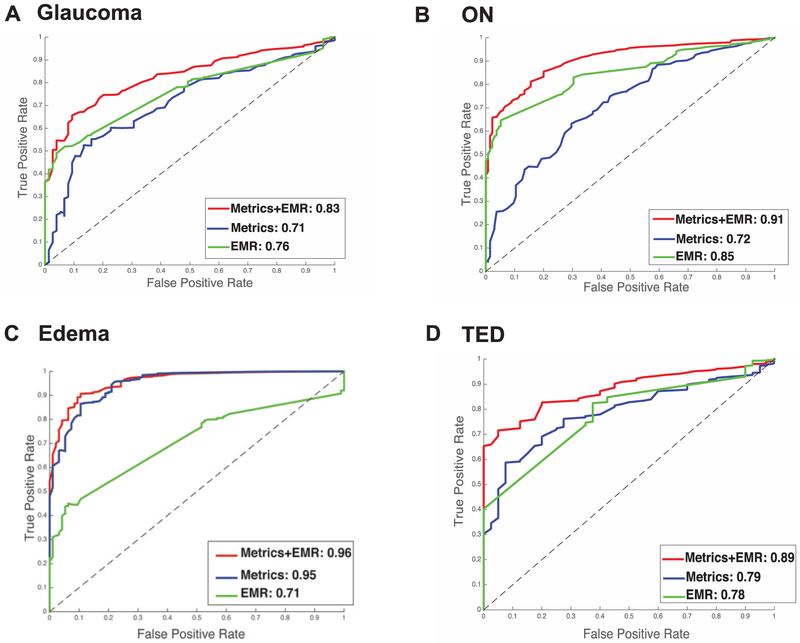
Structural metrics derived from CT imaging are moderately successful in distinguishing disease and control groups with an AUC of 0.71 (Fig. 5A). The EMR context signature vector results in slightly more successful prediction with an AUC of 0.76. However, the model that was built upon using both sets of data has much higher prediction accuracy, with an AUC of 0.83.

Fig. 5.

Disease vs. healthy control results of elastic net classifier for study. Green line indicates the curve for EMR data, blue line indicates the curve for imaging data, and the red line indicates the curve for EMR + imaging data.1. 5A. shows the result for glaucoma, 5B shows the result for intrinsic optic nerve disease, 5C shows the result for optic nerve edema, and 5D shows the result for thyroid eye disease.

2). Case-control experiment: Intrinsic optic nerve disease vs. healthy controls

Structural metrics derived from CT imaging are successful in distinguishing disease and control groups with an AUC of 0.72 (Fig. 5B). The EMR context signature vector results in an AUC of 0.85. The model that was built upon using both sets of data has higher prediction accuracy than either of the former models, with an AUC of 0.91.

3). Case-control experiment: Optic nerve edema vs. healthy controls

Structural metrics derived from CT imaging have a high AUC of 0.96 (Fig. 5C). The EMR context signature vector results in an AUC of 0.95. The model that was built upon using both sets of data has slightly higher prediction accuracy with an AUC of 0.96.

4). Case-control experiment: Thyroid eye disease vs. healthy controls

Structural metrics derived from CT imaging are successful in distinguishing disease and control groups with an AUC of 0.79 (Fig. 5D). The EMR context signature vector results in an AUC of 0.78. The model that was built upon using both sets of data has higher prediction accuracy than either of the former models, with an AUC of 0.89.

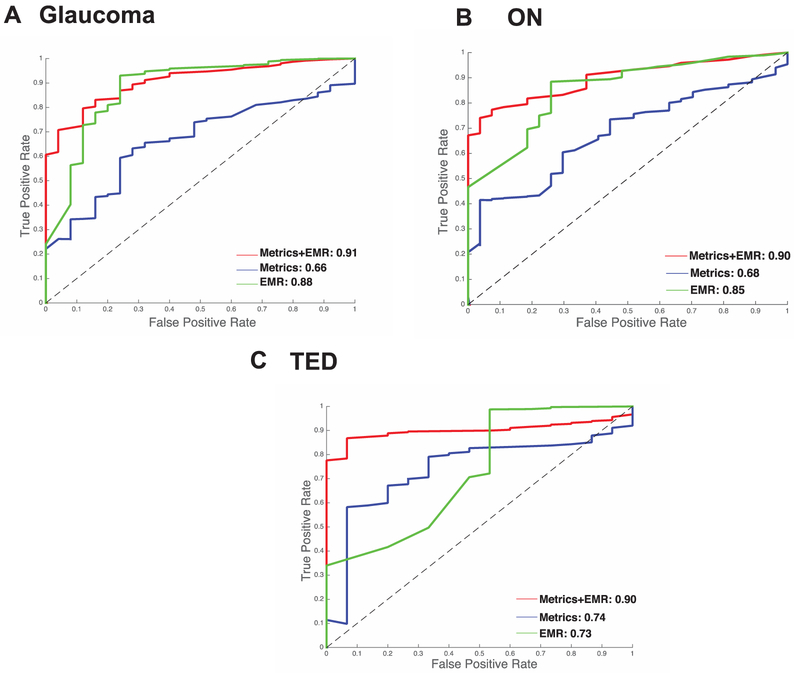
5). Case-control experiment: Glaucoma vs. other diseases

Structural metrics derived from CT imaging are mildly predictive in distinguishing disease and control groups with an AUC of 0.66 (Fig. 6A). The EMR context signature vector is more predictive with an AUC of 0.88. The predictive value of the combined model that was built using both sets of data has an improved prediction accuracy with an AUC of 0.91.

Fig. 6.

Disease vs. other results of elastic net classifier for study 1. Green line indicates the curve for EMR data, blue line indicates the curve for imaging data, and the red line indicates the curve for EMR + imaging data.1. 6A. shows the result for glaucoma, 6B shows the result for intrinsic optic nerve disease, 6C shows the result for thyroid eye disease.

6). Case-control experiment: Intrinsic optic nerve disease vs. other diseases

Structural metrics derived from CT imaging are mildly successful in distinguishing disease and control groups with an AUC of 0.68 (Fig. 6B). The EMR context signature vector results in an AUC of 0.85. The model that was built upon using both sets of data has higher prediction accuracy than either with an AUC of 0.90.

7). Case-control experiment: Thyroid eye disease vs. other diseases

Structural metrics derived from CT imaging are successful in distinguishing disease and control groups with an AUC of 0.74 (Fig. 6C). The EMR context signature vector results in an AUC of 0.73. The combined model has a much higher prediction accuracy than either with an AUC of 0.90.

B. Study 2: Diabetes

Structural metrics derived from MR are slightly better than chance, with an AUC of 0.58, as seen in Fig. 7. The EMR context signature vector has an AUC of 0.83. The model that was built upon using both sets of data does not select any imaging features in the elastic net model, and demonstrated an AUC of 0.85 using abnormal glucose as the only selected feature.

Fig. 7.

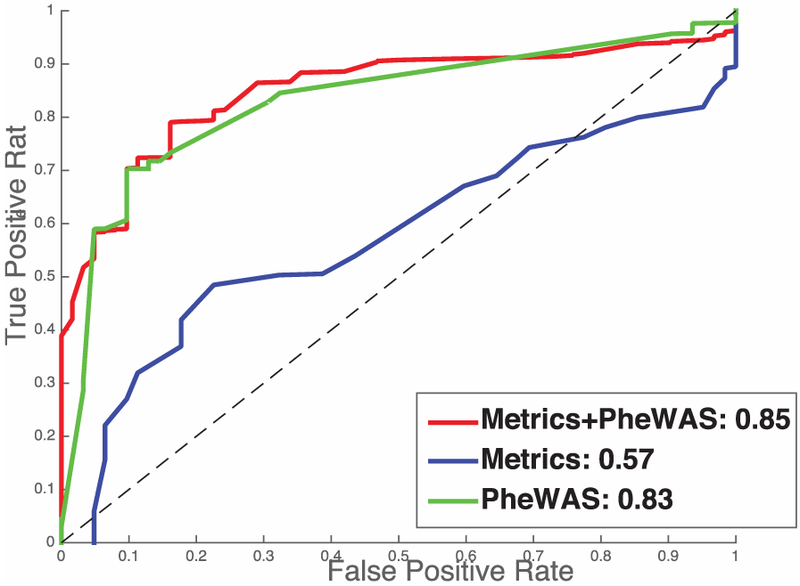
Results for study 2. Diabetes vs. controls.

IV. DISCUSSION

Although success has been reported in several studies that were able to train diagnostic classifiers using medical imaging data in various domains, these studies do not consider the variability of presentation in radiology due to individual patient histories. One way to circumvent this problem is to use data available in electronic medical records to develop context-based diagnostic classifiers. In this paper, we develop methods for multi-modal big data studies in medical image processing that use EMR information, i.e., data from medical images as well other EMR data such as ICD-9 codes. One of the challenging problems in such studies is to consolidate data from EMR records that can be integrated with imaging data. We develop PheDAS, a method to extract diagnostic phenotypes associated with a given condition and transform it into a binary EMR signature vector. In fact, our custom Python package provides provisions to transform the data using other aggregate measures such as counts of the diagnostic phenotypes, and duration of the diagnostic phenotypes [14].

Our main contribution in this paper is evaluation of these context-based diagnostic classifiers using two large-scale studies. In our two studies, we look at two different datasets: study 1 in which significant predictive value for imaging data is observed and study 2 in which the predictive value of imaging data is minimal. In study 1, we find that both structural metrics and PheWAS phenotypes are moderately successful in distinguishing disease groups from controls for diseases of the optic nerve. However, in all four of the disease groups, we saw that addition of the EMR context signature vectors increases the predictive power of the classifiers, making a strong case for context-based imaging studies that take into account the whole story of the patient with the help of information readily available in EMR. In study 2, which was considered to be our validation dataset to evaluate the EMR-phenotype extraction, abnormal glucose, the most important clinical predictor of diabetes[18], [37], is selected as the only predictor by our final model, thus validating the methodology. The context-based classifier for diabetes does not select any imaging features and shows a final AUC of 0.85 using abnormal as a sole feature.

Upon further evaluation of the EMR and imaging phenotypes identified in study 1, several findings align with those reported in medical literature. Thyroid eye disease is associated with a history of Grave’s disease, an autoimmune disorder that causes problems with thyroid regulation [38], [39]. The final model for thyroid eye disease selects phenotypes associated with thyroid imbalances such as hyperthyroidism. The imaging phenotypes selected in this model are proptosis, optic nerve length, and inferior muscle volume and diameter. According to radiology literature, these are some of the most distinct features of TED [40], [41] and inferior muscle is the most commonly affected muscle[42].

The final model for glaucoma identified systemic problems such as diabetes, hyperlipidemia, hypertension, and miscellaneous visual changes as the most predictive, which coincide with common glaucoma co-morbidities reported in medical literature [43]. The EMR context vector for intrinsic optic nerve disease shows a history of multiple sclerosis and other demyelinating diseases of the central nervous system as significant, which is reported widely in medical literature as well[44], [45]. For both glaucoma and intrinsic optic nerve disease the structural changes from imaging calculated in this study were shown to be predictive in differentiating the subject population from controls.

The optic nerve edema disease group consists of papilledema and idiopathic intracranial hypertension. Previous studies show that volumetric changes of the optic nerve are important features used for diagnosis of these conditions [46]–[49]. Our final model identified optic nerve volume, length and intensity, as some of the important predictors of this disease group, thereby achieving a very high AUC of 0.95. The systemic causes for idiopathic intracranial hypertension are not known [50]. The presentation is variable and is associated with other co-morbidities such as obesity, migraine, nausea, depression and so on. Our final model identifies these EMR features as significant, however they do not significantly improve the final prediction over imaging features. The reason for this could be that EMR features for this condition are inconsistent and variable, whereas imaging features are quite distinct and consistent across the subjects.

In future studies, we will develop methods to incorporate other data routinely available in EMR such as procedure codes and labs into the context vectors to develop comprehensive clinical decision support models.