Understanding the binding specificities of mRNA targets by the mammalian Quaking protein

Abstract

Mammalian Quaking (QKI) protein, a member of STAR family of proteins is a mRNA-binding protein, which post-transcriptionally modulates the target RNA. QKI protein possesses a maxi-KH domain composed of single heterogeneous nuclear ribonucleoprotein K homology (KH) domain and C-terminal QUA2 domain, that binds a sequence-specific QKI RNA recognition element (QRE), CUAAC. To understand the binding specificities for different mRNA sequences of the KH-QUA2 domain of QKI protein, we introduced point mutations at different positions in the QRE resulting in twelve different mRNA sequences with single nucleotide change. We carried out long unbiased molecular dynamics simulations using two different sets of recently updated forcefield parameters: AMBERff14SB+RNAχ_OL3 and CHARMM36 (with CMAP correction). We analyzed the changes in intermolecular dynamics as a result of mutation. Our results show that AMBER forcefields performed better to model the interactions between mRNA and protein. We also calculated the binding affinities of different mRNA sequences and found that the relative order correlates to the reported experimental studies. Our study shows that the favorable binding with the formation of stable complex will occur when there is an increase of the total intermolecular contacts between mRNA and protein, but without the loss of native contacts within the KH-QUA domain.

INTRODUCTION

In eukaryotes, gene expression is regulated extensively by RNA-binding proteins (RBPs) or ribonucleoprotein complexes (RNPs). These proteins modulate at the post-transcriptional level and are responsible for stability, transport, editing, and translation of target RNAs. One such family that constitute evolutionary conserved mRNA-binding proteins is STAR family (1). STAR is an acronym for mRNA Signal Transducer and Regulator of RNA. The family broadly comprises three groups: mammalian quaking (QKI); QKI-related (QR) proteins, such as GLD-1 (defective in germ line development) in Caenorhabditis elegans or How (held out wing) in Drosophila melanogaster; and splicing regulators such as SF1 (Splicing Factor 1 in humans) (2–4) and SAM (Src-associated during mitosis 68-kDa protein). These proteins play essential role in developmental processes such as embryogenesis in mice (QKI) (5), myelination process of central nervous system (QKI) (5,6), metazoan germline determination (GLD-1) (7–11), muscle and tendon differentiation in flies (HOW) (12–15), cell death processes (Kep-1) (15,16); and motor defects (17,18) and tumor progression (Sam68) (17,19–21). In mammals, expression of qkI isoforms is tissue-specific (5,22); and are expressed in brain, heart, lung, testis (5), muscle, prostate (23), colon (24), stomach (25) and cells of myeloid lineage (22). In humans, QKI proteins are thus associated with a growing number of diseases (22,26), such as myelination disorders, cancer, cardiovascular disease and schizophrenia.

All STAR proteins from worms to mammals, share similar architecture constituting hallmark STAR domain of ∼200 amino acids that recognize and bind mRNA (1,26,27). The major QKI isoforms possess an identical tripartite STAR domain: mRNA binding extended single heterogeneous nuclear ribonucleoprotein K-Homology (KH) domain, flanked by an N-terminal dimerization QUA1 domain and a C-terminal QUA2 domain (3,17,27–29). The QKI isoforms are sequence specific RNA-binding proteins (28,30), termed as QKI response element (QRE). Using in vitro SELEX (systemic evolution of ligands by exponential enrichment), QRE, was defined as a bipartite sequence with a core (ACUAAY) and a half site (UAAY) separated by 1–20 nucleotides. Comprehensive mutational analysis of similar GLD-1-binding sites in the 3′-UTR of tra-2 mRNA identified UACU(C/A)A as RNA regulatory element (31). Another transcriptome-wide analysis of GLD-1 interactions by RNA immunoprecipitation (RIP) followed by microarray analysis (RIP-chip) identified sequences that were enriched with YUAAY core motif (32). The studies (27,33,34) on human embryonic kidney cells (HEK293) and C. elegans using PAR-CLIP (photoactivable ribonucleoside-enhanced cross-linking and immunoprecipitation) method found similar RREs, with >90% of the 2500 cross-linked binding sites present in 1500 transcripts containing at least one five nucleotide long RNA regulatory element (YUAAY). This preference of binding almost identical RREs is attributed to high sequence and structural similarity of the STAR family of proteins.

The X-ray structure of the QKI STAR domain bound to RNA (27), revealed the relative arrangement of QUA1, KH, and QUA2 domains within each subunit of STAR homodimer. The QKI KH domain along with C-terminal QUA2 domain interacts with the bound mRNA (Figure 1A), and homodimerization is mediated exclusively by QUA1. The KH domain of QKI protein possesses β₁α₁α₂β₂β₃α₃ topology which recognizes four nucleotides of RNA by van der Waals forces, hydrophobic and electrostatic interactions (35). Further downstream 2–3 nucleotides are recognized by the fourth helix of C-terminal QUA2 domain (27). The crystal structure is shown to bind mRNA sequence: ACUAACAA. Herein, we will refer ACUAAC as cognate QRE element, and any other sequence as the non-cognate sequence. Our previous studies (36) on mRNA (QRE) bound and mRNA free STAR domain show that the presence of QRE stabilizes the overall STAR domain by reducing the structural deviations and maintaining the native contacts. We also observed that mRNA binds initially to the maxi-KH domain through a conformational selection of extended mRNA backbone conformations followed by the induced fit of nucleobases to the protein.

Figure 1.

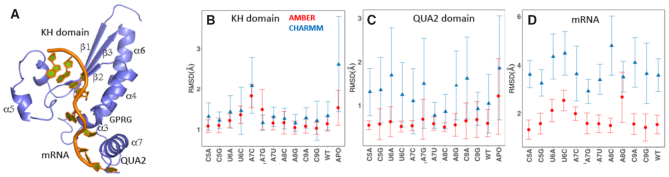
(A) Crystal structure of monomeric QKI STAR-RNA complex (PDBid: 4JVH). Average RMSD values for backbone atoms of (B) KH domain, (C) C-terminal QUA2 domain and (D) mRNA determined with respect to the experimental structure over the production run RMSD values for all simulations of cognate and noncognate sequence bound complexes. Values calculated for simulations with AMBER forcefields are red, and those with CHARMM forcefields are blue.

The question that arises is what makes the QKI STAR domain specific to QRE. In this study, we explored the influence of non-cognate mRNA sequences (sequences other than QRE) on the conformational dynamics of STAR domains. MD simulations have been reliably used to investigate the dynamics of protein-mRNA complexes, such as RRM (RNA Recognition Motif) proteins: U1A protein (37–40), Fox-1 (41) and SRSF1 (41), and core mRNA binding protein, YB-1 (42). In this study, we generated single point nucleobase mutant variants of QREs within the bound complex by substituting the nucleobases at different positions with other purine or pyrimidine within the mRNA cognate RRE. We carried out extensive molecular dynamics of these complexes using two most widely used and recently updated forcefield parameters: AMBERff14SB+RNAχ_OL3 and CHARMM36 (with CMAP correction); and analyzed the changes in intermolecular dynamics as a result of mutation. Throughout this study, we will refer x-ray crystal structure with bound QRE sequence CUAAC as wildtype (WT) and STAR domain with in silico generated mutated mRNA sequences will be referred to as mutants. Assuming that the non-cognate single mutant mRNA sequences should be capable of binding STAR domain in a similar fashion as cognate QRE, we attempted to correlate the relative binding of mRNA sequences with the dynamics of the complex. The aim of this study is, thus 3-fold: How these non-cognate sequences influence the stability and dynamics of STAR proteins? Is the change in intermolecular dynamics between QREs and STAR domain sufficient enough reason to explain the binding specificity of STAR domain? How different forcefields affect protein and mRNA interactions?

MATERIALS AND METHODS

Generation of mRNA mutants

As we aim to understand mRNA recognition and binding, we considered only mRNA binding KH-QUA2 domain for this study. Coordinates for the mRNA bound KH-QUA2 domain (residues 69–204) of QKI protein were extracted from PBDid: 4JVH. Nucleobases within the bound mRNA were mutated to another purine or pyrimidine using mutate_base module of 3DNA (43). For instance, a cytosine at position 5 (nucleotide numbering is similar to the assigned residue index in the crystal structure) was mutated to adenosine. Likewise, different mutations were introduced at positions from 5 to 9, covering cognate mRNA element: CUAAC, and generated mutants, as shown in Table 1. Hereafter, X-ray crystal structure with bound CUAAC (QRE) will be referred to as WT and in silico generated non-cognate mutant mRNA sequences (other than QRE) will be referred to as mutants. We also simulated one artificially generated mRNA free state by removing the bound mRNA coordinates, hereafter termed as APO state.

Table 1.

Simulation systems used in this study

S.No.	Mutant ID	Sequence
1	WT	5′-ACUAACAA-3′
2	C5A	5′-AAUAACAA-3′
3	C5G	5′-AAGAACAA-3′
4	U6A	5′-ACAAACAA-3′
5	U6C	5′-ACCAACAA-3′
6	A7C	5′-ACUCACAA-3′
7	A7G	5′-ACUGACAA-3′
8	A7U	5′-ACUUACAA-3′
9	A8C	5′-ACUACCAA-3′
10	A8G	5′-ACUAGCAA-3′
11	C9A	5′-ACUAAAAA-3′
12	C9G	5′-ACUAAGAA-3′
13	APO	No mRNA bound

Simulation protocol used

The WT and mutants indicated in Table 1 were simulated with the GROMACS simulation package (version 2016.5) (44). The complexes were solvated in rectangular TIP3P solvent box of ∼92 Å × 91 Å × 92 Å; and neutralized with seven Na⁺ ions, resulting in simulation box sizes consisting of ∼65 000 atoms. Long-range interactions were treated using the Particle Mesh Ewald (PME) (45) technique, and a non-bonded cutoff of 12 Å was used. An integration step of 2 fs was used while all bonds were constrained using LINCS algorithm (46,47). The systems were minimized to eliminate any possible clashes and bad contacts using the steepest descent algorithm. Minimization was followed by equilibration under NVT ensemble carried out in two steps. Initially, heavy atoms of the protein and RNA were restrained using position restraints of 1000 kJ/mol/nm² for 2 ns; and during this step, minimized structures were heated gradually from 0 K to 300 K at a rate of 30 K/100 ps while maintaining the restraints. Then, restraints were applied only on Cα atoms of protein, and backbone atoms of mRNA with a reduced force constant of 100 kJ/mol/nm². The structures were further equilibrated for another 1 ns using NPT ensemble while maintaining simulation temperature of 300 K, and pressure of 1 atm. The restraints were removed, and the final structures were further equilibrated for 5 ns under NPT ensemble before entering the production phase. Finally, production runs were carried out twice for 500 ns and 1 μs at 300 K and 1 atm, with no restraints. Temperature coupling was done using velocity rescaling method (48) with a time constant of 0.1 ps, and pressure coupling was done using Parrinello-Rahman pressure coupling algorithm with a time constant of 2.0 and compressibility value as 4.5e–5.

Each of the systems is simulated twice and with two different sets of forcefield parameters, thus resulting in 52 simulations, and an overall simulation time of 39 μs.

Force field evaluations

We used two widely used forcefield sets of parameters with current updated versions: CHARMM and AMBER. For simulations with AMBER forcefields, we used a combination of AMBER ff14SB (49) and RNA χ_OL3 (50,51) to describe protein and mRNA interactions, respectively. ff14SB is reported to improve the accuracy of the protein side chain and backbone parameters (49), and χ_OL3 is shown to perform better than the other reported glycosidic torsion parameterizations (51). For simulations with CHARMM forcefields, we used CHARMM36m (52) forcefield for proteins and CHARMM36 for mRNA (53) to describe the molecular interactions.

Structural deviation analysis

Structural analyses such as root mean square deviations (RMSD) and Root mean square fluctuations (RMSF) were done using VMD-1.9.3 (54). RMSD were calculated for all backbone atoms with reference to the experimental structure. Since the complexes were simulated twice, the mean and standard deviation of the RMSD values for each system was determined. RMSF were calculated for Cα atoms in all the trajectories. Three measures were used to evaluate inter-residue contacts: hydrogen bonds between protein and mRNA; Q, the fraction of native contacts within the protein; and intermolecular contacts between protein and mRNA. Hydrogen bonds were calculated using hbond plugin of VMD with cutoff values of 3.5 Å and 30° for donor–acceptor distances and for donor–hydrogen–acceptor angles, respectively. A native contact is defined when a Cα atom of one residue of protein interacts with another Cα atom of another residue of protein (excluding the adjacent three neighboring residues) within a cutoff distance of 6.0 Å in the starting experimental structure. The fraction of native contacts was calculated using cpptraj (55) implemented in Amber16 (56). For intermolecular contacts between protein and mRNA, a contact is defined when a heavy atom of the protein (KH-QUA2 domain) interacts with another heavy atom of mRNA within a cutoff distance of 5.0 Å, and the calculation was performed using in-house written tcl script for VMD-1.9.3.

Dynamic cross-correlation analysis

The extent of correlated motion between two residues was calculated as the magnitude of the correlation coefficient between Cα atoms of two residues. The cross-correlation coefficient 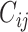for each pair of Cα atoms of residues 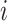and 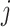is calculated as, 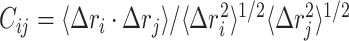where 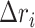is the displacement from mean position of atom 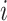and the < > symbol represents the time-average. Dynamic cross-correlation (DCC) analyses was carried out using Bio3d package (57) for Cα atoms by pooling in all the conformations sampled at every 2 ps during multiple simulations runs.

Structural analyses of mRNA conformations

The backbone conformations of mRNA were analyzed during the simulations using four different measures: glycosidic torsions (χ), pseudo-torsion angles (η,θ), backbone torsions (δ) and phosphodiester torsions (BI/BII conformations). Glycosidic torsions, backbone torsions (δ) and phosphodiester torsions (BI/BII conformations as suggested by the difference of ϵ-ζ) calculations were computed out using MDAnalysis suite (58). The backbone pseudo-torsion angles were calculated using in-house written tcl script for VMD-1.9.3 where torsions are defined as (59); η: C4′(i-1)-P(i)-C4′(i)-P(i+1) and θ: P(i)-C4′(i)-P(i+1)-C4′(i+1).

Clustering analyses and generation of residue interaction networks

The conformations of the mRNA bound QKI complexes sampled during the simulation runs were pooled in and clustered into five clusters using kmeans clustering algorithm implemented in cpptraj module (55) of AMBERTools16. Structures representative of the cluster centers were deduced, and representative structure corresponding to the largest cluster center was used to generate residue interaction network (RIN) graph using RINAnalyzer (60) and structureViz2 (61) module of Cytoscape 3.7.1 (62,63). Closeness centrality and average shortest path lengths were also analyzed for each generated network using NetworkAnalyzer (64). This was followed by community clustering (65) using the Girvan-Newman algorithm (66), that uses edge betweenness to detect community peripheries. Community detection is an iterative process, where each cycle consists of calculation of betweenness of all edges in the network, followed by removal of edge with the highest betweenness until no edge remain.

mRNA binding affinities calculations

In this work, the relative free energies associated with the binding of mRNA sequences to the QKI domain were calculated using MM-PB(GB)SA method (67–70). For free energy calculation, conformations sampled at 5 ps (resulting in 50 000 frames) from both the trajectories were pooled and energies were calculated according to the equation: 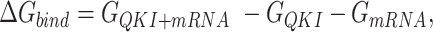where 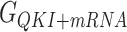, , 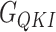and 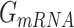denotes the average Gibbs free energy for the mRNA-QKI domain complex, receptor QKI protein domain, and mRNA sequence, respectively over the entire simulation trajectories. The binding energy is estimated as a sum of terms:

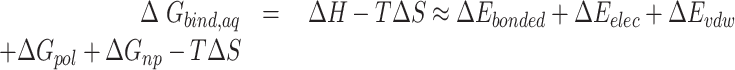(1)

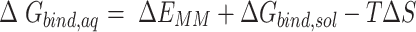(2)

The first three terms in Equation (1) are standard molecular mechanics energy (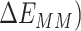 terms associated with bonded (bond, angle, and dihedral), electrostatic and van der Waals interaction. The fourth (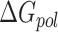) and fifth (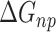) terms in Equation (1) are polar and non-polar contributions to solvation free energy change (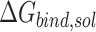). 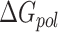is obtained by solving PB or GB model equation, and 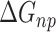is estimated from solvent accessibilities values. The last term (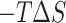) in Equation (1) is the conformational entropy change upon binding. The first five terms in Equation (1) or first two terms in Equation (2) were calculated using MMPBSA.py (71) available in Amber16 for systems simulated using both CHARMM and AMBER forcefields. For the determination of polar solvation energy with Poisson Boltzmann equation (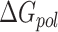), values of 1.0 and 80.0 were used for the dielectrics of solute and solvent, respectively. T and S are absolute temperature (taken here as 300K) and entropy estimated by normal mode analysis of vibrational frequencies. The entropy of the system was computed using normal mode analysis module mmpbsa_py_nabnmode implemented in Amber16 (56,71). All structures were completely energy-minimized prior to normal mode analysis. Due to the high computational cost associated with entropy calculations, a subset of 500 frames from the last 100 ns of both the trajectories simulated with AMBER forcefields was used for normal mode analysis.

RESULTS

We have carried out unbiased simulations of 12 systems comprising of KH-QUA2 domain of QKI protein bound with 12 different sequences, as shown in Table 1. Also, we also simulated mRNA free KH-QUA2 domain, termed as APO state. We used two different forcefields parameters for simulations. For brevity sake, we will refer simulations carried out using AMBERff14sb (protein) +RNAχ_OL3 (mRNA) as AMBER simulations; and simulations carried out using CHARMM36 (both protein and mRNA) as CHARMM simulations.

Structural stabilities of the mRNA-QKI complexes

We assessed the stabilities of QKI domain bound with cognate and non-cognate QREs by computing the root mean square deviations (RMSD) for backbone atoms of KH domain, C-terminal QUA2 domain, and mRNA with respect to the experimental starting structure. We also computed the RMSD for mRNA free APO state. The average RMSD values computed for AMBER and CHARMM forcefields are shown in Figure 1B-D, and the corresponding time evolution plots are shown in Supplementary Figures SI1 and SI2 for AMBER and CHARMM forcefields, respectively. As a general trend, we observed that (a) RMSD values fluctuate less for simulations carried out using AMBER forcefields than those observed with CHARMM forcefields; (b) C-terminal QUA2 domain and mRNA backbone show higher structural deviations with CHARMM forcefields than with AMBER forcefields; (c) Both KH and QUA2 domains in absence of mRNA show higher deviations (as observed for APO state simulations using both AMBER and CHARMM forcefields) than those in presence of mRNA; (d) certain mutations, such as A7C, A7G, U6C destabilize the structure as observed from their higher deviations; and (e) though higher deviations are observed for CHARMM simulations, the variations in average RMSD values with respect to the mutations (except A8C and A8G) are similar using both forcefields.

We analyzed time-averaged root mean square fluctuations (RMSF) for Cα atoms of the KH-QUA2 domain of QKI proteins (Supplementary Figure SI3). We also converted B-factors of crystal structure to RMSF and observed that using AMBER simulations, the KH-QUA2 domain show minor fluctuations than the experimental values. RMSF peaks are observed primarily for residues belonging to α5 helix and adjoining loop. We observed that mRNA, whether cognate or non-cognate stabilizes the KH-QUA2 domain as lower RMSF peaks are observed for WT and mutants (except A7G) than those observed for APO state. On the other hand, CHARMM forcefields show higher RMSF peaks for KH-QUA2 domain, especially for C-terminal QUA2 domain, in the presence of cognate mRNA sequence than for non-cognate sequences. We observed that simulation of KH-QUA2 in the absence of bound mRNA using CHARMM forcefields show considerable higher RMSF values (in comparison with simulations using AMBER forcefields). Though the values of RMSD and RMSF are different for different forcefields, these data highlight the importance of mRNA in stabilizing the KH-QUA2 domain.

Correlated dynamics within the complexes

We assessed the domain-dependent motions by computing the correlation matrix for Cα atoms of the simulated systems in the presence and absence of mRNA (Figure 2, Supplementary Figures SI4 and SI5). In human QKI, mRNA binds onto KH domain within the cleft formed by helices α3, α4, α6, and strands β1, β2, β3 on one side and α5 on the other side. The binding is further extended by helix α7 of QUA2 domain. mRNA specifically interacts with the residues from helices α3, α4, strand β2, conserved GPRG, and loops connecting β2 and α5 of KH domain. A glance at the correlation maps computed using two different forcefields, and we observed that the extent of correlations is less for simulations using AMBER forcefields as indicated by the sparsely located colored islands than those observed for simulations using CHARMM forcefields.

Figure 2.

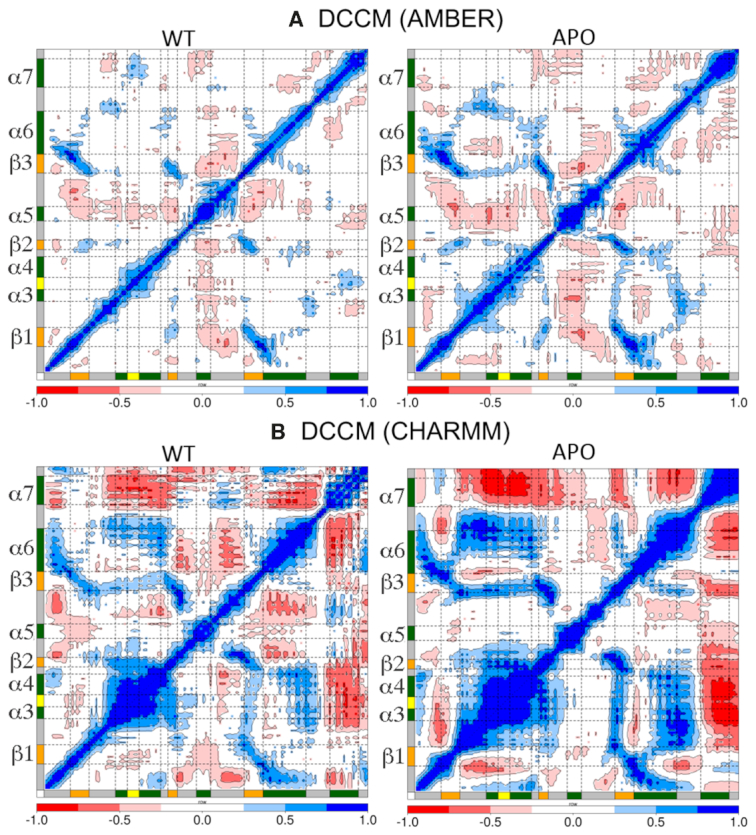
Dynamic cross correlation maps calculated as the time-average for Cα atoms of KH-QUA2 domain of QKI protein in presence of (WT) and in absence of (APO) bound mRNA sequence (WT) using (A) AMBER forcefields and (B) CHARMM forcefields. Secondary structure elements: alpha helices, beta sheets and loops are annotated with boxes of green color, orange color and grey color. ‘GPRG’ motif is annotated with yellow colored box. The whole range of correlation from −1 to + 1 is represented in three ranges: blue color corresponding to positive correlation values ranging from 0.25 to 1; red color corresponding to negative correlation values ranging from −0.25 to −1; and white color corresponding to weak or no-correlation values ranging from −0.25 to + 0.25. The extent of correlation or anti-correlation is indicated by variation in the intensity of respective blue or red color. DCC maps computed for conformations bound to non-cognate sequences are shown in Supplementary Figure SI4 for AMBER forcefields and Supplementary Figure SI5 for CHARMM forcefields.

Nonetheless, there is a difference in correlation when mRNA is not bound as shown by the variations in colored islands in dynamic cross-correlation (DCC) maps of WT versus APO (Figure 2). Looking at the correlation between two sides of the cleft of mRNA binding region of KH domain, we observed that in the absence of mRNA, α5 on one side of the cleft is negatively correlated with rest of the domain, and the extent of negative correlation decreases once mRNA is bound. The beta strands are positively correlated with each other, and with the neighboring helices and the extent of correlation increases in the absence of mRNA. As, mRNA interacts within the cleft, the correlation decreases.

Interestingly, the two forcefields show different correlation patterns for helix α7 of QUA2 domain. For simulations using AMBER forcefields, in the presence of mRNA helix α7 of QUA2 domain is positively correlated with helices α3, α4 and connecting GPRG loop; negatively correlated with helix α5, and uncorrelated with the beta strands. In the absence of mRNA, the positive correlation is lost as there is no mRNA present to correlate KH and QUA2 domain, and instead helix α7 gets negatively correlated with α5 and α6 (Figure 2A). For simulations using CHARMM forcefields, in the presence of mRNA, helix α7 of QUA2 domain is negatively correlated with other helices, and in absence of mRNA, the extent of negative correlation increases as observed for DCC map of APO state (Figure 2B).

Looking at the DCC maps of non-cognate mRNA bound complexes simulated using AMBER forcefields (Supplementary Figure SI4), we found that most of these DCC maps show similar trend as cognate mRNA bound WT complex, except A7G, C9A and C9G. The latter three non-cognate complexes show trend much similar to APO state of AMBER forcefield. Comparing DCC maps of KH-QUA2 bound to cognate (WT) and non-cognate mRNA sequences for simulations using CHARMM forcefields (Supplementary Figure SI5), we observed that the extent of correlation (either positive or negative) decreases when non-cognate mRNA is bound, except for C9A where an increase in the extent of correlation is observed. Together, these data show that KH-QUA2 domain is highly correlated (either negative or positive) in the absence of mRNA, and as mRNA binds within the cleft, the extent of intra-correlation is decreased.

Sampling of mRNA conformations during simulations

To investigate the effect of nucleobase mutations on the conformational sampling of bound mRNA sequences, we calculated four parameters: (a) glycosidic χ angles, (b) backbone pseudotorsion angles (η and θ), (c) torsions around C4′–C3′ bond (δ), and (d) BI/BII transitions (variations in ϵ-ζ).

Supplementary Figure SI6 illustrates the ridge plots depicting the distributions of glycosidic χ angle for conformations sampled using different forcefields. Except for A4 which has χ value of 65.1°, all the nucleotides have anti χ values. CHARMM 36 simulations maintained these χ values except for the terminal A4 and A11. Interestingly, AMBER χ^OL3 simulations followed different trends. The experimental χ values for adenine nucleotides were primarily maintained, whereas those corresponding to the nucleotides cytosine, uracil, and guanine were not maintained during the simulations with AMBER χ^OL3 forcefields. The initial anti χ values of adenine nucleotides in cognate and mutant sequences were maintained during the simulations, except for A10 in A7U and A8G mutation. For guanine and uracil nucleotides, χ seemed to be stabilized in syn region, and for cytosine nucleotides, χ populates anti, high-anti and syn values.

Distributions of pseudotorsion angles, η (torsion around C4′(i-1)-P(i)-C4′(i)-P(i+1)) and θ (torsion around P(i)-C4′(i)-P(i+1)-C4′(i+1)) (Supplementary Figure SI7) showed that similar sampling of mRNA backbone is observed with both the forcefields. The experimental values observed for the crystal structure bound mRNA are maintained for all the nucleotides, except C5 and A10 residues. Drastic changes in η values are observed for mutation at 6^th position as uracil is mutated to adenine (U6A) or cytosine (U6C). Interestingly, backbone changes are not significantly observed for mutations of nucleotides at seventh, eighth or ninth position. We also calculated the backbone δ torsions around sugar C4′-C3′ bond (Supplementary Figure SI8). For the δ torsions, CHARMM36 forcefields maintained the initial values (except for terminal nucleotides A4 and A11). On the other hand, AMBER χ^OL3 forcefields shifted the δ values of A8, C9, and A10. Except for C6 mutation where uracil at sixth position is mutated to cytosine (non-cognate sequence U6C), all the non-cognate sequences showed similar distribution patterns as observed for cognate WT sequence.

We determined the position of backbone phosphate groups with respect to the sugar of the preceding nucleotide by calculating the BI/BII transitions during the simulations (Supplementary Figure SI9). BI/BII conformation of the phosphate group is characterized by the difference of two angles (ϵ-ζ), where ϵ is the torsion angle about the C3′-O3′ bond and ζ is about the O3′-P bond. In the experimental structure, all phosphates are in BI conformation, except for the phosphates of C5 and A7 in BII conformation. With CHARMM36 forcefields, we observed that U6 and A7 phosphates are mostly kept in their initial conformation, whereas other phosphate groups keep swapping temporarily between BI/BII conformations. Similarly, dynamic swapping between BI and BII is observed for AMBER χ^OL3 forcefields, with C5, U6 and A7 phosphates kept in their initial phosphate conformations for most of the sequences.

These data suggest the dynamic nature of mRNA even in the presence of bound KH-QUA2 domain, and also that similar backbone conformations are observed for both cognate and non-cognate single mutant mRNA sequences when simulated with either CHARMM or AMBER forcefields.

Influence of mRNA binding on intra- and inter-molecular interactions

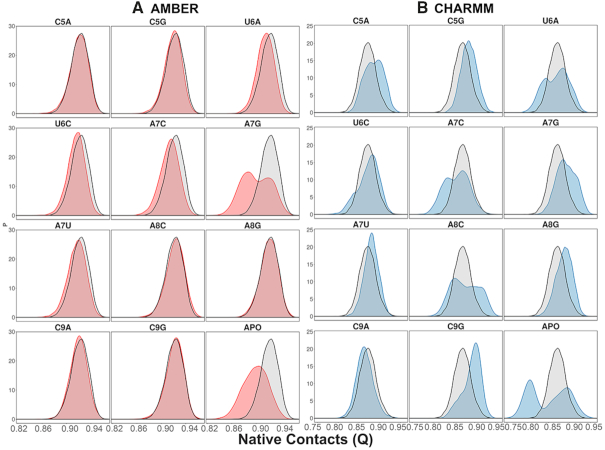
To assess the impact of binding of cognate and non-cognate mRNA sequences on the KH-QUA2 domain with respect to the experimental crystal structure, we calculated the native contacts for conformations of the KH-QUA2 domain sampled during all simulation runs. We plotted the probability distribution functions for Q for these proteins in the presence and absence of different mRNA sequences (Figure 3). Regarding the probabilities of Q calculated for different forcefields, we found that the AMBER forcefields maintain the native contacts of the KH-QUA2 domain in comparison with the CHARMM forcefields. In the absence of mRNA, APO state with both AMBER and CHARMM showed a decrease in native contacts. Using AMBER forcefields, presence of mRNA with non-cognate sequences: U6A, A7G and A7U showed slight decrease that the cognate WT sequence; and considerable broadening of the curve depicting significant decrease in native contacts is observed for mRNA with non-cognate sequence A7G. Using CHARMM forcefields, we observed different trends. Comparative analysis of native contacts with cognate and non-cognate mRNA sequences show that certain non-cognate sequences such as C5A, C5G, U6C, A7U, A8G and C9G maintain the native contacts better than WT cognate sequences; and some sequences such as U6A, A7C, A8C and C9A decrease the native contacts.

Figure 3.

Probability distribution functions for fraction of native contacts, Q observed during simulations using (A) AMBER forcefields and (B) CHARMM forcefields. Distribution of native contacts within STAR domain of QKI proteins in presence of non-cognate sequences and in absence of bound mRNA (APO state) is shown in red and blue states for AMBER and CHARMM forcefields, respectively. For comparison, the native contacts observed for STAR domain with cognate mRNA sequences (WT) using two forcefields are shown in black.

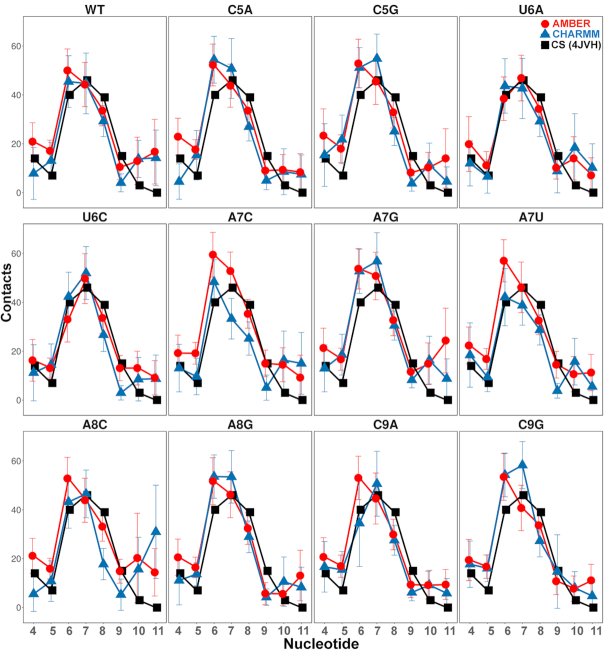
We further calculated the nucleotide-wise contacts between nucleotide and amino acid residues of the KH-QUA2 domain (Figure 4) and compared with those observed in the experimental crystal structure. In the experimental crystal structure, the nucleotides that form a large number of contacts are U6, A7 and A8, followed by A4, C9 and C5; and the last two A10 and A11 lack the contacts with KH-QUA2 domain. The trend is maintained for non-cognate sequences as well, though the order may vary depending on the mutation. For each nucleotide belonging to WT cognate sequence simulated using both AMBER and CHARMM forcefields, we observed on an average, same number of intermolecular contacts with protein residues as those found in experimental structure. For the mutated nucleotide sequences (non QREs), we found that there is an increase in intermolecular contacts with KH-QUA2 for mutations as cytosine at fifth position is mutated to adenine and guanine (C5A, C5G) using both CHARMM and AMBER forcefields. The mutations at sixth position of uracil and ninth position of cytosine (U6A, U6C, C9A, C9G) show no difference in the number of intermolecular contacts (with both forcefields). Mutations of adenine at eighth position to cytosine (A8C) or guanine (A8G) show a decrease in intermolecular contacts for both forcefields.

Figure 4.

Nucleotide-wise intermolecular contacts between nucleotide and residues belonging to KH-QUA2 domain averaged over the simulation trajectories. Blue triangles and lines correspond to the simulations using CHARMM forcefields, and red circles and lines correspond to simulations using the AMBER forcefields. The black squares and lines correspond to the values observed in the crystal structure. The error bars are standard deviation values.

Interestingly, mutation of adenine at seventh position show different trends with different forcefields. Mutation of adenine at seventh position to cytosine (A7C) and guanine (A7G) showed a slight increase in the number of intermolecular contacts using AMBER forcefields, whereas mutation to uracil (A7U) showed no effect. On the contrary, using CHARMM forcefields, we observed that as adenine at seventh position is mutated to any pyrimidine, there is a decrease in intermolecular contacts for nucleotide at seventh position (A7C and A7U); and for A7G mutation, there is an increase in intermolecular contacts. For AMBER simulations, surprisingly we found that any mutation of the nucleotide sequence other than that at sixth position increases the total intermolecular contacts of U6.

We further decomposed the total number of intermolecular contacts to the residue-wise list of interactions. In the experimental crystal structure of mRNA bound QKI protein (Supplementary Figure SI10), it is observed that nucleotides A4, C5 and U6 interact with the residues of C-terminal QUA2 domain. A4 interacts with amino acid residues L194, A198, T203 and Y204. C5 interacts with amino acids R130, K190, and L197. U6 interacts with amino acids K190, Q193 and L197. Besides these, U6 also interacts with N97, G100, R101 and GPRG motif of KH domain. The interaction of nucleotide U6 with ‘G¹⁰⁴PRG¹⁰⁷’ motif is via hydrogen-bonding interactions with G104 and R106, and nonbonded contacts with P105. The nucleobase of A7 is observed sandwiched between the side chains of residues V99 and R130. A7 also interacts with N97 and L103. A8 forms nonbonded contacts with L103, M122 and V123, and backbone sugar-phosphate interactions with G107 and K111. C9 forms hydrogen bonding interactions with side chains of K120 and R124, and nonbonded interactions with M122. Nucleotides A10 and A11 do not form substantial interactions, except weak nonbonded interactions with N143 and W144.

Combining the total intermolecular contacts data with the residue-wise intermolecular contacts plotted in Supplementary Figure SI11 for AMBER forcefields and Supplementary Figure SI12 for CHARMM forcefields, we observed that most of the intermolecular contacts present in the crystal structure are maintained during the simulations, especially with the AMBER forcefields. The quantitative analysis of the intermolecular contacts is provided in Supplementary Figure SI13. The native interactions of nucleotides at fourth and fifth position with C-terminal QUA2 domain; and nucleotides at ninth and tenth with helix α4 residues (amino acids 108–117) are intermittently maintained with CHARMM forcefields even for cognate WT sequence. On the other hand, AMBER forcefields maintain these native interactions, besides forming other non-native interactions suggesting that the mutant nucleotides are capable of interacting with similar residues. These atomistic interaction data suggest that the AMBER forcefields can model and capture these mRNA and protein interactions more accurately than the CHARMM forcefields.

Interestingly, for the flanking 3′ terminal residues, A10 and A11 we observed that during dynamics (Supplementary Figure SI13), they tend to form interactions primarily with the residues 140–144 on the left side of the mRNA binding cleft of KH domain. Another set of interactions of A10 and A11 are also observed with the residues of β2, namely 120–122 on the right side of the cleft. With AMBER forcefields, for all the mutations, except A7G, A8C, A8G and even WT, only the first set of interactions are observed. With CHARMM forcefields, however, a third set of interactions are also observed as A10 and A11 interact with residues 133–138 of helix α5. The data suggest the dynamic nature of flanking nucleotides in the absence of strong interactions.

Variation in interaction networks for complexes bound with different mRNA sequences

We pooled in the conformations of mRNA bound complexes and clustered using k-means clustering algorithm into five clusters. For each cluster, the best representative structure was identified and compared with the experimental structure. Comparative analysis of the representative structures generated using AMBER (Supplementary Figure SI14) and CHARMM forcefields (Supplementary Figures SI15), we observed that the CHARMM generated representative structures have higher RMSD values for backbone atoms (with respect to the initial crystal structure) than those observed for representative structures identified using AMBER forcefields. In line with the RMSD analysis, deviations are observed primarily because of C-terminal QUA2 domain and mRNA backbone.

We utilized the representative structure of the largest cluster center of each simulated system to compute the residue interaction network (RIN) and clustered them based on the communities they belong. RIN analysis followed by community clustering of crystal structure (Figure 5) shows that there are major five communities observed for mRNA bound KH-QUA2 domain. Comparative analysis of crystal structure RIN with RINs of representative structures of simulated data, we found that the interaction networks varies as the structures are simulated. View of the different RINs using both AMBER (Supplementary Figures SI16, SI17) and CHARMM forcefields (Supplementary Figures SI18, SI19) suggests a general trend for distinct community formation of KH-QUA2 domain: (a) helix α5 and the adjoining loops on the left side of the mRNA binding cleft form one community; (b) C-terminal QUA2 domain forms another distinct community; (c) N-terminal proximal region of beta strands and upper half of helix α6 pair up for another community; (d) lower portion of beta strands and lower half of helix α6 forms another community and (e) helices α3 and α4 forms one community or (f) when helices α3 and α4 pair up with lower half of community (d). The differences are observed in pairing up of the nucleotides within these distinct communities. In all the simulated systems using AMBER forcefields (except C5G), nucleotides at fourth, fifth and sixth position always pair in a community consisting of QUA2 domain. Interestingly, CHARMM forcefields are not able to capture these interactions even in WT state, where nucleotide at sixth position loses its connection with QUA2 domain, and pair with a community (e). Similar behavior is observed for C5G, U6C, C9A and C9G simulated with CHARMM forcefields.

Figure 5.

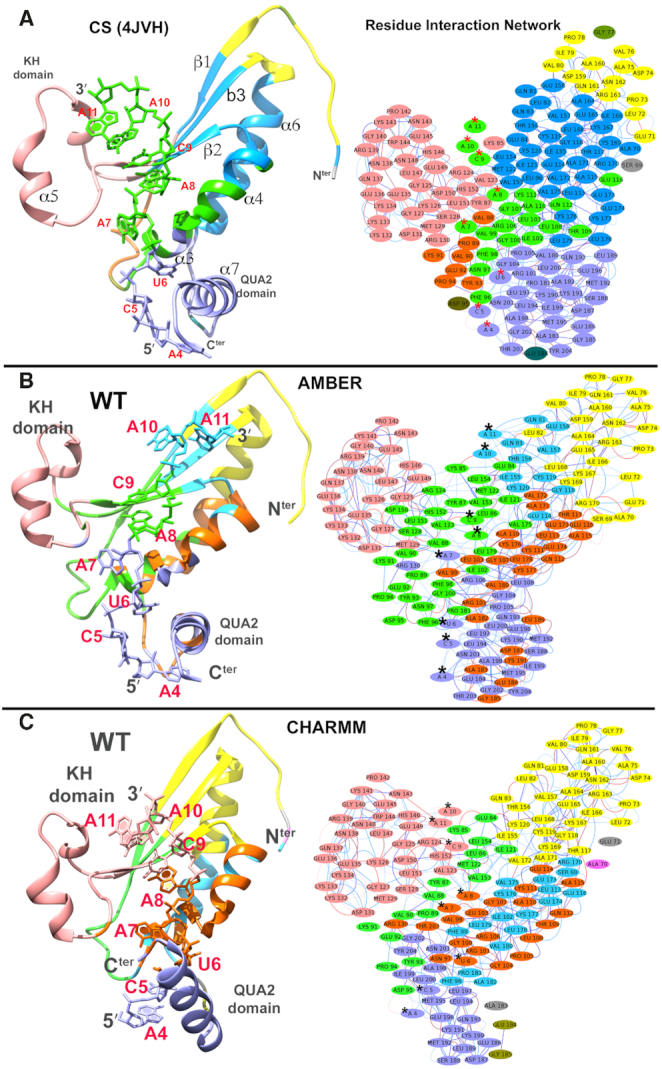
Residue interaction networks (RINs) for (A) the crystal structure of QKI-mRNA complex. The residues are color-mapped according to the communities they belong to. There are five major communities observed. Helix α5 and the adjoining loops on the left side of the mRNA binding cleft form one community, and helix α6 and beta strands (β1,β2,β3) on the right side of cleft form another community. mRNA nucleotides A4, C5, and U6 forms another community with C-terminal QUA2, and rest of the nucleotides A7, A8, C9, A10 and A11 forms community with helices α3 and α4. Interestingly, ‘GPRG’ motif is at the crossroad of the latter two communities with G104, P105 form similar community as mRNA nucleotides A4-U6 and the R106, G107 forms community with nucleotides A7-A11. Panels (B) and (C) show RINs for structures representing the largest cluster center as obtained from the kmeans clustering algorithm during the simulations of WT state carried out using B. AMBER forcefields and C. CHARMM forcefields. RINs for rest of simulated states are shown in Supplementary Figures SI16–S19.

We mapped these RINs with variations in closeness centrality values (Supplementary Figure SI20) and average shortest path lengths (Supplementary Figure SI21) for the nucleotides. In theory, closeness centrality value is reciprocal to the sum of the shortest paths between the node and all other nodes in the network. Therefore, the more central a node is, the lower the average shortest path length will be and the closer that node will be to the other nodes in the network. So, the connected nodes are critical for the network. Looking at the comparative values for these two parameters with respect to the experimental crystal structure, we found that: (a) in crystal structure, nucleotides U6, A7, A8, C9 have high closeness centrality values and low shortest path lengths (with highest/lowest for A7 and A8) and this trend is observed in simulated structures as well; (b) the effect of the mutation at any position is observed substantially for the values of A7, A8 and C9; (c) for cognate WT sequence, CHARMM forcefields show reduction in the values with respect to AMBER forcefields; (d) as a general trend, CHARMM forcefields for most of the mutations (except A8G, C9A) show decrease in centrality values and increase in shortest path length than those observed with AMBER forcefields or in crystal structure.

Effect of mutation on the structural aspects of the complexes

Our results show that the presence of mRNA stabilizes the KH-QUA2 domain in comparison to the mRNA free APO state. Results from the simulations with two different forcefields showed that large structural deviations are observed with CHARMM parameters for both protein and mRNA than with AMBER parameters, with loss of interactions with the C-terminal QUA2 domain. Thus, we are using the trajectories generated using AMBER forcefields to map the point mutations in QRE of mRNA sequence with the variations in the dynamical and structural aspects of mRNA bound complexes.

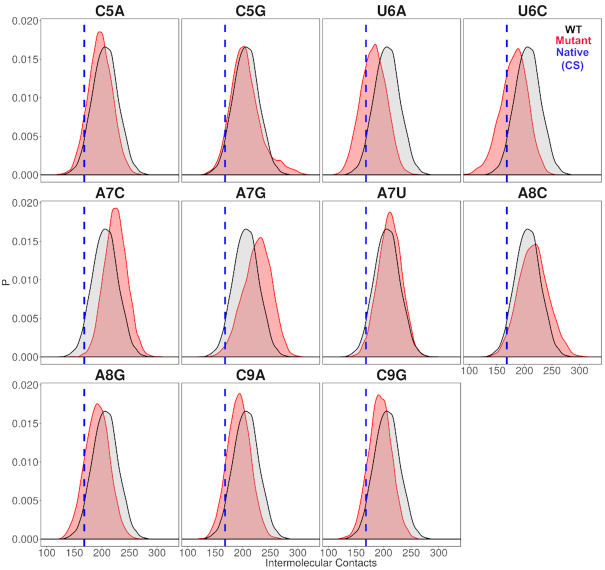
1. Mutations of the fifth nucleotide, which is cytosine in crystal structure to adenine (C5A) or guanine (C5G) show similar structural deviations and correlation pattern as WT, with C5G showing higher structural deviation values. Looking at the interaction analyses and RINs for C5A vs. C5G, it is observed that C5A RIN resembles crystal structure RIN thus, C5A is capable of binding KH-QUA2 domain in a similar fashion. Mutations at fifth position do not change the values for closeness centrality or average shortest path length value associated with nucleotide mutation in comparison with CS. However, this mutation reduces the total number of intermolecular contacts between mRNA and KH-QUA2 domain (Figure 6).

2. Mutations of the sixth nucleotide, which is uracil in crystal structure to adenine (U6A) or cytosine (U6C) show a decrease in the fraction of native contacts maintained during the simulations with AMBER forcefields. Higher RMSD values are observed in mRNA backbone for C6 in U6C followed by A6 in U6A. U6A mutation does not affect the total number of intermolecular contacts between A6 and KH-QUA2 domain. U6C mutation results in a slight reduction in the number of intermolecular contacts with the KH-QUA2 domain. However, this mutation results in a significant overall decrease in intermolecular contacts between mRNA and KH-QUA2 domain (Figure 6). U6C also modifies the RIN in comparison with WT RIN. Mutation at sixth position slightly reduces the values of closeness centrality or slightly increases the average shortest path length associated with nucleotide mutation in comparison with CS.

3. Mutation of the seventh residue, which is adenine in crystal structure to cytosine (A7C), guanine (A7G), or uracil (A7U) has varied effects during the simulations. A7C shows higher fluctuations in KH domain, whereas A7G induces higher deviations in both KH and QUA2 domain. A7U, on the other hand, shows minor deviations similar to WT. A similar trend is observed for the fraction of native contacts observed within the KH-QUA2 domain with A7U maintaining the most of native contacts, followed by A7C, and A7G significantly reduces the native contacts. As far as intermolecular contacts between mRNA and KH-QUA2 domain is concerned, mutation of adenine to cytosine increased the intermolecular contacts, followed by mutation of adenine to guanine, whereas mutation of adenine to uracil did not affect (Figure 6) the number of intermolecular contacts. These mutations also significantly changed the RINs in comparison to the RINs observed for the crystal structure and WT. In the crystal structure RIN, A7 forms community with ‘GPRG’ loop connecting helix α3 and α4. For the mutant RINs, C7 in A7C and G7 is A7G also belongs to similar community as ‘GPRG’ loop, whereas U7 is A7U completely loses its interaction with ‘GPRG’ and forms communities with the left side of the binding cleft. Mutation C7 in A7C increases the closeness centrality value and reduces the average shortest path length value. A7G does not affect these parameters, whereas A7U decreases the closeness centrality value and increases the average shortest path length.

4. Mutation of the eighth residue, which is adenine in crystal structure to cytosine (A8C) and guanine (A8G) show similar correlation patterns as WT. Guanine at eighth position induced higher deviations for mRNA backbone as shown by higher RMSD values than those observed for A8C or WT. A8C and A8G retain the native contacts for the KH-QUA2 domain similarly as observed for WT. However, the intermolecular contacts show minor increase as A8 in WT is mutated to C8 in A8C and significantly reduces for G8 in A8G (Figure 6). The mutations also varied the RINs for the complexes. In the crystal structure, A8 interacts with helix α3/α4 and forms community with these residues, and in WT, A8 pairs up with another community consisting of the lower portion of beta strands and helix α6. C8 in A8C pairs up with α5 on the left side of cleft along with the following 9th–11th nucleotides. G8 in A8G show similar partners as WT as it pairs with the lower portion of beta strands and helix α6. Mutation of A8C and A8G both slightly increases the closeness centrality value and slightly decreases the average shortest path length associated with the nucleotide at eighth position.

5. Mutation of the ninth residue, which is cytosine in crystal structure to adenine (C9A) and guanine (C9G) show higher deviations in C-terminal QUA2 domain. This mutation to either purine reduces the number of intermolecular contacts between mRNA and KH-QUA2 domain (Figure 6) but maintains the fraction of native contacts in the KH-QUA2 domain. In the crystal structure, C9 interacts with residues of helix α4, and in crystal structure RIN, C9 is observed to be part of a larger community consisting of nucleotides A7–A11 and residues spanning helices α3 to α4. For both mutants, A9 in C9A and G9 in C9G breaks off from the larger community and forms a small community with the interacting residues of helix α4. The values of closeness centralities decrease, and average shortest path lengths increase as cytosine mutates to either adenine (C9A) or guanine (C9G).

Figure 6.

Distributions of total intermolecular contacts observed between mRNA and KH-QUA2 domain for conformations sampled using AMBER forcefields. Red colored peaks correspond to non-cognate mRNA sequences and black colored peaks correspond to cognate WT sequence. The blue colored vertical dotted line corresponds to the number of contacts observed between KH-QUA2 domain and bound mRNA in the experimental structure (pdbid: 4JVH).

Energetics of binding of different mRNA sequences to KH-QUA2 domain

We assessed the relative binding energies of cognate and non-cognate mRNA sequences using MMGBSA and MMPBSA approach. Table 2 shows the values of the energetic contributions to the calculation of binding energies. The contributions favoring the binding include van der Waals interactions and coulombic interactions and is opposed by the unfavorable desolvation of polar groups and loss in entropy due to the translational, rotational and vibrational degrees of freedom lost in the binding process. Although the GBSA model provided more favorable estimates of the binding energies than the PBSA model, the relative order of computed energies is similar for both. Our aim with the MMPBSA studies is not getting the absolute binding mRNA energies, but to look at their relative orders with respect to the mutations. For the binding energies (excluding the entropic contributions) calculated (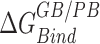 in Table 2) for conformations sampled with CHARMM forcefields, the we observe the relative order of binding energies as: A7G > C5G >A8G > C5A > A8C > WT ≈ C9G/A7U > U6C/A7C > C9A > U6A. Though the most and the least stable mutation remains the same, the relative order changes in between for the conformations sampled using AMBER forcefields. With AMBER forcefields, the relative order of favorable binding energies 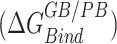, without the entropic contributions, turns out as: A7G > A7C/A7U/A8C > WT > A8G > C5G > U6C/C9A > C5A > C9G > U6A. For the AMBER simulations, we calculated the MM/PBSA entropic contributions, 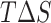at 300K and observed the relative order of stability based on entropy alone as: C9G > A7G > U6A/U6C/A8C > C5G/A7U > A7C/C9A > A8G > C5A > WT. Combining these entropic contributions to the MMPBSA binding energies (calculated for AMBER forcefields) changed the relative order 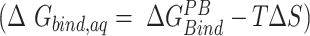of favorable binding energies as: A7G > A7C > A7U ≈ WT/A8C > A8G > C5G > C9A > C5A > U6C > C9G > U6A (Supplementary Figure SI22). These data combined suggest that the mRNA binding to the KH-QUA2 domain is energetically favorable process.

Table 2.

MMPB/GBSA free energies of mRNA complexes with STAR domain of QKI protein. Values are in kcal/mol

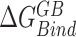
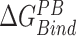
		Evdw	Ecoul	EGB	Esurf		EPB	Enpolar		TΔS	#
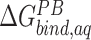WT	AMB*	−126.3 (0.3)	−680.2 (1.5)	706.9 (1.4)	−15.3 (0.03)	−114.9 (0.3)	726.9 (1.4)	−11.8 (0.02)	−91.0 (0.3)	−54.8	−36.2
	CHM#	−106.8 (0.3)	−672.1 (1.9)	713.6 (1.7)	−13.1 (0.03)	−78.5 (0.3)	715.1 (1.9)	−10.7 (0.02)	−74.5 (0.3)	–	–
C5A	AMB	−125.5 (0.2)	−670.2 (1.7)	703.8 (1.6)	−14.8 (0.02)	−106.7 (0.3)	723.9 (1.7)	−11.7 (0.01)	−83.6 (0.3)	−55.1	−32.0
	CHM	−99.6 (0.2)	−749.1 (2.0)	768.5 (2.2)	−12.0 (0.03)	−74.1 (0.2)	779.4 (2.0)	−9.7 (0.02)	−79.0 (0.2)	–	–
C5G	AMB	−125.7 (0.2)	−703.6 (1.9)	733.3 (1.8)	−15.0 (0.02)	−111.2 (0.3)	754.6 (1.9)	−11.8 (0.01)	−86.6 (0.3)	−57.3	−29.3
	CHM	−103.4 (0.2)	−716.2 (1.7)	751.9 (1.7)	−12.7 (0.03)	−80.4 (0.3)	746.5 (1.7)	−10.4 (0.02)	−83.5 (0.3)	–	–
U6A	AMB	−119.6 (0.2)	−694.8 (1.8)	727.5 (1.7)	−14.2 (0.02)	−101.1 (0.3)	750.1 (1.7)	−11.4 (0.02)	−75.7 (0.4)	−58.8	−16.9
	CHM	−89.6 (0.5)	−768.2 (1.9)	804.2 (1.9)	−12.6 (0.03)	−66.2 (0.6)	809.3 (2.1)	−10.4 (0.02)	−58.9 (0.7)	–	–
U6C	AMB	−109.2 (0.2)	−791.1 (1.8)	803.5 (1.7)	−13.3 (0.02)	−110.1 (0.4)	825.5 (1.8)	−10.8 (0.01)	−85.7 (0.3)	−58.3	−27.4
	CHM	−99.8 (0.2)	−806.9 (1.9)	842.5 (1.9)	−12.1 (0.03)	−76.2 (0.3)	842.8 (1.9)	−10.0 (0.02)	−73.9 (0.3)	–	–
A7C	AMB	−129.6 (0.2)	−704.3 (1.6)	719.7 (1.4)	−15.2 (0.01)	−129.4 (0.4)	750.3 (1.5)	−11.4 (0.01)	−94.9 (0.3)	−57.7	−37.2
	CHM	−95.6 (0.3)	−806.0 (1.9)	839.3 (2.5)	−12.2 (0.03)	−74.5 (0.4)	837.9 (2.0)	−10.1 (0.02)	−73.8 (0.3)	–	–
A7G	AMB	−128.8 (0.2)	−806.4 (1.9)	828.3 (1.8)	−15.7 (0.02)	−122.6 (0.3)	846.1 (1.9)	−12.1 (0.01)	−101.2 (0.3)	−60.7	−40.5
	CHM	−108.5 (0.3)	−748.4 (1.8)	774.6 (1.6)	−13.3 (0.03)	−95.6 (0.4)	774.5 (1.7)	−10.5 (0.02)	−93.0 (0.4)	–	–
A7U	AMB	−124.7 (0.2)	−720.8 (1.6)	741.5 (1.4)	−15.0 (0.02)	−119.1 (0.3)	762.2 (1.5)	−11.3 (0.01)	−94.8 (0.3)	−57.9	−36.9
	CHM	−96.6 (0.2)	−800.1 (2.1)	830.8 (1.9)	−12.6 (0.02)	−78.4 (0.3)	832.8 (2.0)	−10.2 (0.02)	−74.1 (0.3)	–	–
A8C	AMB	−130.4 (0.2)	−759.6 (1.9)	778.4 (1.7)	−15.4 (0.02)	−127.0 (0.3)	807.0 (1.8)	−11.7 (0.01)	−94.6 (0.3)	−58.3	−36.3
	CHM	−102.8 (0.3)	−778.9 (2.0)	814.8 (1.8)	−12.7 (0.03)	−79.9 (0.4)	815.6 (2.3)	−10.4 (0.03)	−76.5 (0.3)	–	–
A8G	AMB	−115.8 (0.2)	−704.4 (1.6)	726.9 (1.5)	−14.0 (0.02)	−107.4 (0.2)	741.4 (1.5)	−10.8 (0.01)	−89.6 (0.3)	−55.7	−33.9
	CHM	−101.5 (0.2)	−726.4 (1.7)	756.3 (1.6)	−12.6 (0.03)	−84.3 (0.3)	756.7 (2.0)	−9.9 (0.02)	−81.2 (0.3)	–	–
C9A	AMB	−123.5 (0.2)	−652.8 (1.6)	682.8 (1.5)	−14.5 (0.02)	−108.1 (0.3)	702.8 (1.5)	−11.4 (0.01)	−85.01 (0.2)	−56.1	−28.9
	CHM	−105.2 (0.3)	−672.3 (2.0)	716.0 (1.9)	−12.9 (0.04)	−74.1 (0.4)	716.8 (2.0)	−10.5 (0.02)	−71.3 (0.3)	–	–
C9G	AMB	−122.4 (0.2)	−686.6 (1.6)	716.6 (1.5)	−14.6 (0.03)	−107.0 (0.3)	740.0 (1.5)	−11.5 (0.01)	−80.6 (0.3)	−61.2	−19.4
	CHM	−88.2 (1.9)	−737.9 (1.9)	763.0 (1.7)	−13.1 (0.04)	−76.1 (1.9)	762.1 (1.7)	−10.2 (0.03)	−74.3 (0.8)	–	–

*AMB results for simulations carried out AMBER forcefields. ^#CHM results for simulations carried out CHARMM forcefields. .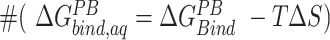

Mapping these binding energies to structural data (Supplementary Figures SI23, SI24), we observed that the these mutants form direct hydrogen bonding interactions with additional amino acid residues, such as G7 in A7G and C7 in A7C interacts with main chain of G127, C9 in A7G and A7C forms hydrogen bonds with R124, and the flanking residues such as A10 and A11 for persistent nonbonded interactions with residues 142–147. For the least stable mutant, U6A we observed that the adenine at sixth position induced changes in 5′ end of mRNA with A4, C5 forming intermittent interactions with QUA2 domain, and the flanking residues at 3′ end A10, A11 also do not form consistent interactions (Supplementary Figure SI13). The data indicates that the relative binding energies of mRNA to KH-QUA2 domain is dependent on the total number of intermolecular contacts between mRNA and KH-QUA2 domain.

DISCUSSION

In the current study, we carried out long-scale MD simulations of the KH-QUA2 domain bound with cognate (WT) and non-cognate mRNA sequences. Non-cognate mRNA sequences were generated by in silico generating point mutations of nucleobases. Also, we simulated the APO state, which is mRNA free KH-QUA2 domain. We employed two recently developed set of forcefields to model mRNA and protein interactions: AMBER simulations with forcefields AMBERff14SB (49) with RNA χ^OL3 (50,51) and CHARMM simulations with parameters CHARMM36m (52) for protein and CHARMM36 for mRNA (53).

In the experimental crystal structure of human QKI protein, we observe that KH-QUA2 domain is complexed with mRNA containing sequence ACUAACAA. In KH-QUA2 domain there is cleft observed formed by helix α5 and adjoining loops on the left side, and rest of the strands (β1,β2,β3) and helices (α3,α4,α6) on the right side. Within this cleft, mRNA is bound, forming various hydrogen bonding interactions as well as non-bonded contacts with the amino acid residues of KH domain. The C-terminal QUA2 domain extends this binding as nucleobases A4, C5 and U6 interact with the residues of α7 helix. We simulated this complex, referred here as WT state with two different forcefields. Our results showed that the CHARMM forcefields show more structural deviations than the AMBER forcefields. From the interactions and deviation analyses, it is observed that the interactions of mRNA with the C-terminal QUA2 domain required for complex stability is not maintained with CHARMM36 forcefields, thus resulting in loss of native contacts and higher deviations. Our data suggest that the combination of AMBER forcefields model the interactions between mRNA and KH-QUA2 domain well enough to stabilize the complex even for the timescale of μs. Here, we also like to add that the complex stability using AMBER forcefields is observed despite the fact that modified RNA χ^OL3 forcefields seem to stabilize the syn glycosidic conformations of uracil, cytosine and guanine.

Removing any bound mRNA sequence destabilizes the KH-QUA2 domain as observed from the structural deviation analyses (RMSD, RMSF) of APO state. In the absence of mRNA, α5 on the left side of the cleft is negatively correlated with rest of the domain; and present on the right side of the cleft, the beta strands are positively correlated with each other, and with the neighboring helices (α3, α4, α6). Once the mRNA is bound, this extent of negative and positive correlation on the left and right side of the cleft, respectively decreases.

We introduced the single point mutations in mRNA sequence at positions 5^th to 9^th and simulated the generated eleven mutants, and analyzed the effect of mutations on various parameters: (a) fraction of native contacts within KH-QUA2 domain, (b) intermolecular contacts between each nucleotide and KH-QUA2 domain, (c) total intermolecular contacts between mRNA and KH-QUA2 domain and (d) difference in residue interaction network. The analysis of detailed atomistic interactions showed that similar residues of the KH-QUA2 interact with the cognate and non-cognate mRNA nucleotides. We also calculated the binding energies associated with mRNA binding to theKH-QUA2 domain using MMPBSA approach and observed that for our study, the inclusion of entropic effects improved the results. Based on the relative binding energies, our results rank the studied mutants in order of favorable binding as: A7G > A7C > A7U/A8C ≈ WT > A8G > C5G > C9A > C5A > U6C > C9G > U6A (Supplementary Figure SI20). We observed a correlation between the binding energies and the total intermolecular contacts between mRNA and KH-QUA2 domain. Mutations with intermolecular contacts more than those observed in WT, such as A7G, A7C, A8C have more favorable MMPBSA binding energies; and those with lower contacts than WT have lower binding energies (Figure 6). Our binding energies results show that A7G mutant forms the most favorable binding complex with the KH-QUA2 domain and U6A mutant is the least favorable.

However, Fluorescence-polarization(FP)/mutagenesis experiments by Ryder and Williamson (28) and FP/(Electrophoretic Gel Mobility Shift (EMSA) experiments by Carmel et al. (72) did not observe any binding for mRNA sequence with guanine nucleotide (at any position). We compared our results with the experimental data (Supplementary Table SI1), and found a loose correlation. Sequences equivalent to A7C (UACUCA in experimental setup) and A7U (UACUUA in experimental setup) showed binding to the QKI domain with lower affinities than WT. In the experimental setup, A7G mutant did not bind to QKI protein, whereas we observed most favorable binding energy for A7G mutant. The probable reason for the favorable binding of A7G in our computations is the increase in the intermolecular contacts between A7G and KH-QUA2 domain. However, the stability of the KH-QUA2 domain in the presence of A7G decreases with higher structural deviations in both KH and QUA2 domain and a significant reduction in native contacts within the protein. Our results show that A7C and A7U are favorable by order of ∼1.5 kcal/mol only, but these mutations also slightly decrease the presence of native contacts within the KH-QUA2 domain. Another sequence equivalent to C5A (AAUAAC) present in 3′-UTR of myelin basic protein (MPB) mRNA was also observed to bind QKI domain, but with low affinity (28,72). Our results show that C5A though has less favorable binding affinities WT, the mutation maintains the native contacts within the KH-QUA2 domain. In an independent study (30) using SELEX strategy, the binding specificity of QKI identified aptamer sequences as bipartite sequences consisting of ‘core’ 5′-NACUAAY-3′ and ‘half-site’ 5′-YAAY-3′ separated by variable spacing. In our study, we lack the half-site as we are simulating the monomeric complex, which is known to bind core site. Our results thus suggest that the favorable binding between mRNA and KH-QUA2 occurs when there is a balance between the intermolecular contacts that mRNA forms and intramolecular native contacts within the KH-QUA2 domain. We like to mention here that we are not discarding the idea that in longer stretches, mRNA with different sequences may form secondary structures which will alter their binding, and thus affect their relative binding affinities. This is beyond the scope of current work.

However, we are proposing one of the probable mRNA binding modes for recognizing the specific nucleotide sequences. From our previous analysis of dissociation of mRNA from KH-QUA2 domain using umbrella sampling simulations (36), it appears that mRNA binding to STAR domain occurs first via a conformational selection of mRNA backbone conformations, followed by induced-fit mechanism as nucleobases interact with the KH-QUA2 domain. Now for the sequences different from the QRE, the initial selection for binding may be made on conformation selection level, but for the sequences similar to QRE such as the ones studied here which have only point mutation, the second selection for binding may be made during induced-fit step. At this step, the strong binding with the formation of stable complex will occur when there is increase between the total intermolecular contacts between mRNA and protein, but without the loss of native contacts within the KH-QUA domain. Thus, any mutation within the mRNA that may increase the intermolecular contacts with the partner protein, but decrease the stability of protein will not bind favorably.

A note on forcefield usage

Modeling of interactions are severely affected by the forcefields approximations used to describe them. Here, we employed two widely used and recently updated nonpolarizable forcefields from AMBER and CHARMM families. AMBER forcefields use QM-derived electrostatic potential (ESP) fit method to parameterize electrostatic term. CHARMM forcefields fit to reproduce QM computations of interaction energies for fragments interacting with water molecules. Another critical parameter used for most of the refinements is tuning of dihedral potentials. For mRNA, earlier AMBER forcefields stabilized the χ potential to anti region and thus, resulting in spurious ladder-like structures (73). The recently updated RNAχ_OL3 minimizes the transitions to ladder-like structures and is known to improve the description of glycosidic syn region. For proteins, CHARMM forcefields have been updated (CHARMM 36m) using grid-base two-dimensional energy correction map (CMAP) obtained by empirically adjusting the map to reproduce experimental data (52). For RNA, CHARMM36 reparameterization was done by modifying the 2′-OH ribose dihedral potential to address the instability of A-RNA (53). A more in-depth overview of the forcefield usage in RNA dynamics is reviewed elegantly in (74).

Based on our studies, both nonpolarizable forcefields show limitations while modeling the protein and mRNA interactions. The updated AMBER RNAχ_OL3 seemed to shift the χ values from experimentally observed anti values to syn region for uracil, cytosine, and guanine. And the CHARMM36 forcefields (though maintained the glyosidic values of nucleobases) fail to maintain the intermolecular contacts between mRNA and C-terminal QUA2 domain, essential for mRNA binding. We are hopeful that once the polarizable forcefields for both protein and RNA are developed, they may be able to accurately depict the biomolecular interactions. Meanwhile based on our studies, in our opinion, a combination of AMBER (AMBERff14SB for proteins and RNAχ_OL3 for mRNA) for modeling both protein-mRNA interactions is a better option for selecting the nonpolarizable forcefields.

CONCLUSION

The results from our unbiased simulation studies provide details about the different binding affinities of the KH-QUA2 for various mRNA sequences. We used two different recently updated forcefield parameters to simulate mRNA binding by KH-QUA2 domain and found that AMBER forcefields more reliable than CHARMM forcefields to model the molecular recognition for mRNA-protein binding interactions. It is evident that the cognate mRNA forms stable interactions with the KH-QUA2 domain and maintains the native contacts within the KH-QUA2 domain. MMPBSA approach, upon inclusion of entropic effects, efficiently provided relative order of binding affinities of different mRNA sequences to the KH-QUA2 domain, which was comparable with the experiments. We hope that this work will stimulate further studies to confirm the hypotheses proposed in this study.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

Department of Science and Technology (DST), India for INSPIRE Award and research grant [IFA14-CH-165 to M.S.].

Conflict of interest statement. None declared.