Abstract
Background:
Children in the UK go through rigorous teacher assessments and standardized exams throughout compulsory (elementary and secondary) education, culminating with the GCSE exams (General Certificate of Secondary Education) at the age of 16 and A-level exams (Advanced Certificate of Secondary Education) at the age of 18. These exams are a major tipping point directing young individuals towards different lifelong trajectories. However, little is known about the associations between teacher assessments and exam performance or how well these two measurement approaches predict educational outcomes at the end of compulsory education and beyond.
Methods:
The current investigation used the UK–representative Twins Early Development Study (TEDS) sample of over 5,000 twin pairs studied longitudinally from childhood to young adulthood (age 7–18). We used teacher assessment and exam performance across development to investigate, using genetically sensitive designs, the associations between teacher assessment and standardized exam scores, as well as teacher assessments’ prediction of exam scores at ages 16 and 18, and university enrollment.
Results:
Teacher assessments of achievement are as reliable, stable and heritable (~60%) as test scores at every stage of the educational experience. Teacher and test scores correlate strongly phenotypically (r ~.70) and genetically (genetic correlation ~ .80) both contemporaneously and over time. Earlier exam performance accounts for additional variance in standardized exam results (~10%) at age 16, when controlling for teacher assessments. However, exam performance explains less additional variance in later academic success, ~5% for exam grades at 18, and ~3% for university entry, when controlling for teacher assessments. Teacher assessments also predict additional variance in later exam performance and university enrolment, when controlling for previous exam scores.
Conclusions:
Teachers can reliably and validly monitor students’ progress, abilities and inclinations. High-stakes exams may shift educational experience away from learning towards exam performance. For these reasons, we suggest that teacher assessments could replace some, or all, high-stakes exams.
Keywords: Educational achievement, teacher assessment, standardized exams, twin models, quantitative genetics
Introduction
Educational achievement is important to children as individuals as well as to society in general. Education enhances the intellectual capital of society; it is one of the most expensive governmental interventions, costing around 6% of the gross domestic product of countries in the Organization for Economic Cooperation and Development (OECD, 2013). For children, educational attainment channels them towards different educational and professional trajectories and is an important predictor of many life outcomes, including health and life expectancy (Arendt, 2005; Bratsberg & Rogeberg, 2017; Cutler & Lleras-Muney, 2012; Gottfredson & Deary, 2004).
The educational curriculum in the UK is highly standardized in terms of content and delivery, as well as assessment of pupils’ performance (The Department for Education: https://www.gov.uk/government/collections/national-curriculum; https://www.gov.uk/government/publications/assessment-principles-school-curriculum). For example, in English, following standardized guidelines, teachers use specific items to rate students’ performance in reading, writing, speaking and listening following standardized rating scales; in mathematics, students are similarly graded on knowledge of numbers, shapes and space, and using and applying mathematics (see Methods for details). In addition to being assessed with standardized teacher assessments, children also go through rigorous UK-wide standardized exams throughout the school years. These exams culminate with the nationwide Generalized Certificate of Secondary Education (GCSE) exams, which are administered at the end of compulsory education when students are around 16 years old. The GCSE exams are critically important for children because they are gatekeepers into academic and vocation tracks at schools and colleges, which include A-level (General Certificate of Education Advanced level) courses and examinations that are required for university entry.
Standardized exam grades, as opposed to teacher assessments, are also used for teacher and school performance management and form the basis of national league tables for schools (Department for Education School league tables: https://www.compare-school-performance.service.gov.uk). About 10% of students go to selective schools (grammar schools or private schools), where entry is determined by entrance exams and prior academic achievement. However, since most secondary schools (both state and private schools) can select students at age 11 and again at age 16, these league tables are to some extent a self-fulfilling prophecy whereby schools at the top of the table select the students who perform best on exams (Smith-Woolley et al., 2018). Seletion to state secondary schools at aget 11 is less common, the majority accept students based on the ‘catchment area’, which is determined by the home address. There is no selection prior age 11 in state secondary schools, admissions are solely based on the ‘catchment area’.
Not all countries make extensive or exclusive use of high-stakes examinations to determine entry to the next stages of education. For example, the High School Certificate in New South Wales and other parts of Australia includes a substantial element of school-based assessment (http://educationstandards.nsw.edu.au/wps/portal/nesa/11–12/hsc/about-HSC/school-assessment). Teacher grades of student achievement are based on assessments of students throughout their classes. This more continuous form of assessment means that each piece of student work is relatively low stakes. In the USA, there is a mix of cumulative assessment via course grades given by teachers using their own metrics and end-of-year standardized testing. The end-of-year standardized testing was introduced by the No Child Left Behind (NCLB) act to make sure that children in grades 3 through 8 (approximately 8 to 13 years old), and at least once in high school, reach adequate levels of reading, arithmetic, and science (https://www2.ed.gov/nclb/overview/intro/execsumm.html). The amount of end-of-year standardized testing done outside of the NCLB requirements, potential use of other standardized testing for progress monitoring, and the stakes of the standardized testing, vary widely across different states of the USA (https://www.ed.gov/news/press-releases/fact-sheet-testing-action-plan).
Although testing arguably consolidates and fosters learning, there are downsides of testing that need to be considered, especially if the exams are very high stakes, as they are in the UK. High-stakes examinations could be detrimental to the learning process if teachers ‘teach to the test’ in a manner that undermines the accumulation of knowledge and understanding of subjects (Cranney, Ahn, McKinnon, Morris, & Watts, 2009; Larsen, Butler, & Roediger, 2009; McDermott, Agarwal, D’Antonio, Roediger, & McDaniel, 2014). In addition, exams are associated with anxiety and distress, and research has shown that high test anxiety is negatively associated with achievement (Embse & Hasson, 2012; Segool, Carlson, Goforth, Von der Embse, & Barterian, 2013; Wood, Hart, Little, & Phillips, 2016), even beyond the anxiety experienced about learning in class (Wang, Shakeshaft, Schofield, & Malanchini, 2018).
High-stakes exams also have an effect on teachers’ morale as well as pupils’ wellbeing and mental health (Hutchings, 2015). Mental health problems in young individuals are increasing in the UK, which is partly associated with increased testing in schools (McDonald, 2001). Childline, a free counseling service for children in the UK, reported that the top concern for children is the stress and anxiety related to school work and exam performance (Childline, 2014). Childline also reports that the number of pupils needing counseling because of school pressures is increasing dramatically (Childline, 2015).
Taken together, these findings raise the issue of the cost-benefit ratio for standardized exams and teacher assessments. The purpose of the current study is to investigate the added benefit of standardized tests over teacher assessments in predicting educational achievement. A novel feature of our study is that we compare teacher assessments and exam performance not just phenotypically but also genetically. Research has shown that variation in educational achievement is substantially heritable for both teacher assessments and test scores (Cesarini & Visscher, 2017; Kovas, Haworth, Dale, & Plomin, 2007; Shakeshaft et al., 2013), and particularly so in contexts like the UK where the educational curriculum is highly standardized (Heath, Berg, Eaves, & Solaas, 1985). Genetic factors are primarily responsible for the long-term prediction of educational achievement (Kovas et al., 2007), so it is important to know the extent to which teachers’ assessments, as compared to test scores, are associated with the heritable component of students’ performance.
Specifically, the current study has two aims: (1) examine phenotypic and genetic associations between teacher assessments and standardized exam scores at ages 7, 11, and 14, and (2) assess the extent to which standardized test scores add to teacher assessments in predicting educational achievement in English, mathematics and science at the end of compulsory education at age 16 (GCSE results), at age 18 (A-level results), and beyond (University enrolment), as well as considering whether this prediction is mediated by genetic or environmental factors.
Methods
Participants
The sample for the study was drawn from the Twins Early Development Study (TEDS). TEDS is a large longitudinal study in the UK that recruited over 16,000 twin pairs born in England and Wales between 1994 and 1996. Although there has been some attrition, more than 10,000 twin pairs remain actively involved in the study. Importantly, TEDS is a representative sample of the UK population (Haworth, Davis, & Plomin, 2013; Kovas et al., 2007; Oliver & Plomin, 2007). Zygosity was assessed using a parent questionnaire of physical similarity, which has been shown to be over 95% accurate when compared to DNA testing (Price et al., 2000). DNA testing was conducted when zygosity was not clear from the physical similarity questionnaire criteria.
A longitudinal sample was used with all available data collected from age 7 to 18. All individuals with major medical or severe psychiatric problems were excluded from the dataset. These included twins with ASD, Cerebral palsy, Down’s syndrome, chromosomal or single-gene disorders, organic brain problems, e.g hydrocephalus, profound deafness, developmental delay. We categorised medical exclusions as any twin medical condition that may have caused mental impairment or that may have interfered in the ability to carry out TEDS activities. Sample size per measure and age is presented in Table S1 in the Supporting Information.
Measures
The TEDS dataset was linked to the National Pupil Database (NPD) for TEDS twins who gave written consent (either self and parent consent). NPD includes data about students’ academic achievement across the school years (https://www.gov.uk/government/collections/national-pupil-database). Data are available for each Key Stage (KS) completed in the UK and follows the National Curriculum (NC). KS1 is completed when children are around 7 years old, KS2 around 11, KS3 around 14, KS4 around age 16 (end of compulsory education, GCSEs), and KS5 data include A-level exam scores at age 18. Teachers reported the NC ratings for each student at the end of each KS according to the standardized rating guidelines. The teacher rating for English combines students’ reading, writing, and speaking and listening; mathematics is a combined score of knowledge in numbers, shapes, space, using and applying mathematics; and science is a score combining life process, scientific enquiry, and physical process. Both teacher ratings and exam scores are available from KS1-KS3; only exam scores are available for KS4 and KS5 (GCSE exams and A-level exams). Only 50% of TEDS participants continue their studies at A-level, which is similar to the national average (42% of students in the 16–18 year cohort in England and Wales continue to do A-levels: https://www.gov.uk/government/uploads/system/uploads/attachment_data/file/502158/SFR03_2016__A_level_and_other_level_3_results_in_England_SFR_revised.pdf), which is why the sample size for KS5 here is halved.
GCSEs are standardized examinations taken at the end of compulsory education at age 16, covering courses taken over 2 or 3 years depending on the course and exam board requirements. Students can choose from a variety of courses including mathematics, science, history, music, physical education, and modern foreign languages. English, mathematics and science are compulsory subjects. The exams are graded from A* to G, with a U grade given for failed exams. Grades were coded from 11 (A*) to 4 (G, lowest pass grade) to have equivalent numerical comparisons. We used exam grades from English, mathematics and science for the current analyses. We created composite measures for English (mean of English language and English literature grades), science (mean of single or double-weighted science, or, when taken separately chemistry, physics and biology grade), and we used the single GCSE grade for mathematics.
A-level examination grades (ranging from A* to E) were coded from 6(A*) to 1(E) to provide numerical comparisons. Because no subjects at A-level are compulsory and the range of subjects chosen is so wide, the sample sizes were too small to provide adequate power for analyses of separate subjects, therefore we created a composite measure of A-level achievement by taking a mean of all A-level exams taken by each student.
At age 18 we also collected data from children’s plans for higher education, specifically if they had enrolled to university course. These data were collected from twins via questionnaires sent through the mail or obtained via telephone. We created a categorical measure of higher education yes/no, assigning 1 to participants who entered university or college and 0 to those who did not.
Analyses
Phenotypic analyses
The measures were described in terms of means and variance, comparing males and females and identical and non-identical twins; mean differences for age and sex and their interaction were tested using univariate analysis of variance (ANOVA).
Correlational analyses were used to investigate the association between teacher ratings and standardized exam scores, from KS1 (age 7) to KS3 (age 14) as well as their correlations with exam grades at age 16 and 18. Hierarchical multiple regression tested the incremental prediction of GCSE grades, A-level grade and university entrance from the standardized exam scores when teacher ratings were entered as the first step in the regression model. Because the present sample was a twin sample, we maintained independence of data by randomly selecting one twin per pair for all phenotypic analyses (phenotypic analyses were repeated with the other twin to partially replicate the results, and are presented in the Additional Supporting material).
Genetic analyses
Twin analyses were used to study the etiology of academic achievement separately for teacher ratings and exam scores. The twin method offers a natural experiment using the known genetic relatedness between monozygotic (MZ) and dizygotic (DZ) twin pairs to estimate the proportion of phenotypic variance explained by genetic, shared environmental and non-shared environmental factors. MZ twins are genetically identical, sharing 100% of the inherited DNA sequence, whereas DZ twins, like other siblings, share on average 50% of DNA variants, while both pairs of twins share 100% of the environmental effects of growing up in the same family. Non-shared environmental influences are unique to individuals and do not contribute to similarities between twins. If MZ correlations on trait similarity are larger than DZ correlations, then genetic influences on a trait can be assumed. These parameters can be estimated using structural equation modelling. The structural equation modeling program OpenMx was used for all model fitting analyses (Boker et al., 2011). Liability threshold model was used for university enrolment as it is a dichotomous measure (Appendix S1).
These univariate analyses can be extended to multivariate analyses to study the etiology of covariance between teacher assessments and test scores. The multivariate genetic method decomposes the covariance between traits into additive genetic (A), shared environmental (C) and non-shared environmental (E) components by comparing the cross-trait cross-twin correlations between MZ and DZ twin pairs. Using the multivariate method it is also possible to estimate the genetic correlation (rG), which indicates the extent to which the same genetic variants influence two traits. The shared environmental correlation (rC) and non-shared environmental correlation (rE) can also be estimated (Knopik, Neiderhiser, DeFries, & Plomin, 2017; Rijsdijk & Sham, 2002). This method can be used to assess the extent to which standardized test scores add to the heritability of teacher ratings in predicting educational achievement at the end of compulsory education and beyond. The method also allows to assess the extent to which the same genetic (and environmental) factors influence teacher ratings and exam scores. Here we used the Cholesky decomposition which allows to examine the genetic and environmental variance shared between two traits after accounting for the variance they both share with variables that have been entered at a previous stage in the model, drawing a parallel with the hierarchical regression analyses that we used in the phenotypic analyses (Appendix S1; Figure S1). When university enrollment was used as an outcome variable, a combined continuous-categorical model was used, where university attendance was used as a categorical variable and was entered as a third variable to the Cholesky model after continuous measures (teacher assessments and test scores). Model fit for all behavioral genetic analyses was assessed by the −2 Log Likelihood (−2LL) value and its corresponding p value, with p > .05 indicating that the behavioural genetic model partitioning the variance into A, C and E components was not a significantly worse fit than the saturated model (baseline model based on the observed means, variances and covariances), and the Akaike information criterion (AIC), with smaller AIC value indicating better model fit. Genetic, shared environmental and non-shared environmental correlations were estimated using the same Cholesky model (correlated factors solution).
Results
Means and standard deviations were calculated for educational achievement across development for the whole sample, males and females separately, and for five sex and zygosity groups: monozygotic (MZ) males, dizygotic (DZ) males, MZ females, DZ females and DZ opposite-sex twin pairs. ANOVA results show that sex and zygosity together explain only 1% of variance on average (Table S1). For the subsequent analyses, the data were corrected for mean sex differences, as described in Methods.
Univariate genetic analyses
Univariate genetic analyses were conducted to estimate ACE for both teacher ratings and test scores in our study. Figure 1 presents the ACE estimates for achievement measures across compulsory education, at A-levels and for university entry. Results are similar for teacher ratings and test scores across subjects and across ages. For both teacher ratings and test scores, heritability (A) is substantial (60% on average, range 50–75%). Shared environment (C) and non-shared environment (E) each accounted of 20% the variance on average (C range 5–29%; E range 15–46%); although the proportion of variance explained by shared environmental factors was slightly higher for Science. Twin intra-class correlations and full model parameters with confidence intervals are presented in Table S2.
Figure 1.
Model fitting results for additive genetic (A), shared environment (C), and non-shared environment (E) components of school performance across school years.
Note: teach= teacher ratings; test= test scores; KS1 = age 7; KS2= age 11; KS3= age 14, GCSE= age 16; A-level= age 18
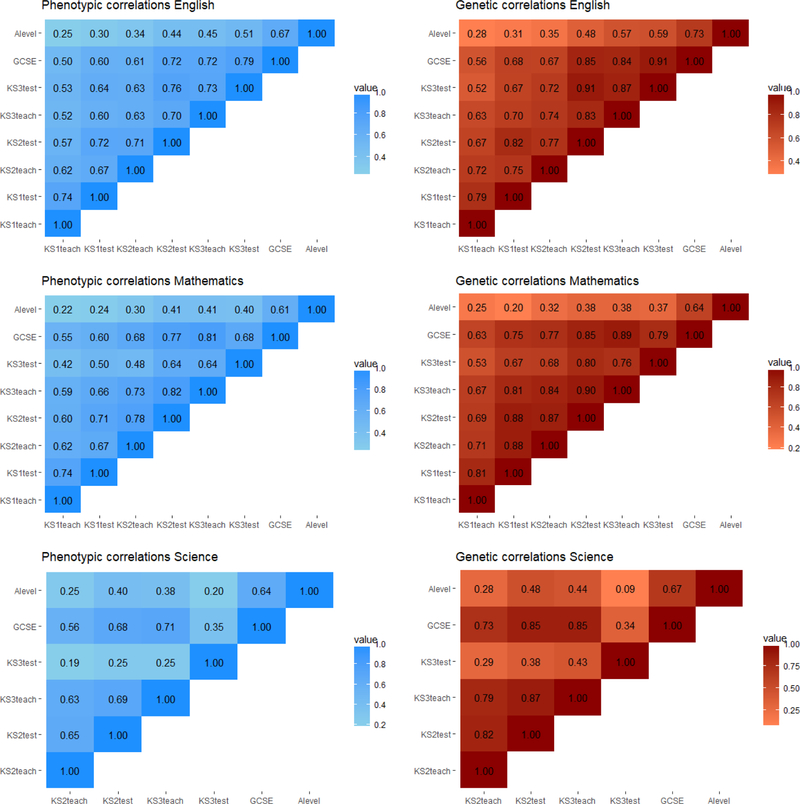
Multivariate analyses
Figure 2 presents the phenotypic and genetic correlations between teacher ratings and exam performance across school years for English, mathematics and science separately. There was high agreement between teacher grades and exam scores (phenotypic correlations ~ .70 and genetic correlations ~ .80) both contemporaneously and over time. These substantial phenotypic and genetic correlations between teacher grades and exam scores contemporaneously indicate that they are largely measuring the same ability, although some specificity is also suggested because the correlations are not 1.0 (Figure S2 presents phenotypic correlations between teacher grades and exams when randomly choosing the other half of the sample). The exception here is the KS3 Science test at age 14, which is less correlated with other achievement measures, possibly due to the lower reliability of the test (https://nationalpupildatabase.wikispaces.com/KS3). In terms of predicting GCSE test results at age 16, the average phenotypic correlation for teacher ratings across English, mathematics and science is 0.64; the average correlation for exam scores is 0.63 (ranging between .50 and .81). For A-level exam scores, the correlations were 0.33 for teachers (ranging between .22 and .45) and 0.36 for exam scores (ranging between .34-.54). (Table S3 presents the phenotypic, genetic, shared environmental and non-shared environmental correlations with 95% confidence intervals). The strongest correlation for A-level performance was with GCSE grades as expected, but no equivalent teacher grade is available at age 16.
Figure 2.
Phenotypic and genetic correlations between teacher ratings and exam performance in English, mathematics and science.
Note: teach= teacher ratings; test= test scores; KS1 = age 7; KS2= age 11; KS3= age 14, GCSE= age 16; A-level= age 18
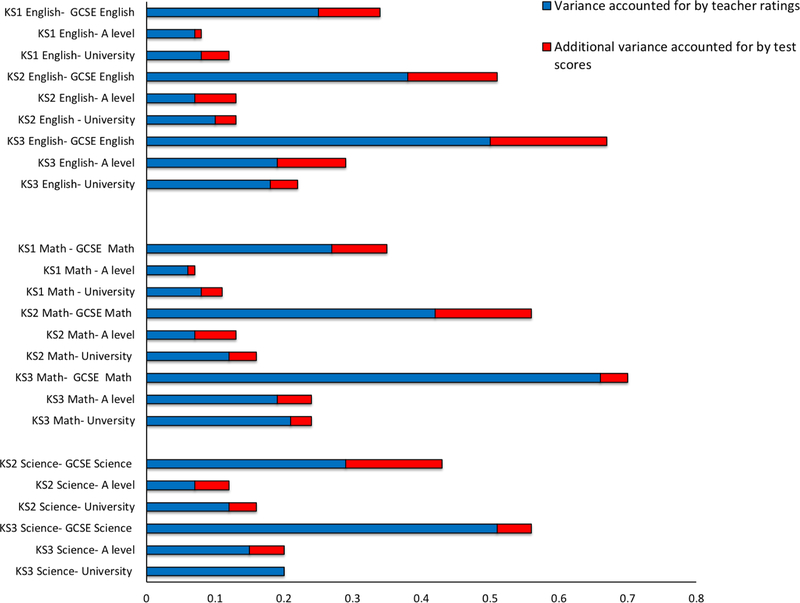
Next we assessed the extent to which standardized test scores add, phenotypically and genetically, to teacher ratings in predicting educational achievement in English, mathematics and science at the end of compulsory education at age 16 (GCSE results), at age 18 (A-level results), and beyond (University enrolment), phenotypically and genetically. Figure 3 summarizes the results of a series of hierarchical multiple regression analyses used to estimate the additional predictive power of test scores over teacher ratings in predicting the educational outcomes of GCSE scores, A-level scores and university entrance. Specifically, KS1 (age 7), KS2 (age 11), and KS3 (age 14) teacher grades were entered in the first step of the regression model and test scores at same ages were entered in the second step. Earlier teacher ratings provided 90% of the combined power of teacher ratings and test scores to predict educational outcomes. After controlling for teacher ratings, test scores explained on average 10% of the variance in GCSE, A-level and university entrance exam scores after controlling for teacher ratings. (See Tables S4–S6 for full results). On average the teacher ratings explained 41% of the variance in GCSE grades, and adding test scores increased the prediction to 51%. For university enrolment teacher assessments explained 13% of the variance, while test scores and teacher grades together explained 16%. The closer in time the teacher assessment was to the outcome variable, the stronger the prediction, but the contribution of teacher ratings compared to test scores remained roughly the same. When we repeated the analyses using the other half of the sample, then the results were highly similar, as presented in Figure S3. We also considered, conversely, the incremental variance explained by teacher assessments, when controlling for exam grades (Figure S4). As expected, teacher ratings also predict variance beyond exam performance.
Figure 3.
Phenotypic variance explained in GCSE exam performance, A-level exam performance and enrollment in a university or college course by teacher ratings in the first step of a hierarchical regression and test scores in the second step at KS1, KS2 and KS3.
Note: KS1 = age 7; KS2= age 11; KS3= age 14, GCSE= age 16; A-level= age 18
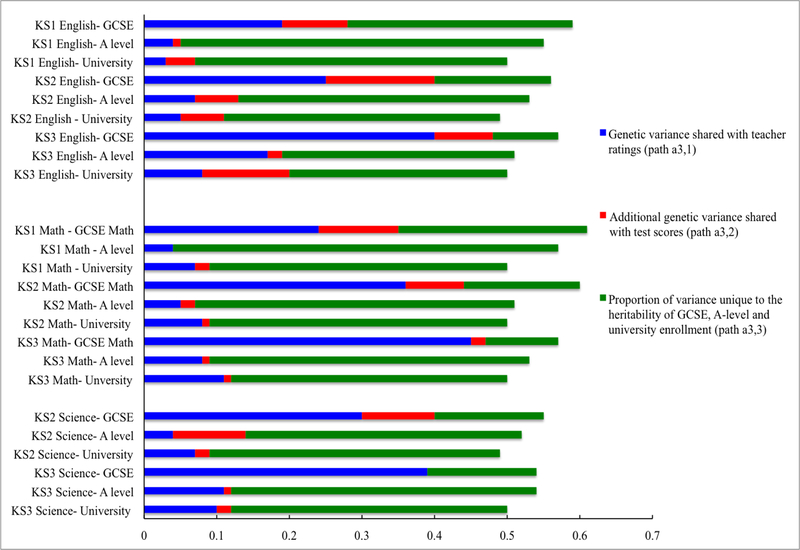
Next, we investigated the genetic etiology of these phenotypic predictions. Figure 4 summarizes the results of a series of trivariate Cholesky analyses (Appendix S1 and Figure S1) that investigated the proportion of heritable variation in GCSE, A-level and university entrance that can be explained by heritable variation in earlier teacher ratings and exam scores. Exam scores explained only a small proportion of additional genetic variance in GCSE, A-level and university entry when controlling for teacher grades. Interestingly, a substantial proportion of the heritability of GCSE, A-level and university entry is not shared with the heritability of earlier school performance, whether measured by teacher ratings or exam scores. (Full model fit statistics are presented in Tables S7- S15). The results of Cholesky analyses when exam scores were entered to the model in the first step are presented in Figure S5.
Figure 4.
Variance explained in the heritability of GCSE exam performance, A-level exam performance and enrollment to university/college course by the heritabilities of teacher ratings and exam performance in compulsory school years (Cholesky decomposition path a3,1 and a3,2; Figure S1).
Discussion
Using a large representative sample of the UK student population, we found that teacher assessments of school achievement correlate substantially (about .7) with standardized test scores across subjects (English, mathematics and science) and across ages (ages 7 to 14). KS3 Science test shows lower correlations with teacher ratings and with earlier assessments, which is most likely be due to lower reliability of this test (https://nationalpupildatabase.wikispaces.com/KS3). Twin analyses showed that heritability is similarly substantial (60% on average) for teacher assessments and test scores across subjects and ages. Multivariate genetic analyses showed that to a large extent the same genetic factors contribute to the prediction of educational outcomes for teacher assessments and test scores; genetic correlations between teacher assessments and test scores were about.
The second aim of the study was to compare teacher assessments and test scores in their ability to predict later educational outcomes. Our results showed that teacher assessments from ages 7 to 14 predict exam scores at ages 16 (GCSE) and 18 (A-levels) just as well as exam scores from ages 7 to 14, although their combined prediction is slightly higher. This result is surprising; the deck is stacked against teacher assessments in these analyses because the educational outcomes we considered (GCSE and A-level outcomes) are themselves test scores; no equivalent teacher assessments were available at ages 16 and 18. We have previously shown that performance in test scores is explained by a range of cognitive and non-cognitive factors (Krapohl et al., 2014), so it is possible that the extra variance explained by test scores in GCSE and A-level performance after controlling for teacher ratings is explained by the same cognitive and non-cognitive factors that contribute to earlier test performance.
Our findings that test scores correlate so highly with the teacher assessments raise questions about the value of the testing culture that characterizes compulsory education in the UK, culminating with the high-stakes GCSE exams at age 16 and A-level exams at the age of 18. Continuous high-stakes testing takes place during the primary as well as secondary education. Testing can be conceived as a stimulating activity that encourages both pupils and teaches to focus their efforts towards a common educational goal that fosters learning, but there are also major downsides to the testing process. First, the economic cost of testing is very high (see response to information request from Department of Education: https://www.gov.uk/government/publications/cost-of-administering-sats-in-primary-school/cost-of-administering-sats-in-primary-schools). Secondly, test taking is associated with narrower curricula, because children are taught only or predominantly what is specifically tested in the exams (Alexander, 2010; Cranney et al., 2009; Hutchings, 2015; Rothstein, 2009). Thirdly, schools that do not meet targets are under increased pressure to improve test results, and these accountability measures are increasingly turning schools into “exam factories” (Hutchings, 2015) that neglect the wellbeing of teachers and pupils (Hutchings, 2015). While the performance in GCSE and A-level (as well as in exams at ages 7, 11, and 14) was originally intended to provide an accurate prediction of future scholastic and life outcomes, it was not intended to replace the outcome (target) itself. This shift of standardized tests from being predictors to criteria is questionable and is in line with Goodhart’s law: once an indicator is used as a target, it loses its value as an indicator (Strathern, 1997).
Although the effect of exams on mental health outcomes was not studied in the present analyses, evidence suggests that these high-stakes exams have a negative impact on children’s wellbeing and mental health (Carmichael et al., 2017; Childline, 2014, 2015; Coldwell & Willis, 2017; Hutchings, 2015; McDonald, 2001). Educational pressures can lead to mental health problems that may cast a long shadow later in life for children (Kelly-Irving et al., 2013; Kessler, Foster, Saunders, & Stang, 1995), for children’s families (Bogels & Brechman-Toussaint, 2006) and for the economy (Prince et al., 2007). Studying the links between school experiences and mental health problems is part of our future research program.
We are not suggesting that students’ progress should not be monitored or arguing against testing in general. For example, it is possible that in an increasingly technological society light-touch frequent testing can aid learning (Dunlosky, Rawson, Marsh, Nathan, & Willingham, 2013). However, we question the value of high-stakes exams so early and regularly in children’s lives. Although teacher assessments do not always accurately reflect students’ ability because of biases and stereotypes held by teachers (Burgess & Greaves, 2013; Campbell, 2015), our results show teacher assessments and exam scores are highly correlated both contemporaneously and over time. The reliability and predictive validity of teacher assessments in the UK may reflect the highly standardized nature of teacher assessments in the UK; validity could be the product of either teachers’ knowledge of pupils’ previous performance or assessments from previous years.
To the extent that assessments and tests are correlated, both during primary as well as secondary education, a case could be made for reducing or eliminating either one of them. We believe that teacher evaluation should play greater role for three reasons. First, teacher ratings assess performance over time, not just a few critical and highly stressful days of testing. Second, ongoing teacher monitoring of student performance is essential for effective teaching (Angelo & Cross, 1993). And third, teacher ratings themselves are to some extent based on in-class tests, which promote consolidation of learning, especially when done regularly and frequently (unlike a single high-stakes examination).
We acknowledge that there has to be an accountability system for monitoring schools and teachers, which may be more challenging to implement without external tests. There are already accountability measures in use such as the Ofsted inspections (The Office for Standards in Education, Children’s Services and Skills: https://www.gov.uk/government/organisations/ofsted/about), which assess aspects of education including teaching, children’s welfare and school management. An additional possible way to reconcile the monitoring of schools without standardized tests is to test random samples of pupils without notice, which is likely to be less stressful, while providing accountability.
One unavoidable limitation of the present study is the absence of teacher assessments at ages 16 and 18. Because the outcome measures used in the analyses, GCSE and A-level exam scores, are also test results, shared method variance is likely to contribute to their prediction from test scores during primary and secondary schools when teacher assessments are controlled. For this reason, it would be interesting to study how the predictions from teacher assessments and exam score compare when considering life outcomes in adulthood that are not test scores -- for example, university graduation, occupational success, as well as life satisfaction and wellbeing. In addition, we know that some of our participants who have not yet enrolled in university courses may do so later in life, therefore, it is important to repeat the analyses at later stages, which is part of our future research program. Another possible limitation is the A-level exam grade we used, which was a mean of all exams taken, rather than taking into account the number of A-levels, although most students take three or four A-level exams. We also acknowledge that our results and interpretations might not generalize to other countries such as the US, which have more decentralized educational systems.
We have demonstrated a remarkably high agreement between teacher assessments and standardized tests, both phenotypically and genetically. We believe that these results, based on a large and population-representative sample, can inform the debate about the appropriate use of high stakes testing during elementary and secondary education. The financial, pedagogical and emotional costs of high-stakes testing are substantial, especially compared to its modest benefits. For these reasons, we view our results as support for the standardization and wider use of teacher assessments and the reduction of testing during compulsory education. We should trust teachers to implement the curriculum and to monitor students’ progress, abilities and inclinations. This would arguably benefit the wellbeing of students as well as teachers, and help to bring joy back to the classroom.
Supplementary Material
Key points.
Teacher assessments are as reliable and heritable as standardized test scores (average heritability around 60%).
Teacher assessments and test scores correlate strongly phenotypically (r ~.70) and genetically (genetic correlation ~ .80) both contemporaneously and over time.
Teacher assessments account for ~90% of the variance of exam performance at ages 16 and 18, although test scores during primary and secondary exams explain some additional variance.
Teacher assessments during compulsory education explain ~ 13% of variance in university enrollment, while test scores add an additional ~3% to that prediction.
Acknowledgements
TEDS is supported by a program grant to RP from the UK Medical Research Council [MR/M021475/1 and previously G0901245], with additional support from the US National Institutes of Health [HD044454; HD059215]. The authors gratefully acknowledge the ongoing contribution of the participants in the Twins Early Development Study (TEDS) and their families. R.P. is supported by a Medical Research Council Research Professorship award [G19/2] and a European Research Council Advanced Investigator award [295366]. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript. M.M. is partly supported by a David Wechsler Early Career Grant for Innovative Work in Cognition. The authors have declared that they have no competing or potential conflicts of interest.
Footnotes
Conflict of interest statement: No conflicts declared.
Supporting information
Additional supporting information may be found online in the Supporting Information section at the end of this article.
Appendix S1. Description of methods.
Table S1. Descriptive statistics. Means (standard deviations in parentheses) for educational achievement.
Table S2. Twin intraclass correlations and model fitting results for univariate analyses of additive genetic (A), shared environmental (C), and non-shared environmental (E) components of variance for educational achievement (95% confidence intervals in parentheses).
Table S3. Phenotypic correlations and proportion of phenotypic correlations explained by A, C, E between teacher ratings versus exam performance across compulsory education and GCSE exam grade at the end of compulsory education (95% confidence intervals).
Table S4-S6. Full results of test scores after controlling for teacher ratings.
Table S7-S15. Full model fit statistics.
Figure S1. Trivariate Cholesky decomposition.
Figure S2. Phenotypic correlations between teacher ratings and exam performance in English, mathematics and science, when randomly choosing the other half of the sample that was not included in the main phenotypic analyses as presented in Figure 2.
Figure S3. Phenotypic variance explained in GCSE exam performance, A-level exam performance and enrollment in a university or college course by teacher ratings in the first step of a hierarchical regression and test scores in the second step at KS1, KS2 and KS3, when randomly choosing the other half of the sample that was not included in the main phenotypic analyses as presented in Figure 3.
Figure S4. Phenotypic variance explained in GCSE exam performance, A-level exam performance and enrollment in a university or college course by test scores in the first step of a hierarchical regression and teacher grades in the second step at KS1, KS2 and KS3.
Figure S5. Variance explained in the heritability of GCSE exam performance, A-level exam performance and enrollment to university/college course by the heritabilities of exam performance and teacher ratings in compulsory school years (Cholesky decomposition path a3,1 and a3,2; see Figure S1).
References
- Alexander R (2010). Children, their world, their education. Final report and recommendations of the Cambridge Primary Review [Google Scholar]
- Angelo TA, & Cross KP (1993). Classroom Assessment Techniques Jossey-Bass Publications Retrieved from http://alh.sagepub.com/cgi/doi/10.1177/1469787411402482
- Arendt JN (2005). Does education cause better health? A panel data analysis using school reforms for identification. Economics of Education Review, 24(2), 149–160. 10.1016/j.econedurev.2004.04.008 [DOI] [Google Scholar]
- Bogels SM, & Brechman-Toussaint ML (2006). Family issues in child anxiety: Attachment, family functioning, parental rearing and beliefs. Clinical Psychology Review, 26(7), 834–856. 10.1016/j.cpr.2005.08.001 [DOI] [PubMed] [Google Scholar]
- Boker S, Neale M, Maes H, Wilde M, Spiegel M, Brick T, … Fox J (2011). OpenMx: an open source extended structural equation modeling framework. Psychometrika, 76, 306–317. 10.1007/s11336-010-9200-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bratsberg B, & Rogeberg O (2017). Childhood socioeconomic status does not explain the IQ-mortality gradient. Intelligence, 62, 148–154. [Google Scholar]
- Burgess S, & Greaves E (2013). Test Scores, Subjective Assessment, and Stereotyping of Ethnic Minorities. Journal of Labor Economics, 31(3), 535–576. 10.1086/669340 [DOI] [Google Scholar]
- Campbell T (2015). Stereotyped at seven? Biases in teacher judgement of pupils’ ability and attainment. Journal of Social Policy, 44(3), 517–547. 10.1017/S0047279415000227 [DOI] [Google Scholar]
- Carmichael N, Allan L, Austin I, Donelan M, Fellows M, Fernandes S, … Wragg W (2017). The House of Commons Educational Committee report: Primary Assesment [Google Scholar]
- Cesarini D, & Visscher PM (2017). Genetics and educational attainment. Npj Science of Learning, 2(1), 4 10.1038/s41539-017-0005-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Childline. (2014). Can I tell you something? ChildLine Review 2012–13 [Google Scholar]
- Childline. (2015). Under pressure ChildLine annual review 2013–2014 [Google Scholar]
- Coldwell M, & Willis B (2017). Tests as boundary signifiers: level 6 tests and the primary secondary divide. Curriculum Journal, 28(4), 578–597. 10.1080/09585176.2017.1330220 [DOI] [Google Scholar]
- Cranney J, Ahn M, McKinnon R, Morris S, & Watts K (2009). The testing effect, collaborative learning, and retrieval-induced facilitation in a classroom setting. European Journal of Cognitive Psychology, 21(6), 919–940. 10.1080/09541440802413505 [DOI] [Google Scholar]
- Cutler DM, & Lleras-Muney A (2012). Education and health: insights from international comparisons (No. 17738) NBER Working Papers. [Google Scholar]
- Dunlosky J, Rawson KA, Marsh EJ, Nathan MJ, & Willingham DT (2013). Improving students’ learning with effective learning techniques: Promising directions from cognitive and educational psychology. Psychological Science in the Public Interest, Supplement 10.1177/1529100612453266 [DOI] [PubMed] [Google Scholar]
- Embse NVD, & Hasson R (2012). Test anxiety and high-stakes test performance between school settings: Implications for educators. Preventing School Failure: Alternative Education for Children and Youth, 56, 180–187. 10.1080/1045988X.2011.633285 [DOI] [Google Scholar]
- Gottfredson LS, & Deary IJ (2004). Intelligence Longevity, Predicts but and Why ? Current Directions in Psychological Science, 13(1), 1–4. [Google Scholar]
- Haworth CMA, Davis OSP, & Plomin R (2013). Twins Early Development Study (TEDS): A genetically sensitive investigation of cognitive and behavioral development from childhood to young adulthood. Twin Research and Human Genetics : The Official Journal of the International Society for Twin Studies, 16(1), 117–25. 10.1017/thg.2012.91 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heath A, Berg K, Eaves L, & Solaas M (1985). Education policy and the heritability of educational attainment. Nature, 314(6013), 734–736. 10.1038/314734a0 [DOI] [PubMed] [Google Scholar]
- Hutchings M (2015). Exam Factories?: The Impact of Accountability Measures on Children and Young People. The National Union of Teachers [Google Scholar]
- Kelly-Irving M, Lepage B, Dedieu D, Bartley M, Blane D, Grosclaude P, … Delpierre C (2013). Adverse childhood experiences and premature all-cause mortality. Eur J Epidemiol, 28(9), 721–734. 10.1007/s10654-013-9832-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kessler RC, Foster CL, Saunders WB, & Stang PE (1995). Social consequences of psychiatric disorders, I: Educational attainment. American Journal of Psychiatry, 152(7), 1026–1032. [DOI] [PubMed] [Google Scholar]
- Knopik VS, Neiderhiser JM, DeFries JC, & Plomin R (2017). Behavioral Genetics 7th ed. Worth Publishers, New York. [Google Scholar]
- Kovas Y, Haworth CMA, Dale PS, & Plomin R (2007). The genetic and environmental origins of learning abilities and disabilities in the early school years. Monographs of the Society for Research in Child Development, 72(3), 1–144. 10.1111/j.1540-5834.2007.00439.x [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krapohl E, Rimfeld K, Shakeshaft NG, Trzaskowski M, McMillan A, Pingault J-B, … Plomin R (2014). The high heritability of educational achievement reflects many genetically influenced traits, not just intelligence. Proceedings of the National Academy of Sciences of the United States of America, 111(42), 15273–15278. 10.1073/pnas.1408777111 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Larsen DP, Butler AC, & Roediger HL (2009). Repeated testing improves long-term retention relative to repeated study: A randomised controlled trial. Medical Education, 43(12), 1174–1181. 10.1111/j.1365-2923.2009.03518.x [DOI] [PubMed] [Google Scholar]
- McDermott KB, Agarwal PK, D’Antonio L, Roediger HLI, & McDaniel MA (2014). Both multiple-choice and short-answer quizzes enhance later exam performance in middle and high school classes. Journal of Experimental Psychology: Applied, 20(1), 3–21. 10.1037/xap0000004 [DOI] [PubMed] [Google Scholar]
- McDonald AS (2001). The Prevalence and Effects of Test Anxiety in School Children. Educational Psychology, 21(1), 89–101. 10.1080/01443410124641 [DOI] [Google Scholar]
- Oliver BR, & Plomin R (2007). Twins’ Early Development Study (TEDS): a multivariate, longitudinal genetic investigation of language, cognition and behavior problems from childhood through adolescence. Twin Research and Human Genetics : The Official Journal of the International Society for Twin Studies, 10, 96–105. 10.1375/twin.5.5.444 [DOI] [PubMed] [Google Scholar]
- Organisation for Economic Co-operation and Development (OECD). (2013). Education at a Glance 2013: Highlights Oecd. [Google Scholar]
- Price TS, Freeman B, Craig I, Petrill SA, Ebersole L, & Plomin R (2000). Infant zygosity can be assigned by parental report questionnaire data. Twin Research : The Official Journal of the International Society for Twin Studies, 3, 129–133. 10.1375/twin.3.3.129 [DOI] [PubMed] [Google Scholar]
- Prince M, Patel V, Saxena S, Maj M, Maselko J, Phillips MR, & Rahman A (2007). No health without mental health. Lancet 10.1016/S0140-6736(07)61238-0 [DOI] [PubMed] [Google Scholar]
- Rijsdijk FV, & Sham PC (2002). Analytic approaches to twin data using structural equation models. Briefings in Bioinformatics, 3(2), 119–133. 10.1093/bib/3.2.119 [DOI] [PubMed] [Google Scholar]
- Rothstein R (2009). Grading education: getting accountability right New York, New York: New York: Teachers’ College Press. [Google Scholar]
- Segool NK, Carlson JS, Goforth AN, Von der Embse N, & Barterian JA (2013). Heightened test anxiety among young children: Elementary school students’ anxious responses to high-stakes testing. Psychology in the Schools, 50(5), 489–499. 10.1002/pits.21689 [DOI] [Google Scholar]
- Shakeshaft NG, Trzaskowski M, McMillan A, Rimfeld K, Krapohl E, Haworth CMA, … Plomin R (2013). Strong genetic influence on a UK nationwide test of educational achievement at the end of compulsory education at age 16. PLoS ONE, 8, e80341 10.1371/journal.pone.0080341 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith-Woolley E, Pingault J-B, Selzam S, Rimfeld K, Krapohl E, von Stumm S, … Plomin R (2018). Differences in exam performance between pupils attending selective and non-selective schools mirror the genetic differences between them. Npj Science of Learning, 3(1), 3 10.1038/s41539-018-0019-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Strathern M (1997). “Improving ratings”: audit in the British University system. European Review Marilyn Strathern European Review Eur. Rev, 55(5), 305–321. 10.1002/(SICI)1234-981X(199707)5:33.0.CO;2-4 [DOI] [Google Scholar]
- Wang Z, Shakeshaft N, Schofield K, & Malanchini M (2018). Anxiety is not enough to drive me away : A latent profile analysis on math anxiety and math motivation. PLoS ONE, 13(2): e01, 1–16. 10.1371/journal.pone.0192072 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wood SG, Hart SA, Little CW, & Phillips BM (2016). Test Anxiety and a High-Stakes Standardized Reading Comprehension Test: A Behavioral Genetics Perspective. Merrill-Palmer Quarterly, 62(3), Article 1. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.