Nanogold Plasmon Resonance-Based Glucose Sensing. 2. Wavelength-Ratiometric Resonance Light Scattering

Abstract

Gold colloids are well known to display strong plasmon absorption bands due to electron oscillations induced by the incident light. When the colloids are in proximity, the plasmon absorption bands are often perturbed. This has enabled us recently to successfully develop a glucose sensing platform based on the disassociation of dextran-coated gold colloids, cross-linked with Con A, by glucose. However, a much more useful and simpler property of gold colloids, which has been ill explored with regard to sensing, is their ability to efficiently scatter excitation light. We have found that our nanogold sensing aggregates are indeed efficient light scatters around the nanogold plasmon absorption band. By measuring the ratio of scattered light intensities at two different arbitrary wavelengths, 560 and 680 nm, glucose concentrations can be readily determined from a few millimolar up to ~60 mM, using a simple white light LED and detection system. Further, by measuring the ratio of the scattered intensities, this sensing approach is independent of the total sensing aggregate concentration and the excitation and detection instrumentation fluctuations or drifts. This simplistic and low-cost approach to glucose sensing, coupled with the sensing aggreagates’ ability to scatter red light, suggests the potential use of these aggregates for use in physiological transdermal glucose monitoring, either for implantable skin sensors or glucose sensing tattoos (discussed later).

Colloidal gold nanoparticles have been studied extensively in recent years due to their optical properties^1–4 and diverse applications.^5–18 Colloidal suspensions display intense colors due to intense light absorption and scattering. These properties are due to electron oscillations in the metallic particles, induced by the incident light field, giving rise to the so-called plasmon absorption.^1–4

Most applications of metallic colloids to date have been concerned with measurements of the plasmon absorption, as seen by direct absorption or even by visual color, and the subsequent changes induced by either aggregation or flocculation of the nanoparticles in solution. Both experimental and theoretical studies have shown that the resonant wavelength of two proximity and coupled nanoparticles is significantly red-shifted from that of the monomers, where the shift decays approximately exponentially with increasing particle spacing, decreasing to almost zero when the distance between the nanoparticles exceeds ~ 2.5 times the particle size.¹⁹ Coupled with the fact that gold and silver nanoparticles are amenable to the attachment of biomolecules or ligands through well-known thiol and amino chemistry, this has led to a wealth of absorption based colloid proximity sensors for pH,²⁰ DNA,^14,15 metal ions,^16,17 and antibodies,¹⁸ to name but just a few.

However, one property of metallic nanoparticles that has received very little attention^21,22 is their ability to efficiently scatter light.^1,2 It has been reported that light scattered from individual colloids can be equivalent to the intensity of 10⁵ fluorescein molecules,^1,2 which has the potential to offer new approaches to bioaffinity based colloid sensing. While the scattered light from colloids does not have the information content of fluorescence, and therefore at first glance is unlikely to provide an opportunity for measurements that are not sensitive to total intensity such as anisotropy or wavelength-ratiometric measurements, we have found that changes in the plasmon absorption can be monitored by changes in the intensity of scattered light and its dependence on wavelength. We have subsequently applied our new approach²¹ to the detection of glucose, using a plasmon absorption based glucose sensing platform, recently reported by us.²³

Resonance light scattering spectroscopy has been used for some years to study the formation of the aggregation of chromophores in complex systems,^24–41 such as dye-protein,^24–27 dye-nucleic acids,^28–35 porphyrin,^36–38 dye-surfactant,³⁹ palladium(II)⁴⁰ and yttrium,⁴¹ to name just a few examples.

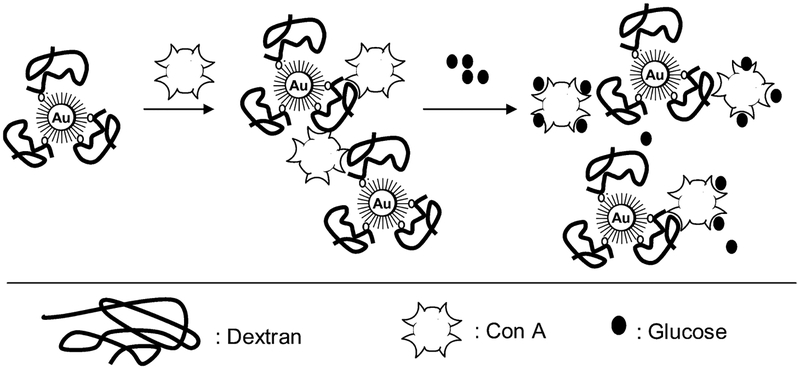
Resonance light scattering occurs when the incident beam is of energy similar to an absorption band produced by an oscillating dipole, the effect amplified when two or more dipoles are strongly coupled. However, there have been very few reports with noble-metal particles and their aggregation to date^21,22 and only one report by us of wavelength-ratiometric scattering measurements using this phenomenon.²¹ Subsequently in this paper we report a wavelength-ratiometric resonance light scattering approach to glucose sensing using a mechanism based on the aggregation and dissociation of gold nanoparticles, Scheme 1. We have recently shown that the tetravalent protein concanavalin A (Con A) can readily cross-link dextran-coated 20-nm gold particles.²³ This results in a broadening and red shift in the gold plasmon absorption. The addition of glucose competitively binds to Con A, reversing the plasmon changes, providing us with a reversible platform for testing our wavelength-ratiometric resonance light scattering approach. Our new approach has several key advantages over traditional colloidal plasmon absorption based sensing schemes including the following:

1. Scattering based sensing can be achieved using a variety of wavelengths, including in the 600–900-nm therapeutic range where the absorption from skin and blood is low.⁴²

2. Glucose sensing based on scattering can be achieved using single or multiple wavelengths, or even wavelength ratiometrically.

3. Wavelength-ratiometric scattering measurements are independent of the total nanogold sensing aggregate concentration.

4. Wavelength-ratiometric scattering measurements are not dependent on the total light intensity and are therefore not perturbed by excitation source instabilities or drifts.

5. Very simple and low-cost instrumentation can be employed for wavelength-ratiometric sensing, enabling the widespread use of the technology and its use in field-deployable devices.

6. Wavelength-ratiometric resonance light scattering measurements can also be done in tandem with absorption and/or fluorescence based measurements.

7. The wavelength-ratiometric resonance light scattering technique can also be applied to the many plasmon absorption schemes already reported, such as for DNA detection, etc.^14,15

8. The detection limits of the sensing system based on scattering measurements can be somewhat tuned by using different size colloids, where the cross section for scatter increases for larger colloids.^1,2

Scheme 1.

Glucose Sensing Scheme Based on the Dissociation of Dextran-Coated Gold Nanoparticles/Con A Aggregates and Their Respective Light Scattering Properties

Finally, for some years our laboratories have been engaged in developing new chromophores based on boronic acid chemistry for glucose sensing.^43–46 While these probes have been successful in colorimetrically determining glucose concentrations greated than a few millimolar, they have not provided opportunities for actual physiological or cellular measurements that are required at red wavelengths. The use of gold metallic colloids for glucose sensing described here may alleviate this problem, the sensing aggregates also having similar glucose dynamic sensing ranges, i.e., ≈1–60 mM.

EXPERIMENTAL SECTION

Materials.

Colloidal gold dispersions (monodisperse, 20-nm average particle diameter), Con A (from Canavalia ensiformis), dextran (average molecular weight 170 000), hydrogen peroxide, sulfuric acid, sodium phosphate monobasic, phosphate-buffered saline (PBS), absolute ethanol, (2-(2-aminoethoxy)ethanol (AEE), and N-hydroxy-2,5-pyrrolidinedione (NHS) were obtained from Sigma. 16-Mercaptohexadecanoic acid (16-MHDA) and polyoxyethylene (20) sorbitan monolaurate (Tween 20), epichlorohydrin, 2-methoxyethyl ether, and nitric acid were obtained from Aldrich. N-3-(Dimethylaminopropyl)-N′-ethylcarbodiimide (EDC) was obtained from Fluka. All chemicals were used as received.

Buffers and Solutions.

Sodium phosphate monobasic buffer solution was prepared to a 10 mM concentration at pH 7. PBS was dissolved in deionized water, and the pH was adjusted to 7.4. Exact pH values for buffer solutions were obtained using a Beckman pH meter. Deionized water (>18 MΩ/cm) was used in the preparation of all buffer solutions. All glassware was washed with “piranha solution” (3:7 30% H₂O₂/H₂SO₄) prior to use. Solutions of 0.50 mM 16-MHDA were prepared in degassed ethanol. Tween 20 solutions were prepared in sodium phosphate buffer at pH 7.

Preparation of the Dextran-Coated Gold Colloids.

The immobilization of dextran onto gold colloids was performed as described previously.²³ In summary, first, the surfaces of the gold colloids are modified with a long-chain carboxyl-terminated alkane thiol (16-MHDA).⁴⁷ The carboxylic acid groups are activated by EDC and NHS to form active NHS-esters, and the AEE reacted with NHS-esters resulting in an addition of a hydroxyl-terminated second layer to the surface of the gold colloids. The hydroxyl groups are activated using epicholorohydrin to which dextran is coupled covalently.⁴⁸ Excess dextran was removed by centrifugation. All solutions of dextran-coated gold colloids were stored in polypropylene centrifuge tubes in the dark to prevent light-induced flocculation of the gold colloids and oxidation of the alkane thiols.⁴⁹ The nanosensing aggregates can be seen in Scheme 1 and have been described in detail previously by the authors.²³

Methods.

All absorption measurements were performed using a Varian UV/VIS 50 spectrophotometer using quartz cuvettes (Starna). Standard Varian kinetic software and Sigma Plot 8.0 were used in the data analysis.

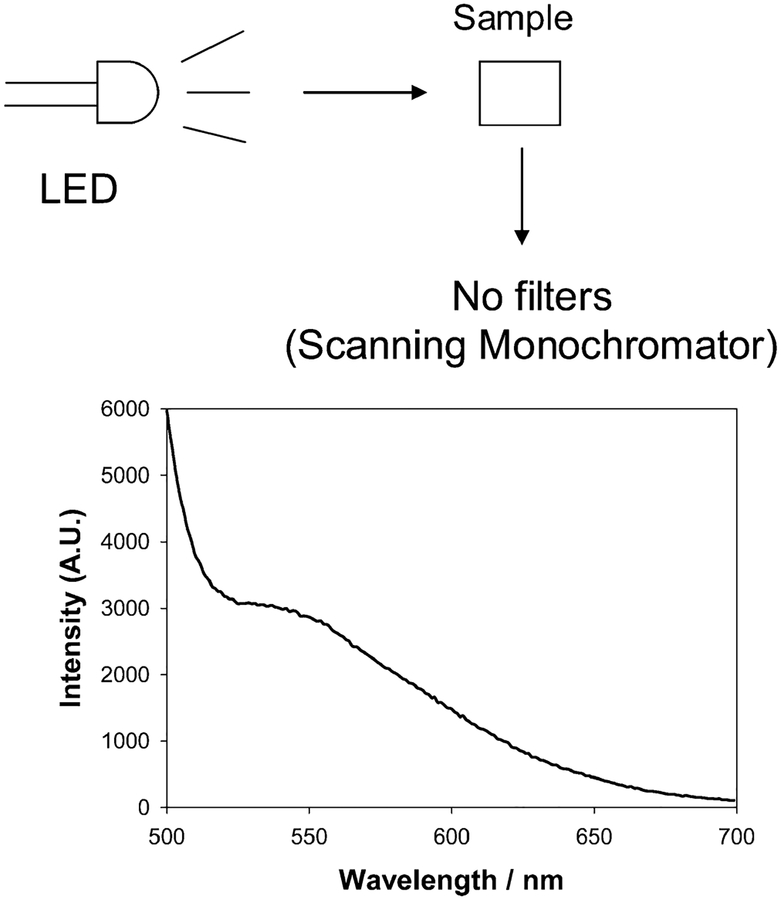
Scattering measurements were performed using a white light LED (RadioShack) and a simple scanning monochromator (no filters), as shown in Figure 1, top, with a simple orthogonal geometry. Figure 1, bottom, shows the scattering profile for the white light LED obtained using Ludox SM30 (DuPont), which is often used as a scattering medium in both steady-state and time-resolved fluorescence measurements.⁴² The LED shows a blue spike in its emission, with a tail toward longer wavelengths. This is indeed typical for white light LEDs and reflects the blue-chip pumped phosphor construction of a white light LED. We examined the stability of the LED and found its spectral profile to be very stable with time. Subsequently for glucose nanosensor scattering measurements, the LED spectrum was not subtracted, allowing the simplicity of the approach to be demonstrated. In control experiments we were able to correct the scattering spectrum with regard to the LED’s spectral profile, but our studies found this to have very little effect on the dynamic glucose sensing range.

Figure 1.

Experimental setup for wavelength-dependent ratiometric-scattering based glucose sensing (top) and wavelength-dependent scattering from LUDOX (30 nm) particles upon white LED illumination (bottom).

RESULTS AND DISCUSSION

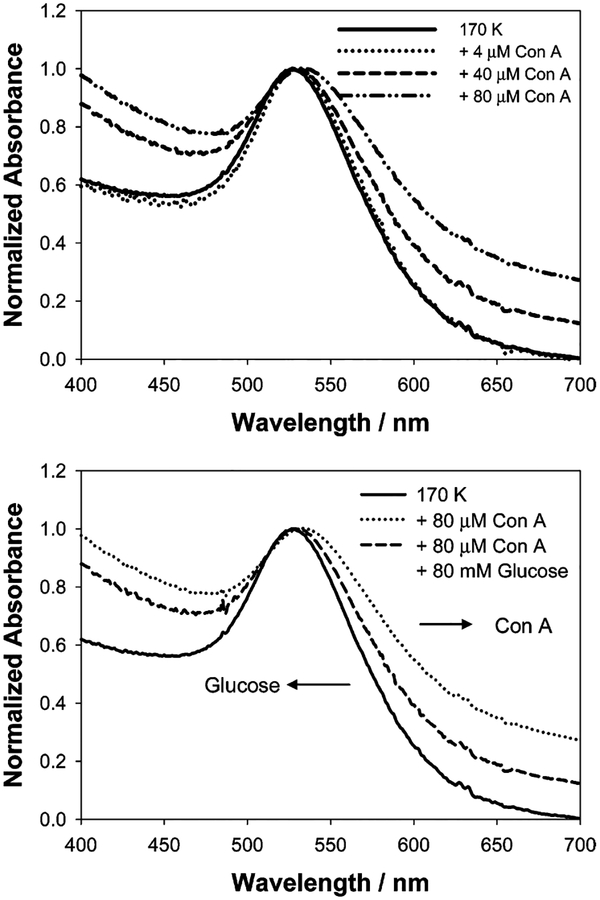
In our recent paper we have shown that the addition of Con A to various compositions and sizes of dextran-coated gold nanoparticles, Scheme 1, results in a broadening of the ~520-nm gold plasmon absorption²³ as the gold colloids are bought into proximity, Figure 2, top. The addition of glucose subsequently disassociates the Con A aggregated complexes, Scheme 1, resulting in a narrowing and blue shift in the plasmon to its original value, depending on the concentrations used, Figure 2, bottom. In the new wavelength-ratiometric scattering studies reported here, we also employed 170 K dextran-coated gold nanoparticles and used Con A concentrations that we previously found resulted in notable plasmon changes. Glucose concentrations of >1 mM were used to reflect the potential role of these scattering sensors for physiological hyperglycemic monitoring.

Figure 2.

Normalized absorbance spectra of dextran-coated gold nanoparticles in the absence and in the presence of Con A (top) and after the addition of glucose (bottom). The absorbance of dextran-coated gold nanoparticles at 535 nm was 0.20 (0.16 nM; this concentration was used for the remainder of the paper).

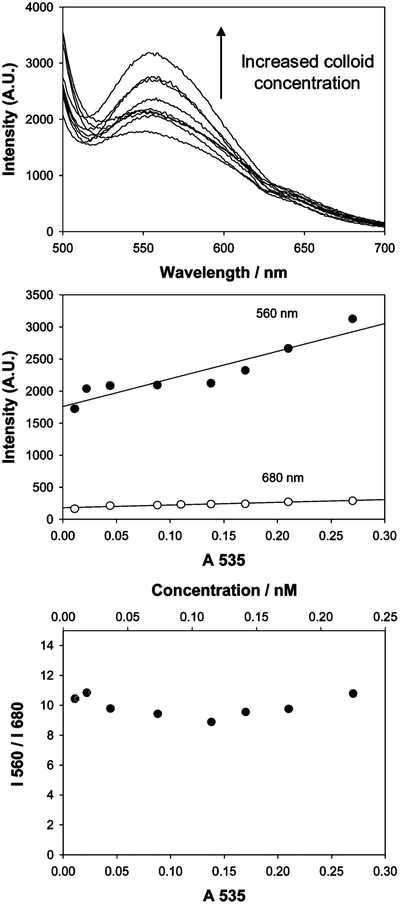
Figure 3, top, shows the wavelength and concentration dependent scattering from dextran-coated gold nanoparticles upon white LED illumination. The concentration of the particles was increased up to 0.25 nM, which corresponded to a gold optical density at 535 nm of 0.3. The scattering intensity at 560 nm increased with increasing nanogold concentration, Figure 3, top and middle, but was approximately constant at 680 nm. This result is most encouraging for scattering based sensors based on plasmon absorption changes and reflects the independent contribution of the scattering process to the gold colloid extinction coefficient, which is composed of both an absorption and a scattering component.^1,2 Subsequently we notice a red-shifted scattering spectrum as compared to the absorption spectrum, cf. Figures 2 and 3, top, noting that the dip in the curves at ~625 nm is a monochromator artifact. Interestingly, the ratio of these arbitrary scattered intensity wavelengths is constant for low optical density solutions, indicating that the wavelength-ratiometric scattering nature of the colloids is not dependent on the total nanogold concentration, an important requirement for sensing applications. Also of significance, Figure 3, bottom, shows a I₅₆₀/I₆₈₀ ratio of ~10, an attractive dynamic range over which to measure a ratio and, therefore, glucose concentrations. While beyond the theme of this text it is informative to consider the fluctuations in the ratiometric scatter presented in Figure 3, bottom. While one would have expected this to be more linear, we have attributed the <10% spread in ratio between the points as due to the inefficient mixing of the dextran-coated gold nanoparticles upon dilution. As we will show later, the data are well described (and reproducible) by the fitted functions to the time-dependent scattering plots, suggesting that there is little statistical scattering of the data points.

Figure 3.

Wavelength-dependent scattering from dextran-coated gold nanoparticles upon white LED illumination (top), scattered intensities at 560 and 680 nm vs concentration of the same nanoparticles (middle), and ratios of the scattered intensities vs concentration of the same nanoparticles (bottom).

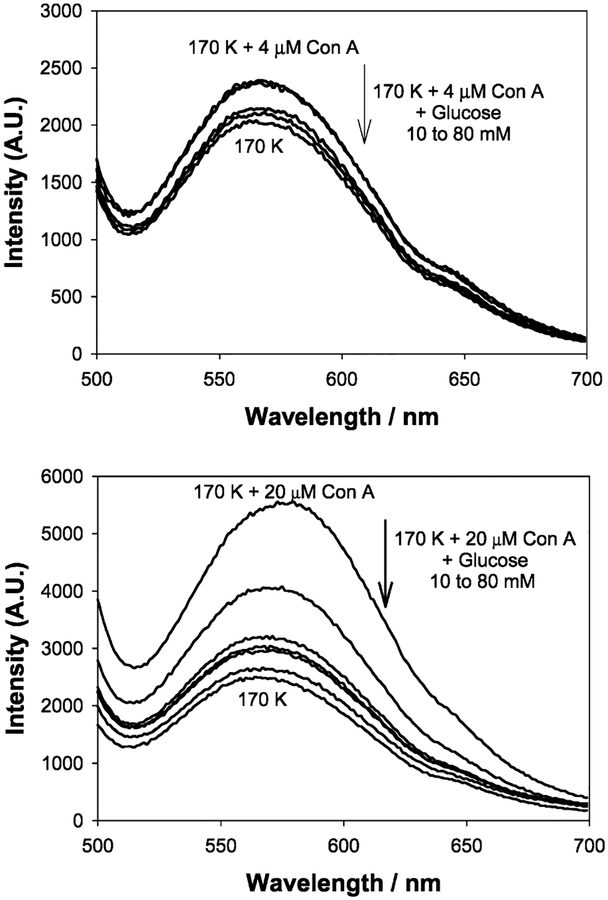
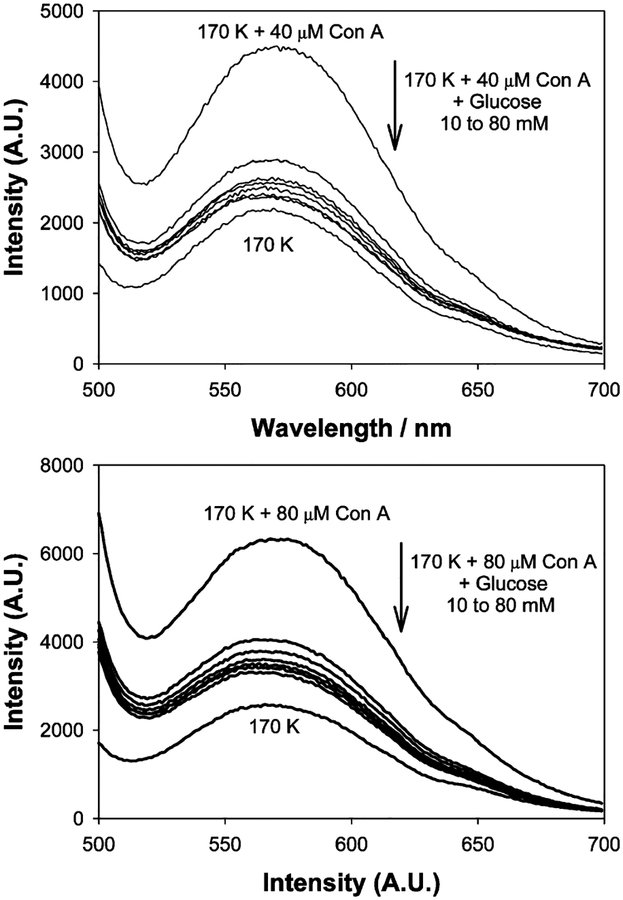
Upon addition of glucose to the Con A aggregated, dextran-coated nanogold, the scattering spectra typically decrease in intensity and slightly blue shift, in accordance with the disassociation of the aggregates, Figures 4 and 5. Similar to previous findings with our absorption based measurements,²³ we found that the greatest scattering changes were obtained for a 170 K dextran sensing aggregate, which had been cross-linked with 20 μM Con A, Figure 4, bottom. These scattering spectra were taken after ~45 min, at the 90% response times, i.e., the time after which the signal had changed by 90% of its original value, as previously described by the authors.²³

Figure 4.

Wavelength-dependent scattering from dextran-coated gold nanoparticles after the addition of glucose with 4 (top) and 20 μM Con A (bottom) upon white LED illumination.

Figure 5.

Wavelength-dependent scattering from dextran-coated gold nanoparticles after the addition of glucose with 40 (top) and 80 μM Con A (bottom) upon white LED illumination.

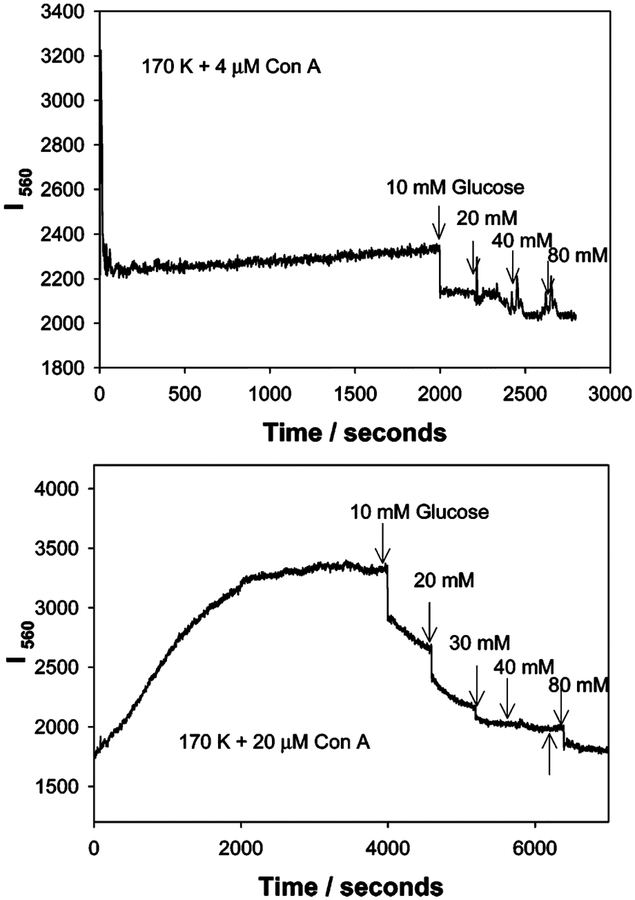
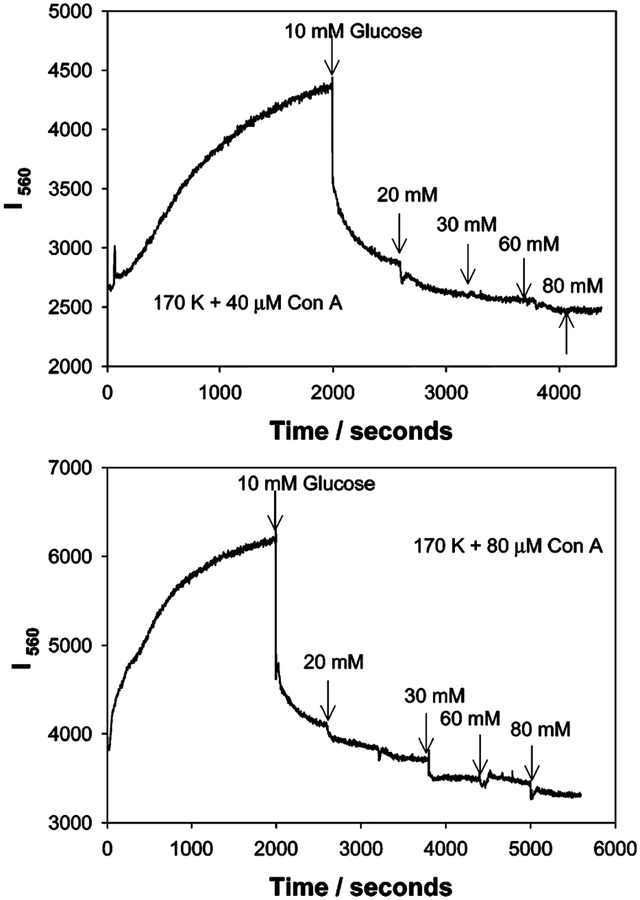
Figures 6 and 7 show the time-dependent scattering at 560 nm for the sensing aggregate compositions shown in Figures 4 and 5. In Figure 6, top, we can clearly see the slow aggregation of the system, indicated by the gradual change in 560-nm scatter, itself induced by 4 μM Con A. The addition of glucose decreases the I₅₅₀ scatter as the aggregates disassociate. In comparison, much greater changes in scatter can be observed at 560 nm by the addition of 20 μM Con A, the addition of glucose after the 90% response time, and returning the scatter value to approximately the initial unaggregated scatter value, i.e., before Con A addition, Figure 6, bottom. As expected, increasing the concentration of Con A results in a greater extent of scattering from the larger aggregates, Figure 7. This result is consistent with previous reports which showed that the scattering cross section increased with colloid size,^1,2 in our case aggregates; however, these reports referred to the size of the colloid monomers and not the aggregates.

Figure 6.

Time-dependent scattering intensity of dextran-coated gold nanoparticles in the presence of glucose and 4 (top) and 20 μM Con A (bottom) upon white LED illumination.

Figure 7.

Time-dependent scattering intensity of dextran-coated gold nanoparticles in the presence of glucose and 40 (top) and 80 μM Con A (bottom) upon white LED illumination.

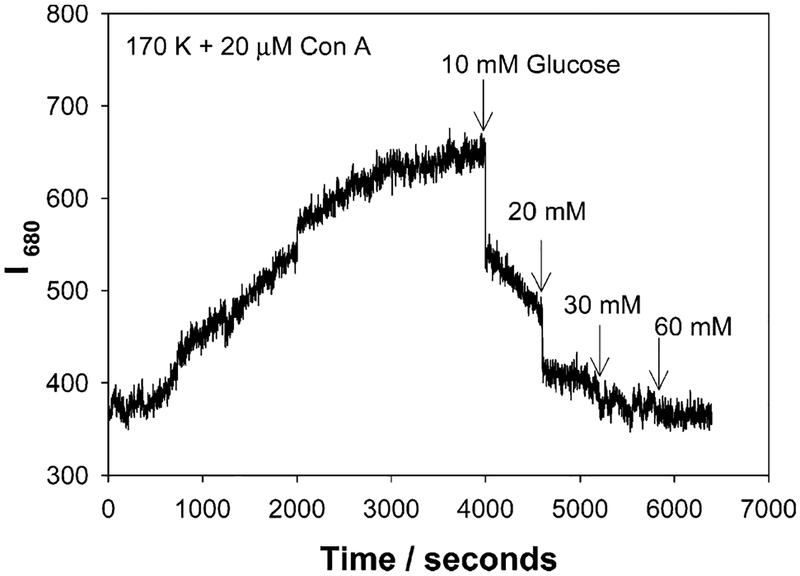
Figure 8 shows the time-dependent scattering intensity at I₆₈₀ nm for 20 μM Con A cross-linked, dextran-coated nanogold, and the subsequent addition of glucose after the 90% response time. The extent of scatter is significantly less at 680 nm as compared to 560 nm. This can also be seen in Figures 4 and 5. The addition of glucose to the Con A cross-linked aggregates reduces the scattered intensity to the original value of the un-cross-linked aggregates, Figure 8.

Figure 8.

Time-dependent scattering intensity measured at 680 nm for 170k dextran-coated gold nanoparticles in the presence of glucose and 20 μM Con A, upon white LED illumination.

The changes for both I₅₆₀₋ and I₆₈₀₋nm scatter versus time, due to nanoparticle aggregation, for the 20, 40, and 80 μM Con A aggregates could be modeled moderately well by a growth exponential of the form

$$I_{560}=I_{560(\text{Final) }}\left(1-\text{exp}\left(-k_{1}t\right)\right)$$ (1)

where I₅₆₀ is the uncorrected scattered intensity at 560 nm at time, t, I_560(final) is the final plateau scattered intensity after 90% Con A induced aggregation, and k₁, the rate constant for the rate of change of scattering, due to the dextran-coated nanogold aggregation (units s⁻¹), Figure 9, top, and Table 1. From Table 1 we can see a greater rate of change of scatter for nanogold compositions containing more Con A and, indeed, a greater final scattered intensity, i.e., I_560(final). It is worth noting that the true form of the scattered light equation with time is likely to be

$$I_{560}=I_0+\left(I_{560(\text{Final) }}-I_0\right)\left(1-\text{exp}\left(-k_{1}t\right)\right)$$ (2)

where I₀ is the initial scattered intensity of the sensing system and ≠ 0. For our studies here, and for the ease of data fitting, we normalized the data so that I₀ = 0.

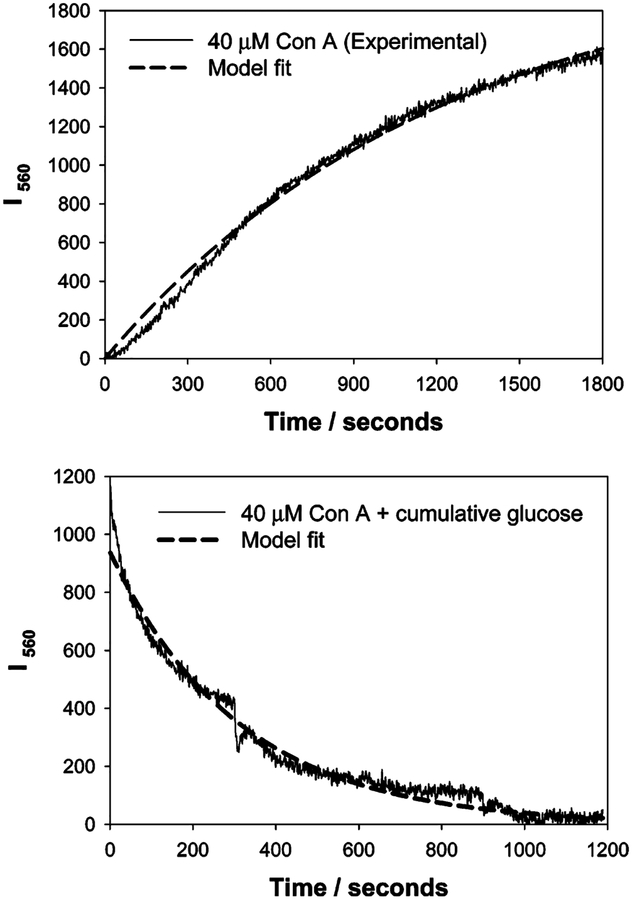
Figure 9.

Fitting of eq 1 to the 560-nm time-dependent scattering for 40 μM Con A induced nanogold aggregation (top), and eq 3 to the dissociation of the same sensing aggregate by glucose (bottom).

Table 1.

Parameters Obtained from Fitting the Aggregation and Disassociation Curves to Eqs 1 and 3, Respectively^a

Con A (μM)	aggregation (Con A induced)			dissociation (glucose)
	I560(Final)	k1 (s−1)	R2	I560(Final)	k1 (s−1)	R2
20	1844	6.6 × 10−4	0.983	1272	1.0 × 10−3	0.982
40	2088	8.2 × 10−4	0.996	939	3.2 × 10−3	0.989
80	2383	1.8 × lO−3	0.991	1265	7.2 × 10−4	0.984

^aAggregation model equation: I₅₆₀ = I_560(Final)[1 - exp(−k₁t)]. Dissociation model equation: I₅₆₀ = I_560(Final)[exp(−k₂t)]. R², regression coefficient.

The decrease in scattered light intensity upon cumulative glucose addition, shown in Figures 6–8, could be modeled well to a simple exponential, Figure 9, bottom, of the form

$$I_{560}=I_{560(\text{Final) }}\left(\text{exp}\left(-k_{2}t\right)\right)$$ (3)

where k₂ is the rate of change of scatter due to glucose addition, noting again the normalization to zero after complete dissociation by glucose, i.e., at t = ∞, Figure 9, bottom. In this regard, normalizing both curves for fitting, Figure 9, top and bottom, is justified as the responses obtained in the scattering versus time plots, Figures 6–8, reversibly change to the same initial scattered intensity value, the I₅₆₀ values of Figure 9, being in essence ΔI₅₆₀ scattering values. It should be noted that the I_560(final) values for association (nanosensor Con A induced aggregation) and disassociation (by glucose) are not the same in Table 1. This is explained by the initial non-diffusion-limited dissociation of the aggregates by glucose, Figure 7, just after the initial addition. Hence our fitting occurred for the data after the first glucose addition.

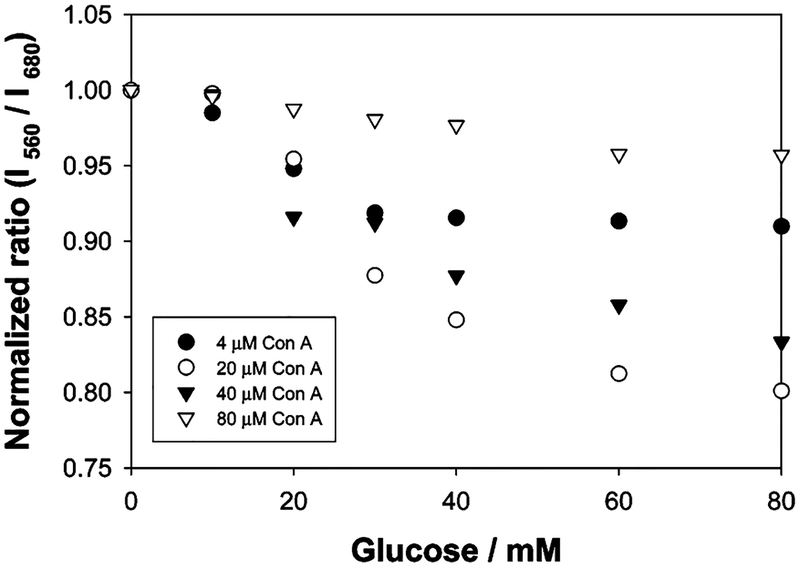
As was shown in Figure 3, bottom, the ratio of the scattered intensities is independent of the total nanogold used, for modest sample optical densities. Hence we were able to plot the scattered ratiometric responses toward glucose for the different sensing compositions of nanogold aggregates studied, Figure 10. In addition the ratiometric plots were normalized to enable the easy visualization of the glucose responses. Nanoaggregates cross-linked with 20 μM Con A showed the greatest glucose response, where the greatest and smallest amounts of Con A used produced the smallest responses and therefore glucose dynamic sensing ranges. This finding was similar for the absorption based glucose measurements previously reported by us.²³ It should be noted that this new approach requires much simpler instrumentation than previously reported, and the wavelength-ratiometric approach is indeed independent of any excitation source fluctuations/drifts and the total nanogold sensing concentration used.

Figure 10.

Normalized ratiometric glucose response for various Con A, dextran-coated nanogold systems.

It is informative to comment on the reversibility of the glucose sensing system. Figures 6–8 clearly show both the aggregation and dissociation of the sensing aggregates and the subsequent changes in excitation scatter. However, additional aggregation/disassociation cycles were not possible in our cuvette based measurements, but the nature of the equilibrium and the competitive binding between dextran–Con A and glucose is well known to afford reversible glucose sensing.^50,51 It is also worth commenting on the specificity of the sensing system for glucose. The affinity of the tetravalent protein Con A for glucopyranosides and manosides has been well studied due to its use in various glucose sensing schemes.^52–55 While glucose is well known to competitively displace other sugars, such as dextran, which only weakly binds,⁵² manosides are low affinity ligands⁵² and galactose does not bind.

We have also studied the stability of the optimal glucose sensing aggregate, namely, 170k Dextran–20 μM Con A, and found that contained samples were stable for many weeks, after which time, flocculation resulted in a precipitate in the bottom of the cuvette. The precipitate could readily be resuspended by agitation, suggesting that any plastic device employing the aggregates would be suitable for continuous use, such as in contact lenses,^56–58 in implantable skin patches,^59–62 or for glucose sensing tattoos.⁶³ In this regard it is informative to speculate further on the applications of this new scattering technology.

Over the past few years, our laboratories have been engaged in developing new technologies to noninvasively and continually monitor physiological glucose, such as a range of glucose sensing contact lenses.^56–58 With these technologies there is a requirement to simplify the technology, from both diabetic patient readout and instrumentation perspectives. Incorporating the sensing aggregates within contact lenses could allow the simple colorimetric determination of tear glucose using ambient light excitation; a patient simply looks in a mirror to see the color change and compares with a precalibrated color strip. In addition, there has been research toward the development of glucose sensing tattoos based on implantable hydrogel beads.⁶³ Given that gold (Gold is used as an injectable suspension for the treatment of arthritis.⁶⁷) and silver colloids are physiologically safe and already used in medicine,^64–67 and the fact that the nanogold aggregates scatter red light, we believe that our approach could additionally be used for glucose sensing transdermally, either for implantable sensors or for glucose sensing tattoos. Further studies by our laboratories are underway.

CONCLUSIONS

Changes in wavelength-ratiometric resonance light scattering, induced by changes in nanogold proximity in the presence of glucose, has enabled a simple glucose sensing platform to be developed. The wavelength-ratiometric approach of the nanogold plasmon scatter is independent of the sensing aggregate concentration and fluctuations in the intensity of the light source. In this paper we have used a simple and inexpensive white light LED for excitation and scanning monochromator for detection, although we envisage that ambient room light, two filters, and a photocell could produce similar results for a significantly lower cost of less than $20.

In addition to wavelength-ratiometric scattering based measurements, we have also shown that scattered intensities at a single wavelength can also report glucose concentrations. These intensity changes have been modeled with intensity versus time functions and could also be used for sensing if a stable light source is used such as an LED or LD.

Finally our approach is readily able to determine glucose concentrations from several millimolar up to ~60 mM, ideal for physiological blood glucose monitoring where red scattering wavelengths (>600 nm) can be selected to eliminate the absorption of hemoglobin, water, and melanin for transdermal-type glucose monitoring.