Finding Diagnostically Useful Patterns in Quantitative Phenotypic Data

Abstract

Trio-based whole-exome sequence (WES) data have established confident genetic diagnoses in ∼40% of previously undiagnosed individuals recruited to the Deciphering Developmental Disorders (DDD) study. Here we aim to use the breadth of phenotypic information recorded in DDD to augment diagnosis and disease variant discovery in probands. Median Euclidean distances (mEuD) were employed as a simple measure of similarity of quantitative phenotypic data within sets of ≥10 individuals with plausibly causative de novo mutations (DNM) in 28 different developmental disorder genes. 13/28 (46.4%) showed significant similarity for growth or developmental milestone metrics, 10/28 (35.7%) showed similarity in HPO term usage, and 12/28 (43%) showed no phenotypic similarity. Pairwise comparisons of individuals with high-impact inherited variants to the 32 individuals with causative DNM in ANKRD11 using only growth z-scores highlighted 5 likely causative inherited variants and two unrecognized DNM resulting in an 18% diagnostic uplift for this gene. Using an independent approach, naive Bayes classification of growth and developmental data produced reasonably discriminative models for the 24 DNM genes with sufficiently complete data. An unsupervised naive Bayes classification of 6,993 probands with WES data and sufficient phenotypic information defined 23 in silico syndromes (ISSs) and was used to test a “phenotype first” approach to the discovery of causative genotypes using WES variants strictly filtered on allele frequency, mutation consequence, and evidence of constraint in humans. This highlighted heterozygous de novo nonsynonymous variants in SPTBN2 as causative in three DDD probands.

Introduction

The clinical phenotype in a single individual has remarkable power to predict the detection of a specific causative ultra-rare genotype, well illustrated by dysmorphic syndrome diagnoses such as Down syndrome (MIM: 190685), Williams-Beuren syndrome (MIM: 194050), and Cornelia de Lange syndrome (MIM: 122470). Such diagnoses are based on a clinically recognizable pattern of physical and behavioral characteristics, most notably pre- and post-natal growth, facial appearance, neurodevelopmental trajectory, and specific sets of malformations. The molecular pathologies associated with these syndromes have shown high levels of mechanistic convergence, particularly when phenotypic similarities between different syndromes are considered. These groups of syndromes (often described as lumped)—RASopathies (e,g., Noonan syndrome,¹ Costello syndrome, neurofibromatosis type 1²), cohesinopathies (e.g., Cornelia de Lange syndrome,³ Roberts syndrome⁴), ciliopathies (e.g., Bardet Biedl Syndrome, Joubert syndrome),⁵ and others—predict biological relatedness of the products of genes harboring causative variants. These characteristics have made the discriminative phenotypic patterns seen in human developmental disorders of interest to basic scientists as well as diagnosticians.

The Deciphering Developmental Disorders (DDD) study aims to develop and use statistically robust, clinically applicable computational genomic approaches to achieve a definite genetic diagnosis within the cohort of >13,000 affected individuals with developmental disorders.^{6, 7} DDD inclusion criteria specifically targeted individuals in whom a clinical diagnosis could not be made and basic genetic investigations were normal.⁸ To date, ∼40% of the DDD probands have a confident diagnosis established using trio-based exome sequencing⁹ most commonly due to a de novo mutation (DNM) affecting the coding region of a single developmentally critical gene. Indeed, the identification of a disruptive DNM in a gene in which monoallelic variants are known to cause developmental disease has, without any reference to the associated phenotype, a positive predictive diagnostic value of >75%.⁹ Unsurprisingly, there is marked locus heterogeneity associated with developmental disorders with no individual locus accounting for >1% of the case subjects. It is likely that many loci remain undiscovered. With sufficient scale and computational power, it is likely that all of these new loci will be discovered using human genetics data alone in the next few years.

Given the strong track record of clinically delineated phenotypic patterns in diagnostic analysis and gene discovery research, we hypothesized that a computational approach to phenotypically driven partitioning of the cohort will increase the power of human genetic analysis to detect loci haboring causative variants and to elucidate the underlying molecular mechanisms. In this study we assessed the utility of computational analysis of phenotypic data for both genetic diagnosis and gene discovery using a large cohort of probands with severe developmental disorders and trio whole-exome sequencing (WES) data. We used median Euclidean distance as a simple measure of similarity, and naive Bayes probabilistic methods, independently, to discover phenotypic patterns, which we have termed in silico syndromes (ISSs). Such models have predictive potential in ranking different plausible variants in an individual and in phenotype-first approaches to gene discovery.

Material and Methods

The quantitative data considered here included measures of growth (proband height, weight, occipital-frontal circumference, and gestation) and of development (proband age for walking independently, sitting independently, uttering first words, and expressing a social smile). Growth data were expressed as z-scores with respect to population norms following the LMS methodology.¹⁰ In addition, we considered categorical data on phenotypic sex and the set of human phenotype ontology (HPO) terms that report clinical observations. To these data we applied a number of distance measures to quantify the similarity, or otherwise, of sets of probands sharing a genetic diagnosis. We then adopted naive Bayes classification as a means of learning probabilistic models from the data, initially following a supervised approach and then learning the models in an unsupervised fashion. These results were assessed using existing tests of classification accuracy and overrepresentation as follows.

Distance Measures from Quantitative Data and HPO Terms

A summary measure of the distance between members a set of probands based on their growth data was calculated as the median Euclidean distance (mEuD) in all pairwise comparisons of growth z-scores between probands in the set. Development data were treated similarly. A summary measure of distance based on proband HPO annotations was calculated as the mean of the maximum information (−log probability of the most informative [parent] HPO term) in all pairwise comparisons between probands in the set. In this case, summary statistics were derived from a matrix of all pairwise distance values, rescaled to increase from 0 by subtracting the overall maximum information value. For growth, development, and HPO data, median (or mean) distances for selected genes were assessed with regard to a distribution of distances for 100,000 random sets of probands of the same size by z-score.

Naive Bayes Classification

Naive Bayes classifiers combine the a priori probability of a proband belonging to a category with the probabilities of phenotypic attributes being “low,” “mid,” or “high” (in the multinomial case) conditional on the sample belonging to the specified category.¹¹ The naive Bayes approach assumes that attributes are conditionally independent and hence the conditional densities can be calculated more easily. Having obtained the probability tables from the observed data, the most probable classification for an observation (maximum a posteriori) can be obtained by Bayes rule. The use of multinomial probability tables requires the phenotypic data to be discretized into a set number of bins. We achieved this by maximizing entropy, that is, by approximately equalizing the number of samples per bin.

The classification error rate of the naive Bayes classifier was calculated by the 0.632 bootstrap method:

$$\left(1-\text{0}\text{.}632\right)\ast \mathit{resubstitution}\text{-}\mathit{error}+0.632\ast \mathit{bootstrap}\text{-}\mathit{error}$$

where the resubstitution-error was¹² calculated after training on the entire dataset and the bootstrap-error from 1,000 bootstraps where the data were resampled with replacement to obtain a new training set and accuracy on samples not in the resampled set was evaluated. These measures of error underestimate and overestimate the true error rate, respectively, and their combination better reflects the true rate.

Unsupervised Naive Bayes Clustering

Naive Bayes approach for unsupervised clustering was performed using phenotype data from the whole cohort. To enable classes to be learned—rather than being specified as above—we adapted a maximum likelihood algorithm^{13, 14} capable of simultaneously assigning labels and calculating probability tables for a given number of classes (k), then selected the optimal value of k by exploring values from 2 to 30 (as we found the trade-off between model complexity and fit to the data to lie below 30). A generalization of the calculation of probabilities in naive Bayes models allows optimal (maximum likelihood) models to be computed for unlabeled samples.^{13, 14} As for supervised naive Bayes models, we are able to inspect the probability tables that make up the model and to calculate model fitting measures such as AIC when exploring alternative values for the number of categories, k. In unsupervised clustering, only the number of categories k is initially specified and all probabilities are calculated through an iterative procedure to generate an unsupervised clustering of the data. For values of k from 2 to 30 (range dependent on the number of data points), we ran the parameter optimization procedure from random starting values 1,000 times and repeated this process 3 times. The best parameter values for each value of k and the best choice of k were found by minimizing AIC. We refer to these clusters as in silico syndromes (ISSs). The clustering algorithms were implemented in R and in Java by the authors, following Collins.¹⁴ The code developed for our analysis is provided in the ISS online repository (see Web Resources).

Of note, conditional probabilities can be calculated in the case of missing values. In contrast, t-SNE clustering was performed on the numerical data directly, but samples with missing values could not be considered and duplicate samples had to be removed.

Tests for Similarity of HPO Terms

The similarity of a set of probands defined by an ISS was assessed through the HPO terms assigned to each proband using the hpo_similarity tools¹¹ (see Web Resources) following the method developed for diagnostic DNMs. This method computes, for a set of probands, the maximum information content pairwise between probands and compares these values to those of a null distribution of values from random sets of the same size.

Tests for Overrepresentation and Significance

Fisher’s exact test was used to determine whether an ISS was overrepresented in alternative categorizations of probands (1) by malformation category (a set of high-level HPO terms) and (2) by DNM. The resulting p values were adjusted for the number of ISSs tested (the threshold for significance was 0.05). In Manhattan plots, the level of genome-wide significance was set by the Bonferroni method: 0.05/(number of ISS ^∗ number of genes tested).

Results

Collection, Characteristics, and Completeness of DDD Phenotypic Data

Throughout the DDD study (during the recruitment period and subsequently), phenotypic information on each recruited proband was entered and/or updated using a custom, secure on-line system within DECIPHER (see Web Resources) by designated professionals at referring centers and authorized by the clinician who had examined the affected individual.

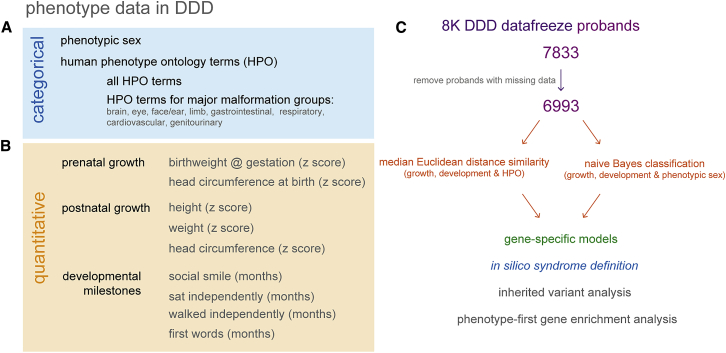
The categorical phenotypic information used in this study consisted of phenotypic sex and the set of human phenotype ontology terms used to describe the clinical issues (Figure 1A). The quantitative data used for analysis consisted of growth data expressed as z-scores and developmental data expressed as proband age (in months) for walking independently, sitting independently, uttering first words, and expressing a social smile (Figure 1B).

Figure 1.

Summary of the Phenotypic Data from DDD Employed in This Study

(A) Description of categorical data types used in the analyses described in the Results.

(B) Description of quantitative data described in the Results.

(C) Overview of the type and purpose of the analyses described in the Results.

6,993 of the first 7,833 probands from the DDD 8K trio exome data freeze had sufficient phenotypic data available to be used for the median Euclidean distance analysis and the naive Bayes classification approaches. The results of these analysis were gene models and in silico syndromes that were then used for analysis of strictly filtered inherited variants and a phenotype first approach to gene enrichment for the purposed of novel locus and/or mechanisms discovery.

Analysis of the DDD data is ongoing and the data used here are derived from the first 7,833 probands that have trio WES data available, of which 6,993 probands had sufficient phenotypic data for analysis (Figure 1C).

Median Euclidean Distance (mEuD) as a Measure of Similarity in DDD Phenotypic Data

To determine whether there is discriminative value in aggregated phenotypic parameters for specific loci in which variants have been confidently associated with disease, we used the median of the pairwise Euclidean distances between all individuals with likely causative de novo variants in a specific gene. The observed mEuD was compared to an expected level derived from multiple random sampling of sets of the same size from the whole group. mEuD is agnostic to the direction or degree of deviation of the phenotypic parameter and only reflects the level of similarity within a set; so, for example, two genes with very similar growth mEuD scores may comprise sets of affected individuals with extremely different growth parameters between the genes.

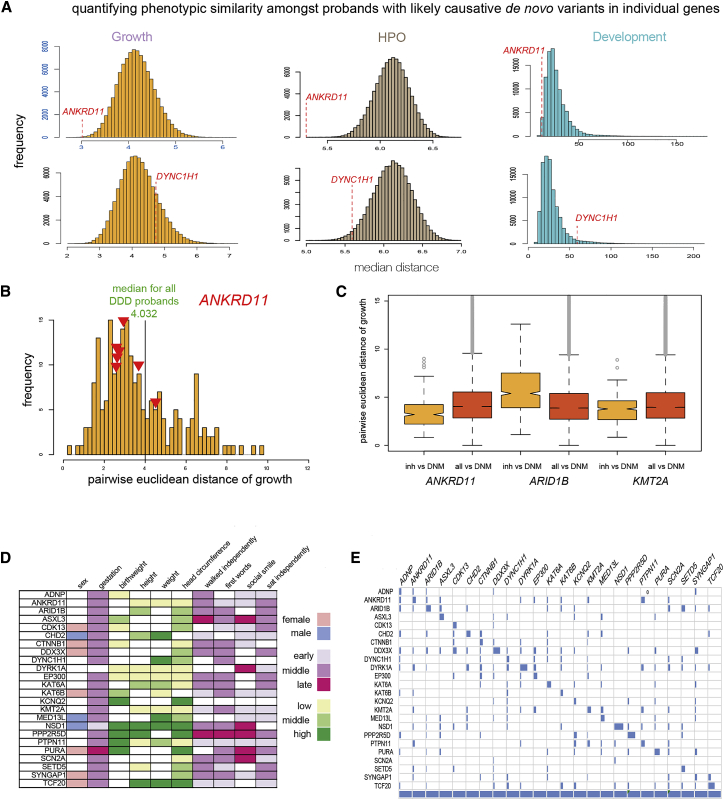
There were 28 genes in which ≥10 individuals had reported DNM and complete growth data (birth weight, gestation, postnatal height, weight, and head circumference). mEuD for growth and development and a previously described¹⁵ distance measure for HPO terms were calculated for each group and compared to a random sampling of groups of the same data in identically sized groups from the DDD data (Figure 2A, Table 1). This showed that 16 of the 28 gene groups showed evidence of similarity; 12 for growth, 10 for HPO (6 overlap with growth) significant at p < 0.05 after Benjamini Hochberg correction, and 1 for development nominally significant at p < 0.05 (overlaps growth and HPO). The group of individuals with DNM in ANKRD11 was exceptional, showing striking levels of similarity for all three parameters (Figure 2A, top) whereas other loci, such as DYNC1H1, showed no significant similarity in any phenotypic domain (Figure 2A, bottom).

Figure 2.

Phenotype-Based Categorization of Individuals with Likely Causative De Novo Mutations in Confirmed Developmental Disorder Genes

(A) Histograms showing the distribution of median distances of random sets of DDD probands for growth (purple), similarity of Human Phenotype Ontology term attributions (brown), and developmental milestone metrics (turquoise). In the upper panel the striking similarities observed in median distances within the group of individuals with de novo mutations (DNM) in ANKRD11 are indicated by the red line. In the lower panel the median distances for the individuals with DNM in DYNC1H1 are indicated by the red lines, which shows no obvious similarity within this group.

(B) Histogram showing the distribution of pairwise Euclidean distances for growth metrics for the individuals with ANKRD11 DNM (purple). The red arrows representing the median of the pairwise comparisons of the individuals with high-impact inherited variants in ANKRD11 with the DNM individuals. The green line represents the mEuD of all DDD probands against the ANKRD11 DNM case subjects.

(C) Boxplot showing the distribution of pairwise distances of individuals with inherited variants and DNM in ANKRD11, ARID1B, and KMT2A (dark purple). For comparison the distribution of distances between the individuals with DNM and all other DDD probands is shown (light purple).

(D) The naive Bayes model for each of the 24 DNM genes with sufficient data is summarized by the discretized values in ten phenotypic categories. Cell shading indicates the discretized value where the value has a probability >0.5 (0.6 for binary variables). A key is provided describing the discrete groupings. These models were based on the observed phenotypes for each gene in isolation but generated apparently discriminative patterns.

(E) To explore the diagnostic potential of the 24 gene models shown in (D), a confusion matrix was created showing the assignments based on each gene model using only phenotypic data from all individuals with diagnostic DNM assignments (columns). The diagonal represents the concordance of the phenotypic and genetic assignment.

Table 1.

Similarity between Individuals with Likely Causative De Novo Variants in 28 Different Genes

Gene	Growth		Development		HPO (Mean of Max IC)
	p Value	z-Score	p Value	z-Score	p Value	z-Score
KMT2A	0.0058∗	−2.3523	0.1854	−0.7322	0.0000∗	−4.3303
ARID1B	0.0091∗	−2.1949	0.1600	−0.8220	0.0000∗	−4.3420
ANKRD11	0.0004∗	−2.9911	0.0074∗	−1.2472	0.0000∗	−4.9775
DDX3X	0.0132∗	−2.0547	0.1875	−0.7794	0.0939	−1.3331
DYRK1A	0.0098∗	−2.1117	–	–	0.0000∗	−4.5538
ADNP	0.1497	−1.0288	–	–	0.0668	−1.5174
MED13L	0.0200∗	−1.8917	0.8971	1.0019	0.0132∗	−2.2639
EP300	0.1282	−1.1087	–	–	0.0001∗	−3.7941
SATB2	0.0016∗	−2.5532	–	–	0.0000∗	−3.9988
MECP2	0.1429	−1.0485	–	–	0.5124	0.0511
DYNC1H1	0.8245	0.9138	0.9580	2.0714	0.0200∗	−2.1047
PURA	0.1306	−1.0952	–	–	0.5964	0.2668
CTNNB1	0.4570	−0.1706	–	–	0.2412	−0.6985
ASXL3	0.0068∗	−2.1506	–	–	0.8509	1.0434
SYNGAP1	0.0013∗	−2.5082	0.3651	−0.4461	0.8891	1.2212
SCN2A	0.5408	0.0357	–	–	0.1092	−1.2397
POGZ	0.1678	−0.9488	–	–	0.4933	0.0021
CDK13	0.0032∗	−2.3295	–	–	0.0316∗	−1.9063
STXBP1	0.4528	−0.1809	–	–	0.0702	−1.5038
SETD5	0.0009∗	−2.5731	–	–	0.5510	0.1525
EHMT1	0.0162∗	−1.8967	–	–	0.5816	0.2266
TCF20	0.2386	−0.7364	–	–	0.0495∗	−1.6879
PTPN11	0.0689	−1.3813	–	–	0.0008∗	−3.2996
PPP2R5D	0.2137	−0.8091	–	–	0.0020∗	−3.0120
KAT6A	0.3261	−0.5026	–	–	0.3382	−0.4030
FOXP1	0.1304	−1.0885	–	–	0.0624	−1.5660
CREBBP	0.3879	−0.3471	–	–	0.0063∗	−2.5684
CASK	0.3241	−0.5091	–	–	0.2016	−0.8301

Asterisk (^∗) indicates significant p values (≤0.05).

The distribution of the mEuD in the randomly selected sets from DDD probands is normally distributed for growth but significantly skewed for development. A z-score could thus be calculated from the growth data which gives directionality to any significant deviation from the expected the mEuD (Table 1). In all 12 gene sets with p < 0.05, the z-score for growth metrics was negative indicating that the groups were more similar than would be expected by chance.

Classifying Inherited Variants using mEuD Growth Models from DNM

To explore the wider diagnostic utility of the mEuD gene-growth models derived from individuals with de novo, likely causative variants, we examined the pairwise Euclidean distances of individuals with inherited variants in the cognate genes. The variants used for analysis were strictly filtered on allele frequency, evolutionary conservation, and predicted consequence to enrich for high impact variants (see Material and Methods; Figures 2B and 2C). Three genes (ANKRD11, ARID1B, and KMT2A) were chosen for study for the following reasons: they are common causes of developmental disorders (each accounting for >0.5% DNM diagnoses in our dataset), each have distinctive clinical features, each shows significant mEuD growth similarity, and there were ≥6 high-impact inherited variants in probands from the 6,993 DDD trio WES data.

The seven individuals with apparently inherited heterozygous high-impact variants in ANKRD11 and adequate phenotype data appeared to have a growth pattern that is more similar to ANKRD11 DNM cases than that expected based on a comparison using the whole cohort (Figures 2B and 2C). In support of these being causative variants, the HPO term distances between each of these probands and the 32 de novo ANKRD11 case subjects were lower than would be expected by chance in six case subjects (p < 0.05; Figure S1). The clinical and genetic information on these individuals was then reviewed and is summarized in Table 2. Individual (258544) was referred to the project with a clinical diagnosis of KBG syndrome made prior to recruitment into DDD. This individual and another (265784) were subsequently shown to have variants that had occurred de novo—these had been previously misassigned due to poor coverage in one or both of the parental exomes. For 265784, the growth was similar (p value 0.0004) but the HPO term usage was not (p value 0.09) whereas 258544 was similar to other individuals with ANKRD11 DNM for both growth and HPO term usage (p values of 0.04 and 0.003, respectively). Clinic reappraisal of the seven probands (referring clinicians and/or DRF and HVF) concluded that six had features consistent with their ANKRD11 genotype with the remaining case subject being considered only possibly consistent (301622).

Table 2.

Clinical and Genetic Features of Individuals with Apparently Inherited, High Impact Variants in ANKRD11

Proband ID	265784	258544	276420	279343	301622	303467	305225
NC_000016.9 Genomic Variant	g.89334964_89334970dup	g.89350555del	g.89350831del	g.89349780_89349781del	g.89351044_89351045del	g.89346281del	g.89348863G>A
NM_013275.5 cDNA	c.7909_7915dup	c.2397del	c.2119del	c.3170_3171del	c.1908_1909del	c.6670del	c.4087C>T
NP_037407.4 Protein	p.Leu2639GlnfsTer113	p.Glu800LysfsTer63	p.Glu707LysfsTer12	p.Lys1057ArgfsTer10	p.His636GlnfsTer26	p.Glu2224ArgfsTer113	p.Arg1363Ter
Inheritance	uncertain (subsequently confirmed de novo)	uncertain (subsequently confirmed de novo)	maternal	maternal	maternal	paternal	paternal
Child/parental VAF	4/4:?	9/5:?	20/20:23/23	32/36:31/49	26/28:26/24	13/10:6/13	35/36:41/46
Consequence	frameshift variant	frameshift variant	frameshift variant	frameshift variant	frameshift variant	frameshift variant	stop gained
Birth weight	−1.23	−0.08	−0.54	−1.29	−1.66	0.32	0.16
Height	−2.39	−1.87	−0.76	−2.92	−2.06	−2.37	−4.02
Weight	−2.49	−0.5	−0.41	−3.58	−1.45	−0.52	−2.97
OFC	−2.38	−0.74	−2.48	−4.78	−3.35	−2.83	−2.64
HPO terms (not used in similarity analysis)	Abnormal facial shape; Intellectual disability; mild; Microcephaly; Short stature	2-3 toe syndactyly; Abnormal facial shape; Abnormality of dental morphology; Avascular necrosis of the capital femoral epiphysis; Broad finger; Clinodactyly of the 5th finger; Cryptorchidism; Global developmental delay; High palate; Short neck; Strabismus	Anteverted nares; Behavioral abnormality; Global developmental delay; Hirsutism; Hypermetropia; Protruding ear; Sensorineural hearing impairment; Short attention span; Synophrys; Wide mouth	Brachycephaly; Clinodactyly of the 5th finger; Conductive hearing impairment; Global developmental delay; Prominent metopic ridge; Short stature; Sparse scalp hair	Fetal fifth finger clinodactyly; Moderate global developmental delay; Short stature	Delayed speech and language development; Edema of the dorsum of feet; Feeding difficulties; Fine hair; Immunologic hypersensitivity; Infra-orbital crease; Moderate global developmental delay; Neonatal hypotonia; Short foot; Thin upper lip vermilion; Upslanted palpebral fissure	2-3 toe syndactyly; Failure to thrive in infancy; Frontal bossing; Long eyelashes; Moderate global developmental delay; Sacral dimple; Short stature
Family history	none	none	father has intellectual disability (variant maternally inherited)	father has mild KBG on clinical reassessment	none	none	none
Clinically confirmed	yes	yes	yes	yes	possible	yes	yes
Notes	DNM in SOX10 not classified	referred with a clinical diagnosis of KBG	also has KMT6A in-frame dup (mat) amd TECTA nonsense mutation (pat) both unclassified	ACAN variant reported (likely benign)	missense in TRIP12 reported (likely benign)	TSC2 variant reported (unclassified)	no variants reported

Abbreviations: VAF, variant allele frequency; DNM, de novo mutation; OFC, occipito-frontal circumference.

In contrast, the growth pattern of individuals with ARID1B apparently inherited high-impact variants were less similar to the individuals with ARID1B DNM than the whole cohort. One of these six had a clinical diagnosis of Coffin Siris syndrome at recruitment and review of the trio WES data following our analysis confirmed that this mutation has occurred de novo. In this individual the HPO term similarity was highly significant (z-score −5.3) but the growth mEuD somewhat dissimilar (z-score −0.99) from individuals with DNM (Figure S1). None of the other five individuals showed significant HPO term similarity and only one had significant growth similarity to the known ARID1B DNM (DDDP120820 z-score −3.1; Figure S1). No differences could be observed between individuals with inherited variants versus DNMs in KMT2A when compared to cohort versus DNM in that gene (Figure 2C).

Supervised Naive Bayes Models Have Diagnostic Potential

We then wished to determine whether naive Bayes models¹⁶ could be used to establish patterns in the quantitative data that would constitute diagnostically useful in silico syndromes. This analysis was performed without using the associated HPO terms. There were 24 genes (a total of 377 probands) in which ≥10 individuals had reported DNM and sufficiently complete growth and developmental milestone data were available. These models were built using ten features, including the four growth and four development measurements described above, plus gender and gestation (Figure 2D, probability tables in Data S1). Each feature was “discretized” (high, middle and low, or high and low groups for continuous features; male and female for sex) as described in Material and Methods.

Each supervised naive Bayes gene-phenotype model was defined independently. No attempt was made to derive models that would distinguish one DNM from another. That said, the performance of the classification models on the training set resulted in 123/377 (32.6%) correct predictions of gene class (Figure 2E) compared to 4% (1/24) expected by chance. This type of analysis can underestimate the true error rate of a classifier, so we also used 0.632 bootstrap method employing resampling with replacement and testing on samples not used in training,¹² which suggested a classification accuracy of 20.1%. The NSD1, DYRK1A, and TCF20 models each had accuracies >30%. KAT6B, DYNC1H1, ADNP, KCNQ2, and SCN2A were poorly predicted with accuracies <10%.

Unsupervised Naive Bayes Models

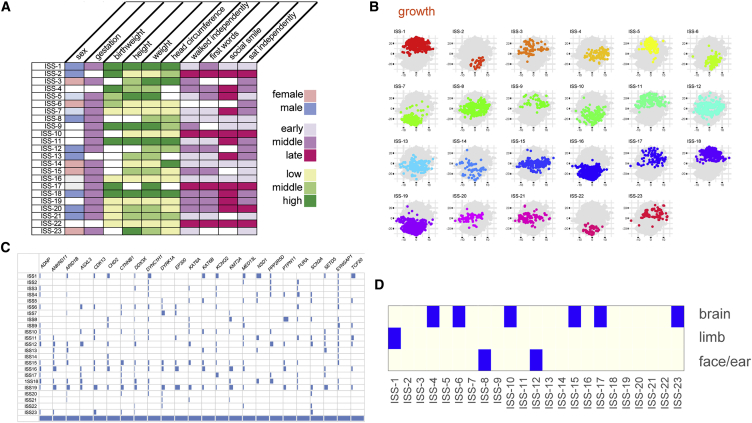
We then applied an unsupervised naive Bayes classifier to the first 6,993 DDD probands with adequate data (see Figure 1C) resulting in 23 classes, which we have termed in silico syndromes. These ISS (Figure 3A, probability tables in Data S1) contained between 49 and 1,049 probands (median 219). Mapping ISS^Bayes:1-23 onto tSNE cluster graphs¹⁷ resulted in visually apparent patterns for growth (Figure 3B) and to a lesser extent for development (Figure S2). It is apparent that seven ISSs have similar predominantly high values for growth but are distinguished by differing combinations of developmental attributes (illustrated by clustering the table, Data S2). Low values for growth features are shared by six ISSs and again these patterns are distinguished by developmental characteristics. 13 of the 23 ISSs have a predominant gender. To quantify the extent to which the ISS classes can be recovered from the data, the proband to ISS labels can be assumed to be correct and the classification error estimated as above for supervised naive Bayes classification by 0.632 bootstrapping. The proposed ISS labels are obtained with an error of 5.6%, giving an accuracy of 94.4% which lends weight to the phenotypic distinctions they make.

Figure 3.

Phenotypic Prototypes and Predictions from Naive Bayes Models

Unsupervised naive Bayes clustering of the 6,993 DDD probands into 23 distinct classes, here termed in silico syndromes (ISS^Bayes).

(A) A graphical representation of the phenotypic characteristics that define each ISS^Bayes using 10 discretized phenotypic values, a key is provided for each of the color-coded groups.

(B) Scatterplots show the projection into two dimensions by t-SNE of growth for each ISS^Bayes where symbols are color coded by ISS.

(C) To determine whether the ISS^Bayes showed any agreement with DNM in 24 different genes, we created a confusion matrix which did not indicate strong evidence of concordance of the phenotypic and genetic assignments.

(D) We also defined eight sets of HPO terms that describe site-specific malformations looked for over-representation of probands when categorized by profile (Fisher’s exact test). Three malformation types were enriched in nine different profiles (p value adjusted for testing 23 profiles, adjusted p ≤ 0.05 considered significant).

Given that HPO terms were not used to generate the ISSs, we reasoned that HPO term similarity between probands within a ISS may be a reasonable test of validity. HPO similarity scores were significantly higher than expected in 13/23 ISS^Bayes (Table 3, p values computed by the method of Akawi and McRae¹⁵). To enrich for terms that would be unambiguously assigned, we created eight subsets for organ-specific malformations (respiratory, GI_abdominal, cardiovascular, limb, face_ear, brain, eye, genitourinary). Of these only brain, limb, and face_ear showed evidence for enrichment in 6, 1, and 2 different, non-overlapping ISSs, respectively (Figure 3D).

Table 3.

HPO Term Enrichment in the 23 ISS^Bayes Derived from Unsupervised Naive Bayes Classification

ISSBayes	p Value	ISSBayes	p Value
ISS-1	0.999	ISS-13	0.079
ISS-2	0.007∗	ISS-14	0.009∗
ISS-3	0.001∗	ISS-15	0.085
ISS-4	0.028∗	ISS-16	0.003∗
ISS-5	0.999	ISS-17	0.001∗
ISS-6	0.001∗	ISS-18	0.375
ISS-7	0.001∗	ISS-19	0.001∗
ISS-8	0.999	ISS-20	0.005∗
ISS-9	0.607	ISS-21	0.376
ISS-10	0.001∗	ISS-22	0.001∗
ISS-11	0.870	ISS-23	0.091
ISS-12	0.035∗	–	–

Asterisk (^∗) indicates significant p values (≤0.05).

Estimating the Potential for Phenotype First Approaches to Gene Discovery

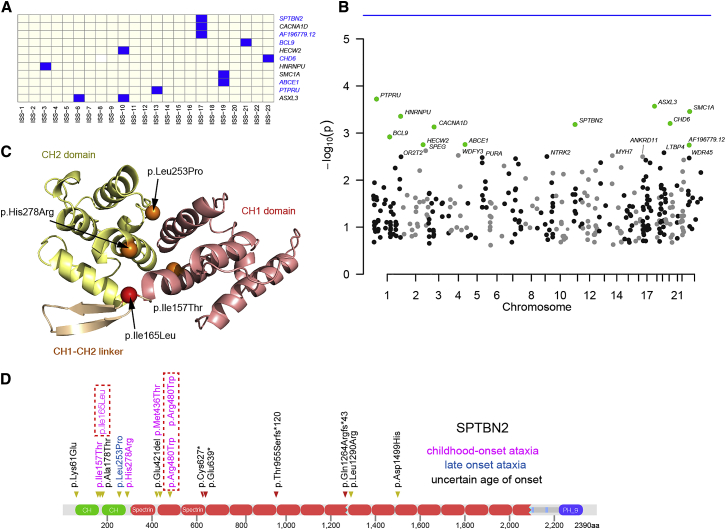
We defined a set of strictly filtered variant calls from the proband exome data. A minor allele frequency of <0.0001 in ExAC, EVS, and 1KG data was used. Any variants with an internal (DDD) variant count of >3 were excluded to minimize the risk of technical artifact. Likely gene disruptive variants were included in genes that showed significant intolerance of such variants at a population level (ExAC pLi > 0.5). Missense variants with CADD score > 30 were included in genes with evidence of missense constraint in human populations (z score > 3 from ExAC). This resulted in a total of 12,458 variants in 6,993 probands (5,858 variant positive probands, 3,617 genes). We then looked for indicative enrichment of genes within the 23 ISS^Bayes using a subset of genes in which variants were identified in at least 8 probands (359/3,617 genes). No gene achieved genome-wide significance. 11/359 genes (SMC1A, WDR45, CHD6, ASXL3, SPTBN2, ABCE1, CACNA1D, HECW2, HNRNPU, BCL9, PTPRU) were enriched above a nominal level (Figures 4A and 4B; Table 4). ASXL3 was the most enriched gene (ISS:6 and ISS:10). 6/11 of these genes (SMC1A, ASXL3, CACNA1D, HECW2, HNRNPU, WDR45) had been previously coded as genes in which variants are known to cause developmental disease in the G2P database¹⁸ constituting an odds ratio of 2.55 (p = 0.11 by Fischer’s test considering the 359 genes with sufficient numbers of probands to be tested as the background set which was itself enriched for genes containing disease-associated variants).

Figure 4.

Discovery of Candidate Diagnostic Genes by Phenotypic Profile

(A) Heatmap of ISS^Bayes 1:23 tested for over-representation of genes passing the variant filtering in the phenotypic profiles (Fisher’s exact test, p value adjusted for testing 23 profiles, adjusted p ≤ 0.05 considered significant, 359 genes had at least 8 probands; mean 1.36 SNV per proband). The variants were derived from proband whole-exome sequencing in the 8k data freeze were filtered by MAF, consequence, pLi, CADD, and NSV scores to produce a set of 12,458 plausible diagnostic SNVs, mean 2.12 per proband in a set of 6,993 probands. Gene names in black are known developmental genes in the G2P database, those in blue are not in the G2P database.

(B) A Manhattan plot shows the p values of enriched genes.

(C) Pathogenic mutations at the CH1:CH2 interdomain interface of SPTBN2. The site of the novel DDD mutation identified here is shown in red, while the sites of the previously identified pathogenic mutations are shown in orange. The crystal structure of alpha-actinin (PDB: 4D1E) was used to build a homology model of SPTBN2 using SWISS-MODEL. The cryoelectron microscopy structure of the SPTBN2 CH1 domain (PDB: 6ANU) was very similar to the model (RMSD = 1.5 Å).

(D) A cartoon of SPTBN2 protein structure. The distribution of pathogenic and likely pathogenic variants recorded in ClinVar is indicated by the yellow (missense) and red (nonsense and frameshift) triangles above the protein. The color of the variant text indicates the age of onset of the ataxia as defined by the key. The dashed line red boxes indicate the position of the de novo variants identified within the DDD cohort.

Table 4.

Clinical Summary of Genes Showing Nominal Enrichment in ISS^Bayes

Gene	ISS	DDG2P	Total Number of Filtered Variants	Variants in Enriched ISS					Variants Not Enriched in ISS					Obvious Clinical Similarity?
				Total	LoF	NSV	DDD Reports Same Variant	DDD Reports Different Gene	Total	LoF	NSV	DDD Reports Same Variant	DDD Reports Different Gene
ABCE1	19	no	9	5	3	2	NA	3	4	4	0	NA	1	no
ASXL3	6	monoallelic:loss of function	26	5	5	0	5	0	21	21	0	14	1
BCL9	21	no	10	3	3	0	NA	1	7	7	0	NA	3	no
CACNA1D	17	monoallelic:activating AND biallelic:loss of function	16	4	2	2	0	1	12	2	10	2	2
CHD6	23	no	19	4	0	4	NA	1	15	1	14	NA	3	no
HECW2	10	monoallelic:all missense/in-frame	14	4	1	3	0	0	10	2	8	0	2
HNRNPU	3	monoallelic:loss of function	9	3	3	0	3	0	6	6	0	4	0
PTPRU	13	no	16	5	1	4	NA	1	11	0	11	NA	2	no
SMC1A	19	X-linked dominant:all missense/in-frame AND X-linked dominant:loss of function	9	6	6	0	5	0	3	2	1	3	0
SPTBN2	17	no	25	5	0	5	NA	0	20	1	19	NA	5	yes
WDR45	17	X-linked dominant:loss of function	9	3	3	0	2	0	6	6	0	6	0
Total			162	47	27	20	15	6	115	52	63	23	25

Abbreviations: LoF, loss-of-function variants; NSV, non-synonymous (missense) variants; ISSs, in silico syndromes.

On clinical review of the individuals with variants in five genes that were not in G2P, only those with variants in SPTBN2 were plausibly diagnostic (Table 5). Mutations in SPTBN2 have been identified in an adult-onset, autosomal-dominant spinocerebellar ataxia 5 (SCA5 [MIM: 600224]).¹⁹ Infantile-onset ataxia and global developmental delay has been reported with biallelic mutations in SPTBN2 (SCA14 [MIM: 615386]). De novo monoallelic variants resulting in p.Arg480Trp have been reported in three individuals in separate case reports with infantile-onset ataxia and global developmental delay.^{20, 21, 22} Three DDD individuals have de novo missense variants in SPTBN2 (Figure 4D), two of which are predicted to result in the p.Arg480Trp substitution (NB: one is the same individual as Parolin Schnekenberg et al.²⁰). The other de novo variant has the consequence p.Ile165Leu. This amino acid substitution is located in the region between CH1 and CH2 domains of SPTBN2, very close to a likely pathogenic de novo variant (GenBank: NM_006946.3 (SPTBN2): c.470T>C [p.Ile157Thr]) reported in ClinVar. Moreover, it is interesting to note that two previously reported missense variants also occur at the CH1:CH2 interface (Figure 4C): p.Leu253Pro associated with adult-onset¹⁹ and p.His278Arg associated with childhood-onset²³ SCA5. It was shown that p.Leu253Pro is damaging because it disrupts the interaction between the two CH domains, which increases actin-binding affinity of SPTBN2.²⁴ It is likely that a similar mechanism underlies the other three mutations at the CH1:CH2 interface, and we can speculate that the degree of disruption may explain the variation in age of onset.

Table 5.

Clinical and Genetic Feature Recorded for Individuals with De Novo Mutations in SPTBN2

DECIPHER ID	261578	282590	274803
NC_000011.9 genomic variant	g.66475202G>A	g.66475202G>A	g.66481869T>G
NM_006946.3 cDNA	c.1438C>T	c.1438C>T	c.493A>C
NP_008877.1 protein	p.Arg480Trp	p.Arg480Trp	p.Ile165Leu
Inheritance	de novo	de novo	de novo
Mother’s age	23	33	37
Father’s age	25	36	38
Birthweight Z score	0.97	−1.13	0.91
Height Z score	–	−0.78	−1.23
Weight Z score	–	0.15	1.75
OFC Z score	−1.75	−1.57	0.5
HPO terms	frontal upsweep of hair; global developmental delay; high forehead; hypopigmentation of hair; tremor	abnormal motor neuron morphology; cerebellar atrophy; intellectual disability; mild	ataxia; cerebral atrophy; dysmetria; global developmental delay; hypertonia; motor delay; strabismus; truncal ataxia
Notes	no other causative variants identified	no other causative variants identified	no other causative variants identified

Discussion

There is a pressing need to develop statistically robust and scaleable methods to incorporate phenotypic data into the analytical pipelines in both diagnostic and clinical research genomics. Statistical approaches to WES/WGS analysis in human disease cohorts have proven to be extremely powerful in identifying new disease associations with individual genes and to identify causative mutations in known genes. This has been particularly true using family-based study designs in developmental disorders due to the very high frequency of causative de novo mutations (DNMs). There is, however, a ∼20% (or greater) false positive rate estimated for plausibly deleterious DNMs in genes containing disease-associated variants.⁹ The difficulty in interpreting the clinical significance of ultra-rare variants becomes significantly greater where the proband is sequenced on their own or with only one parent. The phenotype of the affected individual represents accessible and independent data which can be used to rank the variants identified using human genetic analysis alone. We found it surprisingly difficult to estimate an expected level of improvement in clinical utility before starting this study. Many published diagnostic criteria for individual mendelian disorders include growth and developmental milestone data as key components of the decision tree (e.g., Cornelia de Lange syndrome²⁵), but we could not identify studies that had assessed the additional clinical utility of such information.

Computational use of structured, categorical, medical terminology—such as the Human Phenotype Ontology (HPO)²⁶—is now in widespread use in clinical research.^{27, 28, 29, 30, 31} The primary aim of this paper has been to assess the diagnostic utility of systematically collected quantitative data (derived from growth and development of the affected individuals) in affected individuals who were recruited to the DDD study with severe/extreme developmental disorders. Such data could be used alone or in combination with existing similarity measures that use HPO terms. Growth has major advantages as a phenotype for computational use; it is quantitative, multi-modal (height, weight, head circumference), routinely documented in pediatric health records, and can be normalized by age using z-scores. Birth weight and gestation can be used as a proxy for prenatal growth. Proportionate or disproportional growth anomalies are common in developmental disorders^{32, 33, 34} and growth parameters are commonly used in diagnostic criteria for individual syndromes.³⁵ The diagnostic use of developmental milestones have received little attention to date. Although these data are quantitative, the measurements are in temporal intervals and are not normally distributed, meaning it is not possible to produce age- and sex-normalized z-scores. It is also true that the developmental milestones are not recorded routinely in many electronic medical records and that parental recall, for example of the precise age at sitting unaided, is of uncertain accuracy. In spite of these limitations, developmental milestone data are multimodal and have obvious potential in the diagnosis of developmental disorder.

Our aim was to utilize the breadth of phenotypic data—HPO terms, growth, and developmental milestones—that was collected systematically on recruitment to the DDD study. An early exploratory analysis, which combined tSNE with nearest neighbor approaches (Figure S3), showed only modest evidence of clustering by genetic diagnosis and it was not possible for us to use this approach to create gene-specific models to apply to individual genomic analyses. In contrast, we found improved clustering by ISS groupings. We then assessed the utility of median Euclidean distances as a method of determining how similar the patterns of z-scores for quantitative phenotypes are among genetically defined sets of probands. mEuD provides a computationally and conceptually simple method of determining which measured feature in a group of individuals with comparable genotypes in a specific gene may be of discriminative value. Individuals with plausibly causative DNM in MED13L show evidence for similarity in growth and HPO term usage but not for developmental milestones (Table 1). This phenomenon means that mEuD models can be tailored to an individual locus and genotype allowing us to identify causative variants in ANKRD11 that have been inherited from apparently unaffected parents. In 6 out of 7 cases, the Euclidean distance between these probands and the 32 DNM case subjects is less than expected by chance (p < 0.05 using HPO terms; Figure S1). mEuD models may improve diagnostic interpretation in proband-only analysis by augmenting the standard genetic approaches to prioritizing variants with a phenotypic match.

Naive Bayes classification allowed us to generate gene-phenotype profiles (or in silico syndromes [ISSs]) with significant diagnostic potential. Although these models are not very discriminative when used alone, in conjunction with independent phenotype data such as HPO terms and facial image-derived measurements,³⁶ the naive Bayes ISS could be of use in clinical diagnostic practice. It is now important to develop statistically robust approaches to integration of such data to allow the combined models to be tested in well-characterized cohorts to determine their impact on precision and recall of confirmed molecular diagnoses.

We used naive Bayes classification-derived ISSs to test whether a quantitative phenotype-driven approach could be used for gene discovery in developmental disorders. We derived 23 different ISSs from 6,993 probands in DDD. Nominal evidence for enrichment of likely deleterious mutations was found in 11 different genes in 8/23 ISSs. 6/11 genes were known monoallelic DD loci, including two X-linked genes. Of the 5 remaining genes, one (SPTBN2) has convincing evidence that it is indeed a monoallelic DD gene, probably acting via a dominant-negative mode of action.

The collection and reproducibility of phenotypic data collection in genetic studies needs to achieve the same status as the sequence data. This requires rigorous and consistent standards to enable the data to be used and replicated computationally within and between studies. The accurate definition of aggregate phenotypic patterns in individuals with comparable genotypes has use beyond clinical diagnostics as it may provide biological insights via the identification of modular functions. At present, quantitative phenotypic data cannot produce causative genotype-disease models with strong discriminative value for many conditions. This may be due to the relatively small numbers of affected individuals in each group but it is equally plausible that many conditions may be genuinely indistinguishable. However, it seems likely that quantitative data used in combination with other phenotypic information (clinical terms, facial image analysis, etc.) will have significant utility in ranking variants that have survived the basic filtering using technical, consequence, and population frequency parameters. Relatively simple modifications to electronic health systems should enable the extraction of data in computational tractable formats. Systematic collection, storage, and retrieval should improve both the completeness and accuracy of the data available for diagnostic analysis in individuals with developmental disorders. We challenge authors and publishers to ensure that all phenotypic data—quantitative and categorical—associated with human genetic disease are accessible using consistent formats that maximize the potential for future meta-analysis.

Declaration of Interests

M.E.H. is a co-founder, consultant, and non-executive director of Congenica Ltd. The remaining authors declare no competing interests.

Published: October 10, 2019

Web Resources

• DECIPHER, https://decipher.sanger.ac.uk/

• G2P, https://www.ebi.ac.uk/gene2phenotype

• HGVS, https://variantvalidator.org

• HPO similarity tools, https://github.com/jeremymcrae/hpo_similarity

• ISS scripts, https://github.com/Stuart-Aitken/ISS

• OMIM, https://omim.org/

• RCSB Protein Data Bank, http://www.rcsb.org/pdb/home/home.do

Supplemental Data

Data S1. Naive Bayes Model Probabilities

Excel file of naive Bayes model probabilities for 24 genes (Figure 2D) and for 23 ISS (Figure 3A). The probability tables for each value for each attribute are listed, for example, the probability of gender=Female in KAT6B is 0.7. The a priori probabilities are listed in the final column.

Data S2. Naive Bayes Summary Tables

Excel file of naive Bayes summary tables for 24 genes and for 23 ISS (as Figure 2D and Figure 3A) reordered by clustering growth values.