Abstract
Fundamental ecological processes, such as extrinsic mortality, determine population age structure. This influences disease spread when individuals of different ages differ in susceptibility or when maternal age determines offspring susceptibility. We show that Daphnia magna offspring born to young mothers are more susceptible than those born to older mothers, and consider this alongside previous observations that susceptibility declines with age in this system. We used a susceptible‐infected compartmental model to investigate how age‐specific susceptibility and maternal age effects on offspring susceptibility interact with demographic factors affecting disease spread. Our results show a scenario where an increase in extrinsic mortality drives an increase in transmission potential. Thus, we identify a realistic context in which age effects and maternal effects produce conditions favouring disease transmission.
Keywords: Age, Daphnia, demography, ecology, epidemiology, evolution, immunity, maternal effects, modelling, senescence
Introduction
The ecological context of a host species will shape key demographic features, which in turn affect disease spread. Extrinsic mortality, for example, will regulate population density, a well‐established demographic feature that modulates disease spread. However, extrinsic mortality will shape other population characteristics such as age structure. The age structure of a population could affect disease dynamics through a number of mechanisms, including (1) when individuals of different ages show different susceptibilities (i.e. age effects) or (2) when the offspring of mothers of different ages show different susceptibilities (i.e. maternal age effects).
The age of a host at exposure to a parasite is well established to affect the probability and severity of infection, this is partly due to the ontogeny of the immune system (Lesser et al. 2006; Nussey et al. 2008; Hasselquist & Nilsson 2009). In vertebrates, this includes the development of adaptive immunity followed by immunosenescence, but invertebrates also appear to show a clear development of the immune system or pathogen resistance (Rheins & Karp 1985; Wilson‐Rich et al. 2008; Piñera et al. 2013; Garbutt et al. 2014a; Izhar & Ben‐Ami 2015; Izhar et al. 2015). The consideration of age‐related effects on epidemiological processes has contributed greatly to disease prevention strategies (Anderson & May 1982; Katzmann & Dietz 1984; Müller 2000).
By contrast, maternal age effects on offspring susceptibility to pathogens have received little attention. Generally, maternal effects have been shown to affect population dynamics and demography through alterations in offspring reproduction, maturation and growth rate (Gaillard et al. 2003; Benton et al. 2005; Beamonte‐Barrientos et al. 2010), and maternal effects have been shown to alter population robustness in the face of ecological challenges (Räsänen & Kruuk 2007; Kuijper & Hoyle 2015). The maternal condition, for example nutrition availability or disease status, is increasingly recognised to affect offspring susceptibility to infection (Huang & Song 1999; Little et al. 2003; Rahman et al. 2004; Mitchell & Read 2005; Gasparini et al. 2007; Lorenz & Koella 2011; Stjernman & Little 2011; Tidbury et al. 2011; Boots & Roberts 2012; Garbutt & Little 2017). This suggests variation in phenotypic traits, as a response to the maternal environment, can drive population and epidemiological dynamics (Beckerman et al. 2002; Mitchell & Read 2005; Garbutt et al. 2014b).
Maternal age has been shown to affect offspring performance as offspring of older mothers are often born larger and mature at a greater size (Priest et al. 2002; Benton et al. 2008). However, although older mothers produce larger offspring, they tend to produce fewer of these, suggesting they are subject to a ‘size vs. number’ trade‐off. These effects on performance measures indicate that maternal age effects may alter the competitive environment experienced by successive generations (Beckerman et al. 2006; Kindsvater et al. 2011; Prior et al. 2011).
To understand how maternal age influences susceptibility, we studied four clutches of offspring from the parthenogenic crustacean Daphnia magna when exposed to a bacterial pathogen. In addition to pathogen resistance, we collected data on reproduction and body size. The experiment showed that older mothers give birth to more resistant offspring. Earlier work from our laboratory (Garbutt et al. 2014a) and others (Izhar & Ben‐Ami 2015; Izhar et al. 2015) showed that older mothers themselves are more resistant to this pathogen. We used these two observations – that older mothers are both more resistant and give birth to offspring that are more resistant – to develop a compartmental model describing how population age structure, the effects of age and maternal effects combine to influence the spread of infection.
Study organisms
Daphnia magna (Crustacea: Cladocera) are filter feeding planktonic crustaceans found in small freshwater ponds. Pasteuria ramosa is a sterilising specialist bacterial pathogen of D. magna that is transmitted horizontally when spores released from infected cadavers are ingested by uninfected filter feeding hosts (Ebert et al. 1996, 2016). In this experiment, we used a Daphnia clone (Kc49a) from a population in a pond in Kaimes in the Scottish borders, and a P. ramosa strain isolated from the same population. This host clone was part of a study of genetic variation in maternal effects (Stjernman & Little 2011) and shows a response that is typical of its population (see Little & Colegrave 2016 for discussion of the merits of single vs. multigenotype studies).
Methods
The basic design of our experiment was to measure the pathogen susceptibility of offspring from first, second, third and fifth clutches. Two newborn Daphnia were isolated from each clutch. One of these offspring was exposed to P. ramosa. The second offspring was used for measurement of reproduction. Each newborn also had their body size measured before being placed into their treatment groups. This experiment ran from July 31–September 24 2014.
Acclimation
Twenty‐four replicates, each an individual Daphnia in a 60 mL glass jar, were acclimatised for three generations under standardised conditions. This process is designed to equilibrate uncontrolled maternal effects and ensure that each replicate is independent. During this time, Daphnia were kept in artificial pond medium (Kluttgen et al. 1994) in an incubator with a light:dark cycle of 12 : 12 L:D at 20 °C. They were fed daily with 7 × 106 cells of green algae, Chlorella spp., and changed into fresh medium twice a week and when offspring were present in the jar. Each new generation was initiated with offspring from the second clutch. After the third homogenising generation, one individual was taken from each replicate and placed in fresh jars to be the mothers of the experimental animals. These individuals were kept in the same conditions as the homogenising generations.
Experimental generation
Experiment 1
Offspring from clutch 1, 2, 3 and 5 of the maternal generation were our experimental animals. Two offspring were taken from each mother and were randomly assigned to either pathogen exposure or control – used for the measurement of fecundity in the absence of infection. For pathogen exposure, 20 000 P. ramosa spores were added to each jar and media was not changed for 5 days. Spore mixes were prepared earlier by crushing infected Daphnia and counting spores with a haemocytometer. At the end of the 5‐day exposure treatment, Daphnia were changed into clean jars with fresh media. Daphnia were maintained for 28 days after the exposure period under the conditions used for acclimation. During this period, the date of birth of each clutch and number of individuals born to each clutch was recorded. At the end of the 28‐day period, infections were diagnosed (infections are easy to discern with the naked eye as Daphnia have a clear carapace and reddish‐brown bacterial growth is visible in the haemolymph in addition to the lack of reproduction). The control Daphnia whose fecundity was measured were handled identically, except they were not exposed to parasite spores. All newborn Daphnia were photographed for later measurement of size at birth.
Independent replication of experiment 1
The design and methodology of this experiment were identical to that detailed above: we measured the fitness of offspring from first, second, third and fifth clutches following identical protocol for pathogen exposure and control individuals.
Analysis
Body size at birth and total reproduction were analysed in a general linear model. Age at first reproduction was studied with a parametric survival analysis following a Weibull distribution. A generalised linear model (with binomial errors and logit link function) was used to study probability of becoming infected. In all cases, the explanatory variable was the clutch the Daphnia originated from. The different response variables were analysed with different subsets of the data: size at birth considered the entire data set, reproduction considered only Daphnia that were unexposed to P. ramosa, while the probability of infection included only Daphnia that were exposed to the pathogen.
Experimental Results
The age of the mother had a significant effect on the probability of offspring infection (χ 2 = 24.8, P < 0.0001) where offspring from young mothers were highly susceptible to infection, as shown in Fig. 1a. Maternal age (or variable ‘Clutch’ for clutch number) also had a significant effect on total reproduction (F 3,72 = 15.8, P < 0.0001) as seen in Fig. 1b and size at birth as seen in Fig. 1c (F 3,91 = 219, P < 0.0001). Age at first reproduction was not influenced by maternal age (χ 2 = 5.07, P = 0.16). These patterns were confirmed through the independent replication of the experiment. Maternal age had a significant effect on the probability of becoming infected (χ 2 = 20.6, P < 0.0001; Fig. 1a), total reproduction (F 3,76 = 3.91, P < 0.002; Fig. 1b) and size at birth (F 3,105 = 96, P < 0.0001; Fig. 1c).
Figure 1.
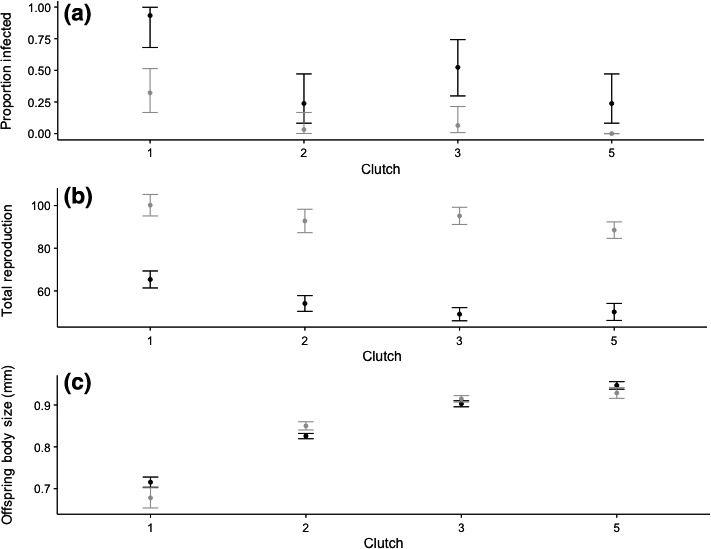
Both the original experiment (shown in black) and independent replication of the experiment (shown in grey) showing (a), proportion of infections resulting from exposure of the treatments groups from clutches 1, 2, 3 and 5, (b) reproductive output and (c) the effect of clutch number (maternal age at reproduction) on offspring body size.
Epidemiological Model
Our experimental results showed a strong effect of maternal age on offspring resistance, with older mothers producing more resistant offspring. Previous research showed that D. magna show age‐specific susceptibility, where older individuals are more resistant to infection than young individuals (Garbutt et al. 2014a; Izhar & Ben‐Ami 2015; Izhar et al. 2015). Host population demography and environmental factors, such as baseline mortality rates, predation and density, have been shown to influence transmission rates and pathogen virulence evolution. Pathogen transmission is a function of an infected individual's rate of contact with other potential hosts. As increased host population density should increase contact rates, it is generally expected that an increase in population density will result in an increase in transmission potential (Anderson & May 1979; Ebert & Mangin 1997; Choo et al. 2003). The theoretical consideration of age‐specific effects on epidemiological dynamics tends to consider age‐specific mortality and age‐specific contact rates rather than the strength or weakness of an age‐associated immune response (Anderson & May 1982; Katzmann & Dietz 1984; Castillo‐Chavez et al. 1989; Müller 2000). In addition to this, the presence of maternal age effects on offspring susceptibility has not been considered. We therefore developed a compartmental model incorporating these age effects on the expected number of secondary infections resulting from the introduction of an individual infected with a novel pathogen into a completely susceptible population (). R 0 depends on the duration of infection, the probability of infecting a susceptible during one contact and the rate of contact per unit of time (Dietz 1993). The output value can be used as a benchmark. If the value of this is > 1, then the disease will spread (Anderson & May 1979).
We divide the population into four age classes, each of which could be infected (I) or uninfected (U), giving a total of eight classes of individuals in the model – U Y,Y, U Y,O, U O,Y, U O,O, I Y,Y, I Y,O, I O,Y, I O,O (Fig. 2). Here, the first subscript indicates the individual's age (Y for young, O for old), and the second subscript indicates the individual's mother's age at that individual's birth.
Figure 2.
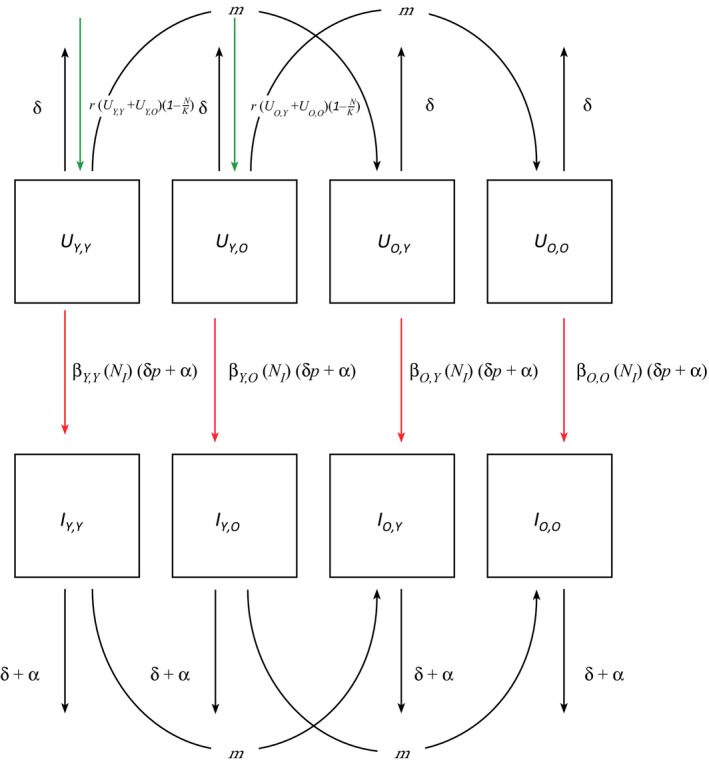
The compartmental model with uninfected and infected groups of four age classes. UY;Y – young individuals with a young mother. UY;O – young individuals with an old mother. UO;Y– old individuals with a young mother. UO;O – old individuals with an old mother. m is the rate at which an individual goes from being a young individual to an old individual. b is the rate of transmission. d is the baseline death rate, with d +a representing baseline death rate plus a measure of virulence. Other parameters are r – maximum reproduction; K – carrying capacity; N – total population number; p ‐ the probability that non‐pathogen induced death of an infected individual will lead to transmission. As p. ramosa is only transmitted upon host death, death rates are included in the transmission terms.
The parameters in the model are: is the baseline transmission rate between infected and uninfected individuals; is the baseline death rate; α is pathogen virulence as measured by disease induced death; p is the probability that non‐pathogen induced death of an infected individual will also lead to transmission; m is the rate of maturation (i.e. the rate at which individuals move from the young age classes to the old); M describes the proportional reduction in an individual's susceptibility as associated by having a mother of the age class ‘Old’ applied to the baseline ; A describes the proportional reduction to an individual's susceptibility by themselves being of the age class ‘Old’ applied to the baseline ; r is the maximum per capita growth rate of hosts; K is the carrying capacity of the host population, controlling density dependent limitation on reproduction. The transmission terms, as shown in Fig. 2, contain the rates of death, due to P. ramosa being transmitted only upon host death. We make the assumptions that there is a constant rate of death across age groups that susceptibility varies between these classes, and that reproduction is resource limited with a constant maximum reproductive rate per day for uninfected individuals. We assume that infected individuals do not reproduce as P. ramosa castrates the host during infection (Ebert et al. 1996). For full details of the model, see the appendix.
In the absence of the pathogen, the equilibrium densities of each age class are
| (1a) |
| (1b) |
| (1c) |
| (1d) |
Here, we see that the equilibrium density of U O,O decrease with increasing mortality δ (as r > δ is necessary for a positive equilibrium). The equilibrium density of both U Y,O and U O,Y initially increases with increasing mortality before decreasing once . Similarly, the density of the age class U Y,Y initially increases with increasing mortality before decreasing once (Fig. 3). This bias of the age structure towards more susceptible younger individuals and individuals from younger mothers occurs as increased mortality frees up resources for reproduction, resulting in the production of more young individuals who will themselves reproduce leading to more individuals from young mothers. At this equilibrium, the total density of uninfected hosts, N U, is
| (2) |
meaning that the total density of uninfected individuals monotonically declines with increasing mortality rate (Fig. 3).
Figure 3.
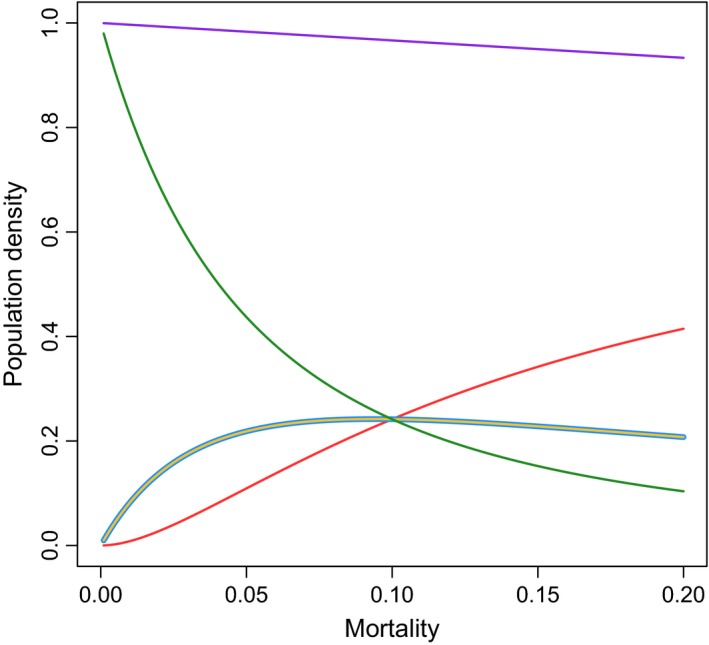
Showing the changes in total population density with increased mortality (purple line). This is broken down into the age classes showing density of young individuals with young mothers (red line), young individuals with old mothers (yellow line), old individuals with young mothers (blue line) and old individuals with old mothers (green line). Due to parameterization of the model, the yellow and blue lines trace one another. Other parameters are r = 3; K = 1; m = 1/10.
To calculate the R 0 of the pathogen, we consider the number of secondary infections caused by a rare pathogen at the pathogen‐free equilibrium given in eqns 1a–d. This yields a pathogen R 0 of
| (3) |
In the appendix, we show that the relationship between pathogen R 0 and the extrinsic death rate, δ, must be negative whenever our age‐related and maternal age‐related effects on susceptibility are absent (i.e. A = 0, M = 0). However, this relationship is humped whenever
| (4) |
with this condition satisfied for sufficiently large reductions in susceptibility with age and maternal age (high A and M). The relationship is illustrated with and without both the age‐ and maternal age‐related reductions in susceptibility in Fig. 4. These qualitative results also hold when an environmental transmission stage of the pathogen is explicitly included in the model (see Appendix).
Figure 4.
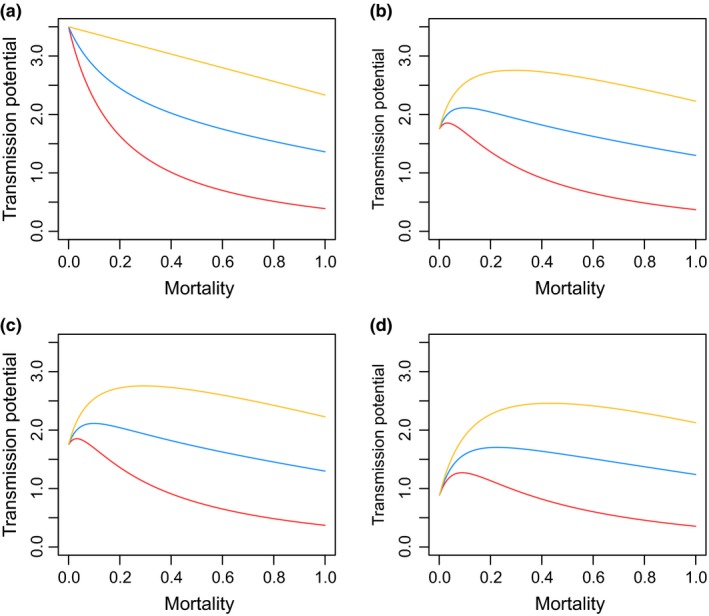
Modelling outputs of the relationship between mortality and transmission potential ( with three different parameter values for p (extrinsic mortality of infected individuals contributing to transmission). p = 1 (yellow line), p = 0.5 (blue line) and p = 0 (red line). (a) No age effects or maternal age effects present, (b) Maternal age effects, (c) Age specific susceptibility, or (d) – Both maternal and age effects present. In the presence of no effects (a), the expected negative relationship between mortality and transmission potential is shown at all levels of extrinsic mortality. The presence of maternal age effects (b), age‐specific susceptibility (c) or both effects (d) within a population results in a humped relationship, where an increase in mortality initially increases transmission, due to the shift in density of susceptible individuals. This positive relationship between mortality and transmission potential is most pronounced at all levels of extrinsic mortality when both effects are present. Other parameters are: r = 3; K = 1; a = 1/5; m = 1/10; = 3.5.
The humped shape can be explained as follows. In the absence of reductions in susceptibility with age and maternal age, reductions in host population density with increasing mortality reduce pathogen R 0 owing to reduced transmission. However, increased mortality also shifts the age structure of the population towards younger individuals and individuals from younger mothers, which can increase in density even as the total population density declines. If these age classes of individual are sufficiently more susceptible to infection, this increase in their density can more than compensate for the total reduction in host population density, leading to an increase in R 0 with increasing non‐pathogen induced mortality. However, at very high mortality rates the total host population density is sufficiently reduced that shifts in age structure no longer compensate, and R 0 declines with mortality, resulting in a humped relationship. Transmission potential begins to decline at lower mortality rates when, p (the probability that non‐pathogen induced death of an infected individual will lead to transmission) is low, as increasing mortality will result in loss of infections with little opportunity for transmission. Note, however that our qualitative results hold even in the case of p = 0.
Discussion
Our experiment makes the novel observation that younger mothers give birth to offspring that are more pathogen susceptible. This data combined with recent observations that younger hosts are themselves more susceptible (Garbutt et al. 2014a; Izhar & Ben‐Ami 2015; Izhar et al. 2015) formed the basis of a compartmental model showing that increasing extrinsic mortality, and thus decreasing total host population density, can lead to increasing transmission. The relationship between mortality and transmission that is classically seen, where higher host densities generate greater transmission, is so pervasive it has become a central assumption of the epidemiological theory that contributes to our understanding of pathogen traits and virulence. (Anderson & May 1979; Read 1994; Levin 1996; Alizon et al. 2009; Schmid‐Hempel 2011). Thus, we have identified a new, and biologically realistic context in which age effects and maternal effects combine to alter the ecological conditions favouring disease transmission.
Our observed effect of maternal age on offspring performance is an example of maternal effect‐driven, delayed life history effects (Beckerman et al. 2002) that lead to whole cohort effects (Ginzburg et al. 1994; Lindström 1999). The maternal condition has previously been shown to have prolonged effects on offspring fecundity, maturation and growth rate over successive generations, influencing population dynamics (Gaillard et al. 2003; Benton et al. 2005; Beamonte‐Barrientos et al. 2010). We now add offspring susceptibility to this list, and can infer from our model that maternal age effects on susceptibility can then impact successive cohorts, by altering the condition of each cohort at reproduction. Considering P. ramosa specifically, the predictions of our model are biologically feasible. This pathogen sterilises hosts, but often one clutch is produced before reproduction stops. If no effect of maturation or maternal effects were present, the transmission potential would decrease as seen in Fig. 4. In the presence of these effects, however, those who are young when infected only reproduce once whilst young and then do not contribute to the population at a later age. Their offspring are therefore expected to be the most susceptible. As mortality increases, the density of young individuals contributing highly susceptible individuals to the population increases, resulting in the dynamic we show.
The maternal effect of increased resistance in offspring born to older mothers could be explained by size at birth. Older mothers are known to produce larger offspring (Marshall et al. 2010; Kindsvater et al. 2011) and therefore the size at birth could be responsible to some degree for the resistance to disease. This correlation of body size to susceptibility has been made before in Daphnia, and it has been suggested this is due to increased resources availability for costly immune defences and somatic maintenance (Garbutt et al. 2014a). In Daphnia spp. and other systems, however, this correlation between increased size and reduced infection probability does not always hold true (Hall et al. 2007; Stjernman & Little 2011). Furthermore, the assumption that increased body size equates to better fitness and performance does not explain how smaller offspring of young mothers are capable of reproducing in higher numbers than their larger counterparts.
The observed trade‐off between offspring size and the decreasing number of offspring in each successive reproductive event could be adaptive if clutches of older mothers were to experience more challenging environments than young mothers. This is plausible given population size could increase, increasing competition, and potentially pathogen prevalence. It has been seen previously that Daphnia produce larger and more resilient offspring in tough conditions (Mitchell & Read 2005; Garbutt et al. 2014b) and larger individuals are better competitors for resources in a more dense populations (Brockelman 1975). In addition, individuals born to older mothers may need to be larger in order to compete with their older siblings (Plaistow et al. 2007).
In summary, our experimental results add evidence to a growing body of work showing maternal age effects on offspring performance (Berkeley et al. 2004; Plaistow et al. 2007; Marshall et al. 2010). Furthermore, our model shows that where age‐related and maternal age‐related effects occur they can fundamentally transform the ecological conditions that favour disease transmission. Divergent host susceptibilities within a population could also have marked effects on pathogen evolution and virulence, and our model lends itself to an extension that includes studies of optimal virulence.
Statement of Authorship
JC wrote manuscript; JC and LM created model; TL and LM provided comments on the manuscript; JG and TL designed experiment; JG carried out laboratory work.
Data Accessibility
Data available from http://doi.org/10.5281/zenodo.322882
Supporting information
Acknowledgements
We thank Phil Wilson for assistance. This work was supported by a NERC grant NE/I026405/1, a Wellcome Trust strategic grant to the Centre for Immunity, Infection and Evolution (grant reference 095831), and the Edinburgh Earth & Environment Doctoral Training Partnership.
References
- Alizon, S., A., H. , Mideo, N. & Van Baalen, M. (2009). Virulence evolution and the trade‐off hypothesis: history, current state of affairs and the future. J. Evol. Biol., 22, 245–259. [DOI] [PubMed] [Google Scholar]
- Anderson, R.M. & May, R.M. (1979). Population biology of infectious diseases: Part I. Nature, 280, 361–367. [DOI] [PubMed] [Google Scholar]
- Anderson, R. & May, R.M. (1982). Directly transmitted infectious diseases: control by vaccination. Science (80‐.)., 215, 1053–1060. [DOI] [PubMed] [Google Scholar]
- Beamonte‐Barrientos, R. , Velando, A. , Drummond, H. & Torres, R. (2010). Senescence of maternal effects: aging influences egg quality and rearing capacities of a long‐lived bird. Am. Nat., 175, 469–480. [DOI] [PubMed] [Google Scholar]
- Beckerman, A. , Benton, T.G. , Ranta, E. , Kaitala, V. & Lundberg, P. (2002). Population dynamic consequences of delayed life‐history effects. Trends Ecol. Evol., 17, 263–269. [Google Scholar]
- Beckerman, A.P. , Benton, T.G. , Lapsley, C.T. & Koesters, N. (2006). How effective are maternal effects at having effects? Proc. R. Soc. B Biol. Sci., 273, 485–493. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Benton, T.G. , Plaistow, S.J. , Beckerman, A.P. , Lapsley, C.T. & Littlejohns, S. (2005). Changes in maternal investment in eggs can affect population dynamics. Proc. Biol. Sci., 272, 1351–1356. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Benton, T.G. , St Clair, J.J.H. & Plaistow, S.J. (2008). Maternal effects mediated by maternal age: From life histories to population dynamics. J. Anim. Ecol., 77, 1038–1046. [DOI] [PubMed] [Google Scholar]
- Berkeley, S.A. , Chapman, C. & Sogard, S.M. (2004). Maternal age as a determinant of larval growth and survival in a marine fish, Sebastes melanops. Ecolo, 85, 1258–1264. [Google Scholar]
- Boots, M. & Roberts, K.E. (2012). Maternal effects in disease resistance: poor maternal environment increases offspring resistance to an insect virus. Proc. R. Soc. B Biol. Sci., 279, 4009–4014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brockelman, W.Y. (1975). Competition, the fitness of offspring, and optimal clutch size. Am. Nat., 109, 677–699. [Google Scholar]
- Castillo‐Chavez, C. , Hethcote, H.W. , Andreasen, V. , Levin, S.A. & Liu, W.M. (1989). Epidemiological models with age structure, proportionate mixing, and cross‐immunity. J. Math. Biol., 27, 233–258. [DOI] [PubMed] [Google Scholar]
- Choo, K. , Williams, P.D. & Day, T. (2003). Host mortality, predation and the evolution of parasite virulence. Ecol. Lett., 6, 310–315. [Google Scholar]
- Dietz, K. (1993). The estimation of the basic reproduction number for infectious diseases. Stat. Methods Med. Res., 2, 23–41. [DOI] [PubMed] [Google Scholar]
- Ebert, D. & Mangin, K.L. (1997). The influence of host demography on the evolution of virulence of a microsporidian gut parasite. Evolution, 51, 1828–1837. [DOI] [PubMed] [Google Scholar]
- Ebert, D. , Rainey, P. , Embley, M.T. & Scholz, D. (1996). Development, life cycle, ultrastructure and phylogenetic position of Pasteuria ramosa Metchnikoff 1888: rediscovery of an obligate endoparasite of Daphnia magna Straus. Philos. Trans. B, 35, 1689–1701. [Google Scholar]
- Ebert, D. , Duneau, D. , Hall, M.D. , Luijckx, P. , Andras, J.P. , Du Pasquier, L. et al (2016). A Population Biology Perspective on the Stepwise Infection Process of the Bacterial Pathogen Pasteuria ramosa in Daphnia In: Advances in Parasitology (ed David Rollinson. & Russell Stothard.). Academic Press, Cambridge, MA, pp. 265–310. [DOI] [PubMed] [Google Scholar]
- Gaillard, J.M. , Loison, A. , Toigo, C. , Delorme, D. & Van Laere, G. (2003). Cohort effects and deer population dynamics. Ecoscience, 10, 412–420. [Google Scholar]
- Garbutt, J.S. & Little, T.J. (2017). Bigger is better: changes in body size explain a maternal effect of food on offspring disease resistance. Ecol Evol., doi: 10.1002/ece3.2709. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Garbutt, J.S. , O'Donoghue, A.J.P. , McTaggart, S.J. , Wilson, P.J. & Little, T.J. (2014a). The development of pathogen resistance in Daphnia magna: implications for disease spread in age‐structured populations. J. Exp. Biol., 217, 3929–3934. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Garbutt, J.S. , Scholefield, J.A. , Vale, P.F. & Little, T.J. (2014b). Elevated maternal temperature enhances offspring disease resistance in Daphnia magna. Funct. Ecol., 28, 424–431. [Google Scholar]
- Gasparini, J. , Boulinier, T. , Gill, V.A. , Gil, D. , Hatch, S.A. & Roulin, A. (2007). Food availability affects the maternal transfer of androgens and antibodies into eggs of a colonial seabird. J. Evol. Biol., 20, 874–880. [DOI] [PubMed] [Google Scholar]
- Ginzburg, L.R. , Taneyhill, D.E. , Ginzburg, L.E.V.R. & Taneyhill, D.E. (1994). Population cycles of forest Lepidoptera : a maternal effect hypothesis. J. Anim. Ecol., 63, 79–92. [Google Scholar]
- Hall, S.R. , Sivars‐Becker, L. , Becker, C. , Duffy, M.A. , Tessier Alan, J. & Caceres, C.E. (2007). Eating yourself sick : transmission of disease as a function of foraging ecology. Ecol. Lett., 10, 207–218. [DOI] [PubMed] [Google Scholar]
- Hasselquist, D. & Nilsson, J.‐A. (2009). Maternal transfer of antibodies in vertebrates: trans‐generational effects on offspring immunity. Philos. Trans. R. Soc. B‐Biological Sci., 364, 51–60. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang, C.C. & Song, Y.L. (1999). Maternal transmission of immunity to white spot syndrome associated virus (WSSV) in shrimp (Penaeus monodon). Dev. Comp. Immunol., 23, 545–552. [DOI] [PubMed] [Google Scholar]
- Izhar, R. & Ben‐Ami, F. (2015). Host age modulates parasite infectivity, virulence and reproduction. J. Anim. Ecol., 84, 1018–1028. [DOI] [PubMed] [Google Scholar]
- Izhar, R. , Routtu, J. & Ben‐ami, F. (2015). Host age modulates within‐host parasite competition. Biol. Lett., 11, 20–23. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Katzmann, W. & Dietz, K. (1984). Evaluation of age‐specific vaccination strategies. Theor. Popul. Biol., 25, 125–137. [DOI] [PubMed] [Google Scholar]
- Kindsvater, H.K. , Bonsall, M.B. & Alonzo, S.H. (2011). Survival costs of reproduction predict age‐dependent variation in maternal investment. J. Evol. Biol., 24, 2230–2240. [DOI] [PubMed] [Google Scholar]
- Kluttgen, B. , Dulmer, U. , Engels, M. & Ratte, H.T. (1994). ADaM, an artificial freshwater for the culture of zooplankton. Water Res., 28, 743–746. [Google Scholar]
- Kuijper, B. & Hoyle, R.B. (2015). When to rely on maternal effects and when on phenotypic plasticity? Evolution (N. Y)., 69, 950–968. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lesser, K.J. , Paiusi, I.C. & Leips, J. (2006). Naturally occurring genetic variation in the age‐specific immune response of Drosophila melanogaster. Aging Cell, 5, 293–295. [DOI] [PubMed] [Google Scholar]
- Levin, B.R. (1996). The evolution and maintenance of virulence in microparasites. Emerg. Infect. Dis., 2, 93–102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lindström, J. (1999). Early development and fitness in birds and mammals. Trends Ecol. Evol., 14, 343–348. [DOI] [PubMed] [Google Scholar]
- Little, T.J. & Colegrave, N. (2016). Caging and uncaging genetics. PLoS Biol., 14, 1–5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Little, T.J. , O'Connor, B. , Colegrave, N. , Watt, K. & Read, A.F. (2003). Maternal transfer of strain‐specific immunity in an invertebrate. Curr. Biol., 13, 489–492. [DOI] [PubMed] [Google Scholar]
- Lorenz, L.M. & Koella, J.C. (2011). Maternal environment shapes the life history and susceptibility to malaria of Anopheles gambiae mosquitoes. Malar. J., 10, 382. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marshall, D.J. , Heppell, S.S. , Munch, S.B. & Warner, R.R. (2010). The relationship between maternal phenotype and offspring quality: do older mothers really produce the best offspring? Ecology, 91, 2862–2873. [DOI] [PubMed] [Google Scholar]
- Mitchell, S.E. & Read, A.F. (2005). Poor maternal environment enhances offspring disease resistance in an invertebrate. Proc. Biol. Sci., 272, 2601–2607. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Müller, J. (2000). Optimal vaccination patterns in age‐structured populations: endemic case. Math. Comput. Model., 31, 149–160. [Google Scholar]
- Nussey, D.H. , Coulson, T. , Festa‐Bianchet, M. & Gaillard, J.‐M. (2008). Measuring senescence in wild animal populations: towards a longitudinal approach. Funct. Ecol., 22, 393–406. [Google Scholar]
- Piñera, A.V. , Charles, H.M. , Dinh, T.A. & Killian, K.A. (2013). Maturation of the immune system of the male house cricket. Acheta domesticus. J. Insect Physiol., 59, 752–760. [DOI] [PubMed] [Google Scholar]
- Plaistow, S.J. , St. Clair, J.J.H. , Grant, J. & Benton, T.G. (2007). How to put all your eggs in one basket: empirical patterns of offspring provisioning throughout a mother's lifetime. Am. Nat., 170, 520–529. [DOI] [PubMed] [Google Scholar]
- Priest, N.K. , Mackowiak, B. & Promislow, D.E.L. (2002). The role of parental age effects on the evolution of aging. Evolution, 56, 927–935. [DOI] [PubMed] [Google Scholar]
- Prior, N.H. , Washington, C.N. , Housley, J.M. , Hall, S.R. , Duffy, M.A. & Cáceres, C.E. (2011). Maternal effects and epidemiological traits in a planktonic host‐parasite system. Evol. Ecol. Res., 13, 401–413. [Google Scholar]
- Rahman, M.M. , Roberts, H.L.S. , Sarjan, M. , Asgari, S. & Schmidt, O. (2004). Induction and transmission of Bacillus thuringiensis tolerance in the flour moth Ephestia kuehniella. Proc. Natl Acad. Sci. U. S. A., 101, 2696–2699. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Räsänen, K. & Kruuk, L.E.B. (2007). Maternal effects and evolution at ecological time‐scales. Funct. Ecol., 21, 408–421. [Google Scholar]
- Read, A.F. (1994). The evolution of virulence. Trends Microbiol., 2, 73–76. [DOI] [PubMed] [Google Scholar]
- Rheins, L.A. & Karp, R.D. (1985). Ontogeny of the invertebrate humoral immune response: studies on various developmental states of the American cockroach. Dev. Comp. Immunol., 9, 395–406. [DOI] [PubMed] [Google Scholar]
- Schmid‐Hempel, P. (2011). Evolutionary Parasitology, 1st edn Oxford University Press, New York. [Google Scholar]
- Stjernman, M. & Little, T.J. (2011). Genetic variation for maternal effects on parasite susceptibility. J. Evol. Biol., 24, 2357–2363. [DOI] [PubMed] [Google Scholar]
- Tidbury, H.J. , Pedersen, A.B. & Boots, M. (2011). Within and transgenerational immune priming in an insect to a DNA virus. Proc. Biol. Sci., 278, 871–876. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilson‐Rich, N. , Dres, S.T. & Starks, P.T. (2008). The ontogeny of immunity: development of innate immune strength in the honey bee (Apis mellifera). J. Insect Physiol., 54, 1392–1399. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Data available from http://doi.org/10.5281/zenodo.322882


