Balancing energy supply during photosynthesis – a theoretical perspective

Abstract

The photosynthetic electron transport chain (PETC) provides energy and redox equivalents for carbon fixation by the Calvin‐Benson‐Bassham (CBB) cycle. Both of these processes have been thoroughly investigated and the underlying molecular mechanisms are well known. However, it is far from understood by which mechanisms it is ensured that energy and redox supply by photosynthesis matches the demand of the downstream processes. Here, we deliver a theoretical analysis to quantitatively study the supply–demand regulation in photosynthesis. For this, we connect two previously developed models, one describing the PETC, originally developed to study non‐photochemical quenching, and one providing a dynamic description of the photosynthetic carbon fixation in C3 plants, the CBB Cycle. The merged model explains how a tight regulation of supply and demand reactions leads to efficient carbon fixation. The model further illustrates that a stand‐by mode is necessary in the dark to ensure that the carbon fixation cycle can be restarted after dark–light transitions, and it supports hypotheses, which reactions are responsible to generate such mode in vivo.

Abbreviations

CBB

Calvin‐Benson‐Bassham

MCA

metabolic control analysis

NPQ

non‐photochemical quenching

ODE

ordinary differential equations

PETC

photosynthetic electron transport chain

PPP

pentose phosphate pathway

PQ

plastoquinone

PS

photosystem

Ru5P

ribulose‐5‐phosphate

SBPase

seduheptulose‐1,7‐bisphosphatase

TPT

triose phosphate transporters

Introduction

Decades of multidisciplinary research of photosynthesis resulted in a detailed understanding of the molecular, regulatory and functional mechanisms of light‐driven carbon fixation. Yet, still much is to uncover, especially in terms of identifying processes limiting photosynthetic productivity, and further basic research will be necessary to redesign and potentially optimize photosynthesis (Ort et al. 2015, Cardona et al. 2018). Historically, the process of photosynthesis has been divided into two parts. The so‐called ‘light reactions’ of the photosynthetic electron transport chain (PETC) convert light into chemical energy, supplying ATP and NADPH. This energy is used to drive the carbon dioxide reduction and fixation processes known as the ‘dark reactions’. Thus, the photosynthetic light and dark reactions can be viewed as a molecular economy supply–demand system (Hofmeyr and Cornish‐Bowden 2000, Rohwer and Hofmeyr 2008, Christensen et al. 2015).

Despite this clear interdependence, these processes are often studied in isolation. This approach permits a detailed and in‐depth analysis of particular components at the cost of simplifying others. This separation is also reflected in theoretical research. Numerous approaches in the past decades aimed at translating the complexity of photosynthesis into a mathematical language, resulting in an impressive portfolio of kinetic models. The majority of these models focus either on the supply or on the demand side. Many classical models of the Calvin‐Benson‐Bassham (CBB) cycle, such as the biochemical models for C3 photosynthetic CO₂ assimilation (Hahn 1986, 1987, Pettersson and Ryde‐Pettersson 1988, Poolman et al. 2000, Farquhar et al. 2007, Zhu et al. 2007, 2009), made no attempt to model the processes of the PETC in any detail. Instead, they simplify the rate of electron transport supplying ATP and NADPH in often just one lumped reaction (e.g. non‐rectangular hyperbola as a function of absorbed irradiance in the study by Morales et al. (2018a)), or even considered key components as constant (NADPH in the study by Pettersson and Ryde‐Pettersson (1988)). Likewise, many models of the PETC made no attempt to include details of the energy consuming reactions and describe ATP and NADPH demand by simple lumped reactions. Such an understandable simplification resulted from the fact that these models were created to study specific light harvesting mechanisms, such as state transitions (Ebenhöh et al. 2014), non‐photochemical quenching (NPQ) (Ebenhöh et al. 2011, Zaks et al. 2012, Matuszyńska et al. 2016) or the role of antenna complexes in photosynthetic productivity (Rubin and Riznichenko 2009).

The purpose of this study is to provide a theoretical understanding of the interactions and interdependencies of the PETC and the carbon fixation cycle, with a focus on investigating the supply–demand control of photosynthesis. For such an exercise, mathematical models are ideally suited, because they allow systematic alterations of parameters, which are not easily accessible experimentally, and thus to draw general conclusions about regulatory principles. Apparently, investigating the delicate supply–demand system of photosynthesis requires a mathematical model that contains both processes. Noteworthy, there exist a few successful attempts to include both electron transport and carbon assimilation processes into a unified mathematical framework. The model proposed by Laisk et al. (2006) provides a solid summary of our knowledge on photosynthesis. The model was constructed with an emphasis on including the electron transport through photosystems PSII and PSI, together with a detailed description of the downstream metabolism. As a result, the model can represent steady state photosynthesis and chlorophyll fluorescence, but is insufficient to reproduce dark–light induction of photosynthesis, a property that is critical in the context of our proposed supply–demand analysis. The ‘e‐photosynthesis’ model by Zhu et al. (2013) is a comprehensive description including ‘as many photosynthesis‐related reactions as possible’. Because of its complexity, using the e‐photosynthesis model (Zhu et al. 2013) for a systematic supply–demand analysis is challenging. Moreover, the highly detailed description of the molecular processes included in the model makes it hard to draw conclusions of general validity. Finally, Morales et al. (2018b) recently developed a thorough model of the PETC, including all relevant processes at the chloroplast and leaf level. Nevertheless, as the emphasis of this model was on the PETC regulation, the CBB cycle has been simplified into two steps. This imbalance in the levels of detail describing the two sub‐processes is the main reason why we decided against using it.

We have therefore developed a new photosynthesis model that contains the key components of both subsystems, yet is simple enough to allow for systematic investigations. The model has been constructed by merging a model of the PETC, originally designed to study photoprotective mechanisms (Ebenhöh et al. 2014, Matuszyńska et al. 2016), with a kinetic model of C3 carbon fixation (Pettersson and Ryde‐Pettersson 1988, Poolman et al. 2000). We demonstrate that coupling these two models into a connected supply–demand system is possible, but far from trivial, and results in new emergent properties. Using metabolic control analysis (Kacser and Burns 1973, Heinrich and Rapoport 1974, Heinrich and Schuster 1996) and metabolic supply–demand analysis (Hofmeyr and Cornish‐Bowden 2000), we provide a quantitative description how the control over the overall photosynthetic flux is distributed under various conditions. Moreover, our model analysis illustrates the need for a stand‐by mode of the carbon fixation cycle in the dark to ensure that it can be restarted after prolonged dark periods. Our model results demonstrate that the oxidative pentose phosphate pathway (PPP) can provide exactly this functionality. Remarkably, deactivation of CBB enzymes in the dark alone is insufficient to enable reactivation. These insights could not have been obtained without a model that merges light‐dependent and ‐independent reactions.

We further expect that our model presented here serves as a basis for future developments. We have specifically constructed the model in a modular architecture, which makes it technically straight‐forward to include other relevant interacting pathways, such as photorespiration or other ATP consuming processes. Together with quantitative experimental data, it will be possible to parameterize the model to specific organisms and conditions. Thus validated, we expect that the model becomes a useful tool to predict how photosynthetic efficiency is affected upon environmental or genetic perturbations. We therefore envision that our model, with suitable modifications, will provide a sound theory that supports attempts to improve photosynthetic performance in a targeted manner.

The model

We are presenting here the result of connecting two previously developed kinetic models of photosynthesis, both based on ordinary differential equations (ODEs). The first model describes the primary photosynthetic reactions through the PETC, leading to the production of ATP and NADPH. The CBB cycle is considered as the main consumer of the produced energy and reducing equivalents. Therefore in this model, the downstream metabolism has been simplified to two consuming reactions governed by mass action kinetics. It has been developed based on our previous work: the core model of the PETC by Ebenhöh et al. (2014) and the model of high‐energy dependent quenching in higher plants developed by Matuszyńska et al. (2016). Using this model, we are able to compute the fluorescence emission under various light protocols, monitor the redox state of the thylakoids and the rate of ATP and NADPH synthesis. The second model is the Poolman (Poolman et al. 2000) implementation of the carbon fixation model by Pettersson and Ryde‐Pettersson (1988), reproduced in our institute using the modelbase software (Ebenhöh et al. 2018). In contrast to the original model (Pettersson and Ryde‐Pettersson 1988), in the Poolman representation the rapid equilibrium assumptions were not solved explicitly, but instead approximated by mass‐action kinetics with very large rate constants. Solving the system of ODEs allows computation of different carbon fixation rates and reaction activities at varying concentrations of external orthophosphate. In the original model, the input of the ETC has been simplified by a single lumped reaction of ATP synthesis (v ₁₆ in the study by Pettersson and Ryde‐Pettersson 1988), while NADPH has been kept as a constant parameter.

Included processes and the stoichiometry

The model, schematically represented in Fig. 1, comprises 35 reaction rates and follows the dynamics of 24 independent state variables (Appendix S1, Supporting Information, for a full list of reaction rates and ODEs). In addition, we compute a number of values such as emitted fluorescence or variables derived from conserved quantities. Light is considered as an external, time‐dependent variable. As the focus of this model is to study basic system properties, such as the response to relative changes in the light intensity, we did not calibrate our simulations to experimentally measured light intensities. Therefore in this work, light is expressed in micromoles of photons per square meter per second (μmol m⁻² s⁻¹) and reflects the quantity of light efficiently used, but the conversion factor to the photon flux density of the incident light is unknown. We included two compartments in our model, the thylakoid lumen and the chloroplast stroma. In the lumen, the reaction kinetics for oxidized plastoquinone (PQ), oxidised plastocyanin, oxidized ferrodoxin, lumenal protons (H) and non‐phosphorylated antenna (light harvesting complexes) were taken from Ebenhöh et al. (2014). The four‐state description of the quencher activity, based on the protonation of the PsbS protein and activity of the xanthophyll cycle, was taken from our mathematical model of NPQ, initially developed to study short‐term light memory in plants (Matuszyńska et al. 2016). The previous description of ATP and NADPH consuming reactions is supplemented by the detailed description of the CBB cycle, taking place in the stroma. Processes of the CBB cycle have been implemented as in the mathematical model of C3 photosynthesis by Poolman et al. (2000), based on the original work of Pettersson and Ryde‐Pettersson (1988). The original model reproduces different carbon fixation rates and reaction activities at different concentrations of external orthophosphate, and includes the conversion of fixed carbon into either triose phosphates or sugar and starch. This model has been parametrized for CO₂ saturating conditions and we kept the same assumption for all our analyses. The previous description of ATP synthesis is supplemented in our model with the new rate v _ATPsynthase, which depends on the proton motive force built up by the PETC activity. Moreover, the stromal concentration of NADPH is dynamic.

Figure 1.

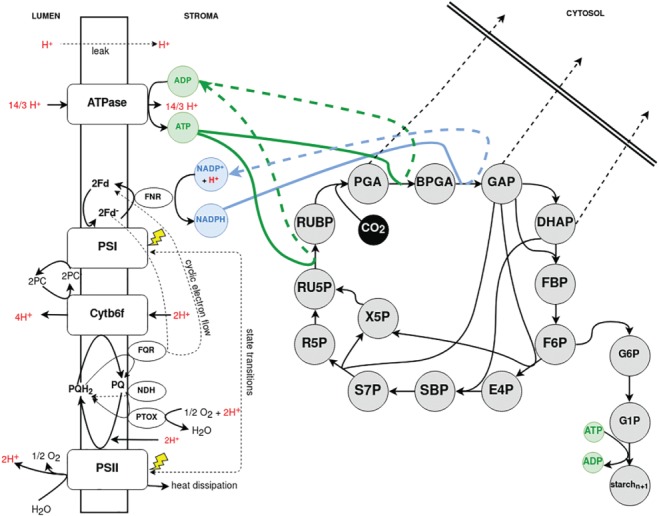
Schematic representation of the photosynthetic processes described by our merged mathematical model. The reactions take place in two compartments. In the lumen, the four protein supercomplexes (PSII, PSI, Cytb6f and ATPase) are embedded, which drive the electron transport in two modes, linear and cyclic; the stroma provides the compartment of C3 photosynthetic carbon fixation. The cytosol defines the system boundary. In color (green and blue) we have highlighted the reactions linking the two submodels: The production and consumption of ATP and NADPH, respectively.

Model compartments and units

The original models were initially developed for different organisms (Ebenhöh et al. (2014) for Chlamydomonas reinhardtii, Matuszyńska et al. (2016) for Arabidopsis thaliana and Pettersson and Ryde‐Pettersson (1988), Poolman et al. (2000) based on data for isolated spinach chloroplasts). Moreover, concentrations and rates were expressed in different units. This patchwork of parameters motivated us to create a general model of photosynthesis, which is not restricted to a single organism. To keep the original structure of the models, but provide consistency, we have kept the original units for each of the compartments and used a conversion factor (p _convf, Appendix S1) to convert quantities where needed. Thus, concentrations of proteins and pool sizes inside the lumen are expressed as in previous models of the electron transport (Ebenhöh et al. 2014, Matuszyńska et al. 2016) in mmol (mol Chl)⁻¹, and the first order rates in mmol (mol Chl)⁻¹ s⁻¹. Concentrations of metabolites and pools inside the stroma are expressed in mM, as in (Pettersson and Ryde‐Pettersson 1988; Poolman et al. 2000). To convert the concentration of ATP produced through the electron transport chain activity, expressed in mmol (mol Chl)⁻¹, to mM, used to express concentrations in the stroma, we made several assumptions, as in our previous models of photosynthesis (Ebenhöh et al. 2011, 2014, Matuszyńska et al. 2016), which were originally derived from Laisk et al. (2006)): (1) chlorophyll content is assumed to be fixed and equal to 350 · 10⁻⁶ mol m⁻² thylakoid membrane, (2) the volume of thylakoid stroma and lumen are 0.0112 and 0.0014 l m⁻², respectively. Thus, 1 mmol (mol Chl)⁻¹ corresponds to 2.5 · 10⁻⁴ M in the lumen and 3.2 · 10⁻⁵ M in the stroma. Although the results presented here have been obtained for these particular values describing the surface‐to‐volume ratios inside the chloroplast, it is in principle easy to change the according parameters to reflect different experimental conditions (Matuszyńska et al. 2016).

Computational analysis

The model has been implemented using the modelbase software, a console‐based application written in Python, recently developed by us (Ebenhöh et al. 2018). Stoichiometry and parameters are provided in Appendix S1, to be found on our GitHub repository (http://www.github.com/QTB-HHU/photosynthesismodel). Moreover, we provide a Jupyter Notebook that allows the user to repeat all the simulations leading to the production of the figures presented in this manuscript.

Reliability of the model

We have assembled the model of photosynthesis adapting previously validated and published mathematical models of two interdependent processes. We have used the same parameters as reported in the previous work and did not perform any further parameter fits (the full list of parameters is provided in Tables S1–S5 in Appendix S1). We have monitored the evolution of several critical parameters to evaluate physiological plausibility of our computational results, including lumenal pH (kept under moderate light around 6), RuBisCO rate (in the order of magnitude of measured values) and the redox state of the PQ pool, used as an estimate of the overall redox state. Moreover, systematic steady state analysis of the model under different light conditions lead to plausible concentrations of CBB cycle intermediates and fluxes, as reported in the literature (Pettersson and Ryde‐Pettersson 1988).

Results and discussion

We used our merged model of photosynthesis and carbon fixation to perform a systematic supply–demand analysis of the coupled system. First, we have integrated the system for various constant light intensities until it reached steady state. Examples are provided in Fig. S1 in Appendix S1. We observed reasonable stationary values of intermediates and fluxes for most of the light intensities. However, under very low light intensities (below 5 μmol m⁻² s⁻¹), the phosphorylated CBB cycle intermediates dropped to zero, and ATP reached the maximal concentration equalling the total pool of adenosine phosphates. Depending on the initial conditions, either a non‐functioning state, characterized by zero carbon fixation rate, or a functioning state, characterized by a positive stationary flux, was reached. This observation of bistability constituted the starting point of our analysis of the tight supply–demand relationship.

In order to analyze this behavior in more detail, we performed time course simulations, in which the light was dynamically switched from constant sufficient light (between 20 and 200 μmol m⁻² s⁻¹), to a ‘dark phase’ of 200 s duration with a light intensity of 5 μmol m⁻² s⁻¹, back to high light, and observed the dynamics of the model variables. In Fig. 2 we display the dynamics of the internal orthophosphate concentration, the sum of all three triose phosphate transporter (TPT) export rates and the RuBisCO rate (from top to bottom, respectively) during such light–dark–light simulations.

Figure 2.

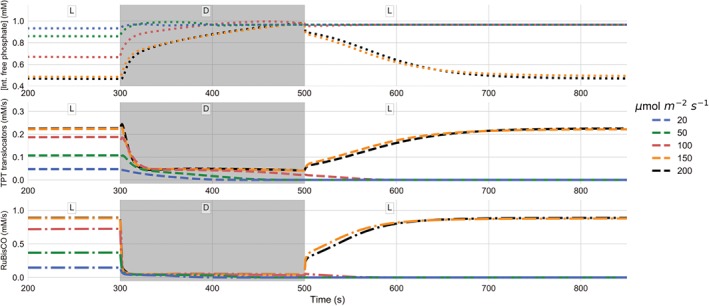
Simulations of light–dark–light transitions for different light intensities, ranging from 20 to 200 μmol m⁻² s⁻¹. Shown are the dynamics of internal orthophosphate concentration, triose phosphate transporter (TPT) export and carbon fixation rates. The simulated time‐courses are shown from 200 s, when the system has reached a stationary state. From 300 to 500 s (gray area), the external light has been set to 5 μmol m⁻² s⁻¹. The figure illustrates that for low light intensities the CBB cycle fails to restart in the second light period.

In agreement with the steady‐state simulations, higher light intensities result in a higher overall flux during the initial light phase. Higher carbon fixation and export fluxes are accompanied by lower orthophsophate concentrations, which reflect higher levels of CBB cycle intermediates. In the dark phase, the non‐functional state with zero carbon flux is approached. While rates decrease, orthophosphate increases, reflecting a depletion of the CBB intermediate pools. In the second light phase, only the simulated transitions to light intensities of 150 and 200 μmol m⁻² s⁻¹ could recover a functional state under the chosen conditions. For lower light intensities, apparently the CBB intermediate pool was depleted to a level, at which re‐illumination fails to recover the CBB cycle activity. Obviously, this behavior disagrees with everyday observations in nature (plant leaves recover from dark periods also under low light intensities). Nevertheless, the model is useful to generate novel insights. First, it illustrates that a critical threshold of intermediate concentrations exists. If levels drop below this threshold, the cycle cannot be re‐activated. Second, it explains the mechanisms leading to intermediate depletion. Under low light conditions, insufficient energy supply results in reduced activity of ATP and NADPH dependent reactions in the carbon fixation cycle, leading to a reduced regeneration rate of ribulose 1,5‐bisphosphate from ribulose‐5‐phosphate (Ru5P). Simultaneously, the reversible (ATP independent) reactions remain active. As triose phosphates are products of reversible reactions, these continue to be exchanged via the TPT export reactions with free phosphate, which leads to a depletion of the CBB cycle intermediates and a concomitant increase of the orthophosphate pool. This further illustrates that even deactivating key light‐regulated CBB enzymes in the dark will not prevent the collapse of the cycle, because the continued activity of the reversible reactions and the triose phosphate translocator will still lead to depleted cycle intermediates (Fig. S2 in Appendix S1).

Clearly, the model is missing important mechanisms that prevent such a functional failure. In particular, we are interested in how a stand‐by mode can be realized, in which intermediate levels are maintained above the critical threshold, while at the same time the resources required to do so, are minimized. A possible strategy to prevent the collapse of the carbon fixation cycle is to resupply important intermediates. One biochemical process in plants that is known to produce Ru5P is the oxidative phase of the PPP, in which one glucose‐6‐phosphate molecule is oxidized and decarboxylated to Ru5P, while producing NADPH and CO₂ (Kruger and Von Schaewen 2003). In order to estimate critical intermediate levels required to prevent the collapse of the carbon fixation cycle, we performed simulations under sufficient light (500 μmol m⁻² s⁻¹), with different initial conditions: the initial concentrations of all carbon fixation intermediates are set to zero, except for Ru5P. The simulated Ru5P concentration, depicted in Fig. 3, displays a characteristic dynamic. In the first seconds, the CBB cycle intermediates are equilibrated by the fast reversible reactions. If the equilibrated Ru5P concentration remains above the critical threshold of approximately 2.5 μM, the cycle reaches a functional state, if it falls below, it will collapse. Interestingly, the threshold concentration is rather independent of the light intensity (Fig. S3 in Appendix S1).

Figure 3.

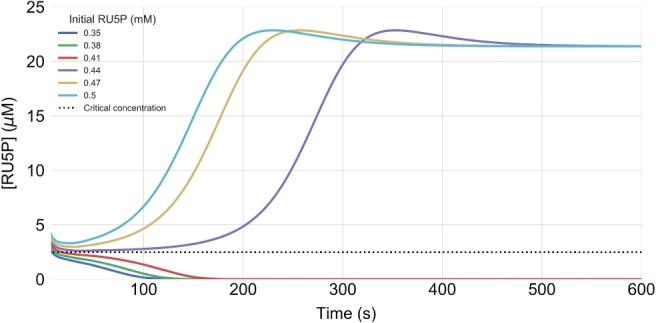
Simulations in light intensity of 500 μmol m⁻² s⁻¹ for different initial concentrations of Ru5P, ranging from 0.35 to 0.5 mM. The Ru5P abundance is shown after 10 s, when the system is approximately equilibrated. The dashed line displays the critical concentration for sufficient cyclic activity after equilibrating. The figure displays that initial Ru5P concentrations below 0.44 mM result in a loss of Ru5P abundance.

To simulate a simple mechanism implementing a stand‐by mode, which maintains sufficient CBB cycle intermediate levels, we introduced a trivial conceptual reaction, exchanging inorganic phosphate with Ru5P. Fig. 4 displays simulated steady state values of the relative stromal ATP concentrations, Ru5P concentrations and lumenal pH in insufficient light conditions (5 μmol m⁻² s⁻¹) as a function of the Ru5P influx. Again, a clear threshold behavior can be observed. If the Ru5P influx exceeds approximately 4 μM s⁻¹, not only CBB intermediates assume non‐zero concentrations, but also the lumenal pH reaches realistic and non‐lethal levels.

Figure 4.

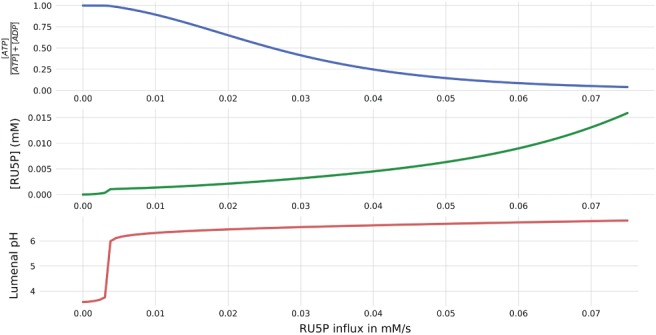
Steady state simulations in low light intensity of 5 μmol m⁻² s⁻¹ and systematically increasing influxes of Ru5P from 0 to 0.08 mM s⁻¹. The figure displays normalized ATP abundance, Ru5P concentration and lumenal pH.

As expected, increased Ru5P influx results in increased stationary Ru5P concentrations, which is accompanied by an increased flux through RuBisCO and the TPT exporter (Fig. S4 in Appendix S1), indicating a higher stand‐by flux, and therefore, a higher requirement of resources to maintain this mode.

These results suggest that a constant flux providing Ru5P in the dark with a rate just above the critical threshold of 4 μM s⁻¹ should maintain intermediate CBB levels sufficiently high, while at the same time minimize the required investment. Indeed, with a constant supply of Ru5P with 5 μM s⁻¹, the system can be restarted and reaches a functional stationary state after a prolonged dark period (Fig. S5 in Appendix S1). Per carbon, this rate translates to 25–30 μM carbon/s, depending whether the pentoses are directly imported or derived from hexoses. Comparing this to stationary carbon fixation in the light of 0.1–1 mM s⁻¹ (for light intensities between 20 and 200 μmol m⁻² s⁻¹, Fig. 2 and Fig. S1 in Appendix S1) shows that resupply under these conditions would consume a considerable fraction of the previously fixed carbon. This calculation demonstrates the importance of down‐regulating the CBB cycle in dark conditions for a positive carbon fixation balance over a day/night cycle. Indeed, key enzymes in the carbon fixation cycle are known to be regulated by the pH and the redox state of the chloroplast stroma. For example, RuBisCO activity is controlled by proton levels and magnesium ions (Tapia et al. 2000, Andersson 2008). Fructose‐1,6‐bisphosphatase, seduheptulose‐1,7‐bisphosphatase (SBPase) and Phosphoribulokinase are all controlled by the redox state through the thioredoxin‐ferredoxin system, and also by pH (Chiadmi et al. 1999, Raines et al. 2000, Raines 2003). Furthermore, Hendriks et al. showed the light dependency of the ADP‐glucose pyrophosphorylase (Hendriks et al. 2003), which is part of the lumped reaction v _Starch in our model. All these mechanisms will lead to a considerable reduction of the required stand‐by flux of the CBB cycle, but are not yet included in our simple merged model.

In the original formulation of our model without constant Ru5P supply or light‐dependent regulation of CBB enzymes, low light intensities lead to a rapid collapse of the cycle. However, in sufficient light ATP levels are very high and carbon fixation rates are already saturated in moderate light conditions (Fig. 2 and Fig. S1 in Appendix S1). These findings indicate that the sets of parameters for the carbon fixation enzymes and the light reactions, derived from the respective original publications, might not be suitably adapted when employed in a merged, cooperating, system. This is not surprising considering that they originate from completely different systems and conditions. However, we wish to highlight here that systems biology models are known to include a ‘sloppy’ spectrum of parameter sensitivities, and yet still provide robust predictions (Gutenkunst et al. 2007).

In order to systematically investigate the supply–demand behavior of the coupled system in different light conditions, we introduce a ‘regulation factor’ f _CBB of the CBB cycle, by which all V _max‐values of the light‐regulated enzymes (see above) are multiplied. This allows for a systematic variation of the energy demand by simulating accelerated or decelerated carbon fixation activity. Performing this variation under different light conditions gives insight into the synchronization of ATP and NADPH production and consumption rates, and thus enables a more profound analysis of the supply–demand regulation of photosynthesis (Brandes et al. 1996, Chiadmi et al. 1999, Raines et al. 2000). For the following steady‐state analysis, the conceptual Ru5P influx reaction is not included.

Fig. 5 displays stationary values of key model variables for different light intensities and regulation factors. In agreement with the observations presented above, that very low light intensities lead to a collapse of the cycle, ATP concentrations (Fig. 5A) are maximal (zero ADP), triose phosphate export (Fig. 5B) and starch production (Fig. 5C) are zero, and the lumenal pH (Fig. 5D) is very low (around 4). The latter is readily explained by the fact that the pH gradient built up by the low light cannot be reduced by the ATPase, which lacks the substrate ADP. Further, it becomes clear that the regulation factor of f _CBB = 1, corresponding to the original parameters, is far from optimal. The ATP:ADP ratio remains very high, and TPT export and starch production rates are well below their optimum, regardless of the light intensities. The stationary lumenal pH further illustrates that parameters are not ideally adjusted. Not only for very low light, but also for moderate to high light conditions (above 300 μmol m⁻² s⁻¹) the lumen is dramatically acidic, indicating a mismatch in production and consumption processes. Increasing the regulation factor to values f _CBB ≈ 4 leads to a dramatic improvement of the performance of the system. The ATP:ADP ratio assumes realistic and healthy values around one, triose phosphate export approximately doubles, and starch production increases by one order of magnitude compared with the original parameter values. Concomitantly, the lumenal pH remains moderate (pH 5.8, as suggested by Kramer et al. 1999). An advantage of mathematical modelling is that one can also predict the behavior of system variables, which are not easy to obtain experimentally. In Fig. S6 in Appendix S1, we exemplarily depict oxidized ferredoxin, oxidized PQ, relative NADP⁺ and violaxanthin levels.

Figure 5.

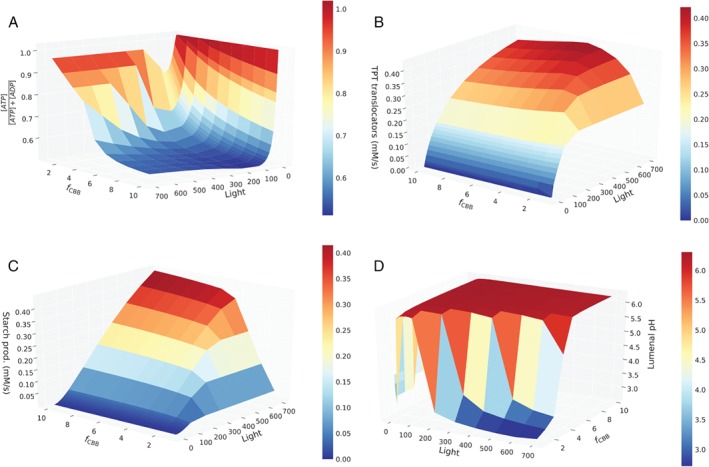
Steady state analysis of the merged photosynthesis model under varying light intensities (x‐axis) and carbon fixation velocities (y‐axis). On the z‐axis (A) the relative ATP abundance, (B) TPT export flux, (C) starch production rate and (D) lumenal pH are displayed.

Quantitative analysis of the supply–demand behavior of the system can be performed by calculating flux control coefficients (Kacser and Burns 1973, Heinrich and Rapoport 1974). To investigate the relative overall flux control of supply and demand reactions, we first divide the set of all reactions in the model (R) into two non‐overlapping sets S and D. S represents the supply set containing all PETC reactions and D represents the demand reaction set including all CBB cycle reactions. We define the overall control of supply (C _Supply) and demand (C _Demand) reactions as the sum of the absolute values of all control coefficients of reactions from S and D, respectively, on the steady‐state flux through the RuBisCO reaction,

$$C_{\text{Demand}}=\sum _{k\in \mathrm{D}}\mid C_k^J\mid$$ (1)

$$C_{\text{Supply}}=\sum _{k\in S}\mid C_k^J\mid ,$$ (2)

where $C_k^J$ denotes the normalized control coefficient of reaction k on the steady‐state carbon fixation rate. Fig. 6 displays the normalized overall control of demand reactions C _Demand/(C _Demand + C _Supply), in dependence on different light intensities and carbon fixation regulation factors. Low light intensities and fast carbon fixation reactions shift the overall flux control to the supply reactions. This can readily be explained because under these conditions (low light and fast CBB enzymes) energy and redox provision by the light reactions are the limiting factor. Interestingly, PSII and PSI contribute strongest to the overall flux control on the supply side (Fig. S7 in Appendix S1). Conversely, high light intensities and slow carbon fixation reactions shift the overall flux control to the demand side, because under these conditions, the system is energetically saturated, and the bottleneck is in the CBB cycle consuming the energy and redox equivalents. Noteworthy, it is the SBPase reaction that exhibits the highest overall flux control (Fig. S8 in Appendix S1), while RuBisCO has only minor control.

Figure 6.

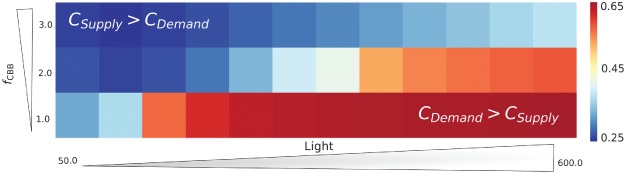
Normalized overall control of the demand reactions (C _Demand) under different light intensities (x‐axis) and CBB cycle activities (y‐axis). The results show how the control shifts from the demand reactions under high light conditions, but low CBB activity, to the supply, under low light conditions but faster CBB cycle.

Conclusions

Merging mathematical models is a highly non‐trivial task. Even if two individual models yield plausible results, there is no guarantee that this is also true after mathematically combining these models. Besides pure technicalities, such as converting concentrations to appropriate units, there are a number of issues that make merging models challenging. Commonly, individual models have been developed with quite different scientific questions in mind, and may therefore display drastically different degrees of details of the involved processes. Moreover, parametrization is often performed for different organisms, tissues or conditions. Most importantly, increasing the system size by integrating two or more models may lead to novel emergent properties that were not observable in the individual models.

In this work, we have successfully merged a model of the PETC, supplying ATP and NADPH, to a model of the CBB cycle, consuming ATP and NADPH. The successful merge was largely facilitated by ensuring a comparable level of simplification of the two individual models (PETC described by 9 ODEs and CBB cycle by 15 ODEs). Our merged model represents a supply–demand system and as such exhibits systemic properties that did not exist in each of the individual models. Linking supply and demand processes into one functional model allowed us to employ metabolic control analysis for a systematic investigation of the regulatory dependence between the PETC and CBB cycle. By simulating the light–dark–light transitions, we could rationalize the importance of the oxidative PPP in providing substrates as a mechanism to operate the CBB cycle in a stand‐by mode. Simultaneously, we illustrate that regulating the activity of the CBB cycle in very low light is critical to avoid excessive investment into the stand‐by mode. Moreover, the model demonstrates that regulation adapting to different light intensities is important to balance the supply by the PETC to the downstream demand. Using metabolic control analysis (MCA), we quantified the control distribution of supply and demand in the system for different light conditions and for varying CBB cycle activities. By introducing a regulation factor, corresponding to the CBB cycle enzyme activities, we demonstrate that the system requires higher input of light to obtain saturation for faster carbon fixation. Our MCA analysis showed that supply reactions exhibit high overall flux control when light is limited. Conversely, the demand reactions control the flux in light‐saturating conditions. Among the supply reactions, the activity of PSII and PSI exhibit the highest overall flux control, while among the demand reactions, SBPase maintains the highest overall flux control (Figs S7 and S8 in Appendix S1). Interestingly, the often considered bottleneck enzyme RuBisCO exhibits only little overall flux control. This observation can be explained by the fact that the model assumes saturated CO₂ conditions.

Our model is freely available as open source software, and we ensure that the results presented here can easily be reproduced. Because of its balanced simplicity and clear modular structure, we envisage that it serves as a platform for future development. Our model results have been obtained for specific experimental values of chlorophyll content and surface‐to‐volume ratios of the chloroplast stroma and lumen. However, these values strongly depend on the growth conditions and vary between plant species. The clear structure of the model and the documented code make it straight‐forward to change model parameters for alternative experimentally determined values. Only relatively minor modifications of the model structure will be necessary to employ it for further analyses of the relationship between the PETC and other subprocesses. For instance, by describing starch as a dynamic variable and by providing a simplified representation of the oxidative PPP, one could improve our understanding of the light dependent turnover of starch (Stitt and Zeeman 2012) and rationalize the resupply of pentoses from hexoses in the chloroplast by the oxidative PPP (Neuhaus and Emes 2000, Kruger and Von Schaewen 2003) and investigate the role of alternative shunts (Preiser et al. 2018). In principle it is also straight‐forward to simulate non‐saturated carbon dioxide concentrations by modifying the RuBisCO rate equation accordingly (e.g. Witzel et al. 2010). However, under these conditions photorespiration can no longer be neglected. Therefore, for a realistic simulation of such scenarios, a simplified representation of the photorespiratory pathway should be included in the model. With such an extension of the model, one could further investigate the energy balance (Igamberdiev et al. 2001) and the distribution of flux control between the PETC, the CBB cycle and the photorespiration reactions. Another model assumption is that all ATP produced by the light reactions is consumed by the CBB cycle. This, however, is of course only an approximation. Under severe stress conditions, or in different organisms, such as C4 plants or nitrogen‐assimilating algae, this approximation is certainly not justified. Our implementation of the model in the modelbase environment (Ebenhöh et al. 2018) is designed to facilitate modifications in an intuitive way. Therefore, adding additional ATP consuming processes is technically simple, allowing theoretical investigations how such an additional demand will influence the behavior of the photosynthetic supply–demand system. The challenge here will be the derivation of realistic rate equations that describe the dependence of the additional ATP consumption rate on the ATP concentration and possibly other system variables.

The process of integrating two models described here illustrates the strength of theoretical approaches. Linking two processes leads to novel properties (here supply–demand balancing), which can be investigated to provide new fundamental insight. The merged model can rationalize the importance of systemic properties, and thus explain why certain mechanisms exist. In particular, none of the individual models could have explained the relevance of the stand‐by mode or the role of adaptive regulation in maximizing efficiency, and thus explain the functional importance of the oxidative PPP or the redox and pH sensitivity of key CBB enzymes in a dynamic environment.

Author contributions

A.M. merged the models and provided all mathematical descriptions. N.P.S. performed the computational analyses and prepared the first draft of the Results. All authors were involved in the interpretation of the results and preparation of the manuscript.

Supporting information

Appendix S1. Supplement.