The sensitivity of the forest carbon budget shifts across processes along with stand development and climate change

Abstract

The future trajectory of atmospheric CO₂ concentration depends on the development of the terrestrial carbon sink, which in turn is influenced by forest dynamics under changing environmental conditions. An in‐depth understanding of model sensitivities and uncertainties in non‐steady‐state conditions is necessary for reliable and robust projections of forest development and under scenarios of global warming and CO₂ enrichment. Here, we systematically assessed if a biogeochemical process‐based model (3D‐CMCC‐CNR), which embeds similarities with many other vegetation models, applied in simulating net primary productivity (NPP) and standing woody biomass (SWB), maintained a consistent sensitivity to its 55 input parameters through time, during forest ageing and structuring as well as under climate change scenarios. Overall, the model applied at three contrasting European forests showed low sensitivity to the majority of its parameters. Interestingly, model sensitivity to parameters varied through the course of >100 yr of simulations. In particular, the model showed a large responsiveness to the allometric parameters used for initialize forest carbon and nitrogen pools early in forest simulation (i.e., for NPP up to ~37%, 256 g C·m⁻²·yr⁻¹ and for SWB up to ~90%, 65 Mg C/ha, when compared to standard simulation), with this sensitivity decreasing sharply during forest development. At medium to longer time scales, and under climate change scenarios, the model became increasingly more sensitive to additional and/or different parameters controlling biomass accumulation and autotrophic respiration (i.e., for NPP up to ~30%, 167 g C·m⁻²·yr⁻¹ and for SWB up to ~24%, 64 Mg C/ha, when compared to standard simulation). Interestingly, model outputs were shown to be more sensitive to parameters and processes controlling stand development rather than to climate change (i.e., warming and changes in atmospheric CO₂ concentration) itself although model sensitivities were generally higher under climate change scenarios. Our results suggest the need for sensitivity and uncertainty analyses that cover multiple temporal scales along forest developmental stages to better assess the potential of future forests to act as a global terrestrial carbon sink.

Introduction

Terrestrial ecosystems, and forests in particular, are contributing substantially to climate change mitigation by absorbing a considerable fraction of anthropogenic carbon dioxide emissions and storing large amount of carbon in biomass and soils (Le Querè et al. 2018). The terrestrial sink, resulting from the balance of photosynthesis and respiration, is extremely sensitive to variation in environmental conditions (climate, seasonality, atmospheric CO₂ concentration, nitrogen deposition) and to disturbances, including management practices (Nolè et al. 2015, Erb et al. 2018). Future changes in the terrestrial carbon budget are therefore very relevant for the trajectory of CO₂ atmospheric concentrations and the Earth's climate (IPCC 2014). To better understand the future role that forests may play in climate change mitigation, and to optimize land‐based mitigation options, it is useful to understand which processes are dominating forest dynamics in the short and even long term. For this purpose, process‐oriented terrestrial ecosystem models embedded into large Earth System Models (ESMs) are important tools (Bonan 2014). These models' predictions have proven to be very uncertain, to the point that the future dynamic of terrestrial ecosystems is one of the most uncertain aspects of the global carbon budget (Friedlingstein et al. 2014, Noce et al. 2016, Mercado et al. 2018). Model construction is based on the representation, at different levels of realism, of specific processes that are subsequently grouped in an ensemble of underlying chains of interacting modules. Within the domain of plant process modeling, the current knowledge of leaf‐level instantaneous responses such as photosynthesis, respiration, and stomatal conductance is rather solid. However, our ability to scale up these responses to larger spatial (e.g., stand level) and longer temporal scales (e.g., decadal to centennial stand development) is less robust (Way and Sage 2008). Ultimately, forest dynamics is considered one of the greatest sources of uncertainty in predicting the future trajectory, in magnitude as well as in direction, of the terrestrial carbon sink under future climate (Friedlingstein et al. 2014).

Uncertainty in model simulations is the quantitative measure of systematic and random variation from the “true” value of a simulated entity (Aubinet et al. 2012). Uncertainty arises from three main sources, which are strongly linked: parameter values, model structure, and input data (Medlyn et al. 2005). In particular, modeling uncertainty can stem from incomplete data for model initialization (i.e., data used to define the initial state of the system), for model parameterization over large spatial scales, and for representing forest development in nonequilibrium conditions. Parameter shifts due to ecosystem perturbations from climate change and disturbances are additional sources of potential uncertainty. These latter factors may increase the relevance of specific processes and decrease the importance of others, ultimately changing the model sensitivity to parameters across temporal scales. To date, models are typically evaluated and optimized with short‐term simulations under present‐day climate (with only some few exceptions, e.g., see TRENDY project; Sitch et al. 2008), and, consequently, leaving open questions on their capability to reproduce robust and less uncertain results in much longer simulations (Wolf et al. 2011a, Bonan 2014). However, the variability of sensitivity and uncertainty over the course of ecosystem development has rarely been studied (Law et al. 2003).

Since forests are long‐lived ecosystems, it is of key interest to understand the causes of such variability also at long‐temporal scales, exploring the relative importance of parameters, processes (and their interactions) and model assumptions that drive variability in model outputs (Huber et al. 2018). This variability extends from young stands, with many small trees with proportionately large foliage biomass, to old stands, with few large trees with proportionately larger stem biomass (Wolf et al. 2011a). Studies at local scales indicate that young and old stands react differently to environmental conditions (Anthoni et al. 2002, Curtis and Gough 2018), due to their developmental stage and to their adjusting physiology with ageing (Zaehle et al. 2006, Sala et al. 2011). The complexity of these interactions has been recognized by forest growth modelers in the last decades, and attempts have been made to devise models that adequately describe the growth response along time of whole ecosystems. Conversely, global models, due to their relatively more abstract nature, usually have considered forests in steady‐state conditions or ignoring stand density and demography (Sitch et al. 2008) leading them to potentially overestimate biomass (Ciais et al. 2008) and underestimate carbon sink (Carvalhais et al. 2010) and neglecting any age‐related effect in forest productivity. Clearly, such results largely vary depending on the model used.

Sensitivity analysis, as the first diagnostic in assessing the uncertainty in model assumptions, process representations and parameterizations, is considered essential to quantifying reliability, robustness, and limitations of models suggesting directions for further improvements aiming to reduce uncertainty (Pappas et al. 2013, Pianosi et al. 2016). Thus, sensitivity analysis (or uncertainty analysis) is the method to quantify the sensitivity in model outputs induced by changes to model inputs (Uusitalo et al. 2015). Despite the growing number of studies that investigate models' sensitivity to parameters controlling “fast” processes (Lombardozzi et al. 2015), and steady‐state conditions (Ricciuto et al. 2018), surprisingly, relatively few studies challenged the inherent hypothesis of changes in model sensitivity to different parameters (even in their magnitude) across forest development at non‐stationary conditions and consequently investigated the impact of such parameters under medium‐ (~50 yr) and/or long‐term (>50 yr) periods (i.e., temporal position relative to the start of simulations). Thus, here we specifically address the question, whether models' sensitivity to parameters or processes changes in medium‐ to long‐term simulations compared to short‐term runs (~10 yr). In particular, we investigate the long‐term emerging patterns of model sensitivity to parameters or processes according to the simulation of forest development and their rates in uncertainty propagation under climate change (i.e., warming and atmospheric CO₂ enrichment). The main objective of this study is to explore variability in the model's sensitivity parameters spectrum for key variables (i.e., net primary productivity [NPP] and standing woody biomass [SWB]) by focusing on the modeled processes along with forest structuring, ageing, and climate change scenarios in a systematic fashion (Fig. 1). In brief, we hypothesize that some parameters may change their influence on modeled processes according to forest development and related functional adjustments because the processes that they control may become more (or even less) relevant with changes in forest structure and at increasing age and tree size. Concurrently, unexpected significance of a parameter or lack of significance can lead to questioning of our mechanistic understanding and the relative role of different processes (Prihodko et al. 2008). Notably, most studies found in literature including forest development and ageing are, to our knowledge, mostly based on Gap Models and Dynamic Vegetation Models (DGVMs) analysis (e.g., LPJ family; see 2013Pappas et al. 2013), with a few studies focused on more general ecosystem process models (Law et al. 2001, 2003).

Figure 1.

Graphical representation of the set of processes, data, and parameters involved in the model sensitivity under forest development and climate change scenarios. Gear wheels with circular arrows refer to processes and data, arrows refer to parameters. NPP, net primary productivity.

In order to address these questions we employed here the process‐based model 3D‐CMCC‐CNR (Collalti et al. 2014, 2016, Marconi et al. 2017), developed to simulate the growth and dynamics in forest ecosystems at three contrasting European forest stands, and specifically (1) to evaluate the model sensitivity bounds to different parameters under different climate change and present‐day climate scenarios for (i) the initialization phase and in the (ii) short‐ (~30 yr), (iii) medium‐ (~60 yr), and (iv) long‐term (>90 yr) runs; (2) to identify key parameters and/or dominant processes, pinpointing their control on the overall physiological and functional responses of forest development and changing climate; (3) to assess and evaluate the physiological and functional plausibility of the model parameter (or process) sensitivity, including the lack of sensitivity, and structural uncertainty; and (4) to discuss whether, as currently considered, some “fixed” (over time) parameters should be otherwise defined as “dynamic” parameters, thus reflecting an endogenous model structural uncertainty.

Since many of the parameters, processes representation and assumptions adopted into 3D‐CMCC‐CNR model are also typical for a large family of other forest stand models (e.g., 3‐PG [Landsberg and Waring 1997], Biome‐BGC‐like models' family [Thornton et al. 2002], G'DAY [Dezi et al. 2010]), age/size‐gap models (ED2 [Medvigy et al. 2009], LPJ‐GUESS [Smith et al. 2001]), and land (or component of) surface models (LPJ‐DGVM [Sitch et al. 2003], CTEM [Arora and Boer 2005], ORCHIDEE [Krinner et al. 2005], JULES [Zaehle and Friend 2010], ACASA [Staudt et al. 2010], Community Land Model, CLM, and its derivates [e.g., Fisher et al. 2015], and the E3SMv0 Land Model [Ricciuto et al. 2018]), we suggest that this work may be of larger and general relevance, offering new insights on forests development and ageing representation.

Materials and Methods

Model description

The 3D‐CMCC‐CNR forest model (v.5.4 BGC) is a biochemical, biophysical, and physiological process‐based model developed to predict carbon, energy, and water fluxes coupled with stand development processes that determine relative stock changes in forest ecosystems at species‐level (Collalti et al. 2014, 2016, 2018, Marconi et al. 2017). The model is designed to simulate the main physiological processes (e.g., photosynthesis and respiration) and hydrological processes (e.g., rain and snow interception) at daily scale, with other processes simulated at monthly and annual scales (e.g., mortality, self‐pruning) and at the species‐specific level. Although the 3D‐CMCC‐CNR is spatially implicit, it embeds a physical representation of forest horizontal and vertical structure with a similar spatial arrangement of crowns as in the “Perfect Plasticity Approximation” (Purves et al. 2008, Strigul et al. 2008, Fisher et al. 2015). The model requires data on initial forest stand condition at the beginning of the run, including species composition, average tree diameter at breast height (DBH), tree height, and stand age and density (number of trees per grid cell). Six main carbon (C) and nitrogen (N) structural biomass pools are considered by the model: leaves, stems, branches, fine and coarse roots, and fruits. A non‐structural tree C pool (NSC, or carbohydrate storage pool; i.e., starch and labile carbon) is also considered. Other C and N sub‐pools are also considered by the model (e.g., sapwood vs. heartwood and live vs. deadwood). These pools are initialized at the beginning of the simulation and are updated daily, monthly, or annually, depending on the processes. All the main equations adopted by the model, as the ways in which they are linked from daily to annual scale, are described in Appendix S1 and Appendix S1: Table S1. Similarities of algorithms, approaches, and assumptions with other vegetation models are also described in detail in Appendix S1: Model description. For a full description of key model principles and theoretical framework see also Collalti et al. (2014, 2016, 2018) and Marconi et al. (2017).

Experimental setup

Overall, across sites 1,665 independent runs were performed encompassing: (1) four different climate change scenarios plus (2) one present‐day baseline climate of ‘no climate change' (The climate‐forcing data) for (3) 55 “perturbed” model parameters (which represent the total number of model parameters), which become twofold considering both positive and negative changes in their values, plus an additional “optimized” parameters samples, (see details in Sensitivity analysis). One modeled annual C flux variable (net primary production [NPP]) and one C pool, namely, standing woody biomass (stem, branch, and coarse root biomass, or SWB), were considered in this analysis as key metrics to represent the autotrophic component of the carbon budget and to quantify vegetation responses at short‐, medium‐ and long‐term changes in model simulations, stand development, and climate (Zaehle et al. 2005). At each site, the model was run for ~100 yr, spanning the period from ~1996 to 2099 depending on the availability of stand data for model initialization.

Study sites

The analysis was applied to three different even‐aged, managed, European forests: an adult (80 yr old), Danish, temperate, European, beech forest (Fagus sylvatica L.; Sorø [Pilegaard et al. 2011]), a moderately young (28 yr old), Finnish, boreal, Scots pine forest (Pinus sylvestris L.; Hyytiälä [Mencuccini and Bonosi 2001, Mäkelä et al. 2006]) and a young (16 yr old), Czech, temperate‐humid, Norway, spruce forest (Picea abies Karst.; Bílý Kříž [Godbold et al. 2015]). The study sites were selected because the three species are representative of the most common types of European deciduous and coniferous species. For the selected sites, at different developmental stages, downscaled and site‐level bias‐corrected ISIMIP‐ESMs (Inter Sectoral Impact Model Intercomparison Project and Earth System Models) climate data were available. General information about the stands and how they are initialized for simulations can be found in Table 1. Model robustness and reliability at these sites under present‐day conditions and considerations about climate change scenario outcomes have been described in earlier works (Collalti et al. 2016, 2018, Marconi et al. 2017).

Table 1.

Sites description with stand initialization data used in simulations

Site name	Species	Climate	DBH (cm)	Age (yr)	Tree height (m)	Density (trees/ha)	LAI (m2/m2)	Source
Hyytiälä	Pinus sylvestris L.	boreal	10.3	28	10	1,800	3	Mencuccini and Bonosi (2001), Mäkelä et al. (2006)
Bílý Kříž	Picea Abies Karst.	cold continental	7.1	16	5.6	2,408	7.5	Godbold et al. (2015)
Sorø	Fagus sylvatica L.	cool temperate, sub‐oceanic	25	80	25	400	5	Pilegaard et al. (2011)

Data correspond to the year 1996 for Hyytiälä and Sorø sites and 1997 for Bílý Kříž. DBH and tree height refer to mean values.

The climate‐forcing data

Input surface weather data include the following variables: daily maximum (T _max, °C) and minimum air temperature (T _min, °C), vapor pressure deficit (VPD, hPa), shortwave solar radiation (MJ·m⁻²·d⁻¹), precipitation (mm/d), and annual atmospheric CO₂ concentration (ppmv [ppm by volume]). For climate change scenarios we used climate data from the ISIMIP Fast Track initiative (Warszawski et al. 2014), based on the Climate Model Intercomparison Project 5 (CMIP5; data available online).¹ The ESMs were driven by four Representative Concentration Pathways (RCPs) associated with different scenarios of greenhouse gas (GHG) concentrations, namely RCP 2.6 (~490 ppmv CO₂‐equivalent), RCP 4.5 (~650 ppmv CO₂‐equivalent), RCP 6.0 (~850 ppmv CO₂‐equivalent), and RCP 8.5 (~1,370 ppmv CO₂‐equivalent; Moss et al. 2010, van Vuuren et al. 2011). To reduce the inherent uncertainty related to climate projections (Morales et al. 2007), the five ESMs (HadGEM2‐ES, IPSL‐CM5A‐LR, MIROC‐ESM‐CHEM, GFDL‐ESM2M, and NorESM1‐M, respectively) were averaged in one single “representative” climate data set, for each of the four RCPs and for each of the sites, which was used to run the model. Finally, to disentangle the effects of forest development to those related to climate change, a “no climate change” scenario was generated by randomly repeating the 1996–2005 climate years up to 2099 with atmospheric CO₂ concentration held fixed at ~370 ppmv and used as reference level.

Sensitivity analysis

The 3D‐CMCC‐CNR forest model uses overall 55 species‐specific eco‐physiological, biophysical, biogeochemical, and structural time‐independent parameters (for a full description, see Table 2 and, for model standard values and references, see Appendix S1: Table S2). Parameter values were previously gleaned mostly from the literature and previous model calibration, optimization, and validation exercises (Collalti et al. 2016, 2018, Marconi et al. 2017), trying to avoid the use of parameters directly measured at the sites, in order to increase generalization of the model use.

Table 2.

List of 3D‐CMCC‐CNR model parameters used in the sensitivity analysis, symbols, units, literature values, and their description (for references in values see Appendix S1: Table S2)

Parameter	Symbols	Units	Fagus sylvatica	Pinus sylvestris	Picea abies	Process(es)	Description
K	k	ratio	0.5	0.51	0.54	L	extinction coefficient for absorption of PAR by canopy
ALBEDO	A	ratio	0.15	0.12	0.06	L	albedo
SLA_AVG0	SLA0	m2/kg DM	40	14.7	7.52	L	average specific leaf area (juvenile)
SLA_AVG1	SLA1	m2/kg DM	20	4.49	3.9	L	average specific leaf area (mature)
TSLA	TSLA	yr	35	10	30	L	age at which average SLA = (SLA_AVG0 + SLA_AVG1)/2
SLA_RATIO	SLAsun:shade	ratio	2.3	2.52	2	L	ratio of shaded to sunlit projected SLA
LAI_RATIO	LAIall:proj	ratio	2	2.6	2.6	L	all‐sided to projected leaf area ratio
FRACB0	PB0	ratio	0.2	0.3	0.6	D	branch fraction (juvenile)
FRACB1	PB1	ratio	0.125	0.1	0.1	D	branch fraction (mature)
TBB	T BB	yr	20	10	30	D	age at which fracB = (FRACB0 + FRACB1)/2
RHO0	ρ0	Mg DM/m3	0.64	0.4	0.425	D	minimum basic wood density (juvenile)
RHO1	ρ1	Mg DM/m3	0.64	0.39	0.374	D	maximum basic wood density (mature)
TRHO	T ρ	yr	50	4	50	D	age at which wood density = (RHO0 + RHO1)/2
COEFFCOND	K D	Pa	800	500	500	C	define stomatal response to VPD
BLCOND	g BL	m/s	0.01	0.01	0.009	C	canopy boundary layer conductance
MAXCOND	g smax	m/s	0.005	0.0025	0.002	C	maximum stomatal conductance
CUTCOND	g cut	m/s	6.00 × 10−5	7.50 × 10−5	6.00 × 10−5	C	cuticular conductance
MAXAGE	agemax	yr	400	300	400	C + M	determines rate of “physiological decline” of forest
RAGE	r age	dimensionless	0.95	0.95	0.95	C + M	relative age to give fAGE = 0.5
NAGE	n age	dimensionless	10	4	4	C + M	power of relative age in function for age
T_MIN	T min	°C	0	−2	−4	P + C	minimum temperature for assimilation/conductance
T_MAX	T max	°C	40	35	35	P + C	maximum temperature for assimilation/conductance
T_OPT	T opt	°C	20	17.5	17.5	P + C	optimum temperature for assimilation/conductance
T_START	T start	°C	60			P + C	thermic sum for starting growth
MINDAYLENGTH	h min	h/d	12			P + C	minimum day length for starting leaf fall
SWPOPEN	SWPopen	MPa	−0.34	−0.5	−0.5	P + C	leaf water potential: start of reduction
SWPCLOSE	SWPclose	MPa	−2.2	−2.2	−2.5	P + C	leaf water potential: complete reduction
OMEGA	ω	dimensionless	0.8	0.8	0.8	A	parameter controlling the sensitivity of allocation to changes in water and light availability
FRACS0	εstem	ratio	0.1	0.15	0.15	A	parameter controlling allocation to stems/minimum ratio to C to stem
FRACR0	εroot	ratio	0.55	0.55	0.55	A	parameter controlling allocation to roots/minimum ration to C to roots
FRACL0	εleaves	ratio	0.35	0.3	0.3	A	parameter controlling allocation to leaves/minimum ration to C to leaves
FRUIT_PERC	εfruit	ratio	0.2	0.2	0.1	A	fraction of NPP allocated for reproduction during the prescribed seasonal period
FRUIT_LIFE_SPAN	Conelife	yr	1	3	3	M	life span for fruits
FINE_ROOT_LEAF	FRL	ratio		1	0.622	A	fine root C:leaf C(initialization)
COARSE_ROOT_STEM	CRS	ratio	0.36	0.29	0.19	A	coarse root C:stem C (initialization)
LIVE_TOTAL_WOOD	LTC	ratio	0.13	0.076	0.076	A	live C:total wood C (initialization)
N_RUBISCO	NR	ratio	0.162	0.055	0.055	P	fraction of leaf N in Rubisco
CN_LEAVES	C:Nleaves	kg C/kg N	27	36	42	A + R	C:N of leaves
CN_FINE_ROOTS	C:Nfroot	kgC/kg N	72	49	58	A + R	C:N of fine roots
CN_LIVEWOOD	C:Nlive	kg C/kg N	70	58	50	A + R	C:N of live wood
BUD_BURST	BB	d	20			Ph	days of bud burst at the beginning of growing season (only for deciduous)
LEAF_FALL_FRAC_GROWING	LFF	dimensionless	0.25			Ph	proportion of the growing season of leaf fall
LEAF_FINEROOT_TURNOVER	ϒgreen	yr−1	1	0.25	0.195	Ph	average annual leaf and fine root turnover
LIVE_WOOD_TURNOVER	ϒlive_wood	yr−1	0.7	0.7	0.7	R	annual live wood turnover
DBHDCMAX	DBHDCmax	ratio	0.5	0.45	0.4	D	maximum DBH to crown diameter
DBHDCMIN	DBHDCmin	ratio	0.14	0.14	0.14	D	minimum DBH to crown diameter
SAP_A	SAPa	dimensionless	0.778	0.974	0.851	D + L	scaling coefficient in sapwood area vs. DBH relationship
SAP_B	SAPb	dimensionless	1.917	1.7979	1.684	D + L	scaling exponent in sapwood area vs. DBH relationship
SAP_LEAF	SAPleaf	m2/m2	5400	1480	2600	D + L	leaf area to sapwood area
SAP_WRES	SAPres	g NSC/g DM	0.11	0.05	0.05	A + R	sapwood to reserve fraction
STEM_A	a S	dimensionless	0.2837	0.127	0.127	D	scaling coefficient in stem mass vs. DBH relationship
STEM_B	n S	dimensionless	2.134	2.3	2.3	D	scaling exponent in the stem mass vs. DBH relationship
CRA	CRA	m	35	32	32	D	Chapman‐Richards maximum tree height
CRB	CRB	dimensionless	0.038	0.04	0.064	D	Chapman‐Richards exponential decay parameter
CRC	CRC	dimensionless	1.104	0.99	1.784	D	Chapman‐Richards shape parameter

The processes column summarizes the main physiological, functional, and structural process(es) that each parameter controls (L, light interception; D, plant structural trait; C, stomatal conductance; M, mortality; P, photosynthesis; A, partitioning and allocation; R, autotrophic respiration; Ph, phenology). PAR, photosynthetically available radiation; DM, dry mass; NSC, non‐structural tree C.

Conceptually, the parameter hyperspace describes species‐specific plant traits by avoiding excessive details and poorly documented parameters, while still aiming to maintain reliable vegetation descriptions. Among the eco‐physiological parameters embedded in the model there are, for example, maximum stomatal conductance or Rubisco nitrogen concentration, while the structural parameters are, for example, leaf area to sapwood area ratio, whereas other parameters are strictly related to species phenology. All model parameters were considered in the sensitivity analysis, as long as they do not violate functional, physical, or phenological relationships, for instance, leaf life span for deciduous species. Some of the parameters are structurally (e.g., allometric parameters) or biologically related (e.g., sapwood to leaf area) and are expected to show covariation among species as also to vary with age. Additionally, some of the parameters are used by the model only at the beginning of the simulation starting from mandatory initial state variables (i.e., DBH, tree height, stand density, and age) to initialize C and N pools at tree and stand level. Conversely, other parameters are used throughout the simulation. The baseline or standard parameterization represents here the benchmark, as the result of previous studies where the model has been evaluated. Results from simulations using different climate change scenarios (which implies also different atmospheric CO₂ concentrations) where compared against the no climate change scenario results to assess model sensitivity to climate‐forcing data.

Due to the high number of model parameters and the potentially high interactions across different processes simulated, a less computationally demanding method was chosen to perform the sensitivity analysis, compared to other much more computationally demanding methods (e.g., Latin hypercube sampling, as in Huber et al. 2018 or Wramneby et al. 2008) or as previously done with 3D‐CMCC‐PSM model but for a much shorter time‐scale (i.e., 3 yr) and under present‐day climate as described in Marconi et al. (2017). Lu et al. (2013) have, however, shown that, in most of the cases, model parameter sensitivities may be dominated by first‐order effects. Following the “one‐[factor]‐at‐a‐time” method (OAT; Morris 1991), in this study, for each simulation, a single parameter has been perturbed by ±10% (constant fraction analysis; Medlyn et al. 2005, Zaehle et al. 2006, Zaehle and Friend 2010, Pianosi et al. 2016), which ideally represent the upper and lower bounds of prior parameter uncertainty, i.e., ±10% represent the tails of this uniform distribution. The OAT and/or the constant fraction analysis have been applied in many other fields and described in numerous other studies (Dufrêne et al. 2005, Medlyn et al. 2005, Tatarinov and Cenciala 2006, Dezi et al. 2010, Campioli et al. 2013). The choice of ±10% is based on several considerations: (1) the variability domain or the most common physical and biological reasonable range of values found in literature for many (but not for all) of the parameters (Hirsch et al. 2004) and (2) to give each of the parameters for each of the species analyzed the same rate of variation avoiding any a priori “expert knowledge” (see Friedlingstein et al. 2014). Furthermore, (3) the use of ±10% helped us to compare against other published studies that have adopted the same level of parameter perturbation. Moreover, (4) the OAT approach allows us to clearly identify and estimate the effects of every tested parameter during the simulated time period, potentially revealing linearity (or non‐linearity) across parameter changes and model outputs and the variations in the model sensitivity to each parameter at different times during the simulation. This is an advantage over more complex and computationally demanding methods that vary multiple parameters at once (global sensitivity), which proved to be infeasible, especially in the case of many parameters to test for long‐simulated periods like those presented in this study. In addition, (5) the treatment of each parameter as a single varying factor (local sensitivity), allows for a simpler and unambiguous synthesis and interpretation of the results by creating a system derivatives space with a number of model simulations lower than the number of derivatives to be estimated (limitations of the OAT method are, however, presented in Discussion). These settings, known as “factor prioritization settings,” allow us to identify and rank parameters that are shown to be the most influential, to minimize the output variance, and to prioritize parameter influence (Cariboni et al. 2007). At the same time (6), this method avoids extreme and implausible results that can be obtained by improbable non‐functional parameter combinations, which might emerge from a multiple parameterization and lead to overestimation of the model sensitivity. Such anomalous parameter combinations are difficult to reject a priori, or from expert judgment, especially under climate change scenarios (Wramneby et al. 2008, Reyer et al. 2016).

The relative changes of model outputs produced by perturbing parameters are computed annually as the relative percentage of change (δ) of the variable x on the time t from the reference (baseline, 0) parameter value (param; Medlyn et al. 2005, van Griensven et al. 2006, Tatarinov and Cenciala 2006) as

$$\frac{d{\mathrm{\delta }}_x}{\mathit{dt}}=\frac{max(|Xparam{n}_0-Xparamn\pm 10\%|)}{Xparam{n}_0}\ast 100$$ (1)

The maximum difference from each of the two perturbations (i.e., positive or negative changes) and the baseline value (0) has been considered as representative of the maximum model sensitivity to changes in parameter value. Eq. 1 is also expressed in relative unit terms (i.e., g C·m⁻²·yr⁻¹ and Mg C/ha, that is, the residual) by excluding denominator and the multiplier factor.

Results were then averaged over the simulation period by summing annual values obtained from Eq. 1 as

$${\mathrm{\delta }}_x=\frac{1}{n}\sum _{i=1}^n\frac{d{\mathrm{\delta }}_x}{\mathit{dt}}\ast 100$$ (2)

To comply with the initial hypothesis that model sensitivity to parameters may not be constant all over the simulation, none of the parameters could be excluded a priori from the analysis.

Results

Outcomes of the sensitivity analysis are reported in Table 3, in three equal‐length reference periods called short (1996–2030), medium (2031–2064), and long (2065–2099), respectively, while in Fig. 2 the model sensitivity with its density distribution in Fig. 3 are shown for each single year. Overall, out of the 55 analyzed parameters, 9 parameters show an effect >5% (assumed arbitrarily as reference level) and can be considered as key parameters potentially critical for the prediction of both NPP and SWB (Appendix S1: Fig. S1).

Table 3.

Maximum model sensitivity (expressed in percentage) for NPP (net primary productivity, upper table) and SWB (standing woody biomass, lower table) for the three sites considered in the study, across four climate change scenarios (RCP) and including the “no climate change” scenario (Cu) from short, medium, to long periods of simulation, respectively

Period and parameter	Hyytiälä					Bílý Kříž					Sorø
	Cu	RCP 2.6	RCP 4.5	RCP 6.0	RCP 8.5	Cu	RCP 2.6	RCP 4.5	RCP 6.0	RCP 8.5	Cu	RCP 2.6	RCP 4.5	RCP 6.0	RCP 8.5
NPP
Short
CN_LIVEWOOD						5.1	6.1	6.2	5.6	5.7	6.3	6.5	6.2	6.2	5.9
K	6.1	6.1	6.1	6.1	6.1
LIVE_TOTAL_WOOD							6.0	6.1	5.3	5.6	6.5	6.1	6.3	6.0	5.8
LIVE_WOOD_TURNOVER											5.9	6.2	6.0	5.5	5.2
SAP_A	7.5	7.5	7.5	7.5	7.5	7.1	7.1	7.1	7.1	7.1
SAP_B	32.9	32.9	32.9	32.9	32.9	22.1	22.1	22.1	22.1	22.1	30.7	30.7	30.7	30.7	30.7
SAP_LEAF	8.6	8.6	8.6	8.6	8.6	7.6	7.6	7.6	7.6	7.6
STEM_B	23.2	23.2	23.2	23.2	23.2	10.3	10.3	10.3	10.3	10.3	37.0	37.0	37.0	37.0	37.0
Medium
CN_LIVEWOOD						6.6	8.6	8.7	7.8	10.1	8.1	9.1	7.8	8.0	8.3
LIVE_TOTAL_WOOD						6.5	8.3	8.2	7.9	9.9	8.1	9.0	7.8	8.8	7.5
LIVE_WOOD_TURNOVER	5.2	6.1	6.2	6.6	7.1	6.1	7.0	7.9	7.7	9.7	10.3	12.8	11.1	12.1	11.0
MAXAGE											9.4	11.5	9.9	10.0	9.7
SAP_B											24.2	23.6	21.7	22.7	22.3
STEM_B	15.0	13.7	13.5	13.3	13.7						31.8	31.5	28.4	30.3	29.9
Long
CN_LIVEWOOD			5.2	5.7	7.1	6.7	8.1	9.2	9.3	11.8	7.3	7.9	8.1	8.2	7.8
LIVE_TOTAL_WOOD			5.2	5.5	6.5	6.7	8.0	9.1	9.2	12.9	7.6	7.8	8.0	8.0	8.0
LIVE_WOOD_TURNOVER	7.0	7.9	9.1	9.2	12.3	8.2	9.6	10.2	10.8	16.8	10.7	12.5	13.0	12.8	14.0
MAXAGE		5.6	6.7	6.5	7.1	7.1	8.0	8.6	9.1	12.7	11.6	12.7	12.4	11.7	12.5
SAP_B											18.0	17.1	16.2	16.5	15.9
STEM_B	11.0	11.2	10.7	9.4	9.5						25.1	23.0	22.8	22.7	22.0
T_MAX					8.6					5.9
All
CN_LIVEWOOD			5.2	5.7	7.1	6.7	8.6	9.2	9.3	11.8	8.1	9.1	8.1	8.2	8.3
K	6.1	6.1	6.1	6.1	6.1
LIVE_TOTAL_WOOD			5.2	5.5	6.5	6.7	8.3	9.1	9.2	12.9	8.1	9.0	8.0	8.8	8.0
LIVE_WOOD_TURNOVER	7.0	7.9	9.1	9.2	12.3	8.2	9.6	10.2	10.8	16.8	10.7	12.8	13.0	12.8	14.0
MAXAGE		5.6	6.7	6.5	7.1	7.1	8.0	8.6	9.1	12.7	11.6	12.7	12.4	11.7	12.5
SAP_A	7.5	7.5	7.5	7.5	7.5	7.1	7.1	7.1	7.1	7.1
SAP_B	32.9	32.9	32.9	32.9	32.9	22.1	22.1	22.1	22.1	22.1	30.7	30.7	30.7	30.7	30.7
SAP_LEAF	8.6	8.6	8.6	8.6	8.6	7.6	7.6	7.6	7.6	7.6
STEM_B	23.2	23.2	23.2	23.2	23.2	10.3	10.3	10.3	10.3	10.3	37.0	37.0	37.0	37.0	37.0
T_MAX					8.6					5.9
Standing woody biomass
Short
K			5.5
SAP_B	12.7	12.7	12.7	12.7	12.7	7.4	7.4	7.4	7.4	7.4	21.7	21.4	21.1	21.7	21.4
STEM_A	8.9	8.9	8.9	8.9	8.9	7.1	7.1	7.1	7.1	7.1	9.3	9.3	9.3	9.3	9.3
STEM_B	67.8	67.8	67.8	67.8	67.8	40.5	40.5	40.5	40.5	40.5	90.6	90.6	90.6	90.6	90.6
Medium
CN_LIVEWOOD							5.3	5.4	5.2	5.4	6.0	6.3	6.4	6.6	6.1
LIVE_TOTAL_WOOD							5.1	5.2	5.1	5.2	5.8	5.8	5.7	6.0	6.4
LIVE_WOOD_TURNOVER											6.4	6.3	6.7	6.5	6.9
MAXAGE											7.9	7.9	7.7	8.1	7.3
SAP_B											24.5	23.8	24.1	24.2	23.7
STEM_B											9.5	7.9	8.9	8.1	8.8
Long
CN_LIVEWOOD						6.1	6.7	7.0	7.0	7.9	7.2	7.5	7.7	7.6	7.4
LIVE_TOTAL_WOOD						6.0	6.6	6.9	6.9	7.8	7.1	7.3	7.2	7.3	7.7
LIVE_WOOD_TURNOVER	5.4	6.0	6.5	6.7	7.8	5.8	6.4	6.8	6.9	7.8	9.5	9.9	10.6	10.3	10.9
MAXAGE	9.8	9.7	9.6	9.6	9.7	7.9	7.7	7.5	7.5	7.7	9.0	8.9	8.4	8.1	8.7
SAP_B											24.8	23.9	24.1	24.2	23.7
SLA_AVG1					5.1	5.2	5.5	5.7	5.6	6.2
STEM_B											12.3	12.4	12.2	12.1	11.9
All
CN_LIVEWOOD						6.1	6.7	7.0	7.0	7.9	7.2	7.5	7.7	7.6	7.4
K			5.5
LIVE_TOTAL_WOOD						6.0	6.6	6.9	6.9	7.8	7.1	7.3	7.2	7.3	7.7
LIVE_WOOD_TURNOVER	5.4	6.0	6.5	6.7	7.8	5.8	6.4	6.8	6.9	7.8	9.5	9.9	10.6	10.3	10.9
MAXAGE	9.8	9.7	9.6	9.6	9.7	7.9	7.7	7.5	7.5	7.7	9.0	8.9	8.4	8.1	8.7
SAP_B	12.7	12.7	12.7	12.7	12.7	7.4	7.4	7.4	7.4	7.4	24.8	23.9	24.1	24.2	23.7
SLA_AVG1					5.1	5.2	5.5	5.7	5.6	6.2
STEM_A	8.9	8.9	8.9	8.9	8.9	7.1	7.1	7.1	7.1	7.1	9.3	9.3	9.3	9.3	9.3
STEM_B	67.8	67.8	67.8	67.8	67.8	40.5	40.5	40.5	40.5	40.5	90.6	90.6	90.6	90.6	90.6

“All” is the average model sensitivity over all simulation periods. An arbitrary threshold of 5% was used as reference level. Within each time period and across sites, values in boldface type represent the most sensitive model parameters. See also Fig. S1 in supplementary material for the sensitivity distribution across scenarios of climate change.

Figure 2.

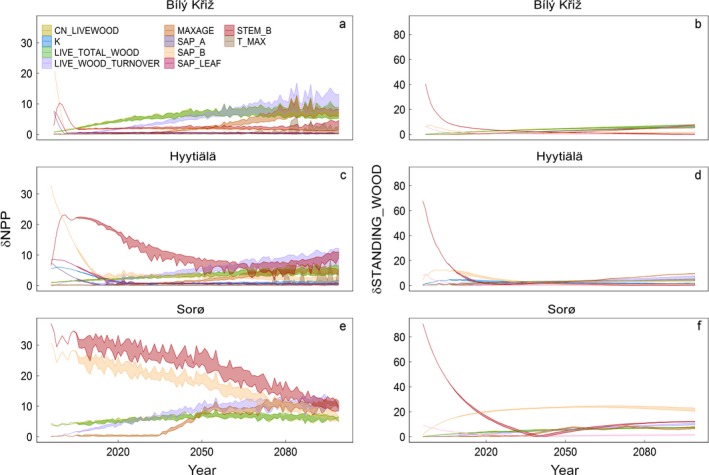
Sensitivity in modeled annual NPP (net primary productivity, left panel) and SWB (standing woody biomass, right panel) expressed in percentage across forest development and climate change scenarios at each of three selected sites. Shaded areas represent the maximum and the minimum relative sensitivity (in absolute values) for the most influential parameters considering that the maximum among the maximum annual values of NPP and SWB changes and the minimum among the maximum annual values of NPP and SWB changes over the climate change and present‐day climate scenarios (RCPs) as summarized in Table 3. An arbitrary threshold of 5% level was used as the reference level.

Figure 3.

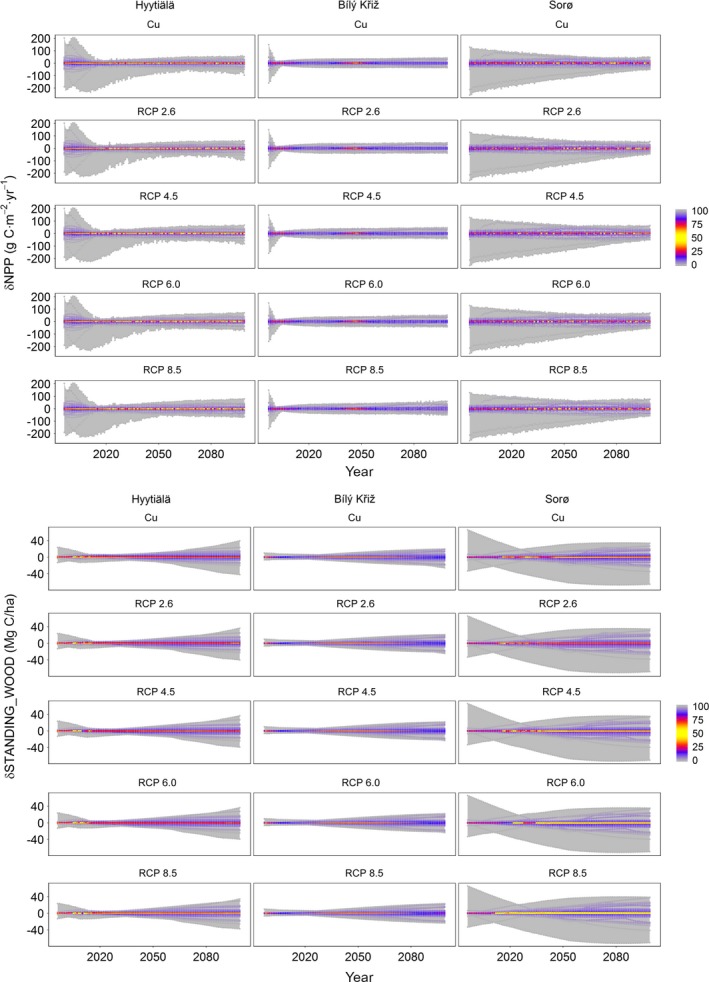
Sensitivity in modeled annual NPP (net primary productivity; upper panel) and SWB (standing woody biomass; lower panel) across forest development and climate change and baseline climate (Cu) scenarios at the three selected sites. Gray‐shaded areas represent the relative modeled sensitivity bounds, considering the maximum annual values of NPP and SWB changes produced by perturbing parameter space across RCPs and the “no climate change” scenario (Cu) as summarized in Appendix S1: Table S2. Colored lines represent the density distribution of sensitivity for 55 parameters using percentiles. The 50th percentile (yellow) represents the median of the values distribution, the 25 and 75 percentiles in red and the 0 and 100 percentiles (grey), the tails of the model results distribution across parameter perturbations.

Sensitivity of NPP

As displayed in Figs. 2 and 3 and summarized in Table 3, modeled NPP sensitivity changes along the simulation where some parameters systematically decrease their importance whereas other appear as progressively dominant at increasing stand age and forest structuring (see also in Appendix S1: Table S3 for the corresponding values in g C·m⁻²·yr⁻¹). Notably, for both NPP and SWB, the model is more sensitive for some parameters (e.g., CN_LIVEWOOD, live‐wood nitrogen concentration; LIVE_TOTAL_WOOD, live‐to‐total wood fraction) at increasing warming and atmospheric CO₂ concentrations, while, for other parameters (e.g., the allometric parameters STEM_B and SAP_B), the model responsiveness decreases. In addition, the model sensitivity and the ranking of parameters show an agreement between evergreen and deciduous species.

In the short period (i.e., 1996–2030, that is, the first 30 yr of simulation) and across sites, the model shows maximum overall responsiveness to a set of eight parameters. The two most important of these are the exponentials of the power‐law allometric equations used to initialize stem biomass (STEM_B) and sapwood biomass (SAP_B), estimated from stand DBH (i.e., the exponential parameters in the y = a × x ^b allometric equation). At the beginning of each modeled year, STEM_B is used to compute the current year DBH from annually increased biomass. Particularly, the SAP_B is the main driver in controlling sensitivity response at two sites (Hyytiälä, 33%, corresponding to 202 g C·m⁻²·yr⁻¹; and Bílý Kříž, 22%, corresponding to 160 g C·m⁻²·yr⁻¹), while at Sorø, the maximum sensitivity values (37%, i.e., 257 g C·m⁻²·yr⁻¹) are showed for the parameter STEM_B. In the short period the perturbation of other parameters such as, e.g., CN_LIVEWOOD, LIVE_TOTAL_WOOD, LIVE_WOOD_TURNOVER (i.e., live‐to‐deadwood turnover), SAP_A, SAP_LEAF (i.e., the relationship between sapwood and leaf area), and k (i.e., the light extinction coefficient) have little influence on NPP, with sensitivity values between ~5% (35 g C·m⁻²·yr⁻¹) and the ~9% (64 g C·m⁻²·yr⁻¹) under all the RCPs. The sensitivity analysis in the short period did not highlight any dependence on the climate scenario also because climatic forcings are similar at the beginning of simulations. In the medium period (i.e., 2031–2064) at the two evergreen sites (Hyytiälä and Bílý Kříž), the model shows a reduced responsiveness to parameter perturbations (the maximum is close to ~15%, 150 g C·m⁻²·yr⁻¹); a similar sensitivity is found at Sorø but, for STEM_B, the model sensitivity was >~28% (168 g C·m⁻²·yr⁻¹). In the long period, the sensitivity is generally close to 10% for all parameters, but, for some of them, the climate scenarios affected model sensitivity, with some effects becoming more notable at increasing temperature and CO₂ concentration. The maximum overall sensitivity is found for STEM_B at Sorø (>23%, 116 g C·m⁻²·yr⁻¹). Conversely, the sensitivity of LIVE_WOOD_TURNOVER tended to increase with increasing warming at Hyytiälä and Bílý Kříž sites. In general, during the entire simulation period, the sensitivity is less than ~17% except for SAP_B and STEM_B, which produce changes in NPP greater than ~22%. At Hyytiälä and Bílý Kříž, the maximum bound of sensitivity is for SAP_B (~33%, 202 g C·m⁻²·yr⁻¹, and ~22%, 160 g C·m⁻²·yr⁻¹, respectively), whereas at Sorø, the STEM_B variation change forest annual productivity by 37% (257 g C·m⁻²·yr⁻¹). Overall, due to the narrow variability of modeled NPP among different RCPs, the model shows to be much more sensitive to parameter values rather than to climate scenarios (Table 3, Fig. 3 and Appendix S1: Table S2).

Sensitivity of standing wood biomass

In the short period, the SWB sensitivity is mainly controlled by perturbations of three parameters, i.e., SAP_B, STEM_A, and STEM_B. The variation of STEM_B shows the highest effect with a change in the annual biomass amount of about 68%, 40%, and 90%, corresponding to 23 Mg C/ha, 10 Mg C/ha, and 67 Mg C/ha at Hyytiälä, Bílý Kříž, and Sorø, respectively. In the medium period, the sensitivity is significant (i.e., >5%) only at Sorø with a maximum value close to 24% (68 Mg C/ha) for SAP_B. In the long period, the modeled SWB sensitivity is almost always less than 10%, although at Sorø for parameter SAP_B, the value is >24% (64 Mg C/ha). Over the whole simulation period, the parameter sensitivities vary between 5% (19 Mg C/ha) and 25% (65 Mg C/ha) at Sorø with very high (>40%) value if the STEM_B is perturbed. Also for SWB, the model shows a transient sensitivity to different parameters across forest development (Fig. 2 and Table 3), as well as on the whole, the model shows to be more responsive to parameter changes rather than to climatic change scenarios (Fig. 3 and Appendix S1: Table S2).

Discussion

Short‐term sensitivity

Initialization and allometry

The 3D‐CMCC‐CNR model outputs are strongly controlled by allometric parameters (e.g., STEM_B or SAP_B) used to initialize the stem biomass and to define the forest structure at the beginning of simulation and (for STEM_B) also along simulations by monthly updating tree diameter increments from biomass growth. The model sensitivity to these parameters is highest for larger initial standing biomass (Bellassen et al. 2010, Song et al. 2012, Marconi et al. 2017). Since many of the other variables are scaled by the initial DBH (which may be itself prone to measurement errors) and stem biomass through other allometric functions, their impact on model sensitivity was expected. However, their influence on NPP is substantially dampened along the forest development, becoming systematically and progressively less influential at the end of simulation because of, among others, saturation of LAI and canopy closure. More generally, the accompanying uncertainty related to the usage of allometric equations is not easily avoidable since most of the field data, concerning some of the physiologically relevant but infrequently sampled pools (i.e., coarse and fine root biomass), are not easily available or directly measurable, while they are more easily obtainable by using generic allometric functions. Allometric equations can be used in the model code to initialize and to update C and N pools, or by the user to produce the model input data, ultimately affecting the sensitivity and the uncertainty of the model outputs in a similar manner. Despite the intrinsic uncertainty, the use of allometric relationships is largely adopted in forest and terrestrial‐land modeling and they are probably necessary scaling tool for both initializing and updating tree pools (e.g., 3‐PG [Landsberg and Waring 1997], LPJ family [Smith et al. 2001, Sitch et al. 2003], Biome‐BGC [Bond‐Lamberty et al. 2005], JULES [Clark et al. 2011], ORCHIDEE [Bellassen et al. 2010]) and for model evaluation (Wolf et al. 2011a).

Different climate scenarios show that allometric parameters progressively increase model sensitivity to changes in climate but tend to decrease in the medium‐ (i.e., 2031–2060) and long‐term (i.e., 2061–2099) simulation. The reasons for this behavior are likely to be traced to the control that these parameters (i.e., SAP_A, SAP_B, and SAP_LEAF) have on LAI and on the maximum annual LAI. In particular, the canopy closure simulated by the model after some years tends to dampen the control of these parameters on LAI. This pattern was also found by Zaehle et al. (2005, 2006) for LPJ‐DGVM. In addition, the greater stem biomass is simulated through the parameter STEM_B: (1) the faster canopy closes, and (2) the more live cells are in stem biomass, leading stem maintenance respiration to increase and ultimately reducing the NPP available for the growth of the subsequent years, and vice versa. Such positive feedback behavior becomes progressively more active under warming conditions as autotrophic respiration in the model is temperature controlled. Consequently, changes in annual NPP will lead to functional plant adjustments and to different increases in stem biomass and different growth and maintenance respiration costs for the subsequent years. Any negative imbalance between photosynthesis and autotrophic respiration is buffered by NSC usage that is refilled at the expense of biomass growth (Fatichi et al. 2014).

Medium‐ to long‐term sensitivity

Over the medium‐ to long‐term periods (i.e., 2031–2099) the 3D‐CMCC‐CNR model shows a greater sensitivity to parameters related to SWB respiration. This analysis approach differs from short‐term sensitivity studies performed, for instance, with the ACASA model (Staudt et al. 2010) or with ED2 (Dietze et al. 2014b). These earlier studies also found that at different years, parameter sensitivity and parameter ranking, as well as parameter values, may vary. The comparison between the results studied in the literature and the results presented in this study, raises a question about the correct representation for the plant traits analyzed: are they constant over time, or do they vary as a function of, for example, forest biomass (i.e., size), structure, or age? Some studies have shown, for instance, changes in specific leaf area (SLA) with age (Forrester et al. 2017), which have been translated in top‐down model parameter values that allow the SLA to decrease with ageing (Landsberg and Waring 1997) and, at the same time, to increase with canopy depth (Thornton and Zimmermann 2007). Other parameters (for instance, LIVE_WOOD_TURNOVER or C:N stoichiometry in tree pools) are expected also to systematically (co)vary with, among others, tree‐size, age, or climate and environmental changes (Machado and Reich 2006, De Kauwe et al. 2014, Walker et al. 2015). These results suggest that underlying ontogenic functional adjustments or acclimation/adaptation processes may lead plants to react differently over the course of their life. However, the same recognition of the dependence on the drivers that should lead processes to be more sensitive to one or another is debated (e.g., see Mencuccini et al. 2005). Ultimately, in‐depth experimental observations in this area are lacking, and we are currently not able to provide a definitive answer to these questions (see also Bond‐Lamberty et al. 2005), therefore, in most cases the use of fixed parameter values represents rather a simplification adopted for the lack of a complete mechanistic understanding about certain processes.

Autotrophic respiration

Parameters controlling maintenance respiration costs also showed high influence on NPP and standing biomass in the long‐term simulations. These include factors controlling tissue nitrogen concentrations (e.g., CN_LEAVES) and connections to the relative size and longevity of live woody pools (LIVE_TOTAL_WOOD and LIVE_WOOD_TURNOVER; see also Zaehle et al. 2006, De Kauwe et al. 2014, Ricciuto et al. 2018). In particular, the allometric parameter controlling the sapwood area (SAP_B), which in turn controls the minimum amount of NSC, maximum annual LAI, and the amount of live tissues, is among the most sensitive parameters over medium‐ to long‐term periods (see Li et al. 2014). As hypothesized by Sala et al. (2011), at increasing sapwood area, more photosynthates are allocated to NSC, which may explain the observed growth decline. Generally, within the model, a decrease in NPP is consistently accompanied by an increase of nitrogen tissue amount, with the connection becoming stronger as substrates (and maintenance respiration) increase, and vice versa.

A relevant aspect of our research deals with the climate and atmospheric CO₂ concentration dependence of the model sensitivity to physiological and structural parameters. Under climate change scenarios, rising temperature acts in two ways: (1) increasing the length of the growing seasons and therefore potentially prolonging the time for photosynthesis (at least in temperature‐limited forests), and (2) increasing respiration costs, that in the model are actively fueled by NSC (negative feedback). NSC however needs to be restored to a critical minimum value, thereby reducing carbon available for increasing SWB (Sala et al. 2011). Conceptually, and following eco‐physiological strategies, the model compensates imbalances in NSC amount by allocating assimilated carbon to reserve pool at first, inhibiting growth in the short term, and only subsequently allocating carbon to other compartments. If these higher respiration rates for plants exposed to higher temperatures are maintained for longer periods (also including both acclimation responses for photosynthesis and respiration, see Model description in Appendix S1), it would mean that a proportionally greater fraction of assimilated carbon is invested (i.e., lost) in respiration, with consequently less C available for growth, entailing a decrease of growth rates with increasing temperature (Kirschbaum 2000).

Tissue turnover

When compared to the two coniferous stands, NPP of the deciduous forest studied here proved to be sensitive to a smaller set of parameters controlling autotrophic respiration (R _a). Among those, CN_LIVEWOOD controls the amount of respiring cells in woody biomass, so that the increase of the fraction of respiring cells leads to an increase in R _a and consequently to a decrease in NPP. In a similar manner, the turnover rate of live tissues (LIVEWOOD_TURNOVER) is shown to affect the annual NPP (as also described for LPJ‐GUESS by Zaehle et al. 2005 and Pappas et al. 2013, for LPJ‐DGVM by Zaehle et al. 2006, and for Biome‐BGC by Cienciala and Tatarinov 2006 and by Wolf et al. [2011b]) by controlling the amount of cells that die and move into the non‐respiring fraction of biomass (heartwood; Larcher 2003) or remain as live tissue. This factor is suggested to be influential also for all models that simulate plants respiration through a mass‐based approach (e.g., CLM; Oleson et al. 2013) and needs further investigation.

On the coupling of photosynthesis and plant respiration

In the model approach, photosynthesis and R _a are considered to be independent (although feed‐forward) processes with different acclimation capacities, resulting in reduced carbon use efficiency (CUE = NPP/GPP, data not shown) at sustained higher temperatures and, across time, with the accumulation of respiring biomass. The hypothesis that respiring substrate and respiration costs increase proportionally with biomass, which is captured in 3D‐CMCC‐CNR behavior, is still a challenge and a matter of debate (Atkin et al. 2007, Drake et al. 2016; A. Collalti and I. C. Prentice, unpublished manuscript). The assumption of a constant R _a to GPP (or NPP to GPP) ratio is particularly critical in trees, for which the ratio between green biomass that support GPP, and the living biomass that respires, may substantially decrease during stand development (Vanninen and Mäkelä 2005). Many forest models attempt to circumvent this problem by considering R _a (or NPP) as a fixed fraction of GPP and maintaining the same relationship under climate change scenarios (e.g.: 3‐PG [Landsberg and Waring 1997], BASFOR [Van Oijen et al. 2005], G'DAY [Dezi et al. 2010]). In doing so, those models assume that the two physiologically processes acclimate at the same rate, although they have different temperature responses (Drake et al. 2016, Reich et al. 2016).

The age effect

Our model includes the parameter MAX_AGE for stomatal conductance and photosynthesis, representing one model assumption in simulating the well‐known age‐related decline in growth (Ryan et al. 2006). Results here show this parameter to affect NPP, through its influence on GPP and, indirectly, by the mortality rate. At Sorø (the oldest stand among the studied sites), MAX_AGE has a strong influence on model responses in the long‐term period and under increasing temperature, with a lower sensitivity at the other sites. At the Hyytiälä and Bílý Kříž sites, and under the warmest scenarios (RCP 8.5), other parameters controlling stomatal conductance and the net leaf assimilation rate (i.e., T_MAX) turned out to be influential; according to this result, these two coniferous species may turn out to be highly susceptible to raising temperature as also recently noted in other modeling exercises and experimental studies (Atkin et al. 2015, Kroner and Way 2016, Mercado et al. 2018).

Sensitivity throughout the course of simulation

Summarizing, for NPP and SWB during the first phase of simulation (short‐term), the model is primarily controlled by parameters (and processes) that define plant architecture and forest structure and that indirectly regulate photosynthesis through LAI, light interception and canopy coverage, and, with secondary influence, by few parameters directly related to photosynthetic processes. As the sensitivity of the model to the aforementioned parameters is progressively reduced, other parameters, mostly related to the carbon storage, biomass accumulation, autotrophic respiration and forest ageing along the stand dynamic, emerge as key factors. The accumulation of SWB coupled warming increases the costs for maintenance respiration while, in parallel, the reduction of stomatal conductance reduces photosynthesis leading to a decrease of NPP. Ultimately, for all of the modeled sites, the parameters affecting NPP are also those controlling the accumulation of SWB.

Our results are in line with the notation of Schulze (2006) and Dietze et al. (2014a), which, based also on field experiments (Körner 2003, Muller et al. 2011, Hoch and Körner 2012), argued that results from complex interactions should not be dominated by the processes of photosynthesis but rather photosynthesis may be more a consequence than a driver of plant structure and architecture.

As displayed in Figs. 2 and 3 and in Table 3, for all the studied sites, forests stages, and climate scenarios, the model sensitivity to changes in parameters regulating NPP shows a considerably lower variability than SWB. This result is mostly due to the compensatory or leveling‐off effects, buffered by NSC, of increases (or decreases) in R_a and the consequent reduction (or increase) in standing wood biomass changes.

In all cases, the model was not shown to be sensitive to parameters controlling the water cycle, as also noted for other models (Zaehle et al. 2005, Pappas et al. 2013, Huber et al. 2018). This is possibly because here we did not consider output variables related to water balance (e.g., evapotranspiration) or due to the specific geographic location of the sites. In fact, as summarized in the fifth IPCC report (IPCC 2013), Northern European sites, even under the most pessimistic warming scenarios (RCP 6.0 and 8.5), will likely not experience significant decreases in precipitation. We also note the lack of model sensitivity for parameters controlling C partitioning ratios, which, as described in the model description in Appendix S1, are forced by limiting factors (i.e., light and soil water content).

In conclusion, we believe that the results of this study could be generalized well beyond the specific 3D‐CMCC‐CNR model, since its structure as well as most of its algorithms, assumptions, and parameters, are commonly embedded and adopted in other terrestrial vegetation models (see Model description in Appendix S1 for similarities and analogies with other vegetation models, e.g., Biome‐BGC, CLM, ORCHIDEE, or JULES). Despite the relative ease of the method, the first‐order partial‐derivative methodology adopted here was aimed at discovering hidden time‐ and forest‐phase‐dependent parameter sensitivities, as well as underlying parameter effects and model feedbacks across processes. Notably, the modeled NPP and SWB proved to be considerably more uncertain and related to the stand development stage, which is determined by the level of standing biomass and long‐term processes that emerge only at forest ageing, rather than to climate change scenarios that only increase model sensitivity for such drivers (i.e., the spread of the changes due to parameter perturbations is larger than those due to different climate‐forcing scenarios). Therefore, this finding suggests that estimates of model sensitivities and their relative uncertainties may change substantially if forest development, that is, changes in forest structure, biomass accumulation, and ageing, would be considered. Thus, the current models' predictions and the associated uncertainties on forest behaviors may be biased in a way potentially larger than previously assumed.

Finally, model behavior and responses may represent a “wake‐up call” for biologists, physiologists, and modelers that should focus in more detail on these aspects: (1) effects of biomass accumulation, the turnover time of live tissues, as well as the key role of the respiration costs and NSC under forest development and particularly, (2) when these are coupled to the acclimatory responses under climate change scenarios in non‐steady‐state systems. In the literature, very little attention has been paid to the analysis of models' sensitivity over decades of forest development and under climate change and, to our knowledge, this work may represent one of the first examples.

Supporting information

 

Collalti A., Thornton P. E., Cescatti A., Rita A., Borghetti M., Nolè A., Trotta C., Ciais P., and Matteucci G.. 2019. The sensitivity of the forest carbon budget shifts across processes along with stand development and climate change. Ecological Applications 29(2):e01837 10.1002/eap.1837

Data Availability

The model code is available at https://github.com/CMCC-Foundation/3D-CMCC-LAND