A Modular Bayesian Salmonella Source Attribution Model for Sparse Data

Abstract

Several statistical models for salmonella source attribution have been presented in the literature. However, these models have often been found to be sensitive to the model parameterization, as well as the specifics of the data set used. The Bayesian salmonella source attribution model presented here was developed to be generally applicable with small and sparse annual data sets obtained over several years. The full Bayesian model was modularized into three parts (an exposure model, a subtype distribution model, and an epidemiological model) in order to separately estimate unknown parameters in each module. The proposed model takes advantage of the consumption and overall salmonella prevalence of the studied sources, as well as bacteria typing results from adjacent years. The latter were used for a smoothed estimation of the annual relative proportions of different salmonella subtypes in each of the sources. The source‐specific effects and the salmonella subtype‐specific effects were included in the epidemiological model to describe the differences between sources and between subtypes in their ability to infect humans. The estimation of these parameters was based on data from multiple years. Finally, the model combines the total evidence from different modules to proportion human salmonellosis cases according to their sources. The model was applied to allocate reported human salmonellosis cases from the years 2008 to 2015 to eight food sources.

1. INTRODUCTION

The main purpose of source attribution methods for foodborne infections is to quantify the likely share of disease cases that could be attributed to a number of predefined food categories denoting the assumed (mutually distinct) origins of bacteria leading to infections. These categories are referred to as “sources” in this context. Consequently, source attribution provides guidance for risk management. In statistical source attribution methods, a probabilistic classifier is constructed to evaluate a conditional probability that a reported human infection originated from the bacterial population of a source, given the characteristics of the case. Two widely used approaches to salmonella source attribution rely either on microbial subtyping or comparative exposure assessment (Pires et al., 2009). The principle of the microbial subtyping approach is to broadly partition human isolates according to the proportions of the same subtypes found in different sources, whereas comparative exposure assessment partitions the proportions according to estimated exposures from different sources (Pires et al., 2009). Foodborne exposure is driven by the occurrence and amounts of pathogens in food, as well as the consumption of food. In addition to food, the environment can also represent a source of infections, but comparative exposure assessment is more challenging with environmental sources. Typically, source attribution focuses on foodborne sources.

Simple subtyping‐based salmonella source attribution is based on point values, as in the Dutch model (Van Pelt et al., 1999), using estimates of the relative proportions of types per source and the total number of reported human cases of each subtype, without addressing statistical uncertainty. A frequently applied typing‐based source attribution model is that described by Hald, Vose, Wegener, and Koupeev (2004), and its modifications (David et al., 2013; Mullner et al., 2009). These methods aim at providing uncertainty for the estimates through the application of a statistical sampling model for the human case counts per subtype and, in the developed version (Mullner et al., 2009), also for the isolate subtypes per source. In this method, the number of human cases of a certain salmonella subtype due to a certain source is assigned a Poisson distribution, with expected value defined as the product of the annual consumption of a particular source and the prevalence of a particular subtype in a source multiplied by the product of the source‐specific parameter and subtype‐specific parameter. The unknown parameters are then estimated by Bayesian methods, with some additional constrains, and assuming that all sources were equally probable to begin with, a priori. However, the challenge has been overparameterization, which leads to poor identifiability and consequently poor convergence of the MCMC (Markov chain Monte Carlo) chain for the model parameters. Therefore, modified versions (David et al., 2013; Mullner et al., 2009) of the Hald model (Hald et al., 2004) have been introduced. These approaches aim to handle the overparameterization by restricting the source‐specific parameters and subtype‐specific parameters (David et al., 2013), as well as by exploiting hierarchical modeling (Mullner et al., 2009). However, these models still tend to be sensitive to the parameterization and the data at hand, particularly with sparse data.

The Bayesian source attribution model presented in this article combines both microbial subtyping and comparative exposure assessment with sparse isolate data. The annual number of isolates derived from the monitored sources was very small. Hence, it would have been impossible to successfully apply any of the existing models as such. Instead, the annual relative proportions of salmonella subtypes were estimated by borrowing strength across different years, assuming that some stability over years persists. The typing information was then combined with the exposure assessment drawn from existing food production chain models (Ranta & Maijala, 2002; Ranta, Mikkelä, Tuominen, & Wahlström, 2013; Tuominen, Ranta, & Maijala, 2006; Tuominen, Ranta, & Maijala, 2007). In addition, the full Bayesian model was modularized in order to separately estimate the unknown parameters in each module (exposure assessment, subtype distribution, and epidemiological model). The model was applied to allocate domestic sporadic human salmonellosis cases in Finland from the years 2008 to 2015 to the following sources: chicken meat, turkey meat, beef, and pork. Domestic and imported foods were treated as separate sources in the model.

2. MATERIALS AND METHODS

2.1. Estimation of the Distribution of Salmonella Subtypes in the Sources

The distribution of salmonella subtypes was modeled for each of the food categories on the basis of the data sets presented in Appendices C–E of the Supporting Information. The annual salmonella findings derived from either production animals or foods derived from these animals were combined to represent the subtype data for each source. These annual counts of the subtypes (X_i,j,t) were modeled with a multinomial distribution:

$$\begin{array}{ccc}& & X_{i,1,t},\dots ,X_{i,J_i,t}\sim \mathrm{Multinomial}\left(u_{i,1,t},\dots ,u_{i,J_i,t},N_{i,t}\right),\hfill \\ & & i=1,\dots ,I,j=1,\dots ,J_i,t=1,\dots ,T,\hfill \end{array}$$

where the multinomial parameters $(u_{i,1,t},\dots ,u_{i,J_i,t})$ indicate the relative proportions of each salmonella subtype j present in source i in year t. The number of all subtypes (J_i) that were considered possible for a source i was based on all its observed subtypes in 2008–2015. Since the annual total counts per source were very low (from 0 to 21; see Appendices C–E of the Supporting Information), an annual sample does not necessarily represent all the subtypes truly existing in a given year. In addition, as some of the salmonella subtypes are characteristic of a particular source, successive years are likely to contain the same subtypes, even when not found in a small sample of isolates. A time series model could be applied to model the distribution of salmonella subtypes in each source, but the data were too limited for seasonal effects or trends. Therefore, a pooled approach was used. A typical uninformative prior distribution for multinomial parameters ({u}) is either Dirichlet(1,…,1) or Dirichlet(1/J_i,…,1/J_i). If applied to annual data, this would directly give the posterior as a Dirichlet distribution with parameters X_i,j,t + w_i,j, with either w_i,j = 1 or w_i,j = 1/J_i. The sum of prior parameters w_i,j is directly comparable to the size of the data sample. With a small data set, the sample weight of the former prior can easily exceed the weight of the data sample, but the sample weight of the latter prior equals just one observation. An informative prior for a single year t was constructed using the pooled results from exclusive years $({\sum }_{k\ne t}{X}_{i,j,k})$, which were divided by their sum over j to obtain prior parameters $w_{i,j,t}=\frac{({\sum }_{k\ne t}{X}_{i,j,k})}{{\sum }_{j=1}^{J_i}({\sum }_{k\ne t}{X}_{i,j,k})},$ so that the (informative) prior sample weight equals one.

Some of the prior parameters could then be zero, that is, the resulting prior could be improper. However, since all types were seen in at least some of the years, the posterior is always a proper Dirichlet distribution with positive parameters. Nevertheless, model diagnostic comparisons between the prior distribution and the posterior distribution can only be carried out when both are proper distributions. An improper prior distribution may also lead to unreasonably small posterior values for multinomial parameters, so for a final default prior, 1 was added to each count before normalizing. Hence, $w_{i,j,t}=\frac{({\sum }_{k\ne t}{X}_{i,j,k})+1}{{\sum }_{j=1}^{J_i}({\sum }_{k\ne t}{X}_{i,j,k})+J_i}$. The effect of this prior choice (adding of 1 or not) is discussed in Section 4.

2.2. Exposure Assessment

In addition to subtyping data, we also used information on the gross exposure to salmonella estimated for each of the sources. A measure of exposure (L_i,t) was defined as the product of the prevalence of Salmonella spp. (π_i,t) and the total annual consumption (M_i,t) for the ith source. The concentration of salmonella bacteria was not taken into account due to insufficient data. The gross exposures $L_{i,t}={\pi }_{i,t}·M_{i,t}$ were obtained as posterior predictive distributions from the existing food chain models (Ranta & Maijala, 2002; Ranta et al., 2013; Tuominen et al., 2007) and import model (Tuominen et al., 2006), which were separately applied to the data from the years 2008 to 2015. The mean and standard deviation of these distributions are presented in Table I. $\mathrm{Gamma}({\alpha }_{i,t},{\beta }_{i,t})$ distributions were then fitted by moment estimation to each distribution of L_i,t, and then used as a prior distribution for L_i,t in the source attribution model.

Table I.

Predictive Mean (m) and Standard Deviation (SD) for the Total Amount of Meat Potentially Contaminated with Salmonella spp. (L_i,t) in Thousands of Kilograms from Domestic (dom.) and Imported (imp.) Sources, Based on the Food Chain Models (Not Accounting for Concentrations)

Meat Type	2008 (m/SD)	2009 (m/SD)	2010 (m/SD)	2011 (m/SD)	2012 (m/SD)	2013 (m/SD)	2014 (m/SD)	2015 (m/SD)
Chicken meat (dom.)	107.6/80.2	355.3/58.9	168.8/96.5	49.6/44.8	49.9/43.3	67.6/55.4	66.1/59.3	65.8/59.0
Turkey meat (dom.)	40.2/26.4	34.7/24.2	26.4/21.2	33.4/23.0	25.7/20.7	21.7/17.8	23.4/19.4	24.3/20.0
Beef (dom.)	21.1/14.6	14.6/13.3	112.9/43.7	63.5/33.5	78.5/31.9	30.3/18.7	59.1/27.8	43.9/26.8
Pork (dom.)	152.8/56.0	154.5/55.0	395.8/154.2	167.2/76.0	277.0/135.5	443.1/439.4	117.1/78.4	133.8/72.2
Chicken meat (imp.)	11.6/5.6	13.1/6.6	15.7/9.8	6.5/3.1	7.8/3.4	11.2/4.0	13.3/4.9	14.2/5.2
Turkey meat (imp.)	3.8/1.7	3.5/1.2	4.9/1.9	2.8/2.2	3.3/2.8	3.0/2.9	2.7/1.2	3.2/1.6
Beef (imp.)	27.4/12.3	27.0/11.9	28.0/34.6	75.2/84.9	93.7/97.9	83.5/80.5	76.8/75.9	66.5/81.8
Pork (imp.)	418.4/162.2	563.2/132.2	1,150.0/354.6	726.6/579.8	407.9/316.0	524.4/181.3	1,042.0/891.2	1,158.0/938.1

Note: Due to large uncertainties, the figures are better compared relative to each other rather than as absolute numbers.

2.3. Epidemiological Model: Reported Human Salmonellosis Cases

The reported total number of human salmonellosis cases by subtype s due to all studied sources in year t (C_s,t) was modeled with a Poisson distribution as an epidemiological model for the population:

$$\begin{array}{ccc}\hfill C_{s,t}& & \sim \mathrm{Poisson}\left(\sum _{i=1}^I{\lambda }_{i,s,t}\right),i=1,\dots ,I,\hfill \\ \hfill s& & =1,\dots ,S,t=1,\dots ,T.\hfill \end{array}$$

The expected value is a sum of the expected number of human cases due to each source i:${\lambda }_{i,s,t}=L_{i,t}·r_{i,s,t}·a_i·q_s$, where s = 1,…,S indicates the different salmonella subtypes detected in any studied sources in 2008–2015, and parameter L_i,t is the gross exposure (Salmonella spp.) from source i in year t (see Section 2.2). The parameter r_i,s,t indicates the relative proportion of salmonella subtype s in source i in year t. The parameters r_i,s,t represent the full set of parameters for the relative proportions (in a source i) of all listed subtypes isolated from any studied source; therefore, r_i,s,t = u_{i, Ind[ i,s ], t} ≥ 0. The index variable Ind[i,s] determines which salmonella subtype in a full list (vector {r}) corresponds to the same subtype in a short (source‐specific) list of subtypes (vector {u}). If subtype s has not occurred at all in a source i during the years 2008–2015, the indicator variable takes the value of zero, and we set u_{i, 0, t}  = 0. The uncertainty related to the short‐listed parameters {u} was modeled in Section 2.1. The source‐specific parameters a_i aim to account for the intrinsic differences between the different sources in their ability to cause a human salmonella infection, and the subtype‐specific parameters q_s similarly for the subtypes. Conventional uninformative prior distributions (Exp(0.001)) were assigned to the parameters a_i and q_s. If {L} and {r} were fixed, the number of unknown parameters would be I + S (source‐specific parameters + subtype‐specific parameters), which is larger than the number of data points (=S) per annum. For a single year, the source‐specific and subtype‐specific parameters could not be freely estimated, even if there were no other unknown parameters, as discussed in the papers by David et al. (2013) and Mullner et al. (2009). In this model, the estimation of a_i and q_s relies on data ({C}) from a longer time period (2008–2015). Hence, the number of data points is considerably larger than the number of unknown parameters $(T·S>S+I)$, and the estimation of {L} and {r} is separated from this.

2.4. Modular Source Attribution

Given all model parameters, the Poisson model can be seen as a competing risk model with Poisson intensities (expected values) for different sources. The relative share of source i in year t (Y_i,t) is then ${\sum }_{s=1}^S{\lambda }_{i,s,t}/{\sum }_{i=1}^I{\sum }_{s=1}^S{\lambda }_{i,s,t}$, which is a function of the model parameters. In full Bayesian modeling, the model works as a whole and information flows freely throughout the model. The model parameters are given by the joint posterior distribution, which consists of the data likelihood functions and the priors (details in Appendix B of the Supporting Information):

$$\begin{array}{c}P(\{L_{i,t}\},\{u_{i,j,t}\},\{a_i\},\{q_s\}|\{X_{i,j,t}\},\{N_{i,t}\},\{C_{s,t}\},\{{\alpha }_{i,t}\},\hfill \\ \{{\beta }_{i,t}\})\propto P(\{C_{s,t}\}|\{a_i\},\{q_s\},\{r_{i,s,t}\}=f(\{u_{i,j,t}\}),\{L_{i,t}\})·\hfill \\ P(\{X_{i,j,t}\}|\{u_{i,j,t}\},\{N_{i,t}\}).\hfill \\ (\{L_{i,t}\}|\{{\alpha }_{i,t}\},\{{\beta }_{i,t}\})·P(\{u_{i,j,t}\}|\{w\})·P(\{a_i\})·P(\{q_s\})\hfill \end{array}$$

However, this full model leads to problems with identifiability between the parameters L_i,t, r_i,s,t, a_i, and q_s because several combinations can give the same value for the product of these parameters (expected number of cases). Hence, these three modules ((1) exposure assessment, (2) subtype distributions, and (3) epidemiological model) were treated as separate modules that do not fully interact as in full Bayesian inference. This method is described as modularization (Liu, Bayarri, & Berger, 2009) in the Bayesian context. It may be beneficial to keep the different modules partly separate because the most valid data for estimating the unknown parameters in modules 1 and 2 are already inside each module, and hence we do not necessarily need interaction between modules for this estimation. The cut function (Plummer, 2015; Spiegelhalter, Thomas, Best, & Lunn, 2004) provided in OpenBUGS software (Lunn, Jackson, Best, Thomas, & Spiegelhalter, 2013; Lunn, Thomas, Best, & Spiegelhalter, 2000) was used to prevent feedback from the other modules to modules 1 and 2 but to allow the information to propagate from these modules to the epidemiological model (module 3) and source attribution. This means that parameters L_i,t only depend on parameters α_i and β_i,t, and not on other quantities in the model. Respectively, parameters {u} only depend on {X}, {w}, and {N}, and not on the other data or parameters in the model (see Fig. 1). The Poisson mean parameter was consequently written using cut functions: ${\lambda }_{i,s,t}^{\ast }=\mathrm{cut}(L_{i,t})·\mathrm{cut}(r_{i,s,t})·a_i·q_s.$ The joint posterior distribution $(\mathrm{cut}(L_{i,t}),\mathrm{cut}(u_{i,j,t}),a_i,q_s|X_{i,j,t},N_{i,t},C_{s,t},{\alpha }_{i,t},{\beta }_{i,t})$ then differs from the fully connected Bayesian posterior distribution.

Figure 1.

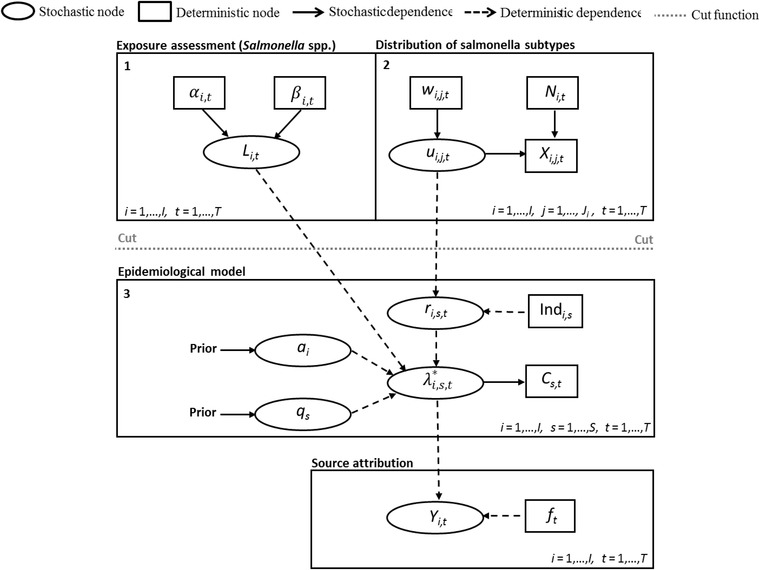
A directed acyclic graph of the modular Bayesian source attribution model. The full Bayesian model was separated into three modules using a cut function (provided in OpenBUGS software).

The Poisson parameter ${\lambda }_{i,s,t}^{\ast }$ describes the expected number of human cases of subtype s due to source i in year t. The predicted proportion of the total burden of domestic human salmonellosis cases attributed to source i in year t (Y_i,t) was then formulated as follows:

$$\begin{array}{ccc}\hfill Y_{i,t}& =& \frac{{\sum }_{s=1}^S\mathrm{cut}\left(L_{i,t}\right)·\mathrm{cut}\left(r_{i,s,t}\right)·a_i·q_s}{{\sum }_{i=1}^I{\sum }_{s=1}^S\mathrm{cut}\left(L_{i,t}\right)·\mathrm{cut}\left(r_{i,s,t}\right)·a_i·q_s}·\hfill \\ \hfill f_t& =& \frac{{\sum }_{s=1}^S{\lambda }_{i,s,t}^{\ast }}{{\sum }_{i=1}^I{\sum }_{s=1}^S{\lambda }_{i,s,t}^{\ast }}·f_t,\hfill \end{array}$$

where the coefficient f_t is the annual percentage of all reported domestic human cases that represented the same salmonella subtypes that were also found in the studied sources during 2008–2015 (see Section 2.1.1). The percentage (1 – f_t) of human salmonellosis cases involving other salmonella subtypes (not previously seen in any studied source) was attributed to other unknown sources. The structure of the whole source attribution model is illustrated in Fig. 1.

2.5. Data

2.5.1. Salmonella Subtypes in the Sources

The salmonella subtype data were collected from the studied sources during 2008–2015. All salmonella isolates from foods (domestic or imported) or living animals represented subspecies of Salmonella enterica. Isolates of Salmonella enterica subspecies enterica were subdivided into serotypes, and salmonella serotypes Typhimurium, Enteritidis, and 1,4,[5],12:i were further subdivided into phage types. The data set also contained a few isolates of Salmonella enterica subspecies diarizoane, which were not further subtyped but used as their own subtype category in the source attribution model. According to this categorization, the total number of different salmonella subtypes detected in either foods or food production animals (chickens, turkeys, cattle, and pigs) during the eight‐year period was 86, of which 17 were not detected in humans over the years 2008–2015. Isolates from food and from the corresponding food production animals were combined due to the lack of data for more refined grouping. In this data set, 54 of 86 salmonella subtypes were uniquely detected in one source. The remaining 32 salmonella subtypes were detected in two or more sources. The number of unique subtypes according to the source is presented in Table II. The salmonella subtypes Enteritidis 3, Infantis, Tennessee, and Typhimurium 120 were detected in four different sources, which was the maximum number of sources for a single subtype in this data set. The salmonella subtype data set is presented as a whole in Appendices C–E of the Supporting Information. In addition, a minor number of Salmonella enterica subspecies enterica isolates were not further subtyped due to an unknown reason. Thus, these observations had to be ignored in the estimation of subtype distributions. The data sets presented in Appendices C–E of the Supporting Information do not offer information on the absolute prevalence of salmonella in the different sources of exposure because the sample sizes are unknown and may vary considerably between sources and years.

Table II.

The Total Number of Salmonella Subtypes and the Total Number of Unique Subtypes Derived from Domestic (dom.) and Imported (imp.) Sources

Source of Exposure	Unique Subtypes	Total Number of Subtypes
Chicken (dom.)	2	6
Turkey (dom.)	1	5
Beef (dom.)	9	28
Pork (dom.)	4	16
Chicken (imp.)	9	22
Turkey (imp.)	10	19
Beef (imp.)	3	11
Pork (imp.)	16	27

2.5.2. Salmonella Subtypes in Humans

Diagnosed human salmonella infections are recorded in the Finnish National Infectious Diseases Register (2018). The domestic cases were separated into their own category to be used in the source attribution. A salmonella case is considered to be of domestic origin if the patient has not traveled abroad during the two‐week period before the illness. Otherwise, it is classified as a foreign acquisition. Salmonella isolates derived from humans were also subtyped (Huusko et al., 2017; Peters et al., 2017) to be able to compare subtype distributions between humans and sources.

A total of 2,767 domestic salmonellosis cases were registered during 2008–2015 (395, 338, 345, 338, 407, 337, 295, and 312, respectively). In total, 67.1% of the reported human salmonellosis cases (66.3%, 71.9%, 55.7%, 57.1%, 77.4%, 67.1%, 70.8%, and 68.6%, respectively) were confirmed to represent salmonella subtypes that had also been found in one or more of the studied sources during 2008–2015. The data set included a small number of salmonella isolates from humans (2008: 4, 2009: 4, 2010: 6, 2011: 2, 2012: 4, 2013: 4, 2014: 3, 2015: 8) that represented Salmonella enterica subspecies enterica, but the phage type or serotype and phage type of these observations were unknown. These isolates were attributed to an unknown source. The total number of domestic sporadic human salmonellosis cases that represented the same salmonella subtypes as findings from the studied sources during 2008–2015 was 1,711 (202, 215, 188, 172, 310, 219, 209, 196) when each confirmed outbreak was included in the data set as an index case (see Appendix F of the Supporting Information). Of these subtypes, the most common in humans were Typhimurium 1 and Typhimurium NST, which together amounted to over 100 reported sporadic cases during the eight‐year period (2008–2015).

3. RESULTS

3.1. MCMC Computation

The computation of the models was performed using OpenBUGS software (Lunn et al., 2000, 2013). The models were run for 50,000 iterations after the burn‐in phase of 10,000 iterations, in which the convergence of the MCMC chains was achieved.

3.2. Estimated Distribution of Salmonella Subtypes in the Sources

The size of the subtype data set was very limited for several of the studied sources. For example, the subtype data sets related to domestic poultry meat included some years completely without salmonella isolates (see Appendices C and D of the Supporting Information), and the total numbers of observations during the eight‐year period were only 16 for chicken and seven for turkey. As an example, the posterior mean and 95% credible interval, as well as the sample‐based prior mean and the 95% credible interval, for the occurrence of the different salmonella subtypes in domestic chicken meat are presented in Fig. 2. Each year, the sample‐based prior distribution takes a unique form depending on the subtype data for other years of the surveillance period. In 2012 and 2014, the posterior distribution equals the sample‐based prior distribution because the annual data set did not provide any information on the occurrence of salmonella subtypes in chicken meat (i.e., no positives were found). The weight of each prior distribution was set to be equal to one observation in order to avoid the prior distribution being too dominant compared to the annual subtype data sets. For 2008, 2011, and 2013, the subtype data set for chicken meat only consists of one observation. Hence, the sample‐based prior distribution and data have the same contribution to the resulting posterior distribution. The subtype sample size for chicken meat was greatest in 2009, when eight salmonella isolates in total were detected. In that case, the main contribution to the posterior distribution came from the observed data of the year. Hence, the occurrence of the unseen subtypes (Albany, Cerro, and Tennessee) in 2009 was estimated to be very small, but higher than zero. The effect of the sample size on the width of the posterior 95% credible interval can be seen in Fig. 2. Even one observed isolate (in 2008, 2011, and 2013) markedly narrows the posterior 95% credible intervals because the prior distributions are only weakly informative.

Figure 2.

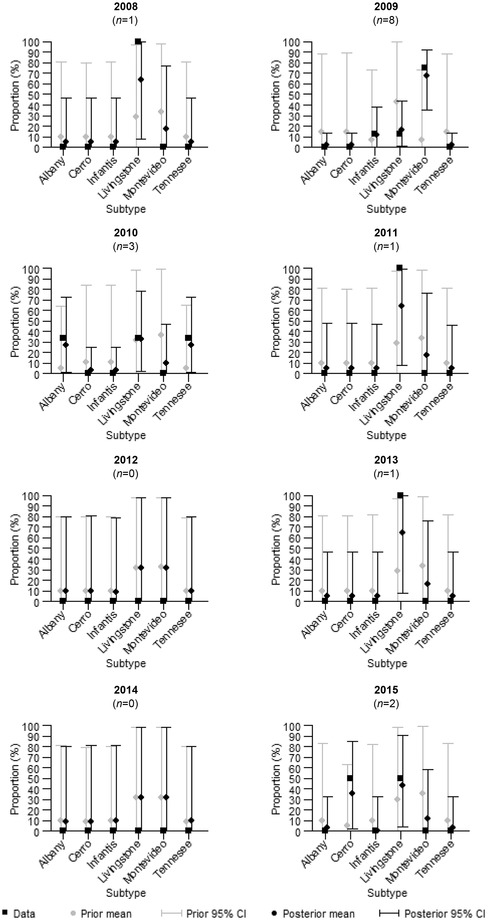
The annual percentages of different subtypes $(X_{1,j,t}/{\sum }_{j=1}^{J_i}{X}_{1,j,t})$ detected from domestic chicken meat (data) and the sample‐based prior, as well as the posterior mean and 95% credible interval for the proportion of different salmonella subtypes in domestic chicken meat ({u ₁}). The annual sample sizes (number of positives) are denoted with n.

The posterior means for the annual proportion of the different salmonella subtypes in all sources ({u_i,t}) are illustrated in Fig. 3. Annually occurring salmonella subtypes can be seen in both domestic and imported sources. For example, the estimated proportion of salmonella subtype Livingstone of all salmonella subtypes in domestic chicken meat remained relatively high over the entire study period (2008–2015).

Figure 3.

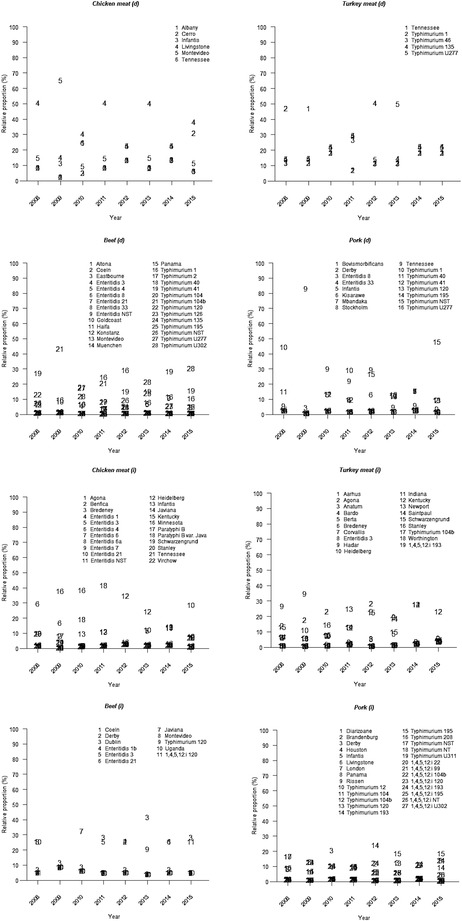
The posterior mean for the annual proportion of different salmonella subtypes in each of the sources ({u_i.t}). Domestic sources are denoted with d and imported sources with i.

3.3. Source Attribution

The source attribution of the reported human salmonellosis cases from 2008 to 2015 was conducted by using the modular Bayesian model presented in Section 2.4. The estimated share for each source of the reported salmonella disease burden obtained with these methods is presented in Table III. Annually, from 55.7% to 77.4% (f_t) of the human cases represented the same salmonella subtypes as isolates found in some of the studied sources during the eight‐year period. The rest of the cases (1 – f_t) were attributed to unknown sources. The proportion (eight‐year average of posterior means) of the total salmonella disease burden attributed to different sources was estimated to be: 14.4% domestic beef, 9.8% imported turkey meat, 10.4% imported pork, 9.3% domestic pork, 9.9% imported chicken meat, 5.7% imported beef, 5.2% domestic turkey meat, 2.2% domestic chicken meat, and 33.1% all other sources.

Table III.

Posterior Mean and 95% Posterior Credible Interval for the Predicted Relative Proportions of the Total Number of Human Salmonellosis Cases Attributed to Domestic (dom.) and Imported (imp.) Sources

	2008	2009	2010	2011	2012	2013	2014	2015
Source of Exposure	Mean/95% CI	Mean/95% CI	Mean/95% CI	Mean/95% CI	Mean/95% CI	Mean/95% CI	Mean/95% CI	Mean/95% CI
Chicken (dom.)	1.6%/0.1–7.6%	10.4%/2.2–26.8%	1.0%/0.1–4.1%	0.6%/0.0–3.0%	0.9%/0.0–4.7%	1.0%/0.0–5.1%	1.2%/0.0–6.5%	0.9%/0.0–4.4%
Turkey (dom.)	12.9%/0.7–40.3%	6.1%/0.2–28.5%	2.6%/0.0–13.4%	3.5%/0.1–15.5%	3.5%/0.1–17.9%	4.3%/0.1–20.0%	4.3%/0.1–21.6%	4.1%/0.1–21.0%
Beef (dom.)	5.2%/0.5–17.0%	6.6%/0.3–23.1%	17.5%/5.4–33.7%	19.7%/4.5–39.6%	29.0%/7.3–55.3%	10.4%/1.1–30.8%	16.6%/3.6–38.1%	10.6%/1.4–29.4%
Pork (dom.)	12.0%/2.0–30.5%	4.8%/0.6–16.5%	7.2%/1.0–21.3%	6.9%/0.9–20.7%	11.3%/1.3–33.8%	18.0%/0.6–49.0%	6.4%/0.5–22.3%	7.9%/1.0–23.5%
Chicken (imp.)	13.5%/2.7–32.0%	10.0%/1.9–26.2%	5.0%/0.5–16.6%	3.6%/0.5–11.8%	6.0%/0.8–19.6%	9.3%/1.7–25.3%	13.7%/2.9–33.6%	18.0%/4.7–38.3%
Turkey (imp.)	9.7%/2.0–24.1%	14.5%/4.0–32.4%	11.7%/3.2–25.7%	10.9%/0.8–32.1%	7.8%/0.4–27.4%	8.0%/0.2–28.7%	7.9%/1.4–22.2%	7.7%/1.1–23.9%
Beef (imp.)	2.7%/0.2–11.1%	4.8%/0.4–20.2%	1.6%/0.0–9.3%	4.2%/0.0–22.0%	13.0%/0.2–50.9%	7.0%/0.1–31.0%	6.6%/0.1–30.1%	5.3%/0.0–27.6%
Pork (imp.)	8.7%/1.9–21.8%	14.7%/4.8–30.1%	9.1%/2.5–20.7%	7.7%/0.5–24.4%	6.0%/0.4–20.7%	9.1%/1.8–23.8%	14.2%/0.9–40.6%	14.1%/1.1–38.7%
Other	33.7%	28.1%	44.3%	42.9%	22.6%	32.9%	29.2%	31.4%

Note: The results were obtained with the modular Bayesian model.

A minor change in the source attribution results was seen if the type‐specific parameters were omitted from the model. The average difference in the results (eight‐year averages of posterior means) between these two approaches was around 0.6 percentage units. The difference was moderately higher (2.9 percentage units) if the source‐specific parameters were omitted, and considerably higher (8.7 percentage units) if both parameters were omitted. The average (all sources and years) width of the 95% credible intervals for the relative proportions was around 23 percentage units with the whole model. No major difference in the average width of the credible intervals was observed between these three options (both parameters included or one omitted). However, the average width of the 95% credible intervals was smaller (13.9 percentage) if both parameters were omitted. The estimated temporal trends in the contribution of the different sources obtained with the whole (both parameters included) modular source attribution model are illustrated in Fig. 4, and the uncertainty related to these results is presented in Table III. The posterior means for the predicted number of human salmonellosis cases by subtype (all years and sources combined) were relatively close to the observed number of human cases, as can be seen in Fig. 5.

Figure 4.

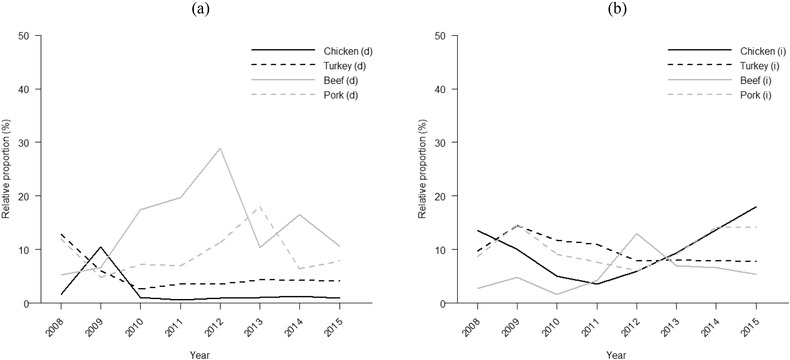
Posterior mean for the predicted relative proportion of the total number of human salmonellosis cases attributed to each of the sources. The results were obtained with the modular Bayesian model. Domestic sources are presented in (a) and imported sources in (b). The sum of all eight proportions in each year is less than 100% because a share (1 – f_t) of the annual cases was attributed to an unknown source.

Figure 5.

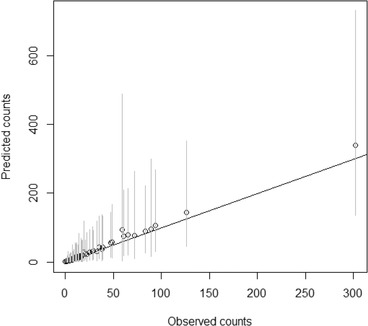
Predicted (posterior mean) versus observed number of cases for salmonella subtypes. Cases summed over years $({\sum }_{t=1}^T{C}_{s,t})$ are represented by dots, and 95% credible intervals for the predicted cases $({\sum }_{i=1}^I{\sum }_{t=1}^T{\lambda }_{i,s,t}^{\ast })$ are shown in the vertical gray lines.

The posterior mean as well as the 95% credible interval for the source‐specific parameters obtained with the modular model are presented in Fig. 6. The value of the source‐specific parameter was estimated to be higher for imported turkey meat and imported chicken meat than for other studied sources. Minor changes in the ranking of the source‐specific parameters were observed if the subtype‐specific parameters were omitted from the model.

Figure 6.

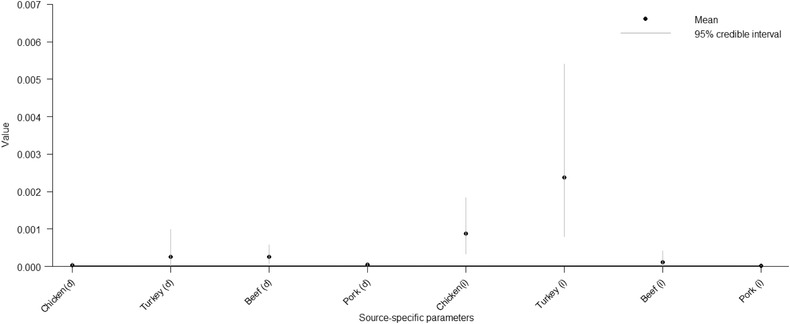
The posterior mean and 95% credible interval for the source‐specific parameters a_i obtained with the modular Bayesian model.

The highest posterior mean for the subtype‐specific parameters obtained with the full model was for Enteritidis 8, followed by Newport, Enteritidis 1b, Enteritidis 1, and Virchow. All of these salmonella subtypes were relatively common in humans during the surveillance (see Appendix F of the Supporting Information). The lowest posterior means for the subtype‐specific parameters were for Paratyphi B var. Java, Typhimurium 46, Minnesota, Altona, and Tennessee, respectively. The posterior means as well as the 95% credible intervals for all subtype‐specific parameters are illustrated in Fig. 7.

Figure 7.

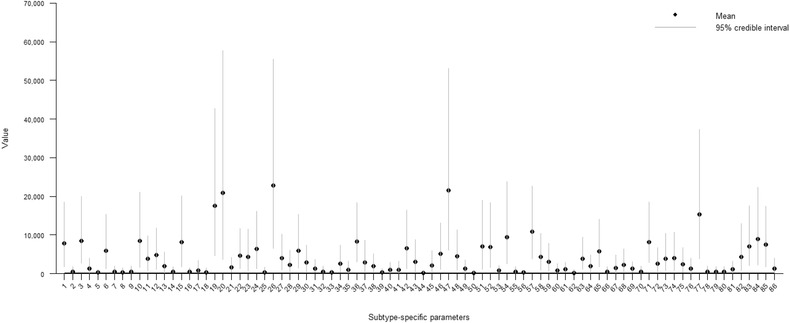
The posterior mean and 95% credible interval for the subtype‐specific parameters q_s obtained with the modular Bayesian model but without outbreak‐related cases (each outbreak was included in the data set as an index case only). The salmonella subtypes in the model were: (1) Diarizoane, (2) Aarhus, (3) Agona, (4) Albany, (5) Altona, (6) Anatum, (7) Bardo, (8) Benfica, (9) Berta, (10) Bovismorbificans, (11) Brandenburg, (12) Bredeney, (13) Cerro, (14) Coeln, (15) Corvallis, (16) Derby, (17) Dublin, (18) Eastbourne, (19) Enteritidis 1, (20) Enteritidis 1b, (21) Enteritidis 3, (22) Enteritidis 4, (23) Enteritidis 6, (24) Enteritidis 6b, (25) Enteritidis 7, (26) Enteritidis 8, (27) Enteritidis 21, (28) Enteritidis 33, (29) Enteritidis NST, (30) Goldcoast, (31) Hadar, (32) Haifa, (33) Heidelberg, (34) Houston, (35) Indiana, (36) Infantis, (37) Javiana, (38) Kentucky, (39) Kisarawe, (40) Konstanz, (41) Livingstone, (42) London, (43) Mbandaka, (44) Minnesota, (45) Montevideo, (46) Muenchen, (47) Newport, (48) Panama, (49) Paratyphi B, (50) Paratyphi B var. Java, (51) Rissen, (52) Saintpaul, (53) Schwarzengrund, (54) Stanley, (55) Stockholm, (56) Tennessee, (57) Typhimurium 1, (58) Typhimurium 2, (59) Typhimurium 12, (60) Typhimurium 40, (61) Typhimurium 41, (62) Typhimurium 46, (63) Typhimurium 104, (64) Typhimurium 104b, (65) Typhimurium 120, (66) Typhimurium 126, (67) Typhimurium 135, (68) Typhimurium 193, (69) Typhimurium 195, (70) Typhimurium 208, (71) Typhimurium NST, (72) Typhimurium NT, (73) Typhimurium U277, (74) Typhimurium U302, (75) Typhimurium U311, (76) Uganda, (77) Virchow, (78) Worthington, (79) 1,4,5,12:i 22, (80) 1,4,5,12:i 99, (81) 1,4,5,12:i 104b, (82) 1,4,5,12:i 120, (83) 1,4,5,12:i 193, (84) 1,4,5,12:i 195, (85) 1,4,5,12:i NT, (86) 1,4,5,12:i U302.

4. SENSITIVITY ANALYSIS

4.1. Prior Choice

The improper prior distribution presented in Section 2.1 was used as another prior choice for multinomial parameters ({u}). However, only a negligible change in the subtype distributions as well as in the results of the source attribution was observed due to this modification. The greatest single difference was 0.7 percentage units (percentual change 14.0%), when the proper prior distribution provided a higher share than the improper prior distribution for domestic chicken meat in 2012 (combined approach). The average difference (all sources and years) between these two options was only 0.2 percentage units (percentual change 2.8%). As both priors correspond to the weight of a sample size of one, only a small difference is expected.

4.2. Number of Possible Subtypes

The total collection of possible salmonella subtypes deemed possible in each of the sources is an issue that cannot be avoided in any source attribution approach. In this model, it was assumed that all salmonella subtypes isolated from a particular source in the long term (2008–2015) are possible, but other subtypes were ruled out from this source. The effect of this choice was studied by assuming that all salmonella subtypes (86 subtypes in total) derived from any of the studied sources are possible in all eight sources, that is, all subtypes have a positive probability of occurring in all studied sources. In this case, it is necessary to use a proper prior distribution because several salmonella subtypes of all the listed subtypes (86 subtypes) represented zero counts in the whole source‐specific data sets. Thus, an improper prior distribution would lead to an improper posterior distribution for the multinomial parameters. The proper prior distribution for the multinomial parameters was constructed in a similar manner to the default model presented in Section 2.1. The results of the source attribution obtained with this alternative assumption are presented in Table IV. The average difference in results (eight‐year averages of posterior means) between the default model and this alternative assumption was 2.6 percentage units. The largest relative proportion of the human cases was related to domestic beef, as observed with the default model (more limited number of possible subtypes). The contributions (eight‐year averages) of the different sources were as follows: domestic beef 10.9%, imported beef 9.3%, imported pork 8.8%, domestic pork 8.5%, imported chicken meat 8.5%, domestic turkey meat 8.1%, imported turkey meat 6.6%, and domestic chicken meat 6.2% The difference between the sources was estimated to be much smaller compared to the default model.

Table IV.

Mean and 95% Posterior Credible Interval for the Predicted Relative Proportion of the Total Number of Human Salmonellosis Cases Attributed to Domestic (dom.) and Imported Sources (imp.)

	2008	2009	2010	2011	2012	2013	2014	2015
Source of Exposure	Mean/95% CI	Mean/95% CI	Mean/95% CI	Mean/95% CI	Mean/95% CI	Mean/95% CI	Mean/95% CI	Mean/95% CI
Chicken (dom.)	6.1%/0.3–22.0%	22.4%/5.5–44.3%	4.9%/0.5–16.2%	2.2%/0.1–9.9%	3.0%/0.1–12.9%	3.7%/0.1–15.6%	4.1%/0.1–17.4%	3.5%/0.1–15.0%
Turkey (dom.)	14.9%/1.5–39.5%	10.4%/0.8–31.9%	4.3%/0.2–16.3%	7.5%/0.5–24.5%	7.2%/0.3–26.8%	6.6%/0.3–24.9%	7.0%/0.3–26.2%	6.7%/0.3–24.9%
Beef (dom.)	3.6%/0.3–11.9%	3.2%/0.1–12.5%	13.9%/3.9–28.8%	15.3%/3.1–34.3%	23.2%/5.5–48.2%	6.4%/0.7–20.2%	12.6%/2.3–31.6%	9.1%/1.2–25.9%
Pork (dom.)	10.5%/1.8–26.9%	4.1%/0.7–12.1%	7.4%/1.3–19.6%	7.5%/1.0–21.5%	10.7%/1.4–30.7%	16.0%/0.4–46.3%	4.6%/0.3–16.2%	7.3%/0.9–22.1%
Chicken (imp.)	11.0%/2.0–27.9%	7.9%/1.3–21.8%	6.0%/0.7–17.9%	3.8%/0.5–11.8%	5.7%/0.9–17.4%	8.1%/1.4–22.6%	12.1%/2.4–30.3%	13.2%/2.9–31.3%
Turkey (imp.)	7.4%/1.3–19.8%	8.1%/1.7–20.2%	7.6%/1.7–18.6%	5.4%/0.3–18.5%	6.9%/0.3–24.4%	5.8%/0.1–22.6%	5.6%/0.8–16.6%	5.8%/0.7–17.9%
Beef (imp.)	5.4%/0.6–17.1%	6.1%/0.8–19.1%	2.9%/0.0–14.4%	8.7%/0.1–32.3%	15.8%/0.3–50.9%	13.0%/0.4–42.2%	12.8%/0.3–42.5%	9.8%/0.0–38.9%
Pork (imp.)	7.6%/1.5–19.9%	9.7%/2.6–22.2%	8.7%/2.2–20.6%	6.8%/0.4–22.6%	5.1%/0.3–18.1%	7.6%/1.4–20.9%	12.1%/0.6–37.2%	13.3%/0.9–37.8%
Other	33.7%	28.1%	44.3%	42.9%	22.6%	32.9%	29.2%	31.4%

Note: The results were obtained with a modular Bayesian model, but assuming that all 86 salmonella subtypes are possible in all studied sources.

Both assumptions provided a significantly higher value of the source‐specific parameter for imported turkey meat and chicken meat than the other sources. The subtype‐specific parameter was estimated to be the largest for Typhimurium 1 (sixth‐largest with default model), followed by Enteritidis 8 (largest with default model) and Newport (second‐largest with default model). In general, small changes in the ranking of the other source‐specific as well as subtype‐specific parameter were observed when these two assumptions were compared. No marked difference was seen in the average width (all sources and years) of the credible intervals for the proportion of human cases attributed to different sources when these two assumptions were compared (default model 23.4 vs. alternative model 23.5 percentage units).

4.3. Outbreaks

Source attribution was conducted by using only sporadic human salmonellosis cases (only one index case per confirmed outbreak was included). However, Finnish register data routinely include both sporadic and outbreak‐related human salmonellosis cases. The effect of the outbreak cases on the attribution results as well as on the estimation of the source‐specific and subtype‐specific parameters was examined in a separate run by including all (sporadic and outbreak‐related) human salmonellosis cases in the model. The domestic outbreaks that represented the same salmonella subtypes as findings from studied sources are presented in Table V.

Table V.

Salmonella Outbreaks that Represented the Same Salmonella Subtypes as Findings from Studied Sources in Finland During the Years 2008–2015 (Infectious Diseases in Finland, 2018)

Year	Serotype	Phage Type	Number of Outbreak‐Related Cases in the Register	Number of Registered Cases
2008	Newport		61	72
2009	Bovismorbificans		29	34
2010	Typhimurium	1	5	60
2011	1,4,5,12:i:‐	195	22	25
2012	Agona		6	33
2013	Typhimurium	135	8	10
2015	Newport		19	27

Note: Outbreaks with weak evidence were ignored.

The effect of the outbreak‐related cases on the attribution results was negligible. The average difference in the source attribution results was only around 0.6 percentage units (eight‐year averages of posterior means) when these two options were compared. The change only exceeded 1 percentage unit for imported turkey (1.8 percentage unit increase). The average width (all sources and years) of the credible intervals for the proportion of human cases attributed to different sources remained almost identical in comparisons (all cases 23.4 vs. sporadic cases 23.3 percentage units). Only a small change was observed in the ranking of the source‐specific, as well as the subtype‐specific, parameters. The average length of the credible intervals for both the source‐specific and the subtype‐specific parameters slightly increased when outbreak‐related cases were included in the data set.

5. DISCUSSION

The combined salmonella source attribution method is based on a synthesis of the microbial subtyping and comparative exposure assessment approaches. Previous studies have emphasized the importance of including source‐specific as well as subtype‐specific parameters in the source attribution model (David et al., 2013; Hald et al., 2004; Mullner et al., 2009). However, the identification of all model parameters has proved to be impossible without additional constructions, even when an extensive annual data set is available (David et al., 2013; Mullner et al., 2009).

In our method, data from multiple years were exploited, and the full Bayesian model was modularized into three parts (exposure assessment, subtype distribution, and epidemiological model) for separate estimation of the unknown model parameters in each module to avoid identifiability issues with the parameters in the multiplicative expressions of the Poisson mean. The advantage of this model compared with the Hald model (Hald et al., 2004) and its modifications (David et al., 2013; Mullner et al., 2009) is that source‐specific as well as subtype‐specific parameters can be freely estimated without additional constraints. The modularization technique has not previously been used in source attribution. However, it was seen as reasonable because the most valid information to estimate the unknown parameters was available inside each module. This model can also be easily connected as an extension to a production chain model to take into account the uncertainty related to the gross exposure (Salmonella spp.) from different sources. However, more direct information on the exposure of consumers can also be used in the model if such dietary data are available.

Uncertainty related to the distribution of salmonella subtypes is also crucial to take into account because an insufficient annual data set does not accurately describe the true occurrences of salmonella subtypes in different sources. Some source attribution models have included uncertainty in the estimation subtype distributions, but it would have been impossible to apply any of the previous models to this type of subtype data set because of the extremely limited and sparse annual data sets. For instance, the subtype data set for domestic turkey included less than one observation per year on average, and several years were completely without positive isolates. This model works without external prior information, but observations are required from several years in order to estimate the annual subtype distribution with better quality by borrowing strength across the different years.

According to the results, the largest relative proportion (eight‐year average) of human salmonellosis cases was attributed to domestic beef and the second largest to imported turkey. This result is explained by the distribution of salmonella subtypes rather than gross exposure. The gross exposure from domestic beef was not particularly large, and only minor from imported turkey. However, a wide selection of salmonella subtypes was detected in these sources during the surveillance. In addition, the salmonella subtype Newport (the second most prevalent of the human subtypes that were also detected in the sources), with the largest value for the subtype‐specific parameters, was uniquely isolated from imported turkey, and the subtypes Typhimurium 1 and Typhimurium NST (respectively, the most prevalent and third most prevalent of the human subtypes that were also detected in the sources) were estimated to be relatively common in domestic beef. The source‐specific parameter for imported turkey was also estimated to be the highest of all source‐specific parameters. The largest gross exposure was related to imported pork. In addition, a wide selection of salmonella subtypes (28) and the highest number of unique subtypes (16) were detected in imported pork. However, the share of imported pork from the total number of disease cases was estimated to be only the third largest (eight‐year average 10.5%) because of the differences in subtype distributions between humans and imported pork. In the data set, three of 16 subtypes that were unique to imported pork represented zero counts in the human data set over the years 2008–2015. The source‐specific parameter for imported pork was also estimated to be the smallest of all source‐specific parameters. The smallest proportion of disease cases was attributed to domestic chicken meat (eight‐year average 2.0%). Only a small selection of salmonella subtypes (6) was detected in this source over the eight‐year period, and these subtypes, excluding salmonella subtype Infantis, were not particularly common in humans. Salmonella subtype Infantis accounted for almost 100 human cases during the surveillance, but there were also several other potential sources for these cases. The source‐specific parameter for domestic chicken meat was estimated to be the second smallest of all source‐specific parameters.

Human salmonellosis cases with salmonella subtypes that were not isolated from the studied sources during the surveillance were attributed to an unknown source. The category “unknown source” included other foods (e.g., vegetables), as well as all other possible sources of human salmonella infections. Nevertheless, the category “unknown source” may include subtypes that were also isolated from the studied sources, while some subtypes truly present in the studied sources may not have been detected. This is an issue that cannot be entirely avoided due to the evidence regarding all existing distinct reservoirs of human infections always being incomplete. However, the total collection of possible subtypes that may occur in the studied sources needs to be defined or estimated in all source attribution models that exploit the microbial subtyping approach. In this model, the total number of possible subtypes per source was taken to be the total number of different salmonella subtypes isolated from that source during 2008–2015. Another option was examined by assuming that all salmonella subtypes isolated from any source have a positive probability of occurring in all sources. A considerable difference in the source attribution results was seen when these two assumptions were compared. Comparison of the results presented in Tables III and IV indicated that the contribution of the sources with a small selection of different observed subtypes (domestic chicken and turkey meat) increases when all 86 salmonella subtypes have a positive probability of occurring in all sources. The weakness of the alternative assumption (all subtypes are possible in all sources) is that a huge amount of probability mass falls on salmonella subtypes that have not been detected at all in the particular sources over the eight‐year period, and some of the subtypes are considered to be implausible according to expert judgment. At the extreme, almost 90% (eight‐year average 89.5%) of the probability mass for the subtype distribution of domestic turkey meat falls on salmonella subtypes that were not detected in domestic turkey meat at all.

In Finland, register data routinely include all (sporadic and outbreak‐related) human salmonellosis cases. The effect of salmonella outbreaks on the source attribution results was examined by including outbreak‐related cases in the data set. The results hardly changed because the number of outbreaks was relatively low (around one per year) and some of them were relatively small. In addition, as the source‐specific and the subtype‐specific parameters were estimated based on data from multiple years, single‐year outbreaks had a smaller effect on the estimation.

This source attribution model only exploits phenotypic typing data (serotypes and phage types) like the majority of previous salmonella source attribution models. However, more advanced molecular typing methods such as whole genome sequencing are already available. Salmonella source attribution models are also moving toward exploiting more accurate typing data (Barco, Barrucci, Olsen, & Ricci, 2013; Mughini‐Gras et al., 2018). These methods may take into account bacterial evolution and aim to find a correlation between the molecular typing of human isolates and isolates derived from the sources. More accurate attribution could then possibly be conducted, but the determination of the acceptable level of correlation may be difficult. A future challenge is the exploitation of molecular typing data together with phenotypic typing data.

Supporting information

APPENDIX A

APPENDIX B

APPENDIX C

APPENDIX D

APPENDIX E

APPENDIX F