Scaling issues of neutral theory reveal violations of ecological equivalence for dominant Amazonian tree species

Abstract

Neutral models are often used as null models, testing the relative importance of niche versus neutral processes in shaping diversity. Most versions, however, focus only on regional scale predictions and neglect local level contributions. Recently, a new formulation of spatial neutral theory was published showing an incompatibility between regional and local scale fits where especially the number of rare species was dramatically under‐predicted. Using a forward in time semi‐spatially explicit neutral model and a unique large‐scale Amazonian tree inventory data set, we show that neutral theory not only underestimates the number of rare species but also fails in predicting the excessive dominance of species on both regional and local levels. We show that although there are clear relationships between species composition, spatial and environmental distances, there is also a clear differentiation between species able to attain dominance with and without restriction to specific habitats. We conclude therefore that the apparent dominance of these species is real, and that their excessive abundance can be attributed to fitness differences in different ways, a clear violation of the ecological equivalence assumption of neutral theory.

Introduction

Why are some species dominant and others rare? Posed by Charles Darwin, this question remains among the most important in ecology (Sutherland et al. 2013) and its answer frames our fundamental understanding of community assembly. Classical Hutchinsonian ecology emphasises the deterministic processes based on niche‐thinking and environmental heterogeneity. Neutral theory, emerging from the theory of Island Biogeography (MacArthur & Wilson 1967), lottery models (Chesson & Warner 1981) and earlier work by population geneticists (Kimura 1983), argues for stochastic processes and environmental stochasticity. The latter was put forward as a null model to test if these interactions and differences between species matter to the assembly of ecological communities. In a way it is similar to the Hardy–Weinberg theorem in population genetics (Hardy 1908; Weinberg 1908), testing assumptions regarding the evolution of populations. Neutral theory likewise tests assumptions regarding the dynamics of communities. The first neutral models of ecology were spatially implicit, with recruitment from either within a local community or from a metacommunity (Fig. S1). These models fail, however, to correctly estimate migration from a spatially explicit world (Pos et al. 2017), even though they generate accurate predictions of community structure. Considering the overwhelming evidence that migration is in all probability very important (Magurran & Henderson 2003; Volkov et al. 2003), spatially explicit models were developed to study the relative importance of migration and neutral processes in determining community structure (Chave & Leigh 2002; Zillio & Condit 2007; de Aguiar et al. 2009; Rosindell & Cornell 2009). These models generated good predictions for species rank abundance distributions and species–area relationships (Hubbell 2001) but focused only on explaining such patterns on regional scales. A lack of previous attempts to combine both regional and local scale predictions has prevented a proper validation of fundamental predictions of neutral theory. Recently, a spatially explicit analytical approach revealed severe scaling issues of neutral theory predictions (O'Dwyer & Cornell 2018). Here it was shown that the number of rare species was severely underestimated by neutral theory predictions. The authors proposed that a lack of stabilising mechanisms, allowing rare species to be maintained, could potentially explain the skew towards the tail of species abundance distributions. This, however, does not include an explanation towards the extreme dominance of species often observed in the field towards which much effort has been devoted, both experimentally and theoretically. Stephen Hubbell in his original publication of neutral theory had already anticipated such use to study what he termed ‘dominance deviations’ using his spatially implicit model (Hubbell 2001). However, as of yet this has not yet been successfully studied theoretically under the assumptions of spatially explicit neutral theory, which would be a far more accurate approach to reality. Here we, therefore, combine regional and local results of a neutral spatially semi‐explicit model (Pos et al. 2017) using parameters based on species characteristics and ask the question if neutral theory can explain the excessive dominance of species as often observed across spatial scales. In other words, we test if there is a biologically sound prediction on regional scales, following from accurate predictions on local scales. If migration is the main process determining community structure (reflecting mainly the neutral perspective), our model should approach empirical data accurately both on regional and local scales. If, however, the model results deviate substantially from empirical data on both or either scale, key assumptions of the model are violated and other processes must be more dominant or at least strongly complementary to migration. To explain such a potential discrepancy and to identify model assumption violations we also performed a number of different (multivariate) analyses on the empirical data, complementary to the simulations and studied distribution of dominant species. Using empirical data from 223 hectares’ worth of forest inventory plots in the Amazon, covering 4493 species and 120.322 individual trees, we simulate forests in the order of 8000 hectares, with 400‐500 individuals per hectare. With the Amazon being one of the most diverse forests of the world in terms of tree species (Hubbell et al. 2008; ter Steege et al. 2013, 2017), such a large data set allows us to test the model on different spatial scales and different communities in terms of diversity.

Materials and Methods

Spatially semi‐explicit models: modelling the green mass

We used a mechanistic model (Pos et al. 2017) simulating not only separate plots and their direct interaction (Fig. S1), but also the intermediate ‘green matrix’ connecting these plots (not unlike the analytic network approach by Economo & Keitt (2008)). Although we often look at the forest using only a relatively small sample of plots, it is this intermediate green matrix that plays a vital role in determining species composition of each local plot, acting as a bridge, exchanging species between the plots being sampled. The model is built up as a three‐dimensional array, with each column representing a single plot within a forest with its individuals stacked as the individual blocks (Fig. S2). The different colours of blocks represent different species and the number of individuals (i.e. amount of stacked blocks) is based on an average amount per plot as observed in the used empirical set. Creating the forests starts with each block (i.e. each individual) being assigned to a species by randomly sampling from a hypothetical metacommunity. This metacommunity follows a logseries, which has been shown to be the best approximation for describing species richness of hyper diverse communities (Hubbell et al. 2008; ter Steege et al. 2013, 2017; Baldridge et al. 2016). The logseries is parameterised using the actual field data to which the simulation is being compared, similar to an earlier study (Pos et al. 2017). With each time step of the simulation the forest is allowed to change with one individual in each plot randomly chosen for replacement. Replacements can come from either of five categories: (1) the plot itself (local recruitment), (2) adjacent plots, (3) the entire forest, (4) the hypothetical metacommunity or (5) a speciation event, which creates a new species neither present in the forest nor in the metacommunity. We estimate probability of migration from adjacent plots using the Corrected Plot Geometry method (Chisholm & Lichstein 2009; Pos et al. 2017) and mean dispersal distance based on phenotypic characteristics, see below. Migration probability of each subsequent category is calculated as 10% of the former following earlier publications (ter Steege et al. 2017), for example if the migration probability from adjacent plots is estimated at 0.071, that from the entire forest is set at 0.0071 and from the hypothetical metacommunity at 0.00071. We calculated speciation as in the original UNTB: theta/(2*J) with theta equal to Fisher's alpha (Hubbell 2001) and J the total number of individuals in the forest. Parallel processing, using either multiple cores on one processor or a cluster using the packages foreach, doParallel and doSnow (Weston 2015), allows multiple forests to be simulated at once, drawing all from the same larger hypothetical metacommunity. These separate forests are indirectly connected as they draw from the same metacommunity, essentially simulating vagrant dispersal from a larger species pool. This allows for much faster computation of a large area. Each step of the simulation itself is explained in chronological order in the Supporting Information S1.

Field data sets

Three independent data sets were used: Guyana/Suriname combined, French Guiana and Ecuador/Peru also combined. All identifications within each data set were harmonised, are independent and non‐overlapping (Pos et al. 2014). Each data set consisted of plots having all trees ≥ 10 cm diameter at breast height (DBH) inventoried. Species ID's were standardised to the W3 Tropicos database within each data set, using TNRS (Boyle et al. 2013; ter Steege et al. 2013). The Guyana/Suriname set consisted of 67 plots all of one hectare in size, yielding 37.446 individual trees distributed among 1042 morphospecies. French Guiana is comprised of 63 plots, ranging between 0.40 and 1 hectares in size (0.40 ha 1 plot, 0.50 ha 3 plots, 0.80 ha 1 plot, 0.98 ha 2 plots and 1 ha 56 plots) accounting for 35.075 individuals belonging to 1204 morphospecies and Ecuador/Peru having 93 plots, ranging in size from 0.2 to 1 hectares in size (0.1 hectares 2 plots, 0.2 ha 1 plot, 0.25 ha 6 plots, 0.5 ha 1 plot and 1 ha 87 plots) yielding 47.801 individuals and 3018 morphospecies. A map of the locations of all plots is provided in the supporting information (Fig. S4).

Parameterising the model

The mean dispersal distance for each data set to be implemented in the Corrected Plot Geometry method (Chisholm & Pacala 2010; Pos et al. 2017) was calculated by assigning a mean dispersal distance depending on the category, based on literature (Yumoto 1999; Seidler & Plotkin 2006; Muller‐Landau et al. 2008) (Table S2). This was done for each plot and ultimately averaged over all plots per data set (see below). As a control, we also simulated the forests for a range of combinations where the total summed amount of migration was randomly divided over all the different categories. A table of all used parameters is provided in the supporting information (Table S2). To test for the influence of severe and absent ecological drift on the difference between local and regional patterns of diversity, we also implemented near null (≪.1) and near‐unity parameters of migration (0.9).

Sampling and analyses

After the simulations, a number of plots equal to the amount of plots in the data set used for comparison were sampled randomly from the forest. Shapes of the rank abundance distributions for both the simulation output and the empirical data were compared using the nonparametric Kolmogorov–Smirnov test (Massey 1959) as it allows for a goodness‐of‐fit test between two distributions without assuming a prior distribution and calculates the statistical distance between the two distributions. The reported D values indicate a maximum distance between the two distributions, with P‐values indicating the probability of such a D statistic being larger or equal to the observed value. Mean number of species in the total sample, number of singletons and Fisher's alpha were compared using the nonparametric Wilcoxon rank sum test (Wilcoxon 1945). Fisher's alpha mathematically describes the relationship between the number of species and their abundance, that is it estimates the parameter alpha in the logseries distribution (Fisher et al. 1943). We posited that if forest dynamics are similar to our neutral model, these aspects of the empirical and simulated data sets should also be similar. Any substantial deviation would represent non‐dispersal related influences on species composition. Thus, we treat the model as a null‐model, much like the Hardy–Weinberg theorem in population genetics (Hardy 1908; Weinberg 1908), with only dispersal as a mechanistic driver. In addition to studying the regional patterns in diversity, we did the same for local patterns studying the average number of species per plot and the ranking in dominance of these species per local community over the whole data set. To complement these comparisons, we performed three different analyses to study the relative importance of geographical distance and environmental filtering. These were non‐metric multidimensional scaling (NMDS) (Fasham 1977; Minchin 1987; Salako et al. 2013) using the Morisita index of diversity (Morisita 1959) as distance measure and a correlation analysis between environmental, geographic and species distance matrices using Mantel tests (Mantel 1967; Legendre & Fortin 2010), using the same distance measure. All are explained in more detail in the Supporting Information S2. A list of all R packages used is given in the supporting information.

Results

No single model parameter setting was capable of reproducing patterns of high dominance on either regional or local scales fitting empirical observations (Figs 1, 2 and 1, 2). Intermediate patterns of regional rank abundance distributions (truncated at ranks 50–750), however, showed a non‐significant difference from empirical distributions (Kolmogorov–Smirnov test, Fig. 1). Total number of species and Fisher's alpha of the total sample (Fig. 2) also showed a reasonable, although not significant fit between observed and predicted patterns for two out of three data sets (Guyana/Suriname and French Guiana). For Guyana/Suriname, there was a significant difference between the complete (i.e. non‐truncated) predicted and field rank abundance distributions, although maximum distance (D, also derived from the Kolmogorov–Smirnov test) between the two distributions was small (Fig. 1). There was also a relatively small yet significant difference in the observed and predicted mean number of species per plot but no significant differences between observed and predicted mean number of singletons (species with only one individual) (Table 1). Complete simulated and empirical regional rank abundance distributions were also significantly different for French Guiana (again with small maximum distance), with a significant difference between observed and predicted mean number of species and mean number of singletons per plot at local scales. For Ecuador/Peru, simulations yielded a much less diverse sample than the empirical data resulting in strong significantly different observed and predicted rank abundance distributions, yielding less than half of the species found in the empirical data as well with a maximum distance over twice as large as for the other two data sets, mainly caused by a lack of rare species from neutral predictions. There were also significant differences in observed and predicted mean number of species and singletons per plot (local scale), although truncated rank abundance distributions again showed no significant difference. All rank abundance distributions on a regional scale showed the familiar logseries (Fig. 1), although comparisons of mean Fisher's alpha per plot revealed significant differences for all data sets between observations and predictions. Regional (total) Fisher's alpha indicated close comparisons for both Guyana/Suriname and French Guiana whereas Ecuador/Peru again showed larger differences between observed and simulated values. From both the rank abundance and maximum dominance distributions it can clearly be seen that in all cases the extremely dominant species are responsible for large distances, which is also indicated by the non‐significant differences for the truncated rank abundance distributions.

Figure 1.

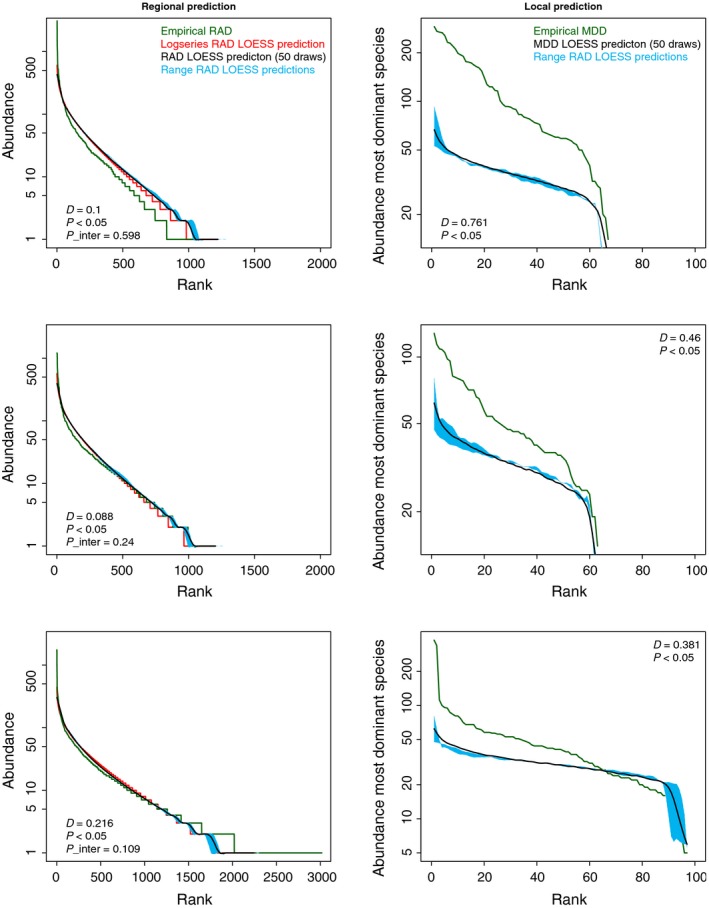
The rank abundance distribution (RAD, left) and maximum dominance distributions (MDD, right) for tree species in 223 Amazon forest plots from Guyana/Suriname (top), French Guiana (middle) and Ecuador/Peru (bottom). Lines indicate empirical (green) and simulated data (black) or fitted logseries (red). Blue shading indicates upper and lower RAD or MDD based on 50 sampling iterations of the total simulated forest. For the RADs, x‐axis indicates the rank from most abundant to least abundant species, with y‐axis showing actual abundances of the species for the ith rank. For the MDDs, x‐axis reflects ranking of plots and y‐axis the maximum dominance of the most abundant species for each plot. D, P and P_inter values represent maximum distance and significance values derived from the Kolmogorov–Smirnov tests with P_inter the comparison between the truncated RADs (ranks 50–750).

Figure 2.

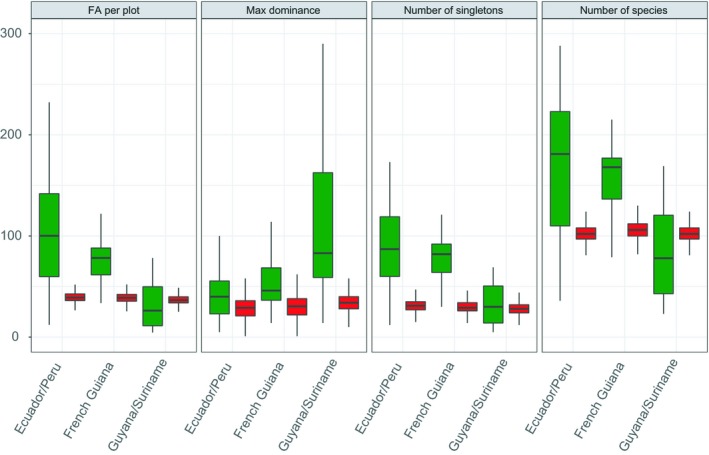
Boxplots summarising features of quantitative variables of composition for Guyana/Suriname, French Guiana and Ecuador/Peru (both simulated and empirical). Statistics are shown by the labels for the plots from the simulation (red) and from the actual empirical data (green) after 50 sampling iterations. Whiskers of boxplots indicate minimum or maximum values (excluding outliers), hinges reflect lower and upper quartiles with bold stripes reflecting median values.

Table 1.

Table comparing simulated (Sim) and empirical data sets (Field) in terms of number of species, singletons and Fisher's Alpha (both total and mean per plot)

	Guyana/Suriname		French Guiana		Ecuador/Peru
	Sim	Field	Sim	Field	Sim	Field
Mean nr species	110***	84***	114***	157***	113***	168***
Total nr of species	1227	1042	1212	1204	2247	3018
Mean nr singletons	34	33	36***	78***	40***	88***
Total nr singletons	215	210	212	208	462	998
Mean FA per plot	46**	31**	48***	76***	58***	101***
FA of total sample	243	199	244	242	489	716

**Indicate significance levels at P ≤ 0.01, *** at P ≤ 0.001.

As a proper test of deviation between neutral expectations and observed rank abundance distribution specific for the (most) dominant species, we tested for departures in the abundances of individual species. For this we bootstrapped sampling to calculate confidence intervals for each species from an equal amount of samples as the respective empirical data sets. Plotted with the empirical rank abundance distribution, it becomes clear that we can reject neutrality especially for these most dominant species in all three data sets (Fig. 3 and Fig. S5). This also shows that for the intermediate to rare species, confidence intervals bracketed the empirical distribution, suggesting neutrality cannot be rejected, in accordance with the non‐significant differences between truncated rank abundance distributions.

Figure 3.

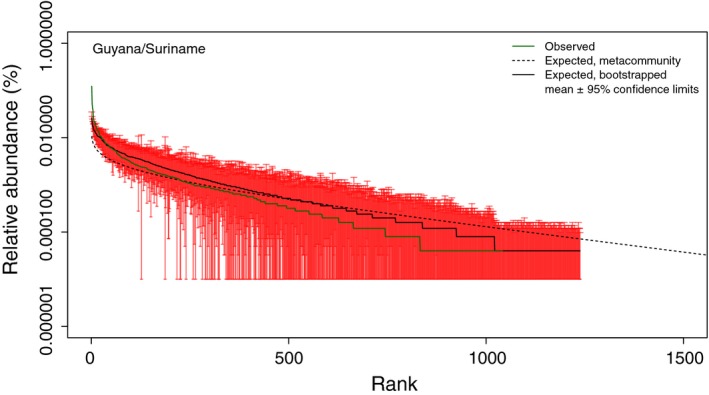
The rank abundance distribution for forests of Guyana and Suriname showing variance in neutral expectation of individual species abundance over 50 iterations and 10 000 bootstraps and metacommunity expectation. Confidence intervals generated by bootstraps clearly indicate neutrality should be rejected for the dominant species, whereas this is not the case for the intermediate and rare species.

As simulations were unable to attain realistic patterns in dominance distribution of species, we redid simulations using near null migration (≪0.1) to mimic extreme ecological drift at the local level. We also performed simulations at the other extreme of near unity (0.9) migration, mimicking a panmictic community. This clearly showed the disagreement between regional and local predictions of the rank abundance distributions (Fig. 4). The first resulted in maximum dominance distributions approaching the empirical data, yet too even and too rich and significantly different at the cost of regional diversity where RAD agreement was lost. With migration probabilities set near unity, regional predicted patterns of rank abundance distributions showed stronger approximation with empirical data although richer and not attaining the excessive dominance. Here, maximum dominance distributions were almost flat, that is individuals were too evenly distributed over the species and strongly different from the observed patterns.

Figure 4.

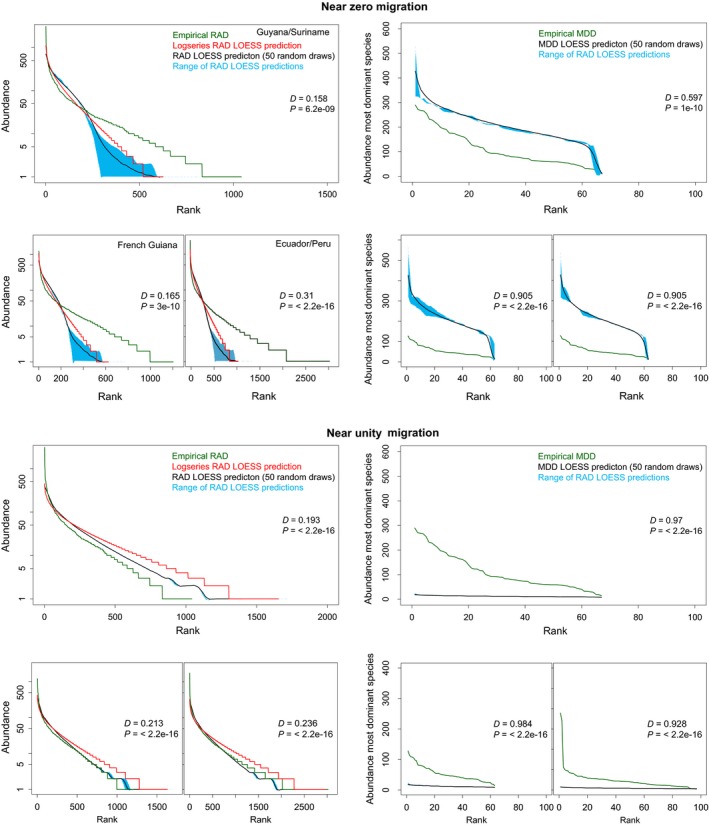
The rank abundance distribution (RAD, left) and maximum dominance distributions (MDD, right) for two limiting cases of near null (top) and near unity migration (below). Distributions are shown in each corner for Guyana/Suriname (top), French Guiana (left) and Ecuador/Peru (right). Distributions clearly show the disagreement between predictions both for rank abundances and the maximum dominance, with migration set near null yielding reasonable regional predictions but not for local predictions as based on MDD, whereas migration set to unity yields the opposite results.

Analyses of composition

For all three data sets, there were significant correlations between spatial distance and composition dissimilarity with relatively high r statistics from the Mantel tests for Guyana/Suriname (0.3101) and French Guiana (0.6723), whereas for Ecuador this was considerably lower (0.2073) (Table S1). Dissimilarity of composition was also compared with environmental distance matrices where local ecology was approximated by Euclidean distances for annual rainfall and a binary distance index of 0 or 1 for forest type (Supporting Information S2). For Guyana/Suriname, this yielded a weaker r statistic of 0.1176 for the former but a similar r statistic of 0.2961 for the latter, both significant. For French Guiana, only comparisons between local ecology and species distances were available as all plots are from the same forest type, yielding a significant r statistic of 0.1713. For Ecuador, in comparing species distances with local ecology yielded an r statistic of 0.1742, with forest type vs. species distances yielding 0.3122, both significant. NMDS also showed distinct grouping for all three different subsets with high agreement between plotted values and observed dissimilarities (all R ² > 0.95) (Fig. S3). Guyana/Suriname showed strong groups based on both country and forest type. French Guiana showed strong overlapping groups based on geographical subdivisions. Ecuador/Peru, with analyses performed separately for all forest types combined and TF separately to show the separation on country‐of‐origin on the axes more discretely, yielded a clear visible segregation along the first axis for both forest type and country of origin. A one‐way anova based on the scores of the first or second axis yielded significant differences for segregation of both country and forest type for Guyana/Suriname. Segregation of geographical subdivision along the second axis of the NMDS for French Guiana also proved to be highly significant as well as segregation of country and forest type for Ecuador/Peru, both along first axis in the separate analyses.

Discussion

Incorporating dispersal in a realistic way and being able to model a considerably large area, we were unable to approach patterns of dominance on local or regional scale for any data set. Such issues with scalability of neutral theory predictions were also shown for the rare species (O'Dwyer & Cornell 2018). This disagreement between observed and predicted patterns of excessive dominance (dominance deviation) suggests that even if regional patterns follow neutral predictions for intermediate abundant species, suggesting neutral dynamics with a significant role for dispersal (e.g. Pyke et al. 2001; Condit et al. 2002), for dominant species these patterns may deviate strongly and indicate non‐neutral dynamics. At regional scales, overall simulation results of both Guyana/Suriname and French Guiana showed high similarity to the actual field data, in particular for the intermediate to rare species. There were only small differences in the total number of species, total FA over all plots or the distribution of species and singletons over the sampled plots according to the rank abundance distributions. For western Amazonian plots, however, the simulation also yielded a much less diverse sample on the regional scale, not only in terms of total number of species (almost 1000 species fewer than the field data) but for total Fisher's alpha as well (almost half of the field data). Simulated data also showed much narrower value ranges compared to the field data for any data set, indicative of much more similar distributions across plots in comparison with field data (Fig. 2). In addition, local community structure showed a much more even distribution of species per plot than the field data (Fig. 1). Our results suggest that with estimates of dispersal limitation based on species characteristics, neutral theory can neither predict the high dominance of some species observed in any of the field data sets (even though they approximate regional patterns quite good) nor the excessive diversity of Western Amazonian forests reflected in the large tail of rare species. Only with severely unrealistic dispersal limitation, patterns in maximal dominance at local scales can be approximated, but at the cost of diversity in comparison with empirical data at regional scales. Similar to the Hardy–Weinberg principle from population genetics testing the null hypothesis of no evolutionary change when assumptions are not violated (Hardy 1908; Weinberg 1908), neutral theory can be used as the null hypothesis of ecological equivalence in ecology. When the assumptions of neutral theory, ecological equivalence, birth and death rates being proportional to abundance in either local or metacommunity and a saturated landscape being the main assumptions, are indeed true, we would expect predicted patterns to follow those observed in the field. If, however, for some reason any of these (or other assumptions) is not met, predictions deviate from empirical data.

Rejection of neutral theory on a regional level

We hypothesise that potential violations are threefold: (1) differences in environmental heterogeneity, even within forest types, and life history strategy among species, (2) geographical distance between plots not being equal and (3) laws of probability. Western Amazonia in general has much richer soils, lower wood density and smaller seed size in comparison with the Guiana Shield and is much more diverse in term of species (ter Steege et al. 2006). Differences in fertility and different life‐history strategies (indicated by wood density and seed mass differences) might allow higher turnover rates of individuals and hence a higher diversity than predicted by neutral theory where the assumption is strict ecological equivalence between species on the individual level (Kraft et al. 2008). This in turn could lead to the higher overall diversity of Ecuador and Peru versus the Guiana Shield. Such signals within each data set, where environmental heterogeneity obviously is to be found, potentially accounts for the significant differences in all data sets, even with small distances between simulated and empirical rank abundance distributions. The average distance between plots in the empirical data set is also larger for Ecuador and Peru in comparison with Guyana, Suriname and French Guiana (mean distance of 195 km for Ecuador/Peru versus 161 for the Guiana Shield data sets) adding to the turnover of species within the sampling scheme and reinforcing this difference in diversity resulting in the larger distance between simulated and empirical rank abundance distributions. The last potential cause for deviation of predictions on regional scale is perhaps not so much a violation of the model assumptions, but rather an indirect result of the modelling process reinforcing earlier mentioned violations. When simulations start, each plot shares roughly the same logseries of the total forest. Ecological drift then slightly changes this logseries for each plot separately causing some species to become more abundant whereas others become less abundant. As this, however, is random across all plots and we have a large number of plots (8000), the law of large numbers will cause the logseries to be preserved in the total sample, even though each separate community might deviate substantially. A similar pattern is observed in population genetics in allele frequencies across communities. Separate samples starting with similar allele frequencies under the influence of drift show that the average frequency over all plots does not change, even though each separate sample might show fixation or loss of the allele (Dobzhansky & Spassky 1962). The same could be happening in simulations of neutral models; even though separate samples are under influence of ecological drift, all plots taken together result in an average rank abundance distribution which hardly changes and will look like the one from field data. This is hiding the fact, however, that each separate plot is quite different, both in terms of composition and structure in comparison with field data. More interestingly, maximum dominance distributions (i.e. local patterns) over all the plots showed remarkably different results compared to regional patterns, with no congruence between field data and simulation output even in extreme cases (Fig. 4). Parameterisation of the model to approach maximum dominance distributions from field data on local scales resulted in a significant drop in regional diversity.

Rejection of neutral theory on a local level

On local levels, we show strong dominance deviations between observed and predicted versus those observed in empirical data. Even on regional levels, some species are more abundant than either predictions or estimations using the logseries distribution (Fig. 1). This suggests some species are better competitors in some way, reaching higher abundances than predicted by neutral theory on both scales. This clearly is a violation of one of its key assumptions, ecological equivalence, which would predict a much more even distribution. Mantel tests supported this view and in accordance, NMDS also showed clear segregation of plot community composition based on both geographical and environmental proxies for all three data sets used. These results would indicate that at least in terms of composition there is a strong effect of both environmental filtering and dispersal limitation, violating at least partly the assumption of ecological equivalence. Although this would be expected for communities of different forest types, many of the dominant species are clearly not restricted to a single forest type. This leaves the question whether being the better competitor related to abiotic conditions is making species more dominant than predicted by neutral theory or that perhaps a greater ability to withstand pests, pathogens and herbivores could account for this pattern.

Identifying key violations of ecological equivalence

If environmental filtering and subsequent selection on certain traits based on abiotic conditions would account mostly for dominance of species we would expect species dominant within one forest type are not necessarily dominant in others as selective regimes would be different. To test this, we correlated species identity and relative abundance, corrected for total abundance and standardised over all plots for the two major forest types found in each data set (Terra Firme and Podzols). This was done within geographical subsets to account for dispersal limitation effects (i.e. the three data sets separate), similar to an approach studying the distribution of species in Peru and Ecuador performed earlier (Pitman et al. 2001). This showed there was a weak but highly significant correlation of .15 between relative abundances on the two forest types. For Ecuador this correlation was twice as high, yielding a correlation of 0.29, again highly significant (Fig. 5). More interestingly, species that attain maximal dominance in any plot (indicated by red) fall in two distinct categories: those dominant on a single forest type or those attaining dominance across forest types. We show this is not due to a mass effect of clustering due to limited dispersal leading to the same dominant species in nearby plots as only between 8 and 15% of dominant species co‐occurred between plots, with only a slight decrease in the proportion of co‐occurrence over larger distances (Fig. S6). Species apparently can attain dominance in two ways: being a good competitor in a specific environment driven by for instance resource competition (confined by forest type in this case, indicated by the blue arrow in Fig. 5) or being a good competitor regardless of the abiotic environment (red arrow). In either case they must have tolerance to frequency dependent mortality (FDM) on the local level (FDM tolerance, as indicated in Fig. 5). Earlier it was already show that the top ten of hyper‐dominant tree species in the Amazon are either species that often occur in very high local dominance or ones that occur almost everywhere at intermediate or low abundances (ter Steege et al. 2013). The interesting differentiation is between those dominant in particular habitats (which could be mechanistically explained by a higher per capita fitness within these environments) and those dominant regardless of habitat for which other explanations are necessary. In terms of violating the assumption of ecological equivalence, we formulate three hypotheses accounting for the excessive dominance of species related to different scales and processes: (1) species could outcompete other species as a result of competitive exclusion based on environmental filtering (Torti et al. 2001; Ribeiro & Brown 2006), (2) species cannot tolerate certain habitats even in the absence of competitors but are vice versa very suitable for other habitats and this differentiation allows different species to dominate in different habitats, adding to deviance on regional scale patterns or (3) they are better competitors in terms of escaping from FDM, resilience to pathogens or predators (Comita et al. 2010; Mangan et al. 2010), specialisation (ter Steege et al. 2013) or migrate easily, all regardless of habitat. We do need to emphasise the escape from FDM primarily acts on the local level as it has been shown previously that regionally, communities experience primarily density‐independent dynamics, which is also predicted by neutral theory (Hubbell 2001; Volkov et al. 2003). As we could not reject neutrality for the intermediate species, it would be interesting to study differences in for instance functional traits or habitat restrictions for these species in comparison with the dominant species. We did this for seed mass class on genus level taxonomy as this information was available (Hans ter Steege, pers. comm.) and because this trait has been shown to correlate strong with other functional traits as well as being indicative of life‐history strategy. Using a generalised linear model, we found a significant difference between dominant and intermediate abundance genera with dominants having larger seed mass classes on average (approximately half a seed mass class higher out of scale from 1 to 5), which might be indicative of differential survival and reproduction allowing for higher dominance (at least for those restricted to habitats), although further study is warranted. Processes such as even severe ecological drift (Peh et al. 2011) are, however, less likely to account for the majority of these patterns in maximum dominance on the local level as this would result in lower regional diversity as shown by our model predictions. In his original book, Hubbell already showed that even a small difference in competitive ability (1%) was enough to explain dominance deviation (Hubbell 2001). Given that we show these dominant species indeed potentially violate the assumption of ecological equivalence, there is a strong need for theories based on empirical evidence (e.g. trait data and dispersal kernels) to explain how fitness differences between species can account for the observed deviance in dominance of tropical trees and how much difference is needed to account for the lack of ecological equivalence.

Figure 5.

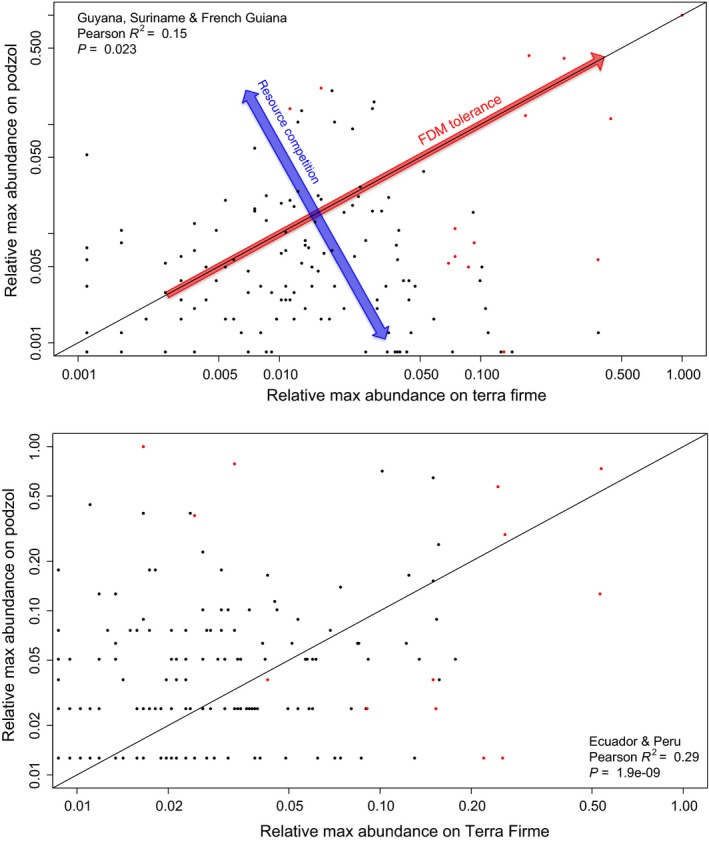
Correlations between species identity and relative abundance corrected for total abundance and standardised over all plots for Guyana, Suriname and French Guiana combined (top) and Ecuador with Peru (bottom). Points indicate standardised relative abundance of species occurring in both Terra Firme (x‐axis) and Podzol forests (y‐axis). Red dots indicate species that attain maximal dominance within any plot. Pearson rank correlation coefficients are noted including the estimated significance levels. Arrows indicate two categories in which species can attain dominance: mainly resource competition in combination with tolerance to frequency dependent mortality (FDM), limiting dominance to a single forest type (blue arrow) or on either forest type indicative of only tolerance to FDM but a lesser degree of resource competition (red arrow).

Conclusions

Our results indicate a severe issue in predictions of neutral theory. It fails to correctly estimate the excessive dominance on either local or regional scales. We hypothesise this is due to violation of model assumptions on different scales, in particular that of ecological equivalence as indicated by the disagreement between distributions of maximum dominance of species across species. In addition, we show that even though (summed) regional patterns in diversity from neutral models may be accurate for intermediate to rare species, there is no guarantee that local plot dynamics and hence the mechanisms behind community composition are also neutral.

Funding

Daniel Sabatier and Jean‐François Molino are supported by an ‘Investissement d'Avenir’ grant managed by Agence Nationale de la Recherche (CEBA, ref. ANR‐10‐LABX‐0025).

Competing interests

Authors declare no competing interests.

Data availability Statement

R scripts including an example data set for Guyana/Suriname supporting the results are available from a GitHub repository (EdwinTPos) https://doi.org/10.5281/zenodo.2587672.

Authorship

EP and HtS designed the experiment. EP wrote R‐scripts, analysed the results and took the lead in writing the manuscript. HtS supervised the writing and provided regular feedback both for the manuscript and the interpretation of the results. All the other authors provided feedback on the manuscript and their data from the Amazon Tree Diversity Network.

Supporting information