Technical Note: Characterization of technology to detect residual injection site radioactivity

Abstract

Purpose

Each year in the United States, approximately 18.5 million nuclear medicine procedures are performed. Various quality control measures are implemented to reduce image errors and improve quantification of radiotracer distribution. However, there is currently no routine or timely feedback about the quality of the radiotracer injection. One potential solution to evaluate the injection quality is to place a topical scintillation sensor near the injection site to record the presence of residual activity. This work investigates a sensor design for identification of injections where the prescribed radioactive activity is not fully delivered into the patient's circulation (an infiltration).

Methods

The sensor consists of a single unshielded bismuth germanate (BGO) crystal (3 mm × 3 mm × 3 mm). Using radioactive sources with gamma energies that span the range commonly used in nuclear medicine, we quantified energy resolution and linearity. Additionally, we computed sensitivity by comparing the calculated incident activity to the activity measured by the sensor. Sensor output linearity was calculated by comparing measured data against the radioactive decay of a source over multiple half‐lives. The sensor incorporates internal temperature feedback used to compensate for ambient temperature fluctuations. We investigated the performance of this compensation over the range of 15°C–35°C.

Results

Energy spectra from four sensors were used to calculate the energy resolution: 67% for ^99mTc (141 keV), 67% for ¹³³Ba (344 keV), 42% for ¹⁸F (511 keV), and 32% for ¹³⁷Cs (662 keV). Note that the energy used for ¹³³Ba is a weighted average of the three photon emissions nearest to the most abundant (356 keV). Sensor energy response was linear with a difference of 1%–2% between measured and predicted values. Energy‐dependent detector sensitivity, defined as the ratio of measured photons to incident photons for a given isotope, decreased with increasing photon energy from 55.4% for ^99mTc (141 keV) to 3.3% for ¹³⁷Cs (662 keV). Without compensation, error due to temperature change was as high as 53%. Temperature compensation reduced the error to less than 1.4%. Sensor output linearity was tested to as high as 210 kcps and the maximum magnitude error was 4%.

Conclusions

The performance of the sensor was adequate for identification of excessive residual activity at an injection site. Its ability to provide feedback may be useful as a quality control measure for nuclear medicine injections.

1. Introduction

Positron emission tomography/computed tomography (PET/CT) data are commonly used for quantitative or semi‐quantitative analyses (e.g., standardized uptake value, PERCIST, and RECIST assessments).1, 2, 3 Furthermore, quantitative single photon emission tomography (SPECT) is gaining popularity. The accuracy of quantitative imaging is assured by processes including clock synchronization, residual syringe activity subtraction, patient weight measurement, and patient blood glucose measurement.4, 5, 6, 7, 8, 9 Inaccuracies can introduce image errors that negatively affect disease staging,1, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29 interpretation of longitudinal disease progression,10, 12, 13, 14, 15, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43 tumor volume measurements,44 myocardial perfusion measurements,1, 31, 45, 46 and neurological assessments.47, 48

However, there is no routine quality control (QC) process for the radiotracer injection itself. During the intravenous access or injection, radiotracer can be inadvertently deposited into the tissue surrounding the vein.49 This is known as an infiltration and can affect the net activity available for circulation or alter the kinetics of availability.10, 26, 29, 42, 43

A potential method of injection QC would be to position a topical scintillation sensor proximal to the injection site (Fig. 1). Scintillation sensors consist of one or more scintillating crystals, light sensors, amplification circuits, energy thresholding circuits, and counting circuitry. When gamma rays interact with the scintillator, light proportional to the absorbed energy is produced. The light sensor then produces electrical pulses whose heights are proportional to the deposited energy. A pulse‐height discriminator is used to reject low‐level pulses resulting from scattered radiation. The remaining pulses are then counted to produce a sensor output in counts per second (cps). For this proposed clinical use, the sensor, along with a second sensor placed on the contralateral arm to collect reference data, could identify the presence of excessive residual radiotracer near the injection site.50, 51 Both sensors would then be removed prior to imaging.

Figure 1.

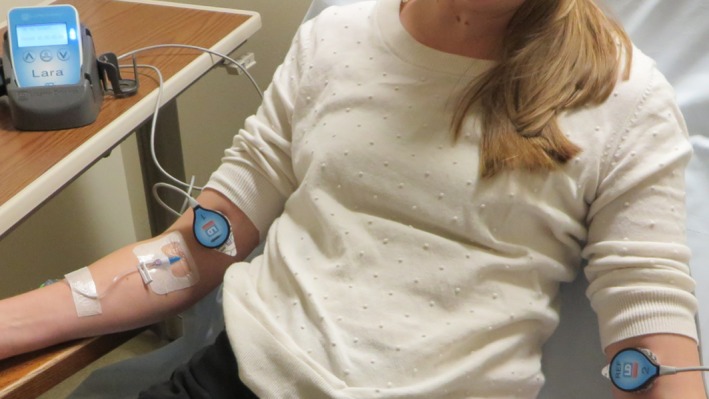
Detectors in use on a patient. Placement is proximal to the injection site.

Based on the sensor design, it may not be possible to provide absolute quantification of the radiotracer near the injection site, but a semi‐quantitative assessment would still be valuable. The goal of this work was to characterize the performance of a topical scintillation sensor for identification of excessive residual activity at the injection site.

2. Materials and methods

We used an uncollimated, unshielded scintillation sensor (Lara^®, Lucerno Dynamics, Cary, NC, USA) with a single 3 mm × 3 mm × 3 mm bismuth germanate (BGO) crystal mated to a silicon photomultiplier (SiPM). The SiPM output is amplified and then discriminated using a single lower level discriminator (LLD). Pulses are counted using a microprocessor‐based asynchronous counter. The design also includes real‐time temperature compensation. Temperature is measured adjacent to the SiPM and crystal, and is used to compensate SiPM bias voltage for fluctuations in temperature. The sensors must be lightweight because they are applied topically with adhesive pads — it is not practical to include significant shielding.

The design of this sensor impacts its performance characteristics. The characteristics we tested were energy resolution, energy linearity, energy‐dependent output sensitivity, temperature sensitivity, and output linearity to determine the device's suitability for its intended clinical function. Sources of ^99mTc, ¹³³Ba, ¹⁸F, and ¹³⁷Cs were used to test the range of energies encountered clinically in nuclear medicine. All sensors used in this testing were calibrated using ¹³⁷Cs.

2.A. Energy resolution

Characterization of the energy resolution is important for setting the pulse‐height discriminator value. We first determined an appropriate step size for energy spectrum analysis. The standard error for full‐width at half‐maximum (FWHM) of a gaussian fit for a 1 keV step size and 10 keV step size was less than 1%. Thus, we used a 10 keV step size to reduce acquisition time. We then measured the energy spectrum for each isotope using four sensors. The sensor design incorporates an LLD but no upper level energy discriminator (ULD). The energy spectrum was measured iteratively over the range of 0–900 keV by adjusting the LLD value. We averaged the output counts from five 1‐s measurements at each step. Without a ULD, the output is an integration of all energies above the threshold, so the resulting iterative spectrum must be differentiated to obtain units of cps/keV. Energy resolution was calculated using the FWHM/E₀ method. Gaussian curves were fit to the average spectrum for each measured isotope using segments of data centered around the measured photopeak: E₀ ± 20% for ^99mTc and ¹³³Ba; E₀ ± 15% for ¹⁸F and ¹³⁷Cs. These gaussian fits were used to calculate the FWHM values. Energy discrimination thresholds for each isotope were then determined and set for the remainder of testing.

2.B. Energy linearity

Knowledge of energy linearity and resolution can be used to determine LLD values for any isotope within the operating range. Using data collected during energy resolution testing, we calculated energy linearity by comparing the center of each gaussian fit to the known photon energy. The differences between calculated and expected values were used to assess performance.

2.C. Sensitivity

Sensitivity with respect to different isotopes is important to anticipate sensor response in clinical applications. Because detector output is dependent on distance to the source, we defined energy sensitivity as the sensor output divided by the calculated number of gamma rays incident upon its crystal. Note that this is unlike sensitivity reported for imaging scanners, but we feel it is appropriate given the design of this detector. To control distance and geometry during testing, we constructed custom fixtures to hold samples of known activity from either standard 1” sealed check sources or single drops of liquid isotope. Sealed source disks were positioned 12.3 mm away from the scintillation crystal and liquid sources were 13.5 mm away. We then calculated the gamma rays from the source that would fall within the solid angle created by the crystal's face in relation to the source. Samples of ¹³⁷Cs and ¹³³Ba consisted of nominally 10 uCi sealed source disks while liquid drops were used for ^99mTc (277 uCi) and ¹⁸F (40 uCi). All test sources were accurately measured with a well counter. Data consisted of an average of 90 1‐s measurements using five devices.

2.D. Temperature sensitivity

Several components of the design are sensitive to temperature including the crystal and SiPM.52, 53 We assessed overall temperature sensitivity with the use of a temperature chamber and isotope samples. Sources consisted of nominally 10 uCi sealed source disks for ¹³⁷Cs and ¹³³Ba and liquid sources of ^99mTc (277 uCi) and ¹⁸F (40 uCi). Each isotope was measured by five sensors using a 1‐s sample rate while ambient temperature was increased from 15°C to 35°C over 15 min. We compared the relationship between sensor output in cps and sensor‐reported temperature. We calculated percent error as a function of the sensor output at 25°C because it is the null‐correction point in the temperature compensation system. Additionally, we calculated the interdevice measurement variation for each isotope with and without temperature compensation.

2.E. Output linearity

For output linearity, we measured a 4.5 mCi source of ^99mTc and an 11.1 mCi source of ¹⁸F as they decayed over multiple half‐lives. We compared the sensor output to known half‐life and calculated the error between the two. Based on existing clinical use of these sensors, we know ¹⁸F injections typically produce 10's of kcps while ^99mTc injections can produce 200 kcps or more. We recorded linearity data up to 210 kcps.

2.F. Detector saturation

Separately, we assessed detector saturation by recording measurements at the maximum sensor output of 250 kcps.

3. Results

3.A. Energy resolution and linearity

Energy resolution results are shown in Table 1 and Fig. 2. Using energy spectra from four sensors, the average values of FWHM/E₀ were 67% for ^99mTc, 67% for ¹³³Ba, 42% for ¹⁸F, and 32% for ¹³⁷Cs. The results of testing for energy linearity are shown in Fig. 3.

Table 1.

Photon energy, location of Gaussian fit, and calculated energy resolution

Isotope	Photon energy (keV)	Gaussian fit center (keV)	FWHM/E0 ± SD
99mTc	141	142 ± 1.3	67% ± 1.3%
133Ba	344	340 ± 1.9	67% ± 2.6%
18F	511	515 ± 4.4	42% ± 3.2%
137Cs	662	666 ± 5.6	32% ± 4.2%

Note that the photon energy used for ¹³³Ba is a weighted average of the three photon emissions near the most abundant (356 keV).

Figure 2.

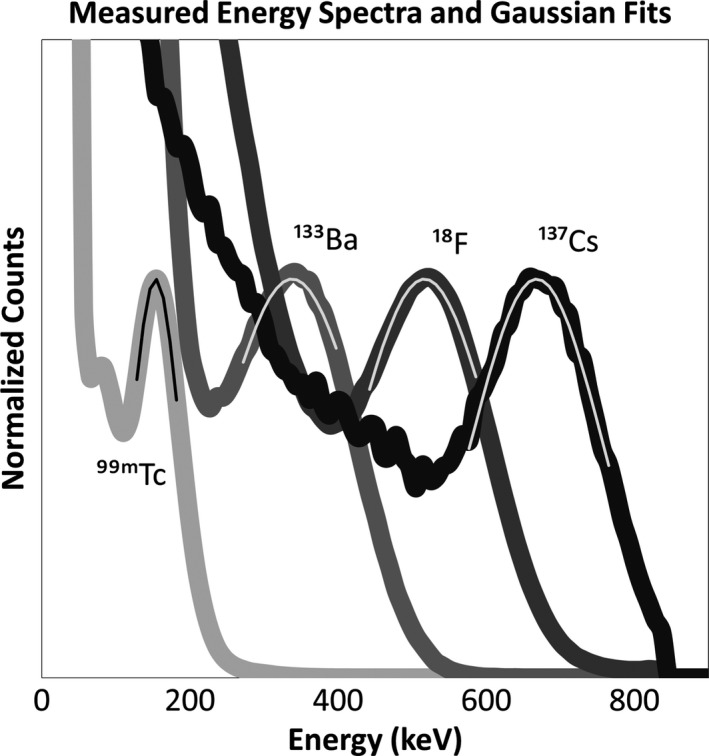
Average measured energy spectra with fit Gaussian curves superimposed.

Figure 3.

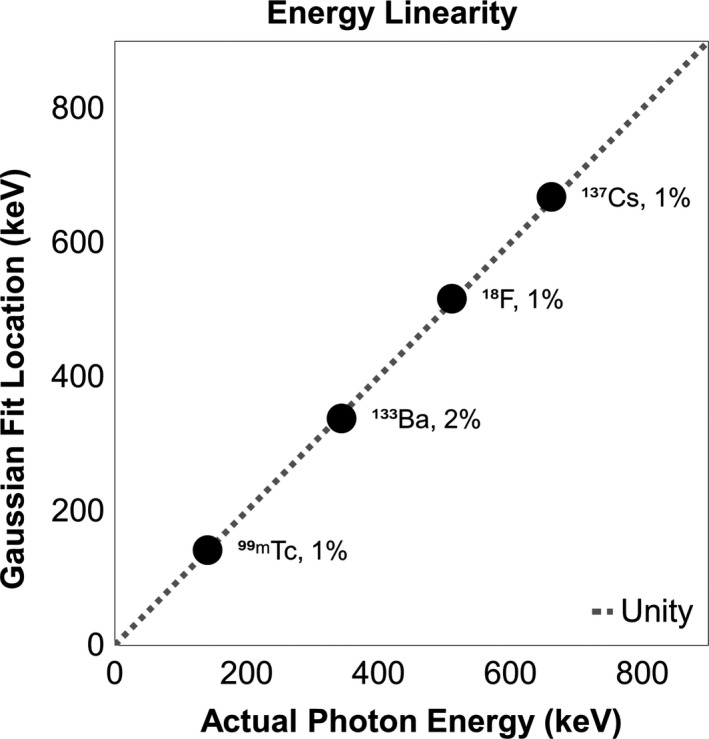
Linearity between photon energy and location of Gaussian curves fit to average measured data. Line of unity is included as a reference along with each point's distance from unity.

3.B. Sensitivity

The average energy sensitivities can be found in Table 2. As expected, sensitivity decreases with increasing photon energy due to reduced stopping power of the scintillation crystal.

Table 2.

Sensitivity of isotopes

Isotope	Calculated incident gammas per second	Detector output (cps)	Average sensitivity ± SD
99mTc	40,276	22,325	55.4% ± 3.1%
133Ba	1,244	308	24.8% ± 0.7%
18F	11,267	396	3.5% ± 0.1%
137Cs	1,649	55	3.3% ± 0.6%

Sources of ^99mTc and ¹⁸F were liquid and positioned 13.5 mm away from the scintillation crystal. Sources of ¹³³Ba and ¹³⁷Cs were sealed source disks and located 12.3 mm away from the crystal.

3.C. Temperature sensitivity

The average bias in sensor output as a function of temperature without compensation is shown in Fig. 4. Maximum uncompensated error was −53% (¹⁸F at 35°C). Measurements taken with compensation indicated the following maximum magnitude percent errors: 0.47% for ^99mTc, 0.63% for ¹³³Ba, 1.41% for ¹⁸F, and 0.93% for ¹³⁷Cs (Fig. 5). Note that error is relative to 25°C because that is the null‐compensation point in the sensor hardware.

Figure 4.

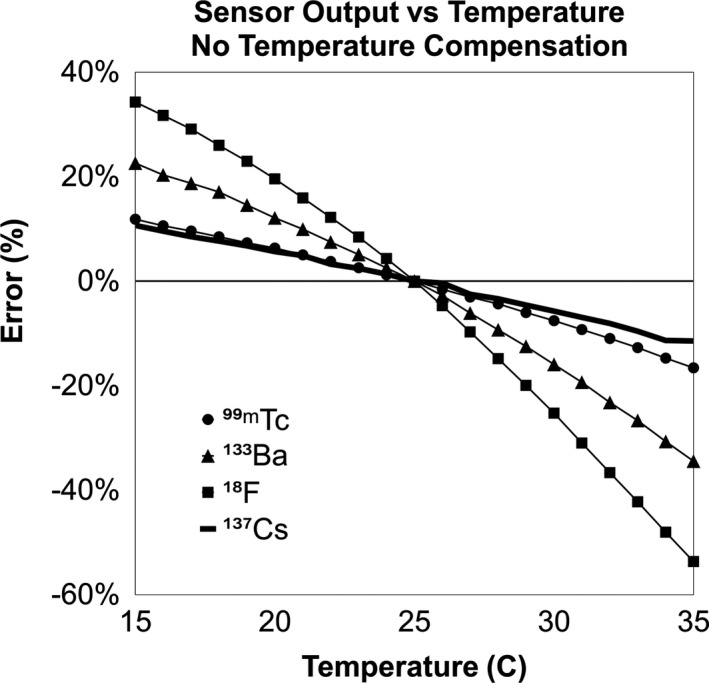
Sensor output vs temperature without compensation enabled as a percent of the value at 25°C.

Figure 5.

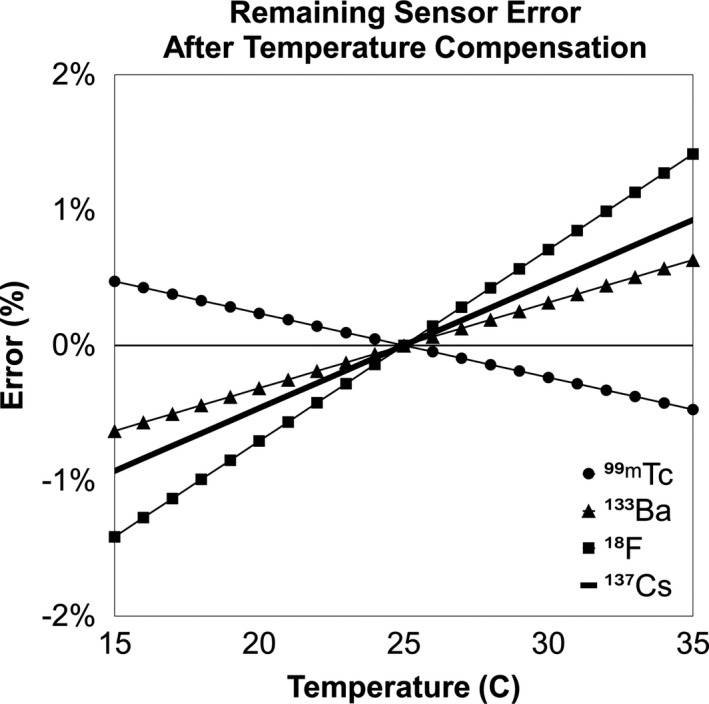
Sensor output vs temperature with compensation enabled as a percent of the value at 25°C.

Temperature compensation had little effect on interdevice measurement variation (Table 3).

Table 3.

Comparison of the impact of temperature compensation on measurement variation

Isotope	Interdevice variation without compensation ± SD	Interdevice variation with compensation ± SD
99mTc	3.59% ± 0.17%	3.50% ± 0.14%
133Ba	3.47% ± 0.17%	3.52% ± 0.17%
18F	4.17% ± 0.48%	3.41% ± 0.09%
137Cs	3.29% ± 0.18%	3.33% ± 0.19%

Average interdevice output variation is shown for each isotope over the temperature range of 15°C–35°C with and without temperature compensation enabled.

3.D. Output linearity

During linearity testing, sensor output ranged from approximately 210 kcps to 10 cps with ^99mTc. Due to the sensor's lower sensitivity for ¹⁸F, its range was from 80 kcps to 10 cps. Performance was evaluated by comparing the output to the known half‐life for each isotope (Fig. 6). The overall error span was approximately 4% for ^99mTc and 1.5% for ¹⁸F.

Figure 6.

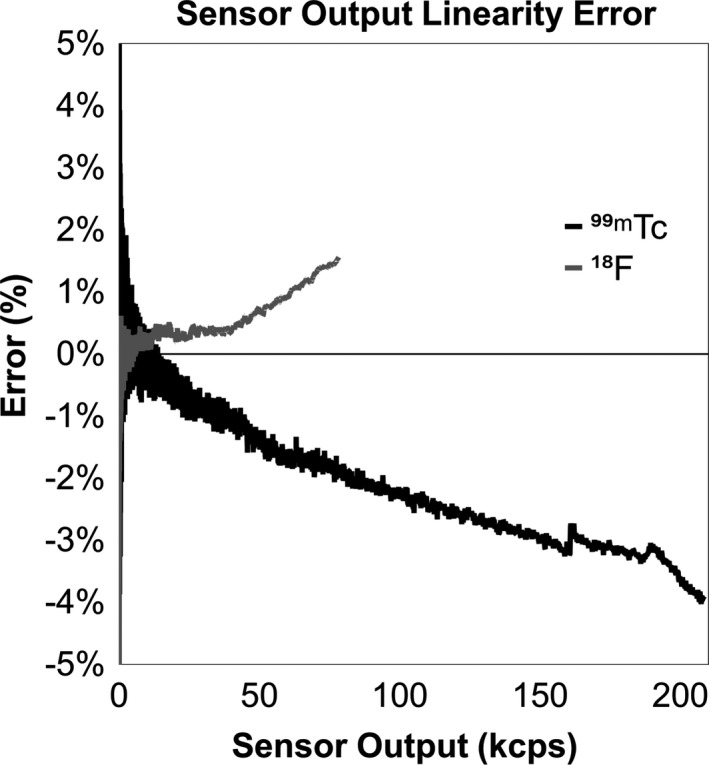
Percent error of measured data vs expected from 0 to 210 kcps for 99mTc and 0 to 80 kcps for 18F.

3.E. Detector saturation

Measurements were taken up to 250 kcps with no indication of detector saturation. The sensor software limits output to 250 kcps.

4. Discussion

Several compromises were made in the design of the investigated sensor in order to support its intended topical application. The use of a single unshielded crystal means that the sensor response is omnidirectional — an advantage for detection of radiotracer with variable and unknown morphology. BGO was chosen for the scintillation crystal because of its high stopping power, high light yield, and nonhygroscopic properties. Its longer optical decay time is not a concern because the sensor is not using coincidence timing to localize positron annihilation; however, it does limit the sensor's maximum count rate and could increase nonlinearity due to pile‐up. Although BGO has advantages, energy resolution and sensitivity are limited by the small crystal size used in this design.

Compared to photomultiplier tubes, SiPMs are advantageous for light detection because of their small size, mechanical robustness, and low bias voltage requirements; however, they exhibit sensitivity to temperature52, 54, 55 which must be accounted for in the design. In clinical applications, sensor temperature can vary due to ambient room conditions, patient body temperature, and use of heated blankets for patient comfort. We found temperature‐induced error without compensation to be as high as 53%, but by using real‐time bias voltage compensation, error was reduced to less than 2%.

Due to the design of this sensor, energy resolution is limited compared to other gamma scintillation detectors.56, 57, 58 Lower resolution is acceptable for the intended application because there is no need to differentiate isotopes based on photon energy. Nonetheless, interdevice energy response was shown to be consistent — photo peak location variability was less than 1% (Table 1). Knowledge of the energy resolution would be necessary if a dual‐threshold energy window were used as opposed to just a single threshold LLD.

The sensors showed strong energy linearity with 1%–2% differences between measured and expected values. This degree of consistency allows standardized LLD values despite variability in the crystal or other hardware. Additionally, it allows for calibration using long‐lived ¹³⁷Cs sources.

The sensitivity for ^99mTc was 16 times that of ¹⁸F. Based on clinical use of this sensor, we know it is common for sensor output to reach 20 kcps for ¹⁸F during the bolus injection. For the same injection with ^99mTc, the rate could be 320 kcps, but the detector software limits output to 250 kcps. Based on the linearity testing done in this work, nonlinearity was within the range expected for pile‐up‐based effects.59

We did not expect the sensor to exhibit positive nonlinearity for ¹⁸F, but the results were consistent and repeatable. We hypothesize the phenomenon could be due to the single‐ended LLD configuration of this design. It is possible that as pulses pile up, those which would normally fall above the upper level discriminator are instead counted causing an increase in output. Further investigation could be done, but clinical use demonstrates typical postbolus output is approximately 25 cps/mCi of injected activity for ¹⁸F and approximately 85 cps/mCi for ^99mTc. At these levels, pile‐up will not be an issue.

The design with a single crystal makes it difficult to quantify the exact amount of radiotracer present near the injection site, but future work could use measured sensitivity and estimates of geometry to perform some quantification. Radioactivity elsewhere in the body is a source of noise when measuring the injection and reference arms. For this reason, the net difference in counts between the two arms is likely better than the injection arm alone. Furthermore, addition of shielding to the sensor could be a mechanism to improve the signal‐to‐noise ratio. A collimated shield could create a focused field of view that would allow for measurement of specific targets within the patient.

5. Conclusion

Nuclear medicine clinicians currently have no effective, routine, and timely feedback about the quality of radiotracer injections. Use of a topical scintillation sensor near the injection site could provide dynamic feedback about the injection quality during the uptake period without dependence on the nuclear medicine image or its field of view. We confirmed the sensor's performance is adequate for its intended function: providing feedback about the presence of residual activity at the injection site. Since infiltrated activity can dynamically alter the systemic availability of radiotracer throughout the uptake time, due to sequestration and reabsorption, this feedback could inform image interpretation and patient management.

Disclosures

All authors of this paper are employed by Lucerno Dynamics, the manufacturer of the Lara^® device.