Skip to main content
PMC home page
Wiley Open Access Collection logoLink to Wiley Open Access Collection
letter
. 2019 Jan 4;22(3):469–479. doi: 10.1111/ele.13204

Foraging efficiency and size matching in a plant–pollinator community: the importance of sugar content and tongue length

Saskia GT Klumpers 1,2,3,✉, Martina Stang 1,2, Peter GL Klinkhamer 1
Editor: Rebecca Irwin
PMCID: PMC6850310  PMID: 30609161

Abstract

A long‐standing question in ecology is how species interactions are structured within communities. Although evolutionary theory predicts close size matching between floral nectar tube depth and pollinator proboscis length of interacting species, such size matching has seldom been shown and explained in multispecies assemblages. Here, we investigated the degree of size matching among Asteraceae and their pollinators and its relationship with foraging efficiency. The majority of pollinators, especially Hymenoptera, choose plant species on which they had high foraging efficiencies. When proboscides were shorter than nectar tubes, foraging efficiency rapidly decreased because of increased handling time. When proboscides were longer than nectar tubes, a decreased nectar reward rather than an increased handling time made shallow flowers more inefficient to visit. Altogether, this led to close size matching. Overall, our results show the importance of nectar reward and handling time as drivers of plant–pollinator network structure.

Keywords: Asteraceae, foraging efficiency, handling time, interaction probability, nectar tube depth, optimal foraging, pollination, proboscis length, size matching

Introduction

The description and understanding of the structure of species interaction networks is growing into a major research field in ecology. Especially mutualistic interactions between plants and pollinators provide an important model system in this field. Studies of these interaction networks have revealed general interaction patterns such as nestedness, connectance and asymmetry in species dependencies (e.g. Bascompte et al. 2003; Vazquez & Aizen 2004; Bascompte & Jordano 2007). These patterns can be explained by a number of non‐mutually exclusive factors, including species abundance, phylogenetic relationships, overlap in spatio‐temporal distributions and matching of phenotypic traits of interacting species (e.g. Vazquez et al. 2009a and references therein; Olesen et al. 2011). In spite of a relatively high ability to predict these aggregate network characteristics, only a few studies have been able to predict pairwise interactions (Stang et al. 2009; Olesen et al. 2011; Verdu & Valiente‐Banuet 2011; Kaiser‐Bunbury et al. 2014; Maglianesi et al. 2014; but see Vazquez et al. 2009b). Nevertheless, insight into the mechanisms that determine pairwise species interactions is important as it can help to understand and better predict commonly observed structural features of ecological communities.

Size matching between floral nectar tube depth and pollinator proboscis length has been shown to be an important determinant of plant–pollinator interactions. In general, flowers with deep nectar tubes restrict access of nectar to visitors with long mouthparts (Haber & Frankie 1989; Corbet 2000; Stang et al. 2007). For specialised and co‐dependent species pairs, evolutionary theory predicts that (1) there should be strong natural selection for pollinator proboscides to exceed floral nectar tubes in order to access all the nectar within the flowers; and (2) that selection on flowers should favour nectar tubes that are longer than their pollinator's proboscis because this ensures contact with the reproductive parts of the flowers and thus maximises pollen transfer (e.g. Alexandersson & Johnson 2002; Anderson & Johnson 2008; Muchhala & Thomson 2009). This co‐evolutionary arms race should lead to ever‐increasing nectar tube depths and proboscis lengths and a close matching between these traits of strongly interacting species (Darwin 1862; Nilsson 1988; Anderson et al. 2010). However, such an arms race cannot explain size matching in multispecies assemblages with a variety of nectar tube depths and proboscis lengths and asymmetrically specialised species pairs. In these systems, flowers with a long nectar tube can only be visited for nectar by pollinators with a long proboscis, but these pollinators can potentially visit plants species with both long‐ and short‐tubed flowers (Harder 1985; Haber & Frankie 1989). Although positive correlations between nectar tube depth of flowers and the average proboscis length of their pollinators have been found (e.g. Brian 1957; Gilbert 1981; Harder 1985; Shmida & Dukas 1990; Plowright & Plowright 1997; Borrell 2005; Stang et al. 2009), such a correlation does not necessarily imply that there is close size matching. For close size matching to occur, pollinators with a long proboscis need to forage preferentially from flowers with a long nectar tube. Only a few community studies have shown close size matching or that size matching can affect interaction strength or interaction probability of pairwise interactions (Stang et al. 2009; Maglianesi et al. 2014 for hummingbirds).

Although insects with a long proboscis can potentially visit a wide variety of flowers, they often seem to avoid relative shallow flowers (Stang et al. 2009) and preferentially forage on plant species with flowers of which the nectar tube matches their proboscis length (Haverkamp et al. 2016). One would expect such a preference if pollinators forage more efficiently on matching flowers. Flower foraging efficiency depends on both handling time and nectar reward. Concerning handling time, it has been shown that long‐tongued bumblebees are generally faster foragers than short‐tongued bumblebees when foraging on a single plant species (Harder 1983), irrespective of whether floral nectar tubes are longer or shorter than their proboscis. In contrast, several studies suggest that it takes pollinators with a long proboscis longer to handle short‐tubed flowers than pollinators with a short proboscis; in other words these studies suggest that tongues can be too long (e.g. Inouye 1980; Plowright & Plowright 1997; Kunte 2007; Karolyi et al. 2013; Bauder et al. 2015). For hummingbirds, it was found that the handling time of nectar resources was related to the degree of matching between bill length and nectar tube depth (Maglianesi et al. 2014). A morphological mismatch (longer bill than nectar tube) led in this study system to longer handling times when accounting for differences in nectar content across plant species. However, other than Maglianesi et al. (2014), we know of no studies that have revealed that handling time and the degree of trait matching of interacting species are related. What is more, the question whether foraging efficiency (defined as sugar extraction rate) of insect pollinators is higher on plant species with matching flowers remains largely unanswered. Insect pollinators seem to prefer more rewarding plants of the same species (Anderson et al. 2016). However, the specific roles of nectar reward and handling time for determining foraging efficiency and its effect on size matching in multispecies assemblages in which both a negative mismatch (proboscis is shorter than nectar tube depth) and a positive mismatch (proboscis is longer than nectar tube depth) occur has not been examined.

In this study, we investigated whether the degree of size matching between floral nectar tube depth and pollinator proboscis length can predict the interaction probability among sixteen co‐occurring subalpine Asteraceae species and their pollinators, and whether foraging efficiency is an important driver of this size matching. As an indicator for foraging efficiency, we used sugar extraction rate. We included flower head display size and flower head density as covariates in this analysis as interaction probability is expected to be related to these floral characteristics (Hegland & Totland 2005; Verdu & Valiente‐Banuet 2011; Kaiser‐Bunbury et al. 2014). In addition, we determined the relationship between degree of size matching and both handling time and sugar extraction rate and examined how sugar extraction rate, handling time and nectar reward are related. Harder (1983) has tested the effect of proboscis length and nectar tube depth on probing time of bumblebees foraging on artificial flowers. The result of this study show that probing time increased gradually with increasing depth for flowers shallower than bees’ glossa. However, beyond that depth, probing time increased much more rapidly. Based on these findings, we hypothesize that the highest interaction probability and sugar extraction rate occur when proboscis length and nectar tube depth match. We expect that interaction probability and sugar extraction rate decrease rapidly when the nectar tube depth exceeds the proboscis length. This is because pollinators cannot reach the nectar in these flowers easily and therefore it will take pollinators longer to handle them. When pollinator proboscis exceeds the nectar tube depth, we expect interaction probability and sugar extraction rate to decrease more gradually, either because pollinators may need longer time to handle these flowers since a longer proboscis may be of hindrance, or because relative shallow flowers produce less nectar than deeper, closely matching, flowers. We choose species of the Asteraceae as a study system, because they are functionally generalised due to their relatively shallow tubular flowers. They have been shown to be visited by a high diversity of insect species, mostly belonging to the insect orders of Hymenoptera, Lepidoptera and Diptera (Lane 1996). This high level of functional generalisation makes these plants an ideal system to analyse the degree of size matching and foraging efficiency and its effect on flower choice in multispecies assemblages.

Material and methods

Study system

Data were collected in the Colorado Rocky Mountains, USA, in the vicinity of the Rocky Mountain Biological Laboratory (RMBL). We included sixteen co‐flowering Asteraceae species which were flowering most abundantly (see Table S1 in Supporting Information). Plant–pollinator interactions were observed from mid‐June to mid‐August 2011 in five different plots of approximately 50 by 50 m. These plots were 100–200 m apart. Pollinators could move freely between these plots. The elevation of the plots was between 2900 and 3200 m above sea level, exposed mainly to the south.

Interaction probability

Each plant species was observed for 4 hours in total by randomly walking through the plots where the focal plant species was flowering abundantly. Total sampling time was divided into eight sampling intervals of approximately half an hour. These sampling intervals were spread over several days, and during different times of day (morning and afternoon). All observations took place between 09:00 and 16:00 h on days without strong wind and rain.

Insect species were not caught to avoid changing their densities, distributions and behaviour. Instead, all insects encountered were filmed with a digital video camera for later identification. Individuals were identified up to the species‐ or morpho‐species level based on video material and a reference collection. In total we observed 610 individuals belonging to 64 (morpho‐)species, mostly Hymenoptera (28 species accounting for 74% of all the individuals), Lepidoptera (18 species, accounting for 16% of all individuals) and Diptera (12 species, accounting for 7% of all individuals). Videos were used to determine whether an insect visited a flower for nectar and/or pollen and whether it touched anthers or stigmata. Only those interactions where insects were foraging for nectar were included in the analyses. All insects touched anthers or stigmata, thus potentially acting as pollinators.

Handling time

Handling time was determined using the video recordings. Video recordings were analysed frame‐by‐frame (50 frames/s) with the software Adobe Premiere Pro CC 2014. We measured handling time as the time that an insect has its proboscis in the flower. Thus, our measurement of handling time includes the time an insect needs to enter a flower with its proboscis and extract the nectar. Not all individuals were filmed long enough to be able to analyse their handling time. In total, we recorded the handling time of 117 unique pairs of interacting plant–pollinator species. Handling time per insect species–plant species combination are averages of several individuals with on average 31 probes per species pair (range between 3 and 260 probes).

Trait matching: degree of (relative) mismatch

To calculate the degree of mismatch, we measured pollinator proboscis length and floral nectar tube depth. Proboscis length measurements of butterflies, flies, solitary bees and wasps were based on specimens from a reference collection. The specimens in this collection were collected in 2008 and 2010, at the same study site as where our study was conducted. The proboscis lengths of these specimens were measured according to the methods described by Stang et al. (2006). Data on the average proboscis lengths for bumblebees were obtained from Macior (1974) (for queens and workers) and from Inouye (1976) (for males), who also collected their specimens in the vicinity of our study sites.

For all plant species, we measured the corolla tube of disk flowers. This corolla tube consists of two parts: a (very) narrow lower part and an upper wider bell‐shaped part. The wider part roughly begins where the stamens insert and ends at the beginning of the corolla lobes, at the base of the deepest cleft in the corolla. Nectar is produced at the base of the narrow part of the corolla tube and migrates up into the wider upper part of this tube. The lower narrow part of the corolla tube is completely filled by the style (see Table S1). Consequently, it can only contain traces of nectar and it is unlikely that insects can access this part of the corolla tube. Therefore, for each plant species, we only measured the depth of the upper wider part of the corolla tube, hereafter referred to as nectar tube (see Fig. S1). We measured the nectar tube depth for at least twenty freshly picked flowers (of at least ten different individuals), to the nearest 0.01 mm, under a dissecting microscope.

The degree of mismatch between pollinator proboscis length and floral nectar tube depth was calculated by subtracting the length of the nectar tube from the length of the proboscis. Consequently, positive values imply that pollinator proboscis is longer than the nectar tube of the flowers they visit. In turn, negative values imply that pollinator proboscis is shorter than the nectar tube of the flowers they visit. In addition, we then calculated the degree of relative mismatch by dividing the degree of mismatch by pollinator proboscis length. The degree of relative mismatch rather than the degree of mismatch might determine whether a long proboscis is of hindrance as e.g. a 0.5 mm longer proboscis would be of more hindrance for an insect with a proboscis of 1 mm than for an insect with a proboscis of 10 mm.

Sugar content and sugar extraction rate

To estimate nectar reward, we measured the sugar content of flowers that were bagged for 24 h. We used nectar production rate (NPR) as an estimate for nectar standing crop (NSC) because we were unable to measure the NSC of eight of the sixteen species. NPR is an appropriate estimate of NSC because these measurements were linearly correlated (Klumpers, unpublished data). NPR and NSC measurements were performed on individuals flowering at the same location as where plant–pollinator interactions were observed. Flowers were bagged between 8 and 9 AM and collected 24 h later. We used bags made of fine gauze that do not change the temperature within the bags and thus do not influence the nectar solute concentration (Corbet 2003). As ray flowers of our species are sterile and do not produce nectar (Mani & Saravanan 1999), we only measured the nectar production of disk flowers. Our video footage also showed that only disk flowers were probed by insects. Nectar volume was measured in the lab under a dissecting microscope, within approximately an hour after collection. Nectar was extracted with microcapillary tubes, ranging in size between 0.2, 0.25, 0.5 and 1.0 μL. Capillary size depended on the quantity of the nectar produced by the flowers and the nectar tube width. With the microcapillary tubes we probed the base of the nectar tube until no more nectar could be removed and then used digital callipers to measure the distance the nectar had migrated up the microcapillary tubes. Nectar volume was determined by converting the distance measured to volumes (μL). Nectar sugar concentration (expressed in % w/w in a solution) was measured with a hand‐held refractometer (Bellingham and Stanley, Tunbridge Wells, UK). Sugar content (mg) was quantified as the product of the nectar sugar concentration, which was first converted from wt/wt to wt/vol, x nectar volume (μL), as suggested by Bolten et al. (1979). When nectar volumes of single flowers were too small, nectar samples of flowers from the same flower head were pooled to obtain an estimate of the average sugar concentration of these flowers. Consequently, sugar content for individual flowers was estimated based on the nectar volume of a single flower and the average sugar concentration of the flowers in a particular flower head.

After the visit of a pollinator, there was no nectar left in flowers that could be extracted with microcapillary tubes. Therefore, we obtained an approximation of sugar extraction rate by dividing the mean sugar content per flower by the handling time for each plant‐pollinator species pair. Thus, sugar extraction rate is the amount of sugar a pollinator ingests per time unit, while handling a single flower.

Flower head display size

For each plant species, we measured the diameter of the flower head (including the rays for the species that have ray flowers) for at least twenty flower heads and calculated the surface area, which we refer to as flower head display size.

Flower head density

For each plant species, we counted the number of open flower heads per square meter. For most species, this number was calculated based on ten quadrats of one square meter which were randomly placed within the plots at places where at least one individual of a species was flowering. For Cirsium sp. 2 and Arnica parryi, we measured flower head density based on one plot of ten square meters. This is because these species were flowering at only one location in our plots.

Statistical analyses

Statistical analyses were performed using R version 3.4.1 (R Development Core Team 2014). To test whether the probability that an interaction between a plant and pollinator species occurred was related to the degree of mismatch, we performed a generalised additive mixed model (GAMM), with presence/absence as response variable and degree of mismatch as explanatory variable, assuming a Binomial error structure. To account for the interspecific differences in flower head display size and flower head density and differences between insect orders, we included these variables as additional explanatory variables. Furthermore, to account for random variation among species, we included insect species as a random effect. As Hymenoptera, Lepidoptera and Diptera made up most of the interactions (97%), we only included these insect orders in the analyses.

To test whether both handling time and sugar extraction rate were related to the degree of mismatch and the degree of relative mismatch, we also used GAMMs, with either handling time or sugar extraction rate as response variable and either degree of mismatch or degree of relative mismatch as explanatory variable, assuming a Gaussian error structure. We calculated the mean handling time and mean sugar extraction rate per plant–pollinator species pair. To account for the differences in handling time among insect orders (Herrera 1989), we included insect order as an additional explanatory variable. For the analyses of handling time, we also included the mean sugar content per flower as an additional explanatory variable. This is to account for the influence of nectar production per flower on handling time. We did not include sugar content in the analyses of sugar extraction rate because the latter was calculated as sugar content divided by handling time and thus would lead to spurious correlations. Finally, to account for the random variation among species, we included insect species as a random factor in these models. We performed GAMMs because this allows for fitting nonlinear and asymmetric relationships between explanatory and response variables. All GAMMs were performed, using the gamm function within the package “mgcv” (Wood 2018).

To analyse whether handling time was affected by sugar content, we used linear regression models with handling time as response variable and sugar content and insect order as explanatory variables. We analysed the effect of sugar content on handling time of negative and positive degree of mismatch separately.

Finally, we analysed the data of those insect species which visited more than three different plant species separately to illustrate the species–specific relationships between handling time or sugar extraction rate and degree of mismatch or relative mismatch. We could only include positive mismatches because of the lack of sufficient data for species with a negative mismatch. We performed linear regression models with handling time or sugar extraction rate as the response variable and either degree of mismatch or degree of relative mismatch and insect species as explanatory variables. In addition, to account for the effect of nectar reward on handling time, we fitted multivariate linear regression models with handling time as response variable and either degree of size mismatch or degree of relative mismatch and sugar content as explanatory variables. For all analyses, we log10‐transformed handling time and sugar extraction rate to normalise residuals.

Results

Interaction probability

The traits of the plant and insect species that were observed are summarised in Tables S1 and S2 respectively. Plants were on average visited by eleven different insect species (range 2–31 species), while insects visited on average three different plant species (range 1–11 species). Thus, plants were more generalised than insects.

Among Hymenoptera and Diptera, the highest interaction probability occurred when their proboscis was slightly longer than the nectar tube (Fig. 1a; Table 1). Among Hymenoptera, we found a rapid decrease in interaction probability when proboscides were increasingly shorter than nectar tubes. When proboscides were increasingly longer than nectar tubes, interaction probability decreased more gradually (Fig. 1a). Diptera experienced the highest interaction probability when their proboscides were approximately four mm longer than nectar tubes. When proboscides were shorter, interaction probability decreased. A mismatch greater than four mm did not occur among Diptera. Lepidoptera did not show a significant relationship between size matching and interaction probability. They did not visit flowers that were much longer than their proboscis (Fig. 1a; Table 1). Interaction probability also increased with flower head display size and flower head density (Figs 1b and 1c; Table 1). Together, the degree of mismatch, flower head display size and flower head density explained 15% of the variance in interaction probability.

Figure 1.

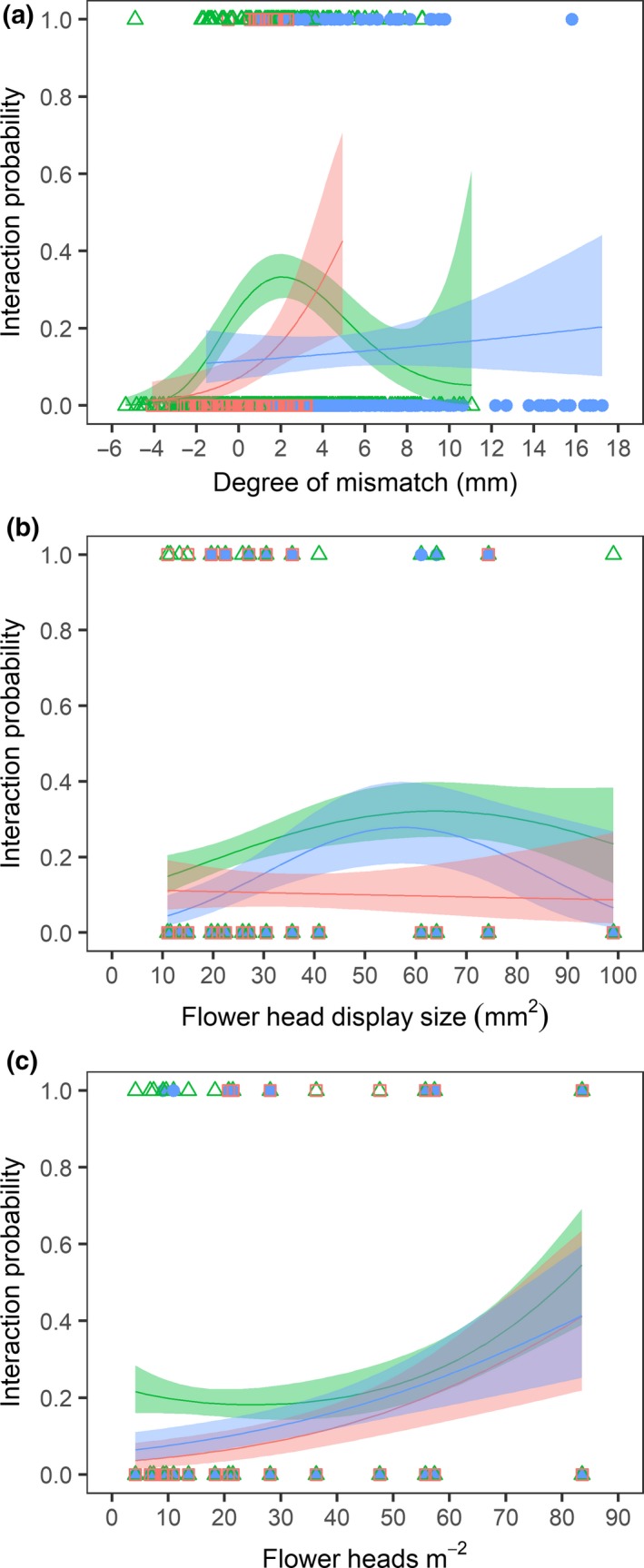
Figure 1

Open in a new tab

Interaction probability as a function of (a) degree of mismatch, (b) flower head display size and (c) flower head density. A degree of mismatch < 0 indicates that floral nectar tube depth exceeds pollinator proboscis length and a degree of mismatch > 0 indicates that pollinator proboscis length exceeds floral nectar tube depth. Each dot represents a particular insect species visiting a particular plant species (1) or not visiting a particular plant species (0). Colours and shapes represent the different insect orders (blue closed circles: Lepidoptera, green open triangles: Hymenoptera and red open squares: Diptera). N = 1040.

Table 1.

Results of the generalised additive mixed model (GAMM) predicting the effect of degree of mismatch, flower head density and flower head display size on interaction probability, fitting a binomial (link=logit) distribution. Insect species was included as a random factor in the model (R 2 adj = 0.15, N = 1040)

Parametric coefficients Smooth terms
Estimate Std.error T‐value P‐value Edf F‐value P‐value
Intercept (Hym) −1.52 0.19 −7.95 <0.001 Degree of mismatch Hym 2.68 12.42 <0.001
Dip −0.31 0.51 −0.61 0.540 Degree of mismatch Dip 1.00 3.76 0.052
Lep −1.15 0.46 −2.54 0.011 Degree of mismatch Lep 1.00 0.02 0.890
Flower head density Hym 2.32 12.35 <0.001
Flower head density Dip 1.00 7.10 0.008
Flower head density Lep 2.19 10.01 <0.001
Flower head display size Hym 1.00 19.06 <0.001
Flower head display size Dip 1.00 2.37 0.124
Flower head display size Lep 2.43 8.42 <0.001
Open in a new tab

Handling time

Handling time when proboscis was shorter than nectar tube

Handling time data are summarised in Table S3. Handling time was exponentially related to the degree of (relative) mismatch as indicated by the linear relationship between degree of (relative) mismatch and log10 handling time (Figs 2a and 2b). Handling time strongly increased when proboscides were increasingly shorter than the nectar tube (negative degree of mismatch) (Figs 2a and 2b; Table 2). This was not because deeper flowers contained more sugar, since handling time was not related to sugar content when the proboscis was shorter than the nectar tube (Fig. 3a). This indicates that it takes insects much longer to extract nectar when they visit flowers of which the nectar tube is longer than their proboscis, not because these flowers contain more nectar but because their proboscis is too short to reach and extract the nectar efficiently.

Figure 2.

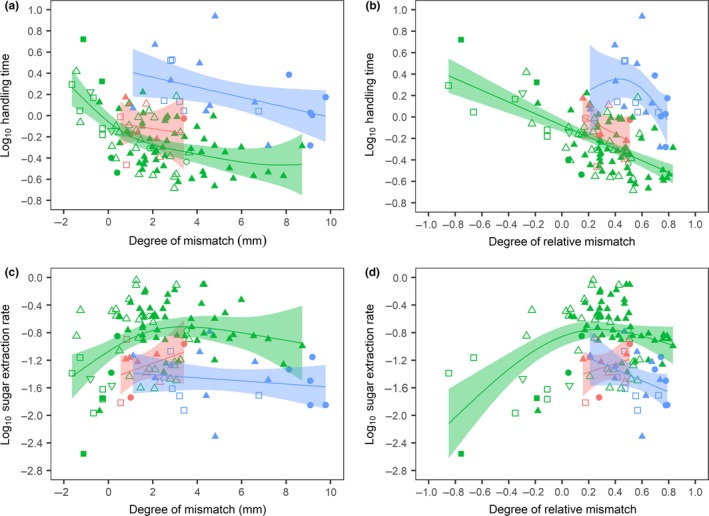
Figure 2

Open in a new tab

Handling time as a function of (a) degree of mismatch (R 2 adj = 0.47, P < 0.001) and (b) degree of relative mismatch (R 2 adj = 0.53, P < 0.001) and sugar extraction rate as a function of (c) degree of mismatch (R 2 adj = 0.28, P = 0.059) and (d) degree of relative mismatch (R 2 adj = 0.37, P < 0.001). A degree of mismatch or relative mismatch < 0 indicates that floral nectar tube depth exceeds pollinator proboscis length and a degree of mismatch or relative mismatch > 0 indicates that pollinator proboscis length exceeds floral nectar tube depth. Each dot represents a particular insect species visiting a particular plant species. Colours represent the different insect orders (blue: Lepidoptera, green: Hymenoptera and red: Diptera) and the shapes represent the different insect families. Plotted lines are based on univariate analyses. N = 117.

Table 2.

Results of the generalised additive mixed models (GAMMs) predicting the effect of degree of mismatch or degree of relative mismatch on handling time or sugar extraction rate, fitting a Gaussian distribution. Handling time and sugar extraction rate were log10 transformed. Sugar content was included as an additional explanatory variable in de models predicting handling time. In all models, insect species was included as a random factor

Parametric coefficients Smooth terms
Estimate Std.error T‐value P‐value Edf F‐value P‐value R 2 adj
(a) Handling time – degree of mismatch
Intercept (Hym) −0.26 0.03 −8.77 <0.001 Degree of mismatch Hym 2.35 17.45 <0.001 0.48
Dip 0.13 0.13 1.00 0.319 Degree of mismatch Dip 1.00 0.28 0.598
Lep 0.62 0.08 7.65 <0.001 Degree of mismatch Lep 1.00 5.34 0.023
Sugar content 1.00 2.72 0.102
(b) Handling time – degree of relative mismatch
Intercept (Hym) −0.27 0.03 −0.01 <0.001 Degree of relative mismatch Hym 1.70 35.18 <0.001 0.54
Dip 0.17 0.08 2.13 0.036 Degree of relative mismatch Dip 1.00 1.64 0.203
Lep 0.42 0.20 2.04 0.044 Degree of relative mismatch Lep 2.27 5.07 0.019
Sugar content 1.00 2.01 0.160
(c) Sugar extraction rate – degree of mismatch
Intercept (Hym) −0.92 0.06 −14.54 <0.001 Degree of mismatch Hym 2.14 3.14 0.059 0.28
Dip −0.24 0.26 −0.94 0.350 Degree of mismatch Dip 1.00 0.55 0.461
Lep −0.50 0.16 −3.08 0.003 Degree of mismatch Lep 1.00 0.56 0.455
(d) Sugar extraction rate – degree of relative mismatch
Intercept (Hym) −0.93 0.06 −15.25 <0.001 Degree of relative mismatch Hym 2.67 9.04 <0.001 0.37
Dip −0.36 0.16 −2.22 0.028 Degree of relative mismatch Dip 1.00 0.41 0.521
Lep −0.31 0.20 −1.57 0.118 Degree of relative mismatch Lep 1.00 2.76 0.099
Open in a new tab
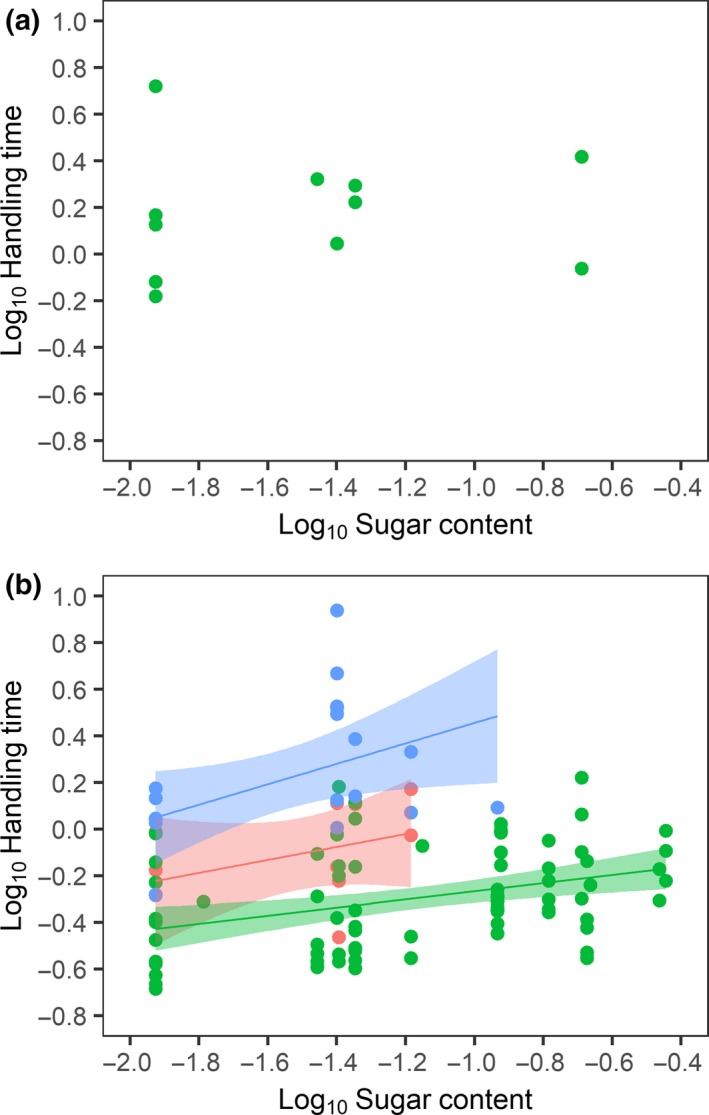
Figure 3.

Figure 3

Open in a new tab

Handling time as a function of sugar content (a) among insects that visit plant species of which the nectar tube is longer than their proboscis (R2 adj = −0.11, P = 0.830, N = 10) and (b) among insects that visit plant species of which the nectar tube is shorter than their proboscis (R 2 adj = 0.48, P < 0.001, N = 105). Colours represent the different insect orders (blue: Lepidoptera, green: Hymenoptera and red: Diptera).

Handling time when proboscis was longer than nectar tube

In contrast to the results when the degree of (relative) mismatch was negative, among Hymenoptera and Lepidoptera, handling time decreased when proboscides were increasingly longer than the nectar tube (Fig. 2a and b; Table 2). This indicates that when a proboscis is longer than the nectar tube, it is not of hindrance to the pollinator. When insects foraged on flowers that were shorter than their proboscis (positive mismatch), handling time increased with increasing sugar content (Fig. 3b). Analysing the data of only those insect species that visited at least three different plant species revealed that for positive mismatches, the degree of (relative) mismatch did not affect handling time when accounted for sugar content (Table S4). When accounting for the degree of relative mismatch, Lepidoptera and Diptera had significantly longer handling times than Hymenoptera, as indicated by a greater intercept in the GAMMs (Table 2).

Sugar extraction rate

Insects experienced the highest sugar extraction rate when their proboscis was slightly longer than the nectar tube, although this relationship was only significant among Hymenoptera (Fig. 2c and d). These were also the flowers that Hymenoptera and Diptera seemed to prefer, as their interaction probability was the highest on these flowers (Fig. 1a). Among Hymenoptera sugar extraction rate rapidly decreased when their proboscides were increasingly shorter than the nectar tubes. Sugar extraction rate decreased more gradually when proboscides were increasing longer than nectar tubes (Fig. 2c and d).

Figure 4 shows that most insect species experienced the highest handling time and sugar extraction rate when their proboscis length matched the nectar tube depth. Mainly the intercept in the regression models of the different insect species, and thus their average handling time and sugar extraction rate, rather than the slopes, differed.

Figure 4.

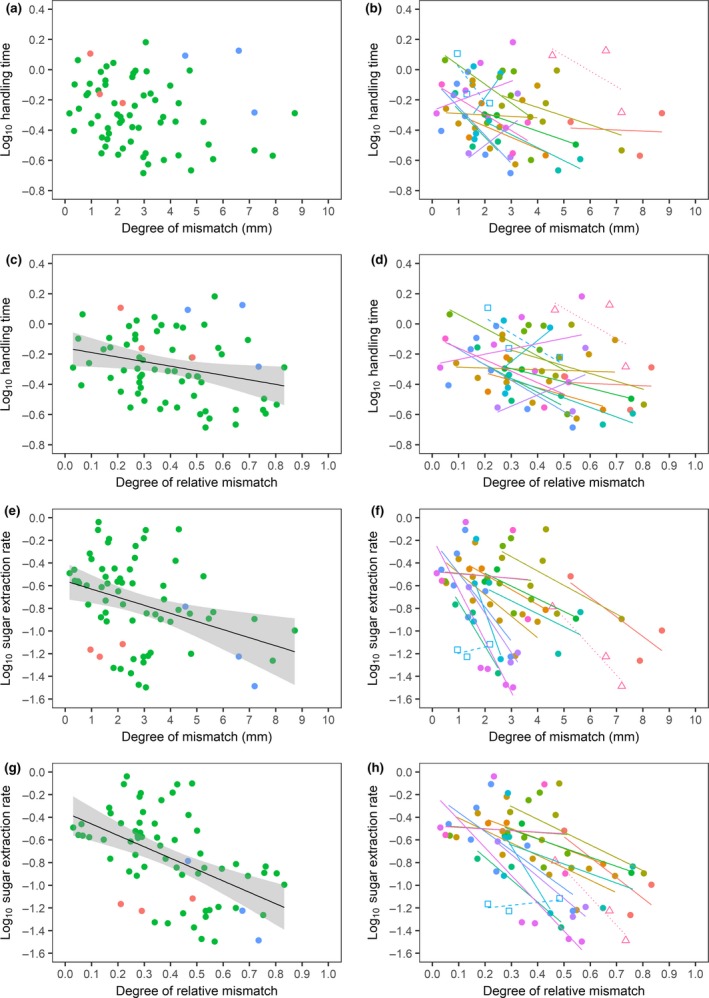
Figure 4

Open in a new tab

Handling time as a function of (a) degree of mismatch (R 2 adj = 0.02, P = 0.109, N = 67), (b) species‐specific degree of mismatch (R 2 adj = 0.19, P = 0.030, N = 67), (c) degree of relative mismatch (R 2 adj = 0.06, P = 0.028, N = 67), (d) species‐specific degree of relative mismatch (R 2 adj = 0.18, P = 0.037, N = 67), and sugar extraction rate as a function of (e) degree of mismatch (R 2 adj = 0.11, P = 0.004, N = 67), (f) species‐specific degree of mismatch (R 2 adj = 0.44, P < 0.001, N = 67), (g) degree of relative mismatch (R 2 adj = 0.25, P < 0.001, N = 67), and (h) species‐specific degree of relative mismatch (R 2 adj = 0.47, P < 0.001, N = 67). Figures only show insect species that visit at least three plant species and only interactions of which the nectar tube depth < pollinator proboscis length (positive mismatch). In Figs a, c, e and g, colours represent different insect orders (blue: Lepidoptera, green: Hymenoptera, red: Diptera). In Figs b, d, f and h, colours represent different insect species and shapes represent different insect orders (open triangles: Lepidoptera, closed circles: Hymenoptera, and open squares: Diptera).

Discussion

Our results show that the probability that plant‐ and pollinator species interact can be predicted by the degree of size matching between floral nectar tube depth and pollinator proboscis length. Among Hymenoptera and Diptera, the highest interaction probability occurred when their proboscis was slightly longer than the nectar tube. On these flowers, insects experienced the highest sugar extraction rate, and thus foraged most efficiently. This suggests that foraging efficiency is an important driver of pairwise plant–pollinator interactions. For Lepidoptera we did not find such a relationship. This finding supports the idea that, in contrast to Hymenoptera, Lepidoptera are mainly opportunistic nectar feeders, using nectar resources as they become available (Shreeve 1992). Other floral traits, such as display or blossom size might also be more important for butterfly flower choice (Corbet 2000).

The role of handling time and nectar reward as determinants of pollinator foraging efficiency depended on the type of mismatch (positive or negative) between floral nectar tube depth and pollinator proboscis length. When proboscides were shorter than the nectar tube (negative mismatch), sugar content did not determine sugar extraction rate while handling time did. For these interactions, a decrease in sugar extraction rate was caused by the fact that it becomes more difficult to handle the flowers efficiently and not because these flowers contain less nectar. The reverse is true when proboscides were longer than the nectar tube (positive mismatch). When pollinator proboscis was longer than the nectar tube, a decrease in sugar extraction rate was not caused by increasing handling times resulting from a morphological mismatch, but from a smaller nectar content in flowers with shorter nectar tubes. Thus, pollinators experienced lower foraging efficiency when foraging on relatively shallow flowers, not because long tongues are of hindrance, as often proposed (Inouye 1980; Plowright & Plowright 1997; Stout 2000; Peat et al. 2005) and shown by Maglianesi et al. (2014) for hummingbirds. It is because those shallow flowers contain less sugar. Furthermore, Hymenoptera visited on average flowers that were more rewarding and handled these flowers faster than Lepidoptera.

Instead of exact matching, interaction probability was the highest in plant species of which flowers were slightly shorter than pollinator proboscides, an average mismatch which was also shown to occur in a Spanish pollination web (Stang et al. 2009). As our results indicate, pollinators may preferentially visit these plants because they forage most efficiently on their flowers. However, as there is intraspecific variability in nectar tube depth, as well as in pollinator proboscis length, by choosing to forage from flowers which are on average slightly shorter than their proboscis, there is a much lower probability that pollinators encounter flowers with nectar tubes that are longer than their proboscis and consequently are not able to feed on the nectar.

The type of mismatch that we found appears to be in contrast to the general trend in co‐evolutionary studies for pollinator tongues to be shorter than the nectar tube of the flowers they pollinate (Anderson et al. 2010; Paudel et al. 2016). This trend is generally explained by asymmetries in specialisation and thus dependence (Anderson et al. 2010). Selection may act more strongly on the interacting partner that is more specialised, as it has more at stake in the interaction (Dawkins & Krebs 1979; Brodie 1999). In coevolved systems, this is usually the plant as they have extremely long nectar tubes. In contrast, in our study system, pollinators were on average more specialised than plants. Thus our results still support the idea that asymmetries in specialisation might drive the degree of mismatch between interacting partners. Moreover, in more generalised pollination systems, of which the flowers are relatively shallow (such as the Asteraceae), flowers produce minute amounts of nectar that can only be found at the bottom of the nectar tube (Pleasants 1981). Therefore, the actual nectar tube depth equals the functional depth and consequently nectar is only accessible to visitors with a proboscis length equal to, or longer than, the nectar tube depth. This is in contrast to extremely long‐tubed flowers in which the nectar wells up in the flowers and becomes accessible to pollinators with shorter mouthparts (Johnson et al. 2017). Deviation from 1:1 phenotypic matching does not necessarily imply a functional mismatch. For example, Toju & Sota (2006) showed experimentally that a functionally perfect phenotypical match (i.e. fitness of the two interacting species is balanced) occurs when weevil rostrums are 1.74 times longer than fruit pericarps. For the Asteraceae, anthers and styles stick out of the flowers. Therefore, functionally perfect phenotypical matching, i.e. optimal pollination and pollen transfer, could actually occur when pollinators’ proboscis is slightly longer than the nectar tube so that the head touches the anthers.

Overall, this study demonstrates that size matching between pollinator proboscis length and floral nectar tube depth can predict plant–pollinator pairwise interactions, and that foraging efficiency is an important driver for such size matching in plant–pollinator communities. As deeper tubed flowers generally produce more nectar (e.g. Galetto & Bernardello 2004; Petanidou 2007; Johnson et al. 2017), it is likely that this is a universal mechanism shaping plant–pollinator interactions. Being able to predict plant–pollinator interactions and understand the underlying mechanisms is of great importance for understanding (the structure of) interaction networks. Generally, short‐tongued insects are not able to visit deep‐tubed flowers (Haber & Frankie 1989; Corbet 2000; Stang et al. 2007) and the absence of these ‘forbidden’ interactions are often assumed to results in a nested network structure (Stang et al. 2006; Olesen et al. 2011; Ibanez 2012). However, our results indicate that interactions between long‐tongued pollinators and short‐tubed flowers do not occur often. Consequently, in quantitative networks, species morphology may lead to a compartmentalised, modular structure, rather than nestedness. Furthermore, most long‐tongued and generalised pollinators are expected to be relatively tolerant (less at risk) to plant species loss because they are not dependent on a single species (Memmott et al. 2004). However, our results indicate that the loss of their ‘matching’ interaction partners may not only increase interspecific resource competition but also decrease their foraging efficiency, which may have negative fitness consequences (Hainsworth et al. 1991). Finally, foraging on the deepest possible flowers (given the length of the proboscis) leads to fitness benefits because these flowers produce more nectar. Therefore, higher pairwise specialisation and a co‐evolutionary arms race between plants and pollinators leading to deeper flowers and longer proboscides is only likely to occur if this is accompanied by larger nectar rewards and consequently increased foraging efficiencies. We are only starting to unravel the role of nectar reward, handling time and foraging efficiency as determinants of pollinator flower choice and thus the structure of plant–pollinator interaction networks. We hope that this paper will stimulate more research on the role of nectar production and handling time as important determinants for pairwise interactions and community wide interaction patterns, especially in more generalised pollination systems.

Authorship

SGTK and MS designed the project and collected data, SGTK conducted statistical analyses and wrote the manuscript, all authors provided feedback on analyses, interpretation of results, and contributed substantially to revisions of the manuscript.

Data accessibility statement

Data available from the Dryad Digital Repository: https://doi.org/10.5061/dryad.r2s74q4.

Supporting information

 

Click here for additional data file. (73.3KB, docx)

 

Click here for additional data file. (21KB, docx)

 

Click here for additional data file. (26.9KB, docx)

 

Click here for additional data file. (31.1KB, docx)

 

Click here for additional data file. (18.5KB, docx)

Acknowledgements

We greatly thank Nick Waser and Mary Price for giving valuable advice during fieldwork and for generously sharing their lab and lab equipment. We thank the Rocky Mountain Biological Laboratory for the permissions to work at the research station, Sabrina van der Velde for her help with data gathering and Ingo Stang and four anonymous reviewers for constructive comments and valuable suggestions on previous versions of the manuscript. This study was supported by grants of the Leiden University Fund and the Dr. Christine Buisman Fund to S.G.T.K., the Catharine van Tussenbroek Fund to S.G.T.K and M.S. and the Royal Netherlands Academy of Arts and Sciences to M.S.

References

  1. Alexandersson, R. & Johnson, S.D. (2002). Pollinator‐mediated selection on flower‐tube length in a hawkmoth‐pollinated Gladiolus (Iridaceae). Proc. R. Soc. Lond. B, 269, 631–636. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Anderson, B. & Johnson, S.D. (2008). The geographical mosaic of coevolution in a plant–pollinator mutualism. Evolution, 62, 220–225. [DOI] [PubMed] [Google Scholar]
  3. Anderson, B. , Terblanche, J.S. & Ellis, A.G. (2010). Predictable patterns of trait mismatches between interacting plants and insects. BMC Evol. Biol., 10, 204. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Anderson, B. , Pauw, A. , Cole, W.W. & Barrett, S.C.H. (2016). Pollination, mating and reproductive fitness in a plant population with bimodal floral‐tube length. J. Evol. Biol., 29, 1631–1642. [DOI] [PubMed] [Google Scholar]
  5. Bascompte, J. & Jordano, P. (2007). Plant‐animal mutualistic networks: The architecture of biodiversity. Annu. Rev. Ecol. Evol. Syst., 38, 567–593. [Google Scholar]
  6. Bascompte, J. , Jordano, P. , Melian, C.J. & Olesen, J.M. (2003). The nested assembly of plant‐animal mutualistic networks. Proc. Natl Acad. Sci. USA, 100, 9383–9387. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Bauder, J.A.S. , Morawetz, L. , Warren, A.D. & Krenn, H.W. (2015). Functional constraints on the evolution of long butterfly proboscides: lessons from Neotropical skippers (Lepidoptera: Hesperiidae). J. Evol. Biol., 28, 678–687. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Bolten, A.B. , Feinsinger, P. , Baker, H.G. & Baker, I. (1979). Calculation of sugar concentration in flower nectar. Oecologia, 41, 301–304. [DOI] [PubMed] [Google Scholar]
  9. Borrell, B.J. (2005). Long tongues and loose niches: evolution of euglossine bees and their nectar flowers. Biotropica, 37, 664–669. [Google Scholar]
  10. Brian, A.D. (1957). Differences in the flowers visited by four species of bumble‐bees and their causes. J. Anim. Ecol., 26, 71–98. [Google Scholar]
  11. Brodie, E.D. (1999). Predator‐prey arms races. Biosciences, 49, 557–568. [Google Scholar]
  12. Corbet, S.A. (2000). Butterfly nectaring flowers: butterfly morphology and flower form. Entomol. Exp. Appl., 96, 289–298. [Google Scholar]
  13. Corbet, S.A. (2003). Nectar sugar content: estimating standing crop and secretion rate in the field. Apidologie, 34, 1–10. [Google Scholar]
  14. Darwin, C. (1862). On the various contrivances by which British and foreign orchids are fertilised by insects, and on the good effects of intercrossing. Murray, London, UK. [PMC free article] [PubMed] [Google Scholar]
  15. Dawkins, R. & Krebs, J.R. (1979). Arms races between and within species. Proc. R. Soc. Lond. B, 205, 489–511. [DOI] [PubMed] [Google Scholar]
  16. Galetto, L. & Bernardello, G. (2004). Floral nectaries, nectar production dynamics and chemical composition in six Ipomoea species (Convolvulaceae) in relation to pollinators. Ann. Bot., 94, 269–280. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Gilbert, F.S. (1981). Foraging ecology of hoverflies: morphology of the mouthparts in relation to feeding on nectar and pollen in some common urban species. Ecol. Entomol., 6, 245–262. [Google Scholar]
  18. Haber, W.A. & Frankie, G.W. (1989). A tropical hawkmoth community: Costa Rican dry forest Sphingidae. Biotropica, 21, 155–172. [Google Scholar]
  19. Hainsworth, F.R. , Precup, E. & Hamill, T. (1991). Feeding, energy processing rates and egg‐production in painted lady butterflies. J. Exp. Biol., 156, 249–265. [Google Scholar]
  20. Harder, L.D. (1983). Flower handling efficiency of bumble bees: morphological aspects of probing time. Oecologia, 57, 274–280. [DOI] [PubMed] [Google Scholar]
  21. Harder, L.D. (1985). Morphology as a predictor of flower choice by bumble bees. Ecology, 66, 198–210. [Google Scholar]
  22. Haverkamp, A. , Bing, J. , Badekel, E.A. , Hansson, B.S. & Knaden, M. (2016). Innate olfactory preferences for flowers matching proboscis length ensure optimal energy gain in a hawkmoth. Nat. Commun., 7, 11644. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Hegland, S.J. & Totland, Ø. (2005). Relationships between species’ floral traits and pollinator visitation in a temperate grassland. Oecologia, 145, 586–594. [DOI] [PubMed] [Google Scholar]
  24. Herrera, C.M. (1989). Pollinator abundance, morphology, and flower visitation rate: analysis of the “quantity” component in a plant‐pollinator system. Oecologia, 80, 241–248. [DOI] [PubMed] [Google Scholar]
  25. Ibanez, S. (2012). Optimizing size thresholds in a plant–pollinator interaction web: towards a mechanistic understanding of ecological networks. Oecologia, 170, 233–242. [DOI] [PubMed] [Google Scholar]
  26. Inouye, D.W. (1976). Resource partitioning and community structure: a study of bumblebees in the Colorado Rocky Mountains. University of North Carolina Chapel Hill, Chapel Hill. [Google Scholar]
  27. Inouye, D.W. (1980). The effect of proboscis and corolla tube lengths on patterns and rates of flower visitation by bumblebees. Oecologia, 45, 197–201. [DOI] [PubMed] [Google Scholar]
  28. Johnson, S.D. , More, M. , Amorim, F.W. , Haber, W.A. , Frankie, G.W. , Stanley, D.A. et al (2017). The long and the short of it: a global analysis of hawkmoth pollination niches and interaction networks. Funct. Ecol., 31, 101–115. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Kaiser‐Bunbury, C.N. , Vazquez, D.P. , Stang, M. & Ghazoul, J. (2014). Determinants of the microstructure of plant‐pollinator networks. Ecology, 95, 3314–3324. [Google Scholar]
  30. Karolyi, F. , Morawetz, L. , Colville, J.F. , Handschuh, S. , Metscher, B.D. & Krenn, H.W. (2013). Time management and nectar flow: flower handling and suction feeding in longproboscid flies (Nemestrinidae: Prosoeca). Naturwissenschaften, 100, 1083–1093. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Kunte, K. (2007). Allometry and functional constraints on proboscis lengths in butterflies. Funct. Ecol., 21, 982–987. [Google Scholar]
  32. Lane, M.A. (1996). Pollination biology of Compositae In: Compositae: Biology and Utilization, Proceedings of the International Compositae Conference, Kew, 1994 (eds Caligari P.D.S. & Hind D.J.N.). Royal Botanic Gardens, Kew, pp. 61–80. [Google Scholar]
  33. Macior, L.W. (1974). Pollination ecology of the front range of the Colorado Rocky Mountains. Melanderia 15. Washington State Entomological Society, Washington, Washington.
  34. Maglianesi, M.A. , Blüthgen, N. , Bohning‐Gaese, K. & Schleuning, M. (2014). Morphological traits determine specialization and resource use in plant‐hummingbird networks in the neotropics. Ecology, 95, 3325–3334. [Google Scholar]
  35. Mani, M.S. & Saravanan, J.M. (1999). Pollination ecology and evolution in Compositae (Asteraceae). Science Publishers Inc, Enfield. [Google Scholar]
  36. Memmott, J. , Waser, N.M. & Price, M.V. (2004). Tolerance of pollination networks to species extinctions. Proc. R. Soc. Lond. B, 271, 2605–2611. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Muchhala, N. & Thomson, J.D. (2009). Going to great lengths: selection for long corolla tubes in an extremely specialized bat–flower mutualism. Proc. R. Soc. B, 276, 2147–2152. 10.1098/rspb.2009.0102. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Nilsson, L.A. (1988). The evolution of flowers with deep corolla tubes. Nature, 334, 147–149. [Google Scholar]
  39. Olesen, J.M. , Bascompte, J. , Dupont, Y.L. , Elberling, H. , Rasmussen, C. & Jordano, P. (2011). Missing and forbidden links in mutualistic networks. Proc. R. Soc. B, 278, 725–732. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Paudel, B.R. , Shrestha, M. , Burd, M. , Adhikari, S. , Sun, Y. & Li, Q. (2016). Coevolutionary elaboration of pollination‐related traits in analpine ginger (Roscoea purpurea) and a tabanid fly in theNepalese Himalayas. New Phytol., 211, 1402–1411. [DOI] [PubMed] [Google Scholar]
  41. Peat, J. , Tucker, J. & Goulson, D. (2005). Does intraspecific size variation in bumblebees allow colonies to efficiently exploit different flowers? Ecol. Entomol., 30, 176–181. [Google Scholar]
  42. Petanidou, T. (2007). Ecological and evolutionary aspects of floral nectars in Meditterranean habitats In Nectaries and nectar. (eds Nicolson S.W., Nepi M., Pacini E.). Springer, Dordrecht, pp. 343–376. [Google Scholar]
  43. Pleasants, J.M. (1981). Bumblebee response to variation in nectar availability. Ecology, 62, 1648–1661. [Google Scholar]
  44. Plowright, C.M.S. & Plowright, R.C. (1997). The advantage of short tongues in bumble bees (Bombus) ‐ analyses of species distributions according to flower corolla depth, and of working speeds on white clover. Can. Entomol., 129, 51–59. [Google Scholar]
  45. R Development Core Team (2014). R: a language and environment for statistical computing. Available at: http://www.R-project.org/. Last accessed 8 November 2018.
  46. Shmida, A. & Dukas, R. (1990). Progressive reduction in the mean body sizes of solitary bees active during the flowering season and its correlation with the sizes of bee flowers of the Mint family (Lamiaceae). Israel J. Bot., 39, 133–141. [Google Scholar]
  47. Shreeve, T.G. (1992). Adult behaviour In The Ecology of Butterflies in Britain. (ed Dennis R.L.H.). Oxford University Press, Oxford, UK, pp. 22–45. [Google Scholar]
  48. Stang, M. , Klinkhamer, P.G.L. & van der Meijden, E. (2006). Size constraints and flower abundance determine the number of interactions in a plant‐flower visitor web. Oikos, 112, 111–121. [Google Scholar]
  49. Stang, M. , Klinkhamer, P.G.L. & van der Meijden, E. (2007). Asymmetric specialization and extinction risk in plant‐flower visitor webs: a matter of morphology or abundance? Oecologia, 151, 442–453. [DOI] [PubMed] [Google Scholar]
  50. Stang, M. , Klinkhamer, P.G.L. , Waser, N.M. , Stang, I. & van der Meijden, E. (2009). Size‐specific interaction patterns and size matching in a plant‐pollinator interaction web. Ann. Bot., 103, 1459–1469. [DOI] [PMC free article] [PubMed] [Google Scholar]
  51. Stout, J.C. (2000). Does size matter? Bumblebee behaviour and the pollination of Cytisus scoparius L. (Fabaceae). Apidologie, 31, 129–139. [Google Scholar]
  52. Toju, H. & Sota, T. (2006). Imbalance of predator and prey armament: geographic clines in phenotypic interface and natural selection. Am. Nat., 167, 105–117. [DOI] [PubMed] [Google Scholar]
  53. Vazquez, D.P. & Aizen, M.A. (2004). Asymmetric specialization: a pervasive feature of plant‐pollinator interactions. Ecology, 85, 1251–1257. [Google Scholar]
  54. Vazquez, D.P. , Blüthgen, N. , Cagnolo, L. & Chacoff, N.P. (2009a). Uniting pattern and process in plant‐animal mutualistic networks: a review. Ann. Bot., 103, 1445–1457. [DOI] [PMC free article] [PubMed] [Google Scholar]
  55. Vazquez, D.P. , Chacoff, N.P. & Cagnolo, L. (2009b). Evaluating multiple determinants of the structure of plant‐animal mutualistic networks. Ecology, 90, 2039–2046. [DOI] [PubMed] [Google Scholar]
  56. Verdu, M. & Valiente‐Banuet, A. (2011). The relative contribution of abundance and phylogeny to the structure of plant facilitation networks. Oikos, 120, 1351–1356. [Google Scholar]
  57. Wood, S. (2018). Package ‘mgcv’. R package version 1.8‐25. Available at: https://cran.r-project.org/web/packages/mgcv/mgcv.pdf. Last accessed 8 November 2018.

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

 

Click here for additional data file. (73.3KB, docx)

 

Click here for additional data file. (21KB, docx)

 

Click here for additional data file. (26.9KB, docx)

 

Click here for additional data file. (31.1KB, docx)

 

Click here for additional data file. (18.5KB, docx)

Data Availability Statement

Data available from the Dryad Digital Repository: https://doi.org/10.5061/dryad.r2s74q4.

Articles from Ecology Letters are provided here courtesy of Wiley

RESOURCES