The syringe potentiometer: a low-cost device for pneumotachograph calibration

Abstract

The purpose of this report was to 1) detail the construction of a low-cost device that provides a “reference” flow waveform for pneumotachograph (PNT) calibration, i.e., the “syringe potentiometer” (SP), and to compare the 2) accuracy and 3) practical performance of “calibration curves” obtained with the SP device to other more established methods of PNT calibration, i.e., the weighted averaging (WA) and polynomial least-squares (PolyLS) methods. Volume and flow waveforms obtained via the SP device were validated against a motion capture system and were deemed accurate surrogates of actual syringe volume and flows. The SP device was used to construct a calibration curve of a PNT by dividing the flow waveform of the SP by the analog output of the PNT amplifier. A total of 187 inspiratory and 187 expiratory strokes were collected. When the entire data set of expiratory strokes was used, the SP, WA, and PolyLS methods together demonstrated acceptable volume and flow errors as per American Thoracic Society/European Respiratory Society recommendations (less than ±3.5% and less than ±5.0% errors, respectively). The “practical” performance of each method was assessed with a nested subsampling procedure, whereby volume and flow errors were evaluated as the number of strokes was increased (in blocks of 5 strokes). To this end, the SP method demonstrated practical performance superior to that of the WA and PolyLS approaches, whereby acceptable volume and flow errors were achieved after only 5 calibration strokes; the WA and PolyLS methods required 15 and 20 strokes, respectively, to achieve the same level of volume and flow accuracy.

NEW & NOTEWORTHY This report describes the construction and validation of a low-cost device for the purposes of pneumotachograph (PNT) calibration: the “syringe potentiometer” (SP). Calibration of a PNT with the SP device yielded acceptable volume and flow errors (<3.5% and 5%, respectively) across a wide range of flows (<0.5 to 15 L/s). The SP device offered superior “practical performance” over other established PNT calibration methods, whereby acceptable volume and flow errors were achieved after only five calibration strokes.

INTRODUCTION

The pneumotachograph (PNT) is one of the most popular devices used to measure respiratory airflows in the laboratory and clinical settings. Airflow (V̇) is obtained from the PNT by measuring the differential pressure (∆P) that develops across the resistive element of the device. This pressure drop is then converted to flow with a calibration factor (k) as follows:

$$\dot{V}=\Delta P\times k$$ (1)

where k is a value of conductance (e.g., L·s⁻¹·cmH₂O). Of note, Eq. 1 implies that a single calibration factor k is sufficient to describe the entire ∆P-V̇ relationship of the device. In practice, however, the value of k for any given PNT is often nonconstant and is instead a unique function of the differential pressure itself, whereby

$$\dot{V}=\Delta P\times k\left(\dot{V}\right)$$ (2)

Equation 2 indicates that for a PNT to provide a valid measure of airflow it is imperative that ∆P is measured with high accuracy and the function k(∆P) is known with high confidence. The former point is of little concern, seeing that even low-cost pressure sensors are capable of measuring ∆P to within ±0.0077 cmH₂O.¹ Rather, it is the latter point that poses the greatest challenge for the investigator.

Assuming the device possesses an adequate frequency response, the “calibration curve” [i.e., k(∆P)] of a PNT may be determined empirically by generating a range of constant, steady flow rates and recording the ∆P developed across the device. The calibration factor k is thus determined as V̇ divided by ∆P at each constant flow. However, to generate a “steady” flow by hand is an exceedingly difficult task, and highly accurate “reference” flow generators are not widely available. To address this issue, previous investigators have developed indirect methods of obtaining the calibration curve of a PNT device with only a 3-liter calibration syringe (14–16). These methods include the weighted averaging (WA) technique first proposed by Yeh et al. (16) and the polynomial least-squares (PolyLS) approach most recently described by Tang et al. (15). Both methods require that multiple syringe strokes are obtained at varying durations of plunger injections/withdrawals. Certainly, the findings of Tang et al. (Ref. 15, see Fig. 3) suggest that an adequate PNT calibration (less than ±3.5% volume error; Ref, 11) may be obtained within 10 syringe strokes with either the WA or PolyLS method. It is worth noting that these calibration techniques use the same objective goal, i.e., to minimize the difference between the known syringe volume (e.g., 3 liters) and the volume obtained from integration of the calibrated PNT waveform during each stroke. It may be argued, however, that although these methods produce a calibration curve that minimizes the average error in syringe volume (volume accuracy), they do not guarantee, ipso facto, that these same curves will yield the least error in V̇ measured instantaneously (flow accuracy). We reason that any given calibration method must demonstrate adequate volume and flow performance across the range of flow rates studied.

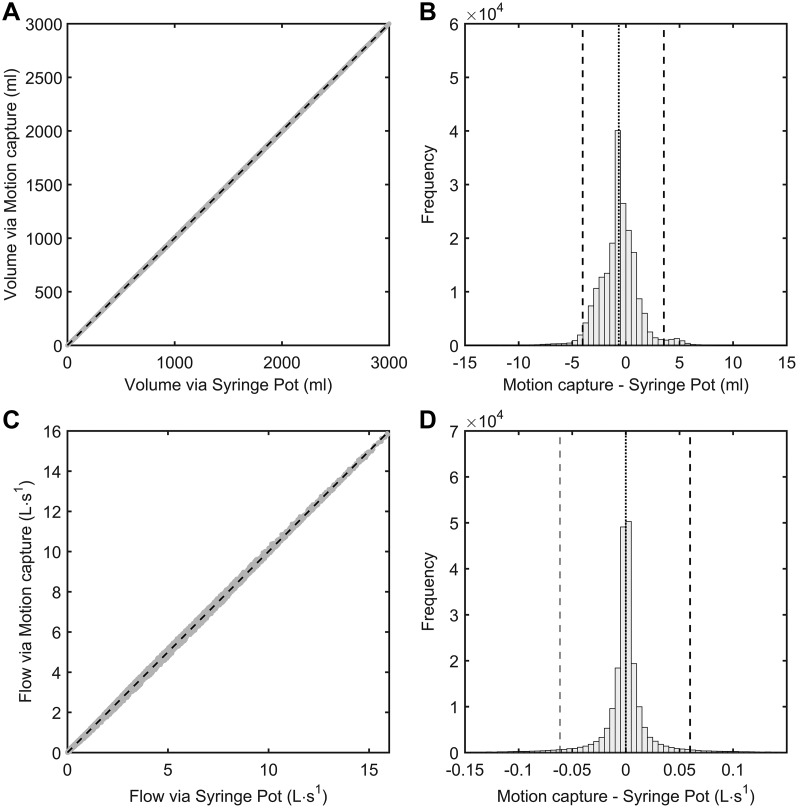
Fig. 3.

Measurement agreement of instantaneous syringe volume (A and B) and flow rate (C and D) obtained via the syringe potentiometer device and motion capture system. The gray points in A and C represent observed values of syringe volumes and flows measured via the syringe potentiometer device and motion capture system. The dashed lines in A and C denote lines of identity (i.e., perfect agreement) for each relationship. The vertical dashed lines in B and D illustrate the 95% confidence percentiles for the distribution of errors incurred by measuring syringe volume and flow via the syringe potentiometer device (whereby values obtained via motion capture are taken as the reference).

To date, no study has examined the flow accuracy of the WA and PolyLS methods of PNT calibration. To address this issue, however, one must obtain some measure of a reference flow that, as mentioned above, poses a great difficulty for the investigator. Therefore, we outline in this report the construction of a low-cost device that can be mounted on any existing calibration syringe. This device uses a draw-wire (“string”) potentiometer to output a voltage proportional to the displacement of the syringe plunger that, in the absence of gas compression/dilation, suffices for instantaneous syringe volume. The first derivative of this signal provides the reference flow waveform. The instantaneous syringe volume and reference flow waveforms from this device were externally validated against those values computed via motion capture of the syringe plunger. We then developed a method of constructing a PNT calibration curve with the syringe potentiometer device (i.e., the SP method). The volume and flow accuracy of the SP method were compared with those obtained via the WA and PolyLS methods.

METHODS

Syringe Potentiometer

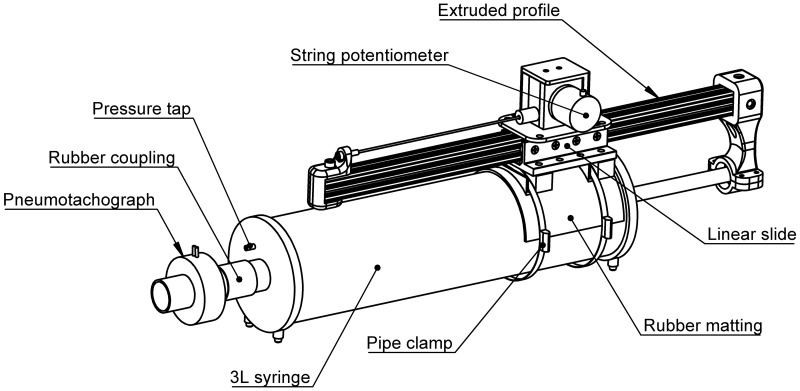
The device under test in this report is a custom-built linear transducer that is affixed to the barrel of a commercially available 3-liter calibration syringe (Hans Rudolph, Shawnee, KS). The linear transducer consists of a draw-wire (string) potentiometer (CWP-S500V1; CALT, Shanghai, China), an extruded aluminum profile (10 Series, ~600 mm in length; 80/20, Columbia City, IN), a linear bearing slide (part no. 6726, 80/20), and a series of three-dimensional (3D)-printed components.² The draw-wire potentiometer and linear bearing slide are affixed to the syringe barrel by a purpose-built 3D-printed platform and two metal pipe clamps (max. diameter 200 mm). A section of rubber matting (2.5- to 4.0-mm thickness) is interposed between the syringe barrel and the 3D-printed platform to prevent slippage at high withdrawal/injection speeds. The syringe plunger is attached to the distal end of the extruded profile by another 3D-printed component; this component also serves as a convenient handle during syringe withdrawals and injections. Finally, the “draw wire” itself is attached to the proximal end of the extruded profile via a separate 3D-printed component. The entire device, inclusive of both the calibration syringe and the linear transducer, is referred to hereafter as the syringe potentiometer. A schematic illustration of the syringe potentiometer is given in Fig. 1.

Fig. 1.

Illustration of the syringe potentiometer assembly.

One can imagine that as the syringe plunger is withdrawn the extruded profile moves in the axial direction via the linear bearing slide, parallel to the syringe barrel. The distance between the proximal end of the extruded profile and the body of the draw-wire potentiometer is thereby decreased. The high retraction forces of the power spring inside the draw-wire potentiometer ensure that the draw wire itself remains under constant tension without slacking. The progressive shortening of the draw wire’s length causes an internal rotation of the potentiometer, changing the internal electrical resistance of the device. The output of the potentiometer is connected to a simple voltage divider circuit. Thus, as the syringe plunger is withdrawn, and the resistance of the potentiometer is reduced, the voltage output of the divider circuit increases. The opposite is seen during injection of the syringe plunger, whereby extension of the draw wire’s length causes an increase in potentiometer resistance, and thus a reduction in voltage output.

In this manner, the analog voltage observed from the divider circuit is, at least in theory, proportional to the displacement of the syringe plunger. The instantaneous volume inside the calibration syringe (V_syr) may be known by the product of plunger displacement (L) and the area of the syringe piston head (A_piston), such that

$$V_{syr}=L\times A_{piston}$$ (3)

where the voltage output from the syringe potentiometer assembly is taken as a surrogate for L. On the other hand, it is not necessary to know A_piston to compute syringe volume. It is a safe assumption that A_piston remains unchanged throughout withdrawals and injections of the plunger. Accordingly, so long as the syringe has been properly calibrated and its value known, a “volume” signal is obtained via a two-point calibration procedure using the extremes of syringe volume (e.g., 0 and 3 liters) and the corresponding analog voltages obtained from the device.

The voltage output from the syringe potentiometer will differ from the actual syringe volume under circumstances of compressible gas flow. The maximum internal volume within the syringe (3 liters) is relatively small and is unlikely to undergo significant gas compression even at high injection speeds (>15 L/s), provided that upstream resistance is negligible. The same point is made for gas expansion during plunger withdrawals. However, the upstream resistance offered by external equipment is liable to change between experiments. To correct for the effects of gas compression/dilation on the instantaneous syringe volume, V_syr, it is necessary to measure pressure within the barrel of the syringe. In turn, a small-bore (~2 mm) pressure tap was drilled into the faceplate of the calibration syringe, whereby the instantaneous pressure inside the syringe barrel (P_syr) could be sampled by a Luer-lock connector. The volume of gas lost to compression or expansion (V_c) may then be calculated (4, 13) as follows:

$$V_c=V_{syr}\times \left[{\left(\frac{P_{syr}+P_b}{P_b}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\gamma $}\right.}-1.0\right]$$ (4)

where P_b is the barometric pressure and γ is the ratio of the molar heat capacity at a constant pressure to the molar heat capacity at a constant volume (i.e., 1.4 for air). Thus the instantaneous syringe volume corrected for gas compression/dilation ($V_{syr}^{\ast }$) is given by

$$V_{syr}^{\ast }=V_{syr}-V_c$$ (5)

With this corrected volume, one may then obtain syringe flow (V̇_syr) by taking the first derivative of $V_{syr}^{\ast }$. The numerical procedure for calculating V̇_syr is described in more detail in Data Analyses.

Motion Capture System

A commercially available eight-camera motion capture system (Optitrack Flex 13; NaturalPoint, Corvallis, OR) was used to record the 3D coordinates (x, y, z) of four passive-reflective markers (hemispheres, ~10-mm diameter). The camera system was calibrated with a standard CWM-250 calibration wand from the manufacturer (size 250 mm). The average residual error achieved after system calibration was 0.2 mm. The 3D trajectories of the four reflective markers were used to compute the linear displacement of the syringe plunger (d) during each calibration stroke. The method of computing d from motion capture data is outlined in Appendix A.

Pneumotachograph

A bidirectional, pressure differential PNT (0–800 L/min range, model 3813; Hans Rudolph) was used to measure airflow at the open port of the syringe potentiometer assembly. The PNT was connected to a specialized amplifier (PA100; Hans Rudolph) and was heated to 37°C for the duration of the study with a heater control unit (model 3850; Hans Rudolph). To account for a “warm-up” drift in zero offset of the PNT, the amplifier and heater control unit were turned on and left running for 60 min before the study began. The pressure inside the PNT assembly (P_PNT) was measured by a lateral tap (2 mm) on the respiratory port affixed to the syringe potentiometer. This pressure, P_PNT, was used in Eqs. 4 and 5 to correct for any gas lost to compression/dilation inside the PNT assembly.

Data Acquisition

The pressures inside the syringe and PNT (P_syr and P_PNT, respectively) were measured via two separate differential pressure transducers (±352 cmH₂O, HSCSNBN005PDAA5; Honeywell International, NJ). The pressure transducers were calibrated with a water manometer before the study. The analog voltage outputs from the pressure transducers, the PNT amplifier, and the syringe potentiometer were sampled continuously at 1,000 Hz (PowerLab 16/35, ADInstruments, Castle Hill, Australia). The 3D trajectories of the four passive-reflective markers (m₁–m₄) were recorded at 120 Hz with commercially available software (Motive:Tracker, version 2.0; NaturalPoint). The “sync out” analog signal from the motion capture system was used to synchronize the recording of data between the camera and data acquisition systems.

Experimental Overview

The principal goals of this report were threefold: 1) to detail the construction and validation of a low-cost device that provides a reference flow waveform for PNT calibration, i.e., the syringe potentiometer; 2) to compare the accuracy of calibration curves obtained via the syringe potentiometer device with two established methods of PNT calibration, the WA (14, 16) and PolyLS (15) methods; and 3) to evaluate the practical performance of each method as progressively more calibration strokes are used by each algorithm. For clarity, the remainder of this report is structured in sections pertaining to each aim where possible. These sections are referred to as experiments 1, 2, and 3.

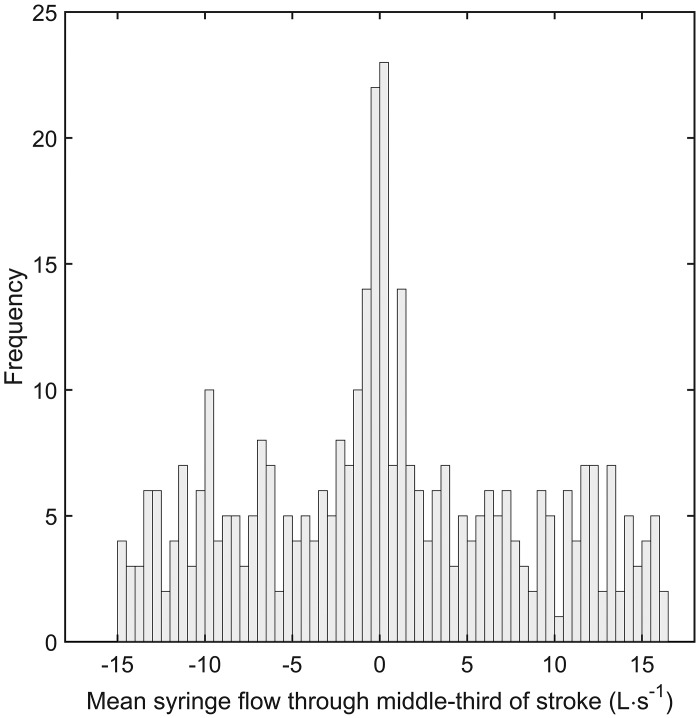
To demonstrate the accuracy of the syringe potentiometer device to measure instantaneous syringe volume (experiment 1), it was first necessary to examine whether the output from the device was indeed a feasible surrogate for plunger displacement. To this end, a validation study was performed in which plunger displacement, as sensed by the syringe potentiometer, was compared to the displacement d measured via the motion capture system (i.e., reference measurement). We performed 187 complete withdrawals and injections of a standard 3-liter calibration syringe (model 5530; Hans Rudolph, Shawnee, KS). The withdrawals and injections of the syringe plunger are defined here as inspiratory and expiratory strokes, respectively. The duration of each stroke was varied between <1 s and 30 s. A frequency distribution of syringe flows through the middle third of each stroke is illustrated in Fig. 2. A commercially available PNT (0–800 L/min range, model 3813; Hans Rudolph) was affixed in series to the open port of the syringe potentiometer assembly throughout experiment 1. The data obtained from the PNT and syringe potentiometer assembly were used to address the aims of experiments 2 and 3.

Fig. 2.

Frequency distribution of syringe flows through the middle third of inspiratory and expiratory calibration strokes. A total of 187 inspiratory and 187 expiratory strokes were obtained.

Data Analyses

Experiment 1: Validation of syringe potentiometer device.

The analog pressure waveforms (P_syr and P_PNT) and voltage output from the syringe potentiometer were downsampled to 120 Hz and time aligned to the motion capture data obtained with the “sync out” signal generated by the motion capture system. The time-aligned pressure, syringe potentiometer, and motion capture data were combined into a single data set. The displacement of the syringe plunger derived from motion capture data (i.e., d) was computed as described in Motion Capture System. The waveforms of the combined data set were low-pass filtered at 25 Hz with a fifth-order Butterworth design.

The voltage output from the syringe potentiometer was calibrated by a two-point calibration procedure. Point 1 was the corresponding signal value when the syringe plunger was in the “fully injected” (end-expiratory) position, and point 2 was taken as the corresponding signal value when the syringe plunger was in the “fully withdrawn” (end-inspiratory) position. The reference values for point 1 and point 2 were set arbitrarily at 0 and 3 liters, respectively. This calibrated waveform therefore represented the instantaneous volume within the barrel of the syringe (i.e., V_syr). This waveform was corrected for gas compression/dilation (i.e., $V_{syr}^{\ast }$) with Eqs. 4 and 5. We then computed a central derivative approximation of the corrected syringe volume waveform to obtain a syringe flow waveform (V̇_syr), using the first-order adaptive windowing (FOAW) technique (5, 6). The calculations used in the FOAW method are outlined in further detail in Appendix B.

The plunger displacement signal obtained from the motion capture system (i.e., d) was also calibrated to the 0–3 liters interval, and is noted hereafter as V_mocap. The resulting V_mocap waveform was corrected for gas compression and/or dilation (i.e., $V_{mocap}^{\ast }$) with Eqs. 4 and 5. The first derivative of $V_{mocap}^{\ast }$ was also obtained with the FOAW algorithm (as above), yielding V̇_mocap.

Experiment 2: Comparison of accuracy between PNT calibration methods.

The raw output voltages from the PNT amplifier were adjusted for gas compression/dilation with Eqs. 4 and 5. The syringe flow waveform (V̇_syr) was used as the reference flow waveform to calibrate the voltage output from the PNT amplifier. With these data, three different methods of PNT calibration were examined in this report. The first method obtained the calibration curve of the PNT by dividing the reference flow signal of the potentiometer (V̇_syr) by the voltage output of the PNT amplifier. We refer to this approach as the syringe potentiometer (SP) method. The second and third calibration techniques were the WA and PolyLS methods. For the sake of brevity, only expiratory calibration curves were used in this report. It is worth noting that both the WA and PolyLS methods require some degree of hyperparameter tuning. For example, one must first decide on the order of the polynomial function before the PolyLS method can be implemented (explained below). To this end, we used repeated K-fold cross-validation (CV) to tune the hyperparameters of the WA and PolyLS methods. Briefly, the 187 expiratory strokes were randomly partitioned into K smaller groups of strokes. The first K − 1 strokes (i.e., training set) are used to build the calibration curve with the desired method. The trained calibration curve is applied to the remaining Kth group (i.e., testing set) of strokes, from which the performance of the calibration method is assessed. This process continues for K times until all combinations of “training” and “testing” sets have been analyzed. Calibration strokes are then randomly repartitioned into a new set of K folds, and the entire process is repeated n times. In this study, we used 5-fold CV partitions repeated 20 times. Accordingly, a total of 100 unique combinations of training and testing data sets were generated, totaling 14,960 training and 3,740 testing strokes. The syringe volume errors from all testing strokes are used to compute the CV mean-square error (MSE_cv). The MSE_cv is a measure of “out-of-sample” error performance, i.e., the expected syringe volume error when the trained calibration curve is applied to new, unobserved calibration strokes. Standard errors of the MSE_CV for each combination of hyperparameters were computed with the standard formula, i.e., SE = SD/√K, where K is the total number of folds used in the repeated K-fold CV procedure. Hyperparameters for the WA and PolyLS methods were chosen as those values that produced a MSE_cv within 1 standard error of the global minimum MSE_cv (1). We selected hyperparameters with this “1 SE rule” because it selects the simplest (most parsimonious) model whose error is comparable to the best model (i.e., global minimum MSE_cv). Once the optimal hyperparameters are chosen, the entire data set is used to build the calibration curve.

syringe potentiometer.

The syringe flow waveform (V̇_syr) and voltage output from the PNT amplifier were bin-averaged with 200-mL intervals across the middle third of each expiratory calibration stroke (i.e., 1 to 2 liters). The middle third was chosen because it avoided nonsteady plunger movements at the beginning and end of each calibration stroke. The bin-averaged values for V̇_syr were divided by the corresponding voltage output from the PNT amplifier, yielding a discrete calibration constant (k) for each bin interval. Accordingly, following this procedure, the 187 expiratory calibration strokes produced 935 discrete values of k. We then used Friedman’s SuperSmoother function to provide a continuous estimate of k as a function of PNT amplifier output (in volts; Ref. 3). The SuperSmoother is a type of scatterplot smoother that uses adaptive bandwidths to provide a nonparametric estimate of the underlying relationship between x and y data. This type of nonparametric smoother is especially useful for data series with nonconstant error variance. The resulting continuous calibration curve was then evaluated for k at any given PNT amplifier output via linear interpolation.

weighted averaging.

The theory and details of the WA method are described elsewhere (12, 14–16). This method uses multiple calibration strokes to provide a “lookup table” of discrete k values corresponding to M sections of the full-span voltage output of the PNT amplifier. There are no heuristic methods of determining the correct value of M to use in the WA method. Whereas some investigators have set M equal to the bit resolution of their data acquisition system (e.g., 2¹² = 2,048) (15), others have used arbitrarily low values (18 sections) (12) or a range of intermediate values (e.g., 20, 100, and 1,000 sections) (14). Moreover, it is emphasized that the lookup table is typically refined by repeating the WA procedure i times until stable estimates of k are obtained within each of the M sections (14–16). As above, there are no well-defined rules for choosing i when using the WA method to construct a PNT calibration curve. To address this uncertainty, we used repeated K-fold CV to tune the hyperparameters M and i of the WA method. The optimal values of M and i were determined as those values that produced a MSE_cv within 1 standard error of the global minimum MSE_cv for syringe volume errors of all testing strokes.

polynomial least squares.

The PolyLS method uses multiple syringe strokes to yield a PNT calibration curve determined by an nth-order polynomial function. The numerical procedures of the PolyLS method are described in detail in Appendix A of Tang et al. (15). The polynomial function used to approximate the underlying calibration curve of the PNT device may be of any arbitrary order, although second- and third-order polynomial functions usually suffice (4). To date, there are no satisfactory criteria used to guide the selection of polynomial order used in the PolyLS method. Hence, as described for the WA method above, repeated K-fold CV was used to determine the polynomial order that produced a MSE_cv within 1 standard error of the global minimum MSE_cv for syringe volume errors of all testing strokes.

volume and flow accuracy.

Volume errors were computed as the difference between the known syringe volume (i.e., 3 liters) and the reconstructed syringe volumes obtained after each calibration method was applied to PNT data. The V̇_syr waveform derived from the syringe potentiometer was taken here as the reference signal. Flow errors were computed as the difference between reference values of V̇_syr and those obtained after each calibration method was applied to PNT data. These flow errors were stratified into five separate groups representing the following ranges of reference flows: very low (<0.5 L/s), low (0.5 to <3.0 L/s), medium (3.0 to <6.0 L/s), high (6.0 to <9.0 L/s), and very high (≥9.0 L/s). The accuracy and precision of calibrated flow data were computed as the average and 95th percentile confidence interval (CI_95%) of flow errors, respectively, within each flow range.

The volume and flow accuracy of each method were evaluated with two data sets: 1) the entire data set of syringe strokes after the selection of optimal hyperparameters and 2) the syringe strokes belonging to the testing data set generated by the repeated K-fold CV procedure. The entire data set was used to demonstrate the accuracy of each calibration method on all available data, whereas the testing data set was used to provide a measure of how well each calibration method may generalize to new, unobserved data.

Experiment 3: Practical performance of calibration methods.

The practical performance of each method was assessed by determining volume and flow errors as progressively more calibration strokes are used to construct the relevant calibration curve. Calibration strokes were added in blocks containing five syringe strokes, one stroke each falling within the very low, low, medium, high, and very high flow ranges described above. A maximum of 12 blocks (60 calibration strokes) were examined. A nested subsampling procedure was used to create 200 surrogate (bootstrapped) data sets. This subsampling process is outlined below:

• 1. Randomly split the entire data set of calibration strokes into 60 training and 127 testing strokes. Ensure that 12 strokes from each of the five flow ranges are represented in the training data set.
• 2. Randomly choose five strokes from the training set. Ensure that each of the five flow ranges is represented in this set of new training strokes.
• 3. If necessary, use repeated K-fold CV (5 folds, 20 repetitions) to find optimal hyperparameters of the given calibration method, using the available number of training strokes.
• 4. Construct the calibration curve with optimal hyperparameters (step 3), using the available number of training strokes.
• 5. Evaluate the volume and flow accuracy of the given calibration method, using the 127 testing strokes set aside during step 1.
• 6. Repeat steps 2–5 until the available number of training strokes is 60 (i.e., 12 blocks of 5 strokes).
• 7. Repeat steps 1–6 until 200 surrogate data sets are generated and analyzed.

The above procedure generated a total of 25,400 testing strokes for each of the 12 blocks.

Statistical Analyses

Experiment 1.

The measurement agreement between the volume waveforms obtained from the syringe potentiometer device and motion capture system ($V_{syr}^{\ast }$ and $V_{mocap}^{\ast }$) were assessed by linear regression and by evaluating the concordance correlation coefficient (CCC) and the root mean square of errors (RMSE). Similar statistical analyses were used to examine the measurement agreement between V̇_syr and V̇_mocap. The CCC indicates the degree to which the relationship between two variables approximates the line of identity (i.e., perfect agreement; Ref. 8). The CCC was interpreted with the following criterion ranges: almost perfect agreement = CCC > 0.99, substantial agreement = 0.95 < CCC < 0.99, moderate agreement = 0.90 < CCC < 0.95, and poor agreement = CCC < 0.90 (9).

Experiment 2.

The volume errors of each calibration method (SP, WA, and PolyLS) were compared by one-way repeated-measures analysis of variance (ANOVA). The flow errors of each method were compared across the five flow ranges (very low, low, medium, high, and very high) with a two-way (3 × 5) repeated-measures ANOVA design. The above statistical tests were performed separately on the entire (n = 187) and testing (n = 3,740) data sets of syringe strokes. Post hoc comparisons were examined with Tukey’s adjustment. Statistical analyses were considered significant if P < 0.05.

Experiment 3.

No formal statistical analyses were used to compare the practical performance between calibration methods. Rather, we examined the distribution of volume and flow errors produced by each method across the 12 blocks of testing strokes generated by the nested subsampling procedure. From these distributions, CI_95% were computed. These confidence intervals were used to determine the minimum number of stroke blocks each method required to produce adequate calibration performance. Adequate calibration performance was observed when the CI_95% of testing volume and flow errors fell within the American Thoracic Society (ATS)/European Respiratory Society (ERS)-recommended error margins for volume and flow measurements (i.e., ±3.50% and ±5.00%, respectively; Ref. 11). We reasoned that a method with good practical performance would require only a small number of stroke blocks to reach this criterion, whereas a method with relatively poorer practical performance would need a larger number of stroke blocks to achieve the same level of calibration performance.

RESULTS AND DISCUSSION

Experiment 1: Validation of Syringe Potentiometer Device

The measurement agreement between the volume waveforms produced by the syringe potentiometer and motion capture system (i.e., $V_{syr}^{\ast }$ and $V_{mocap}^{\ast }$) is displayed in Fig. 3, A and B. The calibrated output from the syringe potentiometer demonstrated near-perfect absolute agreement with $V_{mocap}^{\ast }$, as evidenced by a very high adjusted coefficient of determination (R²) and CCC and the correspondingly low RMSE (adjusted R² = 99.99%; CCC = 0.999; RMSE = 1.4 mL). Moreover, the distribution of measurement errors between $V_{syr}^{\ast }$ and $V_{mocap}^{\ast }$ displayed a trivial bias (–0.7 mL) and a relatively narrow CI_95% (–4.0 to 3.6 mL). The measurement agreement between flow waveforms produced by the syringe potentiometer and motion capture system (i.e., V̇_syr and V̇_mocap) is displayed in Fig. 3, B and C. Similar to the above, V̇_syr demonstrated near-perfect absolute agreement with V̇_mocap, as given by the higher adjusted R² and CCC values, and a low RMSE (adjusted R² = 99.99%; CCC = 0.999; RMSE = 0.014 L/s). The distribution of measurement errors between V̇_syr and V̇_mocap showed negligible bias (<0.001 L/s) and a very narrow CI_95% (–0.06 to 0.06 L/s). We are therefore confident that the voltage output from the syringe potentiometer may be used to provide valid surrogates for instantaneous syringe volumes and flows ($V_{syr}^{\ast }$ and V̇_syr) across a wide range of plunger injection/withdrawal speeds.

Experiment 2: Comparison of Accuracy Between PNT Calibration Methods

Optimal hyperparameters.

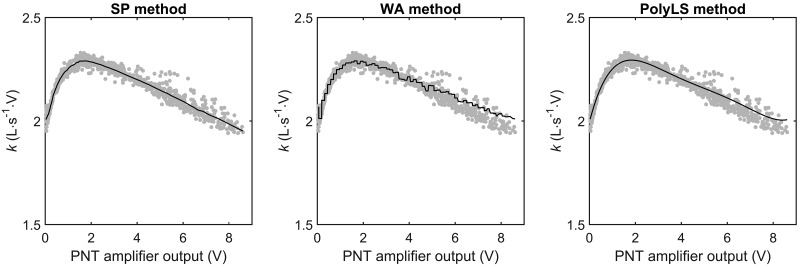
The optimal hyperparameters for the WA were 71 bin intervals and three repetitions. The optimal polynomial order for the PolyLS method was 6. The calibration curves for the SP, WA, and PolyLS methods are displayed in Fig. 4; note that these curves are built on the entire data set of expiratory calibration strokes. It is of particular note that our hyperparameters differ from those values used by other investigators when applying the WA and PolyLS methods (12, 14–16). For example, previous implementations of the WA method have used bin intervals ranging from 18 to 2,048 segments (12, 14–16). Moreover, Tang et al. (15) examined the volume accuracy of the PolyLS method using polynomial orders 1, 2, and 3, orders much smaller than that used in our study (i.e., 6th order). That our hyperparameters are different from those reported in other investigations is not surprising. Whereas the PNT under investigation in this study was an adult-sized Lilly type (screen) device, other investigators have used pediatric-sized Lilly (15) or Fleisch (i.e., capillary tube; 12, 14, 16) PNTs in their studies. The varying geometries and resistances of each type of PNT are likely to produce unique calibration curves, curves that, for example, would require different polynomial orders for the PolyLS method to adequately capture the nonlinear pressure-flow characteristics of the PNT under investigation. Nevertheless, we used the repeated K-fold CV procedure to determine the optimal set of hyperparameters for the WA and PolyLS methods. To the best of our knowledge, we are the first to implement this procedure of hyperparameter selection for any PNT calibration method. We recommend this approach for selecting the hyperparameters of the WA and PolyLS methods because it is an automated, data-driven process, i.e., hyperparameters are chosen so as to minimize volume errors obtained from a distribution of testing (out of sample) calibration strokes. Accordingly, the repeated K-fold CV procedure, as described in our study, will yield a set of hyperparameters that is likely to produce the smallest volume errors on future data.

Fig. 4.

Calibration curves obtained via the syringe potentiometer (SP), weighted averaging (WA), and polynomial least-squares (PolyLS) methods of pneumotachograph (PNT) calibration. k, Calibration constant at the corresponding voltage output from the PNT amplifier. The solid lines represent calibration curves obtained via the 3 methods with the entire data set of calibration strokes. The gray points represent empirical values of k obtained by dividing the reference flow waveform (from the syringe potentiometer) by the analog voltage output of the PNT amplifier.

Volume accuracy.

The syringe volume errors produced by the SP, WA, and PolyLS calibration methods are reported in Table 1. When calibration curves were built on the entire data set of strokes, the SP method produced, on average, larger volume errors compared with either the WA or PolyLS methods (P < 0.05). There were no differences in average volume error between WA and PolyLS when the calibration curves of each method were built on the entire data set of strokes. However, the average volume errors for the testing data set of strokes were significantly different between all three methods (P < 0.05), whereby the largest errors were observed with the SP method and the smallest errors (most accurate) were observed with the PolyLS method. Notwithstanding these significant differences, it is emphasized that all three methods produced volume errors whose respective CI_95% lay inside the ATS/ERS-recommended error margin of ±3.50% (i.e., ~105 mL for a 3-liter calibration syringe; Ref. 11).

Table 1.

Syringe volume errors produced by SP, WA, and PolyLS methods of pneumotachograph calibration

	Entire Data Set		Testing Data Set
Method	Average, %	CI95%	Average, %	CI95%
SP	0.29*†	–0.39 to 1.00	0.29*†	–0.46 to 0.97
WA	0.03	–0.88 to 0.62	0.03†	–1.02 to 0.61
PolyLS	0.01	–1.04 to 0.47	0.01	–1.15 to 0.50

Volume errors are expressed as % of 3 liters. CI_95%, 95th percentile confidence interval of volume errors; PolyLS, polynomial least squares; SP, syringe potentiometer; WA, weighted averaging. Note: The CI_95% of volume errors for the 3 methods all lie within the American Thoracic Society/European Respiratory Society-recommended error margin of ±3.50%.

^*Significantly different from WA method, P < 0.05.

^†Significantly different from PolyLS method, P < 0.05.

Flow accuracy.

The flow errors produced by the three methods of PNT calibration are reported in Table 2. When considering the full range of flows (i.e., 0 to >9.0 L/s), the SP method demonstrated the smallest average flow error (bias) and narrowest CI_95% of all three methods for both the entire and testing data sets of calibration strokes (P < 0.05). A less consistent pattern was observed across the different ranges of flow (i.e., very low through very high). Importantly, however, all three methods produced a distribution of flow errors whose respective CI_95% fell within the ATS/ERS-recommended ±5.00% error margin for flow-sensing devices (11); this finding was consistent irrespective of the data set used to generate flow errors (i.e., entire vs. testing data sets). The above findings indicate that when the user has the luxury of obtaining a large database of calibration strokes (>100) at varying injection/withdrawal speeds, the SP, WA, and PolyLS methods all display levels of volume and flow accuracy within acceptable margins of error.

Table 2.

Flow errors produced by SP, WA, and PolyLS methods of pneumotachograph calibration

		Entire Data Set		Testing Data Set
Range	Method	Average, %	CI95%	Average, %	CI95%
Very low (<0.5 L/s)	SP	–0.04*†	–1.78 to 1.62	–0.01*†	–1.78 to 1.98
	WA	–0.49	–2.91 to 1.52	–0.47	–2.75 to 1.65
	PolyLS	–0.56	–2.13 to 1.38	–0.55	–2.12 to 1.46
Low (0.5–3.0 L/s)	SP	0.09	–1.08 to 1.12	0.10*†	–1.11 to 1.16
	WA	–0.04†	–1.51 to 1.30	–0.11†	–1.60 to 1.22
	PolyLS	0.26	–1.00 to 1.31	0.26	–1.00 to 1.31
Medium (3.0–6.0 L/s)	SP	0.07	–1.59 to 1.28	0.09*†	–1.50 to 1.41
	WA	0.15†	–1.41 to 1.42	0.19†	–1.23 to 1.50
	PolyLS	–0.20	–1.77 to 1.08	–0.19	–1.70 to 1.06
High (6.0–9.0 L/s)	SP	0.02	–1.04 to 1.40	0.01†	–1.04 to 1.36
	WA	–0.14	–1.38 to 1.10	–0.05†	–1.31 to 1.29
	PolyLS	–0.29	–1.36 to 1.07	–0.28	–1.31 to 1.03
Very high (>9.0 L/s)	SP	0.04*†	–2.00 to 3.20	0.03†	–2.00 to 3.16
	WA	–1.05†	–3.49 to 2.18	–0.98†	–3.46 to 2.10
	PolyLS	–0.71	–2.95 to 2.51	–0.72	–2.96 to 2.50
Entire range	SP	0.04*†	–1.57 to 1.68	0.05*†	–1.60 to 1.77
	WA	–0.43	–2.90 to 1.46	–0.40†	–2.88 to 1.52
	PolyLS	–0.34	–2.34 to 1.40	–0.34	–2.34 to 1.41

Flow errors are expressed as % of the corresponding “reference” flow. CI_95%, 95th percentile confidence interval of flow errors within the given range; PolyLS, polynomial least squares; SP, syringe potentiometer; WA, weighted averaging. Note: The CI_95% of flow errors for the 3 methods all lie within the American Thoracic Society/European Respiratory Society-recommended error margin of ±5.00%.

^*Significantly different from WA method, P < 0.05.

^†Significantly different from PolyLS method, P < 0.05.

Experiment 3: Practical Performance of Calibration Methods

Optimal hyperparameters.

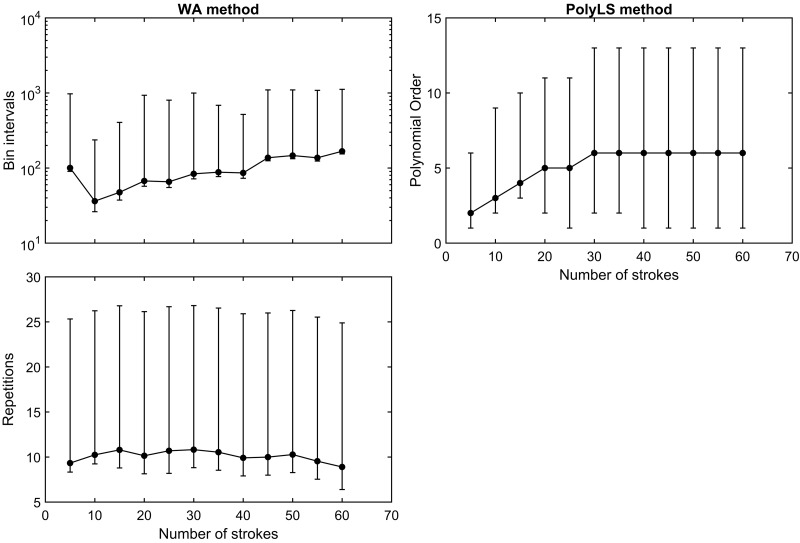
Figure 5 displays the trend in optimal hyperparameters across the 12 stroke blocks used to examine the practical performance of each PNT calibration method. The distributions of optimal bin intervals and algorithm repetitions for the WA method were heavily skewed toward higher values at each block of calibration strokes (Fig. 5, left). There was a tendency for bin interval size to increase as more calibration strokes were used, whereas the average number of algorithm repetitions remained relatively constant. The optimal orders used for the PolyLS method displayed a trend toward higher values as the number of calibration strokes increased. Our impression from these data is that optimal hyperparameter selection is highly sensitive to the particular set of strokes used by each PNT calibration method; one cannot assume that hyperparameters that are optimal for a small number of calibration strokes (<20) will perform equally well on a larger set of calibration strokes. This observation emphasizes the importance of using the repeated K-fold CV procedure to redetermine the optimal hyperparameters for a given PNT calibration method as new syringe strokes are collected.

Fig. 5.

Hyperparameters for the weighted averaging (WA) and polynomial least-squares (PolyLS) calibration methods as a function of increasing numbers of calibration strokes. Values are presented as means ± 95th percentile confidence interval.

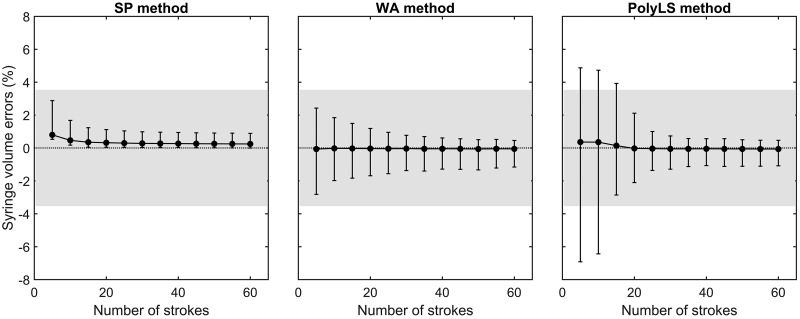
Volume accuracy.

Figure 6 illustrates the change in volume errors with increasing numbers of syringe strokes associated with each calibration method. This figure shows that both the SP and WA methods produced a CI_95% of volume errors that fell within the recommended margins by the end of the first block of five calibration strokes. Importantly, the CI_95% of volume errors produced by the PolyLS method fell within the recommended ±3.50% margin only after 20 calibration strokes (4 blocks) were used to build a calibration curve. It is noted that although the SP method displayed ideal volume errors (less than ±3.50%) within the first block of strokes, the range of its CI_95% did not include 0.00% at any number of calibration strokes. Thus the SP method consistently overestimated the calibrated syringe volume (3 liters) by <0.80%. Conversely, the CI_95% of volume errors produced by the WA and PolyLS methods included 0.00% at each block of strokes.

Fig. 6.

Syringe volume errors produced by syringe potentiometer (SP), weighted averaging (WA), and polynomial least-squares (PolyLS) calibration methods as a function of increasing numbers of calibration strokes. Values are presented as means ± 95th percentile confidence interval (CI_95%). The gray shaded region denotes the ±3.5% error margin of volume errors as recommended by the American Thoracic Society and the European Respiratory Society (11). Note that CI_95% of volume errors produced by the SP and WA methods fall within the recommended error margin after only 5 calibration strokes, whereas it takes 20 strokes with the PolyLS method to achieve the same level of volume accuracy.

Our observation that the PolyLS method required ≥20 calibration strokes to obtain acceptable volume accuracy contrasts with the findings of others. For example, Tang et al. (15) concluded that only 10 calibration strokes were necessary to achieve an acceptable level of volume accuracy when the PolyLS method was examined with second- and third-order polynomial functions. The principal reason for these discrepant findings is likely differences in how volume errors were evaluated in our study and that of Tang et al. (15). Whereas these investigators used the same set of 70 validation syringe strokes to compute volume errors as the number of calibration strokes was increased (from 6 to 50; see Fig. 3 in Ref. 15), we used a nested subsampling procedure to create a larger distribution of testing (validation) strokes for each of the 12 blocks of calibration strokes. We prefer our approach of evaluating the practical performance for PNT calibration methods to that of Tang et al. (15) because it mitigates the risk of bias associated with an arbitrary selection of a predetermined set validation strokes, strokes that may be, by chance, poorly representative of future data. Our nested subsampling procedure, on the other hand, protects against such bias by repeatedly generating unique sets (200 surrogates) of testing/validation data sets (127 strokes each) for every one of the 12 stroke blocks examined (25,400 validation strokes per block). In so doing, we smoothed out “noise” in our estimates of volume errors due to random splitting of training and testing data sets. Further to the above, our approach ensured that within each block of five strokes the very low, low, medium, high, and very high ranges of flow were equally represented (see step 2 in Experiment 3: Practical performance of calibration methods). This particular constraint on the nesting procedure was included to reflect how one might perform ongoing routine calibrations of flow-sensing devices with commercially available equipment, i.e., perform five or six calibration strokes at varying speeds of injection/withdrawals of the syringe plunger. For these reasons, we believe that our nested subsampling approach provided a fairer evaluation of the practical performance of the SP, WA, and PolyLS calibration methods than if we had used a predetermined (unchanging) set of validation strokes as others have done (15).

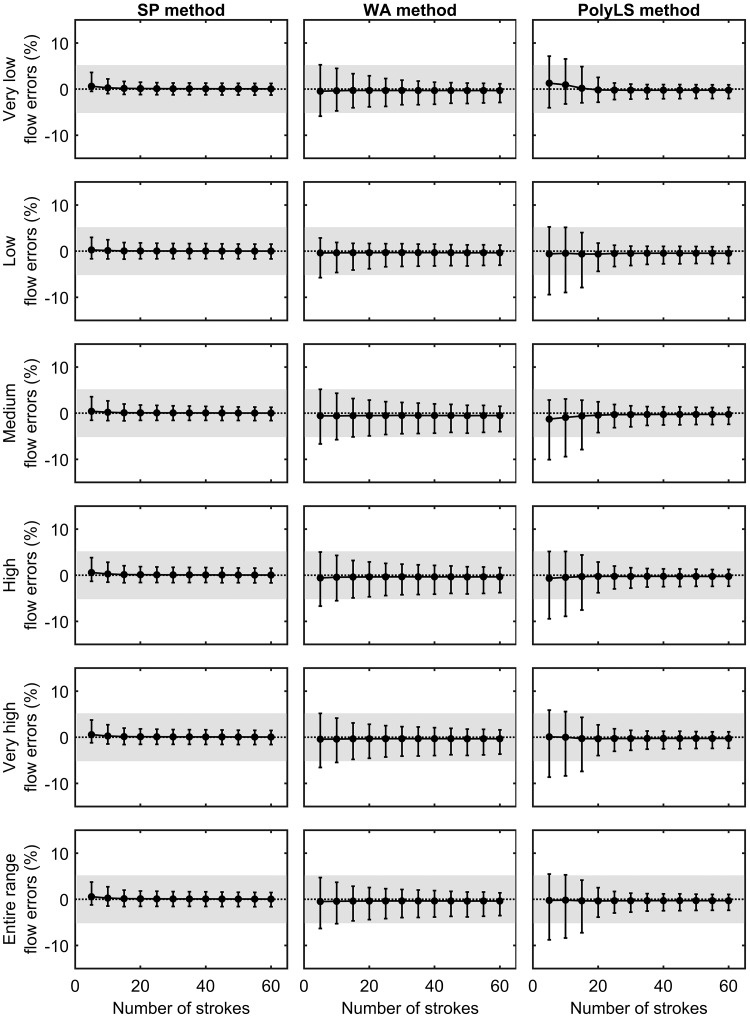
Flow accuracy.

Figure 7 displays the change in flow errors as further calibration strokes are used by the SP, WA, and PolyLS methods. The SP method displayed the best overall flow accuracy across all blocks of strokes, whereby only five calibration strokes (1 block) were necessary to produce CI_95% within the recommended error margin of ±5.00% across the entire range of flows examined (i.e., very low, low, medium, high, and very high). Conversely, it was not until the third block of strokes (15 total strokes) that the CI_95% of flow errors associated with the WA method fell within ±5.00% for all ranges of flow. The PolyLS method demonstrated the worst overall flow accuracy, in that this method required 20 calibration strokes (4 blocks) until the CI_95% of flow errors fell within ±5.00% across all ranges of flows. That the SP method yielded the best overall flow accuracy within the least amount of calibration strokes is perhaps not surprising. The calibration curve of the SP method is empirically determined by dividing the reference flow of the syringe potentiometer by the voltage output of the PNT amplifier (i.e., k = V̇_syr/volts). The WA and PolyLS methods do not empirically compute k, however. These methods instead arrive at calibration curves, using numerical procedures that minimize the average error between a known syringe volume (3 liters) and that obtained via integration of the calibrated flow signal (i.e., the “reconstructed” syringe volume). Notwithstanding the above points, the following is clear: PNT calibration methods that prioritize reducing volume errors do not always, ipso facto, provide the smallest errors in flow.

Fig. 7.

Flow errors produced by syringe potentiometer (SP), weighted averaging (WA), and polynomial least-squares (PolyLS) calibration methods as a function of increasing numbers of calibration strokes. Values are presented as means ± 95th percentile confidence interval. The gray shaded region denotes the ±5.0% error margin of volume errors as recommended by the American Thoracic Society (ATS) and the European Respiratory Society (ERS) (11). Note that flow errors produced by the SP method fall within the ATS/ERS-recommended error margin across all ranges of flow rates after only 5 calibration strokes.

Recommendations

The syringe volume and flow errors produced by the SP, WA, and PolyLS methods all fell within the ATS/ERS-recommended ranges when the entire set of calibration strokes was used (Tables 1 and 2). Similar results were observed when each calibration method was applied on the testing data set. Thus, if one has the luxury of manually generating >100 calibration strokes on a given breathing circuit, there does not appear to be any specific advantage of choosing one of the three PNT calibration methods examined here over another. The choice between SP, WA, and PolyLS methods may be guided by more practical concerns, however. If it is feasible to construct a syringe potentiometer, the user may opt for the SP calibration method because of the relative simplicity of its numerical procedures (i.e., simple division). However, if a syringe potentiometer is not available, the choice between the WA and PolyLS methods is more difficult. On the one hand, the PolyLS method may be preferred because the calibration curve obtained via this approach is relatively easier to implement in real time (online) compared with the WA method. For example, to apply a calibration curve obtained with a second-order polynomial via the PolyLS method in real time, the user has only to apply the following equation to obtain a calibrated flow signal:

$$\dot{V}={\beta }_1\cdot \text{volts}+{\beta }_2\cdot \text{volt}{\text{s}}^2$$ (6)

where β denotes the polynomial coefficient. Many commercially available data acquisition (DAQ) software packages offer support for evaluating this type of simple mathematical expression in real time as a “calculation” or “transformation” channel (e.g., LabChart, AcqKnowledge). In contrast, it is correspondingly more difficult to apply a calibration curve obtained via the WA method in such DAQ software packages. Here, a complex formula syntax is required to implement what is essentially a lookup table of calibration constants (i.e., k), requiring a slew of “if-then” statements to be evaluated each time a new sample is acquired. On the other hand, a polynomial function (of any order) may not adequately describe the nonlinear pressure-flow characteristics of a given PNT device (i.e., Eq. 2). As such, the WA method may instead be preferred, given that no parametric constraints are imposed on the specific shape of the PNT calibration curve with this approach.

It must be remembered that the shape of the pressure-flow characteristic (i.e., calibration curve) for any given PNT is altered by changing the up- and downstream resistance of a breathing circuit (2, 7, 14, 16). It is common that the effective geometry of a breathing circuit will change frequently within a given experimental design. For example, these changes may include 1) the addition of external resistors to impose added loads on breathing; 2) changes to the density/viscosity of gas flowing through the circuit (i.e., normal air vs. 100% O₂ vs. He-O₂ mixtures); and/or 3) varying the effective length of the breathing circuit by redirecting gas flow through two- and three-way valve manifolds (e.g., directing expired gas into a series of Douglas bags). Each time the configuration of the breathing circuit is changed, the user is obliged to create a new calibration curve from the PNT device. And if the geometry of the breathing circuit is changed regularly (e.g., between days, within an experiment, etc.), the luxury of obtaining >100 calibration strokes quickly disappears. Under such circumstances, the SP method of PNT calibration displays superior performance compared with the WA and PolyLS methods (Fig. 6 and Fig. 7). The SP method is able to provide a calibration curve with acceptable volume and flow errors within only five syringe strokes (provided that these strokes cover the very low to very high flow ranges). Thus in situations where the configuration of the breathing circuit is changed frequently, the SP method of PNT calibration is preferred.

The SP method, as implemented here, used only data obtained during the middle third of each calibration stroke. We chose to analyze only this portion to avoid any nonsteady behavior that may be present at the beginning and end of the stroke (i.e., due to poor manual control or “stickiness” of the plunger at the extremes of its excursion). Moreover, we made the somewhat arbitrary choice to bin average these data into 200-mL intervals within the middle third of the stroke. Preliminary analysis revealed that this interval was large enough to improve the stability of our estimates of k using the SP method while being small enough to provide multiple values of k per stroke. A thorough investigation of different bin intervals and volume ranges was outside the scope of the present report; however, it would be prudent to investigate the optimal values for these parameters in a future investigation.

Conclusions

This report outlines a method of construction of a low-cost device used for the purposes of PNT calibration, the syringe potentiometer. We demonstrated that the syringe potentiometer device provides an accurate and valid reference flow waveform, from which a PNT calibration curve may be empirically constructed (i.e., the SP method). When the user has the luxury of collecting >100 calibration strokes, the SP method does not offer any distinct advantages over more established methods of PNT calibration (i.e., the WA and PolyLS methods). However, under circumstances in which the effective geometry of a breathing circuit is likely to change frequently (e.g., between or within days), the SP method offers superior calibration performance compared with the WA and PolyLS methods, insofar as it requires only five syringe strokes to produce a calibration curve with acceptable volume and flow errors. Therefore, the syringe potentiometer and, by extension, the SP method offer users a low-cost, accurate, and expedient method of PNT calibration.

GRANTS

T. J. Cross was supported by an Irene Diamond Fund/American Federation for Aging Research Postdoctoral Transition Award. This study was supported by National Heart, Lung, and Blood Institute Grant HL-71478.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

T.J.C. conceived and designed research; T.J.C., E.F.K., and T.A.H. performed experiments; T.J.C. analyzed data; T.J.C., J.M.I., and B.D.J. interpreted results of experiments; T.J.C. prepared figures; T.J.C., E.F.K., T.A.H., J.M.I., and B.D.J. drafted manuscript; T.J.C., E.F.K., T.A.H., J.M.I., and B.D.J. edited and revised manuscript; T.J.C., E.F.K., T.A.H., J.M.I., and B.D.J. approved final version of manuscript.

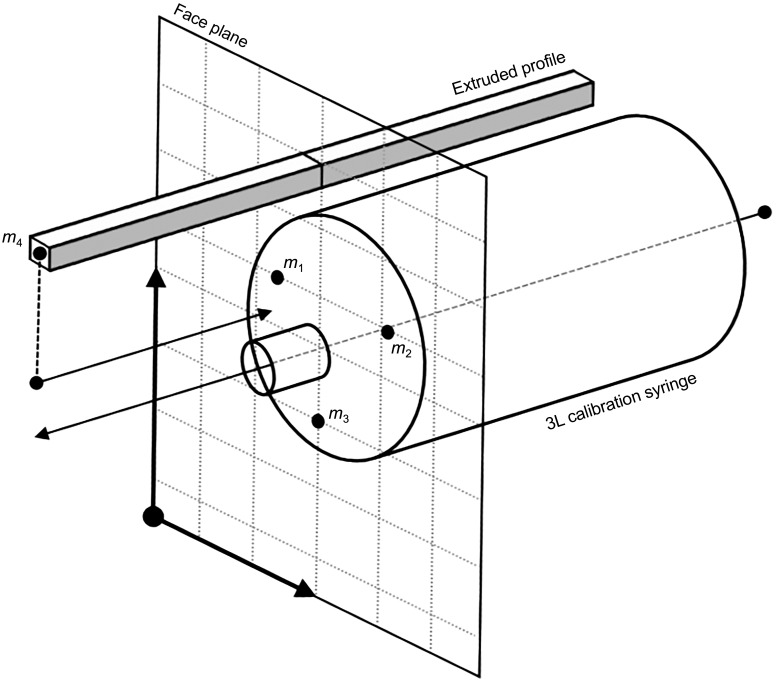
APPENDIX A: MEASUREMENT OF LINEAR DISPLACEMENT OF SYRINGE PLUNGER WITH MOTION CAPTURE

A commercially available eight-camera motion capture system (Optitrack Flex 13; NaturalPoint, Corvallis, OR) was used to record the 3D coordinates (x, y, z) of four passive-reflective markers (hemispheres, ~10-mm diameter). The camera system was calibrated with a standard CWM-250 calibration wand from the manufacturer (size 250 mm). The average residual error achieved after system calibration was 0.2 mm. The first three markers (m₁–m₃) were affixed to the faceplate of the syringe potentiometer (Fig. A1). The fourth marker (m₄) was attached to the distal end of the extruded aluminum profile of the syringe potentiometer assembly. It was assumed that movement of the extruded profile during each calibration stroke occurred solely along the principal axis of the syringe (i.e., axial direction). Accordingly, the markers m₁, m₂, and m₃ defined the surface of a two-dimensional plane coincident with the faceplate of the syringe. The displacement of the syringe plunger was then calculated as the orthogonal distance between m₄ and this planar surface. To obtain this value, it was necessary to first compute the normal vector (n) of the plane, as given by

$$\mathbf{n}=\frac{\overrightarrow{m_1{m}_2}\times \overrightarrow{m_1{m}_3}}{‖\overrightarrow{m_1{m}_2}\times \overrightarrow{m_1{m}_3}‖}$$ (A1)

where $\overrightarrow{m_1{m}_2}$ and $\overrightarrow{m_1{m}_3}$ are direction vectors formed by the marker pairs m₁ and m₂ and m₁ and m₃, respectively. The orthogonal distance (d) of m₄ from the plane was then calculated as the dot product of the direction vector $\overrightarrow{m_1{m}_4}$ and the surface normal n. The value of d was taken to represent the displacement of the syringe plunger during calibration strokes.

APPENDIX B: CALCULATION OF FIRST DERIVATIVES WITH FIRST-ORDER ADAPTIVE WINDOWING METHOD

We computed the central derivative of the corrected syringe volume waveform to obtain a syringe flow waveform (V̇_syr). Numerical differentiation is a noisy procedure, however. Approximating this derivative over a relatively large number of samples (or time) yields a low-noise estimation of the “true” derivative. Yet, although this approximation may be accurate in sections where the signal varies slowly (i.e., low flows), a wide basis of support will tend to underestimate the true derivative where the signal changes rapidly (i.e., high flows). Thus an adaptive window is required to provide an accurate estimation of V̇_syr at both low and high flows. To this end, we used a method similar to the first-order adaptive windowing (FOAW) technique (5, 6) to calculate V̇_syr. (This method is used widely in the engineering field to estimate velocity from displacement sensors.) Briefly, for each time point i of the syringe volume waveform, a linear segment is least-squares fit to a window of n samples (centered on i) where n is initialized at 1. The best-fit linear segment is then evaluated between the margins of n − i to n + i, and the residual errors between the line-fit and observed syringe volumes are computed. If all residuals lie within a prespecified uncertainty band, ε, then n is increased by 1 and the process is repeated again. The FOAW algorithm continues until the largest value of n is found where all residual errors remain within ±ε. The derivative of the syringe volume waveform, V̇_syr, at time point i is then calculated as the slope of the linear segment fitted over this largest value of n. The FOAW algorithm is repeated for every time point in the syringe volume waveform until a continuous V̇_syr waveform is obtained. In this study, we set the uncertainty band ε at 0.24 mL. This value roughly corresponded to the bit resolution of the data acquisition system after the syringe potentiometer output was calibrated.

Fig. A1.

Method for quantifying the instantaneous displacement of the syringe plunger via motion capture. m₁–m₄, passive-reflective markers 1–4. The instantaneous displacement of the syringe plunger is calculated as the perpendicular distance between m₄ and the planar surface formed by m₁, m₂, and m₃.