Effects of habitat area and spatial configuration on biodiversity in an experimental intertidal community

Abstract

Isolating the effects of fragmentation per se (i.e., spatial configuration of habitat patches) on species richness is an ongoing challenge as habitat configuration often covaries with the amount of habitat. Consequently, there is a lack of experimental evidence for configurational effects on species richness in the whole landscape. Here, we developed a novel experimental system for testing the independent and interactive effects of habitat area and configuration on tropical intertidal species richness. Our results confirmed the expectation that average species richness would increase monotonically with habitat area. More intriguingly, we found mixed evidence for a non‐monotonic relationship between species richness and fragmentation per se, with the highest richness at intermediate fragmentation configuration, that is, when habitat tiles were placed in a “several‐small” configuration. The effect of habitat configuration was not due to passive sampling (since area was controlled for), variation in total individual abundance, or niche specialization of species to different landscape configurations. We postulate that a combination of processes, including local negative density dependence and dispersal limitation, could give rise to the observed pattern. We emphasize the importance of considering configurational effects on biodiversity at broader spatial scales and for more experimental research to delve into the mechanisms driving the patterns seen here.

Introduction

Species–area relationships (SARs) have long been considered a general “law” in ecology (Lawton 1999, Tjørve 2003, Triantis et al. 2012) and are commonly used as a tool in conservation biology to predict species loss (extinctions) with habitat reduction (Brown and Lomolino 1998, Brooks et al. 2002). However, theoretical predictions based on classic SAR models have been criticized in light of reported discrepancies between actual and predicted species loss in fragmented landscapes (Kinzig and Harte 2000, Hanski et al. 2013). One limitation of the classic SAR model is that it ignores the spatial configuration of habitat patches (also known as the effect of “habitat fragmentation per se”, sensu Fahrig 2003, 2017). Here, we use the terms “fragmentation per se,” “configuration,” and “arrangement” interchangeably. Using Fahrig's (2003, 2017) definition, fragmentation is thus viewed as a “pattern” (spatial configuration of habitat patches at one point in time) rather than a “process” over time (Fig. 1a). Therefore, “greater fragmentation per se” independent of habitat area loss in this sense would refer to spatial configurations with a greater number of smaller patches (Fig. 1b). The species richness of an ecological community in a landscape can be related to both total habitat area and configuration of patches (Tscharntke et al. 2012). While habitat area has an almost universally positive influence on species richness (Preston 1960), the effects of habitat configuration are much more uncertain (Ewers and Didham 2006, Villard and Metzger 2014) and a subject of great debate (Fletcher et al. 2018, Fahrig et al. 2019, Miller‐Rushing et al. 2019). Research into the topic of habitat fragmentation per se and biodiversity reached an apogee during the single‐large‐or‐several‐small (SLOSS) debate (Triantis and Bhagwat 2011), which had its roots in island biogeography (MacArthur and Wilson 1963, 1967) and dealt with the problem of optimal reserve design. The essential question is whether biodiversity conservation would be better served by a single large reserve or several small ones of equivalent total area. Reductio ad absurdum shows both the single‐large and several‐small scenarios to be suboptimal in general (Rosenzweig 2004). For example, the contiguous United States contains over 1 million km² of protected areas, and this system is almost certainly more effective for biodiversity conservation than would be a single giant reserve of 1 million km² or 1 million scattered reserves of 1 km² each; the former would not capture the variety of habitats present across the country, while the latter would be inhospitable for many sensitive species (e.g., species with large territorial requirements or forest‐interior species). There is thus an ongoing need to answer the question of what habitat configuration is optimal for biodiversity.

Figure 1.

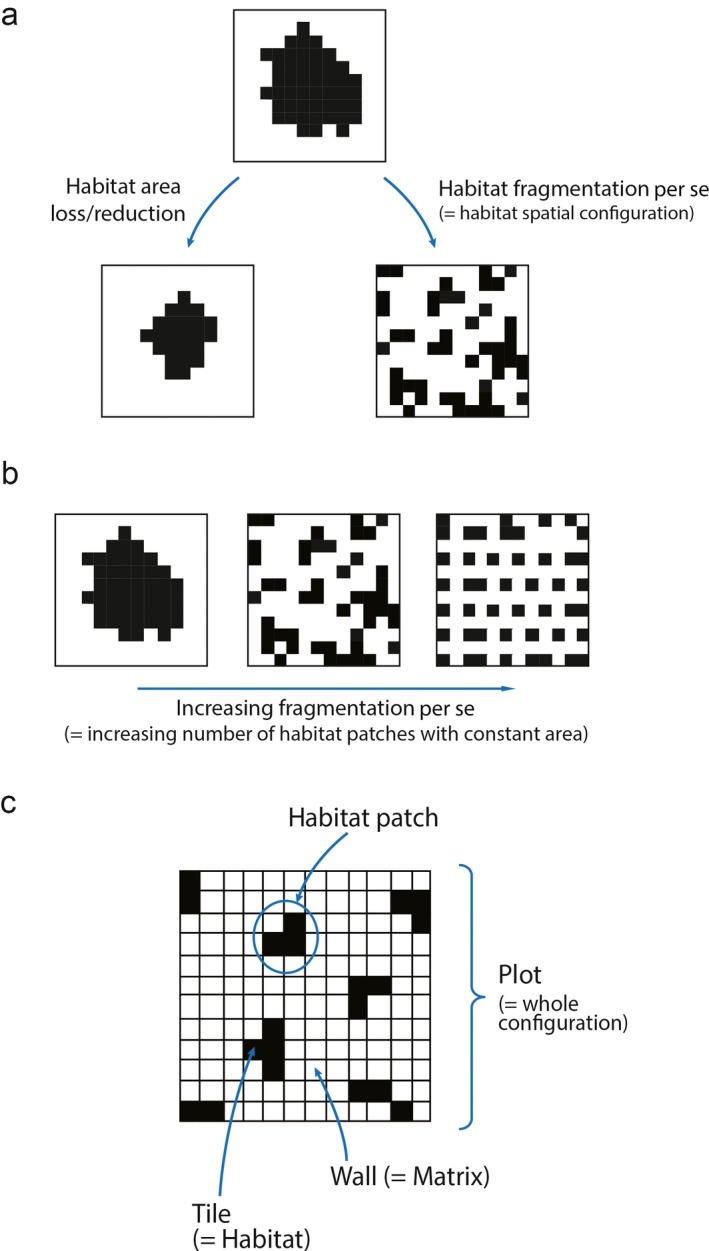
(a) Conceptual diagram illustrating how the definition of habitat fragmentation per se (sensu Fahrig 2003; i.e., change in habitat configuration with area staying constant) is independent of habitat area loss (i.e., reduction of area irrespective of arrangement); (b) increasing fragmentation per se thus refers to an increase in the number of habitat patches and how the patches are configured given the same total area; (c) illustration of the key terms used in our study.

Ecological theory provides a variety of mechanisms that could produce negative or positive relationships between more‐fragmented configurations and diversity. Negative relationships can arise from edge effects, which can reduce species richness by eliminating species intolerant of edge‐associated disturbance (Ries et al. 2004, Laurance et al. 2007). For example, forests with high edge‐to‐interior ratios can be more prone to predation that reduces animal diversity or to desiccation and wind that reduces plant diversity (Murcia 1995, Laurance and Curran 2008, Damschen et al. 2014). Other mechanisms that can theoretically alter diversity in fragmented landscapes are reduced/increased habitat diversity (i.e., number of niches/habitat types) and demographic stochasticity due to smaller population size (Burkey 1989, Hoyle and Harborne 2005). Mechanisms that could produce greater diversity in more‐fragmented configurations include increased beta diversity due to dispersal limitation (Andrén 1994, Jamoneau et al. 2012), and lower likelihood of species extinction arising from environmental stochasticity (e.g., large‐scale disturbances or diseases; Mangel and Tier 1993, Fahrig 2017). Many other mechanisms have been proposed, but most of them are constitutive explanations that fall under one or more of those described above. For instance, negative effects of habitat fragmentation per se due to decreased “landscape complementation” relates to dispersal limitation because when habitat patches with non‐substitutable resources are spaced too far apart they can impede access by mobile species that require the combination of these resources (Dunning et al. 1992). Others have suggested that more‐fragmented configurations can lead to reduced competition (Fahrig 2017); for example, small mammals can use fragmented edges as boundaries of their territory and consequently defend them more easily (Wolff et al. 1997). This is essentially a positive edge effect.

Empirical evidence suggests that the fragmentation–diversity relationship can be positive or negative (assuming area is controlled). A recent review of studies examining fragmentation per se found that, among statistically detectable ecological responses, approximately 76% were positive and 24% negative (Fahrig 2017), but a subsequent critique argued that the studies reviewed were non‐representative and that negative effects of fragmentation per se may in fact be more pervasive (Fletcher et al. 2018). Effects of habitat fragmentation on species richness have been documented across very different systems, from insect communities in grasslands (Collinge and Forman 1998, Tscharntke et al. 2002) to fish communities in coral reefs (Bonin et al. 2011) to tropical forests (e.g., BDFFP and SAFE projects; Laurance et al. 2002, Ewers et al. 2011). The majority of these studies, however, either did not control for area, or measured species richness only within patches (Gibson et al. 2013) and did not examine the whole configuration (which is what ultimately matters for conservation). Many of these studies were also conducted at very small scales so that the effects of different habitat configurations were often so weak as to be statistically undetectable. An experimental study of mite communities, for instance, showed little effect of configuration when controlling for area (Hoyle and Harborne 2005). A complicating factor in studying the fragmentation–diversity relationship is context: the strength and direction can vary with factors such as taxonomic group and habitat area (Andrén 1994, Hanski 2015, Fahrig 2017). For example, in an observational study of heathland habitat, Olff and Ritchie (2002) found that fragmentation per se had a negative effect on bird richness but not on butterfly richness.

The state of knowledge regarding the effect of configuration on diversity is limited by reliance on observational studies rather than experiments where habitat area and configuration are directly and independently manipulated. The paucity of manipulative field experiments is due to their inherent logistical complexity (McGarigal and Cushman 2002, Fahrig 2003). As McGarigal and Cushman (2002:336) note, the effects of habitat fragmentation per se are “exceedingly difficult to isolate experimentally” as they often operate at spatial and temporal scales larger than those being studied. The experimental studies that have been conducted have usually been at very small scales; Gonzalez et al. (1998) for example, considered a total habitat area of 0.012 m² in a plot of area 0.25 m². While large‐scale terrestrial “fragmentation experiments” do exist and have produced invaluable insights into the negative effects of fragmentation per se on biodiversity in individual patches, they are not designed to assess the effect of the configuration of different patches within a landscape (Laurance et al. 2002, Ewers et al. 2011).

Even more challenging to test are the interactive effects of habitat loss and spatial configuration (Villard and Metzger 2014). Simulation models suggest that species’ responses to more‐fragmented configurations can be abrupt and nonlinear when little habitat remains (With and King 1999), compounding the negative effects of habitat loss. This is often referred to as the “20% rule” or “20–30% threshold”: the threshold value of habitat area below which the effects of fragmentation per se “kick in” (Fahrig 2003, Hanski 2015). However, “the literature belies such a simple rule of thumb” (Ewers and Didham 2006:122). Actual thresholds are likely to vary among different species groups (due to trait and sensitivity differences; Henle et al. 2004), environmental heterogeneity (Vellend 2016), the type of ecosystem (e.g., marine vs. terrestrial; Tjørve 2010), and the scale of observation (Yeager et al. 2016).

One other limitation of the classic SAR model is that it ignores the role of the “matrix,” i.e., the areas of cleared habitat that now comprise human‐modified or novel landscapes but are not completely hostile or impervious to biodiversity (Pereira et al. 2012). To incorporate this wider context, Pereira and Daily (2006) developed the “countryside biodiversity model” or “countryside SAR,” which categorizes species into different functional groups with particular affinities for different habitat types in a landscape and showed that their model was able to forecast extinction rates and minimum area required for species persistence, and to describe diversity patterns in human‐modified landscapes (Pereira et al. 2014).

To address the issues raised above, we developed a novel experimental system for testing the independent and interactive effects of habitat area and configuration on species richness in 2.4 × 2.4 m intertidal plots. To our knowledge, no previous manipulative experiment has simultaneously manipulated both these factors independently in marine ecosystems. Nor have any such studies been conducted in the tropics. We used molded concrete tiles to create standard units of “habitat patches” and arranged them in nine different, fully replicated, plot configurations on seawalls in Singapore (Fig. 2). The seawall matrix and the “habitat patches” represented by the tiles differ greatly in their species richness and composition: while most species are associated with the tile habitat, some species also have an affinity for the matrix. In analyzing the experimental data, we treated tiles and seawall matrix as two habitat types and fitted a modified version of the countryside biodiversity model that allows the z‐slope of the species–area curve to vary with the spatial configuration of habitat patches. We hypothesized that: (1) consistent with the traditional SAR, greater tile habitat area would support greater species richness S independent of habitat configuration (fragmentation per se); (2) consistent with the majority of previous “fragmentation studies,” more‐fragmented configurations would have mostly positive effects on S independent of total habitat area; and (3) consistent with threshold models, more‐fragmented configurations would have more negative effects on S at low habitat area.

Figure 2.

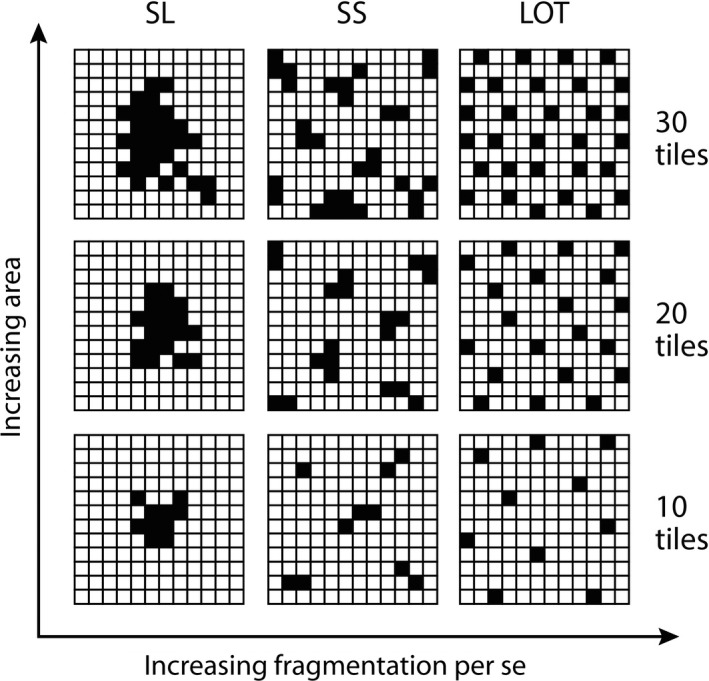
Experimental plots (2.4 × 2.4 m) representing the spatial configurations of tiles (habitat; black cells) installed on seawall substrate (matrix; white cells). Variation in area is represented by rows (10 tiles = 7% area; 20 tiles = 14%; and 30 tiles = 21%) while variation in fragmentation is represented by columns (SL, single large; SS, several small; and LOT, lots of tiny).

Materials and Methods

Experimental design

We manipulated habitat area and spatial configuration within 2.4 × 2.4 m experimental plots on seawalls (each divided into a 12 × 12 grid) using various numbers and arrangements of concrete tiles (see Tile design and fabrication). Previous work has shown that intertidal biodiversity is higher on tiles than on unmodified seawalls (Loke and Todd 2016, Loke et al. 2016, 2017); therefore, we refer to the tiles as “habitat” and the surrounding seawall as “matrix” (Fig. 1c). We created three different levels of total tile (habitat) area (7%, 14%, and 21%) and three different levels of spatial configuration: single large (SL), several small (SS), and lots of tiny (LOT), resulting in nine possible plot configurations (treatments, Fig. 2). Four replicates of each configuration, i.e., 36 treatment plots in total (using 720 concrete tiles) were installed, along with 12 plots with zero tiles (the Area = 0 treatment).

Tile design and fabrication

The concrete tiles used to create the treatment plots measured 20 × 20 × 6 cm (width × length × depth). Only one tile design was used and it incorporated two basic structural component types, “pits” and “grooves” with a size range of 2–56 mm (based on results of Loke and Todd 2016). The software CASU (Loke et al. 2014) was used to generate the arrangement of these components. Once the design was finalized, a wooden master tile was fabricated, from which silicone rubber (Freeman Bluesil V‐340, Freeman Manufacturing & Supply Co., Avon, Ohio, USA) molds were made. The experimental tiles were then cast using a 1:3 Portland cement to sand mix (Appendix S1: Fig. S1).

Study sites and tile deployment

The study was conducted along sloping granite seawalls at Pulau Hantu (1°13′34″ N, 103°45′0″ E), a small island pair located 7 km south of Singapore's main island. The seawalls were constructed in 1974–1975 to retain the ~10 ha of land that was reclaimed from the coral reef flats that once surrounded Pulau Hantu (that originally comprised ~2.4 ha of land above the high tide mark). The mean slope of the seawall is approximately 36°. Tides are semi‐diurnal and tidal stream velocities can reach up to 2.0 m/s. Deployment of the 720 tiles (on seawalls around the entire perimeter of the island pair, ~2 km) was carried out during low tide in February 2014. To ensure the installed tiles closely resembled the plot configurations in Fig. 2, we used 2.4 × 2.4 m aluminum frames (gridded using steel cables) to mark the tile locations. Each tile was attached to the wall with a single stainless steel bolt screwed into an expanding fastener (drop‐in anchors) that had been inserted into a 10 mm diameter hole drilled into the granite. The plots were placed in random order along the seawalls and spaced at least 15 m apart. The experimental plots spanned the intertidal from ~0.2–0.3 m (lowest tile position) to ~1.6–1.7 m (highest tile position) above chart datum.

Field sampling, data extraction, and laboratory procedures

After leaving the experimental plots for a year to allow colonization by organisms, we photographed and then sampled the plots in February 2015. The duration and timing of deployment is appropriate, as Lai et al. (2018) found no seasonal variation in diversity patterns and community composition across various seawall and natural rocky shore sites in Singapore (a tropical aseasonal environment) and Loke et al. (2016) found that succession of the intertidal assemblages on artificial substrates installed at the same site, Pulau Hantu, climaxed after 6–7 months. Samples were obtained by scraping and picking the epibiota off each plot (from both tiles and seawall), and placing them immediately into self‐sealing plastic bags. Organisms found on tiles were bagged separately from those found on the seawall matrix. All samples (labeled by plot numbers 1–36) were brought back to the laboratory and kept in a −20°C freezer before they were sorted, identified, and counted. All organisms were identified to species except for polychaetes, which were identified to family level, and algae, which were classified into seven functional groups following Loke et al. (2016; Appendix S1: Table S1).

Model and statistical analysis

Species–area curves spanning local to continental scales typically exhibit an overall triphasic shape, with the middle phase having an approximate power law shape over intermediate scales characteristic of many problems in ecology and conservation (Rosindell and Cornell 2007). For this reason, a power law is typically fit to species–area data on intermediate scales (larger than the average dispersal scale but smaller than the average species range size), and hence we used approaches based on power laws here.

We first fitted to the data the countryside biodiversity species–area model (Pereira and Daily 2006), which is a modified power law that weights the area of each habitat by the affinity of species for that habitat:

$$S=c{\left(h_{\mathrm{tile}}{A}_{\mathrm{tile}}+h_{\mathrm{wall}}{A}_{\mathrm{wall}}\right)}^z.$$ (1)

here S is species richness, $h_i$ is the affinity of species to habitat i, $A_i$ is the area of habitat i (measured as a proportion of plot area), and c and z are the species–area coefficient and exponent. This model takes account of the areas of the two habitat types but not their spatial configuration. Using the fact that $A_{\mathrm{tile}}+A_{\mathrm{wall}}=1$ and defining $k=h_{\mathrm{tile}}/h_{\mathrm{wall}}$ and $C=c{h}_{\mathrm{wall}}^z$, we can rewrite Eq. (1) as

$$S=C{\left(k{A}_{\mathrm{tile}}+1-A_{\mathrm{tile}}\right)}^z.$$ (2)

The model thus has three parameters (C, k and z) that must be fitted to the data.

We next extended the countryside model (Eq. (1)) to include the effects of different configurations:

$$S_j\left(A_{\mathrm{tile}}\right)=c_j{\left(h_{\mathrm{tile}}{A}_{\mathrm{tile}}+h_{\mathrm{wall}}{A}_{\mathrm{wall}}\right)}^{z_j}.$$ (3)

Now $c_j$ and $z_j$ are the species–area coefficient and exponent for configuration $j$. Enforcing the constraint that all configurations should tend to the same species richness (i.e., the species richness of the Area = 0 treatment plots) as $A_{\mathrm{tile}}\to 0$, we can re‐express Eq. (3) as

$$S_j\left(A_{\mathrm{tile}}\right)=C{\left(k{A}_{\mathrm{tile}}+1-A_{\mathrm{tile}}\right)}^{z_j}$$ (4)

where now $C=c_j{h}_{\mathrm{wall}}^{z_j}$. For this model five parameters must be fitted to the data: $C,k,z_{\mathrm{SL}},z_{\mathrm{SS}}$ and $z_{\mathrm{LOT}}$.

For completeness, we also fitted a third model to include the effects of habitat configuration only:

$$S_j=C_j$$ (5)

where $C_j$ is the average species richness in plots with configuration $j$.

To test whether the effects of area and habitat spatial configuration on species richness were mediated simply by variation in total individual abundance, we fitted another model that relates species richness directly to total individual abundance:

$$S\left(N\right)=S_0+b{N}^w$$ (6)

where N is the total number of individuals observed on a plot and $S_0$ (the number of species that are not measured as counts of individuals, such as algae), w and b are fitted parameters. If the species–individual model (Eq. (6)) were to provide as good a fit as the species–area–fragmentation model (Eq. (4)), this would suggest that the effects of area and configuration on species richness are mediated mainly by variation in total individual abundance, i.e., certain levels of area and certain configurations provide more suitable habitat for all organisms, and therefore higher levels of species richness via a simple sampling effect. Conversely, if the species–individual model (Eq. (6)) were to provide a poorer fit, this would suggest that the observed species–area–fragmentation relationship is mediated mainly by higher‐order mechanisms such as beta diversity and niche specialization.

All models were fitted to the seawall data by non‐linear least squares (function nls in R version 3.3.0 [R Development Core Team, 2016]; see Data S1). We performed 1,000 bootstraps, stratified by total tile area and configuration treatment, to obtain confidence intervals on the parameter estimates and fitted values.

We also performed a two‐way ANOVA to test the robustness of our results to different statistical methods. The experimental design consisted of two factors: “Area,” with three levels and “Configuration,” also with three levels (Fig. 2), which were both fixed and orthogonal to each other (i.e., the Area = 0 treatments were excluded). All ANOVAs were preceded by Cochran's test for heterogeneity of variances and all post‐hoc pairwise comparisons were made with Student–Newman–Keuls (SNK) tests.

To test whether niche specialization to different configurations (treatments) was an important factor underlying observed variation in species richness, we analyzed the co‐occurrence matrix of our whole data set to assess evidence for non‐random assembly across treatments. The number of rows of the co‐occurrence matrix is equal to the total number of species observed, and the number of columns is equal to the number of treatment plots (36). Entry {i, j} of the co‐occurrence matrix is equal to 1 if species i was present in plot j or equal to 0 otherwise. We then randomized the species co‐occurrence matrix, while maintaining the row and column sums, to create 10,000 null matrices (refer to Data S1). Lastly, we compared the species–treatment associations in the null matrices with those in the observed matrix to assess evidence of association between species and different plot configurations. For example, high prevalence of species restricted to a single plot configuration in the observed matrix, relative to the null matrices, would constitute evidence that the observed relationship between species richness and that configuration was driven by habitat specialists.

Results

In total, we counted 6,436 individuals of 68 faunal species. A further eight taxa without easily counted individuals were recorded as present: one colonial ascidian and seven algal functional groups (Appendix S1: Table S1). Species richness generally increased with increasing total tile area and was highest for the intermediate configuration, treatment SS (Fig. 3).

Figure 3.

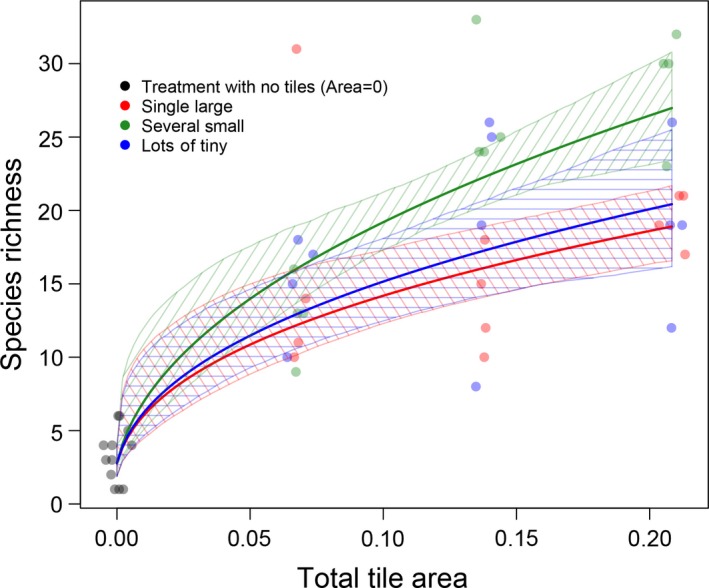
Plot species richness vs. total tile area measured as a fraction of plot area (points). The fitted model is shown with solid curves and 95% confidence intervals from 1,000 bootstraps. The x‐coordinates of points have been jittered to improve their visibility.

The species–area‐only model (Eq. (2)) explained 77.4% of the variance in the data (AIC = 65.8), with best‐fit parameters c = 2.77, k = 750.0, z = 0.407. The parameter k here measures the ratio of the habitat affinity parameters (Pereira and Daily 2006) of tiles and matrix, and the fitted value therefore indicates that the matrix was of negligible importance for plot diversity. Nevertheless, we still needed to include matrix area in our model to account for positive richness in the plots with no tiles, where 100% of the area is matrix (i.e., $A_{\mathrm{wall}}=1$ and $A_{\mathrm{tile}}=0$ but S > 0). The species–area–fragmentation model (Eq. (4)) provided a statistically indistinguishable fit to that of the species–area‐only model, explaining 79.1% of the variance (AIC = 66.2), with C = 2.78, k = 608, z _SL = 0.395, z _SS = 0.469, z _LOT = 0.411. A large fraction of the explained variance of the species–area–fragmentation model was due to the area effect and the Area = 0 treatment specifically (Fig. 3). Two‐tailed tests on the bootstrapped estimates indicated that z _SS was statistically significantly greater than the fitted estimates of z _SL and z _LOT (P = 0.004 and P = 0.014, respectively), but that z _SL and z _LOT were not statistically distinguishable (P = 0.608). The species–fragmentation‐only model (Eq. (5)) explained 75.9% of the variance in the data, with best‐fit parameters $C_{\mathrm{AREA}=0}=2.77$, $C_{\mathrm{SL}}=15.68$, $C_{\mathrm{SS}}=21.07$, $C_{\mathrm{LOT}}=16.81$. The fit of this model (AIC = 70.9) was poorer than that of the species–area‐only model and the species–area–fragmentation model (Table 1).

Table 1.

Summary of models fitted to the experimental data

Model name	Equation	Variance explained	AIC
Species–area‐only model	$S=C{\left(k{A}_{\mathrm{tile}}+1-A_{\mathrm{tile}}\right)}^z$	77.4%	65.8
Species–area–fragmentation model	$S_j\left(A_{\mathrm{tile}}\right)=C{\left(k{A}_{\mathrm{tile}}+1-A_{\mathrm{tile}}\right)}^{z_j}$	79.1%	66.2
Species–fragmentation‐only model	$S=C_j$	75.9%	70.9
Species–individual model	$S(N)=S_0+b{N}^w$	67.2%	83.7

Note: AIC, Akaike information criterion.

The species–individual model (Eq. (6)) also provided a poorer fit to the data than the species–area only and species–area–fragmentation models (best‐fit parameter estimates S ₀ = 0.985, b = 1.61, and w = 0.444; variance explained = 67.2%; AIC = 83.7; Table 1).

The two‐way ANOVA corroborated the results above, revealing significant differences in species richness among the Area (df = 2, 27; MS = 183.44; F = 6.14; P = 0.0063) and Configuration treatments (df = 2, 27; MS = 123.86; F = 4.15; P = 0.027; Fig. 4). Plots with 20 or 30 tiles (14% or 21% tile cover) generally hosted significantly greater S than plots with only 10 tiles (7% cover); while plots with tiles arranged in the SS configuration hosted significantly greater S than SL configurations (Fig. 4). A significant Area × Configuration interaction was present (df = 4, 27; MS = 87.03; F = 2.91; P = 0.040) as fragmentation per se (spatial configuration) did not have a significant effect on plots with the lowest Area treatment (10 tiles or 7% cover; Fig. 4). Treatment plots with no tiles (Area = 0) attached to the seawall substrate hosted significantly fewer species (S, 3.33 ± 1.83 [mean ± SD], SE = 0.53) than any of the plots with tiles (one‐way ANOVA; df = 3, 44; MS = 861.24; F = 26.34; P < 0.0001).

Figure 4.

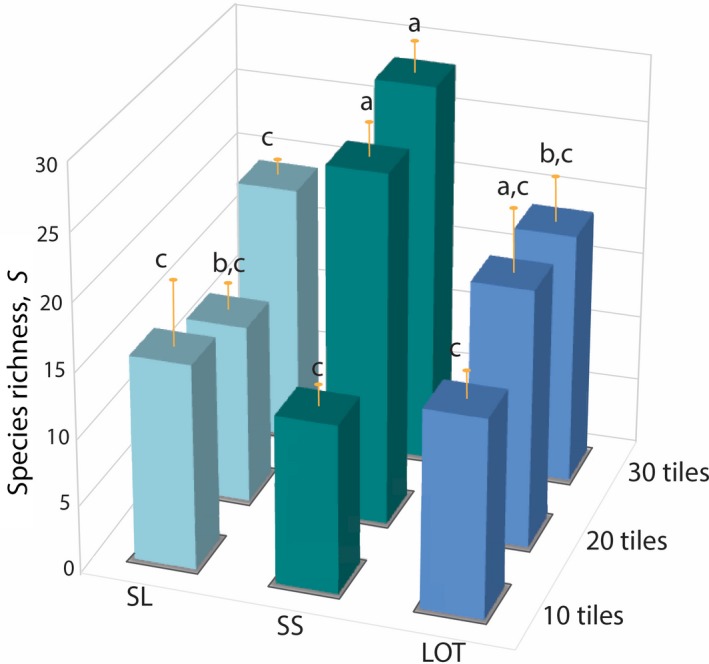
Species richness (S [mean + SE]) found within the nine different plot configurations. Different letters indicate significant differences among means (SNK tests, P < 0.05).

The co‐occurrence matrix for our data was consistent with a random assembly model, i.e., there was no statistically significant evidence that particular species were strongly associated with particular plot configurations (Fig. 5).

Figure 5.

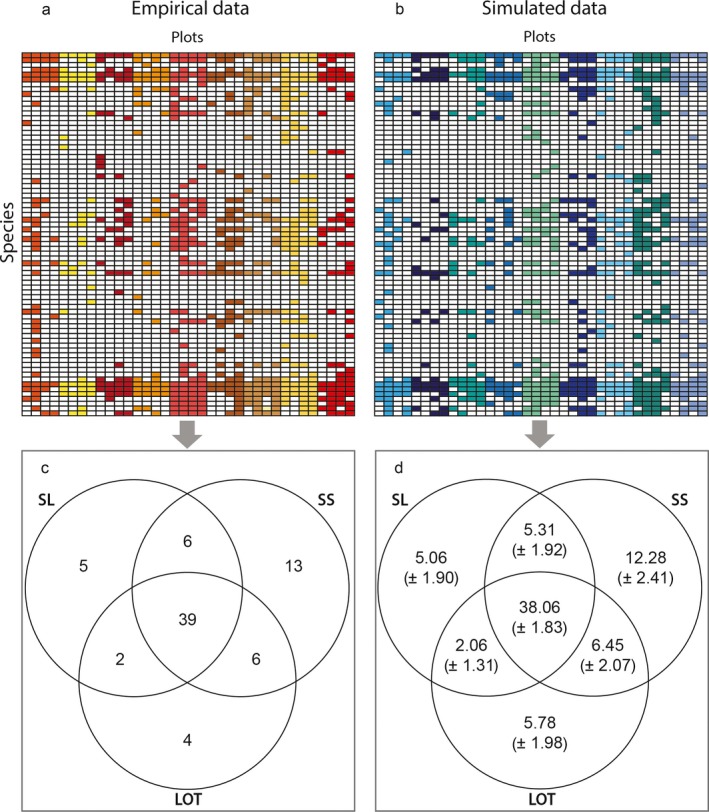
(a) Species (presence–absence) co‐occurrence matrix based on our empirical data, and a Venn diagram showing counts of species associated with each possible combination of plot configurations; (b) null matrix model based on randomizing the presence–absence matrix while maintaining the row and column sums and the mean species richness (n = 10,000; ±SD), along with the corresponding Venn diagram. The observed Venn diagram (c) is statistically indistinguishable from the Venn diagrams of the randomized co‐occurrence matrices (d).

Discussion

There exists a general consensus that both habitat loss and fragmentation per se are key drivers of global biodiversity change (Lindenmayer and Fischer 2007, Hanski et al. 2013, Haddad et al. 2015). However, isolating the effects of habitat configurations (i.e., fragmentation per se, sensu Fahrig 2003, 2017) experimentally is considered especially difficult as the habitat configuration often covaries with area and effects can be confounded by other explanatory variables, such as climatic conditions, and habitat identity and complexity, leading to unreliable inferences (McGarigal and Cushman 2002, Lindenmayer and Fischer 2007, Vellend 2016). Nevertheless, there have been repeated calls for manipulative field experiments or “small‐landscape” (sensu Swift and Hannon 2010) studies to investigate both area and configuration (fragmentation per se) independently (McGarigal and Cushman 2002, Fahrig 2003, Swift and Hannon 2010) so as to clarify the underlying mechanisms and system dynamics of these two complementary aspects of habitat destruction (Fahrig 2003, Lindenmayer and Fischer 2007). Empirical work is also considered to be lagging behind theoretical advances despite habitat fragmentation being one of the largest areas of study in conservation biology (Fazey et al. 2005, Lindenmayer and Fischer 2007, Miller‐Rushing et al. 2019).

Using artificial substrates on seawalls, we were able to test the independent and interactive effects of habitat area and configuration. We also measured species richness at the level of the entire system, i.e., habitat patch plus matrix, which is rarely examined in manipulative field experiments (Hoyle and Harborne 2005, Bonin et al. 2011) even though there is considerable evidence that the surrounding matrix and its quality can have a large influence on the dynamics within fragments (Ricketts 2001, Jules and Shahani 2003, Kupfer et al. 2006). Our results confirmed the expectation (hypothesis 1) that, on the whole, average species richness would increase with habitat area: average species richness was just 3.3 on control plots with zero tiles, but rose to 22.4 on plots with the maximum number of tiles (30 tiles = 21% habitat; Appendix S1: Table S2). More intriguingly, species richness did not increase monotonically with fragmentation per se as expected (hypothesis 2), but was highest at intermediate fragmentation configuration, i.e., when tiles were placed in a SS configuration (center column of Fig. 2). However, the statistical support for this result was equivocal: although the several‐small configuration on average had 37% more species than the SL and 27% more species than the lots‐of‐tiny (LOT) configurations, and although pairwise comparisons reported these differences to be significant, the area–fragmentation model was not clearly superior to the area‐only model as a predictor of species richness (as judged by AIC). We found little evidence that the matrix was an important contributor to species richness. The estimated habitat affinity (Pereira and Daily 2006) of tiles was several hundred times greater than that of matrix. Together, our results suggest that species richness of seawalls peaks at maximum tile density and intermediate fragmentation configuration, with the evidence strongest for tile density.

We found no evidence for threshold effects, i.e., the effect of configuration on species richness was not greater when total tile area was smaller (Fig. 3), although this may be because our maximum total tile area (21% in the LOT treatment; Fig. 2) was already below the threshold at which these effects have previously been observed in other systems (Andrén 1994, Swift and Hannon 2010). This result is interesting as it is contrary to the widely accepted view that configuration only makes a difference when the amount of habitat is low (see Hanski 2015), but is similar to the experimental results of With (2016), who reported that, at low habitat area (10–20%), more fragmented landscapes supported greater richness compared to those with clumped configurations. The lack of a significant difference in species richness among plots of different configurations with low habitat area (i.e., plots with 10 tiles = 7% habitat cover), but not among plots with 20 and 30 tiles, also explains why there was a significant Area × Configuration interaction in the ANOVA results. It suggests that habitat configuration only matters when there is a minimum habitat amount; when the habitat area in a landscape is simply too low, configuration does not matter. This amount/proportion should also be dependent on the spatial extent of the landscape as it affects inter‐patch distances and dispersal ability of mobile species. For instance, at very small scales (mm to cm), configuration is unlikely to matter even when there is low habitat amount because organisms are unlikely to be dispersal limited (we discuss this in detail below), that is, they will be able to traverse the matrix and move between patches easily because the inter‐patch distances are too small to be barriers to dispersal. Organisms are only dispersal limited when their dispersal ability is lower than the distances between patches. Thus, when habitat amount is low at larger spatial scales, organisms are likely to invest a greater proportion of their time in migration within the poorer quality matrix, and experience an overall increase in mortality (Moilanen and Hanski 2001).

What mechanisms can explain the peak of species richness at intermediate fragmentation configuration? We found that the mechanisms that act indirectly via effects on total individual abundance cannot alone explain the results, because our model relating species richness to total individual abundance (Eq. (6)) performed worse than our species–fragmentation‐only, species–area‐only and species–area–fragmentation models (Eq. (2), Eq. (4) and Eq. (5); Table 1). We also found no evidence that certain species were niche‐adapted to certain kinds of arrangement patterns, i.e., there was no significant departure from non‐randomness in the species‐by‐plot co‐occurrence matrix (Fig. 5). In addition, there were no significant differences in community composition among the nine plot treatments (Appendix S1: Table S3).

Having rejected standard hypotheses for why richness would peak at intermediate fragmentation configuration, we are left to speculate that some combination of processes independent of niche adaptations and individual density is driving the result. One possibility is that the dispersal scale of intertidal organisms is such that dispersal limitation acts most strongly in the SS configurations. Dispersal data are scarce for most species in our system, but one species, the knobbly periwinkle (Echinolittorina malaccana) has been observed to disperse a maximum of 25 cm over four days and a maximum of 100 cm over two months (Chapman and Underwood 1994). Congeners of the tropical neritid snails observed in our system have been recorded to disperse roughly 40–100 cm on average over four days (Levings and Garrity 1983). Given these numbers, our intermediate and most‐fragmented configurations are likely more impervious to dispersal since habitat patches are interspersed within the matrix compared to our least‐fragmented configuration (Fig. 2), and thus one would expect dispersal limitation to act more strongly and diversity to be higher in these more‐fragmented configurations because organisms cannot easily disperse from one patch to another (i.e., they are dispersal limited), which would result in greater beta diversity (species turnover in space). But why would diversity be highest at intermediate fragmentation configuration specifically? Our speculative explanation is that the mean patch separation in the intermediate scenario (48.3 cm) is larger than that of the most‐fragmented configuration (32.0 cm), which results in dispersal limitation and hence diversity being highest in the intermediate configuration. We encourage future empirical work that directly measures and manipulates (by translocation) dispersal ability of organisms to test these ideas.

Another possible explanation, also consistent with all our evidence, is that while dispersal limitation enhances diversity with fragmentation per se, another mechanism, local conspecific negative frequency‐dependent selection mediated by predation, acts in the opposite direction. This would occur if predators are more efficient when prey are clumped together on seawalls. There is ample evidence for negative frequency‐dependent selection in intertidal communities, on similar scales to those considered here (Connell 1985, Ortega 1985, Dunmore and Schiel 2003, Jenkins et al. 2008), and in at least one case there is evidence linking the selection to predation (Seitz et al. 2001). Again, our hypotheses for what drives the observed diversity pattern in plots with different patch configurations on seawalls could be tested with further manipulative experiments.

A caveat of our study is that, by design, it examines the “fragmentation problem” in reverse, by starting with a non‐habitat substrate and adding habitat tiles to it. In contrast, in most conservation problems, the starting condition is 100% habitat and habitat is progressively removed. A different experiment, more representative of how fragmentation (i.e., as process) occurs in practice (i.e., loss of area with change in habitat configuration), would be to remove tiles from a completely tiled seawall. We expect that in the short term such an experiment would reveal maximum diversity in the highly fragmented configuration (LOT), because the tiny patches characteristic of this configuration would have inflated species richness due to unpaid extinction debts and the legacy of past negative frequency dependent selection. But, in the long term, after the extinction debt is paid, such an experiment should equilibrate to conditions similar to those in our study and reproduce comparable results. Indeed, in a similar way, other studies have used natural island systems as an analogue of fragmented systems (MacDonald et al. 2018). These considerations highlight the suitability and tractability of seawalls as a model system for exploring the relationship between spatial habitat configuration and biodiversity. Further, many species on intertidal seawalls have relatively short life‐spans, manageable sizes, and are slow‐moving or sessile.

Our findings inform the long‐running debate about how habitat configuration and habitat area jointly determine landscape species richness (Tscharntke et al. 2012, Villard and Metzger 2014, Fahrig 2015, Hanski 2015). Specifically, we found equivocal support for the notion that only total habitat area need be considered when estimating species loss (Fahrig 2013). On the one hand, our area–only model (Eq. (2)) performed just as well as our area–fragmentation model (Eq. (3)). On the other hand, there were statistically significant differences between the fitted SAR exponents for the three configurations (SL, SS, and LOT) in the area–fragmentation model (Eq. (3); Fig. 3). More fundamentally, the importance of configuration is very likely to depend on the spatial extent under consideration. It may well be that at the small scales characteristic of experimental studies, where species can disperse between patches relatively easily, the effects of habitat spatial configuration are secondary to those of total area. However, at the larger (regional) scales of real‐world conservation problems, the situation may be quite different. Simple arguments such as the reduction ad absurdum argument in the Introduction show that when the spatial scale becomes large enough, habitat configuration must have important effects on species richness, above and beyond those of total habitat area. The applied goal of research into species–area–fragmentation relationships is to design better conservation reserve systems. For conservation and ecological engineering programs involving seawall enhancement with concrete tiles (Lai et al. 2015, Loke et al. 2015), we recommend, based on the insights achieved in this study, that tiles be placed in an intermediate configuration to maximize their effectiveness (Fig. 2, middle column, SS). However, our results also suggest that when habitat area is very low, it matters little how these tiles are arranged.

In summary, we note that experimental studies on the area‐independent effect of habitat configuration on species diversity are rare outside of computer simulations (Hanski et al. 2013, Chisholm et al. 2018). Furthermore, the few real‐world experiments that have been conducted have mostly focused on diversity in single patches, whereas what is ultimately needed to inform landscape conservation are experiments that consider diversity in multiple patches and the surrounding matrix. Our contribution is a novel seawall experimental system that allowed the independent effects of habitat area and spatial configuration on species richness to be replicated and tested. Overall, habitat area had the greatest effect on richness. Habitat configuration had weaker effects, with species richness greatest at intermediate fragmentation configuration, the first time this has been shown in a manipulative field experiment. The effect of habitat configuration was not due to passive sampling (since area was controlled for), or solely to variation in total individual abundance or niche specialization of species to different arrangement patterns (treatments). We speculate that this could be due to dispersal limitation alone or a combination of dispersal limitation and local negative density dependence, two fundamental ecological mechanisms, but we emphasize the need for more experimental research to delve into these mechanisms.

Supporting information

 

 

 

Loke, L. H. L. , Chisholm R. A., and Todd P. A.. 2019. Effects of habitat area and spatial configuration on biodiversity in an experimental intertidal community. Ecology 100(8):e02757 10.1002/ecy.2757