Deep learning‐based carotid media‐adventitia and lumen‐intima boundary segmentation from three‐dimensional ultrasound images

Abstract

Purpose

Quantification of carotid plaques has been shown to be important for assessing as well as monitoring the progression and regression of carotid atherosclerosis. Various metrics have been proposed and methods of measurements ranging from manual tracing to automated segmentations have also been investigated. Of those metrics, quantification of carotid plaques by measuring vessel‐wall‐volume (VWV) using the segmented media‐adventitia (MAB) and lumen‐intima (LIB) boundaries has been shown to be sensitive to temporal changes in carotid plaque burden. Thus, semi‐automatic MAB and LIB segmentation methods are required to help generate VWV measurements with high accuracy and less user interaction.

Methods

In this paper, we propose a semiautomatic segmentation method based on deep learning to segment the MAB and LIB from carotid three‐dimensional ultrasound (3DUS) images. For the MAB segmentation, we convert the segmentation problem to a pixel‐by‐pixel classification problem. A dynamic convolutional neural network (Dynamic CNN) is proposed to classify the patches generated by sliding a window along the norm line of the initial contour where the CNN model is fine‐tuned dynamically in each test task. The LIB is segmented by applying a region‐of‐interest of carotid images to a U‐Net model, which allows the network to be trained end‐to‐end for pixel‐wise classification.

Results

A total of 144 3DUS images were used in this development, and a threefold cross‐validation technique was used for evaluation of the proposed algorithm. The proposed algorithm‐generated accuracy was significantly higher than the previous methods but with less user interactions. Comparing the algorithm segmentation results with manual segmentations by an expert showed that the average Dice similarity coefficients (DSC) were 96.46 ± 2.22% and 92.84 ± 4.46% for the MAB and LIB, respectively, while only an average of 34 s (vs 1.13, 2.8 and 4.4 min in previous methods) was required to segment a 3DUS image. The interobserver experiment indicated that the DSC was 96.14 ± 1.87% between algorithm‐generated MAB contours of two observers' initialization.

Conclusions

Our results showed that the proposed carotid plaque segmentation method obtains high accuracy and repeatability with less user interactions, suggesting that the method could be used in clinical practice to measure VWV and monitor the progression and regression of carotid plaques.

1. Introduction

Ischemic stroke caused 2.69 million deaths worldwide,1 primarily caused by formation of plaques at the carotid arterial bifurcations.2 When a carotid arterial plaque ruptures, ischemic stroke may result due to cerebral embolism from a thrombotic plaque or thrombosis at the site of plaque rupture. Plaques at the carotid bifurcation are a major source of thrombosis and subsequent cerebral emboli.3 Since the probability of many strokes caused by carotid plaques can be prevented by lifestyle changes, dietary, or medical treatment,4 noninvasive and local carotid plaque quantification is important for monitoring progression of the disease in patients at risk and regression in response to treatment.5

Ultrasound (US) image assessment of carotid plaques plays an important role because of its noninvasive nature, low cost, short examination time, widespread availability, and US image‐based features revealing valuable information on plaque composition and stability.6, 7 Intima‐media thickness (IMT) measurement8 using two‐dimensional ultrasound (2DUS) images is the most commonly used assessment method at present in clinical practice,9 in which the distance is measured between the lumen‐intima boundary (LIB) and the media‐adventitia boundary (MAB).10, 11 Compared to two‐dimensional US (2DUS) images, 3DUS images provide a more repeatable and effective tool to analyze plaque characteristics, composition, and morphology, as well as to monitor the progression and regression of plaques for evaluating the effect of treatment.12 Wannarong et al reported that in patients attending vascular prevention clinics, progression of the total plaque volume (TPV) was more predictive of cardiovascular events than measurement of total plaque area, and progression of IMT did not predict events.13 Several 3DUS‐based measurements have been reported to be more sensitive to changes in carotid plaques with treatment than the widely used IMT measurement; these include carotid total plaque volume (TPV),13, 14 vessel wall volume (VWV),15, 16 vessel‐wall‐plus‐plaque thickness (VWT)17 and VWT‐Change.18, 19 For measurement of TPV, segmentations of the MAB and LIB are required.20 Moreover, MAB and LIB segmentations are also required to obtain VWV, VWT, and VWT‐Change biomarkers.

Delineations of MAB and LIB can be performed manually by experienced observers or medical experts. However, it is time consuming for an observer to learn and practice manual MAB and LIB segmentation, and the variability in the measurement relies on the experience of the observer.17, 19 As well, manual segmentation is a time‐consuming procedure that requires about 20 min per vessel. Thus, a computer‐assisted segmentation method for MAB and LIB segmentation has the potential to reduce the subjectivity and variability in the manual approach and segmentation time without training observers.

Some studies only segmented the carotid LIB, such that Gill et al21 and Solovey22 proposed direct 3D segmentation methods only for LIB segmentation. Gill et al proposed a dynamic balloon model‐based method to approximate to the vessel wall and further used edge‐based energies to refine the LIB.21 Solovey segmented the LIB of 3D carotid ultrasound images using weak geometric priors.22 However, both of those methods were based on geometric priors, where the shape of LIB was not regular due to plaques, especially in the bifurcation. There were also some algorithms presented to segment both LIB and MAB from 3DUS images of carotid arteries. Yang et al used an active shape model to segment the common carotid artery from 3DUS images to monitor changes in carotid plaques in response to drug therapy23. In this method, the authors used manual segmentation of the baseline data for training and follow‐up data for segmentation, which yielded a Dice Similarity Coefficient (DSC) of 93.6% ± 2.6% and 91.8% ± 3.5% for MAB and LIB segmentations, respectively. Ukwatta et al developed a 2D level set‐based approach to delineate the MAB and LIB of the common carotid artery (CCA) from 2DUS image slices of 3DUS images with the DSC of 95.4% ± 1.6% and 93.1% ± 3.1%, respectively.24 Since these approaches required user interactions on every individual slice, they were time‐consuming, requiring 4.4 ± 0.6 min and 2.8 ± 0.4 min, respectively. Furthermore, in order to reduce user interaction, Ukwatta et al. used 3D sparse field level set (3D SFLS) algorithm to directly segment the MAB and LIB of the CCA from 3DUS images.25 However, the user interaction of this method was still complex, which required the observer to choose several anchor points on both MAB and LIB of a set of transverse slices, locate the bifurcation point (BF), and define the long axis of the artery.

These previous methods used to segment the MAB and LIB have two limitations. First, user interactions in the previous publications are complex and laborious and rely on the experience of the observers. Second, they are sensitive to the initial points making generalization ability of the methods poor. Thus, these limitations are motivating investigators to develop a segmentation method based on deep learning, which is easier to use and more robust to different subjects and US imaging systems.

Some recent studies used deep learning methods to segment B‐mode 2DUS images of CCA. Rosa‐Maria et al. applied extreme learning machine (ELM)‐based autoencoders to segment the intima and media boundaries to obtain an IMT measurement from longitudinal B‐mode 2DUS images of CCA.26 Although, the ELM‐based autoencoders achieved a good performance to measure the IMT, it can only be used in the early‐stage atherosclerosis detection. Shin et al used a CNN to segment the intima and media boundaries automatically from videos of the carotid artery.27 For both these methods, a sliding window approach was applied to the whole image to detect the intima and media boundaries and both were applied to longitudinal US images of CCA. Azzopardi et al used deep CNN and phase congruency maps to segment MAB from B‐mode 2DUS images of CCA.28 However, there was a correlation among images used in training and testing since all images were obtained from only five subjects.

In this paper, we propose novel methods to segment MAB and LIB from 3DUS images of the CCA based on a dynamic CNN and U‐Net. The main contributions are as follows:

First, a data preprocessing method is proposed to enhance the edge‐contrast of CCA US images. Second, a semiautomatic method, dynamic CNN, is proposed for MAB segmentation, which fine‐tunes the CNN model dynamically to fit carotid images of different subjects. The user interaction in our method is simpler than previous methods,24, 25 as it reduces the number of anchor points and does not need the user to define the long axis of the artery. The user interaction time is reduced by more than half compared to the algorithm proposed by Ukwatta.25 Third, LIB segmentation is automated based on an improved U‐Net29 network, which converts the segmentation task to a two‐object classification problem of the lumen and nonlumen regions. Moreover, this study is the first to apply a deep learning technique for carotid segmentation from 3DUS CCA images of subjects with carotid stenosis over 60%.

The remainder of this paper is organized as follows. Section II describes the experimental dataset and the details of the proposed method, which includes the preprocessing, the design of dynamic CNN architecture for MAB segmentation, details of the improved U‐Net for LIB segmentation and evaluation metrics. Section III presents the experimental results, which are compared to other methods. In section IV, we discuss the results and characteristics of the proposed method. Finally, the last section (Section 5) discusses the potential use of the method for research and clinical use.

2. Materials and methods

Our method is based on deep learning algorithms used to segment the MAB and LIB from carotid 3DUS images to determine the VWV measurement of carotid plaques. Since it is difficult to obtain a large number of labeled 3DUS images to train a 3D deep CNN network, we converted the task into a 2D segmentation task by slicing the 3DUS images into 2DUS images. Figure 1 shows the flowchart of the algorithm. A dynamic convolutional neural network is proposed for the MAB segmentation to fine‐tune the learned CNN parameters and obtain a more accurate segmentation. Since other authors have shown that U‐Net performs well for medical image segmentation tasks, a modified U‐Net deep learning network was used for LIB segmentation, which allows training of the network for pixel‐wise classification.

Figure 1.

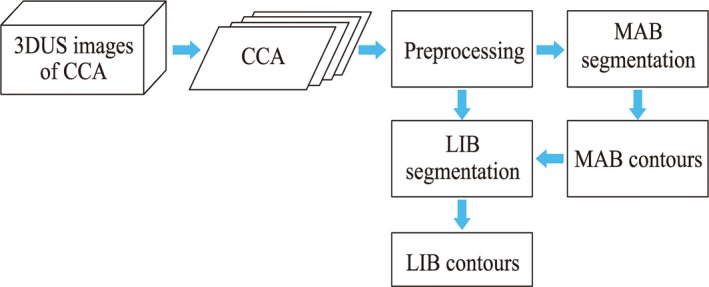
The process flow diagram of the presented algorithm. [Color figure can be viewed at http://wileyonlinelibrary.com]

2.1. Experimental dataset

Thirty‐eight subjects (a mean age ± SD of 69 ± 9 yr) were enrolled in our experiments who had carotid stenosis over 60% confirmed from Doppler US flow velocity measurements.30 These data were chosen since the plaques were relatively large and posed a risk to these patients. All subjects were recruited from the Stroke Prevention and Atherosclerosis Research Centre at Robarts Research Institute, London, Canada (Western University). Patients provided written informed consent to a study protocol approved by the University of Western Ontario Standing Board of Human Research Ethics.

For all subjects, 3DUS images were obtained of both the left and right carotid arteries at baseline and at 3 months follow‐up, using a Philips/ATL HDI 5000 US transducer with an L12‐5 probe (8.5 MHz central frequency) attached to a motorized linear 3DUS acquisition system that moved the transducer along the neck at a constant speed of 3 mm/s.30 The 2DUS images were acquired into a computer via a digital frame grabber and saved and reconstructed into a 3DUS image with 0.1 mm × 0.1 mm × 0.15 mm voxel size. This study generated a set of 3DUS carotid images with segmented MAB and LIB, which were available to us. A total of 152 3DUS images of carotid plaques were acquired from the 38 objects. Of these 3DUS images, there were three 3DUS images in which the length of the acquired common carotid artery part was too short (<3 mm) and it was difficult to place the initial anchor points by the observers in another five 3DUS images. The remaining 144 3DUS images were used in the experiments.

Since training the deep net requires a large number of labeled samples, 144 3DUS images were not sufficient to train a 3D deep learning network. We used the original acquired 2DUS images for LIB and MAB segmentation, which were used to reconstruct the 3DUS images. According to Chui's researches,17, 19 LIB and MAB contours with 1‐mm intervals were used to generate the measurements of VWV, VWT, and VWT‐change. Thus, in our experiment, a total of 2021 2DUS images with pixel dimensions of 0.1 mm × 0.1 mm were obtained with the slice interval of 1 mm.

The multiplanar 3D viewing software was used to present 2D images slice‐by‐slice from the transversal view of the carotid artery 3DUS image.31, 32 An expert then outlined the MAB and LIB boundaries of all the 3DUS images.

2.2. Preprocessing of CCA ultrasound images

Since the original CCA ultrasound images have low tissue contrast, we first applied a linear grey level stretch to enhance the contrast of the images. Then, an improved adaptive region‐based distribution function (ARBD)33 was used to eliminate high‐intensity speckle in the images and increase the contrast of edges. The modified the ARBD function was used to obtain a “compensation” image, g. Then, the edge‐enhanced image, I', was generated by subtracting the compensation term, γg, from the original image I:

$$\begin{array}{cc}\hfill I^{\prime }& =I-\gamma g\hfill \\ \hfill g& =(I·h)-(I·p)\hfill \end{array}$$ (1)

where h and p are two Gaussian filters with different kernel sizes and g is the difference between the convolution of the original image I with the two Gaussian filters h and p. The constant γ is a coefficient of the compensation term. In our experiments, the value of 2 was chosen for γ. The kernel sizes of g and h were 3 × 3 and 9 × 9 pixels, respectively.

2.3. Segmentation of MAB using dynamic convolutional neural network

Training a CNN with a great generalization ability requires a large number of labeled training samples. However, it is hard to obtain many labeled CCA ultrasound images with a specific pathology. Thus, our aim was to design a deep network, which could fine‐tune the model dynamically during testing.

The dynamic convolutional neural network, which adjusts the model to adapt to different subjects, was used to segment the MAB of CCA from 3DUS images. The proposed method consists of two parts: pretraining the CNN model, and dynamically fine‐tuning the CNN model during segmentation. Figure 2 shows the workflow details of our approach, which is the MAB segmentation part of the high‐level flowchart shown in Fig. 1. In our approach, we convert the segmentation problem to a two‐class classification problem by classifying each pixel around the initial contour as to whether it is on the media‐adventitia boundary or not. First, a CNN is pretrained for the initialization of the dynamic CNN, and then, for each 2D CCA image, MAB is segmented by the dynamic CNN, which is fine‐tuned to classify patches generated by sliding windows along the norm line of the initial MAB. Details of this approach are provided in the next two subsections.

Figure 2.

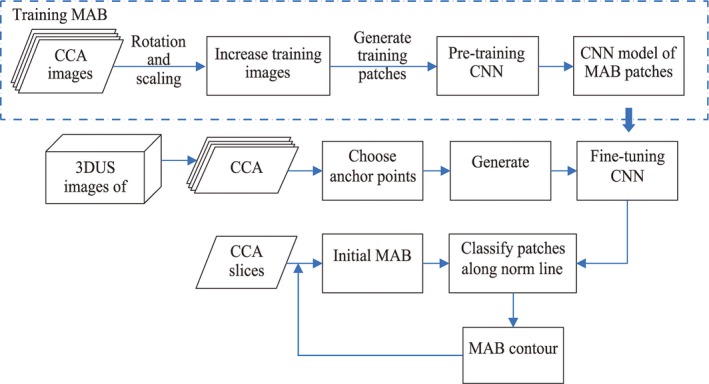
The flow chat of MAB segmentation including the process of training stage and testing stage. [Color figure can be viewed at http://wileyonlinelibrary.com]

2.3.1. Pretraining CNN

First, patches were generated for pretraining a CNN model by sliding a window along the norm lined of each point on the manually delineated MAB of all CCA slices in the training dataset. Since the CNN input images are small, the patches with a size of 64 × 64 pixels were used in our experiments, we used a simple CNN architecture rather than the popular CNN architectures, such as AlexNet,34 VGG,35 GoogLeNet.36 The architecture of our pretrained CNN is shown in Fig. 3, which contains three convolution‐pooling blocks, two fully connected (FC) layers, and a softmax output layer. The kernel sizes of the three convolution layers are 9 × 9, 7 × 7, and 3 × 3 pixels, respectively. Compared to the sigmoid function, the ReLU active function converges faster to the optimal value.37 Thus, the local response normalization (LRN) layer was applied after a ReLU layer, which normalizes the input in a local region across or within feature maps.34 The output of LRN normalization $\left(b_{x,y}^i\right)$ is described by the Eq. (2), thus:

$$b_{x,y}^i=a_{x,y}^i/{(k+\alpha \sum _{j=\text{max}(0,i-n/2)}^{\text{min}(N-1,i+n/2)}{(a_{x,y}^j)}^2)}^{\beta }$$ (2)

where $a_{x,y}^i$ is the activity of a neuron computed by applying kernel i at position (x, y), the sum runs over n “adjacent” kernel maps at position (x, y), and N is the total number of kernels in the layer. The hyperparameters α, β, k and n are constants, and we used α = 10⁻⁴, β = 0.75, k = 2, and n = 5 in our experiments.34

Figure 3.

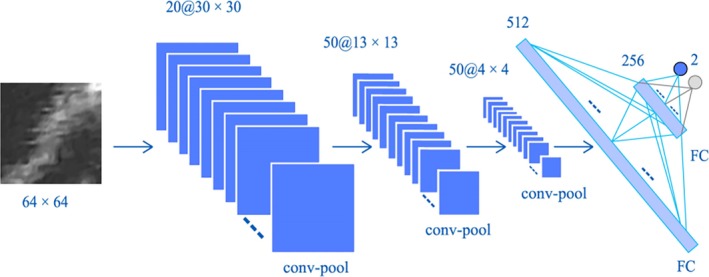
The architecture of our pretraining convolutional neural network (CNN), which contains two convolutional‐pooling blocks and two full connection layers. The inputs of the CNN are 64 × 64 patches generated along norm lines of the initial contours. [Color figure can be viewed at http://wileyonlinelibrary.com]

A stack of convolutional layers is followed by two fully connected layers. The first fully connected layer has 512 channels and the following one contains 256 channels. In optimization of the pretrained CNN, Mini‐batch Stochastic Gradient Descent (SGD) was used and a weight decay, λ, (regularization term coefficient) was used to prevent over‐fitting. The update rule for weight w is given by:

$$w_{i+1}=w_i+m·v_i-\lambda \eta w_i-\eta \frac{\partial E}{\partial w}$$ (3)

where i is the iterations count, v_i is the momentum, m is the momentum coefficient, λ is weight decay, η is the learning rate, and $\frac{\partial E}{\partial w}$ is the derivative of the energy function with respect to w. In our experiments, m and λ were set to 0.9 and 0.0005, respectively.34

2.3.2. MAB segmentation using dynamic CNN

In order to fine‐tune the CNN model dynamically, the observer is required to choose several anchor points on the MAB in the 3DUS images. These anchor points are also used to generate initial MAB contours to limit the search region of the sliding window. Figure 4 shows the process of generating initial MAB contours in a 3DUS CCA image. The observer chooses four or eight anchor points on the MAB of a set of transverse slices with a user‐specified interslice distance (ISD), as shown in Fig. 4(a). According to Ukwatta's publication,25 the value of ISD used in this paper was 3 mm. Figure 4(b) shows initial contours on each user interaction plane generated from the anchor points using the cubic spline interpolation method. A symmetric correspondence algorithm was used to match the corresponding points between two adjacent parallel slices.17, 19 This symmetric correspondence method provides a method to overcome mismatching problems caused by complicated shapes of the initial contours. As shown in Fig. 4(c), a 3D surface of initial the MAB boundaries was generated and the initial MAB contours of slices without userinteraction were obtained from the 3D surface.

Figure 4.

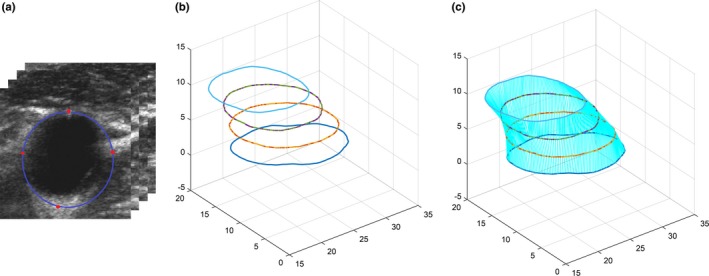
The initialization of MAB segmentation. (a) User interaction on transverse slices of three‐dimensional ultrasound common carotid artery images every 3 mm (i.e., every three slices). The red points are located manually and the blue contours are generated using cubic spline interpolation. (b) Generated initial contours of all slices in (a). (c) Interpolated initial MAB contours from the corresponding points of the two adjacent user interaction slices in (b). [Color figure can be viewed at http://wileyonlinelibrary.com]

The dynamic CNN is then applied in the test procedure to fine‐tune all layers of the pretrained CNN with patches extracted from the generated initial contours. The final MAB is obtained by classifying pixels along the norm line of the initial MAB contours. Patches extracted along the norm line are applied to the dynamic CNN to generate energy probability maps. Each point with the highest probability along a norm line is considered as a point on the MAB. An example result is shown in Fig. 5, where the initial contour is in red, the generated norm line is in yellow, and the blue rectangle represents a patch extracted along the norm line. The architecture of deep tuning is the same as the pretrained CNN, as shown in Fig. 3.

Figure 5.

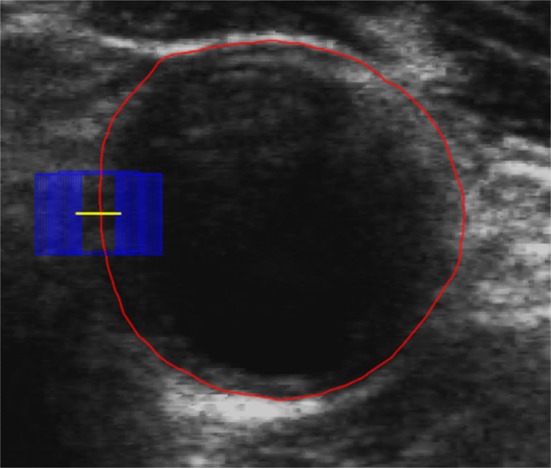
Generate patches along norm line of each initial MAB. The red contour is the initial contour, the yellow line is the generated norm line and the blue rectangle is a patch extracted along the norm line. [Color figure can be viewed at http://wileyonlinelibrary.com]

2.4. Segmentation of LIB using U‐Net deep network

The contours of LIB in CCA US images are difficult to visualize due to the low contrast of some plaque‐lumen boundaries, shadowing from calcified plaques and the irregular shape of some plaques. However, the lumen in US images of the CCA is dark and homogeneous. Thus, we convert the LIB segmentation problem to a lumen classification task, where the goal is to classify each pixel into two categories: a pixel in the lumen and outside the lumen regions.

First, the ROIs of CCA images were obtained according to the segmented MAB and these were all normalized to a size of 128 × 128 pixels. The lumen segmentation was performed using an improved U‐Net, which has achieved excellent performance in a related medical image segmentation task.29 The U‐Net provides a fully automatic method for LIB segmentation without any user interaction. The U‐Net architecture consists of an encoder network to extract features from an input image, a corresponding decoder network to reconstruct feature maps with the same size of the original image, and a soft‐max layer to classify the features maps to lumen and nonlumen regions on a pixel‐by‐pixel basis.

As illustrated in Fig. 6, the encoder part (left side) is the architecture of a convolutional network including four blocks, each of which is composed of a repeated application of two 3 × 3 convolutions followed by a rectified linear unit (ReLU), a 2 × 2 max‐pooling operation with a stride of 2 and a drop‐out layer. The dropout layer randomly sets input elements to zero with a given probability to prevent the network from overfitting. A shortcut connection is applied, which connects the input of each convolutional block to the output directly by skipping two stacked convolutional layers. As shown in Fig. 6, the red arrow lines are the shortcut connections.

Figure 6.

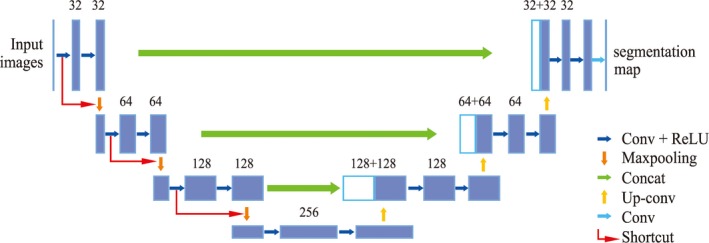
The modified U‐Net architecture. Blue boxes represent feature maps. The number of channels is denoted above each feature map. [Color figure can be viewed at http://wileyonlinelibrary.com]

The decoder part (right side) is an up‐sampling process where an up‐sampling block consists of a 2 × 2 up‐convolution, a concatenation with the corresponding feature map from the encoder part and two 3 × 3 convolutions, each is followed by a ReLU. The last layer is a 1 × 1 convolution to map each 64‐component feature vector to a 2D vector. Then a pixel‐wise soft‐max layer is used to classify each pixel into two categories, within the lumen or outside the lumen.

Assuming $a_{x,y}^i$ is the activity of a neuron computed by applying channel i at position (x, y), the output of the pixel‐wise soft‐max layer is given by:

$$p^i(x,y)=\frac{\text{exp}(a_{x,y}^i)}{\sum _{j=\mathrm{1}}^K\text{exp}(a_{x,y}^j)}$$ (4)

where K is the number of classes.

The energy function is computed by the cross‐entropy loss function. In our application, it is a binary classification problem, where the foreground is the lumen and the region outside the lumen is the background. Assuming the lumen region is labeled by 1 and the background is labeled by 0. Then, the cross entropy penalizes the deviation of the output of the soft‐max layer from 1 using:

$$E=\sum _{(x,y)\in Z^2}w(x,y)\text{log}(p_{l(x,y)}(x,y))$$ (5)

where l is the true label of each pixel, p_{l ( x , y )}(x,y) is the probability output of the soft‐max layer for pixels classified to 1, and w is a weight map.

The weight map is precomputed using masks of images used for training, and is used to calculate the probability of a pixel belonging to a certain class at every position in the training images. Equation (6) gives the weight map belonging to the lumen.

$$w(x,y)=\frac{1}{N}\sum _i^{N}mas{k}_i(x,y)$$ (6)

where N is the number of training images, i is the index of images, and mask(x, y) is the label in a training image at position (x, y) where lumen pixels in a mask image are labeled as 1 and background pixels are 0.

We improved the basic U‐Net to adapt it to the LIB segmentation task as follows:

1. Network architecture: Since the size of our input ROI images of the CCA are 128 × 128 pixels, which is smaller than the size of input images in the original U‐Net,29 we simplified the U‐Net architecture from five convolutional to four convolutional blocks and reduced the number of basic convolutional kernels from 64 to 32. This modified network architecture takes a shorter time to train and converges faster to the optimal value.

2. Dropout: To avoid overfitting in the designed U‐Net, we added a drop‐out hidden layer after each convolutional block of the encoder part, which randomly sets input elements to zero with a probability of 50%.

3. Shortcut connections: In order to avoid overfitting, shortcut connections were added to the original U‐Net architecture, which connect the input to the output of each convolutional block, skipping two convolutional layers. As shown in Fig. 7, the output of a traditional plain convolutional block F(x) is modified by a short connection between the input to the output, giving an output of F(x) + x which could be realized by a feed‐forward propagation, and the entire network can still be trained by backward propagation. Identity shortcut connections add neither extra parameters nor computational complexity and they can solve the vanishing/exploding gradient problem33, 34 during training.

4. Optimization method: The adaptive moment estimation method (Adam) is used in the training, which is an adapted learning rate algorithm.35 The Adam algorithm dynamically adapts parameters and learning rate using first‐order and second‐order moment estimation that can effectively accelerate the convergence of optimization.

5. Weight map in the loss function: A weight map was added to the original cross‐entropy loss function according to the class frequencies at every position of the map in the training data set.

Figure 7.

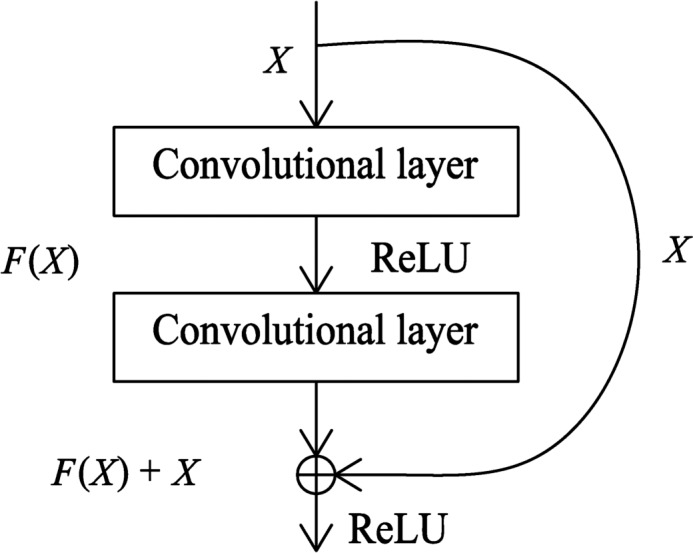
The architecture of convolutional block with a shortcut

2.5. Data augmentation

We used scaling and rotation transformations to increase the training samples, where the scale ratios were [0.5000， 0.7000，0.9000，1.1000，1.3000，1.5000] and six rotation angels were randomly chosen from 0° to 90° for each image. This increased the number of images by a factor of 13 for a total of 26,273 2D images.

2.6. Evaluation metrics

In order to compare our results with a previous method,23 the same volume‐based, region‐based, and distance‐based metrics were used to evaluate the performance of our segmentation method. Volume‐based metrics included VWV difference (∆VWV), MAB volume difference (∆MABV), LIB volume difference (∆LIBV), absolute VWV difference (|∆VWV|), absolute MAB volume difference (|∆MABV|), and absolute LIB volume difference (|∆LIBV|), all expressed as percentages.

The Dice similarity coefficient (DSC) was used to quantify the area overlap between the algorithm segmentation with the ground truth boundaries, thus:

$$\text{DSC}=\frac{2\left|M\cap A\right|}{\left|M\right|+\left|A\right|}=\frac{2TP}{2TP+FP+FN}$$ (7)

where M and A denote the region enclosed by the manual and algorithm‐generated boundaries, and TP, FP, FN are the true positive, false positive, and false negative rates, respectively.

The symmetric correspondence method17, 19 was used to establish a point‐wise correspondence between the manual and algorithm‐generated boundaries. The corresponding boundary points were then used to calculate two boundary distance‐based metrics: the absolute distance (MAD) and the maximum absolute distance (MAXD). Considering M = {m_i, i = 1,2,3…K} is a set of points on the manual boundary and A = {a_i, i = 1,2,3…K} is a set of points on the algorithm‐generated boundary, MAD is expressed as:

$$\text{MAD}=\frac{1}{K}\sum _{i=\mathrm{1}}^K\left|d(m_i,a_i)\right|$$ (8)

The MAXD is calculated by Eq. (9):

$$MAXD=\underset{i\in \{i,k\}}{\text{max}}\{\left|d(m_i,a_i)\right|\}$$ (9)

where m_i and a_i are two correspondence points in M and A, and d(m_i, a_i) is the distance between the two points.

3. Results

A threefold cross‐validation technique was used in the following experiments. All objects in the dataset were randomly divided into three groups. Images of one group were left out for testing and images obtained from the remaining objects were used as the training set, and the process was repeated three times, where the objects in the training set were different from those in the testing set.

Since Ukwatta et al25 performed the most comprehensive experiments using the 3D SFLS method for MAB and LIB segmentation, we compared the same volume‐based, region‐based, and distance‐based metrics of the proposed segmentation method with the 3D SFLS method25 in the experiments. For MAB segmentation, we also compared the results of the presented dynamic CNN with the traditional CNN without fine‐tuning. For LIB segmentation, the performance of the improved U‐Net was compared to several previous works, such as original U‐Net,29 traditional CNN,26 and Jodas's work.38

3.1. Parameters selection in preprocessing algorithm

The Edge Preservation Index (EPI) is commonly used to measure the ability of a filter to maintain details of the image.39 The EPI measurement was calculated for images filtered with different gamma values of 0.5, 2, 4, and 6. Table 1 shows that a larger value of γ obtained a higher EPI. The Peak Signal Noise Rate (PSNR)40 was also used to evaluate the performance of filters with different γ values. Table 1 indicates that the highest PSNR value is achieved when γ = 0.5. In order to balance the image quality and the edge‐contrast, γ of 2 and 4 were considered. Through the subjective assessment by an observer, the compensation coefficient γ value was set to 2.

Table 1.

Average edge preservation index (EPI) and peak signal noise rate (PSNR) of the enhanced US images using different compensation coefficient γ

Gamma (γ)	0.5	2	4	6
EPI	1.084	1.083	1.611	1.974
PSNR	37.59	37.24	36.50	35.94

3.2. Results of MAB segmentation

Different patch sizes (16, 32, 48, 64 pixels) were used to train the proposed CNN network. It did not converge to a local optimum using patches with a size of 16 × 16 pixels in the training. The classification accuracies of the patches were 95.1%, 92.8%, and 98.7% with respect to window sizes of 32, 48, and 64 pixels in the training stage. When a patch size equaled 64, we obtained the best classification accuracy. Thus, the sliding window size was chosen as 64 pixels in the following experiments.

Comparisons between the algorithm and manual MAB segmentations for one subject are shown in Fig. 8. The yellow contours are the manual segmentations and the red contours are the algorithm segmentations. These results indicate qualitatively that the algorithm‐segmented contours are close to the manual contours for this subject.

Figure 8.

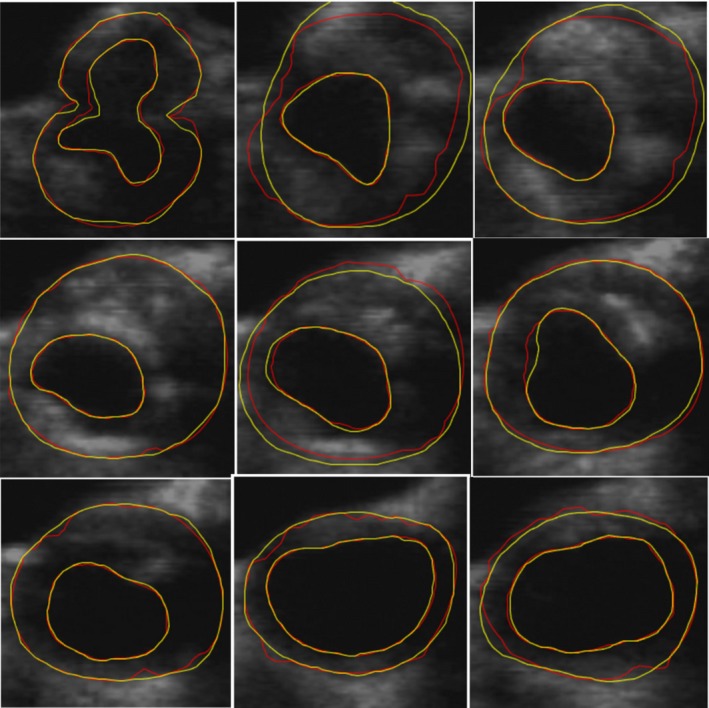
A comparison between the performance of algorithm and manual MAB and lumen‐intima boundary segmentations. The manual segmentations were generated at an interslice distance of 1 mm. The yellow contours show the manual segmentations and the red contours are the algorithm segmentations. [Color figure can be viewed at http://wileyonlinelibrary.com]

A quantitative comparison of the MAB segmentation results using four and eight initial points are shown in Table 2, which demonstrates that initialization with eight points results in better performance with the DSC of 96.46 ± 2.22%, MAD of 0.19 ± 0.11 mm, MAXD of 0.63 ± 0.57 mm, ∆MABV of −0.99 ± 1.37%, and |∆MABV| of 1.36 ± 0.99%. The performance obtained from four initialization points was a little lower but close to the eight‐point initialization and also acceptable.

Table 2.

Media‐adventitia boundary (MAB) segmentation results with different number of initial points

Number of initial points	8	4
DSC (%)	96.46 ± 2.22	95.4 ± 2.39
MAD (mm)	0.19 ± 0.11	0.24 ± 0.13
MAXD (mm)	0.63 ± 0.57	0.77 ± 0.63
∆MABV (%)	−0.99 ± 1.37	2.11 ± 1.70
|∆MABV| (%)	1.36 ± 0.99	2.34 ± 1.37

DSC, dice similarity coefficients; MAXD, maximum absolute distance, MABV, media‐adventitia volume difference.

The dynamic CNN proposed in this paper fine‐tuned the CNN model dynamically during testing in order to adapt the model to fit different vessels. During fine‐tuning the network, the number of epochs was set to 500, since we found when we exceeded 500, the loss value calculated by the loss function decreased slightly. We believe that when the number of epochs is set too large, overfitting during training might occur.

Table 3 shows the results of the traditional CNN and the proposed dynamic CNN. The proposed dynamic CNN with fine‐tuning obtained slightly better segmentation results than the CNN without fine‐tuning, with a DSC of 96.5 ± 2.22%. The distance‐ and volume‐based errors for the dynamic CNN (MAD, MAXD, and ∆MABV) were all smaller than the errors from the traditional CNN. A paired t‐test was applied, which failed to show a statistically significant difference of the DSC between the proposed dynamic CNN and the traditional CNN (P > 0.1).

Table 3.

DSC, MAD, MAXD, ∆MABV of MAB segmentation using different methods

Methods	Dynamic CNN with fine‐tuning	Traditional CNN without fine‐tuning	3D SFLS	U‐Net
DSC (%)	96.5 ± 2.22	96.0 ± 2.66	94.4 ± 2.24	91.45 ± 4.8
MAD (mm)	0.19 ± 0.11	0.21 ± 0.14	0.28 ± 0.18	0.42 ± 0.26
MAXD (mm)	0.63 ± 0.57	0.67 ± 0.53	0.92 ± 1.00	1.63 ± 1.39
∆MABV (%)	−0.99 ± 1.37	1.11 ± 1.66	0.85 ± 9.25	13.2 ± 6.11
|∆MABV| (%)	1.36 ± 0.99	1.61 ± 1.17	1.55 ± 2.45	13.27 ± 6.08

3D, three‐dimensional; CNN, convolutional neural network; DSC, dice similarity coefficients; MAXD, maximum absolute distance, MAB, media‐adventitia boundary; MABV, MAB volume difference; SFLS, sparse field level‐set.

Comparisons of the results from the proposed dynamic CNN, 3D SFLS,25 and U‐Net29 are also shown in Table 3. This table shows that the results with the dynamic CNN method are better than the previous 3D SFLS and the U‐Net methods. A paired t‐test with a Holm–Bonferroni correction showed that the DSC from the dynamic CNN method was statistically significantly different than the SFLS and U‐Net methods (P < 0.0002).

Table 3 also shows that the standard deviation values of MABV and |∆MABV| errors of the proposed method are smaller than the 3D SFLS method. An F‐test showed that the variances results from the dynamic CNN were statistically significantly different than 3D SFLS method (P < 0.0001) demonstrating that the consistency and robustness of the proposed dynamic CNN was better.

3.3. Results of LIB segmentation

The LIB segmentation problem was converted to a segmentation of the lumen region from the CCA US image. This procedure was a fully automatic using the modified U‐Net with the selected ROI in the CCA images obtained from the segmented MAB contours. Figure 8 shows a comparison between algorithm and manual segmentation results, where the red contours are the manually delineated LIB and the yellow contours are the algorithm results, showing that the two segmentations are qualitatively similar.

Table 4 shows a comparison of the segmentation results of the CCA lumen using the proposed method and four other methods. The traditional CNN26 was used to classify LIB patches using sliding windows resulting in a DSC of 85.50 ± 7.22%. Jodas et al. segmented the lumen region using the K‐means algorithm and mean roundness38 and obtained the DSC of 86.30 ± 6.71%. Ukwatta et al. applied the 3D SFLS method25 to segment the LIB and obtained a DSC of 90.64 ± 4.97% for an ISD of 3 mm. We used the traditional U‐Net algorithm29 to segment the LIB, but the DSC result of 89.50 ± 4.91% was a little lower than the 3D SFLS method. Thus, we modified the architecture and improved the U‐Net resulting in a highest DSC of 92.84 ± 4.46%. T‐tests of the DSCs with a Holm–Bonferroni correction (adjusted p‐values in Table 4) for the four tests showed that the proposed improved U‐Net was the statistically significantly different from the other methods (P < 0.05).

Table 4.

Comparisons for the DSC of LIB segmentations using different methods

Methods	Improved U‐Net	Traditional U‐Net	3D SFLS method	CNN using sliding windows	Jodas's method
DSC (%)	92.84 ± 4.46	89.50 ± 4.91	90.64 ± 4.97	86.30 ± 6.71	85.50 ± 7.22
Adjusted P‐valuea	–	0.007	0.033	0.0003	0.0004

3D, three‐dimensional; CNN, convolutional neural network; DSC, dice similarity coefficients; LIB, lumen‐intima boundary; SFLS, sparse field level‐set.

^aThe original P‐values were multiplied by the appropriate factors (4, 3, 2, 1) to give the adjusted P‐values, which were compared to a P‐value of 0.05.

Using the segmented LIB we calculated the volume‐, region‐, and distance‐based metrics using the proposed method and compared the results to the 3D SFLS method with ISD of 3 mm, as shown in Table 5. The DSC of the improved U‐Net method is higher than the 3D SFLS method. A paired t‐test showed that there is a statistically significant difference (P < 0.02) between the improved U‐Net method and the 3D SFLS method. Table 5 also shows that the MAD error metric is smaller for the proposed method than 3D SFLS and the MAXD error metric of the proposed method is similar with the 3D SFLS method. Although the average ∆LIBV of the proposed U‐Net method is similar to that of 3D SFLS method, the standard deviation of ∆LIBV is 5.9%, which is much smaller than the 3D SFLS method with a standard deviation of 49.5%. An F‐test indicated that there is a statistically significant difference (P < 0.0001) between the two methods. The standard deviation of |∆LIBV| is also smaller than the 3D SFLS method (P < 0.02). This large difference is due to the sensitivity of the level‐set based method to the initial contour and the proposed U‐Net method is more robust to different objects.

Table 5.

DSC, MAD, MAXD, △LIBV of LIB segmentation using different methods

Methods	Improved U‐Net	3D SFLS
DSC (%)	92.84 ± 4.46	90.64 ± 4.97
MAD (mm)	0.23 ± 0.14	0.35 ± 0.16
MAXD (mm)	0.86 ± 0.86	0.97 ± 0.62
∆LIBV (%)	3.8 ± 5.9	−0.37 ± 49.5
|∆LIBV| (%)	5.4 ± 4.5	4.43 ± 6.26

3D, three‐dimensional; DSC, dice similarity coefficients; LIBV, lumen‐intima boundary volume; MAXD, maximum absolute distance; SFLS, sparse field level‐set.

3.4. Generating the 3DUS VWV measurement

Since VWV measurements have been observed to be sensitive to temporal changes in carotid plaques,15, 16 we evaluated the accuracy of VWVs obtained from our algorithm generated MAB and LIB in this experiment.

Figure 9(a) shows a correlation plot of the algorithm and manually generated 3DUS VWV for the data using an ISD of 3 mm. This figure shows that the algorithm and manually generated VWVs are a highly correlated with correlation coefficient of 96%. Figure 9(b) shows a Bland–Altman plot of the difference between algorithm and the manual segmentations where the standard deviation is represented by SD. This plot shows good agreement between the mean VWVs generated by the algorithm and manual with a mean difference of −2.45 ± 9.21%, where the range of VWV is 167–1623 mm³.

Figure 9.

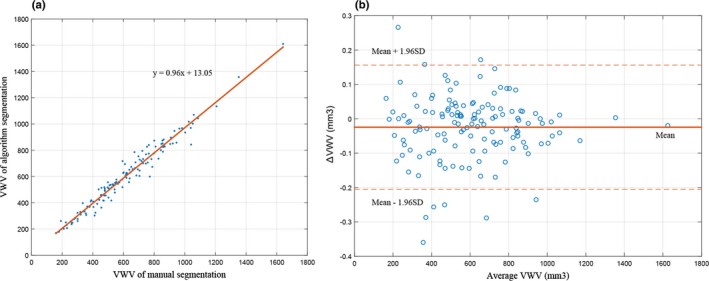
(a) Correlation plot for algorithm‐ and manually generated three‐dimensional ultrasound vessel‐wall‐volume (VWV). (b) Bland–Altman plot of the difference between VWVs generated by algorithm and manual segmentations. The red continuous line labeled as mean indicates the bias, the dotted lines labeled as 1.96 SD indicate the level of agreement. [Color figure can be viewed at http://wileyonlinelibrary.com]

Table 6 shows ∆VWV and |∆VWV| errors between the proposed and manual segmentations as well as the results from the 3D SFLS method.25 The average error of ∆VWV using the proposed segmentation method was 1.62 ± 8.7%, which is similar with the 3D SFLS method (0.56 ± 12.42%). A t‐test failed to show a statistically significant difference between the methods (P > 0.1). Furthermore, the standard deviations of ∆VWV and |∆VWV| are both lower for the proposed method. The F‐test showed that the variance of the ∆VWV (P < 0.01) and |∆VWV| (P < 0.05) metrics are both statistically significant different with the 3D SFLS method.

Table 6.

Results for VWV measurement using different methods

Methods	The proposed method	3D SFLS
∆VWV (%)	1.62 ± 8.7	0.56 ± 12.42
|∆VWV| (%)	6.48 ± 6.14	5.64 ± 8.10

3D, three‐dimensional; SFLS, sparse field level‐set; VWV, vessel‐wall‐volume.

3.5. Computational time

A timer was created in the program to record the elapsed time in each stage. Our proposed algorithm required the observer to locate four or eight anchor points on the MAB contours for initialization, requiring an average of 13.8 ± 6 s to choose eight points, and half that time for four points. The computation time for fine‐tuning the dynamic model was 8.73 ± 2.1 s. The MAB and LIB mean segmentation times were 9.5 ± 1.2 and 1.3 ± 0.5 s, respectively. Thus, the total mean time of 34.4 ± 9.8 s was required to segment a single 3D image. The dynamic CNN was built using Caffe,41 the U‐Net was implemented using the Keras platform42 and a computer with an Intel Core i7 7700K (base frequency: 4.20 GHz) and an NVIDA Geforce GT 1080Ti graphics card was used in the experiments. Table 7 shows a comparison of the average time to segment the MAB and LIB from a 3DUS image using the proposed method, Ukwatta's method (3D SFLS25 and 2D level set24) and Yang's method,23 showing that the proposed method reduced the processing time.

Table 7.

Comparison of segmentation time using different methods

Methods	The proposed method	3D SFLS	2D level set	Yang's method
Time (s)	34.4 ± 9.8	68.4 ± 49.8	168 ± 24	264 ± 36

2D, two‐dimensional; 3D, three‐dimensional; SFLS, sparse field level‐set.

3.6. Reproducibility

Two observers (R. Z. and Y. J.) were required to place 4 initial anchor points on the MAB contours in 117 transverse slices from 20 3DUS images, where both observers were blinded to each other's placement. The interobserver variability results of generating the MAB are shown by the DSC, MAD, MAXD, ∆MABV, and |∆MABV| metrics. The MAB algorithm segmentations using different observers' initializations were compared to manual segmentations. Table 8 shows that the performance of the two MAB algorithm segmentations were similar with DSC (compared to manual segmentation) of 95.77 ± 0.20% and 95.52 ± 1.75%, respectively. A t‐test indicated that the algorithm failed to show a statistically significant difference for the observers' initializations (P > 0.1). All metrics were also calculated to compare the MAB segmentations between the two observers' initializations. The algorithm generated DSC due to the two observers' initializations was 96.14 ± 1.87%, and all the differences between the other distance‐based and volume‐based metrics were small, which demonstrated that the MAB segmentations initialized by two observers were very close.

Table 8.

Comparison of the proposed algorithm segmentations initialized by different observers

Metrics	Algorithm1 — Manual	Algorithm2 — manual	Algorithm1 — Algorithm2
DSCMAB (%)	95.77 ± 0.20	95.52 ± 1.75	96.14 ± 1.87
MADMAB (mm)	0.25 ± 0.12	0.26 ± 0.10	0.23 ± 0.12
MAXDMAB (mm)	0.79 ± 0.42	0.81 ± 0.73	0.81 ± 0.41
∆MABV (%)	0.31 ± 2.40	0.07 ± 2.36	0.20 ± 3.11
|∆MABV| (%)	1.74 ± 1.62	1.78 ± 1.49	2.66 ± 1.51

DSC, dice similarity coefficients; MAXD, maximum absolute distance; MABV, media‐adventitia boundary volume.

Algorithm1: Results of the proposed method using initial points placed by Observer R. Z. Algorithm1: Results of the proposed method using initial points placed by Observer Y. X. Manual: results of manual segmentation.

4. Discussion

In this study, we report on a new algorithm used to delineate the MAB and LIB of the CCA from 3DUS images and generate VWV measurement, which can be used to quantify and monitor changes of atherosclerosis in the common carotid artery. This technique may also be used to calculate other 3DUS‐based biomarkers, such as TPV,20 VWT,17 and VWT‐Change.19

Compared to the previous reports, the deep learning technique was first utilized to segment both MAB and LIB from 3DUS images of carotid arteries, which greatly reduces user interactions and processing time. In the MAB segmentation, we proposed a dynamic convolutional neural network rather than a popular deep learning network, such as U‐Net29, SegNet43 et al, for two main reasons. First, the proposed method could dynamically fine‐tune the CNN model in practice. Second, the boundary contrast of the MAB and LIB on the distal side of the artery is poor due to the ultrasonic attenuation. The initial contours could help to locate the ROI of the carotid artery and improve the accuracy of segmentation. In the LIB segmentation, we improved the network architecture of the original U‐Net in order to avoid the overfitting problem during training.

In the experiment, the dynamic convolutional neural network was fine‐tuned using patches generated from the user interaction initial MAB contours. For both four and eight initial anchor points, it resulted in satisfactory segmentation, where the segmentations using four initial points obtained the average DSC of 95.4 ± 2.39% and the results improved with DSC of 96.46 ± 2.22% for eight initial anchor points. Thus, observers can vary the number of anchor points and ISD depending on the complexity of the plaque surface and the number of plaques.

Comparing the proposed method with the traditional CNN and 3D SFLS methods, we showed that the dynamic CNN generated better performance with a DSC of 96.46 ± 2.22%, MAD of 0.19 ± 0.11%, MAXD of 0.63 ± 0.57%, ∆MABV of −0.99 ± 1.37%, and |∆MABV| of 1.36 ± 0.99%. The DSC of the proposed method was statistically significantly different from the previous 3D SFLS method (P < 0. 0001). The standard deviation values of MABV and |∆MABV| errors of the proposed method are smaller and F‐test showed there was a statistical significant difference between the variances results from the dynamic CNN and 3D SFLS method (P < 0.0001). This result indicates that the proposed method is more robust to different objects.

Comparison of the DSC of LIB segmentation to other published results showed that our method produced the best results with DSC of 92.84 ± 4.46%. From the result of t‐tests of the DSCs with a Holm–Bonferroni correction, it showed that the DSC of the proposed improved U‐Net is the statistically significantly different from that of the other methods (P < 0.05).

The average errors of VWV and |VWV| using the segmented MAB and LIB with the proposed method were comparable to the 3D SFLS method; however, the standard deviations of the error metrics were smaller, which was more desirable for clinical use or trials. These results indicate that the variability of VWV and the generalization ability of the proposed algorithm were better.

The analysis of computational time shows that the proposed method greatly reduced the user interactions and the processing time with a total of 34 s to segment a 3DUS image. This is approximately 93% reduction in time (34 s vs 8.3 min) in comparison to manual segmentation. Compared to the 3D SFLS method, the proposed method reduced the total of user interaction time and processing time by half (34 vs 68 s). However, the time cost for MAB segmentation is much more than the LIB segmentation, since the MAB segmentation algorithm is still not fully automated due to the low‐contrast of media‐adventitia boundaries on the side far away from the probe and the inhomogeneity of peripheral tissue. Thus, future work will focus on improving the MAB segmentation method and reducing its time.

Due to the limitation of the small dataset of 3DUS images and the requirement of a large number of 3DUS images to train a 3D deep learning network, we sliced the 3DUS images into 2DUS images. Although the DSCs of the MAB and LIB segmentations in 2DUS images are already sufficient for clinical use and showed statistically significant difference compared to the 3D SFLS method, the volume metrics fail to show a statistical significance difference. Since we resliced our 3DUS images and segmented them with a spacing of 1 mm, our method did not guarantee connectivity between slices. Moreover, although the threefold cross‐validation technique was used to randomly divide all objects into two groups for training and testing in the experiments, the lack of using an independent testing dataset is another limitation of our work. Thus, in the future, we will collect more clinic 3DUS images for developing an automated 3D deep learning network to segment MAB and LIB and have the independent testing. Since the proposed dynamic CNN required at least two slices of 2D carotid US images for initialization, 3DUS images acquired over a short distance of the common carotid artery were not considered in the experiments. Another limitation of the presented work is that this study lacked a consensus ground truth in the experiments.

Future work will also include the use of our proposed segmentation method to evaluate other useful 3DUS metrics of the carotid arteries, such as VWT,17 VWT‐Change,19 TPV,13 and 3D texture features44 for plaque monitoring and treatment evaluation.

5. Conclusion

In this paper, we presented a dynamic CNN for MAB segmentation and improved U‐Net for LIB segmentation. To our knowledge, this work is the first applying a deep learning technique to segment carotid plaques from 3DUS images of CCA with carotid stenosis over 60%. This method overcomes the limitation of other methods, which are sensitive to initialization points and reduces the need for operator interaction. It provides higher mean segmentation accuracy and smaller standard deviations than the previous methods in terms of volume‐, region‐, and distance‐based metrics. With sufficient accuracy and low variability, the proposed method could be used clinically for monitoring patients' response to therapy. In addition, our segmentation methods could also provide a tool to be used in clinical trials used to investigate new therapy methods by providing a reproducible method to monitor progression and regression of carotid plaques.

Conflict of interest

The authors have no conflicts to disclose.