Large‐scale functional LIPA variant characterization to improve birth prevalence estimates of lysosomal acid lipase deficiency

Abstract

Lysosomal acid lipase (LAL) deficiency is an autosomal recessive disorder caused by LIPA gene mutations that disrupt LAL activity. We performed in vitro functional testing of 149 LIPA variants to increase the understanding of the variant effects on LAL deficiency and to improve disease prevalence estimates. Chosen variants had been reported in literature or population databases. Functional testing was done by plasmid transient transfection and LAL activity assessment. We assembled a set of 165 published LAL deficient patient genotypes to evaluate this assay's effectiveness to recapitulate genotype/phenotype relationships. Rapidly progressive LAL deficient patients showed negligible enzymatic activity (<1%), whereas patients with childhood/adult LAL deficiency typically have 1–7% average activity. We benchmarked six in silico variant effect prediction algorithms with these functional data. PolyPhen‐2 was shown to have a superior area under the receiver operating curve performance. We used functional data along with Genome Aggregation Database (gnomAD) allele frequencies to estimate LAL deficiency birth prevalence, yielding a range of 3.45–5.97 cases per million births in European‐ancestry populations. The low estimate only considers functionally assayed variants in gnomAD. The high estimate computes allele frequencies for variants absent in gnomAD, and uses in silico scores for unassayed variants. Prevalence estimates are lower than previously published, underscoring LAL deficiency's rarity.

1. INTRODUCTION

Lysosomal acid lipase (LAL) deficiency (MIM# 278000) is a rare, autosomal recessive lysosomal storage disorder. LAL is encoded by the LIPA gene (HGNC 6617; MIM# 613497), and its function is to de‐esterify cholesteryl esters and triglycerides inside the lysosome. LIPA mutations that disrupt this enzyme’s ability to degrade its substrates cause LAL deficiency. In infants, disease progression occurs rapidly, presenting with a severe and life‐threatening manifestation; rapidly progressive LAL deficiency (RP‐LALD), historically referred to as Wolman disease, typically presents in the first year of life with diarrhea, failure to thrive, abdominal distension with massive hepatosplenomegaly, anemia, and rapidly progressive liver disease. Untreated infants have a median age at death of 3.7 months (Jones et al., 2016). A more variable presentation and the disease course are seen in children and adults. Children/adult LAL deficiency (CA‐LALD), historically referred to as cholesteryl ester storage disease (CESD), typically presents later in life with such findings as serum lipid abnormalities, hepatosplenomegaly, and/or elevated liver enzymes and can cause significant morbidities from atherosclerosis, liver disease, and other chronic conditions (Reiner et al., 2014; Bernstein, 2018).

Over 60 LIPA mutations have been reported in the literature to be associated with either form of LAL deficiency (Bernstein, Hülkova, Bialer, & Desnick, 2013; Stenson et al., 2017). RP‐LALD is typically caused by biallelic loss‐of‐function mutations that completely abolish LAL enzymatic activity, whereas CA‐LALD typically occurs when some residual enzymatic activity remains (~2% to 10% of wild‐type expression levels; Fasano et al., 2012). The most prevalent genetic variant in European and Hispanic‐ancestry patients with CA‐LALD is variant c.894G>A (rs116928232), a synonymous exonic splice junction mutation (commonly referred to as E8SJM) that provokes skipping of exon 8 and a deletion of 24 amino acids in the resulting protein. This variant is present in a significant fraction (~50–70%) of the patient with CA‐LALD cohorts from these ancestries (Bernstein et al., 2013; Scott et al., 2013).

Obtaining accurate epidemiological estimates of LAL deficiency incidence or prevalence is important for designing diagnostic and treatment strategies, but has proven to be challenging, and estimates vary widely. A birth prevalence value of 0.27 per 100,000 (~1 in 370,000) was estimated for the Czech Republic (Poupětová et al., 2010) for both LAL deficiency forms. In contrast, CA‐LALD prevalence in Germany was estimated as 2.5 in 100,000 (1 in 40,000) (Muntoni et al., 2007). A methodologically similar study (Scott et al., 2013) reported an estimated CA‐LALD prevalence of approximately 1.2 per 100,000 in Causasian populations, and of approximately 0.8 per 100,000 in combined Caucasian and Hispanic populations in the USA. Both Muntoni et al. (2007) and Scott et al. (2013) relied on measuring the E8SJM carrier frequency on the population, assuming Hardy–Weinberg equilibrium (HWE) conditions, and assuming that E8SJM represented about half of the CA‐LALD causing alleles. More recently, CA‐LALD birth prevalence was estimated to be approximately 1/160,000 using a meta‐analysis of existing genetic studies that rely on measuring the E8SJM allele frequency (Carter, Brackley, Gao, & Mann, 2019), whereas LAL deficiency prevalence was estimated in the same work to be about 1/177,000, by aggregating pathogenic variant frequency information from the Genome Aggregation Database (gnomAD; Karczewski et al., 2019).

The main goal of this study is to refine and improve LAL deficiency birth prevalence estimates by characterizing in vitro a sample of approximately 150 LIPA variants, and by developing a novel statistical framework that combines these in vitro data with population allele frequencies.

This large‐scale variant characterization was necessitated by the fact that interpreting pathogenicity of genetic variants is challenging, especially with missense variants. In vitro assays are an essential tool for missense variant interpretation (Raraigh et al., 2018; Starita et al., 2017). However, such in vitro assays can be slow and expensive and cannot cover novel variants that are being constantly discovered in patients and in the general population. The results of this large‐scale variant characterization were then used to assess the ability of in silico variant scoring algorithms to predict LIPA variant pathogenicity and to measure the resulting impact of mutations of unknown effect in LAL deficiency prevalence estimates.

2. MATERIALS AND METHODS

2.1. Variant selection for functional assays

One hundred fifty LAL functional assays were performed to determine the functional spectrum of LIPA variants. Wild‐type LIPA complementary DNA (cDNA), along with 149 variants, were selected for in vitro functional assessment as follows.

• All missense, nonsense, and 1/2 base pair frameshift variants from the patients with LAL deficiency are reported in references (Himes et al., 2016; Hooper, Tran, Formby, & Burnett, 2008; Kuranobu et al., 2016; Pisciotta et al., 2017; Reiner et al., 2014; Ries et al.,1996; Santillán‐Hernández et al., 2015; Scott et al., 2013; Valayannopoulos et al., 2014). This resulted in 47 known pathogenic variants from the literature being chosen. Table S3 lists these variants, as well as variants that were identified at later points in time from literature sources (Jones et al., 2016; Kim et al., 2017; Sjouke et al., 2016), and variants that were not amenable to plasmid‐based transfection due to being splicing mutations (Maciejko et al., 2017; Ruiz‐Andrés et al., 2017).

• All novel missense, frameshift or nonsense variants identified in patients participating in Sebelipase Alfa clinical studies ARISE (NCT0757184) and CL06 (NCT02112994) were selected. This resulted in seven more variants to be assayed. Two novel LIPA mutations detected from these clinical studies (c.822+1G>C and c.538+5G>A) were not assayed because these were splice‐site mutations and therefore not amenable to plasmid‐based transfection.

• All known missense LIPA polymorphisms, with an allele frequency of at least 1%, were additionally chosen. This resulted in two missense variants being selected (c.46A>C/p.Thr16Pro and c.67G>A/p.Gly23Arg).

• The remaining 93 variants were selected uniformly at random from the 138 ExAC missense or frameshift variants with allele count of at least one. This total pool of possible variants to test was expanded to 231 after the gnomAD dataset was made available, which happened after this variant selection process had already taken place. This left 138 candidate gnomAD variants left out of the list of the variant to test in vitro.

2.2. Functional assay preparation

2.2.1. Expression of LAL variants

The reference amino acid sequence encoding LAL was UniProtKB/SwissProt P38751.1. cDNA encoding wild‐type LAL, as well as truncated and scrambled variants, were generated with terminal 6X histidine tags by using the Thermo Fisher Scientific (Carlsbad, CA) GeneArt platform. Sequences were optimized for expression in human cells using GeneArt’s proprietary GeneOptimizer algorithm (Regensburg, Germany). GeneArt was also used to perform mutagenesis on wild‐type LAL cDNA. Resulting coding regions were cloned into vector pBNJ391, a derivative of expression vector pEE12.4 (Lonza Biologics, Basel, Switzerland) described in Fan, Frye, & Racher (2013). Plasmids were sequence verified to confirm the presence of desired mutations.

The resulting constructs were transiently transfected into Expi293F cells using ExpiFectamine 293 and the methodology recommended by the manufacturer (Thermo Fisher Scientific). We have previously reported transfection efficiency in the Expi293F system to be over 90% based on the expression of a green fluorescent protein plasmid (N. K. Jain et al., 2017). Transfections were carried out at the 2‐milliliter scale in 12‐well tissue culture plates (Fisher Scientific, Waltham, MA). Transfected cultures were harvested 3 days after transfection. Briefly, cultures were spun down at 500g for 5 min, supernatants transferred to fresh plates, and cell pellets were washed twice in phosphate‐buffered saline (GE Healthcare, Marlborough, MA). Transfected cultures were incubated with 0.5 ml lysis buffer (1% Triton X‐100, 10 mM sodium phosphate [pH 7.0], 10 mM dithiothreitol, and 1 mM ethylenediaminetetraacetic acid in water) for 45 min at 4°C and centrifuged for 15 min at 3,000g to remove insoluble materials.

2.2.2. LAL enzyme assay

Cell lysates and supernatants from transfected cultures were diluted 25 fold in assay buffer (200 mM sodium acetate [pH 5.5], 1% Triton X‐100%, and 1% human serum albumin). Ten microlitres of this dilution were added to 40 µl  assay buffer in a black 384 well Optiplate (Perkin Elmer, Waltham, MA) for a total dilution of 150 fold. The LAL reaction was started by adding 10 µl of the substrate 4‐methylumbelliferyl (4‐MU) oleate (Sigma‐Aldrich) to a final concentration of 100 µM in a total reaction volume of 60 µl. A BioTek Synergy 2 plate reader was used to follow 4‐MU fluorophore production at excitation/emission wavelengths of 360/460 ± 40 nm. The initial velocity for each LAL variant was determined from the first 10–20 min of the reaction and then normalized to total cell lysate protein content as measured by Pierce BCA assay (Thermo Fisher Scientific). The basal expression for the Expi293 system was determined by performing a mock transfection without any plasmid and measuring resulting LAL activity. The resulting value was subtracted from each mutant’s result. Finally, all data were expressed relative to the wild‐type sample.

2.2.3. Statistical estimation of LAL deficiency birth prevalence

Proposed here is a general hierarchical statistical framework to estimate the birth prevalence of rare, monogenic, and autosomal recessive disorders for which the causal gene is known, with LAL deficiency being an example thereof. This formulation assumes that only variants in a single gene (LIPA in the case presented here) can cause disease, but the effect of alleles and their combination to form a biallelic genotype might not be known. Such is the case for many rare monogenic disorders, where genotype to phenotype relationships might not be deterministic nor fully characterized, and even the effect of a single variant in homozygous state might yield variable penetrance or variable disease forms (see Cooper, Krawczak, Polychronakos, Tyler‐Smith, & Kehrer‐Sawatzki, 2013 for a review and discussion).

2.2.4. Basic general model

Let $\mathcal{A}$ denote the set of possible alleles for the gene of interest, with $a_1,\dots ,a_N$ denoting $N$ possible disease alleles and $a_0$ denoting a wild‐type allele. Let $\mathcal{G}=\mathcal{A}\times \mathcal{A}$ denote the space of possible diploid genotypes, with $G=(A_1,A_2),A_1,A_2\in \mathcal{A}$ denoting a particular diploid genotype.

Let $\mathrm{\Phi }$ denote a particular patient phenotype, and it will be assumed that, for a rare disease of interest, $\mathrm{\Phi }\in \{{\varphi }_1,\dots ,{\varphi }_K\}\doteq \mathcal{P}$ will be a categorical random variable that can only take on discrete values that describe $K$ different disease subtypes in phenotype space $\mathcal{P}$. For the particular LAL deficiency case, $K=2$ and $\mathcal{P}=\{{\varphi }_{\text{CA}-\text{LALD}},{\varphi }_{\text{RP}-\text{LALD}}\}$, respectively denote the CA‐LALD and RP‐LALD phenotypes.

If the genotype frequency distribution of $G$ for a particular population is known, and if there is a deterministic or probabilistic genotype–phenotype model in place such that the distribution for $\text{Pr}(\mathrm{\Phi }={\varphi }_k|G=(a_1,a_2))\forall {\varphi }_k\in \mathcal{P},\forall G\in \mathcal{G}$ is also known, then the probability of an individual carrying a particular disease phenotype ${\varphi }_k$ in the population can be expressed as

$$\text{Pr}(\mathrm{\Phi }={\varphi }_k)=\sum _{G\in \mathcal{G}}\text{Pr}(\mathrm{\Phi }={\varphi }_k|G=(a_1,a_2))\text{Pr}(G=(a_1,a_2))$$ (1)

Assuming that carrying a disease phenotype is compatible with live birth (i.e., no increased risk for miscarriage or fatal congenital malformations), Equation (1) also provides an estimate for the birth prevalence of phenotype ${\varphi }_k$, that is the proportion of live births with a particular disease phenotype in the population.

The immediate problem with Equation (1) is that, for most practical applications, neither a genotype frequency distribution in the population nor a probabilistic relationship of genotype to phenotype is readily available. To make this problem tractable, the following assumptions and simplifications were introduced.

• Variant‐allele equivalency. This analysis is based on the assumption that each allele in the gene of interest comprises exactly one genomic variant. As a consequence, allele frequency can be equated with variant frequency, and the effect that two variants in cis may have on a protein product can be ignored. Such assumption is justified based on what is known of rare recessive disorders, where deleterious, disease‐causing variants are rare in the population due to evolutionary pressures. As shown in Section 3, such an assumption is furthermore guaranteed when examining actual collected patient variants and genotypes. As a further consequence of this assumption, possible disease‐modifying effects of polymorphisms and other factors are ignored and terms including variants, mutations, and alleles are used interchangeably. In addition, possible effects of de novo mutations or uniparental disomy are also ignored for the purposes of this analysis.

• HWE assumes no inbreeding or consanguinity in the population and no population sub‐structure. In the context of LAL deficiency, this assumption has been used before to compute LAL deficiency birth prevalence estimates in the Hispanic and Caucasian populations in the US (Scott et al., 2013) or to estimate LAL deficiency birth prevalence in Germany (Muntoni et al., 2007). Mathematically, this means that $\text{Pr}\left(G=(a_i,a_j)\right)=\text{Pr}(A_1=a_i)\text{Pr}(A_2=a_j)$.

• Variant effect on phenotype assumes that the phenotypic effect of a genotype is solely dependent on the residual variant enzymatic activity that results from this genotype. It is also assumed that this enzymatic activity can be measured via an in vitro assay for a particular gene/protein of interest. Mathematically, this effect is modeled by variable $e\left(A\right)$ representing the effect of a genetic allele $A$ on the enzymatic activity. In addition, the resulting effect of a particular genotype is modeled by simply averaging the effects of individual alleles. That is,

$$e(G)=\frac{e(A_1)+e(A_2)}{2},G=(A_1,A_2)$$ (2)

The model assumes that the probabilistic effect of genotype on phenotype solely depends on $e$, and that a phenotype will become independent of a genotype $G$ once a particular value of $e$ is given. Recalling from Equation (2) that the enzymatic activity of a given genotype is assumed to be the simple average of the measured enzymatic activity of each individual allele, the following is obtained:

$$\text{Pr}(\mathrm{\Phi }={\varphi }_k|G=(a_1,a_2))=\text{Pr}(\mathrm{\Phi }={\varphi }_k|(a_i,a_j))\doteq f({\varphi }_k,(e(a_i)+e(a_j))/2)$$ (3)

Collected functional enzymatic assay data and knowledge of LAL deficiency phenotypes and genotypes taken from literature and case reports can be used to model function $f$ in Equation (3) above. In particular, given a collection of patient genotype and phenotype data of the form $D=\left\{(a_1^i,a_2^i),{\varphi }^i\right\}$, if all alleles in the patient data collection’s genotypes have been functionally tested, then the resulting activity/phenotype pairs $\left\{e(a_1^i,a_2^i),{\varphi }^i\right\}$ can be used to build a conditional probability distribution $f$ specified in Equation (3).

For the case of LAL deficiency, it has been shown that null enzymatic activity normally accompanies the severe RP‐LALD phenotype, whereas the CA‐LALD phenotype might be present when some residual enzymatic activity remains (Fasano et al., 2012). However, the exact enzymatic activity cutoff between these two forms, or between CA‐LALD and a healthy phenotype, might not be well‐defined or might depend on the particular assay protocol. Furthermore, it has recently been appreciated, as mentioned above, that there is a continuum of phenotypes that does not fall neatly into the historical Wolman (RP‐LALD) or CESD (CA‐LALD) descriptions (Santillán‐Hernández et al., 2015). Experimental data indicates that the relationship between residual enzymatic activity and phenotype might not be deterministic, even though, as mentioned, lower enzymatic values are typically associated with more severe phenotypes. Proposed here is a simple stepwise phase‐transition parametric model, where below an enzymatic activity threshold $T_1$ the RP‐LALD probability takes on a value ${\alpha }_1$ (expected to be high), with the CA‐LALD probability taking on a value $1-{\alpha }_1$. For enzymatic thresholds between $T_1$ and $T_2$ the RP‐LALD probability takes on value ${\alpha }_2$ (expected to be much lower), with the CA‐LALD probability taking on a value $1-{\alpha }_2$. Above $T_2$ both RP‐LALD and CA‐LALD probabilities take on an infinitesimal value $ϵ$. Formally:

$$\text{Pr}(\mathrm{\Phi }={\varphi }_{\mathrm{R}\mathrm{P}\mathrm{-}\mathrm{L}\mathrm{A}\mathrm{L}\mathrm{D}}|e(a_i,a_j)=e)=\{\begin{array}{ll}{\alpha }_1\hfill & \text{if}e<T_1\hfill \\ {\alpha }_2\hfill & \text{if}{T}_1\le e<T_2\hfill \\ \epsilon \hfill & \mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e}\hfill \end{array}$$

And, conversely,

$$\text{Pr}(\mathrm{\Phi }={\varphi }_{\mathrm{C}\mathrm{A}\mathrm{-}\mathrm{L}\mathrm{A}\mathrm{L}\mathrm{D}}|e(a_i,a_j)=e)=\{\begin{array}{ll}1-{\alpha }_1\hfill & \text{if}e<T_1\hfill \\ 1-{\alpha }_2\hfill & \text{if}{T}_1\le e<T_2\hfill \\ \epsilon \hfill & \mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e}\hfill \end{array}$$ (4)

The model above assumes full phenotypic penetrance for either RP‐LALD or CA‐LALD phenotypes as long as $e<T_2$.

To estimate model parameters $({\alpha }_1,{\alpha }_2,T_1,T_2)$ from subject data $D$, the log‐likelihood function can be derived as

$$\log L(D\mathrm{;}{\alpha }_1,{\alpha }_2,T_1,T_2)=n_{\text{RP}\mathrm{-}\text{LALD}}^1\log {\alpha }_1+n_{\text{RP}\mathrm{-}\text{LALD}}^{12}\log {\alpha }_2+n_{\text{CA}\mathrm{-}\text{LALD}}^1\log \left(1-{\alpha }_1\right)+n_{\text{CA}\mathrm{-}\text{LALD}}^{12}\log (1-{\alpha }_2)+(n_{\text{RP}\mathrm{-}\text{LALD}}^2+n_{\text{CA}\mathrm{-}\text{LALD}}^2)\log ϵ$$ (5)

Where $n_k^1$ is the number of patients with phenotype $k$ and enzymatic activity $e<T_1$, $n_k^{12}$ is the number of patients with phenotype $k$ and enzymatic activity $T_1\le e<T_2$, and $n_k^2$ is the number of patients with phenotype $k$ and enzymatic activity $e>T_2$. These parameters will be treated as unknown deterministic quantities to simplify the formulation, but in principle a prior distribution could be put on these values to develop a full posterior parameter distribution given subject data. With this simplification, maximum‐likelihood estimates for $({\alpha }_1,{\alpha }_2,T_1,T_2)$ can be obtained by maximizing Equation (5) above.

With these three assumptions in place, Equation (1) becomes

$$\text{Pr}(\mathrm{\Phi }={\varphi }_k)=\sum _{a_i\in \mathcal{A}}\sum _{a_j\in \mathcal{A}}f(\mathrm{\Phi }={\varphi }_k|e(a_i,a_j))p_{a_i}{p}_{a_j}$$ (6)

2.2.5. Modeling allele frequency uncertainty

Equation (6) gives a simple, general framework that links allele frequencies in a population with measured variant enzymatic activity to form an estimate of rare autosomal recessive disease birth prevalence. However, in practice, population allele frequencies $p_{a_i}$ are not known. Given a particular large‐scale genomic dataset like ExAC or gnomAD (Lek et al., 2016) where a particular variant appears with a particular allele count $A{C}_i$ and allele number $A{N}_i$ (the latter corresponding to twice the number of sampled subjects in a population for autosomal variants), the uncertainty on allele frequency knowledge can be incorporated by modeling $p_{a_i}$ as a Beta random variable with distribution $p_{a_i}\sim \beta ({\alpha }_i,{\beta }_i)$, where ${\alpha }_i=A{C}_i$, ${\beta }_i=A{N}_i-A{C}_i$ so that Equation (6) becomes

$$\text{Pr}(\mathrm{\Phi }={\varphi }_k)=\sum _{a_i\mathcal{\in }\mathcal{A}}\sum _{a_j\mathcal{\in }\mathcal{A}}\iint f(\mathrm{\Phi }={\varphi }_k|e(a_i,a_j\left)\right)p_{a_i}{p}_{a_j}\mathbf{\beta }(p_{a_i}\mathrm{;}{\alpha }_i,{\beta }_i\left)\mathbf{\beta }\right(p_{a_j}\mathrm{;}{\alpha }_j,{\beta }_j)d{p}_{a_i}d{p}_{a_j}$$ (7)

Where $\mathbf{\beta }(p_{a_i};{\alpha }_i,{\beta }_i)$ is the Beta probability density function for allele frequency $p_{a_i}$ with parameters $({\alpha }_i,{\beta }_i)$. Normally, solving Equation (7) in closed form is not feasible, but the distribution for $\text{Pr}\left(\mathrm{\Phi }={\varphi }_k\right)$ can be readily obtained using Monte Carlo simulation by just drawing $p_{a_i}$ and $p_{a_j}$ from their corresponding distributions and then computing $\text{Pr}\left(\mathrm{\Phi }={\varphi }_k\right)$ from Equation (6).

2.2.6. Estimating allele frequency of missing variants

Many pathogenic LIPA variants reported in the clinical literature are expected to be private or have such a low allele frequency in the overall population that they won’t be present in gnomAD or other such large‐scale variant database. Other disease variants might be relatively more frequent but may have been missed by sampling in the population. This presents a problem when estimating their contribution to the disease genotype population frequency. Two simple methodological approaches are proposed here to deal with these variants with missing allele frequency estimates.

• Lower frequency bound: In this scenario, the contribution of these variants is ignored by assuming that their cumulative allele frequency in the population is equal to zero. This is equivalent to setting parameter $\alpha =0$ in the Beta distribution corresponding to this allele in Equation (7) so that all terms involving each of these alleles is equal to zero.

• Upper frequency bound: In this scenario, parameters are set as $({\alpha }_i=1,{\beta }_i=\mathit{AN}-1)$ for all alleles with missing allele frequency estimates. That is, the allele frequency of these alleles is treated as if they were a singleton allele.

Both of the scenarios above represent modeling extreme, which might not be realistic, but they set bounds on birth prevalence estimates that provide useful when tight enough.

2.3. Estimating effect of variants not tested in vitro and assessing in silico variant classification algorithms

The statistical prevalence estimation method presented here requires the presence of in vitro functional data for each potentially disease‐contributing variant. This presents a practical limitation because, as described before, not all potentially pathogenic variants present in ExAC or gnomAD were tested, and future population sequencing efforts are bound to produce novel missense variants with uncertain significance. The effect of novel variants can be accounted for by building a predictor $e$ that estimates residual enzymatic activity resulting from a genotype $(a_i,a_j)$ by, as before, first estimating the effect of a single allele on resulting enzymatic activity $e\left(a_i\right)$ and then averaging the effect of both alleles in a genotype.

A natural approach to build these estimators is to use standard in silico algorithms like PolyPhen‐2 (Adzhubei, Jordan, & Sunyaev, 2013), sorting intolerant from tolerant (SIFT; Sim et al., 2012), combined annotation dependent depletion (CADD; Kircher et al., 2014) or others. One possible way to use these algorithms is to set the estimated enzymatic effect of a variant to zero if an in vitro algorithm deems such variant as pathogenic. Furthermore, untested variants which are predicted in silico to produce no enzymatic activity, that is classical loss‐of‐function (LoF) variants like nonsense, splice‐site or frameshift mutations, will also be estimated to have zero activity. That is,

$$\hat{e}(a_i)=\{\begin{array}{ll}e(a_i)\hfill & \text{if}{a}_i\text{tested}\text{in}\text{vitro}\hfill \\ 0\hfill & \text{if}{a}_i\text{is}\text{LoF}\text{or},\text{optionally},\text{marked}\text{as}\text{deleterious}\mathrm{b}\mathrm{y}\mathrm{a}\mathrm{n}\mathrm{}\mathrm{i}\mathrm{n}\mathrm{s}\mathrm{i}\mathrm{l}\mathrm{i}\mathrm{c}\mathrm{o}\text{algorithm}\hfill \\ 1\hfill & \mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e}\hfill \end{array}$$ (8)

Results presented here show the effect of algorithm choice on LAL deficiency phenotype probabilities at birth, as well as individual algorithm performance if the functional in vitro assay data is used as a truth set to assess these algorithms.

2.3.1. Comparison with existing CA‐LALD birth prevalence estimation methods

Previously published methods to compute LAL deficiency (and more specifically, CA‐LALD) birth prevalence relied, broadly, on three steps.

• Estimating the allele frequency of the E8SJM variant on a control population.

• Estimating the allele frequency of the E8SJM variant inside a CA‐LALD patient cohort.

• Computing a birth prevalence estimate assuming HWE conditions.

Formally, assume all disease‐causing alleles can be partitioned into two groups: An allele $a_1$ (like the E8SJM variant) with known allele frequency $f_1$ in the population, and a set of alleles with combined allele frequency $f_2$, which is unknown. In this case, a birth prevalence estimate of an autosomal recessive phenotype (e.g., CA‐LALD) will be, from the HWE assumption, $\text{Pr}(\mathrm{\Phi }={\varphi }_{\mathit{CA}-\mathit{LALD}})={\left(f_1+f_2\right)}^2$ assuming all variants are fully penetrant.

If allele $a_1$’s allele frequency is equal to a constant $\gamma$ within a patient cohort, it can be shown that $\gamma =\frac{f_1}{f_1+f_2}$ under the assumptions above, from which $f_2$ can be estimated as

$$f_2=f_1\frac{1-\gamma }{\gamma }$$

From this, it simply follows that

$$\text{Pr}(\mathrm{\Phi }={\varphi }_{\text{CA}\mathrm{-}\text{LALD}})={\left(f_1/\gamma \right)}^2$$ (9)

As mentioned before, CA‐LALD birth prevalence was estimated to be approximately 25 per million in Germany using this method (Muntoni et al., 2007), with data later expanded to get an estimate of 12 per million in combined US and German Caucasian populations (Scott et al., 2013).

It is possible to refine this method to account for uncertainty on the estimation of $f_1$ by simulating it as a random variable with distribution $\mathbf{\beta }(p_{a_1};{\alpha }_1,{\beta }_1)$ and measuring the resulting distribution estimate for $\text{Pr}(\mathrm{\Phi }={\varphi }_{\text{CA}\mathrm{-}\text{LALD}})$ by performing Monte Carlo simulations of Equation (9).

3. RESULTS

3.1. In vitro assays and LAL variant residual activity

Intracellular enzymatic activity was measured for one wild‐type LAL and 149 variants. Figure 1a plots results obtained, listing LAL variants and resulting enzymatic activity relative to wild‐type. Figure 1b plots this same fraction, split according to variant provenance (i.e., patient cohorts, clinical studies, known polymorphisms or ExAC). Measured values for all 149 variants, as well as the original source LIPA cDNA relative to RefSeq cDNA transcript NM_000235.3 (O’Leary et al., 2016), the produced LAL protein variant and the variant source, are listed on Table S1. As expected, most variants from the CL06 and ARISE clinical studies, as well as variants curated from the LAL deficiency clinical literature, showed very low levels of enzymatic activity, whereas known polymorphisms showed values comparable to or higher than the wild‐type level. ExAC/gnomAD variants spanned the whole range of enzymatic activities. Of note on Figure 1 were three variants reported as pathogenic in the literature in two Japanese patients:

• c.607G>C/p.Val203Leu and c.791T>C/p.Leu264Pro. These two novel variants appeared in compound heterozygous form in a patient reported in Kuranobu et al. (2016)

• c.811A>C/p.Asn271His. This variant appeared in the homozygous form on Reiner et al. (2014) which referenced Kojima et al. (2013).

Figure 1.

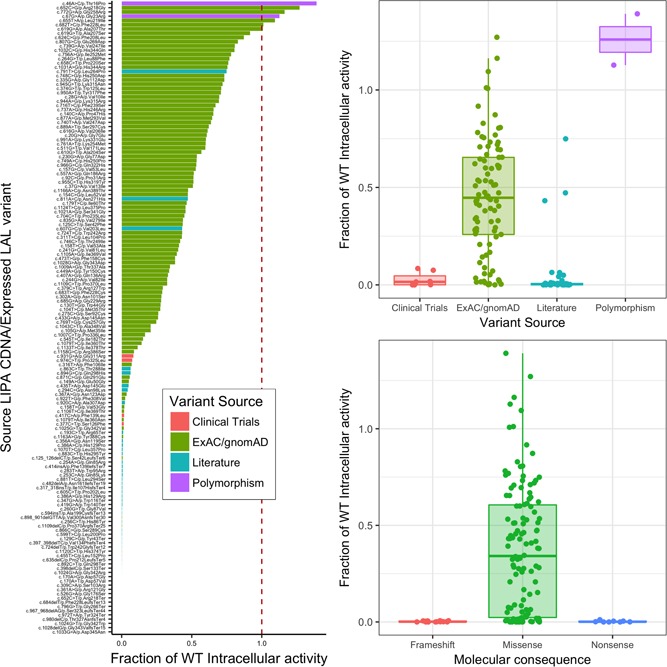
Measured fraction of wild‐type enzymatic activity for all tested LIPA mutants. (a) Listing each individual variant with cDNA source, relative to RefSeq transcript NM_000235.3, (b) Box plot, and scatter plots according to the variant source. (c) Box plot and scatter plots according to variant molecular consequence. CDNA, Coding DNA; ExAC, exome aggregation consortium; gnomAD, Genome Aggregation Database; WT, wild‐type

These three variants were the only studied variants that were reported in the literature as disease‐causing and that showed relatively high intracellular enzymatic activity on enzymatic assays (43.2% to 74.9% of wild‐type value; Table S1).

From the 149 assayed LIPA variants, 126 of them were missense variants, whereas 15 were frameshift variants (small insertions/deletions) and 8 of them were nonsense variants (resulting in stop‐introducing codons). Figure 1c plots the resulting enzymatic activity relative to wild‐type for each variant, split by variant molecular consequence. As expected, frameshift and nonsense variants resulted in null measured enzymatic activity, whereas missense mutations spanned the whole range of enzymatic activity values.

3.2. Genotype to phenotype probabilistic model estimation

Patient genotype and phenotype data were collected retrospectively from the literature, and the expected combined residual enzymatic activity for each patient was computed by looking up the residual enzymatic activity for each patient’s allele and averaging results for both alleles. To maximize the number of points with complete data, alleles which were classified as high‐confidence LoF variants such as frameshift, splice‐site, or nonsense mutations, were assigned a residual activity of zero. E8SJM alleles were assigned a residual activity of 5%, corresponding to a consensus estimated percentage of wild‐type transcript produced from the literature (Aslanidis et al., 1996; Fasano et al., 2012).

Table S2 shows corresponding patient genotype and estimated combined LAL activity from the 165 patients, where 99 had reported CA‐LALD phenotype, 41 had an RP‐LALD phenotype, and 25 had an unspecified LAL deficiency phenotype. Figure 2 plots corresponding mean enzymatic activity values, categorized by reported patient phenotype. The two outlier results, corresponding to the above‐mentioned patients reported in (Kojima et al., 2013; Kuranobu et al., 2016), can be seen on the corresponding CA‐LALD column in this figure. Given the overlap of estimated activity values corresponding to unspecified LAL deficiency phenotypes with the values from the patients with CA‐LALD, it is reasonable to infer that most of the 25 documented patients with unspecified LAL deficiency phenotypes were actually patients with CA‐LALD.

Figure 2.

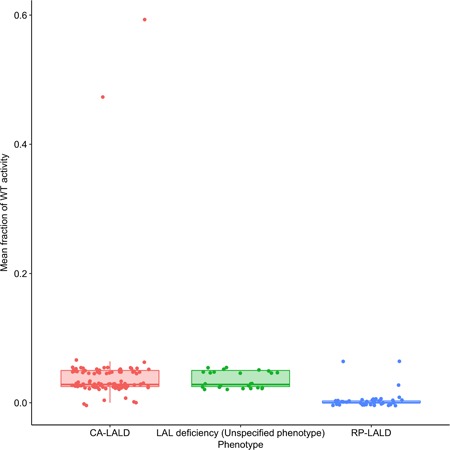
Mean fraction of wild‐type enzymatic activity for both genotypes for all subjects from literature according to their described phenotype. CA‐LALD, childhood/adult lysosomal acid lipase deficiency; LAL, lysosomal acid lipase; RP‐LALD, rapidly progressive lysosomal acid lipase deficiency; WT, wild‐type

To maximize Equation (5), note that, for any fixed value of $T_1,T2$, the maximum likelihood (ML) estimate of $({\alpha }_1,{\alpha }_2)$ is given by

$$\begin{array}{c}{\alpha }_1^{\text{ML}}=\frac{n_{\text{RP}\mathrm{-}\text{LALD}}^1}{n_{\text{RP}\mathrm{-}\text{LALD}}^1+n_{\text{CA}\mathrm{-}\text{LALD}}^1}\\ {\alpha }_2^{\text{ML}}=\frac{n_{\text{RP}\mathrm{-}\text{LALD}}^{12}}{n_{\text{RP}\mathrm{-}\text{LALD}}^{12}+n_{\text{CA}\mathrm{-}\text{LALD}}^{12}}\end{array}$$

ML estimates for $(T_1,T_2)$ were computed by doing a numeric grid search on $(T_1,T_2),0\le T_1\le T_2\le 1$, since the log‐likelihood function in Equation (5) is not continuously differentiable with respect to $T_1$ nor $T_2$. Given input data from Table S2, the following values were obtained for ML parameter estimates:

$$\begin{array}{c}{\alpha }_1^{\text{ML}}=0.86\\ {\alpha }_2^{\text{ML}}=0.04\\ T_1^{\text{ML}}=0.01\\ T_2^{\text{ML}}=0.07\end{array}$$

The parameters obtained by ML estimation match intuitively what Figure 2 shows graphically: For enzymatic activity values below around 0.01 relative to wild‐type, most reported patients to show RP‐LALD phenotype, whereas, for thresholds from around 0.01–0.07, CA‐LALD is the dominant LAL deficiency phenotype form, with no patients showing higher residual enzymatic activities (except for the two outlier points described above). However, the relationship between residual activity and presenting phenotype is not deterministic.

From the 149 tested variants, a total of 63 had measured intracellular enzymatic activity below threshold $T_2^{\text{ML}}$. Forty‐four out of the Forty‐seven variants curated from the literature showed low activity, whereas five out of seven variants from clinical trials showed activity below this threshold. The two clinical trial variants that showed activity above the threshold (c.931G>A/p.Gly311Arg and c.974C>T/p.Pro325Leu) showed activity between 0.07 and 0.08 relative to wild‐type (Table S1), a value possibly within bounds of measurement error. In contrast, only 14 out of the 93 tested variants from ExAC/gnomAD showed low residual activity.

3.3. In silico estimation of variant pathogenicity

After choosing the 149 LAL variants for enzymatic activity tests, there were still variants present in ExAC/gnomAD that remained to be assayed. One hundred thirty‐eight candidate LIPA variants present in ExAC were marked as missense, nonsense, frameshift or in‐frame deletions, and thus, amenable in theory for plasmid‐based in vitro testing. This candidate variant pool was later on expanded to 231 possible variants after the gnomAD 2.1.1 release was published (Karczewski et al., 2019). From this set of candidate gnomAD variants, there were 127 variants (listed in Table S3) that did not have in vitro functional data, 109 of which being missense variants and thus amenable to scoring by most in vitro algorithms. From the total of 54 LoF variants collected from either ExAC/gnomAD or literature, based on their molecular consequence, 23 had already been assayed in vitro (15 frameshift and 8 nonsense variants are described above). The remaining 31 were assumed to have null enzymatic activity as defined in Equation (8).

The presence of in vitro functional data permitted then the building of a validation set with which to assess each in silico algorithm’s performance. From the 126 assayed missense variants, there were 40 whose enzymatic activity (relative to wild‐type) fell below computed threshold $T_2=0.07$, and which were then classified as “deleterious.” The remaining 86 missense variants had measured enzymatic activity above $T_2$, and hence were classified as “nondeleterious.” Given this validation truth set, receiver operating curves (ROCs) and the area under the ROC (AUC) were computed for each of the in silico missense variant prediction algorithms.

• Combined annotation dependent depletion (CADD; Kircher et al., 2014)

• Deleterious annotation of genetic variants using neural networks (DANN; Quang, Chen, & Xie, 2015)

• MutationTaster (Schwarz, Cooper, Schuelke, & Seelow, 2014)

• PolyPhen‐2 (Adzhubei et al., 2013)

• Protein variation effect analyzer (PROVEAN; Choi, Sims, Murphy, Miller, & Chan, 2012)

• Sorting intolerant from tolerant (SIFT; Sim et al., 2012)

ROC and AUC scores were computed using each algorithm’s rank scores obtained from the dbNSFP variant annotation database, version 3.4 (Liu, Wu, Li, & Boerwinkle, 2015) accessed through the variant effect predictor annotation tool (McLaren et al., 2016). To estimate the variability of AUC estimates, and to assess the statistical significance of differences in performance among in silico algorithms, a classical bootstrap procedure was performed by sampling data with replacement, measuring resulting AUC for each in silico algorithm, and repeating sampling 10,000 times. Table 1 shows summarized results of this experiment for all considered in silico predictors. Figure 3 plots the corresponding ROC’s for each algorithm. Pairwise comparisons between each of the possible 15 in silico algorithm pairs revealed all AUC differences to be statistically significant ( for all pairwise Wilcoxon rank‐sum tests). As seen, PolyPhen‐2 performed better than other algorithms in this application.

Table 1.

Mean bootstrap AUC for all tested in silico missense variant effect prediction algorithms

In silico algorithm	Bootstrap AUC mean	Bootstrap AUC 95% CI
SIFT	0.8714170	(0.810–0.925)
PolyPhen‐2	0.9028099	(0.846–0.950)
CADD	0.8157466	(0.740–0.883)
DANN	0.7842790	(0.700–0.857)
MutationTaster	0.6940488	(0.635–0.751)
PROVEAN	0.7906035	(0.711–0.864)

Abbreviations: AUC, area under receiver operating curve; CADD, combined annotation dependent depletion; CI, confidence interval; DANN, deleterious annotation of genetic variants using neural networks; PROVEAN, protein variation effect analyzer; SIFT, sorting intolerant from tolerant.

Figure 3.

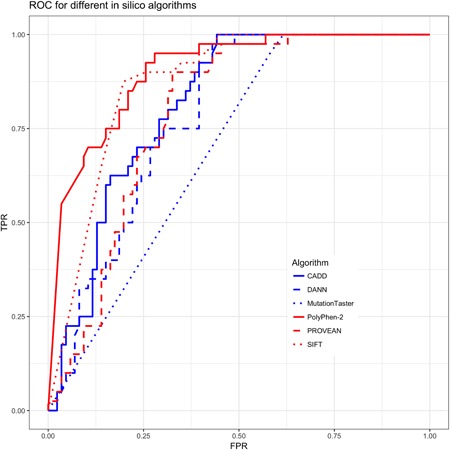
ROC for different in silico algorithms. CADD, combined annotation dependent depletion; DANN, deleterious annotation of genetic variants using neural networks; FPR, false positive rate; ROC, receiver operating characteristic; SIFT, sorting intolerant from tolerant; TPR, true positive rate

3.4. LAL deficiency birth prevalence estimation

With all model pieces in place, it was then possible to compute the LAL deficiency birth prevalence estimate for European‐ancestry populations. As mentioned above, computing an estimate for $\text{Pr}(\mathrm{\Phi }={\varphi }_k)$ was possible by performing Monte Carlo simulations of Equation (6) and analyzing the resulting estimate distribution. The RP‐LALD, CA‐LALD, and combined LAL deficiency birth prevalence estimates were computed under four scenarios, corresponding to the combination of two possible ways to assess variant activity and two possible ways of using gnomAD allele frequencies to evaluate Equation (6), as described above.

• 1.A “Stringent variant evaluation” scenario, which assessed variant activity as defined in Equation (8) only with in vitro functional data, and which set the variant activity of high‐confidence LoF variants to zero as explained on the Section 2.
• 2.A “Loose variant evaluation” scenario where variants which were marked as “Damaging” or “Possibly Damaging” by PolyPhen‐2 and which had not been tested for in vitro residual activity had activity set to zero to evaluate Equation (8).

Similarly, as described above, the two possible ways of using gnomAD allele frequencies were the “Lower Frequency Bound” that set the allele frequency of any variant absent in gnomAD to 0, and the “Upper Frequency Bound” that treated variants absent in gnomAD as singletons.

Each scenario was evaluated by performing 10,000 Monte Carlo runs. Table 2 shows the resulting average estimates for overall LAL deficiency, RP‐LALD, and CA‐LALD, and Figure 4 shows box plots with the spread in estimate values for the LAL deficiency case.

Table 2.

Summarized mean birth prevalence estimate for RP‐LALD, CA‐LALD, and overall LAL deficiency phenotypes as a function of different estimation scenarios

Estimation scenario	LAL deficiency probability (mean)	RP‐LALD probability (mean)	CA‐LALD probability (mean)
Stringent variant evaluation, lower frequency bound	3.45e−06	3.25e−07	3.13e−06
Loose variant evaluation, lower frequency bound	4.05e−06	4.97e−07	3.56e−06
Stringent variant evaluation, upper frequency bound	4.95e−06	7.36e−07	4.21e−06
Loose variant evaluation, upper frequency bound	5.97e−06	1.11e−06	4.86e−06

Abbreviations: CA‐LALD, childhood/adult lysosomal acid lipase deficiency; LAL, lysosomal acid lipase; RP‐LALD, rapidly progressive lysosomal acid lipase deficiency.

Figure 4.

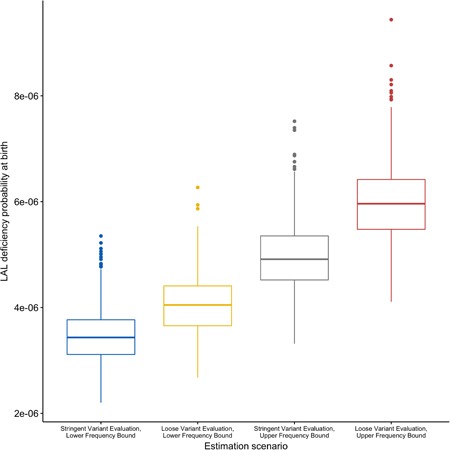
Total LAL deficiency birth prevalence estimates for European‐ancestry populations according to different variant sets. gnomAD, Genome Aggregation Database; LAL, lysosomal acid lipase

As can be seen from these data, the use of the upper frequency bound where missing gnomAD variants are treated as singletons had a significantly larger effect on the estimate than the loose variant evaluation scenario which added variants marked as deleterious by PolyPhen‐2.

3.5. Comparison of birth prevalence method with Scott’s

The results are shown in Table 2 indicate mean CA‐LALD birth prevalence estimates of 3.45–5.97 cases per million births, depending on the variant frequency bound and variant evaluation approach taken. These values are significantly lower than the mentioned estimates for European‐ancestry CA‐LALD birth prevalence of around 12 cases per million births or higher (Muntoni et al., 2007; Scott et al., 2013). This discrepancy follows mainly from the apparent overestimation of the E8SJM population allele frequency in these works. To validate this, E8SJM allele frequency estimates for European‐ancestry populations were collected from the following public data sources.

• Scott (Scott et al., 2013)

• Exome Variant Server (EVS; NHLBI GO Exome Sequencing Project & Exome Variant Server)

• UK10K (UK10K Consortium, 2015)

• ExAC, version 1.0 (Lek et al., 2016)

• gnomAD, version 2.1.1 (Karczewski et al., 2019)

Table 3 shows resulting E8SJM allele counts, allele number and allele frequency for each of these sources. It is clear even from this table that the E8SJM allele frequency from Scott et al. (2013; around 0.002, corresponding roughly to a carrier frequency of about 1/250) is substantially higher than the rest of the data sources, and is about 60% higher than the gnomAD allele frequency, which is the largest allele frequency public data source so far identified in terms of sampled subjects. Because the quadratic relationship between allele frequency and birth prevalence estimates from Equation (9), it was hence expected that the CA‐LALD birth prevalence estimate obtained from gnomAD would be less than half of the one from (Scott et al., 2013). Figure 5 shows resulting European‐ancestry CA‐LALD birth prevalence estimates for each of these data sources, with numerical results listed on Table 4. Also, plotted as horizontal lines, are the lowest and highest mean birth prevalence bounds obtained by in vitro functional testing as described in the previous section.

Table 3.

E8SJM European‐ancestry population allele counts, allele numbers, and allele frequencies for different public genomic data sources

Data source	Allele count	Allele number	Allele frequency
Scott	17	8224	0.0020671
EVS	5	8600	0.0005814
UK10K	7	7428	0.0009424
ExAC	77	66446	0.0011588
gnomAD	167	128942	0.0012952

Abbreviations: EVS, exome variant server; ExAC, exome aggregation consortium; gnomAD, Genome Aggregation Database; UK10K, the UK10K Project.

Figure 5.

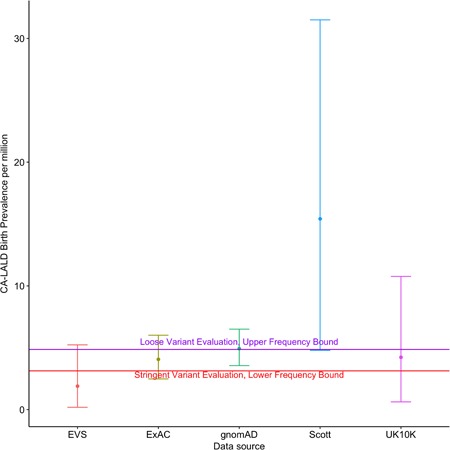
Comparison of different CA‐LALD birth prevalence estimates for European‐ancestry populations based on E8SJM allele frequency estimation according to different data sources. CA‐LALD, childhood/adult lysosomal acid lipase deficiency; EVS, exome variant server; ExAC, exome aggregation consortium; gnomAD, Genome Aggregation Database; UK10K, the UK10K Project

Table 4.

Mean, median, and 95% CI points for CA‐LALD birth prevalence estimates in European‐ancestry populations using E8SJM allele frequency estimates for all collected data sources

E8SJM AF source	Low 95% CI	Median	High 95% CI	Mean
EVS	1.86e−07	1.20e−06	5.20e−06	1.90e−06
ExAC	2.48e−06	3.90e−06	6.00e−06	4.10e−06
gnomAD	3.56e−06	4.80e−06	6.50e−06	4.90e−06
Scott	4.79e−06	1.32e−05	3.15e−05	1.54e−05
UK10K	6.23e−07	3.00e−06	1.08e−05	4.20e−06

Abbreviations: AF, allele frequency; CA‐LALD, childhood/adult lysosomal acid lipase deficiency; CI, confidence interval; EVS, exome variant server; ExAC, exome aggregation consortium; gnomAD, Genome Aggregation Database; UK10K, the UK10K Project.

4. DISCUSSION

The findings discussed here show how integrating in vitro functional data with large‐scale genomic datasets and novel statistical methods can give new insights into rare diseases, especially around genotype/phenotype relationships and the genetic epidemiology of recessive Mendelian disorders. The importance of this study is three‐fold.

• 1.It provides a novel statistical methodology to quantify the birth prevalence of any single‐gene autosomal recessive disorder, under the assumption of known or quantifiable phenotype probability given genotype and under HWE assumptions.
• 2.It is the most extensive catalog of functional assay data for LIPA variants to this date, and it provides a blueprint to further extend it for variants not yet assayed.
• 3.It shows how to combine this statistical methodology with the functional assay data to obtain more accurate bounds for LAL deficiency birth prevalence. In particular, the data shown here support LAL deficiency birth prevalence bounds of approximately 3.45 to 5.97 cases per million births, a range which is broadly concordant with values obtained by the previously used method of computing the E8SJM mutation frequency, once larger cohorts are used to estimate this variant’s frequency. This discrepancy in E8SJM allele frequency estimates with previous values had already been noted before (Stitziel et al., 2013), where a much larger sample size of around 27,000 subjects (which became later a proper subset of ExAc/gnomAD) was used for analysis.

As mentioned in Section 1, a recent publication (Carter et al., 2019) has also attempted to quantify the LAL deficiency prevalence using similar methods as the ones presented here. This study yielded an estimate for CA‐LALD birth prevalence in European‐ancestry populations at 1/160,000 using a meta‐analysis of existing genetic studies that rely on measuring the E8SJM allele frequency, and an overall LAL deficiency birth prevalence estimate of 1/177,000 using allele frequency information from gnomAD coupled with an HWE assumption as in the work presented here. The main differences between this study and the work presented here are the validation of variant pathogenicity by in vitro analysis presented here, and the statistical model used here, which uses measured or estimated in vitro activity to probabilistically classify a genotype as CA‐LALD or RP‐LALD instead of relying on the literature for variant classification. Also, a stricter criteria is used here on which LoF variants to include from either the literature or gnomAD.

The present study has certain limitations, mostly borne out of limited power from available data. In particular, attempts were made to only quantify LAL deficiency birth prevalence in populations of European ancestry, due to the much larger available allele frequency information for this population in comparison to others. The significantly smaller sample sizes available in other populations limit the applicability of the methodology presented here to these populations, because most pathogenic variant‐allele frequencies will be missing, and the resulting bounds obtained yield ranges, which are too wide to be useful. Also, the framework presented here fundamentally relies on the HWE assumptions to estimate birth prevalence. Situations where HWE does not apply, such as populations with significant consanguinity, would make this model inapplicable. We also recognize that more sophisticated genotype/phenotype models could be used, and the model presented here could be extended in several ways to account for more realistic conditions.

Much of the model presented here is dependent on characterizing LAL variants based on in vitro recombinant expression and assessing intracellular lipase activity. A limitation of this approach is that it is not able to provide information on other types of mutations known to give rise to enzyme deficiencies. Examples of these include splicing mutations such as the aforementioned E8SJM/c.894G>A pathogenic mutation found in the majority of patients with CA‐LALD (Bernstein et al., 2013; Scott et al., 2013) as well as mutations that inhibit trafficking beyond the endoplasmic reticulum and trans‐Golgi network as has been observed in other lysosomal storage diseases (Parenti et al., 2007; Ron & Horowitz, 2005; Spratley et al., 2016; Zhang et al., 2000). Another potential limitation of our analysis is the use of the artificial 4‐MU oleate substrate rather than naturally occurring substrates such as cholesteryl esters or triglycerides. Due to the difference in the chemical structure of these substrates, it is possible that some variants may retain substrate specificity against the 4‐MU oleate substrate yet lose the ability to cleave natural substrates or vice versa. In this regard, it is interesting to note that there were three LAL variants mentioned above (c.607G>C/p.Val203Leu, c.791T>C/p.Leu264Pro, and c.811A>C/p.Asn271His), which have been reported to be pathogenic (Kojima et al., 2013; Kuranobu et al., 2016; Reiner et al., 2014), that showed relatively high levels of intracellular lipase activity in our assay. This could be due to any of the reasons discussed, or through a yet to be defined mechanism. Nevertheless, understanding the pathogenesis behind these mutations warrants further investigation, which may lead to a further refinement of our model.

Even though the contribution of these three variants to our birth prevalence estimates is not expected to be significant due to their absence from ExAC/gnomAD, we cannot discount the possibility that some of the ExAC/gnomAD variants that showed high reported levels of intracellular activity might still be pathogenic.

Furthermore, LAL deficiency cannot always be divided up into the two discrete phenotypic manifestations (RP‐LALD and CA‐LALD), but is rather a more complex disease with a continuum of severities and clinical manifestations (Santillán‐Hernández et al., 2015), yielding a more complex model than the simple two‐tier stepwise genotype to phenotype model presented here.

Finally, caution should be taken to not use birth prevalence values obtained here to directly obtain estimates of total prevalent LAL deficiency cases in a geographic region. The total prevalent LAL deficiency population in a region will be affected by other factors such as disease onset and survival.

To conclude, the novel methods presented here, coupled with our large‐scale LIPA variant characterization, have enabled us to derive new estimates for the birth prevalence of both traditional forms of LAL deficiency. The range we derived, of approximately 3.45–5.97 cases per million births in European‐ancestry population, represents a significant decrease from previously published estimates that relied on estimating E8SJM’s carrier frequency but are concordant with values obtained from this methodology once larger sample sizes are used for estimation. Finally, the statistical framework presented here is not limited to LAL deficiency estimation but can be used for birth prevalence estimation of any autosomal recessive Mendelian disease.

Supporting information

Supplementary information

Supplementary information

Supplementary information

del Angel G, Hutchinson AT, Jain NK, Forbes CD, Reynders J. Large‐scale functional LIPA variant characterization to improve birth prevalence estimates of lysosomal acid lipase deficiency. Human Mutation. 2019;40:2007–2020. 10.1002/humu.23837