Abstract
In this work, we report the development of Drude polarizable force-field parameters for the carboxylate and N-acetyl amine derivatives, extending the functionality of existing Drude polarizable carbohydrate force field. The force field parameters have been developed in a hierarchical manner, reproducing the quantum mechanical (QM) gas-phase properties of small model compounds representing the key functional group in the carbohydrate derivatives, including optimization of the electrostatic and bonded parameters. The optimized parameters were then used to generate the models for carboxylate and N-acetyl amine carbohydrate derivatives. The transferred parameters were further tested and optimized to reproduce crystal geometries and J-coupling data from NMR experiments. The parameter development resulted in the incorporation of D-glucuronate, L-iduronate, N-acetyl-D-glucosamine (GlcNAc) and N-acetyl-D-galactosamine (GalNAc) sugars into the Drude polarizable force field. The parameters developed in this study were then applied to study the conformational properties of glycosaminoglycan polymer hyaluronan, composed of D-glucuronate and N-acetyl-D-glucosamine, in aqueous solution. Upon comparing the results from the additive and polarizable simulations it was found that the inclusion of polarization improved the description of the electrostatic interactions observed in hyaluronan resulting in enhanced conformational flexibility. The developed Drude polarizable force field parameters in conjunction with the remainder of the Drude polarizable force field parameters can be used for the future studies involving carbohydrates and their conjugates in complex, heterogeneous systems.
Graphical Abstract
Introduction
The ubiquity of carbohydrates and their scaffolds in biological systems reflects their involvement in a broad range of cellular processes including cell signaling1-2, inflammation3-4, immune response5, and protein stabilization,6 including cryoprotection7-8. In addition, glycosylation of proteins is the most frequent and diverse post-translational modification which profoundly affects their folding9-10, stability,11 and function12. Owing to their structural and functional diversity, carbohydrates represent both therapeutic targets and tools.13-16 For example, glycans decorating the eukaryotic cell surface are often the hallmark of cancer17-18 and inflammation18-19, while aberrant O-glycosylation may result in neurodegenerative disorders like Alzheimer’s20-21, Parkinson’s22 and Huntington’s20 disease. Altered glycosylation patterns (often termed as oncofetal) observed in cancerous cells include increased N-glycan branching, abnormal core fucosylation or an increase in sialyl Lewis structures23-25. Altered glycosylation pattern on some Immunoglobins isotypes, a crucial component of humoral immunity, have been identified in chronic inflammatory, autoimmune and infectious disease26-30, such as rheumatoid arthritis31-32 (RA), systemic lupus erythematosus33 (SLE) and HIV infection34. Indeed, glycosylation pattern differentially affects the functional roles of immunoglobulins35-38. Therefore, understanding the physical and conformational properties of carbohydrates alone and in combination with their molecular scaffolds is essential to elucidate their biological functions and their utilization as therapeutic agents.
Carbohydrate derivatives such as acidic sugars (glucuronic acid, iduronic acid) and amine derivatives (N-acetylglucosamine and N-acetyl galactosamine) are inherent components of complex eukaryotic glycans. These sugar derivatives are the key component of glycosaminoglycans (GAGs) such as heparins, dermatan, and their sulfate derivatives39-40 and play an essential role in various physiological and pathophysiological functions like morphogenesis41, viral invasion, cancer metastasis42, anticoagulation43-44, cell-cell interactions44, the HIV protein surface shield45 and lubrication44. The inherent structural complexity and variable length complicate the experimental structural characterization of these molecules46-47. Detailed analysis of these molecules with NMR or crystallography is usually carried out on smaller, isolated or synthetic oligomer units. Therefore, the experimental studies are generally augmented with theoretical methods like quantum mechanics48-50 (QM) calculations and classical molecular dynamics (MD)51-55 simulations. The most frequently used additive force fields for molecular simulations of carbohydrate derivatives include: CHARMM56, GROMOS57-58, OPLS-AA59, GLYCAM06,60 and CHARMM Carbohydrate Solution Force Field (CSFF)61. Most of the above-mentioned force fields are additive in nature with fixed partial charges, which limits the accurate description of the diverse environment observed in biological systems. For example, quantum mechanical (QM) calculations49-50 have shown that MD simulations with additive force fields do not satisfactorily describe inter and intra-molecular properties like solvent effect, counterion interactions, hydrogen bonding and molecular dipole variations which involve both inter-molecular and intra-molecular charge redistributions. To this end polarizable force fields, which can incorporate polarization allow us to bridge the gap between QM studies and classical MD simulations.
In recent years, several review articles have been dedicated to the facets of research on polarizable force fields62-71. A wide range of methods such as the fluctuating charge model72-76, induced point dipole model69, 77-81 and classical Drude oscillator model82-89 have been used to incorporate polarization in MD simulations. The fluctuating charge (FQ) model, also known as chemical potential equilibration or charge equilibration (CHEQ), is based on the theory of electronegativity equalization90. In the fluctuating charge model, the atomic charges can be redistributed in response to the electric field, while the overall charge on the molecule remains fixed. The CHARMM CHEQ polarizable force field75, 91 is based on fluctuating charge (FQ) model. The CHEQ force fields have been successfully implemented to study ion solvation92, protein-ligand binding,93 and lipid-membrane systems94-95. In the induced point dipole model, in addition to the partial atomic charge, a point dipole is assigned to each contributing site (i.e. atom); and the polarization solution for the induced dipole moment is treated through either iterative self-consistent field96-97 (SCF) methods or perturbation theory98-99. The induced dipole model is employed in several force fields including OPLS/PFF, AMBER (ff02EP100/ff02r1101) and AMOEBA78. The classical Drude oscillator model, also known as the Shell102 or Charge-On-Spring103 (COS) model, uses auxiliary charged particles (e.g. the Drude oscillators) to model the variability of the electronic structure, such that the approach retains most of the pairwise features from the additive force field model while explicitly treating electronic polarizability.
In the Drude polarizable force field, which is based on the classical Drude oscillator model, the charged auxiliary (Drude) particles are attached to the atomic core of the non-hydrogen atoms via a harmonic spring to incorporate induced polarization effects (Figure 1(a)). The induced polarization arises due to the displacement of the Drude particle under an applied electric field. The Drude particles, carrying a negative charge, embody the electronic degrees of freedom in the system (Figure 1(b)). In the Drude oscillator model, the sum of the charge on each atom is the sum of the charge on the atom core (qC) and the Drude particle (qD); and the induced dipole moment (μ) and the displacement (d) between the Drude particle and the core atom in response to an electric field E is defined as
| (1) |
and
| (2) |
and the atomic polarizability is evaluated as
| (3) |
where kD is the harmonic spring force constant for the Drude-core atom bond and is assigned a value of 1000 kcal mol−1 for all Drude particle-atom pairs, where the value of kD/2 or 500 kcal mol−1 is used directly as the input in CHARMM and NAMD.
Figure 1.
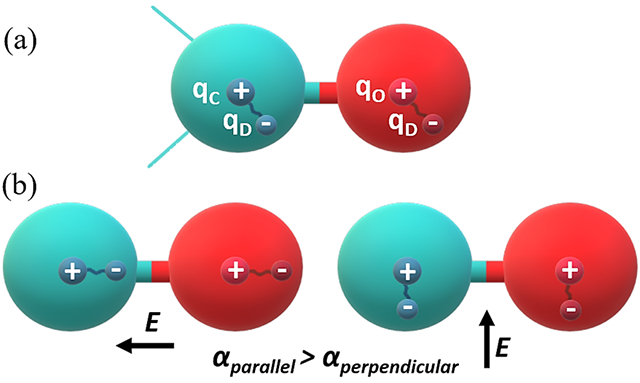
Schematic representation of Drude oscillator model for carbonyl functional (C=O) group. (a) The carbon and oxygen atoms are represented as sphere with the partially positively charged nucleus and partially negatively charged Drude particle. (b) Orientation of the Drude particle in the influence of electrical field, E, parallel and perpendicular to the interatomic covalent bond.
The functional form of the Drude polarizable force field for treating bonded and non-bonded interactions are similar to the additive force fields. The electrostatic potential energy term is extended to incorporate the unscreened Coulombic potential between ith and jth core atoms and their Drude particles, which can be evaluated as104
| (4) |
where qi and qj are the partial charges on ith and jth core atoms; qD,i and qD,j are the partial charges on the Drude oscillator attached to ith and jth core atoms, respectively; and di and dj are the bond lengths between the Drude oscillators and ith and jth core atoms, respectively. The electrostatic term explicitly includes the induced dipole interactions between the neighboring atoms (i.e., 1-2 and 1-3 atom pairs), which are scaled using the Thole screening function105:
| (5) |
Where rij is the distance between ith and jth atoms, and ai and aj are the respective Thole damping parameters that modulate the screening strength of Sij. The Drude force field using atom-specific ai and aj terms allows for improved treatment of molecular polarizability tensors106. This screening function can also be implemented for intermolecular interactions (known as NBTHOLE), which is important to model ions107-108. The Drude model also incorporate NBFIX for selected off diagonal atom-pair specific Lennard Jones (LJ) interactions to obtain better agreement with intermolecular interaction energies as well as condensed phase properties such a hydration free energies109.
The Drude polarizable force field covers a wide range of molecules62 such as water110-112, organic compounds (including alkanes113, aromatic compounds114, linear and cyclic ethers115, alcohols85, amides116, nitrogen109 and sulfur117 containing compounds), ions107, peptides and proteins118, DNA119, RNA120, carbohydrates86, 89, 121-122 and lipid membranes123; and has been applied to a variety of molecular systems124-130. The availability of the Drude polarizable force field in different simulation packages like CHARMM104, NAMD131, GROMACS132, ChemShell QM/MM133 and OPENMM87, 134 have made it convenient to run the polarizable force field simulations at the microsecond time scale. The present work extends the applicability of Drude polarizable force field to enable the modelling of carboxylate and N-acetyl amine carbohydrate derivatives.
Methods
Quantum Mechanical (QM) Calculations:
All QM calculations were carried out using Gaussian 03135 and Psi4136-137programs. Adiabatic potential energy scans (PES) were carried out by gas phase geometry optimization at the MP2/6-31G(d) level and single point energy evaluation at the RIMP2/cc-pVQZ model chemistry. QM solute-water interaction energies were obtained at the RI-MP2/cc-pVQZ//MP2/6-31G* model chemistry with counterpoise correction139 for basis set superposition error140 (BSSE) using the model compound gas phase molecular geometries or the SWM4-NDP111 geometry for water. The level of theory was chosen to maintain consistency with the published Drude polarizable CHARMM carbohydrate FF. 86, 89, 121-122
Molecular Mechanic (MM) Calculations.
All molecular mechanical (MM) calculations were performed using the CHARMM141 program with the Drude polarizable force field for all the polarizable simulations and the CHARMM36 carbohydrate force field56, 121, 142-143 for all the additive simulations unless otherwise stated. The SWM4-NDP111 water model is used to model water molecules in all the polarizable simulations while the CHARMM TIP3P144 water model was used for all the additive simulations. All gas phase monomer and dimer calculations included all possible nonbond pairs.
Dihedral Parameter Optimization.
Gas phase QM potential energy scans (PES) were taken as target data for dihedral parameter optimization. Initially the dihedral force constants of the target dihedrals were set to zero and MM potential energies (MM0) were calculated for the corresponding optimized geometries obtained from QM scans. The energy difference between MM0 and QM energies were used to fit the dihedral parameters using a least-square fit algorithm145 with multiplicity n =1,2,3, and 6 and phase angle δ =0 or 180.
Bond Length, Valence Angle, and Dihedral Angle calculations.
Starting from the QM optimized structure, minimizations were performed initially on only the Drude particles with the atoms constrained using the Steepest Descent (SD) optimizer, followed by Adopted-Basis Newton Raphson (ABNR) method to a gradient of 10−4 kcal/mol/Å. Minimization of all particles was next performed using SD algorithm followed by ABNR method to a gradient of 10−4 kcal/mol/Å.
Solute-water interaction calculations.
Solute-water interaction geometries were constructed based on the donor-acceptor properties of the solute heteroatoms. Solute-water interaction analysis was performed by distance scanning along a fixed orientation with the increment of 0.1 Å in both the QM and MM scans. For the MM scans the solute was constrained to the QM optimized geometry and the minimizations were performed on only the Drude particles with the atoms constrained using the SD optimizer, followed by the ABNR method to a gradient of 10−4 kcal/mol/Å. Interaction energies were calculated as the total energy of the solute-water complex at each distance minus the sum of the energies of the individual isolated monomers.
Crystal Simulations:
The crystal simulations were performed according to a previously established protocol86. Crystal coordinates for the crystal MD simulations were retrieved from Cambridge Structure Database146 (CSD). Missing hydrogen atoms were built and minimized using CHARMM36 additive and Drude polarizable force field parameters for the additive and polarizable crystal MD simulations. For each of the crystalline systems a 2×2×2 super cell was built which was used in the subsequent MD simulations. Crystal simulations under the NPT ensemble were carried out for 20 ns on each supercell system using both the additive and Drude polarizable force fields. All crystal simulations were performed at constant temperature (298 K) and pressure (1 ATM) using velocity-Verlet algorithm104 with Nose-Hoover thermostat. For Drude simulation, the thermostat coupled to the Drude oscillator was set to 1 K, while thermostat for the real atoms was set to 298 K. Electrostatic interactions were evaluated using particle mesh Ewald (PME) method with a real space cutoff of 12 Å, a sixth order B spline interpolation and a KAPPa value of 0.34. The van der Waals interactions were truncated by a switching function over 10-12 Å with an isotropic long-range Lennard-Jones (LJ) correction. Neighbor lists were updated with a 14 Å and 16 Å cutoff for additive and Drude simulations, respectively. In all the Drude simulations, to avoid polarization catastrophe (which may occur when the forces acting on drude particle cause large displacement from its core atom62), a “hard wall constraint” was used with a Drude-atom bond length cutoff of 0.2 Å.
Results and Discussion
I. Parameter Development.
The aim of this work was to develop polarizable force field parameters to extend the functionality of the Drude polarizable force field to include carboxylate and N-acetyl amine carbohydrate derivatives. The carboxylate derivatives of hexopyranose include D-glucuronate, L-iduronate, while amine derivatives include N-acetyl-D-glucosamine (GlcNAc) and N-acetyl-D-galactosamine (GalNAc). Carboxylates were specifically targeted owing to their relevance at physiological pH147. Among carboxylate derivatives, α-L-iduronic acid is an extensively explored component of heparin and heparan sulphates148-149, which exists as interconvertible 1C4 and 4C1 conformers148-149(Figure 2(a)). It is difficult to experimentally quantify the interconversion of the two conformers. While α-L-iduronic acid is assumed to favor the 1C4 configuration, glucuronic acid (C-5 epimer of iduronic acid) prefers to be in the 4C1 conformation150 (Figure 2(b)). Despite the presence of two destabilizing 1-3 diaxial oxygen groups, iduronic acid prefers to be in 1C4 state due to the anomeric effect150. The carboxylate group present on the C5 atom exerts a strong stabilizing effect on the equatorial conformation, while for axial conformation, it shows a destabilizing effect.
Figure 2.
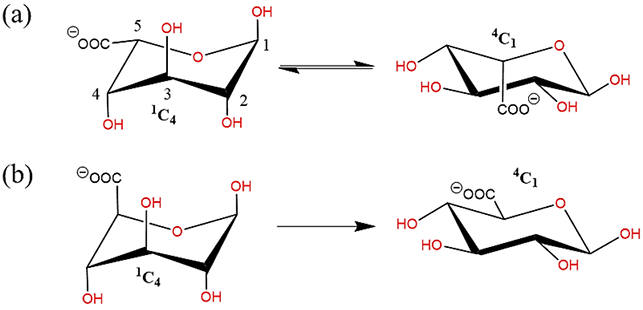
Schematic illustration of (a) interconversion of 1C4 chair to 4C1 configuration in Iduronate, (b) preferential occurrence of 4C1 configuration in Glucuronate. (all schematic diagrams were prepared with ChemBioDraw Ultra 13.0151)
In case of hexopyranose amine derivatives, N-acetylglucosamine (GlcNAc) is considered to exist in the 4C1 configuration in solution152. However, crystallographic data153 identifies rare ring flips in GlcNAc which may assert specific molecular recognition processes. To this end, MD simulations equipped with an accurate force field can facilitate a better understanding of atomistic properties of carbohydrate systems, thereby underlining the motivation of present work to develop Drude polarizable force field parameters for carboxylate and N-acetyl amine sugar derivatives.
In carboxylate sugar derivatives the carboxylate moiety is attached at the C5 position of the hexopyranose ring, while in the case of N-acetylamine derivatives, N-acetyl amine moiety is attached to the C2 position of hexopyranose. The parametrization of the derivative side chains, carboxyl and N-acetyl amine moieties, required the introduction of model compounds M1 (2-methoxy propionate) and M2 (N-isopropyl acetamide), respectively (Figure 3). Subsequent to the development of the parameters for the model compounds the same were transferred to full sugars, D-glucuronate, L-iduronate, N-acetyl-D-glucosamine (GlcNAc) and N-acetyl-D-galactosamine (GalNAc) (Figure 4), to test their transferability. Additional parameter optimization was performed for the full sugars when required. For the full sugars, parameters corresponding to the carbohydrate rings were transferred from the available Drude carbohydrate force field86, 89, 121-122 to maintain the parameter transferability for atoms with the same local chemical environment. In the subsequent sections, we discuss the parametrization process and the various issues faced during the parametrization for the carboxylate and N-acetylamine sugars separately.
Figure 3.
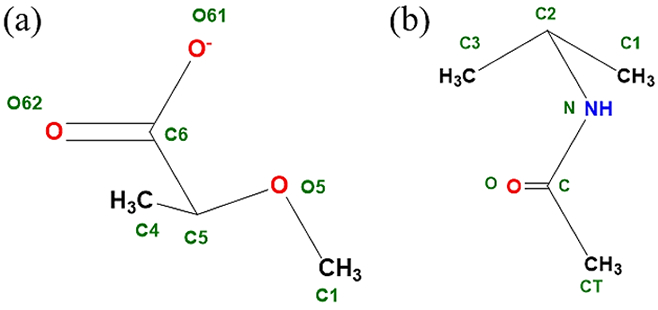
Model compounds used to develop parameters for carbohydrate derivatives (a) M1 (2- methoxy propionate): for glucuronate and iduronate, and (b) M2 (N-isopropyl acetamide): for GlcNAc and GalNAc. (all schematic diagrams were prepared with ChemBioDraw Ultra 13.0151)
Figure 4.
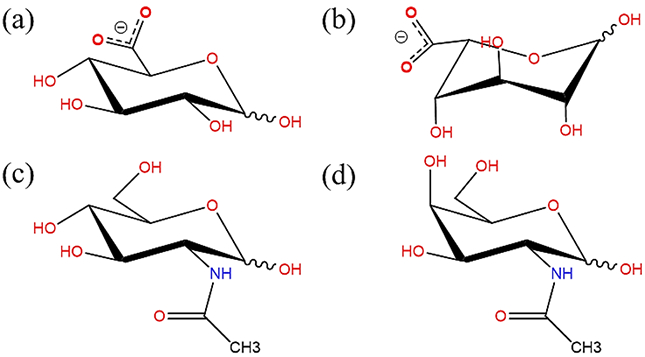
Chemical structures of glucopyranose derivatives (a) D-glucuronate, (b) L-iduronate, (c) N-acetyl-D-glucosamine (GlcNAc) and (d) N-acetyl-D-galactosamine (GalNAc). (all schematic diagrams were prepared with ChemBioDraw Ultra 13.0151)
Parametrization of Carboxylate derivatives
Model Compounds:
We used a model compound-based approach to develop the initial parameters for glucuronates and iduronates. 2- methoxy propionate (M1) was used as the model compound to target the C6 carboxylate, the C5, C4, and C1 ring carbon atoms and O5 ring oxygen (Figure 3). The same model compound was previously used to develop the parameters for the glucuronates and iduronates in the CHARMM additive carbohydrate force field, thereby enabling direct comparison with the additive force field. Parameters developed for the model compound were transferred to the full sugar to model carboxylate sugars for additional validation, as described below.
Model compound (M1):
The initial bonded, Lennard-Jones and electrostatic parameters for M1 were transferred from the existing ether, alkane and acidic residues already available in the polarizable force field85, 113, 115, 154. This identified the dihedral parameters about the C5-C6 bond that required to be parametrized. To parametrize the dihedral around the C5-C6 bond one-dimensional QM scans were performed for the O62-C6-C5-O5 dihedral in 15˚ increment resulting in 24 conformations. A least square fit method developed for parameter optimization145 was used to simultaneously fit the dihedral parameters for the O61/O62-C6-C5-O5 and O61/O62-C6-C5-C4 dihedrals. After fitting the low energy regions (Figure 5) are well represented by the polarizable force field and are consistent with the conformational energies obtained from QM and additive force-field calculations. The transferred and the developed parameters satisfactorily reproduce the minimized geometry of M1, wherein the C1-O5-C5-C6 dihedral was held restrained to an equilibrium value of −162.3˚ (Table 1). To verify the compatibility of the electrostatic parameters with the LJ parameters, the Drude model was validated against M1-water pair QM interaction energies for various geometries (Figure 6 and Table 2). The M1-water pair interaction energies show good agreement with the QM data with an average difference of 0.22 kcal/mol and 0.10 Å for interaction energies and distances, respectively. The parameters also satisfactorily reproduce the vibrational frequencies in agreement with the QM data (Table S1 of the supporting information (SI) file).
Figure 5.
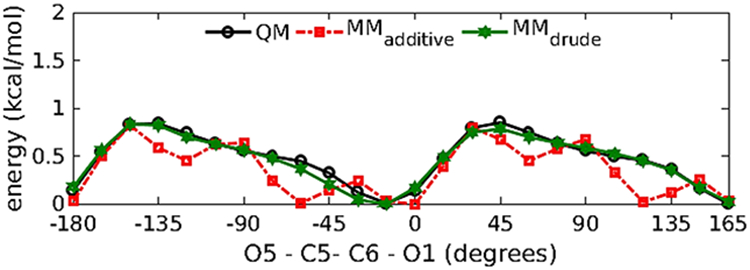
Relaxed potential energy scans of O5-C5-C6-O61 dihedral in compound M1.
Table 1.
Bond lengths, valence angles, and dihedral angles for model compound M1. Bond lengths are in Å, while valance angles and dihedral angles are in degree.
| Parameter | QM | Additive | Drude | ||||||
|---|---|---|---|---|---|---|---|---|---|
| MM | MM - QM |
MM* | MM* - QM |
MM | MM - QM |
MM* | MM* - QM |
||
| BONDS | |||||||||
| C4-C5 | 1.52 | 1.55 | 0.03 | 1.55 | 0.03 | 1.54 | 0.02 | 1.54 | 0.02 |
| C5-O5 | 1.44 | 1.44 | 0.00 | 1.44 | 0.00 | 1.53 | 0.09 | 1.53 | 0.09 |
| C5-C6 | 1.57 | 1.58 | 0.01 | 1.58 | 0.01 | 1.64 | 0.08 | 1.64 | 0.08 |
| C6-O61 | 1.25 | 1.26 | 0.00 | 1.26 | 0.00 | 1.27 | 0.01 | 1.27 | 0.01 |
| C6-O62 | 1.27 | 1.26 | −0.01 | 1.26 | −0.01 | 1.27 | 0.00 | 1.27 | 0.00 |
| Average | 0.01 | 0.01 | 0.04 | 0.04 | |||||
| Standard deviation | 0.01 | 0.01 | 0.04 | 0.04 | |||||
| ANGLES | |||||||||
| C4-C5-O5 | 111.2 | 109.3 | −1.9 | 110.5 | −0.7 | 110.5 | −0.8 | 110.0 | −1.3 |
| C4-C5-C6 | 109.7 | 110.6 | 0.9 | 109.9 | 0.2 | 110.6 | 0.9 | 111.2 | 1.5 |
| O5-C5-C6 | 111.3 | 112.8 | 1.5 | 112.3 | 1.0 | 112.6 | 1.3 | 112.8 | 1.5 |
| C5-C6-O61 | 117.7 | 118.0 | 0.4 | 118.1 | 0.4 | 118.7 | 1.1 | 118.8 | 1.2 |
| C5-C6-O62 | 111.5 | 112.8 | 1.3 | 112.8 | 1.3 | 110.7 | −0.8 | 110.6 | −0.9 |
| O61-C6-O62 | 130.9 | 129.2 | −1.7 | 129.2 | −1.7 | 130.6 | −0.3 | 130.6 | −0.3 |
| Average | 0.1 | 0.1 | 0.2 | 0.3 | |||||
| Standard deviation | 1.5 | 1.1 | 1.0 | 1.3 | |||||
| DIHEDRALS | |||||||||
| O5-C5-C6-O61 | −3.4 | −6.7 | −3.3 | −8.9 | −5.5 | −18.2 | −14.9 | −15.6 | −12.3 |
| C1-O5-C5-C6 | −162.3 | −151.4 | 11.0 | −162.3 | 0.0 | −168.7 | −6.4 | −162.3 | 0.0 |
| Average | 3.8 | −2.7 | −10.6 | −6.1 | |||||
| Standard deviation | 10.1 | 3.9 | 6.0 | 8.7 | |||||
Figure 6.
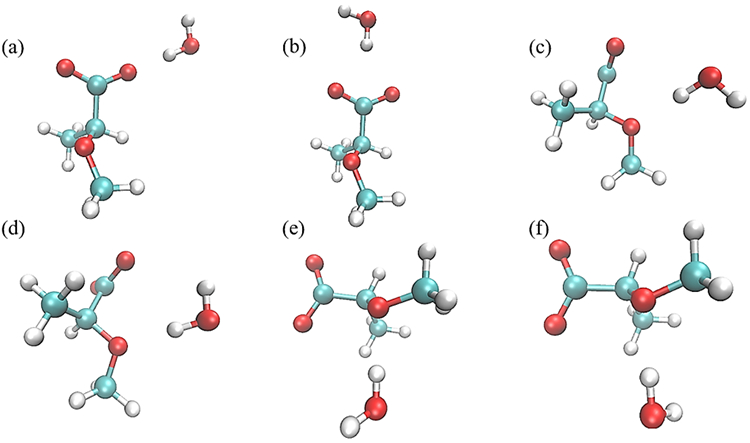
Monohydrate water interaction geometries with model compound M1. Interactions (a) and (b) have the M1 C6-O61 and C5-C6 bonds collinear with the water HO bond, respectively, and with the water molecule in the same plane as the carboxyl group; interactions (c) and (d) have the water HO bond collinear with the ether C1-O5-C5 angle bisector and with the water molecule in the same plane as the C1-O5-C5 atoms; and interactions (e) and (f) have the water molecule forming a tetrahedral interaction with the ether and with the water molecule perpendicular to the plane of the C1-O5-C5 atoms. All molecular graphics were prepared with VMD155.
Table 2.
Solute-water pair interaction energies and distances for model compound M1.
| Water Orientation |
Energy (kcal/mol) | Distance (Å) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| QM | Additive | Drude | QM | Additive | Drude | |||||
| MM | MM-QM | MM | MM-QM | MM | MM-QM | MM | MM-QM | |||
| a | −13.46 | −15.64 | −2.18 | −13.35 | 0.11 | 1.79 | 1.64 | −0.15 | 1.85 | 0.06 |
| b | −12.92 | −14.60 | −1.68 | −12.57 | 0.35 | 2.40 | 2.22 | −0.18 | 2.47 | 0.07 |
| c | −5.85 | −2.70 | 3.14 | −5.15 | 0.70 | 2.03 | 2.04 | 0.01 | 1.88 | −0.15 |
| d | −13.31 | −16.30 | −2.99 | −13.57 | −0.27 | 1.88 | 1.69 | −0.19 | 1.70 | −0.18 |
| e | −9.28 | −10.12 | −0.83 | −10.15 | −0.87 | 1.92 | 1.81 | −0.11 | 1.73 | −0.19 |
| f | −7.28 | −6.14 | 1.14 | −8.60 | −1.32 | 1.97 | 1.89 | −0.08 | 1.76 | −0.21 |
| Average | −0.57 | −0.22 | −0.12 | −0.10 | ||||||
| Standard deviation | 2.30 | 0.76 | 0.07 | 0.13 | ||||||
Full Sugars.
Parameters obtained from the model compounds were then transferred to the full sugar derivatives to model α/β-D-glucuronate and α/β-L-iduronate, in which the carboxylate moiety was attached to the C5 carbon of the hexopyranose ring. To check the transferability of the dihedral parameters obtained for the model compounds to full sugars, 1D QM scans were performed about the C5-C6 bond (for O61/O62-C6-C5-O5 dihedrals) for all the 4 systems; α/β-D-glucuronate is hereto referred as AGLCA/BGLCA and α/β-L-iduronate to be referred as AIDOA/BIDOA. To cover the probable conformational space both the chair conformations, 4C1 (regular chair) and 1C4 (inverted chair) were included for the QM scans. To avoid intramolecular hydrogen bonding between the terminal carboxyl group and the hydroxyl group at C4 carbon atom, the HO4-O4-C4-C3 dihedral was constrained to a value of 60˚ for all the QM and MM scans. The scans for all the systems performed in increments of 15˚ increment yielded a total of 161 conformations.
It was observed that while the transferred parameters were able to reproduce the individual QM energy profiles, they were not able to reproduce the energy differences between the α-and β-anomers (Figure 7). Therefore, transferred dihedral parameters still needed further improvement. To ensure faithful reproduction of conformational energies, out of 161 conformations obtained from QM scans, 62 QM conformations with relative conformational energies <20 kcal/mol from the global minimum for all the anomers were selected for further dihedral parameter optimization. Parameters obtained from the least-squares-fit procedure with the selected low-lying energy conformations as the goal was to be able to reproduce both the low-energy regions of the QM profile as well as the relative energy differences between the α-and β-anomers (Figure 7).
Figure 7.
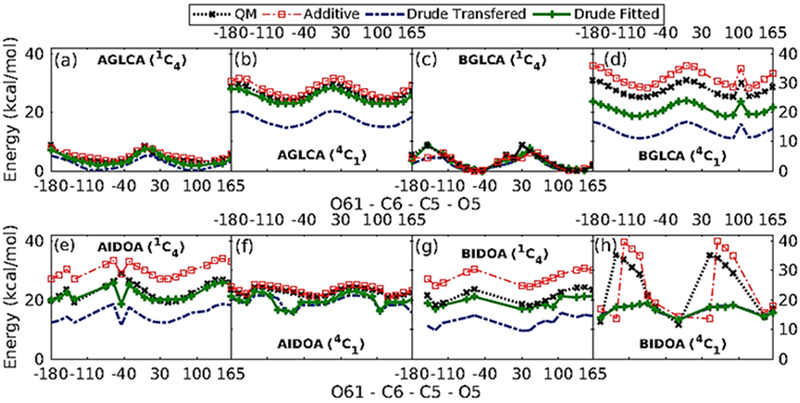
1D dihedral potential energy scans about O61-C6-C5-O5 dihedrals for α-/β- Glucuronate (a, b, c and d), and α-/β- Iduronate (e, f, g and h). Only those conformers with relative energies < 20 kcal/mol are included in the figure.
To check the compatibility of the electrostatic and LJ parameters, the parameters were validated against full sugar-water pair interaction energies for seven different water-solute conformations for all the systems that probe the charges on the O5 and C5 atoms of the carboxylates (Figure 8). The interaction energies and minimum distances for all the systems are tabulated in Table 3. The polarizable force field reproduces the energies and distances better when compared to the additive force field, with the average value for interaction energy differences (MM - QM, in kcal/mol) from the polarizable (additive) force field being 0.49(0.96), 0.33(0.81), −0.83(0.55) and −1.69(0.52) for AGLCA, BGLCA, AIDOA and BIDOA, respectively. We observe a similar trend for the distances, with the average values for the distance differences (MM - QM, in Å) from the polarizable (additive) force field being 0.12 (0.19), −0.52 (−0.47), −0.12 (−0.12) and −0.17 (−0.14) for AGLCA, BGLCA, AIDOA and BIDOA, respectively. The improved agreement with the Drude model is in part due to the additive force field nonbond parameters originally optimized targeting HF/6-31G* without BSSE QM model chemistry data.
Figure 8.
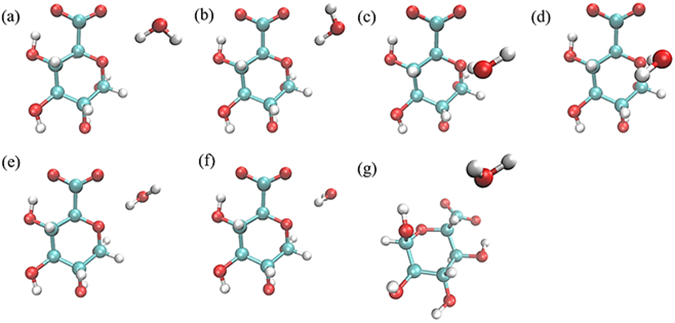
Water pair interaction geometries with acidic sugars. Interactions (a) and (b) have the water HO bond collinear with the C5-O5-C1 angle bisector, with the water molecule in the same plane as the C5-O5-C1 atoms; interactions (c) and (d) have the water molecule forming a tetrahedral interaction with the O5, with the water molecule perpendicular to the plane of the C5-O5-C1 atoms; interactions (e) and (f) have the water HO bond collinear with the C5-O5-C1 angle bisector, with the water molecule perpendicular to the plane of the C5-O5-C1 atoms; and interaction (g) has the C5-H5 vector collinear with the water HOH angle bisector. (All molecular graphics were prepared with VMD155)
Table 3.
Solute-water pair interaction energies and distances for sugar carboxylates.
| Water Orientation | Energy (kcal/mol) | Distance (Å) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| QM | Additive | Drude | QM | Additive | Drude | |||||
| MM | MM-QM | MM | MM-QM | MM | MM-QM | MM | MM-QM | |||
| AGLCA | ||||||||||
| a | −4.89 | −0.95 | 3.94 | −3.28 | 1.61 | 2.25 | 3.71 | 1.46 | 2.54 | 0.29 |
| b | −11.77 | −15.64 | −3.87 | −10.54 | 1.24 | 2.10 | 1.74 | −0.36 | 1.99 | −0.11 |
| c | −7.59 | −7.46 | 0.13 | −7.12 | 0.46 | 1.91 | 1.76 | −0.15 | 1.87 | −0.04 |
| d | −6.16 | −2.94 | 3.21 | −6.26 | −0.10 | 1.98 | 1.96 | −0.02 | 1.91 | −0.07 |
| e | −6.75 | −6.35 | 0.40 | −5.35 | 1.40 | 2.20 | 2.16 | −0.04 | 2.64 | 0.44 |
| f | −4.80 | −2.97 | 1.83 | −5.35 | −0.55 | 2.34 | 2.80 | 0.46 | 2.64 | 0.30 |
| g | 2.20 | 3.30 | 1.10 | 1.57 | −0.64 | 3.00 | 3.00 | 0.00 | 3.00 | 0.00 |
| Average | 0.96 | 0.49 | 0.19 | 0.12 | ||||||
| Standard deviation | 2.55 | 0.94 | 0.61 | 0.22 | ||||||
| BGLCA | ||||||||||
| a | −4.27 | −0.97 | 3.31 | −2.77 | 1.50 | 2.10 | 3.84 | 1.74 | 2.45 | 0.35 |
| b | −11.67 | −15.90 | −4.23 | −10.75 | 0.92 | 2.97 | 1.72 | −1.25 | 1.88 | −1.09 |
| c | −7.29 | −7.35 | −0.06 | −7.97 | −0.68 | 2.89 | 1.82 | −1.07 | 1.83 | −1.06 |
| d | −5.97 | −3.12 | 2.85 | −7.69 | −1.72 | 2.96 | 2.08 | −0.88 | 1.85 | −1.11 |
| e | −6.54 | −5.93 | 0.62 | −4.50 | 2.04 | 2.98 | 1.92 | −1.06 | 2.63 | −0.35 |
| f | −5.57 | −2.73 | 2.84 | −4.51 | 1.06 | 3.02 | 2.28 | −0.74 | 2.64 | −0.38 |
| g | 2.13 | 2.45 | 0.31 | 1.33 | −0.80 | 3.00 | 3.00 | 0.00 | 3.00 | 0.00 |
| Average | 0.81 | 0.33 | −0.47 | −0.52 | ||||||
| Standard deviation | 2.61 | 1.40 | 1.05 | 0.58 | ||||||
| AIDOA | ||||||||||
| a | −4.54 | −1.16 | 3.38 | −4.67 | −0.13 | 2.04 | 1.97 | −0.07 | 1.93 | −0.11 |
| b | −9.65 | −12.12 | −2.47 | −9.97 | −0.31 | 1.93 | 1.71 | −0.22 | 1.84 | −0.09 |
| c | −6.20 | −6.19 | 0.01 | −7.87 | −1.67 | 1.93 | 1.77 | −0.16 | 1.75 | −0.18 |
| d | −4.23 | −2.46 | 1.77 | −6.05 | −1.83 | 2.01 | 1.95 | −0.06 | 1.81 | −0.20 |
| e | −5.05 | −5.26 | −0.21 | −5.91 | −0.86 | 2.05 | 1.85 | −0.20 | 1.95 | −0.10 |
| f | −5.65 | −5.21 | 0.45 | −5.92 | −0.27 | 2.07 | 1.92 | −0.15 | 1.95 | −0.12 |
| g | 2.08 | 3.00 | 0.92 | 1.32 | −0.76 | 3.00 | 3.00 | 0.00 | 3.00 | 0.00 |
| Average | 0.55 | −0.83 | −0.12 | −0.12 | ||||||
| Standard deviation | 1.81 | 0.68 | 0.08 | 0.07 | ||||||
| BIDOA | ||||||||||
| a | −5.79 | −2.80 | 3.00 | −6.49 | −0.70 | 2.01 | 1.89 | −0.12 | 1.85 | −0.16 |
| b | −10.10 | −12.57 | −2.46 | −12.23 | −2.13 | 1.93 | 1.71 | −0.22 | 1.77 | −0.16 |
| c | −6.22 | −5.90 | 0.32 | −7.11 | −0.89 | 2.00 | 1.85 | −0.15 | 1.86 | −0.14 |
| d | −5.83 | −5.22 | 0.60 | −7.34 | −1.51 | 2.10 | 1.91 | −0.19 | 1.86 | −0.24 |
| e | −6.59 | −6.98 | −0.39 | −9.22 | −2.63 | 1.97 | 1.78 | −0.19 | 1.78 | −0.19 |
| f | −5.85 | −4.78 | 1.07 | −9.23 | −3.38 | 2.07 | 1.93 | −0.14 | 1.78 | −0.29 |
| g | 2.21 | 3.74 | 1.53 | 1.65 | −0.56 | 3.00 | 3.00 | 0.00 | 3.00 | 0.00 |
| Average | 0.52 | −1.69 | −0.14 | −0.17 | ||||||
| Standard deviation | 1.69 | 1.07 | 0.07 | 0.09 | ||||||
Crystal Simulation.
Crystal MD simulations were performed to validate the combination of the bonded and non-bonded parameters in the condensed phase. The quality of the optimized parameters was assessed by comparing the intramolecular descriptors of the chemical system (bonds, angles and dihedrals), as well as the descriptors of the crystal lattice (lattice parameters and unit cell volumes) with available experimental values for the crystal structure obtained from Cambridge structural database146 (CSD). A CSD survey yielded one crystal (NABDGC156) for β-D-glucuronate monohydrate, having the full monoclinic unit cell consisting of two monosaccharides, two water molecules, and two sodium ions. MD simulation of the infinite crystal lattice was performed on this system. Analysis of the bond, angles, and dihedrals showed that the intramolecular descriptors of the systems were well reproduced by the polarizable force field. The average errors in the bonds and angles were found to be 0.02 Å and 1.00˚, while the average error for the dihedral was found to be −3.89˚. The results are comparable to the additive force field. The discrepancy in the dihedrals corresponds to the very low barriers for rotation for the exocyclic torsion <1 kcal/mol (Figure 5) around the local minima, especially for the Drude FF when compared to the additive FF. Unit cell geometries were consistent with the experimental values (Table 4), while unit cell volume is overestimated by 3.74 % (Table 5).
Table 4.
Crystalline intramolecular geometries for α-galacturonate crystal. Bond lengths are in Å, while valance angles and dihedral angles are in degree.
| CRYS | MDadd | MDdrude | MDadd – CRYS (%err) |
MDdrude – CRYS (%err) |
|
|---|---|---|---|---|---|
| NABDGC (β-D-glucuronate monohydrate) | |||||
| C4-C5 | 1.535 | 1.527 | 1.536 | −0.01 (0.00) | 0.00 (0.00) |
| C5-O5 | 1.429 | 1.449 | 1.452 | 0.02 (0.00) | 0.02 (0.00) |
| C5-C6 | 1.533 | 1.536 | 1.587 | 0.00 (0.00) | 0.05 (0.00) |
| C6-O61 | 1.244 | 1.257 | 1.271 | 0.01 (0.00) | 0.03 (0.00) |
| C6-O62 | 1.254 | 1.261 | 1.274 | 0.01 (0.00) | 0.02 (0.00) |
| C4-C5-O5 | 109.587 | 108.65 | 108.616 | −0.94 (−0.02) | −0.97 (−0.10) |
| C4-C5-C6 | 108.647 | 110.012 | 113.979 | 1.37 (−0.02) | 5.33 (−0.05) |
| O5-C5-C6 | 108.059 | 109.568 | 110.802 | 1.51 (−0.01) | 2.74 (−0.19) |
| C5-C6-O61 | 116.528 | 116.756 | 114.923 | 0.23 (−0.02) | −1.61 (−0.12) |
| C5-C6-O62 | 118.05 | 116.366 | 115.561 | −1.68 (−0.01) | −2.49 (−0.03) |
| O61-C6-O62 | 125.229 | 126.614 | 128.238 | 1.39 (−0.02) | 3.01 (−0.07) |
| O5-C5-C6-O61 | −28.028 | −27.72 | −41.909 | 0.31 (−0.17) | −13.88 (−0.29) |
| O5-C5-C6-O62 | 156.756 | 159.977 | 148.045 | 3.22 (−0.08) | −8.71 (−0.04) |
| C1-O5-C5-C6 | −177.661 | −173.44 | −166.728 | 4.21 (−0.05) | 10.93 (−0.51) |
additive force field,
drude: Drude polarizable force field parameters.
Table 5.
Crystalline unit cell geometries and volumes
| carbohydrate | Crystal ID | A(Å) | %error | B(Å) | %error | C(Å) | %error | Volume (Å)3 |
%error | |
|---|---|---|---|---|---|---|---|---|---|---|
| β-D-glucuronate monohydrate | NABDGC | Crystal | 9.21 | 7.01 | 7.38 | 472.59 | ||||
| Additive | 9.58 | 4.01 | 7.09 | 1.16 | 7.09 | −3.95 | 478.87 | 1.33 | ||
| Drude | 9.26 | 0.61 | 6.79 | −3.16 | 7.86 | 6.47 | 490.27 | 3.74 |
Parametrization of N-acetylamine derivatives
Similar to carboxylate derivative parametrization, we used a fragment-based approach to parameterize N-acetylamine derivatives. The model compound N-isopropyl-acetamide (M2) was used to target the C1, C2, C3 ring carbon atoms and CT, C, O, and N atoms of the N-acetyl group. The N-isopropyl-acetamide model compound was also used in the additive force field parametrization of N-acetylglucosamines and N-acetylgalactosamines, enabling direct comparison with the additive force field. The developed model compound parameters were then transferred to the full sugar to model N-acetylamine sugars for further validation.
Model Compounds M2.
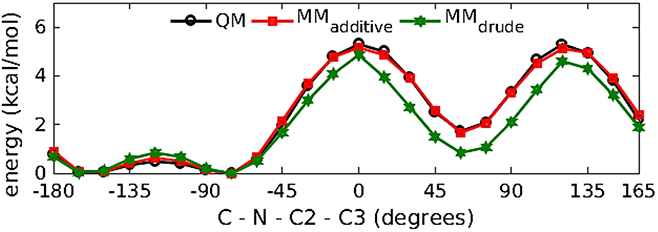
Model compound M2 (Figure 3(b)) was used to parameterize the N-acetyl amine moieties linkages to the C2 carbon of hexopyranose backbone to enable the modeling of N-acetylamine sugars. Initial bonded, LJ and electrostatic parameters for M2 were transferred from existing alanine dipeptide parameters available in the Drude polarizable force field. To check the transferred dihedral parameters in M2, 1D QM potential energy scans were performed about the C2-N bond for the C-N-C2-C3 dihedral. The transferred parameters well represented the low energy region with the conformational energies being comparable to results obtained from the QM and additive force-field calculations (Figure 9). The transferred parameters satisfactorily reproduced the minimized geometry of M2 (Table 6).
Figure 9.
Relaxed potential energy scans of the C-N-C2-C3 dihedral in compound M2.
Table 6.
Bond lengths, valence angles, and dihedral angles for model compound M2. Bond lengths are in Å, while valance angles and dihedral angles are in degrees.
| QM | Additive | Drude | |||
|---|---|---|---|---|---|
| MM | MM-QM | MM | MM-QM | ||
| BONDS | |||||
| C1-C2 | 1.526 | 1.532 | 0.006 | 1.524 | −0.002 |
| C2-C3 | 1.522 | 1.531 | 0.008 | 1.523 | 0.001 |
| C2-N | 1.459 | 1.427 | −0.032 | 1.444 | −0.015 |
| N-C | 1.367 | 1.338 | −0.028 | 1.358 | −0.009 |
| C-CT | 1.516 | 1.506 | −0.010 | 1.524 | 0.008 |
| C-O | 1.234 | 1.224 | −0.011 | 1.257 | 0.023 |
| Average | −0.010 | 0.000 | |||
| Standard deviation | 0.020 | 0.010 | |||
| ANGLES | |||||
| N-C2-C1 | 111.20 | 110.90 | −0.40 | 113.40 | 2.20 |
| N-C2-C3 | 109.10 | 109.50 | 0.40 | 111.70 | 2.70 |
| C1-C2-C3 | 112.50 | 110.90 | −1.60 | 107.70 | −4.80 |
| C2-N-C | 121.50 | 123.60 | 2.10 | 120.80 | −0.60 |
| N-C-CT | 115.40 | 116.10 | 0.70 | 121.80 | 6.50 |
| N-C-O | 122.30 | 123.10 | 0.80 | 124.80 | 2.40 |
| O-C-CT | 122.30 | 120.80 | −1.50 | 113.40 | −8.90 |
| Average | 0.07 | −0.09 | |||
| Standard deviation | 1.32 | 5.19 | |||
| DIHEDRALS | |||||
| C1-C2-N-C | −77.8 | −78.9 | −1.2 | −74.9 | 2.8 |
| C3-C2-N-C | 157.6 | 158.4 | 0.8 | 163.2 | 5.6 |
| Average | −0.2 | 4.2 | |||
| Standard deviation | 1.4 | 1.9 | |||
To verify the compatibility of the electrostatic and LJ parameters, the parameters were validated against M2-water pair interaction energies for various geometries of M2-water system (Figure 10 and Table 7). The M2-water pair interactions obtained from transferred parameters showed good agreement with the QM water pair interactions with average differences of 0.11 kcal/mol and 0.004 Å for interaction energies and distances, respectively. The vibrational frequencies obtained from transferred parameters showed reasonably good agreement to the vibrational frequencies obtained from QM calculations (Table S2 of the supporting information (SI) file).
Figure 10.
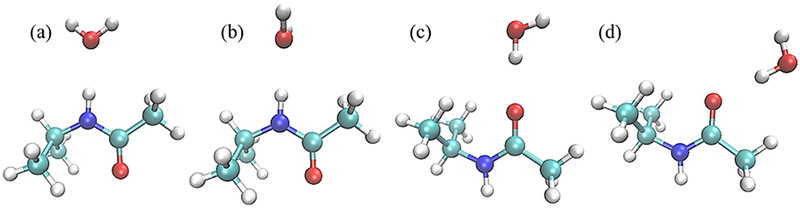
Water pair interaction geometries with model compound M2. Interactions (a) and (b) have the NH vector collinear with water HOH angle bisector; in (a) the water molecule is coplanar with the amide group and in (b) the water molecule is perpendicular. Interaction (c) has the CO vector collinear with the water HO vector and interaction (d) has these two vectors forming a 120°angle; in both (c) and (d) water molecule is coplanar with the amide group. (All molecular graphics were prepared with VMD155)
Table 7.
Solute-Water Pair Interaction Energies and Distances for Model Compound M2.
| Water Orientation |
Energy (kcal/mol) | Distance (Å) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| QM | Additive | Drude | QM | Additive | Drude | |||||
| MM | MM-QM | MM | MM-QM | MM | MM-QM | MM | MM-QM | |||
| a | −5.60 | −7.04 | −1.44 | −5.40 | 0.20 | 1.96 | 1.75 | −0.21 | 1.97 | 0.01 |
| b | −6.81 | −7.37 | −0.57 | −6.77 | 0.04 | 1.94 | 1.77 | −0.17 | 1.90 | −0.04 |
| c | −4.58 | −6.45 | −1.87 | −4.41 | 0.18 | 2.03 | 1.89 | −0.14 | 2.02 | −0.01 |
| d | −4.79 | −6.65 | −1.86 | −4.75 | 0.04 | 2.01 | 1.89 | −0.12 | 2.02 | 0.01 |
| Average | −1.43 | 0.11 | −0.16 | 0.00 | ||||||
| Standard deviation | 0.61 | 0.09 | 0.04 | 0.02 | ||||||
Full Sugar.
Parameters obtained from the model compound M2 were then transferred to the full sugar derivatives to model α/β-N-acetylglucosamines (referred to as AGLCNA/BGLCNA) and α/β-N-acetyl galactosamines (referred to as AGALNA/BGALNA), in which the N-acetyl amine moiety is attached to the C2 carbon of the hexopyranose ring. To examine the transferability of the dihedral parameters obtained from M2 to the full sugar, 1D potential energy scans of C-N-C2-C1 dihedral were conducted for each N-acetylamine derivative (AGLCNA, BGLCNA, AGALNA and BGALNA) at 15˚ interval from 0˚ to 345˚. During both the QM and MM scan, to avoid intramolecular hydrogen bonding between terminal N-acetyl group and the hydroxyl group at C1 carbon atom, O5-C1-O1-HO1 dihedral was constrained to 60˚.
The transferred parameters failed to reproduce the low energy region of the QM profile (Figure 11). Therefore, the refinement of C-N-C2-C1 dihedral was warranted. The least square fitting protocol was applied by targeting MP2/6-31G*//RIMP2/cc-pVTZ QM energies with the dihedral parameter phase angles restricted to either 0˚ or 180˚. Energy surfaces were offset to zero at the lowest energy conformation and the conformations with relative QM energies > 12 kcal/mol were excluded during the fitting. The refined dihedral parameters obtained from the least square fitting protocol were able to reproduce the low energy profile for both α- and β- anomers of N-acetylamine derivative (Figure 11).
Figure 11.
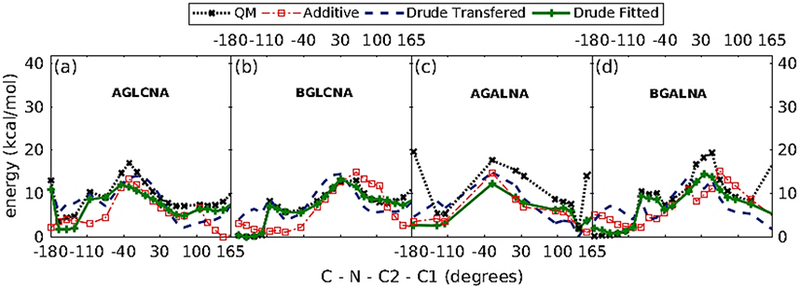
1D dihedral potential energy scans about C-N-C2-C1 dihedrals for α-/β- N-acetyl-D-glucosamine (a and b), and N-acetyl-D-galactosamine (c and d).
To validate the compatibility of electrostatic and LJ parameters, the parameters were examined against the N-acetylamine derivative-water pair interaction energies for three different solute-water conformations (Figure 12) for all the acetyl-amine sugars, which probe the charges on C1 and C2 atoms of the carbohydrate ring. The statistical summary of the interaction energies and minimum distances for all the systems is presented in Table 8.
Figure 12.
Water pair interaction geometries with N-acetylamines (α-/β- GlcNAc and α-/β- GalNAc). Interaction (a) has the C1-H1 vector collinear with the water HOH angle bisector; and interaction (b) has the C2-H2 vector collinear with the water HOH angle bisector. All molecular graphics were prepared with VMD155.
Table 8.
Solute-water pair interaction energies and distances for N-acetylamine sugar derivatives.
| Water Orientation | Energy (kcal/mol) | Distance (Å) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| QM | Additive | Drude | QM | Additive | Drude | |||||
| MM | MM-QM | MM | MM-QM | MM | MM-QM | MM | MM-QM | |||
| AGLCNA | ||||||||||
| a | −2.43 | −3.12 | −0.70 | −1.84 | 0.59 | 2.32 | 2.59 | 0.27 | 2.64 | 0.32 |
| b | −2.77 | −2.23 | 0.54 | −1.54 | 1.23 | 2.13 | 2.57 | 0.44 | 2.60 | 0.47 |
| Average | −0.08 | 0.91 | 0.36 | 0.40 | ||||||
| Standard deviation | 0.87 | 0.46 | 0.12 | 0.11 | ||||||
| BGLCNA | ||||||||||
| a | −2.53 | −3.15 | −0.62 | −1.85 | 0.68 | 2.28 | 2.56 | 0.28 | 2.62 | 0.34 |
| b | −2.42 | −2.63 | −0.22 | −1.62 | 0.80 | 2.28 | 2.61 | 0.33 | 2.64 | 0.36 |
| Average | −0.42 | 0.74 | 0.30 | 0.35 | ||||||
| Standard deviation | 0.29 | 0.09 | 0.04 | 0.02 | ||||||
| AGALNA | ||||||||||
| a | 0.75 | 0.88 | 0.13 | 1.33 | 0.58 | 3.00 | 3.00 | 0.00 | 3.00 | 0.00 |
| b | −1.81 | −2.29 | −0.48 | −2.01 | −0.20 | 2.34 | 2.61 | 0.27 | 2.60 | 0.26 |
| Average | −0.18 | 0.19 | 0.14 | 0.13 | ||||||
| Standard deviation | 0.43 | 0.55 | 0.19 | 0.18 | ||||||
| BGALNA | ||||||||||
| a | −2.10 | −3.17 | −1.08 | −1.91 | 0.19 | 2.36 | 2.58 | 0.22 | 2.64 | 0.28 |
| b | −2.05 | −2.62 | −0.57 | −1.80 | 0.24 | 2.29 | 2.60 | 0.31 | 2.64 | 0.35 |
| Average | −0.82 | 0.22 | 0.26 | 0.31 | ||||||
| Standard deviation | 0.36 | 0.03 | 0.07 | 0.05 | ||||||
Crystal Simulation.
A CSD search yielded three crystal structures ACGLUA11 (compound name: N-acetyl-α-D-glucosamine, R factor: 0.0237), AGALAM10 (compound name: N-acetyl-α-D-galactosamine, R factor: 0.04) and NACMAN10 (compound name: N-acetyl-β-D-mannosamine monohydrate, R factor: 0.07). The ACGLUA11 crystal structure consists of two molecules of α-GlcNAc in the unit cell; the AGALAM10 crystal structure consists of two molecules of α-GalNAc in the unit cell; and NACMAN10 crystal structure consists of four molecules of β-ManNAc and four water molecules in the unit cell. MD simulations were performed on each crystal supercell (2 X 2 X 2-unit cells) constructed from corresponding crystal structures in the NPT ensemble with both additive and Drude polarizable force fields. The results comparing the intramolecular geometrical descriptors (bond lengths, angles and dihedrals) retrieved from additive and Drude polarizable simulations for all the three crystals are tabulated in Table 9. The intramolecular geometrical descriptors are well reproduced by the developed force-field parameters. The average errors in the bonds and angles were found to be 0.02, 0.64˚; 0.02, 0.66˚; and 0.01, 0.42˚ for the three crystals ACGLUA11, AGALAM10 and NACMAN10, respectively. The average errors in dihedrals are 2.0˚, −4.9˚ and −15.6˚ for the three crystals ACGLUA11, AGALAM10 and NACMAN10, respectively. The overall results from crystal simulations are comparable to the additive simulations. Unit cell geometries were consistent with the experimental values, while unit cell volumes were overestimated by 3.42%, 4.29% and 5.73% for the three crystals ACGLUA11, AGALAM10 and NACMAN10, respectively (Table 10).
Table 9.
Crystalline intramolecular geometries for α-GlcNAc, α-GalNAc, β-ManNAc crystals. Bond lengths are in Å, while valance angles and dihedral angles are in degree.
| CRYS | MDadd | MDdrude | MDadd – CRYS (%err) | MDdrude – CRYS (%err) | |
|---|---|---|---|---|---|
| ACGLUA11 (N-acetyl-α-D-glucosamine) | |||||
| C1-C2 | 1.534 | 1.523 | 1.557 | −0.01 (0.00) | 0.02 (0.00) |
| C2-C3 | 1.53 | 1.512 | 1.548 | −0.02 (0.00) | 0.02 (0.00) |
| C2-N | 1.457 | 1.463 | 1.469 | 0.01 (0.00) | 0.01 (0.00) |
| C-CT | 1.508 | 1.502 | 1.523 | −0.01 (0.00) | 0.02 (0.00) |
| C-O | 1.235 | 1.225 | 1.259 | −0.01 (0.00) | 0.02 (0.00) |
| C1-C2-N | 111.055 | 113.41 | 114.732 | 2.36 (−0.03) | 3.68 (−0.01) |
| C3-C2-N | 110.338 | 111.7 | 114.007 | 1.36 (−0.01) | 3.67 (−0.01) |
| C1-C2-C3 | 110.075 | 110.686 | 109.231 | 0.61 (−0.04) | −0.84 (−0.02) |
| C2-N-C3 | 35.802 | 34.781 | 33.976 | −1.02 (−0.01) | −1.83 (−0.01) |
| N-C-CT | 116.011 | 116.455 | 121.857 | 0.44 (−0.02) | 5.85 (−0.01) |
| N-C-O | 123.056 | 123.093 | 124.496 | 0.04 (−0.02) | 1.44 (−0.01) |
| O-C-CT | 120.931 | 120.247 | 113.452 | −0.68 (−0.02) | −7.48 (−0.01) |
| C1-C2-N-C | 140.89 | 124.569 | 140.417 | −16.32 (−0.52) | −0.47 (−0.04) |
| C3-C2-N-C | −96.769 | −109.356 | −92.367 | −12.59 (−0.56) | 4.4 (−0.06) |
| AGALAM10 (N-acetyl-α-D-galactosamine) | |||||
| C1-C2 | 1.52 | 1.525 | 1.552 | 0.01 (0.00) | 0.03 (0.00) |
| C2-C3 | 1.529 | 1.519 | 1.549 | −0.01 (0.00) | 0.02 (0.00) |
| C2-N | 1.454 | 1.46 | 1.463 | 0.01 (0.00) | 0.01 (0.00) |
| C-CT | 1.503 | 1.505 | 1.525 | 0 (0.00) | 0.02 (0.00) |
| C-O | 1.239 | 1.227 | 1.259 | −0.01 (0.00) | 0.02 (0.00) |
| C1-C2-N | 111.776 | 113.371 | 115.99 | 1.59 (−0.06) | 4.21 (−0.01) |
| C3-C2-N | 110.094 | 111.953 | 114.331 | 1.86 (−0.05) | 4.24 (−0.02) |
| C1-C2-C3 | 110.222 | 110.377 | 108.63 | 0.16 (−0.04) | −1.59 (−0.02) |
| C2-N-C3 | 35.962 | 34.794 | 33.897 | −1.17 (−0.02) | −2.07 (−0.01) |
| N-C-CT | 116.003 | 116.012 | 121.261 | 0.01 (−0.02) | 5.26 (−0.01) |
| N-C-O | 123.923 | 122.74 | 124.385 | −1.18 (−0.02) | 0.46 (−0.02) |
| O-C-CT | 120.063 | 121.036 | 114.165 | 0.97 (−0.03) | −5.9 (−0.01) |
| C1-C2-N-C | 81.588 | 76.039 | 74.151 | −5.55 (−0.23) | −7.44 (−0.08) |
| C3-C2-N-C | −155.558 | −158.119 | −157.993 | −2.56 (−0.26) | −2.43 (−0.07) |
| NACMAN10 (N-acetyl-β-D-mannosamine monohydrate) | |||||
| C1-C2 | 1.537 | 1.514 | 1.547 | −0.02 (0.00) | 0.01 (0.00) |
| C2-C3 | 1.537 | 1.519 | 1.548 | −0.02 (0.00) | 0.01 (0.00) |
| C2-N | 1.459 | 1.465 | 1.468 | 0.01 (0.00) | 0.01 (0.00) |
| C-CT | 1.503 | 1.505 | 1.524 | 0 (0.00) | 0.02 (0.00) |
| C-O | 1.248 | 1.228 | 1.26 | −0.02 (0.00) | 0.01 (0.00) |
| C1-C2-N | 110.03 | 112.903 | 114.727 | 2.87 (−0.02) | 4.7 (−0.01) |
| C3-C2-N | 114.082 | 114.222 | 115.817 | 0.14 (−0.02) | 1.74 (−0.01) |
| C1-C2-C3 | 107.223 | 107.351 | 104.809 | 0.13 (−0.05) | −2.41 (−0.01) |
| C2-N-C3 | 33.921 | 33.565 | 33.049 | −0.36 (−0.01) | −0.87 (−0.01) |
| N-C-CT | 116.757 | 116.153 | 121.437 | −0.6 (−0.01) | 4.68 (−0.01) |
| N-C-O | 122.048 | 123.043 | 124.24 | 0.99 (−0.01) | 2.19 (−0.02) |
| O-C-CT | 121.194 | 120.591 | 114.121 | −0.6 (−0.01) | −7.07 (−0.01) |
| C1-C2-N-C | −126.826 | −130.526 | −141.428 | −3.7 (−0.11) | −14.6 (−0.03) |
| C3-C2-N-C | 112.635 | 106.304 | 96.048 | −6.33 (−0.18) | −16.59 (−0.03) |
additive force field,
drude: Drude polarizable force field parameters.
Table 10.
Crystalline unit cell geometries and volumes
| carbohydrate | Crystal ID | A(Å) | %error | B(Å) | %error | C(Å) | %error | Volume (Å)3 |
%error | |
|---|---|---|---|---|---|---|---|---|---|---|
| N-acetyl-α-D-glucosamine | ACGLUA11 | Crystal | 11.57 | 4.85 | 9.74 | 488.19 | ||||
| Additive | 11.66 | 0.75 | 4.87 | 0.40 | 10.06 | 3.27 | 508.38 | 4.14 | ||
| Drude | 11.88 | 2.61 | 4.91 | 1.28 | 9.66 | −0.77 | 504.89 | 3.42 | ||
| N-acetyl-α-D-galactosamine | AGALAM10 | Crystal | 9.16 | 6.32 | 9.21 | 507.30 | ||||
| Additive | 9.88 | 7.82 | 5.78 | −8.54 | 9.73 | 5.65 | 527.84 | 4.05 | ||
| Drude | 9.46 | 3.23 | 6.20 | −1.84 | 9.45 | 2.58 | 529.06 | 4.29 | ||
| N-acetyl-β-D-mannosamine monohydrate | NACMAN10 | Crystal | 7.56 | 7.73 | 18.61 | 1088.23 | ||||
| Additive | 7.70 | 1.85 | 7.75 | 0.20 | 19.01 | 2.17 | 1134.75 | 4.27 | ||
| Drude | 7.71 | 1.93 | 7.57 | −2.15 | 19.73 | 6.01 | 1150.57 | 5.73 |
II. Application of parameters to example systems.
Glycosaminoglycans (GAGS), extracellular polysaccharides play vital roles in various physiological157 and pathophysiological157-158 functions. Most of the GAGs are comprised of repetitive units of uronic acid ( D-glucuronic acids (AGLCA/BGLCA) or L-iduronic acids ( AIDOA/BIDOA)) and amino sugars ( D-glucosamine (AGLCNA/BGLCNA) or D-galactosamine (AGALNA/BGALNA)). Based on the chemical structures and biological activities, GAGs are subdivided into following groups: chondroitin sulfate (CS), heparin sulfate (HS), dermatan sulfate (DS), keratan sulfate (KS), heparin and hyaluronan. Sulfated GAGs constitute a major part of proteoglycans, which are multifaceted macromolecules that are involved in diverse cellular processes159, such as structural components of the extracellular cellular environment; regulatory component of cell signaling pathways by interacting with chemokines160, cytokines161, growth factors162 and proteases163; immunomodulators in acute inflammatory responses159.
Hyaluronan is the only unsulfated subtype of the GAGs and is elegantly discussed as a key immune modulator in several reviews164-166. To demonstrate the utility of the developed Drude polarizable force field parameters, MD simulations were performed on the linear carbohydrate polymer hyaluronan system (CN6, PDB ID: 2KQO167). The covalently conjugated carbohydrate system consists of three repeating units of β-N-acetyl galactosamine and β-D-glucuronate, as represented in Figure 13(a). 60 ns simulations were run using the additive and the polarizable force fields. Complete details of the simulation setup have been described in the SI file.
Figure 13.

Conformational properties of the glycosidic linkages in unsulfated chondroitin (CN6). Figure (a) shows the crystal structure (PDB ID: 2KQO) of unsulfated chondroitin demonstrating β-D-glucuronate (1→3) β-N-acetyl galactosamines linkage and β-N-acetyl galactosamines (1→4) β-D-glucuronate linkage. The BGLCA and BGALNA units are represented as U and N, respectively. Boltzmann-inverted probability distribution of β (1→3)-glycosidic linkage (ϕ = O5(U)-C1(U)-O3(N)–C3(N) and ψ = C1(U)-O3(N)–C3(N)-C4(N)) is shown in Figure (b, c, d) and (e, f, g) for additive and Drude, respectively.
Glycosidic torsion analysis.
The 60 ns simulation trajectories obtained from additive and Drude polarizable simulations were used to calculate the ϕ/ψ torsions about the β (1→3) [(ϕ = O5(U)-C1(U)-O3(N)–C3(N) and ψ= C1(U)-O3(N)–C3(N)-C4(N)]; and β (1→4) ) [ϕ = O5(N)-C1(N)-O4(U)–C4(U) and ψ= C1(N)-O4(U)–C4(U)-C5(U)] linkages, where U and N represent BGLCA (β-D-glucuronate) and BGALNA (β-N-acetyl galactosamine), respectively. 2D plots of the relative free energies, obtained from the Boltzmann-inverted probability distribution of β (1→3) and β (1→4)-glycosidic linkage dihedrals are presented in Figures 13 and 14. The CN6 glycosidic torsion angles from additive and Drude simulations are consistent with the average torsions obtained from the NMR study and are reported in Table 11. The global free energy minima coincide well with the average values of ϕ/ψ obtained from model structures. In comparison to additive simulation, the glycosidic linkage dihedrals extracted from Drude simulation trajectory showed enhanced conformational flexibility. The conformational flexibility of the glycosidic linkages governs the dynamics of polysaccharides168-169. In earlier studies the conformational flexibility of glycosidic linkages has been captured by using Hamiltonian replica exchange (HREX) enhanced sampling protocols170. The fact that drude simulation exhibits additional flexibility enables the simulation of glycosidic linkages in oligosaccharide models. We believe that the enhanced conformational flexibility is captured by the accurate description of the interactions between the hydroxyl groups of the carbohydrates and the surrounding solvent in the Drude simulations, which in turn influences the conformational behavior of polysaccharides. The inherent flexibility and ring puckering of the carbohydrate ring is also found to be important in xylose or heparin and their derivatives171-172. In Figure S5 of the SI file we plot the Mercator plots obtained from the additive and drude simulations. The distribution of the Cremer-Pople puckering parameters173 highlights the higher ring flexibility in the drude simulations. The drude simulation accesses more conformational states, especially the boat and skew forms when compared to the additive simulations.
Figure 14.
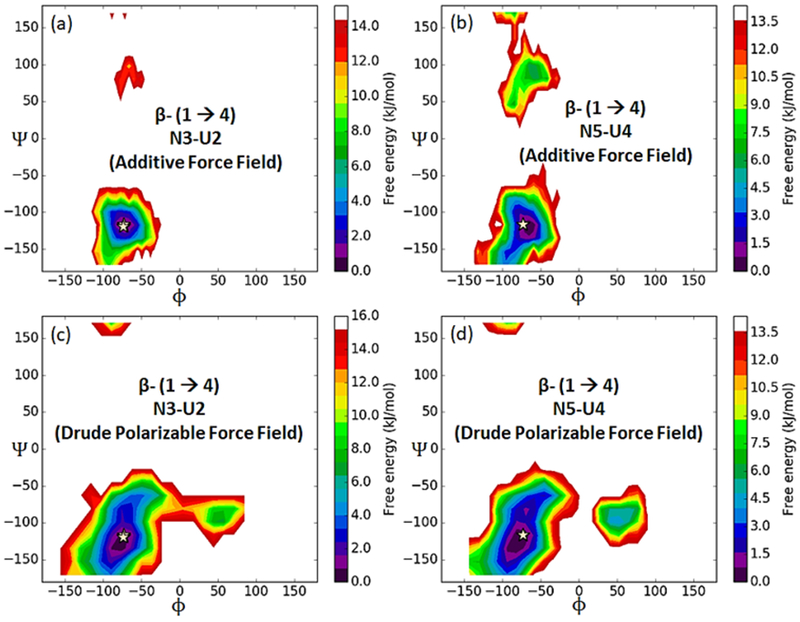
Boltzmann-inverted probability distribution of β (1→4)-glycosidic linkage (ϕ = O5(N)-C1(N)-O4(U)–C4(U) and ψ = C1(N)-O4(U)–C4(U)-C5(U)) in unsulfated chondroitin (CN6) is shown for additive (a and b) and Drude (c and d) simulations, respectively.
Table 11.
Average glycosidic torsion angles in the ensemble of CN6 conformers.
| Torsion | B (1→3) | B (1→4) | ||||
|---|---|---|---|---|---|---|
| U2-N1 | U4-N3 | U6-N5 | N3-U2 | N5-U4 | ||
| CN6 NMRa | ϕ | −73 (2) | −73 (0) | −72 (0) | −73(0) | −73 (0) |
| Ψ | 108 (8) | 107 (0) | 109 (0) | −118 (1) | −116 (0) | |
| Additive | ϕ | −75.8 (15.1) | −74.9 (14.2) | −76.9 (14.8) | −73.3 (13.4) | −72.9 (16.0) |
| Ψ | 96.7 (19.6) | 96.6 (20.2) | 94.9 (19.9) | −115.4 (27.1) | −102.5 (69.3) | |
| Drude | ϕ | −83.5 (26.4) | −83.1(23.9) | −83.8 (24.7) | −72.5 (28.6) | −67.3 (40.0) |
| Ψ | 109.7 (24.1) | 111.7 (23.4) | 110.3 (25.9) | −114.9 (35.9) | −110.7 (38.2) | |
Torsion angles are given in degrees and standard deviations are given in bracket.
Experimental values are taken from Sattelle et. el.167.
3JHN, H2 coupling constant calculation.
In addition to the glycosidic dihedrals analysis, the 3JHN, H2 coupling constants were evaluated for both additive and Drude simulation trajectories. CN6 contains three β-GlcNAc residues (N1, N3 and N5), allowing for the calculation of three vicinal 3JHNH2 coupling constant from H-N-C2-H2 dihedrals using Karplus equations143, 174-175 (6) and (7). The values for the same have been tabulated in Table 12.
Table 12.
Comparison of 3JHN, H2 coupling constant values (in Hz) for H-N-C2-H2 dihedrals from simulation trajectories of unsulfated chondroitin NMR structure, using additive and Drude polarizable force fields.
| Ring | Experimenta | Additive | Drude | ||
|---|---|---|---|---|---|
|
3JHN, H2 (from Eq. 6) |
3JHN, H2 (from Eq. 7) |
3JHN, H2 (from Eq. 6) |
3JHN, H2 (from Eq. 7) |
||
| N1 | 8.98 | 8.71 (1.11) | 7.76 (1.29) | 9.17 (2.06) | 8.94 (2.23) |
| N3 | 9.75 | 10.14 (1.98) | 10.16 (2.02) | 9.24 (2.07) | 9.00 (2.26) |
| N5 | n/d | 8.65 (0.93) | 7.67 (1.04) | 9.04 (1.88) | 8.65 (2.13) |
Standard deviations are given in bracket.
Experimental values are taken from Sattelle et. al.167.
| (6) |
| (7) |
The 3JHN, H2 coupling values are consistent with the observed experimental NMR data (Table 12). The mean 3JHN, H2 coupling values, for all the three β-GlcNAc residues (N1, N3 and N5), were evaluated as 8.71 (8.98), 10.14 (9.75) and 8.65 (n/d) from additive simulation while the same from Dude simulations is found to be 9.17 (8.98), 9.24 (9.75) and 9.04 (n/d). The experimental NMR J coupling constant values are given in parentheses. From the population analysis, it is observed that β-GlcNAc either occupied the cis or trans (trans+/trans-) configuration, as illustrated in Table 13. In the additive simulation, the H-N-C2-H2 dihedral was found to sample the cis conformation for N1 (Figure S6), trans conformation for N3 (Figure S7) and the cis conformation for N5 (Figure S8). In the Drude simulation, it was observed that the H-N-C2-H2 dihedral sampled both the cis and trans conformations for N1 (Figure S6), N3 (Figure S7) and N5 (Figure S8). The conformational preferences were found to be dependent on both intra-residue and inter-residue hydrogen bonding.
Table 13.
Conformational population of H-N-C2-H2 dihedrals from simulation trajectories of unsulfated chondroitin NMR structure, using additive and Drude polarizable force fields.
| Ring | Additive (% population) | Drude (% population) | ||
|---|---|---|---|---|
| cis | trans | cis | trans | |
| N1 | 90.38 | 9.49 | 22.75 | 75.35 |
| N3 | 0.02 | 99.03 | 24.72 | 73.70 |
| N5 | 93.74 | 6.20 | 39.15 | 59.84 |
From the additive simulation, we observe that for the first β-GlcNAc residue (N1) the absence of H-bonding interactions causes the H-N-C2-H2 dihedral to predominantly sample the cis conformation (Figure S6). In the Drude simulation, the formation of the inter-molecular H-bond (O(N1)…HO2(U2)) stabilized the trans conformation while the weak intra-molecular H-bond (O(N1)…HO1(N1)) stabilized the cis conformation (Figure S6).
For the central β-GlcNAc residue (N3) in additive simulation, we observe two significant inter-molecular H-bond interactions (O(N3)…HO2(U4) and HN(N3)…O61/O62(U2)), which facilitate the stabilization of the trans conformation. In the Drude simulation, these two inter-molecular H-bonds also favor the trans-conformation, as the absence of these interactions results in the dihedral adopting a cis conformation (Figure S7). For the terminal β-GlcNAc residue (N5) in the additive simulation, the absence of the inter-molecular H-bond interactions (O(N5)…HO2(U6) and HN(N5)…O61/O62(U4)), results in cis conformation of the H-N-C2-H2 dihedral. In the Drude simulation, transient inter-molecular hydrogen bond O(N5)…HO2(U6), along with HN(N5)…O61/O62(U4)) H-bond favors trans-conformation of the H-N-C2-H2 dihedral, while the absence of these interaction results into cis-conformation (Figure S8).
Inter-residual proton-proton distance calculation.
In addition to the glycosidic dihedrals and 3JHN, H2 coupling constant analysis, the inter-residual proton-proton distance was calculated using additive and the Drude polarizable force field. The results were compared with the inter-residual NOEs (Nuclear Overhauser Enhancements) reported in Sattelle et. al.167 work and tabulated in Table 14. In comparison to the additive simulation, the results obtained from Drude simulation are in better agreement with the NOE data. All the strong and medium signals reported from the NMR experiment are reproduced well by the MD simulations.
Table 14.
Comparison of inter-residual proton-proton distance obtained from NOEs data and simulation data, using additive and Drude polarizable force fields.
| Linkage | BGALNA | BGLCA | distance range (NOE intensity)a |
rb (Additive) | rb (Drude) |
|---|---|---|---|---|---|
| U2:N1 (β1→3) | HN | H-1 | 2.8 - 3.8 (Medium) | 4.0 (0.6) | 3.7 (0.8) |
| H-3 | H-1 | 1.8 - 2.7 (Strong) | 2.2 (0.2) | 2.2 (0.2) | |
| N3:U2 (β1→4) | H-1 | H-4 | 1.8 - 2.7 (Strong) | 2.4 (0.2) | 2.4 (0.4) |
| U4:N3 (β1→3) | HN | H-1 | 2.8 - 3.8 (Medium) | 3.5 (0.7) | 3.7 (0.8) |
| H-3 | H-1 | 1.8 - 2.7 (Strong) | 2.3 (0.2) | 2.2 (0.2) | |
| N5:U4 (β1→4) | H-1 | H-4 | 1.8 - 2.7 (Strong) | 2.5 (0.4) | 2.5 (0.5) |
| U6:N5 (β1→3) | HN | H-1 | 2.8 - 3.8 (Medium) | 4.2 (0.6) | 3.8 (0.8) |
| H-3 | H-1 | 1.8 - 2.7 (Strong) | 2.2 (0.2) | 2.2 (0.2) |
Standard deviations are given in bracket.
distance range and NOE intensity are taken from Sattelle et. al.167.
Intra-residual reference proton-proton distance.
Conclusion
In this work Drude polarizable force field parameters for carboxylate and N-acetyl amine carbohydrate have been developed. The developed Drude polarizable parameters are an extension of the existing Drude polarizable force field to enable the modeling of carbohydrate derivatives. The developed parameters were validated by evaluating condensed phase properties like crystal unit cell parameters and NMR J-coupling constants. Crystal simulation of carbohydrate derivatives showed a slight improvement over the additive CHARMM force field parameters; although, as reported in the previous studies121-122, 176, both the force fields overestimate the crystal unit cell volumes. MD simulation of the glycosaminoglycan complex hyaluronan, using Drude polarizable parameters, showed improvement in NMR J-coupling constants values over the additive simulation. Notably, in comparison to the CHARMM additive force field, the Drude model showed more conformational flexibility as depicted from ϕ/ψ distributions corresponding to the β(1→3) and β(1→4) linkages obtained from the MD simulations. Thus, the developed Drude polarizable force field parameters for carboxylate and N-acetyl amine carbohydrate derivatives can be used to model these carbohydrate derivatives to study their structural and functional properties, either alone or in conjunction with other macromolecules, including carbohydrates, nucleic acids, lipids and proteins in heterogenous systems using Drude polarizable force field parameters for carbohydrates86, 89, 121-122, DNA119, lipids123, peptides and proteins118.
Supplementary Material
Acknowledgements
SSM thanks Department of Science and Technology, INDIA for INSPIRE fellowship (IFA-13 CH-104) and Science and Engineering Research Board, INDIA for Extra Mural Research grant (EMR/2015/000701). ADM acknowledges financial support from the NIH (GM070855) and computational support from the University of Maryland Computer-Aided Drug Design Center and the Extreme Science and Engineering Discovery Environment (XSEDE), which is supported by National Science Foundation Grant Number OCI-1053575 are acknowledged. PP acknowledges fellowship from Indian Institute of Technology (IIT) Gandhinagar and Ministry of Human Resource Development (MHRD), Government of India.
Footnotes
Supporting Information
Supporting Material S1: NMR structure simulation protocol. Figure S1: Pictorial representation of average and standard deviation for MM - QM values of Bond Lengths, Angles and Dihedrals for model compound M1 and M2. Figure S2: Pictorial representation of average and standard deviation for MM -QM values of Solute-Water Pair Interaction energies and distances for model compound M1 and M2. Figure S3: Pictorial representation of average and standard deviation for MM - QM values of Solute-Water Pair Interaction energies and distances for sugar carboxylates. Figure S4: Pictorial representation of average and standard deviation for MM - QM values of Solute-Water Pair Interaction energies and distances for N-acetylamine sugar derivatives. Figure S5: Figure illustrating Cremer-Pople puckering parameters for BGLCA from 60 ns MD simulation trajectory of unsulfated chondroitin structure using additive and Drude polarizable force fields. Figure S6: Figure depicting the conformational properties of the first GlcNAc (N1) acetamido group obtained from 60 ns MD simulation trajectory of unsulfated chondroitin structure using additive and Drude polarizable force fields. Figure S7: Figure depicting the conformational properties of the second GlcNAc (N3) acetamido group obtained from 60 ns MD simulation trajectory of unsulfated chondroitin structure using additive and Drude polarizable force fields. Figure S8: Figure depicting the conformational properties of the third GlcNAc (N5) acetamido group obtained from 60 ns MD simulation trajectory of unsulfated chondroitin structure using additive and Drude polarizable force fields. Table S1 and Table S2: Vibrational Frequency analysis of model compounds M1 and M2. Table S3: Final force field parameters for carboxylate and N-acetyl amine carbohydrate derivatives.
This material is available free of charge via the Internet at http://pubs.acs.org.
References
- 1.Kannagi R, Regulatory roles of carbohydrate ligands for selectins in the homing of lymphocytes. Curr Opin Struct Biol 2002, 12 (5), 599–608. [DOI] [PubMed] [Google Scholar]
- 2.Bucior I; Burger MM, Carbohydrate–carbohydrate interactions in cell recognition. Curr Opin Struct Biol 2004, 14 (5), 631–637. [DOI] [PubMed] [Google Scholar]
- 3.Lasky LA, Selectin-carbohydrate interactions and the initiation of the inflammatory response. Annu Rev Biochem 1995, 64 (1), 113–39. [DOI] [PubMed] [Google Scholar]
- 4.Weis WI; Drickamer K, Structural basis of lectin-carbohydrate recognition. Annu Rev Biochem 1996, 65 (1), 441–73. [DOI] [PubMed] [Google Scholar]
- 5.Lowe JB, Glycosylation, immunity, and autoimmunity. Cell 2001, 104 (6), 809–12. [DOI] [PubMed] [Google Scholar]
- 6.Parodi AJ, Protein glucosylation and its role in protein folding. Annu Rev Biochem 2000, 69 (1), 69–93. [DOI] [PubMed] [Google Scholar]
- 7.Mochizuki K; Molinero V, Antifreeze Glycoproteins Bind Reversibly to Ice via Hydrophobic Groups. J Am Chem Soc 2018, 140 (14), 4803–4811. [DOI] [PubMed] [Google Scholar]
- 8.Meister K; DeVries AL; Bakker HJ; Drori R, Antifreeze Glycoproteins Bind Irreversibly to Ice. J Am Chem Soc 2018, 140 (30), 9365–9368. [DOI] [PubMed] [Google Scholar]
- 9.Helenius A, How N-linked oligosaccharides affect glycoprotein folding in the endoplasmic reticulum. Mol Biol Cell 1994, 5 (3), 253–265. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Trombetta ES; Helenius A, Lectins as chaperones in glycoprotein folding. Curr Opin Struct Biol 1998, 8 (5), 587–592. [DOI] [PubMed] [Google Scholar]
- 11.Opdenakker G; Rudd PM; Ponting CP; Dwek R, Concepts and principles of glycobiology. The FASEB Journal 1993, 7 (14), 1330–1337. [DOI] [PubMed] [Google Scholar]
- 12.Helenius A; Aebi M, Intracellular functions of N-linked glycans. Science 2001, 291 (5512), 2364–2369. [DOI] [PubMed] [Google Scholar]
- 13.Wan Q; Chen J; Chen G; Danishefsky SJ, A potentially valuable advance in the synthesis of carbohydrate-based anticancer vaccines through extended cycloaddition chemistry. The Journal of organic chemistry 2006, 71 (21), 8244–8249. [DOI] [PubMed] [Google Scholar]
- 14.Cipolla L; Peri F; Airoldi C, Glycoconjugates in cancer therapy. Anti-Cancer Agents in Medicinal Chemistry (Formerly Current Medicinal Chemistry-Anti-Cancer Agents) 2008, 8 (1), 92–121. [DOI] [PubMed] [Google Scholar]
- 15.Hasan SS; Ashraf GM; Banu N, Galectins–potential targets for cancer therapy. Cancer letters 2007, 253 (1), 25–33. [DOI] [PubMed] [Google Scholar]
- 16.Wong C-H, Carbohydrate-based Drug Discovery, 2 Volume Set. John Wiley & Sons: 2003; Vol. 1. [Google Scholar]
- 17.Meezan E; Wu HC; Black PH; Robbins PW, Comparative studies on the carbohydrate-containing membrane components of normal and virus-transformed mouse fibroblasts. II. Separation of glycoproteins and glycopeptides by sephadex chromatography. Biochemistry 1969, 8 (6), 2518–2524. [DOI] [PubMed] [Google Scholar]
- 18.Mackiewicz A; Mackiewicz K, Glycoforms of serum α1-acid glycoprotein as markers of inflammation and cancer. Glycoconjugate journal 1995, 12 (3), 241–247. [DOI] [PubMed] [Google Scholar]
- 19.Turner G, N-glycosylation of serum proteins in disease and its investigation using lectins. Clinica chimica acta 1992, 208 (3), 149–171. [DOI] [PubMed] [Google Scholar]
- 20.Yuzwa SA; Vocadlo DJ, O-GlcNAc and neurodegeneration: biochemical mechanisms and potential roles in Alzheimer’s disease and beyond. Chemical Society Reviews 2014, 43 (19), 6839–6858. [DOI] [PubMed] [Google Scholar]
- 21.Wang AC; Jensen EH; Rexach JE; Vinters HV; Hsieh-Wilson LC, Loss of O-GlcNAc glycosylation in forebrain excitatory neurons induces neurodegeneration. Proceedings of the National Academy of Sciences 2016, 113 (52), 15120–15125. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Wani WY; Ouyang X; Benavides GA; Redmann M; Cofield SS; Shacka JJ; Chatham JC; Darley-Usmar V; Zhang J, O-GlcNAc regulation of autophagy and α-synuclein homeostasis; implications for Parkinson’s disease. Molecular brain 2017, 10 (1), 32. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Reily C; Stewart TJ; Renfrow MB; Novak J, Glycosylation in health and disease. Nature Reviews Nephrology 2019, 1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Holmes E; Ostrander G; Clausen H; Graem N, Oncofetal expression of Lex carbohydrate antigens in human colonic adenocarcinomas. Regulation through type 2 core chain synthesis rather than fucosylation. Journal of Biological Chemistry 1987, 262 (23), 11331–11338. [PubMed] [Google Scholar]
- 25.Pinho SS; Reis CA, Glycosylation in cancer: mechanisms and clinical implications. Nature Reviews Cancer 2015, 15 (9), 540. [DOI] [PubMed] [Google Scholar]
- 26.Biermann M; Griffante G; Podolska M; Boeltz S; Stürmer J; Munoz L; Bilyy R; Herrmann M, Sweet but dangerous–the role of immunoglobulin G glycosylation in autoimmunity and inflammation. Lupus 2016, 25 (8), 934–942. [DOI] [PubMed] [Google Scholar]
- 27.Go MF; Schrohenloher RE; Tomana M, Deficient galactosylation of serum IgG in inflammatory bowel disease: correlation with disease activity. Journal of clinical gastroenterology 1994, 18 (1), 86. [DOI] [PubMed] [Google Scholar]
- 28.Rademacher TW; Williams P; Dwek RA, Agalactosyl glycoforms of IgG autoantibodies are pathogenic. Proceedings of the National Academy of Sciences 1994, 91 (13), 6123–6127. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Pfeifle R; Rothe T; Ipseiz N; Scherer HU; Culemann S; Harre U; Ackermann JA; Seefried M; Kleyer A; Uderhardt S, Regulation of autoantibody activity by the IL-23–T H 17 axis determines the onset of autoimmune disease. Nature immunology 2017, 18 (1), 104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Lauc G; Huffman JE; Pučić M; Zgaga L; Adamczyk B; Mužinić A; Novokmet M; Polašek O; Gornik O; Krištić J, Loci associated with N-glycosylation of human immunoglobulin G show pleiotropy with autoimmune diseases and haematological cancers. PLoS genetics 2013, 9 (1), e1003225. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Tomana M; Schrohenloher RE; Koopman WJ; Alarcän GS; Paul WA, Abnormal glycosylation of serum IgG from patients with chronic inflammatory diseases. Arthritis & Rheumatism: Official Journal of the American College of Rheumatology 1988, 31 (3), 333–338. [DOI] [PubMed] [Google Scholar]
- 32.Van Zeben D; Rook G; Hazes J; Zwinderman A; Zhang Y; Ghelani S; Rademacher T; Breedveld F, Early agalactosylation of IgG is associated with a more progressive disease course in patients with rheumatoid arthritis: results of a follow-up study. Rheumatology 1994, 33 (1), 36–43. [DOI] [PubMed] [Google Scholar]
- 33.Tomana M; Schrohenloher R; Reveille J; Arnett F; Koopman W, Abnormal galactosylation of serum IgG in patients with systemic lupus erythematosus and members of families with high frequency of autoimmune diseases. Rheumatology international 1992, 12 (5), 191–194. [DOI] [PubMed] [Google Scholar]
- 34.Moore JS; Wu X; Kulhavy R; Tomana M; Novak J; Moldoveanu Z; Brown R; Goepfert PA; Mestecky J, Increased levels of galactose-deficient IgG in sera of HIV-1-infected individuals. Aids 2005, 19 (4), 381–389. [DOI] [PubMed] [Google Scholar]
- 35.Ohmi Y; Ise W; Harazono A; Takakura D; Fukuyama H; Baba Y; Narazaki M; Shoda H; Takahashi N; Ohkawa Y, Sialylation converts arthritogenic IgG into inhibitors of collagen-induced arthritis. Nature communications 2016, 7, 11205. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Li W; Zhu Z; Chen W; Feng Y; Dimitrov DS, Crystallizable fragment glycoengineering for therapeutic antibodies development. Frontiers in immunology 2017, 8, 1554. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Brückner C; Lehmann C; Dudziak D; Nimmerjahn F, Sweet SIGNs: IgG glycosylation leads the way in IVIG-mediated resolution of inflammation. International immunology 2017, 29 (11), 499–509. [DOI] [PubMed] [Google Scholar]
- 38.Lin C-W; Tsai M-H; Li S-T; Tsai T-I; Chu K-C; Liu Y-C; Lai M-Y; Wu C-Y; Tseng Y-C; Shivatare SS, A common glycan structure on immunoglobulin G for enhancement of effector functions. Proceedings of the National Academy of Sciences 2015, 112 (34), 10611–10616. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Hsieh P-H; Thieker DF; Guerrini M; Woods RJ; Liu J, Uncovering the relationship between sulphation patterns and conformation of iduronic acid in heparan sulphate. Scientific reports 2016, 6, 29602. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Singh A; Tessier MB; Pederson K; Wang X; Venot AP; Boons G-J; Prestegard JH; Woods RJ, Extension and validation of the GLYCAM force field parameters for modeling glycosaminoglycans. Canadian journal of chemistry 2016, 94 (11), 927–935. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Nowak M; Freudenberg U; Tsurkan MV; Werner C; Levental KR, Modular GAG-matrices to promote mammary epithelial morphogenesis in vitro. Biomaterials 2017, 112, 20–30. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Sasisekharan R; Shriver Z; Venkataraman G; Narayanasami U, Roles of heparan-sulphate glycosaminoglycans in cancer. Nature Reviews Cancer 2002, 2 (7), 521. [DOI] [PubMed] [Google Scholar]
- 43.Capila I; Linhardt RJ, Heparin–protein interactions. Angewandte Chemie International Edition 2002, 41 (3), 390–412. [DOI] [PubMed] [Google Scholar]
- 44.Gandhi NS; Mancera RL, The structure of glycosaminoglycans and their interactions with proteins. Chemical biology & drug design 2008, 72 (6), 455–482. [DOI] [PubMed] [Google Scholar]
- 45.Yang M; Huang J; Simon R; Wang L-X; MacKerell AD, Conformational Heterogeneity of the HIV Envelope Glycan Shield. Scientific reports 2017, 7 (1), 4435. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.DeMarco ML; Woods RJ, Structural glycobiology: a game of snakes and ladders. Glycobiology 2008, 18 (6), 426–440. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Rudd T; Skidmore M; Guerrini M; Hricovini M; Powell A; Siligardi G; Yates E, The conformation and structure of GAGs: recent progress and perspectives. Current opinion in structural biology 2010, 20 (5), 567–574. [DOI] [PubMed] [Google Scholar]
- 48.Cilpa G; Hyvönen MT; Koivuniemi A; Riekkola ML, Atomistic insight into chondroitin-6-sulfate glycosaminoglycan chain through quantum mechanics calculations and molecular dynamics simulation. Journal of computational chemistry 2010, 31 (8), 1670–1680. [DOI] [PubMed] [Google Scholar]
- 49.Hricovíni M, Solution structure of heparin pentasaccharide: NMR and DFT analysis. The journal of physical chemistry B 2015, 119 (38), 12397–12409. [DOI] [PubMed] [Google Scholar]
- 50.Hricovíni M; Driguez P-A; Malkina OL, NMR and DFT analysis of trisaccharide from heparin repeating sequence. The journal of physical chemistry B 2014, 118 (41), 11931–11942. [DOI] [PubMed] [Google Scholar]
- 51.Forster MJ; Mulloy B, Molecular dynamics study of iduronate ring conformation. Biopolymers: Original Research on Biomolecules 1993, 33 (4), 575–588. [Google Scholar]
- 52.Pol-Fachin L; Verli H, Depiction of the forces participating in the 2-O-sulfo-α-L-iduronic acid conformational preference in heparin sequences in aqueous solutions. Carbohydrate research 2008, 343 (9), 1435–1445. [DOI] [PubMed] [Google Scholar]
- 53.Samsonov SA; Theisgen S; Riemer T; Huster D; Pisabarro MT, Glycosaminoglycan Monosaccharide Blocks Analysis by Quantum Mechanics, Molecular Dynamics, and Nuclear Magnetic Resonance. BioMed research international 2014, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Muñoz-García JC; López-Prados J; Angulo J; Díaz-Contreras I; Reichardt N; de Paz JL; Martín-Lomas M; Nieto PM, Effect of the Substituents of the Neighboring Ring in the Conformational Equilibrium of Iduronate in Heparin-like Trisaccharides. Chemistry–A European Journal 2012, 18 (51), 16319–16331. [DOI] [PubMed] [Google Scholar]
- 55.Muñoz-García JC; Corzana F; de Paz JL; Angulo J; Nieto PM, Conformations of the iduronate ring in short heparin fragments described by time-averaged distance restrained molecular dynamics. Glycobiology 2013, 23 (11), 1220–1229. [DOI] [PubMed] [Google Scholar]
- 56.Guvench O; Mallajosyula SS; Raman EP; Hatcher E; Vanommeslaeghe K; Foster TJ; Jamison FW; MacKerell AD Jr, CHARMM additive all-atom force field for carbohydrate derivatives and its utility in polysaccharide and carbohydrate–protein modeling. Journal of chemical theory and computation 2011, 7 (10), 3162–3180. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Hansen HS; Hünenberger PH, A reoptimized GROMOS force field for hexopyranose-based carbohydrates accounting for the relative free energies of ring conformers, anomers, epimers, hydroxymethyl rotamers, and glycosidic linkage conformers. Journal of computational chemistry 2011, 32 (6), 998–1032. [DOI] [PubMed] [Google Scholar]
- 58.Plazinski W; Lonardi A; Hünenberger PH, Revision of the GROMOS 56A6CARBO force field: Improving the description of ring-conformational equilibria in hexopyranose-based carbohydrates chains. Journal of computational chemistry 2016, 37 (3), 354–365. [DOI] [PubMed] [Google Scholar]
- 59.Kony D; Damm W; Stoll S; Van Gunsteren WF, An improved OPLS–AA force field for carbohydrates. Journal of computational chemistry 2002, 23 (15), 1416–1429. [DOI] [PubMed] [Google Scholar]
- 60.Kirschner KN; Yongye AB; Tschampel SM; González-Outeiriño J; Daniels CR; Foley BL; Woods RJ, GLYCAM06: a generalizable biomolecular force field. Carbohydrates. Journal of computational chemistry 2008, 29 (4), 622–655. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Kuttel M; Brady JW; Naidoo KJ, Carbohydrate solution simulations: producing a force field with experimentally consistent primary alcohol rotational frequencies and populations. Journal of computational chemistry 2002, 23 (13), 1236–1243. [DOI] [PubMed] [Google Scholar]
- 62.Lemkul JA; Huang J; Roux B; MacKerell AD Jr, An empirical polarizable force field based on the classical drude oscillator model: development history and recent applications. Chemical reviews 2016, 116 (9), 4983–5013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Jing Z; Liu C; Cheng SY; Qi R; Walker BD; Piquemal J-P; Ren P, Polarizable force fields for biomolecular simulations: Recent advances and applications. Annual Review of biophysics 2019, 48. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Baker CM, Polarizable force fields for molecular dynamics simulations of biomolecules. Wiley Interdisciplinary Reviews: Computational Molecular Science 2015, 5 (2), 241–254. [Google Scholar]
- 65.Chu H; Cao L; Peng X; Li G, Polarizable force field development for lipids and their efficient applications in membrane proteins. Wiley Interdisciplinary Reviews: Computational Molecular Science 2017, 7 (5), e1312. [Google Scholar]
- 66.Cisneros GA; Karttunen M; Ren P; Sagui C, Classical electrostatics for biomolecular simulations. Chemical reviews 2013, 114 (1), 779–814. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Halgren TA; Damm W, Polarizable force fields. Current opinion in structural biology 2001, 11 (2), 236–242. [DOI] [PubMed] [Google Scholar]
- 68.Cieplak P; Dupradeau F-Y; Duan Y; Wang J, Polarization effects in molecular mechanical force fields. Journal of Physics: Condensed Matter 2009, 21 (33), 333102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Ponder JW; Wu C; Ren P; Pande VS; Chodera JD; Schnieders MJ; Haque I; Mobley DL; Lambrecht DS; DiStasio RA Jr, Current status of the AMOEBA polarizable force field. The journal of physical chemistry B 2010, 114 (8), 2549–2564. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Ren P; Chun J; Thomas DG; Schnieders MJ; Marucho M; Zhang J; Baker NA, Biomolecular electrostatics and solvation: a computational perspective. Quarterly reviews of biophysics 2012, 45 (4), 427–491. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Warshel A; Kato M; Pisliakov AV, Polarizable force fields: history, test cases, and prospects. Journal of Chemical Theory and Computation 2007, 3 (6), 2034–2045. [DOI] [PubMed] [Google Scholar]
- 72.Rick SW; Stuart SJ; Berne BJ, Dynamical fluctuating charge force fields: Application to liquid water. The Journal of chemical physics 1994, 101 (7), 6141–6156. [Google Scholar]
- 73.Rick SW; Berne B, Dynamical fluctuating charge force fields: the aqueous solvation of amides. Journal of the American Chemical Society 1996, 118 (3), 672–679. [Google Scholar]
- 74.Stern HA; Rittner F; Berne BJ; Friesner RA, Combined fluctuating charge and polarizable dipole models: Application to a five-site water potential function. The Journal of chemical physics 2001, 115 (5), 2237–2251. [Google Scholar]
- 75.Patel S; Brooks CL III, CHARMM fluctuating charge force field for proteins: I parameterization and application to bulk organic liquid simulations. Journal of computational chemistry 2004, 25 (1), 1–16. [DOI] [PubMed] [Google Scholar]
- 76.Patel S; Mackerell AD Jr; Brooks CL III, CHARMM fluctuating charge force field for proteins: II protein/solvent properties from molecular dynamics simulations using a nonadditive electrostatic model. Journal of computational chemistry 2004, 25 (12), 1504–1514. [DOI] [PubMed] [Google Scholar]
- 77.Kaminski GA; Stern HA; Berne BJ; Friesner RA; Cao YX; Murphy RB; Zhou R; Halgren TA, Development of a polarizable force field for proteins via ab initio quantum chemistry: first generation model and gas phase tests. Journal of computational chemistry 2002, 23 (16), 1515–1531. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Ren P; Ponder JW, Consistent treatment of inter-and intramolecular polarization in molecular mechanics calculations. Journal of computational chemistry 2002, 23 (16), 1497–1506. [DOI] [PubMed] [Google Scholar]
- 79.Jorgensen WL; Jensen KP; Alexandrova AN, Polarization effects for hydrogen-bonded complexes of substituted phenols with water and chloride ion. Journal of chemical theory and computation 2007, 3 (6), 1987–1992. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Shi Y; Xia Z; Zhang J; Best R; Wu C; Ponder JW; Ren P, Polarizable atomic multipole-based AMOEBA force field for proteins. Journal of chemical theory and computation 2013, 9 (9), 4046–4063. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.Liu Y-P; Kim K; Berne B; Friesner RA; Rick SW, Constructing ab initio force fields for molecular dynamics simulations. The Journal of chemical physics 1998, 108 (12), 4739–4755. [Google Scholar]
- 82.Drude P; Millikan R; Mann R, The Theory of Optics Longmans. Green, and Co 1902. [Google Scholar]
- 83.Lemkul JA; MacKerell AD Jr, Polarizable force field for DNA based on the classical drude oscillator: I. Refinement using quantum mechanical base stacking and conformational energetics. Journal of chemical theory and computation 2017, 13 (5), 2053–2071. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84.Lemkul JA; MacKerell AD Jr, Polarizable force field for DNA based on the classical Drude oscillator: II. Microsecond molecular dynamics simulations of duplex DNA. Journal of chemical theory and computation 2017, 13 (5), 2072–2085. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85.Anisimov VM; Vorobyov IV; Roux B; MacKerell AD, Polarizable empirical force field for the primary and secondary alcohol series based on the classical Drude model. Journal of chemical theory and computation 2007, 3 (6), 1927–1946. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 86.Aytenfisu AH; Yang M; MacKerell AD Jr, CHARMM Drude Polarizable Force Field for Glycosidic Linkages Involving Pyranoses and Furanoses. Journal of chemical theory and computation 2018, 14 (6), 3132–3143. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87.Huang J; Lemkul JA; Eastman PK; MacKerell AD Jr, Molecular dynamics simulations using the drude polarizable force field on GPUs with OpenMM: Implementation, validation, and benchmarks. Journal of computational chemistry 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 88.Huang J; MacKerell AD, Force field development and simulations of intrinsically disordered proteins. Current opinion in structural biology 2018, 48, 40–48. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 89.Yang M; Aytenfisu AH; MacKerell AD Jr, Proper balance of solvent-solute and solute-solute interactions in the treatment of the diffusion of glucose using the Drude polarizable force field. Carbohydrate research 2018, 457, 41–50. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 90.Mortier WJ; Ghosh SK; Shankar S, Electronegativity-equalization method for the calculation of atomic charges in molecules. Journal of the American Chemical Society 1986, 108 (15), 4315–4320. [Google Scholar]
- 91.Patel S; Brooks CL III, Fluctuating charge force fields: recent developments and applications from small molecules to macromolecular biological systems. Molecular Simulation 2006, 32 (3-4), 231–249. [Google Scholar]
- 92.Ou S; Patel S, Temperature Dependence and Energetics of Single Ions at the Aqueous Liquid–Vapor Interface. The Journal of Physical Chemistry B 2013, 117 (21), 6512–6523. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 93.Zhong Y; Patel S, Binding structures of tri-N-acetyl-β-glucosamine in hen egg white lysozyme using molecular dynamics with a polarizable force field. Journal of computational chemistry 2013, 34 (3), 163–174. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 94.Hu Y; Ou S; Patel S, Free energetics of arginine permeation into model DMPC lipid bilayers: coupling of effective counterion concentration and lateral bilayer dimensions. The Journal of Physical Chemistry B 2013, 117 (39), 11641–11653. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 95.Lucas TR; Bauer BA; Patel S, Charge equilibration force fields for molecular dynamics simulations of lipids, bilayers, and integral membrane protein systems. Biochimica et Biophysica Acta (BBA)-Biomembranes 2012, 1818 (2), 318–329. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 96.Young D, Iterative Solutions of Large Linear Systems (New York: Academic). 1971. [Google Scholar]
- 97.Aviat F; Levitt A; Stamm B; Maday Y; Ren P; Ponder JW; Lagardere L; Piquemal J-P, Truncated conjugate gradient: an optimal strategy for the analytical evaluation of the many-body polarization energy and forces in molecular simulations. Journal of chemical theory and computation 2016, 13 (1), 180–190. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 98.Simmonett AC; Pickard IV FC; Ponder JW; Brooks BR, An empirical extrapolation scheme for efficient treatment of induced dipoles. The Journal of chemical physics 2016, 145 (16), 164101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 99.Simmonett AC; Pickard IV FC; Shao Y; Cheatham TE III; Brooks BR, Efficient treatment of induced dipoles. The Journal of chemical physics 2015, 143 (7), 074115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 100.Cieplak P; Caldwell J; Kollman P, Molecular mechanical models for organic and biological systems going beyond the atom centered two body additive approximation: aqueous solution free energies of methanol and N-methyl acetamide, nucleic acid base, and amide hydrogen bonding and chloroform/water partition coefficients of the nucleic acid bases. Journal of Computational Chemistry 2001, 22 (10), 1048–1057. [Google Scholar]
- 101.Wang ZX; Zhang W; Wu C; Lei H; Cieplak P; Duan Y, Strike a balance: optimization of backbone torsion parameters of AMBER polarizable force field for simulations of proteins and peptides. Journal of computational chemistry 2006, 27 (6), 781–790. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 102.Van Maaren PJ; Van Der Spoel D, Molecular dynamics simulations of water with novel shell-model potentials. The Journal of Physical Chemistry B 2001, 105 (13), 2618–2626. [Google Scholar]
- 103.Kunz A-PE; van Gunsteren WF, Development of a nonlinear classical polarization model for liquid water and aqueous solutions: COS/D. The Journal of Physical Chemistry A 2009, 113 (43), 11570–11579. [DOI] [PubMed] [Google Scholar]
- 104.Lamoureux G; Roux B. t., Modeling induced polarization with classical Drude oscillators: Theory and molecular dynamics simulation algorithm. The Journal of chemical physics 2003, 119 (6), 3025–3039. [Google Scholar]
- 105.Thole BT, Molecular polarizabilities calculated with a modified dipole interaction. Chemical Physics 1981, 59 (3), 341–350. [Google Scholar]
- 106.Harder E; Anisimov VM; Vorobyov IV; Lopes PE; Noskov SY; MacKerell AD; Roux B, Atomic level anisotropy in the electrostatic modeling of lone pairs for a polarizable force field based on the classical Drude oscillator. Journal of chemical theory and computation 2006, 2 (6), 1587–1597. [DOI] [PubMed] [Google Scholar]
- 107.Yu H; Whitfield TW; Harder E; Lamoureux G; Vorobyov I; Anisimov VM; MacKerell AD Jr; Roux B, Simulating monovalent and divalent ions in aqueous solution using a Drude polarizable force field. Journal of chemical theory and computation 2010, 6 (3), 774–786. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 108.Lemkul JA; MacKerell AD Jr, Balancing the Interactions of Mg2+ in Aqueous Solution and with Nucleic Acid Moieties For a Polarizable Force Field Based on the Classical Drude Oscillator Model. The Journal of Physical Chemistry B 2016, 120 (44), 11436–11448. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 109.Lopes PE; Lamoureux G; MacKerell AD Jr, Polarizable empirical force field for nitrogen-containing heteroaromatic compounds based on the classical Drude oscillator. Journal of computational chemistry 2009, 30 (12), 1821–1838. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 110.Lamoureux G; MacKerell AD Jr; Roux B, A simple polarizable model of water based on classical Drude oscillators. The Journal of chemical physics 2003, 119 (10), 5185–5197. [Google Scholar]
- 111.Lamoureux G; Harder E; Vorobyov IV; Roux B; MacKerell AD Jr, A polarizable model of water for molecular dynamics simulations of biomolecules. Chemical Physics Letters 2006, 418 (1-3), 245–249. [Google Scholar]
- 112.Yu W; Lopes PE; Roux B; MacKerell AD Jr, Six-site polarizable model of water based on the classical Drude oscillator. The Journal of chemical physics 2013, 138 (3), 034508. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 113.Vorobyov IV; Anisimov VM; MacKerell AD, Polarizable empirical force field for alkanes based on the classical drude oscillator model. The Journal of Physical Chemistry B 2005, 109 (40), 18988–18999. [DOI] [PubMed] [Google Scholar]
- 114.Lopes PE; Lamoureux G; Roux B; MacKerell AD, Polarizable empirical force field for aromatic compounds based on the classical drude oscillator. The Journal of Physical Chemistry B 2007, 111 (11), 2873–2885. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 115.Vorobyov I; Anisimov VM; Greene S; Venable RM; Moser A; Pastor RW; MacKerell AD, Additive and classical drude polarizable force fields for linear and cyclic ethers. Journal of chemical theory and computation 2007, 3 (3), 1120–1133. [DOI] [PubMed] [Google Scholar]
- 116.Harder E; Anisimov VM; Whitfield T; MacKerell AD; Roux B, Understanding the dielectric properties of liquid amides from a polarizable force field. The journal of physical chemistry B 2008, 112 (11), 3509–3521. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 117.Zhu X; MacKerell AD Jr, Polarizable empirical force field for sulfur-containing compounds based on the classical Drude oscillator model. Journal of computational chemistry 2010, 31 (12), 2330–2341. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 118.Lopes PE; Huang J; Shim J; Luo Y; Li H; Roux B; MacKerell AD Jr, Polarizable force field for peptides and proteins based on the classical drude oscillator. Journal of chemical theory and computation 2013, 9 (12), 5430–5449. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 119.Savelyev A; MacKerell AD Jr, All-atom polarizable force field for DNA based on the classical drude oscillator model. Journal of computational chemistry 2014, 35 (16), 1219–1239. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 120.Lemkul JA; MacKerell AD Jr, Polarizable force field for RNA based on the classical drude oscillator. Journal of computational chemistry 2018, 39 (32), 2624–2646. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 121.Patel DS; He X; MacKerell AD Jr, Polarizable empirical force field for hexopyranose monosaccharides based on the classical drude oscillator. The Journal of Physical Chemistry B 2014, 119 (3), 637–652. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 122.Jana M; MacKerell AD Jr, CHARMM drude polarizable force field for aldopentofuranoses and methyl-aldopentofuranosides. The Journal of Physical Chemistry B 2015, 119 (25), 7846–7859. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 123.Chowdhary J; Harder E; Lopes PE; Huang L; MacKerell AD Jr; Roux B, A polarizable force field of dipalmitoylphosphatidylcholine based on the classical drude model for molecular dynamics simulations of lipids. The Journal of Physical Chemistry B 2013, 117 (31), 9142–9160. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 124.Huang J; MacKerell AD Jr, Induction of peptide bond dipoles drives cooperative helix formation in the (AAQAA) 3 peptide. Biophysical journal 2014, 107 (4), 991–997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 125.Pandey P; Mallajosyula SS, Influence of polarization on carbohydrate hydration: a comparative study using additive and polarizable force fields. The Journal of Physical Chemistry B 2016, 120 (27), 6621–6633. [DOI] [PubMed] [Google Scholar]
- 126.Huang J; Lopes PE; Roux B; MacKerell AD Jr, Recent advances in polarizable force fields for macromolecules: microsecond simulations of proteins using the classical Drude oscillator model. The journal of physical chemistry letters 2014, 5 (18), 3144–3150. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 127.Lemkul JA; Huang J; MacKerell AD Jr, Induced Dipole–Dipole Interactions Influence the Unfolding Pathways of Wild-Type and Mutant Amyloid β-Peptides. The Journal of Physical Chemistry B 2015, 119 (51), 15574–15582. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 128.Savelyev A; MacKerell AD Jr, Differential impact of the monovalent ions Li+, Na+, K+, and Rb+ on DNA conformational properties. The journal of physical chemistry letters 2014, 6 (1), 212–216. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 129.Savelyev A; MacKerell AD Jr, Differential deformability of the DNA minor groove and altered BI/BII backbone conformational equilibrium by the monovalent ions Li+, Na+, K+, and Rb+ via water-mediated hydrogen bonding. Journal of chemical theory and computation 2015, 11 (9), 4473–4485. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 130.Lemkul JA; Savelyev A; MacKerell AD Jr, Induced polarization influences the fundamental forces in DNA base flipping. The journal of physical chemistry letters 2014, 5 (12), 2077–2083. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 131.Jiang W; Hardy DJ; Phillips JC; MacKerell AD Jr; Schulten K; Roux B, High-performance scalable molecular dynamics simulations of a polarizable force field based on classical Drude oscillators in NAMD. The journal of physical chemistry letters 2010, 2 (2), 87–92. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 132.Lemkul JA; Roux B; van der Spoel D; MacKerell AD Jr, Implementation of extended L agrangian dynamics in GROMACS for polarizable simulations using the classical D rude oscillator model. Journal of computational chemistry 2015, 36 (19), 1473–1479. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 133.Sherwood P; de Vries AH; Guest MF; Schreckenbach G; Catlow CRA; French SA; Sokol AA; Bromley ST; Thiel W; Turner AJ, QUASI: A general purpose implementation of the QM/MM approach and its application to problems in catalysis. Journal of Molecular Structure: THEOCHEM 2003, 632 (1-3), 1–28. [Google Scholar]
- 134.Eastman P; Friedrichs MS; Chodera JD; Radmer RJ; Bruns CM; Ku JP; Beauchamp KA; Lane TJ; Wang L-P; Shukla D, OpenMM 4: a reusable, extensible, hardware independent library for high performance molecular simulation. Journal of chemical theory and computation 2012, 9 (1), 461–469. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 135.Frisch M; Trucks G; Schlegel H; Scuseria G; Robb M; Cheeseman J; Montgomery J Jr; Vreven T; Kudin K; Burant J, GAUSSIAN 03, Revision B. 04, Gaussian Inc., Pittsburgh, PA, 2003. Google Scholar 2005. [Google Scholar]
- 136.Turney JM; Simmonett AC; Parrish RM; Hohenstein EG; Evangelista FA; Fermann JT; Mintz BJ; Burns LA; Wilke JJ; Abrams ML, Psi4: an open-source ab initio electronic structure program. Wiley Interdisciplinary Reviews: Computational Molecular Science 2012, 2 (4), 556–565. [Google Scholar]
- 137.Parrish RM; Burns LA; Smith DG; Simmonett AC; DePrince AE III; Hohenstein EG; Bozkaya U; Sokolov AY; Di Remigio R; Richard RM, Psi4 1.1: An open-source electronic structure program emphasizing automation, advanced libraries, and interoperability. Journal of chemical theory and computation 2017, 13 (7), 3185–3197. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 138.Shao Y; Fusti-Molnar L; Jung Y; Kussmann J; Ochsenfeld C; Brown S; Gilbert A; Slipchenko L; Levchenko S; O’Neill D, Q-Chem, version 3.0. Q-Chem, Inc. Pittsburgh, PA: 2006. [Google Scholar]
- 139.Boys SF; Bernardi F. d., The calculation of small molecular interactions by the differences of separate total energies. Some procedures with reduced errors. Molecular Physics 1970, 19 (4), 553–566. [Google Scholar]
- 140.Ransil BJ, Studies in molecular structure. IV. Potential curve for the interaction of two helium atoms in single-configuration LCAO MO SCF approximation. The Journal of Chemical Physics 1961, 34 (6), 2109–2118. [Google Scholar]
- 141.Brooks BR; Bruccoleri RE; Olafson BD; States DJ; Swaminathan S. a.; Karplus M, CHARMM: a program for macromolecular energy, minimization, and dynamics calculations. Journal of computational chemistry 1983, 4 (2), 187–217. [Google Scholar]
- 142.Raman EP; Guvench O; MacKerell AD Jr, CHARMM additive all-atom force field for glycosidic linkages in carbohydrates involving furanoses. The Journal of Physical Chemistry B 2010, 114 (40), 12981–12994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 143.Guvench O; Hatcher E; Venable RM; Pastor RW; MacKerell AD Jr, CHARMM additive all-atom force field for glycosidic linkages between hexopyranoses. Journal of chemical theory and computation 2009, 5 (9), 2353–2370. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 144.Jorgensen WL; Chandrasekhar J; Madura JD; Impey RW; Klein ML, Comparison of simple potential functions for simulating liquid water. The Journal of chemical physics 1983, 79 (2), 926–935. [Google Scholar]
- 145.Vanommeslaeghe K; Yang M; MacKerell AD Jr, Robustness in the fitting of molecular mechanics parameters. Journal of computational chemistry 2015, 36 (14), 1083–1101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 146.Allen FH, The Cambridge Structural Database: a quarter of a million crystal structures and rising. Acta Crystallographica Section B: Structural Science 2002, 58 (3), 380–388. [DOI] [PubMed] [Google Scholar]
- 147.Essentials of Glycobiology. 2009.
- 148.Sattelle BM; Bose-Basu B; Tessier M; Woods RJ; Serianni AS; Almond A, Dependence of pyranose ring puckering on anomeric configuration: methyl idopyranosides. The Journal of Physical Chemistry B 2012, 116 (22), 6380–6386. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 149.Perlin A; Casu B; Sanderson G; Tse J, Methyl α-and β-D-idopyranosiduronic acids synthesis and conformational analysis. Carbohydrate Research 1972, 21 (1), 123–132. [Google Scholar]
- 150.Woods RJ, Predicting the Structures of Glycans, Glycoproteins, and Their Complexes. Chemical reviews 2018, 118 (17), 8005–8024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 151.Ultra C, version 13.0. 2.3021. PerkinElmer: Cambridge, MA: 2013. [Google Scholar]
- 152.Sattelle BM; Almond A, Is N-acetyl-d-glucosamine a rigid 4 C 1 chair? Glycobiology 2011, 21 (12), 1651–1662. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 153.Topin J; Lelimousin M. l.; Arnaud J; Audfray A; Pérez S; Varrot A; Imberty A, The hidden conformation of Lewis x, a human histo-blood group antigen, is a determinant for recognition by pathogen lectins. ACS chemical biology 2016, 11 (7), 2011–2020. [DOI] [PubMed] [Google Scholar]
- 154.Baker CM; MacKerell AD, Polarizability rescaling and atom-based Thole scaling in the CHARMM Drude polarizable force field for ethers. Journal of molecular modeling 2010, 16 (3), 567–576. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 155.Humphrey W; Dalke A; Schulten K, VMD: visual molecular dynamics. Journal of molecular graphics 1996, 14 (1), 33–38. [DOI] [PubMed] [Google Scholar]
- 156.DeLucas LJ; Gartland G; Bugg CE, Sodium binding to d-glucuronate residues: Crystal structure of sodium d-glucuronate monohydrate. Carbohydrate Research 1978, 62 (2), 213–221. [DOI] [PubMed] [Google Scholar]
- 157.Jackson RL; Busch SJ; Cardin AD, Glycosaminoglycans: molecular properties, protein interactions, and role in physiological processes. Physiological reviews 1991, 71 (2), 481–539. [DOI] [PubMed] [Google Scholar]
- 158.Lindahl U; Kjellén L, Pathophysiology of heparan sulphate: many diseases, few drugs. Journal of internal medicine 2013, 273 (6), 555–571. [DOI] [PubMed] [Google Scholar]
- 159.Kang I; Chang MY; Wight TN; Frevert CW, Proteoglycans as immunomodulators of the innate immune response to lung infection. Journal of Histochemistry & Cytochemistry 2018, 66 (4), 241–259. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 160.Tanino Y; Coombe DR; Gill SE; Kett WC; Kajikawa O; Proudfoot AE; Wells TN; Parks WC; Wight TN; Martin TR, Kinetics of chemokine–glycosaminoglycan interactions control neutrophil migration into the airspaces of the lungs. The Journal of Immunology 2010, ji_0903274. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 161.Lortat-Jacob H; Garrone P; Banchereau J; Grimaud J-A, Human interleukin 4 is a glycosaminoglycan-binding protein. Cytokine 1997, 9 (2), 101–105. [DOI] [PubMed] [Google Scholar]
- 162.Rosengart TK; Kuperschmid JP; Maciag T; Clark RE, Pharmacokinetics and distribution of heparin-binding growth factor I (endothelial cell growth factor) in the rat. Circulation research 1989, 64 (2), 227–234. [DOI] [PubMed] [Google Scholar]
- 163.LeMosy EK; Hong CC; Hashimoto C, Signal transduction by a protease cascade. Trends in cell biology 1999, 9 (3), 102–107. [DOI] [PubMed] [Google Scholar]
- 164.Jiang D; Liang J; Noble PW, Hyaluronan as an immune regulator in human diseases. Physiological reviews 2011, 91 (1), 221–264. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 165.Petrey AC; de la Motte CA, Hyaluronan, a crucial regulator of inflammation. Frontiers in immunology 2014, 5, 101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 166.Wight TN, Provisional matrix: a role for versican and hyaluronan. Matrix Biology 2017, 60, 38–56. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 167.Sattelle BM; Shakeri J; Roberts IS; Almond A, A 3D-structural model of unsulfated chondroitin from high-field NMR: 4-sulfation has little effect on backbone conformation. Carbohydrate research 2010, 345 (2), 291–302. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 168.Widmalm G, A perspective on the primary and three-dimensional structures of carbohydrates. Carbohydrate research 2013, 378, 123–132. [DOI] [PubMed] [Google Scholar]
- 169.Jo S; Myatt D; Qi Y; Doutch J; Clifton LA; Im W; Widmalm G. r., Multiple Conformational States Contribute to the 3D Structure of a Glucan Decasaccharide: A Combined SAXS and MD Simulation Study. The Journal of Physical Chemistry B 2018, 122 (3), 1169–1175. [DOI] [PubMed] [Google Scholar]
- 170.Patel DS; Pendrill R; Mallajosyula SS; Widmalm G. r.; MacKerell AD Jr, Conformational properties of α-or β-(1→ 6)-linked oligosaccharides: Hamiltonian replica exchange MD simulations and NMR experiments. The Journal of Physical Chemistry B 2014, 118 (11), 2851–2871. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 171.Ochsenbein P; Bonin M; Schenk-Joß K; El-Hajji M, The 2SO Skew-Boat Conformation in L-Iduronic Acid. Angewandte Chemie 2011, 123 (49), 11841–11843. [DOI] [PubMed] [Google Scholar]
- 172.Thorsheim K; Siegbahn A; Johnsson RE; Stålbrand H; Manner S; Widmalm G; Ellervik U, Chemistry of xylopyranosides. Carbohydrate research 2015, 418, 65–88. [DOI] [PubMed] [Google Scholar]
- 173.Cremer D. t.; Pople J, General definition of ring puckering coordinates. Journal of the American Chemical Society 1975, 97 (6), 1354–1358. [Google Scholar]
- 174.Mobli M; Almond A, N-Acetylated amino sugars: The dependence of NMR 3 J (HNH2)-couplings on conformation, dynamics and solvent. Organic & biomolecular chemistry 2007, 5 (14), 2243–2251. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 175.Mallajosyula SS; MacKerell AD Jr, Influence of solvent and intramolecular hydrogen bonding on the conformational properties of O-linked glycopeptides. The Journal of Physical Chemistry B 2011, 115 (38), 11215–11229. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 176.He X; Lopes PE; MacKerell AD Jr, Polarizable empirical force field for acyclic polyalcohols based on the classical drude oscillator. Biopolymers 2013, 99 (10), 724–738. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


