Drude Polarizable Force Field Parametrization of Carboxylate and N-acetyl Amine Carbohydrate Derivatives

Abstract

In this work, we report the development of Drude polarizable force-field parameters for the carboxylate and N-acetyl amine derivatives, extending the functionality of existing Drude polarizable carbohydrate force field. The force field parameters have been developed in a hierarchical manner, reproducing the quantum mechanical (QM) gas-phase properties of small model compounds representing the key functional group in the carbohydrate derivatives, including optimization of the electrostatic and bonded parameters. The optimized parameters were then used to generate the models for carboxylate and N-acetyl amine carbohydrate derivatives. The transferred parameters were further tested and optimized to reproduce crystal geometries and J-coupling data from NMR experiments. The parameter development resulted in the incorporation of D-glucuronate, L-iduronate, N-acetyl-D-glucosamine (GlcNAc) and N-acetyl-D-galactosamine (GalNAc) sugars into the Drude polarizable force field. The parameters developed in this study were then applied to study the conformational properties of glycosaminoglycan polymer hyaluronan, composed of D-glucuronate and N-acetyl-D-glucosamine, in aqueous solution. Upon comparing the results from the additive and polarizable simulations it was found that the inclusion of polarization improved the description of the electrostatic interactions observed in hyaluronan resulting in enhanced conformational flexibility. The developed Drude polarizable force field parameters in conjunction with the remainder of the Drude polarizable force field parameters can be used for the future studies involving carbohydrates and their conjugates in complex, heterogeneous systems.

Graphical Abstract

Introduction

The ubiquity of carbohydrates and their scaffolds in biological systems reflects their involvement in a broad range of cellular processes including cell signaling^1-2, inflammation^3-4, immune response⁵, and protein stabilization,⁶ including cryoprotection^7-8. In addition, glycosylation of proteins is the most frequent and diverse post-translational modification which profoundly affects their folding^9-10, stability,¹¹ and function¹². Owing to their structural and functional diversity, carbohydrates represent both therapeutic targets and tools.^13-16 For example, glycans decorating the eukaryotic cell surface are often the hallmark of cancer^17-18 and inflammation^18-19, while aberrant O-glycosylation may result in neurodegenerative disorders like Alzheimer’s^20-21, Parkinson’s²² and Huntington’s²⁰ disease. Altered glycosylation patterns (often termed as oncofetal) observed in cancerous cells include increased N-glycan branching, abnormal core fucosylation or an increase in sialyl Lewis structures^23-25. Altered glycosylation pattern on some Immunoglobins isotypes, a crucial component of humoral immunity, have been identified in chronic inflammatory, autoimmune and infectious disease^26-30, such as rheumatoid arthritis^31-32 (RA), systemic lupus erythematosus³³ (SLE) and HIV infection³⁴. Indeed, glycosylation pattern differentially affects the functional roles of immunoglobulins^35-38. Therefore, understanding the physical and conformational properties of carbohydrates alone and in combination with their molecular scaffolds is essential to elucidate their biological functions and their utilization as therapeutic agents.

Carbohydrate derivatives such as acidic sugars (glucuronic acid, iduronic acid) and amine derivatives (N-acetylglucosamine and N-acetyl galactosamine) are inherent components of complex eukaryotic glycans. These sugar derivatives are the key component of glycosaminoglycans (GAGs) such as heparins, dermatan, and their sulfate derivatives^39-40 and play an essential role in various physiological and pathophysiological functions like morphogenesis⁴¹, viral invasion, cancer metastasis⁴², anticoagulation^43-44, cell-cell interactions⁴⁴, the HIV protein surface shield⁴⁵ and lubrication⁴⁴. The inherent structural complexity and variable length complicate the experimental structural characterization of these molecules^46-47. Detailed analysis of these molecules with NMR or crystallography is usually carried out on smaller, isolated or synthetic oligomer units. Therefore, the experimental studies are generally augmented with theoretical methods like quantum mechanics^48-50 (QM) calculations and classical molecular dynamics (MD)^51-55 simulations. The most frequently used additive force fields for molecular simulations of carbohydrate derivatives include: CHARMM⁵⁶, GROMOS^57-58, OPLS-AA⁵⁹, GLYCAM06,⁶⁰ and CHARMM Carbohydrate Solution Force Field (CSFF)⁶¹. Most of the above-mentioned force fields are additive in nature with fixed partial charges, which limits the accurate description of the diverse environment observed in biological systems. For example, quantum mechanical (QM) calculations^49-50 have shown that MD simulations with additive force fields do not satisfactorily describe inter and intra-molecular properties like solvent effect, counterion interactions, hydrogen bonding and molecular dipole variations which involve both inter-molecular and intra-molecular charge redistributions. To this end polarizable force fields, which can incorporate polarization allow us to bridge the gap between QM studies and classical MD simulations.

In recent years, several review articles have been dedicated to the facets of research on polarizable force fields^62-71. A wide range of methods such as the fluctuating charge model^72-76, induced point dipole model^{69, 77-81} and classical Drude oscillator model^82-89 have been used to incorporate polarization in MD simulations. The fluctuating charge (FQ) model, also known as chemical potential equilibration or charge equilibration (CHEQ), is based on the theory of electronegativity equalization⁹⁰. In the fluctuating charge model, the atomic charges can be redistributed in response to the electric field, while the overall charge on the molecule remains fixed. The CHARMM CHEQ polarizable force field^{75, 91} is based on fluctuating charge (FQ) model. The CHEQ force fields have been successfully implemented to study ion solvation⁹², protein-ligand binding,⁹³ and lipid-membrane systems^94-95. In the induced point dipole model, in addition to the partial atomic charge, a point dipole is assigned to each contributing site (i.e. atom); and the polarization solution for the induced dipole moment is treated through either iterative self-consistent field^96-97 (SCF) methods or perturbation theory^98-99. The induced dipole model is employed in several force fields including OPLS/PFF, AMBER (ff02EP¹⁰⁰/ff02r1¹⁰¹) and AMOEBA⁷⁸. The classical Drude oscillator model, also known as the Shell¹⁰² or Charge-On-Spring¹⁰³ (COS) model, uses auxiliary charged particles (e.g. the Drude oscillators) to model the variability of the electronic structure, such that the approach retains most of the pairwise features from the additive force field model while explicitly treating electronic polarizability.

In the Drude polarizable force field, which is based on the classical Drude oscillator model, the charged auxiliary (Drude) particles are attached to the atomic core of the non-hydrogen atoms via a harmonic spring to incorporate induced polarization effects (Figure 1(a)). The induced polarization arises due to the displacement of the Drude particle under an applied electric field. The Drude particles, carrying a negative charge, embody the electronic degrees of freedom in the system (Figure 1(b)). In the Drude oscillator model, the sum of the charge on each atom is the sum of the charge on the atom core (q_C) and the Drude particle (q_D); and the induced dipole moment (μ) and the displacement (d) between the Drude particle and the core atom in response to an electric field E is defined as

$$\mu =\frac{{q_D}^{2}E}{k_D}$$ (1)

and

$$d=\frac{q_{D}E}{k_D}$$ (2)

and the atomic polarizability is evaluated as

$$\alpha =\frac{{q_D}^2}{k_D}$$ (3)

where k_D is the harmonic spring force constant for the Drude-core atom bond and is assigned a value of 1000 kcal mol⁻¹ for all Drude particle-atom pairs, where the value of k_D/2 or 500 kcal mol⁻¹ is used directly as the input in CHARMM and NAMD.

Figure 1.

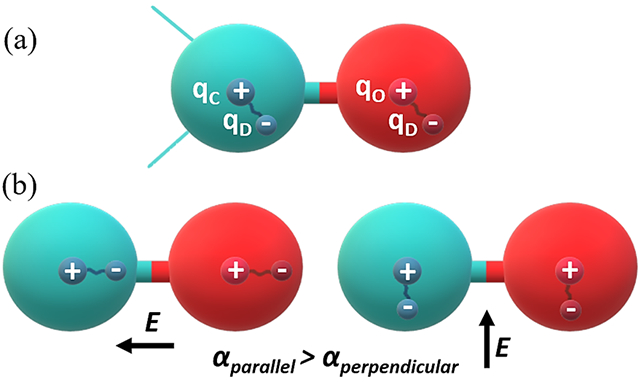
Schematic representation of Drude oscillator model for carbonyl functional (C=O) group. (a) The carbon and oxygen atoms are represented as sphere with the partially positively charged nucleus and partially negatively charged Drude particle. (b) Orientation of the Drude particle in the influence of electrical field, E, parallel and perpendicular to the interatomic covalent bond.

The functional form of the Drude polarizable force field for treating bonded and non-bonded interactions are similar to the additive force fields. The electrostatic potential energy term is extended to incorporate the unscreened Coulombic potential between i^th and j^th core atoms and their Drude particles, which can be evaluated as¹⁰⁴

$$U_{elec}={\sum }_i{\sum }_{j>i}\left[\frac{q_i{q}_j}{\mid r_i-r_j\mid }+\frac{q_i{q}_{D,j}}{\mid r_i-r_j-d_j\mid }+\frac{q_j{q}_{D,i}}{\mid r_i-d_i-r_j\mid }+\frac{q_{D,i}{q}_{D,j}}{\mid r_i-d_i-r_j-d_j\mid }\right]$$ (4)

where q_i and q_j are the partial charges on i^th and j^th core atoms; q_D,i and q_D,j are the partial charges on the Drude oscillator attached to i^th and j^th core atoms, respectively; and d_i and d_j are the bond lengths between the Drude oscillators and i^th and j^th core atoms, respectively. The electrostatic term explicitly includes the induced dipole interactions between the neighboring atoms (i.e., 1-2 and 1-3 atom pairs), which are scaled using the Thole screening function¹⁰⁵:

$$S_{ij}(r_{ij})=1-\left[1+\frac{(a_i+a_j)r_{ij}}{2({\alpha }_i{\alpha }_j{)}^{\frac{1}{6}}}\right]\mathit{exp}\left[\frac{-(a_i+a_j)r_{ij}}{({\alpha }_i{\alpha }_j{)}^{\frac{1}{6}}}\right]$$ (5)

Where r_ij is the distance between i^th and j^th atoms, and a_i and a_j are the respective Thole damping parameters that modulate the screening strength of S_ij. The Drude force field using atom-specific a_i and a_j terms allows for improved treatment of molecular polarizability tensors¹⁰⁶. This screening function can also be implemented for intermolecular interactions (known as NBTHOLE), which is important to model ions^107-108. The Drude model also incorporate NBFIX for selected off diagonal atom-pair specific Lennard Jones (LJ) interactions to obtain better agreement with intermolecular interaction energies as well as condensed phase properties such a hydration free energies¹⁰⁹.

The Drude polarizable force field covers a wide range of molecules⁶² such as water^110-112, organic compounds (including alkanes¹¹³, aromatic compounds¹¹⁴, linear and cyclic ethers¹¹⁵, alcohols⁸⁵, amides¹¹⁶, nitrogen¹⁰⁹ and sulfur¹¹⁷ containing compounds), ions¹⁰⁷, peptides and proteins¹¹⁸, DNA¹¹⁹, RNA¹²⁰, carbohydrates^{86, 89, 121-122} and lipid membranes¹²³; and has been applied to a variety of molecular systems^124-130. The availability of the Drude polarizable force field in different simulation packages like CHARMM¹⁰⁴, NAMD¹³¹, GROMACS¹³², ChemShell QM/MM¹³³ and OPENMM^{87, 134} have made it convenient to run the polarizable force field simulations at the microsecond time scale. The present work extends the applicability of Drude polarizable force field to enable the modelling of carboxylate and N-acetyl amine carbohydrate derivatives.

Methods

Quantum Mechanical (QM) Calculations:

All QM calculations were carried out using Gaussian 03¹³⁵ and Psi4^136-137programs. Adiabatic potential energy scans (PES) were carried out by gas phase geometry optimization at the MP2/6-31G(d) level and single point energy evaluation at the RIMP2/cc-pVQZ model chemistry. QM solute-water interaction energies were obtained at the RI-MP2/cc-pVQZ//MP2/6-31G* model chemistry with counterpoise correction¹³⁹ for basis set superposition error¹⁴⁰ (BSSE) using the model compound gas phase molecular geometries or the SWM4-NDP¹¹¹ geometry for water. The level of theory was chosen to maintain consistency with the published Drude polarizable CHARMM carbohydrate FF. ^{86, 89, 121-122}

Molecular Mechanic (MM) Calculations.

All molecular mechanical (MM) calculations were performed using the CHARMM¹⁴¹ program with the Drude polarizable force field for all the polarizable simulations and the CHARMM36 carbohydrate force field^{56, 121, 142-143} for all the additive simulations unless otherwise stated. The SWM4-NDP¹¹¹ water model is used to model water molecules in all the polarizable simulations while the CHARMM TIP3P¹⁴⁴ water model was used for all the additive simulations. All gas phase monomer and dimer calculations included all possible nonbond pairs.

Dihedral Parameter Optimization.

Gas phase QM potential energy scans (PES) were taken as target data for dihedral parameter optimization. Initially the dihedral force constants of the target dihedrals were set to zero and MM potential energies (MM₀) were calculated for the corresponding optimized geometries obtained from QM scans. The energy difference between MM₀ and QM energies were used to fit the dihedral parameters using a least-square fit algorithm¹⁴⁵ with multiplicity n =1,2,3, and 6 and phase angle δ =0 or 180.

Bond Length, Valence Angle, and Dihedral Angle calculations.

Starting from the QM optimized structure, minimizations were performed initially on only the Drude particles with the atoms constrained using the Steepest Descent (SD) optimizer, followed by Adopted-Basis Newton Raphson (ABNR) method to a gradient of 10⁻⁴ kcal/mol/Å. Minimization of all particles was next performed using SD algorithm followed by ABNR method to a gradient of 10⁻⁴ kcal/mol/Å.

Solute-water interaction calculations.

Solute-water interaction geometries were constructed based on the donor-acceptor properties of the solute heteroatoms. Solute-water interaction analysis was performed by distance scanning along a fixed orientation with the increment of 0.1 Å in both the QM and MM scans. For the MM scans the solute was constrained to the QM optimized geometry and the minimizations were performed on only the Drude particles with the atoms constrained using the SD optimizer, followed by the ABNR method to a gradient of 10⁻⁴ kcal/mol/Å. Interaction energies were calculated as the total energy of the solute-water complex at each distance minus the sum of the energies of the individual isolated monomers.

Crystal Simulations:

The crystal simulations were performed according to a previously established protocol⁸⁶. Crystal coordinates for the crystal MD simulations were retrieved from Cambridge Structure Database¹⁴⁶ (CSD). Missing hydrogen atoms were built and minimized using CHARMM36 additive and Drude polarizable force field parameters for the additive and polarizable crystal MD simulations. For each of the crystalline systems a 2×2×2 super cell was built which was used in the subsequent MD simulations. Crystal simulations under the NPT ensemble were carried out for 20 ns on each supercell system using both the additive and Drude polarizable force fields. All crystal simulations were performed at constant temperature (298 K) and pressure (1 ATM) using velocity-Verlet algorithm¹⁰⁴ with Nose-Hoover thermostat. For Drude simulation, the thermostat coupled to the Drude oscillator was set to 1 K, while thermostat for the real atoms was set to 298 K. Electrostatic interactions were evaluated using particle mesh Ewald (PME) method with a real space cutoff of 12 Å, a sixth order B spline interpolation and a KAPPa value of 0.34. The van der Waals interactions were truncated by a switching function over 10-12 Å with an isotropic long-range Lennard-Jones (LJ) correction. Neighbor lists were updated with a 14 Å and 16 Å cutoff for additive and Drude simulations, respectively. In all the Drude simulations, to avoid polarization catastrophe (which may occur when the forces acting on drude particle cause large displacement from its core atom⁶²), a “hard wall constraint” was used with a Drude-atom bond length cutoff of 0.2 Å.

Results and Discussion

I. Parameter Development.

The aim of this work was to develop polarizable force field parameters to extend the functionality of the Drude polarizable force field to include carboxylate and N-acetyl amine carbohydrate derivatives. The carboxylate derivatives of hexopyranose include D-glucuronate, L-iduronate, while amine derivatives include N-acetyl-D-glucosamine (GlcNAc) and N-acetyl-D-galactosamine (GalNAc). Carboxylates were specifically targeted owing to their relevance at physiological pH¹⁴⁷. Among carboxylate derivatives, α-L-iduronic acid is an extensively explored component of heparin and heparan sulphates^148-149, which exists as interconvertible ¹C₄ and ⁴C₁ conformers^148-149(Figure 2(a)). It is difficult to experimentally quantify the interconversion of the two conformers. While α-L-iduronic acid is assumed to favor the ¹C₄ configuration, glucuronic acid (C-5 epimer of iduronic acid) prefers to be in the ⁴C₁ conformation¹⁵⁰ (Figure 2(b)). Despite the presence of two destabilizing 1-3 diaxial oxygen groups, iduronic acid prefers to be in ¹C₄ state due to the anomeric effect¹⁵⁰. The carboxylate group present on the C5 atom exerts a strong stabilizing effect on the equatorial conformation, while for axial conformation, it shows a destabilizing effect.

Figure 2.

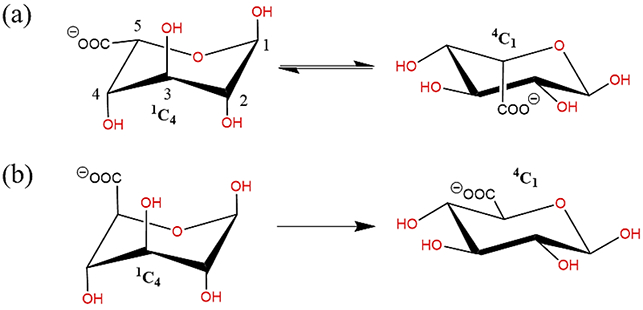
Schematic illustration of (a) interconversion of ¹C₄ chair to ⁴C₁ configuration in Iduronate, (b) preferential occurrence of ⁴C₁ configuration in Glucuronate. (all schematic diagrams were prepared with ChemBioDraw Ultra 13.0¹⁵¹)

In case of hexopyranose amine derivatives, N-acetylglucosamine (GlcNAc) is considered to exist in the ⁴C₁ configuration in solution¹⁵². However, crystallographic data¹⁵³ identifies rare ring flips in GlcNAc which may assert specific molecular recognition processes. To this end, MD simulations equipped with an accurate force field can facilitate a better understanding of atomistic properties of carbohydrate systems, thereby underlining the motivation of present work to develop Drude polarizable force field parameters for carboxylate and N-acetyl amine sugar derivatives.

In carboxylate sugar derivatives the carboxylate moiety is attached at the C5 position of the hexopyranose ring, while in the case of N-acetylamine derivatives, N-acetyl amine moiety is attached to the C2 position of hexopyranose. The parametrization of the derivative side chains, carboxyl and N-acetyl amine moieties, required the introduction of model compounds M1 (2-methoxy propionate) and M2 (N-isopropyl acetamide), respectively (Figure 3). Subsequent to the development of the parameters for the model compounds the same were transferred to full sugars, D-glucuronate, L-iduronate, N-acetyl-D-glucosamine (GlcNAc) and N-acetyl-D-galactosamine (GalNAc) (Figure 4), to test their transferability. Additional parameter optimization was performed for the full sugars when required. For the full sugars, parameters corresponding to the carbohydrate rings were transferred from the available Drude carbohydrate force field^{86, 89, 121-122} to maintain the parameter transferability for atoms with the same local chemical environment. In the subsequent sections, we discuss the parametrization process and the various issues faced during the parametrization for the carboxylate and N-acetylamine sugars separately.

Figure 3.

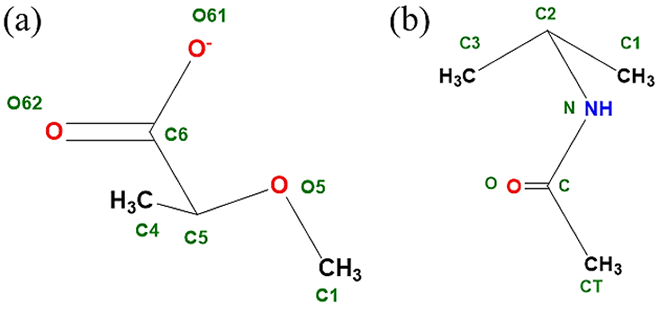
Model compounds used to develop parameters for carbohydrate derivatives (a) M1 (2- methoxy propionate): for glucuronate and iduronate, and (b) M2 (N-isopropyl acetamide): for GlcNAc and GalNAc. (all schematic diagrams were prepared with ChemBioDraw Ultra 13.0¹⁵¹)

Figure 4.

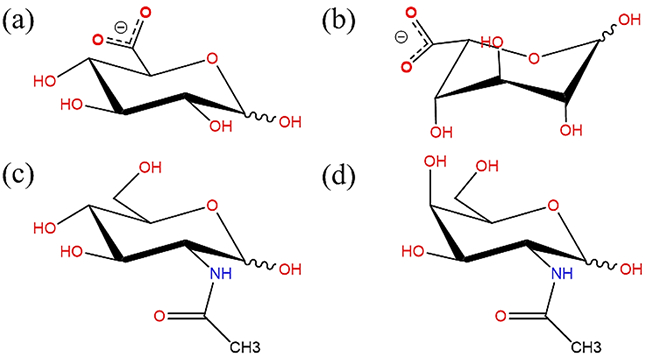
Chemical structures of glucopyranose derivatives (a) D-glucuronate, (b) L-iduronate, (c) N-acetyl-D-glucosamine (GlcNAc) and (d) N-acetyl-D-galactosamine (GalNAc). (all schematic diagrams were prepared with ChemBioDraw Ultra 13.0¹⁵¹)

Parametrization of Carboxylate derivatives

Model Compounds:

We used a model compound-based approach to develop the initial parameters for glucuronates and iduronates. 2- methoxy propionate (M1) was used as the model compound to target the C6 carboxylate, the C5, C4, and C1 ring carbon atoms and O5 ring oxygen (Figure 3). The same model compound was previously used to develop the parameters for the glucuronates and iduronates in the CHARMM additive carbohydrate force field, thereby enabling direct comparison with the additive force field. Parameters developed for the model compound were transferred to the full sugar to model carboxylate sugars for additional validation, as described below.

Model compound (M1):

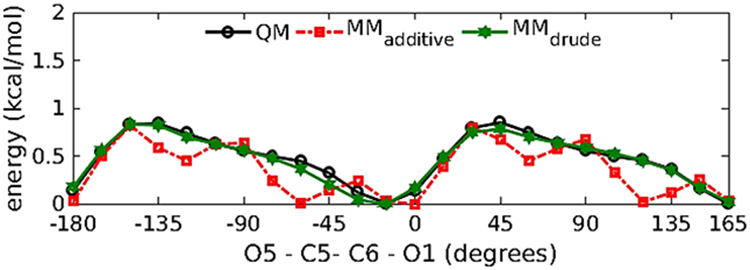
The initial bonded, Lennard-Jones and electrostatic parameters for M1 were transferred from the existing ether, alkane and acidic residues already available in the polarizable force field^{85, 113, 115, 154}. This identified the dihedral parameters about the C5-C6 bond that required to be parametrized. To parametrize the dihedral around the C5-C6 bond one-dimensional QM scans were performed for the O62-C6-C5-O5 dihedral in 15˚ increment resulting in 24 conformations. A least square fit method developed for parameter optimization¹⁴⁵ was used to simultaneously fit the dihedral parameters for the O61/O62-C6-C5-O5 and O61/O62-C6-C5-C4 dihedrals. After fitting the low energy regions (Figure 5) are well represented by the polarizable force field and are consistent with the conformational energies obtained from QM and additive force-field calculations. The transferred and the developed parameters satisfactorily reproduce the minimized geometry of M1, wherein the C1-O5-C5-C6 dihedral was held restrained to an equilibrium value of −162.3˚ (Table 1). To verify the compatibility of the electrostatic parameters with the LJ parameters, the Drude model was validated against M1-water pair QM interaction energies for various geometries (Figure 6 and Table 2). The M1-water pair interaction energies show good agreement with the QM data with an average difference of 0.22 kcal/mol and 0.10 Å for interaction energies and distances, respectively. The parameters also satisfactorily reproduce the vibrational frequencies in agreement with the QM data (Table S1 of the supporting information (SI) file).

Figure 5.

Relaxed potential energy scans of O5-C5-C6-O61 dihedral in compound M1.

Table 1.

Bond lengths, valence angles, and dihedral angles for model compound M1. Bond lengths are in Å, while valance angles and dihedral angles are in degree.

Parameter	QM	Additive				Drude
		MM	MM - QM	MM*	MM* - QM	MM	MM - QM	MM*	MM* - QM
BONDS
C4-C5	1.52	1.55	0.03	1.55	0.03	1.54	0.02	1.54	0.02
C5-O5	1.44	1.44	0.00	1.44	0.00	1.53	0.09	1.53	0.09
C5-C6	1.57	1.58	0.01	1.58	0.01	1.64	0.08	1.64	0.08
C6-O61	1.25	1.26	0.00	1.26	0.00	1.27	0.01	1.27	0.01
C6-O62	1.27	1.26	−0.01	1.26	−0.01	1.27	0.00	1.27	0.00
Average			0.01		0.01		0.04		0.04
Standard deviation			0.01		0.01		0.04		0.04
ANGLES
C4-C5-O5	111.2	109.3	−1.9	110.5	−0.7	110.5	−0.8	110.0	−1.3
C4-C5-C6	109.7	110.6	0.9	109.9	0.2	110.6	0.9	111.2	1.5
O5-C5-C6	111.3	112.8	1.5	112.3	1.0	112.6	1.3	112.8	1.5
C5-C6-O61	117.7	118.0	0.4	118.1	0.4	118.7	1.1	118.8	1.2
C5-C6-O62	111.5	112.8	1.3	112.8	1.3	110.7	−0.8	110.6	−0.9
O61-C6-O62	130.9	129.2	−1.7	129.2	−1.7	130.6	−0.3	130.6	−0.3
Average			0.1		0.1		0.2		0.3
Standard deviation			1.5		1.1		1.0		1.3
DIHEDRALS
O5-C5-C6-O61	−3.4	−6.7	−3.3	−8.9	−5.5	−18.2	−14.9	−15.6	−12.3
C1-O5-C5-C6	−162.3	−151.4	11.0	−162.3	0.0	−168.7	−6.4	−162.3	0.0
Average			3.8		−2.7		−10.6		−6.1
Standard deviation			10.1		3.9		6.0		8.7

^*restraining potential applied to the dihedral C1-O5-C5-C6 to maintain QM geometry.

The average and standard deviations of the difference between the MM and QM values (MM-QM) for the Bond Lengths, Angles and Dihedrals for M1 are also presented pictorially in Figure S1 of the SI file.

Figure 6.

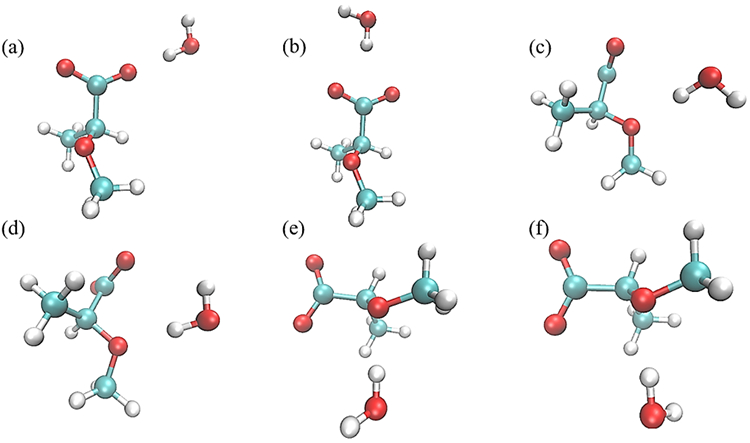
Monohydrate water interaction geometries with model compound M1. Interactions (a) and (b) have the M1 C6-O61 and C5-C6 bonds collinear with the water HO bond, respectively, and with the water molecule in the same plane as the carboxyl group; interactions (c) and (d) have the water HO bond collinear with the ether C1-O5-C5 angle bisector and with the water molecule in the same plane as the C1-O5-C5 atoms; and interactions (e) and (f) have the water molecule forming a tetrahedral interaction with the ether and with the water molecule perpendicular to the plane of the C1-O5-C5 atoms. All molecular graphics were prepared with VMD¹⁵⁵.

Table 2.

Solute-water pair interaction energies and distances for model compound M1.

Water Orientation	Energy (kcal/mol)					Distance (Å)
	QM	Additive		Drude		QM	Additive		Drude
		MM	MM-QM	MM	MM-QM		MM	MM-QM	MM	MM-QM
a	−13.46	−15.64	−2.18	−13.35	0.11	1.79	1.64	−0.15	1.85	0.06
b	−12.92	−14.60	−1.68	−12.57	0.35	2.40	2.22	−0.18	2.47	0.07
c	−5.85	−2.70	3.14	−5.15	0.70	2.03	2.04	0.01	1.88	−0.15
d	−13.31	−16.30	−2.99	−13.57	−0.27	1.88	1.69	−0.19	1.70	−0.18
e	−9.28	−10.12	−0.83	−10.15	−0.87	1.92	1.81	−0.11	1.73	−0.19
f	−7.28	−6.14	1.14	−8.60	−1.32	1.97	1.89	−0.08	1.76	−0.21
Average			−0.57		−0.22			−0.12		−0.10
Standard deviation			2.30		0.76			0.07		0.13

The average and standard deviations of the difference between the MM and QM values (MM-QM) for interaction energies and the distances for M1 are also presented pictorially in Figure S2 of the SI file.

Full Sugars.

Parameters obtained from the model compounds were then transferred to the full sugar derivatives to model α/β-D-glucuronate and α/β-L-iduronate, in which the carboxylate moiety was attached to the C5 carbon of the hexopyranose ring. To check the transferability of the dihedral parameters obtained for the model compounds to full sugars, 1D QM scans were performed about the C5-C6 bond (for O61/O62-C6-C5-O5 dihedrals) for all the 4 systems; α/β-D-glucuronate is hereto referred as AGLCA/BGLCA and α/β-L-iduronate to be referred as AIDOA/BIDOA. To cover the probable conformational space both the chair conformations, ⁴C₁ (regular chair) and ¹C₄ (inverted chair) were included for the QM scans. To avoid intramolecular hydrogen bonding between the terminal carboxyl group and the hydroxyl group at C4 carbon atom, the HO4-O4-C4-C3 dihedral was constrained to a value of 60˚ for all the QM and MM scans. The scans for all the systems performed in increments of 15˚ increment yielded a total of 161 conformations.

It was observed that while the transferred parameters were able to reproduce the individual QM energy profiles, they were not able to reproduce the energy differences between the α-and β-anomers (Figure 7). Therefore, transferred dihedral parameters still needed further improvement. To ensure faithful reproduction of conformational energies, out of 161 conformations obtained from QM scans, 62 QM conformations with relative conformational energies <20 kcal/mol from the global minimum for all the anomers were selected for further dihedral parameter optimization. Parameters obtained from the least-squares-fit procedure with the selected low-lying energy conformations as the goal was to be able to reproduce both the low-energy regions of the QM profile as well as the relative energy differences between the α-and β-anomers (Figure 7).

Figure 7.

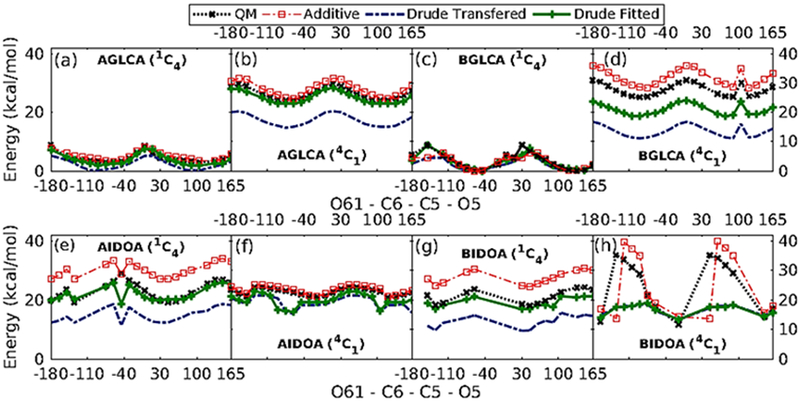
1D dihedral potential energy scans about O61-C6-C5-O5 dihedrals for α-/β- Glucuronate (a, b, c and d), and α-/β- Iduronate (e, f, g and h). Only those conformers with relative energies < 20 kcal/mol are included in the figure.

To check the compatibility of the electrostatic and LJ parameters, the parameters were validated against full sugar-water pair interaction energies for seven different water-solute conformations for all the systems that probe the charges on the O5 and C5 atoms of the carboxylates (Figure 8). The interaction energies and minimum distances for all the systems are tabulated in Table 3. The polarizable force field reproduces the energies and distances better when compared to the additive force field, with the average value for interaction energy differences (MM - QM, in kcal/mol) from the polarizable (additive) force field being 0.49(0.96), 0.33(0.81), −0.83(0.55) and −1.69(0.52) for AGLCA, BGLCA, AIDOA and BIDOA, respectively. We observe a similar trend for the distances, with the average values for the distance differences (MM - QM, in Å) from the polarizable (additive) force field being 0.12 (0.19), −0.52 (−0.47), −0.12 (−0.12) and −0.17 (−0.14) for AGLCA, BGLCA, AIDOA and BIDOA, respectively. The improved agreement with the Drude model is in part due to the additive force field nonbond parameters originally optimized targeting HF/6-31G* without BSSE QM model chemistry data.

Figure 8.

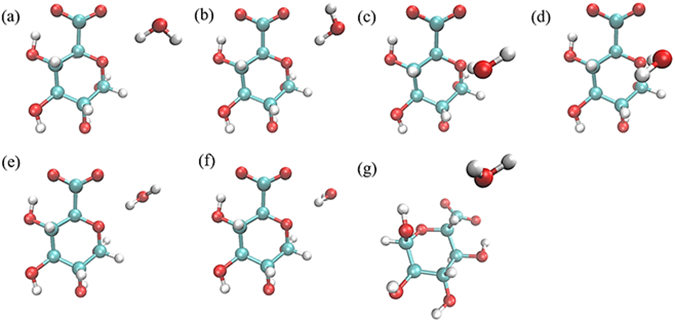
Water pair interaction geometries with acidic sugars. Interactions (a) and (b) have the water HO bond collinear with the C5-O5-C1 angle bisector, with the water molecule in the same plane as the C5-O5-C1 atoms; interactions (c) and (d) have the water molecule forming a tetrahedral interaction with the O5, with the water molecule perpendicular to the plane of the C5-O5-C1 atoms; interactions (e) and (f) have the water HO bond collinear with the C5-O5-C1 angle bisector, with the water molecule perpendicular to the plane of the C5-O5-C1 atoms; and interaction (g) has the C5-H5 vector collinear with the water HOH angle bisector. (All molecular graphics were prepared with VMD¹⁵⁵)

Table 3.

Solute-water pair interaction energies and distances for sugar carboxylates.

Water Orientation	Energy (kcal/mol)					Distance (Å)
	QM	Additive		Drude		QM	Additive		Drude
		MM	MM-QM	MM	MM-QM		MM	MM-QM	MM	MM-QM
AGLCA
a	−4.89	−0.95	3.94	−3.28	1.61	2.25	3.71	1.46	2.54	0.29
b	−11.77	−15.64	−3.87	−10.54	1.24	2.10	1.74	−0.36	1.99	−0.11
c	−7.59	−7.46	0.13	−7.12	0.46	1.91	1.76	−0.15	1.87	−0.04
d	−6.16	−2.94	3.21	−6.26	−0.10	1.98	1.96	−0.02	1.91	−0.07
e	−6.75	−6.35	0.40	−5.35	1.40	2.20	2.16	−0.04	2.64	0.44
f	−4.80	−2.97	1.83	−5.35	−0.55	2.34	2.80	0.46	2.64	0.30
g	2.20	3.30	1.10	1.57	−0.64	3.00	3.00	0.00	3.00	0.00
Average			0.96		0.49			0.19		0.12
Standard deviation			2.55		0.94			0.61		0.22
BGLCA
a	−4.27	−0.97	3.31	−2.77	1.50	2.10	3.84	1.74	2.45	0.35
b	−11.67	−15.90	−4.23	−10.75	0.92	2.97	1.72	−1.25	1.88	−1.09
c	−7.29	−7.35	−0.06	−7.97	−0.68	2.89	1.82	−1.07	1.83	−1.06
d	−5.97	−3.12	2.85	−7.69	−1.72	2.96	2.08	−0.88	1.85	−1.11
e	−6.54	−5.93	0.62	−4.50	2.04	2.98	1.92	−1.06	2.63	−0.35
f	−5.57	−2.73	2.84	−4.51	1.06	3.02	2.28	−0.74	2.64	−0.38
g	2.13	2.45	0.31	1.33	−0.80	3.00	3.00	0.00	3.00	0.00
Average			0.81		0.33			−0.47		−0.52
Standard deviation			2.61		1.40			1.05		0.58
AIDOA
a	−4.54	−1.16	3.38	−4.67	−0.13	2.04	1.97	−0.07	1.93	−0.11
b	−9.65	−12.12	−2.47	−9.97	−0.31	1.93	1.71	−0.22	1.84	−0.09
c	−6.20	−6.19	0.01	−7.87	−1.67	1.93	1.77	−0.16	1.75	−0.18
d	−4.23	−2.46	1.77	−6.05	−1.83	2.01	1.95	−0.06	1.81	−0.20
e	−5.05	−5.26	−0.21	−5.91	−0.86	2.05	1.85	−0.20	1.95	−0.10
f	−5.65	−5.21	0.45	−5.92	−0.27	2.07	1.92	−0.15	1.95	−0.12
g	2.08	3.00	0.92	1.32	−0.76	3.00	3.00	0.00	3.00	0.00
Average			0.55		−0.83			−0.12		−0.12
Standard deviation			1.81		0.68			0.08		0.07
BIDOA
a	−5.79	−2.80	3.00	−6.49	−0.70	2.01	1.89	−0.12	1.85	−0.16
b	−10.10	−12.57	−2.46	−12.23	−2.13	1.93	1.71	−0.22	1.77	−0.16
c	−6.22	−5.90	0.32	−7.11	−0.89	2.00	1.85	−0.15	1.86	−0.14
d	−5.83	−5.22	0.60	−7.34	−1.51	2.10	1.91	−0.19	1.86	−0.24
e	−6.59	−6.98	−0.39	−9.22	−2.63	1.97	1.78	−0.19	1.78	−0.19
f	−5.85	−4.78	1.07	−9.23	−3.38	2.07	1.93	−0.14	1.78	−0.29
g	2.21	3.74	1.53	1.65	−0.56	3.00	3.00	0.00	3.00	0.00
Average			0.52		−1.69			−0.14		−0.17
Standard deviation			1.69		1.07			0.07		0.09

The average and standard deviations of the difference between the MM and QM values (MM-QM) for interaction energies and the distances for AGLCA, BGLCA, AIDOA and BIDOA are also presented pictorially in Figure S3 of the SI file.

Crystal Simulation.

Crystal MD simulations were performed to validate the combination of the bonded and non-bonded parameters in the condensed phase. The quality of the optimized parameters was assessed by comparing the intramolecular descriptors of the chemical system (bonds, angles and dihedrals), as well as the descriptors of the crystal lattice (lattice parameters and unit cell volumes) with available experimental values for the crystal structure obtained from Cambridge structural database¹⁴⁶ (CSD). A CSD survey yielded one crystal (NABDGC¹⁵⁶) for β-D-glucuronate monohydrate, having the full monoclinic unit cell consisting of two monosaccharides, two water molecules, and two sodium ions. MD simulation of the infinite crystal lattice was performed on this system. Analysis of the bond, angles, and dihedrals showed that the intramolecular descriptors of the systems were well reproduced by the polarizable force field. The average errors in the bonds and angles were found to be 0.02 Å and 1.00˚, while the average error for the dihedral was found to be −3.89˚. The results are comparable to the additive force field. The discrepancy in the dihedrals corresponds to the very low barriers for rotation for the exocyclic torsion <1 kcal/mol (Figure 5) around the local minima, especially for the Drude FF when compared to the additive FF. Unit cell geometries were consistent with the experimental values (Table 4), while unit cell volume is overestimated by 3.74 % (Table 5).

Table 4.

Crystalline intramolecular geometries for α-galacturonate crystal. Bond lengths are in Å, while valance angles and dihedral angles are in degree.

	CRYS	MDadd	MDdrude	MDadd – CRYS (%err)	MDdrude – CRYS (%err)
NABDGC (β-D-glucuronate monohydrate)
C4-C5	1.535	1.527	1.536	−0.01 (0.00)	0.00 (0.00)
C5-O5	1.429	1.449	1.452	0.02 (0.00)	0.02 (0.00)
C5-C6	1.533	1.536	1.587	0.00 (0.00)	0.05 (0.00)
C6-O61	1.244	1.257	1.271	0.01 (0.00)	0.03 (0.00)
C6-O62	1.254	1.261	1.274	0.01 (0.00)	0.02 (0.00)
C4-C5-O5	109.587	108.65	108.616	−0.94 (−0.02)	−0.97 (−0.10)
C4-C5-C6	108.647	110.012	113.979	1.37 (−0.02)	5.33 (−0.05)
O5-C5-C6	108.059	109.568	110.802	1.51 (−0.01)	2.74 (−0.19)
C5-C6-O61	116.528	116.756	114.923	0.23 (−0.02)	−1.61 (−0.12)
C5-C6-O62	118.05	116.366	115.561	−1.68 (−0.01)	−2.49 (−0.03)
O61-C6-O62	125.229	126.614	128.238	1.39 (−0.02)	3.01 (−0.07)
O5-C5-C6-O61	−28.028	−27.72	−41.909	0.31 (−0.17)	−13.88 (−0.29)
O5-C5-C6-O62	156.756	159.977	148.045	3.22 (−0.08)	−8.71 (−0.04)
C1-O5-C5-C6	−177.661	−173.44	−166.728	4.21 (−0.05)	10.93 (−0.51)

^addadditive force field,

drude: Drude polarizable force field parameters.

Table 5.

Crystalline unit cell geometries and volumes

carbohydrate	Crystal ID		A(Å)	%error	B(Å)	%error	C(Å)	%error	Volume (Å)3	%error
β-D-glucuronate monohydrate	NABDGC	Crystal	9.21		7.01		7.38		472.59
		Additive	9.58	4.01	7.09	1.16	7.09	−3.95	478.87	1.33
		Drude	9.26	0.61	6.79	−3.16	7.86	6.47	490.27	3.74

Parametrization of N-acetylamine derivatives

Similar to carboxylate derivative parametrization, we used a fragment-based approach to parameterize N-acetylamine derivatives. The model compound N-isopropyl-acetamide (M2) was used to target the C1, C2, C3 ring carbon atoms and CT, C, O, and N atoms of the N-acetyl group. The N-isopropyl-acetamide model compound was also used in the additive force field parametrization of N-acetylglucosamines and N-acetylgalactosamines, enabling direct comparison with the additive force field. The developed model compound parameters were then transferred to the full sugar to model N-acetylamine sugars for further validation.

Model Compounds M2.

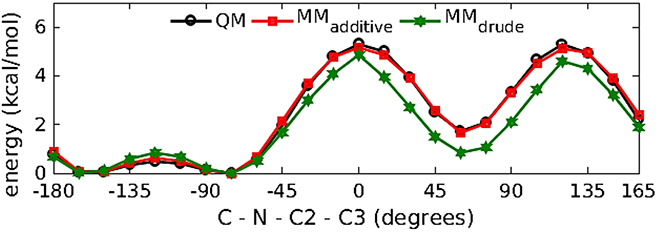
Model compound M2 (Figure 3(b)) was used to parameterize the N-acetyl amine moieties linkages to the C2 carbon of hexopyranose backbone to enable the modeling of N-acetylamine sugars. Initial bonded, LJ and electrostatic parameters for M2 were transferred from existing alanine dipeptide parameters available in the Drude polarizable force field. To check the transferred dihedral parameters in M2, 1D QM potential energy scans were performed about the C2-N bond for the C-N-C2-C3 dihedral. The transferred parameters well represented the low energy region with the conformational energies being comparable to results obtained from the QM and additive force-field calculations (Figure 9). The transferred parameters satisfactorily reproduced the minimized geometry of M2 (Table 6).

Figure 9.

Relaxed potential energy scans of the C-N-C2-C3 dihedral in compound M2.

Table 6.

Bond lengths, valence angles, and dihedral angles for model compound M2. Bond lengths are in Å, while valance angles and dihedral angles are in degrees.

	QM	Additive		Drude
		MM	MM-QM	MM	MM-QM
BONDS
C1-C2	1.526	1.532	0.006	1.524	−0.002
C2-C3	1.522	1.531	0.008	1.523	0.001
C2-N	1.459	1.427	−0.032	1.444	−0.015
N-C	1.367	1.338	−0.028	1.358	−0.009
C-CT	1.516	1.506	−0.010	1.524	0.008
C-O	1.234	1.224	−0.011	1.257	0.023
Average			−0.010		0.000
Standard deviation			0.020		0.010
ANGLES
N-C2-C1	111.20	110.90	−0.40	113.40	2.20
N-C2-C3	109.10	109.50	0.40	111.70	2.70
C1-C2-C3	112.50	110.90	−1.60	107.70	−4.80
C2-N-C	121.50	123.60	2.10	120.80	−0.60
N-C-CT	115.40	116.10	0.70	121.80	6.50
N-C-O	122.30	123.10	0.80	124.80	2.40
O-C-CT	122.30	120.80	−1.50	113.40	−8.90
Average			0.07		−0.09
Standard deviation			1.32		5.19
DIHEDRALS
C1-C2-N-C	−77.8	−78.9	−1.2	−74.9	2.8
C3-C2-N-C	157.6	158.4	0.8	163.2	5.6
Average			−0.2		4.2
Standard deviation			1.4		1.9

The average and standard deviations of the difference between the MM and QM values (MM-QM) for the Bond Lengths, Angles and Dihedrals for M2 are also presented pictorially in Figure S1 of the SI file.

To verify the compatibility of the electrostatic and LJ parameters, the parameters were validated against M2-water pair interaction energies for various geometries of M2-water system (Figure 10 and Table 7). The M2-water pair interactions obtained from transferred parameters showed good agreement with the QM water pair interactions with average differences of 0.11 kcal/mol and 0.004 Å for interaction energies and distances, respectively. The vibrational frequencies obtained from transferred parameters showed reasonably good agreement to the vibrational frequencies obtained from QM calculations (Table S2 of the supporting information (SI) file).

Figure 10.

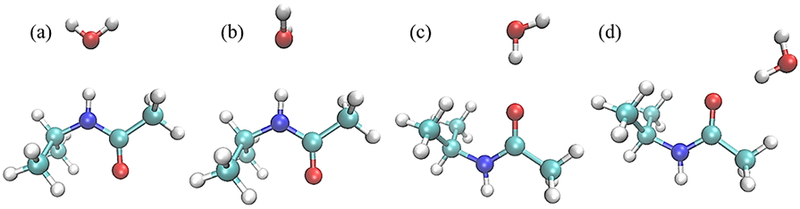
Water pair interaction geometries with model compound M2. Interactions (a) and (b) have the NH vector collinear with water HOH angle bisector; in (a) the water molecule is coplanar with the amide group and in (b) the water molecule is perpendicular. Interaction (c) has the CO vector collinear with the water HO vector and interaction (d) has these two vectors forming a 120°angle; in both (c) and (d) water molecule is coplanar with the amide group. (All molecular graphics were prepared with VMD¹⁵⁵)

Table 7.

Solute-Water Pair Interaction Energies and Distances for Model Compound M2.

Water Orientation	Energy (kcal/mol)					Distance (Å)
	QM	Additive		Drude		QM	Additive		Drude
		MM	MM-QM	MM	MM-QM		MM	MM-QM	MM	MM-QM
a	−5.60	−7.04	−1.44	−5.40	0.20	1.96	1.75	−0.21	1.97	0.01
b	−6.81	−7.37	−0.57	−6.77	0.04	1.94	1.77	−0.17	1.90	−0.04
c	−4.58	−6.45	−1.87	−4.41	0.18	2.03	1.89	−0.14	2.02	−0.01
d	−4.79	−6.65	−1.86	−4.75	0.04	2.01	1.89	−0.12	2.02	0.01
Average			−1.43		0.11			−0.16		0.00
Standard deviation			0.61		0.09			0.04		0.02

The average and standard deviations of the difference between the MM and QM values (MM-QM) for interaction energies and the distances for M2 are also presented pictorially in Figure S2 of the SI file.

Full Sugar.

Parameters obtained from the model compound M2 were then transferred to the full sugar derivatives to model α/β-N-acetylglucosamines (referred to as AGLCNA/BGLCNA) and α/β-N-acetyl galactosamines (referred to as AGALNA/BGALNA), in which the N-acetyl amine moiety is attached to the C2 carbon of the hexopyranose ring. To examine the transferability of the dihedral parameters obtained from M2 to the full sugar, 1D potential energy scans of C-N-C2-C1 dihedral were conducted for each N-acetylamine derivative (AGLCNA, BGLCNA, AGALNA and BGALNA) at 15˚ interval from 0˚ to 345˚. During both the QM and MM scan, to avoid intramolecular hydrogen bonding between terminal N-acetyl group and the hydroxyl group at C1 carbon atom, O5-C1-O1-HO1 dihedral was constrained to 60˚.

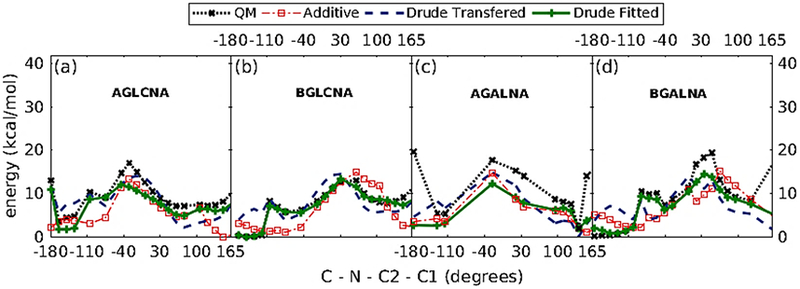
The transferred parameters failed to reproduce the low energy region of the QM profile (Figure 11). Therefore, the refinement of C-N-C2-C1 dihedral was warranted. The least square fitting protocol was applied by targeting MP2/6-31G*//RIMP2/cc-pVTZ QM energies with the dihedral parameter phase angles restricted to either 0˚ or 180˚. Energy surfaces were offset to zero at the lowest energy conformation and the conformations with relative QM energies > 12 kcal/mol were excluded during the fitting. The refined dihedral parameters obtained from the least square fitting protocol were able to reproduce the low energy profile for both α- and β- anomers of N-acetylamine derivative (Figure 11).

Figure 11.

1D dihedral potential energy scans about C-N-C2-C1 dihedrals for α-/β- N-acetyl-D-glucosamine (a and b), and N-acetyl-D-galactosamine (c and d).

To validate the compatibility of electrostatic and LJ parameters, the parameters were examined against the N-acetylamine derivative-water pair interaction energies for three different solute-water conformations (Figure 12) for all the acetyl-amine sugars, which probe the charges on C1 and C2 atoms of the carbohydrate ring. The statistical summary of the interaction energies and minimum distances for all the systems is presented in Table 8.

Figure 12.

Water pair interaction geometries with N-acetylamines (α-/β- GlcNAc and α-/β- GalNAc). Interaction (a) has the C1-H1 vector collinear with the water HOH angle bisector; and interaction (b) has the C2-H2 vector collinear with the water HOH angle bisector. All molecular graphics were prepared with VMD¹⁵⁵.

Table 8.

Solute-water pair interaction energies and distances for N-acetylamine sugar derivatives.

Water Orientation	Energy (kcal/mol)					Distance (Å)
	QM	Additive		Drude		QM	Additive		Drude
		MM	MM-QM	MM	MM-QM		MM	MM-QM	MM	MM-QM
AGLCNA
a	−2.43	−3.12	−0.70	−1.84	0.59	2.32	2.59	0.27	2.64	0.32
b	−2.77	−2.23	0.54	−1.54	1.23	2.13	2.57	0.44	2.60	0.47
Average			−0.08		0.91			0.36		0.40
Standard deviation			0.87		0.46			0.12		0.11
BGLCNA
a	−2.53	−3.15	−0.62	−1.85	0.68	2.28	2.56	0.28	2.62	0.34
b	−2.42	−2.63	−0.22	−1.62	0.80	2.28	2.61	0.33	2.64	0.36
Average			−0.42		0.74			0.30		0.35
Standard deviation			0.29		0.09			0.04		0.02
AGALNA
a	0.75	0.88	0.13	1.33	0.58	3.00	3.00	0.00	3.00	0.00
b	−1.81	−2.29	−0.48	−2.01	−0.20	2.34	2.61	0.27	2.60	0.26
Average			−0.18		0.19			0.14		0.13
Standard deviation			0.43		0.55			0.19		0.18
BGALNA
a	−2.10	−3.17	−1.08	−1.91	0.19	2.36	2.58	0.22	2.64	0.28
b	−2.05	−2.62	−0.57	−1.80	0.24	2.29	2.60	0.31	2.64	0.35
Average			−0.82		0.22			0.26		0.31
Standard deviation			0.36		0.03			0.07		0.05

The average and standard deviations of the difference between the MM and QM values (MM-QM) for interaction energies and the distances for AGLCNA, BGLCNA, AGALNA and BGALNA are also presented pictorially in Figure S4 of the SI file.

Crystal Simulation.

A CSD search yielded three crystal structures ACGLUA11 (compound name: N-acetyl-α-D-glucosamine, R factor: 0.0237), AGALAM10 (compound name: N-acetyl-α-D-galactosamine, R factor: 0.04) and NACMAN10 (compound name: N-acetyl-β-D-mannosamine monohydrate, R factor: 0.07). The ACGLUA11 crystal structure consists of two molecules of α-GlcNAc in the unit cell; the AGALAM10 crystal structure consists of two molecules of α-GalNAc in the unit cell; and NACMAN10 crystal structure consists of four molecules of β-ManNAc and four water molecules in the unit cell. MD simulations were performed on each crystal supercell (2 X 2 X 2-unit cells) constructed from corresponding crystal structures in the NPT ensemble with both additive and Drude polarizable force fields. The results comparing the intramolecular geometrical descriptors (bond lengths, angles and dihedrals) retrieved from additive and Drude polarizable simulations for all the three crystals are tabulated in Table 9. The intramolecular geometrical descriptors are well reproduced by the developed force-field parameters. The average errors in the bonds and angles were found to be 0.02, 0.64˚; 0.02, 0.66˚; and 0.01, 0.42˚ for the three crystals ACGLUA11, AGALAM10 and NACMAN10, respectively. The average errors in dihedrals are 2.0˚, −4.9˚ and −15.6˚ for the three crystals ACGLUA11, AGALAM10 and NACMAN10, respectively. The overall results from crystal simulations are comparable to the additive simulations. Unit cell geometries were consistent with the experimental values, while unit cell volumes were overestimated by 3.42%, 4.29% and 5.73% for the three crystals ACGLUA11, AGALAM10 and NACMAN10, respectively (Table 10).

Table 9.

Crystalline intramolecular geometries for α-GlcNAc, α-GalNAc, β-ManNAc crystals. Bond lengths are in Å, while valance angles and dihedral angles are in degree.

	CRYS	MDadd	MDdrude	MDadd – CRYS (%err)	MDdrude – CRYS (%err)
ACGLUA11 (N-acetyl-α-D-glucosamine)
C1-C2	1.534	1.523	1.557	−0.01 (0.00)	0.02 (0.00)
C2-C3	1.53	1.512	1.548	−0.02 (0.00)	0.02 (0.00)
C2-N	1.457	1.463	1.469	0.01 (0.00)	0.01 (0.00)
C-CT	1.508	1.502	1.523	−0.01 (0.00)	0.02 (0.00)
C-O	1.235	1.225	1.259	−0.01 (0.00)	0.02 (0.00)
C1-C2-N	111.055	113.41	114.732	2.36 (−0.03)	3.68 (−0.01)
C3-C2-N	110.338	111.7	114.007	1.36 (−0.01)	3.67 (−0.01)
C1-C2-C3	110.075	110.686	109.231	0.61 (−0.04)	−0.84 (−0.02)
C2-N-C3	35.802	34.781	33.976	−1.02 (−0.01)	−1.83 (−0.01)
N-C-CT	116.011	116.455	121.857	0.44 (−0.02)	5.85 (−0.01)
N-C-O	123.056	123.093	124.496	0.04 (−0.02)	1.44 (−0.01)
O-C-CT	120.931	120.247	113.452	−0.68 (−0.02)	−7.48 (−0.01)
C1-C2-N-C	140.89	124.569	140.417	−16.32 (−0.52)	−0.47 (−0.04)
C3-C2-N-C	−96.769	−109.356	−92.367	−12.59 (−0.56)	4.4 (−0.06)
AGALAM10 (N-acetyl-α-D-galactosamine)
C1-C2	1.52	1.525	1.552	0.01 (0.00)	0.03 (0.00)
C2-C3	1.529	1.519	1.549	−0.01 (0.00)	0.02 (0.00)
C2-N	1.454	1.46	1.463	0.01 (0.00)	0.01 (0.00)
C-CT	1.503	1.505	1.525	0 (0.00)	0.02 (0.00)
C-O	1.239	1.227	1.259	−0.01 (0.00)	0.02 (0.00)
C1-C2-N	111.776	113.371	115.99	1.59 (−0.06)	4.21 (−0.01)
C3-C2-N	110.094	111.953	114.331	1.86 (−0.05)	4.24 (−0.02)
C1-C2-C3	110.222	110.377	108.63	0.16 (−0.04)	−1.59 (−0.02)
C2-N-C3	35.962	34.794	33.897	−1.17 (−0.02)	−2.07 (−0.01)
N-C-CT	116.003	116.012	121.261	0.01 (−0.02)	5.26 (−0.01)
N-C-O	123.923	122.74	124.385	−1.18 (−0.02)	0.46 (−0.02)
O-C-CT	120.063	121.036	114.165	0.97 (−0.03)	−5.9 (−0.01)
C1-C2-N-C	81.588	76.039	74.151	−5.55 (−0.23)	−7.44 (−0.08)
C3-C2-N-C	−155.558	−158.119	−157.993	−2.56 (−0.26)	−2.43 (−0.07)
NACMAN10 (N-acetyl-β-D-mannosamine monohydrate)
C1-C2	1.537	1.514	1.547	−0.02 (0.00)	0.01 (0.00)
C2-C3	1.537	1.519	1.548	−0.02 (0.00)	0.01 (0.00)
C2-N	1.459	1.465	1.468	0.01 (0.00)	0.01 (0.00)
C-CT	1.503	1.505	1.524	0 (0.00)	0.02 (0.00)
C-O	1.248	1.228	1.26	−0.02 (0.00)	0.01 (0.00)
C1-C2-N	110.03	112.903	114.727	2.87 (−0.02)	4.7 (−0.01)
C3-C2-N	114.082	114.222	115.817	0.14 (−0.02)	1.74 (−0.01)
C1-C2-C3	107.223	107.351	104.809	0.13 (−0.05)	−2.41 (−0.01)
C2-N-C3	33.921	33.565	33.049	−0.36 (−0.01)	−0.87 (−0.01)
N-C-CT	116.757	116.153	121.437	−0.6 (−0.01)	4.68 (−0.01)
N-C-O	122.048	123.043	124.24	0.99 (−0.01)	2.19 (−0.02)
O-C-CT	121.194	120.591	114.121	−0.6 (−0.01)	−7.07 (−0.01)
C1-C2-N-C	−126.826	−130.526	−141.428	−3.7 (−0.11)	−14.6 (−0.03)
C3-C2-N-C	112.635	106.304	96.048	−6.33 (−0.18)	−16.59 (−0.03)

^addadditive force field,

drude: Drude polarizable force field parameters.

Table 10.

Crystalline unit cell geometries and volumes

carbohydrate	Crystal ID		A(Å)	%error	B(Å)	%error	C(Å)	%error	Volume (Å)3	%error
N-acetyl-α-D-glucosamine	ACGLUA11	Crystal	11.57		4.85		9.74		488.19
		Additive	11.66	0.75	4.87	0.40	10.06	3.27	508.38	4.14
		Drude	11.88	2.61	4.91	1.28	9.66	−0.77	504.89	3.42
N-acetyl-α-D-galactosamine	AGALAM10	Crystal	9.16		6.32		9.21		507.30
		Additive	9.88	7.82	5.78	−8.54	9.73	5.65	527.84	4.05
		Drude	9.46	3.23	6.20	−1.84	9.45	2.58	529.06	4.29
N-acetyl-β-D-mannosamine monohydrate	NACMAN10	Crystal	7.56		7.73		18.61		1088.23
		Additive	7.70	1.85	7.75	0.20	19.01	2.17	1134.75	4.27
		Drude	7.71	1.93	7.57	−2.15	19.73	6.01	1150.57	5.73

II. Application of parameters to example systems.

Glycosaminoglycans (GAGS), extracellular polysaccharides play vital roles in various physiological¹⁵⁷ and pathophysiological^157-158 functions. Most of the GAGs are comprised of repetitive units of uronic acid ( D-glucuronic acids (AGLCA/BGLCA) or L-iduronic acids ( AIDOA/BIDOA)) and amino sugars ( D-glucosamine (AGLCNA/BGLCNA) or D-galactosamine (AGALNA/BGALNA)). Based on the chemical structures and biological activities, GAGs are subdivided into following groups: chondroitin sulfate (CS), heparin sulfate (HS), dermatan sulfate (DS), keratan sulfate (KS), heparin and hyaluronan. Sulfated GAGs constitute a major part of proteoglycans, which are multifaceted macromolecules that are involved in diverse cellular processes¹⁵⁹, such as structural components of the extracellular cellular environment; regulatory component of cell signaling pathways by interacting with chemokines¹⁶⁰, cytokines¹⁶¹, growth factors¹⁶² and proteases¹⁶³; immunomodulators in acute inflammatory responses¹⁵⁹.

Hyaluronan is the only unsulfated subtype of the GAGs and is elegantly discussed as a key immune modulator in several reviews^164-166. To demonstrate the utility of the developed Drude polarizable force field parameters, MD simulations were performed on the linear carbohydrate polymer hyaluronan system (CN6, PDB ID: 2KQO¹⁶⁷). The covalently conjugated carbohydrate system consists of three repeating units of β-N-acetyl galactosamine and β-D-glucuronate, as represented in Figure 13(a). 60 ns simulations were run using the additive and the polarizable force fields. Complete details of the simulation setup have been described in the SI file.

Figure 13.

Conformational properties of the glycosidic linkages in unsulfated chondroitin (CN6). Figure (a) shows the crystal structure (PDB ID: 2KQO) of unsulfated chondroitin demonstrating β-D-glucuronate (1→3) β-N-acetyl galactosamines linkage and β-N-acetyl galactosamines (1→4) β-D-glucuronate linkage. The BGLCA and BGALNA units are represented as U and N, respectively. Boltzmann-inverted probability distribution of β (1→3)-glycosidic linkage (ϕ = O5(U)-C1(U)-O3(N)–C3(N) and ψ = C1(U)-O3(N)–C3(N)-C4(N)) is shown in Figure (b, c, d) and (e, f, g) for additive and Drude, respectively.

Glycosidic torsion analysis.

The 60 ns simulation trajectories obtained from additive and Drude polarizable simulations were used to calculate the ϕ/ψ torsions about the β (1→3) [(ϕ = O5(U)-C1(U)-O3(N)–C3(N) and ψ= C1(U)-O3(N)–C3(N)-C4(N)]; and β (1→4) ) [ϕ = O5(N)-C1(N)-O4(U)–C4(U) and ψ= C1(N)-O4(U)–C4(U)-C5(U)] linkages, where U and N represent BGLCA (β-D-glucuronate) and BGALNA (β-N-acetyl galactosamine), respectively. 2D plots of the relative free energies, obtained from the Boltzmann-inverted probability distribution of β (1→3) and β (1→4)-glycosidic linkage dihedrals are presented in Figures 13 and 14. The CN6 glycosidic torsion angles from additive and Drude simulations are consistent with the average torsions obtained from the NMR study and are reported in Table 11. The global free energy minima coincide well with the average values of ϕ/ψ obtained from model structures. In comparison to additive simulation, the glycosidic linkage dihedrals extracted from Drude simulation trajectory showed enhanced conformational flexibility. The conformational flexibility of the glycosidic linkages governs the dynamics of polysaccharides^168-169. In earlier studies the conformational flexibility of glycosidic linkages has been captured by using Hamiltonian replica exchange (HREX) enhanced sampling protocols¹⁷⁰. The fact that drude simulation exhibits additional flexibility enables the simulation of glycosidic linkages in oligosaccharide models. We believe that the enhanced conformational flexibility is captured by the accurate description of the interactions between the hydroxyl groups of the carbohydrates and the surrounding solvent in the Drude simulations, which in turn influences the conformational behavior of polysaccharides. The inherent flexibility and ring puckering of the carbohydrate ring is also found to be important in xylose or heparin and their derivatives^171-172. In Figure S5 of the SI file we plot the Mercator plots obtained from the additive and drude simulations. The distribution of the Cremer-Pople puckering parameters¹⁷³ highlights the higher ring flexibility in the drude simulations. The drude simulation accesses more conformational states, especially the boat and skew forms when compared to the additive simulations.

Figure 14.

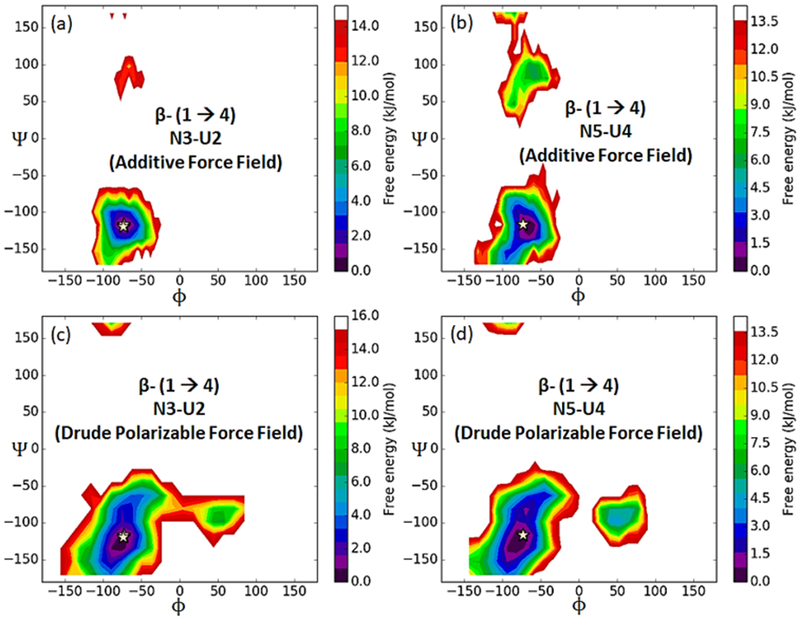
Boltzmann-inverted probability distribution of β (1→4)-glycosidic linkage (ϕ = O5(N)-C1(N)-O4(U)–C4(U) and ψ = C1(N)-O4(U)–C4(U)-C5(U)) in unsulfated chondroitin (CN6) is shown for additive (a and b) and Drude (c and d) simulations, respectively.

Table 11.

Average glycosidic torsion angles in the ensemble of CN6 conformers.

	Torsion	B (1→3)			B (1→4)
		U2-N1	U4-N3	U6-N5	N3-U2	N5-U4
CN6 NMRa	ϕ	−73 (2)	−73 (0)	−72 (0)	−73(0)	−73 (0)
	Ψ	108 (8)	107 (0)	109 (0)	−118 (1)	−116 (0)
Additive	ϕ	−75.8 (15.1)	−74.9 (14.2)	−76.9 (14.8)	−73.3 (13.4)	−72.9 (16.0)
	Ψ	96.7 (19.6)	96.6 (20.2)	94.9 (19.9)	−115.4 (27.1)	−102.5 (69.3)
Drude	ϕ	−83.5 (26.4)	−83.1(23.9)	−83.8 (24.7)	−72.5 (28.6)	−67.3 (40.0)
	Ψ	109.7 (24.1)	111.7 (23.4)	110.3 (25.9)	−114.9 (35.9)	−110.7 (38.2)

Torsion angles are given in degrees and standard deviations are given in bracket.

^aExperimental values are taken from Sattelle et. el.¹⁶⁷.

³J_{HN, H2} coupling constant calculation.

In addition to the glycosidic dihedrals analysis, the ³J_{HN, H2} coupling constants were evaluated for both additive and Drude simulation trajectories. CN6 contains three β-GlcNAc residues (N1, N3 and N5), allowing for the calculation of three vicinal ³J_HNH2 coupling constant from H-N-C2-H2 dihedrals using Karplus equations^{143, 174-175} (6) and (7). The values for the same have been tabulated in Table 12.

Table 12.

Comparison of ³J_{HN, H2} coupling constant values (in Hz) for H-N-C2-H2 dihedrals from simulation trajectories of unsulfated chondroitin NMR structure, using additive and Drude polarizable force fields.

Ring	Experimenta	Additive		Drude
		3JHN, H2 (from Eq. 6)	3JHN, H2 (from Eq. 7)	3JHN, H2 (from Eq. 6)	3JHN, H2 (from Eq. 7)
N1	8.98	8.71 (1.11)	7.76 (1.29)	9.17 (2.06)	8.94 (2.23)
N3	9.75	10.14 (1.98)	10.16 (2.02)	9.24 (2.07)	9.00 (2.26)
N5	n/d	8.65 (0.93)	7.67 (1.04)	9.04 (1.88)	8.65 (2.13)

Standard deviations are given in bracket.

^aExperimental values are taken from Sattelle et. al.¹⁶⁷.

$${}^3{J}_{{\mathrm{HNH}}_2}=9.60{\cos }^2\theta -1.51\cos \theta +0.99$$ (6)

$${}^3{J}_{{\mathrm{HNH}}_2}=9.45{\cos }^2\theta -2.08\cos \theta +0.63$$ (7)

The ³J_{HN, H2} coupling values are consistent with the observed experimental NMR data (Table 12). The mean ³J_{HN, H2} coupling values, for all the three β-GlcNAc residues (N1, N3 and N5), were evaluated as 8.71 (8.98), 10.14 (9.75) and 8.65 (n/d) from additive simulation while the same from Dude simulations is found to be 9.17 (8.98), 9.24 (9.75) and 9.04 (n/d). The experimental NMR J coupling constant values are given in parentheses. From the population analysis, it is observed that β-GlcNAc either occupied the cis or trans (trans⁺/trans^-) configuration, as illustrated in Table 13. In the additive simulation, the H-N-C2-H2 dihedral was found to sample the cis conformation for N1 (Figure S6), trans conformation for N3 (Figure S7) and the cis conformation for N5 (Figure S8). In the Drude simulation, it was observed that the H-N-C2-H2 dihedral sampled both the cis and trans conformations for N1 (Figure S6), N3 (Figure S7) and N5 (Figure S8). The conformational preferences were found to be dependent on both intra-residue and inter-residue hydrogen bonding.

Table 13.

Conformational population of H-N-C2-H2 dihedrals from simulation trajectories of unsulfated chondroitin NMR structure, using additive and Drude polarizable force fields.

Ring	Additive (% population)		Drude (% population)
	cis	trans	cis	trans
N1	90.38	9.49	22.75	75.35
N3	0.02	99.03	24.72	73.70
N5	93.74	6.20	39.15	59.84

From the additive simulation, we observe that for the first β-GlcNAc residue (N1) the absence of H-bonding interactions causes the H-N-C2-H2 dihedral to predominantly sample the cis conformation (Figure S6). In the Drude simulation, the formation of the inter-molecular H-bond (O(N1)…HO2(U2)) stabilized the trans conformation while the weak intra-molecular H-bond (O(N1)…HO1(N1)) stabilized the cis conformation (Figure S6).

For the central β-GlcNAc residue (N3) in additive simulation, we observe two significant inter-molecular H-bond interactions (O(N3)…HO2(U4) and HN(N3)…O61/O62(U2)), which facilitate the stabilization of the trans conformation. In the Drude simulation, these two inter-molecular H-bonds also favor the trans-conformation, as the absence of these interactions results in the dihedral adopting a cis conformation (Figure S7). For the terminal β-GlcNAc residue (N5) in the additive simulation, the absence of the inter-molecular H-bond interactions (O(N5)…HO2(U6) and HN(N5)…O61/O62(U4)), results in cis conformation of the H-N-C2-H2 dihedral. In the Drude simulation, transient inter-molecular hydrogen bond O(N5)…HO2(U6), along with HN(N5)…O61/O62(U4)) H-bond favors trans-conformation of the H-N-C2-H2 dihedral, while the absence of these interaction results into cis-conformation (Figure S8).

Inter-residual proton-proton distance calculation.

In addition to the glycosidic dihedrals and ³J_{HN, H2} coupling constant analysis, the inter-residual proton-proton distance was calculated using additive and the Drude polarizable force field. The results were compared with the inter-residual NOEs (Nuclear Overhauser Enhancements) reported in Sattelle et. al.¹⁶⁷ work and tabulated in Table 14. In comparison to the additive simulation, the results obtained from Drude simulation are in better agreement with the NOE data. All the strong and medium signals reported from the NMR experiment are reproduced well by the MD simulations.

Table 14.

Comparison of inter-residual proton-proton distance obtained from NOEs data and simulation data, using additive and Drude polarizable force fields.

Linkage	BGALNA	BGLCA	distance range (NOE intensity)a	rb (Additive)	rb (Drude)
U2:N1 (β1→3)	HN	H-1	2.8 - 3.8 (Medium)	4.0 (0.6)	3.7 (0.8)
	H-3	H-1	1.8 - 2.7 (Strong)	2.2 (0.2)	2.2 (0.2)
N3:U2 (β1→4)	H-1	H-4	1.8 - 2.7 (Strong)	2.4 (0.2)	2.4 (0.4)
U4:N3 (β1→3)	HN	H-1	2.8 - 3.8 (Medium)	3.5 (0.7)	3.7 (0.8)
	H-3	H-1	1.8 - 2.7 (Strong)	2.3 (0.2)	2.2 (0.2)
N5:U4 (β1→4)	H-1	H-4	1.8 - 2.7 (Strong)	2.5 (0.4)	2.5 (0.5)
U6:N5 (β1→3)	HN	H-1	2.8 - 3.8 (Medium)	4.2 (0.6)	3.8 (0.8)
	H-3	H-1	1.8 - 2.7 (Strong)	2.2 (0.2)	2.2 (0.2)

Standard deviations are given in bracket.

^adistance range and NOE intensity are taken from Sattelle et. al.¹⁶⁷.

^bIntra-residual reference proton-proton distance.

Conclusion

In this work Drude polarizable force field parameters for carboxylate and N-acetyl amine carbohydrate have been developed. The developed Drude polarizable parameters are an extension of the existing Drude polarizable force field to enable the modeling of carbohydrate derivatives. The developed parameters were validated by evaluating condensed phase properties like crystal unit cell parameters and NMR J-coupling constants. Crystal simulation of carbohydrate derivatives showed a slight improvement over the additive CHARMM force field parameters; although, as reported in the previous studies^{121-122, 176}, both the force fields overestimate the crystal unit cell volumes. MD simulation of the glycosaminoglycan complex hyaluronan, using Drude polarizable parameters, showed improvement in NMR J-coupling constants values over the additive simulation. Notably, in comparison to the CHARMM additive force field, the Drude model showed more conformational flexibility as depicted from ϕ/ψ distributions corresponding to the β(1→3) and β(1→4) linkages obtained from the MD simulations. Thus, the developed Drude polarizable force field parameters for carboxylate and N-acetyl amine carbohydrate derivatives can be used to model these carbohydrate derivatives to study their structural and functional properties, either alone or in conjunction with other macromolecules, including carbohydrates, nucleic acids, lipids and proteins in heterogenous systems using Drude polarizable force field parameters for carbohydrates^{86, 89, 121-122}, DNA¹¹⁹, lipids¹²³, peptides and proteins¹¹⁸.