Dynamical important residue network (DIRN): network inference via conformational change

Abstract

Motivation

Protein residue interaction network has emerged as a useful strategy to understand the complex relationship between protein structures and functions and how functions are regulated. In a residue interaction network, every residue is used to define a network node, adding noises in network post-analysis and increasing computational burden. In addition, dynamical information is often necessary in deciphering biological functions.

Results

We developed a robust and efficient protein residue interaction network method, termed dynamical important residue network, by combining both structural and dynamical information. A major departure from previous approaches is our attempt to identify important residues most important for functional regulation before a network is constructed, leading to a much simpler network with the important residues as its nodes. The important residues are identified by monitoring structural data from ensemble molecular dynamics simulations of proteins in different functional states. Our tests show that the new method performs well with overall higher sensitivity than existing approaches in identifying important residues and interactions in tested proteins, so it can be used in studies of protein functions to provide useful hypotheses in identifying key residues and interactions.

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

Protein structure and biological activity are determined by its complex inter-residue interactions (Di Paola et al., 2013). Residue interaction network is a class of computational methods intended to tackle the high dimensionality issue in analyzing inter-residue interactions and have been used to gain interesting new insights in many applications (Albert et al., 2000; Assenov et al., 2008). Often times, these methods can identify important residues that play key roles in problems such as protein folding, allosteric pathway and enzyme catalysis (Del Sol et al., 2007; Dokholyan et al., 2002; Soundararajan et al., 2010; Suel et al., 2003). They can also be used to identify key residues on signaling or allosteric pathways in a range of problems (Chen, 2008; Chen and Luo, 2007; Guo et al., 2017; Jinmai et al., 2016; Li and Chen, 2018; Liu et al., 2017; Rahman et al., 2016; Wang et al., 2016; Yang et al., 2016; Ye et al., 2017; Zhang et al., 2017).

In analyzing protein structures with Interaction Network (IN) (Amitai et al., 2004) methods, every residue is used to define a network node. If all-atom structures are used, computation of interactions between nodes requires going over all pairs of atoms between any two nodes involved. This can be computationally demanding for complex molecular systems. That is why many variants such as Protein Contact Network (PCN) (Di Paola et al., 2013) only pick Cα atoms in the construction of the network to reduce the computational burden in setting up a residue interaction network (Di Paola et al., 2013). Another issue is that many residues/nodes play structural roles and are less important for regulation/function. When considering all residues in the interaction network, nodes that are of little importance for function are included in the network, adding noises in post-analysis while increasing the computational burden. Furthermore, the use of all residues requires us to develop post-analysis methods to remove structural residues, such as filtering by degree, cluster size or betweenness (Di Paola et al., 2013).

Another limitation of IN methods, in general, is that apparently network or structural alone is often not enough in deciphering biological functions, because there is no strict corresponding relationship between structures and functions (Di Paola et al., 2013). This is why Dynamic Cross-Correlation Network (DCN) (Sethi et al., 2009) was introduced that incorporates dynamical/fluctuation correlational information into the network analysis. DCN improves over IN in that dynamical information is elegantly incorporated in the network analysis. However, practical applications show that fluctuation correlation is very hard to converge in molecular dynamics (MD) simulations (Hospital et al., 2015). Thus, it is often the case that the dynamical network is trajectory dependent or simulation time dependent, leading to inconclusive statements.

In this development, we explored a different strategy to incorporate protein dynamics information into the residue interaction network analysis. It is well known that certain residues play important roles for structural and/or functional purposes, but finding which residues are for which purposes is not an easy task by analyzing protein structures alone. This is where MD simulations may provide the valuable additional information as proteins are flexible molecules that undergo both conformational fluctuations and conformational changes due to their functional interactions with other proteins, nucleic acids or ligand molecules. These changes can be described by internal coordinates, or torsional changes in both side chains and/or the main chain. Tracing the changes in torsion angles, or related secondary structures and NMR properties, in MD simulations thus offer a possibility to identify important residues responsible for the conformational changes due to functional interactions. Once we zoom in on the important residues, residue interaction networks can be dramatically simplified by constructing networks using these important residues only. This leads to much reduced noise in subsequent network analysis, improving predictability.

Based on the above reasoning, we developed a robust and efficient residue interaction network method combining both structural and dynamical information. We tested the new method on three non-trivial proteins with 282–518 residues, each with structures and MD trajectories of multiple complexes bound to different ligands to probe receptor conformational changes extensively. The validation shows that most important residues and their interactions as reported in the literature to be functionally importance in experiment which can be identified by the new method.

2 Materials and methods

2.1 Overview of the method

Dynamical important residue network (DIRN) is a residue interaction network approach based on MD-related information as input. This analysis facilitates the identification of important residues that are changed noticeably upon binding to different partners. Inter-residue interactions are then analyzed among important residues and a residue interaction network can be constructed with only important residues as nodes and their stable interactions as edges. Specifically, there are following steps in the algorithm.

1. Conduct Assisted Model Building with Energy Refinement (AMBER) MD simulations (Abdul-Ridha, 2014) of a target protein in different conditions. Here different conditions could mean that the protein is associated with different ligands, in active/inactive states and simulated in different temperatures or salt concentrations. MD simulations for each condition are conducted in multiple trajectories with different random seeds to consider the random effect intrinsic to the MD approach.

2. Compute structural data and NMR observables for each residue frame-by-frame using MDTraj (McGibbon et al., 2015). The structural data include main-chain dihedral angles (Dih), main-chain omega angles (Omega), angles of three consecutive main-chain Carbon Alpha (CA) atoms (T-ang), side-chain dihedrals (Chi1–Chi4). NMR observables include scalar coupling constants between Hydrogen-atoms and Nitrogen-atoms (HN) and CA (Jnhc), HN and CB (Jnhb), and HN and HA (Jnha). All these data types are collectively referred as structural data below.

3. Conduct pairwise alignment for each residue and each structural data type. Here pairwise alignment means compare a structural data type for the same residue in different conditions. Since multiple trajectories are used for each condition, the pairwise alignment is conducted for each pair of trajectories from the two different conditions, as discussed in detail in Section 3.1 below. This step yields an overlap rate between each pair of trajectories for each structural data of each residue to be used in later steps. Here the overlap rate ($\upsilon$) is used to characterize the degree of overlap between the two samples (frame-by-frame structural data) of interest.

4. Identify important residues that vary by a notable amount as analyzing the disjoint rates ($\mathrm{\delta }=1-\upsilon )$ of all pairs of trajectories. If$\mathrm{ }\mathrm{\delta }$ for any monitored structural data of a residue exceeds a given threshold, the residue is said to vary by a notable amount and is recorded as an important residue. It is important to minimize intrinsic noise in MD simulations at this step by using multiple trajectories in each condition. Thus, every pair of trajectories between two different conditions is analyzed and the residue is only identified as an important residue when the disjoint rate exceeds the threshold with a high frequency. The detailed procedure is elaborated in Section 3.1. This step intends to focus on the residues most responsible for the protein conformation changes upon change of conditions.

5. Performing interaction analysis among the important residues to identify stable interactions (García-García et al., 2003).

6. Build residue interaction network with important residues as nodes and stable interactions as edges (Csermely, 2008).

The flow chart of DIRN is shown in Figure 1. Apparently Steps (1), (2), (5) and (6) follow standard published protocols, so we will devote Section 3.1 to discuss the development of the algorithm at Steps (3) and (4) in more detail.

Fig. 1.

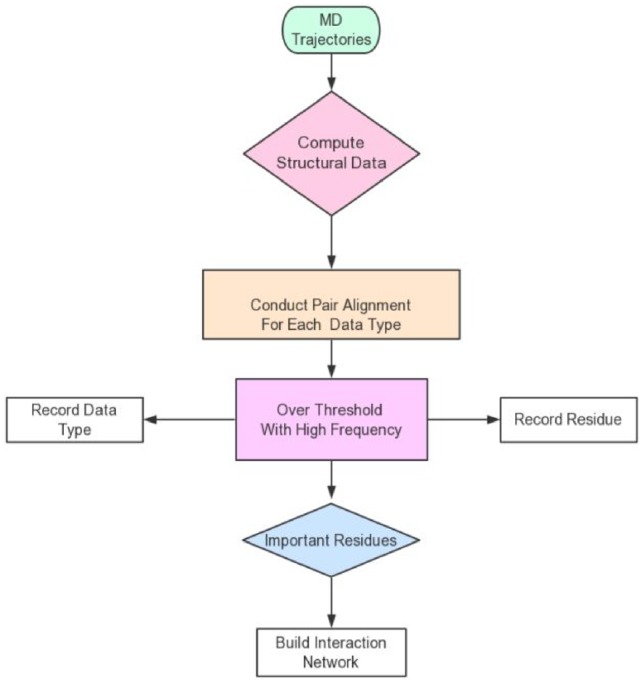
Flow chart of the DIRN approach

2.2 MD simulations

G protein-coupled receptors (GPCR), human M2 muscarinic acetylcholine receptor and Opioid receptor κ, as well as a non-GPCR protein, pyruvate kinase M2 (PKM2) binding specific ligands were performed MD simulations with AMBER16 (Abdul-Ridha, 2014). The detailed structure information and initial conditions of each system can be found in the Supplementary Method. To study the different conformational dynamics in different conditions, five independent trajectories of 160 ns each were simulated for every system listed in Supplementary Table S1. Further simulation details are shown in the Supplementary Method.

2.3 MD simulation post-analysis

MD post-analysis included two parts, structural data processing and interaction analyses. The first part was to identify important residues with notable changes by analyzing their structural data. This was handled with in-house python programs revised from MDTraj (McGibbon et al., 2015). All structural data introduced earlier, Dih, T-ang, Chi1–Chi4, Omega, Jnhc, Jnhb and Jnha were computed for each residue frame-by-frame in each trajectory. Data collection was conducted only after extensive equilibration. The datasets can be classified into three subclasses by data type. For example, Dih, T-ang, Chi1–Chi4 and Omega are radian types; and Jnhc, Jnhb and Jnha are float types. In addition, these data can further be classified into two groups—whether they depend on single or multiple residues. For example, T-ang depends on three residues.

The second part was to analyze interactions among important residues to identify the driving forces of conformational changes. Protein conformation changes can be attributed to inter-residue interactions such as hydrogen-bonding, hydrophobic and electrostatic interactions. Therefore, we identified all possible interactions by an analysis program (Li and Chen, 2018; Wang et al., 2014). Hydrophobic and electrostatic interactions were identified if the inter-residue distance is <0.6 nm. Here the distance is computed on the atomic level with all atoms considered. Hydrogen-bonding interactions were identified if donor–acceptor distance is <0.35 nm and the bond angle is larger than 2.09 radians. All three types of interactions were searched for all important residues and all MD frame so that stable interactions of each type can be defined as follows. For hydrophobic and electrostatic interactions, they are stable if their populations are higher than 75% (García-García et al., 2003). For hydrogen bonds, they are stable if their populations are higher than 30% (Chen, 2008).

2.4 Residue interaction network and shortest-path analysis

Residual-level interaction networks were constructed following published methods with identified important residues/ligands as network nodes (Csermely, 2008; Liu and Hu, 2011) (more detail information are shown in Supplementary Material).

3 Results

In the following, we first present the detailed developmental efforts of our method by focusing on Steps (3) and (4) of the algorithm. This is followed by validation of the method in one nuclear kinase PKM2 and two GPCR M2 and κOR. Finally the method is also compared with existing methods.

3.1 Algorithm development

Given the collected structural data from MD simulations, the first step in the algorithm is to conduct pair alignment for each residue and each structural data for each pair of trajectories taken from two simulation conditions. The output is the overlap rate ($\upsilon$) which characterizes the degree of overlap between the two samples (structural data) for the pair of trajectories. Given the overlap rates of all pairs of trajectories, the next step is to identify important residues by using disjoint rates ($\mathrm{\delta }\hspace{0.5em}=\hspace{0.5em}1-\upsilon )$ of all pairs of trajectories. Specifically, if the disjoint rates of a structural data of a residue in all pairs of trajectories exceed a given threshold with a high frequency, the residue is said to vary by a notable amount and is recorded as an important residue of structural significance.

Pair alignment. After MD simulations, each data type of each residue of each trajectory is saved as a dataset. Supplementary Figure S1 shows several sample datasets collected for different systems. It is clear that these data types distributed in wide ranges of values but may also cluster around a few preferred values. As MD was only used to sample conformations, its time information (or kinetic properties) is of little importance to us. Therefore, we need not consider the time series when analyzing any of the sampled data types. Thus the useful information in a typical time series for a dihedral angle as in Supplementary Figure S2A is only the 1-D dihedral angle values, shown in Supplementary Figure S2B.

To study the difference and similarity between two datasets of the same frame length (denoted as k below) from two different trajectories, the distance (i.e. unsigned difference) of each pair of data (one from each set) was first computed and stored in a distance matrix of dimension $k\times k$.

All the pairwise distances are checked against a cutoff value (Parameter I, to be optimized) so that a data value u_n in set 1 is said to overlap with a data value v_m in set 2 if their pairwise distance is less than the cutoff. The overlapped data are said to belong to an overlapping cluster, an intersection of the two sets. The overlap rate is then defined to be the ratio of the number of overlapping data and the number of total number of data, i.e. the frame length. When inspecting the overall overlap between the two sets, there can be three general situations:

1. Every data in set 1 overlaps with one and only one data in set 2. Thus, there can be a one-to-one mapping defined between set 1 and set 2. The overlapping cluster is the full set, so the overall overlap rate between the two sets is defined as k/k = 1.

2. Certain number of data (a) in set 1 does not overlap with any data in set 2, but all data in set 2 can be found to overlap with some data in set 1. Or the opposite, certain number of data (a) in set 2 does not overlap with any data in set 2, but all values in set 1 can be found to overlap with some data in set 2. The overlapping cluster is the k − a data, the overall overlap rate in both cases can be defined to be (k − a)/k.

3. Certain number (a) of data in set 1 do not overlap with any data in set 2, and certain number (b) of data in set 2 do not overlap with any data in set 1. The overlapping cluster is the min{k − a, k − b} data, the overall overlap rate is defined as min{(k − a), (k − b)}/k.

Supplementary Figure S2D shows an example of the overlapping analysis, where circle d1 represents an overlapping cluster centered at data d1 for Dih Pro198 in M2/2CU, its radius represents the cutoff value. All data for Dih Pro198 in M2/IXO that are within circle d1 are paired with d1, saved and can be later retrieved and used to compute the overlapping rate.

In the pair alignment step, we need to determine the cutoff used in the clustering analysis. A proper way to set the optimal cutoff value for clustering is to analyze the functional dependence of cluster number versus cutoff value as shown in Supplementary Figure S3. The optimal cutoff value is usually chosen at the flex point (Tan et al., 2005). Supplementary Figure S3 further shows that the optimal cutoff is not a fixed value but depends on the sampled dataset, by illustrating three different choices of picking the MD frames for clustering analysis.

After processing all structural data, we arrive at the intermediate results ($\upsilon$, overlap rate) for each residue by each structural data type of each pair of trajectories. The final results ($\mathrm{\delta }$, disjoint rate) can be calculated as $1-\upsilon$, to be used next step.

Identification of important residues. To determine whether a structural data changes noticeably we need to select a benchmark cutoff value, termed threshold. To define the threshold in a logical and rational way, we first analyzed the average disjoint rate of each structural data type for all residues and all pairs of trajectories in the same condition. The results shows the average disjoint rates for all structural data types, which suggests the average disjoint rates in the same condition are mostly <30% (i.e. mean + standard deviation, Supplementary Table S2), regardless of structural data types. Most population of the analyzed residues is centered on the disjoint rate <30% and only fewer residues get a notable change in structure (Supplementary Figs S4–S6). Therefore, if the disjoint rate of any structural data between two trajectories of different conditions is over 30%, we can say that the structural data are changed noticeably between the two trajectories. Thus, the threshold was set as 30% to identify data type that changed noticeably when comparing different pairs of trajectories from different conditions.

Another issue that we must consider in the identification of important residues is the intrinsic noise in MD simulations. It is very common that computed overlap rates and their disjoint rates depend on the specific pairs of trajectories used. Thus, when computing disjoint rates between two different conditions, we need to analyze every pair of trajectories. For example, if each system is simulated in n different trajectories (different random seeds), there are $N=n^2$ pairs of trajectories to be analyzed. If there are M disjoint rates showing a structural data type being changed noticeably, i.e. higher than the threshold, then a frequency ratio of M/N of the pairs are observed to be with significantly changed data types. If the MD simulations were deterministic, the frequency ratio would be either 100% or 0%, i.e. either changed or not with 100% certainty. However, this is not the case. To set a reasonable frequency lower bound, an initial analysis was first conducted for several pairs of systems. As each system was simulated with 5 independent trajectories, there were 25pairs of trajectories to be compared. For example, in the comparison of M2 and M2/IXO/2CU simulations, the pair alignment step leads to a total of 131 candidate residues with at least one noticeably changed structural data in at least one pairs of trajectories. A detailed distribution of these candidates is shown in Supplementary Figure S7A. It is clear that occurrence of candidate residues is not 100% clear cut among the pairs analyzed. However, the analysis shows that majority (85%) of the candidate residues were observed in over 90% of the pairs analyzed. Supplementary Figure S7B and C show the distributions for the other two comparisons, and the conclusion is the same. Therefore in this study, a residue is recorded as an important residue if at least 90% of the 25 pairs of trajectories are observed with at least one structural data changed noticeably for the residue.

Upon completion of Steps (3) and (4), we will be able to identify a list of important residues that have changed noticeably in collected MD trajectories for each protein. Their stable hydrophobic, electrostatic and hydrogen-bonding interactions are then identified as described in Section 2. Residue interaction network edges are identified for all stable interactions among all important residues. Then the shortest-path analysis was performed to identify potential signaling pathways.

3.2 Algorithm validation

3.2.1 PKM2

Important residues responsible for Serine (SER) activation in PKM2. We performed analysis of all four simulated PKM2 systems to identify important residues (Supplementary Table S3). Among these there are 36 residues at the binding site and domain A from the literature (Supplementary Table S4). Twenty-six important residues notably changed based on the MD simulations. Experiments report a total of eight key residues playing roles in activating PKM2, six of them can be identified by our method in this study (Chaneton et al., 2012). Supplementary Table S4 shows that these important residues were observed in very large changes in their side chain torsions (Chi1 and Chi2) as indicated by the high disjoint rates (≥70%$\ge 70\mathrm{\%}$). It further shows that our approach has a high sensitivity (80.00%) but a low specificity (30.77%) in identifying important residues in the PKM2 system.

Distribution of the important residues in each segment is listed in Supplementary Table S5. Supplementary Figure S8A and B shows that about half of the important residues are located in the catalytic domain (A domain). This indicates that the catalytic domain is changed most upon binding to the allosteric activator.

Residue interaction networks. Figure 2 shows the residue interaction networks constructed for the important residues identified by DIRN. The important residues are clearly clustered into left (A and C domain) and right groups (B domain) separated by the dash lines. No network connection was found between substrate OXL and any node in the left group in PKM2/OXL and PKM2/OXL/FBP, but a connection through Met 360 was found in PKM2/OXL/SER and PKM2/OXL/FBP/SER. This indicates that information cannot be transferred to OXL in PKM2/OXL with or without FBP present, while allosteric regulator SER can lead to connections from the left group to OXL through interactions among the important residues. These are consistent with the experiment report that the PKM2 can be inhibited by OXL in the presence FBP (Dombrauckas et al., 2005) while such effect can be reduced by SER (Chaneton et al., 2012).

Fig. 2.

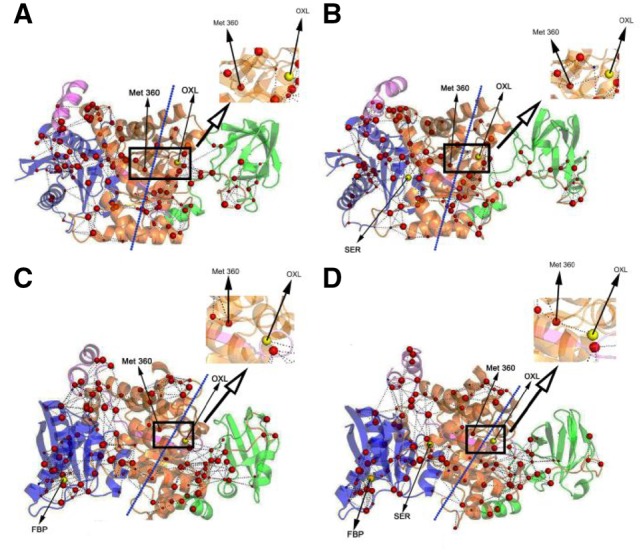
Residue interaction networks formed by important residues in PKM2 systems simulated. OXL is the substrate for PKM2, SER and FBP act as activators. All three are shown as yellow spheres. Red-colored spheres are placed at the CA atoms of important residues. Sphere size represents the disjoint rate of the represented residue. (A) PKM2/OXL. (B) PKM2/OXL/SER. (C) PKM2/OXL/FBP. (D) PKM2/OXL/FBP/SER

Supplementary Table S6 lists the 33 interactions as reported in the literatures (Chaneton et al., 2012; Dombrauckas et al., 2005; Morgan et al., 2013). Among these there are 19 key interactions, while our approach identified 17 of these to be important. Most are identified as hydrogen bonds. This shows that hydrogen-bonding interactions are the primary forces responsible for the PKM2 activation at the binding site and A domain. Comparing with the identification of important residues, our method is more sensitive in identifying key interactions among the important residues, with a true positive rate of ∼89%. The method’s specificity is also a bit better at ∼57%. This shows that additional refinement of our algorithm in identifying important residues is necessary.

It is worth pointing that multiple key residues, such as His464, Trp482, Trp515 and Arg516, which play key role and are identified in both experiment and computation (more information in Supplementary Material).

3.2.2 GPCR M2

Important residues responsible for GPCR M2 activation. We performed alignments between the inactive and each of the active states one by one to investigate the important residues responsible for its activation. Supplementary Table S8 lists the overlapping residues of three sets of about 100 important residues, believed to be the most important for the M2 activation. Among these residues, many of them, such as Tyr80, Asp103, Tyr104, Asp120, Tyr206, Tyr400, Tyr403 and Asn404, are reported frequently in experiment for they are very crucial for M2 activation in the presence of agonist (Haga et al., 2012; Kruse et al., 2013; Miao et al., 2013, 2014). There are total 20 residues analyzed in these experiments as listed in Supplementary Table S9. Among all these residues, 17 residues were identified to be essential both in the literatures and by our method. MD simulations show that most of their changes are on Chi1 or Chi2 side chain angles, with disjoint rates over 90%. Supplementary Table S9 shows that the sensitivity of the method can reach 100%, but its specificity is at 67%. The overall distribution of important residues in each segment is listed in Supplementary Table S10 and Figure S9.

Residue interaction networks. There are hundreds of interactions among all identified important residues. Here only the 22 interactions analyzed in the literatures are shown in Supplementary Table S11 (Kruse et al., 2013; Miao et al., 2014). Out of the 22 interactions, 20 are key interactions for activating M2 receptor and most of them are hydrogen-bond interactions between ligand and surrounding residues. The sensitivity and specificity of our approach in the M2 receptor analysis are 100.00 and 50.00%, respectively. This indicates that most key interactions involving the important residues can be identified by DIRN with high accuracy. The lower specificity here is consistent among all systems analyzed.

The residue interaction network analysis shows the important residues can be divided into left and right regions (Fig. 3). There is no connection between left and right regions in the network of the inactivated M2 while connections emerge in the networks of the activated states, including M2/IXO, M2.2CU and M2/IXO/2CU. In M2/IXO, there is only one bridge (Phe396–Tyr206) linking the two regions, so it is very crucial for signaling. This is consistent with the report that the Y206F mutant receptor cannot be activated by acetylcholine and has very weak functional response upon treatment with IXO (Kruse et al., 2013). In M2/2CU, there are two bridges found (Phe396–Tyr440 and Phe396–Cys439). In M2/IXO/2CU there are also two bridges (Phe396–Tyr440 and Phe396–Tyr206). Our analysis thus shows that M2/IXO/2CU and M2/2CU have very similar connections between the left to right regions. In summary for all activated systems, it is clear that Phe396 is very crucial for linking the left and right regions of the residue interaction network (Li and Chen, 2018).

Fig. 3.

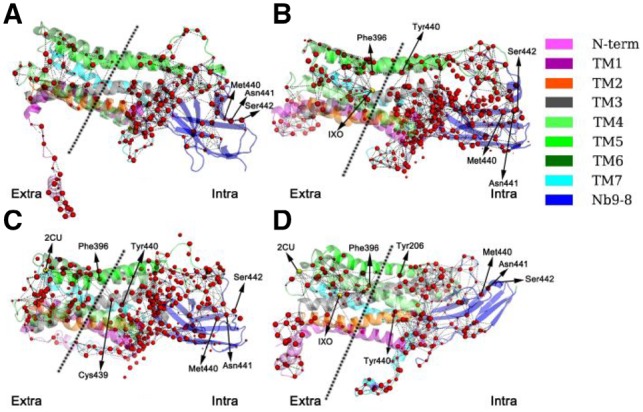
Residue interaction networks formed by identified residues in GPCR M2 systems simulated. IXO and 2CU are activators for M2 which are shown as yellow spheres. Red-colored spheres represent the CA atoms of important residues. Sphere size represents the disjoint rate of the represented residue. (A) M2. (B) M2/IXO. (C) M2/2CU. (D) M2/IXO/2CU

3.2.3 GPCR κOR

Important residues responsible for GPCR κOR signal transduction. The overlapping residues of three sets of about 100 important residues are listed in Supplementary Table S13. Previous experiments studied 11 residues thought to be important in the activation of κOR (Supplementary Table S14) (Cheng et al., 2016). Out of the 11 residues analyzed, 9 were found to be important, and 7 residues were identified to be essential in both literatures and this study (Cheng et al., 2016). Supplementary Table S14 shows that our method achieves both high sensitivity (77.78%) and high specificity (100.00%) for this receptor. Worth pointing out are Asp138, Tyr139, Trp287, Ile294 and Glu297 that play important roles in both 6′-GNTI and κOR/5′-GNTI systems, although the former is active while the latter is inactive, this indicates these residues perform significant functions in different ways to transform the receptor status (Cheng et al., 2016). The distribution of identified residues in each segment is listed in Supplementary Table S15 and shown in Supplementary Figure S10.

Residue interaction networks. All interactions analyzed in the literature are shown in Supplementary Table S16 (Cheng et al., 2016). Out of the 18 interactions, 15 were found to be important for activating κOR receptor and there are mix of hydrogen-bond, salt-bridge and hydrophobic interactions. The sensitivity and specificity of our approach in the κOR receptor analysis are both very high, at 93.33 and 66.67%, respectively. The residue interaction networks are shown in Figure 4.

Fig. 4.

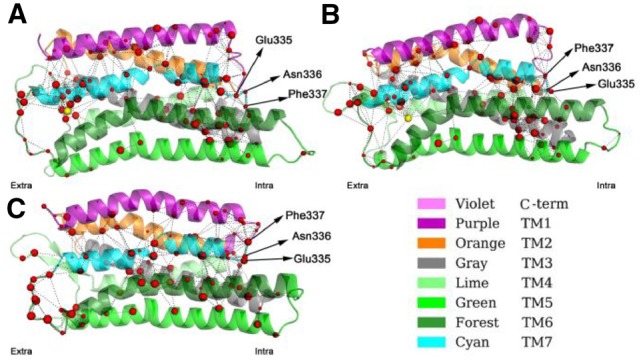
Residue interaction networks formed by important residues in GPCR κOR systems simulated. (A) κOR/5′-GNTI. (B) κOR/6′-GNTI. (C) κOR. 5′-GNTI acts as the inhibitor and 6′-GNTI acts as the activator, both shown as yellow spheres. Red-colored spheres represent CA atoms of important residues. Sphere size represents the disjoint rate of the represented residue

3.3 Comparison with other methods

In this study, we improved the protein network method by pre-selecting functionally important residues in the setup of the residue interaction network. Supplementary Figure S11 shows that there are many other residues (blue spheres) and edges involved in the networks by IN and DCN. Their network topologies are listed in Supplementary Table S18. The presence of these residues in the network is a non-trivial burden when identifying signaling pathways.

Our strategy in pre-selecting important residues with the MD-based approach clearly improves the sensitivity of the method. Supplementary Table S19 shows that DIRN has the highest sensitivity in identifying both important residues and important interactions among the three methods compared.

We also compared the allosteric pathways for the three tested proteins (Supplementary Tables S20–S22). Here we have also highlighted the important residues identified in previous experiments to be important on the pathways. It is clear that IN and DCN identify fewer such key residues on the pathways. Indeed, none of the key residues can be identified in both PKM2 and κOR.

4 Conclusion

We developed a new approach, termed DIRN, to identify important residues responsible for allostery by monitoring the conformational changes induced by ligand binding. In this approach, MD simulations were first conducted for a target protein in different conditions when bound to different ligands. Next torsional and related data were monitored for potential conformational changes. This is followed by pair alignment between different conditions to screen for important residues that are found to change significantly according to monitored structural data. Once important residues are identified, they are utilized as nodes to construct a residue interaction network to understand key signaling pathways for allostery. The new approach was validated by comparing with experimental findings and also with existing methods such as the residue interaction network and dynamical correlation network methods.

Our analysis shows that DIRN tends to yield a higher sensitivity but lower specificity than the residue interaction network and dynamical correlation network methods. Thus DIRN is more robust in screening for important residues/interactions with more true positive results, though it is also less satisfactory in finding true negative residues/interactions. After a careful analysis, we found one reason for the very low true negative rate in PKM2 to be the false positive residues identified by NMR scalar coupling constants. If we repeat the analysis without the scalar coupling constants, overall the specificity can be improved as shown in Supplementary Table S23. Specifically, the specificity increased from 30.77 to 50.00% for PKM2, without much change in the sensitivity ratios for all three systems. It is likely the use of scalar coupling constants requires different set of parameters as the torsional angles that our method heavily relies on. It is also arguable that DIRN’s tendency to predict a large portion of residues to be important may lead to its higher sensitivity. For example, there are 281 residues in GPCR κOR, about 140 of which are predicted to be important residues by DIRN (Supplementary Table S15). We will continue optimizing our approach to improve its performance. Nevertheless, the current method can serve as a useful filtering tool facilitating experimental studies by providing useful initial hypotheses in studies of protein allostery.

Funding

This work was supported by Center for HPC at Shanghai Jiao Tong University, the National Key Research and Development Program of China (2018YFC0310803 and 2017YFE0103300), the National Natural Science Foundation of China (31770771 and 31620103901), Medical Engineering Cross Fund of Shanghai Jiao Tong University (YG2017MS08) and National Institutes of Health/NIGMS (GM093040 and GM079383).

Conflict of Interest: none declared.