Abstract
Motivation
The availability of numerous ChIP-seq datasets for transcription factors (TF) has provided an unprecedented opportunity to identify all TF binding sites in genomes. However, the progress has been hindered by the lack of a highly efficient and accurate tool to find not only the target motifs, but also cooperative motifs in very big datasets.
Results
We herein present an ultrafast and accurate motif-finding algorithm, ProSampler, based on a novel numeration method and Gibbs sampler. ProSampler runs orders of magnitude faster than the fastest existing tools while often more accurately identifying motifs of both the target TFs and cooperators. Thus, ProSampler can greatly facilitate the efforts to identify the entire cis-regulatory code in genomes.
Availability and implementation
Source code and binaries are freely available for download at https://github.com/zhengchangsulab/prosampler. It was implemented in C++ and supported on Linux, macOS and MS Windows platforms.
Supplementary information
Supplementary materials are available at Bioinformatics online.
1 Introduction
Gene transcriptional regulation is mainly carried out by interactions between transcription factors (TF) and specific DNA sequences called TF binding sites (TFBSs), with a length of 6–20 base pairs (bp). Different TFBSs recognized by the same TF are highly similar and are called a motif. Identifying motifs of all TFs in a genome is a central but highly challenging task (Deplancke et al., 2016). Fortunately, datasets produced by chromatin immunoprecipitation (ChIP) followed by sequencing (ChIP-seq) (Park, 2009) and its derivatives such as MNChIP-seq (Tsankov et al., 2015) have provided an unprecedented opportunity to identify all TFBSs in genomes.
In a ChIP-seq experiment, one can obtain hundreds of thousands of binding peaks of the target TF in a tissue sample, with a length from hundreds to thousands bp (Zhang et al., 2008). Although TFBSs of the target TF are usually enriched, identification of all the TFBSs in such a large number of binding peaks has been a highly challenging task. First, the sheer volume of such a dataset dwarfs existing classic motif-finding tools that were mainly aimed at datasets of a small size (Prakash and Tompa, 2005). Consequently, in many ChIP-seq studies, only a few hundred of top-scored binding peaks were used for motif finding (Kheradpour and Kellis, 2014), which under-exploited the valuable datasets. Although faster algorithms have been developed using various algorithmic approaches (Bailey, 2011; Ettwiller et al., 2007; Grau et al., 2013; Hartmann et al., 2013; Heinz et al., 2010; Hu et al., 2010; Huggins et al., 2011; Kulakovskiy et al., 2010; Ma et al., 2012; Mason et al., 2010; Quang and Xie, 2014; Reid and Wernisch, 2011; Thomas-Chollier et al., 2012; Yao et al., 2014; Zhang et al., 2017), they are still too slow for convenient application on very big ChIP-seq datasets. Second, most of these tools are aimed to identify only the motif of the target TF (primary motif) in shortened binding peaks (Colombo and Vlassis, 2015). Nonetheless, since TFBSs of cooperative TFs tend to be closely located, forming cis-regulatory modules (CRMs), there is increasing interest in identifying motifs of cooperative TFs in addition to the primary motif in longer binding peaks with a length of typical enhancers (∼1000 bp) (Bailey and Machanick, 2012). Third, faster tools such as DREME (Bailey, 2011) are based on the discriminative motif-finding schema (Sinha, 2003) by finding overrepresented k-mers in a dataset, but they often fail to identify TFBSs with subtle degeneracy (Bailey, 2011). Fourth, most existing motif-finding tools return too many false positive motifs, making it difficult for the user to decide which ones are likely to be authentic, whereas some other tools are even unable to determine the number of motifs in a dataset, requiring the user to specify it. Finally, most current motif finding algorithms can only identify motifs with a pre-specified length, while those that are able to determine the length of motifs employ an exhaustive enumeration strategy within an interval of length, requiring large memory and running time (Bailey, 2011).
In order to circumvent these obstacles, we have developed an ultrafast and accurate motif-finding algorithm and tool named ProSampler (Profile Sampler) with the ability to automatically determine the number of motifs in a dataset and the length of each motif, using a combination of novel discriminative heuristic seeding (Bailey, 2011), Gibbs sampling (Lawrence et al., 1993) and length extension methods. When evaluated on both synthetic and real MNChIP-seq datasets, ProSampler is orders of magnitude faster than existing fastest motif-finding tools, while identifying all the implanted motifs in the synthetic datasets with the highest specificity, and more primary motifs as well as cooperative motifs in the real datasets.
2 Materials and Methods
2.1 Datasets
2.1.1 Synthetic datasets
We downloaded the known vertebrate TF binding motifs (pfmVertebrates.txt) and the background sequences (upstream1000.fa) from the JASPAR database (Mathelier et al., 2016). The pfmVertebrates.txt file contains 519 motifs with a length ranging from 4 to 21 bp. The upsteam1000.fa file contains 43 632 upstream regions of genes with a length of 1000 bp. To generate six synthetic datasets D1∼D6, we first randomly selected (500, 1000, 2000, 5000, 10 000 and 20 000) sequences from upstream1000.fa and shuffled the sequences in each dataset. Then for each dataset Di containing sequences, we randomly chose 10 motifs M1, M2, …, M10 from pfmVertebrates.txt for distinct TF families, with a length ranging from 6 to 15 bp, and implanted them at a frequency = 0.1, 0.2, …, 1.0 site/sequence, respectively, in the sequences in the dataset. Specifically, for each selected motif, we randomly chose sequences with replacement from the dataset, randomly selected a position in a sequence chosen, and substituted the subsequence starting at this position with a DNA sequence generated according to the motif’s position frequency matrix (PFM) within a Hamming Distance cut-off to the consensus string of this PFM. We recorded the substituted positions and avoided overlapping implanting. Note that with replacement sampling, we allow the ZOOPS (zero-or-one occurrence per sequence) motif distribution model. The implanted motifs and their JASPAR logos in each dataset are listed in Supplementary Table S1.
2.1.2 ChIP-seq datasets
We downloaded a total of 204 ChIP-seq datasets from Gene Expression Omnibus with accession number GSE61475 (Tsankov et al., 2015), generated using a MNase-based ChIP-seq technique from early stages of endoderm, mesoderm, ectoderm and mesendoderm tissues derived from human ES cells. Since motifs of some target TFs are not documented in the JASPAR database, therefore we excluded 99 datasets for these TFs from our analysis, resulting in a total of 105 datasets for 21 TFs with documented motifs in JASPAR. We generated three groups of datasets G1, G2 and G3 by extracting 200, 500 and 1000 bp, respectively, genomic sequence for each called binding peak in each dataset, with the summit of the binding peak being the center. We masked the repeat regions using Repeat Masker (Bedell et al., 2000) and Tandem Repeat Finder (Benson, 1999) with the default parameter settings.
2.2 Algorithms
The details of the ProSampler algorithm are described as follows and its pseudocode is given in Supplementary Figure S1.
Step 1: Generating background sequences: Given a ChIP-seq dataset, we generate a background sequence set with the same number and length of sequences using the third-order Markov chain model based on the frequencies of nucleotides in the dataset.
Step 2: Identifying significant -mers: We count all possible -mers () in both the ChIP-seq and background sequence sets and at the same time, record the two flanking -mers ( by default) of each -mer. Let and be the counts of the occurrences of a -mer in the ChIP-seq and background sequence sets, respectively. If search on both strands is desired, we combine the counts of each pair of reverse complementary -mers. We evaluate each -mer for its significance using the following two-proportion -test with the null hypothesis that its frequencies in the ChIP-seq () and background sequence ) sets are the same:
| (1) |
| (2) |
| (3) |
where
| (4) |
We consider that a k-mer is significant or subsignificant if is greater than a preset value or respectively (by default, corresponding to a -value of , and corresponding to a -value of ). Let all the significant and subsignificant -mers be the sets and , respectively. Note that is a subset of .
Step 3: Constructing preliminary motifs and their position weight matrices (PWMs): For each significant -mer we combine it with all other subsignificant -mers if their Hamming Distance to form a preliminary motif. We construct its PWM mi using the counts of the combined -mers. Let be the set of these PWMs. Notably, a -mer can be included in multiple preliminary motifs. Then we sort the preliminary motifs according to their -scores in the descending order.
Step 4: Constructing the motif similarity graph: We construct a graph using the PWM set as the nodes, and connecting two nodes mi and mj if their Sandelin–Wasserman (SW) similarity (Sandelin and Wasserman, 2004) is greater than a preset value (by default, , which is defined as
| (5) |
where mi (b, c) and mj(b, c) are the frequencies of base b in column c of motifs mi and mj, respectively.
Step 5: Gibbs sampling: Our Gibbs sampler starts by combining the currently most highly ranked (’s -score) with its neighbors in the graph to form a seed motif with redundant -mers removed. In each cycle of sampling, we randomly select a motif in , and then identify the motif from the neighbors of that are not in () with the highest SW similarity to with removed. We add to , if the resulting is the better than (replacing by ) and (the original score); we replace by in if the resulting is the better than and , where
| (6) |
where is the total count of the combined -mers in motif , the probability of base appearing at position and the probability of base in the dataset. We removed redundant -mers in after each updating. After cycles of iteration, we predict as a core motif with a length of . We remove all the nodes in and inscribed edges from the graph to create a new smaller graph. We identify the next core motifs by repeatedly applying this process to the updated graphs until the graph becomes empty or a specified number of motifs are found.
Step 6: Extending core motifs: To identify a motif longer than , for each -mer in each core motif, we pad its two flanking -mers in the genome to the corresponding ends, extending the alignment with a length of . We compare the frequencies of each nucleotide in each flanking columns starting from the closest ones to the core motif, with that in the dataset using the two-proportion -test. We pad a flanking column to the core motifs if at least one of the column’s nucleotides has a significantly different frequency from that in the dataset (by default, , corresponding to -value ). We stop the extension in a direction once an insignificant column is encountered. We rank and output the motifs according to the order they are found, i.e. the rank of the z-value of the initial significant k-mer, which largely reflects their statistically significance.
2.3 Evaluation of the programs
For each of predicted motifs, we compared it with motifs in JASPAR (Mathelier et al., 2016) using TOMTOM with Euclidean distance being the metric (Gupta et al., 2007), and considered the best hit as a match if the -value . If one of motifs returned by a program matches the known motif of the target TF in the JARPAR database, we consider that the primary motif is found by the program. To quantify the performance of the programs for identifying motif lengths, we computed three metrics: performance coefficient (PC), positive predictive value (PPV) and sensitivity (SN) (Ikebata and Yoshida, 2015), based on the overlap between the predicted motif and the hit, defined as follows,
| (7) |
| (8) |
| (9) |
where N is the number of predicted motifs with a hit in JASPAR.
We present the results as mean ± standard error when appropriate, and compared the result of ProSampler with those of other programs evaluated using Wilcoxon rank sum test or two-tailed t-test as indicated in the text.
3 Results
3.1 Comparison of the programs on synthetic datasets
We first compared ProSampler with five state-of-the-art motif-finding tools, i.e. BioProspector (Liu et al., 2001), Homer (Heinz et al., 2010), DREME (Bailey, 2011), XXmotif (Hartmann et al., 2013) and motifRG (Yao et al., 2014) for their speed and ability to find at least a subset of the binding sites of 10 implanted JASPAR motifs (Supplementary Table S1) with different lengths (8–15 bp) in six synthesized datasets, i.e. D1∼D6, containing various number of sequences (D1: 500, D2: 1000, D3: 2000, D4: 5000, D5: 10 000 or D6: 20 000) with a length of 1000 bp (Supplementary Material). Dimont (Grau et al., 2013) was not included in this evaluation as it requires a ChIP-seq quality score of the binding peaks. The 10 motifs were implanted in each dataset at different occurrence frequencies ranging from 0.1 to 1.0 site/sequence to mimic a broad spectrum of cooperation between the ChIP-ed TF and its cooperators. As BioProspector needs the user to specify the number of motifs to be found in a dataset, we let it output 150 motifs in each dataset. For the five other programs that are able to automatically determine the number of motifs to be output in a dataset, we let them output all the motifs they found. As expected, the running time of ProSampler scaled linearly to the size of the datasets, and it was orders of magnitude faster than the second fastest program Homer (Fig. 1A). Remarkably, ProSampler identified all the 10 implanted motifs in datasets D1∼D5 by its top 10 motifs (Table 1 and Fig. 1B) while returning the smallest number (65) of predicted motifs, achieving the lowest false discovery rate (FDR) of 0.08 among all the programs (Table 1). Moreover, the 60 motifs predicted by ProSampler match more significantly [P < 0.01, Wilcoxon rank sum test for -log (q-value)] the implanted ones by TOMTOM than those predicted by all the other five programs (Fig. 1D, see Supplementary Table S1 for the motif logos).
Fig. 1.
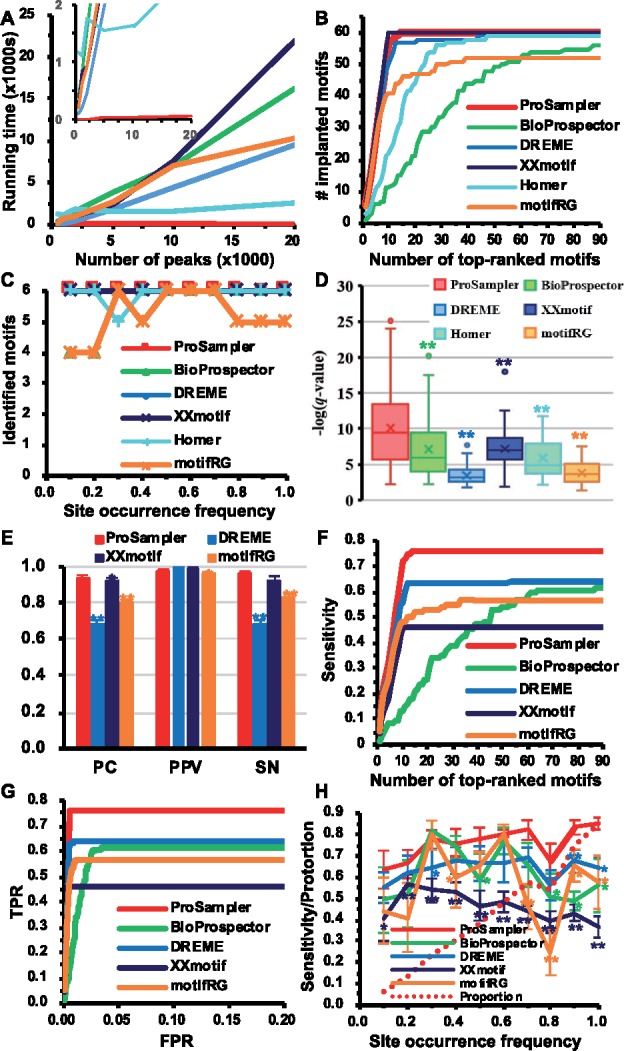
Comparison of the performance of the programs on the six synthetic datasets D1∼D6 with various sizes. (A) Running time of the six programs as a function of the number of sequences in the datasets. The inset is a blow-up view with the running time below 2000 s. (B) Number of recovered implanted motifs as a function of the number of top-ranked motifs predicted by the programs in the six datasets. (C) Number of recovered implanted motifs as a function of the occurrence frequency of the implanted binding sites in the six datasets. (D) Box-plot of the q-values of predicted motifs of the programs, matching the implanted motifs in the datasets. (E) Performance of the programs for predicting the lengths of implanted motifs in the datasets. (F) Average sensitivity of the programs for predicting the binding sites of implanted motifs as a function of the number of top-ranked motifs predicted by the programs in the six datasets. (G) Average ROC curves of the programs for predicting the binding sites of implanted motifs in the six datasets. (H) Average sensitivity of the programs for predicting the implanted binding sites as a function of their occurrence frequency in the six datasets. The dotted line is the proportion of sequences found by ProSampler to contain the implanted binding sites. Labels *P < 0.05 and **P < 0.01 are significant levels between the result of the labeled program and that of ProSampler
Table 1.
Prediction of motifs by the six programs in the synthetic datasets
| Datasets | D1 (500a) |
D2 (1000) |
D3 (2000) |
D4 (5000) |
D5 (10 000) |
D6 (20 000) |
Total true motifs found | Total false motifs found | SN | PPV | PC | FDR | FNR | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| True motifs | Discovered motifs | True motifs | Discovered motifs | True motifs | Discovered motifs | True motifs | Discovered motifs | True motifs | Discovered motifs | True motifs | Discovered motifs | ||||||||
| ProSampler | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 15 | 60 | 5 | 1.00 | 0.92 | 0.92 | 0.08 | 0.00 |
| BioProspector | 10 | 150 | 10 | 150 | 9 | 150 | 9 | 150 | 8 | 150 | 10 | 150 | 56 | 844 | 0.93 | 0.06 | 0.06 | 0.94 | 0.07 |
| DREME | 10 | 14 | 10 | 20 | 10 | 23 | 10 | 36 | 10 | 48 | 10 | 58 | 60 | 139 | 1.00 | 0.30 | 0.30 | 0.70 | 0.00 |
| XXmotif | 10 | 17 | 10 | 10 | 10 | 11 | 10 | 11 | 10 | 12 | 10 | 11 | 60 | 12 | 1.00 | 0.83 | 0.83 | 0.17 | 0.00 |
| Homer | 9 | 300 | 10 | 300 | 10 | 300 | 10 | 300 | 10 | 300 | 10 | 300 | 59 | 1741 | 0.98 | 0.03 | 0.03 | 0.97 | 0.02 |
| motifRG | 10 | 40 | 8 | 95 | 10 | 91 | 8 | 133 | 7 | 196 | 9 | 150 | 52 | 653 | 0.87 | 0.07 | 0.07 | 0.93 | 0.13 |
Number of sequences in the dataset.
We also compared ProSampler with three other programs DREME, motifRG and XXmotif for their ability to identify the length of implanted motifs in the synthetic datasets. BioProspector and Homer were not included in this comparison as both are unable to automatically determine the lengths of motifs. As shown in Figure 1E, ProSampler achieved the highest PC (0.94) and SN (0.96), both are significantly (P < 0.05 or P < 0.01, t-test) higher than those obtained by the other three programs except XXmotif for SN, for which the difference is not significant. ProSampler had comparable PPV (0.97) to the best PPV performer DREME (1.0), although ProSampler predicted the more implanted motifs.
We have so far compared the accuracy of the tools at the motif level by comparing the returned motifs to the implanted ones. However, an ideal motif finder should be able to identify all the binding sites of all motifs in a dataset, not just submotifs containing a subset of the binding sites of the motifs. To compare ProSampler with the programs for such capability, we computed the sensitivity of each program for recovering the binding sites of the implanted motifs by its top-ranked motifs in the six datasets. Homer was not included in this evaluation as it only returns the PWMs rather than the binding sites of predicted motifs. Though DREME also only outputs PWMs, we obtained the binding sites by scanning the sequences using the ‘fasta-grep’ program in the MEME suite (http://meme-suite.org/doc/fasta-grep.html). As shown in Figure 1F, ProSampler substantially outperformed the four other programs by identifying an average of 76.0% of the binding sites of the 60 implanted motifs by its 65 predicted motifs in the six datasets. Receiver operator characteristic (ROC) curve analyses indicate that ProSampler achieved this sensitivity (76.0%) at the lowest false positive rate of 0.005, substantially outperforming the four-other programs (Fig. 1G). We also evaluated the impacts of the occurrence frequency of implanted binding sites in a dataset on the ability of the programs to identify them. As shown in Figure 1H, ProSampler found an average of 63.6%, 66.2%, 77.6%, 76.2%, 77.7%, 80.6%, 82.1%, 67.6%, 83.3% and 85.2% of the binding sites of motifs implanted with an occurrence frequency of 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9 and 1.0 site/sequence, respectively, significantly (P < 0.05 or P < 0.01, t-test) outperforming the four other programs at all the occurrence frequencies except 0.3 and 0.6 site/sequence, at which Prosampler, Bioprospector and motifRG had similar performance (P > 0.05). However, the Bioprospector (56) and motifRG (52) predicted fewer motifs than did ProSampler (60). As expected, the performance of ProSampler generally increased with the increase in the occurrence frequency of implanted motifs (Fig. 1H), but this was not the case for the other programs as their performance tended to decrease at higher frequencies (>0.3 site/sequence) with large oscillations (Fig. 1H). This is rather counter-intuitive, but the causes remain to be elucidated. Taken together, all these results indicate that ProSampler is not only substantially faster, but also generally more accurate and robust for finding binding sites of multiple implemented motifs in the synthetic datasets.
3.2 Comparison of the programs for speed on real ChIP-seq datasets
We next compared ProSampler with six programs (BioProspector, DREME, XXmotif, Homer, motifRG and Dimont) on 105 real ChIP-seq datasets for 21 TFs, collected from embryonic stem (ES) cell-derived early human embryonic tissues using a micrococcal nuclease-based ChIP-seq (MNChIP-seq) technique (Tsankov et al., 2015) (Supplementary Material). Each of these datasets contains 599∼100 778 binding peaks (Supplementary Fig. S2) with an average length of 92∼1151 bp (Supplementary Fig. S3). To evaluate the effect of sequence lengths on the performance of the programs, we re-extracted binding peaks for each dataset with a length of 200, 500, and 100 bp centering on the summit of the originally called binding peaks, forming three groups of 105 datasets: G1 (200 bp), G2 (500 bp) and G3 (1000 bp). We let BioProspector output 150 motifs in each dataset, and the six other programs output all the motifs they found, but only considered up to the top 150 motifs in subsequent analyses. As shown in Figure 2A–C, ProSampler was again orders of magnitude faster (85×) than the second fastest program Homer in the three groups of datasets (motifRG even crashed on some larger datasets in G1∼G3, thus its running times on these datasets were not included). Notably, with the increase in the size of datasets, the running time of ProSampler increased largely linearly with little oscillations (Fig. 2A–C). In contrast, those of the six other programs increased with large oscillations (Fig. 2A–C) that were not seen on the synthetic datasets (Fig. 1A). These results suggest that the real datasets might be structurally more heterogeneous than the synthetic ones, and the running times of the six other programs could be largely affected by the structures of the datasets, which had little effect on ProSampler’s running time. Therefore, ProSampler is not only orders of magnitude faster, but also more robust to the structures of real ChIP-seq datasets than the fastest existing tools.
Fig. 2.
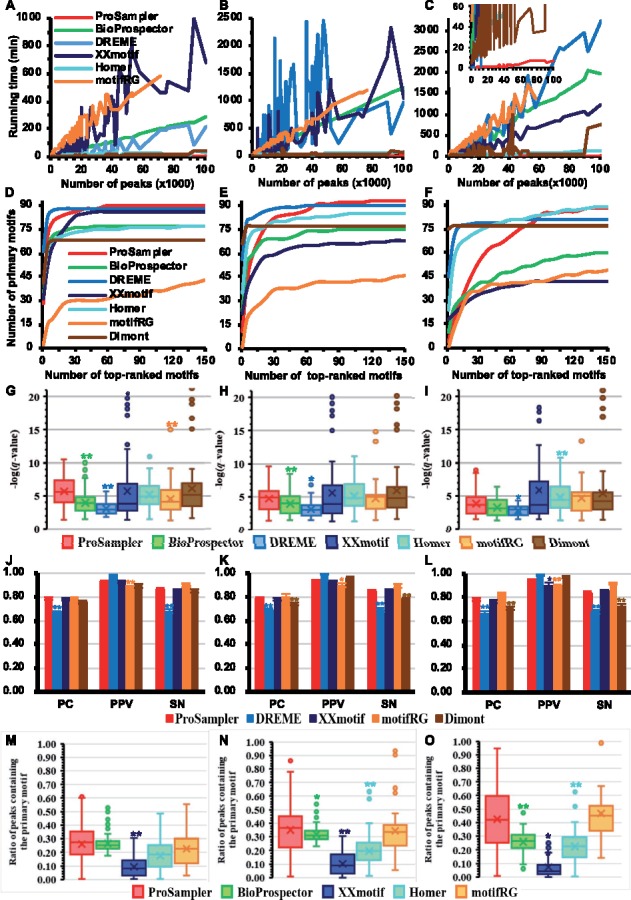
Performance comparison of the six programs for speed and identifying the primary motifs in real ChIP-seq datasets. (A, B and C). Running time of the programs as a function of the size of the datasets in G1, G2 and G3, respectively. The inset in (C) is a blow-up view with the running time below 60 min. (D, E and F) Cumulative number of primary motifs recovered by top-ranked motifs in the datasets in G1, G2 and G3, respectively. (G, H and I) Box plot of the q-values of predicted motifs of the programs, matching the primary motifs in the datasets in G1, G2 and G3, respectively. (J, K and L) Performance of the programs for predicting the lengths of primary motifs in the datasets in G1, G2 and G3, respectively. (M, N and O) Proportion of sequences found by the programs to contain the binding sites of primary motifs in the datasets in G1, G2 and G3, respectively. Labels * and ** have the same meanings as in Figure 1
3.3 Comparison of the programs for identifying primary motifs in real ChIP-seq datasets
To compare ProSampler with the other programs for identifying the primary motifs of the ChIP-ed TFs, we counted the number of primary motifs recovered by each program in its top-ranked motifs in the 105 datasets in G1∼G3. As shown in Figure 2D and E, ProSampler was the runner-up slightly outperformed by DREME for ranking the returned motifs matching primary motifs in both G1 and G2, but ProSampler outperformed all the other programs by identifying the highest number 90 (85.7%) and 93 (88.6%) of primary motifs in the 105 datasets (Table 2). Therefore, increase in the binding peak length from 200 bp (G1) to 500 bp (G2) increased the performance of most programs including ProSampler (90 versus 93) for finding the primary motifs, presumably because the longer (500 bp) peaks include more binding sites of the target TFs than do the shorter (200 bp) peaks (see below), although most of the datasets have an average called binding peak length shorter than 500 bp (Supplementary Fig. S2). In G3, ProSampler held the fourth place for ranking the returned motifs matching the primary motifs (Fig. 2F), presumably because it identified a far larger number of putative cooperative motifs (see below). Nonetheless, ProSampler was the runner-up by identifying 88 (83.8%) primary motifs in the 105 datasets, which is one fewer than the number 89 (84.8%) found by Homer (Fig. 2F and Table 2). Therefore, further increase in the peak length from 500 bp (G2) to 1000 bp (G3) reduced the performance of ProSampler (93 versus 88) and most of the other programs. Increase in the peak length to 1500 bp reduced the performance of all the programs (data not shown), presumably because too long binding peaks might include more noise that interferes with motif finding.
Table 2.
Comparison of performance of seven programs on all 105 MNChIP-seq datasets without running time limit
| Programs | G1 (200 bp) |
G2 (500 bp) |
G3 (1000 bp) |
|||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| No. of datasets with the PM found | Ave. no. of motifs found | Ave. no. of known motifsb | Ave. no. of cooperative motifsc | No. of datasets with the PM found | Ave. no. of motifs found | Ave. no. of known motifs | Ave. no. of cooperative motifs | No. of datasets with the PM found | Ave. no. of motifs found | Ave. no. of known motifs | Ave. no. of cooperative motifs | |
| ProSampler | 90 (85.7%) a | 49.6 | 12.9 | 2.7 | 93 (88.6%) | 93.8 | 17.9 | 3.4 | 88 (83.8%) | 119.0 | 17.5 | 3.7 |
| BioProspector | 77 (73.3%) | 150.0 | 8.7 | 0.9 | 75 (71.4%) | 150.0 | 7.9 | 1.1 | 60 (57.1%) | 150.0 | 5.9 | 0.8 |
| DREME | 88 (83.8%) | 22.7 | 8.0 | 2.5 | 90 (85.7%) | 42.1 | 9.0 | 2.4 | 81 (77.1%) | 48.0 | 6.6 | 1.6 |
| XXmotif | 86 (81.9%) | 49.4 | 12.4 | 2.7 | 68 (64.8%) | 50.5 | 10.3 | 2.4 | 42 (40.0%) | 54.3 | 6.4 | 1.5 |
| Homer | 77 (73.3%) | 121.2 | 20.6 | 3.5 | 85 (81.0%) | 136.9 | 18.9 | 3.2 | 89 (84.8%) | 147.1 | 17.0 | 2.8 |
| motifRG | 43 (41.0%) | 126.8 | 9.4 | 1.8 | 46 (43.8%) | 134.6 | 11.5 | 2.0 | 49 (46.7%) | 132.5 | 13.1 | 2.2 |
| Dimont | 68 (64.8%) | 4.3 | 1.6 | 0.6 | 77 (73.3%) | 2.8 | 1.4 | 0.6 | 77 (73.3%) | 2.0 | 1.3 | 0.5 |
Numbers in bold type represent the best performance in the column.
Average number of predicted motifs matched to those in JASPAR in each dataset.
Average number of predicted motifs matched to those in TCoF-DB for the target TF in each dataset.
The motifs returned by ProSampler in all the three groups of datasets G1∼G3 are significantly (P < 0.05 or P < 0.01) more similar to the known primary motifs than those found by the other programs, or have the same level of similarity to those found by the other programs (P > 0.05) (Fig. 2G–I), although ProSampler generally identified more primary motifs (Fig. 2F and Table 2). The primary motifs identified by ProSampler in the G1, G2 and G3 datasets and their matched motifs in JASPAR are shown in Supplementary Tables S2–S4, respectively. We also compared ProSampler with XXmotif, DREME, motifRG and Dimont for identifying the lengths of primary motifs in the three groups of datasets. As shown in Figure 2J–L, ProSampler had significantly (P < 0.05 or P < 0.01) better performance than, or comparable performance to the other four programs for PC, PPV and SN.
Similar to the cases in the synthetic datasets, motifs predicted by different programs in the same ChIP-seq dataset may match the target motifs significantly, but they may contain varying numbers of target binding sites located in varying numbers of peaks. A ChIP dataset is generally assumed to be enriched for binding peaks containing at least one binding site of the primary motif, thus a better motif finder can find binding sites of the primary motif in more binding peaks than can a worse one. As shown in Figure 2M–O, ProSampler significantly (P < 0.05 or P < 0.01, t-test) outperformed the other programs by finding binding sites of primary motifs in the highest average proportions of binding peaks in the three groups of datasets (Fig. 2D–F). However, the proportion of binding peaks found even by ProSampler to contain binding sites of primary motifs is surprisingly low with a median of 28%, 36% and 42% in G1, G2 and G3, respectively, and varies widely from as low as 0% to as high as 95% (Fig. 2M–O). In most datasets, this ratio was lower than the proportion of sequences found by ProSampler (48.3%) to contain the implanted binding sites in the synthetic datasets with a concentration of 0.6 site/sequence (the dotted line in Fig. 1H). These results suggest that on average more than 40% of ‘binding peaks’ returned by a peak-calling algorithm might actually not contain the binding sites of the target TF, due probably to the low quality of the original data for various technical artifacts such as low specificity of the TF antibody used. Alternatively, the target TF might bind the sequences indirectly through cooperative TFs, or the TF might bind other motifs in addition to the primary one. Nonetheless, the superior performance of ProSampler suggests that it might be used to identify these technical artifacts and their impacts on ChIP-seq data analyses.
3.4 Comparison of the programs for identifying cooperative motifs in real ChIP-seq datasets
We designed ProSampler to identify not only the primary motifs of target TFs, but also the motifs of cooperators in the binding peaks. Thus, we compared ProSampler with the six other programs for identifying cooperative motifs in the three groups of datasets. As shown in Figure 3A–C and Table 2, the programs returned a highly varying number of putative motifs in each group of the datasets. Interestingly, ProSampler identified an intermediate average number of 49.6, 93.8 and 119.0 motifs in G1, G2 and G3, respectively, which are significantly (P < 0.05 or P < 0.01, Wilcoxon rank sum test) larger or smaller than those obtained by the other programs except XXmotif in G1 (Fig. 3A–C). Since there is no golden standard benchmark to validate the predictions of cooperative motifs, we resorted to an alternative approach: we counted the number of known motifs as well as the number of known cooperative motifs of the primary motifs recovered by top-ranked motifs returned by each program. As shown in Figure 3D and Table 2, in the G1 datasets, the cumulative number of known motifs recovered by the top-ranked motifs by both ProSampler and XXmotif increased rapidly and entered the saturation phase around the top 50 predicted motifs, close to the average number of predicted motifs in each dataset by both programs (Fig. 3A). ProSampler recovered a total of 1357 known motifs in the G1 datasets, which is larger than those recovered by the other programs except Homer that recovered a total of 2160 known motifs. In the G2 (Fig. 3E and Table 2) datasets, ProSampler (1857) recovered approximately the same number of known motifs with that of Homer (1968). In the G3 datasets (Fig. 3F and Table 2), ProSampler outperformed all the six other algorithms by recovering the largest number of known motifs by most choices of top-ranked motifs. Since the probability to find known motifs by chance is low, these matching motifs are likely to be true motifs, and may cooperate with the primary motifs in transcriptional regulation.
Fig. 3.
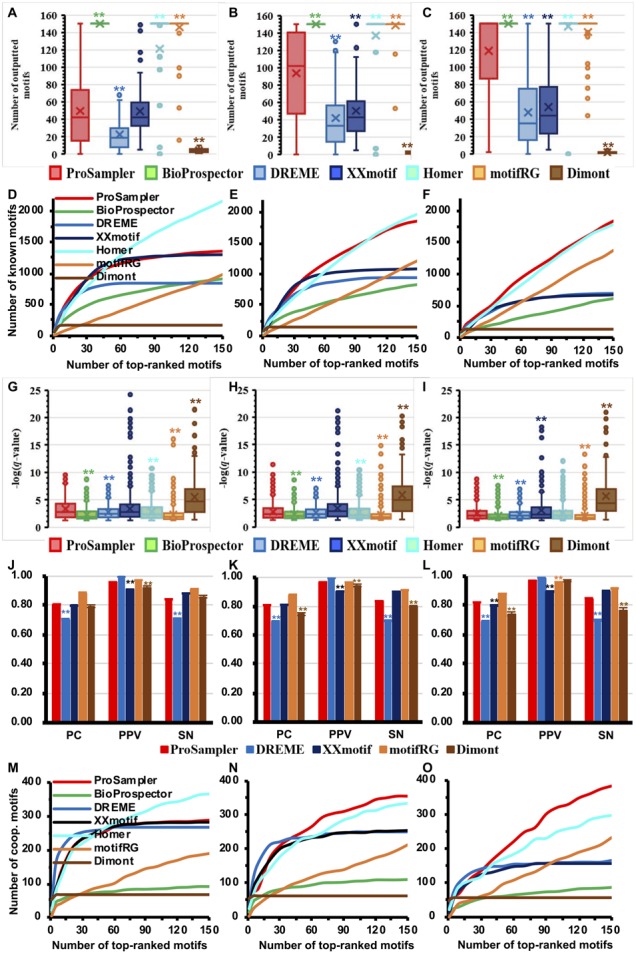
Performance comparison of the programs for identifying cooperative motifs in real ChIP-seq datasets. (A, B and C) Number of motifs returned by the programs in the G1, G2 and G3 datasets, respectively. (D, E and F) Cumulative number of known motifs matched by top ranked motifs of the programs in the G1, G2 and G3 datasets, respectively. (G, H, I) Box plot of the q-values of motifs predicted by the programs matching known motifs in the G1, G2 and G3 datasets, respectively. (J, K and L) Performance of the programs for predicting the lengths of known motifs in the G1, G2 and G3 datasets, respectively. (M, N and O) Cumulative number of the target TFs’ known cooperative motifs matched by top ranked motifs of the programs in the G1, G2 and G3 datasets, respectively. Labels * and ** have the same meanings as in Figure 1
Moreover, as shown in Figure 3G–I and Table 2, the motifs returned by ProSampler in all the three groups of datasets are significantly (P < 0.05 or P < 0.01) more similar to the known motifs than those predicted by all the other programs except that XXmotif performed significantly (P < 0.01) better in G3 and Dimont in G1∼G3 (P < 0.01). However, as a trade-off, both XXmotif and Dimont predicted far fewer known motifs (Fig. 3D–F). For identifying the lengths of the matched known motifs in the three groups of datasets, ProSampler had significantly (P < 0.01) better performance than, or comparable performance to the other four programs for PC, PPV and SN (Fig. 3J–L). The results are largely similar to those obtained for the primary motifs (Fig. 2J–L).
ProSampler also identified the largest average number (3.4 and 3.7) of motifs in G2 and G3 matching those of known cooperative TFs of the target TFs documented in the TcoF-DB database (Fig. 3M–O and Table 2) (Schaefer et al., 2011; Schmeier et al., 2017) (see Supplementary Table S5 for all known cooperative factors of the 21 target TFs), although Homer (3.5) outperformed ProSampler (2.7) in G1. These matching motifs are likely to be true cooperative motifs of the primary ones. As expected, with the increase in the binding peak length of the datasets, ProSampler identified an increasing average number of known cooperative motifs. However, the reverse, an unexpected result, was true for Homer for unknown reasons.
4 Discussion
We designed ProSampler aiming at finding not only the primary motifs of the target TFs, but also motifs of cooperators in the binding peaks with a length of typical CRMs (500∼1000 bp) in very big ChIP-seq dataset. To this end, we took the following tactics: (i) instead of performing Gibbs sampling on original sequences directly (Liu et al., 2001), we sample on preliminary motifs formed by combining highly similar significant k-mers, with the aid of the motif similarity graph. As the number of possible k-mers is fixed in any size of a ChIP-seq data, this step runs in an almost constant time. (ii) Unlike most of the existing algorithms that identify the motif length by exhaustively evaluating each length within a specified interval (Bailey, 2011), we determine the motif length by extending the k-mer core motif using a two-proportion z-test, saving a few fold of CPU time. (iii) By storing the flanking l-mers in memory, we avoid extensive I/O. (iv) We combine the strength of k-mer numeration and Gibbs sampling approaches to identify subtle weak motifs. Indeed, as we demonstrated in this work, these strategies render ProSampler to outperform the six state-of-the-art tools in speed, accuracy and robustness in identifying the primary motifs as well as cooperative ones in very big ChIP-seq datasets with a length of typical CRMs. Thus, ProSampler allows researchers to fully exploit valuable ChIP-seq datasets and identify all possible TFBSs enriched in them. The results can provide new insights into the cooperative regulation of gene transcription by multiple TFs and possible technical issues in generating the datasets. Therefore, by enabling fast and accurate mining of the entire big ChIP-seq datasets, ProSampler can greatly facilitate the efforts to identify the entire cis-regulatory code in genomes.
Supplementary Material
Acknowledgements
The authors thank Dr Meng Niu for assisting in preprocessing the original MNChIP-seq datasets, and members in the Su Lab for discussion, and members in the Li Lab for advices on manuscript writing.
Funding
The work was partially supported by US National Science Foundation [DBI-1661332] and NIH [R01GM106013 to Z.S.]; National Natural Science Foundation of China [61572358] and the Natural Science Foundation of Tianjin Science and Technology Committee [16JCYBJC23600 to S.Z.] and National Science Foundation of China [61432010, 31571354 and 61771009 to G.L.].
Conflict of Interest: none declared.
References
- Bailey T.L. (2011) DREME: motif discovery in transcription factor ChIP-seq data. Bioinformatics, 27, 1653–1659. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bailey T.L., Machanick P. (2012) Inferring direct DNA binding from ChIP-seq. Nucleic Acids Res., 40, 128. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bedell J.A. et al. (2000) MaskerAid: a performance enhancement to RepeatMasker. Bioinformatics, 16, 1040–1041. [DOI] [PubMed] [Google Scholar]
- Benson G. (1999) Tandem repeats finder: a program to analyze DNA sequences. Nucleic Acids Res., 27, 573–580. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Colombo N., Vlassis N. (2015) FastMotif: spectral sequence motif discovery. Bioinformatics, 31, 2623–2631. [DOI] [PubMed] [Google Scholar]
- Deplancke B. et al. (2016) The genetics of transcription factor DNA binding variation. Cell, 166, 538–554. [DOI] [PubMed] [Google Scholar]
- Ettwiller L. et al. (2007) Trawler: de novo regulatory motif discovery pipeline for chromatin immunoprecipitation. Nat. Methods, 4, 563–565. [DOI] [PubMed] [Google Scholar]
- Grau J. et al. (2013) A general approach for discriminative de novo motif discovery from high-throughput data. Nucleic Acids Res., 41, e197. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gupta S. et al. (2007) Quantifying similarity between motifs. Genome Biol., 8, R24. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hartmann H. et al. (2013) P-value-based regulatory motif discovery using positional weight matrices. Genome Res., 23, 181–194. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heinz S. et al. (2010) Simple combinations of lineage-determining transcription factors prime cis-regulatory elements required for macrophage and B cell identities. Mol Cell, 38, 576–589. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hu M. et al. (2010) On the detection and refinement of transcription factor binding sites using ChIP-Seq data. Nucleic Acids Res., 38, 2154–2167. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huggins P. et al. (2011) DECOD: fast and accurate discriminative DNA motif finding. Bioinformatics, 27, 2361–2367. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ikebata H., Yoshida R. (2015) Repulsive parallel MCMC algorithm for discovering diverse motifs from large sequence sets. Bioinformatics, 31, 1561–1568. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kheradpour P., Kellis M. (2014) Systematic discovery and characterization of regulatory motifs in ENCODE TF binding experiments. Nucleic Acids Res., 42, 2976–2987. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kulakovskiy I.V. et al. (2010) Deep and wide digging for binding motifs in ChIP-Seq data. Bioinformatics, 26, 2622–2623. [DOI] [PubMed] [Google Scholar]
- Lawrence C.E. et al. (1993) Detecting subtle sequence signals: a Gibbs sampling strategy for multiple alignment. Science, 262, 208–214. [DOI] [PubMed] [Google Scholar]
- Liu X. et al. (2001) BioProspector: discovering conserved DNA motifs in upstream regulatory regions of co-expressed genes. Pac. Symp. Biocomput., 127–138. [PubMed] [Google Scholar]
- Ma X. et al. (2012) A highly efficient and effective motif discovery method for ChIP-seq/ChIP-chip data using positional information. Nucleic Acids Res., 40, e50. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mason M.J. et al. (2010) Identification of context-dependent motifs by contrasting ChIP binding data. Bioinformatics, 26, 2826–2832. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mathelier A. et al. (2016) JASPAR 2016: a major expansion and update of the open-access database of transcription factor binding profiles. Nucleic Acids Res., 44, D110–115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Park P.J. (2009) ChIP-seq: advantages and challenges of a maturing technology. Nat. Rev. Genet., 10, 669–680. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prakash A., Tompa M. (2005) Statistics of local multiple alignments. Bioinformatics, 21, i344–350. [DOI] [PubMed] [Google Scholar]
- Quang D., Xie X. (2014) EXTREME: an online EM algorithm for motif discovery. Bioinformatics, 30, 1667–1673. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reid J.E., Wernisch L. (2011) STEME: efficient EM to find motifs in large data sets. Nucleic Acids Res., 39, e126.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sandelin A., Wasserman W.W. (2004) Constrained binding site diversity within families of transcription factors enhances pattern discovery bioinformatics. J. Mol. Biol., 338, 207–215. [DOI] [PubMed] [Google Scholar]
- Schaefer U. et al. (2011) TcoF-DB: dragon database for human transcription co-factors and transcription factor interacting proteins. Nucleic Acids Res., 39, D106–110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schmeier S. et al. (2017) TcoF-DB v2: update of the database of human and mouse transcription co-factors and transcription factor interactions. Nucleic Acids Res., 45, D145–d150. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sinha S. (2003) Discriminative motifs. J. Comput. Biol., 10, 599–615. [DOI] [PubMed] [Google Scholar]
- Thomas-Chollier M. et al. (2012) RSAT peak-motifs: motif analysis in full-size ChIP-seq datasets. Nucleic Acids Res., 40, e31. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tsankov A.M. et al. (2015) Transcription factor binding dynamics during human ES cell differentiation. Nature, 518, 344–349. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yao Z. et al. (2014) Discriminative motif analysis of high-throughput dataset. Bioinformatics, 30, 775–783. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Y. et al. (2008) Model-based analysis of ChIP-Seq (MACS). Genome Biol., 9, R137. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang H. et al. (2017) WSMD: weakly-supervised motif discovery in transcription factor ChIP-seq data. Sci. Rep., 7, 3217. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


