Working memory gating mechanisms explain developmental change in rule-guided behavior

Abstract

Cognitive control requires choosing contextual information to update into working memory (input gating), maintaining it there (maintenance) stable against distraction, and then choosing which subset of maintained information to use in guiding action (output gating). Recent work has raised the possibility that the development of rule-guided behavior, in the transition from childhood to adolescence, is linked specifically to changes in the gating components of working memory (Amso, Haas, McShane, & Badre, 2014). Given the importance of effective rule-guided behavior for decision making in this developmental transition, we used hierarchical rule tasks to probe the precise developmental dynamics of working memory gating. This mechanistic precision informs ongoing efforts to train cognitive control and working memory operations across typical and atypical development. The results of Experiment 1 verified that the development of rule-guided behavior is uniquely linked to increasing hierarchical complexity but not to increasing maintenance demands across 1st, 2nd, and 3rd order rule tasks. Experiment 2 then investigated whether this developmental trajectory in rule-guided behavior is best explained by change in input gating or output gating. Further, as input versus output gating also tend to correlate with a more proactive versus reactive control strategy in these tasks, we assessed developmental change in the degree to which these two processes were deployed efficiently given the task. Experiment 2 shows that the developmental change observed in Experiment 1 and in Amso et al. (2014) is likely a result of increased efficacy of output gating processes, as well as greater strategic efficiency in that adolescents opt for this costly process less often than children.

1. Introduction

An important factor in human cognitive development is the emergence of rule-guided action selection. Every situation confronting a child is associated with appropriate and inappropriate behaviors. Flexible and adaptive function requires being able to use rules to plan and execute appropriate action. This ability depends on cognitive control and permits appropriate actions to be selected based on goals, plans, or a particular context. In the simplest instance, rules can be concrete in that they map a given context directly to action. For example, the common household rule “when going outside, wear sunblock” directly relates a context (being outside) to an action routine (apply sunblock).

However, in the complexity of the real world, rules are rarely so direct. Rather, they become nested hierarchically to the extent that they relate increasingly higher order contexts and contingencies to classes of simpler rules (Badre, 2008; Barto & Mahadevan, 2003; Frank & Badre, 2012). Hierarchical rules can be assigned a rule order based on the number of contingency levels they include. Thus, to extend our example from above, the validity of the described rule for wearing sunblock might further depend on whether it is sunny (valid) or cloudy (invalid). This defines a new, second order rule signifying appropriate first order rules (i.e., “when going outside, wear sunblock”) in a given context (i.e., sunny day). And, of course, all of these contextual relationships may change if the child is currently with a caregiver or with their friends. From this example, it is easy to see how the ability to contingently relate contexts to one another in order to specify a rule is crucial for everyday planning and adaptive behavior. Thus, hierarchical rule use of this type supports complex contingent action selection (Badre & D’Esposito, 2007; Badre, Hoffman, Cooney, & D’Esposito, 2009; Chatham, Frank, & Badre, 2014), learning and generalization (Badre & Frank, 2012; Badre, Kayser, & D’Esposito, 2010; Botvinick, 2008; Collins & Frank, 2013; Frank & Badre, 2012), planning (Koechlin, Corrado, Pietrini, & Grafman, 2000), decision making (Badre, Doll, Long, & Frank, 2012), and fluid reasoning (Bunge, 2004; Speed, 2010). It follows that successfully developing this ability is important for flexible function, especially as children become increasingly self-directed and less dependent on caregivers in the transition from childhood to adolescence.

Developmental improvements in rule-guided behavior are evident in early childhood (Munakata, Snyder, & Chatham, 2012; Zelazo, 2004), continue into adolescence (Crone, Bunge, Van der Molen, & Ridderinkhof, 2006; Huizenga, Crone, & Jansen, 2007), and relate to the maturation of the prefrontal cortex (Bunge & Zelazo, 2006; Crone, Donohue, Honomichl, Wendelken, & Bunge, 2006; Wendelken, Munakata, Baym, Souza, & Bunge, 2012). Most of the developmental evidence on rule-guided behavior comes from task-switching studies (Best & Miller, 2010; Chevalier & Blaye, 2009; for review, see Diamond, 2013). For example, children 3- and 4-years old are able to successfully shift between two independent rules, such as “in the color game, red ones go on the left and blue ones go on the right” (e.g., Moriguchi & Hiraki, 2011; Zelazo, 2004). This is a 1st order rule in that the context (color) directly governs action selection (red/left, blue/right). However, young children typically show perseverative errors on tasks where two or more rules or contexts can govern state-action mappings. For example, the 2nd order context specifying which sorting game to play can be hierarchically layered on top of the lower (1st) order color or shape rules. In this case, if we are playing the color game, the previously described state-action mappings apply (red/left, blue/right), but if we are playing the shape game alternative mappings apply, namely “trucks go on the left and stars go on the right”. Since color and shape games are associated with conflicting mappings for red stars or blue trucks, some additional, higher order context is required to determine which game to play. Similar designs in older children have shown that lower order, concrete rule use matures prior to higher order rule use. Indeed, this latter ability is still developing beyond late childhood and into adolescence (Bunge & Zelazo, 2006).

What mechanisms might underlie younger children’s difficulties following rules with a complex hierarchical structure? Research on hierarchical rule use in adults indicates that behaving according to higher order rules places increasing demands on working memory gating (Chatham & Badre, 2015). In particular, there is emerging evidence that execution and learning of complex, hierarchical rules relies on gating mechanisms controlling the output of working memory—as opposed to gating mechanisms controlling its input.

Prevailing models of cognitive control require a working memory that maintains contextual information robust to interference (Desimone & Duncan, 1995; Miller & Cohen, 2001; O’Reilly & Frank, 2006). Once maintained, this information can provide a top-down signal to bias response choices and attentional systems (working memory output). However, working memory is also capacity limited, and so it must be selective about what it maintains. One way to conceptualize such a process is as a gate that is selective about what information is permitted access to working memory (Braver & Cohen, 2000; Chatham et al., 2014; Frank, Loughry, & O’Reilly, 2001; Gruber, Dayan, Gutkin, & Solla, 2006; Hochreiter & Schmidhuber, 1997). When the gate is open, information flows into working memory where it can serve as a context that guides action selection. When the gate is closed, irrelevant information is kept out. For instance, if you are listening to the local traffic report on the radio while driving to work, you will probably update only those road incidents that are relevant to your current route into working memory. This regulation of the input to working memory or input gating has received considerable attention in cognitive neuroscience and is thought to be mediated by the basal ganglia via cortico-striatal-thalamo-cortical loops (e.g., Cools, Miyakawa, Sheridan, & D’Esposito, 2010; Kühn et al., 2013; McNab & Klingberg, 2008; Moustafa, Cohen, Sherman, & Frank, 2008; Murty et al., 2011; Nee & Brown, 2013; O’Reilly & Frank, 2006).

However, not all information maintained in working memory is necessarily behaviorally relevant at any given point in time. Recent evidence in adults indicates that a second gate could operate on the output of working memory by controlling what subset of the currently maintained information is selected to exert an influence on behavior (Chatham et al., 2014). Only when the output gate is open, relevant working memory representations are capable of providing a top-down contextual signal to bias action selection. When the output gate for a given working memory representation is closed, that representation remains in an accessible but inert state.

Output gating may be particularly important for behaving according to complex, hierarchical rules because the child must choose which of the various contexts held in working memory should govern behavior based on a higher order, prevailing context. One such example is the sorting game described above that requires children to maintain the rules for both color (red/left, blue/right) and shape (trucks/left, stars/right) while only one of these contexts will be relevant on a given trial. The higher-order context (color game vs. shape game) determines whether shape or color context need to be output gated to guide action selection. While output gating (relative to input gating) has been shown to be particularly crucial in the execution and learning of higher order rules in adults (e.g., Badre & Frank, 2012; Badre et al., 2010; Chatham et al., 2014; Frank & Badre, 2012), it has not been demonstrated that changes in output gating underlie developmental changes in rule-guided behavior observed in the transition from childhood to adolescence.

Beyond increased demands on working memory gating with higher order rules, there is also often a concomitant increase in the fan of alternatives competing for action. For example, consider a 1st order rule task in which only a single context, such as color, governs response selection (e.g., red/left, blue/right). Here, there are two alternatives for action that need to be maintained in working memory. However, a 2nd order rule may require responding based on either color rules or shape rules (e.g., truck/up, star/down) depending on some other element of context (like an instruction). In this case, not only has the rule order increased, there are also four rule alternatives to be maintained in working memory, namely the rules relating to red, blue, truck, or star. Thus, tasks involving hierarchical rule use and more gating are typically accompanied by a correlated increase in demands on working memory maintenance.

Initial evidence suggests that when working memory load is controlled, the additional contingency or selection step (i.e., the putative output gating demand) entailed by the higher order rule drives developmental change more so than working memory capacity limitations. Recent work (Amso, Haas, McShane, & Badre, 2014) used 1st and 2nd order rule tasks to show that developmental improvements in rule-guided behavior in the transition from late childhood to adolescence were linked to the ability to update rules in working memory, rather than arbitrate between multiple rule alternatives as such. Each increment of the rule order from 0 to 1st order or 1st to 2nd order rules was associated with a cost in performance, and this cost diminished with development from late childhood (7–10 years) to adolescence (12–15). However, there was no additional developmental cost to maintenance of more lower order items, as manipulated by increasing the number of 1st and 2nd order rule sets. In a similar vein, Zelazo, Muller, Frye, and Marcovitch (2003) demonstrated that most 3- and 4 year old children were able to flexibly use as many as four lower order rules, as long as these rules were not in conflict. These observations support the hypothesis that working memory gating, and output gating in particular, may be a core mechanism that undergoes developmental change and drives the maturation of cognitive control.

Importantly, however, the 1st and 2nd order rules used in Amso et al. (2014) might not have been sufficiently challenging to maintain in working memory. It is possible that even higher order rules, involving more contingencies, will expose developmental differences in the ability to arbitrate between multiple alternatives for action. Thus, the first aim of the present study is to replicate and extend the original findings from the 1st and 2nd order tasks to a 3rd order task. In Experiment 1, children (7–11 years), adolescents (12–16 years), and young adults (19–27 years) completed three tasks that involved action selection in the context of increasingly higher order rules (adapted from Badre & D’Esposito, 2007): Rule order increased from the response task (0 order and 1st order rules), to the feature task (1st and 2nd order rules) to the dimension task (2nd and 3rd order rules). Working memory load was manipulated parametrically across different trial blocks within each task by varying the number of rules participants had to choose from at (1, 2, or 4 rules). In the 3rd order task, if participants were to maintain all the rules in working memory at once, then this would require adjudicating among 8 or 16 different lower order rules depending on the condition: a demand that exceeds the putative working memory capacity limits of all age groups. As such, this supra-capacity working memory demand should expose any developmental change in the working memory maintenance component of these rule tasks. If, however, the ability to manage higher order contingencies undergoes the most pronounced developmental change then children should show a greater cost when confronted with rules of increasing hierarchical complexity, relative to costs incurred by increasing numbers of alternatives for action in working memory.

A second aim of the present study is to test the hypothesis that output gating is specifically at the root of the developmental change in higher order rule use. As already noted, many neurocomputational models of working memory updating assume separate mechanisms for gating task-relevant information to be maintained in working memory (input gating) and gating which of the currently maintained working memory representations can exert an influence over behavior (output gating) (Frank & Badre, 2012; Hazy, Frank, & O’Reilly, 2007; Huang, Hazy, Herd, & O’Reilly, 2013; Kriete & Noelle, 2011). Importantly, however, the tests of higher order rule use in children to this point have presented all the relevant contextual elements at the same time. Thus, it is equally plausible that the demand to update working memory (input gating) is driving developmental change, as selecting which rule is relevant from within working memory (output gating). In order to distinguish these alternatives, it is necessary to manipulate when information is available in the environment and in working memory, thereby controlling for the opportunity to input versus output gate working memory.

In Experiment 2, we manipulated the order of presentation of contextual information during a second order rule task in order to bias use of an input or output gating strategy. In this way, we investigated both the mode of control strategy (i.e., input versus output gating) that children (7–11 years) and adolescents (12–17 years) prefer using during rule-guided behavior and also the efficacy of the input and output gating mechanisms themselves across this developmental period. Understanding the precise mechanisms underlying these developmental challenges in hierarchical rule use is particularly important given their broad relevance for managing the explosion in rich decision making opportunities faced by children transitioning into adolescence. Here we ask whether developmental improvements in rule-guided behavior are a function of the ability to use existing information in working memory to guide action (output gating) or the ability to better update information offered by the environment (input gating).

2. Experiment 1

2.1. Methods

2.1.1. Participants

Thirty children (7–11 years, M = 9.4, SD = 1.4; 17 females), 30 adolescents (12–16 years, M = 14.2 SD = 1.4; 15 females), and 30 young adults (19–27 years, M = 22.9, SD = 2.6; 15 females) participated in two separate testing sessions. Participants were recruited from local public schools as well as from the community using flyers and brochures. Adults gave written informed consent consistent with the Brown University Institutional Review Board (IRB) rules and guidelines. For children and adolescents, caretakers’ consent and participants’ assent were obtained in accord with the IRB requirements. According to self-report or caregivers’ report, all had normal or corrected-to-normal visual and auditory abilities and no history of diagnosed neurological or psychiatric disorders. Intact color vision was confirmed using the Ishihara test for color deficiency.

2.1.2. Materials and task

2.1.2.1. Response task

On each trial, a colored square appeared in the middle of the computer screen on a black background for a maximum of 2 s until participants made a response. Trials were separated by a randomly jittered fixation interval of 0–2 s. Within a given block of trials, the response key was chosen based on the color of the square according to an instructed set of rules. There were three different block types, each of which included four colors that mapped onto one (R1 block), two (R2 block), or four (R4 block) different keys (see Fig. 1). On R1 blocks, each of the four colors was assigned to the same response key (e.g., “If the square is red/green/blue/yellow, press button 1.”). Since participants were not faced with a choice, this defined a 0 order rule with no competition between response alternatives. R1 blocks thus provided a control condition for baseline RT differences. During R2 blocks, two colors mapped onto one response key, while the other two colors mapped onto a second response key (e.g., “If the square is red/green, press button 1. If the square is orange/grey, press button 2.”). Hence, in order to select the correct response, participants had to use a 1st order rule that involved a single-level decision over two response alternatives (0 order rules). On R4 blocks, the four colors mapped onto four different keys such that participants were required to choose between four response alternatives (e.g., “If the square is blue, press button 1. If the square is orange, press button 2. If the square is purple, press button 3. If the square is white, press button 4.”). Note that only working memory load but not rule order increased from R2 to R4 as both block types comprised 1st order rules.

Fig. 1.

Schematic depicting trial events (left) and rule mappings (right) across working memory load conditions for the response, feature, and dimension tasks. In the response task (top row), participants respond by pressing one of four keys (1–4) that was cued by the color of the square. Across three, blocked working memory load levels, four color cues to be encountered during a block could map to either one (R1), two (R2), or four (R4) potential responses. The example trials on the left use the R2 rule mappings shown on the right. In the feature task (middle row), participants respond by pressing one of two keys (“match” vs. “nonmatch”) depending on whether or not an arrow pointed in the target direction, as cued by color. Across three, blocked working memory load levels, four color cues could map to one (F1), two (F2), or four (F4) potential target directions. The example trials on the left use the F2 rule mappings shown on the right. In the dimension task (bottom row), participants responded by pressing “match” or “nonmatch” depending on whether the presented objects match along a certain dimension (shape, size, orientation, or shading) as cued by color. Across three, blocked working memory load levels, four color cues could map to one (D1), two (D2), or four (D4) candidate dimensions for a given block. The example trials on the left use the D2 rule mappings shown on the right. Thus, across the three tasks, rule order increases from response task (0 order [R1] and 1st order [R2/R4]), to feature task (1st [F1] and 2nd order [F2/F4]), to dimension task (2nd [D1] and 3rd order [D2/D4]). Note that moving from load 1 to load 2 within each task is associated with an increase in both rule order and maintenance demands, whereas rule order is kept constant and only maintenance demands increase when moving from load 2 to load 4. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

2.1.2.2. Feature task

Participants saw a colored square with a white arrow inside that pointed in one of four directions (up, down, left, right). Trials followed the same procedure as in the response task, except that stimuli were presented for a maximum of 4 s. The task required participants to decide whether the arrow pointed in a given target direction by pressing one of two response keys. The target direction was indicated by the color of the square. Analogous to the experimental logic of the response task, trials were grouped into three alternate block types, each of which included four color-direction mappings that defined one (F1 block), two (F2 block), or four (F4 block) different target directions (see Fig. 1). On F1 blocks, each color mapped onto the same target direction. Hence, similar to R2 blocks, participants had to follow a 1st order rule by making single-level decisions over two response alternatives (match vs. non-match; e.g., “If the square is red/green/ blue/yellow, press the match button if the arrow is pointing up but if the arrow is pointing in a different direction, press the nonmatch button.”). By contrast, F2 and F4 blocks involved 2nd order rules requiring a two-level decision over two (F2) vs. four (F4) 1st order rules (first level) that mapped a given direction onto a match vs. non-match response (second level; e.g., “If the square is red/green, press the match button if the arrow is pointing up but if the arrow is pointing in a different direction, press the nonmatch button. If the square is orange/grey, press the match button if the arrow is pointing to the right but if the arrow is pointing in a different direction, press the nonmatch button.”).

2.1.2.3. Dimension task

On each trial, two objects were displayed inside a colored square. Participants were asked to press one of two response keys to indicate whether the objects match along a certain dimension (shape, size, orientation, or shading). The object pairs were selected such that there were always two matching and two nonmatching dimensions. The relevant dimension was cued by the color of the square. The general trial procedure was the same as in the feature task. Following the experimental design of response and feature tasks, working memory load was manipulated across three types of blocks, in which four colors were mapped onto one (D1 blocks), two (D2 blocks), and four (D4 blocks) different dimensions (Fig. 1). On D1 blocks, each of the four colors were assigned to the same dimension (e.g., direction), so participants had to use a 2nd order rule that requires a decision on relationships between features corresponding to the relevant dimension (e.g., “Is the first object pointing in the same direction as the second object?”). Note that this decision involves an additional selection step compared to F1 blocks, where participants make responses based on a simple stimulus feature (e.g., “Is this arrow pointing down?”). D1 blocks thus contained the same rule structure as F2 blocks. On D2 and D4 blocks, participants followed 3rd order rules that required them to arbitrate between two (D2) vs. four (D4) dimensions in order to select the correct 2nd order rule to make a match/nonmatch decision.

2.1.3. General procedures

Participants completed two experimental sessions on two different days, separated by one to four weeks. In one session, they performed the response and the feature task, in the other session, the dimension task. The order of sessions was counterbalanced across participants, as was the order of response and feature tasks within a session. Each task included six training blocks (two blocks for each load condition) that were followed by six experimental blocks. Training and experimental blocks were fully counterbalanced for order across participants.

At the beginning of the training, the experimenter explained the task and then taught the participant the first set of rules. The corresponding color-rule mappings were shown on the computer screen and participants were given as much time as they needed to memorize them. Before the start of the first practice block, the experimenter covered the computer screen and quizzed the participant on the rule set. If the participant failed to correctly and promptly recall all four mappings, they were given additional time to learn the rule. After successful completion of the quiz, participants started the first training block. Training blocks were identical to experimental blocks except that during the initial block (easy practice) there was no response time limit. Moreover, participants were asked to speak out loud their response along with pressing the button and were reminded of the correct mappings whenever necessary. During the second training block (hard practice), all settings were identical to the experimental blocks. Participants repeated both easy and hard practice as needed until their performance was above chance level.

Training and experimental blocks contained 33 trials for the response task, 32 trials for the feature task, and 25 trials for the dimension task, resulting in a total of 198 trials, 192 trials, and 150 trials, respectively, across the entire experiment. At the beginning of each experimental block, participants had the chance to review the mappings they would encounter during that block. Responses were given on a standard computer keyboard. During feature and dimension tasks, participants used index and middle finger of their dominant hand to make a response, while for the response task, each finger of the dominant hand was assigned to one response key. Each of the two experimental sessions lasted between 1 h and 1.5 h. All participants were tested individually.

2.1.4. Data analyses

The first trial of each experimental block was excluded from analyses, as were RTs for incorrect responses, and trials with latencies faster than 200 ms or slower than the outlier criterion determined on the basis of individual RT distributions (Tukey, 1977). Since mean response latencies differed between the three age groups, F(2,87) = 83.49, p < 0.001, ${\mathit{\eta }}_{\mathrm{p}}^2=0.66$, we included R1 baseline RT as a covariate in the analyses of data from feature and dimension tasks. R1 RT was mean centered prior to running the ANCOVAs (Delaney & Maxwell, 1981). For analyses that included R1 RT as dependent variable (feature task, cross-tasks comparison), we applied a square root transformation to each subject’s mean response latencies per block type in order to increase the homogeneity of variance.

RT and accuracy data were subjected to separate ANOVAs (response task) and ANCOVAs (feature and dimension tasks) including the between-subject factor age group (children, adolescents, adults) and the within-subject factor load (1, 2, vs. 4 alternatives for action). Whenever necessary, the Geisser-Greenhouse correction was applied (Geisser & Greenhouse, 1958) and corrected p-values are reported. Significant interactions were examined further using planned contrasts including pairwise comparisons between age groups specifically regarding their performance differences on load 1 vs. load 2 (combined effect of increasing rule order and maintenance demands) and load 2 vs. 4 (effect of increasing maintenance demands alone). Any developmental change observed in the rule order + working memory load contrast that is associated with maintenance demands should be evident and measurable when rule order is held constant and only the number of alternatives for action in working memory (load 2 to load 4) increases (Amso et al., 2014; Badre & D’Esposito, 2007).

2.2. Results

2.2.1. Response and feature tasks

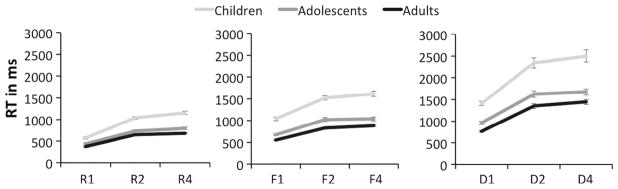
We first sought to replicate the findings of Amso et al. (2014) on the 1st order (response task) and 2nd order (feature task) rule tasks. Accuracy was high in all age groups for the response task (children: M = 0.95, SD = 0.06; adolescents: M = 0.98, SD = 0.02; adults: M = 0.98, SD = 0.01) as well as the feature task (children: M = 0.92, SD = 0.07; adolescents: M = 0.95, SD = 0.04; adults: M = 0.96, SD = 0.03). Fig. 2 presents mean RTs as a function of load (R1, R2, R4 and F1, F2, F4, respectively) and age group (children, adolescents, adults) for response (A) and feature (B) tasks.

Fig. 2.

Response times from Experiment 1. Plotted are mean RTs (in ms) across loads 1, 2, and 4, separately for the three age groups. RT is plotted separately for the (A) Response task, (B) Feature task, and (C) Dimension task. Error bars plot standard error of the mean.

The results are largely consistent with the findings of Amso et al. (2014). For the response task, an omnibus analysis of the RT data revealed a significant main effect of load, F(2,174) = 623.38, p < 0.001, ${\mathrm{\eta }}_{\mathrm{p}}^2=0.88$, that was qualified by an age group × load interaction, F(4,174) = 10.03, p < 0.001, ${\mathrm{\eta }}_{\mathrm{p}}^2=0.19$. Similarly, for the feature task, there was a significant main effect of load, F(2,172) = 377.02, p < 0.001, ${\mathrm{\eta }}_{\mathrm{p}}^2=0.82$, and an age group × load interaction, F(4,172) = 7.65, p < 0.001, ${\mathrm{\eta }}_{\mathrm{p}}^2=0.15$.

We first addressed developmental change in the combined effect of increasing rule-order + working memory load by comparing RTs on R1 blocks (0 order) vs. R2 blocks (1st order) and F1 blocks (1st order) vs. F2 blocks (2nd order) across age groups. Analyses revealed that going from 0 order to 1st order in the response task was associated with an increase in RT, F(1,87) = 644.32, p < 0.001, ${\mathrm{\eta }}_{\mathrm{p}}^2=0.88$. Performance costs were greater for children compared to both adolescents, F(1,87) = 11.32, p = 0.001, ${\mathrm{\eta }}_{\mathrm{p}}^2=0.12$, and adults, F(1,87) = 12.07, p = 0.001, ${\mathrm{\eta }}_{\mathrm{p}}^2=0.12$ (Fig. 2A). Correspondingly, RTs increased when going from 1st order to 2nd order in the feature task, F(1,86) = 422.01, p < 0.001, ${\mathrm{\eta }}_{\mathrm{p}}^2=0.83$. Again, this effect was greater for children compared to both adolescents, F (1,86) = 6.40, p = 0.013, ${\mathrm{\eta }}_{\mathrm{p}}^2=0.07$, and adults, F(1,86) = 18.72, p < 0.001, ${\mathrm{\eta }}_{\mathrm{p}}^2=0.18$ (Fig. 2B). These developmental effects could be a consequence of increases in rule order, increases in working memory load, or both. We thus isolated the RT costs between loads 2 and 4 that are specific to increasing maintenance demands, while holding rule order constant. We compared R2 vs. R4 blocks and F2 vs. F4 blocks, respectively. RTs were slower on R4 than R2 blocks, F (1,87) = 47.03, p < 0.001, ${\mathrm{\eta }}_{\mathrm{p}}^2=0.35$. This effect was significantly larger in children than adults, F(1,87) = 6.89, p = 0.010, ${\mathrm{\eta }}_{\mathrm{p}}^2=0.07$, but did not reliably differ between either children and adolescents or adolescents and adults (ps > 0.13). By contrast, adding competing choices in 2nd order rule use i.e., from F2 to F4 blocks, resulted in a main effect of load, F(1,87) = 13.59, p < 0.001, ${\mathrm{\eta }}_{\mathrm{p}}^2=0.14$, that did not differ across age groups (ps > 0.32).

2.2.2. Dimension task

Next, we asked whether developmental cost due to working memory capacity limitations is evident when participants have to use 3rd order rules in the dimension task. As was the case for response and feature tasks, the omnibus ANCOVA on RTs yielded a main effect of load, F(2,172) = 195.29, p < 0.001, ${\mathrm{\eta }}_{\mathrm{p}}^2=0.69$, that was qualified by an age group by load interaction, F(4,172) = 3.56, p = 0.022, ${\mathrm{\eta }}_{\mathrm{p}}^2=0.08$. Follow-up comparisons of D1 blocks vs. D2 blocks showed that children had greater RT cost due to the combined effect of increasing rule order and working memory load (D1 vs. D2) than did either adolescents, F(1,86) = 6.82, p = 0.011, ${\mathrm{\eta }}_{\mathrm{p}}^2=0.07$, or adults, F(1,86) = 5.98, p = 0.016, ${\mathrm{\eta }}_{\mathrm{p}}^2=0.07$, whereas costs did not differ between the latter two age groups (p = 0.64) (Fig. 2C). In addition, increasing the number of 3rd order rule sets from D2 to D4 blocks was associated with a general RT cost, F(1,86) = 19.21, p < 0.001, ${\mathrm{\eta }}_{\mathrm{p}}^2=0.18$, but there was no evidence for developmental change in the effect of higher maintenance demands (all ps > 0.23).

Accuracy was high on D1 blocks for all age groups, but markedly dropped on D2 and D4 blocks in children. Accordingly, the omnibus ANOVA revealed main effects of age group, F(2,87) = 30.03, p < 0.001, ${\mathrm{\eta }}_{\mathrm{p}}^2=0.39$ (children: M = 0.82, SD = 0.12; adolescents: M = 0.93, SD = 0.12; adults: M = 0.96, SD = 0.12), and load F (2,174) = 33.94, p < 0.001, ${\mathrm{\eta }}_{\mathrm{p}}^2=0.28$ (D1: M = 0.96, SD = 0.06; D2: M = 0.87, SD = 0.02; D4: M = 0.88, SD = 0.02), and an age group by load interaction, F(4,174) = 12.43, p < 0.001, ${\mathrm{\eta }}_{\mathrm{p}}^2=0.22$. When comparing the combined effect of rule order and working memory load (D1 vs. D2) across the three age groups, we found significantly greater performance costs in children (M_D1-D2 = 0.12) compared to both adolescents (M_D1-D2 = 0.06), F(1,87) = 20.46, p < 0.001, ${\mathrm{\eta }}_{\mathrm{p}}^2=0.19$, and adults (M_D1-D2 = 0.01), F(1,87) = 41.06, p < 0.001, ${\mathrm{\eta }}_{\mathrm{p}}^2=0.32$, as well as a trend towards higher cost in adolescents compared to adults, F(1,87) = 3.55, p = 0.063, ${\mathrm{\eta }}_{\mathrm{p}}^2=0.04$. However, once again, we did not find evidence for age differences in maintenance-specific cost (D2 vs. D4; children: M_D4-D2 = 0.01, adolescents: M_D4-D2 = 0.00, adults: M_D4-D2 = 0.01) (all ps > 0.81).

2.2.3. Cross-task comparison

The single-task analyses did not answer the question of whether the observed age differences in performance cost were due to an interaction of rule order and maintenance demands or were specific to improvements in managing higher rule order. Therefore, were ran a task comparison that orthogonally crossed the two factors by including only loads 2 and 4 of each task. RTs were subjected to an ANCOVA with the between-subject factor age group, the within-subject factors rule order (1st [response task], 2nd [feature task], 3rd [dimension task]) and load (2 vs. 4) and R1 baseline RT as covariate. The analysis yielded significant main effects of rule order, F(2,172) = 247.94, p < 0.001, ${\mathrm{\eta }}_{\mathrm{p}}^2=0.74$, and an interaction of age group and rule order, F(4,172) = 6.14, p = 0.002, ${\mathrm{\eta }}_{\mathrm{p}}^2=0.13$. Pairwise comparisons showed that children had greater response cost than did either adolescents or adults when going from 1st to 2nd order rules [F(1,86) = 8.19, p = 0.005, ${\mathrm{\eta }}_{\mathrm{p}}^2=0.09$ and F(1,86) = 18.78, p < 0.001, ${\mathrm{\eta }}_{\mathrm{p}}^2=0.18$, for the comparison of children with adolescents and adults, respectively] as well as from 2nd order to 3rd order rules [F(1,86) = 6.60, p = 0.012, ${\mathrm{\eta }}_{\mathrm{p}}^2=0.07$ and F(1,86) = 5.70, p = 0.019, ${\mathrm{\eta }}_{\mathrm{p}}^2=0.06$, respectively]. Furthermore, we obtained a main effect of load, F(1,86) = 41.55, p < 0.001, ${\mathrm{\eta }}_{\mathrm{p}}^2=0.33$. There was, however, no significant interaction of age group and load (p = 0.28) or age group, load, and rule order (p = 0.58), indicating that the effect of rule complexity on response speed was specifically related to increasing rule order as opposed to working memory load or their interaction.

One potential caveat of the cross-task analysis is that it might be confounded by differences between the three tasks that are unrelated to the experimental manipulations of rule order and working memory load, such as physical properties of the stimuli, instructions, or task-specific cognitive operations. In order to rule out this possibility, we capitalized on the fact that both rule order and total number of contingencies are identical for R2 and F1 conditions as well as for F2 and D1 conditions. Specifically, R2 and F1 conditions involve 1st order rules and require choices between two response alternatives (i.e., 2 contingencies). Correspondingly, F2 and D1 conditions involve 2nd order rules and choices between two contexts (2nd order) and two response alternatives (1st order; i.e., 4 contingencies). Thus, any age-related variations in RT differences between (a) R2 and F1 blocks and (b) F2 and D1 blocks would be due to differences between feature, and dimension tasks other than rule order and maintenance demands.

To address this possibility, we ran separate ANCOVAs with the factors age group and task, and R1 baseline RT as covariate to compare R2 vs. F1 conditions and F2 vs. D1 conditions. Neither of the two analyses yielded a significant age group × task interaction [F (2,86) = 0.36, ns, and F(2,86) = 0.13, ns, respectively]. Thus, we did not find evidence that age differences in RT were modulated by differences between the response vs. feature tasks or feature vs. dimension tasks when these tasks involved the same rule order.

2.3. Discussion

Experiment 1 shows that developmental change in rule-guided behavior can best be explained by improvements in hierarchical rule use and not in the ability to manage an increasing number of alternatives for action in working memory. Across three tasks using both RT and accuracy measures, only one contrast of working memory load showed any age-related difference, and this was a difference between children and adults for the lowest order response task. Given the specificity of this effect to RT and the absence of this effect in the other higher order rule tasks, we suspect that this outlier effect may derive from the unique motor demands of the response experiment, namely that four finger responses are required versus two. Overall, the present results confirm and extend the findings of Amso et al. (2014) and demonstrate that the pattern of developmental differences does not change even when using a more complex, supra-capacity task involving 3rd order rules. Thus, developmental benefit is linked to factors related to higher-order contextual contingencies, but there is no evident developmental cost to the need to maintain multiple rule sets. Lucenet and Blaye (2014) similarly found that increasing working memory load did not impact the dynamics of cognitive control operations in 5- and 6-year-olds.

While Experiment 1 rules out working memory capacity limitations as an explanation for developmental differences in higher order rule use, it does not answer the question what specific mechanisms may underlie the observed effects of rule order. As introduced previously, research in adults has demonstrated that hierarchical rule use strongly relies on efficient working memory gating. Importantly, recent neurocomputational models distinguish two gating functions: an input gate for updating task-relevant information into working memory and an output gate for selecting which of the currently maintained representations exerts a top-down influence on attention and behavior (reviewed in Chatham & Badre, 2015). Modeling and empirical work in adults has highlighted output gating, in particular, as potentially important for higher order rules (Badre & Frank, 2012; Chatham et al., 2014). This motivates the hypothesis that developmental change in the output gating component may be particularly important for changes in hierarchical cognitive control. To test this hypothesis, we next asked to which degree working memory updating in the transition from childhood to adolescence is constrained by inefficiencies in selective input and/or output gating mechanisms. Since Experiment 1 showed that the most pronounced developmental change in higher order rule use occurs between late childhood and adolescence, the second experiment exclusively focused on these two age groups.

3. Experiment 2

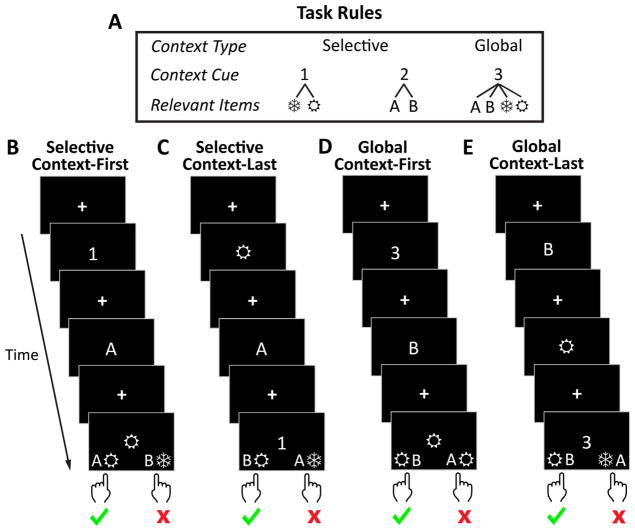
In Experiment 2, we capitalized on an established paradigm that independently manipulates demands on input vs. output gating using a 2nd order conditional rule task (Chatham & Badre, 2013; Chatham et al., 2014). We collected data from children and adolescents within the same age range as in Experiment 1 (7–17 years). On each trial, participants were shown sequences of three items: a digit, a letter, and a symbol. The digit cued whether responses should be made on the basis of the letter, the symbol, or both (Fig. 3A). So, the digit was a 2nd order context that specified which items (letters, symbols, or both) would provide the 1st order context for the motor response. Importantly, the presentation order of the digit, letter, and symbol was unpredictable. Thus, on context first trials, the 2nd order context (i.e., the digit) appeared prior to the lower-order items (letters or symbols), permitting participants to update only the relevant upcoming item into working memory. Thus, an input gating strategy could be used on context first trials. When the context appeared last (context last) participants had to input both of the items into working memory, as they did not know which would be relevant. Then, at the final context presentation, they selected an item from working memory to guide their response. Thus, context last trials required output gating.

Fig. 3.

Task rules (A) and example trial events for the four different conditions (B–E). (A) A second order rule related three contextual elements, a digit (1, 2, 3), a letter (A, B), and a symbol ( ,❄), to a response. As depicted, the digit acts as higher order context such that its identity determines whether the symbol (digit = 1), the letter (digit = 2), or both (digit = 3) determines the response. (B–E) On each trial of the experiment, a digit, letter, and symbol are presented in an unpredictable order. At the end of each trial, participants use response mappings presented at the bottom of the screen to indicate whether the target item, as specified by the rule, is shown on the left or right side of the screen. Left or right is indicated by a button press. The correct response in all example trials is “left”. (B) When the “1” appears first (context first-selective), participants know that they need only input the “ ” into working memory and can ignore the “A”. Thus, an input gating strategy is available. (C) When the “1” appears last, (context last-selective), participants have to input both “ ” and “A” into working memory, as they do not know which will be relevant. Then, at the final context presentation, they select the “ ” from working memory to guide their response. Hence, they must use an output gating strategy. (D and E) In order to control for differences in working memory load in context first vs. context last conditions, a global context cue (the digit “3”) specifies that a conjunction of both lower-level items determines the correct response. In contrast to the selective context cues (the digits “1” or “2”), a global context cue always requires holding two items in working memory, irrespective of whether it appears first (D) or last (E).

Notably, using the input gating strategy on context first trials would require holding only one lower order item in working memory. Whereas on context last trials, two lower order items must be maintained because participants do not know which will be relevant until the context appears. As such, working memory load would always be lower on context first than context last trials and would confound the input vs. output gating difference between these conditions. Thus, to control for working memory load, we also included a global context cue (the digit “3” in Fig. 3A) that specified that a conjunction of both lower-level items determined the correct response (Fig. 3D & E). So, in contrast to the selective context cues (the digits “1” or “2” in Fig. 3A), a global context cue always required holding two items in working memory. Context first and context last were crossed with selective/global to produce four conditions: context first-selective, context first-global, context last-selective, and context last-global.

Beyond controlling for working memory load, the selective-global distinction also provides a purer measure of output gating than the more general comparison of context first and context last conditions, which is likely to reflect other process differences between the two conditions besides output gating demands. One such factor is that in the context last conditions, the higher order context cannot be updated until the end of the trial, i.e., the appropriate rule needs to be set and maintained before selection from working memory can begin. Thus, the additional time required for input gating of the context contributes to the RT differences between context first and context last conditions. By contrast, context last-selective and context last-global conditions differ only in terms of the higher output gating demand associated with singling out one of the two maintained items on context last-selective trials— as opposed to uniformly output gating all working memory representations on context last-global trials.

In a similar vein, the comparison of context first-selective and context first-global conditions provides a measure of the efficiency of selective input gating. As stated above, successful use of a selective input gating strategy on context first-selective trials is associated with reduced working memory load. Consequently, the more efficiently participants use a selective input gating strategy in the context first-selective condition, the more their performance should benefit compared to the context first-global condition, where this strategy is not applicable.

A final point to consider is that when the context appears last (context last conditions), one must use an output gating strategy, as it is not possible to know which of the preceding items will be relevant to the response. However, when the digit (higher order rule/context) appears first (context first conditions), participants can use either a selective input gating strategy or an output gating strategy, as they could choose to wait until both items are presented to select one for responding. So, in Fig. 3B, a child might update the “1”, “ ”, and “A” into working memory and then select the “ ” from working memory based on the “1”. Employing an input gating strategy in this task is a form of proactive control or preparedness (Braver, 2012) and can reduce working memory load when only one lower order item needs to be maintained (i.e., in the selective condition). By contrast, the output gating strategy is reactive and may be more costly both in terms of working memory load and the demands on gating. Despite these potential disadvantages to reactive control, previous work suggests younger children mix modes of control—acting at times proactively and at other times reactively—even when contextual information is available in advance (Blackwell & Munakata, 2014; Chatham, Frank, & Munakata, 2009; Lorsbach & Reimer, 2010; Lucenet & Blaye, 2014).

Thus, one must control for developmental change in reactive and proactive control in order to isolate developmental changes in the efficiency of input and output gating mechanisms. That is, we must first isolate context first trials where participants are using a proactive versus reactive strategy, and then compare RTs separately for these two trial types across our age range. We applied a hierarchical Bayesian mixture model to identify two mixture components: one representing a fast or proactive RT distribution, characterizing trials on which subjects select the appropriate rule upon presentation of the context stimulus, and the other representing a slow or reactive RT distribution, characterizing trials on which subjects select the appropriate rule only upon presentation of the response prompt at the end of the trial.

3.1. Methods

3.1.1. Participants

The sample included a total of 37 typically developing children (N = 18; ages 7–11, M = 9.2, SD= 1.0; 8 females) and adolescents (N = 19; ages 12–17, M = 14.2, SD = 1.6; 11 females). One further adolescent and three further children were tested but excluded from analyses because performance was at chance level in at least two out of the four experimental conditions. All consenting and screening procedures were as in Experiment 1.

3.1.2. Materials and task

As illustrated in Fig. 3, each trial consisted of a sequence of a three stimuli (digit, letter, and symbol) appearing in random order. Stimuli were drawn from three possible digits (“1”, “2”, “3”), two possible letters (“A”, “B”) and two possible wingdings ( , ❄). Simultaneously with the last stimulus in each sequence, two probes (each consisting of a letter and a symbol) were displayed at the bottom left and right of the screen. Participants pressed a button (“F” and “J” on a standard computer keyboard) corresponding to the side (left or right) where the relevant item appeared (Fig. 3B–E). Target and distractors positions were unpredictable, that is, the individual letters and symbols could appear in each of the four probe locations.

The digit acted as higher order context such that depending on its identity, participants chose one of three lower order response rules. Digits 1 and 2 were selective conditions and indicated that only the letter or only the symbol was response-relevant, respectively. The digit 3 was the global condition and indicated that both the letter and symbol in that sequence was the target. In order to make sure that participants process all relevant lower order items, one of the presented items (either symbol or letter) appeared as distractor on the incorrect side of the screen on 50% of trials in both selective and global conditions (Fig. 3C and D). Thus, for example, if participants paid attention to only one of the two items in the global condition, they would not be able to make a decision on trials where both response probes contain this item.

To dissociate input and output gating mechanisms, the context digit was presented either before (context first) or after (context last) the remembered items. For instance, in Fig. 3B, seeing the “1” first, meant a participant need only input the “ ” into working memory and ignore the “A” (selective input gating). In Fig. 3C, in contrast, the “ ” and “A” were first input to working memory and then the “ ” was selected from working memory when “1” was presented (selective output gating). Context first and context last were crossed with selective/global to produce four conditions: context last-selective, context first-selective, context last-global, and context first-global.

In order to make the position of the context cue within a sequence less predictable, the task also included trials on which the digit context cue appeared between the two lower level items. Though of theoretical interest (see Chatham & Badre, 2013; Chatham & Badre, 2015), these context middle events will not be considered further in the present work that is focused on gating mechanisms.

3.1.3. Procedure

Participants were presented with white digits, letters, and symbols displayed in the center of a computer screen on a black background. Each stimulus within a sequence was shown for 500 ms. The fixation interval between the presentation of the first and second stimulus as well as the second and third stimulus was jittered between 1000 ms (~60%), 3000 ms (~30%), and 5000 ms (~10%). Simultaneously with the onset of the last item in a sequence, the probes appeared on the screen for a maximum of 4000 ms until a response was made. The inter-trial-interval was jittered between 700 ms (~75%), 1400 ms (~25%), and 2300 ms (~5%). There were 30 sequences for each of the four experimental conditions (context first-selective, context first-global, context last-selective, context last-global), resulting in a total of 120 trials. Different trial types were presented in random order throughout the experiment. Participants were tested individually in a single test session that took about 45 min to complete.

Before the start of the experiment, participants were taught the use of global and selective rules in the different conditions. After a detailed explanation of task procedure and response requirements, the experimenter walked the participant trough a series of demo trials—one for each experimental condition. The participant then performed the demo trials by themselves, verbalizing their decisions at each step. The experimenter provided feedback after each trial and reminded the participant of the correct rules if necessary. There was no response time limit and training was continued until the participant responded correctly to all trial types. Participants then completed a practice block of 30 trials under experimental settings. Practice was repeated until performance was above chance level.

3.1.4. Analysis of accuracy and RTs

The first ten experimental trials were excluded from analysis, as were responses with latencies faster than 200 ms or slower than the outlier criterion (Tukey, 1977). Since overall means and variances of response latencies differed between the age groups, F (1,35) = 18.89, p < 0.001 and F(1,35) = 6.10, p = 0.019, respectively, mean RTs were square-root transformed prior to analysis as in Experiment 1. All Figures depict raw means, as is the proper convention. Accuracy rates and RTs for correct responses were analyzed by separate ANOVAs with the between-subject factor age group (children, adolescents) and the within-subject factors context order (context first vs. context last) and selection demand (selective vs. global).

3.1.5. Mixture model of reaction time distributions

As noted above, the context first-selective condition can either be performed using a proactive input gating strategy or a reactive output gating strategy. Thus, in order to test estimate the proportion of proactive versus reactive context first trials across the two age groups, we fitted a hierarchical Bayesian Gaussian mixture model (adapted from Almond, 2014) to individual RT distributions. Hierarchical Bayesian techniques assume that individual parameter values are drawn from group-level distribution and take into account similarity between individuals to obtain more reliable subject-specific parameters, which are estimated simultaneously with the group distribution. This approach is particularly suited for developmental studies because it efficiently pools information across individuals and thus requires fewer numbers of trials per subject and condition (e.g., Kruschke, 2010; Lee & Wagenmakers, 2013). The model included two mixture components that represent a fast and a slow RT distribution. For context first-selective trials, we reasoned that the fast distribution was more likely to include trials on which a proactive input gating strategy was used, whereas the slow distribution was more likely to include trials on which a reactive output gating strategy was employed.

It should be noted that the RT distribution analysis by itself cannot tell whether participants actually used an input or output gating strategy; it just estimates whether the RTs come from two different distributions (slow vs. fast). Theoretically, many factors, such as inattention, forgetting, or fatigue, could cause this kind of mixture distribution. Those factors, however, should affect the experimental conditions in a uniform manner. As a result, their effects should not systematically differ across context first and context last conditions. Instead, we expected age differences in the proportion of trials from the slow distribution vs. fast distribution to be greater in the context first condition than in the context last condition. Context last trials thus served as an important control to make sure that the age-differential effects in the mixture distribution analysis do not simply due to children being generally more inattentive or forgetful than adolescents.

Model fitting yielded estimates of three Level 1 (subject-specific) parameters for each of the two components, representing mean (μ_i), precision (τ_i),² and a mixing probability π_i, that determines the likelihood that a given trial will be drawn from the fast or slow distribution. On context first-selective trials, then, the mixing probability corresponds to the proportions of proactive and reactive trials. Components were identified by placing an ordering constraint on the parameter vector μ₀. The proactive distribution was identified as the component with the faster mean RT. Note that since the proportions of fast and slow trials add to one, the corresponding parameters were not estimated independently. The prior distributions for Level 1 parameters were given by

$$\begin{gathered} {\mu }_{i,\mathit{fast}[\mathit{slow}]}~\mathcal{N}({\mu }_{0,\mathit{fast}[\mathit{slow}]},{\beta }_{0,\mathit{fast}[\mathit{slow}]}) \\ log({\tau }_{i,\mathit{fast}[\mathit{slow}]})~\mathcal{N}(log({\tau }_{0,\mathit{fast}[\mathit{slow}]}),{\gamma }_{0,\mathit{fast}[\mathit{slow}]}) \\ {\pi }_i~\text{Dirichlet}({\alpha }_{\mathit{fast}},{\alpha }_{\mathit{slow}}) \end{gathered}$$

where i ∈ {1,…,N} is the subject index, while fast and slow indicate the fast (proactive) and slow (reactive) distributions, respectively. The script 𝒩 denotes the normal distribution. These subject-specific parameters were assumed to be drawn from group distributions, specified by Level 2 (across-subject) parameters α, μ₀, β₀, η₀, and γ₀ with the following hyperpriors

$$\begin{gathered} {\alpha }_0~\text{Dirichlet}(0.5,0.5) \\ {\mu }_{0,\mathit{fast}[\mathit{slow}]}~\mathcal{N}(0,1000) \\ log({\beta }_{0,\mathit{fast}[\mathit{slow}]})~\mathcal{N}(0,1) \\ log({\tau }_{0,\mathit{fast}[\mathit{slow}]})~\mathcal{N}(0,1) \\ log({\gamma }_{0,\mathit{fast}[\mathit{slow}]})~\mathcal{N}(0,1) \end{gathered}$$

The joint posterior distribution of all model parameters was obtained using Markov chain Monte Carlo (MCMC) sampling (Gamerman & Lopes, 2006). The results represent averages across 30 Markov chains, each of which was run 10,000 iterations (the first 1000 iterations were discarded as burn-in). In order to test for pseudo-convergence of the chains, the Gelman-Rubin R̂ statistic (Gelman & Rubin, 1992; Gelman & Shirley, 2011) was computed. This statistic will be close to 1 if the samples of the different chains are indistinguishable, i.e., if the chains mix well. All R̂ coefficients were less than 1.02, indicating proper convergence. Model fit was evaluated by calculating the Watanabe-Akaike information criterion (WAIC; Watanabe, 2010) and the deviance information criterion (DIC; Spiegelhalter, Best, Carlin, & van der Linde, 2002). In both cases, lower values indicate better fit. We also tested whether the two-component mixture model fits the observed data better than a single component (i.e., non-mixture) or a three-component mixture model. All Bayesian analyses were performed using RStan (Stan Development Team, 2014).

3.2. Results

3.2.1. Accuracy and reaction time

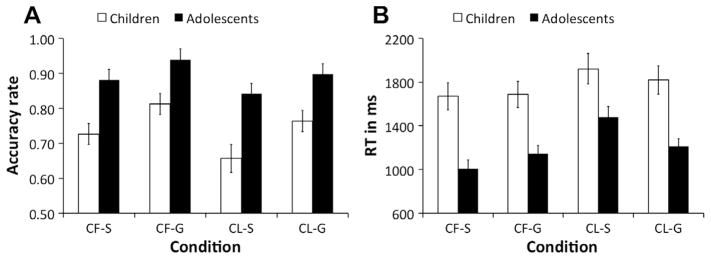
As plotted in Fig. 4A, accuracy in both groups was higher in the context first than context last conditions (F(1,35) = 15.24, p < 0.001, ${\mathrm{\eta }}_{\mathrm{p}}^2=0.30$) and for global than selective conditions (F (1,35) = 14.39, p = 0.001, ${\mathrm{\eta }}_{\mathrm{p}}^2=0.29$), largely mirroring prior observations in adults (Chatham et al., 2014). Adolescents were more accurate overall than children F(1,35) = 17.30, p < 0.001, ${\mathrm{\eta }}_{\mathrm{p}}^2=0.33$. No interactions with age group reached significance (all ps > 0.28).

Fig. 4.

Behavioral results from Experiment 2. Bars plot mean accuracy rates (A) and mean RT (B) for children and adolescents across context first-selective (CF-S), context first-global (CF-G), context last-selective (CL-S), and context last-global (CL-G) conditions. Error bars plot standard error of the mean.

The ANOVA on mean RT revealed a main effect of context order, F(1,35) = 56.81, p < 0.001, ${\mathrm{\eta }}_{\mathrm{p}}^2=0.62$, indicating that responses were slower in context last conditions relative to context first conditions (Fig. 4B). This difference was also evident when comparing RTs in context last conditions only to the load-matched context first-global condition, F(1,35) = 45.89, p < 0.001, ${\mathrm{\eta }}_{\mathrm{p}}^2=0.57$. These results are consistent previous findings in adults (Chatham et al., 2014) showing that the additional output gating demand in context last conditions (compared to context first conditions) is associated with an increase in RT independent of working memory load. However, since other factors than output gating may contribute to performance differences between context first and context last conditions, it was important to determine whether higher output gating demands also resulted in slower RTs in the context last-selective compared to context last-global conditions. This was confirmed by a context order × selection demand interaction, F(1,35) = 58.55, p < 0.001, ${\mathrm{\eta }}_{\mathrm{p}}^2=0.63$. While the context first-selective condition benefitted performance relative to the context first-global condition (by reducing working memory load), t(36) = −3.04, p = 0.004, the context last-selective condition was associated with greater RT cost, even relative to the context last-global condition, t (36) = 5.27, p < 0.001.

In order to make sure that the latter finding did not reflect a differential impact of distractor items on response selection in context last-selective vs. context last-global conditions, we compared RTs on trials containing a distractor in the probe display to those without distractors. As expected, RTs were slower on trials with distractors than those without distractors, F(1,35) = 8.16, p = 0.009, ${\mathrm{\eta }}_{\mathrm{p}}^2=0.19$. However, there was no evidence for a distractor × selection demand interaction in either children or adolescents (ps > 0.35) nor was there a significant age group × distractor × selection demand interaction (p = 0.61). Responses to context last-selective trials (children: M_NoDistractor = 1846 ms vs. M_Distractor = 2026 ms; adolescents: M_NoDistractor = 1418ms vs. M_Distractor = 1471 ms) were always slower than to context last-global trials (children: M_NoDistractor = 1783 ms vs. M_Distractor = 1859 ms; adolescents: M_NoDistractor = 1164ms vs. M_Distractor = 1200 ms). Thus, even when both target and irrelevant item are associated with the same response (no distractor), the context last-selective condition imposes an additional performance cost.³

Furthermore, performance differed by age group. The ANOVA on mean RT revealed a main effect of age group, F(1,35) = 18.37, p < 0.001, ${\mathrm{\eta }}_{\mathrm{p}}^2=0.34$, reflecting overall slower responses in children (Fig. 4B). Moreover, there was context order × selection demand × age group interaction, F(1,35) = 21.49, p < 0.001, ${\mathrm{\eta }}_{\mathrm{p}}^2=0.38$, indicating that the effects of context order and selection demand differed across age groups. We followed this final interaction with separate analyses of the context first and context last conditions. We begin with a comparison of the context last-selective and context last-global conditions, which is a purer measure of output gating performance than the comparison of context first and context last conditions. This is because the context last-selective condition differs from the context last-global condition primarily in terms of the higher output gating demands associated with selecting only one item – as opposed to all information – maintained in working memory, while nuisance factors are mostly identical for the two conditions.

When context information was presented last, we found a selection demand × age group interaction, F(1,35) = 8.41, p = 0.004, ${\mathrm{\eta }}_{\mathrm{p}}^2=0.19$. Both groups were faster on global than selective trials (ps < 0.022), and adolescents overall outperformed children in both context last-selective and context last-global conditions (ps < 0.010). This benefit, however, was greater on context last-global than context last-selective trials. In line with findings in adults (Chatham et al., 2014), these data suggest that singling out only one working memory representation (instead of simply output gating everything from working memory) is more challenging to both age groups, and adolescents benefit more from lower selection demands in the global condition. Nevertheless, adolescents performed better than children in both context last-selective and context last-global conditions.

While RT differences between context last-selective and context last global conditions were smaller in children compared to adolescents, accuracy rates showed the opposite pattern (Fig. 4A). This indicates that children might have responded faster at the cost of higher error rates in context last-selective condition. In order to account for this speed-accuracy trade-off, we ran an additional analysis that combined the two measures. For each participant, we calculated the inverse efficiency score by dividing mean RT for a given condition by the corresponding accuracy rate. An ANOVA with the factors context order (first vs. last) and selection demand (global vs. selective) yielded a marginally significant age group × selection demand interaction, F(1,35) = 3.42, p = 0.07, ${\mathrm{\eta }}_{\mathrm{p}}^2=0.09$, indicating that age differences in performance were relatively larger for selective ( $M_{\text{context}\text{first-selective}}^{\text{diff}}=1258,M_{\text{context}\text{last-selective}}^{\text{diff}}=1346$) compared to global conditions ( $M_{\text{context}\text{first-global}}^{\text{diff}}=896,M_{\text{context}\text{last-global}}^{\text{diff}}=1090$). Thus, when considering RT and accuracy simultaneously, children show greater performance costs in the conditions that require selective (output) gating.

Furthermore, we hypothesized that children’s disproportionally low accuracy rates in the context last-selective condition would reflect a relatively higher proportion of fast guesses. This might have reduced children’s mean RT in the context last-selective condition. In order to test this hypothesis, we calculated accuracy rates separately for each quartile of the RT distribution (including both correct and incorrect responses) for all four conditions in both age groups. As expected, this analysis revealed that accuracy for the fastest responses (first quartile) in the context last-selective condition was at chance level in children (M = 0.52, SE = 0.21) but well above chance in adolescents (M = 0.83, SE = 0.16). In all other conditions, performance for the fastest responses was above chance in both children (M > 0.63) and adolescents (M > 0.87). Thus, a relatively higher proportion of correct responses resulting from fast guesses in children might have diminished age-related RT differences in context last-selective condition.

The comparison of context first-selective and context first-global conditions provides a measure of how efficiently participants used selective input gating to reduce working memory load on context first-selective trials. This analysis also resulted in a selection demand × age group interaction, F(1,35) = 6.37, p = 0.016, ${\mathrm{\eta }}_{\mathrm{p}}^2=0.14$, reflecting that only adolescents, t(18) = −3.45, p = 0.003, but not children, t(17) = −0.61, p = 0.55, were faster in context first-selective than context first-global conditions. Thus, adolescents appeared to be taking advantage of context information when it is presented first to constrain input gating of information needed for action selection. By contrast, children showed no benefit from having received contextual information when it allowed reducing working memory load (context first-selective condition) as compared to when it did not (context first-global condition). However, as noted above, performance in the context first condition can be driven by the use of a proactive control strategy, a reactive control strategy, or a mixture. We address these alternatives next using a hierarchical mixture distribution modeling approach.

3.2.2. Developmental dissociations in control strategy and gating efficiency

The observed lack of RT benefits on context first-selective trials in children could result from a failure of input gating or be due to the greater use of reactive control. Predominant use of a reactive control strategy would slow children’s RTs to approximate those of the output gating conditions (context last). Age-related differences in performance might be thereby diminished. To test this possibility, we first established differences in the dynamics of control across groups by fitting a hierarchical mixture model with two components – one representing the slower (reactive) distribution and the other one representing the faster (proactive) distribution – to each participant’s RT data in the context first-selective and context last-selective conditions.⁴ Importantly, while mixing a proactive and reactive strategy could occur in the context first condition, participants could use only one strategy (output gating) on context last trials. The context last condition thus served as a control to test the validity of the premise that the two components of the mixture model reflect proactive vs. reactive strategy use rather than other, non-specific factors that could result in a mixture of slow and fast distributions. General variables, such as children’s greater susceptibility to distraction or fatigue, should have similar effects on the proportion of slow trials in context first-selective and context last-selective conditions and hence should result in similar mixing probabilities and model fit. By contrast, if the components reflect proactive vs. reactive strategy use, the mixture model should not fit as well or show as large a difference in mixing between age groups for context last-selective compared to context first-selective.

The estimated group-level mixing probabilities (α) and the corresponding estimates of mean RTs for the fast (μ_0,fast) and slow(μ_0,slow) distributions are given in Table 1. In the context first-selective condition, children drew more often from the reactive (slow) distribution than adolescents (0.46 vs. 0.26), while age differences in mixing probabilities were strongly reduced in the context last-selective condition (0.42 vs. 0.43).

Table 1.

Estimated group-level mixing probabilities (α) and mean RTs (μ₀) for the fast and slow distributions in context first-selective and context last-selective conditions.

Parameter	Context first-selective		Context last-selective
	Fast	Slow	Fast	Slow
Children
α	0.54	0.46	0.58	0.42
μ0	1202	2375	1707	2410
Adolescents
α	0.74	0.26	0.57	0.43
μ0	788	1490	1199	1813

Note. The α parameters correspond to the probability that a given trial draws its RT from mutually exclusive fast or slow RT distributions, respectively. For context first-selective only, these two distributions can reflect the use of a proactive input gating strategy versus a reactive output gating strategy.

We used Bayesian parameter estimation to determine whether the across-condition changes in the mixing probabilities differed significantly between the two age groups. Specifically, we computed the 2.5 and 97.5 percentiles of the posterior of a group-level variable ( ${\alpha }_{\mathit{slow}}^{(\mathit{diff})}$) that models the difference between mixing probabilities for the slow distribution in context first-selective vs. context last-selective conditions (i.e., ${\alpha }_{\mathit{slow}}^{(\mathit{diff})}={\alpha }_{\mathit{slow}}^{(cf)}-{\alpha }_{\mathit{slow}}^{(cl)}$), separately for children and adolescents. A significant difference is detected when the Bayesian 95% credible intervals of the posterior distributions for children and adolescents do not overlap. Results showed that this was indeed the case; the 95% credible interval for ${\alpha }_{\mathit{slow}}^{(\mathit{diff})}$ extended from −0.15 to 0.08 in children and from 0.10 to 0.30 in adolescents. Both WAIC and DIC values indicated that the 2-component mixture model fitted the observed data in the context first-selective condition better than models with either 1 or 3 components (Table 2). In contrast, for the context last-selective condition, neither WAIC nor DIC clearly favored the 2- component model over the 1-component or 3-component models.

Table 2.

WAIC and DIC values indicating model fit for models with 1 component (non-mixture), 2, or 3 mixture components. Lower values indicate better fit.

Number of components	WAIC		DIC
	Context first-selective	Context last-selective	Context first-selective	Context last-selective
1	429	557	531	589
2	421	559	518	588
3	456	555	625	612

The finding that children showed a higher proportion of trials from the slow distribution selectively in the context first-selective condition and the fact that only the context first-selective condition was fit well by the mixture model suggest that children are indeed using a mixture of reactive and proactive control modes when context information is presented first.

The critical question then is whether, when RTs are confined to those trials in which participants do use a proactive (selective input gating) vs. reactive (selective output gating) strategy, there are developmental differences in performance that would indicate developmental change in efficiency of input gating or output gating. If children are inefficient input gaters, then they should be particularly slow compared to adolescents when using a proactive input gating strategy. That is, age difference should be relatively greater for trials from the fast distribution compared to trials from the slow distribution in the context first-selective condition. However, if children are disproportionally slower when using a reactive output gating strategy in the context first-selective condition, this would indicate that they are inefficient output gaters. In the latter case, age differences should be relatively greater for the slow compared to the fast distribution. Again, we expected to find age-specific effects in mean RT differences for the two distributions specifically in the context first-selective condition—where both proactive and reactive strategies are available—rather than in the context last-selective condition.

For each participant, each trial of the context first-selective and context last-selective conditions was assigned to either the fast or slow distribution by calculating the posterior probability that the RT was drawn from either of the two components, using Bayes’ theorem

$$p_{i,j,k}^{(c,r)}\propto {\pi }_{i,k}^{(c,r)}\varphi \left(\frac{Y_{i,j}-{\mu }_{i,k}^{(c,r)}}{{\sigma }_{i,k}^{(c,r)}}\right),$$

where ϕ(·) denotes the unit normal density and $p_{i,j,k}^{(c,r)}$ is the posterior probability of the component k (fast vs. slow) for draw r of chain c given the data (RT) observed on trial j in subject i. The estimate for p_i,j,k is then calculated as the average over all MCMC draws of $p_{i,j,k}^{(c,r)}$

$$\frac{1}{CR}\sum _C\sum _R{p}_{i,j,k}^{(c,r)}.$$

A trial was assumed to be sampled from the fast distribution if p_{i,j,fast >} p_i,j,slow and otherwise from the slow distribution.

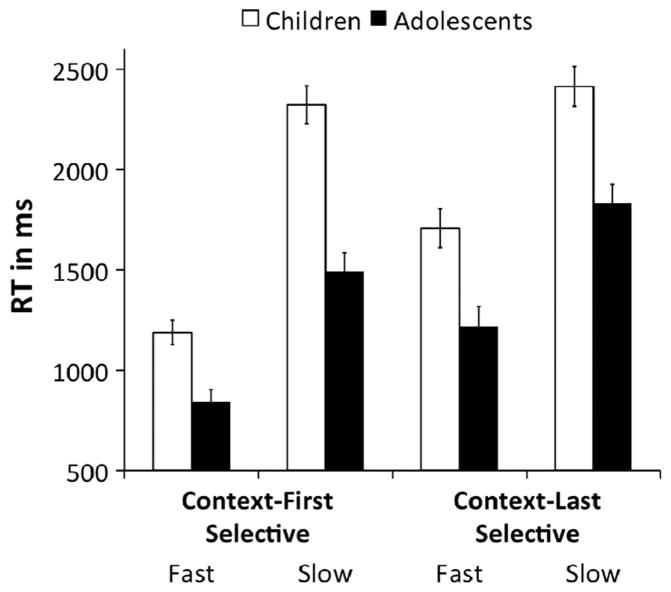
Fig. 5 shows mean RTs for trials from the fast vs. slow distribution in context first-selective and context last-selective conditions, separately for the two age groups. An ANOVA with the factors age group, component (fast vs. slow), and context order (context first vs. context last) revealed a significant three-way interaction, F(1,34) = 11.13, p = 0.002, ${\mathrm{\eta }}_{\mathrm{p}}^2=0.25$. We followed this interaction with separate analyses for context first and context last conditions. For the context first condition, the analysis yielded a significant age group by component interaction, F(1,34) = 36.99, p < 0.001, ${\mathrm{\eta }}_{\mathrm{p}}^2=0.52$, indicating that the difference between children and adolescents was much greater when children adopted a reactive strategy (slow distribution). While a reactive strategy was unsurprisingly costly for both groups on context first trials, children showed a greater decrease in RT on trials from the fast relative to the slow distribution than adolescents (1134 ms vs. 651 ms). In contrast, there was no significant age group by component interaction in the context last condition (p > 0.25), confirming the specificity of the developmental differences in the context first condition. In sum, these findings indicate that children use a selective input gating strategy less often. However, when they do engage in a selective input gating strategy, they approximate adolescent performance more closely than when they rely on more slowly developing output gating mechanisms.

Fig. 5.

Bars plot mean RT for the proactive vs. reactive distributions as a function of condition (context first-selective [CF-S]/context last-selective [CL-S]) and age group (children/adolescents). Greater slowing for children relative to adolescents is evident for reactive versus proactive distributions in context first-selective relative to context last-selective. Error bars plot standard error of the mean.

4. General discussion

In two experiments, we examined potential mechanisms underlying developmental improvements in rule-guided behavior from late childhood through adolescence. In particular, we tested the hypothesis that hierarchically organized gating mechanisms that control information flow into and out of working memory provide a key to understanding this developmental trajectory. Experiment 1 verified that age-related improvements in the capacity to manage increasingly higher order rules cannot be explained by working memory maintenance limitations alone. The results of Experiment 2 then provided evidence for more pronounced developmental change in output gating mechanisms that select which of the currently maintained working memory representations can exert an influence over behavior, above and beyond those that select task-relevant information to be updated into working memory (input gating). Further, we found that despite being more inefficient at output gating, younger children tended to rely more on output gating than input gating when given the option, showing a preference for reactive rather proactive control.

The results of Experiment 1 replicated and extended prior work (Amso et al., 2014) by demonstrating that the development of rule-guided behavior is uniquely linked to the hierarchical complexity of the rule (i.e., rule order) not only in 1st and 2nd order, but also in 3rd order rule tasks. By contrast, we found no clear evidence to suggest that increasing working memory demands, in the form of a larger number of alternatives for action at any single level of the hierarchy, affected performance differentially across the three age groups. These results are consistent with arguments that preschool-aged children’s difficulties with flexible rule switching on the Dimensional Change Card Sort cannot be explained by constraints on working memory capacity alone. In a series of studies, Zelazo et al. (2003) also showed that 3- and 4 year old children are able to flexibly use four lower order rules, as long as these rules are not in conflict. The authors interpreted their findings as indicating that children’s performance is limited by the degree to which lower order rules need to be embedded under higher order rules, rather than the number of parallel rules at a given level of the hierarchy (as formulated in the framework of the Cognitive Complexity and Control theory; e.g., Zelazo & Frye, 1998). Along with the work by Amso et al. (2014), the present study provided a stringent test of this hypothesis by using a paradigm that orthogonally manipulates increases in hierarchical rule order vs. increases in the number of rule alternatives at each hierarchical level.

With respect to working memory gating, Experiment 2 was motivated by emerging evidence that separate mechanisms control input gating of information to be maintained in working memory and output gating of information from working memory to bias thought and action (Chatham & Badre, 2015). Specifically, output gating has been shown to be particularly important, relative to input gating, for the execution and learning of abstract, higher order rules in adults (Badre & Frank, 2012; Chatham et al., 2014; Frank & Badre, 2012). However, selecting items from within working memory (output gating) can be more resource demanding than the selection of items to update working memory (input gating). And further, selecting specific items from working memory (i.e., selective output gating) is more resource demanding than having to gate out all the presented information (i.e., global output gating). We observed similar patterns here and further saw differences in age groups, suggesting that selective output gating may undergo a more protracted developmental change, possibly extending beyond childhood and adolescence into young adulthood. While it seems somewhat surprising that we found larger age-related RT differences for global relative to selective output gating, accuracy rates showed the opposite pattern. Indeed, combined analysis of RT and accuracy data revealed disproportionally larger performance costs for selective compared to global (output) gating in children. Moreover, a more detailed inspection of accuracy rates across quartiles of the RT distribution suggested that children’s responses in the context last-selective condition were more likely to reflect fast guesses than their responses in all other conditions. Taken together, these findings support the notion that children’s mean RTs in the context last-selective condition do not fully reflect the true efficacy of the underlying gating mechanisms.

There are at least two possible explanations of why selection of subsets of information from working memory is more demanding than allowing all information to jointly influence response selection. First, faster RTs in the context last-global condition might reflect a congruency effect on gating. Note that on global trials, the output gates for both working memory representations should be opened in order to allow the two maintained items to jointly bias attention towards the conjunction match (congruent gating policy). By contrast, in the context last-selective condition only the gate on the relevant item should be opened, whereas the gate on the irrelevant item must remain closed (incongruent gating policy). The current findings suggest that adolescents may benefit more from the congruent gating policy in the context last-global condition than children. Second, some computational models of working memory gating assume that the closure of the output gate for one of the two items in the context last-selective condition requires an inhibitory pathway (e.g., the NoGo pathway in the basal ganglia, Frank & Badre, 2012). Activation of an inhibitory pathway could account for the behavioral slowing in this condition. From our results, it appears that children and adolescents are similarly affected by such an inhibitory effect.

Our findings from the context first condition further revealed that the costs of output gating in childhood might be compounded by a strategic tendency toward reactive control. Specifically, the results indicate that while both age groups use a mixture of reactive and proactive control when provided with context first, adolescents are more likely than children to engage proactive control and the more efficient selective input gating strategy. This notion is consistent with previous work in younger children demonstrating that there is a shift in the temporal dynamics of control from a purely reactive control mode to a more mixed reactive/proactive control mode by early childhood, with proactive control continuing to improve throughout adolescence (Andrews-Hanna et al., 2011; Blackwell & Munakata, 2014; Chatham et al., 2009; Lorsbach & Reimer, 2010; Lucenet & Blaye, 2014). However, the present findings also suggest that children can and do use a proactive input gating strategy, and when they do so, they approximated adolescents’ performance. Thus, in context first conditions, differences in performance between children and adolescents might be due to the use of an inefficient strategy (output gating) rather than inefficiency of the input gating strategy itself.

Though the present results do not provide evidence for developmental change in the efficiency of the input gating, we also cannot fully rule out that such inefficiency might be evident if probed differently. For example, it is possible that initial costs in updating working memory with the higher order context can be made up during the slack period of the trial. On this view, the higher proportion of reactive (or unprepared) context first trials could reflect input gating failures, i.e., trials where children failed to update proactively and so had to output gate. Nevertheless, the present data indicate that (1) output gating is less efficient in children than in adolescents and (2) children preferentially adopt a reactive control strategy, thereby utilizing less efficient mechanism more often.

Given that the output gating strategy is less efficient across all age groups—and especially so in children—one might ask why children nonetheless opt for this less efficient option more often? One answer to this question was provided in the preceding discussion: children are simply forced to engage in output gating more often because of a higher frequency of input gating failures. However, another possibility relates to deficiencies in stable meta-task control, such as the sustained maintenance of the meta-task-set or task instructions. This kind of sustained control may be supported by a different and relatively later maturing functional brain network than adaptive trial-to-trial control (Fair et al., 2008; Power, Fair, Schlaggar, & Petersen, 2010), and/or could depend on an additional super-ordinate 3rd order rule or across-trial context (cf. Herd et al., 2014). Indirect evidence for this possibility comes from previous research indicating that children’s deficits in flexible rule use largely derive from their difficulties to translate higher order task cues into rule representations (Chevalier & Blaye, 2009; Lorsbach & Reimer, 2010). The effort in anticipation of an outcome may also play a role in less proactive control, regardless of its relative efficiency. It is notable, in this regard, that elderly populations also tend to use a reactive control strategy more often than young adults (Braver, Paxton, Locke, & Barch, 2009). Accounts of this difference similarly depend on how older adults weigh the relative costs and benefits of a sustained proactive mode versus a periodic reactive strategy (Braver, 2012). Children and adolescents might, correctly or not, differ regarding in the anticipated cost of proactively updating higher order rules versus the benefit to performance of using this strategy.

Connecting the development of rule-guided behavior to output gating also holds intriguing implications for the specific neural systems that might undergo developmental change, as research in adults has begun to elaborate the neurobiological mechanisms that support output gating. Selective input and output gating of higher and lower order information is thought to be controlled by dynamic gating signals from the basal ganglia that are connected with prefrontal cortex via parallel, hierarchically organized corticostriatal loops (reviewed in Chatham & Badre, 2015). Chatham et al. (2014) used the same task as in Experiment 2 and showed that frontostriatal connectivity correlates with the reliability of selective output gating mechanisms in adults. Likewise, there is growing evidence from functional neuroimaging studies for experience-dependent developmental plasticity of connectivity patterns in widespread cognitive control networks in general and corticostriatal circuits in particular (e.g., Fair et al., 2008; Gianaros et al., 2011; Kelly et al., 2009; van den Bos, Cohen, Kahnt, & Crone, 2011). Accordingly, developmental improvements in output gating could be indicative of experience-dependent changes in corticostriatal dynamics that determine the efficiency of hierarchical gating (Chatham et al., 2014). This hypothesis will be important to test in future research.

Finally, it should be acknowledged that our interpretation of the developmental differences we observed in terms of output gating is necessarily indirect and so need to be confirmed by future studies. There are, however, several reasons why we believe our results can be most parsimoniously explained by developmental differences in output gating. First, Experiment 2 used an established paradigm that has been specifically designed to dissociate frontostrial input an output gating mechanisms as inspired by neurocomputational modeling of the relevant pathways (Frank & Badre, 2012). Using this paradigm, Chatham et al. (2014) found that frontostriatal structures supporting output gating are selectively recruited when context is presented last as compared to first and this effect was stronger on context last-selective than on context last-global trials (Chatham et al., 2014). Further, these frontostriatal dynamics predicted individual differences in behavioral measures exclusively in the context last-selective condition. Second, while alternative explanations for the observed age differences in the mixture of slow and fast distributions in the context first-selective condition are possible, it is not easy to see how they account for the differential pattern in context first and context last conditions. By contrast, the results of the mixture model analysis exactly matched the predictions deriving from the assumption that the participants used two strategies (proactive and reactive) in the context first condition but only one strategy (output gating) in the context last condition. Importantly, the notion that children opt more often for a reactive rather than a reactive strategy in the context first condition is also consistent with previous work on the development of the two control strategies (e.g., Andrews-Hanna et al., 2011; Blackwell & Munakata, 2014; Chatham et al., 2009).

Our findings, along with other recent work (e.g., Blackwell, Chatham, Wiseheart, & Munakata, 2014; Blackwell & Munakata, 2014), have important implications for programs that aim to improve executive functions across development. As cognitive control is multifaceted, it is important to characterize the specific mechanisms that are undergoing developmental change in order to direct interventions accordingly. As one example, results from training studies in developmental populations suggest that transfer depends on the engagement of working memory updating—as opposed to mere maintenance—during training (Pereg, Shahar, & Meiran, 2013; von Bastian & Oberauer, 2013; Zinke et al., 2014). Moreover, robust transfer effects have been consistently found for interventions that used task-switching paradigms as training tasks, especially in children and older adults (e.g., Karbach & Kray, 2009; Karbach & Unger, 2014; Zinke, Einert, Pfennig, & Kliegel, 2012). We suggest that this training-induced increase in cognitive flexibility is largely mediated by more efficient output gating of abstract rule representations that support generalization, learning and fluid reasoning. Training programs in children should be determined with respect to the goal they are intending to fulfill, but in any case are unlikely to be successful if the focus is on strengthening working memory from a maintenance capacity only perspective. If the goal is to improve behavioral regulation in children, an effective intervention might focus on shifting children to a more dominantly proactive mode of control, thereby engaging relatively more efficient input gating mechanisms. Braver et al. (2009), for example, showed that specific instruction was a powerful tool in shifting control dynamics from predominantly reactive to proactive in elderly populations. By contrast, interventions targeted at improving rapid generalization of learning might instead emphasize practice with reactive control, thereby taking advantage of the greater efficiency of output gating mechanisms and the benefits they may confer to generalization (Kriete & Noelle, 2011).