Assessing Long-Term Survival Benefits of Immune Checkpoint Inhibitors Using the Net Survival Benefit

Abstract

Background

The treatment effect in survival analysis is commonly quantified as the hazard ratio, and tested statistically using the standard log-rank test. Modern anticancer immunotherapies are successful in a proportion of patients who remain alive even after a long-term follow-up. This new phenomenon induces a nonproportionality of the underlying hazards of death.

Methods

The properties of the net survival benefit were illustrated using the dataset from a trial evaluating ipilimumab in metastatic melanoma. The net survival benefit was then investigated through simulated datasets under typical scenarios of proportional hazards, delayed treatment effect, and cure rate. The net survival benefit test was computed according to the value of the minimal survival difference considered clinically relevant. As comparators, the standard and the weighted log-rank tests were also performed.

Results

In the illustrative dataset, the net survival benefit favored ipilimumab [Δ($0$) = 15.8%, 95% confidence interval = 4.6% to 27.3%, P = .006]. This favorable effect was maintained when the analysis was focused on long-term survival differences (eg, >12 months, Δ($12$) = 12.5% (95% confidence interval = 4.4% to 20.6%, P = .002). Under the scenarios of a delayed treatment effect and cure rate, the power of the net survival benefit test compared favorably to the standard log-rank test power and was comparable to the power of the weighted log-rank test for large values of the threshold of clinical relevance.

Conclusion

The net long-term survival benefit is a measure of treatment effect that is meaningful whether or not hazards are proportional. The associated statistical test is more powerful than the standard log-rank test when a delayed treatment effect is anticipated.

Innovative research in recent years has led to the development of modern anticancer immunotherapies, such as monoclonal antibodies, T cell infusion, and cancer vaccines. These modern immunotherapies have been shown to result in a proportion of patients who remain alive or progression free even after a long-term follow-up. For example, ipilimumab, a monoclonal antibody targeting cytotoxic T lymphocyte-associated protein 5, has demonstrated a statistically significant improvement vs placebo in progression-free survival (PFS) and overall survival (OS) in phase III trials (1,2). The benefit in PFS and OS was mainly observed late during follow-up, with survival curves diverging after being superimposed during the early follow-up. The long-term survival benefit may herald a new era of therapeutic progress in oncology, but the statistical tests that served us well until now are no longer optimal to address such situations.

The treatment effect in survival analysis is most commonly quantified and reported as the hazard ratio (HR), a relative measure of the difference between two survival curves. In general, the hazard ratio is a function of time, but most of the methods used to estimate the hazard ratio assume the hazard rates are proportional over time. Under the assumption of proportional hazards, the hazard ratio can be estimated using the Cox proportional hazards model and comparisons between groups carried out with the log-rank or other rank tests. When the proportional hazards assumption is not met, the computed hazard ratio does not reliably reflect the treatment benefit, because the true hazard ratio is changing over time (3,4). Moreover, the standard log-rank test that is optimal under proportional hazards may lack statistical power to compare two treatment groups when treatment effects are delayed, and the interpretation of the hazard ratio comes into question (5,6). Weighted log-rank tests are used in situations where the proportional hazards assumption does not apply, by allocating different weights to events according the events’ times. The Fleming and Harrington family of weights $G^{\rho ,\gamma }$ is a subclass of weighted log-rank statistics (7,8). When $\rho$ = 0 and $\gamma$ = 1, more weight is given to late event times and less weight is given to early event times. We will refer to this test as the “weighted log-rank test” throughout this article.

Here, we investigate a new statistical approach based on generalized pairwise comparisons (9) that presents two key benefits when treatment effects are delayed. First, the approach leads to a measure of treatment effect that is meaningful whether or not hazards are proportional (9–11). This measure of treatment effect was previously named the net chance of a better outcome, and we call it “net benefit” here for simplicity. The net benefit can focus on long-term survival differences. Second, a statistical test based on the net benefit can be shown to have higher statistical power than the standard log-rank test under situations of delayed treatment effects. The estimation of the net benefit using generalized pairwise comparison can be stratified for baseline prognostic factors if required.

We illustrate the properties of the net benefit using an illustrative dataset from an actual trial comparing ipilimumab plus dacarbazine vs placebo plus dacarbazine in metastatic melanoma (2). Then, we study the power of the proposed test using simulated datasets for a randomized clinical trial under typical scenarios of delayed treatment effect.

Methods

The Net Benefit

The net benefit, denoted Δ, is defined as the probability that a patient chosen at random in the experimental group survives longer than a patient chosen at random receiving the control intervention minus the probability of the opposite situation (9,10). Δ is equal to zero if treatment does not differ from control, it is positive if treatment is better than control, and it would be equal to 100% if all patients in the treatment group fared better than all patients in the control subject group (conversely, it would be equal to −100% if all patients in the control subject group fared better than all patients in the treatment group). For instance, if the net benefit was estimated equal to 0.10, a patient chosen at random would have a 10% higher probability of enjoying a longer survival if receiving treatment rather than control. Of note, the net benefit Δ is a straightforward transformation of the hazard ratio under situations of proportional hazards and no censoring (12).

We will use a specified Δ, the net benefit of at least $m$ months, denoted Δ($m$). The net benefit of at least $m$ months is defined as the probability that a patient chosen at random in the experimental group survives by at least $m$ months longer than a patient chosen at random receiving the control intervention, minus the probability of the opposite situation. The net benefit can be computed, and its statistical significance tested, for any value of $m$ using generalized pairwise comparisons of prioritized outcomes. An adjusted procedure will be used to estimate the net benefit of at least $m$ months to avoid dependency of the net benefit on censoring (10). The approach is briefly summarized in the Supplementary Methods (available online) and has been described in detail elsewhere (9,10).

Illustrative Dataset

The CA184-024 trial (ClinicalTrials.gov no. NCT00324155) was an international study in which 502 patients with previously untreated metastatic melanoma were randomly assigned in a 1:1 ratio to receive ipilimumab plus dacarbazine or dacarbazine plus placebo 2. The protocol of the CA184-024 trial was approved by the appropriate institutional review boards or independent ethics committees. Written, informed consent was obtained from each subject or from his or her guardian. The primary outcome was OS. PFS was a secondary outcome. The assumption of proportionality was assessed graphically using scaled Schoenfeld residuals.

The net benefit of at least $m$ months was estimated for OS and for PFS. Analyses were stratified using the two stratification factors of the trial: metastasis stage and Eastern Cooperative Oncology Group performance status. Values for $m$ ranged from $m=$ 0 months to $m=$ 42 months for OS and to $m=$ 27 months for PFS. The maximum values chosen for $m$ were such that there were at least five patients at risk in the control subject group. Standard and weighted stratified log-rank tests for OS and PFS were also performed. All tests were two-sided, and P values of less than .05 were considered statistically significant.

Simulations

We simulated three scenarios of typical survival differences. In scenario 1, the hazards were proportional between the two treatment groups, with a constant hazard ratio of 0.65, 0.75, or 1. In the two other scenarios, the hazards were nonproportional. In scenario 2, the hazard ratio stayed equal to 1 (no effect) for 4 months, then decreased progressively to 0.4 or 0.6 (delayed effect on survival). In scenario 3, the hazard ratio decreased continuously over time from 1 (no effect) to 0 (cure rate) at 20 or 24 months. For each scenario, 10 000 trial datasets were generated. Each trial dataset included two treatment groups, each with 100 patients. The simulation parameters are summarized in the Supplementary Methods (available online). Three arbitrary dates of analysis were chosen to provide 0%, 20%, or 40% of administrative censoring (ie, the event was not observed for some patients because of the shortened follow-up). For each dataset, the net survival benefit was calculated for values of $m$ ranging from 0 to 42 months. The statistical significance (P value) of the net survival benefit was obtained for each value of $m$ using permutation tests. Standard and weighted log-rank tests were performed for comparison purposes. The power or the type-1 error (in the scenario corresponding to HR = 1, the null hypothesis) for the net survival benefit test was equal to the proportion of tests, among the 10 000 generated datasets in each scenario, that reached a two-sided P value less than .05. Generalized pairwise comparisons were performed with the package BuyseTest in the R software, available on CRAN. All tests were two-sided.

Results

Illustrative Dataset

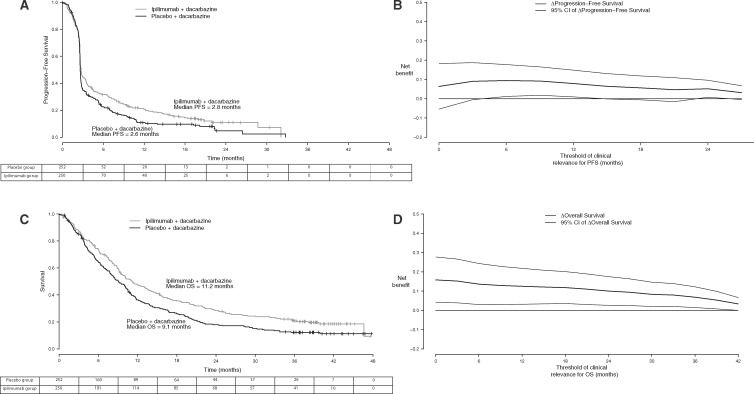
An analysis of PFS on the CA184-024 trial was conducted after 426 events had been documented. Median PFS was similar in the two groups: 2.8 months (95% confidence interval [CI] = 2.6 to 3.3) vs 2.6 months (95% CI = 2.6 to 2.7), near the time of the first tumor assessment. The PFS curves separated after the median, violating the proportional hazards assumption (Figure 1A). The stratified hazard ratio for PFS was 0.76 (95% CI = 0.63 to 0.93, standard stratified log-rank P = .006; weighted stratified log-rank P = .011). When $m$= 0 months, the net PFS benefit was Δ($0$) = 6.2% (95%CI = −5.4% to −17.7%, P = .30). The net PFS benefit increased and became statistically significant when the analysis was focused on long-term PFS differences (Figure 1B). For $m$= 12 months, the net PFS benefit was Δ($12$) = 7.7% (95% CI = 1.3% to 14.0%, P = .018). The elevated and sustained values of Δ, even for high values of $m$, suggested a delayed treatment effect (9).

Figure 1.

Survival and progression-free survival (PFS) benefits in the trial comparing ipilimumab plus dacarbazine vs placebo plus dacarbazine in metastatic melanoma. A) Kaplan-Meier estimates of PFS functions over time. B) Net PFS benefit of at least $m$ months. C) Kaplan-Meier estimates of overall survival functions over time. D) Net survival benefit of at least $m$ months. $\Delta$ = net benefit; CI = 95% confidence interval; OS = overall survival.

An OS analysis was performed after 414 deaths occurred, 37 months after the last patient was enrolled. Median OS was statistically significantly longer in patients treated with ipilimumab plus dacarbazine (11.2 months [95% CI = 9.5 to 13.8 months] vs 9.1 months [95% CI = 7.9 to 10.5 months]; stratified hazard ratio for death estimated through a Cox proportional hazard model = 0.72; 95% CI = 0.59 to 0.87, standard stratified log-rank P < .001; weighted stratified log-rank P = .008). Differences in OS rates favored the ipilimumab plus dacarbazine group and were similar at 1, 2, and 3 years, suggesting that a proportion of the patients achieved a long-term benefit (Figure 1C). When any OS benefit was considered clinically relevant ($m$= 0 months), the net OS benefit was Δ($0$) = 15.8% (95% CI = 4.6% to 27.3%, P = .006) in favor of the ipilimumab plus dacarbazine group. The OS benefit was maintained when the analysis was focused on long-term OS differences (Figure 1D). For $m$= 12 months, the net OS benefit was Δ($12$) = 12.5% (95% CI = 4.4% to 20.6%, P = .002). The elevated and sustained values of Δ, even for high values of $m$, suggested again a prolonged treatment effect (9).

Simulations

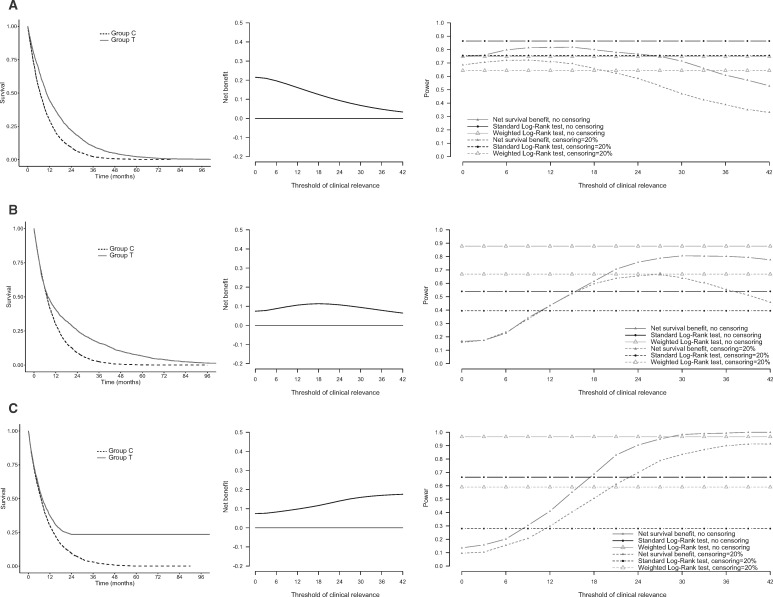
Figure 2A (left) shows typical survival curves generated under scenario 1 of proportional hazards and hazard ratio set at 0.65. The net survival benefit decreased when long-term survival differences were evaluated (middle). The standard log-rank test was uniformly more powerful than the net survival benefit test (Figure 2A, right). In particular, when survival differences longer than 24 months were considered relevant ($m$ = 24), the power of the net survival benefit test began to drop substantially as compared with the power of the log-rank tests. Similar patterns were observed with censoring and when the hazard ratio was set at 0.75 (Figure 2; Supplementary Figure 1, available online).

Figure 2.

Survival benefits in three scenarios of proportional hazards or nonproportional hazards. Survival benefits in a scenario of proportional hazards (A) and two scenarios of nonproportional hazards (delayed treatment effect [B] and cure rate [C]). Left panels: Kaplan-Meier estimates of survival functions over time. Middle panels: net survival benefit of at least $m$ months. Right panels: power of the standard log-rank test, weighted log-rank test, and of the test of a net survival benefit of at least $m$ months. Powers are plotted for two situations: no censoring (solid lines) and administrative censoring of 20% (dotted lines). Group C = control group; Group T = treatment group.

In the presence of a delayed treatment effect (Figure 2B, left), the power of the net survival benefit test increased when the value of $m$ increased (Figure 2B, right). The net survival benefit increased when medium-term survival differences were evaluated, and decreased when only very long-term survival differences were considered (middle). When any survival benefit was considered clinically relevant ($m$= 0 months), the power of the net survival benefit test was low compared with the power of the log-rank tests (17% vs 54% for the standard log-rank test and 88% for the weighted log-rank test in the absence of censoring). In contrast, the power of the net survival benefit test increased when larger survival differences were considered relevant and was substantially higher than the power of the standard log-rank test for $m$= 24 (76% vs 54% for the standard log-rank test and 88% for the weighted log-rank test in the absence of censoring). Similar patterns were observed with censoring, though the log-rank tests were more affected by censoring than the test of the net survival benefit (Figure 2B; Supplementary Figures 2 and 3, available online).

In the presence of a cure rate (Figure 2C, left), the power advantage of the net survival benefit test over the standard log-rank test was even more pronounced (Figure 2C, right; Supplementary Figures 4 and 5, available online). For $m$= 24, the power of the test based on the net survival benefit was 90% vs 66% for the standard log-rank test and 97% for the weighted log-rank test in the absence of censoring, and 70% vs 28% for the standard log-rank test and 59% for the weighted log-rank test in the presence of censoring (20% of censored observations). The power advantage of the net survival benefit test over the standard logrank test (and the weighted logrank test in the presence of censoring) was even more pronounced when the cure rate occurred earlier in time (Supplementary Figures 4 and 5, available online). The type 1 error rate was near 5% in the three scenarios.

Discussion

In this work, we reported on a new statistical measure of treatment effect called the net benefit. The net survival benefit of at least $m$ months addresses the question of a treatment benefit from the point of view of a patient asking “What is my chance of surviving longer by at least $m$ months on treatment than on control?” This measure of benefit addresses the patient-centric question “How long have I got?” for which others have proposed to use percentiles of the survival curves to simulate typical, best-case, and worst-case scenarios (1,2,13). The net survival benefit has a probabilistic interpretation: it is the probability that a patient chosen at random in the experimental arm has a survival longer by at least $m$ months than a patient chosen at random in the control subject group, minus the probability of the opposite situation (ie, a difference between two probabilities, or a “net” probability). $m$ is specified as a minimal clinically relevant difference in survival, such as 12 months. When $m$ is large, the net survival benefit allows one to quantify and focus on long-term survival differences.

When a delayed treatment effect is anticipated, the net benefit is appealing because it stresses benefits that are worthwhile on the time scale, which is arguably more relevant to the individual patient. In contrast, dealing with a difference in median OS does not directly reflect the potential benefit to individual patients. For example, in the ipilimumab trial, the difference in median OS was only 2 months, which may not be viewed as clinically worthwhile. However, the net OS benefit of at least 12 months was 12.5%, stressing the important long-term survival benefit of ipilimumab for patients with metastatic melanoma.

In randomized clinical trials comparing modern anticancer immunotherapies to placebo or best standard therapy, it is now accepted that survival curves commonly display late divergences (1,2,13). The phenomenon has usually been interpreted as a delayed effect of the treatment, in contrast to the immediate effect and early curve divergence seen with cytotoxic chemotherapy. The standard log-rank test is optimal to detect differences between survival curves under proportional hazards, and the Cox proportional hazards model is appropriate in this case. However, it is not true anymore in immunotherapeutic trials, in which late divergences of survival curves may occur (6). The power of the net survival benefit test was higher than the power of the standard log-rank test when long-term survival differences ($m$ large) were of interest. A weighted log-rank test, giving more weight to later events, was as expected more powerful than the standard log-rank test in scenarios of delayed treatment effect or cure rate. In these scenarios and when focusing on long-term survival differences, the power of the net survival benefit test was comparable to that of the weighted log-rank test (sometimes higher and sometimes lower depending of scenarios and thresholds). Long-term differences are arguably more meaningful to an individual patient than the overall risk reduction captured by the hazard ratio. As such, the net survival benefit test may be more intuitively appealing than weighted rank tests that can be used to improve the power of the log-rank test, such as the weighted log-rank test used in this paper (1,2,13).

One limitation of the net benefit occurs when the average follow-up of a trial is much shorter than the longest event time. Such early analyses might be conducted during interim analyses of a clinical trial, or for practical reasons when a trial is conducted in a population with a low event rate. In these scenarios, the survival function can only be estimated up to a finite time. The bias of the net survival benefit has been shown to be small when hazards are proportional (10). However, when the treatment effect varies over time, the net benefit is biased if the follow-up is too short.

When analyzing the ipilimumab trial dataset, the net OS benefit and the net PFS benefit were both large when all OS or PFS differences were considered clinically relevant. More interestingly, the net OS and PFS benefits were mainly maintained in the long run, that is, for $m$ = 12 months for OS and PFS, and beyond. The P values for tests based on the long-term net benefit were lower than the P values for tests based on the overall net benefit, and also lower than the P values of the standard log-rank tests. It confirms the potential power advantage of tests based on large values of $m$ when designing or analyzing trials with a late treatment effect, at least when compared to the standard log-rank test. The graphs representing the net OS and PFS benefit as a function of the minimal clinically relevant difference $m$ allows a patient-centered assessment of the treatment effect. These graphs provide the net probabilities that the new treatment prolongs PFS or OS for a patient by at least $m$ months.

The simulation study was limited to several scenarios representative of the survival benefit that is expected when an immunotherapy is compared to a nonimmune anticancer treatment. It might not be representative of trials comparing to immunotherapy regimens or comparing two combinations each including an immunotherapy.

According to the individual context of each clinical trial, the net survival benefit might be used for primary analysis of clinical trials investigating immunotherapies. It might also be used in hierarchical analyses or as secondary analyses. When the net survival benefit test is used for sample size calculations, simulations should be based on precise hypotheses about the expected survival distributions in the control and experimental groups, the predefined threshold of clinical relevance ($m$), and the planned duration of follow-up. We recommend performing sensitivity analyses exploring a large range of thresholds $m$. These sensitivity analyses might be performed without adjustment for multiplicity, but should then be reported as exploratory.

Individual patients and clinicians may have different opinions regarding the survival benefit considered to be worthwhile, depending on a host of factors related to the patient’s condition and potential tolerance as well as to the treatment tolerance, convenience, and toxicity. The approach presented here allows such a benefit-risk assessment to be made for varying values of $m$. As such, it is a useful approach for personalized medicine.

Notes

Affiliations of authors: Hospices Civils de Lyon, Oncology department, Pierre-Benite, France (JP); Hospices Civils de Lyon, Service de Biostatistique et Bioinformatique, Lyon, France (JP, JG, PR, DMB); Université de Lyon, Lyon, France; Université Lyon 1, Villeurbanne, France (JP, JG, PR, DMB); CNRS, UMR 5558, Laboratoire de Biométrie et Biologie Evolutive, Equipe Biostatistique-Santé, Villeurbanne, France (JP, PR, DMB); Global Biometric Sciences, Bristol-Myers Squibb, Braine-l’Alleud, Belgium (AL, SM); Neurobiology Research Unit, Rigshospitalet, Copenhagen, Denmark (BO); University of Copenhagen, Department of Public Health, Section of Biostatistics, Copenhagen, Denmark (BO); Hospices Civils de Lyon, Cancer Research center of Lyon, ImmuCare (Immunology Cancer Research), Dermatology Department, Pierre-Benite, France (SD); Interuniversity Institute for Biostatistics and Statistical Bioinformatics (I-Biostat), Hasselt University, Hasselt, Belgium (AM, MB); International Drug Development Institute (IDDI), San Francisco, CA (MB).

AL and SM are employees of BMS. MB is a shareholder of IDDI. SD is Principal investigator in clinical trials conducted by BMS, has received research grant to institution, and has been provided congress expenses by BMS. The other authors declare no conflict of interest.

JP and MB developed the analysis plan and prepared the report. AL and SM provided the data. JP performed the statistical analyses. All authors interpreted the analyses, revised, and approved the manuscript. The authors agree collectively to be accountable for all aspects of the work.

The corresponding author attests that all listed authors meet authorship criteria and that no others meeting the criteria have been omitted. The lead author affirms that the manuscript is an honest, accurate, and transparent account of the study being reported; that no important aspects of the study have been omitted; and that any discrepancies from the study as originally planned have been explained.

This work was performed within the framework of the SIRIC LYriCAN grant INCa-DGOS-Inserm_12563.