Modeling the impact of liana infestation on the demography and carbon cycle of tropical forests

Abstract

There is mounting empirical evidence that lianas affect the carbon cycle of tropical forests. However, no single vegetation model takes into account this growth form, although such efforts could greatly improve the predictions of carbon dynamics in tropical forests. In this study, we incorporated a novel mechanistic representation of lianas in a dynamic global vegetation model (the Ecosystem Demography Model). We developed a liana‐specific plant functional type and mechanisms representing liana–tree interactions (such as light competition, liana‐specific allometries, and attachment to host trees) and parameterized them according to a comprehensive literature meta‐analysis. We tested the model for an old‐growth forest (Paracou, French Guiana) and a secondary forest (Gigante Peninsula, Panama). The resulting model simulations captured many features of the two forests characterized by different levels of liana infestation as revealed by a systematic comparison of the model outputs with empirical data, including local census data from forest inventories, eddy flux tower data, and terrestrial laser scanner‐derived forest vertical structure. The inclusion of lianas in the simulations reduced the secondary forest net productivity by up to 0.46 t_C ha⁻¹ year⁻¹, which corresponds to a limited relative reduction of 2.6% in comparison with a reference simulation without lianas. However, this resulted in significantly reduced accumulated above‐ground biomass after 70 years of regrowth by up to 20 t_C/ha (19% of the reference simulation). Ultimately, the simulated negative impact of lianas on the total biomass was almost completely cancelled out when the forest reached an old‐growth successional stage. Our findings suggest that lianas negatively influence the forest potential carbon sink strength, especially for young, disturbed, liana‐rich sites. In light of the critical role that lianas play in the profound changes currently experienced by tropical forests, this new model provides a robust numerical tool to forecast the impact of lianas on tropical forest carbon sinks.

This is the first dynamic vegetation model that simulates lianas. We predict a strong impact on the carbon stocks, especially for younger (secondary) forests where liana density is higher.

1. INTRODUCTION

Tropical forests are a critical component of the Earth system, storing half of the global forest carbon stocks (Pan et al., 2011) and accounting for a third of terrestrial photosynthesis (Beer et al., 2010). Their contribution to the global carbon cycle is increasingly acknowledged even though both the magnitude of their role (Malhi, 2010) and model predictions (Fisher et al., 2010) remain uncertain. These uncertainties mainly stem from our limited understanding of tropical forest functioning in response to perturbations (Powell et al., 2013). As a consequence, it is unclear whether tropical forests still constitute a net carbon sink or source globally (Popkin, 2017) after decades of declining sequestration capacity among old tropical forests (Brienen et al., 2015). Although the drivers of this transition are not yet fully understood, lianas (woody vines) have been proposed as a possible cause of tropical forest structural changes (Lewis, Malhi, & Phillips, 2004).

Lianas use the architecture of trees to climb to the top of the canopy without the need to invest in fully self‐supporting structures. They have complex growth forms and are very diverse, making them difficult to study. Because relatively little was known about lianas prior to the 1990s, many researchers assumed that they play a limited role in the carbon cycle, and therefore, most community‐level forest field and modeling studies did not consider them at all (Schnitzer & Bongers, 2002). However, host trees infested by lianas experience intense above‐ and below‐ground competition and mechanical damage, resulting in reduced growth (Schnitzer & Carson, 2010) and increased mortality (Ingwell, Joseph, Becklund, Hubbell, & Schnitzer, 2010). As a result, liana abundant forests are believed to possess substantially smaller carbon stocks as compared to forests with lower liana density (Durán & Gianoli, 2013); this hypothesis was recently confirmed by a liana removal experiment conducted in Gigante, Panama (van der Heijden, Powers, & Schnitzer, 2015). Although such studies need to be confirmed with long‐term observations across multiple forests (Schnitzer, van der Heijden, & Powers, 2016), they provided, for the first time, empirical evidence that lianas have a substantial negative impact on whole‐forest carbon uptake/sequestration. Furthermore, approximately half of the tropical forest area is currently covered with secondary forest (Poorter et al., 2016), where lianas peak in abundance (Schnitzer, 2018), which might reduce the potentially rapid rates of carbon sequestration in such secondary forests (Durán & Sánchez‐Azofeifa, 2015) and further impact the global carbon cycle.

Including lianas in vegetation models is particularly important in the age of climate change and increasing anthropogenic disturbance, since liana proliferation might be driven by these external factors (Lewis, Edwards, & Galbraith, 2015; Schnitzer, 2018). Numerous studies have shown that liana density consistently increases in disturbed parts of forests (Putz, 1984; Schnitzer & Bongers, 2002), peaks in late secondary forest, and eventually decreases with forest succession (Barry, Schnitzer, Breugel, & Hall, 2015; DeWalt et al., 2015; Gerwing & Farias, 2000; Letcher & Chazdon, 2012; Schnitzer & Bongers, 2002), thus making forest demography models the most suitable tool for understanding changes in liana dominance over time.

Despite the demand of the scientific community for the inclusion of lianas in models (van der Heijden, Schnitzer, Powers, & Phillips, 2013; Kumar & Scheiter, 2019; McDowell et al., 2018; Phillips et al., 2002) and the increase in liana abundance in the Neotropics, no single dynamic global vegetation model (DGVM) so far includes lianas (Verbeeck & Kearsley, 2015). Given that an increasing amount of data on different aspects of liana ecology has emerged (Gianoli, 2015; Laurance et al., 2014; Schnitzer, 2018; Schnitzer & Bongers, 2011), we argue that now is the time to start building such models (Verbeeck & Kearsley, 2015). Because of the potential impact of lianas on forest succession and carbon sequestration, the development of validated tools to understand their role in forest ecosystems is paramount.

In this study, we present the first effort toward incorporating lianas in a cohort‐based DGVM, the Ecosystem Demography Model (Moorcroft, Hurtt, & Pacala, 2001). The core development consisted of adding a mechanistic representation of lianas as a novel plant functional type (PFT) within the model and parameterizing it according to the available data. To evaluate and demonstrate the predictive capacity of the model, we performed simulations of the new model version for two different Neotropical forest sites. The simulations were systematically confronted with multiple (existing and newly collected) datasets, including data from forest inventories and eddy flux tower observations. Our main objective was to quantify the role of lianas in the fully integrated forest carbon cycle at old‐growth and secondary tropical forest sites, which we achieved by comparing model simulations with and without lianas. Due to the observed high density of lianas in young forests, we hypothesized that their impact on carbon uptake will be larger for secondary forests than for old‐growth forests.

2. MATERIALS AND METHODS

2.1. The Ecosystem Demography Model

The Ecosystem Demography Model, version 2 (ED2), is an integrated terrestrial biosphere model incorporating state‐of‐the‐art information on physiology and biogeochemistry and a multilayer canopy structure that scales up competition for light and soil resources from the tree to the ecosystem scale (Medvigy & Moorcroft, 2011; Medvigy, Wofsy, Munger, Hollinger, & Moorcroft, 2009). Plant diversity is represented through PFTs differing in their photosynthetic, water use, energy balance, and mortality characteristics (Levine et al., 2016; Xu, Medvigy, Powers, Becknell, & Guan, 2016).

The model has a hierarchical structure in which only the meteorological grid cell is spatially explicit. Within each grid cell, the spatial heterogeneity of the forest structure is represented by patches. Patches represent the discretized distribution of forest gaps as a function of age since the last disturbance (Moorcroft et al., 2001). In the ED2 framework, forest gaps represent the area that would be disturbed by the falling of a large tree. The total number of patches controls the resolution of the discrete age distribution, and the relative patch area corresponds to the probability of finding forest gaps with ages similar to the patch age. Importantly, forest gaps grouped into a patch are not necessarily adjacent: they are grouped based on the similarity of vertical forest structure. Likewise, patches do not possess any geographic information within the grid cell. Within any patch, the position of each individual plant is also not retained; instead, plants are grouped into cohorts based on their size (diameter at breast height, DBH) and their PFT, and the abundance of plants belonging to each cohort within each patch is represented by the cohort plant density.

The stochastic nature of mortality, reproduction, and dispersal processes is represented through a size and age structure approximation of a gap model. For further details about the simulated processes, we refer to the ED2.2 model description (Longo et al., 2019).

2.2. Model development

In comparison to previous efforts of including new PFTs into the ED2 (Ise & Moorcroft, 2010; Wang, LeBauer, & Dietze, 2013), the incorporation of lianas entails the additional complexity of representing the parasitic relationship with infested trees: lianas, in that sense, are unique because they climb host trees and invade the same spatial location (Stewart & Schnitzer, 2017). From a modeling point of view, this means that some cohorts (attached lianas and their hosts) can no longer be considered independent from one another. The core of the model development procedure consisted of creating new processes to realistically represent the liana–tree interaction and parameterizing them appropriately. These new processes as well as the model parameterization are briefly presented below. All details regarding implementation features are available in the supplementary material of this paper (Supporting Information 1 and 3). The source code is publicly available at https://github.com/manfredo89/ED2/releases/tag/3.

2.2.1. Liana allometry and cohort tracking

Allometric relationships represent one of the key differences between liana and tree growth forms, as relatively small lianas (typically 2–3 cm in DBH) have a high probability of reaching the top of the forest canopy (Kurzel, Schnitzer, & Carson, 2006) and may have large leaf and root biomass pools (Putz, 1983; Wyka, Oleksyn, Karolewski, & Schnitzer, 2013). ED2 uses allometric relations to partition the assimilated carbon into different plant pools. Available carbon is integrated daily from the photosynthetic activity, which is calculated on a fine time step (typically 10 min). The values for living tissues (leaves, fine roots, and sapwood) are updated daily, while those for structural tissues are updated monthly. The different pools are linked to one another through DBH‐dependent allometries.

Liana‐specific allometries were chosen based on an extensive literature meta‐analysis (see Supporting Information 1). For structural biomass, we used the pantropical liana equation of Schnitzer, DeWalt, and Chave (2006), which is derived from the most comprehensive liana allometry dataset available. For leaf biomass, we used the latest published equation (Gehring, 2004), corrected for small individuals: we used the early successional tree allometric parameterization of the ED2 for lianas with small DBH because the aforementioned equation for lianas would lead to unrealistically low leaf biomass compared to trees (see Supporting Information 1 for details), thus preventing their establishment.

In ED2, plant height is one of the most important properties of a given cohort because of its direct impact on light interception and photosynthetic rates. To represent the liana height, we created a new ontogenic allometric equation because, to the best of our knowledge, no such description of the relation across life stages exists in the literature. Upon establishment, each liana is assigned to a host tree. Once the liana's height matches the host tree's height, the liana is constrained to be a maximum of 20 cm taller than its host (see Supporting Information 1 and 2). When it reaches the maximum height, the attached liana can continue growing in diameter without obeying the original diameter–height allometric relation. This means that unlike for trees, the diameter–height allometry of lianas cannot be represented by a bijective function; that is, the height of attached lianas can no longer be determined from their diameter and vice versa. The current model implementation allows tree cohorts to support more than one liana cohort; however, we assumed that each liana cohort is attached to a single tree cohort, which means that the lianas are attached to their initial host until a disturbance or a cohort splitting event occurs (see Supporting Information 2).

In ED2, allocation to growth and reproduction occurs once all maintenance costs are deducted from the carbon balance (e.g., respiration and turnover of living tissues). The parameter controlling the allocation of excess carbon to stem growth was tuned for lianas by targeting the observed average annual increase in DBH at the Barro Colorado Island (BCI) site in Panama (Putz, 1990). In contrast to that of trees, the reproduction pool of the liana PFT is assumed to contain both the carbon used for seeds and fruits as well as the carbon used for vegetative reproduction. To account for the high proportion of clonal stems found in recently disturbed forests (30% of upright shoots were vegetative offshoots in the 50 ha plot on BCI; Schnitzer et al., 2012), we set the height threshold for liana reproduction to be shorter than that for trees (see Supporting Information 3).

2.2.2. Liana tree‐fall survivorship and resprouting

Another aspect that makes lianas functionally different from trees is their greater ability to survive disturbance events. In ED2, disturbances lead to the creation of new patches (with age 0). The initial population in the recently disturbed patch corresponds to the survivors of the disturbance. The model assumes that within the patch area, only a limited fraction of small (<10 m) plants survive (see Supporting Information 3). Unlike trees, lianas often survive in gaps after the falling of their host (Putz, 1984), potentially giving them a competitive advantage in highly disturbed areas (Schnitzer, 2018; Schnitzer & Carson, 2001). Therefore, we assumed a higher survivorship probability for attached lianas in the case of tree‐fall (0.8, Table S1).

The height of the surviving fallen lianas is recalculated to be consistent with the height distribution within that patch, as in the model, lianas cannot vertically outgrow their potential hosts. With $t$ representing the initial time and t + Δt the time after the disturbance, the new height ($h$) is determined by h(t + Δt) = H · (h(t)/h _max), where $H$ is the height of the tallest cohort in the newly created patch (typically 10 m) and $h_{\mathrm{m}\mathrm{a}\mathrm{x}}$ is the maximum height lianas can reach. This scaling scheme ensures that lianas have a height distribution that is consistent with the height of the surviving trees in the patch.

Since surviving lianas become free standing, the other plant tissues are rescaled according to the allometries described in the previous section. The difference in biomass is transferred to the litter pool to represent the damage caused to the tissues of the fallen lianas by the tree‐fall event.

2.2.3. Direct light competition

Light competition in ED2 implements the flat‐top crown concept (i.e., the leaf area of each plant cohort is distributed evenly across the patch), and the crown depth is assumed to be infinitesimally small (i.e., all leaves are located at the same vertical position). Because of this specific implementation, each cohort is considered to be partially shaded by all leaves of any taller cohorts in that specific patch. As a result, lianas cast their shade not only onto their host but also onto all shorter cohorts within the patch. To account for the particularly intense light competition between the liana and its host, as well as the damage caused by lianas in the tree crown, we assumed a high cost of leaf maintenance for the liana and its host tree. More specifically, both cohorts in a liana–host tree association experience a similar relative increase in their respective leaf turnover rate depending on the liana–tree leaf biomass ratio (see Supporting Information 2).

2.3. Model parameterization

PFTs reflect the strategic diversity that plants exhibit in nature, from the fast‐growing, resource‐acquisitive, early successional species to the more conservative, slow‐growing late successional species. For the tropical trees, we used the same parameterization as Longo et al. (2019). For the lianas, we used a parameterization based on data derived from a comprehensive trait analysis (similar to the work of Asner & Martin, 2012 and Wyka et al., 2013, extended to other liana traits). At the photosynthetic level, although not all liana species are fully light demanding (Sanches & Válio, 2008), the majority are assumed to have an acquisitive and light‐demanding leaf physiology (Asner & Martin, 2012; Cai, Schnitzer, & Bongers, 2009). We therefore assumed liana leaf properties to be similar to those of early successional trees, including similar values for the maximum rate of carboxylation (V _cmax) and specific leaf area. A list of most relevant liana parameters and their derivation can be found in Table S2 (Supporting Information 3).

2.4. Simulation sites and additional data

We evaluated the model for two forest sites, Paracou (French Guiana) and the Gigante Peninsula (Panama). We chose these two sites because they present key differences in terms of forest successional stage and liana infestation (see Table S1 and Supporting Information 4 for more details) and because supporting datasets exist for these sites to benchmark the model.

The Paracou research station is located in the coastal part of French Guiana and is classified as a lowland moist primary forest. Records indicate a mean annual precipitation (MAP) of 3,088 mm, with a well‐marked dry season from mid‐August to mid‐November (Table 1; Figure S4). The meteorological forcing data span from 2004, when the flux tower was installed, to 2016. For this study, we used the flux tower measurements using the eddy covariance technique as described in Bonal et al. (2008; Aguilos, Hérault, Burban, Wagner, & Bonal, 2018), as well as the meteorological forcing data from the tower measurements. Tree inventories have been conducted in 10 plots of 70 × 70 m established in 2004 in the flux tower footprint, recording all trees with DBH ≥ 10 cm. Liana inventories have been performed in the same plots since 2004 (DBH ≥ 10 cm) and included smaller individuals from 2015 (DBH ≥ 2 cm, see Supporting Information 5).

Table 1.

Main features of the two forest sites used for the simulation

Site name	Paracou	Gigante peninsula
Country	French Guiana (France)	Panama
Forest type	Tropical moist	Semi‐deciduous, seasonally moist
Forest successional stage	Old growth	Secondary (approximately 70 years old)
Coordinates (latitude, longitude)	5.3N, 52.9W	9.2N, 79.8W
Mean altitude (m a.s.l.)	40	80
Mean annual temperature (°C)	26.0 ± 0.3	25.6 ± 0.4
Mean annual precipitation (mm)	3,088 ± 117	2,394 ± 94
Available years of meteorological data	2004–2016	2003–2016
Above‐ground biomass (kgc/m2)	18.5–21.2 (16.9)	7.1–10 (8.2)
Liana basal area (m2/ha)	0.42 (0.48)	2.42 (1.53)
Tree basal area (m2/ha)	32.6 (29.7)	18.7 (15.7)
Liana stem density (DBH ≥ 2.5 cm; per ha)	131 (481)	1,332 (996)
Tree stem density (DBH ≥ 10 cm; per ha)	576 (778)	409 (575)

Mean annual temperature and mean annual precipitation are reported with averages ± standard deviation. Numbers in parentheses are model outputs for the simulation with lianas.

The second site used to test our model is the secondary forest located on the Gigante Peninsula, which is part of the Barro Colorado Nature Monument in Panama. The forest is estimated to be approximately 70 years old (Schnitzer, 2014), and, like the forest at Paracou, it is a lowland moist tropical forest. On average, Gigante receives approximately 2,400 mm of rainfall annually. The dry season runs from mid‐December to mid‐April (Table 1 and Figure S4). Meteorological data were collected from the nearby field station of BCI (Powell, Faybishenko, Kueppers, & Paton, 2019). Tree and liana inventories were carried out in eight plots of 60 × 60 m used as control plots for a liana removal experiment. For both sites, we recycled the meteorological forcing data throughout the entire simulation.

Most of the data used in this study to evaluate the model predictions come from published studies (see Table S3). Whenever possible, we used data specifically available for the two study sites. However, some other empirical data were added to the model–data comparison from experimental plots in different locations close to the sites of interest.

Additional observational data were also collected in this study, specifically those from the liana inventories conducted at Paracou in 2015 mentioned above and plant area index (PAI) values from terrestrial laser scans (TLSs). The scans were performed in three different control plots and three removal plots in Gigante in 2016. Removal plots are forest plots from which all lianas were removed in 2011 and that were maintained liana‐free through the successive extirpation of new lianas (van der Heijden et al., 2015). The detailed steps and formulas used to derive the vertically resolved PAI from TLSs are described (Krishna Moorthy, Calders, Porcia e Brugnera, Schnitzer, & Verbeeck, 2018). We used the allometric equation generated from the community‐level analysis of Bohman and O'Brien (2006) to calculate the crown depth from the simulated DBH for the comparison between simulated LAI and TLS PAI. The leaf area was assumed to be uniformly distributed within the crown depth. Simulated leaf area below 1.2 m (the tripod height) was not considered, and the simulated wood area was ignored.

2.5. Model setup

The model runs were initialized from near bare ground (all PFTs have an initial sapling density of 0.1/m²) and were continued for 500 years to reach an equilibrium state. The atmospheric CO₂ concentration was assumed to be constant over the simulated period and fixed at 370 ppm. The runs with and without lianas were performed with the same conditions but turning on and off the liana PFT. All results shown in this study come from simulations achieved with 34 cohorts per patch and an upper limit of 34 patches. For comparison to the field observations, the simulated results for the Paracou site were averaged over a 400–500 year period (corresponding to the equilibrium), and the results for Gigante were averaged over a 50–100 year period (around the approximate age of the forest).

Relative changes (RC, in %) in fluxes or pools (F) were calculated as

$$\text{RC}=100\left(\frac{F_L-F_{\text{NL}}}{|F_{\text{NL}}|}\right),$$

where the subscripts L and NL refer, respectively, to the simulations with and without lianas. By convention, positive RC values represent increases in the corresponding flux or pool when the liana PFT is included in the model simulation regardless of the sign of the flux/pool in the baseline simulation.

For the tuning of the liana growth parameter (allocation to stem growth), we ran a batch of simulations with a reduced number of patches (18) and cohorts per patch (18), exploring the whole parameter range, and found the best value with a bisection algorithm (see Supporting Information 3 for details). The optimal value was then used to run the final simulations presented in this study.

3. RESULTS

3.1. Carbon pools and fluxes

With values of 16.9 kg_c/m² in Paracou (Figure 1) and 8.2 kg_c/m² in Gigante (Figure S6), wood biomass was the largest simulated carbon pool and accounted for more than 95% of the above‐ground biomass (AGB), or approximately two‐thirds of total plant biomass, at both sites. In Paracou, lianas constituted approximately 1.1% of the forest AGB, consistent with the observed 1.3 ± 0.8% (average ± standard deviation). For Gigante, the percentage of liana AGB was 8.2%, in agreement with the observed value of 12.0 ± 4.9% (Figure S6).

Figure 1.

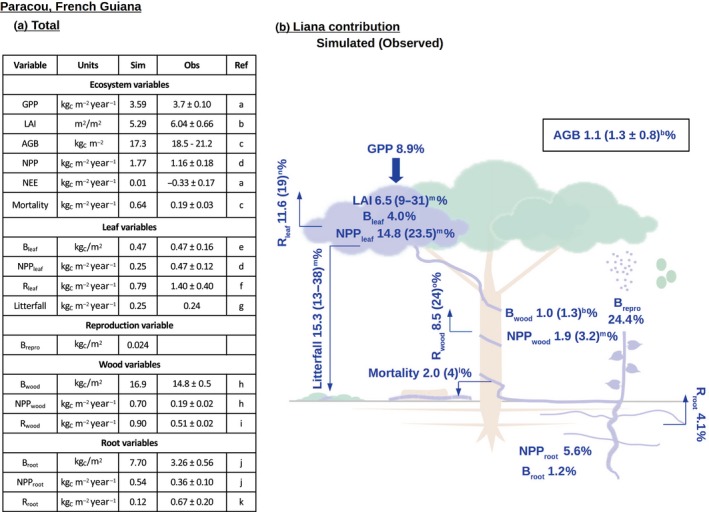
Total forest carbon pools and fluxes (left panel) and liana contributions (right panel). The table shows simulated (Sim) and observed (Obs) values for Paracou and the corresponding references (Ref). The sketch shows simulated liana contributions, with observed liana contributions in parentheses. B, biomass; GPP, gross primary productivity; NEE, net ecosystem exchange (negative values mean carbon uptake); NPP, net primary productivity; R, respiration. References for observations: ^aParacou, French Guiana (Aguilos et al., 2018); ^bParacou, French Guiana (TLS data, this study); ^cParacou, French Guiana (Rutishauser, Wagner, Herault, Nicolini, & Blanc, 2010); ^dParacou, French Guiana (Longo et al., 2019); ^eParacou, French Guiana (Domenach et al., 2004); ^fParacou, French Guiana (Stahl, 2010); ^gParacou, French Guiana (De Weirdt et al., 2012); ^hParacou, French Guiana (Baker et al., 2004); ⁱParacou, French Guiana (Stahl, Burban, Goret, & Bonal, 2011); ^jParacou, French Guiana (Bréchet, 2009; Stahl et al., 2013); ^kDifference between total soil and heterotrophic respiration (Bréchet, 2009; Bréchet, Ponton, Alméras, Bonal, & Epron, 2011; Epron, Bosc, Bonal, & Freycon, 2006); ^lNouragues, French Guiana (Chave et al., 2008); ^mDifferent sites in South America and Asia (van der Heijden et al., 2013); ⁿLa Selva Biological Station, Costa Rica (Cavaleri, Oberbauer, & Ryan, 2008); ^oLa Selva Biological Station, Costa Rica (Cavaleri et al., 2008)

The liana contribution to leaf net primary productivity (NPP) was higher in Gigante (36.2% modeled) than in Paracou (14.8% modeled vs. 23.5% observed), and as a result of the high leaf turnover, the relative contribution of lianas to litterfall was higher than their contribution to leaf biomass. In Paracou, the simulated liana litterfall accounted for 15.3% of the total litterfall carbon flux (measurements in the field vary between 13% and 38%; van der Heijden et al., 2013), while liana leaves only contributed to 4.0% of the total standing leaf biomass. For the simulations at Gigante, lianas accounted for 16% of the forest leaf biomass and 38% of the litterfall carbon flux. The general trend observed at both sites was consistent with the observation that, given their biomass, lianas disproportionally contribute to leaf litter production (Tang, Kitching, & Cao, 2012). The total simulated litterfall for Paracou was in good agreement with the empirical data (0.25 vs. 0.24 kg_c m⁻² year⁻¹). The simulated liana component of the LAI was approximately 7% for Paracou and 22% for Gigante. The data collected from the plots in the field indicate that lianas contribute between 9% and 31% of the ecosystem LAI (van der Heijden et al., 2013). Removal experiments carried out in gaps and intact forest in Gigante found the liana LAI to account for 17% and 20% of the total LAI, respectively (Rodríguez‐Ronderos et al., 2016; Schnitzer & Carson, 2010).

Overall, the model overestimated the NPP in Paracou (1.77 vs. 1.16 kg_c m⁻² year⁻¹), while the simulated forest gross primary production (GPP) was close to the observed value (3.59 vs. 3.7 kg_c m⁻² year⁻¹). For both sites, the simulated liana contribution to the reproductive biomass was large (70.3% and 24.4% for Gigante and Paracou, respectively), mainly due to the high investment in vegetative reproduction among lianas.

The inclusion of lianas in the model did not negatively affect the predicted GPP or latent heat fluxes for the Paracou site or their seasonality, which were both well reproduced by the model (Figure S7). Similarly, including the lianas in the simulation did not significantly impact the estimated GPP fluxes in Gigante.

3.2. Forest structure and demography

The simulation results showed significantly more lianas at the Gigante site than at Paracou, with densities of 996 stems/ha (DBH ≥ 2.5 cm) for Gigante and 481 stems/ha for Paracou (Table 1; Figure 2). The field measurements indicate a liana density of 1,332 stems/ha and 131 stems/ha for Gigante and Paracou, respectively. By comparing these numbers with those in the Global Liana Database (DeWalt et al., 2015), it appears that Gigante and Paracou stand at the opposite sides of the liana density spectrum for the Neotropics (min = 105 stems/ha at km 41, Brazil; max = 1,414 stems/ha at Fazenda Sete, Brazil). According to our simulations, lianas were most abundant in the canopy of young forest, such as that in Gigante, and progressively declined in older patches (Figure 4a) to become almost absent in the top canopy of old‐growth forests. The simulated liana basal area was 1.53 cm²/m² for Gigante (2.41 cm²/m² in the field data) and 0.48 cm²/m² for Paracou (0.42 cm²/m² in the field data). The experimental data showed significantly different demography for the two sites. The simulated liana size distributions exhibited an exponential decrease, similar to what is observed in Gigante but different from the flatter distribution observed in Paracou. The percentage of the total liana basal area represented by large lianas (DBH ≥ 10 cm) was 7.6% for Gigante (15% in the field data) and 2.6% (40% in the field data) for Paracou. We stress that while the model represents a landscape average, field data come from a limited number of plots and are therefore not necessarily representative of the average forest.

Figure 2.

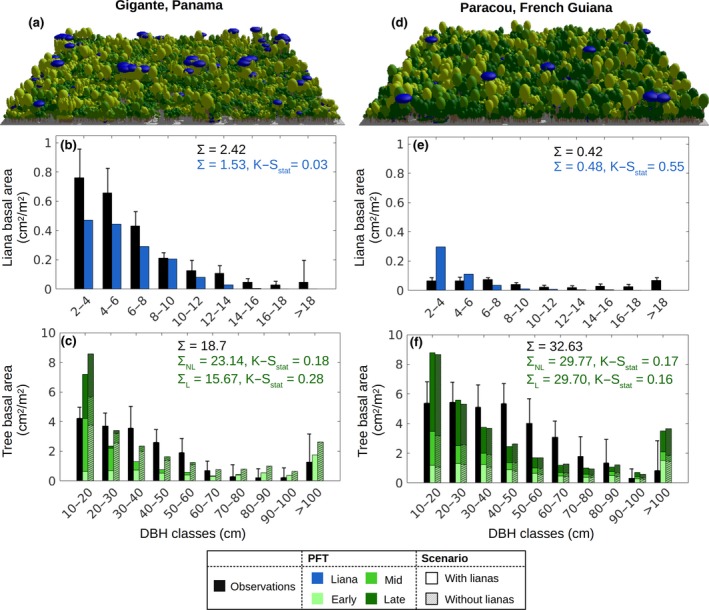
Forest demographic composition for the two simulated sites: Gigante, Panama (a–b–c), and Paracou, French Guiana (d–e–f). Panels (a) and (d) show a representative area of modeled forest of 1 ha. To visualize the forest composition, the forest is decomposed into patches according to their simulated relative area, and the three cohort densities and sizes are preserved (as well as the liana tree tracking). Panels (b–c) and (e–f) compare the basal area distributions of liana and tree PFTs, respectively, as observed locally (black) or simulated according to the ED2 (shades of blue and green). Tree basal area values (panels c and f) are compared for the simulations with (solid bars) or without (hatched bars) lianas. Σ represents the total basal area according to the model (blue or green) and field observations (black). Error bars represent the standard deviation of the different plot measurements (smaller error bars correspond to more homogeneous plots). The K–S_stat is the test statistic of the two‐sample Kolmogorov–Smirnov test between the observed and simulated size distributions (with a sampling size of 250 for each distribution). Liana basal area in Gigante was the only case in which the observed and simulated distribution did not significantly differ

Figure 4.

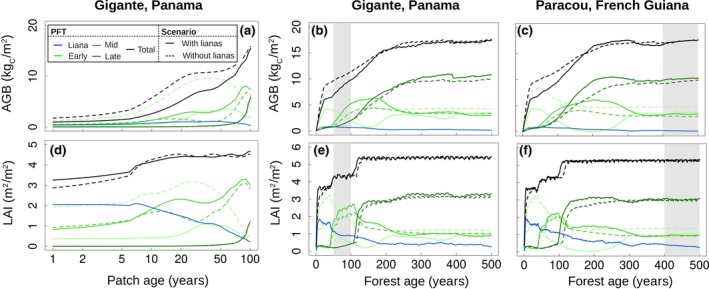
Comparison of simulations with (solid lines) and without (dashed lines) lianas. The upper graphs (a–c–e) show the above‐ground biomass (AGB), while the bottom graphs (b–d–f) represent LAI as a function of time for one patch (a–d) and for the forest aggregate (b–c–e–f). The gray zones represent the period during which the model outputs were averaged for all other plots (corresponding to the approximate stand age of the forest sites). The increases in LAI are caused by the crossing of the reproductive thresholds for the different plant functional types (PFTs)

The tree size distribution was rather poorly represented by the model regardless of the inclusion of lianas. For the Gigante site, the introduction of lianas into the model reduced the basal area across the entire size range (Figure 2c) and decreased the tree stem density from 705/ha to 575/ha, while the Paracou tree density was reduced from 858/ha to 778/ha. Given that the tree stem density calculated for Paracou was almost 10% lower when lianas were included in the simulations, the similar total tree basal area implies that the average tree DBH was slightly larger when we included lianas. The inclusion of lianas had a noticeable effect on the simulated PFT composition. Early successionals were significantly affected by lianas and went almost extinct when the forest was approximately 150 years old. The strong competition between lianas and pioneer trees benefited the shade‐tolerant PFT, which at the same forest age comprised more than 50% of the total biomass (compared to less than 40% when lianas were not included).

The trends in the simulated demography were largely governed by the forest stand age, while the climatic differences between the two test sites had very little impact on the overall forest carbon cycle and demography (Figures S8 and S9). For example, the simulated liana basal area for Paracou was 1.80 cm²/m² at the Gigante stand age, while the value was 1.71 cm²/m² for the actual Gigante simulation. Similarly, Gigante experienced a decrease in liana basal area after approximately 50 years according to the simulation.

In addition to the total LAI (Figure 1 for Paracou and Figure S6 for Gigante), we also examined whether the model captured the main peaks in the vertical stand structure in Gigante, measured with TLS in the control and removal plots (Figure 3). We compared the simulated LAI vertical distribution with the vertically resolved PAI derived from the TLS data. The observed vertical distribution was poorly captured by the model, with systematic underestimation of the PAI. The source of this underestimation is twofold: first, the simulations are the results of a landscape average that included recently disturbed patches, with lower LAI values (Figure 4a); this clogged phase leads to a significant peak in liana LAI at approximately 5 m. Second, the wood area index contribution was not accounted for in the simulations.

Figure 3.

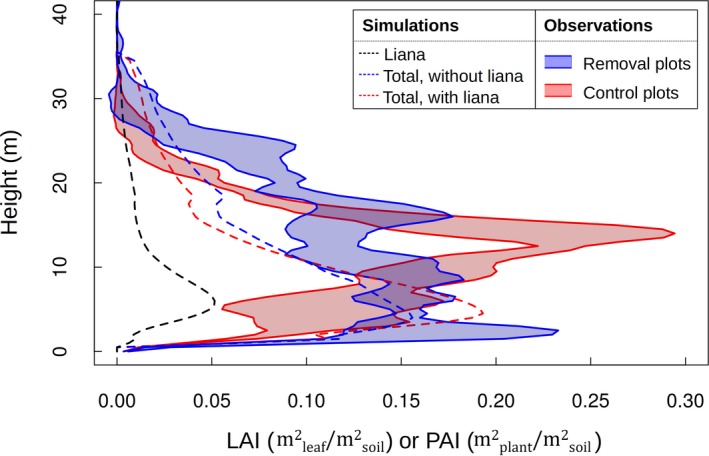
Modeled vertical distribution of the LAI in simulations with (red dashed line) or without (blue dashed line) lianas and TLS‐derived PAI profiles in control (red envelopes) and removal (blue envelopes) plots for Gigante, Panama. The shaded areas delimit the mean plus or minus one standard deviation, as calculated from the three vertical distributions scanned for each treatment. The black dashed line is the liana contribution to the total LAI vertical distribution. The modeled vertical distributions were calculated as the area‐weighted average of all patches in the simulated forest using 0.5 m height intervals and were reconstructed by distributing the LAI of the flat‐top crown over a DBH‐dependent crown depth (Bohman & O'Brien, 2006)

Despite this underestimation, the model was able to qualitatively reproduce some observed trends. In particular, adding lianas to the simulations led to a reduced PAI for trees taller than 16 m, as observed in the control plots. Measurements in gaps that were in a state of arrested succession indicated that they have lower canopies than liana‐dominated patches (average ± standard error was 16.5 ± 0.3 m vs. 30.4 ± 0.2 m; Tymen et al., 2015), which was confirmed by our model: the average top‐of‐canopy height was 9.9 m in liana‐dominated patches (where the liana LAI is more than half the total) and 25.6 m after arrested succession.

Even if liana leaves persist in old patches (the simulated liana LAI is strictly positive up to 35 m), the bulk of liana leaves are found in young patches. This result is consistent with the liana size distribution, which shows that the model underestimated the contribution of large lianas.

3.3. Trends in carbon dynamics and PFT composition

Simulations with ED2 result in the aggregation of patches with different disturbance histories across the landscape. In our simulations, only natural tree‐fall disturbance was considered. Figure 4 illustrates the differences between the results for the individual patches and the patches aggregated across the landscape. At the single patch level (Figure 4a), lianas slowed down forest carbon sequestration, leading to lower AGB stocks until the patch was approximately 100 years old (with a reduction of approximately 50% after 20 years). Figure 4b,c shows the AGB time series as an aggregate for the 34 patches considered in the landscape. For Gigante, the reduced growth rate translated into a reduction in the AGB stocks (−19%); in Paracou, the lower abundance of lianas and the lower mortality (on a per kg_C basis) resulted in a nonsignificant AGB difference with the nonliana scenario.

The low allocation of lianas to wood (in Paracou, the mean individual stem biomass was 5.95 kg_C versus 131 kg_C for adult lianas and trees, respectively) had a strong negative impact on the forest woody biomass growth rate (which decreased by 0.03 and 0.16 kg_C m⁻² year⁻¹, representing relative reductions of 5% and 28%, for Paracou and Gigante, respectively; see Figure S10), which is consistent with the approximate 10% reduction observed by van der Heijden and Phillips (2009). Given their small investment in structural stem tissues, lianas are left with a greater fraction of carbon to allocate to living tissues and reproduction. In fact, despite the total leaf biomass and LAI being almost not affected by the introduction of lianas, the leaf NPP was substantially higher (+8% and +20% for Paracou and Gigante, respectively, Figure 5) due to the high leaf turnover of lianas and the increased competition for light. At the whole forest level, the total leaf biomass and LAI were uninfluenced by the inclusion of lianas (Figures 4 and 5), showing that liana leaf abundance caused a proportional decrease in the tree leaf abundance (Figure 2). Since the model does not account for trait plasticity, this reduction of tree LAI was caused by a lower tree density. Only patches younger than 5 years, where lianas are highly dominant, displayed a significant increase in the total LAI (Figure 4d).

Figure 5.

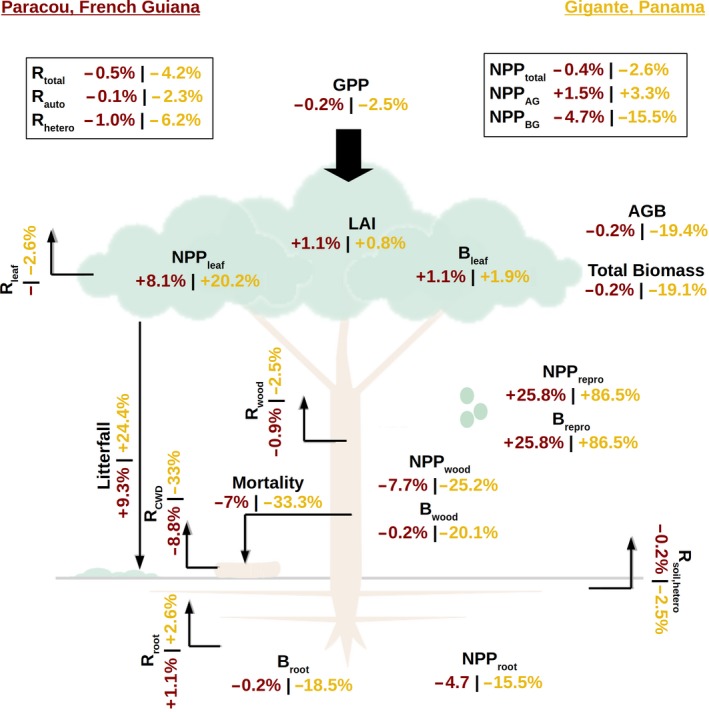
Relative changes in carbon pools and fluxes for Paracou, French Guiana (brown), and Gigante, Panama (yellow), upon inclusion of the liana plant functional type in the simulations. B, biomass; GPP, gross primary productivity; NPP, net primary productivity; R, respiration

The simulated vegetation composition was significantly affected by the presence of lianas. During the early stages of growth, early‐ and mid‐successional tree biomass significantly declined (−58% and −36%, respectively, for Gigante). For mature forest, such as that in Paracou, the total biomass was approximately the same, with a slight increase in the fraction of late successionals (+6%) and a marked decrease in early successionals (−25%). After the forest is around 100 years old, late‐successional trees display a large increase in biomass, especially for Paracou where they comprised as much as 65% of the total AGB. During the same period, early successionals decline steeply, only to recover after year 200.

For both sites, the GPP is only slightly impacted by the introduction of lianas (Figure 5). This raises a fundamental question: where is the canopy‐assimilated carbon going in liana‐rich forests?

For the Gigante forest, the simulation that included lianas showed 33% lower tree mortality on a kg_c lost basis (0.44 vs. 0.66 kg_c m⁻² year⁻¹). This finding does not imply that lianas reduce tree mortality but rather reflects the observation that liana‐infested forests have a reduced carbon stock, leading to a lower carbon flux from mortality. Despite being less impacted by lianas, the Paracou forest displayed qualitatively similar trends in mortality. Compared to simulations without lianas, the leaf NPP was 8% higher in Paracou and 20% higher in Gigante (Figure 5). Reproductive NPP was 26% higher in Paracou and 87% higher in Gigante, mainly driven by the contribution of lianas. Stem NPP was considerably lower in both Paracou (−8%) and Gigante (−25%). This shift in the production of plant material with a shorter residence time was consistent with empirically observed data (van der Heijden et al., 2015) and resulted in an overall decrease in carbon stocks for the liana forest.

4. DISCUSSION

One of the advantages of our modeling approach is the possibility of tracking the role of lianas in the dynamics of the different carbon pools and fluxes. This is not possible with observations in the field, as many of the variables are rarely measurable simultaneously or cannot be measured at all for practical or financial reasons, for example, GPP contributions and below‐ground biomass. In the following paragraphs, we provide an overview of the impacts of lianas on the tropical forest dynamics as well as a critical analysis of the results and suggest possible improvements for the parameterization and representation of the liana PFT.

4.1. Liana impacts on tropical forest

As a consequence of the contrasting abundance of lianas in young and old forests, their impact on the carbon cycle in these ecosystems is markedly different. At the younger site of Gigante, lianas account for one‐fourth of the total LAI, and due to their competition with early successional trees, they reduce the total AGB by approximately 19%. Paracou displays a similar effect of lianas during the same early stage of succession; however, their impact is significantly weaker during the 400–500 year period: liana contribution to the LAI is lower (approximately 7%), and the total forest AGB stocks are similar for simulations with and without lianas. Liana density significantly differs between the two sites (Table 1), and the impact of lianas on carbon dynamics was greater where they were more abundant. While these findings cannot be extrapolated to all primary and secondary forests (within which liana abundance varies substantially), the results indicate that the impact of lianas on forest demography and the carbon cycle is correlated with liana density.

In Gigante, the presence of lianas has a strong impact on the different above‐ground fractions of NPP (Figure 5). Although total NPP is not strongly impacted by the introduction of lianas, the greater allocation to leaves and lower allocation to stem reduces the potential for medium term (150 years) carbon sequestration in liana‐rich forests. As of 2008, the amount of secondary (between 1 and 60 years old) forest in the Neotropics was estimated to be 2.4 million km². Over the next 40 years, this land can potentially accumulate a total above‐ground carbon stock of 8.48 Pg_C (Chazdon et al., 2016). Our findings suggest that this carbon sink potential could be severely affected by liana proliferation.

The differences between Gigante and Paracou are consistent with the evidence that lianas are most abundant in young forests and recently created gaps (Barry et al., 2015; Putz, 1984; Schnitzer & Carson, 2010). Young patches are dominated by lianas and persist in a state of arrested succession for approximately 10 years (Figure 4d); this leads to size distributions that are highly skewed toward small individuals of relatively low height in young patches and a very low liana density in older patches (Figures 3 and 4). When looking at the simulated single patch dynamics (Figure 4a,d), the disappearance of lianas is likely too rapid. In fact, experimental evidence suggests that lianas persist in mature forests (Roeder, Hölscher, & Ferraz, 2010; Schnitzer et al., 2012) and that their contribution to the total basal area remains constant even as the liana stem density declines (Dewalt, Schnitzer, & Denslow, 2000). These model predictions are likely driven by a high liana mortality parameter as well as the inability for lianas to change hosts during the course of their life in silico. Currently, the range of reported mortality rate values is very broad, varying from 0.27%/year (Putz, 1990) to 9.4%/year (Mascaro, Schnitzer, & Carson, 2004). The current liana mortality parameterization could be improved in the future with additional field data.

The model predicts differential impacts of lianas on trees of different functional types: lianas negatively impact pioneer trees and favor shade‐tolerant trees. Although this differentiated effect of liana infestation is still debated (Schnitzer & Carson, 2010), a recent study by Visser et al. (2017) tends to corroborate the model output by finding that shade tolerance correlates with tolerance of liana infestation. In the model, the low density‐independent mortality of shade‐tolerant species translates to longer residence times than those shown by the occupying lianas. Late successionals can therefore survive liana infestation by outliving their liana colonists. This effect is consistent with empirical evidence of shade‐tolerant trees living with high levels of liana infestation for decades (Ingwell et al., 2010).

4.2. Model limitations and perspectives

Our model is able to capture some important features of a liana‐infested forest. However, our implementation relies on a number of assumptions that should be re‐evaluated as additional data become available. For example, the liana PFT was assumed to be representative of all lianas in tropical forests, whereas in nature, lianas display a wide diversity of growth forms, climbing mechanisms, dispersal types, leaf photosynthetic properties, and allocation patterns (Isnard & Silk, 2009; Wyka et al., 2013). Like for trees, liana species variability translates to a large range of allometric models and trait distributions. For example, liana wood density varies between 0.28 and 0.84 g/cm³ in the BCI inventory data, a range similar to that observed for trees (Muller‐Landau, 2004). Even more importantly, the use of different published allometric equations leads to 15‐fold differences in predicted liana AGB (Figure S2). In fact, a seminal study on liana allometry suggests that “stem diameter does not appear to be as good of a predictor for above‐ground stem biomass for lianas as it is for trees” (Schnitzer et al., 2006). The inclusion of a representation of stem length in the model could lead to improved biomass estimates (Gehring, 2004). For these new types of allometry to be considered in the model, there is a need for larger allometric datasets, especially those that include large lianas.

Our model predicts that the burden of hosting lianas is borne disproportionately by early‐ and mid‐successional trees: lianas colonize the first established community and mostly die with it. This is due to mortality, competition within that community, and the impossibility of recruiting in the shade. The experimental data regarding the impact of lianas on specific functional groups or on single species are still debated (van der Heijden & Phillips, 2009; Martínez‐Izquierdo, García, Powers, & Schnitzer, 2016); however, we acknowledge that some mechanisms of liana colonization (e.g., the colonization of multiple trees by the same liana) or of liana loss (e.g., by branch shedding) were not represented in the model and could have different impacts on tree PFTs. The transition rates from and to a liana‐infested state have recently been investigated (Visser et al., 2018) and could be used in the future to improve the model parameterization. We consider the direct competition for light between lianas and their hosts as one of the most speculative parts of our current model implementation; this process needs further attention in observational studies for future model improvement.

One of the key parameters to accurately represent lianas was the high allocation to reproduction and the low allocation to DBH growth; this contrasts with trees, which mainly allocate their excess carbon to stem growth (Supporting Information 3). It is worth noting that in the model, the contribution of lianas to the reproduction pool accounts not only for seeds but also for vegetative reproduction through the production of new shoots. Both of these mechanisms are considered to have a low rate of success in the model; that is, only 5% of the carbon invested in reproduction is eventually transformed into actual saplings (Table S1). Similar to the increased litterfall, this process contributes to the higher turnover rate of the liana‐infested forests. Several studies have demonstrated the importance of clonal reproduction for lianas and support our parameterization: even if the frequency of clonal reproduction is highly variable among liana species (Schnitzer et al., 2012), the ability to spread vegetatively is very common among lianas, and species that seem to lack this capacity are rare (Caballe, 1994). Vegetative reproduction has potentially huge impacts on liana proliferation, distribution, and overall impact on the forest. For instance, Schnitzer et al. (2012) showed that the highly clonal liana species may be more disturbance adapted and may account for the clumped distribution pattern observed among lianas (Ledo & Schnitzer, 2014). A future improved model could benefit from a mechanistic representation of liana clonal reproduction, as we currently simply increase the allocation of excess carbon by lianas to reproductive tissues to represent this process.

The two sites considered in this study are both relatively wet, but some noticeable climatic differences exist between them: the dry season in central Gigante is longer than that in Paracou (4 months vs. 3 months), and the cumulative rainfall in Gigante is 20% lower than that in Paracou (2,400 vs. 3,000 mm). The simulated forest dynamics were, however, very similar for both sites (Figures S8 and S9), which are explained by the dominance of above‐ground competition over below‐ground competition in the simulations. For example, for the Gigante site, the mid‐afternoon water stress coefficient (unitless factor between 0 and 1 reducing the stomatal aperture due to drought stress, see Medvigy et al., 2009) was 0.94 ± 0.02; that is, the overall forest transpiration was only marginally reduced by water stress. This finding was confirmed in all simulations and was not affected by the presence of lianas. While drought stress has been experimentally observed in the Gigante Peninsula (Álvarez‐Cansino, Schnitzer, Reid, & Powers, 2015), it was not reproduced in our simulations, and a better representation of below‐ground competition between growth forms should be the focus of future research. When comparing trees and lianas, hydraulic properties display significant differences between the two growth forms (e.g., Johnson, Domec, Woodruff, McCulloh, & Meinzer, 2013). These differences likely contribute to the observed negative correlation between liana abundance and MAP and the positive correlation between liana abundance and mean dry season length (DeWalt et al., 2009). Simulating tree–liana competition across a broader range of environmental conditions (drier sites and periods) would require taking these differences in water uptake and transport strategies into account. From a modeling point of view, a new physically based implementation of water uptake and transport toward the canopy for ED2 was recently developed by Xu et al. (2016) and offers the opportunity to account for these hydraulic differences in future studies.

Despite the significant limitations that emerged from the analysis of our results, we can conclude that the model simulations with the new liana PFT, captured many peculiarities of the carbon dynamics of liana‐rich forests. This first implementation of lianas into a DGVM should open new avenues to forecast the impact of liana infestation on the demography and biogeochemical cycles of tropical forests.

CONFLICT OF INTEREST

The authors declare no conflict of interest.

AUTHOR CONTRIBUTIONS

H.V., M.D.P., and F.M. designed the study. M.D.P. developed the model code, with contributions from M.L. and F.M. M.D.P. carried out the simulations. M.D.P., F.M., and M.L. analyzed the results. S.M. provided the LIDAR data. M.D.P. and F.M. led the manuscript writing, with additional contributions from M.L. and H.V. All other authors contributed to discussions and revised the final version of the manuscript.

Supporting information

 

di Porcia e Brugnera M, Meunier F, Longo M, et al. Modeling the impact of liana infestation on the demography and carbon cycle of tropical forests. Glob Change Biol. 2019;25:3767–3780. 10.1111/gcb.14769