Coexisting representations of sensory and mnemonic information in human visual cortex

Abstract

Traversing sensory environments requires keeping relevant information in mind while simultaneously processing new inputs. Visual information is kept in working memory via feature selective responses in early visual cortex, but recent work had suggested that new sensory inputs obligatorily wipe out this information. Here we show region-wide multiplexing abilities in classic sensory areas, with population-level response patterns in early visual cortex representing the contents of working memory alongside new sensory inputs. In a second experiment, we show that when people get distracted, this leads to both disruptions of mnemonic information in early visual cortex and decrements in behavioral recall. Representations in the intraparietal sulcus reflect actively remembered information encoded in a transformed format, but not task-irrelevant sensory inputs. Together these results suggest that early visual areas play a key role in supporting high resolution working memory representations that can serve as a template for comparing incoming sensory information.

When trying to attain behavioral goals, the ability to flexibly juggle thoughts is key. Visual Working Memory (VWM) provides the mental workspace to keep visual information online, allowing this information to guide visual search or to be recalled at a future moment in time. Neuroimaging studies have firmly established that VWM contents can be decoded from occipital cortex including primary visual area V1^1,2,3,4, and that the quality of this information predicts behavioral performance^5,6, suggesting that early sensory areas are involved in the representation of visual memories.

That said, previous studies typically relied on a traditional delayed-match-to-sample (DMTS) task in which a sample memory stimulus is encoded and remembered across a blank delay interval before a test stimulus appears for comparison. However, in everyday perception, VWM maintenance needs to be robust to the continuous influx of new visual inputs that come with each exploratory saccade or change in the environment. Thus, a delay period devoid of other visual inputs is quite divorced from typical visual experience. Based on this mismatch between experimental and real-world scenarios, some have argued that recruiting early sensory areas to store relevant VWM information would be counterproductive in everyday life, as new sensory inputs would destructively interfere with concurrent mnemonic representations^6,7,8.

Based on this logic, one recent study⁶ employed a DMTS task with task-irrelevant pictures of faces and gazebos sometimes presented during the delay period. The authors used functional magnetic resonance imaging (fMRI) and found that activation patterns in early visual cortex represented the contents of VWM during blank delays, but not when delays were filled with predictable distractors (i.e. the task-irrelevant pictures). The authors concluded that representations initially encoded in early visual cortex were recoded in a more durable format in parietal cortex to insulate mnemonic representations from interference induced by new sensory input. Furthermore, the authors argued that the disengagement of primary sensory regions was strategic as it occurred only when participants expected the task-irrelevant pictures. This study challenged the importance of early visual cortex during VWM, attributing previous findings of sensory recruitment to overly artificial tasks (cf.⁹ for potential caveats of this work).

Importantly, this proposed framework⁶ implies a fundamental limitation of cortical information processing: a sensory area such as primary visual cortex cannot represent both top-down biasing signals associated with internal cognitive operations like VWM and bottom-up sensory inputs evoked by newly encountered stimuli in the environment. However, this strong stance is questionable for at least two reasons. First, from a functional point of view, success on a DMTS task relies on comparing an internally stored representation to a new sensory input. For this, a ‘local comparison circuit’, able to jointly represent remembered and perceived items in the same local circuit, could be ideal. Second, separable bottom-up and top-down inputs could theoretically support the co-existence of multiple simultaneous representations, a concept we term ‘region-wide multiplexing’ (after the more common usage of ‘multiplexing’ to refer to flexible coding in single neurons). Bottom-up input from the lateral geniculate nucleus primarily projects to layer 4 of primary visual cortex, whereas top-down input arrives primarily in superficial layers and layer 5^10,11. When information from layer 4 is conveyed to the superficial layers, different populations of neurons might be recruited to keep bottom-up and top-down inputs anatomically segregated¹². In addition, the format of the codes might differ, with bottom-up signals driving changes in spike rate, and top-down signals modulating membrane potentials⁷. Such a system could promote match detection via response gain when memory and sensory information are aligned¹³.

Results

In Experiment 1 we evaluated the ability of early visual areas to act as a multiplexing comparison circuit during VWM. Participants performed a working memory task where they remembered randomly oriented visual gratings while looking at either a blank screen or a sequence of contrast-reversing visual distractors (Fig. 1a). Each trial started with a 100% valid cue (1.4s) indicating the distractor condition during the subsequent delay. Next, a target orientation was shown for 0.5s, and remembered throughout a 13-second delay. To ensure a relatively uniform sampling of orientation space, the target orientation was pseudo-randomly drawn from one of six orientation bins (each bin contained 30 orientations, in integer increments), with an equal number of draws from each bin. During the middle portion of the delay, participants viewed either a grey screen, or an 11-second contrast-reversing distractor. Distractors were either a Fourier filtered white noise stimulus (an example is shown in Fig. 1a – a novel noise structure was generated on every trial) or an oriented grating with pseudo-random angular offset relative to the memory target orientation (its orientation was similarly drawn from one of six bins, counterbalanced with respect to the target orientation bin; see Supplementary Fig. 1a). After the delay, participants had 3 seconds to rotate a recall probe to match the remembered orientation as precisely as possible before continuing to the next trial. While the presence or absence of distractors was fully predictable, distractors were irrelevant to the task, and had no observable impact on behavior during fMRI scanning (Fig. 1b, Supplementary Fig. 2a). As expected, distractors effectively drove a sustained and highly robust increase in the overall univariate response amplitude in V1 and other visual areas (Supplementary Fig. 3a). Note that the distractors, when presented, function as visual masks. This was a deliberate choice, optimizing the design to be most favorable to the no-distractor condition (i.e. a blank screen without any visual interference during the delay).

Figure 1.

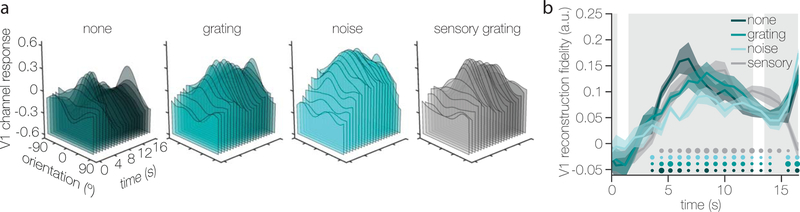
Experiment 1 paradigm and results (a) After a valid cued about the distractor condition (here, the blue fixation cued a noise distractor) a 0.5s target orientation was remembered for 13 seconds. During this delay, participants viewed a grey screen or an 11-second contrast-reversing distractor. Distractors could be a Fourier filtered noise stimulus (depicted), or an oriented grating (its orientation pseudo-randomly selected on every trial). After the delay participants had 3 seconds to rotate a recall probe to match the remembered orientation. (b) There were no differences in behavioral error between the three distractor conditions, as indicated by a non-parametric one-way repeated measures within-subject ANOVA (F_(2,10) = 0.044; p = 0.943). Grey lines indicate individual subjects. (c) Model-based reconstructions of the remembered orientation during the three different distractor conditions (left), and of the physically-present orientation on trials with a grating distractor (right). Reconstructions were based on the average activation patterns 5.6–13.6 seconds after target onset. (d) The degree to which memory and sensory stimuli were represented during the delay was quantified by projecting the channel response at each degree onto a vector centered on the true orientation (i.e. zero), and taking the mean of all these projected vectors. On the left, a cartoon reconstruction is defined by 18 points/degrees (note: in reality there were 180 degrees). On the right, this cartoon reconstruction is wrapped onto a circle. We show for one point/degree how the channel response (h) is projected onto the true orientation (remembered or sensed) resulting in vector b. Knowing the angle (A) between the true orientation and the orientation at this particular point/degree, we solve for b using trigonometric ratios for right triangles (i.e.$\cos A=b/h$). The mean of all projected vectors (all b) indexes the amount of information at the true orientation, and is our metric for reconstruction fidelity. (e) Reconstruction fidelity for remembered (shades of teal) and sensed distractor (grey) orientations is significantly above chance in almost all ROIs (based on one-sided randomization tests comparing fidelity in each condition and ROI to zero; see Methods). Black asterisks next to ROI names (under the x-axis) indicate significant differences in memory fidelity between the three distractor conditions in that ROI, as determined by non-parametric one-way repeated-measures within-subjects ANOVA’s performed separately for each ROI (see Methods; for exact p-values and post-hoc tests see Supplementary Tables 1 and 2). One, two, or three asterisks indicate significance levels of p ≤ 0.05, p ≤ 0.01, or p ≤ 0.001, respectively (uncorrected for multiple comparisons). Dots indicate individual subject fidelities in each condition and ROI. For b, c, and e, error bars / areas represent ± 1 within-subject SEM around the average across n=6 independent subjects.

Next, using a multivariate ‘inverted encoding model’^14,15 (or IEM; Supplementary Fig. 4) trained on independent data, we generated model-based reconstructions of the remembered orientation from delay period activity patterns in primary visual cortex (Fig. 1c, left panel), and all other early retinotopic areas that we mapped along the visual hierarchy (Supplementary Fig. 5a), irrespective of whether a distractor was present during the delay. The baseline offset observed between distractor conditions (vertical shift up/down the y-axis in Fig. 1c) largely reflects the univariate effect of distractor presence during the delay interval, with higher baselines during trials with distractors (see Supplementary Fig. 3a). As a measure of tuning fidelity, we projected the channel response at each degree in orientation space onto the remembered orientation and then took the mean of these projected vectors (Fig. 1d). Fidelity was significantly above zero, indicating that there was information about the remembered orientation during all distractor conditions (Fig. 1e, teal bars) and in all regions of interest (ROIs), except areas in the intraparietal sulcus (IPS). Note that the independent data used to train the IEM were collected while participants directly viewed orientation stimuli. Thus, generalization from sensory evoked response patterns to memory-related response patterns during the delay epoch implies that mnemonic information was represented in a sensory-like format.

Importantly, we were also able to reconstruct the orientation of the distractor that was physically present on the screen during grating distractor trials (Fig. 1c, right panel; Fig. 1e, grey bars), using the exact same delay-period data. This demonstrates that, contrary to simple feedforward models that posit V1 as a passive filter, early visual cortex can represent incoming sensory information alongside mnemonic information that is no longer tethered to external inputs. While the fidelity of remembered and sensed orientations was roughly equivalent in V1–V2 (Fig. 1e, compare mid-teal bars and grey bars), the fidelity of the sensed distractor grating dropped against the fidelity of the remembered grating when ascending the visual hierarchy to V3–V4 (interaction: F_(4,20) = 5.67, p = 0.002; note that this analysis does not include IPS and LO1, as their relative hierarchical relationships are less clear). This finding captures the top-down nature of mnemonic signals, as top-down signals are thought to have more traction than bottom-up sensory inputs in higher-level regions.

Notably, timepoint-by-timepoint reconstructions reveal that remembered and perceived representations evolve together over time in primary visual cortex (Fig. 2), indicating that these representations coexist throughout most of the delay period. This is also true for other early retinotopic areas along the visual hierarchy, but not for later retinotopic IPS areas (Supplementary Fig. 6a). Note that claims about the coexistence of information are limited by the temporal resolution of our measurement (i.e. 800ms TR’s). The notion of a comparison circuit at the level of early sensory cortex is further supported by a boost in representational quality when target and distractor orientations are similar, compared to dissimilar (Supplementary Figs. 7 and 8b). This finding is mirrored by behavioral demonstrations showing higher fidelity memory recall for similar targets and distractors^16,17 (Supplementary Fig. 9b).

Figure 2.

Model-based reconstructions of remembered orientations and sensed distractor orientations over time in V1. (a) The time axis starts at “0” which is trial onset, and each slice shows the mean reconstruction across participants at each 800ms TR (for a total of 21 TRs). Reconstructions for the remembered orientation are shown in the three left-most panels (shades of teal), and sensed distractor orientation reconstructions are shown in the right-most panel (grey). (b) The fidelity of timepoint-by-timepoint reconstructions in V1 (quantification of (a)), with time 0 representing target onset. The three gray background panels represent the target, distractor, and recall epochs of the working memory trial. Small, medium, and large dots at the bottom indicate significance at each time point at p ≤ 0.05, p ≤ 0.01, and p ≤ 0.001, respectively (based on one-sided randomization tests comparing fidelity in each condition and at each timepoint to zero, uncorrected for multiple comparisons; see Methods). Shaded error areas represent ± 1 within-subject SEM around the average across n=6 independent subjects.

In a second experiment we evaluated the impact of more naturalistic distractors, namely, face and gazebo pictures (after ref.⁶). Moreover, instead of contrast-reversing our visual distractors (as in Experiment 1), we flickered distractors on (250ms) and off (250ms) for 11s during the delay to maximize the unpredictability of contrast changes at every pixel. The task structure (Fig. 3a) was similar to that of Experiment 1, with participants again remembering a pseudo-randomly oriented grating while ignoring other inputs during the delay. A 100% predictable cue (1.4s) was presented before the to-be-remembered memory target (0.5s), with the cue indicating one of three possible events during the 12s delay: no distractor (i.e. blank screen), an 11s grating distractor (with pseudo-random angular offset relative to the target orientation, Supplementary Fig. 1b), or 11 seconds of picture distractors (example shown in Fig. 3a). Participants had 4s to report the remembered orientation as precisely as possible by rotating a dial. Distractors drove robust univariate responses in all of our ROIs (Supplementary Fig. 3b).

Figure 3.

Experiment 2 paradigm and results (a) Irrelevant but fully predictable distractors were cued by a change in fixation color (here, blue indicated that picture distractors would be shown during the delay) prior to a 500ms target presentation. Participants remembered the target orientation for 12 seconds, while they either viewed a grey screen, or an 11-second on-off flickering distractor (a pseudo-randomly oriented grating, or pictures of faces or gazebos). After the memory delay participants rotated a dial to match the remembered orientation. Photo used with permission. (b) Distractor presence negatively impacted behavioral performance, as indicated by a non-parametric one-way repeated measures within-subject ANOVA (F_(2,12) = 10.154; p < 0.001). Errors were smaller when no distractor was shown during the delay, compared to when distractor gratings (t₍₆₎ = 6.272; p < 0.001) or pictures (t₍₆₎ = 3.375; p = 0.018) were shown. Performance did not differ between grating and picture distractors (t₍₆₎ = 1.184; p = 0.184). Post-hoc tests were non-parametric uncorrected paired-sample t-tests. Grey lines indicate individual subjects. (c) Model-based reconstructions of the remembered orientation during the three different distractor conditions (left), and of the sensed distractor orientation on trials with a grating distractor (right). There reconstructions were generated with an IEM trained on independent localizer data, and based on the average activation patterns 5.6–13.6 seconds after target onset. (d) Reconstruction fidelity for remembered orientations without distraction (dark teal) and for sensed distractor orientations (grey) is significantly above zero in all ROIs except IPS0 and IPS1 (based on one-sided randomization tests in each condition and ROI; see Methods). However, reconstruction fidelity is less robust when a distractor was presented throughout the delay (mid-teal and yellow for grating and picture distractors, respectively). Black asterisks next to ROI names indicate significant differences in memory fidelity during the three distractor conditions in that ROI, as determined by non-parametric one-way repeated-measures within-subjects ANOVA’s performed separately for each ROI (see Methods; for exact p-values and post-hoc tests see Supplementary Tables 3 and 4). Dots indicate individual subject fidelities in each condition and ROI. (e) The fidelity of timepoint-by-timepoint reconstructions in V1. Time “0” represents target onset, and the three gray panels represent the target, distractor, and recall epochs of the working memory trial. One, two, or three asterisks in b and d (small, medium, or large dots at the bottom of e) indicate significance levels of p ≤ 0.05, p ≤ 0.01, or p ≤ 0.001, respectively (uncorrected). For b, c, d, and e, error bars / areas represent ± 1 within-subject SEM around the average across n=7 independent subjects.

Notably, the presence of distractors in Experiment 2 negatively impacted behavioral performance during fMRI scanning (Fig. 3b, Supplementary Fig. 2b). This drop in behavioral performance was accompanied by qualitatively poorer memory reconstructions when distractors were presented during the delay (Fig. 3c, left panel; Supplementary Fig. 5b). Indeed, memory fidelity in V1–V4 and LO1 was reduced when grating and picture distractors were shown during the delay, compared to fidelity without distractors (Fig. 3d; Supplementary Tables 3 and 4). Alongside these (reduced) memory representations, the directly sensed distractor orientation was represented in a robust manner (Fig. 3c, right panel; Fig. 3d, grey bars), as were the directly sensed picture distractors (Supplementary Fig. 10). As in Experiment 1, the IEM was trained on independent data, collected while participants were directly viewing oriented gratings. Generalization to data from the memory delay implies that a sensory-like code is used to represent mnemonic information, and that this representation is less robust when people are distracted by visual inputs during the delay. Note that in IPS0 and IPS1 there was no evidence of mnemonic information, nor did these regions represent the sensed distractor grating, implying that these areas do not represent information in a manner that is generalizable from directly viewed sensory inputs.

A direct comparison between the remembered and sensed orientations on trials with a grating distractor (compare mid-teal bars and grey bars in Fig. 3d) again revealed a relative increase in mnemonic compared to sensed information when ascending the visual hierarchy (interaction: F_(4,24) = 7.418, p = 0.001) – a hallmark of top-down processing^18,19,20,21. Timepoint-by-timepoint analyses (Fig. 3e) showed sustained memory representations throughout the delay when there was no distractor present, while memory fidelity was less sustained in the presence of visual distraction. Note that this did not hold true for IPS, where there was no evidence of representations of the either the remembered orientation or the sensed distractor orientation, sustained or otherwise (Supplementary Fig. 6b).

In the analyses presented thus far, we trained the IEM solely on data from independent sensory localizers, demonstrating that visual areas up to IPS encode remembered features in a sensory-like format. Here, ‘sensory-like’ refers to a format akin to that of a stimulus-driven sensory response. An independent sensory localizer makes no demands on memory, and gives rise to information in a stimulus-driven format. However, not all mnemonic signals are necessarily stored in this format, and might also be stored in a format that is somehow transformed. For example, pixel-by-pixel representations in early visual cortex might undergo some dimensionality reduction in upstream cortical sites^22,23. To look for a mnemonic code that is not necessarily sensory-like, we trained the IEM on data from the memory delay via a leave-one-out procedure (see Methods). In both Experiments 1 and 2 we see robust VWM representations, despite visual distraction, in all retinotopic ROIs including IPS0 and IPS1 (Fig. 4; Supplementary Figs. 11 and 12), and including more anterior and non-visually responsive IPS ROIs (Supplementary Fig. 13). Despite the ubiquity of mnemonic information in IPS revealed by this analysis, there is still no apparent information about the directly sensed distractor grating (grey bars) in IPS (Fig. 4; Supplementary Fig. 13). Taken together, this implies that IPS does represent mnemonic information, and that it uses a code that is transformed away from the stimulus-driven driven response. Furthermore, representations in IPS were impervious to visual distraction, with equivalent memory fidelities during all distractor conditions even in Experiment 2 (Supplementary Fig. 13), despite differences at the behavioral level (Fig. 3b). Thus, representations in V1–V4 and LO1 (lower fidelity during visual distraction), but not IPS (stable fidelity), mirrored how well people did on a VWM task.

Figure 4.

Reconstruction fidelity when training and testing an IEM on data from the memory delay in Experiment 1 (a) and Experiment 2 (b). There are robust memory representations throughout the visual hierarchy, including retinotopic IPS. This implies that the representational format in IPS is not in a stimulus-driven format. The proposed transformed nature of the IPS code is also supported by the lack of information about the directly sensed grating distractor (grey bars). As before, differences in memory fidelity between the three distractor conditions (black asterisks next to ROI names) were virtually absent in Experiment 1 (a; for exact p-values and post-hoc tests see Supplementary Tables 5 and 6), while in Experiment 2 the presence of distractors was accompanied by a drop in memory fidelity in many ROIs (b; for exact p-values and post-hoc tests see Supplementary Tables 7 and 8). Note however that mnemonic representations in IPS were unaffected by visual distraction (see also Supplementary Fig. 13). One, two, or three asterisks indicate significance levels of p ≤ 0.05, p ≤ 0.01, or p ≤ 0.001, respectively. Dots indicate individual subject fidelities in each condition and ROI. Error bars represent ± 1 within-subject SEM (for n=6 and n=7 independent subjects in a and b respectively). Statistical testing was identical to Figs. 1e and 3d. When ascending the visual hierarchy from V1 to V4, a weakening sensory representation paired with a strengthening mnemonic representation illustrates the top-down nature of VWM (compare grey and mid-teal bars). This signature interaction was present in both Experiment 1 (F_(4,20) = 13.6, p < 0.001) and Experiment 2 (F_(4,24) = 7.769, p < 0.001), as indicated by non-parametric two-way repeated measures within-subject ANOVA’s.

Note that this analysis does not necessarily speak to the representational format in early visual areas V1–V4 or LO1. While generalization from independent sensory data demonstrated a sensory-like mnemonic format, generalization within the memory delay does not by definition indicate a non-stimulus driven format. After all, training and testing on a sensory-like mnemonic code would yield robust reconstructions as long as there was information present. Thus, we can only ascertain the presence of non-stimulus driven transformed codes in IPS, as uncovering mnemonic information in IPS is only possible after training the IEM on memory (and not sensory) data.

Finally, none of the findings reported here depend on our choice of analysis approach (IEM model), and conventional decoding analyses yield similar patterns of results (Fig. 5).

Figure 5.

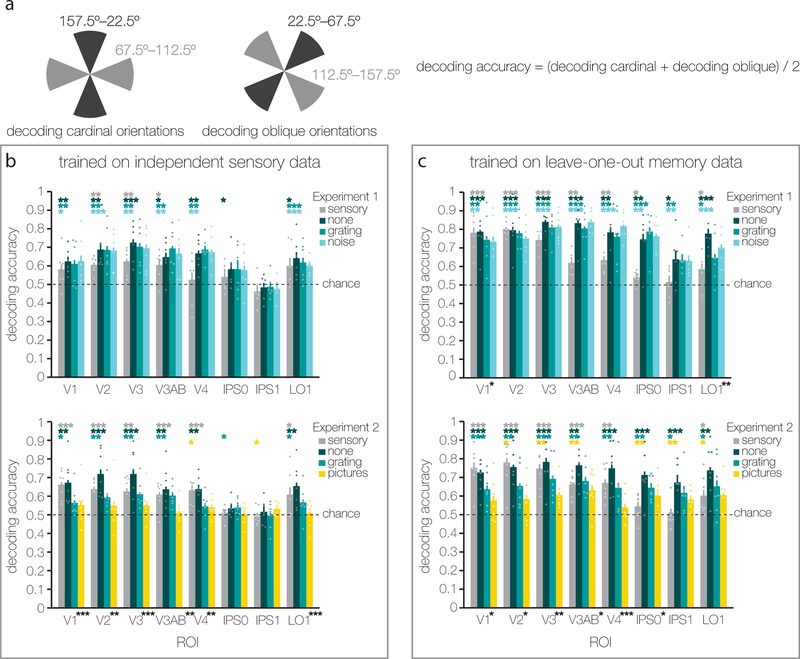
Decoding analyses yield highly comparable results to the IEM analyses. (a) In Experiments 1 and 2 we used random orientations (1°–180°), while relevant previous work has used orthogonal orientations^1,6. To closely mimic the two-way classification performed in previous work, we divided our random orientations into four bins, and performed two two-way classifications: The first classification determined whether orientations were around vertical (between 157.5° and 22.5°) or horizontal (between 67.5° and 112.5°) – shown schematically in the left diagram. The second classification determined whether orientations were around one or the other oblique (i.e. between 22.5°–67.5° or between 112.5°–157.5°) – shown schematically in the right diagram. Decoding performance was averaged across these two-way classifications to yield an overall classification accuracy for each ROI. For all decoding analyses we ensured balanced training sets. (b) We trained the SVM on independent data from the visual mapping tasks. Results mirrored those from the IEM analyses. In Experiment 1 (top) we found above chance decoding in V1–V4 and LO1, but not IPS0 and IPS1. There were no differences between the three distractor conditions in any of the ROIs (all F_(5,10) < 1.024, all p > 0.429). Also in Experiment 2 (bottom) there was little above chance decoding in IPS regions. In V1–V4 and LO1, memory decoding in Experiment 2 differed between the three distractor conditions (all F_(5,10) > 10.419, all p < 0.004), and was generally better when no visual distraction was presented during the delay, compared to delays with a grating or a picture distractor. In both Experiments 1 and 2, the grating distractor condition revealed an interaction between remembered and sensed representations (compare mid-teal and grey bars), considered a signature of top-down processing (F_(4,20) = 2.469, p = 0.046 and F_(4,24) = 3.198, p = 0.024, respectively). (c) We also trained the SVM on data from the memory delay via a leave-one-out cross-validation procedure. This led to robust decoding of mnemonic information in IPS0 and IPS1 for both Experiments 1 (top) and 2 (bottom), implying a non-stimulus driven mnemonic code in these areas. Lack of information about the ignored sensory distractor orientation (grey bars) further corroborates that IPS uses non-stimulus driven codes to represent task-relevant information. In Experiment 1 (top) the three distractor conditions differed in V1 and LO1 (F_(2,10) = 3.517, p = 0.045 and F_(2,10) = 12.723, p = 0.003, respectively) but not in any other ROIs (all F_(2,10) < 1.062, all p > 0.386). In Experiment 2 (bottom) the three distractor conditions differed in almost all ROIs (V1–IPS0, all F_(2,12) > 5.399, all p < 0.022;). Again, both Experiments 1 and 2 revealed an interaction between remembered and sensed representations (compare mid-teal and grey bars) in the grating distractor condition (F_(4,20) = 11.499, p < 0.001 and F_(4,24) = 3.331, p = 0.029, respectively). For both b and c, statistical testing was identical to that in Figs. 1e, 3d, and 4 with the exception that randomization tests were against chance (0.5) instead of zero (see also Methods). One, two, or three asterisks indicate significance levels of p ≤ 0.05, p ≤ 0.01, or p ≤ 0.001, respectively. Dots indicate individual subject decoding in each condition and ROI. Error bars represent ± 1 within-subject SEM (for n=6 and n=7 independent subjects in Experiments 1 and 2, respectively).

Discussion

Visual information held in mind to attain behavioral goals should withstand interference from ongoing sensory inputs. In Experiment 1 we demonstrated that recall of an orientation was unimpeded by irrelevant visual distractors, and that the fidelity of mnemonic representations in visual cortex was similar with and without distractors. By contrast, participants in Experiment 2 did get distracted, showing impairments at both the behavioral and neural level. Participants viewed noise distractors in Experiment 1, and picture distractors (faces and gazebos) in Experiment 2. Different distractor types might result in different degrees of distractibility, which could explain the discrepancy between the two experimental outcomes. However, grating distractors were shown during both experiments, and even for this shared condition there was a drop in the fidelity of behavioral and brain responses in Experiment 2. This was true also for the three participants who completed both experiments, and had not been affected by distractors in Experiment 1. Instead of distractor type, a likely variable causing the differences in distractibility is the “intensity” of the distractors, namely, whether they were contrast-reversing (Experiment 1) or flickering on and off (Experiment 2). The contrast at every pixel, integrated over a contrast-reversal cycle, is always mean grey. Instead, flickering between a grating with a random phase (“on”) and a mean grey screen (“off”) results in contrast fluctuations from cycle to cycle, and thus a stronger temporal gradient of change at every pixel.

A previous paper reported one experiment claiming that task-irrelevant visual distraction wiped out mnemonic representations in V1 at no behavioral cost^6,9. Our results from Experiment 2 are reminiscent of these findings, where distractor presence caused a marked drop in mnemonic information in early retinotopic areas. However, information did not generally dissipate altogether (Figs. 3d, 4b and 5, Supplementary Figs. 5b, 6b, 11b, and 12b). More importantly, this reduction of information was mirrored by a clear decline in behavioral performance (Fig. 3b). Prior failures to uncover behavioral effects when only a single feature is remembered can be readily explained by the need for statistical power in paradigms where memory fidelity tends to be high²⁴. Instead of a traditional DMTS task with only two answer alternatives, the recall procedure we used here allowed a much more fine-grained detection of small effect sizes. Thus, differences in distractor intensity, as well as a behavioral paradigm that lacks sensitivity, can account for the biggest discrepancies between previous work⁶ and our current findings.

The coexistence of local information about current sensory inputs, combined with feature-selective top-down inputs that carry information about remembered items, could provide a powerful local mechanism for comparing memory contents to the sensory environment^12,25,26. To support this functionality, sensory and memory information could be multiplexed by different populations of neurons¹². For example, if neurons tuned to the features of a memory target were selectively activated during the delay, the output of a local comparison circuit would be relatively high when a matching test stimulus was encountered that selectively excited similarly tuned neurons. On the other hand, a mismatch test stimulus would drive a set of differently tuned neurons, which may lead to a lower overall response due to inhibitory competition with the already active neurons tuned to the sample feature^13,27. The same logic also applies if the top-down modulations supporting VWM do not lead to sustained patterns of spiking in sensory cortices, and instead only influence sub-threshold potentials^7,28. Differences in the local comparison circuit output would still be expected due to interactions between the top-down feature-selective bias and the sensory response evoked by the test stimulus. Moreover, content-specific patterns of sub-threshold membrane potentials could persevere through bouts of local spiking driven by sensory inputs during a delay, and thus protect mnemonic contents from distraction¹³. Because fMRI measures an aggregate of signals (i.e. spikes, local field potentials, etc.), here we can only speculate about the exact nature of this comparison circuit, and cannot draw inferences about single neurons, the likely scale of anatomical separation, or precise temporal integration of the comparison circuit.

Here we find distractor resistant mnemonic representations throughout the delay (Experiment 1), while classic single-neuron physiology has generally found mnemonic representations in later stages of visual cortex disrupted by visual transients^12,29,30. For example, when monkeys viewed a target image and subsequently looked for matches in a series of test images, neuronal responses in inferior temporal (IT) cortex signaled an active memory trace via enhanced firing for matches³¹. However, this memory signal did not bridge the intervening delays between test images. By contrast, delay activity in prefrontal cortex survived intervening test stimuli and was maintained during each delay^32,33. Note how this task, unlike ours, requires the animal to perform a matching operation on each intervening stimulus and thus each ‘distractor’ is actually a behaviorally relevant image that requires attentive processing. Instead, in a set of studies that is more directly comparable to our experiments, monkeys had to mentally trace a curved line that was no longer in view, which led to sustained delay-period spiking in V1. Spiking was briefly interrupted by an irrelevant mask, but reinstated soon thereafter¹¹. Thus, the status of a distractor as relevant or irrelevant might play an important role in how memories are maintained. Also, different memory contents (i.e. highly familiar categorical objects versus fine-grained line orientations) might require different levels of representational precision.

Prefrontal and parietal cortices play a central role in maintaining distractor resistant memory representations^32,33,34, and feedback from these regions likely supports the persistent mnemonic representations in early visual cortex found here. Early retinotopic representations were sensory-like in nature, as evidenced by the generalization from independent sensory data (used to train our multivariate models) to delay epoch data. A sensory-like format would indeed be well suited for a local comparison circuit, readily able to contrast mnemonic information and ongoing sensory inputs. By contrast, sensory information did not generalize to the memory delay in IPS. Instead, only training and testing on data obtained during the memory delay itself revealed information in IPS. This implies a code that is transformed away from a purely stimulus-driven format. The notion of such a non-stimulus driven code in IPS which is further supported by the absence of information about the directly sensed grating distractor. Maintaining multiple replicas of a remembered sensory stimulus at all cortical levels would be computationally expensive and inefficient. Instead, high-resolution pixel-by-pixel representations might be condensed into stable and low dimensional representations in higher cortical regions²². Accordingly, these stable and potentially compressed representations might not support high-fidelity mnemonic information. Indeed, behavioral performance in Experiment 2 was impaired in the same conditions where representations in early visual areas were disrupted, while mnemonic representations in IPS remained intact. Of course, our failure to find sensory-like representations in IPS doesn’t mean they don’t exist there. For one, IPS doesn’t have orientation columns in the same way that early retinotopic regions do, which could impede our ability to pick up on macroscopic information at the voxel level. Moreover, participants did not attend the orientations of the sensory stimuli used to train our model (instead they performed an orthogonal task). A confluence of both perception and attention might be required to get reliable sensory responses from IPS^35,36. Even though we cannot exclude the possibility of a mnemonic code in IPS that reflects stimulus-driven responses, our data do demonstrate that a transformed non-stimulus driven code exists in IPS.

Previous studies have shown that there are interactions between remembered and seen stimuli, such as interference by^{16,17,37,38,39,40,41} and attraction towards^{16,17,42,43,44,45,46,47} irrelevant distractors (see also Supplementary Fig. 9). One recent fMRI study⁴⁶ looked at visual cortex representations of a remembered orientation in the delay period before and after a brief (0.5s) irrelevant grating. The irrelevant grating always differed 40°–50° from the target orientation. In the delay before the irrelevant grating, the remembered orientation could be recovered from early visual areas V1–V3 combined. In the delay after the irrelevant grating, the recovered orientation was shifted in the direction of the distractor, dovetailing with known behavioral attraction biases towards irrelevant orientations^16,17,47 (see also Supplementary Fig. 9a). However, this previous study only looked at memory representations before and after distraction, so nothing can be said about the joint representation of information. Furthermore, the target and distractor orientations were yoked together, so the representations associated with the target and the distractor could not be independently assessed. In the present work we were able to detect biases towards irrelevant gratings during distraction (Supplementary Figs. 7 and 8a) while using randomized target–distractor differences (Supplementary Fig. 1). When people remember an orientation while viewing a grating distractor, both the target and distractor orientations contribute to the measured brain response. At the single-trial level, the relative contributions of mnemonic and perceived signals to an IEM reconstruction can be hard to untangle. Nevertheless, the uncorrelated nature of target and distractor orientations enables the assessment of memory representations in the presence of an orientation distractor across many trials. The finding that mnemonic representations in Experiment 1 were unaltered by concurrent sensory inputs can therefore not be an artifact of the distractor orientation. This is further supported by comparably durable memory representations in the presence of grating and noise distractors alike – the latter having no discernible orientation information.

What if instead of coexisting mnemonic and sensory representations, people were exclusively representing either the target or the distractor orientation on some fraction of trials? This alternative account is unlikely for a several reasons. First, switching between representations would impose a drop in the representation of the memory target. No such drop from the no-distractor condition to the grating-distractor condition was observed in Experiment 1. Second, the 11s continuous presentation of distractors necessarily activates V1. Thus, while V1 is representing ongoing sensory inputs, mnemonic information can still be recovered at every TR throughout the delay.

Neuroimaging studies on working memory routinely use a retro-cue paradigm where two stimuli are presented in quick succession, followed by a numerical cue indicating which of the two to remember¹. Using this paradigm, information can be decoded equally well when the first stimulus was cued instead of the second¹, demonstrating a robustness to potential interference from the second stimulus. In Experiment 1 we extend this finding by showing that mnemonic representations persisted in the presence of visual masks shown for 11s (the distractors). Mnemonic representations were just as robust during distractor and no-distractor conditions – the latter entirely without visual interference by deliberate omission of the retro-cue paradigm. Furthermore, mnemonic information could be recovered at every time point during the 13s delay (Fig. 2) despite the poorer signal-to-noise of single TR data (compared to data averaged over multiple TR’s). Note that this timeframe far surpasses the duration of the stimulus-evoked BOLD response. A comprehensive body of work has shown that stimulus-evoked BOLD alone is generally insufficient for stimulus information to persist into the working memory delay. For example, when people make their response immediately after a retro-cue stimulus sequence, instead of after a long delay, the cued target cannot be decoded¹. In addition, when presented with a stimulus that has two independent features, only the attended and remembered feature can be decoded during the delay period². This means that, despite identical sensory inputs and task demands at encoding, stimulus-evoked BOLD responses do not carry information about a cued target in the absence of a continued memory requirement. Indeed, once active maintenance of a stimulus feature is no longer needed, information about that feature rapidly drops to chance^{1,2,3,48,49,50}. Thus, active mnemonic maintenance, and not stimulus-evoked BOLD, can drive the information contained in multivariate fMRI signals during the working memory delay.

In sum, new sensory inputs do not automatically purge working memory information from early retinotopic cortex. Salient and distracting information can, not surprisingly, negatively impact neural representations and behavioral performance. Together, these data suggest that early visual areas actively participate in both sensory and mnemonic processing, possibly serving as a local comparison circuit, and that high-fidelity memories rely on sustained representations in early visual cortex.

Methods

Participants.

Six volunteers (5 female) between the ages of 21 and 32 years (sd = 3.67) participated in Experiment 1, and seven volunteers (5 female) between the ages of 24 and 35 years (sd = 3.994) participated in Experiment 2. Three volunteers (S03, S04, and S05) participated in both experiments. No statistical methods were used to pre-determine sample sizes, but our sample sizes are similar to those reported in previous publications^1,2,6. Participants had varying amounts of experience with fMRI experiments, ranging from scanner-naïve (S02, S07, and S09) to highly experienced (i.e. > 10 hours in the scanner; S01, S04, S05, and S10). For a separate behavioral experiment (Supplementary Fig. 9) we recruited 21 participants (14 female; mean age = 20.12, SE = 0.647), of whom 17 were included in the analysis (3 dropped out and 1 was excluded due to chance-level performance). The study was conducted at the University of California, San Diego, and approved by the local Institutional Review Board. All participants provided written informed consent, had normal or corrected-to-normal vision, and received monetary reimbursement for their time ($10 an hour for behavior, $20 an hour for fMRI, except for S10, one of the authors).

Stimuli and procedure Experiment 1.

All stimuli in Experiment 1 were projected on a 120 × 90 cm screen placed at the foot-end of the scanner and viewed through a tilted mirror from ~370 cm in an otherwise darkened room. Stimuli were generated on a Macbook Air running OS X using MATLAB 2013a (Natick, MA) and the Psychophysics toolbox^51,52. The luminance output from the projector was linearized in the stimulus presentation code. All stimuli were presented against a 62.82 cd/m² uniform grey background. Stimuli presented during the memory task (targets and distractors; Fig 1A) were configured in a donut-shaped circular aperture with a 1.5° and 7° inner and outer radius, respectively, and smoothed edges (1° Gaussian kernel; sd = 0.5°). Memory targets were full contrast sinusoidal gratings with a spatial frequency of 2 cycles/°. Distractors were either gratings or Fourier filtered noise stimuli, both with a Michelson contrast of 50%. Noise distractors were created by filtering white noise to include only spatial frequencies between 1 and 4 cycles/° (all stimulus code will be available on OSF for more stimulus details if desired).

To ensure that the distribution of remembered orientations was approximately uniform across all trials in the experiment, the orientation of the memory target on each trial was chosen from one of six orientation bins. Each bin contained 30 orientations, in integer increments, and orientations were drawn randomly from each of the six bins with equal probability. Importantly, the orientation of the distractor, on trials that contained an oriented grating distractor, was chosen using the same procedure. Moreover, we counterbalanced the orientation bins from which target and distractor orientations were drawn. This ensured that distractor orientations were also distributed uniformly across all trials in the experiment and that the target and distractor orientations were uncorrelated across trials (see also Supplementary Fig. 1a).

On every trial we randomly chose the spatial phase of the memory target grating. Depending on the distractor condition, we also selected either a random spatial phase for the distractor grating or a random seed to generate the noise distractor. Each initial stimulus was then toggled back and forth between its original and inverted contrast at 4Hz, without blank gaps in between, for as long as the stimulus was on the screen. Thus, the memory target (500ms total duration) cycled through 1 contrast-reversal (i.e. 250ms per contrast). This single counter-phase contrast reversal was specifically designed to minimize afterimages induced by the memory target⁵³. Similarly, distractors (11s total duration) contrast-reversed for 22 cycles. The recall probe consisted of two white line segments that were 5.5° long and 0.035° wide, with each segment presented at the same distance from fixation as the donut-shaped target and distractor stimuli. A 0.4° central black dot was presented continuously on each block of trials to facilitate fixation.

Each trial of the memory task (Fig. 1a) started with a 1.4s change in the color of the central fixation dot, indicating with 100% validity the distractor condition during the delay (e.g. no distractor, grating distractor, noise distractor). Cues could be blue, green, or red. The pairing of cue-colors with distractor-conditions was randomized across participants. Following the cue, a memory target was shown for 500 ms and participants remembered its orientation over a 13 second delay. A contrast-reversing noise (1/3 of trials) or grating (1/3 of trials) distractor was presented for 11 seconds during the middle portion of the delay, or the screen remained grey throughout the 13s delay (1/3 of trials). After the delay, participants used four buttons to rotate the recall probe around fixation, matching the remembered orientation as precisely as possible. The left two buttons rotated the line counter clockwise, while the right two buttons rotated it clockwise. Using the outer- or inner-most buttons would result in faster or slower rotation of the recall probe, respectively. Participants had 3 seconds to respond before being presented with the next memory target 3, 5, or 8 seconds later. Each run consisted of 12 memory trials, and lasted 4 minutes and 40.8 seconds. Distractor type (none, grating, or noise) and the orientation bin (one of six) from which the target or distractor grating orientations were drawn, were fully counterbalanced across 9 consecutive runs of the memory task. Data for 27 total runs were acquired across 3 separate scanning sessions. Before starting the fMRI experiment, participants practiced the memory task outside the scanner until they were comfortable using the response buttons to recall the target orientation within the temporally restricted response window and mean absolute response error was <10° (this took between 6 and 12 trials for all participants).

In addition to the memory task, Experiment 1 also included an independent mapping task. During this task, participants viewed 9-second blocks of donut-shaped gratings (same dimensions as in the memory task) or circle-shaped gratings (1.5° radius) that were contrast-reversing at 5 Hz. The orientation of each grating was chosen at random from one of ten orientation bins, and from each bin equally often during a run, to approximate an even sampling of orientation space. Per run, 20 blocks of donut-shaped gratings were alternated with 20 blocks of circle-shaped gratings, with 4 fixation blocks interspersed. Each run took 7 minutes. Participants performed a detection task to ensure attention at the physical location of the stimuli: Grating contrast was probabilistically dimmed twice every 9 seconds, from 100% to 80% for 200 ms. Because the contrast change was probabilistic, there was no change on some stimulus blocks, while on others there were >2 changes. Participants maintained fixation on a 0.4° mean-grey dot with a 0.2° magenta dot on top. Note that the donut-shaped stimuli in the mapping task occupied the same physical location as the donut-shaped target and distractor stimuli in the main memory task. This allowed us to independently identify voxels in early visual areas that selectively responded to the spatial position of the memory target. During each scanning session, participants completed 4–6 runs of the mapping task (15–17 total runs across days). Three participants (S02, S03, and S04) practiced 1 block of the mapping task prior to the experiment.

Stimuli and procedure Experiment 2.

In Experiment 2, all stimuli were projected on a 16 × 21.3 cm screen placed inside the scanner bore, viewed from ~40 cm through a tilted mirror. Stimuli were generated using Ubuntu 14.04, Matlab 2017b (Natick, MA), and the Psychophysics toolbox^51,52. During the memory task, memory targets were full contrast circular sinusoidal gratings (radius = 14.58°) with smoothed edges (1.33° kernel; sd = 0.67°) and a spatial frequency of 1.5 cycles/°. Distractor stimuli were either gratings shown at 50% Michelson, or pictures of faces⁵⁴ and gazebos⁶ (maximal extent = 27.83°, adapted after⁶). All pictures had the same mean luminance, which was equal to the grey background. The memory target contrast-reversed once, just as in Experiment 1. However, unlike Experiment 1 (where distractors were also contrast-reversing), distractors in Experiment 2 were toggled on and off at 4Hz (i.e. one cycle consisted of a 250ms distractor image and a 250ms blank screen). On a picture distractor trial, we either showed the full set of 22 unique face images, or the full set of 22 unique gazebo images, in randomly shuffled order. On a grating distractor trial, we showed 22 gratings, each with the same orientation but a randomly chosen phase $\left(0-2\pi \right)$. Target and distractor grating orientations were pseudo-randomly chosen from one of six orientation bins to ensure a roughly uniform sampling of orientation space, identical to the procedure used in Experiment 1 (see also Supplementary Fig. 1b). The recall probe consisted of a 0.056° wide and 29.17° long black line. This line was interrupted by a 0.53° black central fixation dot presented on top of a 0.81° mean grey circle. This fixation dot was presented throughout to aid fixation.

The procedure during the memory task (Fig. 3a) was identical to that of Experiment 1, with the following exceptions: The noise distractor condition was replaced with a picture distractor condition. On half of these trials pictures of faces were shown, and on the other half pictures of gazebos were shown. In both the grating and picture distractor conditions, the distractors started flickering on and off one second into the 12-second delay, and the recall probe appeared immediately after the last off period. Participants had 4 seconds to rotate the dial. Participants were scanned on 3 separate days, completing a total of 27 total runs (9 runs per day, 12 trials per run) of the memory task. Prior to scanning, participants practiced for 12–24 trials, until their absolute performance was <10°. Only S09 did not quite reach this criterion during practice, with a performance of 11.5° after 36 practice trials.

Experiment 2 used two different mapping tasks: During the first mapping task, participants viewed a series of gratings (50% of trials), face pictures (25% of trials), or gazebo pictures (25% of trials) that were flickered on (250ms) and off (250ms) at 4Hz for a total of 5.5 seconds (i.e. 11 stimuli per trial). Each trial was followed by a 3, 5, or 8s inter-trial interval. Grating and picture stimuli were identical to the ones described above for the Experiment 2 memory task. On grating trials, the orientation was chosen at random from one of 12 orientation bins (to ensure approximately uniform sampling of orientation space as in Experiment 1). Each of the 22 unique face images was shown 3 times during a run. Face images were randomly shuffled across all trials in a run, with the restriction that the same image was never shown twice in a row. The same was true for gazebo images. Participants completed 24 trials per run (4 minutes and 31.2s per run). Across the three scanning days, participants completed between 20 and 29 total runs of this first mapping task. Three participants (S04, S05, and S09) practiced one run of the task before going into the scanner.

The second mapping task of Experiment 2 was comprised of trials showing either a circle-shaped (1.06° radius) or donut-shaped (1.06° inner and 14.74° outer radius) grating stimulus (spatial frequency 1.43 cycles/°; edges smoothed with 0.69° kernel and sd = 0.36°). On every trial, a 6s grating was contrast-reversing (as in Experiment 1) at 4Hz (i.e. 250ms per contrast), followed by a 3, 5, or 8s inter-trial interval. Grating orientation was randomly chosen from one of 9 orientation bins on each trial, and equally often from each bin within a run. Participants completed 36 trials per run (18 circle-shaped grating trials, and 18 donut-shaped grating trials, randomly interleaved), and each run took 7 minutes and 5.6s. A central black dot (0.56°) aided fixation throughout. Data for this second mapping task were collected separately from the other Experiment 2 data (i.e. different scanning sessions). Participants completed between 10–20 total runs of the second mapping task.

During both mapping tasks in Experiment 2, we occasionally (0–3 times per trial) superimposed small smoothed circles (of a uniform light grey color) on the mapping stimuli for 250ms. These brief ‘blobs’ could be centered at any distance from fixation occupied by a stimulus (though no closer than 0.056° and no further than 13.78°), and at any angle relative to fixation (1–360°). Blobs were scaled for cortical magnification⁵⁵, such that all blobs (i.e. at every distance from fixation) stimulated roughly 1mm of cortex. In terms of visual angle, this means blobs had radii spanning from 0.18° to 0.75°. No blobs were presented during the first or last 500ms of a trial, or within 500ms of each other. Participants pressed a button every time they detected a blob superimposed on a stimulus image, such that they stayed alert and attending the location of the mapping stimuli.

Magnetic Resonance Imaging.

All scans were performed on a General Electric (GE) Discovery MR750 3.0T scanner located at the University of California, San Diego (UCSD), Keck Center for Functional Magnetic Resonance Imaging (CFMRI). High resolution (1 mm³ isotropic) anatomical images were acquired during a retinotopic mapping session, using an Invivo 8-channel head coil. Functional echo-planar imaging (EPI) data for the current experiment were acquired using a Nova Medical 32-channel head coil (NMSC075–32-3GE-MR750) and the Stanford Simultaneous Multi-Slice (SMS) EPI sequence (MUX EPI), utilizing 9 axial slices per band and a multiband factor of 8 (total slices = 72; 2 mm³ isotropic; 0 mm gap; matrix = 104 × 104; FOV = 20.8 cm; TR/TE = 800/35 ms, flip angle = 52°; inplane acceleration = 1). At sequence onset, the initial 16 TR’s served as reference images critical to the transformation from k-space to image space. Un-aliasing and image reconstruction procedures were performed on local servers using CNI based reconstruction code. Forward and reverse phase-encoding directions were utilized during the acquisition of two short (17 s) “topup” datasets. From these images, susceptibility-induced off-resonance fields were estimated⁵⁶ and used to correct signal distortion inherent in EPI sequences using FSL topup^57,58.

Preprocessing.

All imaging data were preprocessed using software tools developed and distributed by FreeSurfer and FSL (free to download at https://surfer.nmr.mgh.harvard.edu and http://www.fmrib.ox.ac.uk/fsl). Cortical surface gray-white matter volumetric segmentation of the high resolution anatomical image was performed using the “recon-all” utility in the FreeSurfer analysis suite⁵⁹. Segmented T1 data were used to define Regions of Interest (ROIs) for use in subsequent analyses. The first volume of every functional run was then coregistered to this common anatomical image. Transformation matrices were generated using FreeSurfer’s manual and boundary based registration tools⁶⁰. These matrices were then used to transform each 4D functional volume using FSL FLIRT^61,62, such that all cross-session data from a single participant was in the same space. Next, motion correction was performed using the FSL tool MCFLIRT⁶² without spatial smoothing, a final sinc interpolation stage, and 12 degrees of freedom. Slow drifts in the data were removed last, using a high pass filer (1/40 Hz cutoff). No additional spatial smoothing was applied to the data apart from the smoothing inherent to resampling and motion correction.

Signal amplitude time-series were normalized via Z-scoring on a voxel-by-voxel and run-by-run basis. Z-scored data were used for all further analyses unless mentioned otherwise. Trial events were jittered with respect to TR onsets, and trial events were rounded to the nearest TR. To recover the univariate BOLD time courses for all three memory distractor conditions in Experiments 1 and 2 we estimated the Hemodynamic Response Function (HRF) for each voxel at each time point of interest (0–19.5 seconds from memory target onset). This was done using a finite impulse response function (FIR) model⁶³ consisting of a column marking the onset of each event (memory target onset) with a “1”, and then a series of temporally shifted version of that initial regressor in subsequent columns to model the BOLD response at each subsequent time point (following sample onset). Estimated HRF’s were then averaged across all voxels in each ROI (see also Supplementary Fig. 3). Analyses performed after preprocessing was completed were all done in MATLAB 2016b using custom functions.

Identifying Regions of Interest (ROIs).

To identify voxels that were visually responsive to the donut-stimuli, a General Linear Model (GLM) was performed on data from the mapping task (for Experiment 2 we used data from the second mapping task) using FSL FEAT (FMRI Expert Analysis Tool, version 6.00). Individual mapping runs were analyzed using BET brain extraction⁶⁴ and data prewhitening using FILM⁶⁵. Predicted BOLD responses were generated for blocks of “donut” and “circle” stimuli by convolving the stimulus sequence with a canonical gamma hemodynamic response function (phase = 0 s, sd = 3 s, lag = 6 s). The temporal derivative was included as an additional regressor to accommodate slight temporal shifts in the waveform to yield better model fits and to increase explained variance. Individual runs were combined using a standard weighted fixed effects model. Voxels that were significantly more activated by the donut compared to the circle (p = 0.05; FDR corrected) were defined as visually responsive and used in all subsequent analyses.

Standard retinotopic mapping procedures^66,67 were employed to define 9 a priori ROIs in early visual (V1–V3, V3AB, hV4) and parietal (IPS0–IPS3) cortex. Retinotopic mapping data were acquired during an independent scanning session that utilized both meridian mapping techniques (with checkerboard “bowtie” stimuli shown alternating between the horizontal and vertical meridian) and polar angle techniques (with a slowly rotating checkerboard wedge) to identify the visual field preferences of voxels (stimuli described in more detail in⁶⁸). Anatomical and functional retinotopy analyses were performed using a set of custom wrappers that encapsulated existing FreeSurfer and FSL functionality. ROIs were combined across left and right hemispheres and across dorsal and ventral areas (for V2–V3) by concatenating voxels.

Only visually responsive voxels, selected using the localizer procedure described above, were included in the ROI of each retinotopic area. We only included data for retinotopic areas in which the number of visually responsive voxels exceeded 20 for every single participant. Exact voxel counts for each participant in each ROI can be found in Supplementary Tables 9 and 10 for Experiments 1 and 2, respectively.

fMRI Analyses: Inverted Encoding Model.

To generate model-based reconstructions of remembered and perceived orientations from voxel responses, an Inverted Encoding Model (IEM) was implemented^14,15 with orientation as the feature dimension. The first step in this analysis is to estimate an encoding model using voxel responses in a cortical region of interest. These data are considered the “training set” (Supplementary Fig. 4a, left), and are combined with 9 idealized tuning functions, or “channels” (Supplementary Fig. 4a, right), to parameterize an orientation sensitivity profile for each voxel. The second step in the analysis combines the estimated sensitivity profiles in each voxel with a novel pattern of all voxel responses in a ROI on a single trial in the experimental data set (the “test set”, Supplementary Fig. 4b, left) to reconstruct a model-based representation of the orientation that was remembered or viewed on that trial (Supplementary Fig. 4b, right). The encoding model for a single voxel has the general form:

$$R_j=\sum _i^9{w}_i{c}_i$$ Equation (1)

Where $R_j$ is the response $R$ of voxel $j$, and $c_i$ is the channel magnitude $c$ at the i^th of 9 channels. A voxel’s sensitivity profile over orientation space is captured by 9 weights $w$. Channels were modeled as:

$$c\left(d\right)=\cos {\left(\left(d-\mu \right)\cdot \frac{\pi }{180}\right)}^8$$ Equation (2)

Where d is the distance in degrees from the channel center $\mu$. Channel centers were spaced 20° apart.

For the first step of the IEM, Equation 1 can be expressed as:

$$B_1=W{C}_1$$ Equation (3)

Here, a matrix of observed BOLD responses $B_1$ (m voxels × n trials) is related to a matrix of modeled channel responses $C_1$ (k channels × n trials) by a weight matrix $W$ (m voxels × k channels). For each trial, $C_1$ is the pointwise product of a stimulus mask (i.e. “1” at the true stimulus orientation, “0” at all other orientations) with the idealized tuning functions. $W$ quantifies the sensitivity of each voxel at each idealized orientation channel, and can be computed with least-squares linear regression:

$$\widehat{W}=B_1{C}_1^T{\left(C_1{C}_1^T\right)}^{-1}$$ Equation (4)

Estimating the sensitivity profiles concludes the first encoding step of the IEM. The second step of the IEM inverts the model, using the estimated sensitivity profiles of all voxels $\widehat{W}$ (m voxels × k channels) in combination with a “test set” of novel BOLD response data $B_2$ (m voxels × n trials) to estimate the amount of orientation information at each channel ${\widehat{C}}_2$ (k channels × n trials):

$${\widehat{C}}_2={\left({\widehat{W}}^T\widehat{W}\right)}^{-1}{\widehat{W}}^T{B}_2$$ Equation (5)

This step uses the Moore-Penrose pseudoinverse of $\widehat{W}$, and it is multivariate in nature since it uses the sensitivity profiles across all voxels to jointly estimate channel responses ${\widehat{C}}_2$ for each trial of the “test set”. This effectively forms a model-based ‘reconstruction’ of the remembered or seen stimulus feature on a trial-by-trial basis.

Because grating orientations could take any integer value between 1° and 180°, both the encoding (Equation 4) and inversion (Equation 5) steps of the IEM were repeated 20 times. On each repeat, the centers of 9 idealized tuning functions were shifted by 1° (Equation 2), and we estimated the channel responses ${\widehat{C}}_2$ at those 9 centers, until the entire 180° orientation space was estimated in 1° steps. This procedure thus yielded estimated channel responses ${\widehat{C}}_2$ for each degree in orientation space. After generating reconstructions for each trial, all single trial reconstructions were re-centered on the remembered orientation (when looking at information for mnemonic orientations) or on the orientation of the directly viewed distractor grating (when looking at information for viewed orientations).

Importantly, for the IEM analyses investigating mnemonic codes based on sensory-driven responses, we utilized independent data from the mapping task as the “training set” and data from the memory task as the “test set”. For Experiment 2, we combined data across the two mapping tasks to comprise the “training set”. For the IEM analyses investigating mnemonic codes that are not necessarily based on sensory-driven responses, we used a within-condition leave-one-out procedure. Here, all but one trial is used as the “training set”, and the left out trial constitutes the “test set”. This procedure is repeated until all trials in a given condition have been left out once. Of note, we also did these analyses leaving one session out, yielding qualitatively similar results. To obtain single trial activity estimates, memory data were averaged over a time window of 5.6–13.6 seconds (7–17 TRs) after target onset. Mapping data in Experiment 1 were averaged over 4.8–9.6 seconds (6–12 TR’s) after donut onset. Mapping data from both Experiment 2 mapping tasks were averaged over 2.4–7.2 seconds (3–9 TR’s) after donut onset.

fMRI Analyses: Reconstruction fidelity.

Model-based reconstructions of orientation were quantified using a fidelity metric derived from trigonometry (Fig. 1d)⁶⁹. Unless specified otherwise, this fidelity metric was applied to the average of 108 single-trial reconstructions (i.e. all trials from a given distractor condition), separately for each condition, participant, and ROI. For each reconstruction, the fidelity metric was calculated by taking the channel response at each degree in orientation space (wrapped onto a 2πcircle), and projecting this vector onto the center of the stimulus space (i.e. onto zero degrees) via $\cos A_{abs\left(0^{\underset{\_}{\circ }}-d\right)}=\frac{b}{h}$, where A is the angle between the tuning function center (at 0°) and the degree in orientation space being evaluated (d), and h is the channel response at d (i.e. the hypotenuse of a right triangle). In other words, we project the length of vector h onto 0° by solving for b (i.e. the adjacent side of a right triangle). This procedure was repeated for all 180 degrees in orientation space, after which we calculated the mean of all 180 projected vectors. Thus, the mean projected vector – our fidelity metric – reflects the amount of ‘energy’ at a remembered or sensed orientation. Note that this metric, by design, gets rid of additive offsets, and captures only the amount of information at the center of the reconstruction.

fMRI Analyses: Decoding.

In addition to using an inverted encoding model to analyze our data (i.e. the IEM analysis described above), we also used a multivariate pattern analysis (MVPA) decoding approach. This allowed us to evaluate the extent to which our results generalized across different analysis techniques. It also allowed us to more directly compare our results to previous work by Bettencourt & Xu⁶, who used a decoder to perform a two-way classification between orthogonal orientations. To analyze our data in an analogues manner, despite our use of continuous orientations (1°:180°), we performed two 2-way classifications. For the first classification, we binned all orientations within a 45° window around vertical, and we binned all orientations within a 45° window around horizontal. We then performed a two-way classification to decode between the two cardinal axes (Supplementary Fig. 14a, left). For the second classification, we binned all orientations within a 45° window around the two oblique axes (i.e. around 45° and 135°) to classify between the two oblique orientations (Supplementary Fig. 14a, right). Finally, decoding performance was averaged across the two two-way classifications (i.e. the cardinal classification and the oblique classification) before performing statistics and plotting (Supplementary Fig. 14b). We used the Matlab built-in multi-class Support Vector Machine (‘fitcecoc’ and ‘predict’ functions). As with our IEM analyses, we performed the decoding analysis in two different ways: (1) Training the SVM on independent localizer data, and decoding the orientation from the working memory delay epoch, and (2) Training and testing on data from the memory delay, using a leave-one-trial-out procedure. Decoding results based on the independent and leave-one-out training schemes are plotted on the left and right side of Supplementary Fig. 14b, respectively. For Experiment 2 we also evaluated whether the picture distractors shown during the delay (faces and gazebos) could be decoded. Using the same classifier described above, we trained an SVM on independent data from the first Experiment 2 localizer (i.e. the one with trials showing pictures of faces and gazebos) to do a two-way classification. We then decoded the presence of either a face of gazebo distractor during the working memory delay period epoch (Supplementary Fig. 10).

Statistical procedures.

All statistical statements reported here were based on permutation (or randomization) testing over 1000 iterations with scrambled data labels. Note that this constrains the resolution of our p-values to a lower limit of p ≤ 0.001. To test if fidelity metrics were significantly greater than zero, we generated permuted null distributions of fidelities for each participant, ROI, and condition (and for each timepoint, in the analyses shown in Fig. 2b, Fig. 3e, and Supplementary Figs. 6 and 12): On each permutation we first reshuffled target orientation labels for all trials before performing the inversion step of the IEM (effectively randomizing single trial reconstructions relative to the true orientation). Second, we calculated the fidelity for the trial-averaged shuffled orientation reconstructions in a manner identical to calculating fidelity for the intact reconstructions. This resulted in one “null” fidelity estimate per permutation. Combining the “null” fidelities across all participants (so 6 and 7 fidelities for Experiments 1 and 2, respectively) resulted in one t-statistic per permutation $t=\frac{\overline{x}-{\mu }_0}{s/\sqrt{n}}$, where $\overline{x}$ and $s$ are the mean and standard deviation of fidelities across participants, ${\mu }_0$ is the null hypothesis mean (i.e. 0), and n is the sample size. To test across-participant fidelities against zero (Figs. 1e, 2b, 3d, 3e, and 4; Supplementary Figs. 6, 12, and 13) we compared the t-tatistic calculated from the intact data against the permuted null distribution of t-statistics for that condition, ROI, and timepoint. Reported tests against zero were one-sided and uncorrected. Note that the same procedure was used for the decoding analyses (Supplementary Figs. 10 and 14), with the exception that the null hypothesis for the t-statistic was 0.5 (i.e. chance level). Significant fidelity (and decoding) is indicated in our figures by colored and grey asterisks.

To test if there were differences in fidelity between distractor conditions (within each ROI; Figs. 1e, 3d, and 4; Supplementary Figs. 8, 13, and 14), we used within-subjects repeated-measures one-way ANOVA’s. First, we calculated the F-statistic from the intact data for the effect of condition. Next, we generated permuted null distributions of F by shuffling the condition labels per subject, and calculating the “null” F-statistic on each permutation. Each data-derived F was then compared to its null distribution of F’s to get the p-value. Significant effects were followed up with post-hoc paired-sample t-tests: We performed pairwise comparisons between each of the conditions, comparing the data derived $t=\frac{{\overline{X}}_D-{\mu }_0}{s_D/\sqrt{n}}$, (with ${\overline{X}}_D$ and $s_D$ denoting the mean and sd of the pairwise differences) against a permuted $t$ distribution generated by reshuffling condition labels on each iteration. Significant comparisons are indicated in our figures by black asterisks.

To look for a signature of top-down related processing, we utilized the grating distractor condition, as it allowed us to directly compare fidelities from remembered and sensed orientations (which were derived from the same exact data). We used a within-subjects repeated-measures two-way ANOVA to track differences in fidelity between ROI and memory/sensory condition (Figs. 1e, 3d, 4 and 5). We only included V1–V4 as our ROIs, as the hierarchical relationship between these areas is still fairly clear. Permutations were done as described above, but now based on F-statistics for the two main effects of ROI and memory/sensory condition, as well as their interaction. Specifically, the aim of this analysis was to look for significant interactions between ROI and memory/sensory condition, and to test if memory and sensory representations became more and less pronounced, respectively, as one ascends the visual hierarchy. There are various ways in which ROIs might systematically differ from one another, such as their size (i.e. number of voxels), sensitivity to neural activity, or signal-to-noise ratio. Because these factors might impact the attainable accuracy of multivariate analysis tools, a direct comparison across ROIs is generally not recommended⁷⁰. However, because here we are looking for an interaction specifically (and not an absolute difference between ROIs), and because we apply our multivariate techniques to the exact same data in each ROI (i.e. information about either the remembered or sensed orientation) these caveats are not of concern in this particular case. One remaining concern is that also the scaling might not be comparable between ROIs (i.e. a difference of X in one ROI may not mean the same as a similar difference of X in another ROI), although this concern is not reflected by the data presented here.

When circular statistics were used, these were calculated using the circular statistics toolbox⁷¹.

Glitches.

S01 completed 4 sessions of scanning, but on the first scanning day the projector settings had been changed such that we were presenting stimuli as ovals rather than circles. Data from this session were excluded from analysis. S02 was also scanned 4 times, but data transfer after one of the sessions failed, and the data were removed from the scanner center’s servers before being backed up – and thus lost forever. For S04 we only collected 4 mapping runs on the first day of scanning because the scanner computer hard drive was full by the time we approached the end of the scan, causing the computer to freeze. On the first day of scanning S05 the scanner computer started spontaneously deleting data files half way through the session. Consequently, data from the 2^nd mapping run were deleted and the 5^th memory run was aborted (with imaging data collection incomplete, while behavioral data collection was complete). To ensure full counterbalancing, an exact replica of this 5^th memory run was repeated as the first run on the second day of scanning. During the last scanning session of S09, the subject reported repeated but brief instances of falling asleep. Probed further, S09 indicated having also slept occasionally during the 3 sessions prior. Because we could no longer determine the runs during which S09 was asleep, we decided to keep all S09 data for analyses, and to scan one additional subject for Experiment 2.

Miscellaneous.

All information detailed in these Methods can also be found in the Life Sciences Reporting Summary, published alongside this paper. During data collection, participants were not blinded to the experimental conditions (i.e. they could clearly perceive the distractor condition on every trial), while experimenters were blinded (i.e. they were not in the room and conditions were interleaved). Analyses were not performed blind to the conditions of the experiments.