A Pragmatic, Adaptive Clinical Trial Design for a Rare Disease: The FOcal Cerebral Arteriopathy Steroid (FOCAS) Trial

Abstract

Background

Pediatric stroke investigators identified as their top research priority a clinical trial of corticosteroids for focal cerebral arteriopathy (FCA). However, FCA is both rare and an acute condition making it infeasible to enroll the large sample sizes needed for standard, confirmatory clinical trials. We present a pragmatic approach to clinical trial design that may inform the approach to other rare disorders.

Methods

We surveyed pediatric stroke experts to determine the level of evidence that would impact their clinical management of FCA. Incorporating survey results, a randomized, group sequential Bayesian adaptive design was proposed based on a quantitative radiologic outcome measure (change from baseline in change in the FCA Severity Score). Using accumulating information, the design determines whether intervention is better than control with high probability.

Results

Among 21 (100%) respondents, the probability of corticosteroid efficacy that would lead the experts to treat was 30% (median). The probability of efficacy that would make them unwilling to randomize (because they would feel all children should receive corticosteroids) was 70%. Simulation studies with the proposed design showed that a total of 42 subjects controls the type I error rate at the desired level 0.20 and yields a smaller average sample size and trial duration compared to a conventional design.

Conclusions

Designs in rare diseases require special considerations; this is especially true for this childhood disease, which is both uncommon and acute. This design has incorporated expert consensus to establish the criteria for success, formal monitoring rules for safety, and early stopping rules.

Introduction

In a Delphi consensus process, pediatric stroke investigators identified a clinical trial of corticosteroids for the treatment of focal cerebral arteriopathy of childhood (FCA) as the highest research priority for their field.¹ FCA is a life-threatening inflammatory disease of cerebral arteries that progresses over days to weeks and causes arterial ischemic stroke in otherwise healthy children.² In the absence of clinical trial data, clinicians have begun to employ corticosteroid therapy.^{3, 4} However, there are potential downsides: experimental evidence suggests that the post-stroke inflammatory response has beneficial (in addition to detrimental) effects, with roles in infarct resolution, and brain remodeling and repair.⁵ Hence, pediatric stroke experts agree on the need for a clinical trial to guide FCA management.¹

However, design of an FCA trial faces two major challenges: the rarity of FCA and its acuity. Although FCA is a common cause of childhood arterial ischemic stroke, ischemic stroke in children is rare, occurring in approximately 1.3 per 100,000 US children (non-neonates) per year.⁶ Although the incidence of FCA has not been established, it causes approximately 10% of childhood arterial ischemic strokes,⁷ so has an annual incidence of approximately 1.3 per 1,000,000 US children. Hence, in the US population of 74 million children, there are likely less than 100 annual FCA cases nationwide. The acuity of FCA presents additional challenges; while most rare disease clinical trials study chronic diseases and take advantage of established patient cohorts, an FCA trial needs to rapidly identify and treat acute, incident cases, before the arteriopathy progresses.

With a traditional trial design, the sample size is chosen such that the study has a certain amount of power for a minimum clinically important effect with the standard two-sided alpha level of 0.05. This allows us to be “95% confident” that if we observe a treatment effect, then it is not due to chance alone. Likewise, if we do not observe a treatment effect, it is not due to lack of power. For a trial of a rare disease like FCA, this approach may result in an infeasible sample size, accomplishable only with hundreds of enrolling sites and a long enrollment window. Biomedical ethicists have argued that, for ethical reasons, the overall significance level should be adjusted in settings when clinicians would change clinical practice with a level of confidence lower than 95%.⁸ A higher alpha level reduces the necessary sample size for a trial, and hence reduces the number of participants randomized to the inferior therapy. Others have suggested that approaches to sample size calculation ought to be different for rare diseases and need to take into account a variety of assumptions about the treatment effect, as well as input from the scientific community.⁹ In this paper, we describe how we designed a FCA corticosteroid trial— the FOcal Cerebral Arteriopathy Steroid (FOCAS) trial—by seeking expert input to establish what would be considered a “good” probability that corticosteroids are better. The trial design’s operating characteristics are provided. This approach may be useful to investigators designing clinical trials for other rare diseases.

Material and methods

We approached the FOCAS trial design with the goal of obtaining the level of evidence sufficient to change current clinical practice while providing a feasible approach for a rare disease in an acute setting. The proposed intervention is corticosteroid therapy (a standard 3-day course of IV methylprednisolone followed by oral prednisone) versus control (standard care); both the treatment and control groups will receive standard therapy of oral aspirin and supportive care. The primary endpoint is the change in the FCA Severity Score (FCASS; a quantitative radiologic measure of the arteriopathy severity) from baseline to 1 month post enrollment.² The safety outcome was defined as any serious adverse event. The maximum sample size is 50 children, enrolled at 25 sites, inflated for lost-to-follow-up expected to be less than 20%. The primary analysis is intention-to-treat and will include all randomized children. We adopt the idea of a Prospective Randomized Open, Blinded End-point (PROBE) design because corticosteroids cause behavioral side effects that preclude double-blinding; a central group of neuroradiologists will measure the FCASS blinded to both treatment arm and time (baseline or post-baseline).¹⁰

Expert Survey

To determine the appropriate criteria for success for the trial, we designed a survey of pediatric stroke experts (full survey available, Online Supplemental Material). The survey first established current practices concerning the use of IV corticosteroids for the treatment of FCA. We also queried, using a Likert scale, current perceptions regarding the safety and benefit of corticosteroid therapy. We then asked, “What probability of efficacy would lead you to treat FCA with corticosteroids?” Although our trial planned to use the FCASS measure, we repeated this question with two definitions of efficacy: improved imaging biomarkers (arteriopathy progression and infarct volume) and improved 12-month neurological outcomes (using the Pediatric Stroke Outcome Measure, or PSOM). The survey provided examples: “If you could tell a family that the treatment has a 50% chance of improving their child’s 12-month outcome, would that be enough for you to treat?” To establish stopping rules for the trial, we also asked what probability of efficacy would make them unwilling to randomize their next patient due to efficacy or due to futility, and asked about acceptable levels of serious adverse effects.

We applied the survey in-person, taking advantage of an investigator meeting for an NIH-funded multicenter observational study of childhood arterial ischemic stroke (the Vascular effects of Infection in Pediatric Stroke, or VIPS, study).¹¹ After distributing paper copies of the survey to 21 experts, the FOCAS PI (H.J.F.) verbally explained the intent of the survey and then guided the respondents through the individual questions. We then collected and compiled the survey responses, and used descriptive statistics to summarize the results.

Overview of FOCAS trial design

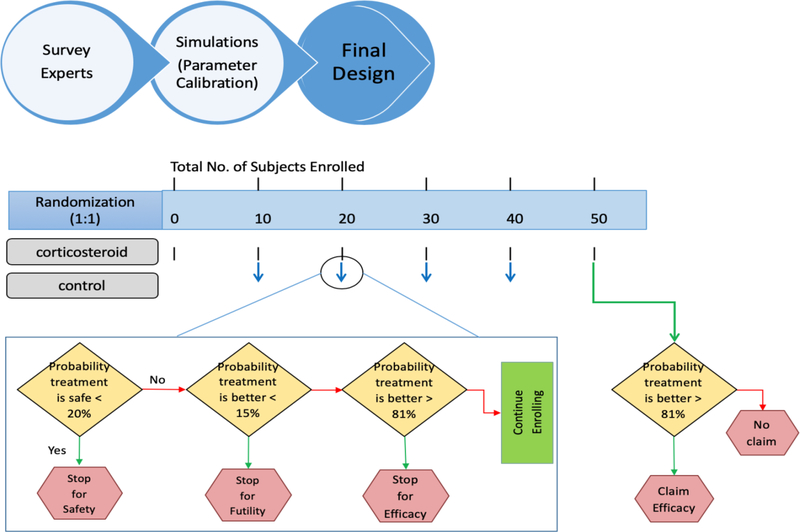
We consider a multi-site, two-arm randomized clinical trial in which patients are enrolled in each site, and patients are randomized to either an intervention arm or control arm in a fixed ratio 1:1. For each enrolled patient, FCASS measurements are collected at baseline and 1 month to assess potential benefit of the intervention based on the change of FCASS measurements, and are followed by 3 months to assess adequacy of 1 month of therapy by identifying relapses. Also, infarct volume at 1 month, arteriopathy relapse, serious adverse events, and prevalence of acute herpesvirus infection will be measured as secondary outcomes. The primary objective is to determine whether corticosteroid intervention improves the change in FCASS between baseline and 1 month of children with symptomatic FCA compared to the control. The outcome was chosen because of its sensitivity to acute changes. Our design has interim analyses to monitor safety, futility, and efficacy. Interim analyses are performed frequently, i.e., after every 10 subjects complete 1 month. The trial may terminate early if the intervention is superior or futile compared to the control. The proposed Bayesian monitoring rules based on the change from baseline to 1 month in FCASS measurements yield type I/II error by rejecting/accepting the null hypothesis, which states that there is no difference between intervention and control. The errors are controlled by the test boundaries calibrated from simulations under the Bayesian framework. In addition to the interim analyses for efficacy and futility, we monitor the safety of the corticosteroid intervention and allow for early stopping of the trial due to a toxic intervention. Moreover, the FOCAS trial design identifies the optimal duration for the intervention at the end of trial by assessing the probability to relapse for subjects showing an initial improvement, i.e., that the FCASS is worsening at 3 months compared to 1 month.

Statistical models

Index patients and sites by i =1, …, n_j and, respectively. j = 1, …J, Let G_ij be an experimental condition indicator denoting E or C for intervention or control, respectively, which the ith subject in the jth site is treated. Let Y_ij denote, for the ith subject in the jth site, the observed change of FCASS measurement from baseline to 1 month (i.e., 1 month FCASS measurement - baseline FCASS measurement) such that a lower change is a better outcome. Let Z_ij denote a binary safety outcome with Z_ij = 1 indicating that the ith subject in the jth site experienced a serious adverse event, Z_ij = 0 otherwise. We model the efficacy outcome as

$$Y_{ij}={\alpha }_j+{\theta }_{G_{ij}}+\beta Z_{ij}+{\epsilon }_{ij},$$

where α_j describes the effect at site j, ${\theta }_{G_{ij}}$ characterizes the effect of treatment which the ith patient in the jth site will be assigned (i.e., G_ij = E or C), β denotes the effect of safety events on the efficacy outcome, and the error term ε_ij follows a normal distribution with mean 0 and variance σ². As in the FCASS derivation study (using the VIPS cohort), the primary efficacy outcome in FOCAS will be centrally determined, and hence we anticipate that the impact of site will be minimal. However, if there is a prior belief that the site effect on the measurement is heterogeneous, our model can be extended with an additional hierarchy on α_j to incorporate the random effect. The parameters α_j, j = 1, …, J, θ_E, θ_C, β and σ² are estimated under a Bayesian framework. We assume that α_j, j = 1, …, J are independently distributed from a normal variable with mean a and variance ξ², the treatment effect θ_g, g = E or C follows a normal distribution with the mean μ_g and variance ${\eta }_g^2$ and the safety effect β follows a normal distribution with the mean b and variance ζ². We also assign σ² an inverse-gamma distribution with shape parameter w₁ and rate parameter w₁/w₂. For rare disease trials, since conventional vague prior distributions are often problematic for small samples, it is necessary to carefully select the hyperparameters – a, ξ, μ_g, η_g, w₁ and w₂. Appendix A provides the details of the prior specifications with reasonable hyperparameters for rare disease trials. We next model the safety outcome as

$$Z_{ij}\sim Ber\left({\pi }_{G_{ij}}\right),$$

where ${\pi }_{G_{ij}}$ denotes the probability of a safety event for treatment G_ij. In this study, we are mostly concerned about the safety of the intervention group, but our proposed safety monitoring approach can be applied to both arms. This approach will be reviewed in addition to ongoing review by an independent medical safety monitor. We assign π_E a non-informative beta prior with shape parameters ϕv and ϕ(1 − v). The selection of hyperparameters ϕ and v are suggested in Appendix A. Lastly, under the Bayesian framework, we generate samples from the posterior distribution, which is proportional to the likelihood function multiplied by the prior distribution. We provide the detail of the posterior distribution based on our statistical model in Appendix B.

Monitoring rules

The FOCAS trial design monitors efficacy, futility and safety. Suppose that the proposed design has K − 1 interims, and an interim analysis will be conducted after the enrollment of each cohort (e.g., every 10 subjects) to determine whether the trial should be terminated early for efficacy, futility or safety. The final analysis will be performed after a follow-up period of 3 months for the last subject. Let Data_k denote the accumulating data at the kth analysis. Let c_1, c₂ and c₃ be the pre-specified boundaries for the efficacy, futility and safety monitoring rules. To save several rounds of calibrations, the initial cutoff values for c_1, c₂ and c₃ were selected according to the survey results and calibrated based upon the simulation studies. See Figure 2. The detailed procedure for the cutoff specification is provided in Appendix C. For the interim analysis at k = 1, …, K − 1, the decision rule are as follows:

1. Stop the trial for superiority of intervention over control if

   $$P\left\{{\theta }_E<{\theta }_C|Dat{a}_k\right\}>c_1.$$
2. Stop the trial for futility of intervention over control if

   $$P\left\{{\theta }_E<{\theta }_C|Dat{a}_k\right\}<c_2.$$
3. Stop the trial for safety if

   $$P\left\{{\pi }_E\le \delta |Dat{a}_k\right\}<c_3$$

   where δ denotes the maximum of acceptable rate of any serious adverse event.

Figure 2.

Schema for the calibration of cutoffs for our Bayesian monitoring rule.

If the trial is not stopped early, then at the last analysis (i.e., k = K), it is concluded that intervention is superior to control if

$$P\left\{{\theta }_E<{\theta }_C|Dat{a}_K\right\}>c_1.$$

Our monitoring rules follow an adaptive, group sequential method in order to allow us to terminate the trial early for superiority, futility or safety based on the accumulating data.^13–16 A similar approach to monitoring futility and toxicity is considered in Bayesian adaptive oncology clinical trials to identify a set of admissible doses – acceptably safe and efficacious doses- for the dose finding problem.^17–19 Also, a futility monitoring rule is considered by many phase II oncology trials based on the response probability.^{20, 21} However, an adaptive sequential rule incorporating efficacy, futility and safety has never been used for pediatric strokes, and we propose a tailored monitoring rule for pediatric stokes.

Consideration of duration of intervention

We define arteriopathy relapse in the corticosteroid intervention arm as a worsening FCASS measurement from 1 month to 3 months after an initial improvement (i.e., reduction in FCASS from baseline to 1 month). Let F₁ and F₃ denote the FCASS measurement at 1 month and 3 months, respectively. Let d = F₁ – F₃. If any 2 subjects with d<0 are observed, then the duration of corticosteroid intervention arm will be extended to 3 months of treatment. The primary outcome and study design will not otherwise be changed. Because relapse is so rare, the intervention duration will be extended if we observed a relapse in only 2 subjects.

Results

Of the 21 pediatric stroke investigators present at the VIPS investigator meeting, all (100%) participated in the survey. All respondents were pediatric stroke clinical experts; 20 were child neurologists and one was a pediatric hematologist. Seventeen (81%) were from U.S. institutions; three were Canadian and one was Swiss. The majority (13/21, 62%) currently treat some cases of FCA with corticosteroids. Among those 13 who sometimes treat, the most common criterion for treatment was progressive FCA severity (11/13 respondents), followed by recurrent ischemic events (9/13 respondents). Regarding the statement, “I think corticosteroids most likely benefit children with FCA”: 4% strongly agreed, 44% agreed, and 52% were neutral (none disagreed or strongly disagreed). Regarding the statement, “I think corticosteroids most likely harm children with FCA”: 9% strongly disagreed, 74% disagreed, and 17% were neutral (none agreed or strongly agreed). All (100%) agreed they would be willing to enroll patients in a trial that randomized children to corticosteroids versus standard therapy.

If efficacy is measured by imaging biomarkers, the probability of efficacy that would lead an investigator to treat was a mean of 38% (median 30%; range 10% to 90%). If efficacy is measured by 12-month PSOM (neurological outcome), the probability of efficacy that would lead an investigator to treat was a mean of 34% (median 25%; range 10% to 90%). With either metric, only a single respondent indicated that they would require a probability of efficacy greater than 80% in order to treat. The probability of efficacy (by either metric) that would make them unwilling to randomize because of efficacy (they would feel all children should receive the effective intervention) was a median 70%. The most common response was 80% (7 of 21 respondents), and only a single investigator (4.8% of 21 respondents) provided a response greater than 80%. The probability of efficacy (by either metric) that would make them unwilling to randomize because of futility (they would feel no children should receive the futile intervention) was a mean of 17% (median 10%). The maximum acceptable proportion of severe/life-threatening adverse effects (assuming corticosteroids are effective) was a mean of 4% (range 1 to 15%). Hence we chose 8% as δ for our safety monitoring rule.

Simulation study

We evaluated the operating characteristics of the FOCAS trial design using simulations. We assumed enrollment occurred at 21 sites (i.e., 2 patients/site) that all 42 subjects reached the final visit. The maximum sample size of 42 in our simulations takes into account the dilution of the treatment effect due missing data from the planned sample size for FOCAS trial (N=50). Data was simulated assuming patients arrived according to a Poisson process with an accrual rate of 0.06 patients per year and were equally randomized to receive either intervention or control. Three interim analyses were performed when the first 10, 20, and 30 enrolled patients completed 1 month. A final analysis was performed after the last patient completed follow-up. We generated the data according to the scenarios described in the first column of Table 1 with the expected change of FCASS measured between baseline and 1 month for control (Δ_c) and intervention (Δ_E). Based on the FCASS data from the VIPS cohort, excluding two patients treated with IV steroids, the mean change in FCASS from baseline to 1 month was 3.8 (standard deviation=3) for the control group.² The simulation setting follows the same control group mean throughout and considers a range of effects for the intervention group with an equal variance for both groups. In other words, for the ith patient in site j which was assigned to the intervention, the change of FCASS between baseline and 1 month follows a normal distribution with mean Δ_E and standard deviation 3. Independently from the FCASS measurement, serious adverse events (SAE) were generated from a Bernoulli distribution with a rate of 4%. This is reasonable for the FCA treatment with corticosteroids, because we do not expect that FCASS would be measured differently if there is a safety issue, and prior publications have not reported serious adverse effects. ^{3, 4} However, our model is generalized by incorporating the correlated outcomes between safety and efficacy, and we investigated this case in Appendix D.

Table 1.

Operating Characteristics of the FOCAS trial and a Conventional trial under five scenarios.

Scenario (ΔC,ΔE)	Rejection probability		Mean sample size		Duration of trial (months)		Early stopping probability
	FOCAS	Conventional	FOCAS	Conventional	FOCAS	Conventional	superiority	futility
(3.8, 4.0)	0.143	0.147	35.56	42	26.32	31.08	0.125	0.136
(3.8, 3.8)	0.193	0.2	35.22	42	26.07	31.08	0.167	0.107
(3.8, 2.8)	0.589	0.582	28.79	42	21.30	31.08	0.502	0.026
(3.8, 2.2)	0.812	0.799	23.07	42	17.07	31.08	0.723	0.008
(3.8, 1.8)	0.910	0.896	19.38	42	14.34	31.08	0.842	0.004

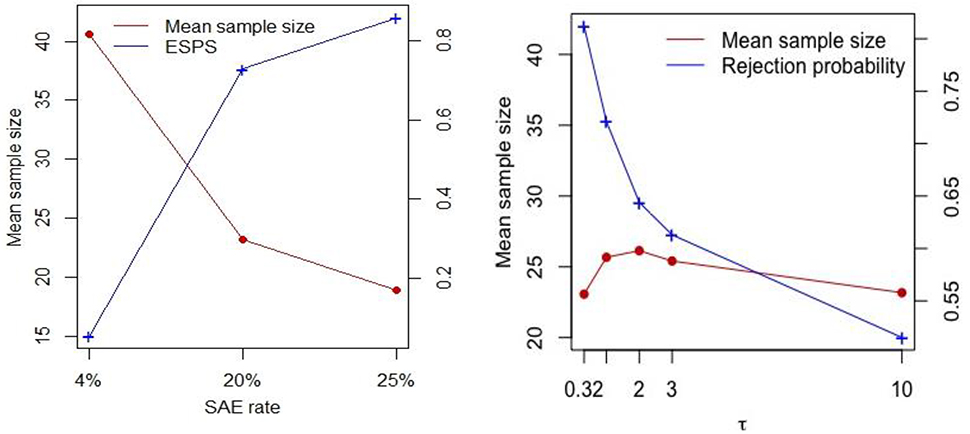
Using an empirical approach to calibrate the cutoffs for the Bayesian monitoring rule (see Appendix C), c₁ = 0.81 and c₂ = 0.15 were identified in order to achieve our desired type I and II error rates of 20% and 20%, respectively. In addition, we set δ = 0.08 as the maximum of acceptable safety rate and identified c₃ = 0.2 as an appropriate safety monitoring cutoff to stop early with 5.5% probability when the true SAE rate π_E was 4% and stop early with 85.7% probability when π_E was 25% (figure 1 and Appendix C). Table 1 shows the operating characteristics based on 10,000 simulations. The FOCAS trial design preserved the overall type I error rate at the level of 0.193 (see the second scenario) and yielded power 81.2% when the difference in mean change of FCASS between corticosteroids and control was 1.6 (i.e., the fourth scenario). The proposed design is compared with a conventional, fixed design using a one-sided two-sample t-test statistics with a significance level of 0.2 at the end of the trial. The conventional design has no interim monitoring, and the total sample size is required to be enrolled. However, our proposed FOCAS design detects a treatment effect earlier to save 30–55% patients and makes the duration of the trial shorter. This is a remarkable benefit of our proposed design especially for a rare disease.

Figure 1.

Plot of sensitivity analyses for the serious adverse event (SAE) rate (left panel) and variability of site effect (right panel) when the difference of FCASS measured between corticosteroids and control was −1.6 (i.e., the fourth scenario).

Sensitivity analyses

We evaluated the proposed design for early stopping for safety when the true SAE rate is 20% and 25%, which are larger than the threshold δ = 0.08, to consider a case where the rate is higher than the maximum acceptable safety range given in the survey. We compared the results to those when the true SAE rate is 4%. The left panel of Figure 1 shows that the trial stops earlier for higher SAE rates with 73–86% early stopping probability, because it clearly detects the SAE rate is higher than 8%. It saves more than 50% of patients from the toxic drug. Also, when the drug is safe (i.e., the SAE rate is 4%), we almost never stopped early, and our trial avoids erroneous decisions from safety monitoring. The right panel of Figure 1 shows the results of the FOCAS trial design when there is a site effect or when the site effect is more variable compared to the fourth scenario of Table 1. Note that the site effect was generated from a normal distribution with mean 0 and standard deviation τ, and the FCASS change is now generated from $Y_{ij}\sim N\left({\mathrm{\Delta }}_{G_{ij}},{\tau }^2+3^2\right)$, where G_ij is either E or C. The rejection probability under the fourth scenario in Table 1 (i.e., when τ² = 0.32) becomes smaller as the variability of the site effect increases. However, the mean sample size is mostly similar regardless of the variability of the site effect. Moreover, we investigated the operating characteristic of the proposed design when the errors are not normally distributed. We generated the data under the same setting as Table 1, but with two different non-normal error distributions, including t distribution with degrees of freedom 2.25 and uniform distribution on interval (−5.2, 5.2). Those parameters are selected to obtain the same variability as Table 1 but the distribution has fat-tail or flat-tail, respectively. The results are presented in Table 2. We notice that a moderate departure from normality does not cause a big difference in the operating characteristics. Both type I and II errors are preserved at the nominal level.

Table 2.

Sensitivity analysis results for FOCAS trial design under non-normal error distribution.

Error distribution	Scenario (ΔC,ΔE)	Rejection probability	Mean sample size	Duration of trial (months)	Early stopping probability for
					superiority	futility
Fat-tailed (t distribution)	(3.8, 4.0)	0.051	39.91	29.53	0.043	0.048
	(3.8, 3.8)	0.085	39.66	29.35	0.067	0.033
	(3.8, 2.8)	0.651	29.18	21.59	0.537	0.004
	(3.8, 2.2)	0.918	19.09	14.12	0.856	0.002
	(3.8, 1.8)	0.976	14.77	10.93	0.946	0.001
Flat-tailed (uniform)	(3.8, 4.0)	0.144	35.41	26.20	0.125	0.141
	(3.8, 3.8)	0.193	35.05	25.93	0.167	0.113
	(3.8, 2.8)	0.587	28.79	21.30	0.502	0.028
	(3.8, 2.2)	0.808	23.27	17.22	0.720	0.011
	(3.8, 1.8)	0.909	19.72	14.59	0.837	0.005

Discussion

We present a pragmatic, adaptive clinical trial design, with criteria for trial success based on the level of evidence needed to impact clinical practice. We have demonstrated the trial operating characteristics under a variety of assumptions.

In the VIPS observational study, the well-performing sites enrolled an average of one FCA case per site per year.⁷ If enrollment in FOCAS, as an interventional trial, is half of enrollment in VIPS, then patients would enroll 0.5 cases/site/year, or 2 cases/site over a 4-year enrollment period. We need 25 sites to enroll 50 patients over four years. The proposed design allows for a feasible study, accomplishable within the typical 5 year NIH funding period.

We propose that several factors make this pragmatic approach reasonable for the FOCAS trial design: (1) FOCAS will study standard doses of old medications with well-established safety profiles commonly used for other pediatric disorders. (We will not seek a new FDA label.) (2) Alternative therapies for FCA do not exist, and untreated FCA often progresses. (3) Most pediatric stroke experts already employ corticosteroids for select cases of FCA, and perceive it to be safe. Hence, to be convinced to treat FCA with corticosteroids, clinicians require a lower than usual level of confidence that the treatment is effective.

We also propose that this approach is more ethical, minimizing the number of children who would ultimately receive the inferior therapy. We anticipate that this assurance—that we will minimize unnecessary randomizations—will improve participation in the clinical trial. Clinicians would be less likely to enroll children into a trial designed to prove efficacy at a higher level than what they feel necessary to change clinical practice.

Conclusions

Other rare diseases may be similar to FCA in that clinicians would be comfortable with a lower level of confidence regarding treatment efficacy because of either the severity of disease or the safety of the intervention. This approach to trial design— applying the probability of efficacy needed to change clinical practice based on expert consensus and incorporating frequent opportunities to stop early—may help make the study of interventions for rare disease more feasible.