Abstract
Purpose
National programs for trachoma control are implementing mass treatment programs in which azithromycin is used as part of the control strategy. Dose is determined by weight, which can be difficult to determine in field conditions. The purposes of this study were to determine whether an accurate dose could be determined by using height as a surrogate for weight and whether a single model of height-based dosage would be applicable in more than one setting.
Methods
Data on height, weight, age, and gender of 5558 children aged 6 months to15 years were obtained from Kongwa and Rombo, Tanzania; Malakal, Sudan; Jareng, The Gambia; and Daboya, Ghana. Models for predicting weight by measuring height were developed that incorporated country-specific parameters. Doses of azithromycin assumed suspension of 40 mg/mL and 250-mg tablets that could be halved. Tolerance limits were defined as 15 to 30 mg/kg.
Results
A regression model, predicting log weight as a function of log height, was the best fit and explained 94% of the variance. In children less than 1 year of age or 60 cm in height, dose determined by weight was preferred. Dosage by height resulted in more than 97% of children receiving doses within the tolerance limits. Children aged 1 to 2 years were the group most likely to be over- or undermedicated, but this occurred in only 6% of this age group.
Conclusions
Height-based determination of dosage of azithromycin in trachoma control programs appears to be feasible, using the height-based schedule proposed. One model was adequate for all the countries in the study. Further expansion to other countries is warranted.
The control of blinding trachoma in endemic countries is based on a four-part strategy that includes the provision of antibiotics to treat active trachoma.1 The World Health Organization recommends that if the prevalence of active trachoma is more than 20% in children aged 1 to 9 years, mass distribution of antibiotic in affected communities is warranted. The current antibiotics of choice are topical tetracycline eye ointment or oral azithromycin. Azithromycin is given as a single dose from 20 mg/kg up to a maximum of 1 g.
Mass treatment campaigns have been performed in several countries, typically giving the drug at once-yearly intervals. Some programs target children, who have the highest rates of active disease and infection in the community.2,3 The dose of azithromycin in persons weighing less than 50 kg is based on weight, which can present logistic problems in the field. Scales are cumbersome to carry, cooperation of young children can be difficult and time consuming to obtain, and the scales can lose calibration. Faced with similar problems, the onchocerciasis control teams have investigated height-based, physical appearance– based, and arm circumference– based dosages for distribution of ivermectin.4–7 In other programs, the utility of using height to determine dose has also been investigated.8 The results suggest that alternative approaches to using weight to determine dosage are feasible. There is considerable interest in determining whether similar approaches, such as that based on height, could be used for dispensing azithromycin.
The purpose of this study was twofold: first, to investigate the predictive power of using height to estimate weight in children receiving azithromycin for the control of trachoma, and to determine how accurate these models are at predicting the dose of azithromycin as 20 mg/kg, and second to investigate the problem of under- or overmedicating with azithromycin based on models for height when the unit of dose is either a suspension at 40 mg/mL or 250-mg tablets, which can be broken in half to provide a dose of 125 mg. In addition, we investigate the likelihood that one predictive equation would be reasonable for more than one country by using five data sets from four trachoma-endemic countries.
Methods
The study protocol adhered to the provisions of the Declaration of Helsinki, and informed consent was obtained from participants or their parents after the intent and risks of the study were explained.
We used 20 mg/kg as an ideal dose of azithromycin, with tolerance limits of 15 mg/kg to 30 mg/kg. Thus, the tolerance limits in terms of absolute dose widened as body weight increased. The choice of tolerance limits was arbitrary, based on what other studies of azithromycin use have suggested.9 Sensitivity analysis was performed broadening the tolerance region to include 13 and 35 mg/kg. The dosages of azithromycin available were liquid at 40 mg/mL reconstituted and 250-mg tablets. We assumed that tablets could be broken in half to provide a 125-mg dose. We optimized the height cutoff for which tablets could be used versus suspension, although the option to use a half tablet is addressed in the Discussion section.
Height-based dosage is only an issue in children and persons weighing less than 33 to 50 kg (based on the tolerance limits), who would not be receiving the full 1-g dose. Therefore, we confined our analyses to children aged less than 15, because, in older persons, the dosage would most likely be 1 g. Azithromycin is not used in children less than 6 months of age, and the data are therefore based on children aged between 6 months and 15 years. Data were collected from sites in four countries: Tanzania, Ghana, The Gambia, and Sudan. In Tanzania, two sites were surveyed, Kongwa and Rombo. Each data set contained the following data:
Height, measured in centimeters. In Kongwa, Tanzania, and The Gambia, a standard height board was used to determine height. In Rombo, Tanzania, a plank of wood with height marked in centimeters was used. In Ghana, community health volunteers measured each child’s height on a straight stick with a piece of chalk. The distance from the ground to the chalk mark was measured with a tape measure. In Sudan, a standard balance scale was used that also had a height scale.
Weight, measured in kilograms. In Kongwa, The Gambia, and Rombo, Tanzania, digital scales were used to collect weight. In Kongwa, Tanzania, the scales were calibrated to zero each day and with an object of known weight. For children unable to stand on a scale, the mother was weighed holding the child, then weighed without the child. The child’s weight was the difference of the two weights. In Ghana, analogue scales were used, with the same procedure used for children unable to stand on a scale. In Rombo, children who could not stand on a scale were weighed with spring scales (TALC, St. Albans, UK). In Sudan, the children stood on the balance scale. No children aged less than 1 year were studied in Sudan.
Age. For analytical purposes, age was rounded to the nearest year. In Kongwa, age above 1 year was rounded to the nearest year as reported by the mother. If necessary, the vaccination card was used to obtain the age. In Sudan; Rombo, Tanzinai; and Ghana, age was reported by the mother and rounded to the nearest year. In The Gambia, vaccination records were used to supplement the mother’s reports of age.
The data were first analyzed by evaluating the raw correlation between height and weight for each data set. Missing data were excluded from analyses. Data from two children whose heights and weights were extreme outliers were excluded (one child weighed <1 kg, and one child was <40 cm in height and weighed outside the 99.9th percentile for that height). The possible nonlinear relationship of weight and height was explored by using descriptive plots of the data. Weight against height was plotted in the log scale, and a smoothed spline was calculated using S-plus (S-plus; Insightful Corp., Seattle, WA). Linear spline regression models were then created to predict weight from height and then including terms for gender and age in an attempt to create the best fitting model that accounted for the most variance. To assess the stability of the model findings, we estimated the relationship between height and weight separately and examined for similarity across randomly selected halves of the total sample. Once the model with the best fit was created, height was used to obtain a predicted weight for each child. The predicted dose was calculated, based on the predicted weight. This dose was then divided by the actual weight to determine whether an under- or overdose had occurred. If the dose was within the tolerance limits, we counted it as acceptable. Doses less than 15 mg/kg were termed an underdose and those over 30 mg/kg were termed an overdose. We then sought to see whether the models created for each country could be used accurately for the other countries.
Results
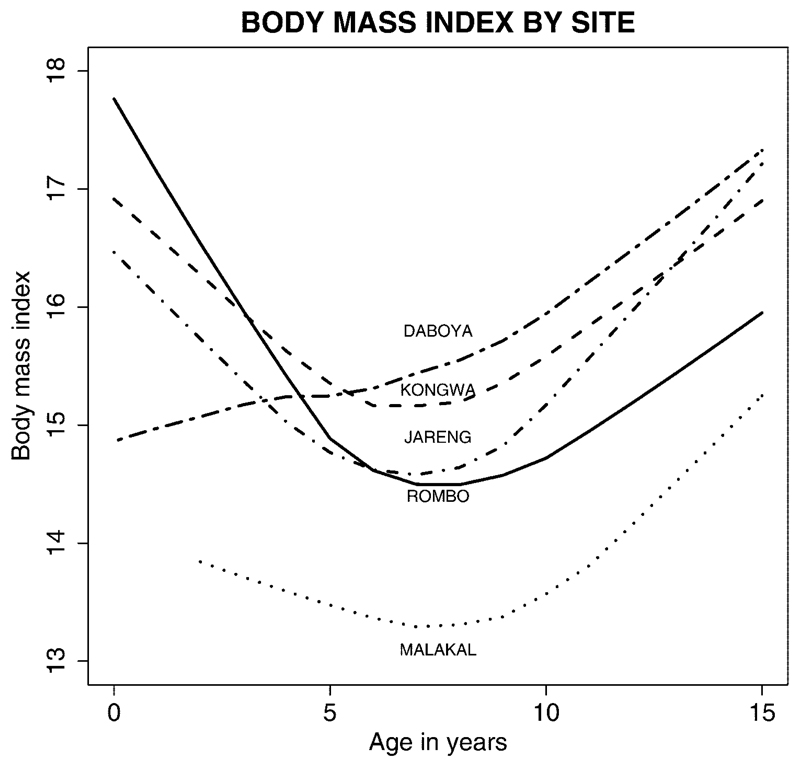
The age and gender distributions for each of the five study sites are shown in Table 1. None of the study sites had enrolled many children below the age of 1 year. The data from Sudan had few children below the age of 5 years, and the study in Ghana had few children older than 12. The study in Rombo, Tanzania, had the largest population, 2846 children. The body mass index, by age, for each of the five study sites suggested that the children in Sudan had much lower weight for height at each age group than children in the other data collection sites (Fig. 1).
Table 1. Demographic Characteristics of the Sample for Each Site.
| Daboya, Ghana | Jareng, The Gambia | Kongwa, Tanzania* | Rombo, Tanzania | Malakal, Sudan | Total | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Age Group (y) | Male n (%) |
Female n (%) |
Male n (%) |
Female n (%) |
Male n (%) |
Female n (%) |
Male n (%) |
Female n (%) |
Male n (%) |
Female n (%) |
Male n (%) |
Female n (%) |
| <1 | 5 (4.3) | 2 (2.0) | 22 (6.0) | 27 (6.7) | 13 (2.0) | 24 (3.2) | 39 (2.8) | 31 (2.2) | 0 (0.0) | 0 (0.0) | 79 (2.9) | 84 (3.0) |
| 1–4 | 42 (35.9) | 39 (39.4) | 109 (30.0) | 109 (27.0) | 283 (44.0) | 267 (35.4) | 377 (27.5) | 379 (26.9) | 19 (9.1) | 17 (9.3) | 830 (30.7) | 811 (28.5) |
| 5–8 | 30 (25.6) | 34 (34.3) | 120 (33.0) | 109 (27.0) | 197 (30.7) | 263 (34.9) | 381 (27.8) | 396 (28.1) | 57 (27.1) | 48 (26.3) | 785 (29.0) | 850 (29.9) |
| 7–12 | 31 (26.5) | 19 (19.2) | 72 (19.8) | 105 (26.0) | 107 (16.6) | 148 (19.6) | 346 (25.2) | 355 (25.2) | 92 (43.8) | 97 (53.3) | 648 (23.9) | 724 (25.3) |
| 13–15 | 9 (7.7) | 5 (5.1) | 41 (11.3) | 53 (13.2) | 43 (6.7) | 52 (6.9) | 229 (16.7) | 248 (17.6) | 42 (20.0) | 20 (11.1) | 364 (13.5) | 378 (13.3) |
| Total | 117 (100) | 99 (100) | 364 (100) | 403 (100) | 643 (100) | 754 (100) | 1372 (100) | 1409 (100) | 210 (100) | 182 (100) | 2706 (100) | 2847 (100) |
Gender is missing for six children.
Figure 1.
Body mass index by site.
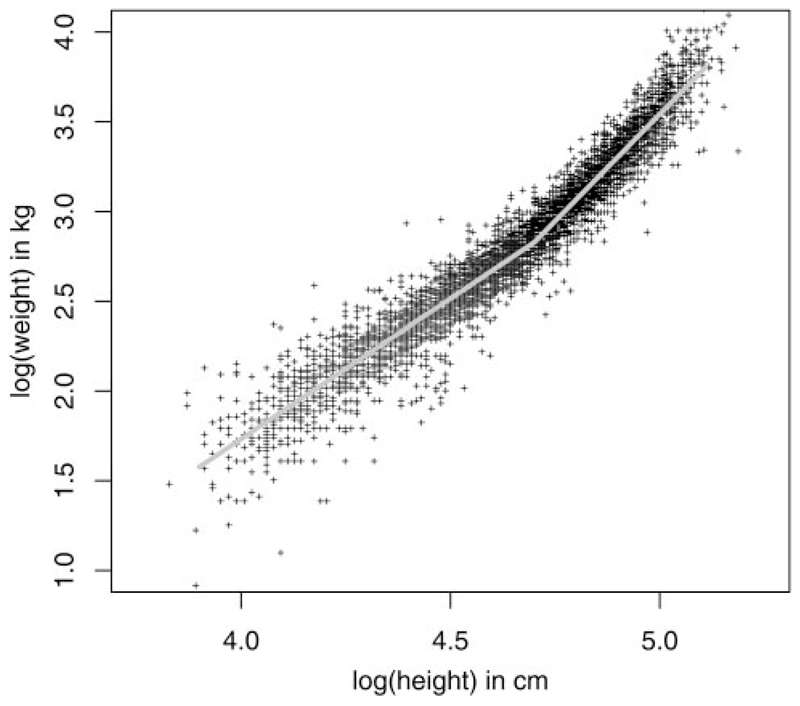
The correlation between height and weight for all countries is shown in Figure 2. The correlation was high and the distribution was not strictly linear, with a more rapid increase in weight for a given height beyond approximately 110 cm.
Figure 2.
Correlation between height and weight in all countries (Malakal, Sudan; Rombo and Kongwa, Tanzania; Jareng, The Gambia; Daboya, Ghana).
The model with the best fit was a spline regression of log height predicting log weight, where height was centered at the node of 110 cm (coincidentally, the median of the distribution of heights; Table 2). Age and gender accounted for very little of the remaining variance in the model and were not studied further. The general model, not accounting for the country-specific parameters, accounted for 94% of the variance. Virtually identical parameter estimates were obtained (to the third decimal place) when using the randomly selected subsamples of the population, providing support for the stability of the final model.
Table 2. Predicting Weight from Height Using a Spline Regression Model in the Log Scale.
| Model | Variable | Parameter Estimate* | 95% CI | P | R2 |
|---|---|---|---|---|---|
| General | Intercept | 2.8286 | (2.8230, 2.8334) | ||
| Log (height/110) (height <110 cm) | 1.5643 | (1.5440, 1.5844) | <0.0001 | 0.944 | |
| Log (height/110) (height ≥110 cm) | 2.3828 | (2.3499, 2.4157) | <0.0001 | ||
| Adding Country-Specific Parameters† | Intercept | 2.8282 | (2.8220, 2.8343) | ||
| Log (height/110) (height <110 cm) | 1.5708 | (1.5511, 1.5905) | <0.0001 | 0.947 | |
| Log (height/110) (height ≥110 cm) | 2.45935 | (2.4099, 2.5088) | <0.0001 | ||
| Malakal, Sudan | −0.11683 | (−0.1292, −0.1045) | <0.0001 | ||
| Daboya, Ghana | 0.00548 | (−0.0102, 0.0211) | 0.48 | ||
| Jareng, The Gambia | −0.00690 | (−0.1600, 0.0022) | 0.13 | ||
| Kongwa, Tanzania | 0.01438 | (0.0071, 0.0217) | 0.0001 |
log (weight) = α + β log (height/110).
Reference Rombo, Tanzania.
We decided that, because so few children were enrolled at less than 1 year of age and because it is likely that such children would be weighed to determine the dose anyway, we would create a model for children age 1 to 15 years and exclude those known to be aged less than 1 year. The mean height for children aged less than 1 year was less than 60 cm, and we therefore presumed that children less than 1 year of age or 60 cm would be weighed to determine the appropriate dose. The sample from Rombo, Tanzania, was used as the reference group, because it contained the most children. There was no significant difference in predicting weight for height using the same parameters comparing Rombo with either Jareng, The Gambia, or Daboya, Ghana. (Table 2). Children in Kongwa, Tanzania, were slightly, but significantly, heavier at each height. However, for each height, children from Malakal, Sudan, had significantly lower weight compared with the children from Rombo, Tanzania. These data imply that a different height-based dosage paradigm may be needed for dosage in Sudan, because using the model based on the other three countries for predicting weight from height would consistently provide more medication for children in Sudan than indicated by their true weights. However, the tolerance limits for over- or underdoses of azithromycin are reasonably wide, as we show herein.
Using the model without the country-specific parameters, we then calculated the proportion that would receive more than 30 mg/kg or less than 15 mg/kg in each site (Table 3). The percentage undermedicated was small, ranging from none to 0.9%. The percentage that received overdoses ranged from 0.3% in Sudan to 1.2% in Kongwa, Tanzania. Thus, although there is the theoretical problem of overdose in Sudan, practically, the tolerance limits were broad enough that it appears not to be an issue. The ages of the children who received over- or underdoses, and the distribution of actual doses they would receive, suggest most of the problem is in the smallest children, ages 1 to 2 years (Table 4). There was one young child who was exceedingly tall for his weight and would have received 40 mg/kg according to this model. Although we do not know whether the height or weight data were in error, it is important to note that most of the overdoses did not exceed approximately 36 mg/kg.
Table 3. The Distribution by Country of Children Who Would Receive a Dose of Azithromycin within the Tolerance Limits and Those Who Would Receive Over- or Underdoses, Presuming Doses as Fine as 20 mg/kg.
| Country | Underdose (<15 mg/kg) | Dose within Limits | Overdose (>30 mg/kg) |
|---|---|---|---|
| Malakal, Sudan | 0 (0.0) | 391 (99.7) | 1 (0.3) |
| Rombo, Tanzania | 14 (0.5) | 2692 (99.3) | 5 (0.2) |
| Kongwa, Tanzania | 5 (0.4) | 1344 (98.5) | 16 (1.2) |
| Jareng, The Gambia | 6 (0.9) | 711 (99.0) | 1 (0.1) |
| Daboya, Ghana | 0 (0.0) | 207 (99.0) | 2 (1.0) |
Children were 1 to 15 years of age. Data are number of children with percentage of the study group in each country in parentheses.
Table 4. Actual Characteristics of the 50 Children Who Would Receive Either Under- or Overdoses, Presuming Doses as Fine as 20 mg/kg.
| Outside Tolerance Limits | Age (n) | Mean and Range of Actual Doses (mg/kg) |
|---|---|---|
| Received <15 mg/kg | 1–2 (10) | 13.8 (13–14) |
| 3–4 (3) | 13.3 (12–14) | |
| 5–8 (4) | 12.8 (12–14) | |
| 9–12 (2) | 13.0 (12–14) | |
| 13–15 (6) | 13.7 (13–14) | |
| Received >30 mg/kg | 1–2 (18) | 33.3 (31–40.0) |
| 3–4 (1) | 31.0 (—) | |
| 5–8 (3) | 32.7 (32–33) | |
| 9–12 (2) | 34 (32–36) | |
| 13–15 (1) | 31.0 (—) |
Children were 1 to 15 years of age.
However, in tablet form, the dose of azithromycin cannot be as fine as 20 mg/kg. We presumed that syrup would be administered to a child less than 71.5 cm, although children between 60 and 64.9 cm could receive a half tablet. Children less than 60 cm or between 64.9 and 71.5 cm would be better served with suspension, which can be dispensed in finer milligram increments. Table 5 shows the dosage, with tablets or suspension, according to height and associated predicted weight. In our model, the height of each child was used to derive a predicted weight, and the dose each child would receive was calculated.
Table 5. The Range of Actual Heights Used for Predicting the Dose of Azithromycin and Range of Weights Predicted Based on the Model.
| Height (cm) |
Predicted Weight (kg) |
|||
|---|---|---|---|---|
| Dose | Lower Limit | Upper Limit | Lower limit | Upper Limit |
| Suspension | ||||
| S 120 mg* | 60.0 | 60.5 | 6.56 | 6.64 |
| S 160 mg* | 60.6 | 71.6 | 6.65 | 8.64 |
| Number of tablets | ||||
| 1 (250 mg) | 71.7 | 100.0 | 8.65 | 14.60 |
| 1.5 (375 mg) | 100.1 | 120.0 | 14.61 | 20.80 |
| 2 (500 mg) | 120.1 | 134.0 | 20.81 | 27.0 |
| 2.5 (625 mg) | 134.1 | 146.2 | 27.1 | 33.3 |
| 3 (750 mg) | 146.3 | 157.1 | 33.4 | 39.6 |
| 3.5 (875 mg) | 157.2 | 167.1 | 39.7 | 45.8 |
| 4 (1000 mg) | 167.2 | — | 45.9 | — |
Children weighing between 60 and 64.9 cm could receive half a tablet.
Table 6 shows the percentages of children who would receive under- or overdoses, if our model of height-based dosage as shown in Table 5 were used in each country. More than 97% of children would receive dosages within the tolerance limits, if our approach were used. Slightly more children would receive doses above 30 mg/kg than would be undermedicated, but the percentages are very small. The problems continue to arise in the youngest children, for whom height predicts either too much or too little medication (Table 7). More than half of the children who received doses outside the tolerance range were aged 1 to 2 years. With the dosage schedule described in Table 5, an estimated 6% of 1- to 2-year-olds would receive either over- or underdoses of azithromycin.
Table 6. The Distribution by Country of Children Who Would Receive Azithromycin within the Tolerance Limits and Those Who Would Receive Over- or Underdoses.
| Tolerance Limits 15–30 mg/kg |
Tolerance Limits 13–35 mg/kg |
|||||
|---|---|---|---|---|---|---|
| Location | Underdose | Within Limits | Overdose | Underdose | Within Limits | Overdose |
| Malakal, Sudan | 0 (0.0) | 389 (99.2) | 3 (0.8) | 0 (0.0) | 392 (100.0) | 0 (0.0) |
| Rombo, Tanzania | 18 (0.7) | 2667 (99.1) | 7 (0.2) | 3 (0.1) | 2688 (99.9) | 1 (0.04) |
| Kongwa, Tanzania | 10 (0.7) | 1316 (97.3) | 26 (1.9) | 0 (0.0) | 1348 (99.7) | 4 (0.3) |
| Jareng, The Gambia | 7 (1.0) | 706 (98.3) | 5 (0.7) | 1 (0.1) | 717 (99.9) | 0 (0.0) |
| Daboya, Ghana | 0 (0.0) | 206 (98.6) | 3 (1.4) | 0 (0.0) | 208 (99.5) | 1 (0.5) |
Children were 1 to 15 years of age. Data are number of children in each country with percentage of whole group in each country in parentheses.
Table 7. Actual Characteristics of the 79 Children Who Received Either an Under- or Overdose with the Proposed Dosage Schedule.
| Outside Tolerance Limits | Age (n) | Mean and Range of Actual Doses (mg/kg) |
|---|---|---|
| Received <15 mg/kg | 1–2 (12) | 13.3 (11–14) |
| 3–4 (5) | 13.4 (11–14.) | |
| 5–8 (9) | 13.7 (13–14) | |
| 9–12 (4) | 13.5 (13–14) | |
| 13–15 (5) | 14.0 (14–14) | |
| Received >30 mg/kg | 1–2 (33) | 33.1 (31–40) |
| 3–4 (5) | 31.8 (31–35) | |
| 5–8 (3) | 31.7 (31–33) | |
| 9–12 (2) | 33 (31–35) | |
| 13–15 (1) | 31.0 |
Field workers have expressed interest in minimizing the number of children needing suspension, to avoid having to mix the solution and dispense the liquid. Therefore, we also undertook analyses of under- and overdoses of children using the scenario of all children between 60 and 71.5 cm receiving a half tablet, instead of those with heights just those between 60 and 64.9 cm. Such a change would increase the absolute number of children who would receive over- or underdoses from 79 to 170. Although more than 95% of children aged 1 to 15 years would still be within tolerance limits, more than 16% of children aged 1 to 2 years would receive doses outside the tolerance limit. It appears that even the half-tablet dose does not provide a dosage in small enough units to be useful in the youngest children.
If the tolerance region is widened to include 13 and 35mg/kg (Table 6), 99.8% of the children would be medicated within the tolerance limits. The six children in Table 6 who received doses above 35 mg/kg were aged 1 to 2 years.
Discussion
Our data suggest that height-based dosage, using the recommended cutoffs displayed in Table 8, provide accurate doses for children aged 1 to 15 years. We recommend the weighing of children aged less than 1 year, and the use of suspension in children of height less than 71.5 cm. Furthermore, reasonable health practice suggests that determination of dose by weight be performed for any child who appears very thin or very heavy for height, to avoid over- or undermedicating.
Table 8. Recommended Azithromycin Dose According to Height.
| Height Range (cm) | Recommended Dose (mg) |
|---|---|
| <60 or (<1 year) | Need to weigh |
| 60.0–60.5 | 120 (suspension)* |
| 60.6–71.6 | 160 (suspension)* |
| 71.7–100.0 | 250 (1 tablet) |
| 100.1–120.0 | 375 (1.5 tablets) |
| 120.1–134.0 | 500 (2 tablets) |
| 134.1–146.2 | 625 (2.5 tablets) |
| 146.3–157.1 | 750 (3 tablets) |
| 157.2–167.1 | 875 (3.5 tablets) |
| >167.1 | 1000 (4 tablets) |
Children weighing between 60 and 64.9 cm could receive half a tablet.
The use of 15 to 30 mg/kg as the tolerance limits was based on prior studies and manufacturer’s recommendations, but in fact the safety margin of azithromycin may be higher than 30 mg/kg. Azithromycin is rapidly distributed to tissues and has a long half-life. Adult doses of azithromycin can vary, depending on indication, from 1 to 3 g over 3 days. For some indications in children the dose is 12 mg/kg once per day for 5 days, or 60 mg/kg total dose. If the tolerance limits are even wider than were used in this study, the proportion of children adequately treated (i.e., within the tolerance limits) would be even higher. More information is needed on safety and efficacy at doses outside the tolerance limits.
The equation we used for predicting dosage from height appears robust enough to encompass inter- and intracountry differences in height for weight in children. For example, although children from Sudan weighed significantly less at each height compared with the children in Tanzania, Ghana, and The Gambia, the prediction of dose resulted in very few over- or underdoses for those children.
There are some limitations to our study. The data from Ghana and Sudan have few children aged 2 years or less. Because over- and undermedication was most problematic in that age range, the absence of significant problems for Ghana and Sudan may reflect the small sample in that age range. In general, the proportion of children aged 1 to 2 years who would be receive doses out of range was still relatively small (6%) suggesting height-based doses and use of suspension for these younger children is reasonable.
We used data from East and West Africa for this study. The model should be tried on data from children in areas in which trachoma is endemic in Asia and the Middle East to determine whether it has even wider applicability.
The data were collected under field conditions by research teams in each setting. No attempt was made to standardize protocols across the different countries, and some of the differences by setting may be due to differences in the scales and calibrations used, determination of height (especially at the youngest ages), and determination of age. Children were measured only once, precluding quantification of the measurement error. Such differences would introduce noise into the overall model of predicting weight based on height without specific country parameters. However, height predicted 94% of the variance in weight, suggesting that noise was relatively minimal. The country parameters, in fact, added very little to the prediction.
In summary, height-based dosages of azithromycin appear to be reasonable for trachoma control programs, with the caveat for weighing children less than 1 year of age. The use of height would expedite treating large numbers of children in mass treatment campaigns in West and East Africa. Further experience in using our model with height and weight data from children in other countries is encouraged, to determine whether the model can be generalized even further.
Acknowledgments
The authors thank the teams who collected the data in each country: Mamoun Homeida in Malakal, Sudan; Patrick Massae in Rombo, Tanzania; Joseph Akudibillah and Peter Abugri in Dabota, Ghana; and Harran Mkocha in Kongwa, Tanzania.
Supported by grants from the Edna McConnell Clark Foundation, International Trachoma Initiative, and The Wellcome Trust. SKW is a Research to Prevent Blindness Senior Scientific investigator.
Footnotes
Commercial relationships policy: N.
The publication costs of this article were defrayed in part by page charge payment. This article must therefore be marked “advertisement” in accordance with 18 U.S.C. §1734 solely to indicate this fact.
References
- 1.The World Health Organization. Global Elimination of Blinding Trachoma. World Health Organization 51st World Health Assembly; May 11-16, 1998; Geneva, Switzerland. Resolution 51.11. [Google Scholar]
- 2.West SK, Muñoz B, Turner V, Mmbaga BBO, Taylor HR. The epidemiology of trachoma in Central Tanzania. Int J Epidemiol. 1991;20:1088–1092. doi: 10.1093/ije/20.4.1088. [DOI] [PubMed] [Google Scholar]
- 3.Schachter J, West SK, Mabey D, et al. Azithromycin in control of trachoma. Lancet. 1999;354:630–635. doi: 10.1016/S0140-6736(98)12387-5. [DOI] [PubMed] [Google Scholar]
- 4.Taylor HR, Gonzales C, Duke Brian. Simplified dose schedule of ivermectin. Lancet. 1993;341:50–51. doi: 10.1016/0140-6736(93)92524-w. [DOI] [PubMed] [Google Scholar]
- 5.Cousens SN, Gemade E, Asha B, Abiose A, Jones BR. Ivermectin dosing based on physical appearance. Int Ophthalmol. 1994;18:215–219. doi: 10.1007/BF00951800. [DOI] [PubMed] [Google Scholar]
- 6.Shu EN, Okonkwo PO. Community based ivermectin therapy for onchocerciasis: comparison of three methods of dose assessment. Am J Trop Med Hyg. 2001;65:184–188. doi: 10.4269/ajtmh.2001.65.184. [DOI] [PubMed] [Google Scholar]
- 7.Alexander ND, Cousens SN, Yahaya H, Abiose A, Jones BR. Ivermectin dose assessment without weighing scales. Bull World Health Organ. 1993;71:361–366. [PMC free article] [PubMed] [Google Scholar]
- 8.Hall A, Nokes C, Wen ST, et al. Alternatives to body weight for estimating the dose of praziquantel needed to treat schistosomiasis. Trans R Soc Trop Med Hyg. 1999;93:653–658. doi: 10.1016/s0035-9203(99)90087-1. [DOI] [PubMed] [Google Scholar]
- 9.Solomon AW, Akudibillah J, Abugri P, et al. Pilot study of the use of community volunteers to distribute azithromycin for trachoma control in Ghana. Bull World Health Organ. 2001;79:8–14. [PMC free article] [PubMed] [Google Scholar]