Accurate quantification of astrocyte and neurotransmitter fluorescence dynamics for single-cell and population-level physiology

Abstract

Recent work examining astrocytic physiology centers on fluorescence imaging, due to development of sensitive fluorescent indicators and observation of spatiotemporally complex calcium activity. However, the field remains hindered in characterizing these dynamics, both within single cells and at the population level, because of the insufficiency of current region-of-interest (ROI)-based approaches to describe activity that is often spatially unfixed, size-varying, and propagative. Here, we present an analytical framework that releases astrocyte biologists from ROI-based tools. The Astrocyte Quantitative Analysis (AQuA) software takes an event-based perspective to model and accurately quantify complex calcium and neurotransmitter activity in fluorescence imaging datasets. We apply AQuA to a range of ex vivo and in vivo imaging data, and uncover novel physiological phenomena. Since AQuA is data-driven and based on machine learning principles, it can be applied across model organisms, fluorescent indicators, experimental modes, and imaging resolutions and speeds, enabling researchers to elucidate fundamental neural physiology.

Introduction

With increased prevalence of multiphoton imaging and optical probes to study astrocyte physiology^1–3, many groups now have tools to study fundamental functions that previously remained unclear. Recent work has focused on new ways to decipher how astrocytes respond to neurotransmitter and neuromodulator circuit signals^4–7 and how the spatiotemporal patterns of their activity shape local neuronal activity^8–10. Recording astrocytic dynamics to decoding their disparate roles in neural circuits has centered on expression of genetically encoded probes to carry out intracellular calcium (Ca²⁺) imaging using GCaMP variants³. In addition, many groups study astrocytic function by performing extracellular glutamate imaging using GluSnFR², and several more recently developed genetically encoded fluorescent probes for neurotransmitters such as GABA¹¹, norepinephrine (NE)¹², ATP¹³, and dopamine¹⁴ are poised to further expand our understanding of astrocytic circuit biology.

Compared to neuronal Ca²⁺ imaging, astrocytic GCaMP imaging presents particular challenges for analysis due to the complex spatiotemporal dynamics observed. Astrocyte-specific analysis software has been developed to capture these Ca²⁺ dynamics, several of which identify subcellular regions-of-interest (ROIs) for analysis^4,15. Likewise, GluSnFR imaging analysis techniques are based on manually or semi-manually selected ROIs, or by analyzing the entire imaging field together as one ROI^2,6,8,16. Thus most, although not all^17,18, other current techniques rely on the conceptual framework of ROIs for image analysis. However, astrocytic Ca²⁺ and GluSnFR fluorescence dynamics are particularly ill-suited for ROI-based approaches, because the concept of the ROI has several inherent assumptions that cannot be satisfied for astrocytic activity data. For example, astrocytic Ca²⁺ signals can occupy regions that change size or location across time, propagate within or across cells, and spatially overlap with other Ca²⁺ signals that are temporally distinct. ROI-based approaches assume that for a given ROI, all signals have a fixed size and shape, and all locations within the ROI undergo the same dynamics, without propagation. Accordingly, ROI-based techniques may over- or under-sample these data, obscuring true dynamics and hindering discovery. An ideal imaging analysis framework for astrocytes would take into account all these dynamic features and be free of ROI-based analytical restrictions. In addition, an ideal tool should be applicable to astrocyte imaging data across spatial scales, encompassing subcellular, cellular, and population-wide fluorescence dynamics.

We set out to design an image analysis toolbox that would capture the complex, wide-ranging fluorescent signals observed in most dynamic astrocyte imaging datasets. We reasoned that a non-ROI-based approach would better describe the observed fluorescent dynamics, and applied probability theory, machine learning, and computational optimization techniques to generate an algorithm to do so. We name this resulting software package Astrocyte Quantitative Analysis (AQuA) and validate its utility by applying it to simulated datasets that reflect the specific features that make analyzing astrocyte data challenging. We next apply AQuA to experimental two-photon (2P) imaging datasets—ex vivo Ca²⁺ imaging of GCaMP6 from acute cortical slices; in vivo Ca²⁺ imaging of GCaMP6 in primary visual cortex (V1) of awake, head-fixed mice; and ex vivo extracellular glutamate, GABA, and NE imaging. In these test cases, we find that AQuA accurately detects fluorescence dynamics by capturing events as they change in space and time, rather than from a single location, as in ROI-based approaches. AQuA outputs a comprehensive set of biologically relevant parameters from these datasets, including propagation speed, propagation direction, area, shape, and spatial frequency. Using these detected events and associated output features, we uncover neurobiological phenomena.

A wide variety of functions have been ascribed to astrocytes, and a key question currently under examination in the field is whether certain types of Ca²⁺ activities correspond to particular neurobiological functions. However, current techniques with which to classify these observed dynamics remain inadequate since they do not capture many of the dynamics recorded in fluorescent imaging of astrocytic activity. The framework we describe allows for a rigorous, in-depth dissection of astrocyte physiology across spatial and temporal imaging scales, and sets the stage for a comprehensive categorization of heterogeneous astrocyte activities both at baseline and after experimental manipulations.

Results

Design principles of the AQuA algorithm

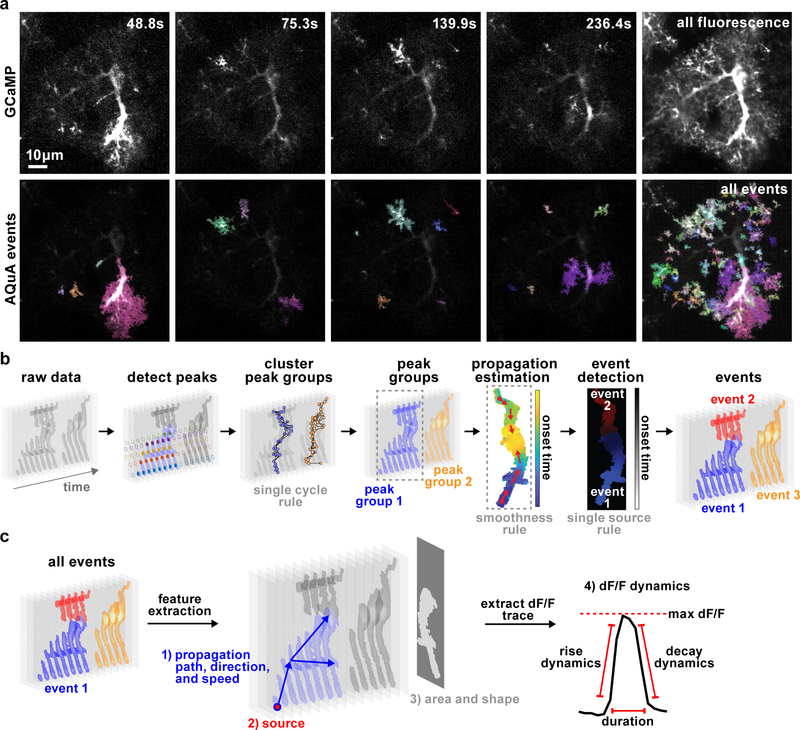
To move away from ROI-based analysis approaches and accurately capture heterogeneous astrocyte fluorescence dynamics, we designed an algorithm to decompose raw dynamic astrocyte imaging data into a set of quantifiable events (Fig 1a, Supp. Video 1, Supp. Fig. 1–3). Here, we define an event as a cycle of a signal increase and decrease that coherently occurs in a spatially connected region defined by the fluorescence dynamics, not a priori by the user or the cell morphology. Algorithmically, this definition is converted to the following two rules: 1) the temporal trajectory for an event contains only one peak (single-cycle rule, Fig. 1b) and 2) adjacent locations in the same event have similar trajectories (smoothness rule, Fig. 1b). The task of the AQuA algorithm is to detect all events, and, for each event, to identify the temporal trajectory, the spatial footprint, and the signal propagation. Briefly, our strategy of event-detection is to a) explore the single-cycle rule to find peaks, which are used to specify the time window and temporal trajectory, b) explore the smoothness rule to group spatially adjacent peaks, whose locations specify the footprint, c) apply machine learning and optimization techniques to iteratively refine the spatial and temporal properties of the event to best fit the data, and d) apply statistical theory to determine whether a detected event is purely due to noise (Fig. 1).

Figure 1. AQuA-based event detection.

(a) Individual representative frames from 5-min ex vivo astrocytic GCaMP imaging experiment (top, Video 1) with AQuA-detected events shown below. Each color represents individual event and is chosen at random. Right column shows the average GCaMP fluorescence (top) and all AQuA-detected events (bottom) from the entire video. Note that contrast differs between rows to highlight events. Similar event detection results are observed in all 48 ex vivo, 46 in vivo GCaMP data sets and 14 GluSnFr data sets used in this report. (b) Flowchart of AQuA algorithm. Raw data is visualized as a stack of images across time with grey level indicating signal intensity. In the detect peaks panel, five peaks are detected and highlighted by solid diamonds, each color denoting one peak. Based on the single-cycle rule and spatial adjacency of the apexes (solid dots) of each peak, peaks are clustered into spatially disconnected groups. Based on smoothness, propagation patterns are estimated for each peak group. By applying the single-source rule, two events are detected for peak group 1. Three total events are detected. (c) Feature extraction. Based on the event-detection results, AQuA outputs four sets of features relevant to astrocytic activity: 1) propagation-related (path, direction, and speed); 2) source of events, indicating where an event is initiated; 3) features related to the event footprint, including area and shape. Event 2 is plotted here; 4) features derived from the dF/F dynamics.

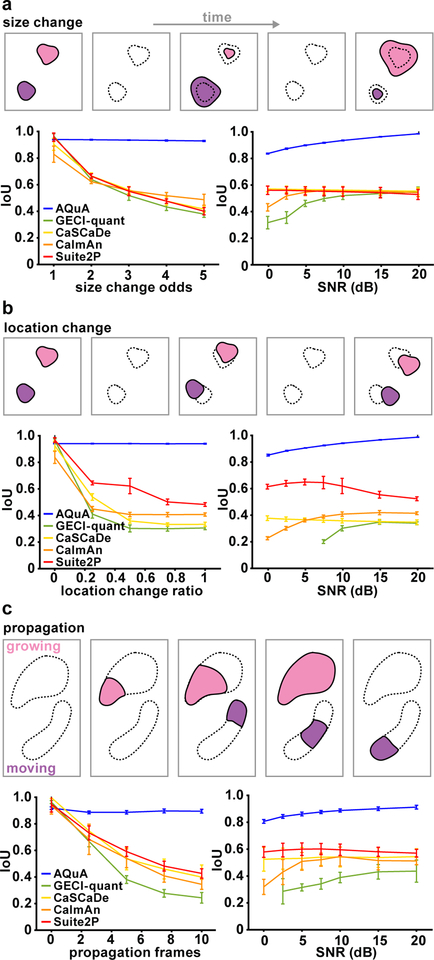
Figure 2. Performance comparison among image-analysis methods.

(a–c) Schematic (top) and results (bottom) of five image analysis methods (AQuA, GECI-quant, CaSCaDe, CaImAn, and Suite2P) on simulated datasets, independently changing event size (a), location (b), and propagation duration (c). In results, independent parameter change is shown in the left panel, and varying SNR in the right. For each, the smallest value of the independent parameter corresponds to a simulation under pure ROI assumptions. The larger the values, the greater the violation of the ROI assumptions. IoU (intersection over union) measures the overlap between detected and ground-truth events. An IoU=1 is the best achievable performance, meaning that all detected events are ground-truth and all ground-truth events are detected. For all graphs, mean value is plotted, and error bars indicate the 95% confidence interval calculated from 10 independent replications of simulation, where each simulation contains hundreds of events.

Full statistical and computational details are provided in the Methods, but we highlight one technical innovation (Graphical Time Warping [GTW])¹⁹ and one new concept (the single-source rule) that jointly enable a nuanced analysis of astrocyte fluorescence dynamics as shown below when applied to experimental datasets. To the best of our knowledge, signal propagation has never been rigorously accounted for and has been considered an obstacle to analysis. With GTW, we can estimate and quantify propagation patterns in the data. With the introduction of the single-source rule (Fig. 1b), each event only contains a single initiation source and we can separate events that are initiated at different locations but meet in the middle. The single-source rule also allows us to divide large-scale activity across an entire field-of-view into individual events, each with a single initiation location.

The output of the event-based AQuA algorithm is a list of detected events, each associated with three categories of parameters: 1) the spatial map indicating where the event occurs, 2) the dynamic curve corresponding to fluorescence change over time (dF/F), and 3) the propagation map indicating signal propagation. For each event, we use the spatial map to compute the event area, diameter and shape of the domain it occupies (Fig 1c). Using the dynamic curve, we can calculate maximum dF/F, duration, onset-time, rise-time and decay-time. Using the propagation map, we extract event initiation location, as well as propagation path, direction, and speed. In addition, AQuA computes features involving more than one event, such as the frequency of events at a position, and the overall number of events in a specified region or cell. A complete list of features is in the Methods.

Validation of AQuA using simulated data

To validate AQuA, we designed three simulation datasets to know the ground truth dynamics of each event. These datasets independently vary the three key phenomena in astrocyte imaging datasets that cause ROI-based approaches to misanalyze the data: size-variability, location-variability, and propagation. While these phenomena usually co-occur in real datasets, we simulated each independently to examine its individual impact and test AQuA’s performance relative to other image analysis tools, including CaImAn²⁰, Suite2P²¹, CaSCaDe¹⁵, and GECI-quant⁴. CaImAn and Suite2P are widely used for neuronal Ca²⁺ imaging analysis while CaSCaDe and GECI-quant were designed specifically for Ca²⁺ activity in astrocytes; all four methods are ROI-based. In our analysis of these simulated datasets, we optimally tuned the ROI-detection for all methods for an objective comparison of the best performance of each method. We also systematically changed the signal-to-noise-ratio (SNR) to examine the effect of noise.

To evaluate the performance on all simulated datasets, we used two measures: IoU and a map of the event counts. IoU (intersection over union) measures the consistency between detected and the ground-truth events, and takes into account both the spatial and temporal accuracy of detected events. IoU ranges from 0 to 1, where 1 indicates perfect detection and 0 indicates a complete failure in detection. The map of the event counts is obtained by counting the number of events at each pixel in the field, and is used to visually assess the accuracy of event-detection results by a comparison to the ground-truth map.

We first studied the impact of size-varying events (Fig. 2a), in which multiple events occurred at the same location and the event centers remain fixed, but sizes changed across different events. The degree of size change is quantified using size-change odds (see Methods) where a size-change odds of 1 indicates events with the same size, while an odds of 5 is the largest simulated size change. For example, when the odds are at 5, events with sizes randomly distributed between 0.2 and 5 times the baseline size are simulated. When there was no size change (odds=1), all methods performed well with IoUs near 0.95 (Fig. 2a). When the size change was increased, AQuA still performed well (IoU=0.95), while all other methods quickly drop to 0.4–0.5. We next studied the impact of SNR on performance by varying SNR, but fixing the size-change odds. AQuA performed better with increasing SNR and achieved nearly perfect detection accuracy (IoU=1) at 20dB. In comparison, all other methods had an IoU less than 0.6, even at high SNR (Fig. 2a). We also examined the results by visualizing event counts at each pixel (Supp. Fig. 4–5). These maps show that AQuA faithfully reported the events under various SNRs but the other methods had erroneous event counts with artificial patterns.

We next focused on shifting event locations. In these simulated datasets, event size was fixed but location changed, the degree of which was represented by a location-change score (Fig. 2b). Zero indicates no location change and greater values represent larger degrees of change. Here, results are similar to changing size, as above. AQuA models the location change well and its performance is not affected by degree of location change. Likewise, AQuA reached near perfect results when SNR was high. In contrast, all other analysis methods performed poorly with changing locations (Fig. 2b, Supp. Fig. 4).

In our third simulated dataset, we asked how fluorescence signal propagation impacts the performance of AQuA and other methods. Two propagation types—growing and moving—were simulated in this dataset (Fig. 2c), although they were also separately evaluated (Supp. Fig 6). Propagation frame number denotes the difference between the earliest and latest onset times within a single event. When propagation frame number is zero, all signals within one ROI are synchronized and there is no propagation. Similar results to the two scenarios above were obtained here, with AQuA out-performing all the other methods by a large margin. These results indicate that AQuA handles various types of propagation well, while the performance of other methods degrades rapidly when propagation is introduced.

In summary, when any of the three ROI-violating factors—size-variability, location-variability, and propagation—is introduced, other methods do not accurately capture the dynamics of the simulated data, and AQuA outperforms them by a large margin. We expect that the performance margin on real experimental data is larger than those quantified in the simulation studies here, since real data exhibits multiple ROI-violating factors. However, these IoU analyses and the event count visualizations informed us about different types of errors observed in ROI-based methods: CaSCaDe tends to over-segment, as it is based on watershed segmentation, and GECI-quant is particularly challenged by noise, causing many lost signals (Supp. Fig. 5). We note that propagation caused ROI-based approaches to quickly decline in performance, with GECI-quant influenced by noise level and CaSCaDe’s assumption of synchronized signals not allowing for accurate capture of event dynamics.

AQuA enables identification of single-cell physiological heterogeneities

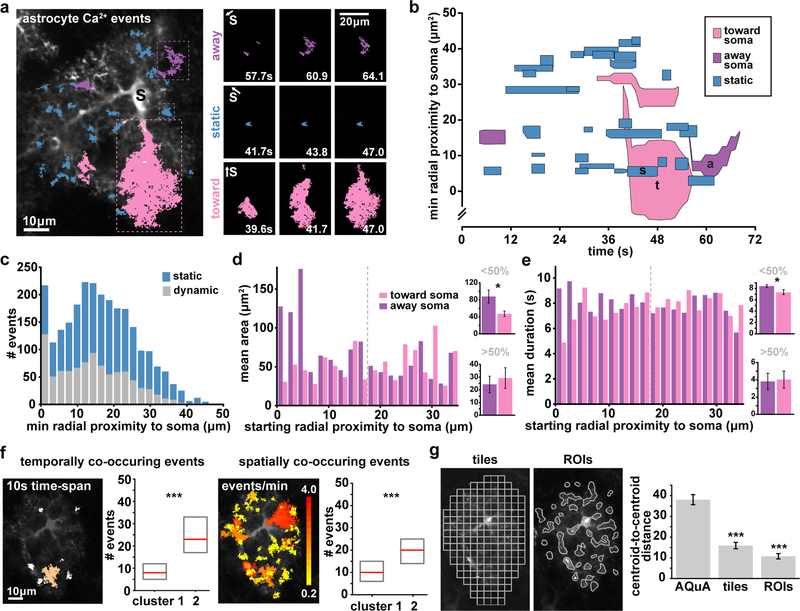
To test AQuA’s performance on real astrocyte fluorescence imaging data and ask whether AQuA could classify Ca²⁺ activities observed in single cells, we next ran AQuA on Ca²⁺ activity recorded from astrocytes in acute cortical slices from mouse V1 using 2P microscopy. We used a viral approach to express the genetically encoded Ca²⁺ indicator GCaMP6f³ in layer 2/3 (L2/3) astrocytes. Unlike ROI-based approaches, AQuA detects both propagative and non-propagative activity, revealing Ca²⁺ events with a variety of shapes and sizes (Fig. 3a, left). Further, since AQuA detects Ca²⁺ events’ spatial footprint and time-course, we can apply AQuA to measure the propagation direction each event travels over its lifetime. Imaging single cells, we used the soma as a landmark, and classified events as traveling toward the soma (pink), away from the soma (purple), or static (blue) for the majority of its lifetime (Fig. 3a, right). We then combined multiple measurements (size, propagation direction, duration, and minimum proximity to soma) into one spatiotemporal summary plot (Fig. 3b). Since astrocytes exhibit a wide diversity of Ca²⁺ activities across subcellular compartments^6,22,23, plotting the signals this way rather than standard dF/F transients highlights these heterogeneities, allows us to map the subcellular location of the Ca²⁺ signals, and enables a quick, visual impression of large amounts of complex data (Supp. Fig. 7). We note that while the expression of GCaMP6 in these experiments enabled us to analyze events within single cells, some probes do not allow clear delineation of single cells. However, a secondary fluorophore (such as TdTomato) often serves the purpose of defining the morphology of single cells, and the AQuA software is designed to overlay morphological masks on the dynamic fluorescence channel.

Figure 3. AQuA features capture heterogeneities among single astrocytes.

(a) Representative GCaMP6f ex vivo image (left) with AQuA events overlaid from 1 min of a 5 min video. Soma marked with black s. (Video 1). Right: Representative image sequence for each propagation direction class (blue = static, pink = toward soma, purple = away from soma. Soma direction marked with s and white arrow. Data from a total of 11 cells from 5 slices. (b) Spatiotemporal plot of Ca²⁺ activity from 1 min of video. Each event is represented by a polygon that is proportional to its area as it changes over its lifetime. (c) Distribution of dynamic and static events as a function of minimum distance from soma. All bin widths calculated by Freedman-Diaconis’s rule. (d) Left: Propagative event size versus starting distance from soma, segregated by propagation direction. Dashed gray line denotes half the distance between the soma and the cell border. Right: Average event area for those that start <50% (top) and >50% (bottom) from the soma, (one-tailed paired t-test, *p=0.0107). Graphs in d and e display mean ± s.e.m. (e) Left: Event duration versus starting distance from soma. Right: Average event duration for those that start <50% (top) and >50% (bottom) from the soma (one-tailed paired t-test, *p=0.0269). (f) Two event-based measurements of frequency are schematized: events with activity overlapping in time (left) and in space (right;). Left: one example event (orange) co-occurs with six other events (white) within 10s. Right: event colors indicate event number/min (0.2–4) at each location. Median (red) and interquartile range (gray) from cells in each cluster in Supp. Fig. 9 (one-tailed Wilcoxon rank sum, ***p<0.001). (g) Centroid distances between cells from two clusters determined by t-SNE plots of Ca²⁺ activity using features calculated from ROIs and 5×5μm tiles (top), (bottom, one-tailed paired t-test, ***p=9.37e-8(tiles), 2.11e-10(ROIs)).

We next asked whether some subcellular regions of astrocytes have more dynamic activity than others. Although we detected more static events than dynamic ones overall (Supp. Fig. 8a), we observed a higher proportion of dynamic events than static events in the soma (59%, Fig. 3c, Supp. Fig. 8b). We then characterized events by propagation direction and event initiation location (Fig. 3d). Events that begin close to the soma and propagate away (purple) were on average larger than the events propagating toward the soma (pink, two-tailed t-test). Similarly, those events that began close to the soma and propagated away showed a longer duration than events propagating toward the soma (two-tailed t-test, Fig. 3e, Supp. Fig. 8).

AQuA automatically extracts many features which can be used to form a comprehensive Ca²⁺ measurement matrix, where each row represents an event and each column an extracted feature (Supp. Fig. 9). Dimensionality reduction applied to this matrix can then be used to visualize each cell’s Ca²⁺ signature (Supp. Fig. 9, white rows separate individual cells). To do this, we applied t-distributed Stochastic Neighbor Embedding (t-SNE)²⁴, followed by k-means clustering to assign the cells to groups (Supp. Fig. 9), revealing clusters marked by cells with large differences in median frequency (Fig. 3f). Astrocytic Ca²⁺ frequency is commonly measured as the number of transients in time within an ROI. Here, we instead define frequency from an event-based perspective in two ways: 1) for each event, the number of other events that overlap in time, and 2) for each event, the number of other events that overlap in space. We used these two measures (temporal and spatial overlap) and several other extracted measures (Supp. Fig. 9) to construct the matrix used for t-SNE visualization and clustering. We then tested how well our AQuA-specific features perform at clustering compared to two ROI-based methods (Fig. 3g), and found that the AQuA-based method outperformed the others. In fact, even when we only use AQuA-specific features—area, temporal overlap, spatial overlap, and propagation speed—for this analysis and remove all features that can be extracted from ROI-based methods, AQuA still significantly outperforms in clustering cells (Supp. Fig. 9g–i). AQuA-extracted features that correspond to those that can be obtained by ROI-based methods—frequency, amplitude, duration—do not allow clustering significantly better than the ROI-based approaches themselves (Supp. Fig. 9g–i), suggesting that AQuA-specific features best capture dynamic fluorescence features that vary among single cells. This indicates that AQuA may be used to extract data from existing ex vivo Ca²⁺ imaging datasets to reveal previously uncovered dynamics and sort cells into functionally relevant clusters.

In vivo astrocytic Ca²⁺ bursts display anatomical directionality

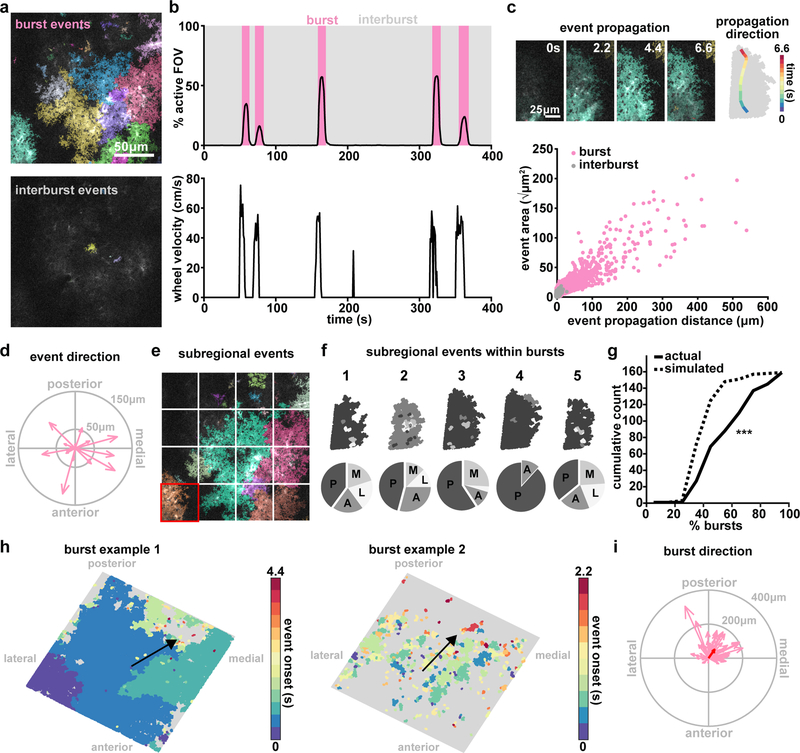
Recent interest in astrocytic activity at the mesoscale has been driven by multi-cellular astrocytic Ca²⁺ imaging^{1,5,7,8,25–27}, so we next applied AQuA to in vivo, population-level astrocyte Ca²⁺ activity. Previous studies have described temporal details of astrocyte activation^4,5,7,8,25, yet have left largely unaddressed the combined spatiotemporal properties of Ca²⁺ activity at the circuit-level, across multiple cells. Here, we explored whether AQuA can uncover spatial patterns within populations of cortical astrocytes in an awake animal, and carried out head-fixed, 2P imaging of GCaMP6f in V1 astrocytes. In vivo cortical astrocytes exhibit both small, focal, desynchronized Ca²⁺ activity²⁵, and large, coordinated activities^4,5 that we refer to as bursts. Importantly, AQuA detected both types of Ca²⁺ activity within the same in vivo imaging datasets (Video 2, Fig. 4a). Similar to previous studies, we observed many of the bursts co-occurring with locomotion (Fig. 4b, pink), and many events within these bursts displayed propagation (Fig. 4c, top). Propagative events were larger in area and propagated greater distances than those occurring during the inter-burst periods (Fig. 4c, bottom). To test whether AQuA could help us discover discrete features of this phenomenon, we next focused our investigation on the burst-period events (Supp. Fig. 10).

Figure 4. AQuA resolves astrocytic Ca²⁺ propagation directionality across scales.

(a) Representative in vivo GCaMP6f images during a burst period (top) and inter-burst period (bottom) with overlaid AQuA-detected events. (b) Population Ca²⁺ events represented as percentage of the imaging field active as a function of time. Burst periods (pink) are defined by Ca²⁺ activity >1% of the field of view and >10% of the maximum number of event onsets. (c) In vivo Ca²⁺ events propagate with specific directionality. Top: representative propagative event from the burst in panel a. The propagation direction (change of centroid relative to its original location) for each frame is overlaid on the event (right). Bottom: Total propagation distance versus event size for all events within bursts (n=6 mice, 66 bursts, 14,967 events for all data in this figure). (d) Event propagation direction from all events over the entire field in the burst in e. Arrow length indicates propagation distance. (e) To test consistency of subregional directionality during bursts, sixteen 96×96μm tiles are overlaid on images. (f) Top: All events within highlighted tile in d (red square) for five burst periods, color-coded by propagation direction (top). Bottom: Event propagation direction distributions (P=posterior; A=anterior; M=medial; L=lateral). (g) Cumulative distribution of percentage of bursts with events (within individual tiles/regions) propagating in the same direction in actual (solid) and simulated (dashed) data (one-tailed Wilcoxon rank sum, ***p=3.77e-15) (h) Two representative maps of population burst propagation direction with each event color-coded by onset time relative to the beginning of the burst, demonstrating variability of burst size. (i) Burst propagation direction calculated from onset maps in h (n=66 bursts). Event locations from the first 20% of the frames after burst onset are averaged together to determine burst origin. Event locations from 20% of the last frames after burst onset are averaged together and the difference between this and the origin determines burst propagation distance. Red arrow denotes average of all bursts.

To analyze the structure of these burst-period Ca²⁺ events, we investigated fluorescence propagation across multiple spatial scales: at the level of individual events, of subregions of the imaging field encompassing multiple events, and of the entire imaging field. At the level of individual events within a single burst, plotting the individual event direction within the entire field of view did not reveal a consistent propagation direction (Fig. 4d). However, when we divided our field-of-view into equivalently sized, subregional tiles (Fig. 4e), we observed more consistent propagation direction within single subregions (Fig. 4f). When we plot the cumulative count of the percentage of bursts with regions that propagate in the same direction, we indeed observe that this curve is right-shifted compared to a simulated random assignment of majority regional propagation direction (Fig. 4g), suggesting regularity in the propagation pattern within bursts that only becomes apparent at larger spatial scales. Thus, we next explored whole imaging field dynamics during Ca²⁺ bursts. The percentage of the active field-of-view varied across burst periods (Fig. 4b), with a wide variability from few to hundreds of events (Fig. 4h). To control for number and size of events, we used the difference between each event’s onset time to calculate a single burst-wide propagation direction (Fig. 4h, black arrow). Doing so revealed a consistent posterior-medial directionality of population Ca²⁺ activity (Fig. 4i). Although Ca²⁺ bursts have been previously observed using GCaMP6 imaging in awake mice^4,5, consistent spatial directionality with respect to the underlying anatomy has never been described. This observed posterior-medial directionality may be revealing anatomical and physiological underpinnings of these bursts, and since they have been shown to be at least partly mediated by norepinephrine^5,7, they could be reflective of responses to incoming adrenergic axons originating in locus coeruleus. Regardless of mechanism(s), these results suggest that in vivo, astrocytic Ca²⁺ propagation dynamics differ depending on the spatial scale examined, which may explain previously described discrepancies.

AQuA-based analysis of extracellular neurotransmitter fluorescence dynamics

We next asked whether AQuA could be used to detect other spatiotemporally complex fluorescent dynamics distinct from astrocytic Ca²⁺. We decided to image extracellular-facing neurotransmitter probes, including GluSnFR^2,6,8 since astrocytes regulate extracellular glutamate. GluSnFR dynamics are much faster than GCaMP dynamics, causing detection to be very susceptible to low SNR. This can be an additional challenge and many previous GluSnFR analyses have relied on averaging across multiple trials. While GluSnFR has been expressed both in astrocytes and in neurons previously^2,8,16,28, how cell type-specific expression and morphology determines its fluorescent dynamics has not been fully explored^16,28. Likewise, no previously applied analytical tools have been reported to automatically detect GluSnFR or other neurotransmitter events to accommodate different event sizes and shapes. Here, we explored whether application of AQuA could be used to detect cell type-specific differences in glutamate dynamics that may be based on heterogeneous underlying morphologies and cell biological mechanisms.

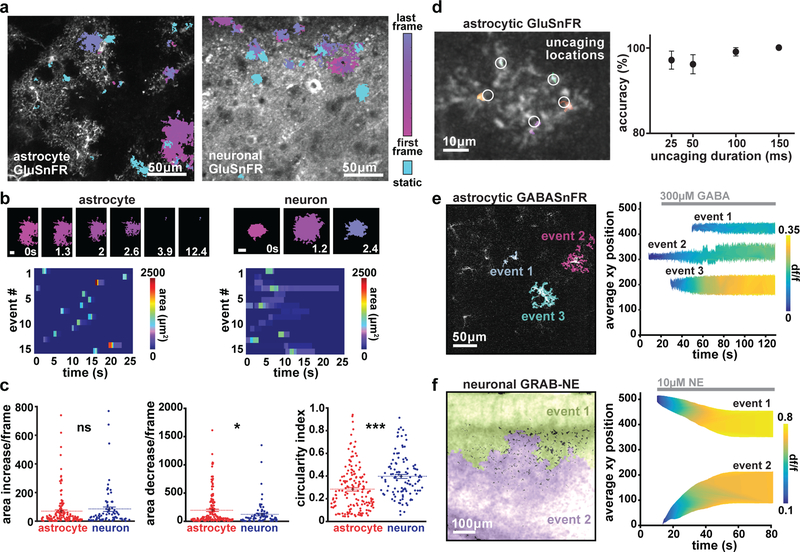
We expressed GluSnFR in either astrocytes or neurons using cell type-specific viruses² and carried out 2P imaging of spontaneous GluSnFR activity in acute cortical V1 slices. Distinct morphological differences between astrocytic and neuronal expression of GluSnFR were evident, as observed previously^8,29,30 (Fig. 5a). We applied AQuA to these datasets to detect significant fluorescent increases, and were able to detect events that were too small and fast to detect by eye (Video 3); AQuA-detected events were confirmed by post hoc ROI-based analysis. 62% of astrocytic events had an area less than the size of a single astrocyte, and 8% of astrocytic and 35% of neuronal glutamate events had a small maximum dF/F (less than 0.5). Because GluSnFR events have previously been detected by spatial averaging or by manual detection, many AQuA-detected event are most likely missed by ROI-based methods^6,8,16 (Supp. Fig. 11). Because AQuA detects events independently from shape or size, events of heterogeneous size and shape were revealed during this analysis (Fig. 5a–b). A large proportion of these spontaneous GluSnFR events changed size over the course of the event, with 42% of total astrocytic and 32% of total neuronal glutamate events exhibiting area changes. On average, astrocytic GluSnFR events were significantly larger (274 ± 39.56 μm²) than neuronal events (172 ± 57.06 μm²), sometimes encompassing an entire astrocyte (Supp. Fig. 11). Neuronal GluSnFR events were significantly more circular (Figure 5b–d), perhaps reflecting morphological differences between cell types. Between cell types, GluSnFR events also exhibited different size dynamics (Fig. 5b–c). We also observed that the rate of size decrease of astrocytic events between frames was larger than that of neuronal events (Fig. 5c), which may reflect differential synaptic and extrasynaptic glutamate dynamics in proximity to subcellular compartments of each cell type.

Figure 5. AQuA-based detection of extracellular dynamics via astrocytic and neuronal expression of genetically encoded neurotransmitter sensors.

(a) Representative images of ex vivo slices with expression of astrocytic (left) or neuronal (right) GluSnFR. Color indicates detected events. Those with dynamic shape are shown in magenta, and static events in cyan. (b) Examples of timecourse of astrocytic (left, top) and neuronal (right, top) glutamate events. Scale bar = 10μm. Raster plot of astrocytic (left, bottom) and neuronal (right, bottom) glutamate event area. (c) Size dynamics (area increase [left] and decrease [middle] per frame) and shape (circularity index, right) of glutamate events when GluSnFR is expressed on astrocytes (red) or neurons (blue). (n=3 slices for each cell type, comparison using two-tailed t-test with mean displayed as center, p=0.414(left), 0.0297(middle), 4.26e-6(right)) (d) Left: Single astrocyte expressing GluSnFR, with AQuA-detected events (colors) with ~100Hz frame rate imaging and 25–150ms uncaging of RuBi-glutamate. Uncaging locations marked with white circles. Right: Percent correct events detected by AQuA, as a function of laser uncaging pulse duration. (n=5 cells, mean ± s.e.m.) (e) Example of three AQuA-detected events at single timepoint (97s) after addition of 300μM GABA to slice with astrocytes expressing GABASnFR (left). Right: Detected events before and after addition of 300μM GABA (gray bar) to circulating bath. Events are plotted to display spatial position in imaging field (y-axis), event area (height), and gradually increasing amplitude (color) over time. (n=1 slice) (f) Left: two detected events in cortical slice expressing GRAB-NE in neurons after addition of 10μM NE. Right: Events plotted to display spatial position (y-axis), event area (height), and amplitude (color) dynamics over the course of the experiment. In (e) and (f), average xy position at each timepoint is calculated using the following equation: (((xLoc-1)*frameSize) + yLoc)/frameSize. (n=1 slice)

After showing that AQuA-based detection was effective for quantification of spontaneous GluSnFR activity, we tested its performance on fast, evoked glutamate events, since GluSnFR is used to measure synaptic glutamate release at fast acquisition rates^2,31. To do this, we performed fast (~100Hz) GluSnFR imaging while photoactivating a caged glutamate compound (RuBi-glutamate^10,32) with a second laser beam. In these experiments, we uncaged glutamate for varying durations (25–150ms), and applied AQuA to detect these small-scale, fast events (Fig. 5d, right). AQuA detection showed high accuracy levels across all uncaging durations, with a minimum of 96% average accuracy across durations (Fig. 5d, right; n=5 cells, 3 replicates/cell), indicateing that AQuA works well for event detection at fast frame rates.

We lastly tested whether AQuA can be used with other probes relevant for astrocyte-neuron physiology by imaging two recently developed genetically encoded probes that report extracellular neurotransmitter dynamics: GABASnFR¹¹ and GRAB-NE¹². We expressed GABASnFR (Fig. 5e, left) in cortical astrocytes and GRAB-NE in cortical neurons (Fig 5f, left), and performed ex vivo imaging with bath application of either GABA or NE. For GABASnFR expression in individual astrocytes, AQuA-detected events increased in amplitude and area with cell-specific dynamics (Fig. 5e, right). The widespread neuronal expression of GRAB-NE allowed us to detect the location, amplitude, and area of NE waves as they progressed across the slice (Fig 5f, right), indicating that AQuA may be useful to quantify propagating wavefronts in other contexts. Together, these results suggest that AQuA-based detection can be used to quantify dynamics of extracellular molecules at a range of speeds and spatial spreads, across multiple cell types and expression patterns.

Discussion

With the development of an event-based analysis tool, we have enabled accurate quantification of fluorescence dynamics that are un-fixed, propagative, and size varying. Here, we demonstrate that AQuA performs better than other image analysis methods on simulated datasets, and describe event detection using several genetically encoded indicators. AQuA can also be applied to datasets not directly tested here, including those captured under different magnifications and spatial resolutions, as well as under confocal or wide-field imaging. Since AQuA functions independently from frame rate, datasets captured faster or slower^17,25 are also amenable to an AQuA-based analysis. Further, AQuA is applicable to fluorescent indicators other than the ones tested here, particularly those that exhibit complex dynamics.

We envision the AQuA software as enabling problem-solving for a wide range of astrocyte physiological questions, because it accurately captures dynamics exhibited by commonly used fluorescent indicators. Since AQuA-specific features captured observed heterogeneities among single cells, these features may be more physiologically relevant than the standard measurements (amplitude, frequency, duration) used to describe astrocytic physiology. Beyond baseline differences, we expect that AQuA will be a powerful tool to quantify physiological effects of pharmacological, genetic, and optogenetic manipulations.

Significant disagreement about basic physiological functions of astrocytes remains. One outstanding issue is whether astrocytes release transmitters such as glutamate. While we don’t address this topic here, we expect that the heterogeneous activities uncovered using in-depth GluSnFR analysis may be key in determining different sources of glutamate under different conditions, and could help untangle conflicting data. AQuA here may be particularly useful in this regard as next-generation GluSnFR variants become available and make multiplexed imaging experiments increasingly accessible³¹. Astrocyte Ca²⁺ imaging data can largely be grouped into two categories: single-cell imaging and population-wide imaging focusing of many cells. Experimental data and neurobiological conclusions from these two groups can differ quite widely. This may be due, in part, to population-wide bursts observed with locomotion onset in vivo. Many ROI-based techniques used to analyze these bursts can under-sample inter-burst events by swamping out smaller or shorter signals. Our technique can sample small- and large-scale activity in the same dataset and may aid researchers in resolving outstanding physiological problems.

As demonstrated by its utility with Ca²⁺, glutamate, GABA, and NE datasets, AQuA can now be applied to many other fluorescence imaging datasets that exhibit non-static or propagative activity, particularly since it is open-source and user-tunable. For example, recently described Ca²⁺ dynamics in oligodendrocytes display some similar properties to astrocyte Ca^2+33,34. Likewise, subcellular neuronal compartments, such as dendrites or dendritic spines can exhibit propagative, wave-like Ca²⁺ signals³⁵ while whole-brain neuronal imaging can capture burst-like, population-wide events³⁶.

We predict that the potential applications of AQuA are wide, but AQuA also has limitations. Since it detects local fluorescence increases, AQuA is not well suited to analyze morphological dynamics, such as those observed in microglia, and it does not improve on tools built for analyzing somatic neuronal Ca^2+20,21, where ROI assumptions are well satisfied. In addition, AQuA was optimized for 2D datasets, as these comprise the majority of current astrocyte imaging experiments. As techniques for volumetric imaging advance, an extension to accommodate 3D imaging experiments will be necessary. AQuA is expandable to 3D datasets since the algorithmic design is not restricted to 2D assumptions. A full 3D AQuA version is beyond the scope of this paper, but a 3D prototype performed well on simulated 3D data based on published¹⁷ astrocytes (Supp. Fig. 12). These results suggest that a full 3D version will work on real volumetric datasets in the future and demonstrate that AQuA is a flexible and robust platform that can accommodate new data types without large changes to the underlying algorithm.

Methods

Viral injections and surgical procedures

All procedures were carried out in accordance with protocols approved by the UCSF Institutional Animal Care and Use Committee. For slice experiments, neonatal mice (Swiss Webster, P0–P4) were anesthetized by crushed ice anesthesia for 3 minutes and injected with 90nL total virus of AAV5-GFaABC1D.Lck-GCaMP6f, AAV5-GFaABC1D.cyto-GCaMP6f, AAV1-GFAP-iGluSnFR, AAV1-hsyn-iGluSnFR, AAV2-GFAP-iGABASnFR.F102G, and AAV9-hsyn-NE2.1 at a rate of 2–3nL/sec. Six injections 0.5μm apart in a 2×3 grid pattern with 15nL/injection into assumed V1 were performed 0.2μm below pial surface using a UMP-3 microsyringe pump (World Precision Instruments). Mice were used for slice imaging experiments at P10–23.

For in vivo experiments, adult mice (C57Bl/6, P50–100) were given dexamethasone (5mg/kg) subcutaneously prior to surgery and then anesthetized under isoflurane. A titanium headplate was attached to the skull using C&B Metabond (Parkell) and a 3mm diameter craniotomy was cut over the right hemisphere ensuring access to visual cortex. Two 300nL injections (600nL total virus) of AAV5-GFaABC1D.cyto-GCaMP6f were made into visual cortex (0.5–1.0mm anterior and 1.75–2.5mm lateral of bregma) at a depth of 0.2–0.3mm and 0.5mm from the pial surface, respectively. Virus was injected at a rate of 2nL/s, with a 10min wait following each injection to allow for diffusion. Following viral injection, a glass cranial window was implanted to allow for chronic imaging and secured using C&B metabond³⁷. Mice were given at least ten days to recover, followed by habituation for three days to head fixation on a circular treadmill, prior to imaging.

Two-photon imaging

All 2P imaging experiments were carried out on a microscope (Bruker Ultima IV) equipped with a Ti:Sa laser (MaiTai, SpectraPhysics). The laser beam was intensity-modulated using a Pockels cell (Conoptics) and scanned with linear or resonant galvonometers. Images were acquired with a 16x, 0.8 N.A. (Nikon, in vivo GCaMP and ex vivo GRAB-NE) or 40x, 0.8. N.A. objective (Nikon, ex vivo GCaMP, GluSnFR, and GABASnFR) via a photomultiplier tube (Hamamatsu) using PrairieView (Bruker) software. For imaging, 950nm (GCaMP), 910nm (GluSnFR and GABASnFR), or 920nm (GRAB-NE) excitation and a 515/30 emission filter was used.

Ex vivo imaging

Coronal, acute neocortical slices (400μm thick) from P10–P23 mice were cut with a vibratome (VT 1200, Leica) in ice-cold cutting solution (in mM): 27 NaHCO₃, 1.5 NaH₂PO₄, 222 sucrose, 2.6 KCl, 2 MgSO₄, 2 CaCl₂. Slices were incubated in standard continuously aerated (95% O₂/5% CO₂) artificial cerebrospinal fluid (ACSF) containing (in mM): 123 NaCl, 26 NaHCO₃, 1 NaH₂PO₄, 10 dextrose, 3 KCl, 2 CaCl₂, 2 MgSO₄, heated to 37°C and removed from water bath immediately before introducing slices. Slices were held in ACSF at room temperature until imaging. Experiments were performed in continuously aerated, standard ACSF. 2P scanning for all probes was carried out at 512×512 pixel resolution. Acquisition frame rates were 1.1Hz (GCaMP), 4–100Hz (GluSnFR), 6Hz (GABASnFR), and 1.4Hz (GRAB-NE). For GluSnFR imaging and RuBi-glutamate uncaging experiments, GluSnFR imaging was performed at 950nm excitation to ensure that no RuBi-glutamate was released during scanning. Acquisition rates were between 95–100Hz, using resonant galvonometers. 300μM RuBi-glutamate was added to the circulating ACSF and using a second MaiTai laser tuned to 800nm, five uncaging points were successively uncaged at each cell at durations indicated in the figure and at power <3mW that were shown in control experiments to cause no direct cell activation.

In vivo GCaMP imaging

At least two weeks following surgery mice were head-fixed to a circular treadmill and astrocyte calcium activity was visualized at ~2Hz effective frame rate from layers 2/3 of visual cortex with a 512×512 pixel resolution at 0.8 microns/pixel. Locomotion speed was monitored using an optoswitch (Newark Element 14) connected to an Arduino.

AQuA algorithm and event detection

Overview of the AQuA algorithm

Astrocytic events are heterogeneous and varying with respect to many aspects of their properties. In AQuA, we extensively applied machine learning techniques to flexibly model these events, so that our approach is data-driven and physiologically relevant parameters are extracted from the data instead of imposing a priori assumptions. Probability theory and numerical optimization techniques were applied to optimally extract fluorescent signals from background fluctuations. Here, we delineate the eight major steps in AQuA (Supp. Fig. 1), discuss motivations behind the algorithm design, and describe key technical considerations in further detail.

Step 1: data normalization and preprocessing. This step removes experimental artifacts such as motion effects, and processes the data so that noise can be well approximated by a standard Gaussian distribution. Particular attention is paid to the variance stabilization, estimate of baseline fluorescence, and variance. Step 2: detect active voxels. Step 3: identify seeds for peak detection. Step 4: detect peaks and their spatiotemporal extension. These three steps work together to achieve peak detection. To detect peaks we start from a seed, which is modeled as a spatiotemporal local maximum. However, since random fluctuations due to background noise can also result in local maxima, we need to detect active voxels such that only the local maxima on the active voxels are considered as seeds. Here, active voxels are those likely to have signals. Step 5: cluster peaks to identify candidates for super-events. Temporarily ignoring the single-source requirement, the set of spatially-adjacent and temporally-close peaks is defined as a super-event. However, clustering results of spatially adjacent peaks are not super-events themselves, because a peak group may consist of noise voxels and temporally distant events. Step 6: estimate the signal propagation patterns. Step 7: Detect super-events. To get super-events from peak clusters, we compute the temporal closeness between spatially adjacent peaks by estimating signal propagation patterns. The propagation pattern for each event is also important for its own sake, by providing a new way to quantify activity patterns. Step 8: split super-event into individual events with different sources. A super-event is split into individual events by further exploiting propagation patterns. Based on propagation patterns within a super-event, the locations of event initiation are identified as local minima of the onset time map. Each initiation location serves as the event seed. Individual events are obtained by assigning each pixel to an event based on spatial connectivity and temporal similarity.

Step 1(Data normalization and preprocessing):

We correct for motion artifacts in the in vivo dataset using standard image registration techniques before applying AQuA. However, AQuA does not necessarily require motion correction because it performs event-based analysis, which is localized temporally and thus less prone to motion artifacts.

We perform data normalization and preprocessing to approximate noise by a Gaussian distribution with mean=0 and standard deviation=1. For those who want to directly modify our code, pseudocode is available (Supp. Table 1). To achieve this normalization, we first apply a square-root transformation to the data to ensure that the noise variance after transformation is not related to the intensity itself, an operation also known as variance stabilization. Variance stabilization is important so that events with bright signals are not over-emphasized and events with dim signals not neglected. Next, the noise variance of the transformed data for each pixel is estimated as half of the median of the square of differences between two adjacent values in the time series at the pixel. Mathematically, denote X_i the time series at the ith pixel, where X_i[t] is the value of the tth time point. Then, the noise variance ${\sigma }_i^2$ at the ith pixel is estimated as

$${\sigma }_i^2=\frac{1}{2}{\text{median}}_{t\text{=2,}\mathrm{\dots }\text{,T}}\left\{{\left(X_i\left[t\right]-X_i\left[t-1\right]\right)}^2\right\}.$$

We do not use the conventional sample variance $\frac{1}{T}{{\sum }_{t=1}^T\left(X_i\left[t\right]-\text{mean}\left(X_i\right)\right)}^2$ as the estimate, which tends to inflate the variance when signals exist in the time series. Third, to estimate the baseline fluorescence F₀ for each pixel, we compute the minimum of the moving average of 25 time-points in a user-specified local time window (default=200 in our experiments). We do not use the full time series to identify the minimum, in order to be robust to image degradation or other long-term trends. Considering the minimum is a biased estimate of the baseline fluorescence, we add a pre-determined quantity to the minimum to serve as the estimate of F₀. Here, the pre-determined quantity depends on the extent of the moving average and the size of the time window, and is found through simulation. Denote V_i[t] as the value of ith pixel at the tth frame in the raw video data. In the following, all modeling is performed on the normalized data,

$$Z_i\left[t\right]=\frac{\sqrt{V_i\left[t\right]}-\sqrt{F_{i0}}}{{\sigma }_i},$$

where the subscript i denotes that the baseline fluorescence and noise variance are location- and pixel-specific. It is worth noting that the data normalization and preprocessing is used to build an accurate statistical model so that signals can be reliably distinguished from noise. When we extract activity-related features such as rise and decay time, raw data is used.

Step 2 (Detecting active voxels):

A voxel is defined as a pixel of a certain frame. For example, voxel (x, y, t) denotes the pixel at location (x, y) in the tth frame in the movie. An active voxel is the voxel that contains an activity signal. If a voxel is not associated with any event, it is not considered active. Since an event often occupies multiple pixels and extends several frames, we first apply 3D Gaussian filtering to smooth the data to reduce the impact of noise. Then, we calculate the z-scores for each voxel in the smoothed data. Here, z-score is computed as the value of the voxel divided by its standard deviation, which can be estimated as in the normalization procedure above, but now on the smoothed data. All voxels that have z-scores larger than a given threshold are considered tentative active voxels. A liberal threshold is used here to retain most signals, often at a z-score of 3. We next calculate the size of groups of connected tentative active voxels, with spatially connected tentative active belonging to the same group and a minimum size threshold (often 4). If a group of tentative active voxels is less than the threshold, all voxels in this group are removed, resulting in a final list of active voxels. Pseudocode is presented in Supp. Table 1.

Our event detection can be roughly described as finding bumps in space-time, and it could be asked why we don’t simply set a threshold on the ΔF data and identify all components larger than the threshold as events. This method is essentially equivalent to our Step 2 (Detecting active voxels), but there are motivations to go beyond this step. Even if simple thresholding detected individual events perfectly, many features of each event—such as propagation patterns—cannot be directly derived. More importantly, no threshold we have found can faithfully detect real events (Supp. Fig. 3). Three types of commonly observed complexities lead to this insufficiency in thresholding (Supp. Fig 3b). First, not all pixels drop below the threshold because of residual signals. Second, neighboring events occurring at different times can be spatiotemporally connected. Third, two events can be temporally separated when they appear, but meet with each other after propagation.

Step 3 (Identifying seeds for peak detection):

Similar to the detection of active voxels, we apply 3D Gaussian smoothing to the normalized data and then find all local maxima, defined as connected components of pixels with a constant intensity value and with all neighboring pixels having a lower value. Considering our time-lapse images as three-dimensional arrays (2D space plus 1D time), each single pixel has 26 neighbors. Although each local maximum generally occupies one pixel due to random fluctuation inherent in the data, this definition allows a local maximum to occupy multiple pixels of the same intensity value. This is helpful for the case in which some pixels have saturated values. Because pure random fluctuation can also lead to local maxima, we restrict the search of local maxima to active voxels only (see pseudocode in Supp. Table 1). The resultant local maxima are considered seeds for the purpose of peak detection, the subsequent step in the algorithm. We start peak detection by identifying the local maxima as seeds because the maxima are likely to contain the strongest signal and thus have a better SNR than other points. The 3D Gaussian smoothing is used to further improve SNR, motivated by the fact that an event occupies multiple pixels and spans multiple time points.

Step 4 (Detecting peaks and their spatiotemporal extent):

We partially and temporally extend each seed detected above to all voxels that are potentially associated with each event. We call the collection of the seed and its extended voxels the super voxel. Seeds are processed one-by-one, with higher intensity seeds processed first. Each seed is first extended temporally, then spatially.

The spatiotemporal index (x₀, y₀, t₀) denotes the seed. When we temporally extend the seed backwards and forwards (Supp. Fig 2b, Supp. Table 2), we encounter two main scenarios. In the first, a voxel before (x₀, y₀, t₀) has a value close to the baseline F₀, and a voxel after (x₀, y₀, t₀) also is close to F₀. If a voxel has an intensity <20% of the seed value, it is defined as close to baseline. In this scenario, the seed is extended temporally until it reaches these two voxels. In the second scenario, extension in at least one of two directions never meets a voxel with value that is considered close to the baseline before meeting another seed. This scenario could happen when one event begins before the previous event drops completely to the baseline fluorescence level. To determine whether these two seeds should be merged and thus belong to the same event, we denote V_min the minimum value between the two seeds and calculate the difference between V_min and value at the seed (x₀, y₀, t₀). If the difference is larger than the threshold Δ_tw, which is 2σ₀ by default for most data, the minimum is considered the end of the extension. Otherwise, these two seeds are merged and the extension continues. For very high peaks, this threshold is too low for perceptually meaningful separation. To split two adjacent high ΔF peaks, a strong decrease between them is needed and the threshold is changed to Δ_tw = max(0.3ΔF(x, y, t₀), 2σ₀).

Once each seed i is temporally extended from (x_i, y_i, t_i) to a peak (x_i, y_i, (t_i − a_i): (t_i + b_i)), (t_i − a_i): (t_i + b_i) denotes a time window spanning from t_i − a_i to t_i + b_i. We define reference curve c_i as the average of nine pixels around (x_i, y_i) in that time window. To spatially extend each peak to cover most signals-of-interest, each seed becomes a set of voxels ${\text{∪}}_{k=1}^K\left(x_{ik},y_{ik},\left(t_i-a_i\right):\left(t_i+b_i\right)\right)$ after extension, where the corresponding spatial footprint, K pixels {(x_ik, y_ik), k = 1 … K}, is spatially connected. During this process, each seed is associated with two sets. The first is Ω_i, which are pixels already associated with seed i. Each pixel in this set, (x_i1, y_i1), e. g., corresponds to a set of voxels: (x_i1, y_i1, t_i – a_i: t_i + b_i). The second set is Θ_i, the set of pixels to avoid. Initially, Ω_i = {(x_i, y_i)} and Θ_i is empty.

The spatial extension operation for each seed is repeated a maximum of 40 rounds. For each seed, the set Ω_i is spatially dilated with a 3×3 square, thus only testing pixels adjacent to the Ω_i boundary. Next, Θ_i is removed from the dilated region. We then test whether each new pixel should be added to Ω_i or not. Because for each given new pixel and each time window we have a time series, we can calculate the Pearson correlation coefficient between this time series and c_i. The correlation coefficient is converted to a z-score using the Fisher transform. If the z-score is higher than the user-defined given threshold, the pixel is added to Ω_i. Otherwise, it is added to Θ_i. Because all seeds are local maxima, no time alignment is needed here.

During the extension process, different super voxels can meet. We want to stop the extension process of one super voxel only when it meets the bright part of other super voxels (50% rising to 50% decaying). For example, we have two peaks from two seeds: (x₁, y₁, (t₁ – a₁): (t₁ + b₁)) and (x₂, y₂, (t₂ – a₂): (t₂ + b₂)). Assume the first seed has already occupied pixel (x₃, y₃). When the second seed tries to determine whether it should extend to (x₃, y₃) or not, we calculate whether (t₁ – a₁: t₁ + b₁) and (t₂ – a₂: t₂ + b₂) sufficiently overlap. Two peaks sufficient overlap if the 50% rising to 50% decay ranges of the two peaks overlap. Thus, if (t₁ – a₁: t₁ + b₁) and (t₂ – a₂: t₂ + b₂) sufficiently overlap, seed two will not include pixel (x₃, y₃) and it is added to Θ₂. Otherwise, it is added to Ω₂. After spatial extension is complete, we remove super voxels with Ω_i < 4 pixels or total voxels < 8 pixels.

Step 5 (Clustering peaks to identify candidates for super-events):

A super-event is defined as a group of events connected spatially but originating from different initiation locations. This step was motivated by the frequent observation in real data that multiple events can be spatially connected at some time point. One example is a large burst in the in vivo dataset, where multiple events start at different places but merge as a burst at later stage. Another example is a set of two events originating from different places, propagating and meeting each other in the middle (Supp. Fig. 3). Thus, in a spatial direction, we may encounter multiple events within the super-event. However, we never encounter two or more events in the temporal direction, which guides the following algorithm. To identify candidates for super-events, we next cluster peaks, but these results are not identical to super-events, because voxels extended to be associated with the peak may have some errors. As discussed below, the candidate super-event must be purified to resolve the final super-event.

Since each super-voxel extends from its seed (representative peak), we also call the process of clustering super-voxels as clustering peaks for conceptual convenience. If two super-voxels are connected and their rise-time difference is less than a given threshold (as discussed below), they are considered neighbors. For two super-voxels, if 10% of pixels of either super-voxel is also occupied by the other, they are a conflicting pair. For each super-voxel, we list all its neighbors and conflicting counterparts. To cluster peaks/super-voxels (Supp. Fig. 2b, Supp. Table 3), we begin with the earliest occurring super-voxel and check each of its neighbors. If a neighbor is not conflicting with that super-voxel, it is combined with the super-voxel. This process is repeated until no new super-voxel can be added. Then we move to the next earliest super-voxel that is not added to any others, and repeat this process. An iterative approach prioritizes events that are close to each other. Supposing the largest rising time difference for super-voxels that is allowed to be neighbors is 10, we start the procedure with the allowed difference as 0 and merge the super voxels. Then we increment the allowed difference by 1 and repeat the step above, until the rising time difference allowed reaches 10.

Step 6 (Estimating signal propagation patterns):

For each spatial location/pixel, an associated time series indicates the signal dynamics. Estimation of propagation patterns is formulated as a mathematical problem of time alignment between the time series at each location and a representative/reference time series. Time alignment results directly relay the delay of a given pixel at a time frame with respect to the representative dynamics. Conventionally, time alignment is accomplished by dynamic time warping (DTW). However, DTW is notoriously prone to noise, which leads to unreliable propagation estimation. Since two adjacent pixels have more similar propagation patterns than two distant pixels, we impose a smoothness constraint on neighboring pixels using our recently developed mathematical model—Graphical Time Warping (GTW)—to explicitly incorporate this constraint. However, since we do not have a representative time series at the very beginning, our strategy is to guess a reference time series from the data and align time series at each pixel to this reference. Then, we use alignment results to obtain an updated reference, and iterate the process of alignment and update of reference until it converges (Supp. Fig. 2b, Supp. Table 3).

To initialize the reference time series, we search for the voxel with the largest ΔF/F value and record that voxel’s location. The initial reference is then estimated as the average time series of the pixels in the 5×5 square around that location, with the square size a user-tunable parameter. The voxel with the largest ΔF/F value is used because it has the best signal-to-noise ratio. We do not use the time series at a single pixel to initiate the reference because it is noisy, nor do we use the average time series over all the pixels, because the average would be a large distortion to the representative dynamics due to signal propagation. Next, we supply the neighborhood graph and the reference time series to GTW to calculate the time alignment between all pixels and the reference. For each pixel, we consider the 8 pixels around the 3×3 grid as neighbors. A GTW parameter controls the balance between fitness and smoothness of the alignment. We empirically found 1 to be a good value. To control computational complexity, GTW has another parameter corresponding to the maximum time delay allowed. In all our experiments, we found no time delay induced by propagation is larger than 11 frames. So, we set that parameter to 11.

Step 7 (Detecting super-events):

Once the time alignment between the representative dynamics and the time series at each pixel is obtained, we refine candidate super-events to obtain final super-events. A super-event is defined as detected when the representative dynamics and all voxels are associated with the super-event. Since each voxel is jointly specified by spatial location and time frame, we next determine which pixels and time frames jointly belong to the super-event. Since representative dynamics are already obtained in the previous step of propagation estimation, here we focus on how to determine which pixels and which time frames are covered by the super-event.

Because each pixel corresponds to a time series, if a pixel belongs to a super-event, its time series should be highly correlated to the representative dynamics of the super-event. Note that the correlation is calculated based on the aligned time series to account for the time distortion due to signal propagation. Thus, we first obtain a new time series for each pixel based on the time alignment obtained previously. Then, we calculate the Pearson correlation between each new time series and the representative dynamics, leading to a correlation map. We further convert the Pearson correlation to z-score using Fisher’s transform. Here, we do not use a threshold for each z-score to determine whether that pixel is statistically significantly associated with the super-event because that ignores the neighborhood information in the correlation map and is less statistically powerful. Instead, incorporating the information from the neighboring pixels, we apply our recently developed order-statistics-based region-growing method to determine which pixels should be associated with the super-event (Supp. Fig. 2b, Supp. Table 3).

To determine which time frames are associated with the super-event, we now examine the representative time series, calculating the maximum intensity along the curve and considering all time frames with intensity >10% of the maximum to be associated with the super-event. Different pixels may have different time frames associated with the super-event. We use the time alignment results above to identify the time frames associated with the super-event for each pixel. A time frame at a given pixel is associated with the super-event as long as its corresponding time frame in the representative curve is associated with the super-event.

Step 8 (Splitting super-events into individual events with different sources):

For each super-event, we have a 2D map of rise-time for each pixel by re-aligning the super-event using GTW. The local minima in this map are potential originating locations for events in this super-event. However, noise may produce random local minima, which do not correspond to true originating locations and are removed by merging with spatially adjacent local minima. We use rise-time to determine whether two local minima should be merged. This idea can be illustrated with the following 1D example: [1 2 4 2 2]. The two local minima are the first and the last pixel (pixel i and j, respectively), occurring at time 1 (t₀) and 2 (t₁), respectively. To determine whether they should be merged, we find all paths connecting them. In this example, there is only one path and the pixel with the latest rise-time in this path is the third pixel (rise-time=4 (t_m)). The distance between pixel i and pixel j induced by this path is therefore defined as max(t_m – t₀, t_m – t₁). If the distance induced by any path is less than the given threshold, these two local minima are merged.

We next separate super-events into individual events by simultaneously extending all remaining local minima. Each remaining local minimum corresponds to one event. Pixels attached to a local minimum are defined as growing. With each iteration, we add the earliest-occurring pixel to a growing event. If the pixel under examination is adjacent to a growing event, it is done, and then we find the next earliest occurring pixels. Otherwise, we add it to the waitlist and continue with the next earliest occurring one. Each time a pixel is successfully added to a growing event, pixels in the waitlist are checked as to whether they can be added to growing events. When the growing process ends, all individual events are obtained. (see pseudocode in Supp. Table 3).

Run-time analysis of AQuA algorithm:

In our implementation, ~ 60–70% of the total running time is spent on propagation estimation, and super-event detection and splitting. The super voxel detection step takes about 15% of the total time. Another 7% extracts features from each detected event. The event cleaning and post-processing takes ~6% of the total time, while it takes <1% of the time to load the data and <2% in the active voxel step, which finds baseline, estimates noise, and gets seeds. Tested on a desktop computer with Intel Xeon E5–2630 CPU and 128 GB memory using Windows and MATLAB version R2018b, the total running time ranges from several minutes to 1.5 hours, depending on file size and data complexity (Supp. Table 4).

Generation of simulation data sets

Spatial footprint templates:

We built a set of templates for event footprints from real ex vivo data which serve as the basis for the ROI maps in the subsequent step. Footprints are processed by morphology closing, hole filling, and morphology opening to clean boundaries, with 1683 templates generated total.

ROI maps:

2D ROI maps generated from spatial footprint are used to generate events in subsequent steps. Different simulation types have a different preference for the size of the ROIs. Maximum number of ROIs is set at 100; ROIs are randomly chosen and placed onto a 2D map <5 pixels from existing ROIs.

Simulation dataset 1 (size-varying events):

To simulate event size changes, we generate events for each ROI and then alter them to have different sizes so that each ROI in the 2D map will be related to multiple events whose centers are inside that ROI, but whose sizes are different. The degree of size change is characterized by the odds ratio (maximum = 5) between the maximum and the minimum allowable sizes of the events associated with that ROI. For example, with an odds ratio of 2, the size of the event will range from 50–200% of the ROI area. The chances for the event size to be larger or smaller than the area of the ROI are the same. To achieve this, we generate a random number between 1 and 2, then randomly assign whether to enlarge size by multiplying or shrink by dividing by this factor. Event duration is four frames.

To determine the frames at which the event occurs, we first put the event 10–30 frames (randomly) after the ROI occurs. Spatial distance of this event from others must be ≥3 pixels and temporal distance ≥4 frames. Part of the event may be inside the spatial footprint of other ROIs, as long as its spatiotemporal distance to other events is larger than the threshold set above. Events are generated for each ROI; on average, we simulate 250 frames with 800 events on 90 ROIs.

Simulation dataset 2 (location-changing events):

To simulate event location changes, we generate events with the same size for each ROI and shift them to nearby locations. Thus, each ROI (450–550 pixel size) is related to multiple events near to that ROI. Denote dist the distance between the event center and the ROI center. Denote diam the diameter of the ROI. The degree of location change is quantified by the ratio between dist and diam. For example, if we set 0.5 as the maximum degree of location change, the distance of the center of a new event to the ROI will be 0–0.5 times the diameter of the ROI. If the ratio is 0, we simulate a pure ROI dataset. The new event may be located any direction from the ROI, randomly picked from 0–2π. Shapes of new events are randomly picked from the templates, so may be different from the ROI while size is constant. Event duration is four frames, and the remaining steps are the same as above. On average, we simulate 250 frames with 800 events on 90 ROIs.

Simulation dataset 3 (propagating events):

We simulated two types of propagation: growing and moving, leading to three types of synthetic datasets: growing only, moving only, and mixed. These three types are generated similarly. The ROI map is generated as above, and ROI sizes are 4,000–10,000 pixels, with events generated inside each ROI. In comparison, events in the size-change and location-change simulations can be (fully or partially) outside their corresponding ROIs. We simulate only one seed (starting propagation point) in each ROI. For each event, we generate a rise-time map (for each pixel in the ROI) and construct event-propagation based on the map. We obtain this map by simulating a growing process starting from the seed pixel, with the seed pixel active at the first time-point. At the next time point, its neighboring pixels are active with a variable success probability. Growth continues until ≥90% of pixels in the ROI are included in the event. Based on the rise-time map, we identify frames at which pixels become active in the event. To determine when the event ends, we treat growing and moving propagation differently. In growing propagation, all pixels are inactive simultaneously 2 frames after the last pixel becomes active. For moving propagation, the duration is 5 frames. Typically, we generate approximately 140 events in 14 ROIs for each synthetic dataset.

Simulate various SNRs:

Gaussian noise is added to the synthetic data to achieve various SNRs. We define the signal intensity as the average of all active pixels in all frames. SNR is defined as

$$20\times {\text{log}}_{10}\frac{\text{average signal intensity}}{\text{noise standard deviation}}.$$

When we change the degree of location change, size change, and propagation duration, we add noise with 10 dB SNR. To study the impact of SNR on size changes, size-change degree is 3. For location changes, distance-change ratio is 0.5 while varying SNRs. For propagation, propagation duration is 5 frames. Seven SNRs are tested: 0, 2.5, 5, 7.5, 10, 15, 20 (all in dB).

Post-processing simulated data:

We set the average signal intensity at 0.2, with a range from 0–1. Synthetic data is spatially filtered to mimic blurred boundaries in real data. The smoothing is performed with a Gaussian filter with a standard deviation of 1. Signals with intensity <0.05 after smoothing are removed. Remaining signals are temporally filtered with a kernel with a decay τ of 0.6 frames. The rising kernel is linear. For propagation simulation, data is down-sampled by five. Next, we perform a cleaning step. For each pixel in each event, we find the highest intensity (x_peak) across frames. For that pixel, we set signals that are <0.2 times of x_peak to 0. Finally, a uniform background intensity of 0.2 is added (except for GECI-quant, where no background is added; see below).

Application of AQuA and peer methods on the simulation data sets

Based on our knowledge about simulated datasets, we apply specific considerations for each analytical method in order to set optimal parameters for each. In this way, we aim to assess the methodological limit of each method, rather than suboptimal performance due to inadequate parameter-setting. We expect that the performance of the peer methods on simulation data is an overestimate of their performance on real experimental data, because here we take advantage of the ground-truth knowledge, which is not available for experimental astrocyte data.

Event detection using peer methods:

AQuA and CaSCaDe report detected events, while other methods report detected ROIs. For a consistent comparison, we detect events from those methods that use ROIs. Once ROIs are detected, we calculate the average dF/F curve for each ROI, as follows: The curve is temporally smoothed with a time-window of 20. The minimum value in the smoothed curve is considered baseline. Assume the minimum value occurs at time t_base. The baseline is then subtracted to obtain the dF curve. The noise standard deviation σ is estimated using 40 frames around t_base. We then obtain a z-score curve as dF/σ. A large z-score indicates an event; we use a z-score threshold of z₀. The value z₀ is set according to ground-truth knowledge, so that the smallest-size event in the simulation data is detected by this threshold. Denote x₀ and s₀ the peak intensity and the size for the smallest event in the ground truth. We also denote the ground truth noise level as σ₀. Then, the threshold is calculated as,

$$z_0=\text{min}(\frac{0.9x_0\sqrt{s_0}}{{\sigma }_0},10).$$

We clip the score to 10 to avoid setting large values for high SNR. For CaSCaDe, we supply this value as the peak intensity threshold parameter.

Using the z-score curves and threshold, we detect events from ROIs for CaImAn, Suite2P, and GECI-quant. For each z-score curve, we find all frames with values >z₀. Each frame is a seed for an event. Assume the z-score for that frame is z₁ and we search before and after that frame. If the intensity of the frame is ≥ 0.2z₁, the frame is associated with the event. If we meet frames with intensities <0.2z₁, we stop searching that direction. Once finished, we obtain all frames associated with the event. We continue with another seed frame to find another event. Note that if a frame is considered part of an event, we do not consider it as a seed for another event, even if it is >z₀. The spatial footprint is fixed for all frames in an event, based on the ROI detected. Combining spatial footprint and frames, we obtain events for each ROI and identify all voxels belonging to an event.

Parameter setting for AQuA:

The parameters of AQuA are based on the ex-vivo-GCaMP-cyto preset with the following modifications: For different noise levels, we apply different smoothness levels. The smoothing is performed only spatially and values are empirically chosen. The smoothness parameter is the standard deviation of the Gaussian smoothing kernel used.

SNR (dB)	0	2.5	5	7.5	10	15	20
Smoothness	1	0.9	0.8	0.7	0.6	0.5	0.1

We do not simulate motion of the field-of-view, so we do not discard any boundary pixels, and we set regMaskGap = 0. We do not simulate Poisson Gaussian noise; we use additional Gaussian noise only, so PG = 0. Event sizes in the simulation are >200 pixels, so we set the minimum event size to be a value much smaller: minSize = 16. An event may not have more than one peak, so we set cOver = 0. We do not simulate temporally adjacent events, so we set thrTWScl = 4. We do not use proofreading, so we choose a more stringent z-score of events: zThr = 5.

Specific considerations for CaSCaDe:

We use the following parameters for CaSCaDe: According to the duration and temporal distances of the simulated events, we can safely set peak distance p.min_peak_dist_ed = 3 and minimum peak length p.min_peak_length = 2. We set the spatial smoothing filter size in the 3D smoothing function (bpass3d_v1) according to the size of the event, so we set p.hb equal to 2x median of the radius of the spatial footprint of all events. We use this setting because the default settings could not detect larger events on the simulation data sets. For temporal smoothing, we set p.zhb=21. We do not need to correct background, so we set p.int_correct= 0. The minimum peak intensity is p.peak_int_ed = z0, as discussed above. Minimum event intensity is p.min_int_ed = min(2, p.peak_int_ed *0.2). We modified the low-frequency part of the watershed segmentation step to allow larger events to be detected, by changing the function bpassW inside the function domain_segment. We replaced the noise estimator in CaSCaDe (function estibkg) with the more robust one used by AQuA.

CaSCaDe uses a supervised approach to classify detected events. Instead of manually labeling a large number of events and training many SVM models, we directly use ground truth to perform training. For example, for each event detected by CaSCaDe, we check the ground-truth data to test whether it is (part of) a true event. If so, it is retained; otherwise, it is discarded.

Specific considerations for GECI-quant:

GECI-quant requires user input at each step. Here, we describe how to automate these steps by taking advantage of ground-truth information. This allows us to test many conditions and repeat many times.

First, we do not add background signals to the synthetic data, so background subtraction is ignored. The domain- and the soma-detection steps require manual thresholding. We estimate the best threshold using the ground-truth data for each simulation. To do so, we scan 255 thresholds and use the one that leads to the best correlation between binarized data and ground truth. We next cleaned the binarized signals with sizes <4 pixels. The data here is also smoothed as it is in GECI-quant (3×3 spatial averaging). Events with spatial footprints < 1,000 pixels are treated as domains and others are treated as somas. The soma segmentation step also uses a threshold. We first process the data as in GECI-quant: for every three frames, a standard-deviation map is calculated so that each voxel in ground-truth data is associated with a standard deviation value. The average of all standard deviations from the ground-truth data is used as the threshold.

We next made the entire analysis pipeline automatic. Fiji is called from the command line in each step and parameters are passed as well. The final ROIs from Fiji are brought back into MATLAB. ROIs are > 15 pixels in area. All other parameters are unchanged, including those for the particle detector. Note that this modification cannot be used as an automated version of GECI-quant for real applications since it relies on ground-truth information.

Specific considerations for CaImAn:

We experimented with different parameters for CaImAn and found the following set of parameters performed best on simulation data. As event size can be large, we enlarge the patch size, so patch_size = [128,128] and overlap = [32,32]. Components to be found is set to K = 50. The standard deviation of the Gaussian kernel (half size of a neuron) is enlarged to tau = 16. Maximum size is 5,000 and the minimum size is 25. Decay time is 0.5. Other parameters are based on default settings. No spatial or temporal down-sampling is used. Adjusting these parameters dis not impact results on our simulated data. We used the 5/5/2018 version downloaded from https://github.com/flatironinstitute/CaImAn-MATLAB.

Specific consideration for Suite2P:

The most critical parameter for Suite2P is neuron size. We set db.diameter equal to the minimum between 50 and the median of the radius of the spatial footprint of all events. Setting the diameter too large leads to an out-of-memory issue. We bypass the registration step. We used the 6/4/18 version downloaded from https://github.com/cortex-lab/Suite2P.

Performance evaluation on the simulated data

To evaluate the accuracy of detected events, we quantify the intersection over the union (IoU). We consider all event voxels, not only pixels as in ROI-based methods. For each detected event i, we find all the ground-truth events that have common voxels with event i. For each such ground-truth event, e.g., event j, we calculate an IoU score (also known as Jaccard index) between this pair of events as the following,

$$Io{U}_{i,j}=\frac{\text{Number}\left(\text{Voxels in event }i\cap \text{Voxels in event }j\right)}{\text{Number}\left(\text{Voxels in event }i\cup \text{Voxels in event }j\right)}.$$

When a detected event can be perfectly matched with a ground-truth event, its IoU score is 1. A score of 0 indicates this pair of events has nothing in common. For each detected event i, we find the maximum IoU score among all pairs between this event and a ground-truth event. We denote this maximum score as IoU_i. Similarly, we can compute a score IoU_j for the ground truth event j. The final IoU score is obtained by averaging over all events, including detected and ground-truth events. Supposing we have I detected events and J ground truth events, where I and J are not necessarily equal, we compute the final score as the following,

$$IoU=\frac{{\sum }_{i=1}^{I}Io{U}_i+{\sum }_{j=1}^{J}Io{U}_j}{I+J}.$$

Each simulation is repeated 10 times. The mean and 95% confidence interval (CI) of IoU score is calculated and plotted. The CI is calculated as [μ_sim – 2σ_sim, μ_sim + 2σ_sim], where μ_sim is the estimated mean and σ_sim is the estimated standard deviation (σ_sim) based on 10 repetitive runs.

Open-source software for analyzing and visualizing dynamic fluorescent signals in astrocytes

Applying software engineering principles, we developed an open-source toolbox for astrocyte fluorescent imaging data with detailed user guidelines. The software not only implements the AQuA algorithm for detecting events, but also provides an integrated environment for users to see the results, interact with the analysis, and combine other types of data such as cell/region masks and landmarks. There are two versions of the software with the same functionality, based on MATLAB or Fiji. The software is freely available at https://github.com/yu-lab-vt/aqua where detailed documents and example applications can be found. A list of extracted features is shown in Supp. Table 5. Highlights of the software follow.

First, the software implements AQuA and provides several options to export the event-detection results, including TIFF files with color-coded events, event features in Excel, and MATLAB or Java data structures to be used by other programs. Second, the software can display analysis results by adding color to the raw video, where color encodes the value of a user-defined extracted feature such as propagation speed. Users can specify which feature to be displayed, either an existing feature in AQuA or a user-designed feature based on features provided by AQuA. We provide several pre-defined colormaps, but allow users to manually define colormaps as well. AQuA also provides a side-by-side view, to simultaneously display two features or a raw video plus one feature. Third, the software provides a convenient way to interactively view detected events and their associated features. By clicking on an event, the dF/F curve for the event is shown in a separate panel below the video, and the time-frames during which the event occurs are highlighted in red. The values of several other features for that event are also shown in another panel. The software allows multiple events to be selected simultaneously, so that their curves and features can be plotted together and compared. Fourth, the software provides both automatic and manual ways to proofread the results. For automatic proofreading, events are filtered by setting desired ranges for features-of-interest. Alternatively, users can choose the ‘delete/restore’ button and manually click an event to remove it. Fifth, the software provides flexible ways to incorporate cell morphology or landmark information. Users can manually supply cell morphology or regional information such as the cell boundary, which can assign events to individual cells. Users can also provide landmark information such as the location of a pipette for pharmacological application. Users can also load cell, region, or landmark information from other data sources, such as another fluorescence channel that captures cell morphology. The software can extract landmark-related features for each event, including the direction of propagation relative to a landmark.

Statistics

The confidence intervals in Fig. 2 and Supp. Fig. 6 (confidence level, 95%) were estimated as 2 times of the standard deviation based on 10 independent simulations. The confidence intervals in Supp. Fig. 12 were based on 5 independent simulations. For imaging experiments, the following statistical tests were employed, as appropriate, and as indicated: one- and two-tailed t-test, Wilcoxon rank sum, chi-square test, k-means clustering, and the Freedman-Diaonis’s rule. No statistical methods were used to predetermine sample sizes but our sample sizes are similar to those reported in previous publications^4–6,8, and statistical significance was calculated using post hoc tests. Data distribution was assumed to be normal but this was not formally tested. In terms of randomization, samples were allocated into experimental groups by cell-type expression of each individual fluorescent sensor, and ex vivo or in vivo methodology. Within each group, imaging datasets were collected at similar ages. Both male and female were used and randomly selected. Data collection and analysis were not performed blind to the conditions of the experiments. For GluSnFR studies, blinding was not possible, because cell-type expression is evident from the images themselves. Likewise, for GABASnFR and GRAB-NE experiments, blinding was not possible because we injected a single virus and bath applied only the relevant neurotransmitter. For GCaMP imaging studies, blinding was not relevant because all data within each dataset were grouped and analyzed together. No animals or data points were excluded from the analyses.

Reporting Summary

Further information on experimental design is available in the Life Sciences Reporting Summary linked to this article.

Code availability

The code has been released under GNU General Public License v3.0 and is available at https://github.com/yu-lab-vt/AQuA.

Data Availability Statement

The data that support the findings of this study are available from the corresponding authors upon request.